 Open Access
Open Access
ARTICLE
Pressure Impulse during Explosive Boiling on the Surface of a High Temperature Melt in Water—Discussion of the Calculation Model
1 Heat Transfer in Power Plants Laboratory, Joint Institute for High Temperatures, Moscow, 125412, Russia
2 Department of Engineering Thermophysics, National Research University “Moscow Power Engineering Institute”, Moscow, 111250, Russia
* Corresponding Author: Stepan Yudin. Email:
(This article belongs to the Special Issue: Heat and Mass Transfer in Energy Equipment)
Frontiers in Heat and Mass Transfer 2024, 22(6), 1805-1821. https://doi.org/10.32604/fhmt.2024.056787
Received 30 July 2024; Accepted 15 October 2024; Issue published 19 December 2024
Abstract
This study explores the mechanism behind the generation of pressure pulses on the outer surface of a molten metal droplet when immersed in water. The absence of any external trigger is assumed, and the droplet is surrounded by a vapor layer with surface hydrodynamic waves at the vapor-liquid interface. The study examines the heating conditions of a cylindrical column of water used to model a volume of cold liquid interacting with a hot metal surface, which explosively boils upon direct contact. Within the framework of classical homogeneous nucleation theory, the relationship between pressure pulse magnitude and rise time and the size of the contact area and surface temperature of the droplet is established. A criterion for determining the magnitude of the pressure pulse is derived, showing that significant pressure pulses occur within a narrow range of values for this criterion. Experimental investigations have been conducted to measure the key parameters—such as the duration and area of contact and pressure amplitude buildup—when room-temperature water comes into contact with a hot steel surface. The experimental results are compared with the theoretical predictions. Incorporating Skripov’s theory of explosive boiling into the model helps explain the relationship between the pressure pulse and contact area, only when the droplet surface temperature is near or exceeds the temperature of the maximum possible water superheating.Keywords
Nomenclature
| C | Speed of sound |
| Cp | Heat capacity at constant pressure |
| D | Diameter of contact spot |
| L | Heat of vaporization |
| P | Pressure |
| R | The radius of vapor bubble |
| Rg | Gas constant |
| T | Temperature |
| T* | Temperature in the liquid at the time of boiling |
| Ts | Temperature of saturation |
| ∆T | Depth of entry into the metastable region |
| a | Thermal diffusivity |
| h | Height of a cylindrical volume of liquid |
| k | Thermal conductivity |
| q | Heat flux density |
| r | Radial distance in a cylindrical coordinate system |
| t | Time |
| t” | The boiling time of the entire liquid |
| z | Axial coordinate in a cylindrical coordinate system |
| Greek Symbols | |
| Overheated vapor thermal diffusivity as a function of temperature | |
| Time from the beginning of the contact | |
| Density | |
| υ | Specific volume |
| The number of ready-made centers per unit volume | |
| Subscripts and Superscripts | |
| 0 | Cooling water |
| m | Melted liquid droplet |
| gr | Contact area |
| l | Direction from water side |
| υ | Direction from vapor side |
| n | Normal direction to the surface |
| s | Spherical coordinate system |
| ′ | Water |
| Vapor | |
| cent | Center of hemispherical steel heated body |
| surf | Surface of hemispherical steel heated body |
| bubble | Bubble |
| max | Maximum value |
| means | Measured value |
| del | Delay |
| cont | Contact |
| interphase | Interphase |
The relevance of the study of the emergence and development of a pressure pulse on the high-temperature surface of a molten metal drop immersed in water (without an external trigger) is related to the problem of the occurrence of a vapor explosion in emergencies in various industries, including nuclear power and metallurgy. A detailed description of this problem, applied mainly to the safety issues of nuclear power plants, can be found in early review papers [1–3]. Modern information on this problem is presented in reviews [4–6]. The results of studies of steam explosions, as applied to metallurgy, are described in [7]. A review of works on the study of heat transfer peculiarities at steam explosions is presented in [8].
In the literature, there is a large amount of experimental data on the interaction of a drop of molten metal with a cooling liquid—usually water at room temperature. In experiments, mainly liquid tin drops falling into the sea [9] or ordinary [10–14] water as well as materials based on lead [13] and bismuth [15–17] have been used. Droplets made of copper [18,19] and iron melts [7,20] have been used to model processes at high temperatures. A comparative analysis of the fragmentation process of iron and corium droplets carried out taking into account heat transfer by radiation, is presented in [21].
In addition to nuclear power and metallurgy, steam explosions have been observed in the paper industry, as well as in the production and transportation of liquefied natural gas [22]. The results of a series of studies on modeling steam explosions in manufacturing paper are presented in [23–26]. In these experiments, performed with drops of table salt falling into the water, it is confirmed that spontaneous steam explosions can be initiated by the accidental crushing of a single drop. A distinctive feature of steam explosions in the interaction of liquefied natural gases with water is the absence (due to the low cryogenic temperatures of the coolant) of the influence of thermal radiation on the process of their occurrence. Possible vapor explosions in devices using liquid sodium as a coolant, such as fast reactors, are discussed in [27].
In most of the experiments performed, in addition to visual observations, temperature characteristics of the process and pressure pulses were measured. In some experiments [14,28,29], along with conventional video cameras, cameras operating in the range of X-rays were used, which made it possible to significantly improve image analysis by separating vapor from metal fragments. More than a dozen physical models devoted to droplet fragmentation can be found in the literature. Among them, one can single out the models based on: the penetration of coolant jets into the volume of the droplet [30], and its destruction due to both internal boiling (cavitation) [31] and thermomechanical stresses during abrupt cooling [32]. The above models describe the initial stage of the fragmentation process with different approximations and are mainly descriptive (and to some extent contradictory) in nature.
Droplets of melted material being immersed in water are surrounded by a vapor film, the boundary of which oscillates with great or small amplitude. Then, if there is a trigger (for example an external pressure impulse), the vapor film surrounding the droplet is destabilized. Thus, the oscillations of the phase boundary may reach a large scale and liquid may approach or touch the heated droplet surface. So, the explosive boiling of the liquid fraction contacting with the metal surface becomes possible. It leads to pressure impulse generation, which causes the fragmentation of the droplet. In addition, an initial pressure impulse generates an acoustic wave in the liquid and the melted droplet. This wave may affect the vapor films around neighboring particles of melted material. It may intensify the process of steam explosion. A detailed description of this behavior of the steam layer, as well as its explosive destruction, is described in [33].
The vapor film oscillations (without external trigger) may appear as a result of a hydrodynamic effect if the droplets are passed over by the liquid flow (instabilities of Kelvin-Helmholtz), or as a result of thermal processes that take place at the liquid-vapor phase boundary (in this case there is a wider circle of phenomena than Rayleigh-Taylor instability).
The object of this work is an investigation of the pressure impulse generation value, the conditions of its generation and the duration of explosive water boiling at the high temperature melted droplet surface (according to [34]). We think that, under some circumstances, this pressure impulse may be the trigger of steam explosion and may cause droplet fine fragmentation.
When water contacts the melted droplet surface due to surrounding vapor film destabilization (the simplest model of the phenomenon is shown in Fig. 1), the pressure impulse may appear. It is connected with explosive boiling, and a rapid decrease in volume density is considered. The formed vapor bubble (expanding at the speed of sound) in some cases does not compensate for the increasing pressure.
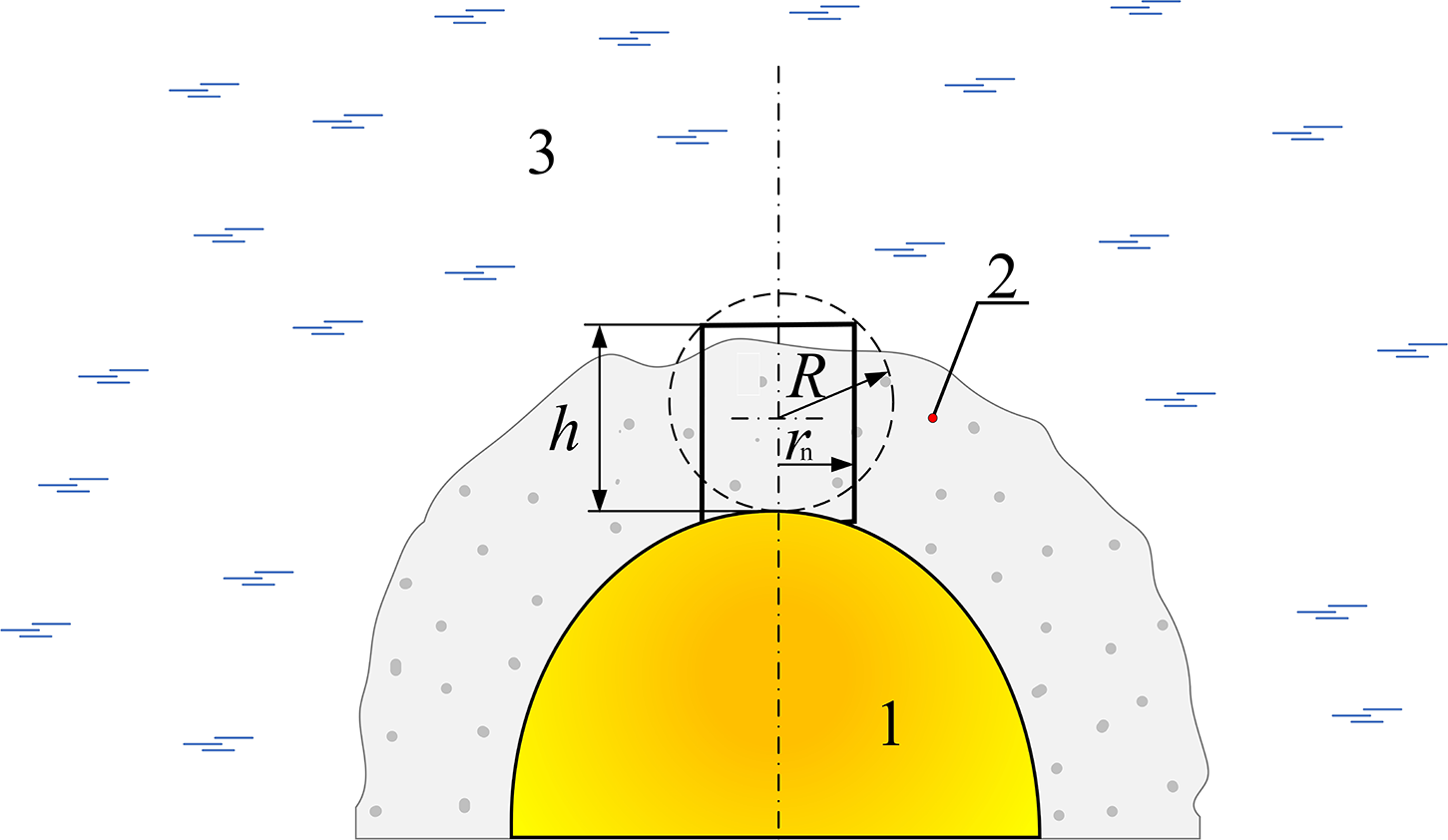
Figure 1: Simplified scheme of water explosive boiling after vapor film continuity breakdown; 1—melted droplet, 2—vapor film, 3—cooling water
There is now a fairly large number of experimental studies of the effects of the vapor film surrounding a drop of heated metal when it enters a coolant. These experimental data, and several qualitative considerations by various authors, show that many mechanisms lead to the effect of the vapor film on the deformation (fracture) of the liquid metal droplet when it interacts with the surrounding liquid.
In the first part of this paper, an attempt is made to evaluate the effect of the vapor film during the transition of a liquid to a metastable state within the framework of the well-known V.P. Skripov model [34].
2.1 The Peculiarities of Heat Transfer Regime
Instabilities of vapor film surrounding the droplet, which may lead to direct contact between water and the hot surface of molten metal (as mentioned above), are described in works [8,35].
Consider heating a water cylinder and its contact with a hot droplet surface. The cylinder models the water volume (which has, in general, a more complicated form). Several mechanisms produce explosive boiling. One of them is related to pressure entry into the metastable zone, which is known to lead to boiling. A necessary condition for explosive boiling, according to [34], is a sufficiently deep entry into the metastable zone, since:
where L, T*, Ts and
It was noted in [34] that the liquid can be superheated even in the presence of artificial centers if heating occurs quickly enough. Moreover, it is necessary to provide such a heating rate, which noticeably exceeds the heat consumption for evaporation on active centers. The analytical solution for two semi-infinite bodies was used to estimate the heating rate of the cylinder and to determine the temperature at the phase boundary. It was also used to determine the boundary condition on the lower surface of the cylinder, the temperature of which is assumed not to exceed the temperature of the limiting overheating of the coolant, as well as to verify the numerical solution for the case of zero heat flow on the side surface of the cylinder. The solution to this problem for the initial temperature distribution independent of the coordinate is found by [36]:
The heat flux on the droplet surface is:
Conjugating by heat flux, temperature in the contact zone is:
where
Figs. 2 and 3 (which illustrates calculations by Eqs. (3)–(5)) show heat flux density variation at the phase boundary and time dependency of temperature in the water cylinder at the z–coordinate 3 μm from the surface. The heat flux decreases several times (Fig. 2) during 1 ms (due to low water thermal conductivity) while the temperature of the metal surface and contact zone change slightly. However, the water cylinder becomes superheated for approximately 200 K at the mentioned coordinate.
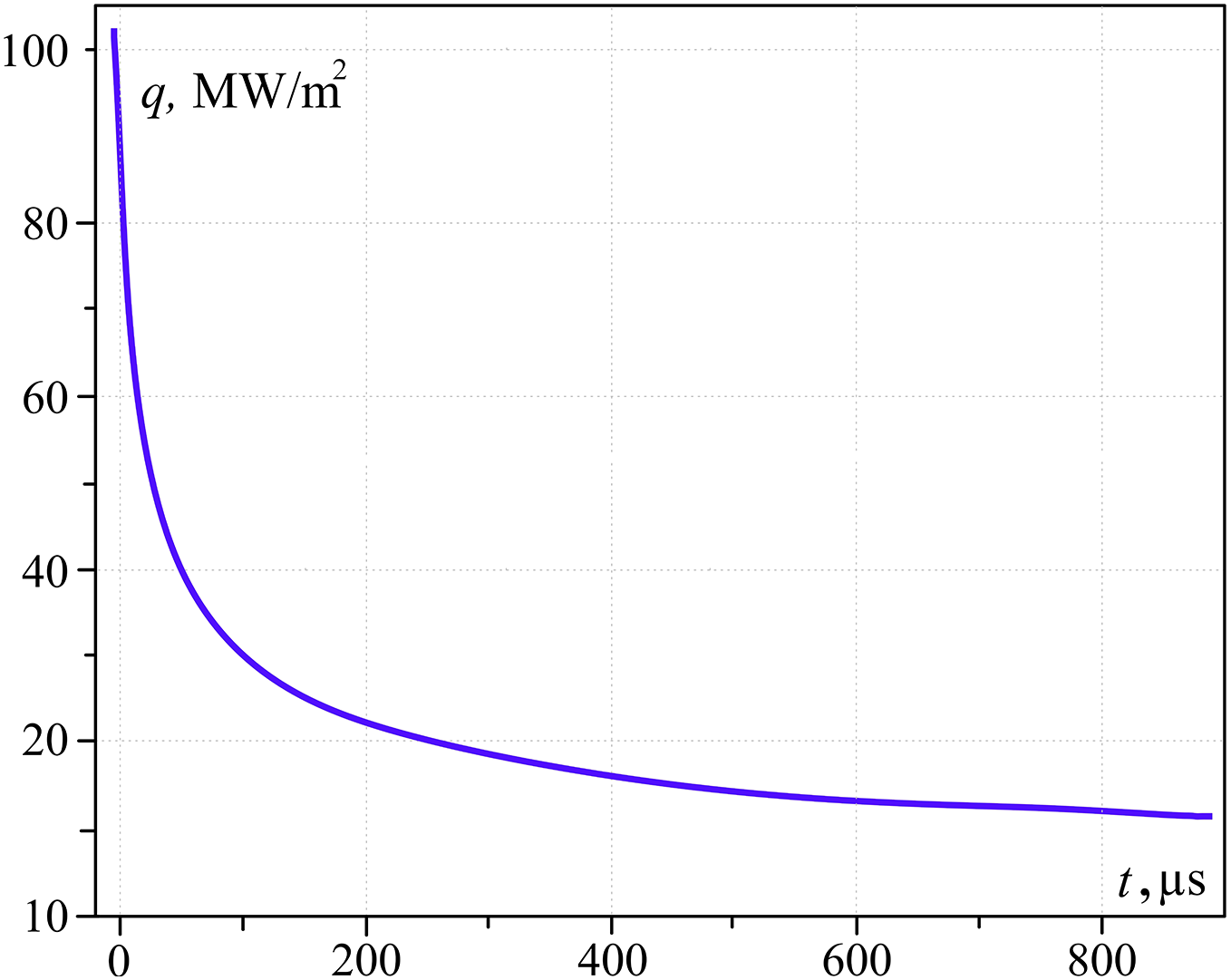
Figure 2: Heat flux dependence on time in contact zone (z = 3 μm; Tgr = 584 K)
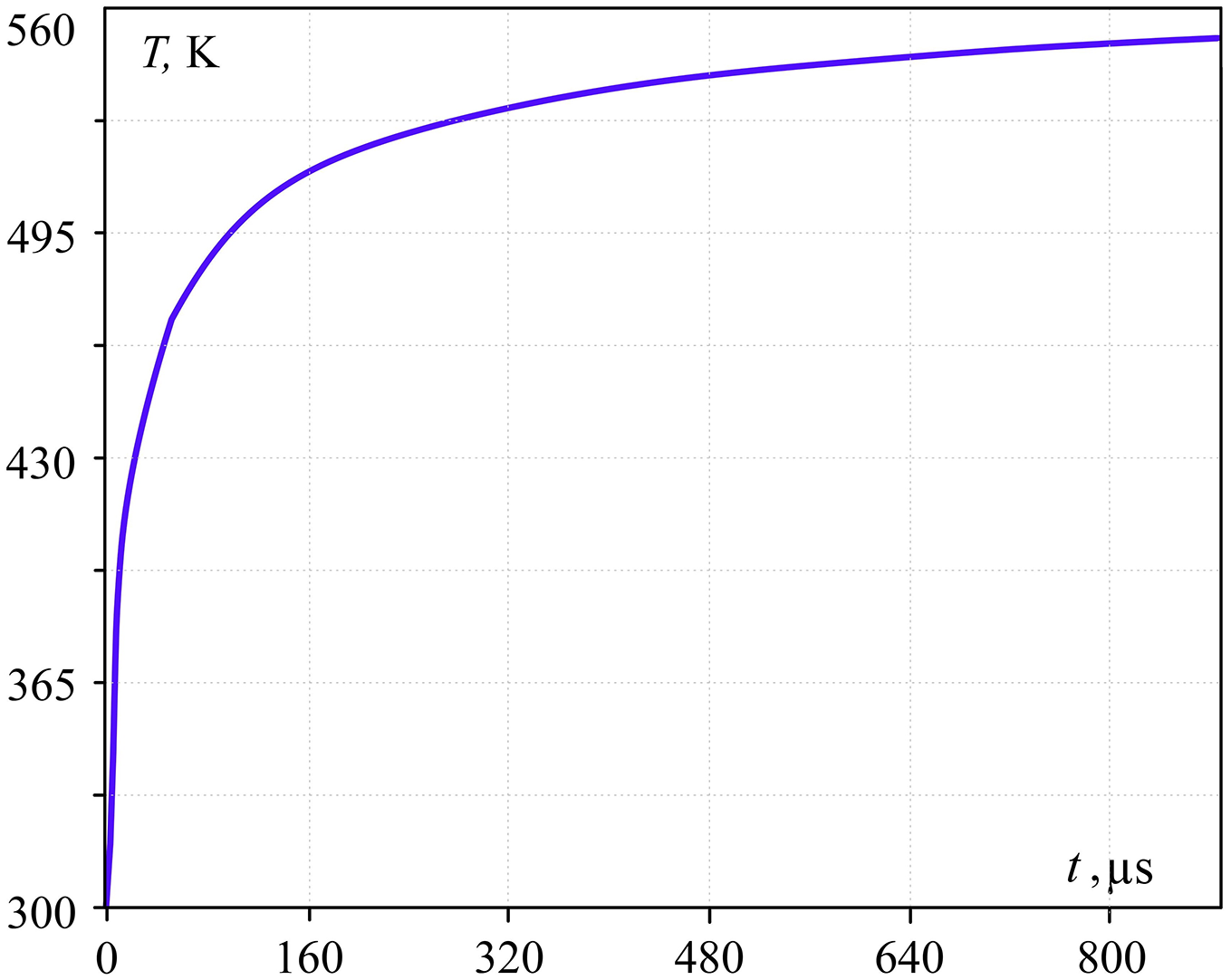
Figure 3: Droplet surface temperature dependence of time (z = 3 μm; Tgr = 584 K)
For a more exact definition of the temperature distribution of a water cylinder in contact with a droplet surface, the heat conduction equation was solved in cylindrical coordinates:
with the following boundary conditions:
where z, r, h, rn, T0, av, ql and qv are the coordinate normal to the droplet surface (z = 0 in the point of inter-phase contact), coordinate along the radius of cylinder (r = 0 at the symmetry axis), height of the cylinder, which is approximately equal to the vapor film thickness, cylinder radius, cooling water temperature, thermal diffusivity (here we considered as constant), heat flux densities at the lateral cylinder surface in liquid and vapor correspondingly.
To determine the boundary conditions on the side surface of the cylinder, the temperature distribution in the vapor film was found. The problem was solved in a one-dimensional approximation in polar coordinates taking into account the temperature variability of superheated vapor properties:
where rs, av (T), T are the distance from droplet center, overheated vapor thermal diffusivity as a function of temperature, temperature as a function of rs in the vapor film.
For numerical calculation, the appropriate explicit schemes of second order for cylinder and polar coordinates were used [37].
Hereinafter, we determine the experimental heating period between the water contact with the droplet surface and the start of explosive boiling, which is measured by the fall of electrical resistance between the droplet and liquid. Correspondingly, the height of the water cylinder in a metastable state is determined, and the overheating satisfies the explosive regime conditions [34].
It is possible to calculate the radius of the sphere (R), the volume of which is equal to the volume of the water cylinder part in which explosive boiling is realized.
The parameter R is used in subsequent dimensionless analysis.
For example, for the following calculation, the temperature of the tin droplet was chosen so that the temperature of the interphase surface corresponds to the ultimate overheating water temperature 311K. Experimental waiting time is assumed to be 1 ms.
The results of calculations for the above example are represented in Fig. 4. The line (2) in Fig. 4 cuts part of the water cylinder heated to the metastable condition that satisfies the condition of explosive boiling [34].
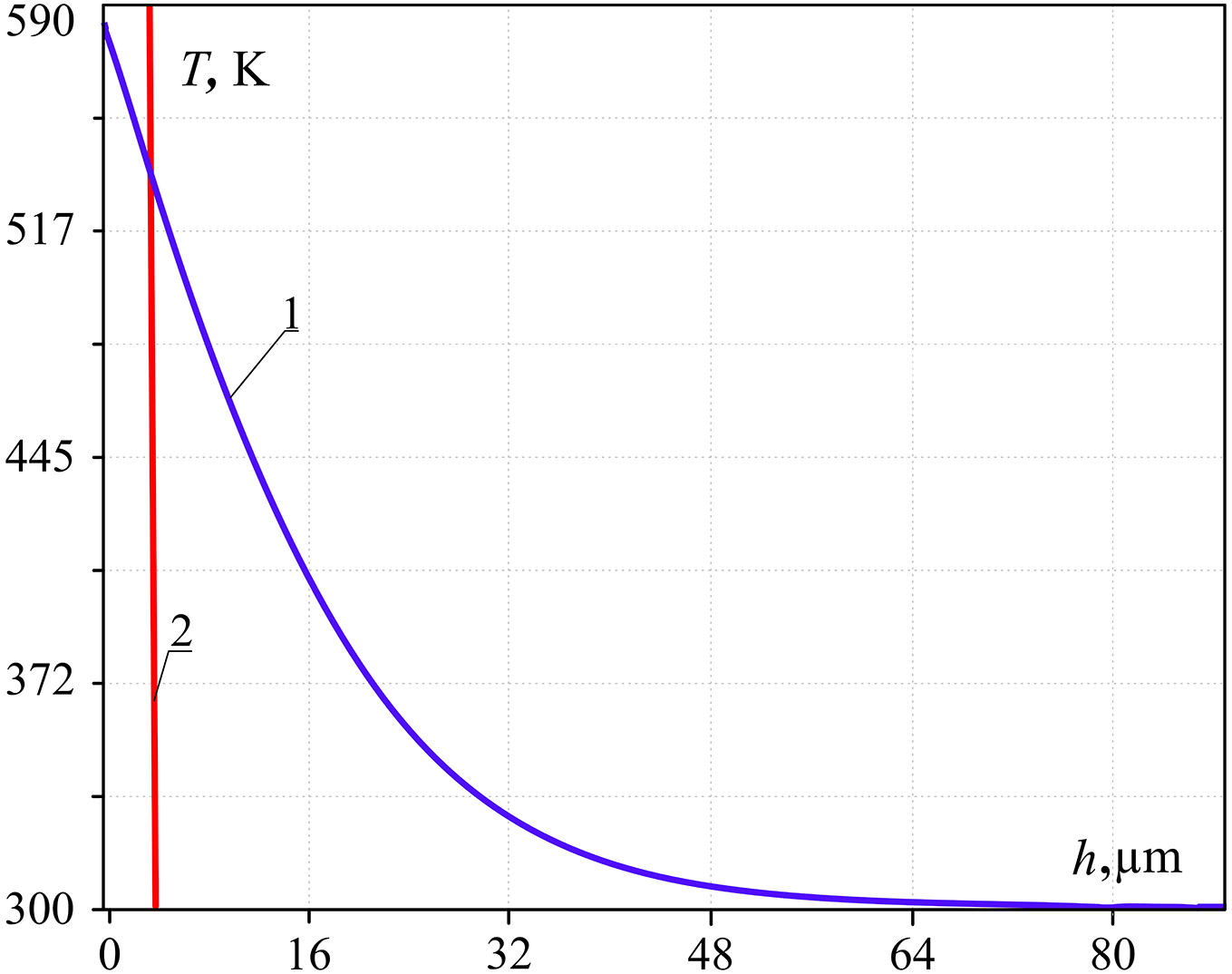
Figure 4: Temperature distribution (1) along the height of the water cylinder (h) at symmetry axis after 1 ms from water droplet surface contact; to the left of (2)—the zone of explosive boiling; (Tgr = 584 K, t = 1 ms)
The time of superheated liquid explosive boiling out at the active centers, according to [30], is:
where
The number of active centers to the moment of explosive boiling beginning is determined as an integral of nucleation speed according to classic theory of homogenous nucleation. Then (the Raleigh case): n = 1. In [30], the law of bubble growth is represented as: an asymptotical Raleigh law for bubble growth.
For a first estimation, φ may be determined from the following considerations [38]:
If we assume in the zone of heating
where L is the heat of vaporization.
The formed vapor spherical bubble expands at the speed of sound, so we’ll describe the growth of its radius R as:
here ∆R is the radius enlarging to the moment of the end of boiling or, putting new variables:
We have:
Defining K, as:
We have the following equation:
Since only positive x are of interest, it may be written:
Then:
or
where T, ∆T, L, C, Rg and K are the vapor temperature, the level of superheating, specific heat of vaporization, speed of sound, vapor gas constant and the dimensionless criterion K (9), which depends upon contact spot radius and droplet surface temperature.
Then the Eq. (10) is solved for x, and thus the vapor density is determined in the enlarged bubble to the end of boiling (ρ″) as a function of K. So, one can determine the pressure in the bubble (12), and it is the pressure impulse, which determines the following events:
The duration of the impulse (the duration of pressure growth inside the bubble until it reaches maximum value) is:
Bellow the dependence of pressure impulse (Fig. 5) and duration of pressure growth in the bubble (time of boiling out) (Fig. 6) are given as a function of sphere radius (R), the volume of which equals the initial volume of the explosive boiling liquid. This dependence refers to the temperature of the contact zone to be the maximum water overheating level at atmospheric pressure and experimental time of water cylinder heating.
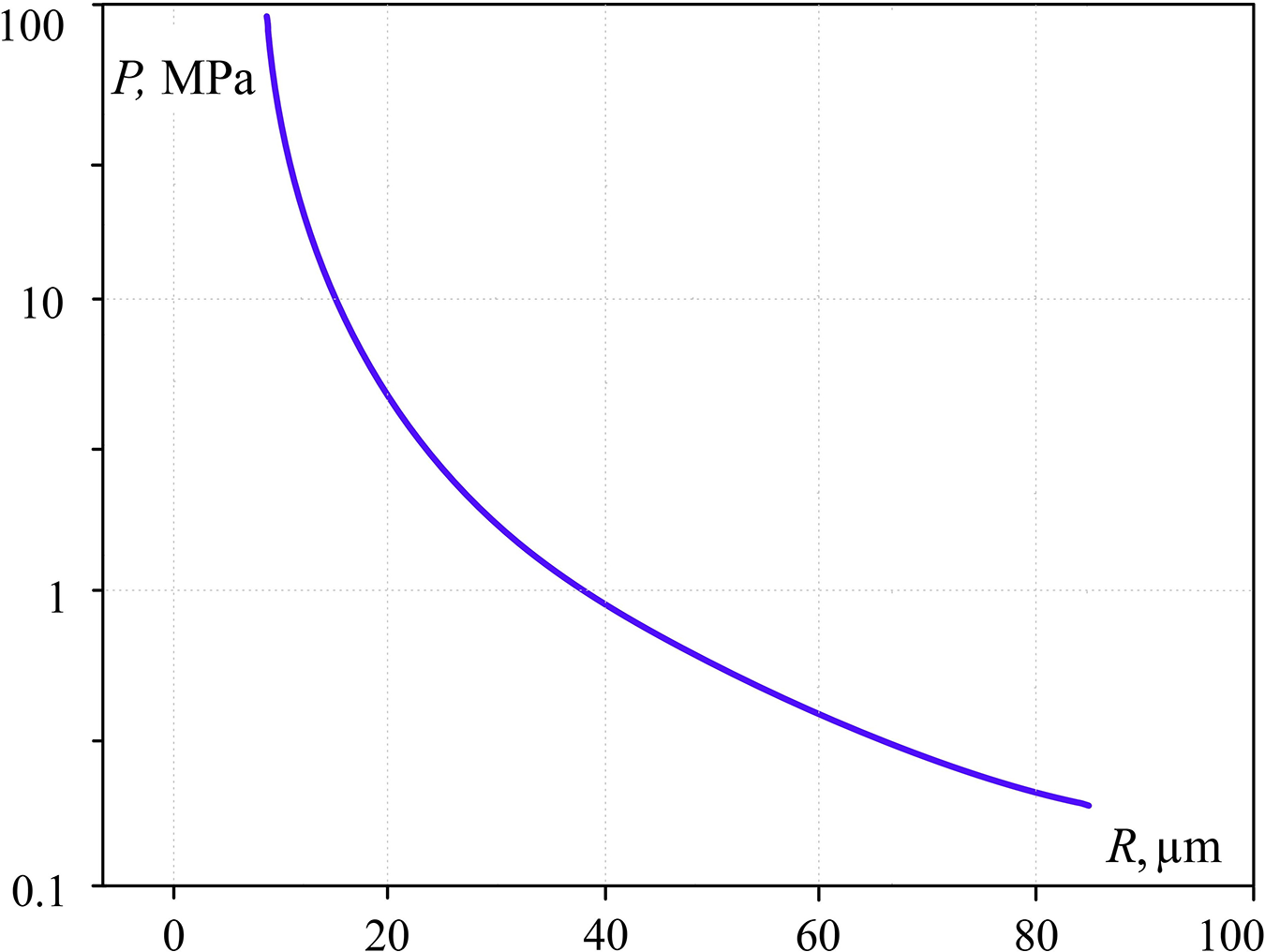
Figure 5: Pressure impulse dependency upon R
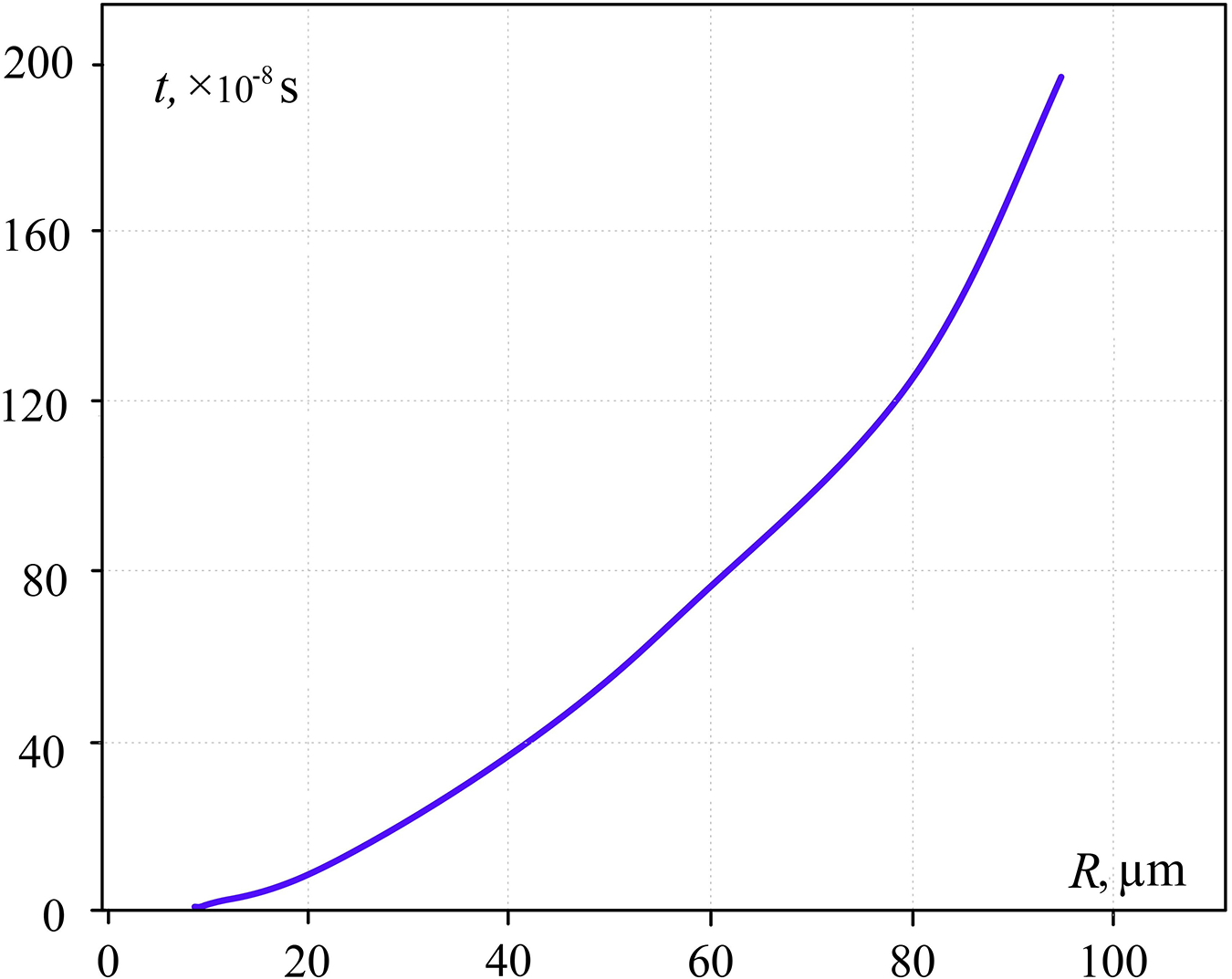
Figure 6: Time of pressure growth (the time of boiling out) in pressure impulse as a function of R
The dependence between vapor density and criterion K (Fig. 7) is physically restricted by the maximum possible vapor density at critical water temperature.
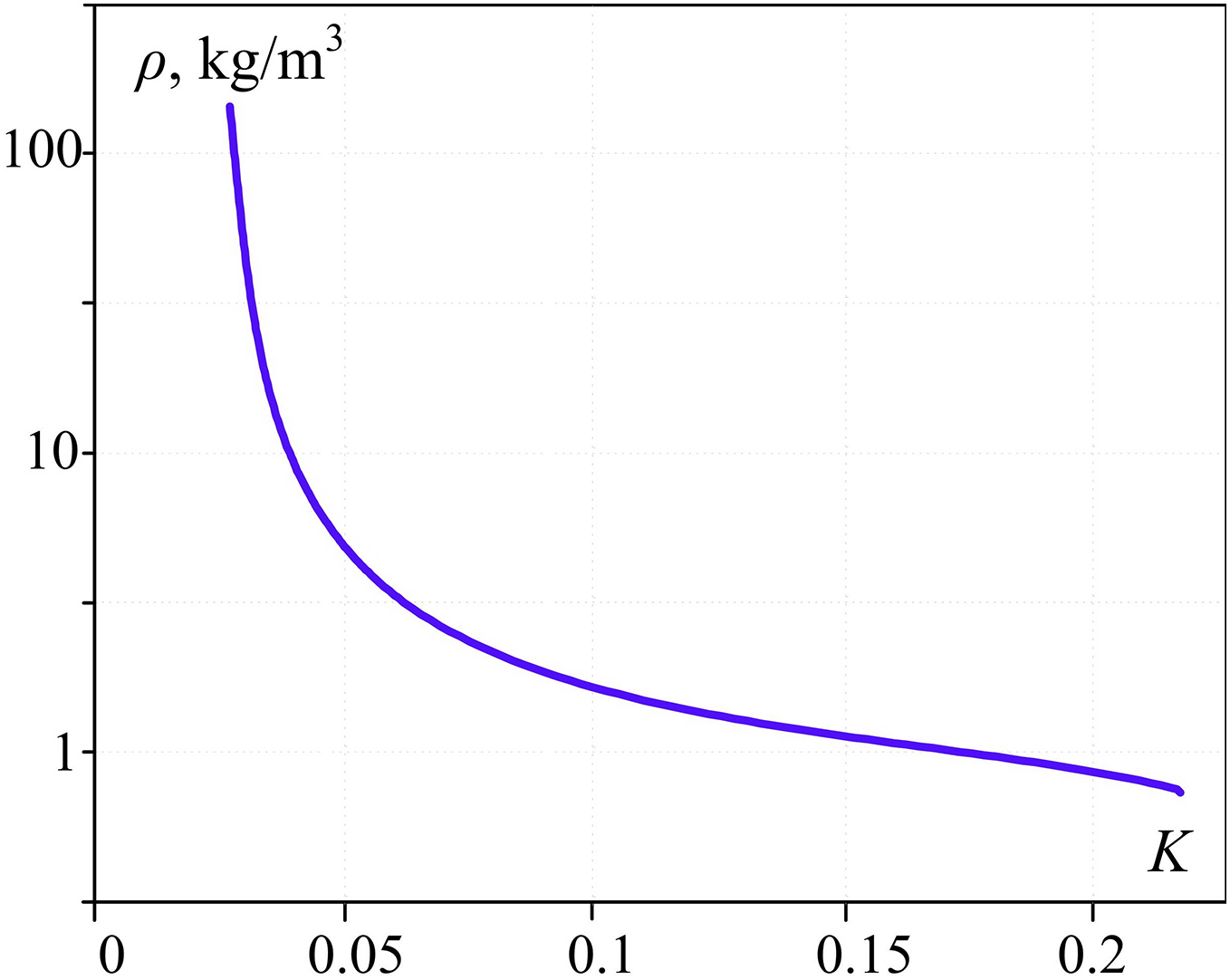
Figure 7: Vapor density (at the end of boiling) dependency upon dimensionless parameter K
It should be noted that there are some problems with the model based on the mechanism described in [34]. One of them is related to the need to know the number of nucleation centers, which for various experiments is known with insufficient accuracy. Another problem is the need for the liquid to enter the metastable zone. In addition, the Skripov model does not take into account the influence of vapor film oscillations (small and with finite amplitude) on the development of instabilities not related to the metastable state of the liquid. Thus, the results presented here demonstrate the main difficulties of the droplet fragmentation model based on shock boiling theory [34]. However, there are other models available. Most notably, in reality, each type of boiling nucleation is heterogeneous. Therefore, the model must include either a heterogeneous factor (the value of which is usually unknown in advance) or there must exist an alternative model of heterogeneous nucleation.
Estimated calculations within the framework of the simplest V.P. Skripov model show its limitations. The essence of its limitations is that it is based on homogeneous nucleation liquid; therefore, a more detailed analysis of other mechanisms is required, some of which have been partially discussed, some of which have not. The analysis of such mechanisms is the aim of further research.
Based on the results of experiments with metal balls [39–41], it can be assumed that the processes of destruction of vapor shells of the coolant near the superheated surfaces of solid and liquid metallic bodies develop similarly. Therefore, additional experiments modeling the initial stage of vapor film destruction on a hot liquid-metal drop and intended to verify the results of the above deductions were performed under conditions of explosive boiling of water on solid samples of hemispherical shape. Experiments using a similar measurement technique were performed earlier in [42].
The scheme of the experimental setup and the main measurements carried out on it are shown in Fig. 8. The working section was a cylindrical rod, the lower end part of which was made of stainless steel AISI 304. The end surface of the cylinder had the shape of a hemisphere with a diameter of 10 mm. The working section, thermally insulated over the entire surface, except for the hemispherical part, was heated by direct electric current, which was passed through an electrically insulated spiral wound on its surface.
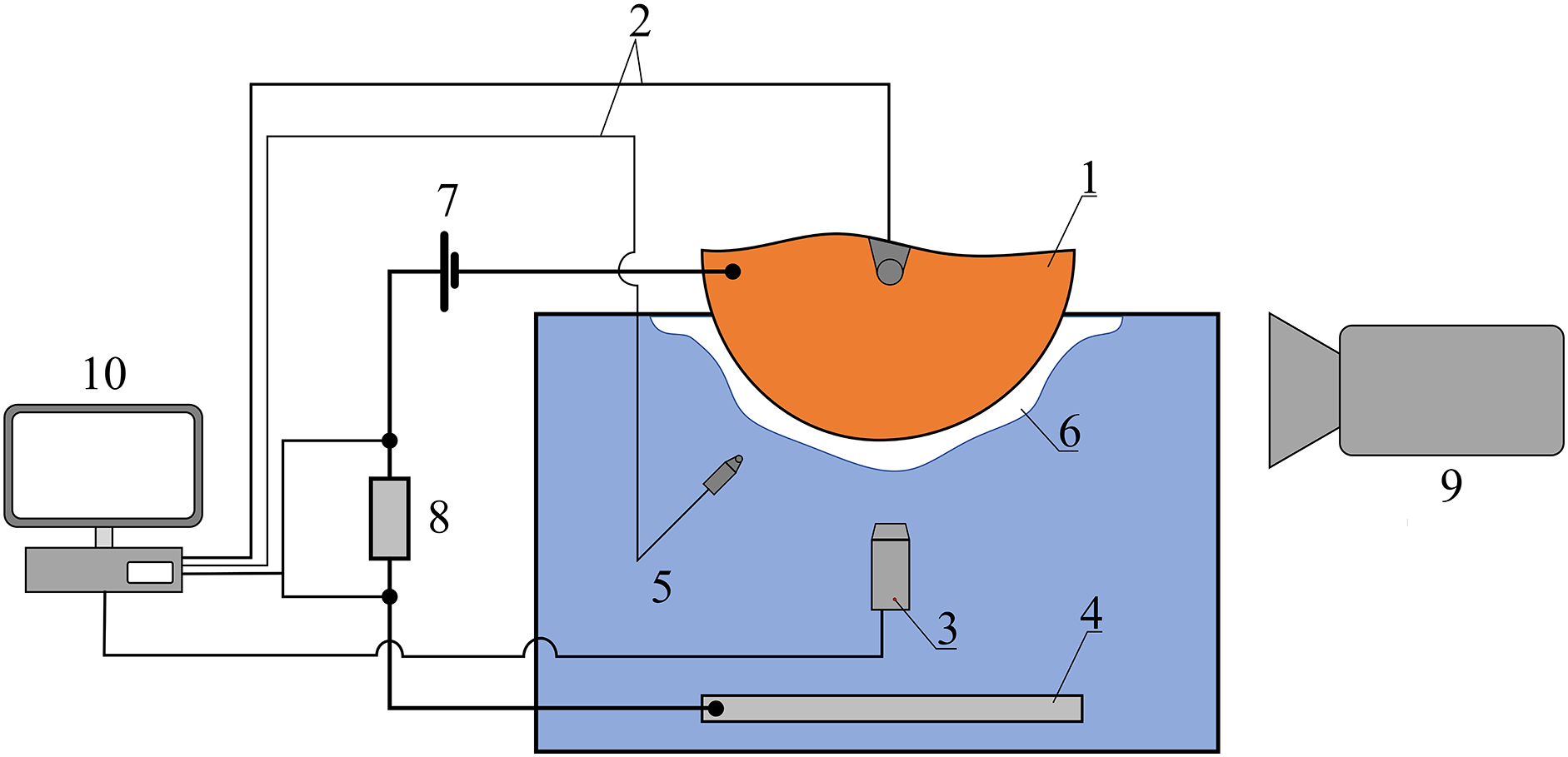
Figure 8: Scheme of the experimental setup and main measurements. 1—sample; 2—thermocouple (K-type); 3—pressure sensor; 4—electrode; 5—water; 6—steam shell; 7—battery: 8—reference resistor; 9—video camera; 10—computer
The experiments were performed in the following sequence. In the initial (raised) position, the working section was heated in air to a temperature of ~773K. After that, the electric heater was switched off, and the hot working section was immersed in the bath filled with distilled water to the depth of the hemisphere radius with the help of a special coordinate device at a speed of several millimeters per second. This method of heating was a simple way to affect the mode of stable film boiling near the hot hemisphere, and also to allow explosive escape of the vapor film from the heated surface of the working section during the cooling process. Distilled water at room temperature (291K) (degassed using two-hour boiling) was used in the experiments.
Temperature measurements were made with the help of chrome-alumni thermocouples, the junction of which were placed in water, in the center of the hemisphere, and different parts of the working area. This made it possible to control with sufficient accuracy the value of heat flux density on the hemispherical surface in the film boiling mode. The estimated value of the temperature of the hot surface of the sample was determined computationally by solving the unsteady heat conduction equation.
In the experiments, pressure pulses were investigated, which were generated at the collapse of the vapor cavity in the process of cooling the working section. High-frequency piezoelectric transducers from PCB PIEZOTRONICS Model: HS113A28, which were located at a distance of 6 mm from the lower end of the hemisphere, were used as pressure transducers.
In addition to pressure transducers, the conductometric technique of determining the parameters of water contact with the heated surface was used in the experiments. The characteristics of this process (area and duration of contact) were determined by the change in the value of the voltage drop on the “exemplary” resistance, which is part of a closed electrical circuit consisting of a direct current source, two electrodes (one of which is the working area and the other is a copper plate placed in water), connecting wires, volumes of water and water vapor. In the absence of water contact with the heater, the total resistance of the circuit, determined by the electrical resistance of the vapor layer, is as large as possible, and the current and voltage drop across the reference resistance are minimal.
At the moment of contact of the heater with water in the measuring circuit the electric current increases sharply, the value of which varies depending on the contact area. The calibration dependence of the voltage drop across the sample resistance on the equivalent diameter of the contact area (Fig. 9) was obtained in a specially designed experiment in which the contact spot was modeled by the area of the end surface of a copper wire insulated from the sides. One of the ends of a piece of wire, which diameter in the experiments varied from 30 µm to 15 mm, was fixed on the hemispherical surface of the working area, and the other was immersed a few millimeters into water.
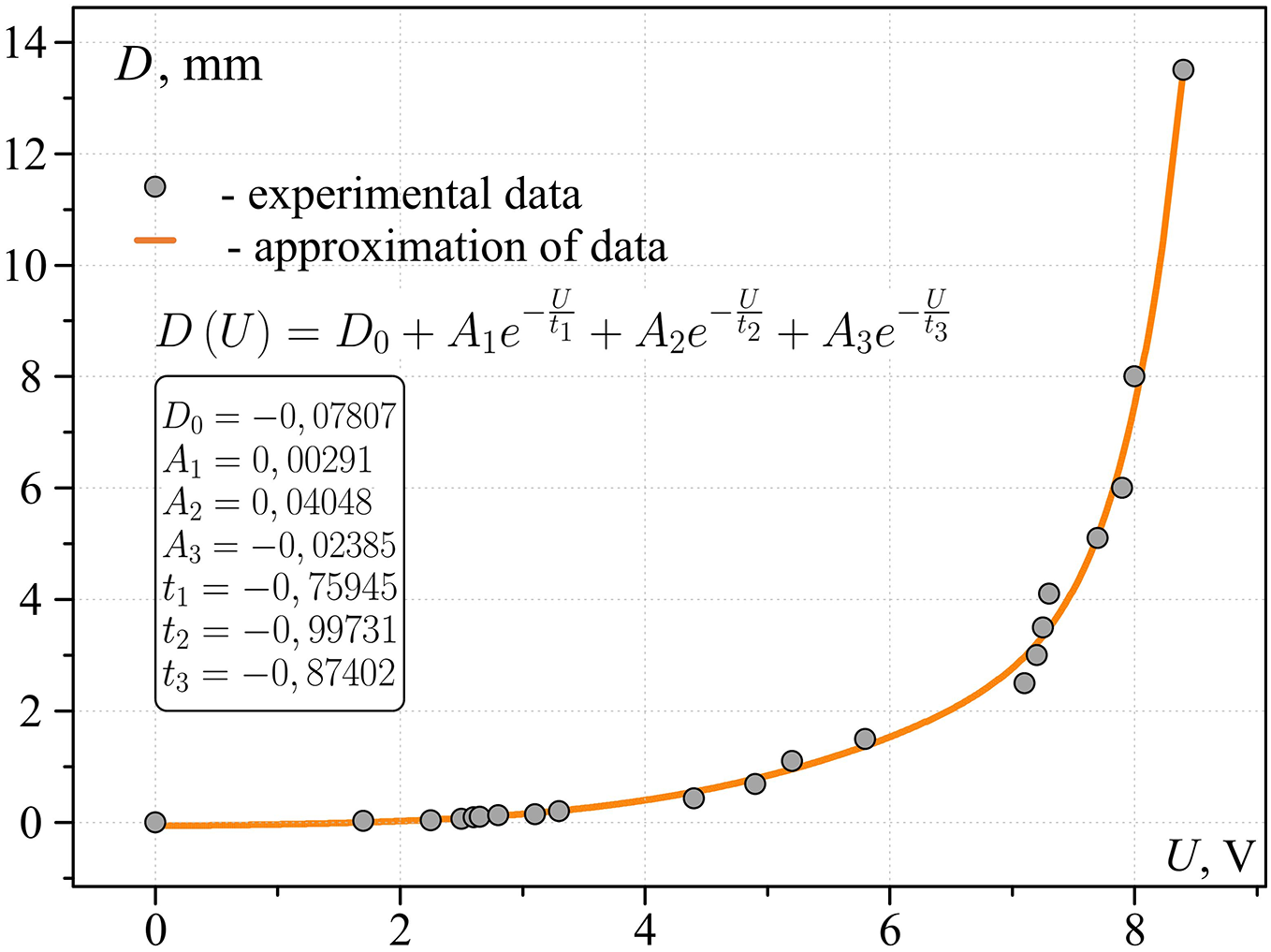
Figure 9: Calibration dependence of the contact diameter on the voltage drop across the reference resistor
Based on the results of video observations (video recording frequency 1000 fps), it was found that the contact of the cooler with the hot surface takes place in the lowermost part of the hemispherical sample, where the thickness of the vapor shell is minimal. The experiments used National Instruments equipment, and the measurements were performed using the Labview software environment. The frequency of digitization of signals from pressure and contact sensors was 5 × 105 Hz.
A characteristic form of oscillograms of pressure Pmeas and the equivalent diameter of the contact spot Dcont, measured at three different temperatures in the center of the heated sample Tcent, are presented in Figs. 10–12. As can be seen from the presented graphs, for all three values of Tcent. There is a time delay tdel. Pressure curve relative to the oscillogram of the contact diameter. Table 1 presents the characteristic values tdel and the contact radius obtained taking into account the calibration dependence in Fig. 9. The same table presents the estimated temperatures of heated metal Tsurf and interphase Tinterphase, (at the moment of contact of water with a hot body) surfaces, as well as the pressure at the explosion point P, calculated taking into account the pressure drops according to the law Pmeas ~ P/r. Here r is the distance from the explosion point to the measurement point (in our case, r = 5 mm).
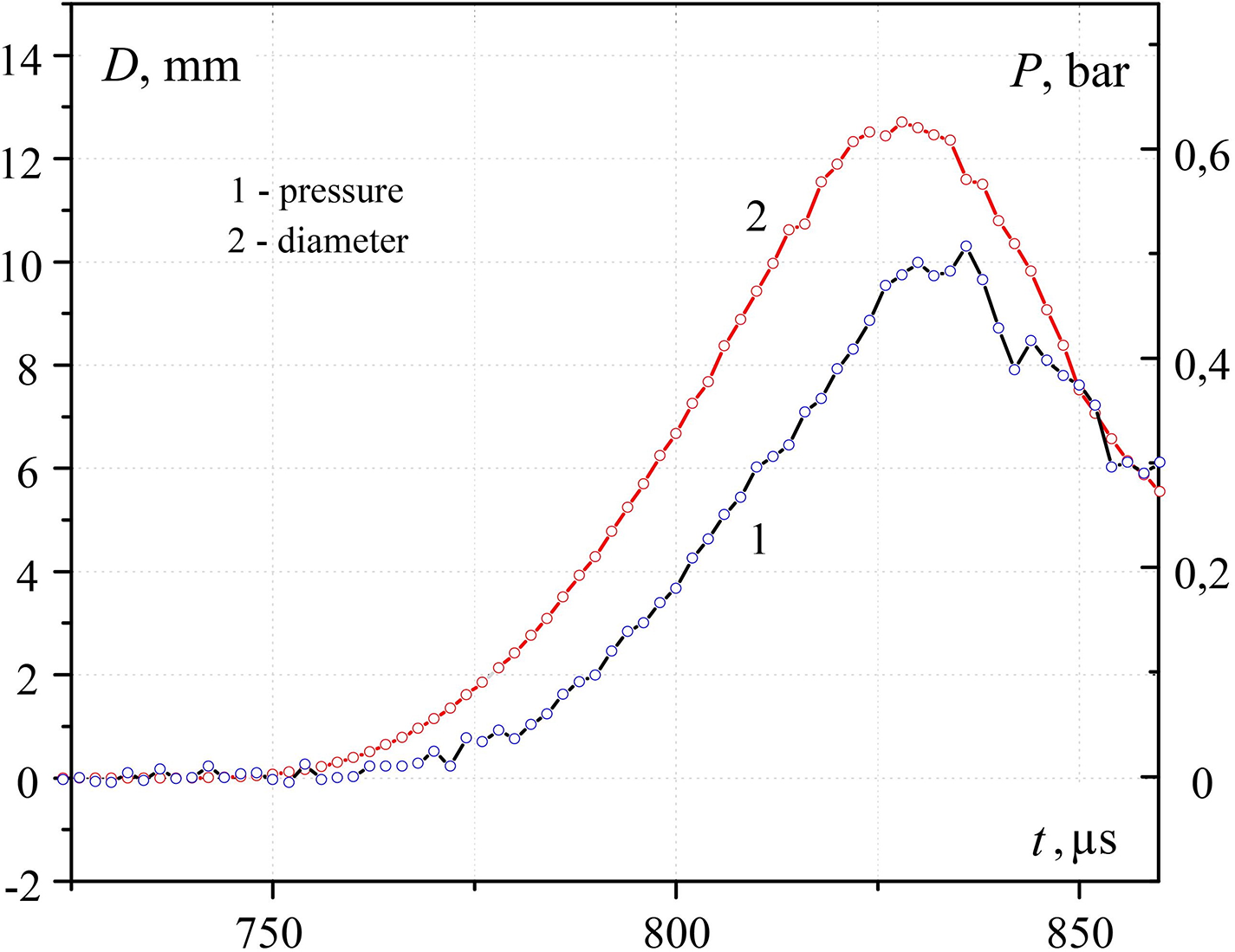
Figure 10: Change over time of pressure (1) and diameter of contact (2) during the initial interaction of water (temperature T~293 K) with hot steel surface (549 K)
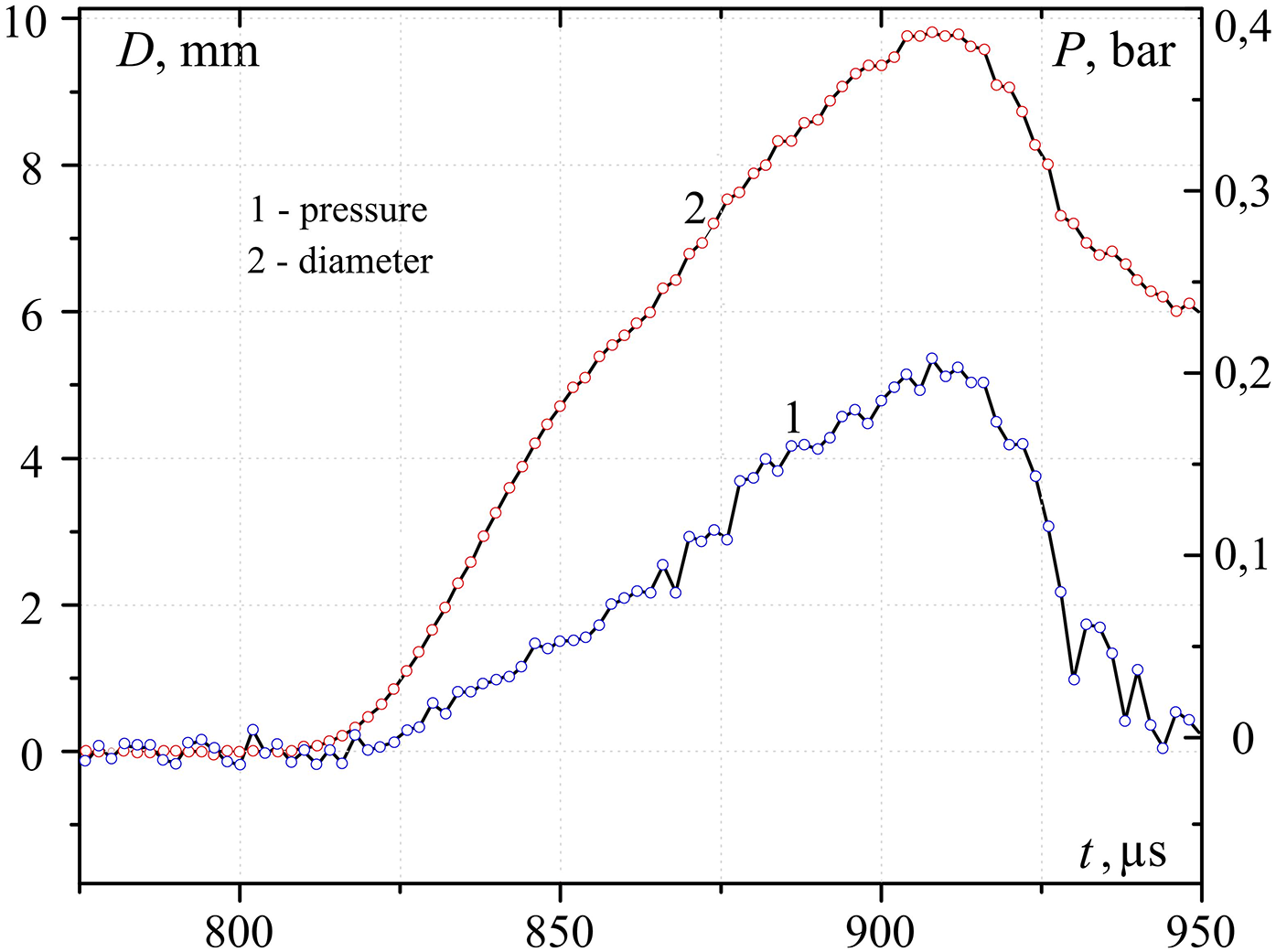
Figure 11: Change over time of pressure (1) and diameter of contact (2) during the initial interaction of water (temperature T~293 K) with hot steel (599 K) hemisphere
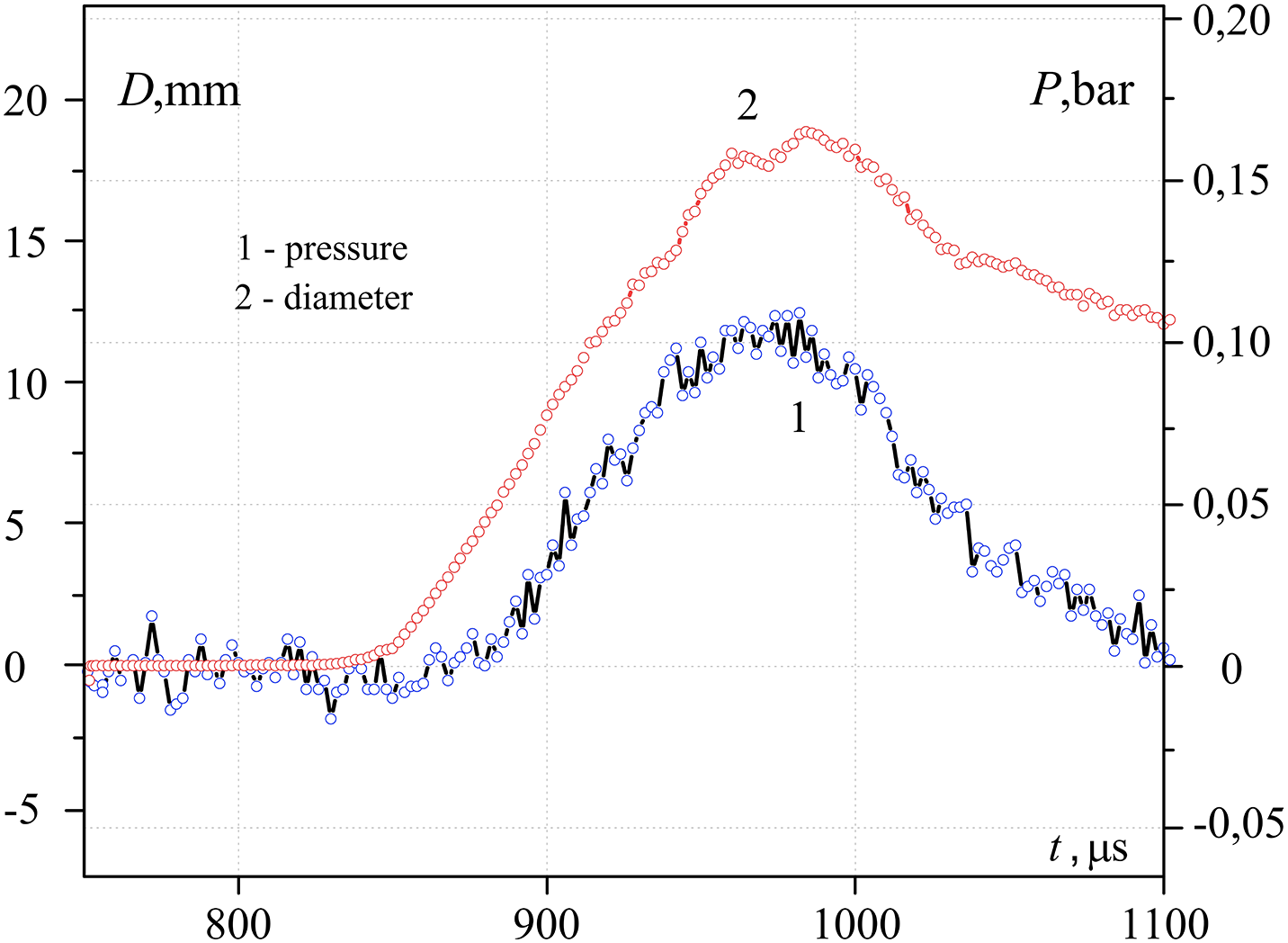
Figure 12: Change over time of pressure (1) and diameter of contact (2) during the initial interaction of water (temperature T~293 K) with hot (489 K) steel hemisphere

The experimental results obtained confirm that the delay time of explosive boiling increases with increasing contact patch, which, in turn, decreases with increasing temperature of the hot surface. The dependence P (Tcent) has a maximum, that is, the pressure amplitude can change in different directions depending on the temperature of the hot surface.
As mentioned above, the comparison of experimental and analytical dependences is relatively restricted nevertheless, it may be marked that there is a good correspondence between pressure impulse value at various squares of contact at the surface temperature close to the temperature of the maximum possible temperature of water overheating. At the same time, the analytical period of pressure growth in pressure impulse is several times less than the experimental one.
The analysis of the experimental data on the pressure rise generated by the boiling liquid at its contact with the heated metal surface given in the current section shows that the model based on the transition of the liquid to a metastable state (explosive boiling) does not allow to describe the observed experimental results accurately enough, in particular, the sharp pressure rise in the boiling region is not clear enough.
The paper proposes and describes a model of pressure pulse formation on the surface of a high-temperature melt drop when it is immersed in water. The model is based on the explosive boiling of coolant at the wave crests generated at the vapor-liquid interface, where it comes into contact with a hot metal surface. Within the framework of the explosive boiling theory based on the classical concept of homogeneous nucleation, a criterion determining the magnitude of the pressure pulse and depending, in particular, on the size of the contact spot and the number of vaporization centers is determined. It is shown that significant pressure pulses occur in a rather narrow range of values of this criterion. Additional experiments have been carried out to determine the main parameters (duration and area of contact, pressure amplitude increase) of the contact of room temperature water with a hot steel surface. The theoretical relationship between the intensity of the pressure pulse and the volume of the boiling liquid, as well as the temperature of the droplet surface, has been established. These calculations enable the determination of the contact spot area corresponding to the observed pressure (P) in the experiment. It should also be noted that the proposed model has several disadvantages associated, in particular, with the absence in the literature of detailed information on the boiling centers, which are little known for specific experiments. In addition, the proposed model does not take into account the influence of both small and finite amplitude vapor film oscillations on the development of instability. The results obtained indicate the need for a deeper study of the nature of the vapor film instability since the area of the hot metal contact with the liquid formed as a result of wave motion largely determines the intensity of the resulting pressure pulse.
Acknowledgement: The authors express their gratitude and deep appreciation to A.N. Kireeva for a useful discussion of the results of the studies.
Funding Statement: This work was supported by the Ministry of Science and Higher Education of the Russian Federation (State Assignment No. 075-00270-24-00).
Author Contributions: The authors confirm contribution to the paper as follows: study conception, mathematical model and analysis: Oleg Sinkevich, Sergei Shchigel, Yuri Ivochkin; data collection: Yuri Ivochkin, Igor Teplyakov; analysis and interpretation of results: Yuri Ivochkin, Stepan Yudin, Igor Teplyakov; computational model and calculations: Stepan Yudin; draft manuscript preparation: Yuri Ivochkin, Stepan Yudin. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: No data was used for the research described in the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Fletcher DF, Theofanous TG. Heat transfer and fluid dynamic aspects of explosive melt–water interactions. Adv Heat Transf. 1997;29:129–213. doi:10.1016/S0065-2717(08)70185-0. [Google Scholar] [CrossRef]
2. El-Genk MS, Matthews RB, Bankoff SG. Molten fuel-coolant interaction phenomena with application to fuel safety. Prog Nucl Energy. 1987;1(2–4):151–98. doi:10.1016/0149-1970(87)90005-9. [Google Scholar] [CrossRef]
3. Berthoud G. Vapor explosions. Annu Rev Fluid Mech. 2000;32:573–611. doi:10.1146/annurev.fluid.32.1.573. [Google Scholar] [CrossRef]
4. Melikhov VI, Melikhov OI, Yakush SE. Thermal interaction of high-temperature melts with liquids. High Temp. 2023;60(2):252–85. doi:10.1134/S0018151X22020274. [Google Scholar] [CrossRef]
5. Simons A, Bellemans I, Crivits T, Verbeken K. Vapor explosions: modeling and experimental analysis in both small- and large-scale setups: a review. JOM. 2021;73(10):3046–63. doi:10.1007/s11837-021-04767-y. [Google Scholar] [CrossRef]
6. Melikhov VI, Melikhov OI, Yakush SE. Hydrodynamics and thermophysics of steam explosions. Report “IPMech RAN”. Moscow; 2020. p. 1–276 (In Russian). [Google Scholar]
7. Li M, Chen Z, Liu L, Shen Z, Wang C. Fragmentation and solidification of fuel-coolant interaction of columnar molten iron and water. J Therm Anal Calorim. 2023;148:10897–906. doi:10.1007/s10973-023-12419-3. [Google Scholar] [CrossRef]
8. Simons A, Bellemans I, Crivits T, Verbeken K. Heat transfer considerations on the spontaneous triggering of vapor explosions—a review. Metals. 2021;11:55. doi:10.3390/met11010055. [Google Scholar] [CrossRef]
9. Deng Y, Guo Q, Xiang Y, Fang D, Ma W. Experimental study on steam explosion of multiple droplets in different chemical solutions. Int J Heat Mass Transf. 2024;226:125477. doi:10.1016/j.ijheatmasstransfer.2024.125477. [Google Scholar] [CrossRef]
10. Simons A.Bellemans I, Crivits T, Verbeken K. The effect of vapour formation and metal droplet temperature and mass on vapour explosion behavior. Int J Heat Mass Transf. 2022;196:12328. doi:10.1016/j.ijheatmasstransfer.2022.123289. [Google Scholar] [CrossRef]
11. Wang C, Wang C, Chen B, Li M, Shen Z. Fragmentation regimes during the thermal interaction between molten tin droplet and cooling water. Int J Heat Mass Transf. 2021;166:120782. doi:10.1016/j.ijheatmasstransfer.2020.120782. [Google Scholar] [CrossRef]
12. Dullforce TE, Buchanan DJ, Perckover RS. Self-triggering of small-scale fuel-coolant interactions: I. Experiments. J Phys D Appl Phys. 1976;9(9):1295–303. doi:10.1088/0022-3727/9/9/006. [Google Scholar] [CrossRef]
13. Wang C, Wang C, Chen B, Lin D, Li M, Shen Z. Comparative study of water drop let interactions with molten lead and tin. Eur J Mech/B Fluids. 2020;80:157–66. doi:10.1016/j.euromechflu.2019.11.010. [Google Scholar] [CrossRef]
14. Pak HS, Hanson RC, Sehgal DR. Fine fragmentation of molten droplet in subcooled water due to vapor explosion observed by X-ray radiography. Exp Therm Fluid Sci. 2005;29(3):351–61. doi:10.1016/j.expthermflusci.2004.05.013. [Google Scholar] [CrossRef]
15. Kouraytem N, Li EQ, Thoroddsen ST. Formation of microbeads during vapor explosions of Field’s metal in water. Phys Rev. 2016;93:063108. doi:10.1103/PhysRevE.93.063108. [Google Scholar] [PubMed] [CrossRef]
16. Tan S, Zhong Y, Cheng H, Cheng S. Experimental investigation on the characteristics of molten lead-bismuth non-eutectic alloy fragmentation in water. Nucl Sci Tech. 2022;33:115. doi:10.1007/s41365-022-01097-9. [Google Scholar] [CrossRef]
17. Hansson RC. Triggering and energetics of a single drop vapor explosion: the role of entrapped noncondensable gases. Nucl Eng Technol. 2009;41(9):1215–22. [Google Scholar]
18. Song J, Wang C, Chen B, Li M, Shen Z, Wang C. Phenomena and mechanism of molten copper column interaction with water. Acta Mech. 2020;231:2369–80. doi:10.1007/s00707-020-02667-x. [Google Scholar] [CrossRef]
19. Zyszkowski W. Experimental investigation of fuel-coolant interaction. Nucl Technol. 1977;33:40–59. doi:10.13182/NT77-A31762. [Google Scholar] [CrossRef]
20. Nelson LS, Duda PM. Steam explosions experiments with single drops of iron oxide melted with CO2–laser. High Temp–High Press. 1982;14:259–22. [Google Scholar]
21. Dombrovsky LA. Steam explosion in nuclear reactors: droplets of molten steel vs core melt droplets. Int J Heat Mass Transf. 2017;107:432–8. doi:10.1016/j.ijheatmasstransfer.2016.11.064. [Google Scholar] [CrossRef]
22. Pitblado RM, Woodward JL. Highlights of LNG risk technology. J Loss Prev Process Ind. 2011;24(6):827–36. doi:10.1016/j.jlp.2011.06.009. [Google Scholar] [CrossRef]
23. Vavilov SN, Vasil’ev NV, Zeigarnik Yu A, Lidzhiev EA. Experimental studies of phenomena occurring during vapor explosion triggering. Therm Eng. 2024;71(7):600–8. doi:10.1134/S0040601524700113. [Google Scholar] [CrossRef]
24. Klimenko AV, Vavilov SN, Vasil’ev NV, Zeigarnik Yu A, Skibin DA. Vapor explosions: experimental observations of the spontaneous triggering phase. Doklady Phys. 2022;67(3):67–9. doi:10.1134/S1028335822010025. [Google Scholar] [CrossRef]
25. Vavilov SN, Vasil’ev NV, Zeigarnik Yu A, Klimenko AV, Skibin DA. Spontaneous triggering of vapor explosion results of experimental studies. Therm Eng. 2022;69(7):484–9. doi:10.1134/S0040601522070072. [Google Scholar] [CrossRef]
26. Vavilov SN, Vasil’ev NV, Zeigarnik Yu A. Vapor explosion: experimental observations. Therm Eng. 2022;69(1):66–71. doi:10.1134/S0040601522070072. [Google Scholar] [CrossRef]
27. Uršič M, Leskovar M. Investigation of challenges related to vapour explosion modelling in sodium. Nucl Eng Des. 2020;363:110646. doi:10.1016/j.nucengdes.2020.110646. [Google Scholar] [CrossRef]
28. Ciccarelli G, Frost DI. Fragmentation mechanisms based on single drop steam explosion experiments using flash X-ray radiography. Nucl Eng Des. 1994;146:109–32. doi:10.1016/0029-5493(94)90324-7. [Google Scholar] [CrossRef]
29. Hansson RC, Park HS, Dinh TN. Dynamics and preconditioning in a single-droplet vapor explosion. Nucl Technol. 2009;167(1):223–34. doi:10.13182/NT09-A8864. [Google Scholar] [CrossRef]
30. Kim B, Corradini M. Modeling of small-scale single droplet fuel coolant interactions. Nucl Sci Eng. 1988;98(2):16–28. doi:10.13182/NSE88-A23522. [Google Scholar] [CrossRef]
31. Kazimi MS, Autruffe MI. On the mechanism for hydrodynamic fragmentation. Trans Am Nucl Soc. 1978;30:366–7. [Google Scholar]
32. Dombrovsky LA. Approximate model for break-up of solidifying melt particles due to thermal stresses in surface crust layer. Int J Heat Mass Transf. 2009;52(1–2):582–7. doi:10.1016/j.ijheatmasstransfer.2008.07.025. [Google Scholar] [CrossRef]
33. Glazkov VV, Zhilin VG, Zeigarnik YA, Ivochkin YP, Igumnov VS, Sinkevich OA, et al. A study into development of instability and collapse of vapor layer on a heated solid hemispherical surface. High Temp. 2000;38:900–8. doi:10.1023/A:1004193307529. [Google Scholar] [CrossRef]
34. Skripov V. Metastable liquids. New York and Toronto: J. Wiley; 1974. [Google Scholar]
35. Sinkevich OA. Waves on the surface of a vapor film under conditions of intensive heat fluxes. Phys Rev E. 2008;78:036318. doi:10.1103/PhysRevE.78.036318. [Google Scholar] [PubMed] [CrossRef]
36. Schneider P. Engineering problems of thermal conductivity. Moscow: Publishing House of Foreign Literature; 1960. p. 1–478 (In Russian). [Google Scholar]
37. Krainov AY, Minkov LL. Computational methods for solving heat and mass transfer problems. Tomsk: Izdatelstvo STT; 2016. p. 1–92 (In Russian). [Google Scholar]
38. Gukhman AA. Application of similarity theory to the study of heat and mass transfer processes. Moscow: Higher School; 1974. p. 1–328 (In Russian). [Google Scholar]
39. Sher I, Harari R, Reshef R, Sher E. Film boiling collapse in solid spheres immersed in a sub-cooled S.R. liquid. Appl Therm Eng. 2012;36:219–26. doi:10.1016/j.applthermaleng.2011.11.018. [Google Scholar] [CrossRef]
40. Yagov VV, Minko KB, Zabirov AR. Two distinctly different modes of cooling high-temperature bodies in subcooled liquids. Int J Heat Mass Transf. 2021;120838. doi:10.1016/j.ijheatmasstransfer.2020.120838. [Google Scholar] [CrossRef]
41. Kanin PK, Yagov VV, Zabirov, Molotova IA, Vinogradov MM, Ryazantsev VA. On the vapor film destabilization mechanism during unsteady film boiling. High Temp. 2023;61:220–28. doi:10.1134/S0018151X23020086. [Google Scholar] [CrossRef]
42. Ivochkin YP, Zeigarnik YA, Kubrikov KG. Mechanisms governing fine fragmentation of hot melt immersed in cold water. Therm Eng. 2018;65(7):462–72. doi:10.1134/S0040601518070029. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools