 Open Access
Open Access
ARTICLE
Optimal Pitch Size of a Biphilic Surface for Boiling Heat Transfer at Subatmospheric Pressures
1 The Laboratory of Low-Temperature Thermophysics, Kutateladze Institute of Thermophysics, Novosibirsk, 630090, Russia
2 Physical Department, Novosibirsk State University, Novosibirsk, 630090, Russia
3 Center of Excellence for Functional Surfaces and Interfaces (EFSUN), Faculty of Engineering and Natural Sciences (FENS), Sabanci University, Orhanli, Tuzla, Istanbul, 34956, Turkey
* Corresponding Author: Ivan Malakhov. Email:
Frontiers in Heat and Mass Transfer 2024, 22(6), 1645-1660. https://doi.org/10.32604/fhmt.2024.056664
Received 27 July 2024; Accepted 24 October 2024; Issue published 19 December 2024
Abstract
To date, using biphilic surfaces is one of the most promising methods for enhancing heat transfer and critical heat flux during boiling simultaneously. However, most of studies on the effect of biphilic surfaces on boiling performance have been carried out under atmospheric pressure conditions. In this context, the issues of heat transfer enhancement and stabilization of the boiling process at subatmospheric pressures are particularly critical due to the interesting characteristics of boiling heat transfer and bubble dynamics at subatmospheric pressures and their practical significance including aerospace applications. This paper investigates the effect of the pitch size between hydrophobic spots on a biphilic surface on heat transfer and bubble dynamics during boiling at subatmospheric pressures (from 11.2 kPa up to atmospheric pressure). The data analysis using infrared thermography demonstrated that the maximum heat transfer rate was achieved on a surface with a uniform pitch size (6 mm) at all pressures. In this case, the heat transfer enhancement, compared a bare surface, reached 3.4 times. An analysis of the departure diameters of bubbles based on high-speed visualization indicated that the optimal configuration of the biphilic surface corresponds to the pitch size equal to the bubble departure diameter. Using high-speed visualization also demonstrated that an early transition to film boiling was evident for configurations with a very high density of hydrophobic spots (pitch size of 2 mm).Graphic Abstract
Keywords
Nomenclature
| A | Area, m2 |
| CHF | Critical heat flux, kW/m2 |
| Ddep | Bubble departure diameter, m |
| h | Heater thickness, m |
| HSV | High speed visualiation |
| HTC | Heat transfer coefficient, kW/m2K |
| I | Current, A |
| IR | Infrared |
| ITO | Indium-tin-oxide |
| lcr | Critical pitch size, m |
| ONB | Onset of nucleate boiling |
| ps | Saturation pressure, kPa |
| q | Heat flux density, kW/m2 |
| U | Voltage, V |
| δ | Relative uncertainty symbol |
| ΔT | Superheat, K |
| ε | HTC enhancement factor |
| Θ | Contact angle |
Boiling at subatmospheric pressures is of interest because the reduction in pressure lowers the absolute boiling temperature, which is crucial for several practical applications, including absorption heat pumps, the cooling of microchips, the cooling of lithium-ion batteries, and the desalination process [1–4]. Nevertheless, the reduction in pressure results in a decline in the heat transfer coefficient and critical heat flux, as well as in significant changes in bubble sizes, bubble departure frequency, nucleation site density, and transition to intermittent boiling [5–9].
A recent trend in boiling heat transfer enhancement involves the control of the wetting properties of the heat-dissipating surface. It has been demonstrated that the activation temperature of nucleation sites is significantly reduced by hydrophobic surfaces. Furthermore, for weakly hydrophobic surfaces (90° < θ ≤ 130°), the density of nucleation sites increases resulting in enhanced heat transfer at low heat fluxes [10–13]. However, these surfaces also result in to an early transition to film boiling, which is a significant drawback for high heat flux systems. At the same time, hydrophilic surfaces are known to enhance significantly the critical heat flux during boiling [14–17]. Several studies have reported that superhydrophilic surfaces increase the temperature of the onset of nucleate boiling (ONB) and reduce the heat transfer performance [15,16].
Recently, attention has shifted to surfaces with heterogeneous wettability. Numerous studies have shown that biphilic surfaces, composed of (super) hydrophobic spots on a (super) hydrophilic base, combine the advantages of both hydrophilic and hydrophobic properties. This combination leads to a reduction in ΔTONB, an increase in the heat transfer rate, and a higher critical heat flux during the water boiling. A comprehensive review of biphilic surfaces was recently performed by Xiang et al. [18]. The heat transfer coefficient and critical heat flux are significantly dependent on the pattern geometry of the biphilic surface, including the pitch size and spot diameters. A substantial body of research have investigated the influence of biphilic configurations on boiling performance. High-speed visualization (HSV) of the boiling process has demonstrated that the maximal heat transfer enhancement is typically observed when the pitch size is equal to the bubble departure diameter [19]. In a numerical study that modeled boiling on biphilic surfaces using the lattice-Boltzmann method, Fedoseev et al. came to the same conclusion [20]. On one hand, it is reasonable to hypothesize that an increase in the density of nucleation sites, i.e., hydrophobic spots, would enhance the heat transfer rate [21,22]. On the other hand, the study by Pontes et al. [23] indicated that if the pitch size is too small, a sessile bubble may extend across multiple hydrophobic spots resulting in local film boiling potentially leading to an early boiling crisis at high heat fluxes. In terms of boiling curves, this is reflected in behavior similar to that observed on homogeneous hydrophobic surfaces [24]. From a hydrodynamic standpoint, the development of the crisis was examined by Xiang et al. [25]. However, experimental data indicate that increasing the density of hydrophobic spots up to a certain threshold results in an improved heat transfer rate [26]. With regard to the pitch size between (super) hydrophobic spots, its impact on local characteristics and heat transfer rate has been studied [19,23,25,27]. It has been demonstrated that reducing the diameter of hydrophobic spots results in a bubble size decrease [23,27,28], theoretically allowing for a higher density of hydrophobic spots on the surface. Simultaneously, a reduction in spot size increases their departure frequency, resulting in a greater total volume of vapor produced per unit of time [23,27]. However, direct measurements of the heat transfer rate while varying spot sizes have yielded different results in various studies. In the study of Mortezaker et al. [24], a two-fold change in the heat transfer coefficient (HTC) was observed when the spot sizes were varied from 50 to 1100 µm. The maximum HTC was observed at a pitch size of 700 µm. In contrast, Može [19] found that spot sizes ranging from 250 to 750 µm had no significant effect on the HTC. These studies indicate that local boiling processes and vapor bubble parameters play a key role in determining the optimal configuration of a biphilic surface. It is also known that pressure has a decisive influence on the local characteristics of the boiling phenomenon and, consequently, on boiling heat transfer.
The heat transfer performance of a biphilic surface at subatmospheric pressures with a pitch size of 10 mm and a spot diameter of 1.5 mm was examined by Serdyukov et al. [29]. The findings revealed that for the biphilic surfaces, the heat transfer rate at different pressures remains unchanged, and the increase in heat transfer reaches 300%. Nevertheless, in contrast to conditions of atmospheric pressure, there are few studies investigating the effect of changing the parameters of a biphilic surface pattern under vacuum conditions. A recent series of studies by Shen et al. [30–33] focused on boiling under vacuum conditions using biphilic surfaces. These studies achieved heterogeneous wetting properties by applying hydrophobic coatings via electroplating [30] and spray deposition [31–33] on a copper base surface. The authors demonstrated that biphilic surfaces markedly reduced the superheat at the onset of boiling and increased the critical heat flux (CHF) by 250% across the entire pressure range (down to 14 kPa) [30]. However, they found that at pressures between 6.9 and 8.8 kPa, there was a sharp transition to intermittent boiling, leading to a steep drop in HTC. To explain this effect, the authors conducted more detailed studies on bubble dynamics at very low pressures. Shen et al. [31] examined bubble dynamics on a single hydrophobic spot under reduced pressure conditions. The authors demonstrated that at various pressures, the conditions governing the growth and departure of vapor bubbles exhibited notable differences due to the varying dynamics of the contact line relative to the hydrophobic spot boundaries. Below a certain pressure threshold, as the bubble growth rate increased, the probability of the contact line exceeding the hydrophobic spot boundaries also increased. This resulted in larger departure diameters and altered bubble departure processes. At larger diameters, bubble departure was accompanied by wetting over hydrophobic spots, which interrupted vapor bubble generation and led to intermittent boiling [32]. Based on these findings, Shen et al. [33] investigated surfaces with simultaneously modified structures and wetting properties. This approach successfully delayed the transition to intermittent boiling by retaining vapor nuclei. However, the authors noted that further research on the detailed dynamics of the triple contact line is necessary to prevent intermittent boiling completely.
The above studies show that biphilic surfaces are a promising method for improving boiling heat transfer and stabilizing boiling at subatmospheric pressures. However, data on the influence of surface parameters on boiling at various pressures are scarce. Although the development and application of biphilic coatings are actively progressing, there is a lack of understanding the local processes on these surfaces and optimal configurations of biphilic coatings for boiling at subatmospheric pressures. This study investigates the effect of the pitch size between hydrophobic spots on a biphilic surface on boiling heat transfer and local evaporation processes during boiling of water at pressures ranging from 11.2 kPa to atmospheric pressure.
In order to study the local pool boiling characteristics and heat transfer in boiling under various pressure conditions, a setup shown in Fig. 1 was made. The working volume consists of a sealed stainless steel chamber placed in a controlled thermostat to maintain the saturation temperature at a specified pressure. The pressure in the chamber was set with an EVP 2XZ-1C rotary vane vacuum pump and monitored with a Thyracont VD81 digital vacuum gauge. To maintain constant pressure during boiling, a closed water-cooled condenser was installed at the top of the working volume. Deionized water prepared with a Merck Direct-Q 3 UV system was used as the working fluid. The experiments were conducted within a pressure range of 11.2–102.8 kPa, corresponding to saturation temperatures of 48.0°C–100.3°C.
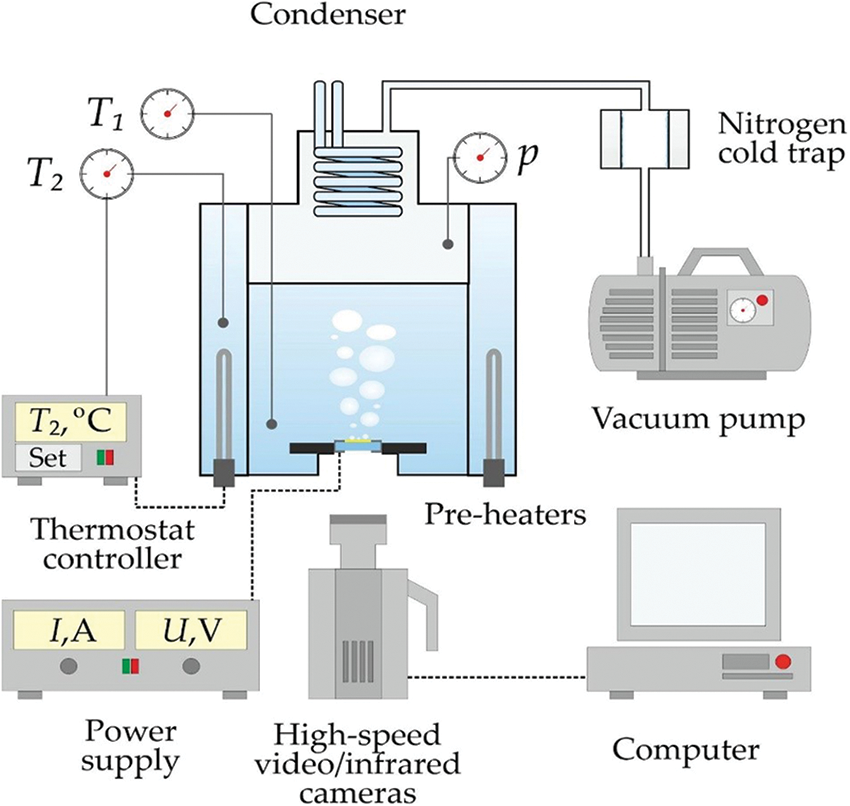
Figure 1: The experimental setup
When determining the pressure on the surface of bubble nucleation, the influence of the liquid column pressure of approximately 1.5 kPa, was taken into account. This significantly affected the saturation temperature on the heater surface during low-pressure experiments, where it was comparable to the chamber pressure. It should be noted that for subatmospheric pressures, the thermostat temperature was set above the saturation temperature to achieve saturation conditions, but at atmospheric pressure, the degree of subcooling was 2°C–3°C in different runs.
The qualitative characteristics of the different regimes as well as bubble departure diameters were investigated using high-speed videography through a transparent heater from below (the design is detailed in Section 3.2). The videography was performed using a Phantom VEO 410 camera with a frame rate of up to 4000 fps and a maximum spatial resolution of 73 μm/pixel. To illuminate the working area during high-speed videography, an LED connected to an external power source through a sealed connector was installed inside the working volume.
To study the heat transfer rate, a high-speed infrared camera, FLIR Titanium HD 570 M, with a spectral response of 3.7–4.8 μm and a noise equivalent differential temperature (NETD) value of 18 mK was used. In this study, the thermographic camera had a frame rate of 1000 fps, an integration time of 300 μs, and a maximum spatial resolution of 220 μm/pixel. To eliminate parasitic reflected rays and to enhance the intensity of the IR signal in experiments with the IR camera, the bottom side of the heater was painted with black matte paint.
A key feature of the experimental setup used in this study is the transparent heater (Fig. 2a), which consists of a 1 µm thick ITO (indium tin oxide) film deposited at the bottom of a sapphire substrate. The transparency of the heater allows for high-speed video recording from below through the heater. This visualization technique provides comprehensive information about the local characteristics of boiling and allows detailed tracking of the evolution of individual bubbles and the behavior of the contact line. The size of the heat dissipation area, i.e., the ITO film area, was 28 × 30 mm², while the sapphire substrate used as the base was a disc with a diameter of 60 mm and a thickness of 2 mm.
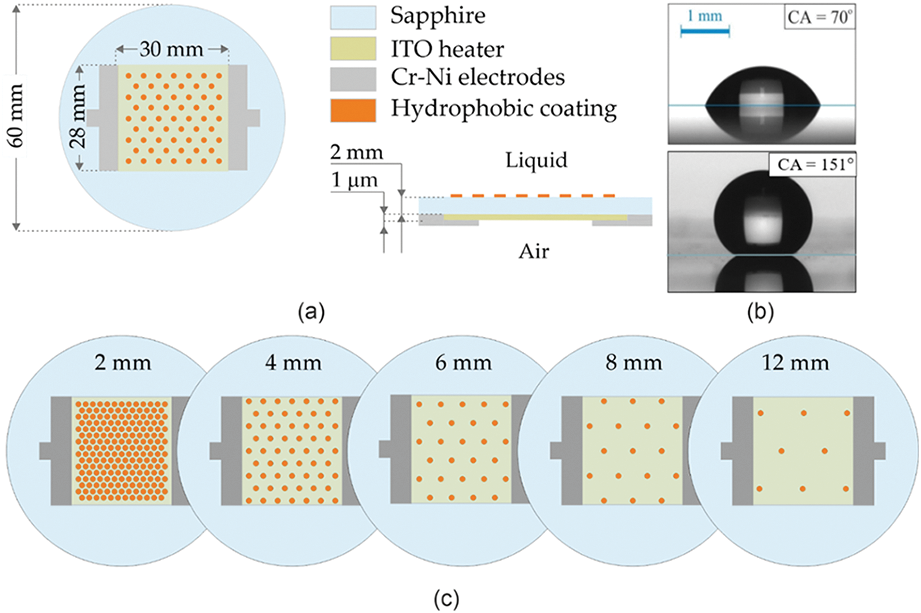
Figure 2: (a) The heater design (b) contact angles of the sapphire surface and hydrophobic coating (c) configurations of biphilic surfaces
Hydrophobic spots were applied by spraying, using a mask to create a pattern with a specific geometry. Vinyl stickers with holes cut at specified distances using a plotter were used as masks of various configurations. In this study, five different configurations of biphilic surfaces with different distances between the hydrophobic spots of 2, 4, 6, 8, and 12 mm (Fig. 2c) were made. The diameter of the hydrophobic spots was constant for all coatings and was set as 1.5 mm. The ratio of the area of hydrophobic spots to the total area, used by some authors to determine the configuration of the biphilic surfaces, was 51.0%, 12.8%, 5.6%, 3.2%, and 1.4%.
To create hydrophobic spots on the surface of the sapphire substrate, a silicone-based coating (Glaco Zero) was used. The results of static contact angle measurements of water droplets which were performed using a KRUSS DSA100 system (Fig. 2b) show that the contact angle is 151° for the hydrophobic coating, while the base sapphire surface was characterized by a contact angle of 70°. During the test experiments, the surface demonstrated stable wettability properties after 6 h of boiling. Furthermore, to ensure that the biphilic surface properties do not change during the experiment, each boiling curve was obtained 3 times.
To obtain the surface temperature data recorded by the IR camera, a calibration procedure was performed using a Honeywell HEL 700 thermosensitive sensor attached to the heater before the experiments. The calibration was performed by gradually increasing the temperature of the entire liquid volume using a thermostat.
To analyze the heat transfer rate, the surface temperatures were averaged over the heater area and a 10-s interval, thus obtaining the mean heater temperature for a fixed heat flux. Since the IR camera recorded the temperature on the lower side of the sapphire substrate where the heat was dissipated, the surface temperature in direct contact with the liquid was determined by calculating the temperature drop across the thickness of the sapphire substrate using Fourier law for steady-state conditions. This procedure was described in detail in a previous study [12].
To ascertain the precise heat flux to the liquid from the surface area covered by the subject biphilic pattern, the heat losses were analyzed in detail. This was performed based on the numerical solution of the heat transfer equation in 3D domain. The boundary conditions for the problem were as follows:
1. A constant heat flux density
2. A heat flux density
3. A constant temperature equal to the saturation temperature was set on the lateral sides.
4. A third-kind boundary condition in the form of a q(T) dependence, determined from the boiling curves for the biphilic surface, was set on the upper side in the biphilic pattern-covered area.
5. A third-kind boundary condition in the form of a q(T) dependence, determined from the boiling curves for the bare surface, was set on the upper side in the area not covered by the biphilic pattern.
Several heat fluxes were assessed. It was found that the heat losses did not exceed 14.0% and exhibited a decrease to 8.3% when the heat flux was increased to 200 kW/m². The calculated heat loss values as a function of heat flux were taken into account when constructing the boiling curves.
The uncertainty in the heat flux was found using the uncertainty in the electrical current supply, as well as the uncertainty in the voltage. In total, it was calculated as 0.5% of the multiplication error in indirect measurements.
The uncertainty in the pressure consists of the sensor accuracy, which is less than 0.3% according to the manufacturer datasheet, and the accuracy of the liquid column height, measured with an uncertainty of <5 mm corresponding to a maximum uncertainty of 0.5% at the lowest pressures. However, since the pressure was set manually, it could be different for different experiments. Therefore, when summarizing the data of different experiments, conditionally at the same pressure, it is necessary to specify the mean square deviation for various tests. It was 1.4 kPa.
To ascertain the temperature of the working surface, it is essential to consider the uncertainties associated with both the temperature measurement with the IR camera and the heat flux, since the heat flux contributes to the calculation of the upper heater surface in direct contact with water, as discussed in the previous section. For the IR camera, there is an uncertainty associated with the calibration procedure and the sensitivity of the IR camera. The absolute value of the uncertainty in the temperature measurement after calibration experiments was no more than 1 K. As a result, the uncertainty in temperature measurement via the IR camera can be found as
In the case of geometric parameters that are measured based on HSV data, it is necessary to take into account the uncertainty in spatial resolution since it is measured based on the high-speed visualization through the transparent heater. This contribution can be estimated as the size of a single pixel divided by the characteristic departure size of the bubble, which is approximately 6 mm. Thus, the uncertainty in Ddep becomes 73 µ/6 mm, which equates to 0.013 (1.3%).
Fig. 3 shows the comparison of boiling curves for biphilic surfaces with different pitch sizes at four different pressures (11.2, 22.3, 41.8, and 102.8 kPa). As a reference, the boiling curve of a bare surface is also displayed at similar pressures [6]. The boiling curves for biphilic surfaces are significantly shifted to the left compared to the bare surface. While the curve slope changes corresponding to the onset of nucleate boiling (ONB) on the bare surface occurs at superheats from ΔTONB = 21 K at 11.2 kPa to ΔTONB = 11 K at 102.8 kPa, the ONB on biphilic surfaces is significantly reduced at all studied pressures. The transition between convection and nucleate boiling on biphilic surfaces was observed at superheats of approximately 5 K ± 2.
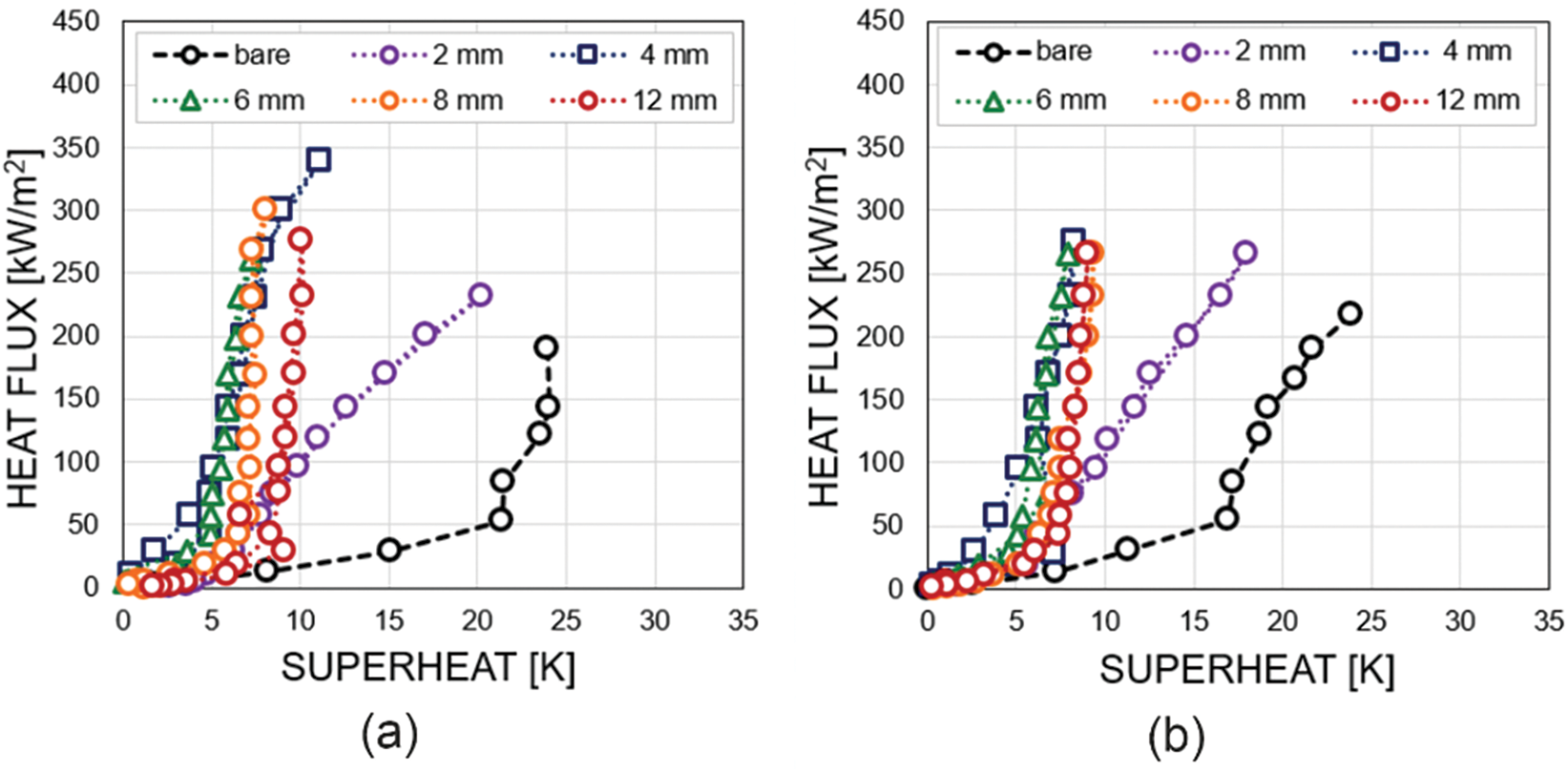
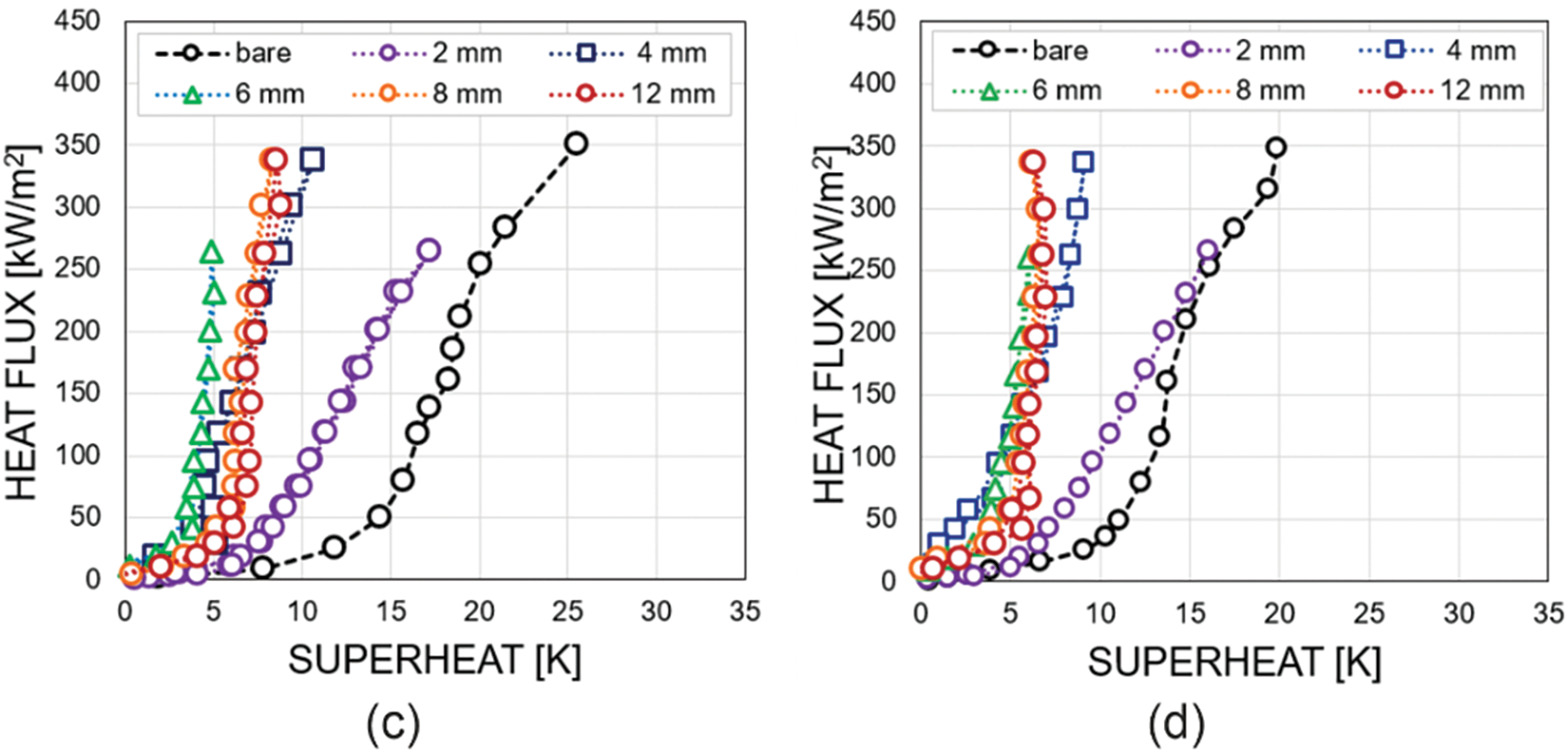
Figure 3: Boiling curves for different configurations of biphilic surfaces at pressures of (a) 11.2 kPa, (b) 22.3 kPa, (c) 74.3 kPa, (d) 102.8 kPa
It should be noted that for biphilic surfaces with a pitch size of l ≥ 4 mm, the boiling curves are similar to each other. However, for the smallest pitch size of 2 mm, a markedly disparate slope is observed in the boiling curve. As the heat flux increases for this type of biphilic surface, the temperature rises sharper as compared to the other biphilic surface configurations. Moreover, a continuous temperature rise can be observed on the surface with a 2 mm pitch size at heat fluxes of approximately 250–300 kW/m² indicating a transition to film boiling and the onset of a boiling crisis. This indicates that there is a lower limit for the pitch size, below which the heat flux that can be dissipated through boiling decreases significantly. The observed values (250–300 kW/m²) are approximately four times lower than the critical heat flux for water calculated using the Kutateladze-Zuber correlation [34,35] for atmospheric pressure.
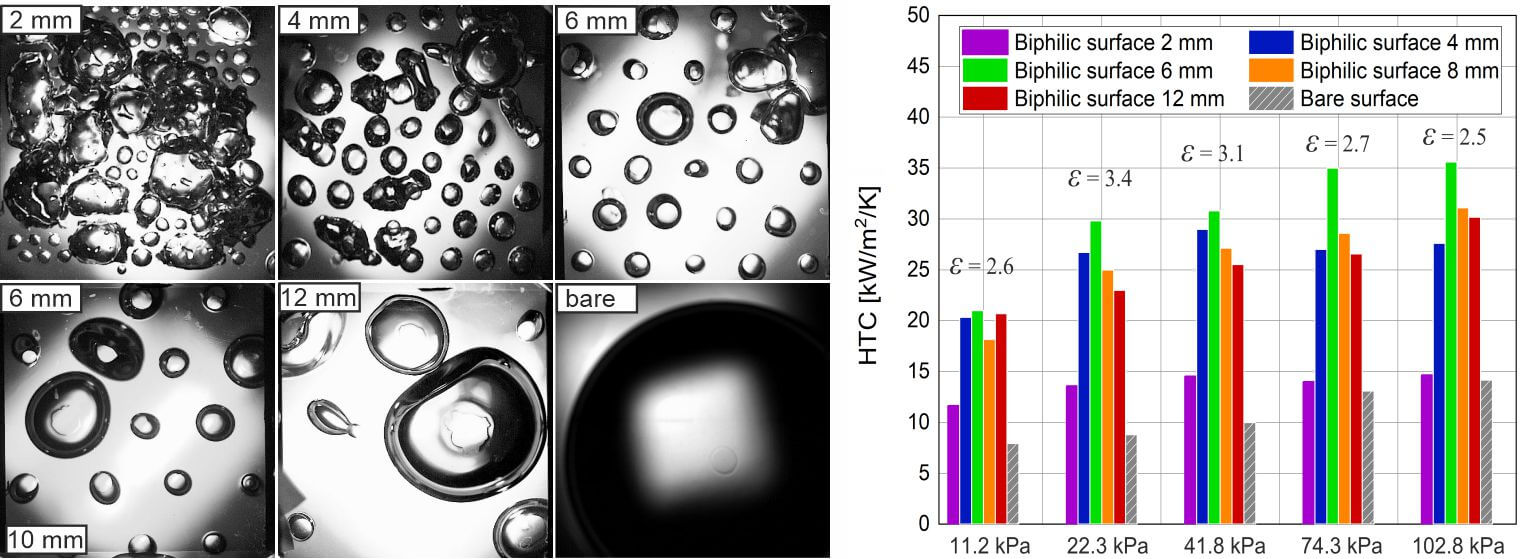
To undertake a quantitative comparison of the influence of biphilic surfaces on boiling heat transfer, the HTC values were determined for different configurations at varying pressures (a comparison diagram for the heat flux of 200 kW/m²) is shown in Fig. 4). It is evident that there is an optimal configuration that yields the highest HTC values. A reduction from 12 to 6 mm has been observed to result in a gradual increase in HTC, with a corresponding increase of 20%–30%, depending on the pressure. The highest HTC values at all pressures were observed for the pitch size of 6 mm. However, with a further reduction in the pitch size to 2 mm, the heat transfer rate drops sharply by 2–2.5 times. In order to gain insight into the mechanisms of the influence of the biphilic surface configuration on boiling heat transfer, high-speed visualization through a transparent heater was conducted, which will be discussed in the following section.
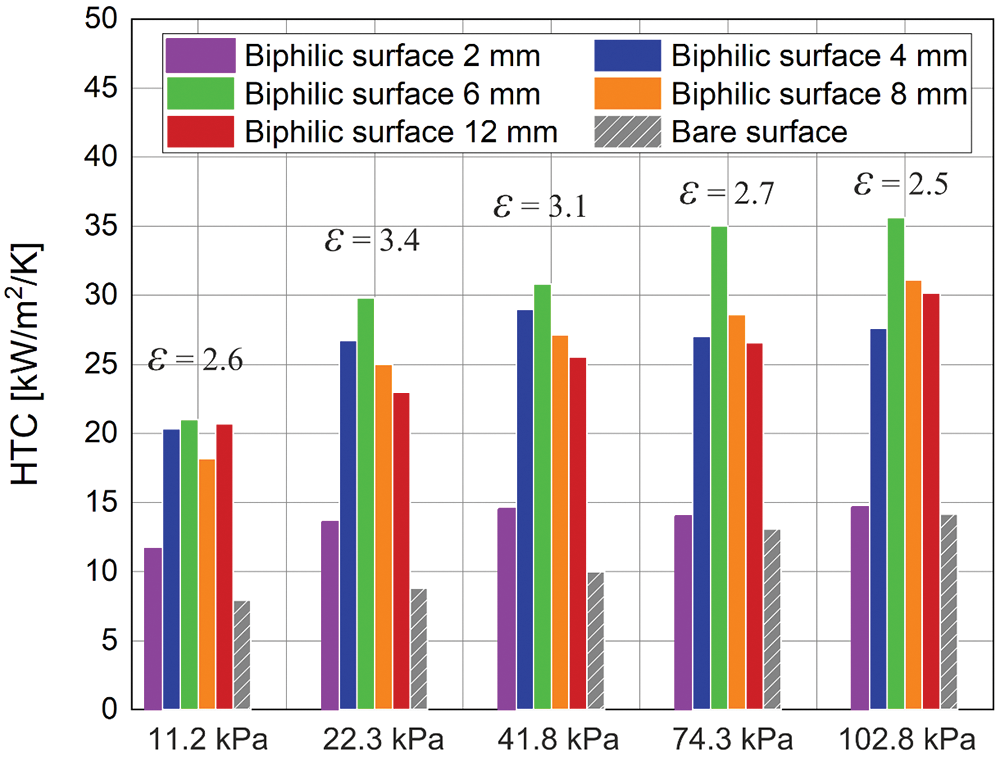
Figure 4: Comparison of heat transfer coefficients for different configurations of biphilic surfaces at different pressures (q = 200 kW/m2). The maximum enhancement factor for the current pressure is marked on the diagram
Fig. 4 also demonstrates that there is a dependence of HTC on pressure for the investigated biphilic surfaces, contrary to the findings of previous studies [29,32]. In comparison to the biphilic surface, the factor of heat transfer enhancement increases with decreasing pressure. As a result, the relative enhancement using biphilic surfaces becomes higher with decreasing pressure, even though the HTC itself decreases, which is a promising outcome for the use of biphilic surfaces at subatmospheric pressure.
To analyze the bubble dynamics during boiling on biphilic surfaces with different pitch sizes at various pressures, high-speed images captured through a transparent heater were acquired. Fig. 5 presents typical frames of boiling on surfaces with varying pitch sizes at the lowest pressure of ps = 11.2 kPa, which clearly demonstrate the influence of the configuration.
Figure 5: Comparison of boiling regimes on surfaces with different pitch size at q = 40 kW/m2 (Ps = 11.2 kPa +/− 0.5 kPa)
First of all, it can be observed that the biphilic surface facilitates continuous nucleation and bubble departure across the entire surface, specifically at each hydrophobic site. This leads to a notable increase in the frequency of bubble detachment (number of bubbles per unit time) compared to a bare surface, where only a single large bubble forms at extended intervals. Moreover, the bubble departure size on the biphilic surface is significantly reduced. Additionally, the nature of bubble detachment from the heating surface changes on the biphilic surface. Specifically, after bubble departure from the hydrophobic sites, a portion of the vapor remains on the surface. As a result, during boiling on a biphilic surface, the waiting period between the detachment of one bubble and the nucleation of the next on individual hydrophobic spots is minimized [29]. Consequently, the bubble departure frequency is considerably higher than that observed on a base hydrophilic surface. This mechanism plays a crucial role in enhancing the heat transfer coefficient (HTC) on biphilic surfaces.
For the pitch size of 2 mm, the contact lines of adjacent bubbles merge, forming a large sessile bubble that occupies a substantial area, covering several spots as it is demonstrated in Fig. 6. The bubble dynamics on such a surface are similar to those observed on a surface with homogeneous hydrophobic properties [12]. This fact indicates that there is a critical value of pitch size lcr at which the transition to a boiling regime similar to boiling on a hydrophobic surface occurs. The region enclosed by the contact line remains insulated from the liquid by vapor for an extended period. In essence, these bubbles act as local sites of film boiling, which cover an increasingly larger area as the heat flux increases. Once the areas enclosed by the contact lines of the sessile vapor bubbles reach a critical size, irreversible growth of dry spots occurs, leading to a boiling crisis. When the pitch size between hydrophobic spots decreases, based on the energy balance, it is more favorable that the contact line covers several spots rather than each spot individually due to the lower total surface energy of the phase boundaries. However, it is evident that the balance is also influenced by the pressure and evaporation rate associated with the heat flux.
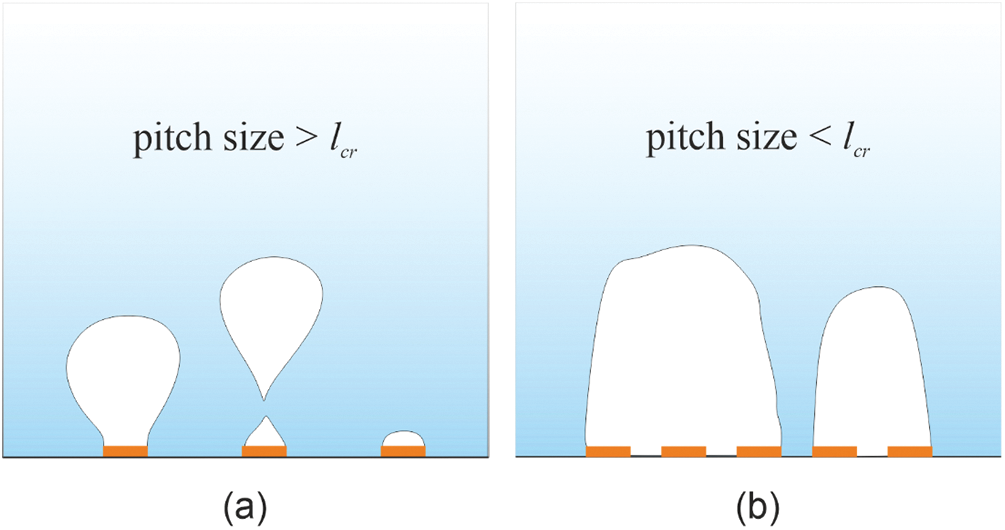
Figure 6: (a) The boiling regime with pitch size >lcr (b) The boiling regime with pitch size >lcr
3.2.2 Bubble Departure Diameters
Using the images obtained via high-speed visualization, departure diameters of vapor bubbles were measured for the biphilic surface configurations at various pressures. Fig. 7a shows the results for different surfaces as a function of pressure. The analysis indicates that during boiling on the biphilic surfaces, the diameters are weakly dependent on pressure for all the configurations as compared to the bare surface. While the departure diameters increase to 38 mm upon a pressure decrease to 11.2 kPa on the bare hydrophilic surface, [12], the average diameters for all configurations range from 3.5 to 7 mm for the biphilic surfaces. Since superheats corresponding to the onset of bubble growth on a biphilic surfaces are significantly lower than those on hydrophilic surfaces, the bubble growth rate is lower, and inertial effects do not strongly influence the bubble departure process [36]. As a result, a weaker dependence of the bubble departure diameter on the pressure is visible as compared to a hydrophilic surface.
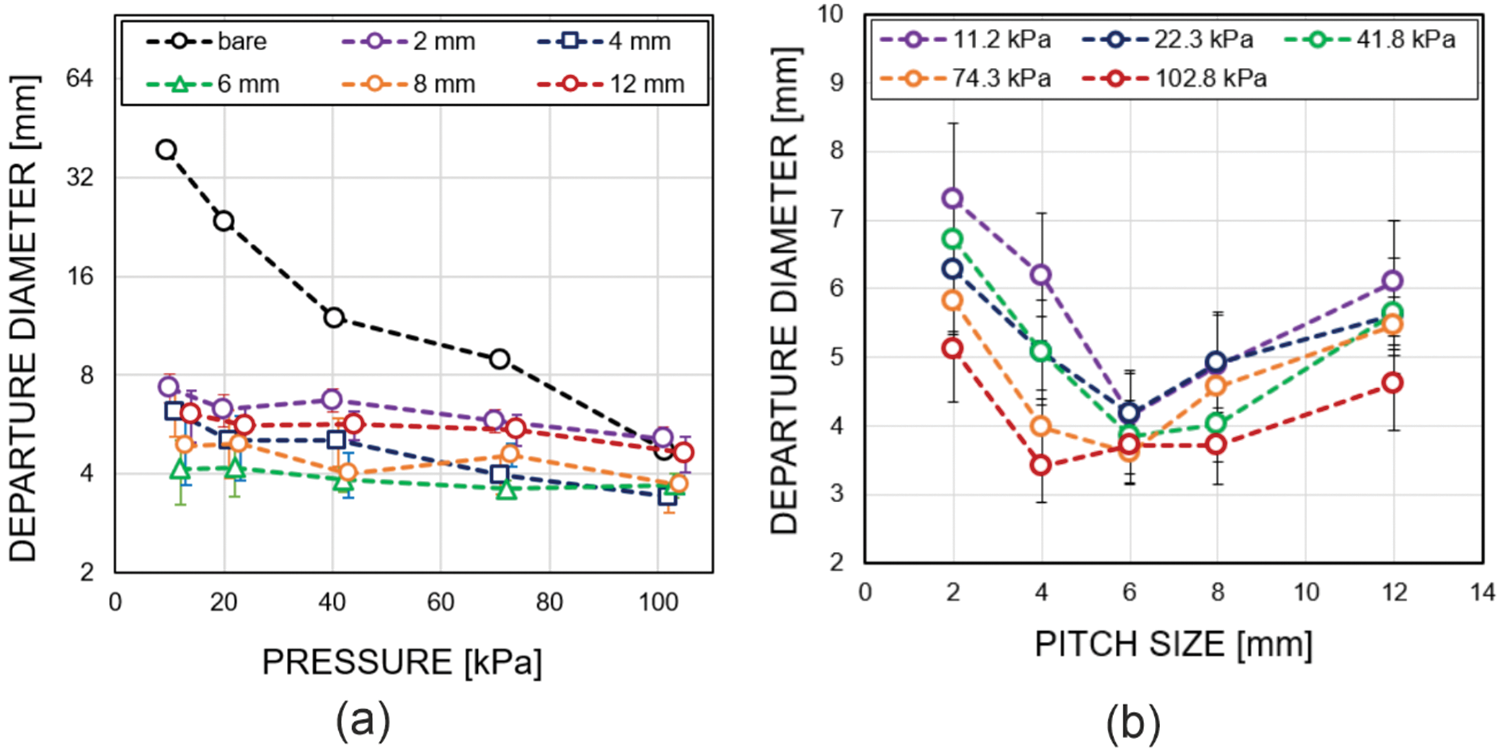
Figure 7: (a) Dependence of bubble departure diameter on pressure for different configurations of biphilic surfaces. (b) Dependence of bubble departure diameter on the pitch size for different pressures
Fig. 7b shows the dependence of the bubble departure diameter on the pitch size at different pressures. When the pitch size is reduced from 12 to 6 mm, the departure diameter of bubbles decreases. However, with a decrease in the pitch size from 6 to 2 mm, the bubble diameter increases. The existence of a minimum on the profiles presented in Fig. 7b can be attributed to the fact that bubble departure occurs depending on different scenarios, as demonstrated in Fig. 7. For distances of 6 mm and more, most bubbles reach the departure stage, showing virtually minimal interaction with neighboring bubbles throughout most of the growth stage (Fig. 6a). As the distance between spots increases, the area around the spot not occupied by bubbles also expands. Since active evaporation and heat dissipation occur in the regions where bubbles originate, for large gaps between spots the superheat of liquid in gaps reaches the higher values than in the case of the dense spot configuration. As a result, the temperature of liquid around the growing bubble becomes higher, which leads to an increased bubble growth rate. As a result, inertial effects begin to influence the departure, to an increase in the duration of the bubble growth stage [36].
In the case of the biphilic surface with a pitch size of 2 mm, bubble departure occurs due to another reason. For this configuration, large stationary bell-shaped slowly growing bubbles form on the surface (Fig. 7b), similar to those on the reference hydrophobic surface [12]. Due to the geometry of their base, at the same diameter, the length of the contact line is greater than for spherical bubbles with a thin stem. As a result, surface tension forces can hold a larger volume of vapor than spherical bubbles, and buoyancy forces exceed surface tension forces at large bubble diameters.
In most studies, the departure diameter of bubbles is indicated as a parameter that determines the optimal geometry of biphilic surfaces. In particular, Fedoseev et al. [20], who investigated the influence of biphilic surfaces on boiling heat transfer using the Lattice Boltzmann method, stated that the optimal distance between unwetted spots corresponds to 0.9–1.3 of the departure diameter of bubbles. In this study, as the bubble departure diameter varies for different biphilic surfaces, its value ranges from 4 to 6 mm, except for the surface with a distance of 2 mm, where a quasi-hydrophobic boiling regime was observed. So, the pitch size, corresponding to the highest values of HTC in our experiments, is also about the bubble departure diameters. In the experimental study by Može et al. [19], which investigated the influence of the distance between spots on a biphilic surface at atmospheric pressure, it was stated that the maximum enhancement was observed for a distance between spots equal to the departure diameter of bubbles, while the bubble diameter differed significantly as compared to this study.
Regarding the departure diameters, the highest HTC is achieved for the same distance between spots at all pressures which is explained by the weak dependence of bubble departure diameter on pressure. The optimum distance between spots in these experiments roughly matches with the bubble departure diameter, which qualitatively agrees with the data of other authors, despite the fact that in other works the changes in the values of the Ddep differed significantly and could be about 1–1.3 mm at atmospheric pressure and diameters of hydrophobic spots of 0.25–1 mm [19].
According to the highlighted above, we should note that the departure diameter is not the only criterion and somewhat not the most critical factor. In the case of a very small distance between spots, which was 2 mm in our experiment with hydrophobic spots diameter of 1.5 mm, there is a significant change in the boiling phenomenon, which leads to a dramatic decrease in both HTC and CHF. In this regard, the most important parameter governing the geometric configuration of the biphilic surface is the criterion of stability for large-scale vapor bubbles, which is determined by the total surface energy of interfacial boundaries, the pressure of liquid, and probably the evaporation rate of liquid near the contact line, influenced by the heat flux and contact angle of the hydrophilic part of the surface. However, this deserves another detailed study and will be addressed in future studies.
The effect of the pitch size of biphilic surface configurations on boiling heat transfer and bubble dynamics during boiling at subatmospheric pressures in the range of 11.2–102.8 kPa was investigated. Surfaces with hydrophobic spots of 1.5 mm diameter and pitch sizes ranging from 2 to 12 mm were examined. Based on the experimental results obtained using IR thermography and high-speed visualization through a transparent heater, the following conclusions can be drawn:
• In the range of heat fluxes studied (0–300 kw/m2), biphilic surfaces were observed to enhance heat transfer by 2.5–3.4 times depending on pressure (at the optimum pitch size). A reduction in pressure leads to an increase in the enhancement of heat transfer with biphilic surfaces, which is a promising result for operating at subatmospheric pressures.
• The pitch size at which the maximum factor of the heat transfer enhancement was achieved in the experiment is 6 mm (the hydrophobic area was 5.6%), the same for all studied pressures.
• The mean bubble departure diameter on biphilic configurations is observed to vary from 3.5 to 7 mm which is significantly smaller than the values obtained in boiling on hydrophilic bare surface at subatmospheric pressures (up to 40 mm at 8.8 kPa). The lowest bubble departure diameter could be observed for the biphilic surface with a 6 mm pitch size, which provides the greatest heat transfer enhancement.
• High-speed visualization shows that for a pitch size of 2 mm, the formation of large-scale sessile vapor bubbles, which cover several hydrophobic spots, can be detected from the onset of boiling, similar to the case of the homogeneous hydrophobic surface. For this surface, a sharp temperature rise is obtained due to the early transition to boiling crisis at the heat flux of 250–300 kW/m².
The data obtained can be used to develop an analytical criterion of the optimal configuration of the biphilic surface, to achieve the highest heat transfer and simultaneously avoid negative trends associated with the transition to a quasi-hydrophobic boiling regime.
Acknowledgement: Not applicable.
Funding Statement: The work was carried out under the state contract of IT SB RAS (No. 121031800216-1) and supported by the joint funding of RFBR (No. 20-58-46008, Anton Surtaev) and TUBITAK (No. 119N401, Ali Kosar).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Anton Surtaev, Alexander Pavlenko, Ali Kosar; data collection: Ivan Malakhov; analysis and interpretation of results: Ivan Malakhov, Anton Surtaev, Vladimir Serdyukov; draft manuscript preparation: Ivan Malakhov, Anton Surtaev, Vladimir Serdyukov. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: For additional information or data presented in the paper, you can contact the corresponding author.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Roe C, Feng X, White G, Li R, Wang H, Rui X, et al. Immersion cooling for lithium-ion batteries–a review. J Power Sources. 2022;525:231094. doi:10.1016/j.jpowsour.2022.231094. [Google Scholar] [CrossRef]
2. Sun C, Guo D, Wang Z, Sun F. Investigation on active thermal control method with pool boiling heat transfer at low pressure. J Therm Sci. 2018;27(3):277–84. doi:10.1007/s11630-018-1009-0. [Google Scholar] [CrossRef]
3. Amaris C, Bourouis M. Boiling process assessment for absorption heat pumps: a review. Int J Heat Mass Transfer. 2021;179:121723. doi:10.1016/j.ijheatmasstransfer.2021.121723. [Google Scholar] [CrossRef]
4. Bilgil A, Hırlakoğlu B. An experimental study on desalination at vacuum environment under low pressure and low condensation temperatures. Desalination. 2017;411:9–18. doi:10.1016/j.desal.2017.02.006. [Google Scholar] [CrossRef]
5. Chan MA, Yap CR, Ng KC. Pool boiling heat transfer of water on finned surfaces at near vacuum pressures. 2010;132(3):031501. [Google Scholar]
6. Surtaev A, Serdyukov V, Malakhov I. Effect of subatmospheric pressures on heat transfer, vapor bubbles and dry spots evolution during water boiling. Exp Therm Fluid Sci. 2020;112:109974. doi:10.1016/j.expthermflusci.2019.109974. [Google Scholar] [CrossRef]
7. Giraud F, Rullière R, Toublanc C, Clausse M, Bonjour J. Experimental evidence of a new regime for boiling of water at subatmospheric pressure. Exp Therm Fluid Sci. 2015;60:45–53. doi:10.1016/j.expthermflusci.2014.07.011. [Google Scholar] [CrossRef]
8. Michaie S, Rullière R, Bonjour J. Experimental study of bubble dynamics of isolated bubbles in water pool boiling at subatmospheric pressures. Exp Therm Fluid Sci. 2017;87:117–28. doi:10.1016/j.expthermflusci.2017.04.030. [Google Scholar] [CrossRef]
9. Mahmoud MM, Karayiannis TG. Bubble growth on a smooth metallic surface at atmospheric and sub-atmospheric pressure. Int J Heat Mass Transfer. 2023;209:124103. doi:10.1016/j.ijheatmasstransfer.2023.124103. [Google Scholar] [CrossRef]
10. Malavasi I, Bourdon B, Di Marco P, De Coninck J, Marengo M. Appearance of a low superheat quasi-Leidenfrost regime for boiling on superhydrophobic surfaces. Int Commun Heat Mass Transfer. 2015;63:1–7. doi:10.1016/j.icheatmasstransfer.2015.01.012. [Google Scholar] [CrossRef]
11. Malavasi I, Teodori E, Moita AS, Moreira AL, Marengo M. Wettability effect on pool boiling: a review. In: Encyclopedia of two-phase heat transfer and flow III: macro and micro flow boiling and numerical modeling fundamentals volume 4: special boiling topics. Singapore: World Scientific; 2018. p. 1–61. [Google Scholar]
12. Surtaev A, Koşar A, Serdyukov V, Malakhov I. Boiling at subatmospheric pressures on hydrophobic surface: bubble dynamics and heat transfer. Int J Therm Sci. 2022;173:107423. doi:10.1016/j.ijthermalsci.2021.107423. [Google Scholar] [CrossRef]
13. Allred TP, Weibel JA, Garimella SV. The petal effect of parahydrophobic surfaces offers low receding contact angles that promote effective boiling. Int J Heat Mass Transfer. 2019;135:403–12. doi:10.1016/j.ijheatmasstransfer.2019.02.002. [Google Scholar] [CrossRef]
14. Serdyukov V, Vladyko I, Starinskiy S, Rodionov A, Shukhov Y, Malakhov I, et al. Pool boiling performance on the textured hemi-wicking surfaces fabricated by nanosecond laser ablation. Appl Therm Eng. 2023;228:120472. doi:10.1016/j.applthermaleng.2023.120472. [Google Scholar] [CrossRef]
15. Hsu CC, Chen PH. Surface wettability effects on critical heat flux of boiling heat transfer using nanoparticle coatings. Int J Heat Mass Transfer. 2012;55(13–14):3713–9. [Google Scholar]
16. Girard AR, Kim J, You SM. Pool boiling heat transfer of water on hydrophilic surfaces with different wettability. In: ASME International Mechanical Engineering Congress and Exposition, 2016 Nov; Phoenix, AZ, USA: American Society of Mechanical Engineers. vol. 50626, V008T10A018. [Google Scholar]
17. Peng C, Song Y, Deng J, Wu J, Chen H, Liu F. The influence of suspension and deposition on pool boiling heat transfer of nanofluids: experiment and engineering model study. Int J Heat Mass Transfer. 2024;227:125614. doi:10.1016/j.ijheatmasstransfer.2024.125614. [Google Scholar] [CrossRef]
18. Xiang L, Song Y, Yang D, Yang X, Vafai K. A comprehensive review of boiling heat transfer characteristics of wettability patterned surface. Exp Therm Fluid Sci. 2024;154:111145. doi:10.1016/j.expthermflusci.2024.111145. [Google Scholar] [CrossRef]
19. Može M, Zupančič M, Golobič I. Pattern geometry optimization on superbiphilic aluminum surfaces for enhanced pool boiling heat transfer. Int J Heat Mass Transfer. 2020;161:120265. doi:10.1016/j.ijheatmasstransfer.2020.120265. [Google Scholar] [CrossRef]
20. Fedoseev AV, Salnikov MV, Ostapchenko AE, Surtaev AS. Lattice Boltzmann simulation of optimal biphilic surface configuration to enhance boiling heat transfer. Energies. 2022;15(21):8204. doi:10.3390/en15218204. [Google Scholar] [CrossRef]
21. Kurul N, Podowski MZ. Multidimensional effects in forced convection subcooled boiling. In: International Heat Transfer Conference Digital Library, 1990; Jerusalem, Israel: Begel House Inc., V008T10A018 [Google Scholar]
22. Zupančič M, Gregorčič P, Bucci M, Wang C, Aguiar GM, Bucci M. The wall heat flux partitioning during the pool boiling of water on thin metallic foils. Appl Therm Eng. 2022;200(23):117638. doi:10.1016/j.applthermaleng.2021.117638. [Google Scholar] [CrossRef]
23. Pontes P, Cautela R, Teodori E, Moita AS, Moreira ALN. Experimental description of bubble dynamics and heat transfer processes occurring on the pool boiling of water on biphilic surfaces. Appl Therm Eng. 2020;178(17–18):115507. doi:10.1016/j.applthermaleng.2020.115507. [Google Scholar] [CrossRef]
24. Motezakker AR, Sadaghiani AK, Celik S, Larsen T, Villanueva LG, Koşar A. Optimum ratio of hydrophobic to hydrophilic areas of biphilic surfaces in thermal fluid systems involving boiling. Int J Heat Mass Transfer. 2019;135(2):164–74. doi:10.1016/j.ijheatmasstransfer.2019.01.139. [Google Scholar] [CrossRef]
25. Xiang L, Song Y, Yang D, Zhang Z, Yao S, Vafai K. Boiling mechanism of biphilic surfaces based on Helmholtz instability and Taylor instability. Int J Multiphase Flow. 2024;173(125):104735. doi:10.1016/j.ijmultiphaseflow.2024.104735. [Google Scholar] [CrossRef]
26. Betz AR, Jenkins J, Attinger D. Boiling heat transfer on superhydrophilic, superhydrophobic, and superbiphilic surfaces. Int J Heat Mass Transfer. 2013;57(2):733–41. doi:10.1016/j.ijheatmasstransfer.2012.10.080. [Google Scholar] [CrossRef]
27. Pereira J, Cautela R, Moita A, Moreira A. Effect of the size of the superhydrophobic regions of biphilic surfaces on the bubble dynamics. Symmetry. 2023;15(4):949. doi:10.3390/sym15040949. [Google Scholar] [CrossRef]
28. Lim DY, Bang IC. Controlled bubble departure diameter on biphilic surfaces for enhanced pool boiling heat transfer performance. Int J Heat Mass Transfer. 2020;150:119360. doi:10.1016/j.ijheatmasstransfer.2020.119360. [Google Scholar] [CrossRef]
29. Serdyukov V, Patrin G, Malakhov I, Surtaev A. Biphilic surface to improve and stabilize pool boiling in vacuum. Appl Therm Eng. 2022;209(2):118298. doi:10.1016/j.applthermaleng.2022.118298. [Google Scholar] [CrossRef]
30. Yamada M, Shen B, Imamura T, Hidaka S, Kohno M, Takahashi K, et al. Enhancement of boiling heat transfer under sub-atmospheric pressures using biphilic surfaces. Int J Heat Mass Transfer. 2017;115:753–62. doi:10.1016/j.ijheatmasstransfer.2017.08.078. [Google Scholar] [CrossRef]
31. Shen B, Yamada M, Mine T, Hidaka S, Kohno M, Takahashi K, et al. Depinning of bubble contact line on a biphilic surface in subatmospheric boiling: revisiting the theories of bubble departure. Int J Heat Mass Transfer. 2018;126:715–20. doi:10.1016/j.ijheatmasstransfer.2018.06.030. [Google Scholar] [CrossRef]
32. Shen B, Mine T, Iwata N, Hidaka S, Takahashi K, Takata Y. Deterioration of boiling heat transfer on biphilic surfaces under very low pressures. Exp Therm Fluid Sci. 2020;113:110026. doi:10.1016/j.expthermflusci.2019.110026. [Google Scholar] [CrossRef]
33. Shen B, Iwata N, Hidaka S, Takahashi K, Takata Y. Limited enhancement of subatmospheric boiling on treated structured surfaces with biphilic pattern. J Heat Transfer. 2021;143(10):101601. doi:10.1115/1.4051056. [Google Scholar] [CrossRef]
34. Kutateladze SS. Hydrodynamic model of heat transfer crisis in free-convection boiling. J Tech Phys. 1950;20(11):1389–92. [Google Scholar]
35. Zuber N. On the stability of boiling heat transfer. Trans Am Soc Mech Eng. 1958;80(3):711–14. doi:10.1115/1.4012484. [Google Scholar] [CrossRef]
36. Kutateladze SS, Gogonin II. Growth rate and detachment diameter of a vapor bubble in free convection boiling of a saturated liquid. Teplofizika Vysokikh Temperatur. 1979;17:792–7. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools