Numerical Study of the Free Convection of a Hybrid Nano-Fluid Filling a Three-Dimensional Cavity Exposed to a Horizontal Magnetic Field

Nomenclature

1  Introduction

The limitations of conventional fluids, such as oil, ethylene glycol, and water, have prompted researchers to explore nanofluids, a novel type of fluid introduced by Choi [1]. Nanofluids are suspensions of nanoparticles uniformly dispersed in a base fluid, offering significant enhancements in convective heat transfer [2] due to their improved thermal conductivity. These fluids have found applications in various heat removal systems, including heat exchangers, radars, electronic cooling, and sensors.

Extensive research has been conducted on the behavior of nanofluids. For example, Khanafer et al. [3] demonstrated that adding nanoparticles enhances heat transfer irrespective of the Grashof number. Similarly, Abu-Nada [4] found that increasing the volume fraction of nanoparticles significantly boosts heat transfer. Other studies have investigated nanofluids under various configurations and boundary conditions [5–9]. While considerable work has been done on two-dimensional natural convection, three-dimensional free convection in cavities filled with nanofluids remains less explored. Ravnik et al. [10] used the boundary element method to study free convection in a cavity filled with nanofluids. Selimefendigil et al. [11] analyzed the impact of cylinder angular velocity on the average Nusselt number in a cubic tube filled with nanofluid, finding that rotation direction affects the Nusselt number. In another study, they examined the effects of various parameters, including Richardson number and nanoparticle volume fraction, on heat transfer with carbon nanotube (CNT)-water nanofluids in a cubic enclosure [12]. Recent numerical simulations have focused on optimizing cavity design and nanoparticle dispersion to maximize heat transfer [13–15].

Atashafrooz [16] conducted a three-dimensional numerical study of nanofluid flow on an inclined step, concluding that temperature distributions are more sensitive to nanoparticle concentration than velocity distributions. An increase in nanoparticle percentage also led to higher friction coefficients, mean bulk temperatures, and Nusselt numbers. Sajjadi et al. [17] performed a three-dimensional mesoscopic simulation of natural magnetohydrodynamic (MHD) convection using the Boltzmann lattice method, showing that an increase in the Hartmann number decreases heat transfer due to reduced Nuavg. Zhou et al. [18] employed a similar Boltzmann method to study mixed convection of Al2O3-water nanofluids in a cubic domain with a magnetic field, finding that heat transfer improves at high Rayleigh numbers compared to low ones. Recent advancements in MHD simulations have explored the use of machine learning to predict heat transfer rates under varying magnetic field strengths [19,20].

Al-Sayegh [21] utilized the finite volume method to study free convection in an open trapezoidal enclosure filled with CNT-nanofluid, discovering that increased Hartmann numbers with high Rayleigh numbers reduce heat transfer, whereas higher nanoparticle volume fractions enhance heat transfer regardless of magnetic field inclination. Bouchta et al. [22] also used the finite volume method to investigate the effect of the Hartmann number on flow in a cube, finding that heat transfer deteriorates under the repulsive effect of the magnetic field. Al-Rashed et al. [23] further explored the impact of Rayleigh number, nanoparticle volume fraction, and Hartmann number, demonstrating improved heat transfer with higher nanoparticle percentages and Rayleigh numbers, though heat transfer decreased significantly with higher Hartmann numbers. Recent studies have focused on the interplay between magnetic field orientation and nanoparticle type in optimizing heat transfer [24,25].

Alongside the exploration of magnetic field effects on nanofluids, there has been growing interest in hybrid nanofluids. These fluids, which combine different types of nanoparticles, offer additional potential for enhancing heat transfer performance, especially in environments with complex conditions such as magnetic fields or unconventional cavity geometries.

Recently, hybrid nanofluids, which combine different types of nanoparticles, have gained attention for their potential to further enhance heat transfer performance. Experimental studies have investigated their rheological behavior and heat transfer characteristics [26–28]. Mehryan et al. [29] conducted a numerical study of hybrid nanofluid (Al2O3-Cu/Water) in a porous medium, finding that heat transfer is reduced compared to single nanofluids. Kalidasan et al. [30] simulated free convection in a square cavity with an adiabatic center element and heating elements on the side walls, concluding that the primary vortex strength decreases with increased hybrid nanoparticle volume fraction for all Rayleigh numbers. Recent research has also explored the synergistic effects of hybrid nanoparticle combinations in enhancing thermal conductivity and reducing viscosity [31–33]. Studies have further examined the natural convection of hybrid nanofluids in inclined enclosures with heat generation [34], the effects of nanoparticle shapes and arrangements in porous cavities [35], and the performance of hybrid nanofluids in microchannel heat sinks [36].

Recent advancements in fractional calculus have provided new perspectives in the study of nanofluid dynamics. Hejazi et al. [37] investigated the effects of velocity slip on mixed convection flow of a nanofluid over an inclined surface using fractional differential equations, contributing to a better understanding of thermal dynamics under varying conditions. Khan et al. [38] developed a fractional model to study the radiative thermal flow of a hybrid nanofluid with Jeffrey base material, incorporating copper aluminum oxide and titanium dioxide nanoparticles, and analyzed the effects of mixed convection, magnetic forces, slip conditions, and porous media on heat and mass transfer. Maatki et al. [39] performed a numerical analysis of entropy generation in a 3D differentially heated enclosure, providing insights into heat and mass transfer influenced by buoyancy ratios and Rayleigh numbers. Kolsi et al. [40] examined double diffusive natural convection in a square cavity filled with a porous medium and a power law fluid separated by a wavy interface, highlighting the role of the wavy interface in enhancing heat transfer. Mahmood et al. [41] analyzed mixed convective stagnation point flow of hybrid nanofluids over a sheet with variable thermal conductivity and slip conditions, demonstrating the significant impact of thermal conductivity models on heat transfer. Zafar et al. [42] studied the effects of thermal conductivity and nanoparticle volume fraction on mixed convective stagnation point flow over a permeable extending surface, showing notable discrepancies in the mean Nusselt values generated by various thermal conductivity models.

Recent work by Bayareh et al. [43] explored the magnetic field effect on heat transfer and entropy generation by convection of a nanofluid in a porous cavity, as well as the application of artificial intelligence to optimize these processes, taking into account the thermodynamic performance according to the second law. Mandal et al. [44] studied natural convection heat transfer with hybrid nanofluids in a porous thermal system under the influence of a magnetic field and multifrequency heating. It shows that multifrequency heating and corrugated walls enhance heat transfer in a porous system with nanofluids, while high Darcy and Hartmann numbers reduce convection. Ain et al. [45] used numerical simulations and a neural network-assisted (ANN) model to analyze heat transfer in a star-shaped cavity filled with hybrid nanoparticles under a magnetic field. Results show that nanoparticles enhance thermal transfer, while the magnetic field reduces fluid velocity. Rabby et al. [46] investigated heat transfer in saw-tooth corrugated pipes carrying a hybrid nanofluid (aluminum oxide and aluminum nitride suspended in water). Results show that corrugations significantly enhance heat transfer compared to straight pipes, with increased Reynolds number and nanoparticle concentration leading to higher thermal transfer. In another study, Chabani et al. [47] numerically analyzed the laminar flow of the Ag-Al2O3/H2O hybrid nanofluid and its effect on convective heat transfer in a modified trapezoidal porous enclosure. Results show that increasing Rayleigh and Darcy numbers improves heat transfer and the average Nusselt number, while reducing the Hartmann number is advantageous.

Additionally, recent studies have explored various aspects of nanofluids and hybrid nanofluids. Feng et al. [48] found that heat transfer in an eccentric tube increases with eccentric distance under laminar flow. Alami et al. [49] reviewed heat transfer enhancement in heat exchangers using nanofluids, noting discrepancies and calling for more research. Kalsi et al. [50] highlighted recent developments in nanofluids and their applications, emphasizing the benefits of hybrid nanofluids. Jiang et al. [51] showed that parameters like the Hartmann number significantly affect heat transfer in iron oxide/multi-walled carbon nanotube (Fe3O4/MWCNT)-water hybrid nanofluids under magnetic fields. Rashad et al. [52] found that increasing nanoparticle volume fraction enhances heat transfer in TiO2–Ag/water hybrid nanofluids, while higher Hartmann numbers reduce it.

The objective of this study is to explore the effect of magnetic fields on heat transfer and the dynamics of a hybrid nanofluid in a three-dimensional cavity, with the aim of optimizing its use in industrial environments with magnetic fields.

2  Mathematical Modelling

The physical model is shown in Fig. 1. It is a cube with side walls that are heated differently, while the other walls are considered adiabatic. A horizontal magnetic field is applied in front of the left wall of the cube. The cube is filled with water-based nanofluid and hybrid nanofluid, consisting of spherical nanoparticles with an average diameter between 20 and 50 nm, with a monodisperse distribution (a single particle size).

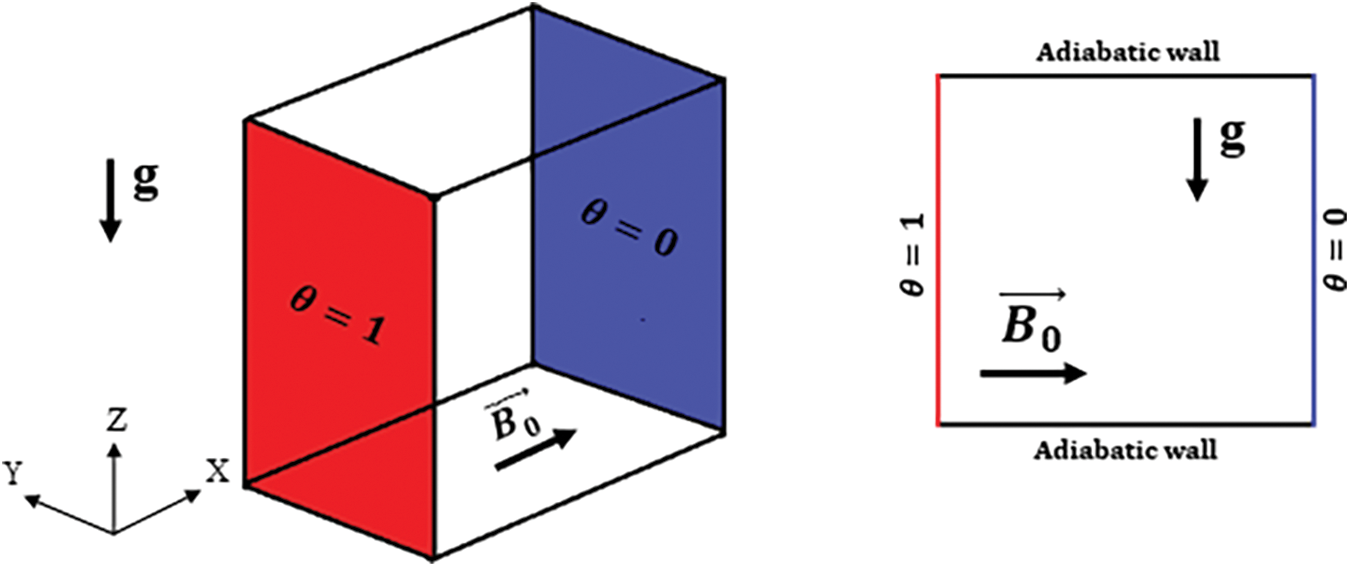
Figure 1: The geometry of the current problem

The flow is assumed to be Newtonian, incompressible, and laminar. This means that the fluid’s viscosity is constant, the density does not change with pressure, and there are no turbulences in the fluid, respectively. The base fluid (water) and the nanoparticles (Al2O3-Cu) are assumed to be in thermal equilibrium, indicating that the temperature is uniform between them with no significant internal temperature gradients. The thermal and physical properties of the nanomaterials and water (at 300K) are listed in Table 1. The different thermal and physical properties of the two fluids (nanofluid and hybrid nanofluid) are considered constant, except for the density, which varies based on the Boussinesq approximation, as described by Bejan [53]. This approximation accounts for buoyancy effects due to temperature variations, which is essential for accurately simulating natural convection movements.

The conservation equations namely those of continuity (1), the amount of motion in the x,y and z directions (2)–(4) and the energy (5) in the stationary state:

∂u∂x+∂v∂y+∂w∂z=0(1)

ρhnf(u∂u∂x+v∂u∂y+w∂u∂z)=−∂p∂x+μhnf∇2u(2)

ρhnf(u∂v∂x+v∂v∂y+w∂v∂z)=−∂p∂y+μhnf∇2v−σhnfB02v(3)

ρhnf(u∂w∂x+v∂w∂y+w∂w∂z)=−∂p∂Z+μhnf∇2w+g(ρβ)hnf(T−Tc)−σhnfB02w(4)

u∂T∂x+v∂T∂y+w∂T∂z=αhnf∇2T(5)

We nondimensionalize the equations by introducing dimensionless variables:

X=xH,Y=yH,Z=zH,U=uHαf,V=vHαf,W=wHαf,P=pH2ρhnfαf2,θ=T−TcTh−Tc(6)

Ra=gβf(Th−Tc)H3αfνf,Pr=νfαf,Ha=B0Lσhnfρhnf.νf(7)

Ultimately, we derive the following dimensionless equations:

∂U∂X+∂V∂Y+∂W∂Z=0(8)

U∂U∂X+V∂U∂Y+W∂U∂Z=−∂P∂X+μhnfρnfαf∇2U(9)

U∂V∂X+V∂V∂Y+W∂V∂Z=−∂P∂Y+μhnfρnfαf∇2V−Ha2PrV(10)

U∂W∂X+V∂W∂Y+W∂W∂Z=−∂P∂Z+μhnfρnfαf∇2W+(ρβ)hnfρhnfβfRaPrθ−Ha2PrW(11)

U∂θ∂X+V∂θ∂Y+W∂θ∂Z=αhnfαf∇2θ(12)

Table 2 groups together the set of thermal and physical properties of the hybrid nanofluid (water/Cu-Al2O3) and of the nanofluid (water/Al2O3).

3  Grid Dependency

The numerical simulation was tested to verify the sensitivity of the results to the mesh with the parameters Pr=6.8, Ra=105, φ=0.05, and Ha=30. As shown in Fig. 2, a 3D mesh of 61×61×61 was used for this analysis. The results presented in Table 3 indicate that the numerical solution is only slightly affected by the chosen mesh size, demonstrating the stability and accuracy of the simulation under these specific conditions. The visualization of the 3D mesh helps to better understand the mesh density and its ability to capture the details of the flow, ensuring a reliable modeling of the studied system.

Figure 2: 3D mesh grid used for numerical simulation with 61 × 61 × 61 elements

4  Numerical Method

We use the finite volume method to discretize the equations of the mathematical model. The obtained equations are solved by the usual iterative method, Tri-Diagonal Matrix Algorithm (TDMA) [56]. The iterative process takes into account the pressure correction by implementing the SIMPLEC algorithm [57], and reaches convergence when the variation of the dependent variables (U,V,W,P or θ) is no longer significant. A test for stopping the iterative process at convergence is established at each stretch according to the following criterion:

∑i,j,k=1imax,jmax,kmax|∅i,j,kn+1−∅i,j,kn||∅i,j,kn|≤10−5(18)

where ∅ is one of the field variables (U,V,W,T,P) and i,j and k are the grid positions. n represents the time step number.

A numerical code is developed in FORTRAN to implement this algorithm, as shown in Fig. 3, which follows several steps to ensure the accuracy and stability of the solution.

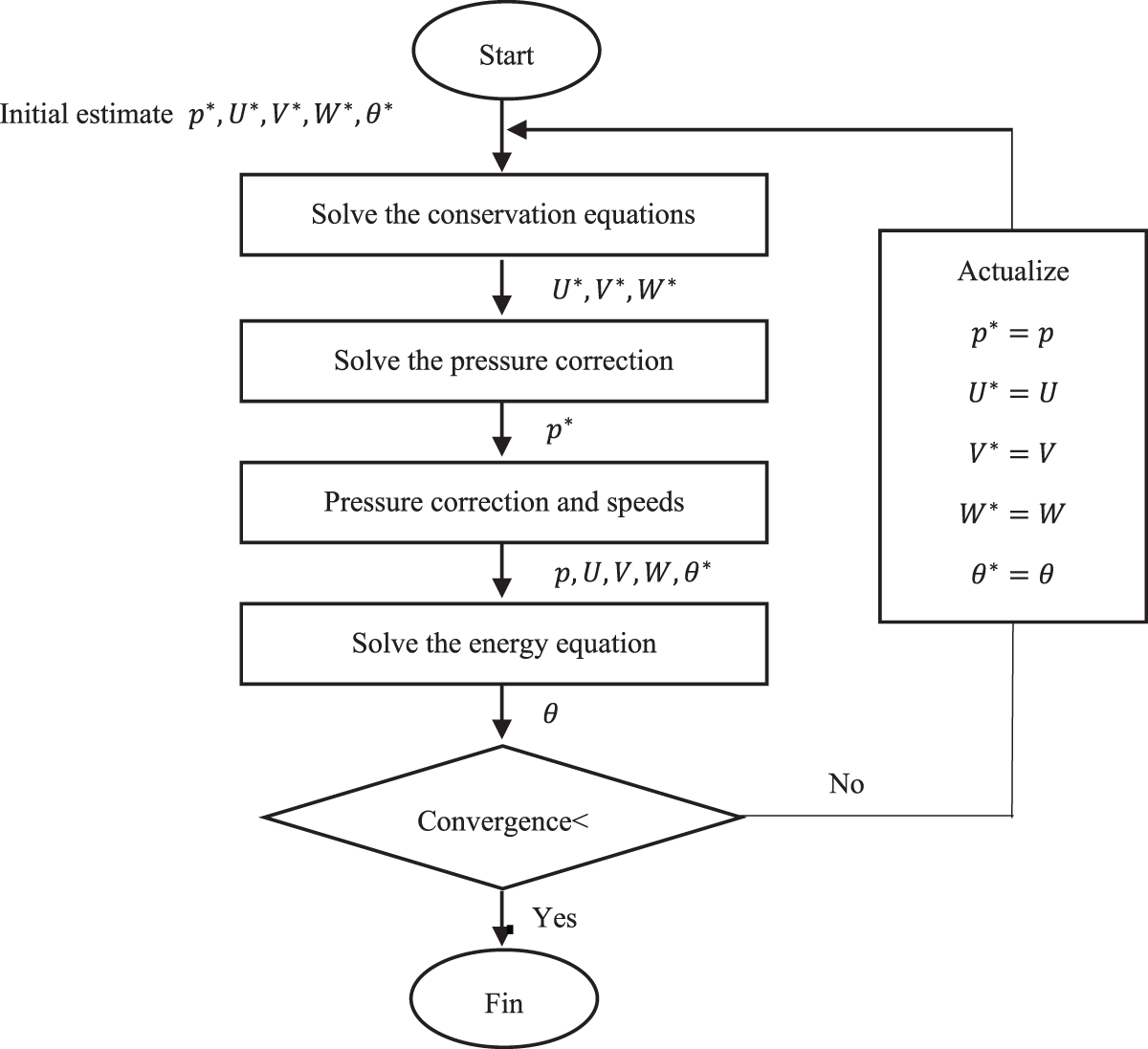
Figure 3: Sequence of steps in the SIMPLEC flowchart

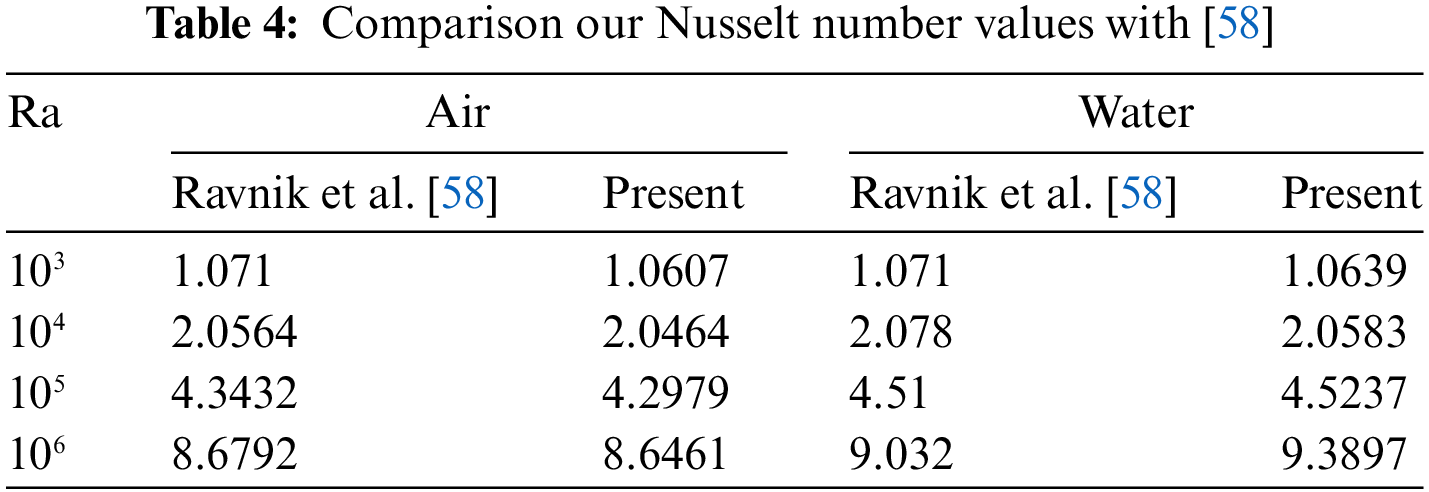
This process is repeated until the convergence criteria are met, ensuring the accuracy of the final results. To verify our numerical program, the results obtained are compared to the results available in the literature. The first comparison involves a three-dimensional numerical simulation of free convection of air and water (Pr=0.71) at Rayleigh numbers ranging from 103 to 106. Table 4 shows the comparisons between our results and those in the literature. After reviewing them, we find that our numerical results are in complete agreement with those in the Reference [58].

The second test is heat transfer in a cubic enclosure containing the nanofluid Cu−water. The results obtained are confronted with the results of Ravnik et al. [58]. Fig. 4 illustrates the variations of the mean Nusselt number found in this simulation, and that of Ravnik et al. [58]. As can be seen in Fig. 2, there is a very good concordance of the two results.

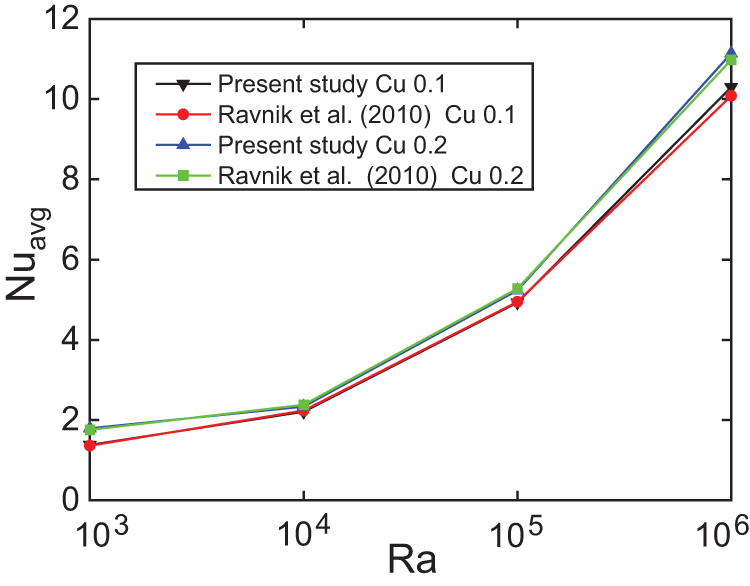
Figure 4: Comparison with the results of Ravnik et al. [58] for water/TiO2 nanofluid

The curve of nondimensional vertical velocity W and nondimensional temperature θ for natural convection of a nanofluid (water-Cu) in a cubic cavity (Ra=10,104,106) is presented in Fig. 5 and compared with the results of Ternik [59]. It is visible that the present simulations are also in agreement, the difference being about 1.82%.

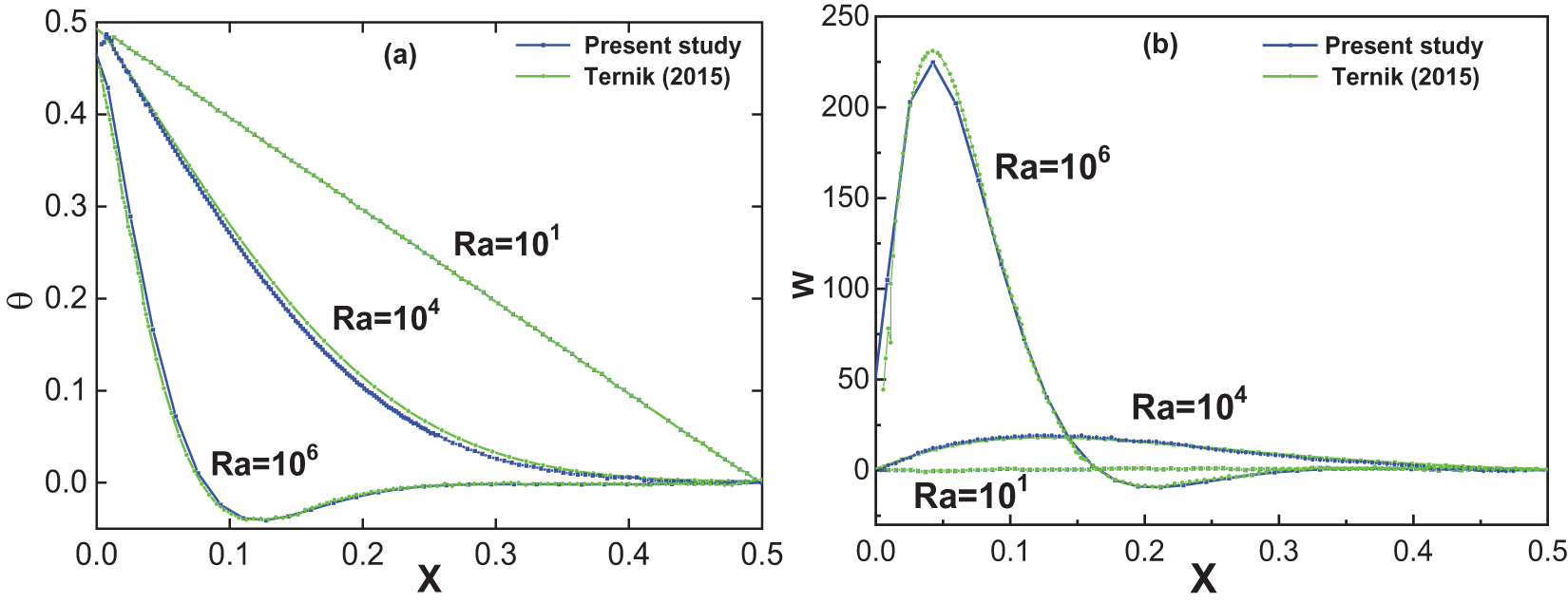
Figure 5: (a) Variation of dimensionless temperature θ, (b) Dimensionless vertical velocity W for Y=Z=0.5

According to these successful comparisons, the present numerical code is considered to be suitable for the present investigation.

5  Results and Discussion

For this study, simulation results are obtained for the case of a pure fluid, nanofluid, and hybrid nanofluid. In order to identify all the impacts of the magnetic field on heat transfer and thermal and dynamic fields, we examine the effects of Ra, Ha and φ of nanoparticles. The results are analysed, through the hydrodynamic and thermal fields, of variations in the average and local Nusselt number and velocity profiles.

Fig. 6 shows the three-dimensional temperature distribution in the cube for three Hartmann numbers: 0,30, and 70. The fluid moves from the hot wall to the cold wall, ensuring that the heat transfer rate is consistently maintained within the cube. As the Hartmann number increases, the flow of the nanofluid is significantly affected. Specifically, at higher Hartmann numbers, the magnetic field exerts a force opposing the fluid movement, which reduces the flow velocity and alters the temperature distribution. This change in nanofluid flow becomes particularly noticeable as the Hartmann number increases from 0 to 70, highlighting the substantial impact of the magnetic field on heat transfer within the system.

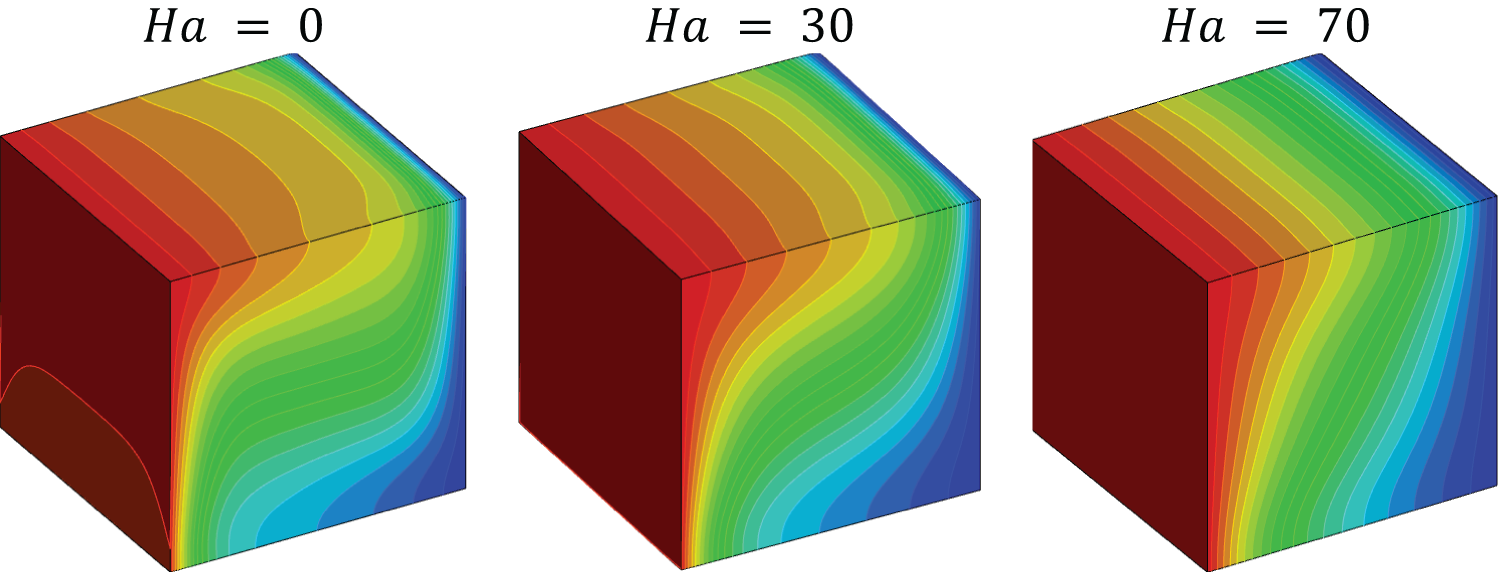
Figure 6: Isotherms in 3D with Ra=105 for Al2O3-Cu/Water (φ=0.05)

Fig. 7 shows the effect of the magnetic field on streamlines and isotherms for a Rayleigh number Ra=105, with three Hartmann numbers (0,30, and 70). These isotherms and streamlines are presented for the case of the hybrid nanofluid (Al2O3-Cu/Water) with a volume fraction φ=0.05.

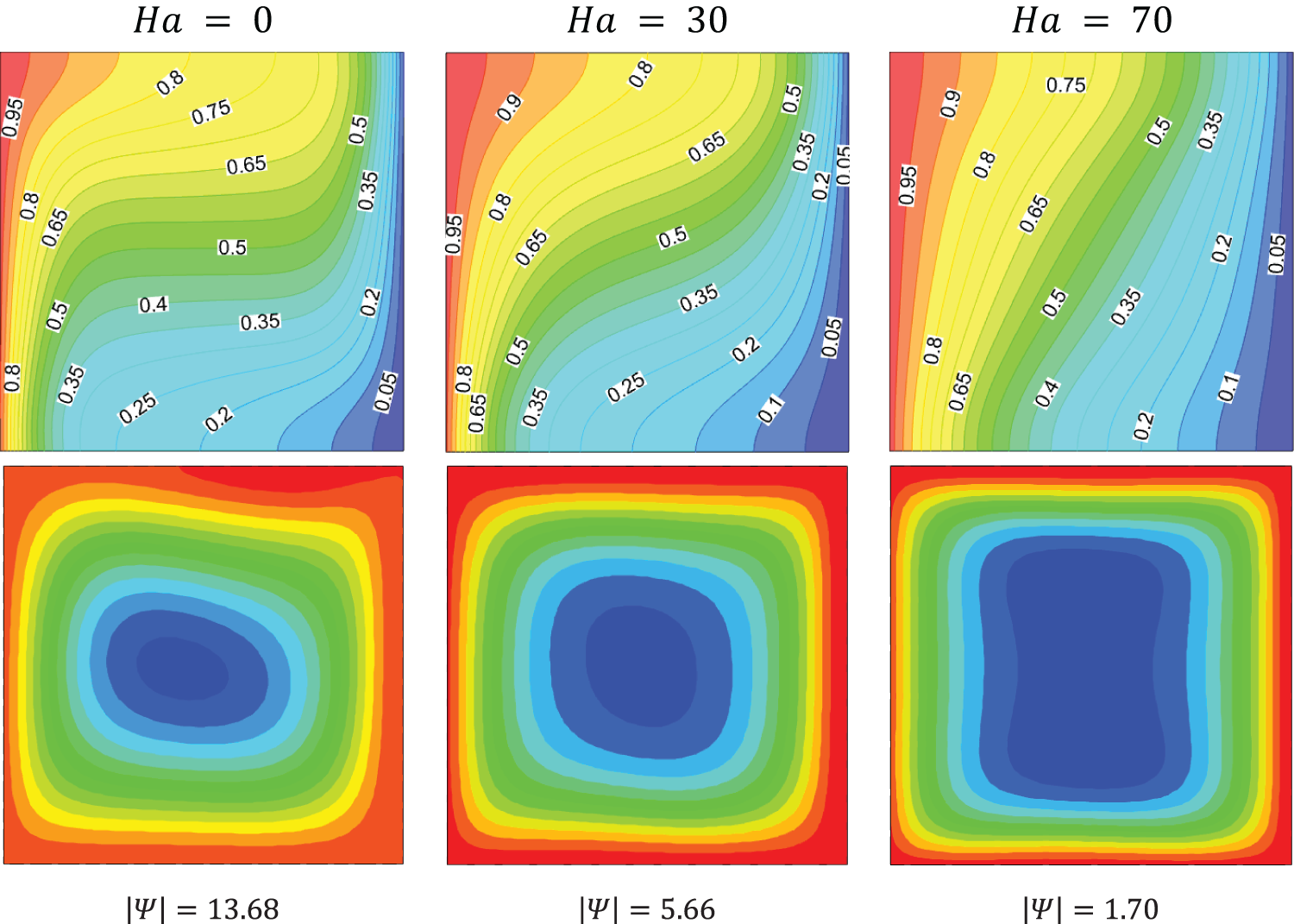
Figure 7: Isotherms and streamlines for different Hartmann numbers, Ra=105 for hybrid Nanofluid Al2O3-Cu/Water (φ=0.05)

In the absence of a magnetic field (Ha=0), the isotherms are horizontally stratified in the middle of the cube and are concentrated near the side walls. This configuration indicates that heat transfer primarily occurs in the vertical direction, with a significant temperature gradient near the walls. The streamlines show relatively uniform circulation throughout the volume, with recirculation cells forming due to the temperature gradients.

As the magnetic field intensity increases (Ha=30 and Ha=70), significant changes are observed in the structure of the isotherms and streamlines. The initially horizontal isotherms tend to become more vertical. This phenomenon is attributed to the Lorentz force, which is perpendicular to both the magnetic field and the fluid flow direction. This force acts as a resistance, decreasing the flow velocity and altering the temperature distribution.

With higher Hartmann numbers, the Lorentz force becomes more pronounced, reducing the fluid’s flow rate and modifying the internal circulation. Specifically, at Ha=30 and Ha=70, the recirculation cell that was circular at Ha=0 rotates clockwise. At Ha=70, this cell becomes almost vertical. This change is a result of the decreased flow rate due to the opposing Lorentz force, which acts against the natural fluid movement.

The reduced fluid circulation due to the magnetic field effect also leads to a decrease in heat transfer. The isotherms become less horizontal and more vertical, indicating less effective convection. The magnetic field exerts a force that constrains the fluid movement, thereby altering the temperature distribution and reducing the overall thermal transfer within the system.

Fig. 8 shows the velocity profiles V at Y=Z=0.5, with a volume fraction φ of 5% and a Rayleigh number Ra=105, for three Hartmann numbers: 0, 30, and 70.

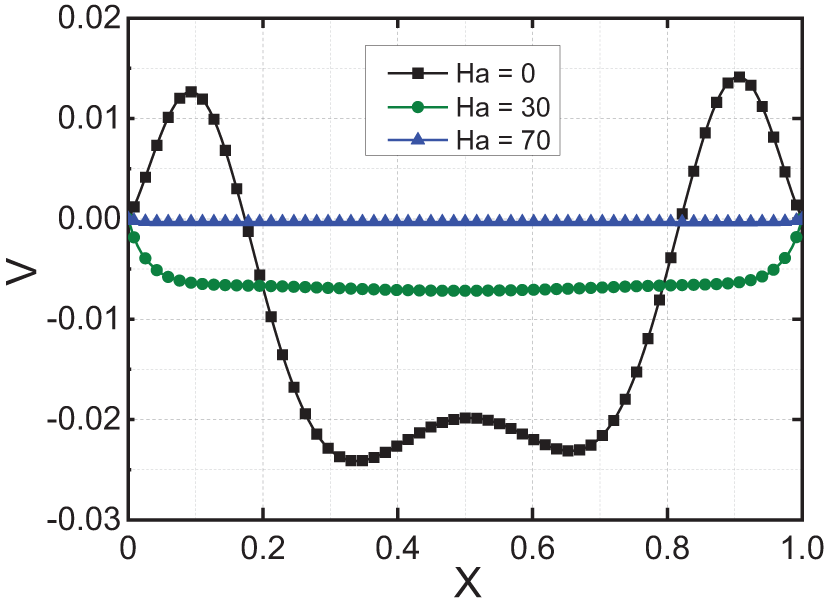
Figure 8: Velocity profiles V=f(X) for different Hartmann numbers Ha; Y=Z=0.5; φ=0.05; Ra=105

Without a magnetic field (Ha=0), the velocity profile displays a typical natural convection pattern. Higher velocities are observed near the heated walls due to buoyancy forces caused by temperature gradients. This creates well-defined convection cells where the hot fluid rises along the walls and sinks in the center, promoting effective thermal mixing within the cavity.

At a moderate Hartmann number (Ha=30), the introduction of a magnetic field starts to influence the fluid flow. The Lorentz force, which acts perpendicular to both the magnetic field and the fluid flow, begins to resist the circulation. This results in a reduction of the convective velocities near the heated walls and a general decrease in the overall circulatory motion of the fluid. While convection cells are still present, they are less pronounced compared to the case without a magnetic field.

At a high Hartmann number (Ha=70), the impact of the magnetic field becomes dominant. The velocity profile flattens out and approaches near-zero values throughout the cavity, indicating that fluid motion is almost entirely suppressed by the Lorentz force. The significant decrease in fluid velocity suggests that natural convection is greatly hindered, limiting thermal mixing and leading to a more uniform but less efficient heat transfer distribution.

Fig. 9 illustrates the effect of the Rayleigh number on the velocity profile for a fixed Hartmann number, Ha=30. As the Rayleigh number (Ra) increases, the velocity within the fluid also increases. This is due to the enhanced inertial forces of the fluid, which amplify convective movements. A higher Rayleigh number corresponds to a larger temperature gradient between the heated and cooled regions, which generates stronger buoyancy forces. These forces drive more intense convective flows, resulting in increased fluid motion.

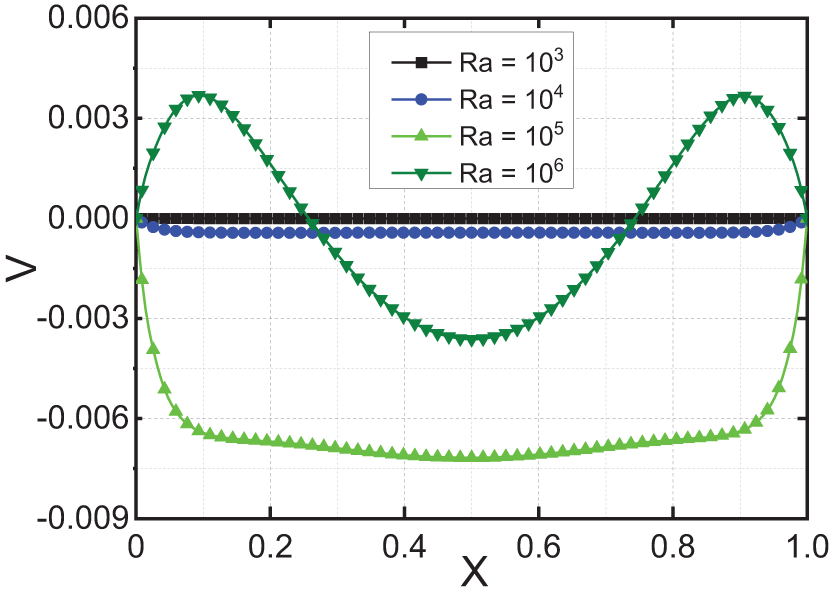
Figure 9: Velocity profiles V=f(X) for different Ra; Y=Z=0.5; φ=0.05; Ha=30

For Ra=106, positive velocities are observed in the regions 0<X<0.25 and 0.70<X<1. These positive velocities are indicative of ascending currents created by the presence of recirculation cells within the fluid. In these regions, the fluid near the heated walls warms up, decreases in density, and rises towards the cooler areas, forming upward currents.

As the Rayleigh number increases, these natural convection currents become more pronounced, leading to higher velocities in the regions where the warm fluid rises, and the cooler fluid descends. This increase in convection enhances thermal mixing within the cavity, resulting in more substantial fluid motion and higher velocity profiles in these areas. Consequently, the overall heat transfer efficiency within the cube is improved due to the intensified circulation and mixing of the fluid.

Fig. 10 shows the temperature isosurfaces for different Hartmann numbers (Ha=0,30, and 70). In the absence of a magnetic field (Ha=0), the isotherms are horizontally stratified within the enclosure. This horizontal stratification indicates that heat transfer is primarily governed by natural convection, with the temperature distribution reflecting the thermal gradients created by the heated and cooled walls.

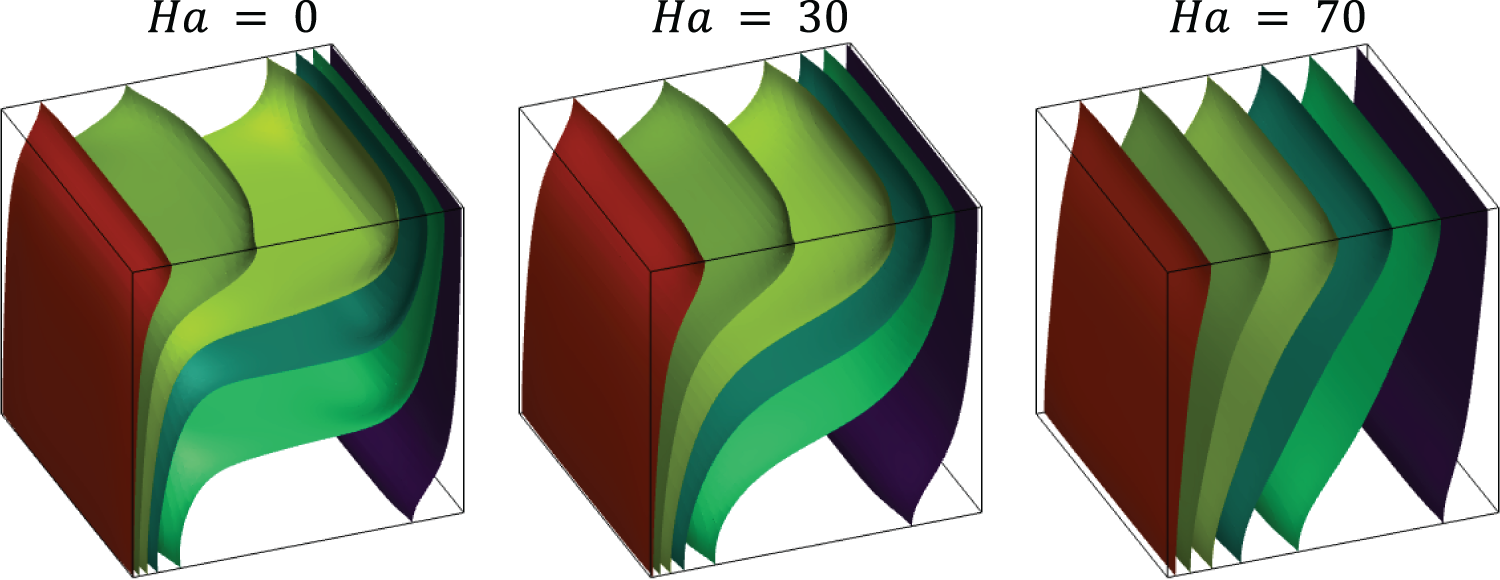
Figure 10: Isosurfaces of temperature for nanofluid hybrid (φ=0.05) at Ra=105

As the Hartmann number increases, this horizontal stratification becomes more vertically aligned. At higher Hartmann numbers (Ha=30 and Ha=70), the increasing strength of the magnetic field restricts convective motion, causing the temperature distribution to resemble that of pure conduction. The magnetic field exerts a force that opposes fluid movement, leading to a more uniform temperature distribution across the enclosure. This uniformity is characteristic of a conduction-dominated regime, where heat spreads more evenly in the absence of significant convective currents.

Fig. 11 illustrates the influence of the Hartmann number on the average Nusselt number Nuavg at different Rayleigh numbers (Ra=103,104,105, and 106) for the three fluids: pure water, nanofluid (water/Al2O3,φ=5%), and hybrid nanofluid (water/Al2O3-Cu,φ=5%). At Ra=103, where heat transfer is predominantly conduction-dominated, the magnetic field has only a minor effect on improving heat transfer. This is because, at low Rayleigh numbers, conduction dominates and the influence of convection, altered by the magnetic field, is minimal. A slight increase in Nuavg with increasing Ha is observed, with the hybrid nanofluid showing a more pronounced effect, likely due to its superior thermal properties compared to the other fluids.

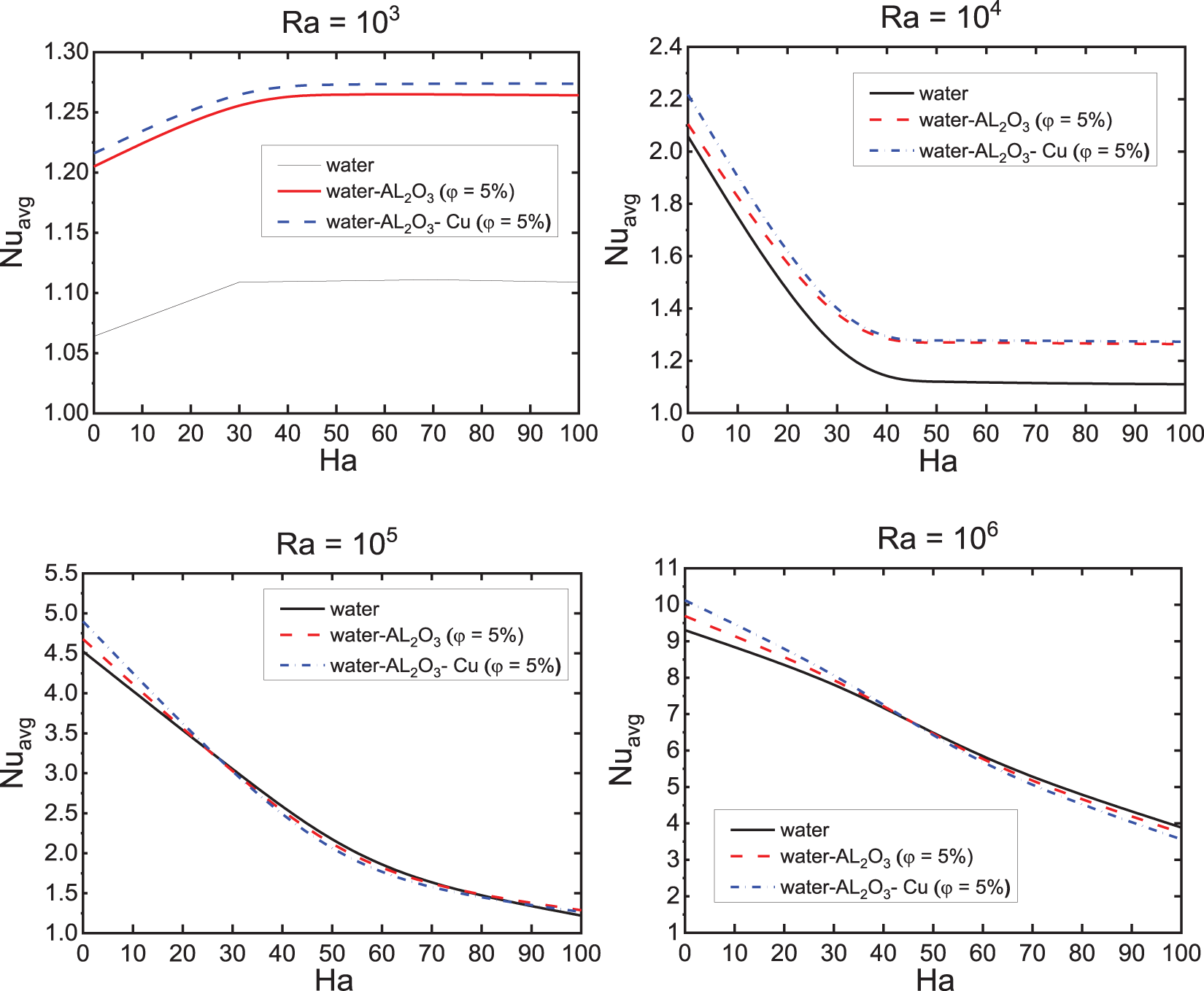
Figure 11: Evolution of Nuavg according to Ha for different Ra, in the case of nanofluid, hybrid nanofluid, and pure water

For Ra=104, during the transitional phase between conduction and convection, the magnetic field begins to negatively impact heat transfer. This is attributed to the interaction between the magnetic field and the fluid, where Lorentz forces oppose the fluid motion, reducing circulation and mixing. This effect is evident in the decrease in Nuavg with increasing Ha. Note that for Ra=103 and 104, Nuavg stabilizes beyond Ha=40, suggesting that the impact of the magnetic field reaches a saturation point at certain Ha values.

At higher Rayleigh numbers, where natural convection dominates, the magnetic field continues to exert a negative influence on heat transfer. As Ha increases, Lorentz forces oppose the fluid flow more strongly, decreasing the effectiveness of thermal transfer. This results in a reduction in Nuavg with increasing Ha, indicating that the magnetic field impedes convective heat transfer by diminishing the fluid’s kinetic energy.

In the absence of a magnetic field (Ha=0), the hybrid nanofluid promotes heat transfer more effectively than pure water and the nanofluid, thanks to the enhanced thermal conductivity of the nanoparticles. However, in the presence of a magnetic field, starting from a certain Ha value, such as for Ra=106 and Ha>40, water and nanofluids exhibit a slight advantage over hybrid nanofluids. This can be explained by the complex interactions induced by the magnetic field on hybrid nanofluids, which may not promote heat transfer as effectively as simpler fluids. Thus, across the range of Ra considered in this study, Ra=106 provides the highest values for the average Nusselt number, emphasizing the importance of high Rayleigh numbers for optimizing heat transfer in the presence of nanofluids.

Fig. 12 illustrates the influence of the nanoparticle percentage on heat transfer. At Ha=0, heat transfer increases with the percentage of nanoparticles for all Rayleigh numbers. This enhancement is due to the improved thermal conductivity of the fluid resulting from the presence of nanoparticles. Nanoparticles enhance the fluid’s ability to conduct heat, leading to higher Nusselt numbers and therefore better heat transfer.

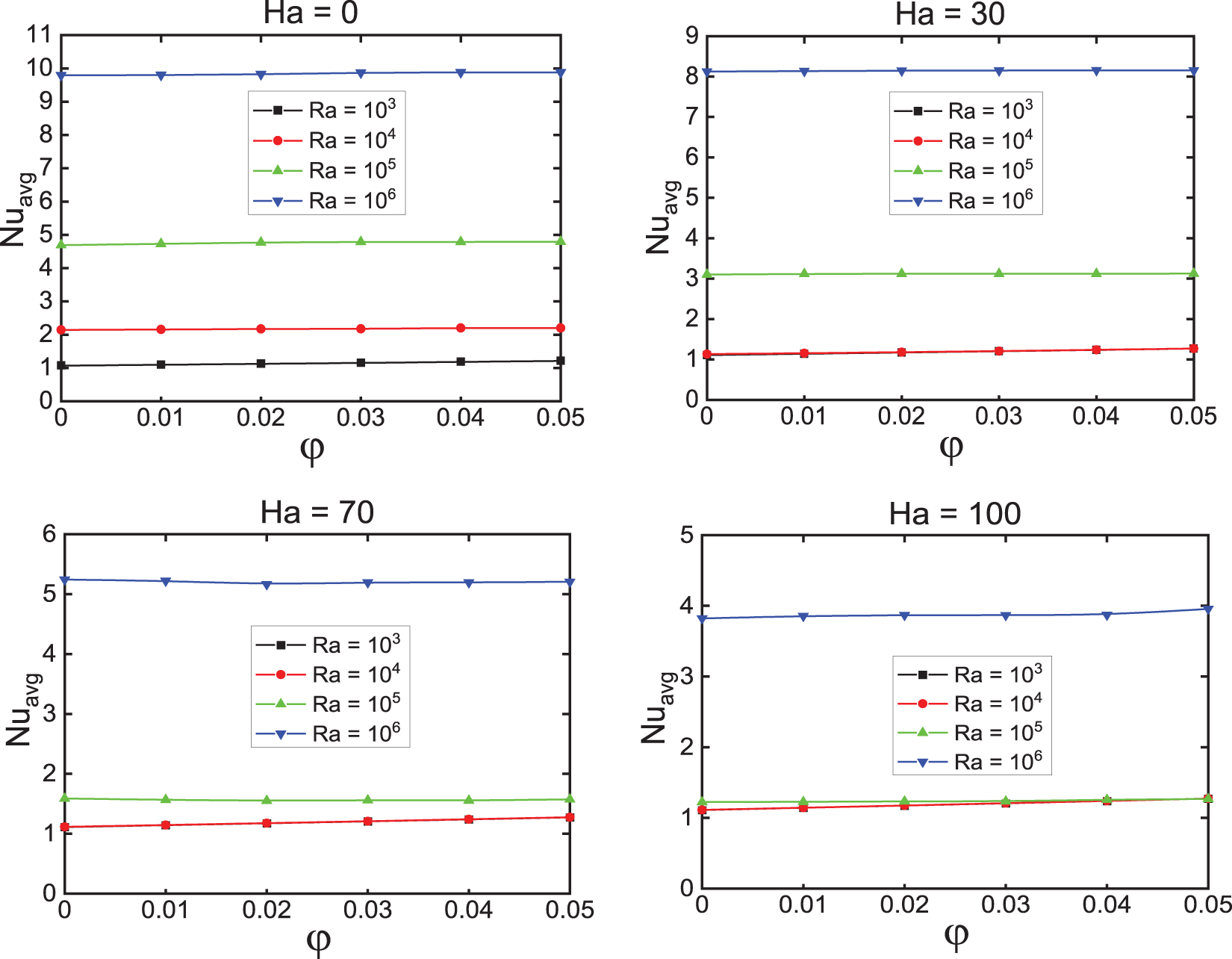
Figure 12: Evolution of Nuavg as a function of φ for different Ra, in the case of hybrid nanofluid (water/Al2O3-Cu)

However, for Ha=70 and 100, the negative effect of the magnetic field becomes evident, particularly at Ra=106. Despite the increase in the percentage of nanoparticles, the average Nusselt number decreases. This phenomenon can be attributed to the complex interaction between nanoparticles and the magnetic field. The Lorentz forces generated by the magnetic field oppose the fluid motion, reducing circulation and mixing within the fluid. While nanoparticles enhance thermal conductivity, their effect is overshadowed by the magnetic field’s impact, which inhibits natural convection. Consequently, the magnetic field diminishes the overall heat transfer efficiency, even with higher concentrations of nanoparticles.

To quantify the heat exchange within the cavity, Fig. 13 illustrates the variation of the local Nusselt number along the Z-axis (at X=0 and Y=0.5) for different Hartmann numbers (Ha). The results show that in the absence of a magnetic field (Ha=0), the heat transfer is most effective. In this scenario, natural convective movements are maximized, allowing for efficient fluid circulation and better thermal mixing, which enhances heat transfer. However, the introduction of a magnetic field significantly alters the flow structure. For Hartmann numbers of 30 and 70, the Lorentz force generated by the magnetic field opposes the direction of fluid flow, drastically reducing fluid movement and circulation. This resistance suppresses natural convection, thereby decreasing the effectiveness of heat transfer. The reduced fluid motion results in flatter isotherms, indicating a more uniform but less effective distribution of heat.

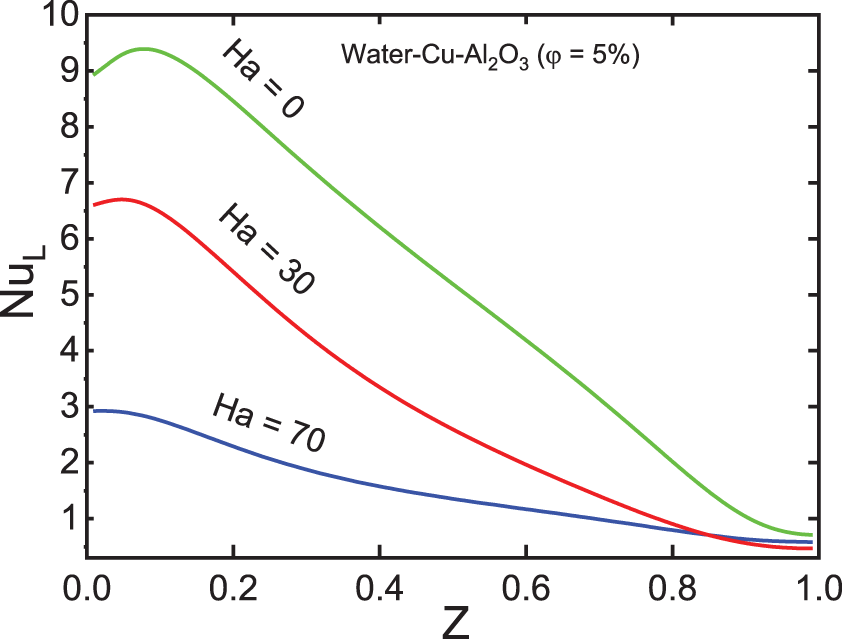
Figure 13: Local Nusselt number along Z (X = 0 and Y = 0.5) for different values of Ha

These observations demonstrate that the influence of the magnetic field becomes more pronounced as the Hartmann number increases, ultimately reducing the overall heat transfer efficiency.

6  Conclusion

The numerical method developed in this study has proven effective in accurately simulating the effect of a magnetic field on a hybrid nanofluid. Several key parameters, such as the Rayleigh number, Hartmann number, and nanoparticle volume fraction, were analyzed to assess their impact on the dynamic and thermal fields as well as heat transfer. The main findings are as follows:

Heat transfer enhancement: Heat transfer improves with an increase in the Rayleigh number due to the intensification of convective effects, which promotes better fluid circulation and more efficient thermal dissipation.

Performance of the hybrid nanofluid: At low Hartmann numbers, the hybrid nanofluid outperforms both the simple nanofluid and pure water due to its superior thermal conductivity. However, at higher Hartmann numbers, the heat transfer efficiency of the hybrid nanofluid decreases because the magnetic field inhibits fluid motion.

Impact of the magnetic field: The negative effect of the magnetic field on heat transfer becomes particularly pronounced at high Rayleigh numbers (Ra=106). The magnetic field impedes natural convection by generating Lorentz forces that oppose fluid movement, thereby reducing thermal transfer.

Reduction in heat transfer: Heat transfer is reduced by approximately 50% when the Hartmann number increases from 0 to 70, due to the magnetic field’s inhibitory effect on convective movements.

Effect of nanoparticle volume fraction: Increasing the nanoparticle volume fraction does not enhance heat transfer at high Hartmann numbers (70 and 100). At these levels, the adverse effects of the magnetic field outweigh the benefits of increased thermal conductivity.

These findings have significant implications for the development of new thermal technologies, highlighting the need to reconsider materials or configurations to maximize efficiency in environments where magnetic fields are present.

For future research, it would be beneficial to experimentally validate numerical results and investigate the effects of magnetic field orientations and intensities on heat transfer. Incorporating chemical interactions such as pH, zeta potential, and redox potential could enhance the understanding of nanoparticle dispersion. Models that consider variable thermophysical properties could also improve simulation accuracy.

Acknowledgement: The authors would like to thank the GEMS Laboratory, ENSA, Ibn Zohr University, Agadir, for providing the computing resources.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Mouna Benshab, Said Bouchta; data collection: Mouna Benshab, M’barek Feddaoui; analysis and interpretation of results: Said Bouchta, Aberrahman Nait Alla, Abdellatif Dayf; draft manuscript preparation: Said Bouchta, Jaouad Bouchta. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. Dev Appl Non Newtonian Flows. 1995;66:99–106. [Google Scholar]

2. Yang Y, Zhang ZG, Grulke EA, Anderson WB, Wu G. Heat transfer properties of nanoparticle-in-fluid dispersions (nanofluids) in laminar flow. Int J Heat Mass Transfer. 2005;48(6):1107–16. doi:10.1016/j.ijheatmasstransfer.2004.09.038. [Google Scholar] [CrossRef]

3. Khanafer K, Vafai K, Lightstone M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int J Heat Mass Transfer. 2003;46(19):3639–53. doi:10.1016/S0017-9310(03)00156-X. [Google Scholar] [CrossRef]

4. Abu-Nada E. Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step. Int J Heat Fluid Flow. 2008;29(1):242–9. doi:10.1016/j.ijheatfluidflow.2007.07.001. [Google Scholar] [CrossRef]

5. Ben Cheikh N, Ben Beya B, Lili T. Aspect ratio effect on natural convection flow in a cavity submitted to a periodical temperature boundary. J Heat Transfer. 2007;129(8):1060–8. doi:10.1115/1.2728908. [Google Scholar] [CrossRef]

6. Charafi MM, Bendaraa A, Hasnaoui A. Numerical modelling of natural convection in a square cavity: effect of nanofluid volume fraction and inclination. MATEC Web Conf. 2018;241(4):01006. doi:10.1051/matecconf/201824101006. [Google Scholar] [CrossRef]

7. Mohebbi R, Izadi M, Chamkha AJ. Heat source location and natural convection in a C-shaped enclosure saturated by a nanofluid. Phys Fluids. 2017;29(12):122009. doi:10.1063/1.4993866. [Google Scholar] [CrossRef]

8. Sheremet MA, Pop I, Mahian O. Natural convection in an inclined cavity with time-periodic temperature boundary conditions using nanofluids: application in solar collectors. Int J Heat Mass Transfer. 2018;116:751–61. doi:10.1016/j.ijheatmasstransfer.2017.09.070. [Google Scholar] [CrossRef]

9. Boualit A, Zeraibi N, Chergui T, Lebbi M, Boutina L, Laouar S. Natural convection investigation in square cavity filled with nanofluid using dispersion model. Int J Hydrogen Energy. 2017;42(13):8611–23. doi:10.1016/j.ijhydene.2016.07.132. [Google Scholar] [CrossRef]

10. Ravnik J, Skerget L. Simulation of flow of nanofluids by BEM. In: WIT transactions on modelling and simulation. UK: WIT Press. 2010;50(12):3–14. doi:10.2495/BE100011. [Google Scholar] [CrossRef]

11. Selimefendigil F, Oztop HF. Mixed convection of nanofluids in a three-dimensional cavity with two adiabatic inner rotating cylinders. Int J Heat Mass Transfer. 2018;117:331–43. doi:10.1016/j.ijheatmasstransfer.2017.09.116. [Google Scholar] [CrossRef]

12. Selimefendigil F, Oztop HF. Conjugate mixed convection of nanofluid in a cubic enclosure separated with a conductive plate and having an inner rotating cylinder. Int J Heat Mass Transfer. 2019;139:1000–17. doi:10.1016/j.ijheatmasstransfer.2019.05.053. [Google Scholar] [CrossRef]

13. Syam Sundar L, Naik MT, Sharma KV, Singh MK, Siva Reddy TC. Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4 magnetic nanofluid. Exp Therm Fluid Sci. 2012;37(4):65–71. doi:10.1016/j.expthermflusci.2011.10.004. [Google Scholar] [CrossRef]

14. Giwa SO, Sharifpur M, Ahmadi MH, Meyer JP. A review of magnetic field influence on natural convection heat transfer performance of nanofluids in square cavities. J Therm Anal Calorim. 2021;145(5):2581–623. doi:10.1007/s10973-020-09832-3. [Google Scholar] [CrossRef]

15. Dey D, Sekhar SD. Experimental study in a natural convection cavity using nanofluids. Mat Today: Proc. 2021;41(11):403–12. doi:10.1016/j.matpr.2020.09.631. [Google Scholar] [CrossRef]

16. Atashafrooz M. Effects of Ag-water nanofluid on hydrodynamics and thermal behaviors of three-dimensional separated step flow. Alex Eng J. 2018;57(4):4277–85. doi:10.1016/j.aej.2017.07.016. [Google Scholar] [CrossRef]

17. Sajjadi H, Delouei AA, Sheikholeslami M, Atashafrooz M, Succi S. Simulation of three-dimensional MHD natural convection using double MRT lattice Boltzmann method. Phys A Stat Mech Appl. 2019;515(6):474–96. doi:10.1016/j.physa.2018.09.164. [Google Scholar] [CrossRef]

18. Zhou W, Yan Y, Xie Y, Liu B. Three-dimensional lattice Boltzmann simulation for mixed convection of nanofluids in the presence of magnetic field. Int Commun Heat Mass Transfer. 2017;80(1):1–9. doi:10.1016/j.icheatmasstransfer.2016.11.012. [Google Scholar] [CrossRef]

19. Ahmad S, Cham BM, Liu D, Islam SU, Hussien MA, Waqas H. Numerical analysis of heat and mass transfer of MHD natural convection flow in a cavity with effects of source and sink. Case Stud Therm Eng. 2024;53:103926. doi:10.1016/j.csite.2023.103926. [Google Scholar] [CrossRef]

20. Mohapatra R, Panda S, Mishra SR. Exploring heat transfer enhancement: machine learning predictions using artificial neural network for water-based Cu and CuO micropolar nanofluid transportation over a radiating surface. BioNanoSci. 2024;14(2):842–56. doi:10.1007/s12668-024-01392-2. [Google Scholar] [CrossRef]

21. Al-Sayegh R. Influence of external magnetic field inclination on three-dimensional buoyancy-driven convection in an open trapezoidal cavity filled with CNT-water nanofluid. Int J Mech Sci. 2018;148(6):756–65. doi:10.1016/j.ijmecsci.2018.09.032. [Google Scholar] [CrossRef]

22. Bouchta S, Feddaoui M. Numerical simulation of free convection in a three-dimensional enclosure full of nanofluid with the existence a magnetic field. Eur J Electr Eng. 2020;22(6):405–11. doi:10.18280/ejee.220602. [Google Scholar] [CrossRef]

23. Al-Rashed AAAA, Kalidasan K, Kolsi L, Aydi A, Malekshah EH, Hussein AK, et al. Three-dimensional investigation of the effects of external magnetic field inclination on laminar natural convection heat transfer in CNT-water nanofluid filled cavity. J Mol Liq. 2018;252(1):454–68. doi:10.1016/j.molliq.2018.01.006. [Google Scholar] [CrossRef]

24. Liao CC, Li WK. Effect of different magnetic field angles on the relationship between nanofluid concentration and heat transfer. Int C Heat Mass Transfer. 2022;135(1):106137. doi:10.1016/j.icheatmasstransfer.2022.106137. [Google Scholar] [CrossRef]

25. Selim MM, El-Safty S, Tounsi A, Shenashen M. Review of the impact of the external magnetic field on the characteristics of magnetic nanofluids. Alex Eng J. 2023;76(2):75–89. doi:10.1016/j.aej.2023.06.018. [Google Scholar] [CrossRef]

26. Hemmat ME, Afrand M, Yan Y, Yarmand H, Toghraie D, Mehidzale M. Effect of temperature and concentration on rheological behavior of MWC-NTs/SiO2(20–80)-SAE40 hybrid nano-lubricants. Int C Heat Mass Transfer. 2016;76(2):133–8. doi:10.1016/j.icheatmasstransfer.2016.05.015. [Google Scholar] [CrossRef]

27. Hemmat ME, Saelak MR. Experimental investigation of switchable behavior of CuO-MWCNT (85%–15%)/10W-40 hybrid nano-lubricants for applications in internal combustion engines. J Mol Liq. 2017;242(4):326–35. doi:10.1016/j.molliq.2017.06.075. [Google Scholar] [CrossRef]

28. Aparna Z, Monisha M, Pabi SK, Ghosh S. Thermal conductivity of aqueous Al2O3/Ag hybrid nanofluid at different temperatures and volume concentrations: an experimental investigation and development of new correlation function. Powder Technol. 2019;343:714–22. doi:10.1016/j.powtec.2018.11.096. [Google Scholar] [CrossRef]

29. Mehryan SAM, Kashkooli FM, Ghalambaz M, Chamaka AJ. Free convection of hybrid Al2O3-Cu water nanofluid in differentially heated porous cavity. Adv Powder Technol. 2017;28(9):2295–305. doi:10.1016/j.apt.2017.06.011. [Google Scholar] [CrossRef]

30. Kalidasan K, Rajesh PK. Natural convection on an open square cavity containing diagonally placed heaters and adiabatic square block and filled with hybrid nanofluid of nanodiamond cobalt oxide/water. Int C Heat Mass Transfer. 2017;81:64–71. doi:10.1016/j.icheatmasstransfer.2016.12.005. [Google Scholar] [CrossRef]

31. Babar H, Ali HM. Towards hybrid nanofluids: preparation, thermophysical properties, applications, and challenges. J Mol Liq. 2019;281:598–633. doi:10.1016/j.molliq.2019.02.102. [Google Scholar] [CrossRef]

32. Vallejo JP, Prado JI, Lugo L. Hybrid or mono nanofluids for convective heat transfer applications: a critical review of experimental research. Appl Therm Eng. 2022;203(5):117926. doi:10.1016/j.applthermaleng.2021.117926. [Google Scholar] [CrossRef]

33. Ma M, Zhai Y, Yao P, Li Y, Wang H. Synergistic mechanism of thermal conductivity enhancement and economic analysis of hybrid nanofluids. Powder Technol. 2020;373:702–15. doi:10.1016/j.powtec.2020.07.020. [Google Scholar] [CrossRef]

34. Armaghani T, Rashad AM, Togun H, Mansour MA, Salah T. Hybrid nanofluid unsteady MHD natural convection in an inclined wavy porous enclosure with radiation effect, partial heater, and heat generation/absorption. Iran J Sci Technol Trans Mech Eng. 2024;48(3):971–88. doi:10.1007/s40997-023-00720-3. [Google Scholar] [CrossRef]

35. Izadi M, Sheremet MA, Mehryan SAM. Natural convection of a hybrid nanofluid affected by an inclined periodic magnetic field within a porous medium. Chin J Phys. 2020;65:447–58. doi:10.1016/j.cjph.2020.03.006. [Google Scholar] [CrossRef]

36. Heyhat MM, Changizi P, Azartakin S, Zabetian Targhi M. Hybrid nanofluids for working fluid in a microchannel heat sink; hydrothermal analysis. Heat Mass Transfer. 2024;60(1):89–100. doi:10.1007/s00231-023-03423-2. [Google Scholar] [CrossRef]

37. Hejazi HA, Khan MI, Raza A, Smida K, Khan SU, Tlili I. Inclined surface slip flow of nanoparticles with subject to mixed convection phenomenon: fractional calculus applications. J Indian Chem Soc. 2022;99(7):100564. doi:10.1016/j.jics.2022.100564. [Google Scholar] [CrossRef]

38. Khan SU, Raza A, Kanwal A, Javid K. Mixed convection radiated flow of Jeffery-type hybrid nanofluid due to inclined oscillating surface with slip effects: a comparative fractional model. Waves Random Complex Media. 2022;1-22(8):1–22. doi:10.1080/17455030.2022.2122628. [Google Scholar] [CrossRef]

39. Maatki C, Ghachem K, Kolsi L, Borjini M, Aissia HB. Entropy generation of double diffusive natural convection in a three-dimensional differentially heated enclosure. Int J Eng Trans B Appl. 2014;27:215–26. doi:10.5829/IDOSI.IJE.2014.27.02B.06. [Google Scholar] [CrossRef]

40. Kolsi L, Hussain S, Ghachem K, Jamal M, Maatki C. Double diffusive natural convection in a square cavity filled with a porous media and a power law fluid separated by a wavy interface. Mathematics. 2022;10(7):1060. doi:10.3390/math10071060. [Google Scholar] [CrossRef]

41. Mahmood Z, Duraihem FZ, Adnan, Khan U, Hassan AM. Model-based comparative analysis of MHD stagnation point flow of hybrid nanofluid over a stretching sheet with suction and viscous dissipation. Numer Heat Transf Pt B Fundam. 2024:1–22. doi:10.1080/10407790.2024.2318457. [Google Scholar] [CrossRef]

42. Zafar M, Rafique K, Khan U, Abd El-Rahman M, Alharbi R. Analysis of mixed convective stagnation point flow of hybrid nanofluid over a sheet with variable thermal conductivity and slip conditions: a model-based study. Int J Heat Fluid Flow. 2024;106(10):109296. doi:10.1016/j.ijheatfluidflow.2024.109296. [Google Scholar] [CrossRef]

43. Bayareh M, Baghoolizadeh M. An overview of the magnetic field effect on heat transfer and entropy generation in cavities: application of the second law of thermodynamics and artificial intelligence. Int C Heat Mass Transf. 2024;151(3):107238. doi:10.1016/j.icheatmasstransfer.2023.107238. [Google Scholar] [CrossRef]

44. Mandal DK, Mondal MK, Biswas N, Manna NK, Al-Farhany K, Mitra A, et al. Convective heat transport in a porous wavy enclosure: nonuniform multi-frequency heating with hybrid nanofluid and magnetic field. Heliyon. 2024;10(9):e29846. doi:10.1016/j.heliyon.2024.e29846. [Google Scholar] [CrossRef]

45. Ain QU, Ali Shah I, Alzahrani SM. Enhanced heat transfer in novel star-shaped enclosure with hybrid nanofluids: a neural network-assisted study. Case Stud Therm Eng. 2024;61(12):105065. doi:10.1016/j.csite.2024.105065. [Google Scholar] [CrossRef]

46. Rabby MII, Sharif MAR, Hossain F. Numerical study of laminar convective heat transfer from a corrugated pipe into an Al2O3–AlN/H2O hybrid nanofluid. Case Stud Therm Eng. 2022;39(1):102454. doi:10.1016/j.csite.2022.102454. [Google Scholar] [CrossRef]

47. Chabani I, Mebarek-Oudina F, Vaidya H, Ismail AI. Numerical analysis of magnetic hybrid nanofluid natural convective flow in an adjusted porous trapezoidal enclosure. J Magn Magn Mater. 2022;564(2):170142. doi:10.1016/j.jmmm.2022.170142. [Google Scholar] [CrossRef]

48. Feng X, Wu H, Sun Y, Zhang J, Yang Y, Zhao B. Numerical simulation study of heat transfer enhancement in a tube based on an eccentric structure. Energy Rep. 2023;9(Suppl 6):275–83. doi:10.1016/j.egyr.2023.04.037. [Google Scholar] [CrossRef]

49. Alami AH, Ramadan M, Tawalbeh M, Haridy S, Al Abdulla S, Aljaghoub H, et al. Un aperçu essentiel sur les nanofluides pour l’amélioration du transfert de chaleur. Sci Rep. 2023;13(1):15303. doi:10.1038/s41598-023-42489-0. [Google Scholar] [CrossRef]

50. Kalsi S, Kumar S, Kumar A, Alam T, Dobrotă D. Thermophysical properties of nanofluids and their potential applications in heat transfer enhancement: a review. Arab J Chem. 2023;16(11):105272. doi:10.1016/j.arabjc.2023.105272. [Google Scholar] [CrossRef]

51. Jiang X, Hatami M, Abderrahmane A, Younis O, Makhdoum BM, Guedri K. Mixed convection heat transfer and entropy generation of MHD hybrid nanofluid in a cubic porous cavity with wavy wall and rotating cylinders. Appl Therm Eng. 2023;226:120302. doi:10.1016/j.applthermaleng.2023.120302. [Google Scholar] [CrossRef]

52. Rashad AM, Togun H, Mansour MA, Salah T, Armaghani T. Unsteady MHD hybrid nanofluid mixed convection heat transfer in a wavy porous cavity with thermal radiation. J Therm Anal Calorim. 2024;149(5):2425–42. doi:10.1007/s10973-023-12690-4. [Google Scholar] [CrossRef]

53. Bejan A. Convection heat transfer. Hoboken: John Wiley & Sons; 1984. [Google Scholar]

54. Abu-Nada E, Oztop HF. Effect of inclination angle on natural convection in enclosure filled with Cu-water nanofluids. Int J Heat Fluid Flow. 2009;30(4):669–78. doi:10.1016/j.ijheatfluidflow.2009.02.001. [Google Scholar] [CrossRef]

55. Takbi B, Shokouhmand H. Effects of Al2O3-Cu/water hybrid nanofluid on heat transfer and flow characteristics in turbulent regime. Int J Mod Phys C. 2015;26(4):1550047. doi:10.1142/S0129183115500473. [Google Scholar] [CrossRef]

56. Patankar SV. Numerical heat transfer and fluid flow. New York: Hemisphere Publishing Corporation, Taylor and Francis Group; 1980. doi:10.1201/9781482234213. [Google Scholar] [CrossRef]

57. Van Doormaal JP, Raithby GD. Enhancements of the SIMPLE method for predicting incompressible fluid flow. Numer Heat Transfer. 1984;7(2):147–63. doi:10.1080/01495728408961817. [Google Scholar] [CrossRef]

58. Ravnik J, Skerget L, Hribersek M. Analysis of three-dimensional natural convection of nanofluids by BEM. Eng Anal Bound Elem. 2010;34(12):1018–30. doi:10.1016/j.enganabound.2010.06.019. [Google Scholar] [CrossRef]

59. Ternik P. Conduction and convection heat transfer characteristics of water-Au nanofluid in a cubic enclosure with differentially heated sidewalls. Int J Heat Mass Transfer. 2015;80(205):368–75. doi:10.1016/j.ijheatmasstransfer.2014.09.041. [Google Scholar] [CrossRef]