Nanofluid Heat Transfer in Irregular 3D Surfaces under Magnetohydrodynamics and Multi-Slip Effects

Nomenclature

1  Introduction

Nanoparticles, such as particles or fibers dispersed in liquids such as water, oil, or ethylene glycol, belong to an advanced group of solid-liquid substances that have brought significant advancements in the field of thermal science. When mixed with nanoparticles that vary in size from 1 to 100 nanometers, these fluids display altered characteristics. These changes affect thickness, mass, heat transfer efficiency, and distribution patterns. As a result, they offer better rates of heat transfer compared to base fluids. This makes them fascinating in engineering disciplines, including biomechanics, the chemical and nuclear industries, and general engineering applications. However, despite the growing interest and range of applications of nanofluids, their dynamics are still poorly understood. This is especially true for the effects of magnetohydrodynamics (MHD) and surface irregularities on nanofluids. The lack of knowledge in this area is particularly critical for applications that require behavioral control. Our study focuses on bridging this gap in understanding by exploring the thermal transfer processes and three-dimensional movement patterns in a nanofluid that consists of a second-grade fluid. A nanofluid is a class of fluid consisting of a base liquid dispersed with nanoparticles exhibiting significant enhancement in heat transfer properties. Nanofluids were first postulated by Choi et al. [1] as an unprecedented class of fluids. Since then, considerable advances have been made to this basic notion, then in Eastman et al. [2] an exceptionally high effective thermal conductivity for nanofluids containing ethylene glycol and copper nanoparticles, which he suggested offered considerable potential for practical improvements in heat transfer applications. Ghalambaz et al. [3] reported that non-uniform magnetic fields can increase the rates of heat and mass transfer in MHD nanofluids inside a cavity. Rashid et al. [4] also found that nanoflow have the best behavior for thermal conductivity followed by lamina-shaped nanoparticles MHD applications in micro-nanotechnologies. Wahid et al. [5] studied hybrid nanofluids influenced by MHD and radiation case which presented significant improvement in heat transfer, whereas Swain [6] analyzed ternary-hybrid nanofluid problem considering viscous dissipation and Lorentz force for the convection flow of water with copper-alumina-silver nanoparticles. Ramzan et al. [7] investigated ternary hybrid nanofluids in kerosene oil and showed that their thermal conductivity can be significantly enhanced. Dash et al. [8] reported that copper kerosene nanofluids are superior compared to their water-based counterpart in terms of heat transfer enhancement. Bhandari et al. [9] optimized nanofluid flow over a shrinking surface, highlighting the impact of Biot and Grashof numbers on heat transfer. Kotha et al. [10] investigated bioconvection in MHD nanofluids with gyrotactic microorganisms, showing enhanced heat and mass transfer. Hussain et al. [11] compared heat transfer in water-based MHD nanofluids, finding Zn-water nanofluids superior to TiO2-water nanofluids.

Studies of non-Newtonian fluids are critical in fluid mechanics due to their unique rheological characteristics, different from the predictable viscosities observed in Newtonian fluids [12]. Davis et al. [13] reported that these fluids exhibit intricate responses to external forces. Therefore, they are essential in numerous industrial and scientific fields, such as biomedical engineering and manufacturing. Second-grade fluids constitute an intriguing subclass of non-Newtonian fluids with a wide variability ([14]). Khan et al. [15] studied the time fractional second-grade MHD dusty fluid flow, highlighting the impact of heat and mass transfer rates on fluid dynamics. Entropy generation in Williamson fluid flow was investigated by Qayyum et al. [16], considering that thermal radiation and magnetic effects have a remarkable impact on entropy generation. Ahmed et al. [17] conducted a study on heat and mass dynamics within the MHD boundary layer flow of a second-grade fluid, discovering that chemical reactions and fluid oscillations reduced concentration levels. Anwar et al. [18] explored the transient MHD behavior of Oldroyd-B fluids, factoring in slip conditions and Newtonian heating effects to assess their influence on shear stress and heat distribution. Concurrently, Hayat et al. [19] conducted a study on the dual transport phenomena and entropy effects in MHD-driven second-grade nanofluid flows along a Riga plate, examining their contributions to thermal efficiency and entropy-related heat transformation. Khan et al. [20] studied how activation energy and complex heating and cooling processes impact the flow of Carreau nanofluids in environments influenced by radiation, focusing on how these factors affect speed and temperature changes. Das et al. [21] looked into how fluid flows with complex fluid properties, influenced by magnetic fields, chemical reactions, and heat transfer, contribute to irreversible energy loss. Chu et al. [22] examined how energy transfers in magnetically influenced nanofluids showing second-grade characteristics impact speed and temperature, highlighting significant effects from intense radiation. Tanveer et al. [23] studied electroosmosis in the peristaltic activity of MHD non-Newtonian fluid and illustrated the applications in micro-fabrication and chemical industries. Heat and mass transport in MHD flow of a non-Newtonian viscoelastic over a stretched magnetized surface were investigated by Aloliga et al. [24] and observed how induced magnetization was affecting heat transfer and flow behavior.

Boundary layer flows over-stretching sheets of various thicknesses are a topic of significant interest owing to their numerous applications in material processing and industrial manufacturing. The requirements for a fundamental understanding of fluid dynamics in flows of the boundary layer over continuously extending surfaces were laid down in the pioneering work of Sakiadis [25]. This represents a theoretical guideline for what has been experimentally demonstrated Tsou et al. [26]. Recent research has significantly progressed the description of boundary layer flows over stretching sheets including fluid dynamics, heat and mass transfer mechanisms as well as the influence of non-uniform sheet thickness. Hussain et al. [27] analyzed the entropy generation in MHD convection flow of hybrid nanofluids within a wavy enclosure, focusing on the impacts of heat generation and thermal radiation on thermal efficiency. Lin et al. [28] examined the behavior of fractional nanofluids in a porous medium, assessing the impact of magnetohydrodynamics and heat modifications on convective flow and heat transfer efficiency. Sharma et al. [29] conducted a numerical study of fractional boundary layer flow over a stretching sheet with variable thickness using a finite difference approach. Flow of a nanoliquid with gyrotactic microorganisms through the boundary layer over a stretching sheet was examined computationally by Hosseini et al. [30]. The nanofluid flow of variable thickness sheet with non-uniform stretching and porous velocities was examined by Alam et al. [31]. Rehman et al. [32] considered the influence of flow distribution on heat and mass transfer in MHD thin liquid film flow over an unsteady stretching sheet with mixed convection. Fatunmbi et al. [33] analyzed convective heat transfer in hydromagnetic micropolar fluid flow past an inclined nonlinear stretching sheet with variable thermo-physical properties.

This study extends the application of the Buongiorno model to explore the dynamic interactions of nanoparticle migration in a mixed convection second-grade fluid over a variable thickness stretching sheet. A comprehensive range of external influences including Joule heating, slip effects, thermal radiation, heat generation, and magnetohydrodynamic forces considered in the current assessment. To the authors’ knowledge, applying the Buongiorno model to study nanoparticle migration in second-grade fluids over variable-thickness sheets with Joule heating and convective boundaries is unprecedented. The model was constructed based on flow assumptions, utilizing boundary layer approximations represented by partial differential equations. These equations were transformed into dimensionless form through appropriate scaling. Subsequently, the dimensionless equations were numerically solved using MATLAB software. The results of physical factors are deliberated through graphs as well as tables. This research not only broadens the theoretical framework but also enhances practical applications in industries where precise control of thermal and fluid dynamics is critical.

2  Methodology

This study investigates the steady incompressible flow of a mixed convection second-grade fluid over a variable thickness stretching sheet, modeled by z=J(x+y+c)0.5(1−n). Here, J acts as a geometric scaling factor that modulates the sheet’s thickness. The parameter n influences surface configurations, as illustrated in Fig. 1. Analyzing the effects of Joule heating, slip conditions, thermal radiation, heat generation, and MHD forces, the study uses the Buongiorno model to examine nanoparticle behavior and the impact on heat and mass transfer efficiency. The governing equations derived from boundary layer approximations are dimensionless for numerical solution (see [34]):

∂xu+∂yv+∂zw=0(1)

u∂xu+v∂yu+w∂zu=ν∂zzu+αsg(u∂xzzu+w∂zzzu−∂xu∂zzu−∂zu∂zzw−2∂zu∂xzu−2∂zw∂zzu)−σcondBmag2ρu+g((T−T∞)βT+(C−C∞)βC)(2)

u∂xv+v∂yv+w∂zv=ν∂zzv+αsg(v∂xzzv+w∂zzzv−∂xv∂zzv−∂zv∂zzw−2∂zv∂xzv−2∂zw∂zzv)−σcondBmag2ρv(3)

u∂xT+v∂yT+w∂zT=kfρcpf∂zzT+χcp(DB∂zC∂zT+DTT∞(∂zT)2)−1ρcpf∂zqrad+Qgaρcpf(T−T∞)+σcondBmag2ρcpf(u2+v2)(4)

u∂xC+v∂yC+w∂zC=DB∂zzC+DTT∞∂zzT(5)

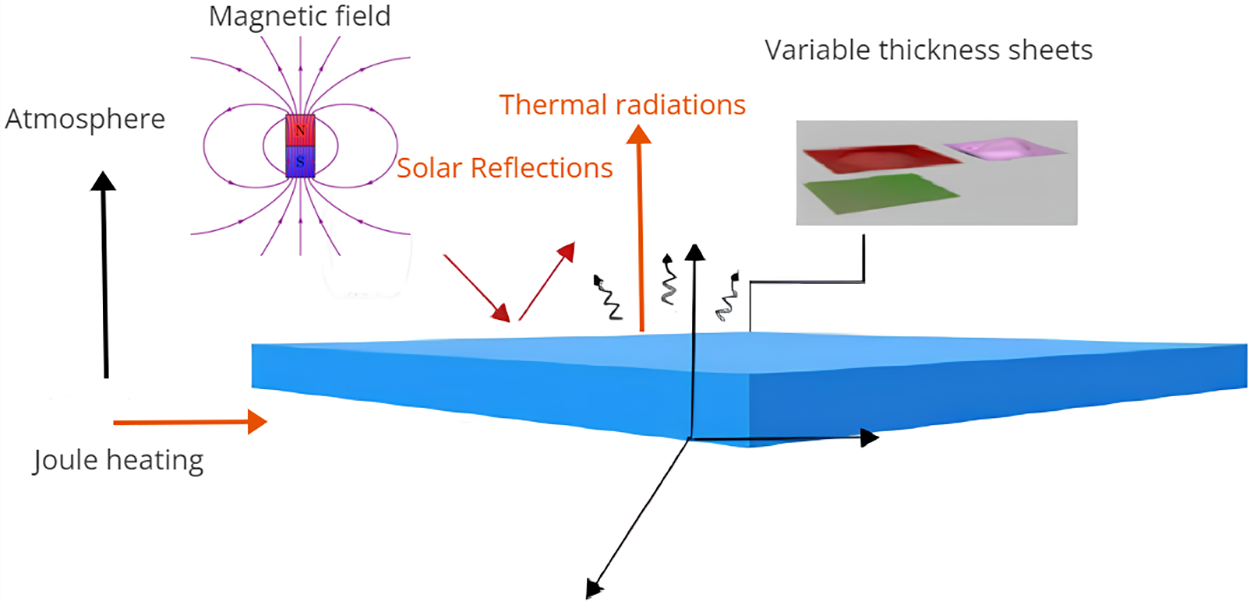
Figure 1: Schematic of flow geometry

The velocity conditions at the surface, where the thickness is variable

u−uw−ϵv∂zu=0,v−vw−ϵv∂zv=0,w=0(6)

whereas boundary conditions for concentration and temperature are detailed as follows:

−kf∂zT=hw(Tw−T),−DB∂zC=hf(Cw−C)(7)

u→0,v→0,T→T∞,C→C∞,as z→∞(8)

The coefficients in the boundary conditions are defined as

ϵv=(2−RmRM)ξ1(x+y+c)1−n2,ξ2=ξ1Pr,ξ3=ξ2Pr,

uw=U0(x+y+c)1−n2,vw=U0(x+y+c)1−n2,

Tw=T∞+T0(x+y+c)1−n2,Cw=C∞+C0(x+y+c)1−n2

Qga=Q0(x+y+c)1−n2,Bmag=B0(x+y+c)n−12,Ec=Ec∗(x+y+c)1−n2

The equation for energy as (4) describes how the radiative heat flow qrad is determined by applying the radiative transport equation [34,35].

qrad=−4σ43k1∂T4∂z4(9)

Simply relying on the T4 expansion around the temperature T∞ is insufficient to explain radiative heat transfer fully. This overlooks some of these aspects. Therefore, we adjusted the energy equation to account for radiative heat flux accurately (see [34,35]).

u∂xT+v∂yT+w∂zT=kfρcpf∂zzT+χcp(DB∂zC∂zT+DTT∞(∂zT)2)

u∂xT+v∂yT+w∂zT=kfρcpf∂zzT+χcp(DB∂zC∂zT+DTT∞(∂zT)2)+1ρcpf∂z(4σ43k144T3∂zT)+Qgaρcpf(T−T∞)+σcondBmag2ρcpf(u2+v2)(10)

We have implemented transformations to simplify the mathematical formulation [34,35].

ζ=[(n+1)U022νf]1/2(x+y+c)(n−1)/2z,Ψ=[2νfU0(n+1)1/2]1/2(x+y+c)(n+1)/2F(ζ),Θ(ζ)=T−T∞Tw−T∞,Φ(ζ)=C−C∞Cw−C∞,u=U0(x+y+c)nF′(ζ),v=U0(x+y+c)nG′(ζ),w=−[2νfU0(n+1)12]12(x+y+c)n−12[n+12(F(ζ)+G(ζ))+n−12ζ(F′(ζ)+G′(ζ))](11)

Here, ζ represents the similarity variable, and Ψ refers to the stream function. By applying the transformation described in Eq. (11) to our set of equations and the specified boundary conditions, we establish the corresponding nonlinear ordinary differential equations (ODEs).

(n+12)F(4)+β1[2n(n+1)G′+(n+1)(3n−1)F′]F′′′−12[(G+F)n+12+(n2−1)ηG′]−MF′+(λ1θ+λ2)−[nF′G′+nF′′′2−n+12(F+G)F′′′]=0(12)

(n+12)G(4)+β1[2n(n+1)F′+(n+1)(3n−1)G′]G′′′−12[(F+G)n+12+(n2−1)ηF′′′]G(4)−MG′−[nG′F′+nG′′2−n+12(G+F)G′′′]=0(13)

Pr(1−nn+1)(F′+G′)Θ−(F+G)Θ′+2n+1IHΘ+NbmΘ′+NtpΘ′2+2n+1Ec(F′2+G′2)+(1+43Πrad)Θ′′=0(14)

Φ′′+Sc((F+G)Φ′−1−nn+1(F′+G′)Φ)+NtpNbmΘ′′=0(15)

The corresponding boundary conditions are

F(ζ)=λ(1−n1+n)(1+τ1F′′(ζ)),F′(ζ)=1+τ1F′′(ζ),Θ′(ζ)=−γ1(1−Θ(ζ)),G(ζ)=λ(1−n1+n)(1+τ1G′′(ζ)),G′(ζ)=1+τ1G′′(ζ),Φ′(ζ)=−γ2(1−Φ(ζ)), atζ=λ,F′(∞)=0,G′(∞)=0,Θ(∞)=0,Φ(∞)=0(16)

To make it easier to analyze the intricate differential Eqs. (12)–(15), and related boundary conditions (16) that were originally established across the range [λ,∞) are now redefined in a different domain [0,∞). This change simplifies the procedure by moving the variable making it simpler and more organized to solve these equations.

The transformed differential equations are given by

(n+12)f(4)+β1[2n(n+1)g′+(n+1)(3n−1)f′]f′′′−12[(g+f)n+12+(n2−1)ηg′′′′]f(4)−Mf′+(λ1θ+λ2)−[nf′g′+nf′′2−n+12(f+g)f′′′]=0(17)

(n+12)g(4)+β1[2n(n+1)f′+(n+1)(3n−1)g′]g′′′−12[(f+g)n+12+(n2−1)ηf′′′′]g(4)−Mg′−[ng′f′+ng′′2−n+12(g+f)g′′′]=0(18)

Pr(1−nn+1)(f′+g′)θ−(f+g)θ′+2n+1IHθ+Nbmθ′+Ntpθ′2+2n+1Ec(f′2+g′2)(1+43Πrad)θ′′=0(19)

ϕ′′+Sc((f+g)ϕ′−1−nn+1(f′+g′)ϕ)+NtpNbmθ′′=0(20)

The corresponding boundary conditions at the transformed domain are:

f(0)=λ(1−n1+n)+τ1f′′(0),f′(∞)=0,f′(0)=1+τ1f′′(0),θ(∞)=0,θ′(0)=−γ1(1−θ(0)),g′(∞)=0,g(0)=λ(1−n1+n)+τ1g′′(0),ϕ(∞)=0,g′(0)=1+τ1g′′(0),ϕ(0)=−γ2(1−ϕ(0))(21)

The following parameters are introduced to thoroughly analyzed the behavior of flow and heat and mass transfer effects in the systems:

M=σcondB02ρfU0,β1=uwαsecν,Pr=μfcpfkf,Πrad=4σ4T∞3kfk1∗,Nbm=χcpDB(Cw−C∞)νf,Ntp=χcpDT(Tw−T∞)νfT∞,Sc=νfDB,τ1=2−RmRmξ1(x+y+c)0.5(1−n),γ1=hwkf(2νf(n+1)uw2)0.5,λ=J((n+1)U022νf)0.5(x+y+c)0.5(n−1),γ2=hfDB(2νf(n+1)uw2)0.5(22)

Frictional resistance coefficient, mass transfer coefficient, and heat transfer coefficient are discussed below to determine the numerical solutions

Rex12CFx=2((n+12)12(f′′′(0)+2β1[g′(0)2f′′(0)+(f′(0)+g′(0))2+2nf′(0)f′′(0)+nf′(0)2f′′(0)−n+12(f(0)+g(0))f′′′(0)])),

Rey12CFy=2((n+12)12(g′′′(0)+2β1[f′(0)2g′′(0)+(g′(0)+f′(0))2+2ng′(0)g′′(0)+ng′(0)2g′′(0)−n+12(g(0)+f(0))g′′′(0)])),

NuxRex−12=−(1+43Πrad)(1+n2)12θ′(0),ShxRex−12=−(1+n2)12ϕ′(0),

Rex=uw(x)(x+y+c)νf

3  Numerical Solution Approach

The dimensionless system, represented by ordinary differential equations (ODEs), is elucidated using numerical techniques. This method transforms higher-order nonlinear differential equations into first-order ones. The process is outlined below (refer to Fig. 2).

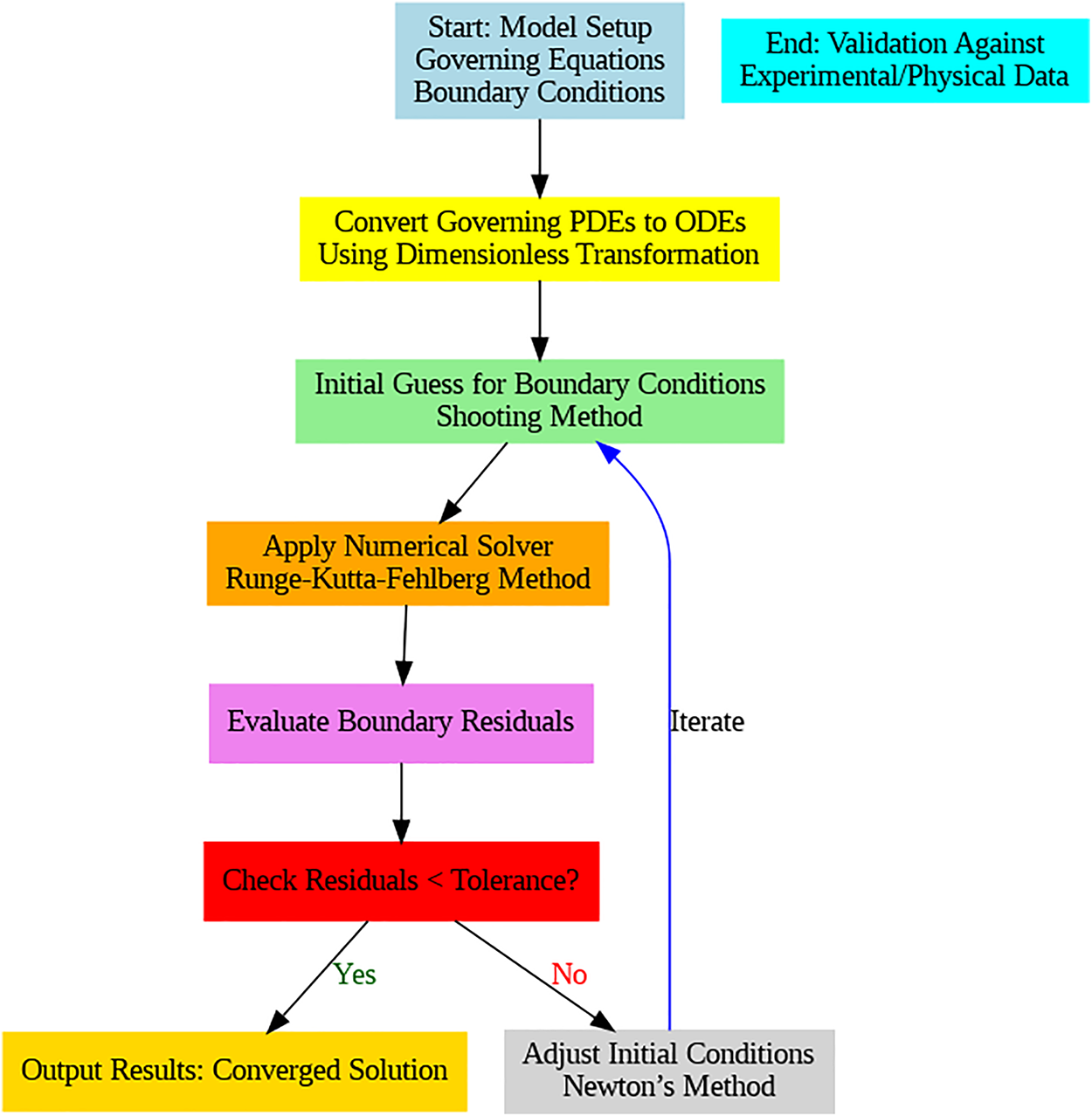
Figure 2: Schematic representation of the computational algorithm

Let’s introduce these variables: - u1=f, u2=f′, u3=f′′, u4=f′′′ - v1=g, v2=g′, v3=g′′, v4=g′′′ - w1=θ, w2=θ′ - z1=ϕ, z2=ϕ′

u1′=u2,

u2′=u3,

u3′=u4,

u4′=(2n+1)(−β1[2n(n+1)v2+(n+1)(3n−1)u2]u4+12[(v1+u1)n+12+(n2−1)ηv2]u4+Mu2−(λ1w1+λ2)+[nu2v2+nu32−n+12(u1+v1)u4])),(23)

v1′=v2,

v2′=v3,

v3′=v4,

v4′=(2n+1)((−β1[2n(n+1)u2+(n+1)(3n−1)v2]v4+12[(u1+v1)n+12+(n2−1)ηu2]v4+Mv2−(λ1w1+λ2)+[nv2u2+nv32−n+12(v1+u1)v4]))(24)

w1′=w2,

w2′=−11+43Πrad(Pr1−nn+1(u2+v2)w1−(u1+v1)w2−2n+1IHw1−Nbmw2−Ntpw22−2n+1Ec(u22+v22))(25)

z1′=z2,

z2′=−1Sc((u1+v1)z2−1−nn+1(u2+v2)z1−NtpNbmw2′)(26)

With boundary conditions

u1(0)=λ(1−n1+n)+τ1u3(0),u2(∞)=0,u2(0)=1+τ1u3(0),w1(∞)=0,w2(0)=−γ1(1−w1(0)),v2(∞)=0,v1(0)=λ(1−n1+n)+τ1v3(0),z1(∞)=0,v2(0)=1+τ1v3(0),z2(0)=−γ2(1−z1(0))(27)

4  Results and Discussion

This investigation explores the complex behavior of nanofluid flow over a surface that is stretched in a manner affected by different factors. It examines the interaction between the nanofluid and irregular surface and the influence of external forces, such as magnetohydrodynamics (MHD) and thermophoresis. This section analyzes the impact of different critical parameters on the velocity, temperature, and concentration profiles. These parameters include the parameter M velocity power index parameter n second-grade fluid parameter β1 and several thermal- and concentration-related parameters. Understanding these variables is crucial for comprehending the complexities of nanofluid behavior and its potential applications in engineering and technology. Fig. 3 illustrates how changes in parameter M affect both the stretch-induced velocity profile f′ and the cross-stretch velocity profile g′. As the strength of the field increases, it causes a Lorentz force to act against the flow, resulting in a decrease in f′. Similarly, in the perpendicular direction (along g′, the cross-flow is also inhibited by the magnetic forces, leading to a decrease in the velocity gradient perpendicular to the primary flow. Fig. 4 shows how the velocity slip parameter τ1 affects both f′ and g′. As τ1 increased, these velocity profiles decreased, indicating a slip at the boundary. A higher value of τ1 signifies an increased slip at the boundary, enabling fluid flow with reduced resistance and consequently resulting in velocity gradients for both f′ and g′.

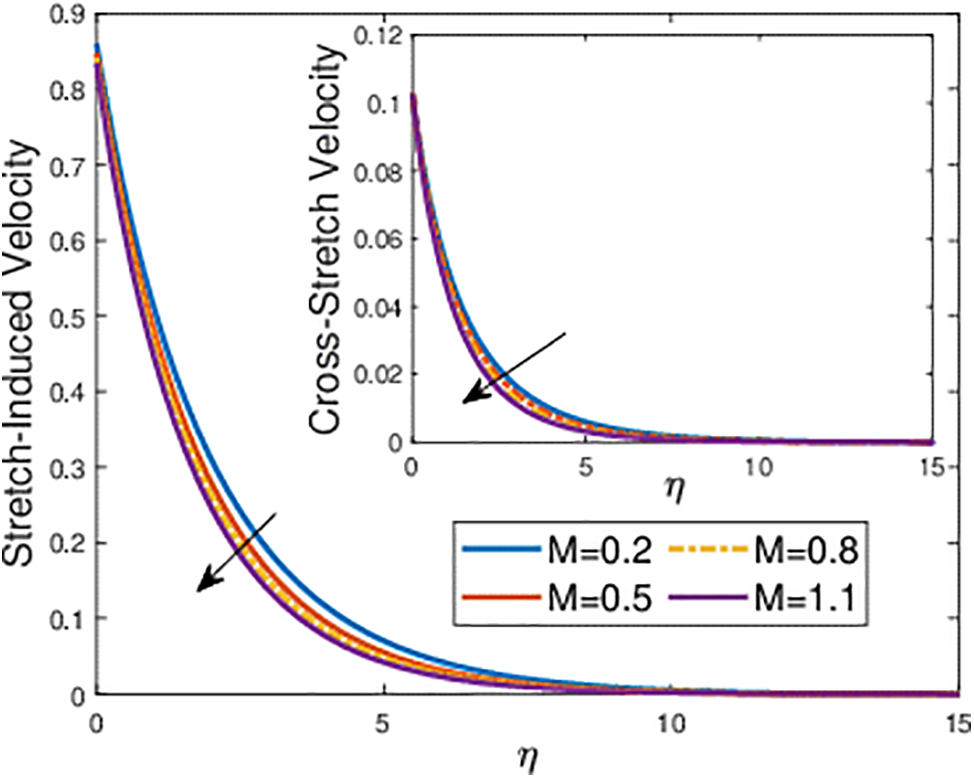
Figure 3: Effects of the magnetic parameter M on f′ and g′

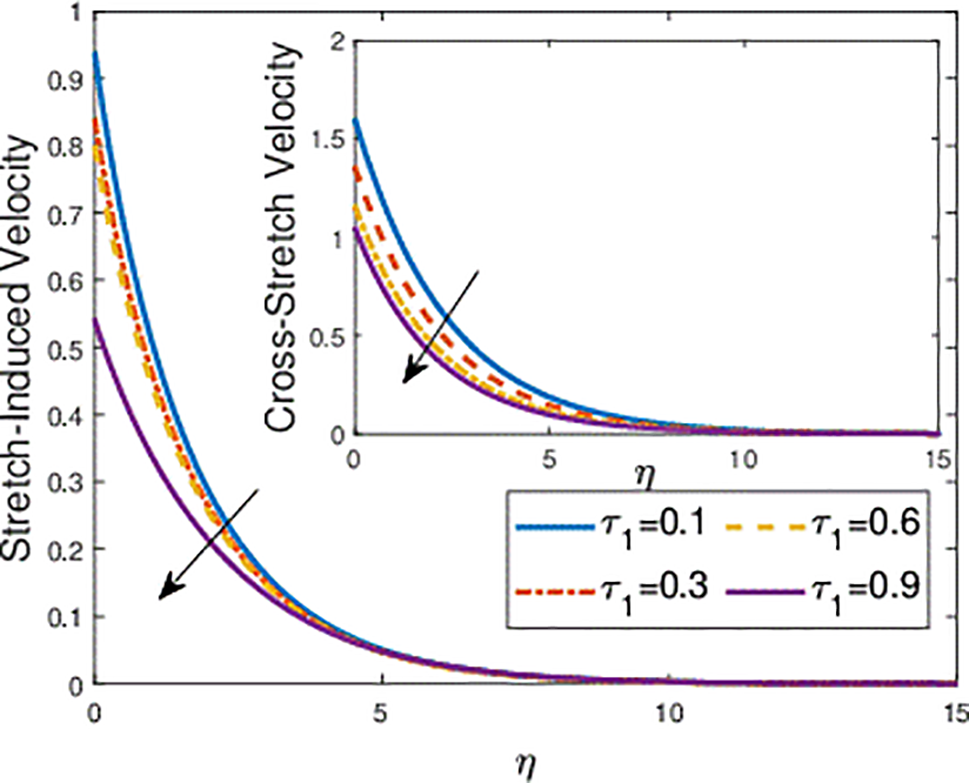
Figure 4: Effects of the velocity slip parameter τ1 on f′ and g′

The impact of the velocity index parameter, denoted by n on the velocity profiles caused by stretching, represented by f′ and g′ is depicted in Fig. 5. This parameter demonstrates that the behavior of the velocity profile follows a power-law pattern. As the value of n increases, both f′ and g′ exhibit a trend indicating a significant variation in the velocity near the surface. With an increasing power index parameter, the velocity gradients in both profiles became more pronounced, accelerating the flow from the surface. Fig. 6 illustrates how the second-grade fluid parameter, β1, affects both f′ and g′. As β1 increases, we consistently observe an increase in these velocity profiles. This trend can be physically justified by the fluid’s enhanced elasticity which allows it to respond more dynamically to changes in flow and boundary interactions. The increase in β1 amplifies the fluid’s ability to store and release elastic energy, leading to higher velocity gradients f′ and g′.

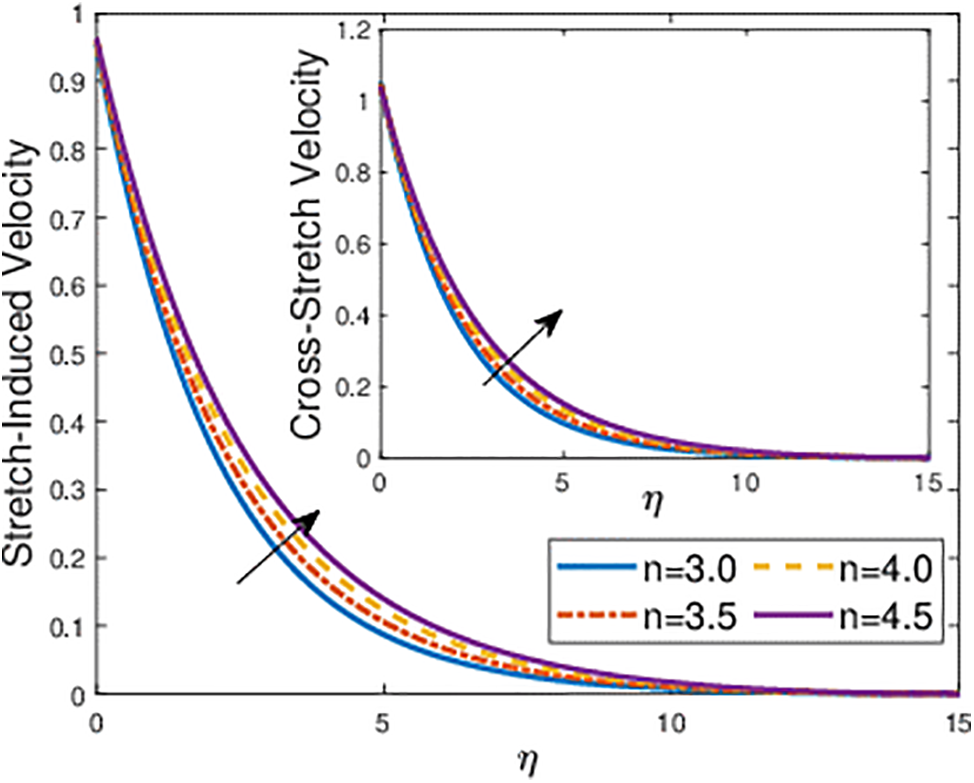
Figure 5: Effects of the velocity power index parameter n on f′ and g′

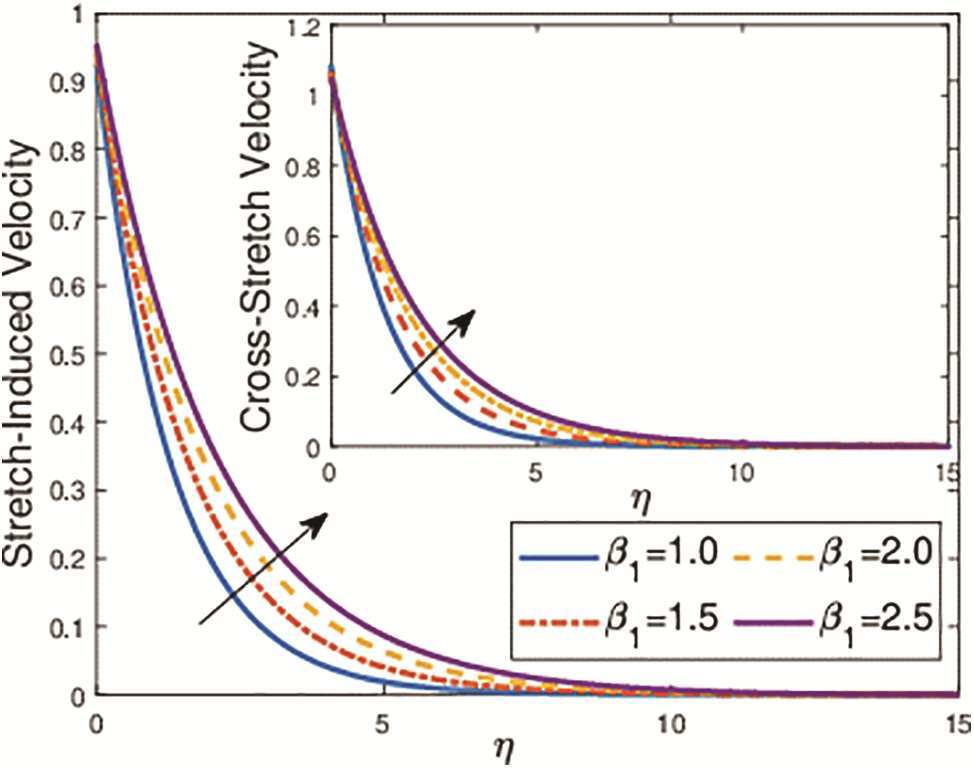
Figure 6: Effects of the second grade fluid parameter β1 on f′ and g′

Fig. 7 shows the effects of increasing the thermal Grashof number λ1 on the velocity gradients f′ and g′. As λ1 increases, there is a clear increase in f′, indicating that the buoyancy-driven flow becomes more pronounced. This enhancement in f′ suggests that the upward buoyant force, which aids in driving the fluid flow against gravitational pull, is strengthened with higher λ1, thereby accelerating the fluid more significantly in the primary flow direction. Conversely, while there is also an increase in g′, its change is minimal, particularly in the curved regions of the flow, suggesting that the cross-flow is less affected by buoyancy. The impact of the Eckert number Ec on the temperature profile θ is exhibited in Fig. 8. An increase in Ec leads to a noticeable increase in the temperature profile θ. This trend highlights the conversion of kinetic energy into thermal energy through viscous dissipation, underscoring a direct relationship between mechanical energy dissipation and temperature increase in the fluid.

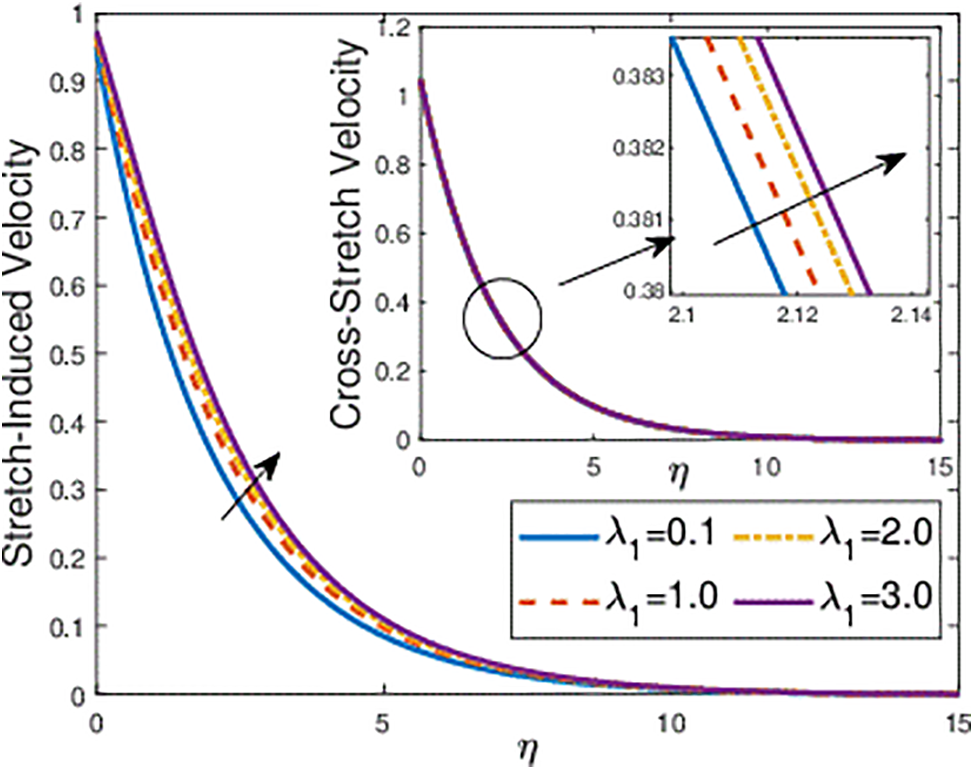
Figure 7: Effects of the thermal Grashof number λ1 on f′ and g′

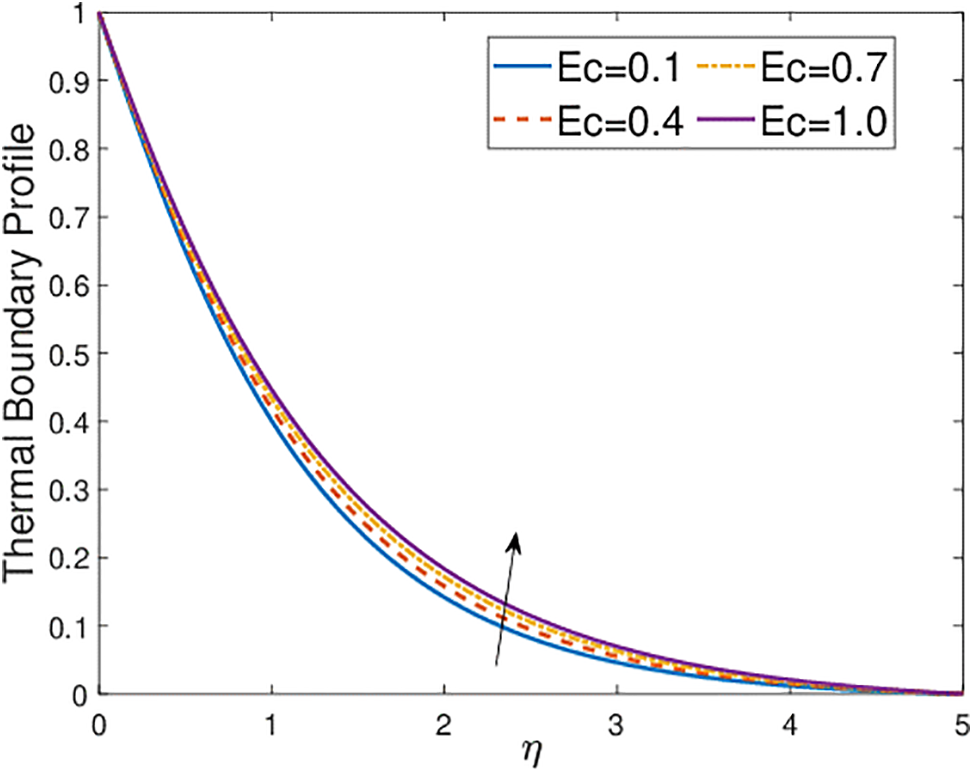
Figure 8: Effects of the Eckert number Ec on θ

The Fig. 9 demonstrates how the thermophoresis parameter Ntp and the Brownian motion parameter Nbm impact the thermal boundary profile θ. As the value of Ntp increases, the value of θ. This is because the stronger thermophoretic force pushes the nanoparticles away from the surface, resulting in a wider thermal boundary layer. Similarly, when Nbm is higher, the energy transfer between the particles and fluid increases, resulting in a boundary layer. Fig. 10 shows how an increase in the thermal Biot number, γ1, affects the temperature profile θ. Higher γ1 indicates increased internal resistance to heat conduction compared to external convective transfer, resulting in a pronounced temperature gradient. This leads to a thicker thermal boundary layer as the surface quickly equilibrates with the environment, while the interior heats up more slowly. The effect is a more distinct temperature variation across the fluid, highlighting the importance of γ1 in thermal management.

Figure 9: Effects of the thermophoresis parameter Ntp and the Brownian motion parameter Nbm on θ

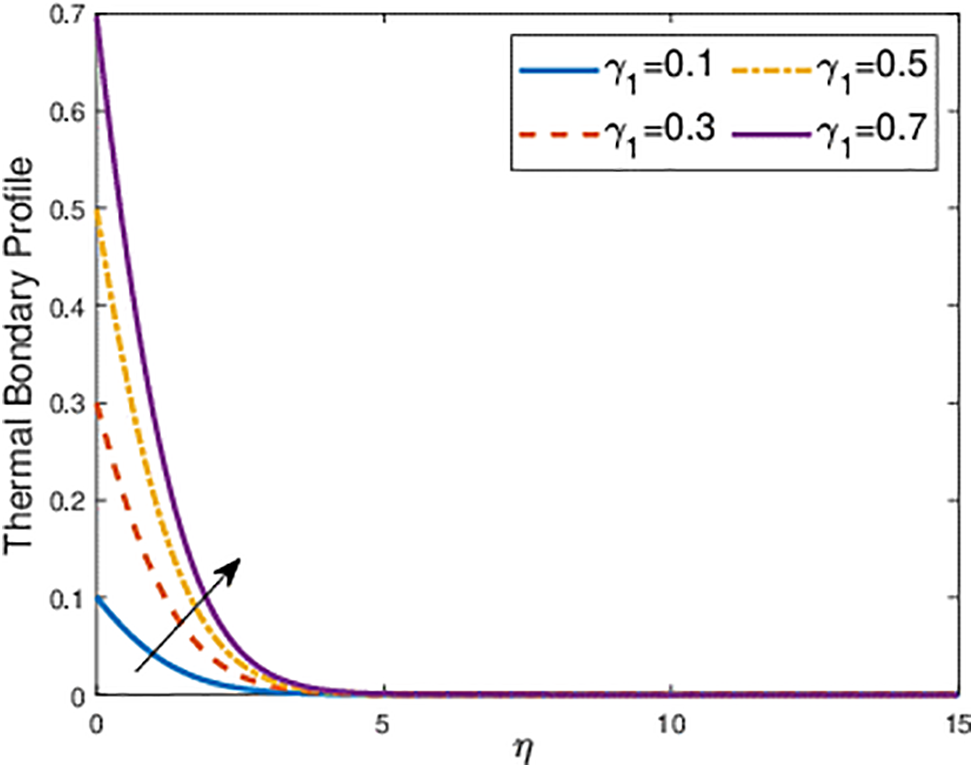
Figure 10: Effects of the thermal Biot number γ1 on θ

In Fig. 11, we observe the impact of the radiation parameter Πrad on the layer. The thermal boundary layer became more noticeable as the value of Πrad increased. This is because of the increased radiative heat transfer, which allows energy dissipation away from the boundary layer and creates a wider temperature difference. As shown in Fig. 12, we can see how the heat-generation parameter IH affects the profile θ of the boundary layer. The growth of this layer was caused by the thermal energy generated within the fluid owing to the increase in IH. The internal heat generation within the enhanced heat distribution resulted in a more extensive thermal boundary layer. This behavior highlights the effect of internal heat sources on the flow properties.

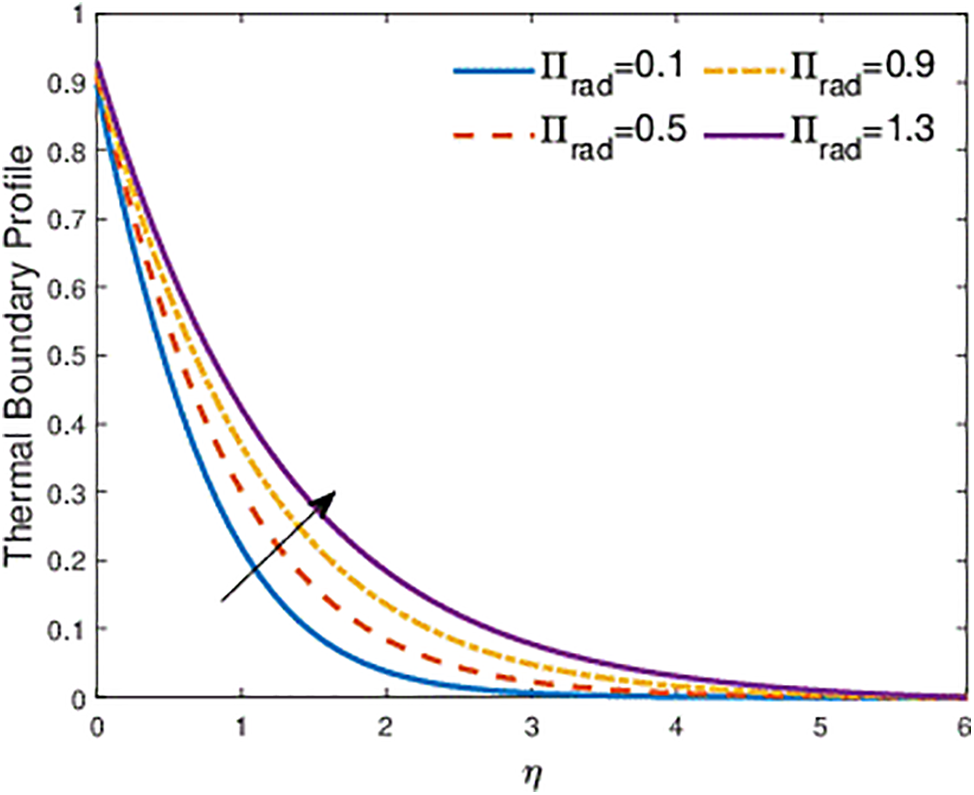
Figure 11: Effects of the radiation parameter Πrad on θ

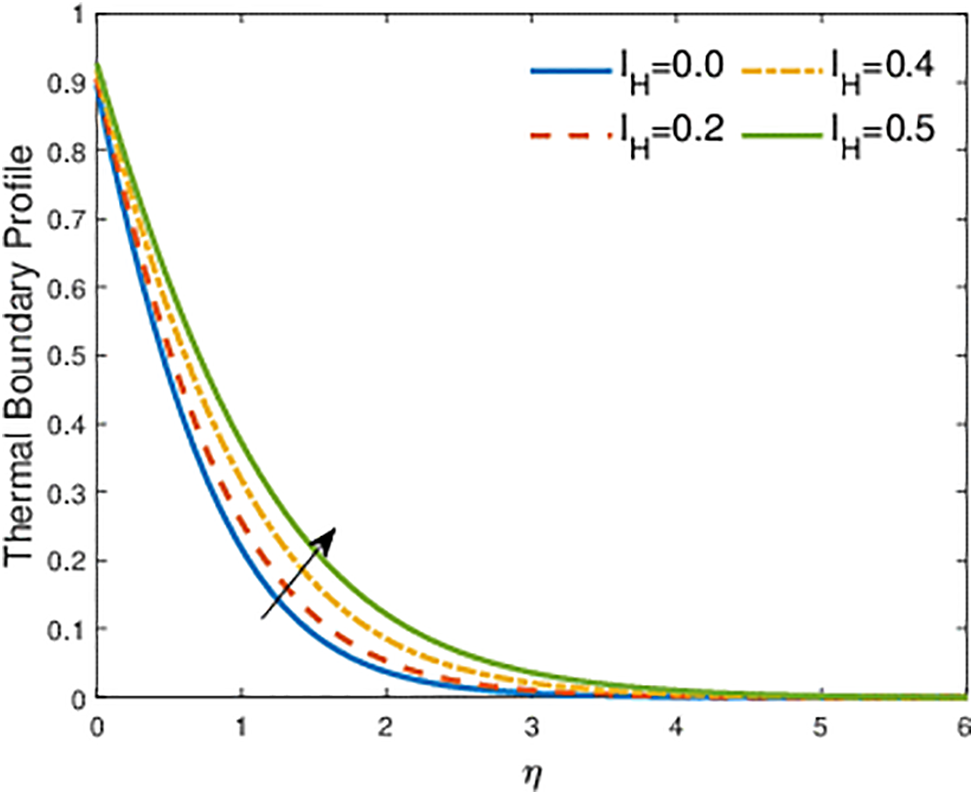
Figure 12: Effects of the internal heat generation parameter IH on θ

Fig. 13 shows how changes in Ntp and Nbm affect the behavior of the concentration boundary profile ϕ. When the thermophoresis parameter Ntp increases, it also leads to an increase in ϕ, indicating that the particles move intensely from the areas to colder ones. This occurs because, as Ntp increases, the thermophoretic force becomes more significant, causing the nanoparticles to be displaced from the surface, resulting in a concentration within the boundary layer. On the contrary, when we increased the motion parameter Nbm we observed a reduction in the value of ϕ. This suggests that increased motion, which refers to particle movement, leads to a more even distribution of the NPs and decreases the concentration gradient near the surface. Fig. 14 demonstrates how an increase in the concentration Biot number, γ2, influences the concentration profile. A higher γ2 suggests greater internal resistance to diffusion compared to the surface mass transfer, resulting in a steeper concentration gradient at the boundary. This differential leads to a more defined concentration boundary layer, as the surface adjusts to environmental changes more rapidly than the interior. Consequently, there is a more pronounced variation in concentration throughout the fluid, underscoring the significance of γ2 in managing diffusion processes.

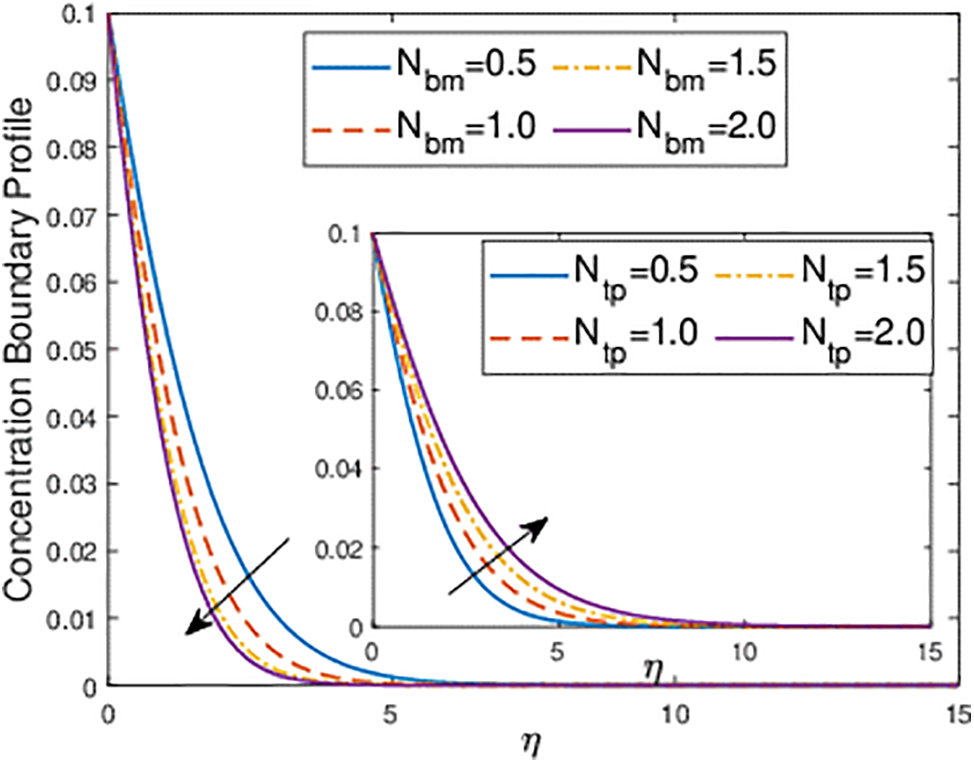
Figure 13: Effects of the thermophoresis parameter Ntp and Brownian motion parameter Nbm on ϕ

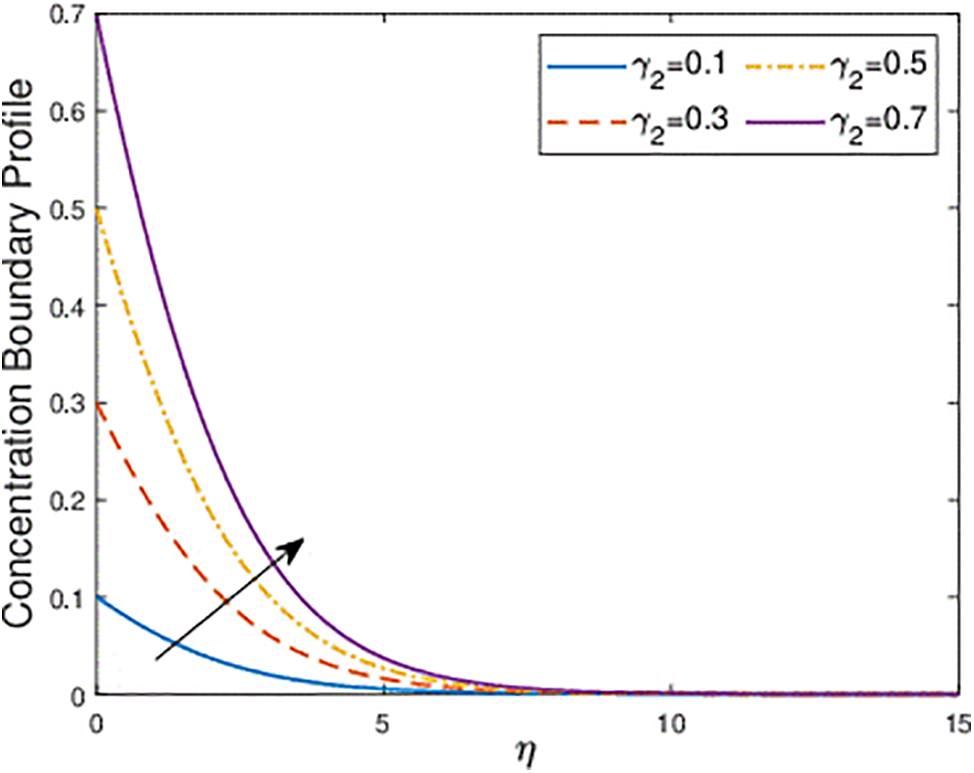
Figure 14: Effect of the concentration Biot number γ2 on ϕ

Our study examines the influence of various physical parameters on skin friction and heat and mass transfer in fluid flow, as detailed in Tables 1 and 2. Table 1 highlights the effects of parameters such as τ1, M, γ1, and λ on the skin friction coefficients CFx. It is evident that even minor adjustments in the velocity slip parameter τ1 can cause significant changes in skin friction. For example, increasing M from 0.22 to 0.88 results in a CFx decrease of 37.5%, indicating a strong influence of magnetic fields on friction. Moreover, changes in the wall thickness parameter λ from 0.33 to 0.99 lead to a decrease in CFx by 1.1%.

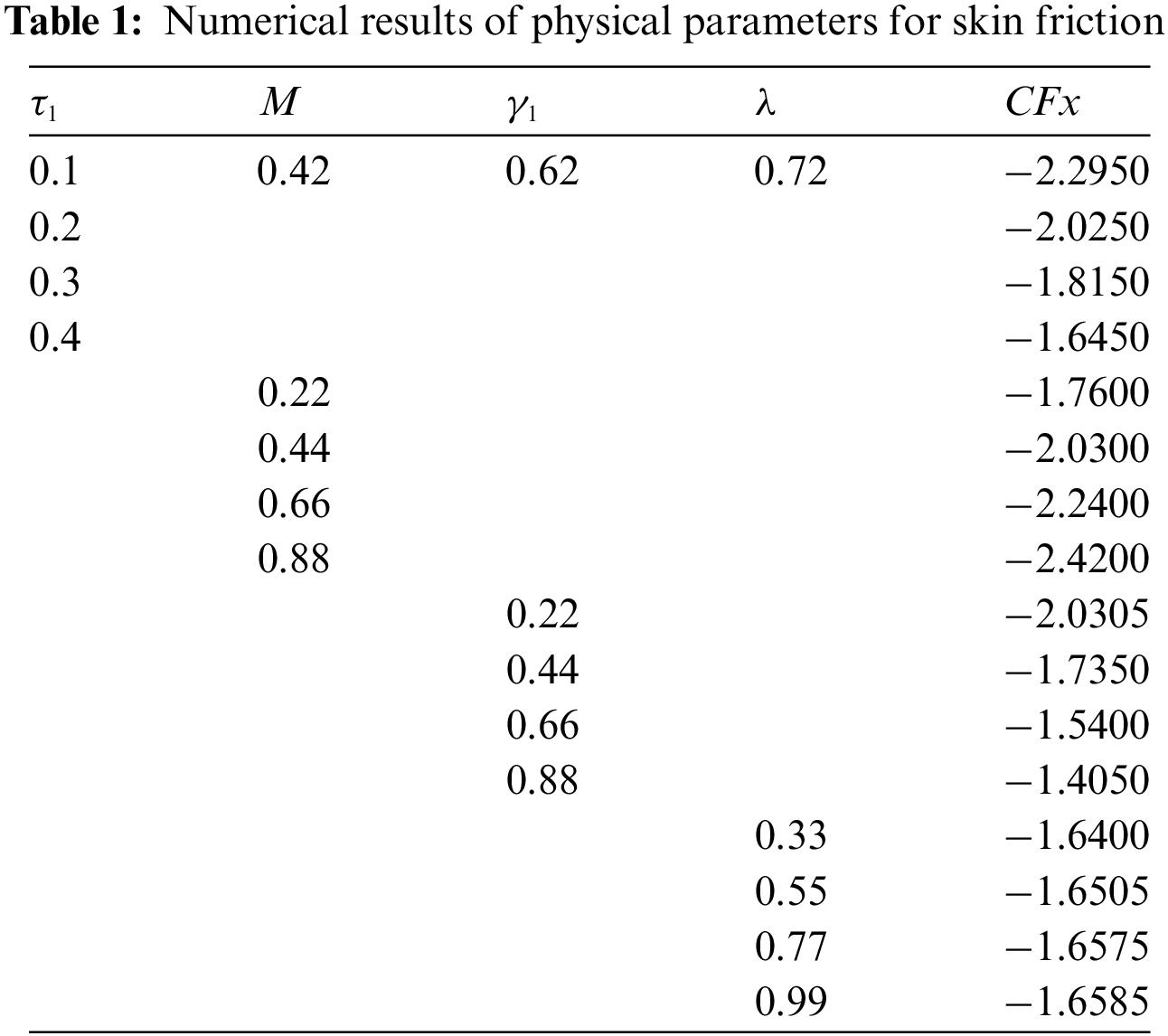
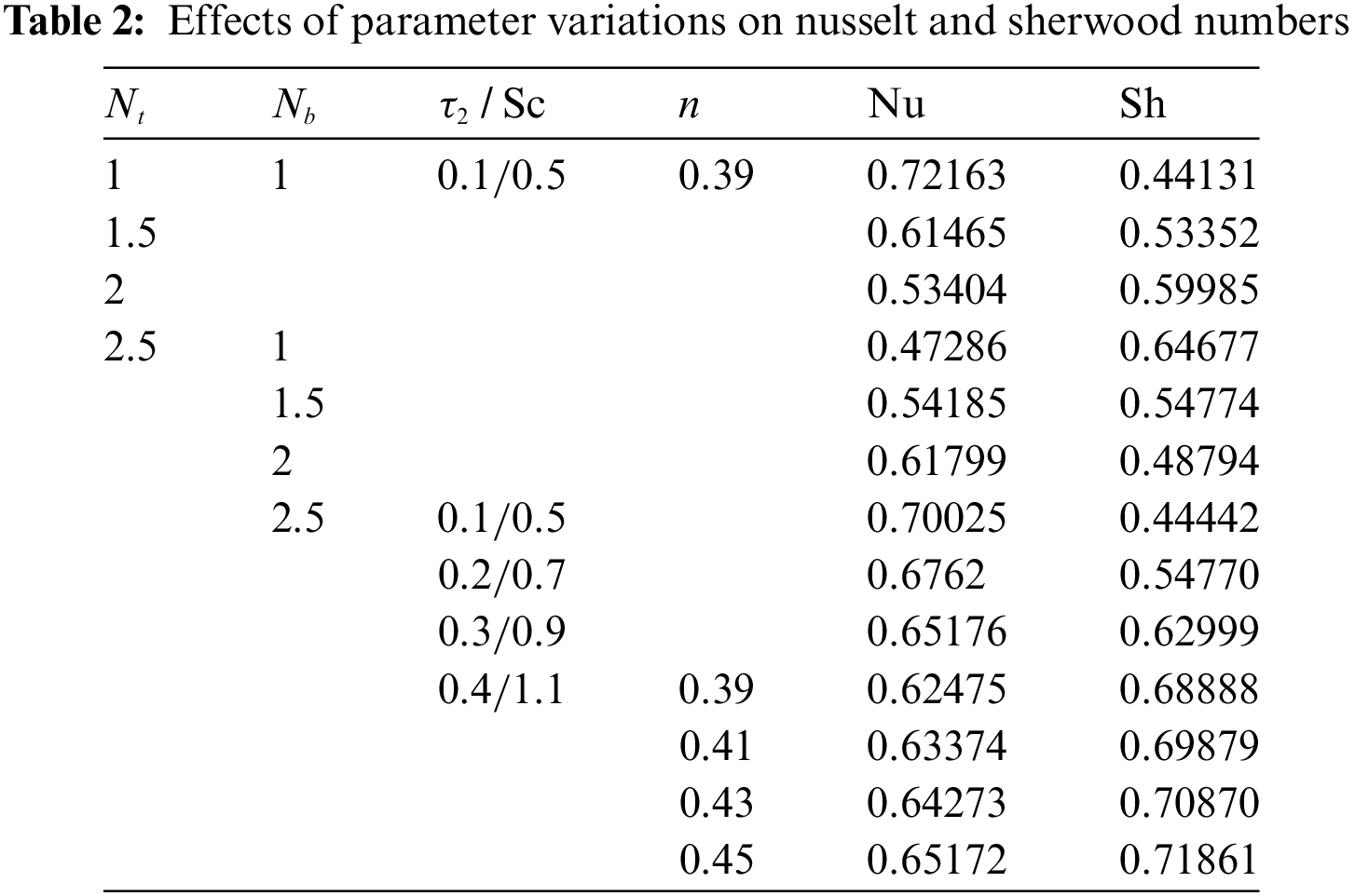
Table 2 analyzes the correlation between parameters Ntp, Nbm, γ1, Sc, and n with the heat and mass transfer characteristics measured by Nusselt (Nu) and Sherwood (Sh) numbers. The Brownian motion parameter Nbm and the thermophoresis parameter Ntp notably increase both Nu and Sh, with Nu seeing increases up to 14.6% and Sh up to 23.2%. Increases in the Biot number (γ1) for heat transfer, reflecting improved heat transfer efficiency at the surface relative to the interior. Similarly, a rise in the thermal Biot number (γ2) for mass transfer, enhances the Sherwood number (Sh), indicating more effective convective mass transfer compared to diffusion. Similarly, an increase in the Schmidt number (Sc) enhances the mass transfer rate as indicated by a rise in Sh, with percentage increases reflecting the direct correlation with Sc. The velocity power index (n) also significantly affects these transfer rates, with increases in n resulting in corresponding rises in both Nu and Sh by approximately 1.4%.

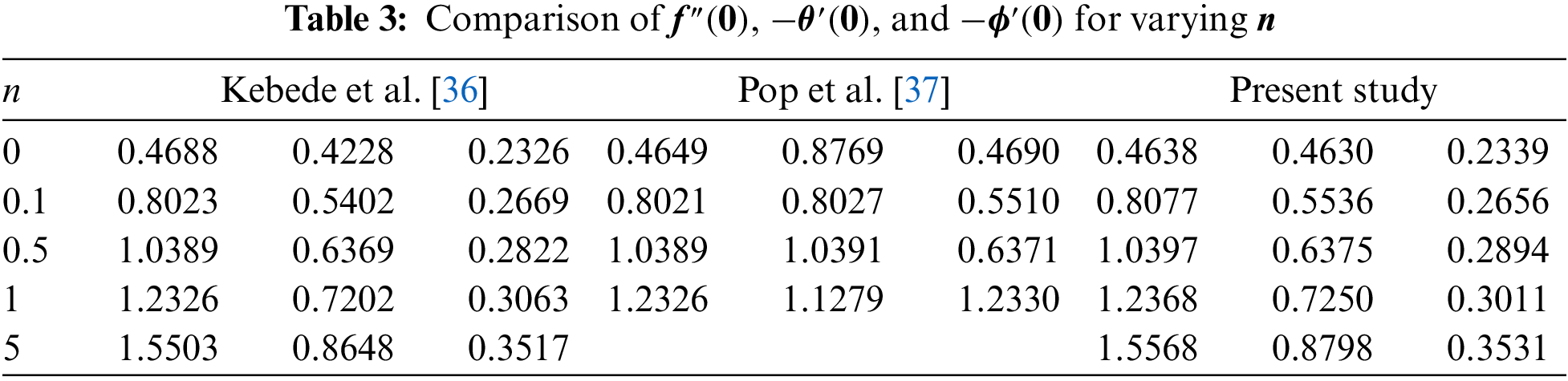
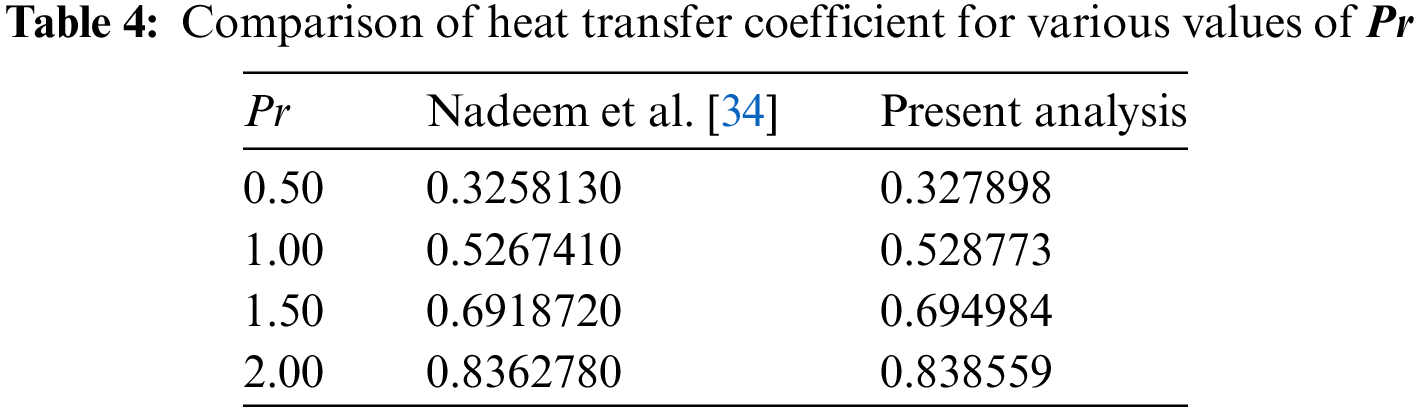
In Tables 3 and 4, we present a comparison of our study findings with the results from previous research by Nadeem et al. [34], Kebede et al. [36], and Pop et al. [37]. These comparisons specifically focus on the behaviors of f′′(0), θ′(0), and ϕ′(0) for different values of n and Pr. Our results are closely aligned with those reported in the literature, reinforcing the validity and precision of our computational approach.

5  Conclusion

This research applies the Buongiorno model to investigate the behavior of nanoparticles in a mixed convection second-grade fluid flowing over a variable thickness stretching sheet. Key features such as Joule heating, slip effects, thermal radiation, heat generation, and magnetohydrodynamic forces are considered. The main findings of this study are as follows:

•   Increasing Πrad enhances the temperature profile, expanding the thermal boundary layer.

•   Increasing the thermal Biot number enhances the temperature gradient at the boundary, while a rise in the concentration Biot number sharpens the concentration gradient at the boundary.

•   Higher second-grade fluid parameters increase velocity profiles due to enhanced fluid elasticity.

•   An increase in the velocity slip parameter reduces velocity gradients by lowering boundary resistance.

•   Nusselt and Sherwood numbers increase by up to 14.6% and 23.2%, respectively, due to higher Brownian motion and thermophoresis parameters.

•   Skin friction coefficients decrease by 37.5% with increasing magnetic field strength.

Investigating different fluid models such as Oldroyd-B and Sisko fluids on complex surfaces could provide further insights into non-Newtonian behaviors under stretching and magnetic influences. This research could enhance applications in industries that demand precise fluid dynamics control.

Acknowledgement: The authors would like to express their gratitude to the reviewers for their insightful and constructive comments, which have significantly contributed to enhancing the quality of this article according to the journal’s standards.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Muhammad Shoaib Anwar; analysis and interpretation of results: Mumtaz Khan; draft manuscript preparation: Muhammad Shoaib Anwar, Mumtaz Khan. Mudassar Imran and Amer Rasheed contributed to addressing reviewer comments and the preparation of the revised manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included within this article.

Ethics Approval: This study did not involve human or animal subjects and, as such, ethical approval was not required.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Choi SUS, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. ASME Fed. 1995;231:99–105. [Google Scholar]

2. Eastman JA, Choi SUS, Li S, Yu W, Thompson LJ. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl Phys Lett. 2001;78:718–20. doi:10.1063/1.1341218. [Google Scholar] [CrossRef]

3. Ghalambaz M, Sabour M, Sazgara S, Pop I, Trambitas R. Insight into the dynamics of ferrohydrodynamic (FHD) and magnetohydrodynamic (MHD) nanofluids inside a hexagonal cavity in the presence of a non-uniform magnetic field. J Magn Magn Mater. 2020;497:166024. doi:10.1016/j.jmmm.2019.166024. [Google Scholar] [CrossRef]

4. Rashid U, Liang H, Baleanu D, Iqbal A, Abbas M. Shape effect of nanosize particles on magnetohydrodynamic nanofluid flow and heat transfer over a stretching sheet with entropy generation. Entropy. 2020;22(10):1171. doi:10.3390/e22101171 [Google Scholar] [PubMed] [CrossRef]

5. Wahid NS, Arifin N, Khashi’ie N, Pop I, Bachok N, Hafidzuddin E. MHD hybrid nanofluid flow with convective heat transfer over a permeable stretching/shrinking surface with radiation. Int J Numer Methods Heat Fluid Flow. 2021;32(5). doi:10.1108/HFF-04-2021-0263. [Google Scholar] [CrossRef]

6. Swain B. Dynamics of ternary-hybrid nanofluid of water conveying copper, alumina and silver nanoparticles when entropy generation, viscous dissipation, Lorentz force are significant. ZAMM. 2023;103(9):e202200254. doi:10.1002/zamm.202200254. [Google Scholar] [CrossRef]

7. Ramzan M, Dawar A, Saeed A, Kumam P, Sitthithakerngkiet K, Lone S. Analysis of the partially ionized kerosene oil-based ternary nanofluid flow over a convectively heated rotating surface. Open Phys. 2022;20:507–25. doi:10.1515/phys-2022-0055. [Google Scholar] [CrossRef]

8. Dash R, Mishra S, Pattnaik PK. Influence of radiative heat energy on the MHD flow of Cu-kerosene nanofluid over a vertical plate: laplace transform technique. Biointerface Res Appl Chem. 2021;12(5):6234–51. doi:10.33263/BRIAC125.62346251. [Google Scholar] [CrossRef]

9. Bhandari A, Pannala R. Optimization of heat transfer properties of nanofluid flow over a shrinking surface through mathematical modeling. Int J Appl Mech Eng. 2020;25(1):40–56. doi:10.2478/ijame-2020-0019. [Google Scholar] [CrossRef]

10. Kotha G, Kolipaula VR, Rao MVS, Penki S, Chamkha AJ. Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. Eur Phys J Plus. 2020;135(6). doi:10.1140/epjp/s13360-020-00606-2. [Google Scholar] [CrossRef]

11. Hussain A, Arshad M, Rehman A, Hassan A, Elagan S, Ahmad H et al. Three-dimensional water-based magneto-hydrodynamic rotating nanofluid flow over a linear extending sheet and heat transport analysis: a numerical approach. Energies. 2021;14(16):5133. doi:10.3390/en14165133. [Google Scholar] [CrossRef]

12. Smith AB, Johnson CD. Advanced rheology of non-Newtonian fluids. J Fluid Mech. 2018;123:45–67. [Google Scholar]

13. Davis LE, Lee MJ. Industrial applications of non-Newtonian fluids. Eng Appl. 2017;15(2):89–102. [Google Scholar]

14. Green P, Thompson K. Characteristics of Second-Grade Fluids. Rheol Today. 2021;20(4):210–25. [Google Scholar]

15. Khan Z, Ali F, Haq S, Khan I. A time fractional second-grade magnetohydrodynamic dusty fluid flow model with variable conditions: application of Fick’s and Fourier’s laws. Front Phys. 2022;10:1006893. doi:10.3389/fphy.2022.1006893. [Google Scholar] [CrossRef]

16. Qayyum S, Khan M, Masood F, Chu Y, Kadry S, Nazeer M. Interpretation of entropy generation in Williamson fluid flow with nonlinear thermal radiation and first-order velocity slip. Math Meth Appl Sci. 2020;44:7756–65. doi:10.1002/mma.6735. [Google Scholar] [CrossRef]

17. Ahmed NA, Krishna MV, Aljohani A. Heat and mass transfer in MHD boundary layer flow of a second-grade fluid past an infinite vertical permeable surface. Heat Transf. 2021;50:6022–42. doi:10.1002/htj.22160. [Google Scholar] [CrossRef]

18. Anwar T, Kumam P, Asifa, Thounthong P, Muhammad S, Duraihem FZ. Generalized thermal investigation of unsteady MHD flow of Oldroyd-B fluid with slip effects and Newtonian heating; a Caputo-Fabrizio fractional model. Alex Eng J. 2021;61(3):2188–202. doi:10.1016/j.aej.2021.06.090. [Google Scholar] [CrossRef]

19. Hayat T, Shah F, Alseadi A. Cattaneo-Christov double diffusions and entropy generation in MHD second grade nanofluid flow by a Riga wall. Int Commun Heat Mass Transf. 2020;119:104824. doi:10.1016/j.icheatmasstransfer.2020.104824. [Google Scholar] [CrossRef]

20. Khan M, Alzahrani F. Dynamics of activation energy and nonlinear mixed convection in Darcy-Forchheimer radiated flow of Carreau nanofluid near stagnation point region. J Therm Sci Eng Appl. 2021;13. doi:10.1115/1.4049434. [Google Scholar] [CrossRef]

21. Das S, Sarkar S, Jana R. Assessment of irreversible losses of non-Newtonian nanofluid flow underlying hall current, chemical reaction and thermal radiation. World J Eng. 2020;18(2):228–50. doi:10.1108/WJE-07-2020-0266. [Google Scholar] [CrossRef]

22. Chu Y, Shah F, Khan M, Kadry S, Abdelmalek Z, Khan W. Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. J Mater Res Technol. 2020;9:13977–87. doi:10.1016/j.jmrt.2020.09.101. [Google Scholar] [CrossRef]

23. Tanveer A, Mahmood S, Hayat T, Alsaedi A. On electroosmosis in peristaltic activity of MHD non-Newtonian fluid. Alex Eng J. 2021;60:3369–77. doi:10.1016/j.aej.2020.12.051. [Google Scholar] [CrossRef]

24. Aloliga G, Seini IY, Musah R. On MHD flow of non-Newtonian viscoelastic fluid over a stretched magnetized surface. Am J Appl Math. 2022;10(2):29. doi:10.11648/j.ajam.20221002.12. [Google Scholar] [CrossRef]

25. Sakiadis BC. Boundary-layer behavior on continuous solid surface: i. boundary-layer equations for two-dimensional and axisymmetric flow. J AIChe. 1961;7:26–8. doi:10.1002/aic.690070108. [Google Scholar] [CrossRef]

26. Tsou FK, Sparrow EM, Goldstain RJ. Flow and heat transfer in the boundary layer on a continuous moving surface. Int J Heat Mass Transf. 1967;10:219–35. doi:10.1016/0017-9310(67)90100-7. [Google Scholar] [CrossRef]

27. Hussain S, Parveen R, Katbar N, Rehman S, Abd-Elmonem A, Abdalla N, et al. Entropy generation analysis of MHD convection flow of hybrid nanofluid in a wavy enclosure with heat generation and thermal radiation. Rev Adv Mater Sci. 2024;63(1):20240037. doi:10.1515/rams-2024-0037. [Google Scholar] [CrossRef]

28. Lin Y, Rehman S, Akkurt N, Shedd T, Kamran M, Imran Qureshi M et al. Free convective trickling over a porous medium of fractional nanofluid with MHD and heat source/sink. Sci Rep. 2022;12:20778. doi:10.1038/s41598-022-25063-y [Google Scholar] [PubMed] [CrossRef]

29. Sharma R, Bisht A, Kumar A. Numerical study of fractional boundary layer flow over a stretching sheet with variable thickness: a finite difference approach. AIP Conf Proc. 2020;2253:020018. doi:10.1063/5.0018931. [Google Scholar] [CrossRef]

30. Hosseini Z, Abidi A, Mohammadi S, Mehryan S, Hulme C. A fully resolved computational fluid dynamics study of the boundary layer flow of an aqueous nanoliquid comprising gyrotactic microorganisms over a stretching sheet: the validity of conventional similarity models. Mathematics. 2021;9(21):2655. doi:10.3390/math9212655. [Google Scholar] [CrossRef]

31. Alam A, Marwat DNK, Ali A. Flow of nano-fluid over a sheet of variable thickness with non-uniform stretching (shrinking) and porous velocities. Adv Mech Eng. 2021;13. doi:10.1177/16878140211012913. [Google Scholar] [CrossRef]

32. Rehman S, Rehman S, Khan A, Khan Z. The effect of flow distribution on heat and mass transfer of MHD thin liquid film flow over an unsteady stretching sheet in the presence of variational physical properties with mixed convection. Physica A. 2020;551:124120. doi:10.1016/j.physa.2019.124120. [Google Scholar] [CrossRef]

33. Fatunmbi E, Okoya S, Makinde O. Convective heat transfer analysis of hydromagnetic micropolar fluid flow past an inclined nonlinear stretching sheet with variable thermo-physical properties. Diffus Found. 2020;26:63–77. doi:10.4028/www.scientific.net/DF.26.63. [Google Scholar] [CrossRef]

34. Abbas N, Tumreen M, Shatanawi W, Qasim M, Shatnawi TA. Thermodynamic properties of second grade nanofluid flow with radiation and chemical reaction over slendering stretching sheet. Alex Eng J. 2023;70:219–30. doi:10.1016/j.aej.2023.02.031. [Google Scholar] [CrossRef]

35. Cortell R. A numerical tackling on Sakiadis flow with thermal radiation. Chin Phys Lett. 2008;25(4):1340. doi:10.1088/0256-307X/25/4/048. [Google Scholar] [CrossRef]

36. Kebede T, Haile E, Awgichew G, Walelign T. Heat and mass transfer analysis in unsteady flow of tangent hyperbolic nanofluid over a moving wedge with buoyancy and dissipation effects. Heliyon. 2020;6:e03776. doi:10.1016/j.heliyon.2020.e03776 [Google Scholar] [PubMed] [CrossRef]

37. Pop I, Ingham DB. Convective heat transfer: mathematical and computational modelling of viscous fluids and porous media. 1st ed. New York: Pergamon; 2001. [Google Scholar]