Artificial Intelligence-Driven FVM-ANN Model for Entropy Analysis of MHD Natural Bioconvection in Nanofluid-Filled Porous Cavities

Nomenclature

1  Introduction

Natural bioconvection is the self-organizing patterns generated by the collective movement of microorganisms in a fluid media, which are primarily driven by density gradients caused by their own motility and biological activity. Gyrotactic microorganisms, such as certain algae species, have a particular swimming habit that is influenced by gravitational and viscous torques, resulting in different bioconvective patterns. When these microorganisms are suspended in a nanofluid (a base fluid containing nanoparticles), the fluid’s thermal and rheological properties change considerably, improving heat transmission and stability.

Jamuna et al. [1] investigated the flow of bioconvective nanofluids containing gyrotactic microorganisms within a porous square cavity. Utilizing the Darcy model under the Boussinesq approximation, they considered the effects of both heat generation and absorption. Obalalu et al. [2] examined bioconvective nanofluid flow using Oswald–DeWaele power-law models, focusing on the swimming behavior of gyrotactic microorganisms and the resulting bioconvection patterns. Tanveer et al. [3] analyzed heat and mass transfer in a copper-water hybrid nanofluid under the influence of ohmic dissipation, also accounting for the presence of gyrotactic microorganisms.

Introducing a magnetic field into these systems adds complexity due to the interaction between the magnetic field and the conductive nanofluid, which affects flow and heat transfer through Lorentz forces. The inclusion of porous materials further complicates the dynamics by adding resistance to fluid flow and introducing additional heat exchange mechanisms. Kotha et al. [4] studied magnetohydrodynamic flow and heat and mass transfer in a water-based nanofluid containing gyrotactic microorganisms over a vertical plate, considering the impacts of heat generation or absorption. Abbas et al. [5] explored the effects of reduced gravity and solar radiation on magnetohydrodynamic fluid flow and heat transfer around a stationary sphere within a porous medium. They developed a dimensionless model using suitable variables and transformed it into a primitive form for efficient computation. Jeelani et al. [6] enhanced heat transfer by dispersing cylindrical-shaped alumina and copper nanoparticles in ethylene glycol, employing a non-Newtonian Maxwell fluid model. Their study analyzed the effects of solar radiation, plate suction, and magnetohydrodynamics on a Maxwell hybrid nanofluid.

Yadav et al. [7] investigated heat and mass transfer in the flow of immiscible couple stress fluids through a curved channel with walls maintained at different temperatures. The fluids are influenced by an external magnetic field perpendicular to the flow direction, and the channel walls are considered porous to allow for suction or injection. Yadav et al. [8] examined how factors like inclination angle, porous media, slip boundary conditions, and magnetic fields affect flow variables such as velocity, wall shear stress, pressure difference, head loss, and volumetric flow rate in a channel containing two electrically conducting, immiscible fluids—Newtonian and couple stress fluids. The inclined channel is divided into two equal sub-regions, each occupied by one type of fluid. Biswas et al. [9] investigated magnetohydrodynamic (MHD) bioconvection driven by the movement of oxytactic microorganisms within a linearly heated square cavity containing porous media and a copper-water nanofluid. They assessed how various multi-physical parameters affect fluid flow, temperature distribution, oxygen concentration, and microbial patterns using both local and global analytical methods. Maheshwari et al. [10] analyzed the effects of an external magnetic field combined with bottom heating on the bioconvection behavior of a nanofluid containing gyrotactic microorganisms. Their research employed modified Maxwell’s equations and an extended Buongiorno model to formulate the governing equations for the nanofluid within a Darcy-Brinkman porous medium. In a separate study, Biswas et al. [11] explored mixed thermos-bioconvection in a magnetically responsive fluid that includes copper nanoparticles and oxytactic bacteria within a uniquely shaped W-configuration porous cavity. The system exhibited buoyant convection due to isothermal heating at a wavy bottom wall, while mixed convection was induced by the shearing action of a top-cooled sliding wall.

Rashed et al. [12] examined laminar mixed convection at the stagnation point in an unsteady, electrically conducting hybrid nanofluid composed of Fe3O4 and Cu nanoparticles in water, flowing over a horizontal porous stretched sheet. Their study focused on the impacts of both external and induced magnetic fields, as well as the roles of viscous and gyrotactic microorganisms. Entropy generation analysis in such systems is essential for understanding the irreversibility associated with heat transfer, fluid friction, and mass transfer. By quantifying entropy production, researchers can pinpoint areas and conditions where energy dissipation peaks, providing insights for enhancing system efficiency and optimizing design parameters for engineering applications. This is particularly important in sectors like biomedical engineering, environmental technology, and renewable energy, where effective thermal management and energy conservation are crucial. Mandal et al. [13] investigated entropy generation in a Maxwell nanofluid with gyrotactic microorganisms flowing over a radiatively heated inclined stretching cylinder.

Meenakshi et al. [14] investigated the influence of Brownian motion and thermophoresis on entropy generation in the bioconvective flow of a nanofluid containing gyrotactic microorganisms within a porous cavity. They utilized Darcy’s Boussinesq approximation to address the porosity term in the momentum equation. Mishra et al. [15] focused on optimizing entropy generation in the flow of a ternary hybrid Jeffery nanofluid (Ag-Au-TiO₂/PVA) through a peristaltic vertical channel that contains swimming gyrotactic microorganisms. Ramzan et al. [16] examined the two-dimensional flow behavior of a Carreau-ternary hybrid nanoliquid subjected to a magnetic field over a stretching surface. Their study explored the heat transfer mechanism, considering the effects of thermal radiation and heat sources or sinks. Li et al. [17] analyzed the effects of activation energy and chemical reactions on the magnetohydrodynamic Darcy-Forchheimer flow of a squeezed Casson fluid through a porous medium within a horizontal channel, where two parallel plates are in motion. For additional research involving magnetohydrodynamics in fluid flows, readers are referred to References [18–20] and the citations within those works.

In recent times, ANNs have gained prominence as a promising alternative to traditional Computational Fluid Dynamics (CFD) methods. Inspired by the neural structures of the human brain, ANNs are computational model’s adept at learning patterns and making data-driven predictions. Their ability to approximate complex nonlinear functions makes them suitable for various applications in CFD, including flow prediction, turbulence modeling, and optimization. The application of ANNs in CFD began gaining traction due to their potential to significantly reduce computational costs while maintaining accuracy. Early studies, such as those by Milano et al. [21], demonstrated the feasibility of using neural networks to model turbulent flows, showing that ANNs could effectively capture the essential dynamics of fluid motion with lower computational overhead compared to traditional methods. Building upon these findings, later research has broadened the exploration by investigating various neural network architectures to tackle specific challenges in computational fluid dynamics (CFD). These include convolutional neural networks (CNNs) [21] and recurrent neural networks (RNNs) [22].

One of the notable advantages of using ANNs in CFD is their ability to generalize from training data, allowing them to predict fluid behavior in new, unseen scenarios. This capability has been leveraged in data-driven turbulence modeling, where ANNs are trained on high-fidelity simulation data or experimental measurements to develop models that can accurately predict turbulent stresses and eddies. Ling et al. [23] presented a groundbreaking study in this area, introducing a deep learning approach for Reynolds-Averaged Navier-Stokes (RANS) models that improved predictive accuracy over traditional models. Furthermore, ANNs have been integrated into CFD workflows to enhance optimization and control processes. For example, Rabault et al. [24] used deep reinforcement learning, a type of ANN, to optimize active flow control strategies, achieving significant improvements in flow performance metrics with reduced computational effort. This integration highlights the potential of ANNs not only to accelerate CFD simulations but also to enable real-time optimization and adaptive control in complex fluid systems. The incorporation of ANNs into CFD represents a transformative development in the field. By leveraging the power of machine learning, researchers and engineers can achieve faster, more efficient, and potentially more accurate simulations, opening new avenues for innovation in fluid dynamics [25–28]. As technology advances, ANNs are anticipated to significantly enhance computational fluid dynamics (CFD) techniques and their uses. Aly et al. [25] investigated the incompressible smoothed particle hydrodynamics (ISPH) with machine learning (ML) to examine the uses of two different domain shapes where it was discovered that the velocity field decreases substantially as the Darcy number decreases due to the increased porous resistance at a lower Darcy number. Recent research on combining numerical methods with ANN models to address heat transfer in intricate geometries is discussed in the referenced studies [26–30]. Zou et al. [31] provided an overview of ANN fundamentals. Sun et al. [32] used ANN to predict heat transfer in supercritical CO2 flow within tubes, showing its effectiveness in thermal systems. Rehman et al. [33] applied ANN to optimize drag coefficients for obstacles. Fuxi et al. [34] assessed how spring turbulators affect solar collectors using ANN. Ali et al. [35] explored ANN and fractional calculus in analyzing blood flow with nanoparticles. Karmakar et al. [36] extended ANN to study bioelectromagnetic in blood circulation, incorporating hybrid nanoparticles and microbes.

This research presents a novel integration of an ANN with FVM to perform entropy analysis of MHD natural bioconvection within a porous cavity filled with a nanofluid. This study uniquely combines ANN with numerical simulation to predict the Nusselt number with high accuracy, which is unprecedented in similar analyses. Furthermore, unlike prior studies that focused on simpler systems, this research examines the effects of complex factors such as cooling area length, heat source location, and porosity on heat and mass transfer processes, providing insights that can optimize thermal management in engineering applications such as heat exchangers and biomedical systems. The model demonstrates high predictive accuracy, as shown by the excellent agreement between ANN-predicted values and simulated results, significantly contributing to the advancement of computational approaches in thermal systems.

Investigating entropy production in MHD natural bioconvection within a porous cavity containing a nanofluid with gyrotactic microorganisms enhances our understanding of fundamental fluid dynamics and thermodynamics. This study also offers practical insights for improving the efficiency and effectiveness of various technological applications. The proposed model has potential applications in fields like biomedical engineering, environmental technology, and renewable energy, where efficient thermal management and energy conservation are crucial. In this research, the applied magnetic field is angled to simulate a more generalized and realistic physical scenario. In many practical applications, magnetic fields are not always aligned with the primary axes (horizontal or vertical); rather, they are inclined due to the configuration of the magnetic source or external environmental conditions. The inclination angle of the magnetic field introduces Lorentz forces that interact with the fluid flow and nanoparticles, influencing heat and mass transfer properties. This interaction between the magnetic field and the nanofluid is crucial for controlling the flow dynamics in MHD systems. The chosen angle helps to investigate how such inclinations impact the behavior of bioconvection in a porous cavity, contributing to the overall entropy generation and heat transfer efficiency. Thus, the specifically directed magnetic field serves as a model to study real-world situations in engineering applications such as cooling systems, energy storage, and bioengineering where magnetic fields are applied to control fluid flow and enhance system performance.

2  Mathematical Modeling

Consider a steady, two-dimensional natural convection flow within a porous square cavity of side length (H), occupied by a nanofluid containing gyrotactic microorganisms as shown in Fig. 1. The horizontal and vertical positions are represented by coordinates (x) and (y), respectively. The flow is laminar, incompressible, and maintains steady-state conditions. The vertical and horizontal walls are partially cooled over a variable length (B), while the remaining portions are insulated (adiabatic). The inner surfaces with a wavy profile are maintained at a higher temperature (Th) and concentration (Ch). Gravity acts uniformly in a single direction throughout the cavity. All walls adhere to no-slip boundary conditions. Table 1 lists the thermal properties of the constituent materials: water, copper, and titanium dioxide.

Figure 1: Initial diagram of a physical model

The equations governing the continuity, momentum, energy, and concentration for the hybrid nanofluid, under the assumptions of incompressible, laminar, single-phase, and steady-state flow, are formulated as follows [37–40]:

∂u∂x+∂v∂y=0,(1)

1ε2(u∂u∂x+v∂u∂y)=−1ρhnf∂p∂x+1ε(μhnf)ρhnf.∇2u−(μhnf)ρhnfuK+σhnfB02ρhnf(vsin⁡Φcos⁡Φ−usin2⁡Φ),(2)

1ε2(u∂v∂x+v∂v∂y)=−1ρhnf∂p∂y+1ε(μhnf)ρhnf∇2v−(μhnf)ρhnfvK−1ρhnf[γΔρm+(ρβ∗)hnfρhnfg(C−Cmin)−(ρβ)hnf(T−Tc)]g+σhnfB02ρhnf(usin⁡Φcos⁡Φ−vcos2Φ),(3)

1ε(u∂T∂x+v∂T∂y)=αnf∇2T+Q0ε(ρcp)nf,(4)

u∂C∂x+v∂C∂y=DB∇2C−δm,(5)

∂∂x[um+u~m−Dm∂m∂x]+∂∂y[vm+v~m−Dm∂m∂y]=0.(6)

In these equations, u~=(lWCΔC)∂C∂x and v~=(lWCΔC)∂C∂y, where x and y are the Cartesian coordinates, u and v are the velocity components along the x and y-axes, T,C are the temperature and concentration, K is the permeability of a porous medium, μ is the dynamic viscosity of the suspension, n is the number density of motile microorganisms, g is the gravity, Q0 is the strength of a heat source, DC is the diffusivity of oxygen, Dn is the diffusivity of the microorganisms. Cmin is the minimum oxygen concentration, b is the chemotaxis constant, WC is the maximum cell swimming speed.

2.1 Dimensionless Forms of Equations

The dimensionless set [37–40] is:

X=xH,Y=yH,U=uHαf,V=vHαf,P=pH2ρfαf2,θ=T−TcΔT,φ=C0−CminΔCM=mm0,ΔT=(Th−Tc),ΔC=(C0−CD)=dH,B=bHmin.(7)

Substitute “Eq. (7)” into Eqs. (1)–(6) returns the dimensionless equations [37–41]:

∂U∂X+∂V∂Y=0,(8)

1ε2(U∂U∂X+V∂U∂Y)=−∂P∂X+Prε.(ρfρhnf)(μhnfμf).∇2U−PrDa.(ρfρhnf)(μhnfμf).U+(ρfρhnf)(σhnfσf).Ha2.Pr.(VsinΦcosΦ−Usin2⁡Φ),(9)

1ε2(U∂V∂X+V∂V∂Y)=−∂P∂Y+Prε.(ρfρhnf)(μhnfμf).∇2V−PrDa.(ρfρhnf)(μhnfμf).V+Pr.Ra.(ρβ)hnfρhnf.βf.(θ−Rb.M)+Rac.φ+(ρfρhnf)(σhnfσf).Ha2.Pr.(UsinΦcosΦ−Vcos2⁡Φ),(10)

1ε(U∂θ∂X+V∂θ∂Y)=αeff.nfαf∇2θ+1ε(ρcp)f(ρcp)nfQ,(11)

U∂φ∂X+V∂φ∂Y=1σSc∇2φ,(12)

Scχ(U∂M∂X+V∂M∂Y)+PePr(M∇2φ+∂M∂X∂φ∂X+∂M∂Y∂φ∂Y)=Pr∇2M.(13)

With the boundary conditions as follows:

U=V=0,0≤X≤1,0≤Y≤1

θ=φ=0,∂M∂X=Pe.M∂φ∂X,(D−0.5B)≤Y≤(D+0.5B),∂θ∂X=∂φ∂X=∂M∂X=0,othrwise,at walls X=0,1

θ=φ=0,∂M∂Y=PeM∂φ∂Y,(D−0.5B)≤X≤(D+0.5B),∂θ∂Y=∂φ∂Y=∂M∂Y=0,othrwise,at walls Y=0,1.

On the obstacles:

θ=φ=M=1.

Ra=gβf(Th−Tc)H3αfυf is Rayleigh number, γ=δeαfH2 is a relaxation parameter, Ha=B0Hσfμf is the Hartmann number, and Pr=υfαf is Prandtl number, and Da=KH2 is Darcy parameter.

The local Nusselt number is stated as:

(Nus)X=0,1=−keff.nfkeff.f(∂θ∂X)X=0,1 and (Nus)Y=0,1=−keff.nfkeff.f(∂θ∂Y)Y=0,1.(14)

The average Nusselt number is stated as:

(Numf)X=0,1=1B∫D−0.5BD+0.5B(Nus)X=0,1dX,(Numf)Y=0,1=1B∫D−0.5BD+0.5B(Nus)Y=0,1dY,(15)

Numf=(Numf)X=0,1+(Numf)Y=0,14.(16)

The local Sherwood numbers are stated as:

Shs(Y=0,1)=−(∂φ∂Y)Y=0,1,Shs(X=0,1)=−(∂φ∂X)X=0,1.(17)

The local microorganism density numbers are stated as:

Mhs(Y=0,1)=−(∂M∂Y)Y=0,1,Mhs(X=0,1)=−(∂M∂X)X=0,1.(18)

2.2 Entropy Generation Analysis

In linear transport theory under local thermodynamic equilibrium, the dimensionless total local entropy generation for the fluid and solid phases is represented as:

s=(keff.hnfT2)[(∂T∂x)2+(∂T∂y)2]+(μhnfT){1K(u2+v2)+2[(∂u∂x)2+(∂v∂y)2]+(∂u∂y+∂v∂x)2}+RDBC⌈(∂C∂x)2+(∂C∂y)2⌉+RDBT⌈∂T∂x∂C∂x+∂T∂y∂C∂y⌉+RDmm⌈(∂m∂x)2+(∂m∂y)2⌉+RDmT⌈∂T∂x∂m∂x+∂T∂y∂m∂y⌉+(σhnfT)B02(usin⁡Φ−vcos⁡Φ)2.(19)

The dimensionless entropy generation, (S), is stated as:

S=s.(H2kf)=1(θ+CT)2.(keff.hnfkf)[(∂θ∂X)2+(∂θ∂Y)2]+1(θ+CT)Θ1.(μnfμf).{1Da(U2+V2)+2[(∂U∂X)2+(∂V∂Y)2]+(∂V∂X+∂U∂Y)2}+1(φ+CC)Θ2.[(∂φ∂X)2+(∂φ∂Y)2]+1(θ+CT).Θ2.[∂φ∂X∂θ∂X+∂φ∂Y∂θ∂Y]+1M4[(∂M∂X)2+(∂M∂Y)2]1(θ+CT)4[∂M∂X∂θ∂X+∂M∂Y∂θ∂Y]+1(θ+CT).Θ1.(σnfσf).Ha2.(Usin⁡Φ−Vcos⁡Φ)2=Sh+Sv+Sφ+Sφ.θ+SM+SM.θ+Sj.(20)

Here, the irreversibility ratios Θ1,Θ2,Θ3andΘ4 are stated as:

Θ1=μfΔT.kf(αfH)2,Θ2=RDB.(ΔCkf),Θ3=keff.sks,kfs=kfks,Θ4=RDm.(m0kf).(21)

The Bejan number is stated as:

Be=ShS.(22)

To describe the influence of nanoparticles, magnetic fields, and temperature differences on the average Nusselt number, total entropy generation, and Bejan number, we define the following dimensionless ratios: Nusselt ratio, entropy generation ratio, and Bejan number ratio.

Numf+=Numf(Numf)ϕ=0,Numf++=Numf(Numf)Ha=0,Numf+++=Numf(Numf)Φ=0,(23)

S+=S(S)ϕ=0,S++=S(S)Ha=0,S+++=S(S)Φ=0,(24)

Be+=Be(Be)ϕ=0,Be++=Be(Be)Ha=0,Be+++=Be(Be)Φ=0,e+=s+Numf+,e++=s++Numf++.e+++=s+++Numf+++.(25)

In the above equations αeff,hnf and αeff,f are equal to:

αeff,hnf=keff,hnf(ρcp)hnf,

αeff,f=keff,f(ρcp)f,

keff,hnf=εkhnf+(1−ε)ks,

keff,f=εkf+(1−ε)ks.

The expressions for the thermal diffusivity, effective density, thermal expansion coefficient, and thermal conductivity of the hybrid nanofluid are as follows:

αhnfαf=khnfkf(ρCp)hnf(ρCp)f,

ρhnfρf=(1−ϕCu)(1−ϕTiO2+ϕTiO2ρTiO2ρf)+ϕCuρCuρf,

βhnfβf=(1−ϕCu)(1−ϕTiO2+ϕTiO2βTiO2βf)+ϕCuβCuβf,

khnfkbf=kCu+2kbf−2ϕCu(kbf−kCu)kCu+2kbf+ϕCu(kbf−kCu),

where kbfkf=kTiO2+2kf−2ϕ1(kf+kTiO2)kTiO2+2kf+ϕ1(kf−kTiO2).

The formula for the heat capacity of the hybrid nanofluid is:

(ρCp)hnf(ρCp)f=(1−ϕCu)(1−ϕTiO2+ϕTiO2(ρCp)TiO2(ρCp)f)+ϕCu(ρCp)Cu(ρCp)f.

The formula for the effective dynamic viscosity of the hybrid nanofluid is:

σhnfσbf=σCu+2σbf−2ϕCu(σbf−σCu)σCu+2σbf+ϕCu(σbf−σCu),

where σbfσf=σTiO2+2σf−2ϕTiO2(σf−σTiO2)σTiO2+2σf+ϕTiO2(σf−σTiO2).

3  ANN Modelling

In this work, the neural network based on the Levenberg-Marquardt training (LMT) method is applied to predict the values of Nu¯. The ANN uses the multilayer perceptron (MLP) due to its layered structure. Also, MLP has a large learning capacity according to Çolak [42]. To obtain reliable forecasts, a dimensionless time τ and fin length LFin are utilized as input factors, and there are sufficient data points with the number 195,230. The values of Nu¯ are included in the output layer. In the hidden layer of the MLP network model, it was found that a model with 14 neurons was effective [42,43]. The following transfer functions are used by the MLP network’s hidden and output layers:

f(x)=tansig(x)=−1+21+e(−2x).(26)

The structure of the generated MLP network is shown in Fig. 2. 195,230 data points make up the input data; 15% are reserved for testing, 15% are used for validation, and 70% of the data are utilized to train the model. Selected performance parameters commonly used in the literature to evaluate the training and prediction performance of the ANN model include the mean squared error (MSE), coefficient of determination (R), and margin of deviation (MoD). The mathematical equations [44] used to calculate these metrics are as follows:

Figure 2: A structure of the created MLP network

MSE=1N∑i=1N(Xtarg(i)−Xpred(i))2,(27)

R=1−∑i=1N(Xtarg(i)−Xpred(i))2∑i=1N(Xtarg(i))2,(28)

MoD =[Xtarg−XpredXtarg].(29)

Fig. 3 showcases the MSE performance of the proposed MLP model during the training phase. The graph illustrates how the MSE values progressively decreased with each epoch, starting from a high initial value. The training process concluded when all three datasets achieved the optimal validation value. Fig. 4 presents the error histogram derived from the training data. A close examination of this histogram reveals that the error values are predominantly clustered around the zero-error line, indicating minimal deviations. Additionally, the numerical values of the errors were found to be relatively low. Fig. 5 introduces the regression profile for the MLP model. In this context, regression refers to the linear relationship (R) between inputs and targets. In our model, all training, validation, and testing datasets exhibited an R value of 1, signifying a perfect linear correlation. Fig. 6 depicts the gradient state of the MLP model. The graphical results demonstrate that the proposed MLP model converged at a small gradient value of 6.0033e-6 and step size Mu = 1e-07, indicating effective training convergence. Fig. 7 displays both the target values for each data point and the average Nusselt number Nu¯ values predicted by the ANN model. Upon scrutinizing the graph, it is evident that the Nu¯ values obtained from the ANN model are in excellent agreement with the target values. This near-perfect alignment demonstrates that the constructed ANN model can predict the Nu¯ values with high accuracy. A significant finding from our study is that the ANN model, utilizing the Levenberg-Marquardt training algorithm and a multilayer perceptron architecture, exhibited exceptional predictive accuracy for the average Nusselt number Nu¯. The near-perfect correlation between the predicted and target values highlights the robustness of the ANN model in capturing the complex thermal behaviors within the MHD natural bioconvection system.

Figure 3: MSE performances for the functioning of the suggested MLP model during training

Figure 4: Errors histogram for the MLP model

Figure 5: Regression profile for the MLP model

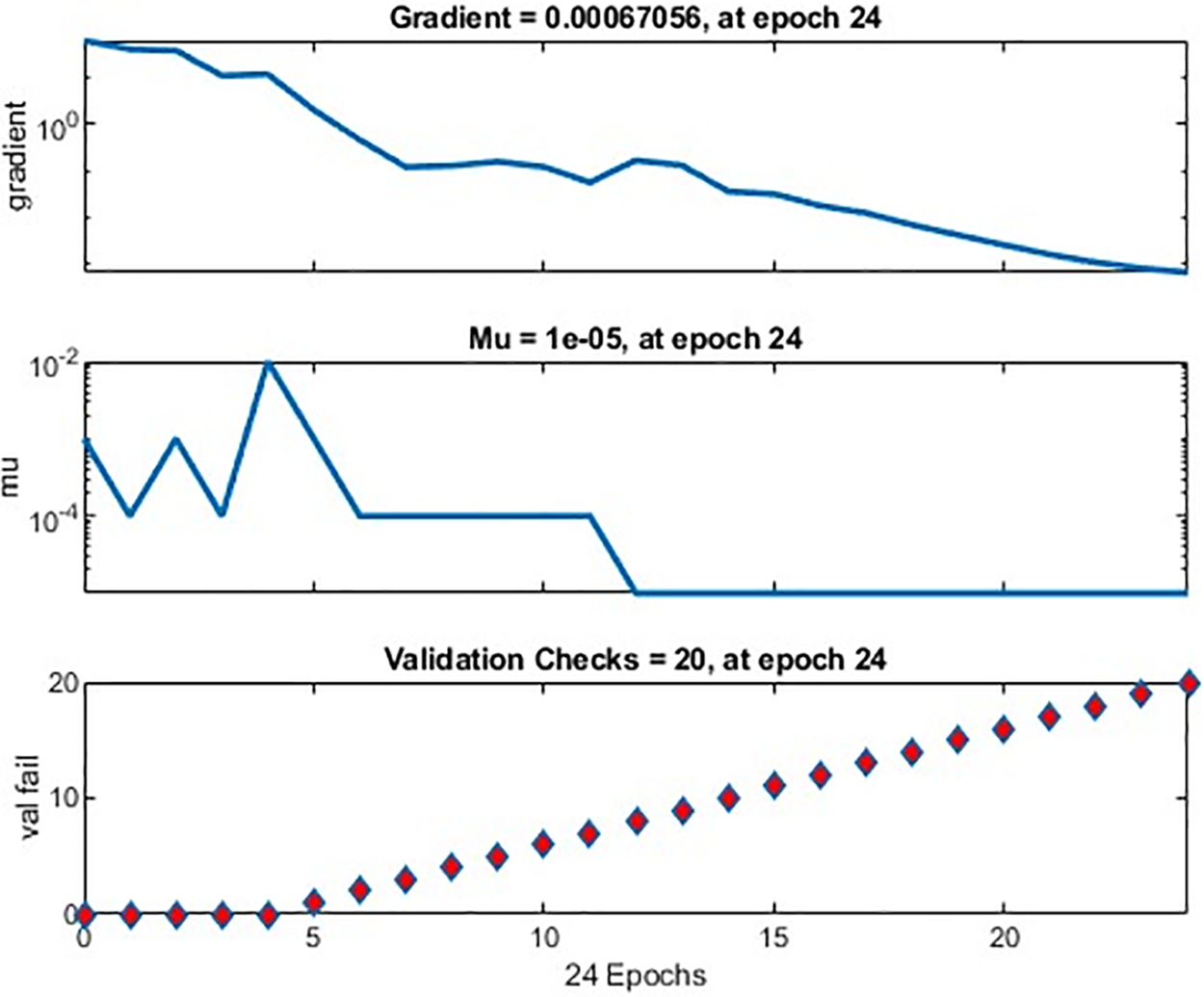
Figure 6: Gradient state of the MLP model

Figure 7: The values of Nu¯ and Sh¯ calculated by the ANN model

The limitations of the AI-driven FVM-ANN model, including reliance on the quality of training data, sensitivity to hyperparameters, difficulties in addressing complex nonlinear dynamics, and issues with interpretability, underscore the importance of a deeper exploration of these constraints to improve the model’s effectiveness and accuracy in analyzing entropy in MHD natural bioconvection within nanofluid-filled porous cavities.

4  Results and Discussion

This section presents the numerical simulation outcomes, analyzing system behavior, key findings, and their implications within the broader research context. Table 2 represents the parameters, symbols, numerical ranges, and references.

Fig. 8 represents the streamlines, isotherms, iso-concentrations, isolines of micro-rotation and local Bejan number under variation of low temperature/concentration length B=0.1,0.3,0.5. The intensity of maximum streamlines boosts as the length of cooling area increases. The isotherms are shrinking across the cavity due to expanded cooling area B. Similar trends of reduction on the iso-concentrations are occurring at expanded B. The micro-rotation is reducing along the cavity when B increases. The local Bejan number decreases by an increment in B. Figs. 9 and 10 show the profiles of the local Nusselt number/Sherwood number along the heat sink for a hybrid suspension under variation of B=0.1,0.3, and 0.5. These profiles are higher at lower B due to low temperatures and concentration distribution. Fig. 11 presents the profiles of local microorganism density along the heat sink for a hybrid suspension, with variations of B=0.1,0.3,0.5. The local microorganism density number along the heat sink has higher values at small B due to low microorganism density. Fig. 12 represents the profiles of the average Nusselt number Numf and Numf+++ along ϕ and Φ under variation of B=0.1,0.3,0.5. Increasing B declines the profiles of Numf and Numf+++. Fig. 13 shows the variation of global entropy e+,e++, and e+++ under variation of B=0.1,0.3,0.5 along ϕ, Ha, and Φ. An expanded B reduces e+ and e++, whilst e+++ enhances by an expanded B. Fig. 14 presents the variation of the Bejan number Be+ and Be+++ under variation of B=0.1,0.3,0.5. The Bejan number Be+ declines by an increase in B and Be+++ enhanced by an increased in B. Fig. 15 presents the streamlines, and isotherms under the variations of Q=−4,0,4. There are minor changes on the streamlines under the variation of Q. The intensity of isotherms decreases across a cavity when Q increases from −4 to 4. Fig. 16 shows the profiles of average Nusselt number Numf and Numf+++ along ϕ and Φ for hybrid suspension of Q. An increase in Q declines the profiles of average Nusselt numbers. Fig. 17 shows the streamlines, isotherms, iso-concentrations, isolines of micro-rotation and local Bejan number under variation of D=0.3,0.4,0.7. An increment in D affects on the contours of streamlines, whilst it has slight changes on the intensity of streamlines. The isotherms, iso-concentrations, isolines of micro-rotation are influenced clearly by changes of D. The distribution of local Bejan number changes its lines due to an increase in D. Figs. 18–20 show the profiles of the local Nusselt number, Sherwood number, and local microorganism density number along the heat sink for a hybrid suspension under variation of D. The locations and strengths of local Nusselt number, Sherwood number, and local microorganism density number are mainly affected by an expanded of D. Fig. 21 shows the streamlines under variation of ε=0.1,0.3,0.9. The strength of streamlines is enhanced by an increment in ε which represents the amount of a porous struggle of a fluid flow. Figs. 22 and 23 represent the profiles of the local Nusselt number along the heat sink and average Nusselt number along ϕ, and Φ for hybrid suspension under variation of ε. An increase in ε enhances the profiles of local Nusselt number. The average Nusselt number Numf enhances by an increment in in ε, whilst Numf+++ declines by an increment in in ε.

Figure 8: Streamlines, isotherms, iso-concentrations, isolines of micro-rotation and local Bejan number under variation of B=0.1,0.3,0.5 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 9: Profiles of the local Nusselt number along the heat sink for hybrid suspension under variation of B=0.1,0.3,0.5 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 10: Profiles of the local Sherwood number along the heat sink for hybrid suspension under variation of B=0.1,0.3,0.5 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 11: Profiles of the local microorganism density number along the heat sink for a hybrid suspension under variation of B=0.1,0.3,0.5 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 12: Profiles of the average Nusselt numbers Numf and Numf+++ along ϕ and Φ under variation of B=0.1,0.3,0.5 at Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 13: Variation of global entropy e+,e++, and e+++under variation of B=0.1,0.3,0.5 along ϕ, Ha, and Φ at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 14: Variation of the Bejan number Be+ and Be+++ under variation of B=0.1,0.3,0.5 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1, and D=0.5

Figure 15: Streamlines, and isotherms under the variations of Q=−4,0,4 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,D=0.5, and B=0.5

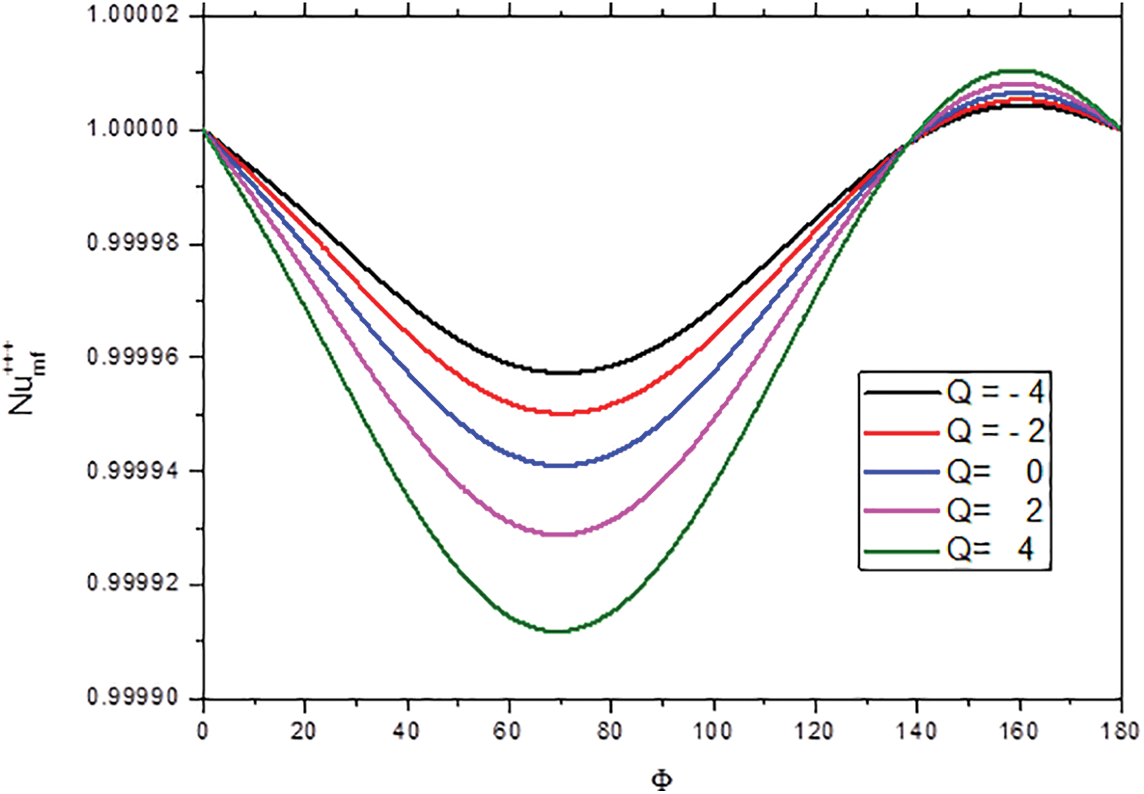
Figure 16: Variation of the average Nusselt number Numf and Numf+++ along ϕ and Φ under the influence of Q at Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,D=0.5, and B=0.5

Figure 17: Streamlines, isotherms, iso-concentrations, isolines of micro-rotation and local Bejan number under variation of D=0.3,0.4,0.7 at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,B=0.5

Figure 18: Profiles of the local Nusselt number along the heat sink for a hybrid suspension under variation of D at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,B=0.5

Figure 19: Profiles of the local Sherwood number along the heat sink for hybrid suspension under variation of D at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,B=0.5

Figure 20: Profiles of the local microorganism density number along the heat sink for a hybrid suspension under variation of D at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,D=0.5,B=0.5

Figure 21: Streamlines under variation of ε=0.1,0.3,0.9 at Φ=600,Ra=104,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,D=0.5,B=0.5

Figure 22: Profiles of the local Nusselt number along the heat sink for hybrid suspension under variation of ε at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,D=0.5,B=0.5

Figure 23: Variation of the average Nusselt number for a hybrid suspension under variation of ε at Φ=600,Ra=103,Rb=10,Sc=1,χ=1,Pr=6.2,Pe=1,σ=1,Q=1,D=0.5,B=0.5

5  Conclusion

This study investigated inclined magneto-hydrodynamic natural convection in a nanofluid-filled porous cavity with gyrotactic microorganisms using a hybrid FVM and ANN model. The ANN model, trained via the Levenberg-Marquardt method, demonstrated excellent predictive accuracy for average Nusselt number Nu¯, with high correlation (R = 1) and low mean squared error, validating its reliability. The finding results are showed that:

•   Increasing cooling area length B reduces the intensity of streamlines, local Nusselt, and Sherwood numbers, while decreasing the Bejan number (Be+) and increasing global entropy (e+++).

•   Variations in heat generation Q slightly affect streamlines but reduce isotherm intensity and average Nusselt numbers.

•   Increasing location of heat source D significantly alters streamlines, isotherms, and local Bejan number distribution.

•   Higher porosity parameter (ε) enhances streamlines and local Nusselt numbers, with mixed effects on average Nusselt numbers. These results can be practically applied to optimize heat transfer efficiency in systems such as heat exchangers, electronic cooling, and solar collectors, where precise thermal management is crucial.

Future work could extend the hybrid FVM and ANN model to more complex geometries and controlled variations in magnetic field orientations. This approach would enhance the understanding of the model’s behavior in diverse scenarios without overextending the study’s scope.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP. 2/610/45). This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R102), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Sara I. Abdelsalam expresses her deep gratitude to Fundación Mujeres por África for supporting this work through the fellowship awarded to her in 2020.

Funding Statement: Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project under Grant Number (RGP. 2/610/45). This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R102), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Noura Alsedais, Mohamed Ahmed Mansour, Abdelraheem M. Aly, Sara I. Abdelsalam; data collection: Abdelraheem M. Aly; analysis and interpretation of results: Mohamed Ahmed Mansour, Noura Alsedais; draft manuscript preparation: Noura Alsedais, Mohamed Ahmed Mansour, Abdelraheem M. Aly, Sara I. Abdelsalam. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on a request from corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Jamuna B, Shekar C. Bioconvection in a porous square cavity containing gyrotactic microorganisms under the effects of heat generation/absorption. Proc Inst Mech Eng E J Process Mech Eng. 2021;235(5):095440892110073. doi:10.1177/09544089211007326. [Google Scholar] [CrossRef]

2. Obalalu A, Salawu S, Olayemi O, Odetunde C, Akindele A. Computational study of bioconvection rheological nanofluid flow containing gyrotactic microorganisms: a model for bioengineering nanofluid fuel cells. Int J Model Simul. 2023;130(4):1–15. doi:10.1080/02286203.2023.2204209. [Google Scholar] [CrossRef]

3. Tanveer A, Aneja M, Ashraf DM, Nawaz R. Bioconvection heat and mass transfer across a nonlinear stretching sheet with hybrid nanofluids, joule dissipation, and entropy generation. ZAMM. 2024;104(5):206. doi:10.1002/zamm.202300550. [Google Scholar] [CrossRef]

4. Kotha G, Kolipaula V, Rao M, Penki S, Chamkha A. Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. Eur Phys J Plus. 2020;135(7):2942. doi:10.1140/epjp/s13360-020-00606-2. [Google Scholar] [CrossRef]

5. Abbas A, Sarris IE, Ashraf M, Ghachem K, Hnaien N, Alshammari BM. The effects of reduced gravity and radiative heat transfer on the magnetohydrodynamic flow past a non-rotating stationary sphere surrounded by a porous medium. Symmetry. 2023;15(4):806. [Google Scholar]

6. Jeelani MB, Abbas A. Al2O3-Cu/ethylene glycol-based magnetohydrodynamic non-Newtonian Maxwell hybrid nanofluid flow with suction effects in a porous space: energy saving by solar radiation. 2023;15(9):1794. [Google Scholar]

7. Yadav PK, Yadav N. Impact of heat and mass transfer on the magnetohydrodynamic two-phase flow of couple stress fluids through a porous walled curved channel using Homotopy Analysis Method. Chaos Sol Frac. 2024;183(20):114961. doi:10.1016/j.chaos.2024.114961. [Google Scholar] [CrossRef]

8. Yadav PK, Srivastava P. Impact of porous material and slip condition on the MHD flow of immiscible couple stress-Newtonian fluids through an inclined channel: head loss and pressure difference. Chin J Phys. 2024;89(50):1198–221. doi:10.1016/j.cjph.2024.03.046. [Google Scholar] [CrossRef]

9. Biswas N, Manna N, Mandal D, Gorla R. Magnetohydrodynamic bioconvection of oxytactic microorganisms in porous media saturated with Cu-water nanofluid. Int J Numer Methods Heat Fluid Flow. 2021;31(1):3461–89. doi:10.1108/HFF-08-2020-0538. [Google Scholar] [CrossRef]

10. Maheshwari S, Sharma R. Analysis of magneto-thermo-bioconvection of nanofluid containing gyrotactic microorganisms through porous media. J Nanofluids. 2022;11(6):979–87. doi:10.1166/jon.2022.1894. [Google Scholar] [CrossRef]

11. Biswas N, Mandal D, Manna N, Benim AC. Magneto-hydrothermal triple-convection in a W-shaped porous cavity containing oxytactic bacteria. Sci Rep. 2022;12(1):18053. doi:10.1038/s41598-022-18401-7. [Google Scholar] [CrossRef]

12. Rashed A, Nasr E, Mabrouk S. Influence of gyrotactic microorganisms on bioconvection in electromagnetohydrodynamic hybrid nanofluid through a permeable sheet. Computation. 2024;12(1):17. doi:10.3390/computation12010017. [Google Scholar] [CrossRef]

13. Mandal S, Shit GC, Shaw S, Makinde O. Entropy analysis of thermo-solutal stratification of nanofluid flow containing gyrotactic microorganisms over an inclined radiative stretching cylinder. Therm Sci Eng Prog. 2022;34(7):101379. doi:10.1016/j.tsep.2022.101379. [Google Scholar] [CrossRef]

14. Meenakshi V, Bodduna J, Mallesh M, Shekar C. Impact of Brownian motion and thermophoresis on entropy generation in a cavity containing microorganisms. Int J Comput Methods Eng Sci Mech. 2023;24(4):1–15. doi:10.1080/15502287.2023.2185554. [Google Scholar] [CrossRef]

15. Mishra N, Sharma P, Sharma B, Almohsen B, Pérez L. Electroosmotic MHD ternary hybrid Jeffery nanofluid flow through a ciliated vertical channel with gyrotactic microorganisms: entropy generation optimization. Heliyon. 2024;10(3):e25102. doi:10.1016/j.heliyon.2024.e25102. [Google Scholar] [CrossRef]

16. Ramzan M, Ali F, Akkurt N, Saeed A, Kumam P, Galal AM. Computational assessment of Carreau ternary hybrid nanofluid influenced by MHD flow for entropy generation. J Magn Magn Mater. 2023;567(1):170353. doi:10.1016/j.jmmm.2023.170353. [Google Scholar] [CrossRef]

17. Li S, Raghunath K, Alfaleh A, Ali F, Zaib A, Khan MI, et al. Effects of activation energy and chemical reaction on unsteady MHD dissipative Darcy-Forchheimer squeezed flow of Casson fluid over horizontal channel. Sci Rep. 2023;13(1):2666. doi:10.1038/s41598-023-29702-w. [Google Scholar] [CrossRef]

18. Fayz-Al-Asad M, Mebarek-Oudina F, Vaidya H, Hasan MS, Sarker MM, Ismail AI. Finite element analysis for magneto-convection heat transfer performance in vertical wavy surface enclosure: fin size impact. Front Heat Mass Transf. 2024;22(3):817–37. doi:10.32604/fhmt.2024.050814. [Google Scholar] [CrossRef]

19. Mebarek-Oudina F, Chabani I, Vaidya H, Ismail AI. Hybrid nanofluid magneto-convective flow and porous media contribution to entropy generation. Int J Numer Methods Heat Fluid Flow. 2024;34(2):809–36. doi:10.1108/HFF-06-2023-0326. [Google Scholar] [CrossRef]

20. Ramesh K, Mebarek-Oudina F, Ismail AI, Jaiswal BR, Warke AS, Lodhi RK, et al. Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sciencia Iran. 2023;30(2):376–90. doi:10.24200/sci.2022.58629.5822. [Google Scholar] [CrossRef]

21. Milano M, Koumoutsakos P. Neural network modeling for near wall turbulent flow. J Comput Phys. 2002;182(1):1–26. doi:10.1006/jcph.2002.7146. [Google Scholar] [CrossRef]

22. Das S, Tariq A, Santos T, Kantareddy SS, Banerjee I. Recurrent neural networks (RNNsarchitectures, training tricks, and introduction to influential research. In: Colliot O, editor. Machine learning for brain disorders. New York, NY, USA: Humana; 2023. p. 117–38. [Google Scholar]

23. Ling J, Kurzawski A, Templeton J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J Fluid Mech. 2016;807:155–66. doi:10.1017/jfm.2016.615. [Google Scholar] [CrossRef]

24. Rabault J, Kuchta M, Jensen A, Réglade U, Cerardi N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J Fluid Mech. 2019;865:281–302. doi:10.1017/jfm.2019.62. [Google Scholar] [CrossRef]

25. Aly AM, Lee S-W, Hussein HS. Integrating ISPH simulations with machine learning for thermal radiation and exothermic chemical reaction on heat and mass transfer in spline/triangle star annulus. Case Stud Therm Eng. 2024;54(1):103948. doi:10.1016/j.csite.2023.103948. [Google Scholar] [CrossRef]

26. Aly AM, Lee S-W, Ho NN, Raizah Z. Thermosolutal convection of NEPCM inside a curved rectangular annulus: hybrid ISPH method and machine learning. Comput Part Mech. 2024. doi:10.1007/s40571-024-00744-9. [Google Scholar] [CrossRef]

27. Elshehabey HM, Aly AM, Lee SW, Çolak AB. Integrating artificial intelligence with numerical simulations of Cattaneo-Christov heat flux on thermosolutal convection of nano-enhanced phase change materials in Bézier-annulus. J Energy Storage. 2024;82(1):110496. doi:10.1016/j.est.2024.110496. [Google Scholar] [CrossRef]

28. Elshehabey HM, Çolak AB, Aly A. Adjoined ISPH method and artificial intelligence for thermal radiation on double diffusion inside a porous L-shaped cavity with fins. Int J Numer Methods Heat Fluid Flow. 2024;34(4):1832–57. doi:10.1108/HFF-11-2023-0677. [Google Scholar] [CrossRef]

29. Alhejaili W, Lee S-W, Hat CQ, Aly AM. Heat and mass transport of nano-encapsulated phase change materials in a complex cavity: an artificial neural network coupled with incompressible smoothed particle hydrodynamics simulations. AIMS Math. 2024;9(3):5609–32. [Google Scholar]

30. Xie GN, Wang QW, Zeng M, Luo LQ. Heat transfer analysis for shell-and-tube heat exchangers with experimental data by artificial neural networks approach. Appl Therm Eng. 2007;27(5):1096–104. [Google Scholar]

31. Zou J, Han Y, So SS. Overview of artificial neural networks. Methods Mol Biol. 2008;458:15–23. [Google Scholar]

32. Sun F, Xie G, Li S. An artificial-neural-network based prediction of heat transfer behaviors for in-tube supercritical CO2 flow. Appl Soft Comput. 2021;102:107110. [Google Scholar]

33. Rehman KU, Çolak AB, Shatanawi W. Artificial neural networking (ANN) model for drag coefficient optimization for various obstacles. Mathematics. 2022;10(14):2450. [Google Scholar]

34. Fuxi S, Sina N, Sajadi SM, Mahmoud MZ, Abdelrahman A, Aybar HŞ. Artificial neural network modeling to examine spring turbulators influence on parabolic solar collector effectiveness with hybrid nanofluids. Eng Anal Bound Elem. 2022;143:442–56. doi:10.1016/j.enganabound.2022.06.026. [Google Scholar] [CrossRef]

35. Ali A, Das S. Applications of neuro-computing and fractional calculus to blood streaming conveying modified trihybrid nanoparticles with interfacial nanolayer aspect inside a diseased ciliated artery under electroosmotic and Lorentz forces. Int Commun Heat Mass Transf. 2024;152:107313. doi:10.1016/j.icheatmasstransfer.2024.107313. [Google Scholar] [CrossRef]

36. Karmakar P, Das S. A neural network approach to explore bioelectromagnetics aspects of blood circulation conveying tetra-hybrid nanoparticles and microbes in a ciliary artery with an endoscopy span. Eng Appl Artif Intell. 2024;133(1):108298. doi:10.1016/j.engappai.2024.108298. [Google Scholar] [CrossRef]

37. Cho C-C. Heat transfer and entropy generation of mixed convection flow in Cu-water nanofluid-filled lid-driven cavity with wavy surface. Int J Heat Mass Transf. 2018;119:163–74. doi:10.1016/j.ijheatmasstransfer.2017.11.090. [Google Scholar] [CrossRef]

38. Hussain S, Öztop HF, Mehmood K, Abu-Hamdeh N. Effects of inclined magnetic field on mixed convection in a nanofluid filled double lid-driven cavity with volumetric heat generation or absorption using finite element method. Chin J Phys. 2018;56(2):484–501. doi:10.1016/j.cjph.2018.02.002. [Google Scholar] [CrossRef]

39. Mejri I, Mahmoudi A. MHD natural convection in a nanofluid-filled open enclosure with a sinusoidal boundary condition. Chem Eng Res Des. 2015;98(5):1–16. doi:10.1016/j.cherd.2015.03.028. [Google Scholar] [CrossRef]

40. Abderrahmane A, Younis O, Mourad A, Laidoudi H, Oreijah M, Guedri K, et al. The baffle shape effects on natural convection flow and entropy generation in a nanofluid-filled permeable container with a magnetic field. Sci Rep. 2024;14(1):2550. doi:10.1038/s41598-024-53001-7. [Google Scholar] [CrossRef]

41. Bondareva NS, Sheremet MA, Öztop HF, Abu-Hamdeh N. Entropy generation due to natural convection of a nanofluid in a partially open triangular cavity. Adv Powder Technol. 2017;28(1):244–55. doi:10.1016/j.apt.2016.09.030. [Google Scholar] [CrossRef]

42. Çolak AB. A new study on the prediction of the effects of road gradient and coolant flow on electric vehicle battery power electronics components using machine learning approach. J Energy Storage. 2023;70(4):108101. doi:10.1016/j.est.2023.108101. [Google Scholar] [CrossRef]

43. Güzel T, Çolak AB. Performance prediction of current-voltage characteristics of Schottky diodes at low temperatures using artificial intelligence. Microelectron Reliab. 2023;147(1–3):115040. doi:10.1016/j.microrel.2023.115040. [Google Scholar] [CrossRef]

44. Çolak AB, Yıldız O, Bayrak M, Tezekici BS. Experimental study for predicting the specific heat of water based Cu-Al2O3 hybrid nanofluid using artificial neural network and proposing new correlation. Int J Energy Res. 2020;44(9):7198–215. [Google Scholar]

45. Raizah Z, Aly AM, Mansour MA. Radiative and heat generation effects on MHD mixed convection of non-Newtonian nanofluids in lid-driven inclined odd-shaped porous cavity containing obstacle using local thermal non-equilibrium condition. Waves Rand Compl Med. 2022;1–28. doi:10.1080/17455030.2022.2071499. [Google Scholar] [CrossRef]

46. Alsedais N, Aly AM, Mansour MA. Local thermal non-equilibrium condition on mixed convection of a nanofluid-filled undulating cavity containing obstacle and saturated by porous media. Ain Shams Eng J. 2022;13(2):101562. [Google Scholar]

47. Raizah Z, Aly AM, Alsedais N, Mansour MA. MHD mixed convection of hybrid nanofluid in a wavy porous cavity employing local thermal non-equilibrium condition. Sci Rep. 2021;11(1):17151. [Google Scholar]