Impact of Viscous Dissipation and Ohmic Heating on Natural Convection Heat Transfer in Thermo-Magneto Generated Plume

Nomenclature

1  Introduction

In environmental monitoring and remediation, we encounter plumes from industrial stacks and wild fires. Thermal plumes generated by energy sources can help track oil spills in water bodies, aiding in the deployment of containment and cleanup measures. Plume behavior is incorporated into climate models to predict the impact of various energy sources on global climate patterns. Plume dynamics are crucial in designing effective ventilation systems for buildings, ensuring proper airflow, and maintaining indoor air quality. Plumes from volcanic eruptions are monitored to predict the dispersion of ash and gases, aiding in disaster response and evacuation planning. These are a few of the important real-life applications of the plumes in different fields. Incorporating Ohmic heating into a system allows for considering electrical resistance effects and the consequent transformation of electrical energy into heat. By incorporating Ohmic heating, we aim to gain a thorough understanding of energy transfer and heat generation within the system. Ohmic heating has applications in various fields such as food processing, chemical synthesis, biomedical applications, environmental remediation, and material fabrication. Viscous dissipation, alternatively termed viscous heating or the effects of viscous heating, describes the process whereby mechanical energy transforms into heat owing to internal friction within a flowing fluid. Viscous dissipation is pivotal across a broad spectrum of engineering and scientific domains, impacting fluid flow dynamics, temperature dispersion, and heat transfer rates in various applications.

Zeldovich [1] is credited as the earliest known researcher to describe the natural convective plume generated by a horizontal line energy source. Sparrow et al. [2] conducted a comprehensive study on heat transfer values, analyzing surfaces under both isothermal and non-isothermal conditions. In contrast, Glauret [3] investigated boundary layer separation under varying electrical conductivity conditions, ranging from small to large values, when subjecting a flat plate to a uniform magnetic field. Notably, one of the significant findings suggested the potential convergence towards zero of the missing conditions in the flow problem. Gebhart et al. [4] provided numerical results across a diverse range of Prandtl numbers and viscous dissipation. They also discussed several similar aspects of flow characteristics for convective plumes and flow over surfaces.

The researchers Gebhart et al. [5] scrutinized the limitations and refined numerous redundancies linked with the boundary conditions of a horizontal line energy source, resulting in the generation of a laminar buoyancy-driven convective plume. Welling et al. [6] delved into an experimental examination of the natural convective plume originating from a vertical cylinder serving as a heat source. Additionally, they analyzed temperature data and velocity fluctuations to gain deeper insights into the dynamics of the turbulent convective plume. Lithgow-Bertelloni et al. [7] focused their study on investigating the thermal plume across a range of Rayleigh numbers, spanning from the shallowest boundary layer to the convective plumes deep beneath the Earth’s mantle. Ashraf et al. [8] investigated the influence of radiation on a magnetized porous plate subjected to a fluctuating magnetic field adjacent to the surface, along with a steady mixed convective flow. Sharma et al. [9] analyzed the consequences of viscous dissipation, along with Ohmic heating and variable thermal conductivity, on buoyancy-induced convective flow under the influence of a magnetic field. Hunt et al. [10] provided solutions to the conservative equations of plumes under distinct scenarios, elucidating the advantages derived from these solutions. The outcome of radiation on irregular hydro-magnetic buoyancy induced convective flow utilizing a magnetized plate was carried out by Ashraf et al. [11]. Their study examines the variations in intensity of surface temperature along with magnetic field about a mean.

Hernandez [12] employed the SIMPLER approach to address the comprehensive numerical modeling of thermal plumes within a cavity of an elongated configuration. Jackson et al. [13] underscored the importance of the structure of a subglacial outlet in governing plume movements. Wang et al. [14] investigated the scaling relations of thickness and velocity for the mountain’s initial plume and its thermal boundary layer. Focusing on the Brownian motion and thermophoresis as governing factors, the dynamics of the boundary layer of nanofluids at various places, like the sphere and the plume surrounding it, were examined by Ashraf et al. [15]. Ahmad et al. [16] concentrated on observing the influence of viscous dissipation and catalyst-induced chemical reactions (which release energy) on buoyancy-driven convective energy transfer.

Khan et al. [17] disclosed the findings from their numerical analysis of the time-dependent, laminar flow of nanofluid around a sphere, both within the plume area and in its vicinity. Fan et al. [18] studied the transitions of plumes over a heated horizontal surface. Their findings indicated that plume flow occurred when the Froude number exceeded the critical Froude number, with the opposite trend observed for dome flow. Ullah et al. [19] conducted an analysis of oscillating forced and free convective flow around a horizontal cylinder. Their study comprehensively addressed aspects such as energy transmission, current density, and oscillating skin friction. The recent advancements in understanding the composition and morphology of plumes, as well as their role in convective processes within the global mantle, were investigated by Koppers et al. [20]. They also explored the potential influences of mantle plumes on climate and other related fields.

Ahmad et al. [21] and Ashraf et al. [22] conducted research on catalyst-assisted exothermic chemical reactions occurring on curved surfaces. Ashraf et al. incorporated these interactions with magnetic fields in their subsequent investigations. Abbas et al. [23] examined the Peristaltic mechanism of micropolar Casson fluid focusing on thermal transportation involving viscous dissipation. Ashraf et al. [24] investigated the influence of viscous dissipation and magnetohydrodynamics on the periodic energy transfer along a cone positioned within porous media. Moreover, Ashraf et al. [25,26] analyzed the influence of the nanofluids in the plume zones. Further, he examined the influence of thermal radiation, along with Brownian motion and thermophoresis, on the behavior of dense gray nanofluid around the surface of a sphere and within its plume area. Li et al. [27] investigated the effects of viscous dissipation, chemical reactions, and Ohmic heating on unsteady radiative flow. Kumar et al. [28] explored the influences of Ohmic heating and an aligned magnetic field on the dynamics of nanofluid’s flow among two coaxial cylinders, considering the rotational effect. Rehman et al. [29] performed a stability analysis prioritizing the shape factor of radiation on a hybrid nanofluid. Thabet et al. [30] examined the thermophoretic diffusion and thermal enhancement, with Brownian motion effects on micropolar nanofluid under the influence of magnetic field over an inclined surface. Where in the most recent studies, Taghavi et al. [31] studied the free convective influences in the insulated layers within cryogenic vessels for storage. Ajibade et al. [32] analyzed the free convective flow under the impacts of viscous dissipation and Darcy in a partially occupied vertical tube. The impacts of viscous dissipation along with Ohmic heating were examined by Ajithkumar et al. [33] on peristaltic convective flow for non-Newtonian fluids in porous media. Anwar et al. [34] investigated the behavior of a magnetized plume considering a non-Newtonian Casson fluid with variable thermal conductivity and solar radiation.

We have considered the natural convective plume by following Gebhart et al. [5]. To address the research gap, we got inspiration from the widespread industrial utilization of magnetic fields and applied the aligned magnetic field to a plume. Inspired by plume dynamics and the widespread industrial utilization of magnetic fields, our research is structured to mitigate the excessive heating within the plume’s system. Our aim is to observe the fluid and heat transfer characteristics of the plume generated by the horizontal line energy source. This plume system is under the impact of an aligned magnetic field. We have incorporated Ohmic heating along with viscous dissipation to observe the heat generation and transfer in the plume system. The preceding work in the literature was on plume generation due to line heat sources. This novel work combines the use of an aligned magnetic field, which helps mitigate excessive heating within the plume’s system. The novelty also includes the presence of Ohmic heating and viscous dissipation. The objective of this study is to comprehensively describe and analyze the results obtained from an in-depth investigation into the complex interactions between thermal phenomena and fluid flow within such intricate structures.

2  The Geometric Scheme and Governing Mathematical Model

The analysis concerns a steady, incompressible, viscous, two-dimensional flow driven by natural convection with laminar characteristics occurring above an infinitely extended horizontal line heat source. This configuration is analyzed with the inclusion of an aligned magnetic field, alongside considerations for viscous dissipation and Ohmic heating. Ohmic heating occurs when electric currents encounter resistance in a conductive medium, leading to the conversion of electrical energy into heat energy. In this context, it contributes to the overall thermal behavior of the system, particularly when combined with the presence of an aligned magnetic field. Meanwhile, viscous dissipation refers to the conversion of mechanical energy into thermal energy due to internal friction or the viscosity of the fluid. As the fluid moves, heat is generated as a result of the friction between its layers. The geometric arrangement and the coordinate system of the flow model are depicted in Fig. 1. The schematic diagram shows that the x-axis corresponds to the plume’s surface, while the y-axis is oriented perpendicular to it. Concerning [5,9,11], the plume system is considered with the inclusion of the magnetic field along with Ohmic heating and viscous dissipation. The magnetic field’s component Bx is taken along the surface of the plume and By is perpendicular to the surface. The continuity Eq. (1), momentum Eq. (2), and energy Eq. (5) are utilized to model the generated plume, as described in Reference [5]. Eq. (2) is adjusted by incorporating a term for the aligned magnetic field following [11]. Additionally, Maxwell Eq. (3) and magnetic diffusion Eq. (4) of the flow model facilitate the magnetic convection within the plume’s system, as indicated by Reference [11]. The viscous dissipation and Ohmic heating terms are added to the energy equation following [9]. Taking into account the assumptions mentioned above, the mathematical model is articulated in terms of conservative equations as follows:

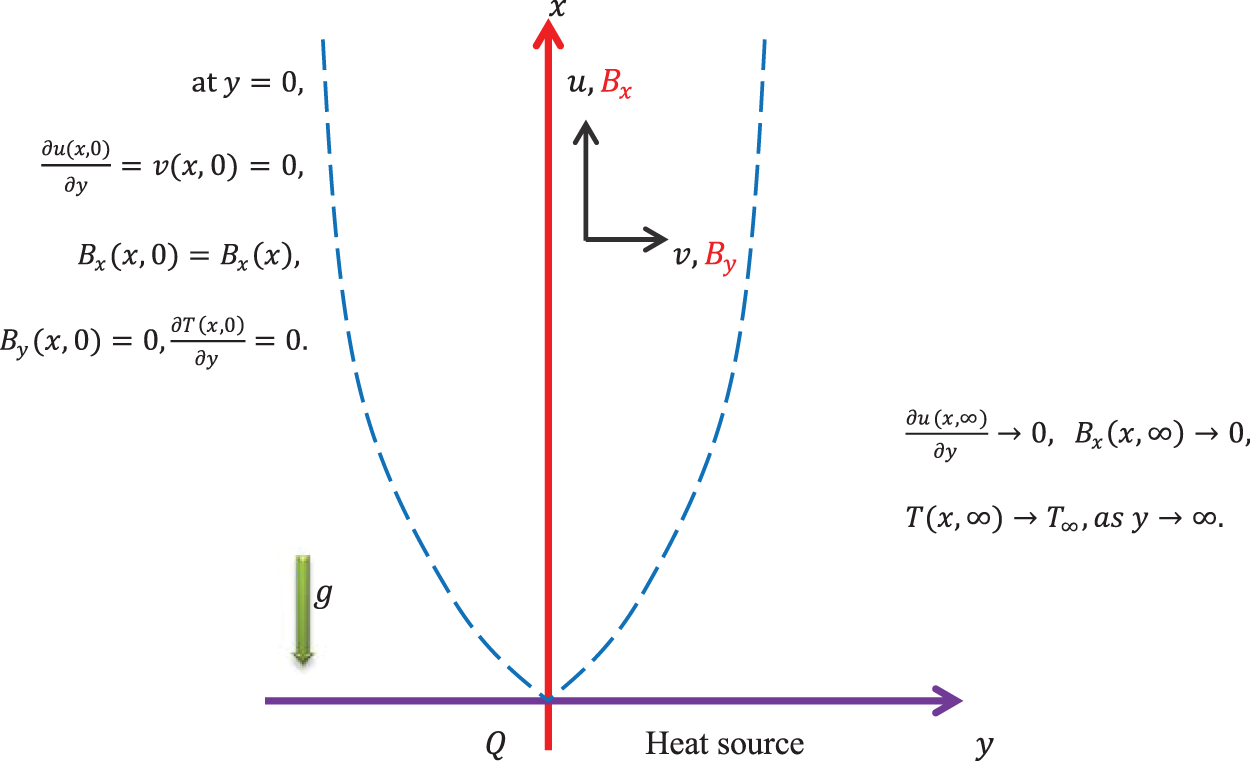
Figure 1: Schematic geometry

The boundary layer equations are:

∂u∂x+∂v∂y=0,(1)

ρ(u∂u∂x+v∂u∂y)=μ∂2u∂y2+μm(Bx∂Bx∂x+By∂Bx∂y)±gβρ(T−T∞),(2)

∂Bx∂x+∂By∂y=0,(3)

u∂Bx∂x+v∂Bx∂y−Bx∂u∂x−By∂u∂y=νm∂2Bx∂y2,(4)

u∂T∂x+v∂T∂y=α∂2T∂y2+μρCp(∂u∂y)2+σB02u2ρCp.(5)

The pivotal boundary conditions dictating the boundary-layer fluid flow of the plume consist of:

∂u(x, 0)∂y=v(x, 0)=0, Bx(x, 0)=Bx(x), By(x, 0)=0, ∂T(x, 0)∂y=0, at y=0,(6)

∂u(x, ∞)∂y→0, Bx(x, ∞)→0, T(x, ∞)→T∞, asy→∞.

Eqs. (1) to (5) combined with boundary conditions (6), involve the velocity components u and v, dynamic viscosity μ of fluid, magnetic permeability μm, coefficient of volumetric thermal expansion β, fluid density ρ, thermal diffusivity α, magnetic field strength B0 and magnetic viscosity νm. In boundary conditions (6), B0(x) is denoted as B0(x)=4B0νx2(Grx4)1/2 that designates magnetization of the surface. Since the plume is generated in the x-direction and an aligned magnetic field is applied in the same direction, B0(x) signifies the magnetization of the plume’s surface along the x-axis. Eq. (6) stipulates that the skin friction ∂u∂y at both the plume’s surface and far from the surface in the undisturbed fluid is zero. Additionally, according to Eq. (6), the heat transfer rate ∂T∂y at the plume’s surface is also zero. These assumptions imply that natural convection occurs on a surface that is adiabatic. Such surfaces, being thermally insulated, inhibit heat exchange between their opposing sides.

3  Stream Function Formulation

To solve the aforementioned flow model, I have chosen the method of transformation using similarity variables. This method entails converting the system of Partial Differential Equations (PDEs) into Ordinary Differential Equations (ODEs). The velocity components u and v are governed by the continuity Eq. (1), which is expressed in terms of the stream function ψ(x, y) as follows:

u=∂ψ∂y, v=−∂ψ∂x.(7)

The function φ(x, y) fulfills the equation governing the divergence-free conduction of the magnetic field (3), as follows:

Bx=∂φ∂y, By=−∂φ∂x.(8)

The Eqs. (2), (4), and (5) along with the boundary conditions (6) are transformed into a set of three ordinary differential equations, accompanied by specified boundary conditions. This transformation is facilitated by introducing the similarity variable η(x, y), the stream function ψ(x, y), and the transformed magnetic field stream function φ(x, y), as elucidated in Reference [5] is given as follows:

η=yx(Grx4)14, ψ=4ν(Grx4)14f(η), φ=4B0νx(Grx4)14ϕ(η)(9)

where

Grx=gβx3(T0−T∞)ν2.(10)

The dimensionless temperature ratio, denoted as θ(η), is expressed as follows:

θ(η)=T−T∞T0−T∞.(11)

Primarily, a power-law relationship of the form Nxn is assumed to describe the variation of plume midline temperature with respect to x, such that:

T0−T∞=Nxn.(12)

The subsequent temperature distribution in the region is determined by:

T−T∞=Nxnθ(η).(13)

By substituting the similarity variables defined in Eqs. (9) through (11) and (13) into Eqs. (1) through (6), Eqs. (2), (4), and (5) are transmuted as follows:

f′′′−(2n+2)f′2+(n+3)ff′′+S(n−1)[2ϕ′2−ϕϕ′′]±θ=0(14)

ϕ′′′+γ[(n+3)fϕ′′+4f′ϕ′−(n−1)ϕf′′]=0,(15)

θ′′+Pr[(n+3)fθ′−4nf′θ+E(f′′)2+EM(f′)2]=0(16)

In the Eqs. (14)–(16), S=μmB02ρx2 is magnetic force parameter which is the ratio of magnetic forces to inertial forces, γ=ννm is magnetic Prandtl number, and Pr=να is Prandtl number, respectively. While in Eq. (16) E=4gβxCp is parameter of viscous dissipation, where M=σB02x2μ(Grx4)−(12) is Magnetic parameter and Grx defined in Eq. (10). Where, “ ′ “ prime denotes derivative with respect to η.

The boundary conditions undergo transformation as below:

At η=0; f′′(0)=f(0)=0, ϕ′(0)=1, ϕ(0)=0, θ′(0)=0,(17)

As η→∞; f′′(∞)→0, ϕ′(∞)→0, θ(∞)→0.

The energy transported by convection across a horizontal plane (at x) within a plume is denoted as (refer to [5]):

Q=ρCp[∫−∞∞(T−T∞)udy].(18)

The Eq. (18) sums up the heat transfer effects over the entire y-direction perpendicular to the plume surface. Here, the velocity component u responsible for how heat is carried away from the heat source Q.

The derivative of the similarity variable from Eq. (9) with respect to y is computed as:

dηdy=1x(Grx4)1/4,

⟹x(Grx4)−14dη=dy.

Upon substituting the above derived expression and similarity variables into Eq. (18), we obtain:

Q=ρCp[∫−∞∞Nxnθ(η){4νxf′(η)(Grx4)12}x(Grx4)−14dη],

Q=4ρνNxnCp(gβNxn+34ν2)1/4∫−∞∞f′(η)θ(η)dη,

Q=4NρνCpx5n+34(gβN4ν2)1/4∫−∞∞f′(η)θ(η)dη.(19)

This Eq. (19) is the transformed expression of the heat source Eq. (18) by utilizing the similarity variable defined in Eq. (9), and using Eq. (13). This transformation is carried out to find the value for exponent n. The exponent n is taken as zero and 15, for an isothermal surface (where temperature remains unchanged) and uniform heat flux state (where temperature changes uniformly), respectively, where Q ought to be proportioned to x. Since Q (representing heat generated solely by the line source) is independent of x, in this case, the value of n is determined by referencing [2,5] and following Eq. (19) as below:

x5n+34=1=x0.

Using the reverse engineering mechanism, as mentioned earlier, the value of n is given as below:

n=−35.(20)

Substituting this value of n mentioned in Eqs. (20), (14)–(16) become as:

f′′′−45f′2+125ff′′−85S[2ϕ′2−ϕϕ′′]±θ=0,(21)

ϕ′′′+γ[125fϕ′′+4f′ϕ′+85ϕf′′]=0,(22)

θ′′+Pr[125(fθ′+f′θ)+E(f′′)2+EM(f′)2]=0.(23)

Accompanied by the specified boundary conditions (17) as follows:

At η=0; f′′(0)=f(0)=0, ϕ′(0)=1, ϕ(0)=0, θ′(0)=0,

As η→∞; f′′(∞)→0, ϕ′(∞)→0, θ(∞)→0.

4  Methodology of Computation

For computational assessment, I chose to employ the well-established Shooting technique alongside MATLAB’s bvp4c method. This allowed us to address the system of third-order differential equations detailed in Eqs. (21) to (23) while ensuring adherence to the boundary conditions specified in (17). The bvp4c function within MATLAB stands out as a reliable tool for tackling boundary value problems (BVPs) linked with ODEs. Its application combines numerical techniques, with particular emphasis placed on leveraging the finite difference method (FDM) as the underlying solver. In the domain of the FDM, the shooting technique stands out as a crucial method employed by bvp4c to handle BVPs effectively. Fundamentally, the shooting technique converts a given BVP into an initial value problem (IVP), enabling the use of conventional ODE solvers. This conversion requires establishing an initial estimate for the boundary conditions and initiating an iterative process to iteratively enhance the solution until it matches the specified boundary conditions. Essentially, the shooting technique initiates trajectories from the initial condition towards the boundary conditions, making adjustments in the initial guess needed to ensure convergence. The optimal step sizes and the values of η at infinity are carefully chosen based on appropriate selections. The convergence criterion in the bvp4c tool within MATLAB hinges significantly on the initial guess quality furnished by the user. Forecasting a precise initial guess for the boundary conditions can pose challenges, especially in scenarios involving complex problems characterized by nonlinearities or discontinuities. To overcome this obstacle, substitutions are frequently utilized to convert the given boundary value problem (BVP) into a set of first-order ordinary differential equations (ODEs). Accordingly, the subsequent replacements are utilized to convert the mentioned equations into first-order differential equations, as below:

F=f′, G=f′′, H=ϕ′, I=ϕ′′, J=θ′(24)

Following this, the ensuing first-order equations are formulated as:

G′=[45F2−125fG]+85S[2H2−ϕI]∓θ,(25)

I′=−γ[125fI+4FH+85ϕG],(26)

J′=−Pr[125(fJ+Fθ)+EG2+EMF2],(27)

At η=0, G(0)=f(0)=0, H(0)=1, ϕ(0)=0, J(0)=0,(28)

as η→∞, G(∞)→0, H(∞)→0, θ(∞)→0.(29)

The bvp4c algorithm in MATLAB is utilized to solve Eqs. (25) through (29), following a methodology consistent with established practices in numerical analysis. For details of coding on MATLAB kindly check the Appendix A.

5  Computational Results and Physical Significances

In this section, we analyze the evolving heat transfer configurations across various scenarios, considering factors such as the magnetic parameter (M), parameter of viscous dissipation (E), magnetic force parameter (S), magnetic Prandtl number (γ), and Prandtl number (Pr) within the context under consideration. The thorough examination provided here reveals the complex interaction among the mentioned parameters and their influence on fluid flow and heat transfer characteristics. The velocity, current density, and temperature distributions are the missing initial conditions. These graphical results of the velocity, current density, and temperature distributions are explicitly mentioned at the end of their captions as missing conditions. As well as a detailed discussion is provided along with these representations. The results of these missing conditions are calculated by utilizing the specified boundary conditions. As it is clear that specified conditions are satisfied, the results of missing conditions are also accurate and strengthened by it. Additionally, it sheds light on skin friction f′′, magnetic flux ϕ′ and heat transfer rate θ′ as specified boundary conditions. Current density refers to the amount of electrical current traveling per unit area. It results from the interaction between the fluid’s motion and the magnetic field, leading to induced currents and Lorentz forces that modify the flow patterns and thermal behavior. Current density directly contributes to Ohmic heating. The higher current densities yield greater electrical resistance and, consequently, higher heat generation within the fluid. While current density does not directly influence viscous dissipation, it can be influenced by the magnetic field’s effects including current density.

The influences of magnetic parameter M are highlighted on temperature distribution, current density, and velocity profiles in Fig. 2a–c as missing conditions. For this objective, the other involved parameters remain fixed while adjusting parameter M across four appropriate different options. These graphical representations depict that the velocity, current density, and temperature profiles are maximum and minimum at the plume’s surface for M=0.4 and M=0.1, respectively. The fluid’s velocity and temperature distribution at the surface of the plume decreases gradually for an enhancing parameter M, as evident from Fig. 2a,c. The Lorentz forces induced by a magnetic field become more significant relative to viscous forces with an enhancing parameter M. This leads to the suppression of fluid motion and turbulences resulting in more smoother and ordered velocity distributions within the plume. This also caused the drop in velocity and temperature distribution. Fig. 2b demonstrates that the current density drops with a slighter difference at the surface for a shorter distance along the x-direction but then the trend reverses and it starts increasing gradually with enhancing parameter M. Due to intense magnetic forces, the close confinement experienced by induced current yields an immediate drop in current density at the surface. As we move slightly away from the surface the confinement effects diminish and current density increases. Fig. 3a–c signifies the skin friction, magnetic flux, and heat transfer rate as specified conditions for distinct values of M. The skin friction and magnetic flux drops with increment in parameter M as claimed by Fig. 3a,b. Due to smoother fluid motion and thinning of the boundary layer by strong magnetic effects, the shear stress exerted by fluid reduces near the surface which leads to a drop the skin friction. Stronger magnetic forces result in tighter confinement of the magnetic flux, reducing its outward expansion within the system. Therefore, the magnetic flux depicted in Fig. 3b descends with a minute difference and depicts a closely packed pattern. The heat transfer rate as depicted in Fig. 3c increases with ascending parameter M. The heat transfer rate is minimum for M=0.3 near the surface. The induced Lorentz forces by magnetic field causes the thinning of the thermal boundary layer which reduces the thermal resistance and enhances the heat transfer rate despite a decline in temperature distribution.

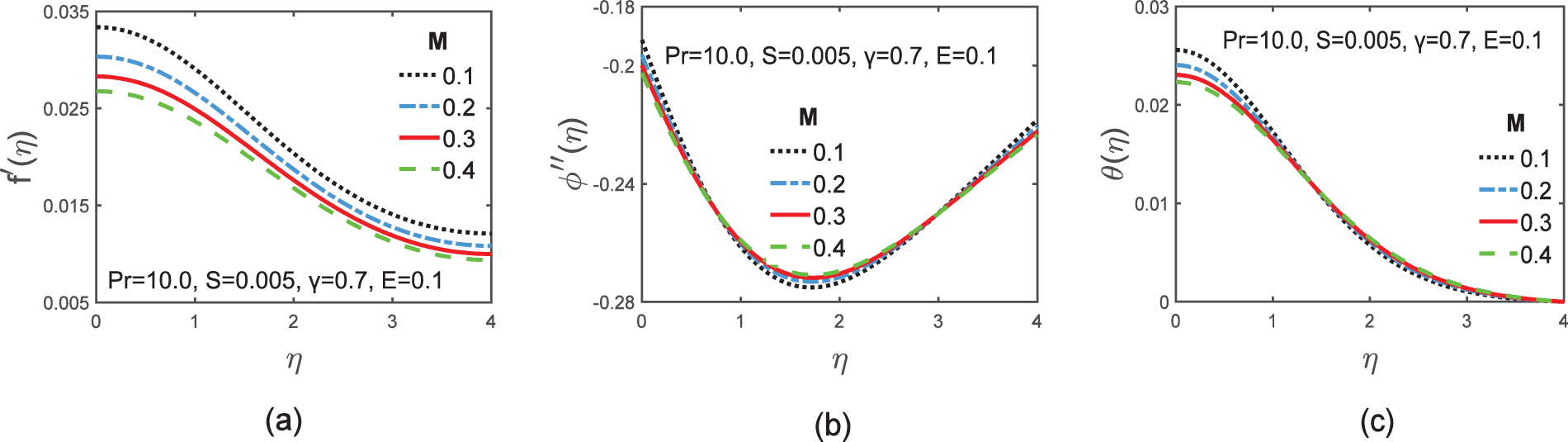
Figure 2: Graphs of velocity f′(η) (a), current density ϕ′′(η) (b) and temperature distribution θ(η) (c) against η for distinct four values of magnetic parameter M with other fixed parameters (Missing conditions)

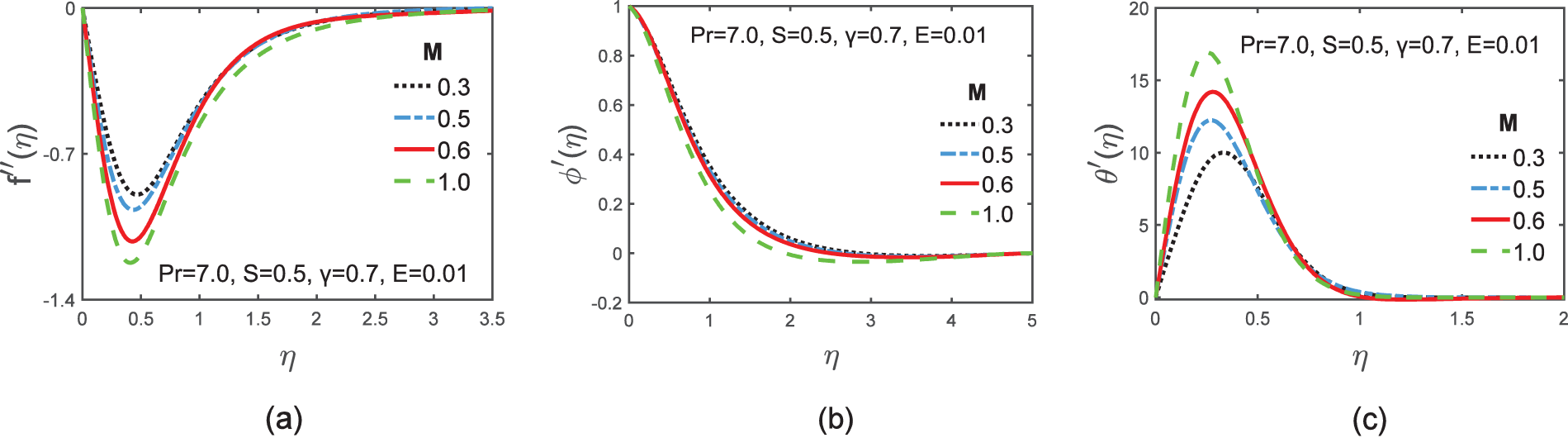
Figure 3: Graphs of skin friction f′′(η) (a), magnetic flux ϕ′(η) (b) and heat transfer rate θ′(η) (c) against η for distinct four values of magnetic parameter M with other fixed parameters (Specified conditions)

The consequences of the parameter of viscous dissipation E on f′, ϕ′′, and θ are represented being missing initial conditions in Fig. 4a–c. The velocity f′, and temperature profiles θ drops while current density ϕ′′ initial drops then it exhibits increasing behavior for enhancing parameter E. The velocity drops because enhanced dissipation leads to higher energy losses within the fluid and causes a reduction in the kinetic energy. The increased dissipation tends to overpower the fluid’s motion, which yields a reduction in current density at the surface. Fig. 5a–c illustrates the influences of parameter E with appropriate values on specified conditions noted as f′′, ϕ′ and θ′. The skin friction f′′ and magnetic flux ϕ′ drops, whereas, the heat transfer rate θ′ also decreases with enhancing values of parameter E. With reduced turbulence caused by an incremented dissipation, the skin friction declines. Further, the magnetic flux drops due to the fact that enhanced dissipation reduces the inductions of current. Higher viscous dissipation leads to lower heat transfer rates θ′ because the enhanced dissipation reduces the efficiency of the fluid’s heat transfer process. This also causes a drop in the temperature distribution of the system.

Figure 4: Graphs of velocity f′(η) (a), current density ϕ′′(η) (b) and temperature distribution θ(η) (c) against η for distinct four values of parameter of viscous dissipation E with other fixed parameters (Missing condition)

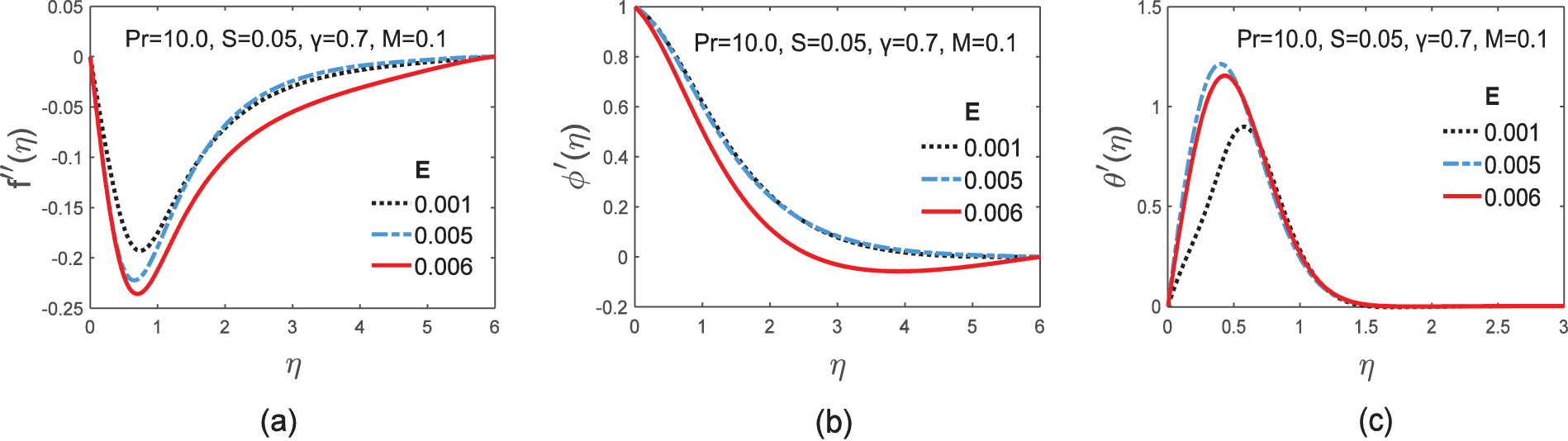
Figure 5: Graphs of skin friction f′′(η) (a), magnetic flux ϕ′(η) (b) and heat transfer rate θ′(η) (c) against η for distinct values of parameter of viscous dissipation E with other fixed parameters (Specified conditions)

For four appropriate choices of magnetic force parameter S the velocity f′, current density ϕ′′, and temperature θ profiles are depicted as missing conditions of the flow problem in Fig. 6a–c. The parameter S is the ratio of magnetic to inertial forces. So, increment in parameter S causes the magnetic forces to dominate over inertial forces. The f′ profiles increased for a shorter distance initially, and then it started decreasing. It maintained the later trend in undisturbed fluid as well, as evident in Fig. 6a. The velocity of the fluid decreases as the magnetic force increases with increasing parameter S. The ϕ′′profiles by Fig. 6b exhibit a descending trend near the surface, and afterwards it reveres that behavior. The negative values indicate a reversal in the direction of the current density, which could be due to a stronger magnetic field altering the original direction of current flow. The temperature profile enhanced gradually, as visible in Fig. 6c. The temperature distribution is minimum for S=0.1 at the plume’s surface. This behavior of temperature is justified by the presence of significant Ohmic heating and viscous dissipation. Fig. 7a–chighlights impact of parameter S on the specified conditions mentioned as skin friction f′′, magnetic flux ϕ′ and heat transfer rate θ′. The f′′ and ϕ′ drop while θ′ increment for enhancing values of parameter S claimed by these figures. Increasing magnetic forces cause a more stabilized laminar flow near the surface, reducing the shear stress. This leads to lower skin friction. The higher magnetic forces induce currents or fields that counteract the primary magnetic field and lead to an overall reduction in the observed magnetic flux. The increased temperature gradient due to enhanced Ohmic heating and viscous dissipation contributes to a higher heat transfer rate with increasing parameter S.

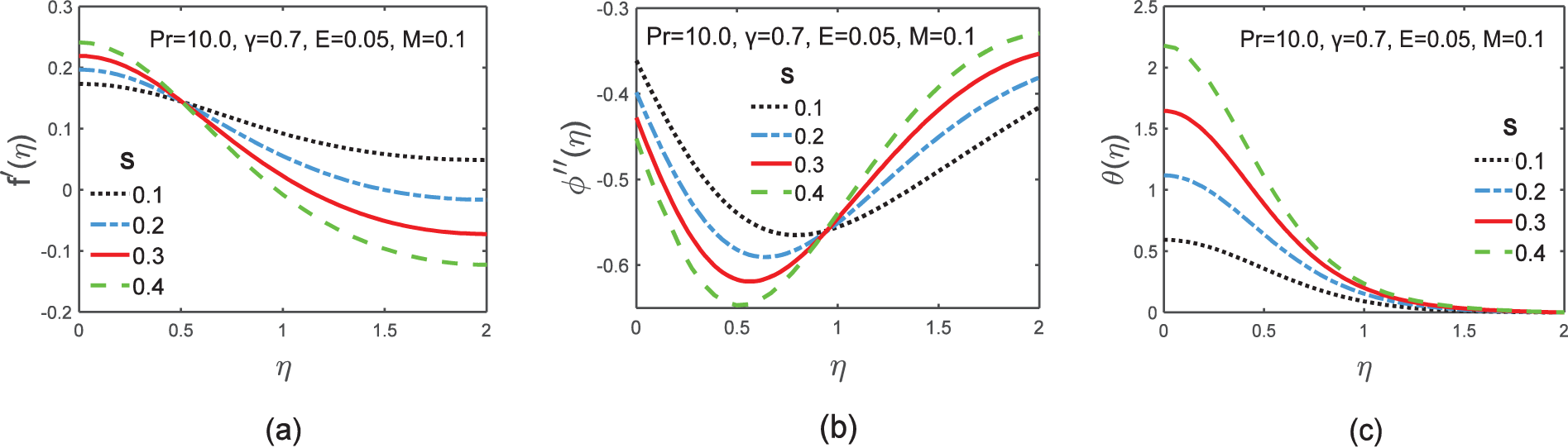
Figure 6: Graphs of velocity f′(η) (a), current density ϕ′′(η) (b) and temperature distribution θ(η) (c) against η for distinct four values of magnetic force parameter S with other fixed parameters (Missing condition)

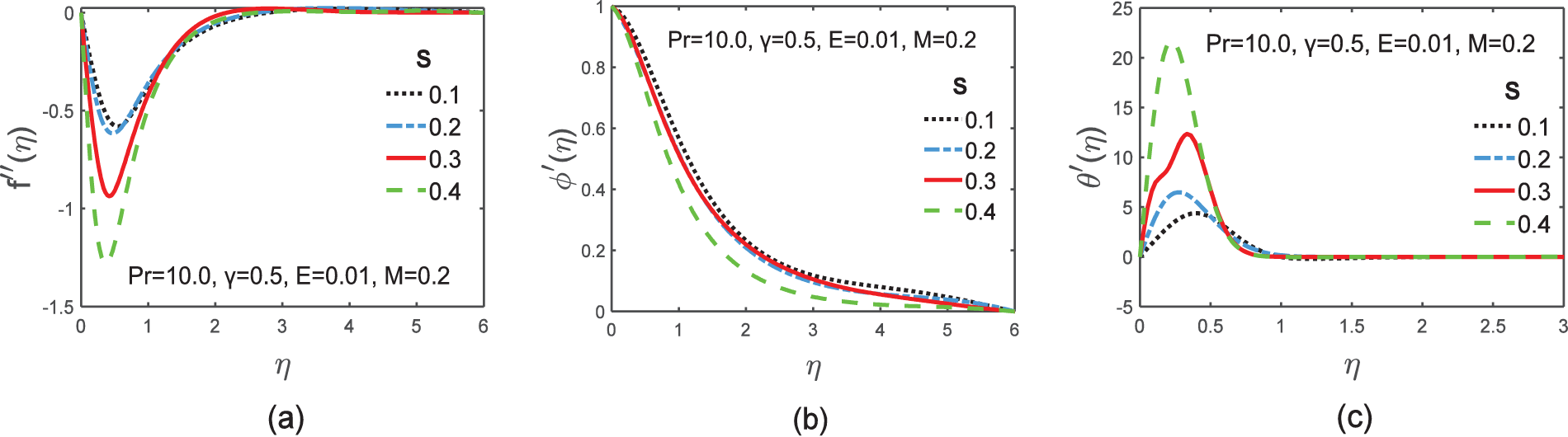
Figure 7: Graphs of skin friction f′′(η) (a), magnetic flux ϕ′(η) (b) and heat transfer rate θ′(η) (c) against η for distinct values of magnetic force parameter S with other fixed parameters (Specified conditions)

The velocity, current density, and temperature distribution profiles are emphasized as missing initial conditions in Fig. 8a–c for four distinct values of magnetic Prandtl number γ. The parameter γ is the ratio of viscous diffusivity to the magnetic diffusivity. Due to the increment in γ, the viscous impacts dominate over magnetic effects. The influences of dominant viscosity due to increased γ are listed here. The temperature and velocity profiles as described in Fig. 8a,c are maximum and minimum for γ=0.5 and γ=3.0, respectively. It is depicted that the velocity primarily drops for a shorter distance and then it reverses its trend. The increased viscous diffusivity causes a stronger damping effect on the velocity due to the viscous forces’ domination. The temperature distribution declines for the escalating values of γ. The lower magnetic diffusivity reduces the heating effect from Ohmic dissipation and causes drop in temperature. Fig. 8b elucidates the current density drop for the ascending values of γ. The physical profiles for specified boundary conditions skin friction, magnetic flux, and rate of heat transfer are illustrated in Fig. 9a–c for appropriate choices of γ. The skin friction is maximum for γ=6.0 near the plume’s surface and gradually enhances with increment in γ as claimed by Fig. 9a. The magnetic flux and rate of heat transfer rise slowly for increments in γ as represented in Fig. 9b,c. The magnetic flux exhibits reverse behavior after some distance. Near the surface, the reduced magnetic diffusivity leads to a lower interaction between the magnetic field and the fluid which reduces skin friction. For increasing magnetic Prandtl number, the resulting slower magnetic field diffusion and reduced penetration into the fluid reduces the overall magnetic flux. Whereas, heat transfer rate increases due to enhanced temperature gradients, and improved thermal conductivity due to reduced Ohmic heating.

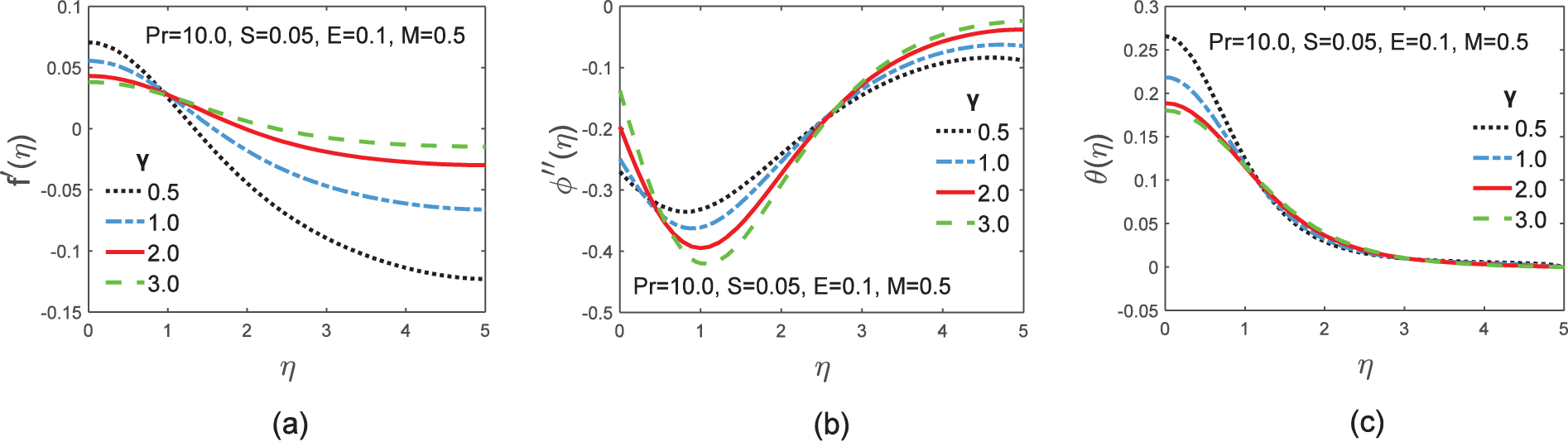
Figure 8: Graphs of velocity f′(η) (a), current density ϕ′′(η) (b) and temperature distribution θ(η) (c) against η for distinct four values of magnetic Prandtl number γ with other fixed parameters (Missing conditions)

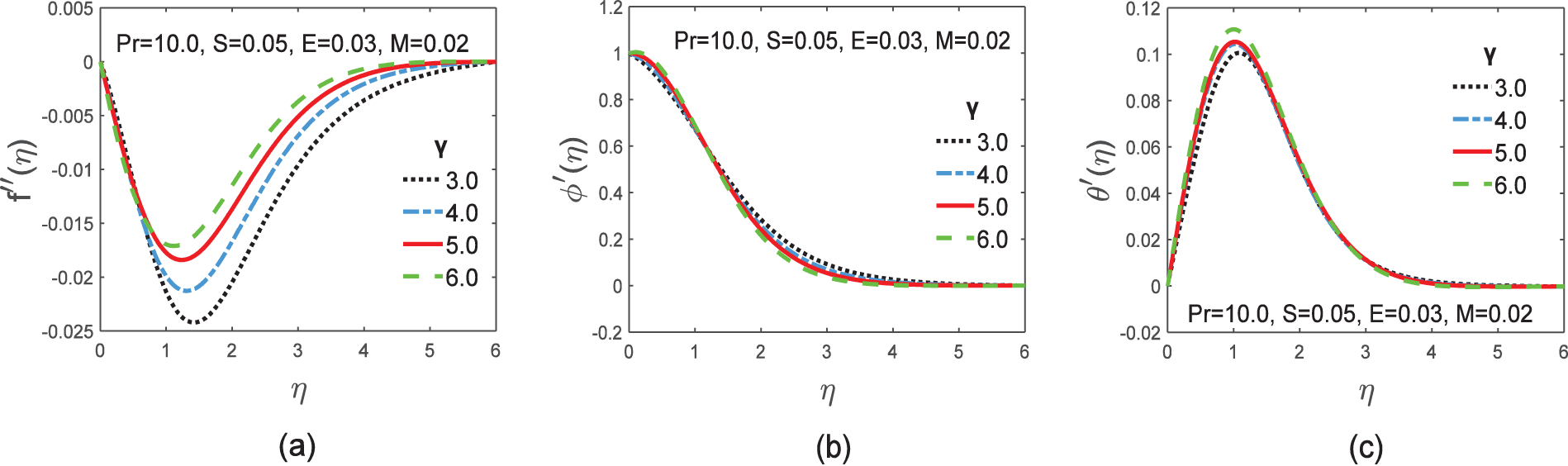
Figure 9: Graphs of skin friction f′′(η) (a), magnetic flux ϕ′(η) (b) and heat transfer rate θ′(η) (c) against η for distinct values of magnetic Prandtl number γ with other fixed parameters (Specified conditions)

The physical conduct for missing initial conditions f′, ϕ′′ and θ are shown in Fig. 10a–c for varying Prandtl number. Fig. 10a,c represents that the velocity and temperature profiles are highest for Pr=0.7 while minimum for Pr=4.0. The θ and f′ profile exhibit a gradual drop for an enhancing Pr. In Fig. 10b, a decreasing trend is observed at the surface, while a similar pattern is noted near the plume’s surface with increasing Pr for current density ϕ′′. The physical elucidation for skin friction f′′, magnetic flux ϕ′ and rate of heat transfer θ for appropriate values of Pr are highlighted in Fig. 11a–c. The results for specified boundary conditions skin friction f′′ and magnetic flux ϕ′ claimed by Fig. 11a,b are lower for Pr=1.0 and Pr=4.0 near the surface, respectively. The skin friction shows enhancing behavior for enhancing Pr. Whereas, the magnetic flux ϕ′ drops gradually with an ascending Pr. Fig. 11c depicts that the θ′ decreases for enhancing Pr whereas abrupt behavior is noted for Pr=2.0. The underlying principle governing the observed behavior of flow and heat transfer characteristics concerning the Prandtl number is that as the Prandtl number increases, the viscosity of the fluid increases while the thermal conductivity of the fluid decreases. Due to increased viscosity, the velocity drops and skin friction enhanced because of the higher shear stress. Higher Prandtl number leads to thicker thermal boundary layer which implies less effective heat transfer from the heat source to the fluid. This causes drop in the temperature distribution as well as heat transfer rate. The drop in magnetic flux is indirectly due to the reduced temperature and current density. However, current density reduces at the surface due to reduced thermal diffusivity with rising Prandtl number.

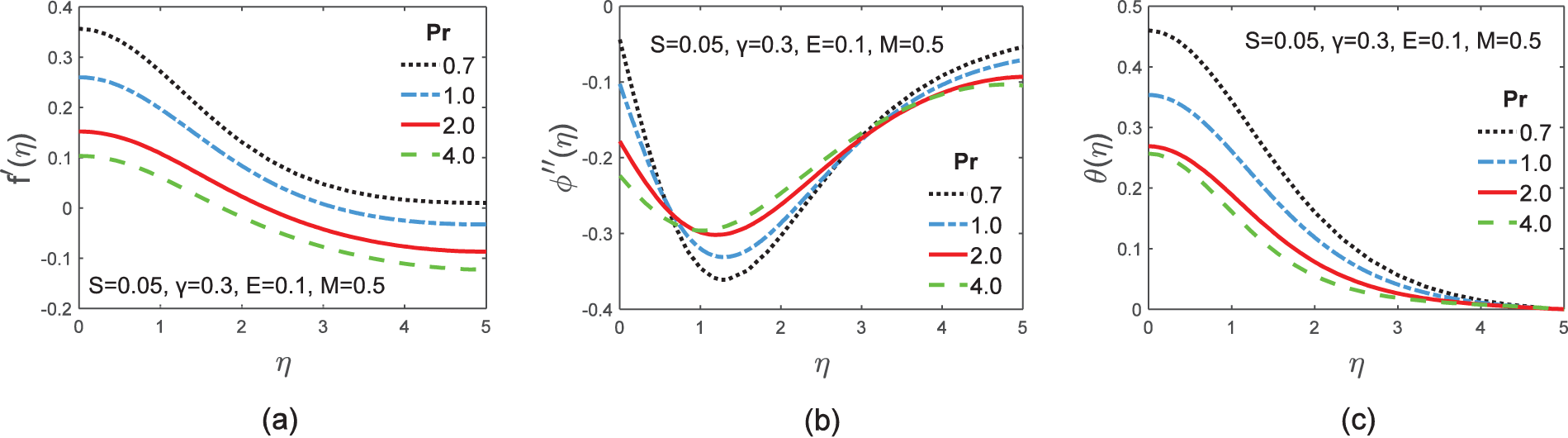
Figure 10: Graphs of velocity f′(η) (a), current density ϕ′′(η) (b) and temperature distribution θ(η) (c) against η for distinct four values of Prandtl number Pr with other fixed parameters (Missing conditions)

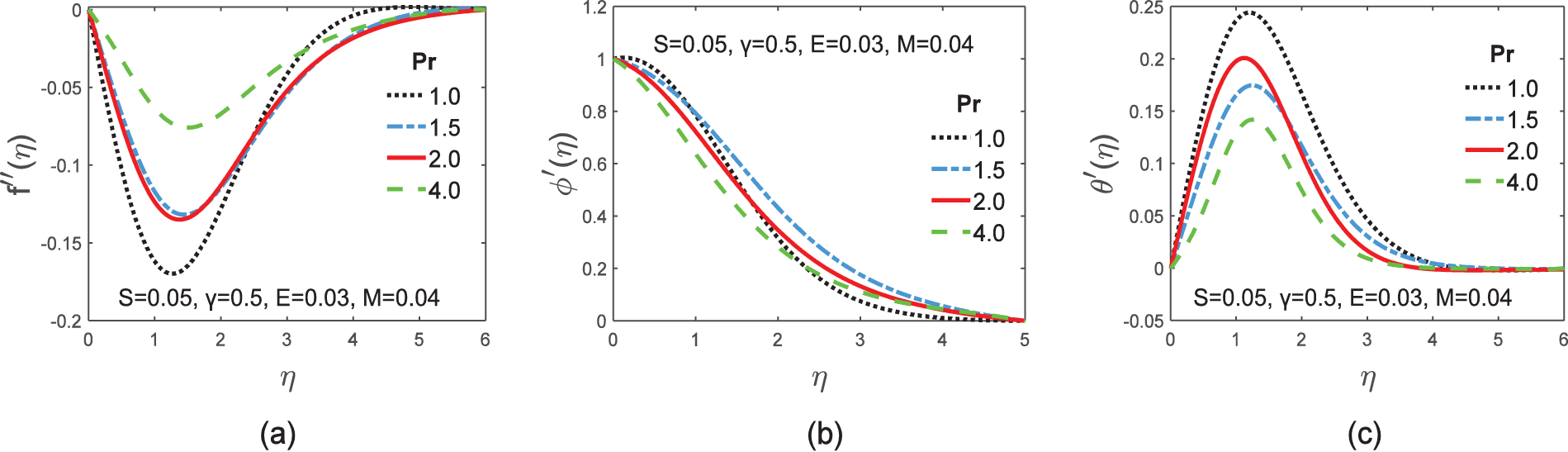
Figure 11: Graphs of skin friction f′′(η) (a), magnetic flux ϕ′(η) (b) and heat transfer rate θ′(η) (c) against η for distinct values of Prandtl number Pr with other fixed parameters (Specified conditions)

6  Validation Analysis

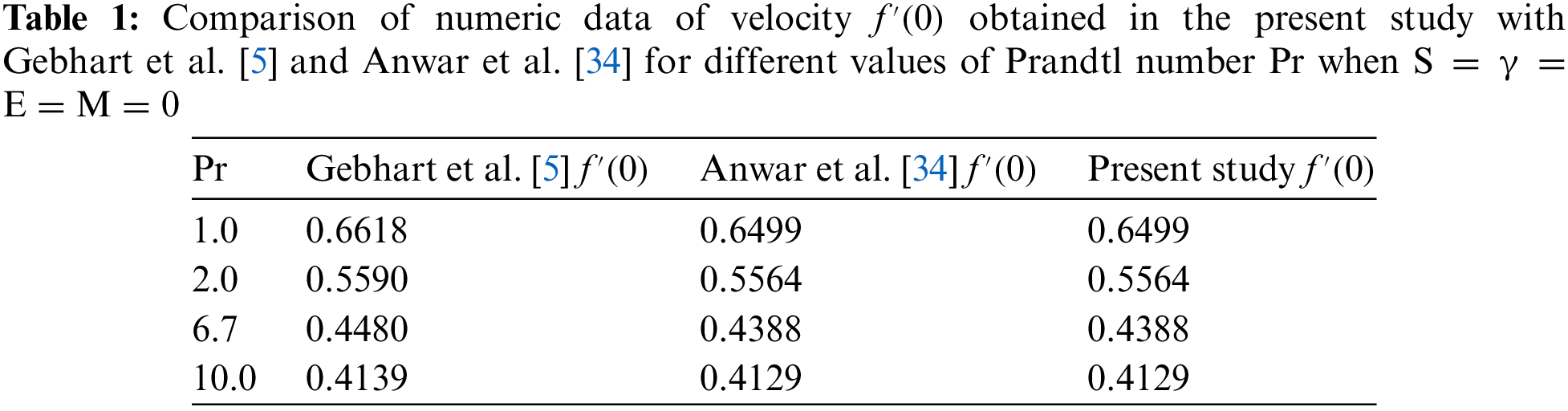
The validation analysis, performed for the velocity f′(0), is presented in Table 1. This examination not only reinforces the credibility of our current research efforts but also demonstrates the close correspondence of our findings with those reported in prior literature, as observed in Gebhart et al. [5] and Anwar et al. [34]. This consistent correspondence further emphasizes the reliability and robustness of the conclusions drawn from our study.

7  Conclusion

In light of the above-detailed discussion on fluid flow and heat transfer properties regarding the parameters involved, the observed outcomes are encapsulated as follows:

For the missing initial conditions:

•   The fluid velocity dropped with increasing magnetic parameter M, viscous dissipation variable, and Prandtl number. But it increases initially for increasing magnetic force parameter S and then declines. It shows a reverse trend for the magnetic Prandtl number compared to the magnetic force parameter.

•   The current density decreased for enhancing the magnetic parameter, viscous dissipation variable, magnetic force parameter, and Prandtl number. However, it increased with increasing magnetic Prandtl number.

•   The temperature distribution dropped for rising values of the magnetic parameter, viscous dissipation variable, magnetic Prandtl number, and Prandtl number. But the temperature of the plume’s system is the lowest for S=0.1.

For specified boundary conditions:

•   The skin friction declined for higher values of the magnetic parameter, viscous dissipation variable, magnetic force parameter, and magnetic Prandtl number. While increasing for a higher Prandtl number.

•   For enhancing values of enhancing the magnetic parameter, viscous dissipation variable, magnetic force parameter, magnetic Prandtl number, and Prandtl number the magnetic flux dropped.

•   The heat transfer rate escalates for rising values of magnetic parameter, magnetic force parameter, and magnetic Prandtl number. However, it dropped for the viscous dissipation variable and the Prandtl number.

Acknowledgement: The authors are grateful to the reviewers for their constructive comments and suggestions.

Funding Statement: The research has been supported by the National Foreign Expert Project-Foreign Youth Talent Program Fund No. QN2023001001, Beijing Natural Science Foundation Project-Foreign Scholar Program Fund No. IS23046/ZW001A00202301, National Natural Science Foundation of China (NSFC) Fund No. 12202019, and Beijing Postdoctoral Research Activities Fund No. Q6001A00202301.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Sahar Anwar, Ghulam Rasool, Muhammad Ashraf; data collection: Uzma Ahmad; analysis and interpretation of results: Sahar Anwar, Ghulam Rasool, Muhammad Ashraf, Uzma Ahmad, Tao Sun; draft manuscript preparation: Sahar Anwar, Ghulam Rasool, Muhammad Ashraf, Uzma Ahmad, Tao Sun. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data is available within the manuscript.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zeldovich YB. Limiting laws of freely rising convection currents. Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki. 1937;7(12):1463–5. Available from: https://www.sid.ir/paper/544407/fa. [Accessed 2024]. [Google Scholar]

2. Sparrow EM, Gregg JL. Similar solutions for free convection from a nonisothermal vertical plate. Trans Am Soc Mech Eng. 1958;80(2):379–86. doi:10.1115/1.4012377. [Google Scholar] [CrossRef]

3. Glauert MB. The boundary layer on a magnetized plate. J Fluid Mech. 1962;12(4):625–38. doi:10.1017/S0022112062000439. [Google Scholar] [CrossRef]

4. Gebhart B, Mollendorf J. Viscous dissipation in external natural convection flows. J Fluid Mech. 1969;38(1):97–107. doi:10.1017/S0022112069000061. [Google Scholar] [CrossRef]

5. Gebhart B, Pera L, Schorr AW. Steady laminar natural convection plumes above a horizontal line heat source. Int J Heat Mass Transfer. 1970;13(1):161–71. doi:10.1016/0017-9310(70)90032-3. [Google Scholar] [CrossRef]

6. Welling I, Koskela H, Hautalampi T. Experimental study of the natural-convection plume from a heated vertical cylinder. Exp Heat Transfer an Int J. 1998;11(2):135–49. doi:10.1080/08916159808946558. [Google Scholar] [CrossRef]

7. Lithgow-Bertelloni C, Richards MA, Conrad CP, Griffiths RW. Plume generation in natural thermal convection at high Rayleigh and Prandtl numbers. J Fluid Mech. 2001;434:1–21. doi:10.1017/S0022112001003706. [Google Scholar] [CrossRef]

8. Ashraf M, Asghar S, Hossain MA. Thermal radiation effects on hydromagnetic mixed convection flow along a magnetized vertical porous plate. Math Probl Eng. 2010;2010:1243. doi:10.1155/2010/686594. [Google Scholar] [CrossRef]

9. Sharma PR, Singh G. Effects of variable thermal conductivity, viscous dissipation on steady MHD natural convection flow of low Prandtl fluid on an inclined porous plate with Ohmic heating. Meccanica. 2010;45:237–47. doi:10.1007/s11012-009-9240-0. [Google Scholar] [CrossRef]

10. Hunt GR, Van den Bremer TS. Classical plume theory: 1937–2010 and beyond. IMA J Appl Math. 2011;76(3):424–48. doi:10.1093/imamat/hxq056. [Google Scholar] [CrossRef]

11. Ashraf M, Asghar S, Hossain A. Fluctuating hydromagnetic natural convection flow past a magnetized vertical surface in the presence of thermal radiation. Therm Sci. 2012;16(4):1081–96. doi:10.2298/TSCI110805045A. [Google Scholar] [CrossRef]

12. Hernandez RH. Natural convection in thermal plumes emerging from a single heat source. Int J Therm Sci. 2015;98:81–9. doi:10.1016/j.ijthermalsci.2015.06.010. [Google Scholar] [CrossRef]

13. Jackson RH, Shroyer EL, Nash JD, Sutherland DA, Carroll D, Fried MJ, et al. Near-glacier surveying of a subglacial discharge plume: implications for plume parameterizations. Geophys Res Lett. 2017;44(13):6886–94. doi:10.1002/2017GL073602. [Google Scholar] [CrossRef]

14. Wang X, Xu F, Zhai H. An experimental study of a starting plume on a mountain. Int Commun Heat Mass Transf. 2018;97:1–8. doi:10.1016/j.icheatmasstransfer.2018.06.004. [Google Scholar] [CrossRef]

15. Ashraf M, Khan A, Gorla RS. Natural convection boundary layer flow of nanofluids around different stations of the sphere and into the plume above the sphere. Heat Transf—Asian Res. 2019;48(3):1127–48. doi:10.1002/htj.21424. [Google Scholar] [CrossRef]

16. Ahmad U, Ashraf M, Khan I, Nisar KS. Modeling and analysis of the impact of exothermic catalytic chemical reaction and viscous dissipation on natural convection flow driven along a curved surface. Therm Sci. 2020;24(Suppl. 1):1. doi:10.2298/TSCI20S1001A. [Google Scholar] [CrossRef]

17. Khan A, Ashraf M, Rashad AM, Nabwey HA. Impact of heat generation on magneto-nanofluid free convection flow about sphere in the plume region. Mathematics. 2010;8(11):2010. doi:10.3390/math8112010. [Google Scholar] [CrossRef]

18. Fan Y, Wang Q, Ge J, Li Y. Conditions for transition from a plume to a dome above a heated horizontal area. Int J Heat Mass Transf. 2020;156:119868. doi:10.1016/j.ijheatmasstransfer.2020.119868. [Google Scholar] [CrossRef]

19. Ullah Z, Ashraf M, Rashad AM. Magneto-thermo analysis of oscillatory flow around a non-conducting horizontal circular cylinder. J Therm Anal Calorim. 2020;142(4):1567–78. doi:10.1007/s10973-020-09571-5. [Google Scholar] [CrossRef]

20. Koppers AA, Becker TW, Jackson MG, Konrad K, Müller RD, Romanowicz B, et al. Mantle plumes and their role in Earth processes. Nat Rev Earth Environ. 2021;2(6):382–401. doi:10.1038/s43017-021-00168-6. [Google Scholar] [CrossRef]

21. Ahmad U, Ashraf M, Al-Zubaidi A, Ali A, Saleem S. Effects of temperature dependent viscosity and thermal conductivity on natural convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. PLoS One. 2021;16(7):e0252485. doi:10.1371/journal.pone.0252485 [Google Scholar] [PubMed] [CrossRef]

22. Ashraf M, Ahmad U, Zia S, Gorla RS, Al-Johani AS, Khan I, et al. Magneto-exothermic catalytic chemical reaction along a curved surface. Math Probl Eng. 2022;2022(1):8439659. doi:10.1155/2022/8439659. [Google Scholar] [CrossRef]

23. Abbas Z, Rafiq MY. Numerical simulation of thermal transportation with viscous dissipation for a peristaltic mechanism of micropolar-Casson fluid. Arab J Sci Eng. 2022;47(7):8709–20. doi:10.1007/s13369-021-06354-4. [Google Scholar] [CrossRef]

24. Ashraf M, Ilyas A, Ullah Z, Ali A. Combined effects of viscous dissipation and magnetohydrodynamic on periodic heat transfer along a cone embedded in porous medium. Proc Inst Mech Eng, Part E: J Process Mech Eng. 2022;236(6):2325–35. doi:10.1177/09544089221089135. [Google Scholar] [CrossRef]

25. Ashraf M, Khan A, Ullah Z. Computational analysis of the transient mixed convective flow of nanofluid in the plume regions. Wave Random Complex. 2022;11:1–7. doi:10.1080/17455030.2022.2084573. [Google Scholar] [CrossRef]

26. Ashraf M, Khan A, Abbas A, Hussanan A, Ghachem K, Maatki C, et al. Finite difference method to evaluate the characteristics of optically dense gray nanofluid heat transfer around the surface of a sphere and in the plume region. Mathematics. 2023;11(4):908. doi:10.3390/math11040908. [Google Scholar] [CrossRef]

27. Li S, Khan MI, Alzahrani F, Eldin SM. Heat and mass transport analysis in radiative time dependent flow in the presence of Ohmic heating and chemical reaction, viscous dissipation: an entropy modeling. Case Stud Therm Eng. 2023;42:102722. doi:10.1016/j.csite.2023.102722. [Google Scholar] [CrossRef]

28. Kumar J, Sandeep N. Dynamics of Ohmic heating and aligned magnetic field on a nanofluid flow between two coaxial cylinders with rotation effect. Numer Heat Transf, Part A: Appl. 2023;231:1–20. doi:10.1080/10407782.2023.2237185. [Google Scholar] [CrossRef]

29. Rehman A, Khun MC, Khan D, Shah K, Abdeljawad T. Stability analysis of the shape factor effect of radiative on MHD couple stress hybrid nanofluid. South Afr J Chem Eng. 2023;46:394–403. doi:10.1016/j.sajce.2023.09.004. [Google Scholar] [CrossRef]

30. Thabet EN, Khan Z, Abd-Alla AM, Bayones FS. Thermal enhancement, thermophoretic diffusion, and Brownian motion impacts on MHD micropolar nanofluid over an inclined surface: numerical simulation. Numer Heat Transf, Part A: Appl. 2023:1–20. doi:10.1080/10407782.2023.2276319. [Google Scholar] [CrossRef]

31. Taghavi M, Sharma S, Balakotaiah V. Natural convection effects in insulation layers of spherical cryogenic storage tanks. Int J Heat Mass Transf. 2024;220:124918. doi:10.1016/j.ijheatmasstransfer.2023.124918. [Google Scholar] [CrossRef]

32. Ajibade AO, Gambo JJ, Jha BK. Effects of darcy and viscous dissipation on natural convection flow in a vertical tube partially filled with porous material under convective boundary condition. Int J Appl Comput Math. 2024;10(2):84. doi:10.1007/s40819-023-01623-2. [Google Scholar] [CrossRef]

33. Ajithkumar M, Lakshminarayana P, Sucharitha G, Vajravelu K. Investigation of convective peristaltic flow of non-Newtonian fluids through a non-uniform tapered porous conduit with Ohmic heating and viscous dissipation. Int J Model Simul. 2024;5:1–4. doi:10.1080/02286203.2024.2345259. [Google Scholar] [CrossRef]

34. Anwar S, Ahmad U, Sun T, Ashraf M, Rasool G. Impact of solar radiation in the presence of temperature-dependent thermal conductivity of non-Newtonian Casson flow on natural convection heat transfer in plume generated due to the combined effects of heat source and aligned magnetic field. Numer Heat Transf, Part A: Appl. 2024;7:1–8. doi:10.1080/10407782.2024.2367089. [Google Scholar] [CrossRef]

Appendix A. Algorithm

The major lines of the algorithm are stated from Eqs. (A1) to (A4). The differential equations are enlisted as:

dFdeta=@(eta,F)[F(2);F(3);((4/5)∗F(2)∗F(2)−(12/5)∗F(1)∗F(3))+((8/5)∗S∗(2∗F(5)∗F(5)−F(4)∗F(6)))+F(7);F(5);F(6);−(γ)∗((12/5)∗F(1)∗F(6)+4∗F(2)∗F(5)+(8/5)∗F(4)∗F(3));F(8);−(Pr)∗(((12/5)∗(F(1)∗F(8)+F(2)∗F(7)))+E∗(F(3)∗F(3))+M∗E∗(F(2)∗F(2)))](A1)

Boundary conditions are enlisted as:

res =@(fa,fb)[fa(1);fa(3);fa(4);fa(5)−1;fa(8);fb(3);fb(5);fb(7)];(A2)

The initial guess and step size adjuster

SolYinit = bvpinit([0:1:5],[0;0;0;0;0;0;0;0]);(A3)

Fsol = bvp4c(dFdeta, res, SolYinit)(A4)