 Open Access
Open Access
ARTICLE
Effect of the Geometrical Parameter of Open Microchannel on Pool Boiling Enhancement
Mechanical Engineering Department, University of Technology-Iraq, Baghdad, 10066, Iraq
* Corresponding Author: Ali M. H. Al-Obaidy. Email:
Frontiers in Heat and Mass Transfer 2024, 22(5), 1421-1442. https://doi.org/10.32604/fhmt.2024.055063
Received 15 June 2024; Accepted 12 August 2024; Issue published 30 October 2024
Abstract
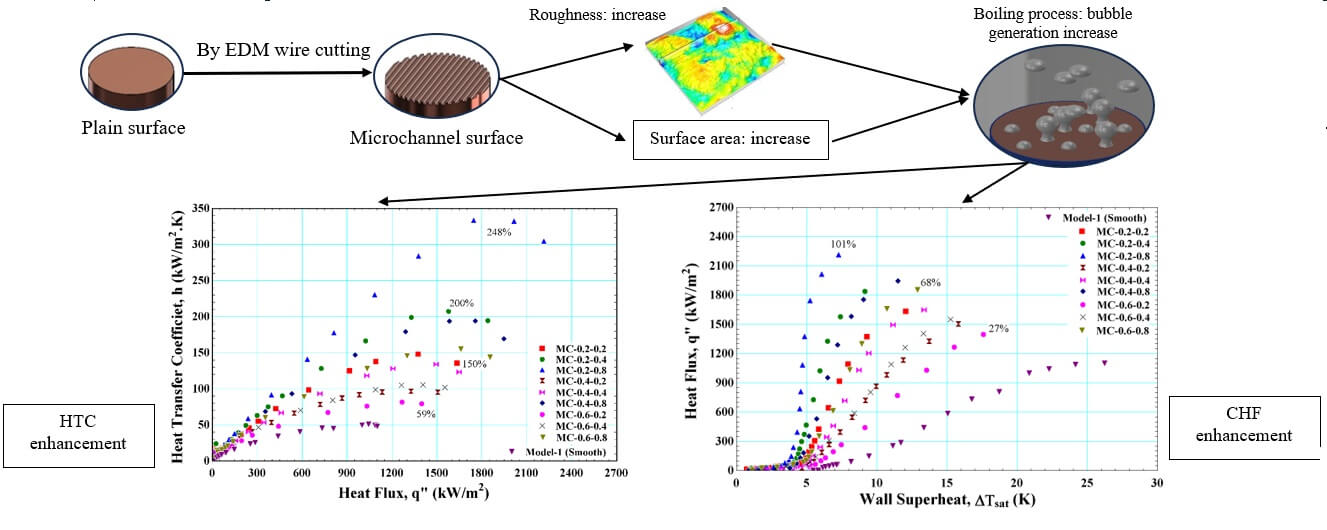
High heat dissipation is required for miniaturization and increasing the power of electronic systems. Pool boiling is a promising option for achieving efficient heat dissipation at low wall superheat without the need for moving parts. Many studies have focused on improving heat transfer efficiency during boiling by modifying the surface of the heating element. This paper presents an experimental investigation on improving pool boiling heat transfer using an open microchannel. The primary goal of this work is to investigate the impact of the channel geometry characteristics on boiling heat transfer. Initially, rectangular microchannels were prepared on a circular copper test piece with a diameter of 20 mm. Then, the boiling characteristics of these microchannels were compared with those of a smooth surface under saturated conditions using deionized water. In this investigation, a wire-cutting electrical discharge machine (EDM) machine was used to produce parallel microchannels with channel widths of 0.2, 0.4, and 0.8 mm. The fin thicknesses were 0.2, 0.4, and 0.6 mm, while the channel depth remained constant at 0.4 mm. The results manifested that the surface featuring narrower fins and broader channels achieved superior performance. The heat transfer coefficient (HTC) was enhanced by a maximum of 248%, and the critical heat flux (CHF) was enhanced by a maximum of 101% compared to a plain surface. Eventually, the obtained results were compared with previous research and elucidated a good agreement.Graphic Abstract
Keywords
Nomenclature
| Latins’ Symbols | |
| A | Area (m2) |
| CHF | Critical Heat Flux |
| EDM | Electrical Discharge Machine |
| D | Diameter (m) |
| HTC/h | Heat transfer coefficient (kW.m−2 K−1) |
| hfg | Latent heat of vaporization (kJ.kg−1) |
| I | Electrical current (A) |
| k | Thermal conductivity (kW.m−1 K−1) |
| MAE | Mean absolute error |
| MC | Microchannel |
| q | Heat flux (kW.m−2) |
| R | Roughness (m) |
| ONB | Onset of nucleate boiling |
| r, min/r, max | Maximum and minimum cavity radius (µm) |
| T | Temperature (K) |
| U | Uncertainty |
| V | Voltage (V) |
| W | Width (µm) |
| y | Distance between thermocouples (m) |
| Greek Symbols | |
| δ | Boundary layer thickness (µm) |
| θ | Contact angle (degree) |
| ρ | Density (kg.m−3) |
| σ | Surface tension (N.m−1) |
| Subscripts | |
| l | Liquid |
| s | Surface |
| Sat | Saturated |
| Sub | Subcooled |
| Th | Thermal |
| v | Vapor |
Recently, there has been a notable focus on two-phase heat transfer due to the growing need for efficient heat dissipation in devices with high heat flux. In contrast to non-phase change processes, pool boiling heat transfer has been shown to be a very dependable and effective method for high heat flux systems [1–3]. It has been used in a variety of technical fields, including nuclear reactors [4,5], high-performance electronics [6–8], power plants [9,10], petroleum refining [11,12], and spacecraft [13,14]. Hence, altering the heat transfer surface can improve the overall heat transfer performance. So, the fabrication of surface micro/nanostructures has garnered significant interest in recent times, as it has been demonstrated to be a successful method of raising both the heat transfer coefficient (HTC) and the critical heat flux (CHF) [15]. Various researchers have tried to change the open microchannel’s geometrical design parameters to enhance pool boiling’s performance. For instance, Ghiu et al. [16] investigated the effect of channel width on the thermal performance of pool boiling using a range of width (0.065–0.36 mm) at a constant value of depth and pitch of open microchannel. The authors found that the heat transfer performance of the enhanced structures was weakly dependent on the channel width. Cooke et al. [17] studied the effect of the different surface geometries of a copper chip on the thermal performance in pool boiling. Experiments were performed at two values of width and fin thickness (0.1 and 0.2 mm) with a range of depth (0.18–0.208 mm) using saturated distilled water as working fluid under atmospheric pressure. The results indicated that the microchannels with a broader and deeper etch are the most effective boiling surfaces. Compared with a plain chip, the heat transfer coefficient can be augmented by up to 3.4. Cooke et al. [18] also extended their work to improve heat transfer by changing the geometric parameters of the microchannel. So, experiments were carried out with a (0.2–0.4 mm) width, a (0.1–0.4 mm) depth, and a (0.1–0.3 mm) fin thickness. The results evinced that the chips with deeper channels, wider channels, and thinner fins performed the best. The best chip dissipated a heat flux of 244 W.cm−2, corresponding to a recorded heat transfer coefficient of (269 kW.m−2 K−1), which didn’t attain the CHF.
Contrary to what was stated above, studies on improved or structured microchannel heat sinks often concluded that the deeper and narrower width of open microchannel favorably impacted the thermal performance of pool boiling, such as Kalani et al. [19]. They investigated the effect of various channel depths (245–470 μm) and widths (194–406 μm) of the microchannel upon the performance of pool boiling using ethanol as a working fluid under atmospheric pressure. Results showed that the heat dissipated by a surface with microchannels is double that of the plain surface. The best-performing chips of microchannels are the narrower and deeper channels. Kalani et al. [20] continued the experimental work using dielectric fluid (FC-87), using the same test rig and specimens from the previous study. It was observed that the type of fluid had no effect on the performance of the microchannel chips but dissipated a heat flux of 1.5 times lower than ethanol compared to a plain surface. Mehta et al. [21] performed pool boiling experiments on cylindrical tubes that were positioned horizontally or vertically and had open microchannels with V-grooves and rectangular shapes that were organized both circumferentially and axially. Their findings depicted that the horizontally oriented circumferential V-groove structured surfaces performed better thermally than the vertically oriented V-grooves. Gheitaghy et al. [22] investigated experimentally the impact of microchannel inclination and geometric parameters. It was noticed that when compared to the vertical channel, the angled channel performed better. Also, it was noted that the heat transfer improved when the pitch and channel depth were increased. Kaniowski et al. [23] studied the effects of the geometric dimensions of a microchannel surface on the CHF and HTC. The microchannel has a width of (0.2–0.4 mm), a depth of about (0.2–0.5 mm), and a channel spacing of twice the width. Also, the experimental outcomes displayed that the highest HTCs and CHFs were determined to employ microchannels with the minimum widths. Additionally, the heat flux of the microchannel surface was augmented by more than (245%) compared to a smooth surface, and the heat transfer coefficient (HTC) was augmented by (2.5–4.9) times. Kaniowski [24] also investigated the effects of the geometric dimensions of an inclined microchannel surface upon the CHF and the HTC. Experiments were performed at a range of fin width and channel width (0.2–0.5 mm) and an inclined range from 0° to 60° with a constant depth of 0.3 mm using Novec-649 as working fluid under atmospheric pressure. The highest heat transfer coefficients (HTCs) were achieved on the microchannel surfaces with the largest surface extensions, meaning the surfaces with the smallest microchannel widths. This is because these surfaces provided a significant number of active nucleation sites at both their bottoms and lateral surfaces. The maximum heat flux was 80% higher, and the heat transfer coefficient was twice as high as it would have been on a smooth surface by straight microchannel surfaces. Kaniowski [25] repeated his work with the same experiment conditions and surface dimensions except that the microchannel inclination range was modified from 30° to 60°, and deionized water was used as working fluid in experiments. The result portrayed that the narrowest microchannel widths, along with the longest extensions of microchannel surfaces, produced the highest heat transfer coefficients. The outcomes indicated the highest recorded heat flux equal to 1730 kW.m−2, while the heat transfer coefficient was equal to 475 kW.m−2 K−1.
However, some researchers have been interested in studying the effect of microchannel depth on the performance during boiling, such as Kaniowski et al. [26], who investigated the influence of microchannel depth on the heat transfer coefficient using saturated deionized water (DI) and Novec-649 as working fluid. The microchannel had a depth of (0.2–0.4 mm), a width of (0.3 mm), and a spacing of (0.1 mm). The authors illustrated that the heat transfer coefficient increased when the channel depth increased from 0.2 to 0.3 mm and then decreased as the depth was increased to 0.4 mm. As a result, the heat transfer coefficient of a microchannel with a depth of 0.3 mm was 3.5 times higher than the plain surface. The same research team (Kaniowski et al.) [27] extended their work to investigate the effects of microchannel depth on the performance of pool boiling using ethanol and FC-72 at atmospheric pressure. The microchannel depth was in the range (0.2–0.5 mm) with a width of 0.3 mm. The result evinced that the microchannel’s uppermost HTC had a depth of 0.3 mm. The same study team (Kaniowski et al.) [28] also compared the heat transfer coefficients (HTCs) and the heat fluxes of plain micro-fins and open microchannels for the pool boiling of water, ethanol, and FC-72. The open microchannel surfaces had a width of (0.3 mm) and a depth of (0.2–0.5 mm). Plain micro-fins were 0.6 to 1.5 mm apart on the base surface and had a height of 0.5 mm. It was found that the surface with 0.3 mm deep open microchannels had the best performance. Pool boiling with ethanol at atmospheric pressure was further studied by Kaniowski et al. [13] to determine the impact of microchannel depth on the pool boiling performance. The microchannel had a depth with a range from 0.2 to 0.5 mm. The widths and the pitches of the microchannels were 0.2, 0.3, and 0.4 mm. The study revealed that the microchannels with a width of 0.2 mm and a depth of 0.5 mm achieved the highest HTC and CHF due to their large surface area, which resulted in a heat transfer coefficient that was three times higher and a critical heat flux that was compared to more than double the plain smooth surface. Guo et al. [29] studied the impact of microchannel depth on the heat transfer coefficient by utilizing saturated deionized water as the working fluid. Three shapes of microchannel surfaces were tested: Rectangular, U-shape, and V-shape, with a depth ranging from 0.04 to 0.08 mm and a width of 0.08 mm. It was observed that the depth of the microchannel has a remarkable impact on the frequency at which the bubbles detach. Also, it was depicted that the greater depth of the microchannel results in increased capillary force, consequently promoting bubble formation.
Some researchers investigated the influence of different structured geometries at the microlevels for substrate, such as Ranjan et al. [30] who performed experiments for two structured heating surfaces: the stepped and the segmented stepped configuration of microchannel surfaces in the pool boiling to evaluate them concerning the performance of heat transfer. The stepped microchannel is comprised of an amalgamation of a big rectangular geometry at the top and a V-groove at the bottom. It was found that the uppermost performance of heat transfer was with the segmented stepped configuration, with an improvement of 224% and 296% in the CHF and HTC, correspondingly, in comparison with a plain copper surface. The heat transfer of pool boiling of the V-shaped open microchannels, and micro-pyramids was investigated by Long et al. [31]. The range of the ratios of the depth-to-width of open microchannels was (0.5–2), and these microchannels had various channel widths of (100 µm) and (50 µm). The V-shaped microchannels were less wickable than the pyramidal microstructures. If a comparison with the V-shaped microchannels was made, the pyramidal microstructures having similar structural depth and spacing caused a rise of (35%–157%) in the HTC and (5%–40%) in the CHF, correspondingly. Ali [15] conducted experiments on three types of heating surfaces, namely the rough surface in a circle (RCD), the rough surface in one direction (ROD), and the microchannel, to assess their heat transmission performance in pool boiling. The study revealed that the microchannel surface had the highest heat transfer performance, with a remarkable enhancement of 131% and 211% in the critical heat flux (CHF) and heat transfer coefficient (HTC), respectively, compared to a plain copper surface.
According to the review provided above, the researchers did not reach a consensus regarding the extent to which the microchannel’s width affects the pool boiling performance. At the same time, one group of researchers discovered that the heat transfer efficiency of the improved structures had only a small association with the width of the channel. Another group of researchers found that a smaller and deeper open microchannel positively affected the thermal efficiency of pool boiling. Therefore, the main objective of this study is to investigate the impact of the width of the top fin and the channel width on the pool boiling performance. Experiments were carried out using fully saturated deionized water at normal atmospheric pressure.
The pool boiling set-up was used to perform the experiments in the current work, as shown in Fig. 1. It consists of a boiling chamber, heating elements, a condenser unit, data acquisition hardware, and a power supply unit. The boiling chamber comprises a cylindrical vessel fabricated from stainless steel, featuring a height of 350 mm and an interior diameter of 120 mm. To enable visual inspection, two sight glass windows have been integrated within the boiling chamber. The boiling chamber was sealed by two cylindrical flanges (top and bottom). For a leak-proof system, four connecting rods, as well as O-rings on both sides, were utilized. The upper flange was constructed of aluminum. It provided an opening for the distilled water inlet, thermocouple probe type K (T1) to measure bulk temperature and outlet and inlet connections for the copper Cu condenser. Also, a coiled Cu tube worked as a condenser for the current system. Thus, to keep the coolant fluid in the condenser at a constant temperature, the chiller unit supplies the cooling water into the condenser at the flow rate and the desired temperature. However, the bottom flange was made from thermal Teflon, which provided an opening as follows: Two auxiliary heaters (each one with A 120 VDC, 200 W) combined with a PID to maintain the temperature of bulk water under saturation circumstances. The PID senses the temperature reading of the liquid boiling chamber through a thermocouple (T1). In addition, a central hole with a diameter of 20 mm had been made to insert the heating element. All the thermocouples were connected to a data acquisition system (Model AT4524-Applent Instruments Company) with an accuracy of ±0.3°C integrated with a USB data logger (Model number ATN2 USBRS232) to acquire the temperature readings.

Figure 1: Experimental rig (a) rig diagram, (b) main heating element, (c) heating surface. 1. Boiling chamber vessel. 2. Upper flange. 3. Lower flange. 4. Connecting rod. 5. Sight glass. 6. Thermocouple probe. 7. Cooling water inlet and outlet. 8. Condenser coil. 9. Auxiliary heater. 10. PID. 11. Variac. 12. Stabilizer. 13. Data logger. 14. PC. 15. Cooling tower. 16. Power source. 17. Heating surface block. 18. Copper block. 19. Main heaters. 20. Heating surface block thermocouple distribution. 21. Microchannel surface shape
2.2 Testing Surface Heating Elements Configuration
The heating element consists of a copper test surface, a copper heat block, thermocouples type K, and a cartridge heater, as shown in Fig. 1, to test the variety of the copper test. In test surfaces, a screw was used at one end to be fitted on the copper heat block. The copper test surface with a diameter of 20 mm and a height of 63 mm involved five thermocouples type K inserted into drilled holes with a (2 mm) diameter in the center of the copper test surface. For measuring the temperature gradient within the test surface, the thermocouples were distributed at two different radial directions with an angle of 90° between them, as depicted in Fig. 1. Microchannels were made upon the Cu test surface’s top surface (heating surface) using wire EDM. In the present work, ten heating surfaces with various configurations were utilized for pool boiling experiments: (i) A plain Cu surface and (ii) Nine heating surfaces with different microchannel dimensions. To reduce the heat losses from the test surface to ambient, it was insulated using a Teflon block that was cut to match the Cu test surface geometry. The heat is transferred from a cartridge heater to the copper test surface through a copper heat block that is fitted with seven cartridge heaters, each having a capacity of 250 W. To ensure a leak-proof joint between the Cu heater block and the Cu test surface, thermal grease with a thermal conductivity of 1.2 W/m.K was used between them. The screw end of the Cu test surface that is tied to the Cu heater block is closely surrounded by thermal insulation from stone wool material having a semi-hollow cylindrical shape. The power supply for the cartridge heaters and auxiliary heaters is provided by two variable transformers (Variac) (Model HSN 0103 220 PLUG). The voltage supply is corrected using a voltage stabilizer model (FA-AVR-90V-200VA).
2.3 Preparing of Microchannel Surface
In this study, a wire-cutting electrical discharge machine (EDM) was employed to fabricate nine surfaces of open longitudinal multi-microchannels with dimensions listed in Table 1. The cutting wire used in the EDM has a diameter of 0.18 mm. To complete the task, acetone and ethanol were employed to clean the Cu test region.

Before carrying out any experiment, the Cu test surface for that experiment was fitted on a Cu heat block after applying thermal grease between them to decrease the thermal resistance. Then, a leak-proof test was conducted by filling the boiling chamber with deionized water and checking for any change over a (10 h) period under atmospheric pressure. After that, the level of deionized water in the boiling chamber was attuned to become somewhat above that of the auxiliary heater. Before each test, the dissolved air was removed from the fluid. This can be done by powering the cartridge heater and the auxiliary heater to permit the fluid degassing through boiling it. Throughout the degassing, the system’s pressure was kept at the atmospheric pressure. As soon as the pressure in the system becomes closer to the atmospheric pressure, the condenser is initiated by circulating the water from the circulation bath at a fixed temperature. The heating process was continued for 45 min, with the inlet valve partially opened for (10 s) to eliminate any non-condensable gases. Beyond a certain time of degassing and keeping the bulk fluid at the saturation temperature, the tests began by gradually giving heat input to the test surface, measured by the wattmeter. After reaching a steady state, measurements of the test surface temperature were recorded at each stage. The readings were taken when the thermocouples remained within a ±0.1°C range for a (2 min) continuous period. Such a process was repeated for different heat flux values. The experiments were carried out within a heat flux range of (0–3400 kW.m−2).
The uncertainty is derived using equations in [32,33]. Therefore, the uncertainty of heat flux can be given by:
The uncertainty of surface temperature can be given by:
where
The surface roughness and morphological analysis of the microchannel models and plane surfaces in the present work were measured using atomic force microscopy (AFM; Naio Nanosurf Switzerland) technology. Also, the wettability of a surface was defined by measuring the static contact angle. Additionally, the easiest and most broadly utilized technique is the Sessile drop technique for determining the angle of contact. A drop of fluid is located upon the test surface, a camera takes its images, and the angles are obtained by sketching a tangent upon these images. Table 2 summarizes the surface roughness results and the wettability measurements for the microchannel models and plane surfaces.

The heat flux applied to the heat sink may be regarded as unidirectional. The evaluations, in this case, adhere to the Fourier’s law of heat transfer in the vertical direction [34–36], as below:
where k is the thermal conductivity of heating surface material (Copper). The temperature gradient is determined using backward Taylor’s series approximation based on three points:
Taylor’s series: validity is contingent upon using equidistant spaces. Therefore, point 2 is excluded from the equation shown above. The coefficient of heat transfer may be obtained by employing Newton’s equation of heat transfer:
where Tl is the saturated temperature of the boiled liquid, and Ts is the heating surface temperature, which can be evaluated by Fourier’s law also [19,20]:
T2, T3, T4, and T5 are the points of thermocouples on the heat sink, as manifested in Fig. 1. y1 is the space between the point of thermocouple 2 and the heating surface.
The heating assembly consists of several components, resulting in significant heat dissipation owing to the presence of gaps and thermal grease, which has a thermal conductivity much lower than that of copper. So, the heat flow has to be determined using the following equation:
Then, Eq. (1) will be subtracted from Eq. (5) to obtain the losses.
Pool boiling curves were performed to confirm the accuracy of the measuring devices and the experimental setup. The findings from the smooth plain copper surface were compared with experimental data, and correlations were established from previous studies found in the literature [37–40]. The comparison with the published data was evaluated using the mean absolute error (MAE) [41,42] in the following manner:
where x is the heat flux in this work, and n is the total number of data points.
The comparison can be displayed in Fig. 2. The current study shows good agreement with the experimental results from Dharmendra et al. [37] and Wang et al. [38] with an MAE value of 8.28% and 13.63%, respectively. In addition, the current experimental results were compared to established correlations, such as Jung et al. [39] and Cooper [40]. Fig. 2 manifests that the correlations for Jung et al. [39] and Cooper [40] give a good prediction with an MAE of 22.97% and 26.01%, respectively.

Figure 2: Comparison between present experimental data and previous works for smooth surface . Dharmendra et al. (2015) [37], Wang et al. (2018) [38], Cooper (1984) [40], Jung et al. (2004) [39]
3.2.1 Effect of Microchannel Width
The boiling curve for smooth copper surfaces and open microchannels with different designs is displayed in Fig. 3A–C as a function of heat flux and wall superheat temperature. The heat flux presented in this figure was calculated based on the projected area of the microchannel interactions between the bubbles forming and developing in and over the surfaces of microchannels. Meanwhile, the bubble’s pinning on the microchannel fins helped reduce the wall’s superheat by helping dissipate heat from the surface. As a result, the smooth surface was the poorest compared to all microchannel models. The figure shows that all the investigated models exhibit a similar boiling curve pattern in which the natural convection predominates initially at lower heat fluxes. Following the start of nucleate boiling, the surface temperature increased, and more nucleation sites were activated, resulting in more heat being released. This means that with the increased heat flux of the wall, the wall superheat temperature also increased. However, further heat is released from the microchannel surface at a wall superheat similar to that of Model 1. It’s obvious from the figure that the microchannel models have a higher slope than Model 1. This is attributed to the enhancement of CHF. As a result, the improved CHF values for the model’s channels MC-0.2-0.2, MC-0.2-0.4, and MC-0.2-0.8 at a fin width of 0.2 were 48.5%, 67.3%, and 101.3%, respectively, compared to Model 1. The model with a broader channel (MC-0.2-0.8) provides the highest CHF. This can be explained as reported by Yao et al. [43,44], Cooke et al. [17,18], and Kaniowski et al. [23] that the broader channels increased the heat transfer, which is thought that the broader channels increased the heat transfer, which is thought to be connected to the generation of bubbles and its dynamics. As a result of its proximity to the heat source, the bubbles formed at the channel bottom. More bubble nucleation sites appeared to be generated by the broader channels. Additionally, widening the channel facilitates the water flow into the microchannels, feeding the nucleation sites and preventing the channel from drying out.

Figure 3: Effect of microchannel width on boiling curve for: (A) fin width of 0.2 mm, (B) fin width of 0.4 mm, and (C) fin width of 0.6
The influence of three values for fin width (0.2, 0.4, and 0.6 mm) on the pool boiling curve can be elucidated for three groups, each with three models with a fixed channel width of (0.2, 0.4, and 0.8 mm), as illustrated in Fig. 4A–C. Model 1 was used as a reference to evaluate the fin width’s effectiveness. In general, for a given channel width, as seen in the figure, with an increase in fin width from 0.2 to 0.6 mm, one can observe that the boiling curve shifted towards the right, resulting in a delay in the onset of nucleate boiling. This means that the slope of the boiling curve is reduced with increasing the fin width, which results in lower CHF values and larger onset nucleation. For example, for a given channel width of 0.2, the onset of nucleation boiling for channel models MC-0.2-0.2, MC-0.4-0.2, and MC-0.6-0.2 was at 3.16, 3.78, and 4.748 K, respectively. Also, the percent enhancement of CHF corresponding to the mentioned models was 48.5%, 36.8%, and 27.2%, respectively, compared to Model 1. From this, one can conclude that the thicker fin demonstrates a reduction in performance. Hence, the model with a thinner fin (MC-0.2-0.2) has better performance. The performance improved when the channel width increased, as portrayed in Fig. 4B,C, which was clear via increasing the slope. Thus, one can conclude that the heat transfer is influenced by the width of the fin as well as the width of the channel since the hottest region (the bottom of channels) will be larger for thinner fins and wider channels. And the nucleation sites number is going to grow long with the size of a larger region with higher temperatures.

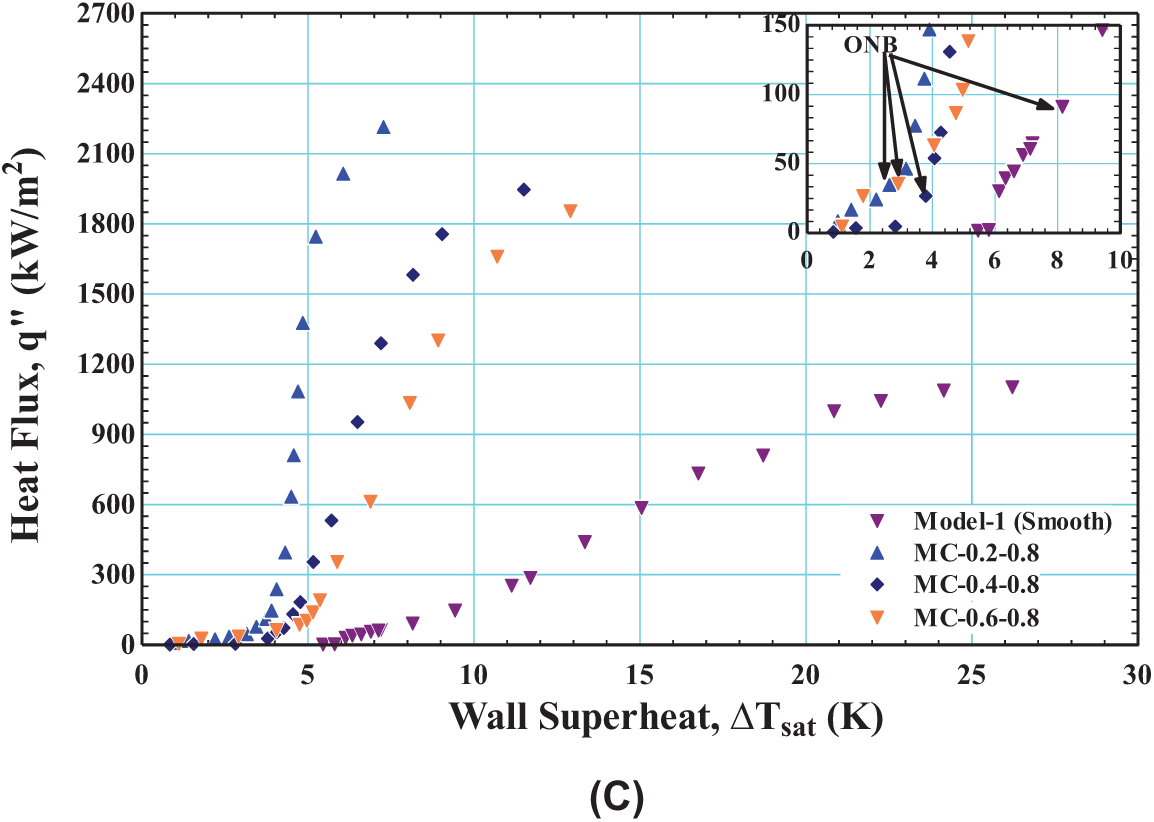
Figure 4: Effect of fin width on boiling curve for: (A) channel width of 0.2 mm, (B) channel width of 0.4 mm, and (C) channel width of 0.8
3.3.1 Effect of Microchannel Width
The heat transfer coefficient against the heat flux is depicted in Fig. 5A–C for three groups of channel models that are classified by fin widths of 0.2, 0.4, and 0.6 mm. These groups have similar channel width values (0.2, 0.4, and 0.8 mm) and have similar channel depths of 0.4 mm. Model 1 (smooth surface) is presented in this figure to evaluate the performance of microchannels. As seen in this figure, the results obtained for all models exhibit a steady increase in the heat transfer coefficient with an increase in the heat flux condition. Also, the HTC is improved by all tested microchannel configurations compared to Model 1. Hence, the factors that result in increased heat transfer may be represented as increased bubble frequency, bubble diameter, and improved microlayer evaporation, as mentioned by Gouda et al. [45]. Referring to this figure, for a given fin width, one can observe that a wider channel causes remarkably increased heat transfer. This may be ascribed to more nucleation sites and promising bubble dynamics compared to the smaller channel width. As mentioned earlier, the nucleation sites are related to the roughness if they are within the range of the active nucleation cavity size. So, it has been calculated using the theory of Kandlikar in 2006 [46] expressed by:


Figure 5: Effect of microchannel width on HTC for: (A) fin width of 0.2 mm, (B) fin width of 0.4 mm, and (C) fin width of 0.6 mm
with the feeding of experimental properties and the outcome is tabulated in Table 3. As indicated in this table, the roughness acts as an active nucleation site for bubble generation because it falls within the calculated cavity size range. In general, the higher roughness causes a larger wetted area, as seen in Table 3, which increases the number of surfaces’ microcavities and increases the density of the active nucleation sites. As a result, the wall temperature required for nucleation decreased, which increased the heat transfer coefficient. According to the figure, the peak of the curve corresponds to the maximum HTC, which is specified as CHF. Beyond the CHF, the HTC reduces with the wall superheat rise. Table 3 presents the enhancement ratio of HTC for nine channel models and the enhancement factor compared to Model 1. The maximum HTC is obtained for the wider channel, and the maximum HTC for the MC-0.2-0.8 channel model is attributed to the higher roughness and wettability. Referring to Table 3, for comparing the augmentation factor for area and heat transfer between them for all channel models, this table shows that the augmentation factor area for the MC-0.2-0.8 channel model is 1.8, whereas the heat transfer enhancement factor is 7.571. With its area enhancement factor identical, it was an MC-0.6-0.4 channel model but had a lower heat transfer enhancement factor of 2.07. Therefore, the MC-0.2-0.8 channel model outperforms the MC-0.6-0.4 channel model for a similar area enhancement factor. So, it can be inferred that increasing the surface area isn’t the only factor increasing the heat transfer rate in pool boiling.

The impacts of three fin width values (0.2, 0.4, and 0.6) on the HTC for three groups, each with three models, are revealed in Fig. 6A–C. The efficiency of fin width was evaluated using Model 1 as a reference point. As seen in this figure, all models have the same pattern as the HTC with heat flux. Where it increases with increased heat flux until it reaches a maximum value of HTC, the heat flux at such point is defined as the CHF. After that, the HTC decreases with the increase in heat flux. According to the figure, for a given channel width, one can note that the maximum heat transfer coefficient was obtained with the thinner fin of 0.2 mm, as indicated in Table 3. This is attributed to the surface’s characteristic of the channel models, as tabulated in Table 2. It is observed that the roughness of the surface and wettability decrease with the increased fin width. Thus, the reduction in roughness reduces the contact area with liquid, which causes the required wall temperature to increase for the incipient boiling. Also, a reduction in surface wettability makes the surface hydrophobic; hence, the contact angle is greater than 90 degrees. This outcome for the hydrophobic surface causes poor heat transfer performance at a high heat flux density, as seen in the figure. The surface wettability has an important influence on the boiling heat transfer. However, the HTC enhancement increased with an increase in channel width from 0.2 to 0.8 mm, as seen in the figure and Table 3. This is related to the increase in the surface wettability and roughness, which is clear in Table 2. It can be inferred that both the channel width and fin width impact the heat transmission since the surface roughness and wettability will be larger for wider channels and thinner fins. With greater surface roughness and wettability, the number of nucleation sites will increase, resulting in a reduced wall temperature and an increase in the HTC. As a result, the MC-0.2-0.8 microchannel model was chosen among all the channel models to improve its performance further by coating the fin tops and the interior channel walls of the microchannel, as manifested in Fig. 6.

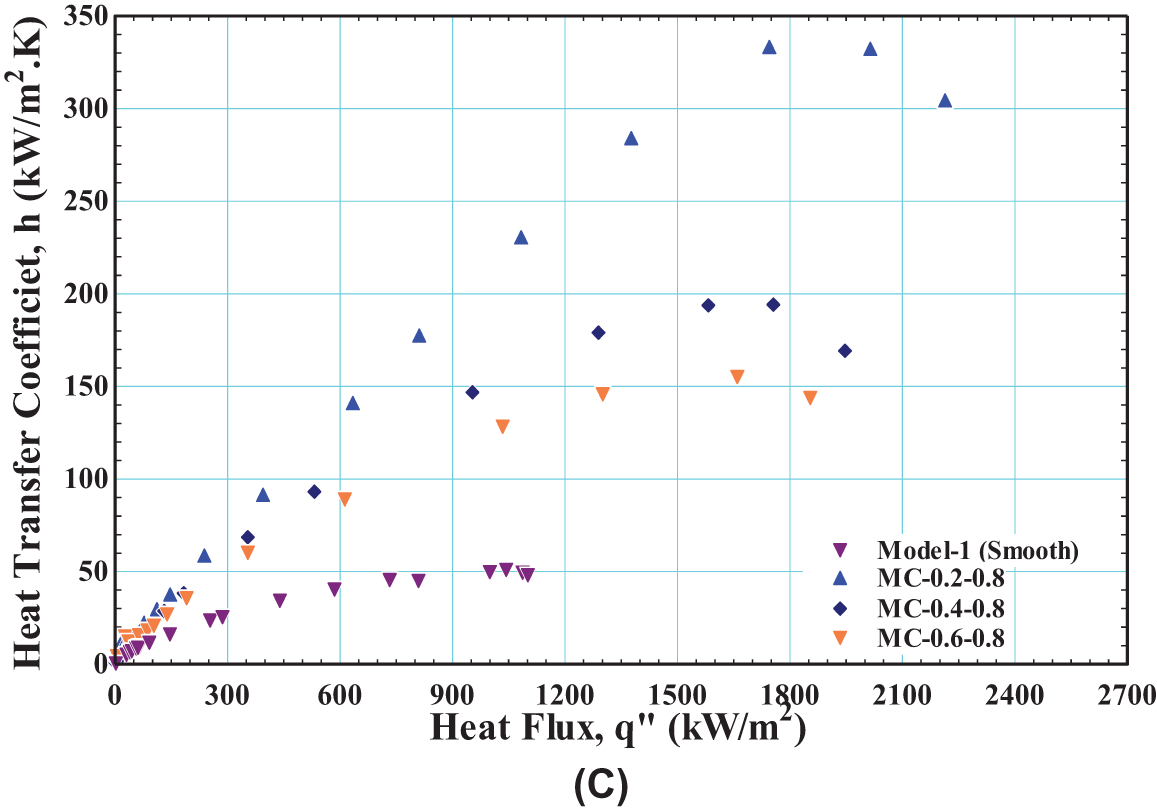
Figure 6: Effect of fin width on HTC for: (A) channel width of 0.2 mm, (B) channel width of 0.4 mm, and (C) channel width of 0.8 mm
3.4 Comparison with Previous Works
The HTC for the all-model microchannel surfaces tested in the present work was compared with published data for Mehta et al. [21], Long et al. [31], Dong et al. [47], Ranjan et al. [30], and Bulut et al. [48], as shown in Fig. 7. The data [21] appeared to have good predictions with the results for the channel models of MC-0.2-0.2, MC-0.2-0.4, MC-0.4-0.2, MC-0.4-0.4, MC-0.6-0.2, MC-0.6-0.4, and MC-0.6-0.8 with an MAE of 18.7%, 29.8%, 14.8%, 17.8%, 25.5%, 15.4%, and 18.8%, respectively.

Figure 7: Comparison of the microchannel with previous works. Mehta and Kandlikar (2013) [21], Long et al. (2022) [31], Ranjan et al. (2023) [30], Bulut et al. (2023) [48], Dong et al. (2023) [47]
Furthermore, it has appeared that the data for Long et al. [31] were accurately predicted by the channel models MC-0.2-0.2 and MC-0.6-0.4, which had corresponding MAEs of 28.1% and 20.4%, respectively. Dong et al. [47] predicted very well the MC-0.2-0.4 and MC-0.2-0.8 channel models with an MAE of 24.1% and 29.1%, respectively. Also, the channel models MC-0.2-0.2, MC-0.4-0.2, MC-0.4-0.4, MC-0.6-0.2, MC-0.6-0.4, and MC-0.6-0.8 evinced good predictions for the data from Ranjan et al. [30], with a MAE of 29.4%, 10.3%, 22.7%, 11.3%, 10%, and 29%, respectively. Additionally, Bulut et al. [48] demonstrated accurate prediction using the MC-0.2-0.2, MC-0.4-0.2, MC-0.4-0.4, MC-0.6-0.2, MC-0.6-0.4, and MC-0.6-0.8 channel models, with the respective MAE values of 28.1%, 11.2%, 21.6%, 10%, 12.4%, and 26.7%, respectively.
Experiments were conducted with deionized water (DI) under atmospheric pressure to investigate the effect of the channel width and the fin thickness at a fixed channel depth on the boiling performance of nine microchannel models. For comparison, plane surfaces were used. The experimental investigations debated in this paper led to the subsequent conclusions:
1. The results elucidated that the performance improvement from the microchannel surfaces was unrelated to the surface area increase.
2. The outcomes also portrayed that the onset of nucleate boiling (ONB) occurs at lower superheat degrees and heat flux when using wider channels and thinner fin surfaces because the increase in channel area provides more nucleation sites.
3. It was found that the broader channels had a higher CHF. The maximum CHF was obtained by the MC-0.2-0.8 channel model with 2214 kW.m−2 and an enhancement ratio of 101.3% compared with the smooth surface because the heat transfer is influenced by the width of the fin as well as the width of the channel since the hottest region (the bottom of channels) will be larger for thinner fins and wider channels.
4. The MC-0.2-0.8 channel model obtained the maximum HTC with 332.3 kW.m−2 K−1, and the enhancement ratio was 248.1% compared with the smooth surface since the surface roughness and wettability will be larger for wider channels and thinner fins. With greater surface roughness and wettability, the number of nucleation sites will increase, resulting in a reduced wall temperature and an increase in the HTC.
Acknowledgement: The authors extend their sincere gratitude to the reviewers for their helpful suggestions, which significantly enhanced the quality and presentation of this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Conceptualization, Ali M. H. Al-Obaidy, Ekhlas M. Fayyadh and Amer M. Al-Dabagh; methodology, Ali M. H. Al-Obaidy; validation, Ali M. H. Al-Obaidy and Ekhlas M. Fayyadh; formal analysis, Ali M. H. Al-Obaidy and Ekhlas M. Fayyadh; investigation, Ali M. H. Al-Obaidy, Ekhlas M. Fayyadh and Amer M. Al-Dabagh; resources, Ali M. H. Al-Obaidy; data curation, Ali M. H. Al-Obaidy and Ekhlas M. Fayyadh; writing original draft preparation, Ali M. H. Al-Obaidy and Ekhlas M. Fayyadh; writing review and editing, Ali M. H. Al-Obaidy and Ekhlas M. Fayyadh; visualization, Ali M. H. Al-Obaidy; supervision, Ekhlas M. Fayyadh and Amer M. Al-Dabagh. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data generated in this study can be made available by the corresponding author following a request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kuznetsov DV, Pavlenko AN, Radyuk AA, Komlev DI, Kalita VI. Features of heat transfer during pool boiling of nitrogen on surfaces with capillary-porous coatings of various thicknesses. J Eng Thermophys. 2020;29(3):375–87. doi:10.1134/S1810232820030017. [Google Scholar] [CrossRef]
2. Cao Z, Wu Z, Abbood S, Sundén. B. An analysis of pool boiling heat transfer on nanoparticle-coated surfaces. Energy Procedia. 2019;158:5880–7. [Google Scholar]
3. Mohammed S, Fayyadh E. Experimental investigation of sub-cooled flow boiling in metallic microchannel. Eng Technol J. 2019;37(10A):408–15. doi:10.30684/etj.37.10A.5. [Google Scholar] [CrossRef]
4. Ali A, Kim HG, Hattar K, Briggs S, Jun Park D, Hwan Park J, et al. Ion irradiation effects on Cr-coated zircaloy-4 surface wettability and pool boiling critical heat flux. Nucl Eng Des. 2020;362(11–12):110581. doi:10.1016/j.nucengdes.2020.110581. [Google Scholar] [CrossRef]
5. Agma O, Yildiz S. Experimental study of nucleate pool boiling with water in atmospheric pressure. Therm Sci. 2024;28(2):1807–18. doi:10.2298/TSCI230627210A. [Google Scholar] [CrossRef]
6. Ali JM, Abid BA, Essa KM. Pool boiling heat transfer using nanofluids. Eng Technol J. 2015;33(7B):512–25. doi:10.30684/etj.33.2A.5. [Google Scholar] [CrossRef]
7. Walunj A, Sathyabhama A. Pool boiling heat transfer enhancement through biphilic stepped microchannel. Int J Chem Eng Mater. 2023;2:8–17. [Google Scholar]
8. Song Y, Díaz-Marín CD, Zhang L, Cha H, Zhao Y, Wang EN. Three-tier hierarchical structures for extreme pool boiling heat transfer performance. Adv Mater. 2022;34(32):e2200899. doi:10.1002/adma.202200899 [Google Scholar] [PubMed] [CrossRef]
9. Kadhim ZK, Mohamed AA, Abed SA. An experimental study for the effect of vertical forced vibration on pool boiling heat transfer coefficient. Eng Technol J. 2012;30(10):1662–76. [Google Scholar]
10. Getan MK, Abid BA. Heat transfer in pool boiling with surfactants. Eng Technol J. 2010;28(17):5421–39. [Google Scholar]
11. Gupta SK, Misra RD. Effect of two-step electrodeposited Cu-TiO2 nanocomposite coating on pool boiling heat transfer performance. J Therm Anal Calorim. 2019;136:1781–93. [Google Scholar]
12. Jabbar SA, Sultan AJ, Maabad HA. Prediction of heat transfer coefficient of pool boiling using back propagation neural network. Eng Technol J. 2012;30(8):1293–305. [Google Scholar]
13. Kaniowski R, Pastuszko R, Dragašius E, Baskutis S. Pool boiling of ethanol on copper surfaces with rectangular microchannels. Energies. 2023;16(23):7883. [Google Scholar]
14. Shil B, Sen D, Das AK, Sen P, Kalita S. Effect of GNP/Ni-TiO2 nanocomposite coated copper surfaces fabricated by electro chemical deposition under nucleate pool boiling regime: a comprehensive experimental study. J Appl Fluid Mech. 2024;17:697–712. [Google Scholar]
15. Ali BM. An experimental study of heat transfer in pool boiling to investigate the effect of surface roughness on critical heat flux. Chem Eng. 2024;8(2):44. [Google Scholar]
16. Ghiu CD, Joshi YK. Visualization study of pool boiling from thin confined enhanced structures. Int J Heat Mass Transf. 2005;48(21–22):4287–99. [Google Scholar]
17. Cooke D, Kandlikar SG. Pool boiling heat transfer and bubble dynamics over plain and enhanced microchannels. J Heat Transfer. 2011;133:163–72. [Google Scholar]
18. Cooke D, Kandlikar SG. Effect of open microchannel geometry on pool boiling enhancement. Int J Heat Mass Transf. 2012;55(4):1004–13. [Google Scholar]
19. Kalani A, Kandlikar SG. Pool boiling heat transfer over microchannel surfaces with ethanol at atmospheric pressure. In: International Conference on Nanochannels, Microchannels, and Minichannels (ICNMM) ASME, 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels, 2012, Jul 8–12; Rio Grande, Puerto Rico, USA: ASME; p. 333–9. doi:10.1115/ICNMM2012-73188. [Google Scholar] [CrossRef]
20. Kalani A, Kandlikar SG. Pool boiling of FC-87 over microchannel surfaces at atmospheric pressure. In: International Conference on Nanochannels, Microchannels, and Minichannels (ICNMM) ASME 2012 International Mechanical Engineering Congress and Exposition, 2012, Nov 9–15; Houston, TX, USA: ASME; p. 2051–7. doi:10.1115/IMECE2012-86186. [Google Scholar] [CrossRef]
21. Mehta JS, Kandlikar SG. Pool boiling heat transfer enhancement over cylindrical tubes with water at atmospheric pressure, part I: experimental results for circumferential rectangular open microchannels. Int J Heat Mass Transf. 2013;64:1205–15. [Google Scholar]
22. Gheitaghy AM, Samimi A, Saffari H. Surface structuring with inclined minichannels for pool boiling improvement. Appl Therm Eng. 2017;126:892–902. [Google Scholar]
23. Kaniowski R, Pastuszko R. Pool boiling of water on surfaces with open microchannels. Energies. 2021;14(11):3062. [Google Scholar]
24. Kaniowski R. Pool boiling of Novec-649 on inclined microchannel. Energies. 2023;16(5):2476. [Google Scholar]
25. Kaniowski RM. Pool boiling for water on surfaces with inclined microchannel. Arch Thermodyn. 2024;45:41–9. [Google Scholar]
26. Kaniowski R, Pastuszko R, Nowakowski L. Effect of geometrical parameters of open microchannel surfaces on pool boiling heat transfer. EPJ Web Conf. 2017;143:02049. doi:10.1051/epjconf/201714302049. [Google Scholar] [CrossRef]
27. Kaniowski R, Pastuszko R. Pool boiling of ethanol and FC-72 on open microchannel surfaces. EPJ Web Conf. 2018;180:02042. doi:10.1051/epjconf/201818002042. [Google Scholar] [CrossRef]
28. Kaniowski R, Pastuszko R. Comparison of heat transfer coefficients of open micro-channels and plain micro-fins. EPJ Web Conf. 2018;180:02041. doi:10.1051/epjconf/201818002041. [Google Scholar] [CrossRef]
29. Guo N, Gao X, Li D, Zhang J, Yin P, Hua M. Experimental and numerical analysis of the influence of microchannel size and structure on boiling heat transfer. Comput Model Eng Sci. 2023;136(3):3061–82. doi:10.32604/cmes.2023.026657. [Google Scholar] [CrossRef]
30. Ranjan A, Priy A, Ahmad I, Pathak M, Khan MK. Pool boiling heat transfer characteristics of a stepped microchannel structured heating surface. Int J Multiphase Flow. 2023;160:104351. [Google Scholar]
31. Long J, Liu Z, Lin H, Li Y, Cao Z, Zhang Z, et al. Pool boiling heat transfer and bubble dynamics over V-shaped microchannels and micropyramids: does high aspect ratio always benefit boiling? Appl Therm Eng. 2022;201:117796. [Google Scholar]
32. Gao Z, Hong S, Dang C. An experimental investigation of subcooled pool boiling on downward-facing surfaces with microchannels. Appl Therm Eng. 2023;226:120283. [Google Scholar]
33. Xu C, Ren J, Qian Z, Zhao L. Investigation of heat transfer performance in deionized water-ethylene glycol binary mixtures during nucleate pool boiling. Processes. 2024;12(2):368. [Google Scholar]
34. Gupta SK, Misra RD. An experimental investigation on pool boiling heat transfer enhancement using Cu-Al2O3 nano-composite coating. Exp Heat Transf. 2019;32(2):133–58. [Google Scholar]
35. khaleel Rashid M, Ali BM, Zorah M, Al-Musawi TJ. Experimental investigation of the effects of grooves in Fe2O4/water nanofluid pool boiling. Fluids. 2024;9(5):110. [Google Scholar]
36. Žalec D, Može M, Zupančič M, Golobič I. Elucidating the effects of surface wettability on boiling heat transfer using hydrophilic and hydrophobic surfaces with laser-etched microchannels. Case Stud Therm Eng. 2024;57:104357. [Google Scholar]
37. Dharmendra M, Suresh S, Kumar CSS, Yang Q. Pool boiling heat transfer enhancement using vertically aligned carbon nanotube coatings on a copper substrate. Appl Therm Eng. 2016;99(3):61–71. doi:10.1016/j.applthermaleng.2015.12.081. [Google Scholar] [CrossRef]
38. Wang YQ, Luo JL, Heng Y, Mo DC, Lyu SS. Wettability modification to further enhance the pool boiling performance of the micro nano bi-porous copper surface structure. Int J Heat Mass Transf. 2018;119(20):333–42. doi:10.1016/j.ijheatmasstransfer.2017.11.080. [Google Scholar] [CrossRef]
39. Jung D, Lee H, Bae D, Oho S. Nucleate boiling heat transfer coefficients of flammable refrigerants. Int J Refrig. 2024;27(4):409–14. doi:10.1016/j.ijrefrig.2003.11.007. [Google Scholar] [CrossRef]
40. Cooper MG. Saturation nucleate pool boiling—a simple correlation. In: First U.K. National Conference on Heat Transfer: The Institution of Chemical Engineers Symposium Series. 1984;2. 86:785–93. [Google Scholar]
41. Habtay G, Buzas J, Farkas I. Heat transfer analysis in the chimney of the indirect solar dryer under natural convection mode. FME Trans. 2020;48(3):701–6. doi:10.5937/fme2003701H. [Google Scholar] [CrossRef]
42. Falsetti C, Chetwynd-Chatwin J, Walsh EJ. Pool boiling heat transfer of Novec 649 on sandblasted surfaces. Int J Thermofluids. 2024;22:100615. doi:10.1016/j.ijft.2024.100615. [Google Scholar] [CrossRef]
43. Yao Z, Lu YW, Kandlikar SG. Pool boiling heat transfer enhancement through nanostructures on silicon microchannels. J Nanotechnol Eng Med. 2012;3(3):031002. doi:10.1115/1.4007425. [Google Scholar] [CrossRef]
44. Yao Z, Lu YW, Kandlikar SG. Fabrication of nanowires on orthogonal surfaces of microchannels and their effect on pool boiling. J Micromech Microeng. 2012;22(11):115005. doi:10.1088/0960-1317/22/11/115005. [Google Scholar] [CrossRef]
45. Gouda RK, Pathak M, Khan MK. Pool boiling heat transfer enhancement with segmented finned microchannels structured surface. Int J Heat Mass Transf. 2018;127(4):39–50. doi:10.1016/j.ijheatmasstransfer.2018.06.115. [Google Scholar] [CrossRef]
46. Kandlikar SG. High flux heat removal with microchannels—a roadmap of challenges and opportunities. Heat Transf Eng. 2005;26(8):5–14. doi:10.1080/01457630591003655. [Google Scholar] [CrossRef]
47. Dong Y, Yu Y, Ibrahim A, Hu X, Hao Y. Influence of liquid height on pool boiling heat transfer over open rectangular microchannels. Appl Therm Eng. 2023;228:120453. doi:10.1016/j.applthermaleng.2023.120453. [Google Scholar] [CrossRef]
48. Bulut M, Shukla M, Kandlikar SG, Sozbir N. Experimental study of heat transfer in a microchannel with pin fins and sintered coatings. Exp Heat Transf. 2023;36(7):1099–1114. doi:10.1080/08916152.2023.2176566. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools