 Open Access
Open Access
ARTICLE
Magneto-Hydro-Convective Nanofluid Flow in Porous Square Enclosure
1 Laboratory Numerical and Experimental Modeling of Mechanical Phenomena, Mechanical Engineering Department, Abdelhamid Ibn Badis University, Mostaganem, 27000, Algeria
2 Department of Physics, Faculty of Sciences, University of 20 Aoút 1955-Skikda, Skikda, 21000, Algeria
3 Mechanical Engineering Department, Mostapha Istambouli University, Mascara, 29000, Algeria
* Corresponding Author: F. Mebarek-Oudina. Email:
(This article belongs to the Special Issue: Advances in Computational Thermo-Fluids and Nanofluids)
Frontiers in Heat and Mass Transfer 2024, 22(5), 1343-1360. https://doi.org/10.32604/fhmt.2024.054164
Received 20 May 2024; Accepted 15 July 2024; Issue published 30 October 2024
Abstract
In this work, a steady mixed convection in a two-dimensional enclosure filled viananoliquid Cu/H2O through a porous medium was numerically analyzed. The nanoliquid flow is designated utilizing the Brinkman-Forchheimer model. The upper and the bottom horizontal walls are considered to be hot (Th) and cold temperature (Tc), respectively, whereas the other walls are thermally insulated. The impact of various dimensionless terms such as the Grashof number (Gr) in the ranges (0.01–20), the Reynolds number (Re) in the ranges (50–500), the Hartman number (Ha) in the ranges (0–20), and three different location cases (0.25, 0.5, and 0.75) are carefully analyzed. The obtained outcomes are established in the form of isotherms, streamlines, and the average Nusselt number. It has been found that heat transport increases significantly through rising Reynolds number (Re). For the location cases L = 0.25, Re = 50, and Gr = 105, the heat transfer is maximum.Keywords
Nomenclature
| CP | Specific heat (J kg−1 K−1) |
| g | Gravitational acceleration (m s−2) |
| Gr | Grashof number |
| k | Heat conductivity (W m−1 K−1) |
| Nuavg | Average Nusselt number |
| Nu | Local Nusselt number |
| p | Static pressure (N/m2) |
| P | Non-dimensional pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| Ri | Richardson number, Gr/Re2 |
| Ha | Hartman number |
| Da | Darcy number (κ/H2) |
| H | Height of the cavity (m) |
| l | Cavitylength (m) |
| L | location of inner elliptical cylinder |
| x, y | Dimensional space coordinates (m) |
| X,Y | Dimensionless space coordinates |
| T | Local temperature (K) |
| Th − Tc | Temperatures gradient |
| ΔT | Temperature difference (K) |
| u, v | Dimensional velocity components (m s−1) |
| U,V | Non-dimensional velocity components |
| U0 | Velocity of the flow at the inlet (m s−1) |
| hi, h0 | Height inlet and outlet of the enclosure (m) |
| Greek Symbols | |
| α | Thermal diffusivity (m2/s) |
| Β | Coefficient of thermal expansion (1/K) |
| Volume fraction of the NPs | |
| Dimensionless temperature | |
| ρ | liquid density (kg/m3) |
| ν | Kinematic viscosity (m2/s) |
| μ | Dynamic viscosity (kg/ms) |
| ϵ | Porosity |
| κ | Permeability of porous medium |
| σ | Electrical conductivity |
| Subscripts | |
| nf | Nanofluid |
| c | Cold |
| h | Hot |
| avg | Average |
| s | Solide |
| f | Fluid |
The convective heat transport problem receives much attention from scientists [1,2]. Ben-Nakhi et al. [3] have demonstrated a computed analysis of convection inside an enclosure. Saeid [4] examined the heat transport in a permeable enclosure with a heated wall. Varol et al. [5] have reconnoitered the coupling between conduction and convection in a triangular enclosure. Chamkha et al. [6] have scrutinized the warm execution of a square walled-in area, which contains a warmed triangular strong divider. In addition, various experimental trainings have been carried out [7–9], and there are several theoretical studies of convection in closed cavities with local heaters [10,11]. In an endeavor to synthesize and scrutinize the impact of NF on liquid motion and heat transport rate, various simulations have been carried out in diverse enclosures. Recently, several researches were conducted to analyze the addition of magnetic hybrid nanofluids (HNFs) in porous enclosures [12–14]. They have examined the exploitation of HNFs in thermal systems used in engineering applications. Sheremet et al. [15] explored the convection transient in an undulated-walled cavity filled with nanoparticles and fluid. They found that the average Nu decreased via a rise in the nanoparticle volume fraction. Bouselsal et al. [16] analyzed the convection inside a tube/shell heat exchanger of various tube shapes filled with Al2O3-MWCNT hybrid nanofluid. Ramesh et al. [17] explored different problems of free convection in various cavities filled with nanofluid. They presented different techniques to boost heat transport (HT). Ismael et al. [18] analyzed the HT in a square medium filled with anNF. The amelioration of HT is reached for very low (Da) numbers and greater than 0.5 of the porous layer thickness. Ismael et al. [19] exposed the coupled convection and conduction modes in a square enclosure. In recent times, the influence of NP volume fractions on the free convection in several cavities under a Lorentz force has enticed the attention of numerous scientists. Ali et al. [20] inspected the impact of Lorenz force with a heat source on ciliated micro-vessels through hybrid nano-blood. Esfe et al. [21] analyzed the effect of distinctive terms on the warm convection in distinctive walled in areas beneath attractive areas with NFs. They stated that Nu decreased with the Ha effect. Mebarek-Oudina et al. [22] scrutinized the thermal-convective performance of the HNF in porous media and its contribution to entropy generation under the power of the Lorentz force. Molana et al. [23] conducted an analysis of convection within a creatively shaped permeable cavity. Their study delved into examining the influence of several physical terms such as Ha, Da, and Ra numbers, alongside geometrical terms, on both the velocity and temperature fields. Giwa et al. [24] delved into the convection study within a square enclosure with a hybrid NF under the influence of magnetic fields. Their research focused on exploring the impact of physical and geometrical terms on both temperature and velocity fields. Hdhiri et al. [25] focused their research on convection within a square-porous cavity. Their findings encompassed a range of parameters including Darcy numbers, porosity, and Richardson numbers and provided insights into the outcomes of their study. Rajarathinam et al. [26] investigated the convection of a Cu-H2O NF in a porous enclosure. They made a significant observation that the orientation of the moving divider has a direct impact on thermal transport in the system. Mebarek-Oudina et al. [27] considered a modified Buongiorno model to verify the influence of magnetite-water NF on hydromagnetic flow. Fayz-Al-Asad et al. [28] studied the heat transfer performance with convection in a wavy surface enclosure adjusted through the fin, they found that the fin size had a significant impact on HT. Abolbashari et al. [29] conducted entropy generation research in a porous enclosure filled with NF. Kameswaran et al. [30] studied the influence of homogeneous-heterogeneous reactions in NF flow. They studied two types of NFs, Cu-H2O and Ag-H2O. Swamy et al. [31] considered the conjugate (conduction-convection) Magneto-Hydro-Dynamic (MHD) incompressible flow in an annular cavity filled via MWCNT-Ag water HNF. It appeared that the most extreme stream quality and warm dissemination rate have been accomplished for a higher conductivity proportion with a lower divider thickness. They found that increasing nanoparticle concentration leads to maximum heat transport. Keerthi Reddy et al. [32] examined the numerical think-about of buoyant convection and warm scattering forms of nanoliquids soaked in a slanted permeable annulus. They found that an increase in Darcy’s number increases the average Nu. In addition, they noticed a substantial control of the magnetic field on liquid flow and heat transport rate. The convection in a square cavity is numerically studied. The 2D Navier-Stokes equations are computed utilizing a control-volume technique based on the model of Darcy-Forchheimer. The solution is achieved for diverse (Gr) numbers, (Ha) numbers, Reynolds numbers (Re), and three locations of the inner cylinder. These studies are attended to improve the impact of physical and geometrical terms on the velocity field, temperature field, and heat transport. Recently, many researches [33–36] were published to examine the convective flow and entropy generation of NF in various cavities. The novelty here and similar works is to study the magnetohydrodynamic convective flow that occurs in a square enclosure with NF made of Cu/H2O in a porous medium with inlet and outlet ports and variously located inner elliptical obstacle. Considering an extensive review of the authors’ expertise and the literature, this particular issue has not yet been studied. Walls are retained at temperatures of hot Th and cold Tc (Th > Tc), respectively, while the left and right vertical walls and the inner elliptical cylinder are considered to be adiabatic.
The physical geometry of the current investigation is displayed in Fig. 1. It is a 2D porous square enclosure filled with Cu-water NF under radial electromagnetic force. The top and bottom horizontally are minted at hot and cold temperatures, respectively. While the vertical walls are adiabatic. The liquid enters the cavity via an inlet port of width (hi) that is positioned on the left vertical wall, prolonging from y = (H–hi) to y = H. An exit port of width (ho) is located on the right vertical wall, scattering from y = zero to y = ho. The widths of the inlet and outlet ports are identical (hi = ho = h). Here, the convection of NF is analyzed by considering three varied locations of the inner cylinder (L).
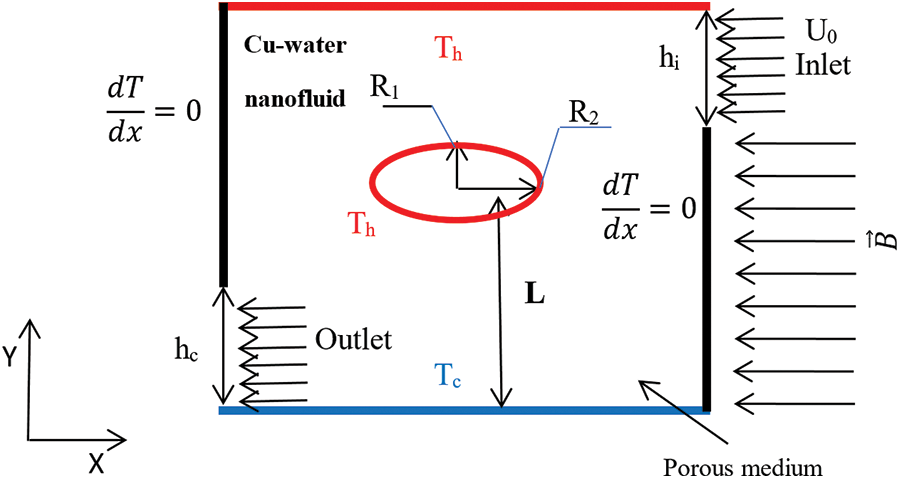
Figure 1: Physical sketch
The NF physical properties are expected to be constant except for the density variation in the buoyancy parameter due to the Boussinesq estimate. Table 1 presents the constant thermo-physical properties of both the NPs and the base liquid. These assumptions are used:
The considered geometry is axisymmetric.
The NF is assumed to be Newtonian and incompressible, and the flow is laminar and unsteady.
The permeable medium is suspicious to be isotropic, homogeneous, and in warm harmony with the fluid.
The NF in the porous enclosure is presumed to be in a single phase. That is, the liquid and NPs are in a warm balance, and no-slip condition happens among them.
With the above expectations and the Boussinesq estimations, 2D equations comprising mass, momentum, and energy can be articulated utilizing the Darcy-Brinkman-Forchheimer model as [22]:
2.1 The Dimensionless Governing Equations
The system is transformed using these variables:
The Eqs. (1)–(4) are shortened by being changed into dimensionless form as shown below:
The problem is convoyed by boundary conditions which are:
• On the inlet side of the enclosure (X = 0, Y = (1–h/H) to 1)
On the outlet side of the enclosure (X = 1, Y = 0 to h/H)
On the vertical left and right walls of the enclosure are adiabatic (X = 0 and X = 1) and the perimeter of the inner cylinderis all so isolated
On the outlet side of the cavity
The thermophysical properties of basic liquid water and Cu are defined in Table 1.
Where:
In the above equations, Cp is the specific heat,
The effective dynamic viscosity and thermal conductivity of the NF can be modeled by Khanafer et al. [38] and Jou et al. [39].
2.3 Heat Transport Characterization
The transferred energy from the heated wall of the annulus is presented in values to obtain the local and average Nu.
2.4 Validation Process & Grid Independence
The investigation of grid independence has successfully confirmed the accuracy of the numerical code with benchmark research published by Saeidi et al. [40]. According to Fig. 2, the comparison between our results and the obtained outcomes from the referred reference shows a respectable agreement.
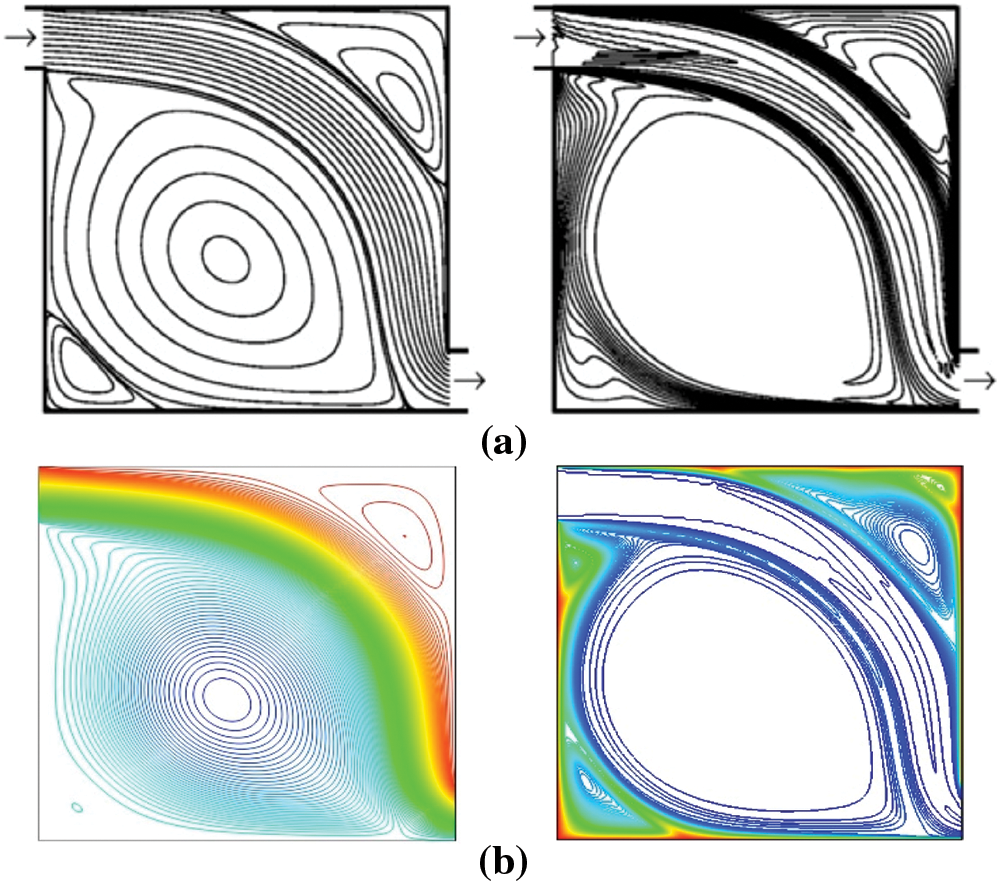
Figure 2: Validation of streamlines and isotherms among the (a) outcomes of Saeidi et al. [40] and (b) current results for Pr = 5, Re = 500
The grid test has been displayed to determine the value of the average Nu via Re = 100, Gr = 105, Da = 10−3, and ϕ = 0.04, as presented in Table 2.

In this study, 2D magneto-convective flow in a square enclosure filled through Cu-water NF soaked with porous medium with an inner circular obstacle is numerically analyzed. The numerical study is performed in order to scrutinize the impacts of some physical and geometrical terms in the specific ranges, such as the Gr in ranges (103–105), the Rein ranges (50–500), the Hartman number (Ha) in the ranges (0–20), and three different location cases L (0.25, 0.5, 0.75) for the fixed Darcy number Da = 10−3 on the plots of streamlines, isotherms, and Nu.
To distinguish the heat transport and flow field features of this problem, various parameters were considered. First, we start studying the effect of Re in the range 50, 100, 250, and 500 for a fixed position of the inner cylinder L = 0.5. The streamlines corresponding case (L = 0.5) with different Grashoft numbers (Gr = 103, 104, and 105) are presented in Fig. 3. Similar isotherms patterns are shown in Fig. 4.
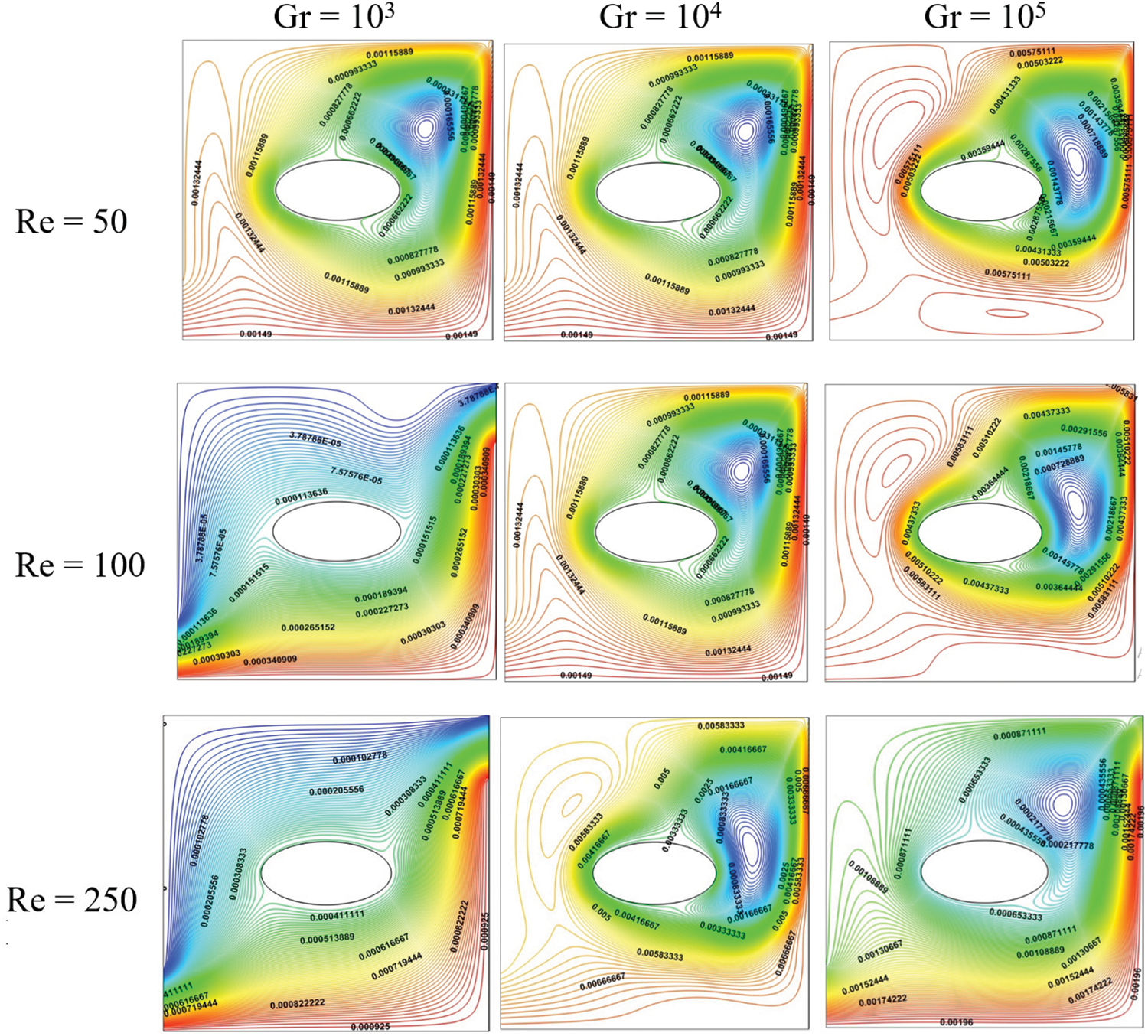
Figure 3: Influence of Re on the streamlines for Da = 10−3, Ha = 0, ϕ = 0.04 and ϵ = 1
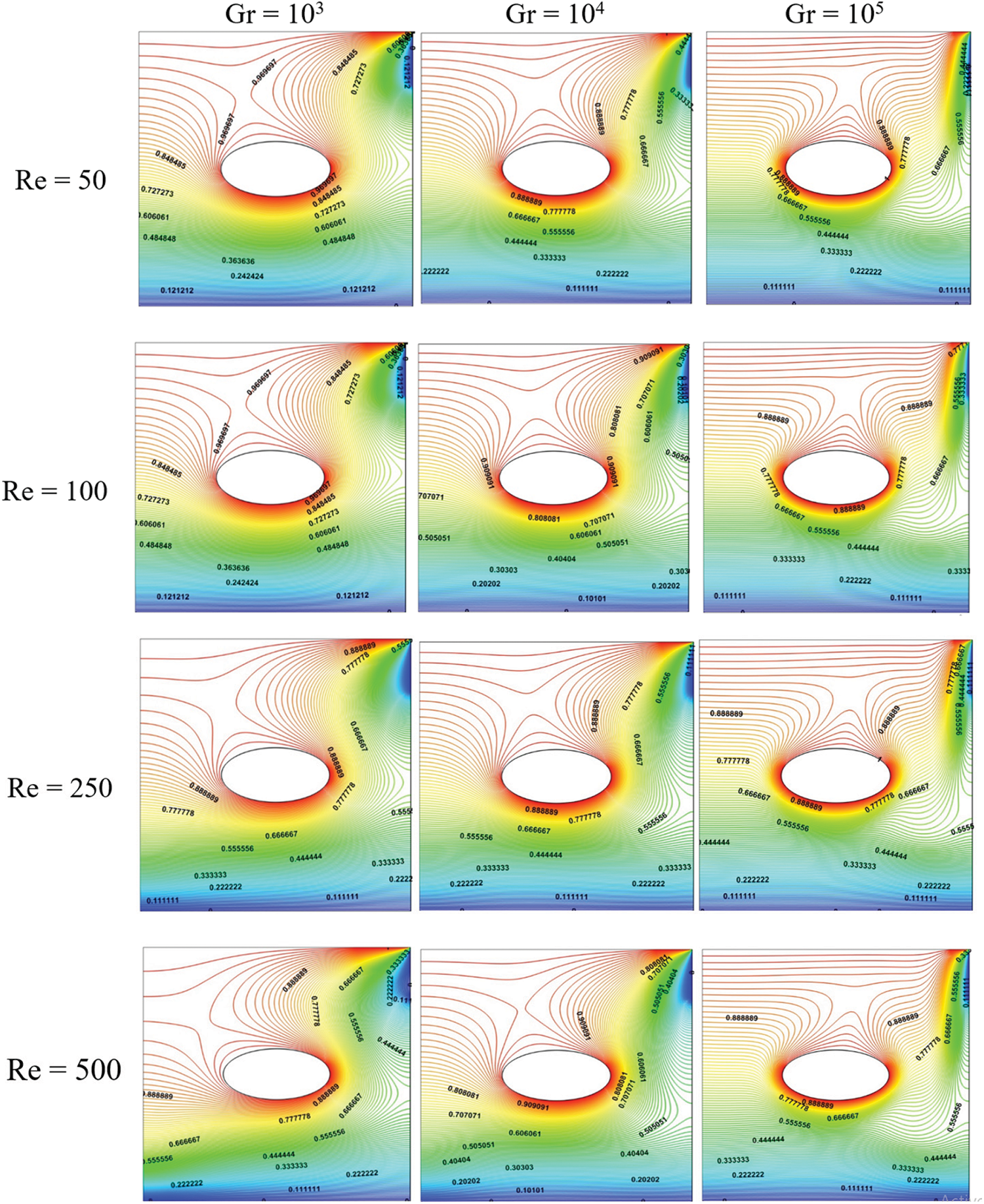
Figure 4: Influence of Re on the isotherms for Da = 10−3, Ha = 0, ϕ = 0.04 and ϵ = 1
It is detected initially for Re = 50 that the flow along the superior inlet port of the cavity is weak. The fresh fluid entering the enclosure travels the shortest distance possible before leaving the enclosure, passing through the lower hemisphere of the cylinder. The magnitude of velocity in the direction of the flow is specified through colors extending from red to blue. Once the colors convert to red, the amplitude of the liquid velocity in the direction of the flow rises. Whereas, colors close to blue specify low-velocity areas. The low-velocity area is focused in the vicinity of the cylinder, which occupies the upper hemi-circle of the cylinder. This area is located in the vicinity of the upper hemisphere of the cylinder. Nonetheless, the magnitude of the velocity is higher in the lower adjacent hemisphere of the cylinder. For Re = 100, the low-velocity region rises via a rising Grashof number (Gr). This region occupies half of the cavity between the upper horizontal wall and the cylinder. Whereas, for Re ≥ 250, the area of this region decreases via rising Gr and becomes smaller.
The isotherm plots are illustrated in Fig. 4. The inertial buoyancy forces are not as sturdy at low Re; the temperature isotherms are parallel to the active upper horizontal walls and are scattered uniformly from bottom to top. The heat transport regime is purely diffusive in this case (conductive). Rising Re up to 250, the inertial buoyancy forces become noticeably stronger, and the heat transfer regime has been removed to the convective mode. The isothermal contours are demolished in the flow direction and clearly indicate a gradient at the top horizontal wall. Due to the hot temperature of the upper horizontal wall of the enclosure, a greater temperature region is concentrated in the vicinity of the upper horizontal wall and the right vertical wall. The reason for the addition of the right-side wall in the hot zone can be attributed to the drying, which enters from the top of the left vertical wall. The ventilation effect confines the high-temperature zones in the upper right corner of the enclosure.
3.2 Effect of Location Cases of the Inner Cylinder
Fig. 5 presents the effect of location cases on the streamlines. The displacement of the elliptical obstacle has a major impact on the velocity and temperature fields. When the elliptical obstacle is near both the horizontal upper wall and bottom, one large vortex can be seen. However, in the case of L = 0.5, the vortices diminish in size, and numerous small vortices can be seen near the cylinder, mostly in the lower section and at the corner of the enclosure. For L = 0.25, we observe a large vortex over most of the cavity. When the cylinder moves upwards, L = 0.5, this large vortex splits into two vortices. The size of this vortex is lost with the displacement of the inner cylinder. At L = 0.75, the cylinder is directly exposed to entering flow through the inlet orifice.
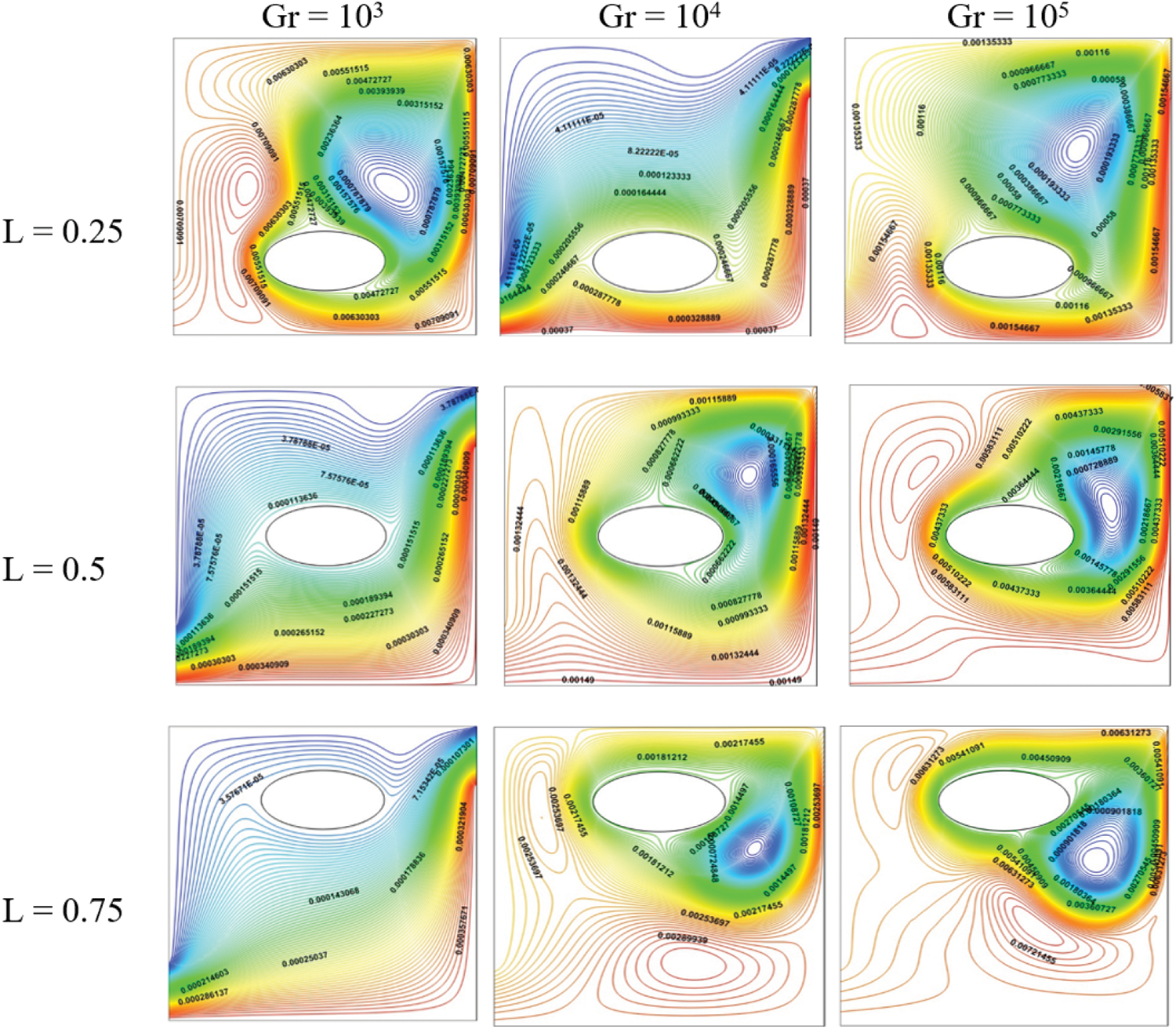
Figure 5: Influence of location cases elliptical cylinder on the streamlines for Re = 100, Ha = 0, Da = 10−3, ϕ = 0.04 and ϵ = 1
The isotherms are stratified at the upper horizontal wall of the enclosure (Fig. 6). When the cylinder moves upwards close to the upper wall at L = 0.75, we observe a plume progressing in the lower part of the enclosure. The isotherms tend to fluctuate. It can be deduced that the displacement of the position of the inner cylinder has a positive impact on the heat transport in the enclosure. The isotherms are confined to the upper horizontal wall of the enclosure for L = 0.25.
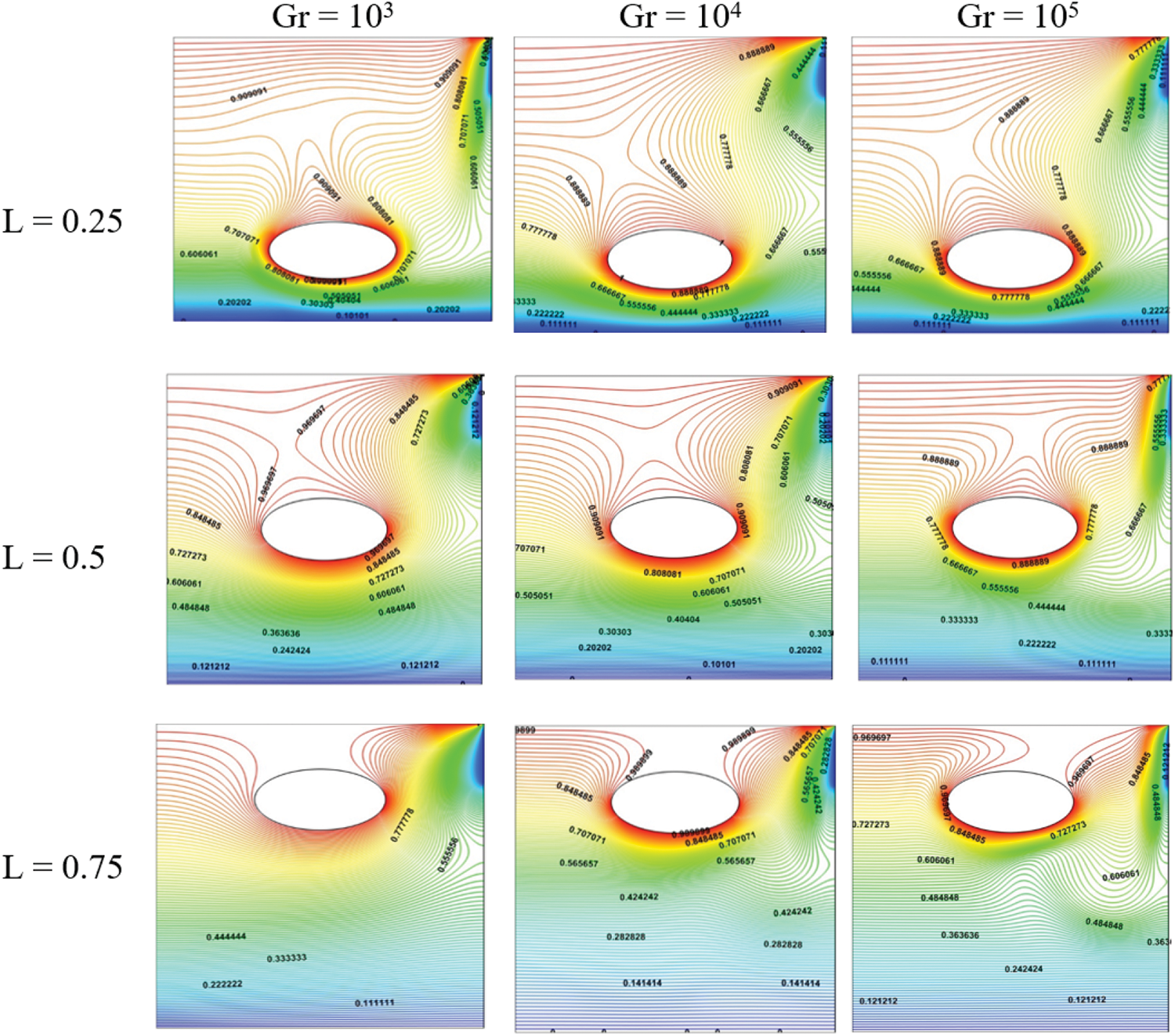
Figure 6: Influence of location cases cylinder on the isotherms for Re = 100, Ha = 0, Da = 10−3, ϕ = 0.04 and ϵ = 1
Figs. 7 and 8 show the behavior of the streamlines and the isothermal contours regarding a range of Ha from 0 to 20. In fact, when the Ha rises, it means that the magnetic field is stronger and affects the NPs, so the motions of the NPs under this stronger field will be lessened. As Hartman number (Ha) increases, the thermal cells become larger, indicating a decrease in the convective flow because the Lorentz forces oppose buoyancy effects. Also, at higher Ha numbers, natural convection occurs more slowly and has a horizontal stratification of temperature.
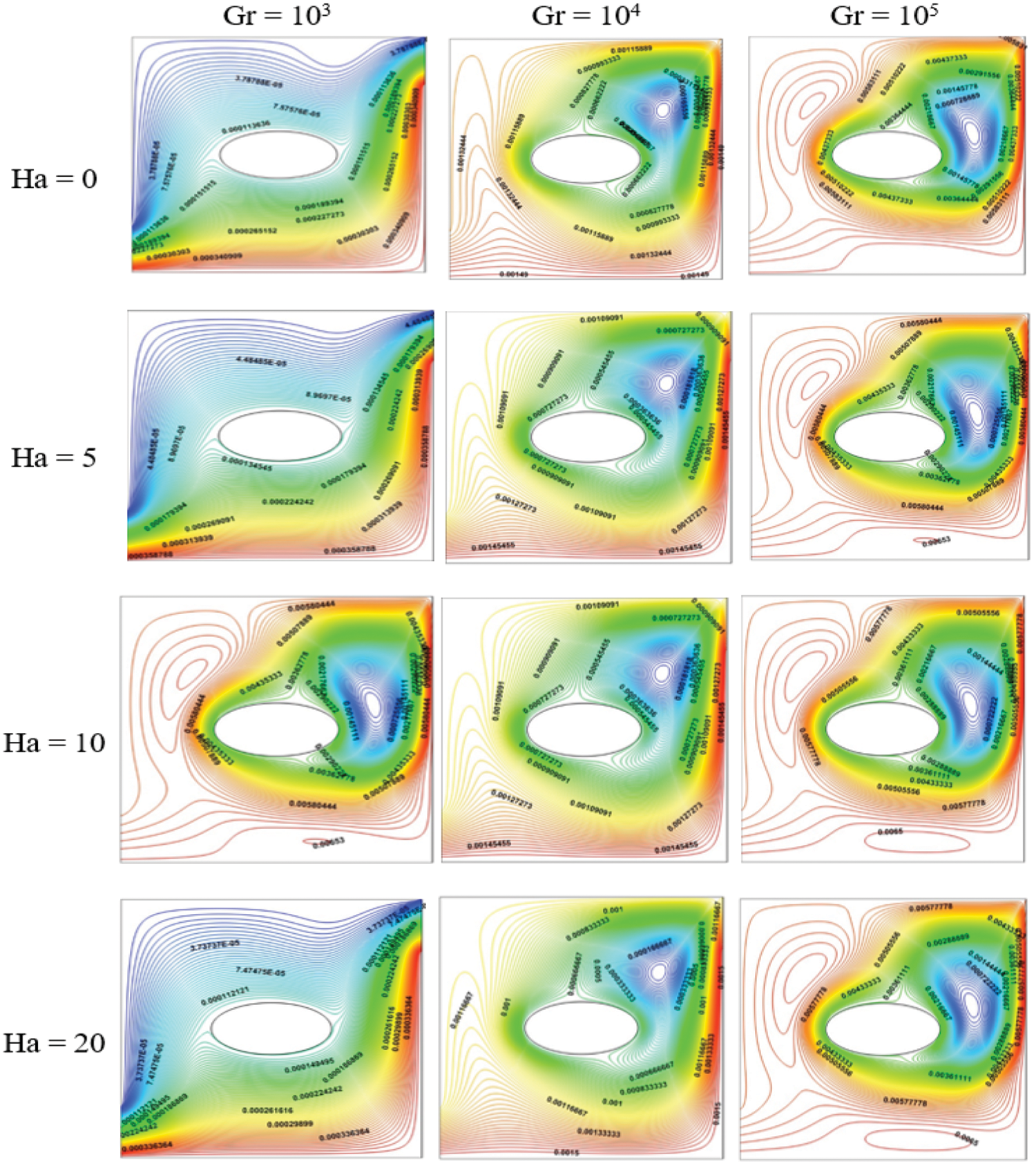
Figure 7: Streamlines for different Ha (Re = 100, Da = 10−3, and ϵ = 1)
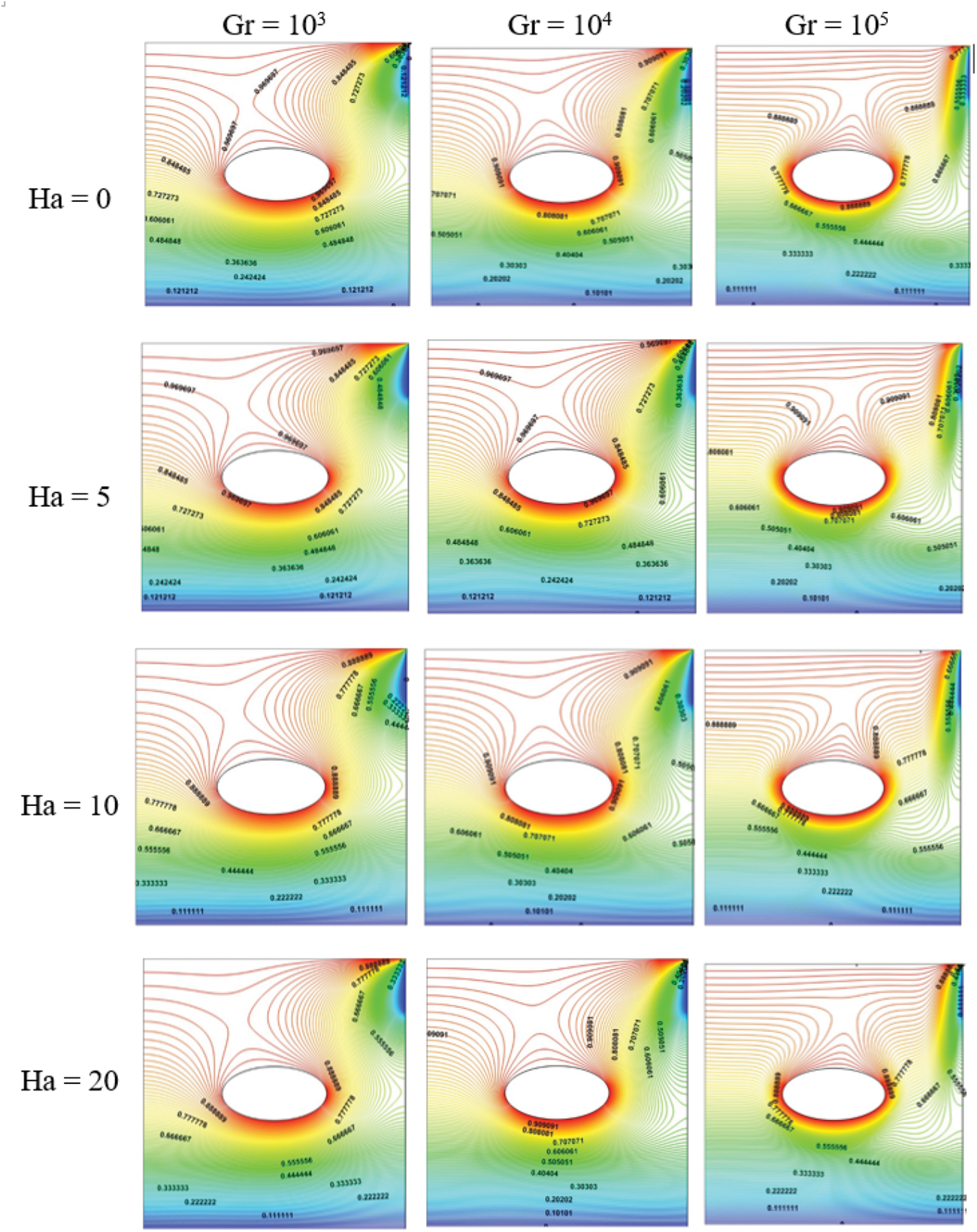
Figure 8: Isopleths of temperature for different Ha (Re = 100, Da = 10−3, and ϵ = 1)
While a slight deviation exists in the temperature field with arising Ha, the temperature profile is not significantly pretentious with the rise in Ha.
3.4 Re on the Average Nu Impact
The effect of Re and Gr on the average Nu is presented in Fig. 9. It is noted that the average Nu increases with the augmentation of Gr for all three cases. The average Nu increases with the intensification of Re due to laminar forced convection domination. The max heat transfer is detected at Re = 50 and L = 0.25 due to the cold flow circulations in the vicinity of this hot area.
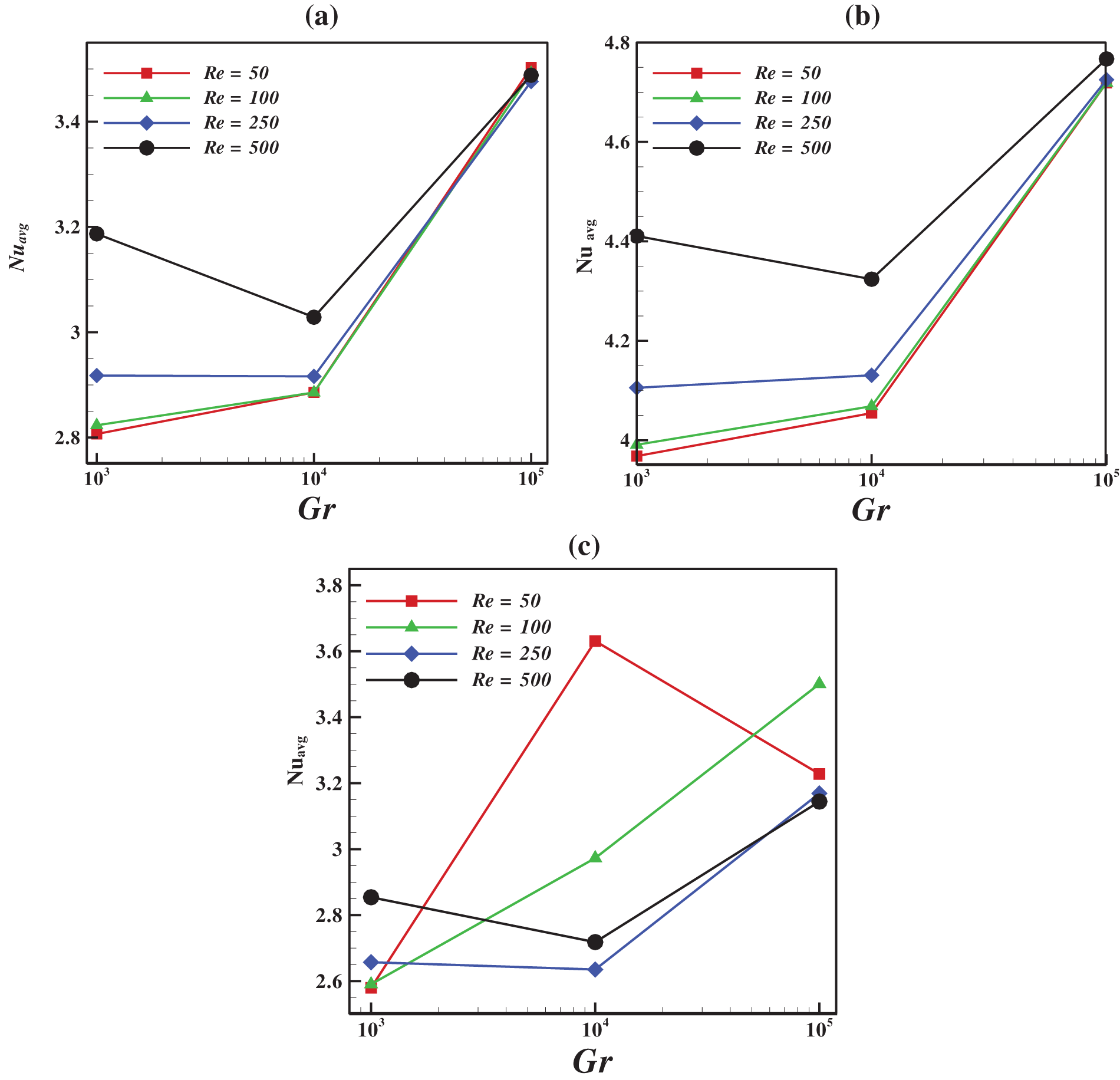
Figure 9: Average Nu vs. Gr and Reynold number Re for three different cases (a) L = 0.5 (b) L = 0.25 (c) L = 0.75 at (Da = 10−3, ϕ = 0.04 and ϵ = 1)
Fig. 10 represents the variation of Nuavg with Gr for various Ha. The heat transfer rates are an increasing function of Gr. It is shown from this figure that boosting the magnitude of the applied magnetic field diminishes the heat transport rates from the heated wall to the NF.
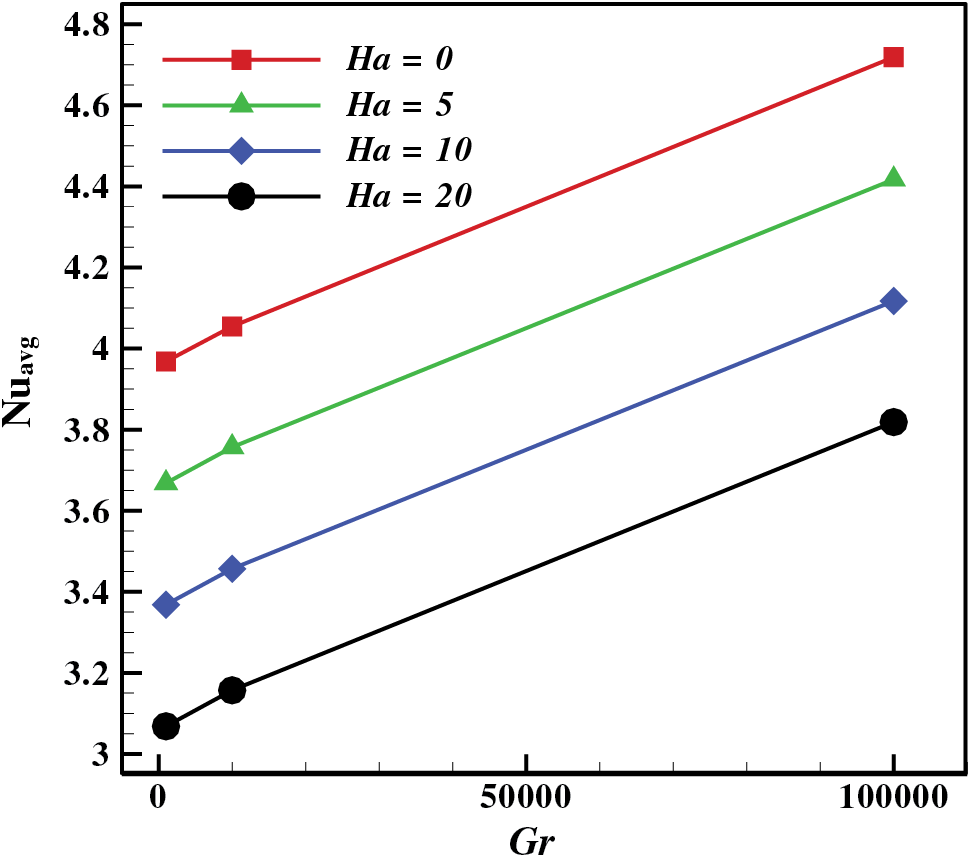
Figure 10: Average Nu vs. Gr and Hartman number (Ha) for the cases L = 0.25 at (Da = 10−3, Re = 50, ϕ = 0.04 and ϵ = 1)
In the analysis of 2D, steady mixed convective flow in a square enclosure filled with Cu NF in a porous medium, a numerical study was conducted utilizing the Darcy-Brinkman-Forchheimer model. The results highlighted significant findings regarding the impact of various physical and geometrical terms on liquid flow and HT within the system:
1. At Reynolds numbers (Re) ≤ 100, higher velocities were observed in the region adjacent to the lower hemisphere of the cylinder.
2. Increasing the Reynolds number to Re ≥ 250 led to a noticeable enhancement in heat transfer.
3. Heat transfer rates exhibited a decrease with rising Hartmann (Ha) numbers.
4. The Ha number significantly influenced the heat transfer of NFs, with heightened Ha values leading to the immobilization of nanoparticles due to Lorentz forces, ultimately affecting Nusselt number plots and emphasizing the role of the magnetic field in altering heat transport.
5. While temperature profiles did not exhibit remarkable changes with increasing Ha numbers, variations in vortex shapes were observed in streamlined profiles.
6. The velocity flow was impacted with rising Ha, primarily due to the intensified magnetic field resulting from Lorentz forces, which restricted NP motions.
7. The positioning of the inner cylinder positively affected heat transfer within the cavity, with a lower cylinder location being preferable in the current physical model.
8. Maximum heat transfer was observed at L = 0.25 for Re = 50 and Gr = 105.
Although this study raises various intriguing questions regarding the interactions of NF and porous medium in a magnetic field, future research will focus on exploring the influence of hybrid NFs on entropy production in the system.
Acknowledgement: The authors express their gratitude to their affiliated universities.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection, analysis and interpretation of results, draft manuscript preparation: B. Ould Said, F. Mebarek-Oudina. Analysis and interpretation of results: M. A. Medebber. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data are available on request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Liaqat A, Baytas AC. Numerical comparison of conjugate and non-conjugate natural convection for internally heated semi-circular pools. Int J Heat Fluid Flow. 2001;22(6):650–6. doi:10.1016/S0142-727X(01)00124-2. [Google Scholar] [CrossRef]
2. Sheremet MA. Interaction of two-dimensional thermal “plumes” from local sources of energy under conditions of conjugate natural convection in a horizontal cylinder. J Appl Mech and Tech Physics. 2012;53(4):566–76. doi:10.1134/S0021894412040116. [Google Scholar] [CrossRef]
3. Ben-Nakhi A, Chamkha AJ. Conjugate natural convection in a square enclosure with inclined thin fin of arbitrary length. Int J Thermal Science. 2007;46(5):467–78. doi:10.1016/j.ijthermalsci.2006.07.008. [Google Scholar] [CrossRef]
4. Saeid NH. Conjugate natural convection in a porous enclosure: effect of conduction in one of the vertical walls. Int J Thermal Science. 2007;46(6):531–9. doi:10.1016/j.ijthermalsci.2006.08.003. [Google Scholar] [CrossRef]
5. Varol Y, Oztop HF, Pop I. Conjugate heat transfer in porous triangular enclosures with thick bottom wall. Int J Num Method Heat Fluid Flow. 2009;19(5):650–64. doi:10.1108/09615530910963571. [Google Scholar] [CrossRef]
6. Chamkha AJ, Ismael MA. Conjugate heat transfer in a porous cavity heated by a triangular thick wall. Num Heat Transfer A. 2013;63(2):144–58. doi:10.1080/10407782.2012.724327. [Google Scholar] [CrossRef]
7. Baïri A, García de María JM, Laraqi N, Alilat N. Free convection generated in an enclosure by alternate heated bands. Experimental and numerical study adapted to electronics thermal control. Int J Heat and Fluid Flow. 2008;29(5):1337–46. doi:10.1016/j.ijheatfluidflow.2008.06.007. [Google Scholar] [CrossRef]
8. Corvaro F, Paroncini M. An experimental study of natural convection in a differentially heated cavity through a 2D-PIV system. Int J Heat Mass Transfer. 2009;52(1–2):355–65. doi:10.1016/j.ijheatmasstransfer.2008.05.039. [Google Scholar] [CrossRef]
9. Atayilmaz SO, Teke I. Experimental and numerical study of the natural convection from a heated horizontal cylinder. Int Commun Heat Mass Trans. 2009;36(7):731–8. doi:10.1016/j.icheatmasstransfer.2009.03.017. [Google Scholar] [CrossRef]
10. Kuznetsov GV, Sheremet MA. Mathematical simulation of conjugate mixed convection in a rectangular region with a heat source. Prikl Mekh Tekh Fiz. 2008;49(6):69–81. doi:10.1007/s10808-008-0117-0. [Google Scholar] [CrossRef]
11. Sarkar S, Dalal A, Biswas G. Mixed convective heat transfer from two identical square cylinders in cross flow at Re = 100. Int J Heat Mass Trans. 2010;53(13–14):2628–42. doi:10.1016/j.ijheatmasstransfer.2010.02.053. [Google Scholar] [CrossRef]
12. Asim M, Siddiqui FR. Hybrid nanofluids and—next-generation fluids for spray-cooling based thermal management of high-heat-flux devices. Nanomaterials. 2022;12(3):507. doi:10.3390/nano12030507 [Google Scholar] [PubMed] [CrossRef]
13. Wohld J, Beck J, Inman K, Palmer M, Cummings M, Fulmer R, et al. Hybrid nanofluid thermal conductivity and optimization: original approach and background. Nanomaterials. 2022;12(16):2847. doi:10.3390/nano12162847 [Google Scholar] [PubMed] [CrossRef]
14. Younes H, Mao M, Sohel Murshed SM, Lou D, Hong H, Peterson GP. Nanofluids: key parameters to enhance thermal conductivity and its applications. Appl Therm Eng. 2022;207:118202. doi:10.1016/j.applthermaleng.2022.118202. [Google Scholar] [CrossRef]
15. Sheremet MA, Pop I. Conjugate natural convection in a square porous cavity filled by a nanofluid using Buongiorno’s mathematical model. Int J Heat Mass Trans. 2014;79(2–3):137–45. doi:10.1016/j.ijheatmasstransfer.2014.07.092. [Google Scholar] [CrossRef]
16. Bouselsal M, Mebarek-Oudina F, Biswas N, Ismail AI. Heat transfer enhancement using Al2O3-MWCNT hybrid-nanofluid inside a tube/shell heat exchanger with different tube shapes. Micromachines. 2023;14(5):1072. doi:10.3390/mi14051072 [Google Scholar] [PubMed] [CrossRef]
17. Ramesh K, Mebarek-Oudina F, Souayeh B. Mathematical modelling of fluid dynamics and nanofluids. 1st ed. Boca Raton, FL, USA: CRC Press (Taylor & Francis); 2023. doi:10.1201/9781003299608. [Google Scholar] [CrossRef]
18. Ismael MA, Chamkha AJ. Conjugate natural convection in a differentially heated composite enclosure filled with a nanofluid. J Porous Media. 2015;18:699–716. [Google Scholar]
19. Ismael MA, Armaghani T, Chamkha AJ. Conjugate heat transfer and entropy generation in a cavity filled with a nanofluid-saturated porous media and heated by a triangular solid. J Taiwan Institute of Chem Eng. 2016;59:138–51. [Google Scholar]
20. Ali A, Mebarek-Oudina F, Barman A, Das S, Ismail AI. Peristaltic transportation of hybrid nano-blood through a ciliated micro-vessel subject to heat source and Lorentz force. J Therm Anal Calorim. 2023;148(14):7059–83. doi:10.1007/s10973-023-12217-x. [Google Scholar] [CrossRef]
21. Esfe MH, Afrand M, Esfandeh S. Investigation of the effects of various parameters on the natural convection of nanofluids in various cavities exposed to magnetic fields: a comprehensive review. J Therm Anal Calorim. 2020;140:2055–75. [Google Scholar]
22. Mebarek-Oudina F, Chabani I, Vaidya H, Ismail AI. Hybrid nanofluid magneto-convective flow and porous media contribution to entropy generation. Int J Num Methods Heat Fluid Flow. 2024;34(2):809–36. doi:10.1108/HFF-06-2023-0326. [Google Scholar] [CrossRef]
23. Molana M, Dogonchi AS, Armaghanid T, Chamkha AJ, Ganji DD, Tlili I. Investigation of hydrothermal behavior of Fe3O4-H2O nanofluid natural convection in a novel shape of porous cavity subjected to magnetic field dependent (MFD) viscosity. J Energy Storage. 2020;30:101395. [Google Scholar]
24. Giwa SO, Sharifpur M, Ahmadi MH, Meyer JP. A review of magnetic field influence on natural convection heat transfer performance of nanofluids in square cavities. J Therm Anal Calorim. 2021;145(5):2581–623. doi:10.1007/s10973-020-09832-3. [Google Scholar] [CrossRef]
25. Hdhiri N, Ben Beya B. Numerical study of laminar mixed convection flow in a lid-driven square cavity filled with porous media: darcy-Brinkman-Forchheimer and Darcy-Brinkman models. Int J Num Methods for Heat & Fluid Flow. 2018;28(4):857–77. doi:10.1108/HFF-04-2016-0146. [Google Scholar] [CrossRef]
26. Rajarathinam M, Nithyadevi N, Chamkha AJ. Heat transfer enhancement of mixed convection in an inclined porous cavity using Cu-water nanofluid. Adv Powder Technol. 2018;29:590–605. [Google Scholar]
27. Mebarek-Oudina F, Preeti, Sabu AS, Vaidya H, Lewis RW, Areekara S. Hydromagnetic flow of magnetite-water nano-fluid utilizing adapted Buongiorno model. Int J Mod Phys B. 2024;38(1):2450003. doi:10.1142/S0217979224500036. [Google Scholar] [CrossRef]
28. Fayz-Al-Asad M, Mebarek-Oudina F, Vaidya H, Hasan MS, Sarker MMA, Ismail AI. Finite element analysis for magneto-convection heat transfer performance in vertical wavy surface enclosure: fin size impact. Front Heat Mass Transfer. 2024;22(3):817–37. doi:10.32604/fhmt.2024.050814. [Google Scholar] [CrossRef]
29. Abolbashari MH, Freidoonimehr N, Nazari F, Rashidi MM. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nanofluid. Powder Technol. 2014;267:256–67. [Google Scholar]
30. Kameswaran PK, Shaw S, Sibanda P, Murthy PVSN. Homoegenous-heterogenous reactions in a nanofluid flow due to a porous stretching sheet. Int J Heat Mass Transf. 2013;57:465–72. [Google Scholar]
31. Swamy HA, Keerthi Reddy N, Sankar M, Peddinti PRT. Conjugate heat transfer of aqueous hybrid nanoliquid between coaxial cylinders subjected to magnetic field. Int J Thermofluids. 2023;17:100299. [Google Scholar]
32. Keerthi Reddy N, Swamy HA, Sankar M, Jang B. MHD convective flow of Ag-TiO2 hybrid nanofluid in an inclined porous annulus with internal heat generation. Case Stud Therm Eng. 2023;42:102719. [Google Scholar]
33. Ali S, Shaiq S, Shahzad A, Sohail M, Naseem T. Numerical thermal investigation of radiative magnetohydrodynamics axisymmetric Cu-Al2O3/H2O hybrid nanofluid flow over an unsteady radially stretched surface. Int J Ambient Energy. 2024;45(1):2321210. [Google Scholar]
34. Sohail M, Rafique E, Singh A, Tulu A. Engagement of modified heat and mass fluxes on thermally radiated boundary layer flow past over a stretched sheet via OHAM analysis. Discover Appl Sci. 2024;6(5):240. [Google Scholar]
35. Rafique E, Ilyas N, Sohail M. Utlization of generalized heat flux model on thermal transport of powell-eyring model via OHAM with heat geneartion aspects: thermal transport of powell-eyring model. Babylonian J of Math. 2024;2024:19–33. [Google Scholar]
36. Wang FZ, Sohail M, Nazir U, Awwad EM, Sharaf M. Utilization of the Crank-Nicolson technique to investigate thermal enhancement in 3D convective Walter-B fluid by inserting tiny nanoparticles on a circular cylinder. AIMS Math. 2024;9(4):9059–90. [Google Scholar]
37. Li J. Computational analysis of nanofluid flow in micro channels with applications to micro-heat sinks and bio-MEMS (Ph.D. Thesis). NC State University: Raleigh, NC, USA; 2008. [Google Scholar]
38. Khanafer K, Vafai K, Lightstone M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int J Heat Mass Trans. 2003;46(19):3639–53. doi:10.1016/S0017-9310(03)00156-X. [Google Scholar] [CrossRef]
39. Jou R-Y, Tzeng S-C. Numerical research of nature convective heat transfer enhancement filled with nanofluids in rectangular enclosures. Int Commun Heat Mass Trans. 2006;33(6):727–36. doi:10.1016/j.icheatmasstransfer.2006.02.016. [Google Scholar] [CrossRef]
40. Saeidi SM, Khodadadi JM. Transient flow and heat transfer leading to periodic state in a cavity with inlet and outlet ports due to incoming flow oscillation. Int J Heat Mass Trans. 2007;50:530–8. doi:10.1016/j.ijheatmasstransfer.2006.07.018. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools