 Open Access
Open Access
ARTICLE
Modeling of the Adsorption Allowing for the Changing Adsorbent Activity at Various Stages of the Process
1 LLP «InnovTechProduct», Industrial Zone Ordabasy, Shymkent, 160006, Republic of Kazakhstan
2 M. Auezov South Kazakhstan University, Laboratory «Monitoring and Ecology of Water», Shymkent, 160012, Republic of Kazakhstan
* Corresponding Author: Marat Satayev. Email:
Frontiers in Heat and Mass Transfer 2024, 22(5), 1533-1558. https://doi.org/10.32604/fhmt.2024.052901
Received 18 April 2024; Accepted 14 August 2024; Issue published 30 October 2024
Abstract
The goal of this work is, first of all, to construct a mathematical model of the mass transfer process in porous adsorption layers, taking into account the fact that in most cases the adsorption process is carried out in non-stationary technological modes, which requires a clear description of its various stages. The scientific contribution of the novel model is based on a probability approach allowing for deriving a differential equation that takes into account the diffusion migration of adsorbed particles. Solving this equation allows us to calculate the reduced degree of the adsorption surface coverage along the flow and, thereby, calculate the efficiency of the mass transfer process. The model also makes it possible to determine the slip coefficient, the internal diffusion coefficient and the degree of filling of the internal surface of the pores of the adsorbent layer, which corresponds to the completion of the initial stage of adsorption and the transition of the process to a stable mode. In this case, the problem is to calculate a non-isothermal turbulent boundary layer when flowing around the surface of an adsorbent. Next, the problem of identifying the main control parameters of the model has been solved. Based on such analysis and experimental studies to assess the influence of process control parameters, the patterns of adsorption purification and solution separation have been established and the design of a highly efficient adsorption apparatus with a fixed layer of porous adsorbent have been developed.Keywords
Nomenclature
| Cp | Concentration of the solute in the solvent; |
| D | Diffusion coefficient; |
| Deff | Effective diffusion coefficient; |
| Jр | Solute flow; |
| Jad | Flow of the adsorbed substance on the surface of the adsorbent layer; |
| Κm | Migration rate; |
| Κpas | Surface passivation coefficient; |
| l | The amount of the overshoot; |
| р | Particle momentum; |
| Pad | Probability of adsorption; |
| Pm | Probability of migration; |
| Pdes | Probability of desorption; |
| P*m | Probability of migration near a busy center; |
| P*des | Probability of desorption near a busy center; |
| s | Local coefficient of adhesion; |
| S1 | Saturation of pores with dissolved matter; |
| S2 | Pore saturation with solvent; |
| T´ | Perturbation of the temperature field caused by turbulent pulsations of the velocity field; |
| u´ | Longitudinal velocity of turbulent pulsations; |
| V1 | Flow rate of the solute; |
| V2 | Solvent flow rate; |
| v | Velocity of particles near the surface in the area of the potential hole; |
| v´ | Transverse velocity of turbulent pulsations; |
| β | Internal mass transfer coefficient; |
| δ | Thickness of the diffusion boundary layer; |
| δ | Thickness of the hydrodynamic boundary layer; |
| ε | Coefficient of turbulent viscosity; |
| ε1 | Porosity for the dissolved component in the zone of “overshoot” porosity; |
| ε2 | Porosity for the solvent in the zone of “overshoot” porosity; |
| εP | “Overshoot” specific porosity; |
| εS | Porosity, which is formed by channels having a characteristic radius less than the radius of the solvated molecule; |
| ε | Energy; |
| θ | Degree of coverage of the adsorbent surface with adsorbate molecules; |
| θ* | Filling degree; |
| Θ | Transitional reduced degree of coverage; |
| λ | Degree of filling. |
Due to the existence of passive surfaces near the interfaces, the quantitative mass transfer indicator decreases [1]. In this study, a continuous particle transport model of molecule transfer based on the phase separation technique [1] is used to simulate the interfacial mass transfer of solutes from the stationary phase of the solution to the mobile phase of the solution. Two processes associated with the surface and porosity values were studied. The dependence of the soluting velocity on the mass transfer indicator is characterized by the immobility area and the characteristic diffusion distance. It was found that the saturation of the stagnation zone can serve as an indicator of the total diffusion distance in the pores of the surface [2].
Changes are observed in the processes of heat and mass transfer in the surface pores. The effective and convenient simulation method for modeling the bidisperse porous media properties was generated by digital image reconstruction [3]. The appropriate was solved by using the finite element numerical scheme. Next, a comparative analysis of stresses and strains in open and closed pore regions has been carried out. It was shown that the deformation of the bidisperse porous sample led to an increase in the fractal dimension of the pore area and to a decrease in the fractal dimension of tortuosity [3].
Based on the obtained results, the need to consider the effect of deformation on the actual volume of flexible porous media, which plays a sufficient role for adequate model building [4].
As the early stage mass transfer coefficient continuously decreases due to the depletion of solute by small NAPL clusters that are in direct contact with the flowing liquid [5], the conclusion is that long-term mass transfer mainly occurs at interfaces associated with large clusters characterized by a larger diffusion length. By this, the mass transfer coefficient is mainly determined by the saturation of the stagnant zone. So, the influence of different mass transfer rates at different stages of the process must be taken into account when modeling [6]. The coordination of the dynamics of the driving force model and the diffusion equations are of great practical importance in the design and optimization of adsorption separation processes [7].
Analysis of the adsorption characteristics has shown that it is impossible to achieve equivalence based on a single parameter. To construct a universal equivalence and determine the mass transfer coefficients, it is necessary to take into account many parameters for the active volume of the particle, the geometries of the sphere, and diffusion. Understanding the mass transfer of matter and determining the diffusion coefficients are necessary to study the mechanisms of the flow of matter and evaluate porous media [8]. In porous media with a complex pore size distribution, numerous mechanisms of substance transfer coexist, including viscous flow, Knudsen diffusion, and many other parameters.
In work [6], an original approach to modeling mass transfer during multicomponent, multiphase flow in porous media has been proposed. This model allows one to derive and solve equations for the concentration of substances in the volume of a porous layer under the condition of thermodynamic equilibrium at the liquid/liquid interface. A special feature of the model is the ability to set physically justified boundary conditions for concentration on solid walls. The validity of the method was verified by comparison with analytical solutions for simplified problem statements. This approach was then used to study and scale mass transfer through interphase surfaces in thin films and mass transfer in complex porous structures under various hydrodynamic conditions. The known experimental results demonstrate the validity of this approach [9]. The experiments were conducted with different main acid substance concentrations and entry velocities into different porous structures. At low acid concentrations, the reaction proceeded in a single-phase regime. In cases with higher acid concentrations, multiphase hydrodynamic instabilities were observed. In experiments with different entry velocities, it was noted that a higher entry velocity leads to an acceleration of the reaction, but at the same time, fewer gas bubbles are formed. On the contrary, at a lower velocity, more gas bubbles are formed, which block the flow and the reaction. In addition, cracks or cavities on the solid walls of the apparatus significantly affect the flow structure [9].
In the article [8], a mathematical model taking into account surface diffusion has been developed. The results show that the equilibrium time of the gas transfer process decreases rapidly with increasing temperature. A higher saturation pressure can speed up the process and increase the amount of gas produced. The surface diffusion coefficient for shale is from 10−18 to 10−16 m2/s. In the article [10], the adsorption and diffusion of lithium ions on various sizes of a graphene monolayer are investigated, and it is proved that they depend on the size. Moreover, the lithium-ion diffuses over the graphene surface rather than through the hexagonal carbon ring to the other side, regardless of the size of the graphene sheet. In the article [11], based on the assumption that the porous medium was quasi-homogeneous, effective diffusion coefficients were calculated based on experimental data for two stages of adsorption and one stage of desorption of 1,2-dichloropropane in activated carbon particles. Although the effective diffusion coefficient calculated from the desorption data corresponded by an order of magnitude to the values obtained from the adsorption data, its absolute value was significantly lower. A comparison of the values of the developed model and experiments on the study of diffusion indices proved that diffusion control is prevailed [12]. A mathematical model is used to analyze the mass transfer in the pores of materials, taking into account pores of different sizes. Meso and micropores are mainly used [13].
Many research works are carried out with the absence of uncertainties, considering only precise parameters under ideal conditions. However, the presence of uncertainties associated with It has been established that depending on their relationship, the improvement of total mass transfer is provided by two fundamentally different mechanisms and the total transfer depends on three independent parameters. The calculated diffusion index, in the range from 4.93 × 10−10 to 5,96 × 10−10 m2/s were obtained on the basis of kinetic data during adsorption on the adsorbent of 14.94–31.51 g/m3 [14]. A significant analysis of the dependence of the diffusion index in the adsorbent on the adsorption and desorption values, may be related to the nonlinear character of the adsorption isotherm. The effective internal diffusion coefficients of Di [15] phenol and p-nitrophenol in an aqueous solution on granular activated carbon were calculated using a diffusion-adsorption mathematical model that takes into account the usual mechanisms of characterizing diffusion in liquid and surface diffusion. Calculations were made for the surface diffusion indices taking into account the temperature. The calculation of the release of heat and energy during adsorption was made. The values obtained are between the values of the characteristic physical and chemical adsorption. Experimental data on the adsorption rate of methylene blue and methyl blue were interpreted using a diffusion model that took into account external mass transfer, intragastric diffusion, and adsorption at the active center [16]. At the same time, internal diffusion considered both pore volume and surface diffusion. The surface diffusion model corresponded well enough to the experimental data, thereby indicating that the overall adsorption rate was controlled by surface diffusion. It is concluded that surface diffusion plays an important role in the adsorption of organic compounds on organoclay. The model of homogeneous surface diffusion (HSDM) of dyes on natural clay was developed on the basis of external mass transfer and surface diffusion to explain the curves of concentration versus time [17]. A computer program was used to create theoretical curves of concentration versus time, and these results were adjusted based on experimental data using the ‘best fit’ approach. The Ds values are 2.3 × 10−8 and 1.9 × 10−8 cm2/s for base blue and base red, respectively.
Interesting studies have been conducted to study and understand the physicochemical and thermal processes associated with methane hydrate dissociation [18]. Of particular interest are the studies conducted at the pore scale, since this allows us to propose approaches to developing more accurate simulation models in the oil industry. In the analyzed work, a numerical model at the pore scale was developed based on the lattice Boltzmann method and a description of the distribution of a multicomponent multiphase flow, heat and mass transfer, heterogeneous reaction, and solid structure evolution during gas hydrate dissociation was given. As a result of the numerical modeling of the study, the characteristics of hydrate dissociation in kinetically limited and diffusion-limited modes were determined. The limitation of mass transfer in the diffusion-limited mode indicates that enriched methane at the hydrate-water interface reduces the rate of hydrate dissociation with increasing water saturation.
In work [19], the yield coefficient approach model for nanoscale flow is used to simulate the flow in the adsorbed layer, and the traditional hydrodynamic flow theory simulates the continuous fluid flow. The calculation shows that the adsorbed layer on the wall surface can have a very significant effect on power losses during multiscale mass transfer. The work [20] used a combination of computational fluid dynamics and a porous media model to simulate the adsorption of benzene on activated carbon and the flow fields in a porous media. Three-dimensional unsteady state gas flow was modeled using laminar single-phase flow equations combined with a mass transfer equation. Diffusion time constants were obtained by fitting a series of curves to an isothermal diffusion model [21]. The results of the analysis showed that the transport of CO2 in granules is well described by a combination of Knudsen mechanisms and viscous diffusion. The pore diffusion model (PDM) was developed based on external mass transfer and pore diffusion to predict the performance of a batch adsorber for the adsorption of basic dyes [22]. A computer program was developed to create theoretical curves of the dependence of the Sherwood number on time, and these results were adjusted with experimental curves of the dependence of the Sherwood number on time using the ‘best fit’ approach. The external mass transfer coefficient (Ks) and the intracellular diffusion rate parameter (Kp) were calculated and evaluated as functions of gas mixing and temperature [23]. It was found that the increase in the adsorption rate caused by gas mixing was twice as large as with an increase in temperature due to the high turbulence caused by the axial and radial flow created by gas mixing. The activation energy (E), equal to 5.95 kcal/mol, demonstrated that the adsorption of the main dye on clay was controlled by diffusion. The diffusion properties of zeolite H-ZSM-5 were measured using a new flow gravimetric method involving sorption of p- and o-xylenes [24]. The sorption rate of p-xylene in all studied samples corresponded to Fick’s second law of diffusion, which led to an effective diffusion capacity of about 1.7 × 10−11 m2/s, regardless of whether the H-form or modified forms were studied. In the study [25], an analytical procedure was investigated to determine the kinetic parameters of Ds and kF adsorption using a single concentration change curve (decay curve) in a reactor with a fixed layer of a circulating type by a test method. Experimental conditions such as the large liquid-solid ratio zϕ, the short contact time z/u, and the low height of the Z layer, which bring the decay characteristics in a reactor with a fixed circulating layer closer to the characteristics of a batch mixing reactor, were quantified on a theoretical basis. In the study [26], fractal theory was used to construct a velocity and surface diffusion model for mesoporous adsorbents. The fractal pore sizes of the adsorbent were obtained using the Dubinin-Astakhov equation and the Yaronets equation. The calculated CO2 adsorption from convective models was significantly higher in the turbulent regime. The rate of adsorption increased with increasing values of ΔT (Tsat – T). The surface diffusion also increased with increasing ΔT, regardless of the flow regime.
Recently, special attention has been paid to the study of adsorption processes in specific nano-systems. For example, paper [27] was devoted to the investigation of the unsteady flow of a hybrid nanofluid (NF) consisting of cobalt ferrite (CoFe2O4) and copper nanoparticle (Cu) with natural convection flow due to an expanding surface implanted into a porous core. In biomedical fields, in very rare cases fluid flows through a static channel in a stable mode [28].
In the article [29], kinetic data were described using intracellular diffusion, and the results of isothermal studies were described using the Langmuir, Freundlich, and Dubinin-Radushkevich equations. It was found that the adsorption of toluene and benzene, considered in the Weber-Maurice model, corresponds to diffusion with the resistance of the liquid phase film. In addition, the physical nature of adsorption is confirmed by the values of free energy (E = 6.92 and 8.41 kJ mol−1 for benzene and toluene, respectively). In studies [30], the effective diffusion time constants (Deff/R2) of alkylbenzene on the ZLC desorption curves increase with increasing mesoporosity in ZSM-5 zeolites, but the diffusion activation energy (Ea) shows the opposite trend. Due to the low interaction of isopropylbenzene with the zeolite surface, the Deff/R2 values of isopropylbenzene with a lower activation energy in all ZSM-5 samples are higher than those of toluene. The size of the molecules of the two alkylbenzenes is not a key factor for their adsorption and diffusion in mesozoic rocks. In [31], it was concluded that the resistance to mass transfer includes diffusion in micropores, diffusion in macropores, surface barriers, and resistance of the outer film. With reasonable application of (FR) frequency response methods, it is possible not only to determine the dominant mass transfer resistances, but also to extract reliable mass transfer coefficients based on appropriate mathematical models.
The effective diffusion coefficients in silicas were estimated on the basis of Fick’s second diffusion law [32]. The obtained diffusion coefficients are quite similar for different samples, demonstrating that diffusion occurs mainly in silica macropores. It was found that the values of the diffusion coefficients go beyond Knudsen’s prediction. In the article [33], diffusion was modeled using Fick’s second law. The relationship between the mass transfer coefficient and the electrical conductivity of the mass was determined by simplex optimization, minimizing percentage errors between experimental and simulated concentrations, obtaining 3.79% (w/v) for NaCl and 5.66% (w/v) of KCl in static brine. In the article [34], the standard diffusion model and the time-separated diffusion model for methane and methanol, respectively, were used to calculate the diffusion coefficients. Studies demonstrate that the mode of anomalous diffusion using spatial scaling of the diffusion coefficient is limited by measuring the diffusion length of a certain diffusion in a porous material. Methane diffusion [35] was measured in the temperature range (298–393 K) and pressure (0–0.9 bar) to study the effect of temperature and pressure on diffusion coefficients. The results showed that the diffusion properties decrease with increasing pressure, while they increase with increasing temperature. Moreover, the activation energy of diffusion decreases with increasing pressure. A new approximate solution [36], relevant to the case of rectangular (Langmuir) adsorption isotherms, was developed based on the integral balance method with the double integration technique. The solution is based on a model developed by Ruthven for slabs and spherical adsorption granules, where adsorption is controlled by diffusion in macropores. The new approximate solution uses the concept of a finite diffusion penetration depth and the shape of concentration profiles. The adsorption and diffusion properties of CH4 in the slit pores of montmorillonite were investigated [37]. As a rule, the pore space can be divided into three parts, namely the inaccessible zone, the adsorption zone and the free zone. It was found that the length of the inaccessible zone does not depend on pore size and pressure. In the article [38], it was concluded that mass transfer over the surface due to surface diffusion depends on the concentration of molecules adsorbed on the surface. This is a significant factor affecting the surface flow and is the that mass transfer is related to the concentration of substances. A combined decrease in the adsorbate concentration during adsorption from a limited volume [39], in the temperature rate change of the adsorbent, and in the rate of intercrystalline diffusion between crystals leads to a decrease in the kinetics of adsorption.
Unlike the decrease in the differential heat of adsorption with the degree of filling, these factors are not necessary conditions for the appearance of extremes on the kinetic curves of adsorption.
Solution of the problem on the equilibrium the dynamics of adsorption dependens on the form of the adsorption isotherm [40].
It is shown in the article [41] that all forms of adsorption isotherms can be used in calculations of adsorption kinetics with diffusion control. Examples of calculations concerning Langmuir, Freundlich, Vollmer, Frumkin, and van der Waals isotherms are given. In [42], the estimates justifying the standard diffusion in adsorbents are critically revised. Examples of incompleteness of the evaluation procedure based on the re-evaluation of data previously published in the literature are presented. Incorrect choice of boundary conditions [43] when estimating diffusion coefficients in solids can lead to very unreliable estimates.
The analysis of experimental and theoretical material on the modes of dynamics and mass transfer in the adsorbent layer showed that in the separation processes, it is necessary to take into account the role of controlling factors: unsteadiness of influences, diffusion migration of molecules of the adsorbed substance from the outer surface of the adsorbent grain into the channels of its pores, turbulence of the boundary layer, heat release and heat exchange between the adsorbent and the flow. However, it is precisely taking into account the influence of parameters characterized by equilibrium and kinetic patterns of the adsorption-desorption cycle, rearrangement of molecules in solutions, an increase in the diffusion coefficient, taking into account heat release and heat transfer, the coefficient of turbulent viscosity, the degree of filling of the inner surface of the adsorbent pores, and the adhesion coefficient that are necessary when calculating and designing systems for adsorption purification of streams [2]. This approach to the problems of adsorption separation, unlike traditional approaches today, opens up fundamentally new possibilities for increasing the selectivity and selectivity of target components during their mass transfer.
The main conclusion made by the authors of the works mentioned here, from the review of literature sources, is that many problems in calculating adsorption processes in porous layers are associated with insufficient consideration of the fundamental non-stationarity of the adsorption process. This is due to the fact that at different stages of the process, control parameters differ significantly.
In the submitted now work, the authors set the problem for building a mathematical model of the mass transfer process in porous adsorption layers allowing for describing the various stages of the adsorption process. The main scientific contribution of the novel model is based on a probability approach that has been used for deriving a differential equation taking into account the variability of adsorption layer properties.
To develop the most economical solution to the problem of deep adsorption purification, we have developed a design of a mass transfer device with a fixed adsorbent layer, combining high intensity of mass and heat transfer, and high productivity.
The mass transfer apparatus developed [44] with a fixed adsorbent layer allows for the most efficient adsorption process in conditions where maintaining a certain temperature is required, increasing the degree of purification of the substance, minimizing the cost of adsorbent regeneration and evenly distributing the temperature control of the adsorbent layer. Fig. 1 shows a general view of the mass transfer apparatus.

Figure 1: An adsorber with a fixed layer
The mass transfer device works as follows. The liquid phase is fed through the nozzle 8 into the upper section of the apparatus, passing through the switchgear 4, the liquid phase is filtered through the adsorbent layer 3 in chamber 2 and is discharged from the apparatus through the nozzle 7. When the solution passes from the upper section of the apparatus into the contact chambers, the volumetric flow density is leveled along the section of the apparatus and evenly distributed.
When filtering the viscous liquid phase, the flow of the mass transfer process depends on temperature and hydrodynamic conditions. To heat the liquid phase to reduce its viscosity and increase fluidity, which makes it possible to effectively use the entire volume of the adsorbent layer, a coolant is introduced through the nozzle 9 into the coolant chamber 11 with a certain temperature, depending on the properties of the liquid phase and the absorbed substance, which allows systematic control of the temperature in the contact chambers of the adsorbent with the liquid phase during filtration.
When the degree of purification of the liquid phase by the adsorbent decreases, as evidenced by an increase in the concentration of the absorbed substance in the purified liquid phase, the filter loading (adsorbent layer) is regenerated. To do this, the supply of the initial liquid phase is turned off using the taps of fittings 7, and 8, and a regenerating agent is introduced through fitting 12 and fed into contact chamber 2, while the temperature in coolant chamber 11 increases. The absorbed substance separated from the adsorbent in a mixture with a regenerating agent is removed through the nozzle 13.
For uniform distribution of the liquid phase, a perforated switchgear made of webs with tunnel cells is used (Fig. 2). After passing the first web of the switchgear package, the liquid takes a direction corresponding to the direction of the edges of the tunnel cells on this web. The liquid passes through the subsequent web of the package, changing direction, as the direction of the edges of the tunnel cells on this web changes relative to the previous one. Moreover, the relative change in the direction of the edges of the tunnel cells on the canvases of the package is carried out with the displacement of each canvas in the package relative to the lower one by screw. In this sequential arrangement of the canvases one under the other, after describing the edges of the 360° cells (one screw approach), the direction of the arrangement of the canvases one under the other changes with their displacement along the screw (the screw approach changes).

Figure 2: Perforated switchgear
The liquid phase, like the arrangement of the cloths in the package, describes the trajectory of one screw, changing, in general, the direction of travel along the height of the package by 360°, after which its approach along the screw changes, and the liquid, again passing through the canvases of the switchgear, describes the trajectory of the screw and so on. The twisting of the liquid flow through the screw as it passes through the switchgear is local, i.e., the entire liquid flow is, as it were, divided into some separate streams (such a division occurs when the liquid phase passes through the tunnel cells of the webs), each of which, passing through some webs of the package, twists. With such a fractional twisting of the liquid flow, force flows of the centrifugal field arise, because of which the volume density of the flow is equalized along the cross-section of the apparatus, i.e., the liquid phase is evenly distributed. After passing through the switchgear, the liquid evenly passes through the active layer.
In modern industries, adsorption processes are now used as the main methods of separation and purification of a wide variety of substances. Adsorption is a process that allows the impurity to be almost completely removed from the liquid medium. Depending on the purpose, the scale of installations varies from miniature cartridges to complexes containing tens of tons of adsorbents. The adsorption process is of particular importance for solving the problem of protecting the environment from harmful products formed during the operation of industrial enterprises.
The vast majority of purification processes from liquid media are carried out in the adsorbent layer. However, the saturation of each adsorbent particle in the adsorber with adsorbate depends on the diffusion rate of the absorbed molecules inside the pellet, which ultimately determines the intensity of mass transfer under a certain hydrodynamic regime. When filtering the liquid phase, the flow of the mass transfer process depends on temperature, hydrodynamic conditions, height, and shape of the layer, i.e., the size and design of the apparatus.
Granular activated carbons developed by us from the shells of fruit seeds (apricot, plum, peach) were used as adsorbents [45–47].
3 Modeling of the Initial Stage of the Adsorption Process in a Porous Adsorbent Layer
Following the stated purpose of the study and modern concepts, the work presents two main mathematical models. The first model is modeling of the initial stage of the adsorption process in a porous adsorbent layer. When developing this model, the following assumptions were made. First, it is assumed that the adhesion coefficient is a function of temperature, and the control parameter in this dependence is the degree of surface coating by adsorbate molecules. Secondly, the process of adsorption and subsequent internal diffusion of molecules is accompanied by competition between associative physicochemical adsorption of molecules and dissociative chemisorption. The model is probabilistic. Therefore, below the main probabilities that determine the kinetics of various stages of the adsorption process at the microlevel have been introduced.
3.1 Initial Stage of the Adsorption Process.
The flow of the substance adsorbed on the surface of the adsorbent layer is written as [48]:
where
The incoming molecule is first captured by an external potential well (presorption state), and then it is captured into an internal potential well. Let’s consider how the degree of coverage of the adsorbent surface affects the adhesion coefficient. In accordance to main suppositions, the coefficients of particle migration, surface passivation and the initial local adhesion coefficient of the part are estimated by introducing special probabilities for these local characteristics.
The effective degree of the surface coverage along the flow changes due to changes in the concentration of captured component along the flow and, accordingly, the equilibrium concentration also changes. This, in turn, leads to a change (a decrease, namely) in the driving force of the mass transfer process. All of the above describes the universal features of mass transfer processes in flow systems.
A molecule near the free chemisorption state can either move
If the molecule is physically adsorbed over the occupied chemisorption state, then the first of these probabilities is zero. Let’s denote the probabilities of particle migration and desorption near the occupied center
Let be
Let’s make a probabilistic balance of particles on the surface of the adsorbent [48,49].
We introduce a local coefficient of adhesion in the form:
For the adhesion coefficient, we have:
From here, we get:
The probabilities of adsorption and desorption are approximated by temperature dependences of the Arrhenius dependence type [50–52]:
The probability of particle migration is assumed to be proportional to the number of neighboring free centers, i.e.,
The rationale for this approach can be given using the idea of the local thermodynamic equilibrium of particles in a potential well during physical adsorption [51,53].
Then, for the initial local coefficient of adhesion, we obtain:
For the probability of desorption of a particle near the occupied center, respectively, we obtain:
Expression (12)can be rewritten as:
Fig. 3 shows the results of a numerical study of the dependence of the probability of desorption of a molecule near the occupied center on the degree of surface coverage at different values of the migration coefficient

Figure 3: The dependence of the probability of desorption of a molecule near the occupied center on the degree of surface coverage at different values of the migration coefficient
It can be seen from the graphs that with an increase in the migration coefficient, the probability of desorption and, accordingly, the efficiency of the capture process decreases rapidly. This effect is especially pronounced at low degrees of surface coating, i.e., at the initial stage of the process, which is most important from the point of view of efficiency.
The estimation of the migration coefficient follows from the ratio (12):
Let us now consider the transition process associated with the establishment of the state of stationary saturation of the adsorbent layer. Fig. 4 shows the results of a numerical study of the relative coefficient of adhesion from the degree of surface coating at different ratios of the probabilities of adsorption and desorption of molecules near free and occupied active centers. For this purpose, an appropriate evaluation parameter has been introduced: the surface passivation coefficient.

Figure 4: The dependence of the relative coefficient of adhesion on the degree of surface coating at different ratios of the probabilities of adsorption and desorption of molecules near free and occupied active centers
It can be seen from the graphs that the degree of passivation of the surface significantly affects the adhesion coefficient. Moreover, with an increase in the passivation coefficient, the adhesion coefficient begins to decrease more sharply with an increase in the degree of coverage of the adsorption surface. The apparent separate porosities for the dissolved component and the solvent in the “slip” porosity zone depend on the saturation of the pores with the filtered components
where, as a hypothesis, we assume that in a non-stationary process, an equality similar to the ratio for a stationary process is observed at any given time:
During stationary adsorption in the flow mode, there is no accumulation of the dissolved component in the adsorbent in the “overshoot” filtration zone. This condition is written as:
In the transition period, the function can be
Also:
Only the solvent moves through this channel system. Moreover, we will assume that the concentration of the dissolved substance near the adsorbent does not exceed the equilibrium one, i.e., there is no clogging of pores with polymer molecules.
We will further assume that the diffusion of adsorbate in the pores of the adsorbent is described by the classical diffusion equation for the probability of migration of adsorbed particles:
Let’s consider a tubular apparatus and rewrite the basic diffusion equation in one-dimensional form:
Hear
In Formulas (26) and (27):
With a known initial function that defines the distribution of the degree of surface coverage along the length of the device
The solution of Eq. (25) can be obtained by the Fourier method [54]. To do this, we will introduce the transitional reduced degree of coverage into consideration
where
Then the task is converted to the form:
Eq. (31) is a first-order equation in the time variable t, and it is a second-order equation in the spatial variable z. Respectively, the initial condition for variable t is written in the form (33) and two boundary conditions for z are written in the form (32).
The boundary conditions take the form:
The initial conditions are converted to the form:
Using the Fourier variable separation method according to [55], the solution of the problem (31)–(33) is obtained in the form:
Based on Formulas (34), (29) and (30), we obtain a description of the change in the degree of coverage of the adsorption surface along the flow in the apparatus.
Since the average distance between the centers of particle migration along the adsorption surface can be taken inversely proportional to the average number of neighboring vacant centers, we obtain an estimate of the magnitude of the “jump”:
where
This leads to an estimate of the value of the internal diffusion coefficient:
where
So, we have:
Fig. 5 shows the dependence of the internal diffusion coefficient in the pores of the adsorbent on the temperature and degree of coating of the pore surface.

Figure 5: Dependence of the internal diffusion coefficient on the temperature and degree of coating of the pores of the adsorbent
As an estimate of the stabilization time of the saturation process of the inner surface of the pores of the adsorbent with the captured component, it is possible to take the time when the characteristic distance between the vacant centers exceeds the path length of the adsorbate molecules at a given temperature. This will happen when the degree of filling of the adsorption surface is of the order:
The corresponding Knudsen number is calculated using the formula:
From here, we obtain a formula for calculating the degree of filling of the inner surface of the adsorbent pores, corresponding to the completion of the initial stage of adsorption and the transition of the process to a stable mode:
The proposed mathematical model allows us to calculate the main characteristics of the transient process of non-isothermal adsorption of a two-component liquid in a porous adsorbent layer. Unlike existing methods, the described model uses a minimum number of empirical data that can be obtained using relatively simple experimental facilities.
The next section devotes the model, which makes it possible to calculate the mass transfer coefficient during adsorption on the grain surface, taking into account the change of the non-isothermal turbulent boundary layer.
3.2 Calculation of a Non-Isothermal Turbulent Boundary Layer at Flow around the Surface of the Adsorbent Layer
The effective diffusion coefficients calculated according to the described method are used to calculate the internal mass transfer coefficient in the apparatus according to the formula:
where
A turbulent boundary layer is usually described as consisting of three regions with different flow patterns. A laminar sublayer with a thickness from 0.001 to 0.01 of the layer thickness is located near the wall. Next is the transition zone-from 0.1 to 0.2 layer thickness. At the outer boundary there is a completely turbularized part of the layer, occupying up to 0.9 of its thickness.
The equations describing free convection in a flat laminar flow near the surface of a vertical plate in the presence of a transverse temperature gradient are written, as a rule, in the Boussinesq approximation. Moreover, when describing a turbulent flow, it is necessary to take into account the transfer of momentum in the liquid layer due to turbulent pulsations. Then the equation of fluid motion takes the form:
where
The thermal conductivity equation for a turbulent layer is written as:
Here is a perturbation of the temperature field caused by turbulent pulsations of the velocity field.
Formula (43) can be rewritten as:
where
The boundary conditions for the equation of motion, as usual, are the conditions of adhesion, i.e., the equality of all components of the velocity field on the wall to zero:
Either a constant temperature or a constant heat flow is also set on the wall:
or
Currently, the most productive approach is the one based on the concepts of turbulent viscosity and turbulent Prandtl number. It is shown that with the help of such model representations, turbulent boundary layers with natural convection can be calculated. In accordance with this approach, the term in the momentum equation due to turbulent pulsations is represented as:
where ε–the coefficient of turbulent viscosity, the determination of which is associated with the main difficulties of calculation.
The corresponding calculation can be performed as follows, based on the ideas proposed in [42].
First, according to the Cebeci model, Bradshaw [56] proposed to use the mixing path length characteristic of boundary layers without buoyant forces to calculate the coefficient of turbulent viscosity, i.e.,:
where δ–the thickness of the hydrodynamic boundary layer.
Secondly, a change in the thickness of the boundary layer is assumed according to a semi-empirical law:
The variable Reynolds number, depending on the longitudinal coordinate, is calculated from the “equivalent” longitudinal velocity associated with an additional term in the momentum equation due to thermal convection. Thus, the closure of thermal and hydrodynamic problems is carried out.
The first approximation of the velocity profile in a turbulent boundary layer obtained in the described way can be used to calculate the second approximation, and so on. The calculation using a simplified method gives a very good match with the results of large-scale numerical experiments by Cebeci and Bradshaw for the first approximation. The calculation of the velocity profile according to the first approximation gave results for the middle part of the boundary layer that are very close to experimental data.
3.3 The Results of the Numerical Experiment and Comparison with Experimental Data
The mathematical model developed in the previous sections was used to conduct numerical experiments and then compare the calculation results with experimental data. Fig. 6 shows the results of calculating the effective diffusion coefficient at different degrees of pore coating of the adsorbent, depending on temperature. The calculation was performed by solving Formula (24) to determine the dynamics of changes in the degree of pore coverage and then using Formula (37). The available array of experimental data does not allow a direct assessment of both the dynamics of changes in the degree of pore coverage of the adsorbent and the average value of this parameter. However, as can be seen from the figure, the experimental data are in good agreement with the calculated curve at temperatures up to 370 K with an average degree of coverage of the order of 0.45.

Figure 6: Comparison of experimental and calculated values of the diffusion coefficient in the pores of the adsorbent at different degrees of coating
At higher temperatures, the best agreement of experimental and calculated data is obtained with a higher degree of adsorbent coating of the order of 0.6. This result can be explained by the fact that, despite the increase in the mobility of molecules of the captured component with increasing temperature, which contributes to an increase in the probability of surface migration, an increase in the activity of adsorption centers still plays a predominant role. Therefore, the degree of coverage is also increasing.
Fig. 7 shows the results of calculating the characteristic distance between the active centers of the adsorption surface, depending on the pore radius and the degree of surface coating. This calculation can be performed only with the combined use of experimental data on pore radii and calculated ratios of the mathematical model. Even in this case, the available experimental data alone do not make it possible to calculate the characteristic distances between active centers. However, the calculated curves obtained make it possible to interpret the experimental data.

Figure 7: Calculation of the characteristic distance between the active centers of the adsorption surface based on experimental data and a mathematical model depending on the pore radius and the degree of surface coating
It can be seen that for a given average degree of pore coverage of the adsorbent (which corresponds to different temperatures) the maximum distance between the active centers of the adsorption surface has extreme values at certain pore radii. With a high degree of coverage of the adsorption surface, this extreme is weakly expressed. However, at the initial stage of the process, with small degrees of coverage, the extremes appear quite vividly. This phenomenon can be explained by the fact that the average pore radius has a complex correlation with the tortuosity of the pores and the average porosity of the adsorbent layer. The geometric nature of this correlation manifests itself more strongly at lower degrees of coverage corresponding to greater activity of the adsorption surface.
Fig. 8 shows the results of comparing the calculated and experimental values of the Bio criterion depending on the diameter of the adsorbent particles. These results are also obtained by indirect calculation, first using the data shown in Fig. 8, and then using the formulas of the mathematical model. The boundary layer thickness was calculated using the model described in the second section. It can be seen from the graphs that the best agreement between the calculated and experimental data was observed with an average particle size of the adsorbent of the order of 0.5 × 10−3 mm or more.

Figure 8: Comparison of calculated and experimental values of the Bio criterion depending on the internal diffusion coefficient
In general, it can be concluded that with very small particle sizes corresponding to a sufficiently dense adsorbent package, the turbulent boundary layer model is not appropriate. At the same time, for large particle sizes, this model works reliably enough, which explains the better agreement of the calculated and experimental values of the mass transfer coefficient and, accordingly, the Bio criterion.
Based on the results of the comparison of calculations performed according to the ratios of the mathematical model and experimental data, it can be concluded that the developed mathematical model qualitatively correctly describes the processes occurring during adsorption and gives fairly good quantitative estimates. In the future, these data may be very useful in assessing the characteristic geometric parameters of the adsorption layer and identifying the main geometric and technological parameters controlling the adsorption process.
Fig. 9 shows the dependence of the diffusion coefficient on the thermal speed of movement of petroleum product molecules and the pore radius of the activated seed shell. If the pores are comparable to the absorbed molecules, the adsorption process becomes activated. By analogy with the Arrhenius concepts developed for a chemical reaction, during activated adsorption, not all molecules of petroleum products can penetrate into the pores and be absorbed there, but only those that have some excess energy reserve. This excess energy is called activation energy.

Figure 9: Diffusion coefficient as a function of the thermal speed of movement of petroleum product molecules and the radius of the pores of the activated seed shell
Fig. 10 shows the dependence of the diffusion coefficient on the activation energy. It can be seen from the figures that the higher the activation energy, the more the adsorption rate changes with temperature changes. With increasing activation energy, the diffusion coefficient increases; with an increase in temperature to 328–343 K, the diffusion coefficient increases to 2.4 × 10−10 m2/s.
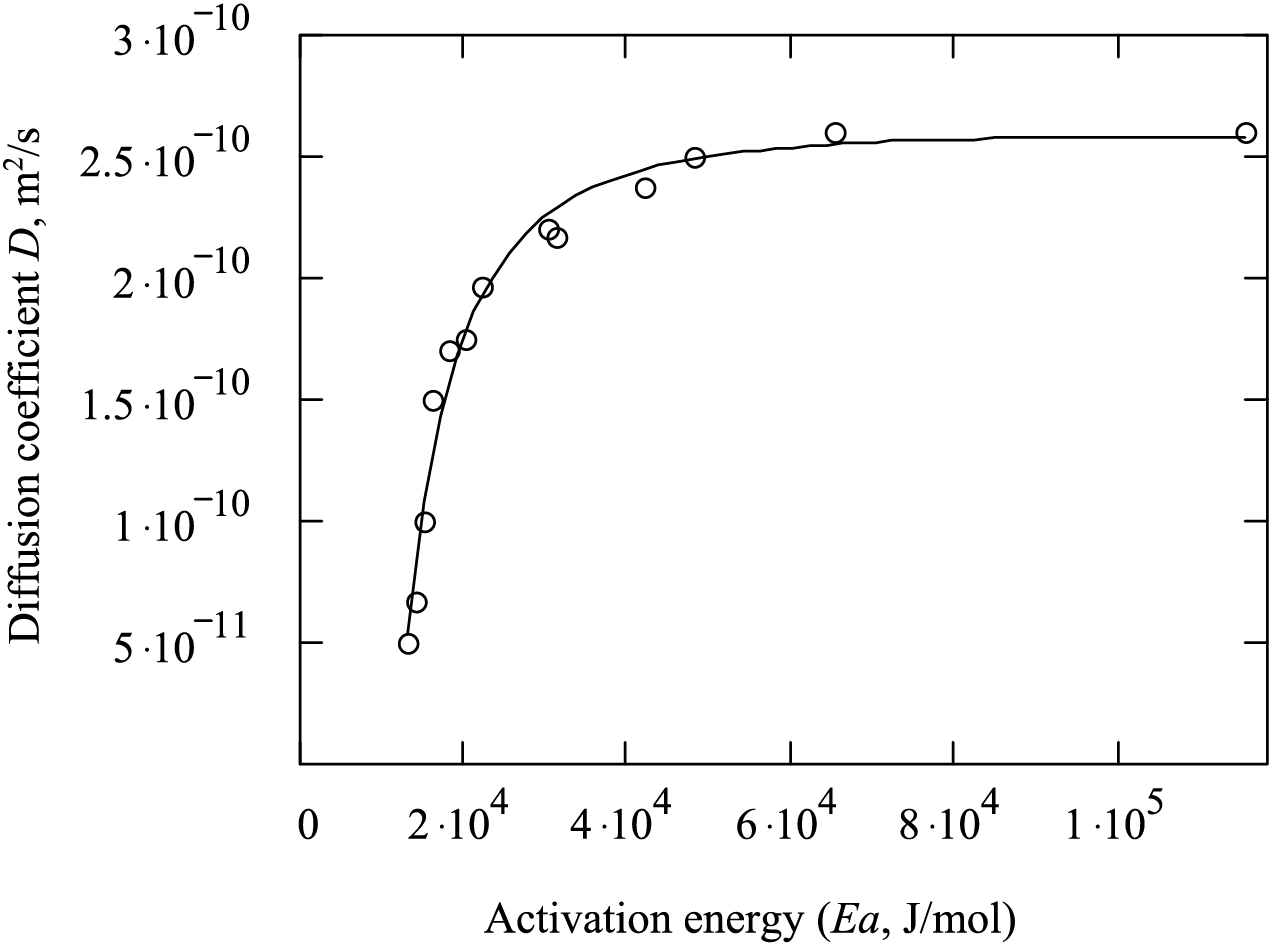
Figure 10: Dependence of diffusion coefficient on activation energy
Using the proposed model, the main characteristics of the adsorption process were calculated, on the basis of which the design parameters of the adsorber were calculated. The results of this work were involved in the production of InnovTechProduct LLP.
A mathematical model allowing for calculating the main characteristics of the initial stage and transient process modes of non-isothermal adsorption of a two-component liquid in a porous adsorbent layer has been carried out. Equations are proposed to determine the probabilities of particle migration and desorption near the occupied center, as well as expressions for determining the coefficient of migration of molecules, passivation of the surface and the initial local coefficient of adhesion.
Based on the established mechanism for changing the degree of coverage of the adsorption surface along the flow in the apparatus, a differential equation is proposed for the probability of diffusive migration of adsorbed particles in the pores of the adsorbent. As a result of solving the differential equation, an expression is obtained for the transiently reduced degree of coating and calculation of the degree of filling of the inner surface of the pores of the adsorbent corresponding to the completion of the initial stage of adsorption and the transition of the process to a stable mode.
To calculate a non-isothermal turbulent boundary layer when flowing around the surface of the adsorbent layer, expressions are proposed for calculating the coefficient of turbulent viscosity of the mixing path, characteristic of boundary layers without buoyant forces.
An efficient design of a fixed-layer adsorber has been developed, combining high mass transfer intensity and high productivity. The mass transfer device allows to increase in the degree of purification, a high level of utilization of the useful volume of the device, an increase in the degree of processing of the adsorption capacity of the adsorbent in the layer, uniform distribution of water in the adsorbent layer.
Further research, in the author’s opinion, should be aimed at a more detailed development of the model, taking into account the multicomponent nature of the mixtures being processed and the characteristics of hydrodynamics in specific apparatuses. It is also necessary to pay special attention to understanding the methods for estimating control parameters and debugging the quantitative calculation of their optimal values for specific systems.
Acknowledgement: We are grateful to the grant project of the Ministry of Science and Higher Education of the Republic of Kazakhstan “Development of Drying Equipment and Mass Transfer Research for Fruit Drying” (АР19678142), which allowed us to complete this work.
Funding Statement: This research was funded by the Ministry of Science and Higher Education of the Republic of Kazakhstan (grant number AP19678142; M. Satayev, A. Azimov, N. Alekseуeva, M. Isak, Z. Shakiryanova, Z. Ashirbaev, S. Duisebaev; https://www.gov.kz/memleket/entities/science?lang=en) (accessed on 13 August 2024).
Author Contributions: Study conception and design: Marat Satayev; data collection: Nina Alekseyeva; analysis and interpretation of results: Abdugani Azimov; draft manuscript preparation: Arnold Brener, Zulfia Shakiryanova. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: No data was used for the research described in the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Gao H, Tatomir AB, Karadimitriou NK, Stee H, Sauter M. Effect of pore space stagnant zones on interphase mass transfer in porous media, for two-phase flow conditions. Transp Porous Media. 2023;146(3):639–67. doi:10.1007/s11242-022-01879-0. [Google Scholar] [CrossRef]
2. Sakhmetova G, Brener A, Satayev M, Korabayeva K. On the mesoscopic model of mass transfer in microporous membranes. Chem Eng Trans. 2016;53. doi:10.3303/CET1653009. [Google Scholar] [CrossRef]
3. Mou X, Chen Z. Pore-scale simulation of heat and mass transfer in deformable porous media. Int J Heat Mass Transf. 2020;158(6):119878. doi:10.1016/j.ijheatmasstransfer.2020.119878. [Google Scholar] [CrossRef]
4. Graveleau M, Soulaine C, Tchelepi HA. Pore-scale simulation of interphase multicomponent mass transfer for subsurface flow. Transp Porous Media. 2017;120(2):287–308. doi:10.1007/s11242-017-0921-1. [Google Scholar] [CrossRef]
5. Pavlenko A. Heat and mass transfer in porous materials. Materials. 2023;16(16):5591. doi:10.3390/ma16165591 [Google Scholar] [PubMed] [CrossRef]
6. Teruel FE, Díaz L. Calculation of the interfacial heat transfer coefficient in porous media employing numerical simulations. Int J Heat Mass Transf. 2013;60:406–12. doi:10.1016/j.ijheatmasstransfer.2012.12.022. [Google Scholar] [CrossRef]
7. Brandani S. Exact equivalence at cyclic steady state between isothermal diffusion and linear driving force models for linear adsorption systems. Adsorption. 2021;27(2):171–80. doi:10.1007/s10450-020-00261-0. [Google Scholar] [CrossRef]
8. Wang J, Yuan Q, Dong M, Cai J, Yu L. Experimental investigation of gas mass transport and diffusion coefficients in porous media with nanopores. Int J Heat Mass Transf. 2017;115(B):566–79. doi:10.1016/j.ijheatmasstransfer.2017.08.057. [Google Scholar] [CrossRef]
9. Wei H, Sha X, Chen L, Wang Z, Zhang C, He P, et al. Visualization of multiphase reactive flow and mass transfer in functionalized microfluidic porous media. Nano-Micro Small. 2024;20(32):2401393. doi:10.1002/smll.202401393 [Google Scholar] [PubMed] [CrossRef]
10. Yu YZ, Guo JG, Zhou LJ. Theoretical investigation on the adsorption and diffusion of lithium-ion on and between graphene layers with size and defect effects. Adsorpt Sci Technol. 2016;34(2–3):212–26. doi:10.1177/0263617415623429. [Google Scholar] [CrossRef]
11. Bobok D, Besedová E. Diffusion of 1,2-Dichloropropane in particles of activated carbon. Adsorpt Sci Technol. 1998;16:217–24. doi:10.1177/026361749801600305. [Google Scholar] [CrossRef]
12. Hwang S, Kärger J, Miersemann E. Diffusion and reaction in pore hierarchies by the two-region model. Adsorption. 2021;27(5):761–76. doi:10.1007/s10450-021-00307-x. [Google Scholar] [CrossRef]
13. Priyadarshini S, Nayak S. A numerical approach to study heat and mass transfer in porous medium influenced by uncertain parameters. Int Commun Heat Mass Transf. 2022;139(11):106411. doi:10.1016/j.icheatmasstransfer.2022.106411. [Google Scholar] [CrossRef]
14. Bobok D, Besedová E. The diffusion of chlorinated hydrocarbons in particles of activated carbon. Adsorpt Sci Technol. 2001;19(10):813–20. doi:10.1260/0263617011494600. [Google Scholar] [CrossRef]
15. Costa E, Calleja G, Marijuan L. Adsorption of phenol and p-Nitrophenol on activated carbon: determination of effective diffusion coefficients. Adsorpt Sci Technol. 1987;4(1–2):59–77. doi:10.1177/0263617487004001-206. [Google Scholar] [CrossRef]
16. Ocampo-Pérez R, Leyva-Ramos R, Padilla-Ortega E. Equilibrium and kinetic adsorption of organic compounds onto organobentonite: application of a surface diffusion model. Adsorpt Sci Technol. 2011;29(10):1007–24. doi:10.1260/0263-6174.29.10.1007. [Google Scholar] [CrossRef]
17. El-Geundi MS. Homogeneous surface diffusion model for the adsorption of basic dyestuffs onto natural clay in batch adsorbers. Adsorpt Sci Technol. 1991;8(4):217–25. doi:10.1177/026361749100800404. [Google Scholar] [CrossRef]
18. Yang J, Dai X, Xu Q, Liu Z, Zan C, Long W, et al. Pore-scale study of multicomponent multiphase heat and mass transfer mechanism during methane hydrate dissociation process. Chem Eng J. 2021;423:130206. doi:10.1016/j.cej.2021.130206. [Google Scholar] [CrossRef]
19. Zhang Y. Power loss in multiscale mass transfer. Front Heat Mass Transf. 2019;13(1):1–4. doi:10.5098/hmt.13.22. [Google Scholar] [CrossRef]
20. Mirzaie M. CFD simulation of benzene adsorption on pistachio activated carbon porous media. Front Heat Mass Transf. 2020;14(1):1–7. doi:10.5098/hmt.14.19. [Google Scholar] [CrossRef]
21. Krishnamurthy S, Blom R, Ferrari MC, Brandani S. Adsorption and diffusion of CO2 in CPO-27-Ni beads. Adsorption. 2020;26(5):711–21. doi:10.1007/s10450-019-00162-x. [Google Scholar] [CrossRef]
22. El-Geundi MS. Pore diffusion model for the adsorption of basic dyestuffs onto natural clay in batch adsorbers. Adsorpt Sci Technol. 1992;9(2):109–20. doi:10.1177/026361749200900205. [Google Scholar] [CrossRef]
23. Fadali OA. Effect of gas stirring on external mass transfer, intraparticle diffusion and energy consumption during adsorption. Adsorpt Sci Technol. 2003;21(10):935–50. doi:10.1260/02636170360744371. [Google Scholar] [CrossRef]
24. Hudek P, Bobok D, Smiešková A, Židek Z. Sorption and diffusion properties of H- and modified forms of ZSM-5 zeolites. Adsorpt Sci Technol. 1996;13(6):495–508. doi:10.1177/026361749601300606. [Google Scholar] [CrossRef]
25. Sonetaka N, Seida Y, Nakano T, Furuya E. Determination of intraparticle diffusivity and fluid-to-solid mass transfer coefficient from single concentration history curve in circulated-type fixed-bed reactor. Adsorpt Sci Technol. 2018;36(1–2):571–85. doi:10.1177/0263617417707866. [Google Scholar] [CrossRef]
26. Othman MR, Martunus Fernando WJN, Kim J. Fractal rate of adsorption and surface diffusivity of carbon dioxide across mesoporous adsorbents. Adsorpt Sci Technol. 2009;27(10):893–906. doi:10.1260/0263-6174.27.10.893. [Google Scholar] [CrossRef]
27. Murtaza S, Kumam P, Bilal M, Sutthibutpong T, Rujisamphan N, Ahmad Z. Parametric simulation of hybrid nanofluid flow consisting of cobalt ferrite nanoparticles with second-order slip and variable viscosity over an extending surface. Nanotechnol Rev. 2023;12(1):20220533. doi:10.1515/ntrev-2022-0533. [Google Scholar] [CrossRef]
28. Murtaza S, Kumam P, Ahmad Z, Ramzan M, Ali I, Saeed A. Computational simulation of unsteady squeezing hybrid nanofluid flow through a horizontal channel comprised of metallic nanoparticles. J Nanofluids. 2023;12(5):1327–34. doi:10.1166/jon.2023.2020. [Google Scholar] [CrossRef]
29. Memetova AE, Burakova IV, Burakov AE, Memetov NR, Tkachev AG. Effective adsorption of toluene and benzene on coconut activated carbon modified with carbon nanotubes: kinetics, isotherms and thermodynamics. Adsorption. 2023;29(5–6):335–49. doi:10.1007/s10450-023-00405-y. [Google Scholar] [CrossRef]
30. Du Y, Zhang H, Yang Y, Jiao J, Ma J, Li R. Adsorption and diffusion of alkylbenzene in microspherical ZSM-5 zeolite assembled with nanocrystals. Adsorption. 2018;24(8):705–14. doi:10.1007/s10450-018-9980-z. [Google Scholar] [CrossRef]
31. Wang Y. Identification of mass transfer resistances in microporous materials using frequency response methods. Adsorption. 2021;27(3):369–95. doi:10.1007/s10450-021-00305-z. [Google Scholar] [CrossRef]
32. Zhokh A, Strizhak P, Maresz K, Ciemięga A, Mrowiec-Białoń J. Diffusion in hierarchical silica monoliths: impact of pore size and probe molecule. Heat Mass Transf. 2020;56(12):3199–207. doi:10.1007/s00231-020-02929-3. [Google Scholar] [CrossRef]
33. Clemente MAJ, de Oliveira TF, Cremasco H, Galvan D, Bordin MSP, Moreira I, et al. Mathematical modeling of NaCl and KCl diffusion in mozzarella cheese using static and stirred brine. Heat Mass Transf. 2020;56(7):2203–10. doi:10.1007/s00231-020-02849-2. [Google Scholar] [CrossRef]
34. Zhokh A, Strizhak P. Investigation of the anomalous diffusion in the porous media: a spatiotemporal scaling. Heat Mass Transf. 2019;55(9):2693–702. doi:10.1007/s00231-019-02602-4. [Google Scholar] [CrossRef]
35. Maghsoudi H, Nozari V, Zamzami SR. Diffusion of methane in high-silica CHA zeolite. Heat Mass Transf. 2019;55(6):1619–25. doi:10.1007/s00231-018-02547-0. [Google Scholar] [CrossRef]
36. Hristov J. A new closed-form approximate solution to diffusion with quadratic Fujita’s non-linearity: the case of diffusion controlled sorption kinetics relevant to rectangular adsorption isotherms. Heat Mass Transf. 2019;55(2):261–79. doi:10.1007/s00231-018-2408-1. [Google Scholar] [CrossRef]
37. Chen C, Hu W, Sun J, Li W, Song Y. CH4 adsorption and diffusion in shale pores from molecular simulation and a model for CH4 adsorption in shale matrix. Int J Heat Mass Transf. 2019;141(6):367–78. doi:10.1016/j.ijheatmasstransfer.2019.06.087. [Google Scholar] [CrossRef]
38. Levdansky VV, Smolik J, Moravec P. Effect of surface diffusion on transfer processes in heterogeneous systems. Int J Heat Mass Transf. 2008;51(9–10):2471–81. doi:10.1016/j.ijheatmasstransfer.2007.08.009. [Google Scholar] [CrossRef]
39. Gorlov VA, Moskovskaya TA, Voloshchuk AM. Study of intracrystalline diffusion in zeolites. 8. Effect of the parameters of the adsorption systems on the kinetics of adsorption in numerical modeling of nonisothermal diffusion in crystals. Russ Chem Bull. 1990;39(8):1541–4. doi:10.1007/BF00961472. [Google Scholar] [CrossRef]
40. Efremov SN, Zolotarev PP, Ulin VI. Approximate solution of the equilibrium adsorption-dynamics problem for certain convex adsorption isotherms considering longitudinal diffusion. Russ Chem Bull. 1980;29(9):1395–8. doi:10.1007/BF01168260. [Google Scholar] [CrossRef]
41. Miller R. On the solution of diffusion controlled adsorption kinetics for any adsorption isotherms. Colloid Polym Sci. 1981;259(3):375–81. doi:10.1007/BF01524718. [Google Scholar] [CrossRef]
42. Zhokh A. Diffusion in zeolites: a critical assessment on an observed “Fickianity”. Int Commun Heat Mass Transf. 2019 Dec;109:104372. doi:10.1016/j.icheatmasstransfer.2019.104372. [Google Scholar] [CrossRef]
43. Dovì VG, Paladino O, Preisig H. The importance of correct boundary conditions in the estimation of diffusion coefficients from mass sorption experiments. Int Commun Heat Mass Transf. 1988;15(5):669–79. doi:10.1016/0735-1933(88)90057-7. [Google Scholar] [CrossRef]
44. Satayev MI, Altynbekov RF, Altynbekov FE, Balabekov OS, Mamitova A. Mass transfer apparatus. Patent of the Republic of Kazakhstan 10182; 2001. Available from: https://kzpatents.com/3-10182-massoobmennyjj-apparat.html/. [Accessed 2003]. [Google Scholar]
45. Satayev MI, Altynbekov FE, Arginbaev DK, Sataev KI. Method for producing activated carbon. Patent of the Republic of Kazakhstan 7613. Available from: https://kzpatents.com/0-7613-sposob-polucheniya-aktivirovannogo-uglya.html/. [Accessed 1999]. [Google Scholar]
46. Sataev MI, Mamitova AD, Shakirov BS, Sataeva LM, Turisbaeva AK, Smagul AT. Method for producing activated carbon. Patent of the Republic of Kazakhstan 10536. Available from: https://kzpatents.com/0-pp10536-sposob-polucheniya-aktivirovannogo-uglya.html/. [Accessed 2001]. [Google Scholar]
47. Sataev MI, Esenbek AS, Azimov AM, Alekseeva NV, ZhS A, ShE D, et al. Method for producing activated carbon. Patent of the Republic of Kazakhstan 6376; 2022. Available from: https://qazpatent.kz/ru. [Accessed 2022]. [Google Scholar]
48. Zenguil E. Surface physics. Moscow: Mir; 1990, p. 536. Available from: https://obuchalka.org/20220805146371/fizika-poverhnosti-zenguil-e-1990.html. [Accessed 2022]. [Google Scholar]
49. Flood EA. The solid-gas interface. 1. New York, 1967, p. 435. Available from: https://books.google.ru/books?id=AJshAQAAMAAJ&hl=ru&source=gbs_navlinks_s. [Accessed 2011]. [Google Scholar]
50. Alekseev BV. Mathematical kinetics of reacting gases. Moscow: Nauka; 1982, p. 421. Available from: https://books.google.ru/books/about/ [Accessed 2008]. [Google Scholar]
51. Frank-Kamenetsky DA. Diffusion and heat transfer in chemical kinetics. Moscow: Nauka; 1967. p. 502. Available from: https://elib.biblioatom.ru/text/frank-kamenetskiy_diffuziya-i-teploperedacha_1987/p0b/ [Accessed 2009]. [Google Scholar]
52. YuB R, MSh R. Thermodynamics, statistical physics and kinetics. Moscow: Nauka; 1977. p. 552. Available from: https://djvu.online/file/IJVKLtHx71wRS. [Accessed 2010]. [Google Scholar]
53. Tashimov LT. Convective heat and mass transfer in film processes of chemical technology/Issues of modeling and stability/. Almaty: Bilim; 1999. p. 200 Available from: https://e-catalog.nlb.by/Record/BY-NLB-br174568 [Accessed 2008]. [Google Scholar]
54. Kosloff R. The Fourier method. In: Numerical grid methods and their application to Schrödinger’s Equation/Dordrecht. Netherlands: Springer; 1993. p. 175–94. [Google Scholar]
55. Wong MW. Partial differential equations: topics in Fourier analysis. New York, USA: Chapman and Hall/CRC; 2022. [Google Scholar]
56. Cebeci T, Bradshaw P. Physical and computational aspects of convective heat transfer. Heidelberg, Germany: Springer Science & Business Media; 2013. doi:10.1007/978-1-4612-3918-5. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools