Droplet Condensation and Transport Properties on Multiple Composite Surface: A Molecular Dynamics Study

Nomenclature

1  Introduction

Vapor condensation is a physical phenomenon characterized by phase transition. Natural occurrences such as the formation of rain and fog, dew condensation on plant leaves, as well as the water-harvesting for desert beetles and cacti [1–3], are all intricately linked to the vapor condensation. Furthermore, condensation heat transfer plays a crucial role in various industrial processes including thermal management of electronic equipment [4,5], power generation [6], and seawater desalination [7].

There are two primary condensation modes on a cold surface, namely dropwise condensation (DWC) [8] and filmwise condensation (FWC) [9]. DWC enables the efficient detachment of condensate droplets, resulting in a significant reduction of thermal resistance from condensate [10]. On average, the heat transfer coefficient for DWC is 5–7 times higher [11,12] than that for FWC. For the DWC, the micro-dynamic processes of nucleation, growth, and transportation are observed for condensate droplets [13–15]. Extensive experiments and theoretical analysis have been conducted to understand the dynamic behavior of multiscale droplets. Furthermore, numerous scholars have successfully achieved directional transportation of dropwise condensation by changing the wettability of condensation surface, which helps to accelerate the removal of condensate and improve the heat transfer coefficient [16–18].

The widespread utilization of molecular dynamics simulations for investigating microscopic mechanisms including vapor droplet nucleation [19], growth and coalescence has been facilitated due to significant improvement of computational capabilities. Numerous researchers have employed the concept of clusters [20,21] to elucidate the formation mechanism of initial droplets using molecular dynamics simulations. For instance, Yasuoka et al. [22] employed molecular dynamics simulation to examine the dynamics of homogeneous nucleation in a Lennard-Jones fluid with a supersaturation ratio of 6.8. Their findings revealed that the critical nucleus size, as determined by kinetics, ranged from 30 to 40 for the Lennard-Jones fluid. Gao et al. [23] studied the coalescence process of two same-sized nanodroplets and found that surface wettability intensity and solid fraction played a remarkable role in the attractive forces of nanodroplets. Additionally, Xu et al. [24] constructed a composite wedge-shaped condensation surface with multiple wettability gradients, which proved to be advantageous for directional transportation of condensate. Mo et al. [25] employed the molecular dynamics method to examine the motion of nanoscale droplets on axisymmetric surfaces, specifically focusing on the effect of surface geometry, wettability, and droplet size, which shed light on the factors influencing droplet movement. Similarly, Niu et al. [26] conducted simulations to accurately manipulate the aspect ratio of nano-structures and further explored the mechanisms of droplet growth and coalescence during the transition from the Wenzel state to the Cassie state. Notably, this simulation was performed on a relatively large system by adopting coarse-grained molecular model.

In comparison to wettability, the inclusion of pore structures significantly affects the transport properties of droplets. The successful implementation of heat and mass recovery is greatly influenced by the configuration of nanopores. Cihan et al. [27] conducted a theoretical investigation on adsorption, capillary condensation, and imbibition in nanoporous media, emphasizing the importance of fluid-fluid and fluid-pore wall interaction forces. de la Llave et al. [28,29] employed a coarse-grained model of water to explore the phase behavior and nucleation dynamics of confined fluids in cylindrical hydrophilic pores through molecular dynamics simulation. Further, Hu et al. [30] carried out numerous studies on the adsorption and condensation of vapor in tunable nanopores, and explored the capillary pressure effect to uncover the relevant mechanisms of the condensate-nanopore interaction for both hydrophilic and hydrophobic nanopores. Wang et al. [31] elucidated the dominant factor behind the spontaneous infiltration of a non-wetting capillary using many bodies dissipative particle dynamics (MDPD) simulations. They found that the capillary forces exerted both inside and outside the droplet surface play a crucial role in this phenomenon. In another study, Pospíšil et al. [32] explored the phase behavior of fluids in undulated nanopores, proposing mesoscopic corrections to macroscopic theory to describe phase transitions. Consequently, these investigations have demonstrated the utility of molecular dynamics simulation in predicting and comprehending the intricate heat and mass transfer behaviors associated with vapor condensation at the nanoscale.

Despite the abundance of recent research on improving condensation heat transfer performance, there has been a lack of focus on efficiently recovering heat and water using functionalized surface by coupling gradient surfaces and nanopores structure. The purpose of this study is to explore the influence mechanisms of complex functional structures on heat and mass transfer during the condensation process. The research findings aim to provide theoretical support and technical guidance for the development of efficient condensation heat exchangers. This investigation employs a combination of simulation conditions and analysis the underlying mechanism from a micro perspective. By considering the characteristics of droplet nucleation, growth, and transport, this study extensively explores the effect of the functionalized surface including wetting gradient and pore structure on the heat and mass recovery in condensation process.

2  Models and Methods

This study employs the simulation software LAMMPS [33] to investigate the heat and mass recovery process on the functionalized surface with wetting gradient and pore structure. Initially, the simulation system is constructed, comprising coarse-grained water vapor and a Cu-like gradient pore structure. The dimensions of the 3D simulation box are 120 Å × 120 Å × 360 Å in the x, y, and z directions, respectively. The x and y directions adopt periodic boundary conditions, while the z direction adopts a reflection boundary condition. The solid surface gradient within the system is constructed using a FCC crystal with a lattice constant S=3.615 A. The configuration of the simulation system is shown as Fig. 1a. Previous studies [34,35] have demonstrated that the GCMD simulation (a combination of Grand Canonical Monte Carlo and molecular dynamics simulation) is a feasible method for the simulation of the phase change process which is also adopted in this study. The bottom region of the simulation box, known as the GCMD region, has a thickness of 40 Å and serves as a reliable source of vapor for maintaining stable temperature and pressure in the saturated state. To create a low-temperature region for heat dissipation, the thermostat is employed near the top of the box with a thickness of 10 Å as heat sink. Furthermore, an initial water layer is situated at the uppermost section of the simulation box to remove the condensate, which can be likened to the cooling water present in the tube during membrane recycling experiments. By implementing this particular configuration, it becomes possible to achieve evaporative condensation for the saturated vapor while maintaining a controllable subcooling degree.

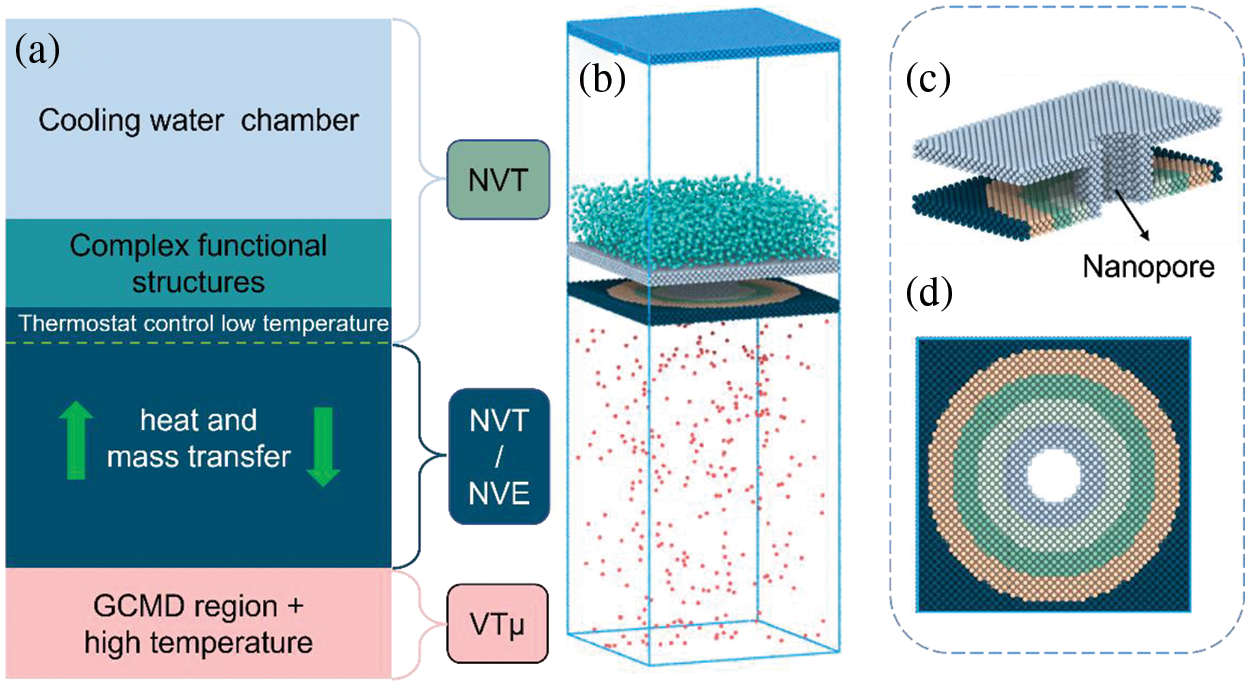
Figure 1: Setup of the simulation system. (a) Setup of system area, (b) simulation box of CG water vapor condensation transport, (c) setup of nanopore structure, (d) condensation surface with functional gradient

The simulations were conducted in two stages. During the first stage, the water molecules in the GCMD region were kept at a temperature of 500 K and a pressure of 5.5 atm using GCMD method. To ensure adherence to the simulation setup, the MC exchange (insertion or deletion) of water molecules was attempted every 20 steps. The NVT ensemble, which maintains a constant number of particles (N), volume (V), and temperature (T), was employed for the entire simulation region until the system reached equilibrium for 1 ns with a timestep of 5 fs. Following the initial phase of relaxation equilibrium, the system parameters achieved stability within their designated regions. Subsequently, a nanochannel was constructed by removing a cylindrical block with a radius of 1.2 nm from the central position of condensation solid surface. Furthermore, the region of vapor delivery situated between the GCMD region and the heat sink underwent a conversion from the NVT ensemble to the NVE ensemble, wherein the number of particles (N), volume (V), and energy (E) remained constant. Apart from these modifications, the remaining area settings remained unchanged from the initial configuration. In summary, a physical model depicting condensation nucleation, coalescence, and transport on a complex functional structure has been constructed as illustrated in Fig. 1b. The cutaway drawing of the complex functional structure including wettability gradient and transport pore are presented in Fig. 1c,d, respectively.

The Morse potential [36], E=D0[e−2α(r−r0)−2e−α(r−r0)], is used to construct coarse-grained water molecules in which D0=0.81265kcal/mol, α=0.5564A−1 and r0=6.29A are the characteristic energy and the reciprocal of the Van der Waals radius and the Van der Waalsctages in describing the dynamic and thermodynamic properties of the system. It is worth noting that the liquid film in the cooling water chamber is also composed of coarse-grained water molecules for which one coarse-grained bead represents four water molecules in all-atom model.

The interaction between solid surface and water molecules is also described using 12-6 revised Lennard-Jones (LJ) potential as follows:

E=4βεij[(σijrij)12−(σijrij)6](1)

where rij, εij and σij are the distance, well depth and equilibrium distance between a pair of atoms. rij and σij are calculated using the Lorentz-Bertholet mixing rule. The cutoff distances for LJ and Coulomb interactions are both 12 Å.

εij=εiεj(2)

σij=(σi+σj)2(3)

The dimensionless number, β, plays a crucial role in regulating the hydrophilicity and hydrophobicity of the condensation solid surface. To investigate the condensation behavior on such complex functional surface, the contact angle of the droplet was measured at a temperature of 300 K, for β serving as the independent variable. Fig. 2 shows the relationship between the contact angle and β. It is observed that as the β increases, the wettability of the solid surface transitions from hydrophobic to hydrophilic.

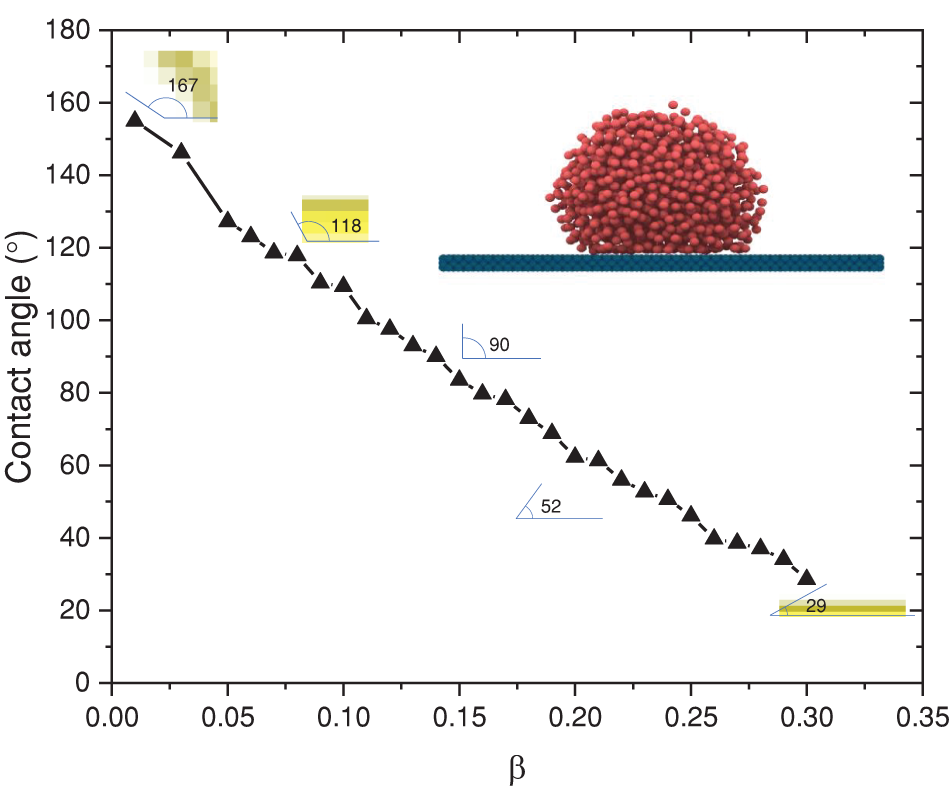
Figure 2: Correlations of contact angle with β

3  Results and Discussion

3.1 Effect of Complex Functional Structure on Heat and Mass Transfer

In accordance with Fig. 3, the initial stage of the simulation involved the introduction of water vapor with a temperature of 500 K and a pressure of 5.5 atm into the system via the GCMD method. Following a relaxation period of 1 ns, the number of water molecules and the total energy gradually approach stabilization. Additionally, it has been ascertained that the atomic parameters within the system can be reliably constructed through the utilization of the GCMD method. Consequently, all subsequent investigations will be conducted based on this relaxation phase to ensure the precision of the simulation.

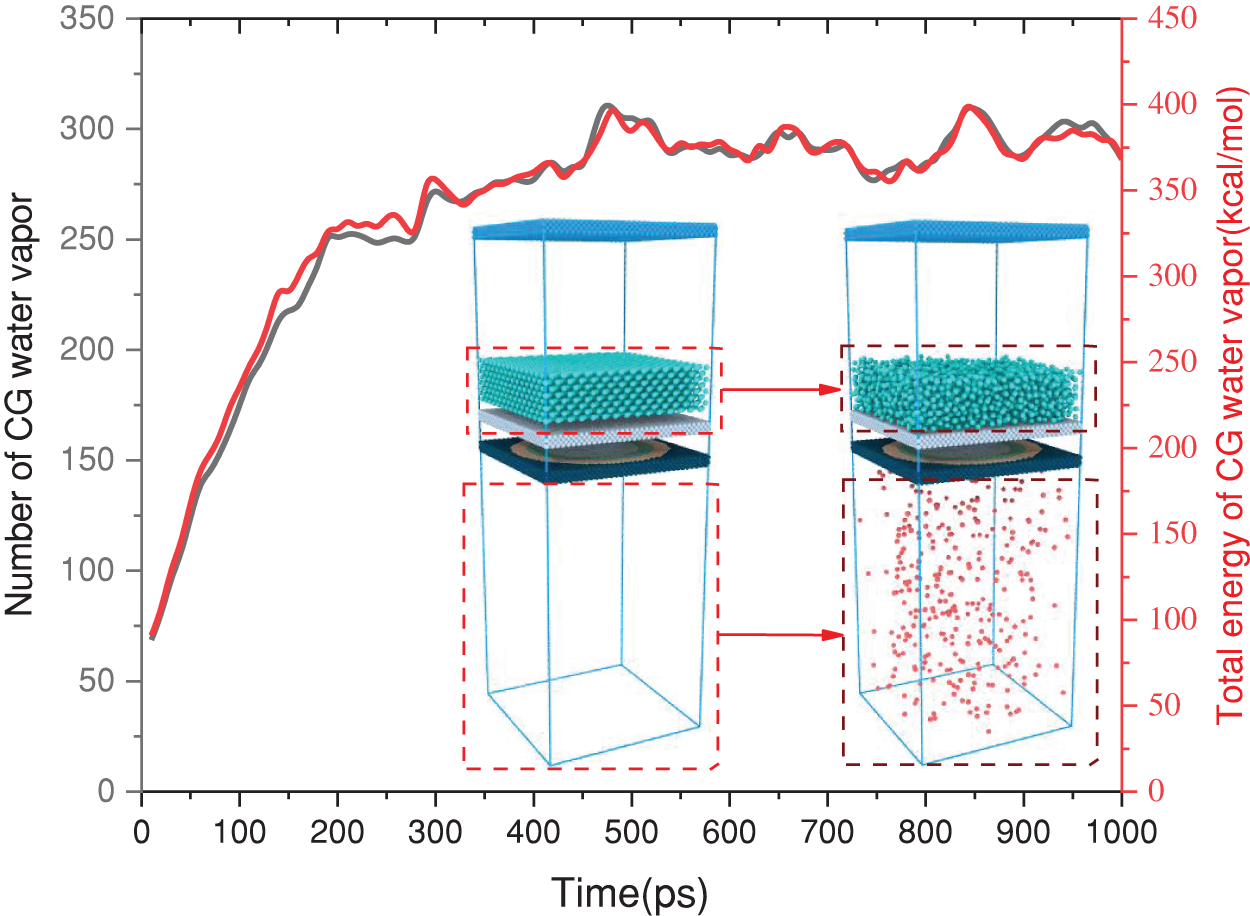
Figure 3: Steady-state verification of CG water vapor in the relaxation stage

The change in the wettability of the cooling surface during heat transfer is a key factor affecting the heat and mass transfer of vapor condensation. In this paper, three different groups of complex functional surface was built: homogeneous surface (Δθh=0∘, θ1=78.2∘), small gradient Δθs=5.4∘ (θ1=78.2∘→θ2=83.6∘), and large gradient (Δθl=14.8∘, θ1=78.2∘→θ3=93.0∘), as depicted in Fig. 4. It is worth noting that the nanopore wettability for all three groups is θ1. Over time, the three groups of systems demonstrate distinct outcomes. As depicted in Fig. 5, the presence of a large wetting gradient significantly increases the quantity of condensed liquid water compared to the other two cases. The simulation results indicate that the gradient effect within the large gradient wetting structure plays a pivotal role in expediting the transportation and elimination of condensed water. This gradient setup establishes favorable circumstances for subsequent vapor condensation and enhances the efficient transport of condensed water.

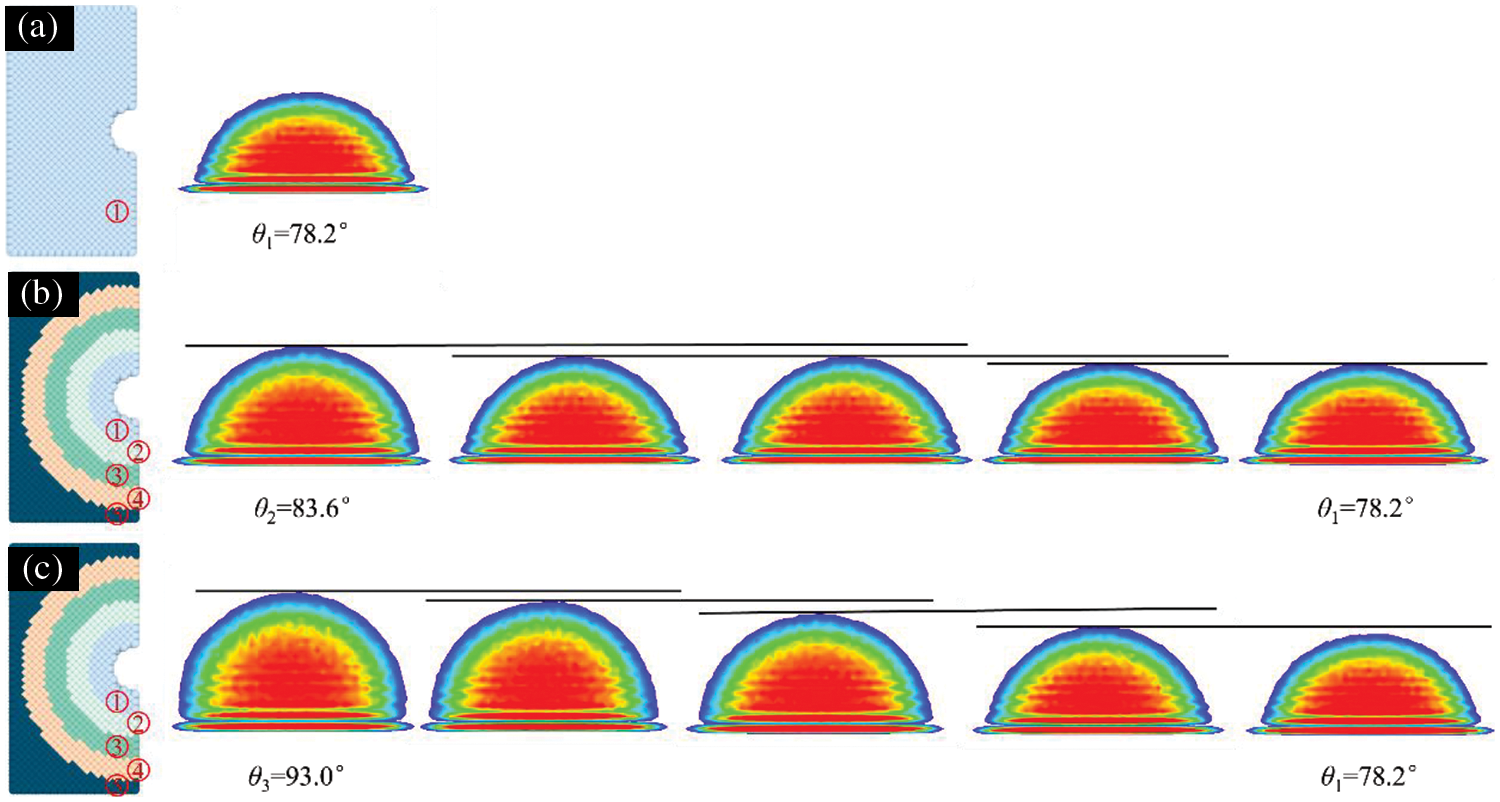
Figure 4: Droplet density cloud diagram on the wetted surface; (a) homogeneous structure; (b) small gradient wetting structure; (c) large gradient wetting structure (wettability gradually increases from left to right)

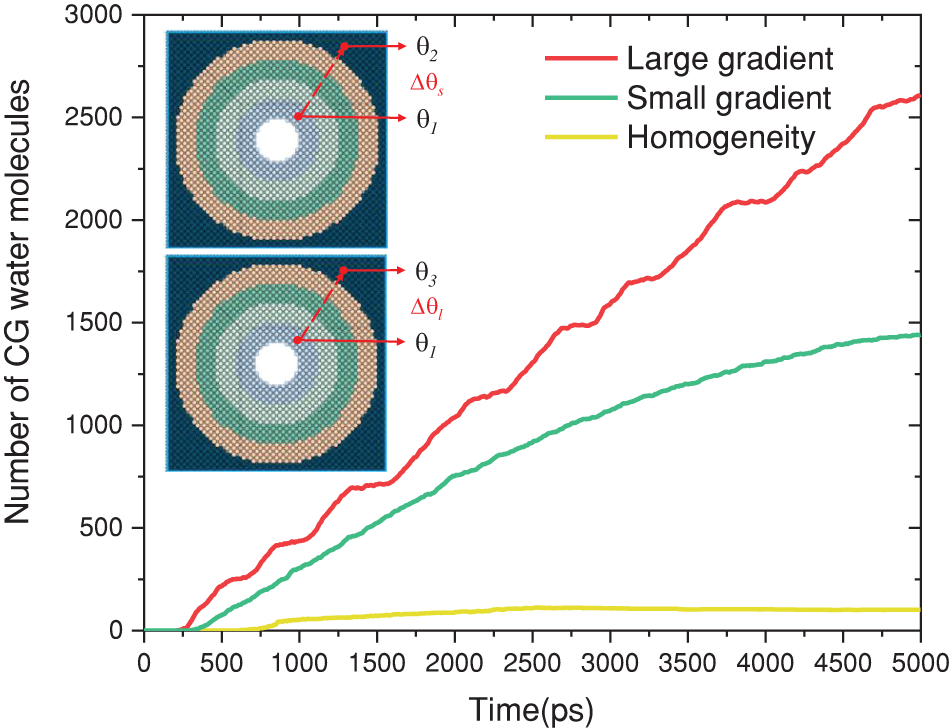
Figure 5: Number of CG water molecules entering the cooling water chamber for different groups

3.2 Enhance Mechanism of New Functional Surface

The research findings demonstrate that a reasonable wetting gradient in conjunction with nanopore can considerably enhance the heat and mass transfer of water vapor condensation. To quantitatively analyze this enhancement principle, we performed investigations on the condensation process occurring on the gradient surface, as well as the mechanisms governing the rates of condensate transport within nanopores. Firstly, the initial stage of condensation involves the generation of condensation nuclei. According to Stillinger’s definition [37], molecules within a certain distance could be considered to form a cluster. In this study, the size of atomic clusters in the system was measured, and clusters were defined as atomic clusters where the intermolecular distance is less than 9 Å and the number of molecules is greater than 7. The transition to nuclei occurred when the number of molecules in a cluster exceeded 45 [38]. Finally, when the number of molecules in the nucleus is greater than 214 [39], we consider it to be a nanoscale droplet or liquid film.

In this study, the wettability of the cold surface was the only variable during the process of condensation heat transfer. Fig. 6 (Fig. 6a,b,e,f,i,j) presents a comprehensive examination of the nucleation phenomena of condensation on micro-nanoscale surfaces with three distinct structures. Within a timeframe of 80 ps, it was observed that water vapor rapidly condensed into clusters on all three condensation surfaces. Subsequently, between 80 ps and 240 ps, the diverse phenomena were observed in the three groups, as depicted in Fig. 7. The clusters observed in Group A are not primarily influenced by gradient forces, but rather by the presence of periodic boundaries. In this particular case, the condensate clusters tend to form more easily at the edges of the cold surface and rapidly transition from a cluster to a droplet state (Fig. 6b,c). On the other hand, condensate clusters in Group B form randomly on the cold surface and exhibit rapid growth and coalescence into nuclei due to a small gradient force (Δθs=5.4∘). However, contrary to the first two cases, condensate clusters in Group C move towards the nanopore with greater wettability. In this case, the larger gradient force (Δθl=14.8∘) makes the small clusters coalesce into a larger cluster around or at the nanopore easier. We found that at 240 ps, the coalescence clusters were located directly below the nanopore and the growth of cluster was stagnant on the cold surface.

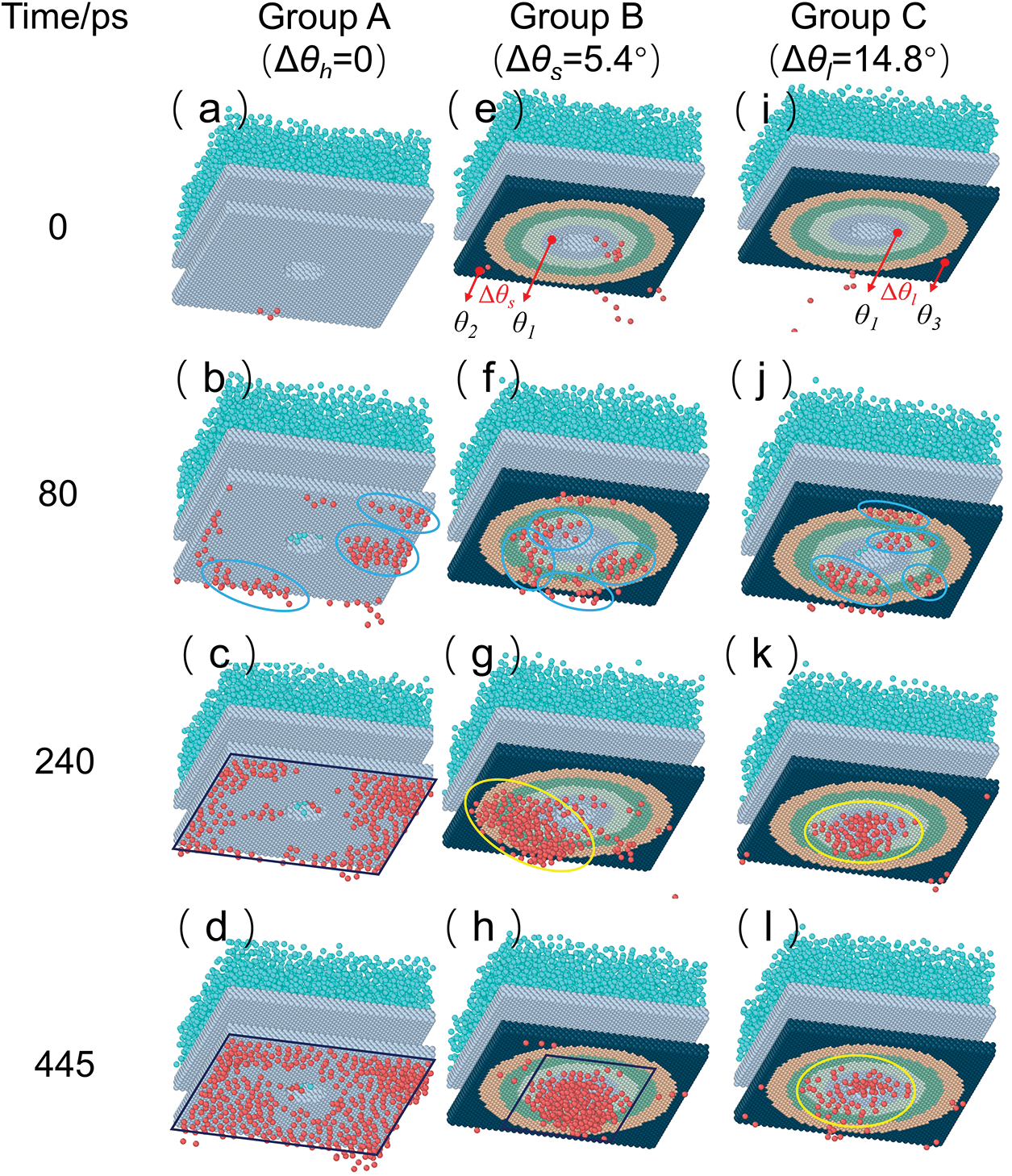
Figure 6: Transient snapshots of vapor condensation on different complex functional structure; (a) Snapshot of Group A at 0 ps; (b) Snapshot of Group A at 80 ps; (c) Snapshot of Group A at 240 ps; (d) Snapshot of Group A at 445 ps; (e) Snapshot of Group B at 0 ps; (f) Snapshot of Group B at 80 ps; (g) Snapshot of Group B at 240 ps; (h) Snapshot of Group B at 445 ps; (i) Snapshot of Group C at 0 ps; (j) Snapshot of Group C at 80 ps; (k) Snapshot of Group C at 240 ps; (l) Snapshot of Group C at 445 ps (“” represents a cluster; “” represents nuclei; “” represents nanoscale droplets or liquid films)

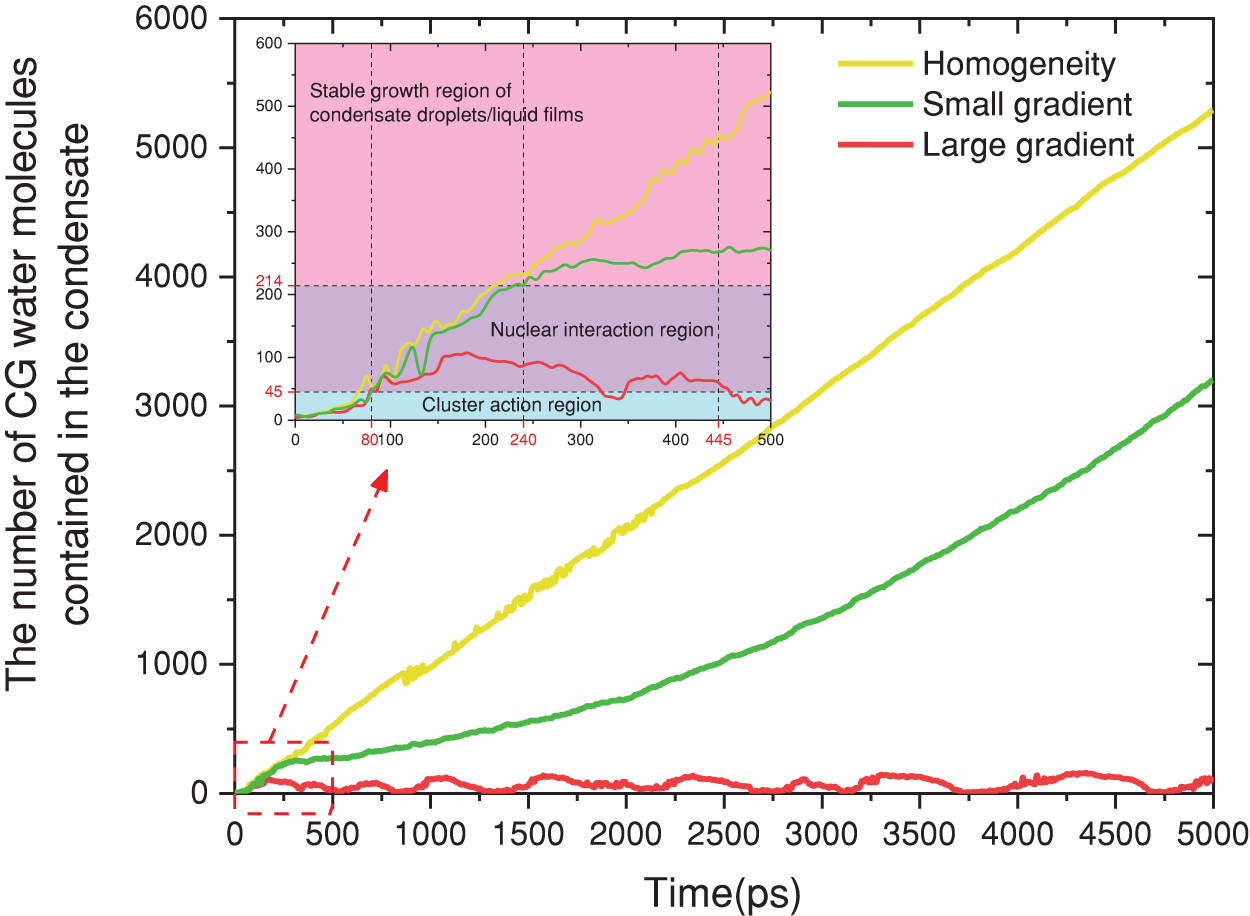
Figure 7: Condensation behavior of water vapor on the condensing surface

Over the course of time, notable differentiations among the three groups become evident beyond 445 ps. In Group A, the condensate exhibits a consistent expansion at the periphery of the uniform structure, as depicted in Fig. 6d. In Group B, propelled by the influence of minute gradient functional surface forces, the condensate initially moves directly beneath the nanopore (Fig. 6h), followed by continuous growth, as illustrated in Fig. 7. The condensate in Group C is observed to exist solely in two states, namely cluster and nucleus (Fig. 6i,l). According to the findings of the quantitative analysis, it is evident that the growth rate of condensate is comparatively lower than the rate of longitudinal transport of condensate in nanopore. Additional elaboration for this phenomenon will be provided in Section 3.3.

3.3 Mechanism of Condensate Transport in Nanopore

The Laplace pressure is the main factor affecting the transport rate of nanopores due to the surface tension. The setting of the condensation surface in the complex functional structure allows different interactions of the condensate with the nanopores. The surface tension force can be derived from the Gibb’s free energy of surface (G=∑γiAi) in an isothermal, isobaric thermodynamic system [40,41], where γi is the interfacial tension of any interface of area Ai within the system. The total surface tension of the system (Fγ=−dG/dx), where the x direction coincides with the direction of meniscus motion. Consequently, the Newtonian equation of motion expressed on the total surface tension in the nanopore, and is written as

d(mU)dt=Fγ(4)

where m is the mass of the liquid inside the nanopore, U is the average axial velocity over the nanopore cross section. The average axial velocity can then be expressed as U=dx/dt. Hence, the alternation of momentum includes the changes due to the column velocity and the column mass [42], and it can be expressed as

d(mU)dt=mdUdt+Udmdt=πR2ρ[xd2xdt2+(dxdt)2](5)

where ρ is the density of liquid and t is the time.

As shown in Fig. 8, the action of the CG water vapor condensate on the nanopore is considered alone, resulting in two gas-liquid interfaces (as marked in green in Fig. 8a,b): the gas-liquid interface (A1−i) of the droplet outside the nanopore and the concave surface (A2) of the meniscus inside the nanopore, respectively. In addition, there is one solid-liquid interface (Asl=2πx) and one solid-gas interface [Asg=2π(L−x)]. Thus the Gibb’s free energy in this state is as follows:

G1=γA1−i−2πRx(γsg−γsl)+(γA2+2πRγslL)(6)

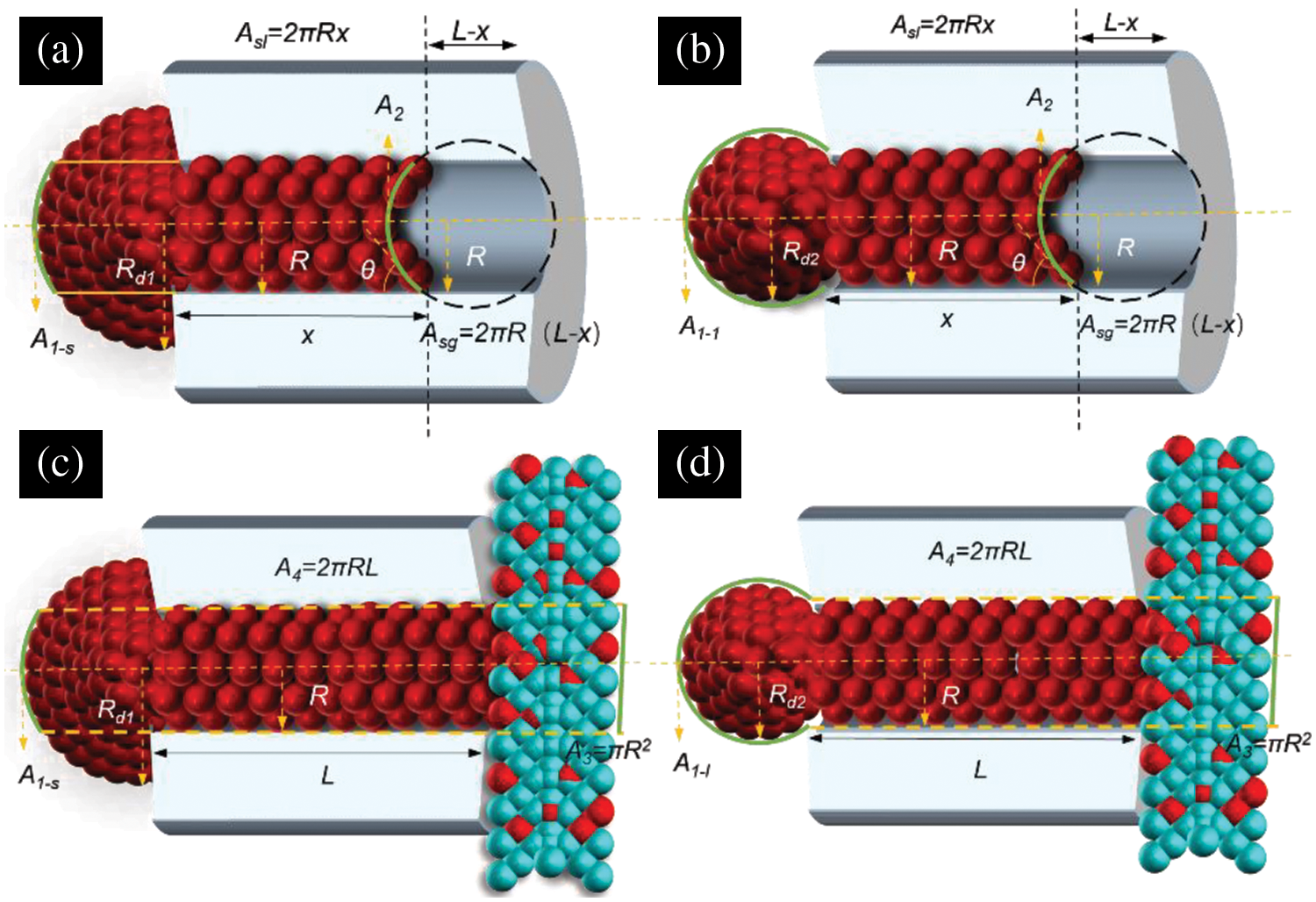
Figure 8: Analysis of the action of different condensate forms with nanopores. (a) Analysis of the force of hemispherical droplet on nanopores, (b) analysis of the force of pendant droplet on nanopores, (c) analysis of the force of hemispherical droplet on nanopores under the action of complex functional structure, (d) analysis of the force of pendant droplet on nanopores under the action of complex functional structure

Inserting Yong’s equation (γcosθ=γsg−γsl) into Eq. (6) [43] and derivation with to x, the following the surface tension expression is obtained:

Fγ−1=−γ(−2πRcosθ+dA1dx)(7)

As shown in Fig. 8c,d, for the complex functional structure action, considering the effect of cooling water on the condensate inside the nanopore, there are two gas-liquid interfaces: the gas-liquid interface (A1−i) of the droplet outside the nanopore and the concave surface (A3) of the meniscus inside the nanopore. The difference is that only one solid-liquid interface (A4) exists in this working condition. Therefore, the total Gibb’s free energy under the action of complex functional structure is obtained as follows:

G2=γA1−i+2πRLγsl−γA3(8)

Similarly, the total surface tension under the action of the complex functional structure can be derived from Eq. (8) for x, as follows:

Fγ−2=−γdA1dx(9)

Substituting Eq. (5) and Eq. (9) into Eq. (4) gives

πR2ρ[xd2xdt2+(dxdt)2]=−γdA1dx(10)

Combined with the analysis of Eq. (10), for the longitudinal driving force of nanopore under the action of complex functional structure, the rate of change of dA1 is the main factor affecting Fγ when dx→0. Thus, the principle of coupling interaction between the functional gradient surface and nanopore is obtained in this paper, i.e., the lateral transport rate of water condensate to nanopore greatly affects the longitudinal transport rate of condensate.

As shown in Figs. 9 and 10, combined with the analysis of Eq. (10), for the homogeneous structure of Group A, the condensate rapidly forms a liquid film during the whole process of vapor condensation heat and mass transfer. The heat and mass recovery effect of condensate only occurs before the liquid film is formed, and Fγ tends to 0 in the steady growth state of the liquid film. When dx→0, dt|t=445 ps→0 (initial moment of condensation), the radius of curvature (rs) in Group B is slightly larger than that in Group C. Similarly, the changing rate of dA1−s is slightly smaller than that of dA1−l, yielding Fγ−s<Fγ−l, but the overall heat and mass transport rate and the condensate accumulation flow rate are both considerable. When dx→0, dt|t=2935ps→0 (continuous condensation moment), the radius of curvature (rs) of Group B increases significantly, and the changing rate of dA1−s is much less than dA1−l, yielding Fγ−s<<Fγ−l, the rate of heat and mass transport of Group B decreases significantly, and the rate of condensate volume flow decreases significantly.

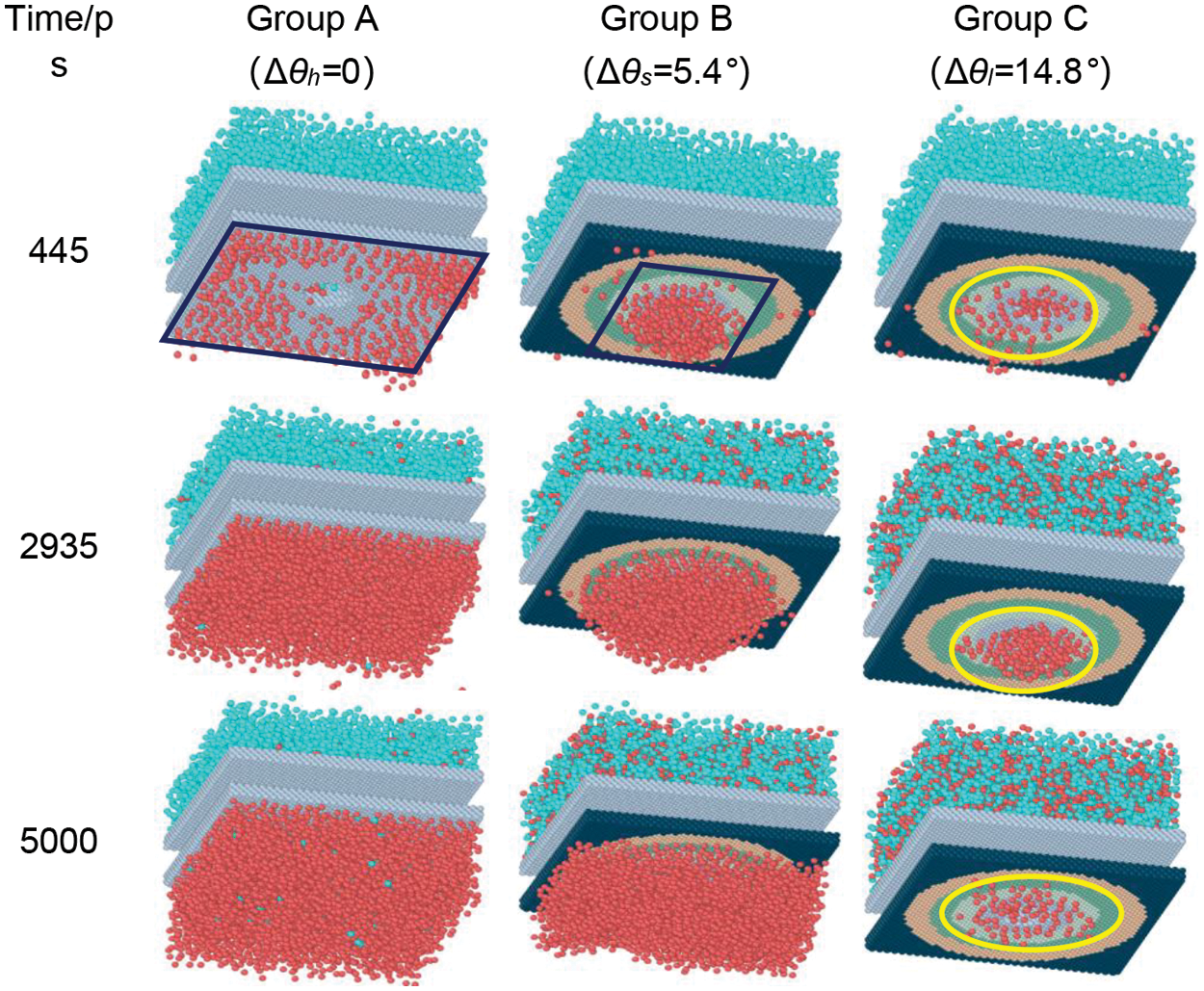
Figure 9: Transient snapshots of vapor condensation on different complex functional structure

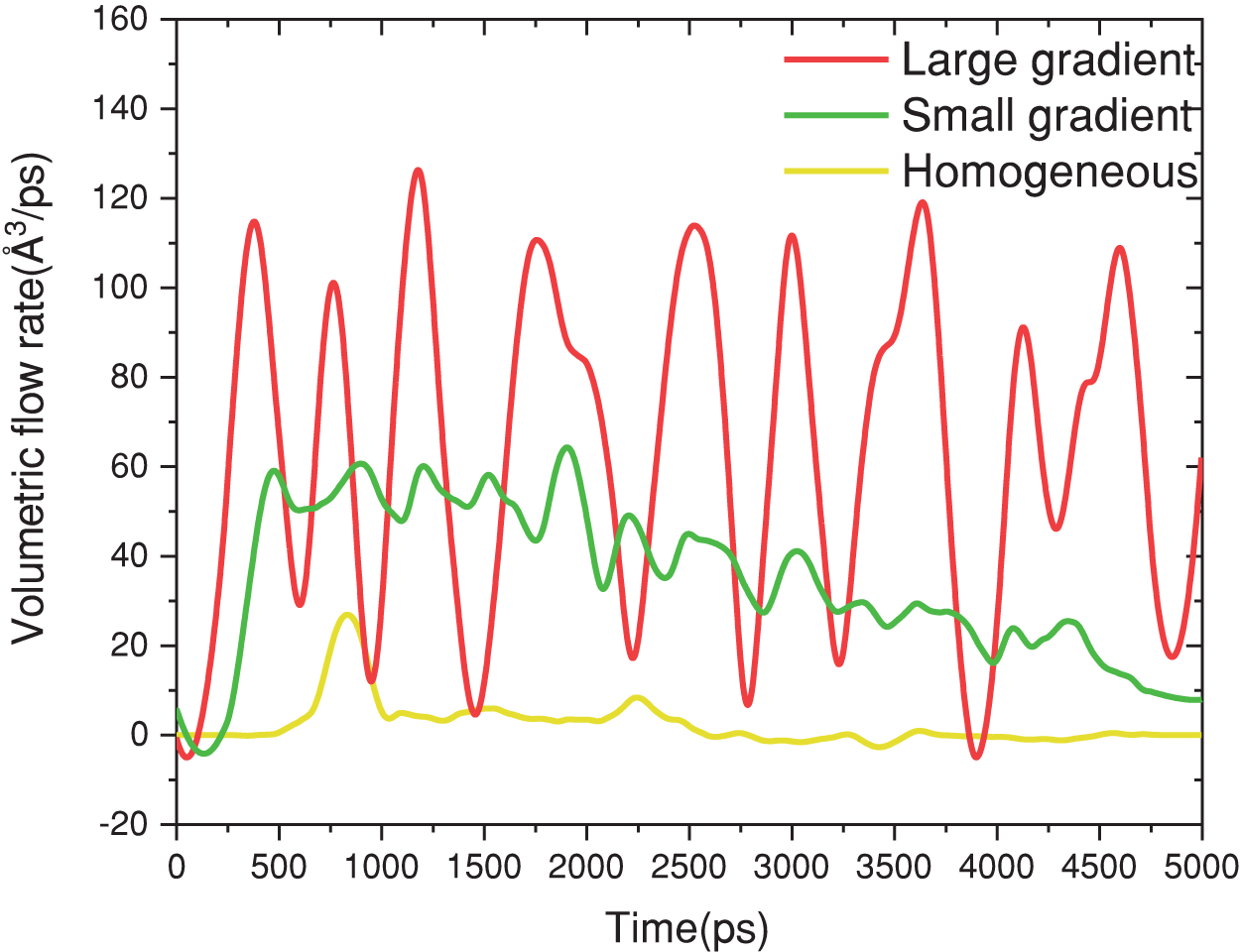
Figure 10: Volume flow rate under the action of different complex functional structure

An in-depth analysis of the process reveals that Group A, with its homogeneous structure, exhibits the lowest condensation heat and mass transfer rates. Initially, Group B is heat and mass transfer rates are on par with those of Group C. However, as condensation progresses and the liquid droplets within Group B coalesce into a liquid film, the performance of its complex functional structure in enhancing condensation becomes equivalent to that of Group A. In contrast, Group C undergoes regular pulsations in transport, consistently maintaining a stable heat and mass transfer rate throughout each cycle, which markedly enhances the condensation process.

4  Conclusions

In this work, we have built a complex condensation functional structure to enhance heat and mass transfer and analyzed the multiple mechanisms of condensation and transport enhancement. The results showed that the complex functional structure including gradient and nanopore allows continuous transport of condensate from the cold surface to the nanopore. The transport velocity of condensate is faster due to the larger wettability gradient which could be 1.85 times faster than that on a conventional surface.

The results showed that the complex functional structure is more effective in enhancing the heat and mass transfer rate of vapor condensation and that the Laplace pressure derived from surface tension is the main factor driving the longitudinal transport of condensate along the nanopore. It was found that condensation surfaces with larger gradient differences contribute to the rapid coalescence transport of condensate to nanopores, which creates extremely favorable conditions for the longitudinal transport of condensate. The complex functional structure provides microscopic mechanisms and theoretical support for the design of efficient condensers for recovering waste heat and waste material at the macroscopic level.

Acknowledgement: The authors would like to acknowledge the constructive remarks by worthy reviewers that led to this revised article.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 52206093), the University Outstanding Youth Fund Project of Anhui Province (Nos. 2022AH020028 and 2022AH030037), the Natural Science Foundation of Anhui Province (Nos. 1908085QF292 and 2308085ME173), Anhui Province Outstanding Young Talents Support Program (No. gxyqZD2022058), Guangdong Basic and Applied Basic Research Foundation (Nos. 2024A1515011379 and 2023A1515110613).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Haowei Hu, Qi Wang; data collection and analysis and interpretation of results: Qi Wang; draft manuscript preparation: Xinnuo Chen; investigation: Qin Li; conceptualization, methodology, writing review & editing: Du Mu; conceptualization, methodology, writing review & editing: Dong Niu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data can be made available from the corresponding author following a special request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Feng L, Li S, Li Y, Li H, Zhang L, Zhai J, et al. Super-hydrophobic surfaces: from natural to artificial. Adv Mater. 2002;14(24):1857–60. doi:10.1002/adma.200290020. [Google Scholar] [CrossRef]

2. Lv F, Zhao F, Cheng D, Dong Z, Jia H, Xiao X, et al. Bioinspired functional SLIPSs and wettability gradient surfaces and their synergistic cooperation and opportunities for enhanced condensate and fluid transport. Adv Colloid Interface Sci. 2022;299:102564. doi:10.1016/j.cis.2021.102564. [Google Scholar] [PubMed] [CrossRef]

3. Guo P, Zheng Y, Liu C, Ju J, Lei J. Directional shedding-off of water on natural/bio-mimetic taper-ratchet array surfaces. Soft Matter. 2012;8(6):1770–5. doi:10.1039/C1SM06631E. [Google Scholar] [CrossRef]

4. Tariq SL, Ali HM, Akram MA, Janjua MM. Experimental investigation on graphene based nanoparticles enhanced phase change materials (GbNePCMs) for thermal management of electronic equipment. J Energy Storage. 2020;30(12):101497. doi:10.1016/j.est.2020.101497. [Google Scholar] [CrossRef]

5. Miao T, Liu Z, Chen D, An M, Ma W. Regulatable thermal conductivity and excellent mass transport of water-filled carbon nanotube as capillary wicks. Int J Heat Mass Transf. 2022;195(8):123211. doi:10.1016/j.ijheatmasstransfer.2022.123211. [Google Scholar] [CrossRef]

6. Boreyko JB, Zhao Y, Chen CH. Planar jumping-drop thermal diodes. Appl Phys Lett. 2011;99(23):234105. doi:10.1063/1.3666818. [Google Scholar] [CrossRef]

7. Shen JW, Li J, Liu F, Zhang L, Liang L, Wang H, et al. A molecular dynamics study on water desalination using single-layer MoSe2 nanopore. J Membr Sci. 2020;595:117611. doi:10.1016/j.memsci.2019.117611. [Google Scholar] [CrossRef]

8. Wang X, Xu B, Chen Z, Yang Y, Cao Q. Lattice Boltzmann simulation of dropwise condensation on the microstructured surfaces with different wettability and morphologies. Int J Therm Sci. 2021;160:106643. doi:10.1016/j.ijthermalsci.2020.106643. [Google Scholar] [CrossRef]

9. Liu J, Grigoriev RO. Analytical solution for filmwise condensation in confined high-aspect ratio geometry. Int J Heat Mass Transf. 2019;133(6):561–71. doi:10.1016/j.ijheatmasstransfer.2018.12.131. [Google Scholar] [CrossRef]

10. Lo CC, Chen LJ. Dropwise condensation on single-micro-scale roughness hydrophobic surfaces. Surf Interfaces. 2022;33:102281. doi:10.1016/j.surfin.2022.102281. [Google Scholar] [CrossRef]

11. Rose JW. Dropwise condensation theory and experiment: a review. P I Mech Eng A—J Pow. 2002;216(2):115–28. doi:10.1243/09576500260049034. [Google Scholar] [CrossRef]

12. Chen X, Derby MM. Droplet departure modeling and a heat transfer correlation for dropwise flow condensation in hydrophobic mini-channels. Int J Heat Mass Transf. 2018;125(2):1096–104. doi:10.1016/j.ijheatmasstransfer.2018.04.140. [Google Scholar] [CrossRef]

13. Lv C, Chen C, Chuang YC, Tseng FG, Yin Y, Grey F, et al. Substrate curvature gradient drives rapid droplet motion. Phys Rev Lett. 2014;113(2):026101. doi:10.1103/PhysRevLett.113.026101. [Google Scholar] [PubMed] [CrossRef]

14. Liu Y, Cheng Y, Du B, Lan Z, Wen R, Ma X. Low-pressure steam dropwise condensation on durable PFA-coated horizontal tube: droplet dynamics in active region. Int J Heat Mass Tran. 2023;214(11):124423. doi:10.1016/j.ijheatmasstransfer.2023.124423. [Google Scholar] [CrossRef]

15. Liu C, Ju J, Zheng Y, Jiang L. Asymmetric ratchet effect for directional transport of fog drops on static and dynamic butterfly wings. ACS Nano. 2014;8(2):1321–9. doi:10.1021/nn404761q. [Google Scholar] [PubMed] [CrossRef]

16. Gao S, Liu W, Liu Z. Tuning nanostructured surfaces with hybrid wettability areas to enhance condensation. Nanoscale. 2019;11(2):459–66. doi:10.1039/C8NR05772A. [Google Scholar] [PubMed] [CrossRef]

17. Goswami A, Pillai SC, McGranaghan G. Surface modifications to enhance dropwise condensation. Surf Interfaces. 2021;25:101143. doi:10.1016/j.surfin.2021.101143. [Google Scholar] [CrossRef]

18. Chavan S, Cha H, Orejon D, Nawaz K, Singla N, Yeung YF, et al. Heat transfer through a condensate droplet on hydrophobic and nanostructured superhydrophobic surfaces. Langmuir. 2016;32(31):7774–87. doi:10.1021/acs.langmuir.6b01903. [Google Scholar] [PubMed] [CrossRef]

19. Paul S, Chakraborty D, Esha SJ, Hasan MN. Role of wettability contrast on nanoscale condensation over hybrid wetting surface with gradient and patterned wetting configuration at various philic-phobic content. Surf Interfaces. 2023;36:102417. doi:10.1016/j.surfin.2022.102417. [Google Scholar] [CrossRef]

20. Song T, Lan Z, Ma X, Bai T. Molecular clustering physical model of steam condensation and the experimental study on the initial droplet size distribution. Int J Therm Sci. 2009;48(12):2228–36. doi:10.1016/j.ijthermalsci.2009.05.004. [Google Scholar] [CrossRef]

21. Meng T, Chen J, E J, Zhang F, Liao G, Leng E. Molecular dynamics study on the dissolution characteristics and cluster formation of Li2CO3 in supercritical water. J Mol Liq. 2023;392(2):123454. doi:10.1016/j.molliq.2023.123454. [Google Scholar] [CrossRef]

22. Yasuoka K, Matsumoto M. Molecular dynamics of homogeneous nucleation in the vapor phase. I. Lennard-Jones fluid. J Chem Phys. 1998;109(19):8451–62. doi:10.1063/1.477509. [Google Scholar] [CrossRef]

23. Gao S, Liao Q, Liu W, Liu Z. Coalescence-induced jumping of nanodroplets on textured surfaces. J Phys Chem Lett. 2018;9(1):13–8. doi:10.1021/acs.jpclett.7b02939. [Google Scholar] [PubMed] [CrossRef]

24. Xu B, Chen Z. Molecular dynamics study of water vapor condensation on a composite wedge-shaped surface with multi wettability gradients. Int Commun Heat Mass Transf. 2019;105(25):65–72. doi:10.1016/j.icheatmasstransfer.2019.03.011. [Google Scholar] [CrossRef]

25. Mo J, Wang C, Zeng J, Sha J, Li Z, Chen Y. Directional passive transport of nanodroplets on general axisymmetric surfaces. Phys Chem Chem Phys. 2022;24(16):9727–34. doi:10.1039/D1CP05905J. [Google Scholar] [PubMed] [CrossRef]

26. Niu D, Gao H, Yan Y. A discussion for the formation of cassie droplet on nanostructured surface using molecular dynamics simulation. Case Stud Therm Eng. 2021;25:100976. doi:10.1016/j.csite.2021.100976. [Google Scholar] [CrossRef]

27. Cihan A, Tokunaga TK, Birkholzer JT. Adsorption and capillary condensation-induced imbibition in nanoporous media. Langmuir. 2019;35(29):9611–21. doi:10.1021/acs.langmuir.9b00813. [Google Scholar] [PubMed] [CrossRef]

28. de la Llave E, Molinero V, Scherlis DA. Water filling of hydrophilic nanopores. J Chem Phys. 2010;133(3):034513. doi:10.1063/1.3462964. [Google Scholar] [PubMed] [CrossRef]

29. de la Llave E, Molinero V, Scherlis DA. Role of confinement and surface affinity on filling mechanisms and sorption hysteresis of water in nanopores. J Phys Chem C. 2012;116(2):1833–40. doi:10.1021/jp206580z. [Google Scholar] [CrossRef]

30. Hu H, Li Q, Liu S, Fang T. Molecular dynamics study on water vapor condensation and infiltration characteristics in nanopores with tunable wettability. Appl Surf Sci. 2019;494(1):249–58. doi:10.1016/j.apsusc.2019.07.132. [Google Scholar] [CrossRef]

31. Wang Y, Chen S, Liu Y. Spontaneous uptake of droplets into non-wetting capillaries. Comput Fluids. 2016;134:190–5. doi:10.1016/j.compfluid.2016.05.017. [Google Scholar] [CrossRef]

32. Pospíšil M, Malijevský A. Phase behavior of fluids in undulated nanopores. Phys Rev E. 2022;106(2):024801. doi:10.1103/PhysRevE.106.024801. [Google Scholar] [PubMed] [CrossRef]

33. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117(1):1–19. doi:10.1006/jcph.1995.1039. [Google Scholar] [CrossRef]

34. Yamashita K, Kashiwagi K, Agrawal A, Daiguji H. Grand canonical Monte Carlo and molecular dynamics simulations of capillary condensation and evaporation of water in hydrophilic mesopores. Mol Phys. 2017;115(3):328–42. doi:10.1080/00268976.2016.1262555. [Google Scholar] [CrossRef]

35. Tang G, Niu D, Guo L, Xu J. Failure and recovery of droplet nucleation and growth on damaged nanostructures: a molecular dynamics study. Langmuir. 2020;36(45):13716–24. doi:10.1021/acs.langmuir.0c02809. [Google Scholar] [PubMed] [CrossRef]

36. Chiu SW, Scott HL, Jakobsson E. A coarse-grained model based on Morse potential for water and n-alkanes. J Chem Theory Comput. 2010;6(3):851–63. doi:10.1021/ct900475p. [Google Scholar] [PubMed] [CrossRef]

37. Stillinger Jr FH. Rigorous basis of the frenkel-band theory of association equilibrium. J Chem Phys. 1963;38(7):1486–94. doi:10.1063/1.1776907. [Google Scholar] [CrossRef]

38. Sheng Q, Sun J, Wang Q, Wang W, Wang H. On the onset of surface condensation: formation and transition mechanisms of condensation mode. Sci Rep. 2016;6(1):1–9. doi:10.1038/srep30764. [Google Scholar] [PubMed] [CrossRef]

39. Antony AC, Liang T, Sinnott SB. Nanoscale structure and dynamics of water on Pt and Cu surfaces from MD simulations. Langmuir. 2018;34(39):11905–11. doi:10.1021/acs.langmuir.8b02315. [Google Scholar] [PubMed] [CrossRef]

40. Yang C, Li D. A method of determining the thickness of liquid-liquid interfaces. Colloids Surf A Physicochem Eng Asp. 1996;113(1–2):51–9. doi:10.1016/0927-7757(96)03544-3. [Google Scholar] [CrossRef]

41. Radiom M, Chan WK, Yang C. A study of capillary flow from a pendant droplet. Microfluid Nanofluidics. 2009;7(5):697–707. doi:10.1007/s10404-009-0429-2. [Google Scholar] [CrossRef]

42. Chan WK, Yang C. Surface-tension-driven liquid-liquid displacement in a capillary. J Micromech Microeng. 2005;15(9):1722–8. doi:10.1088/0960-1317/15/9/014. [Google Scholar] [CrossRef]

43. Marmur A. Kinetics of penetration into uniform porous media: testing the equivalent-capillary concept. Langmuir. 2003;19(14):5956–9. doi:10.1021/la034490v. [Google Scholar] [CrossRef]