 Open Access
Open Access
ARTICLE
Droplet Self-Driven Characteristics on Wedge-Shaped Surface with Composite Gradients: A Molecular Dynamics Study
1 School of Environment and Energy Engineering, Anhui Jianzhu University, Hefei, 230601, China
2 Engineering Research Center of Building Energy Efficiency Control and Evaluation, Ministry of Education, Anhui Jianzhu University, Hefei, 230022, China
3 School of Materials and Chemical Engineering, Anhui Jianzhu University, Hefei, 230601, China
4 Institute of Refrigeration & Cryogenics Engineering, Dalian Maritime University, Dalian, 116026, China
5 Shenzhen Research Institute of Shandong University, Shandong University, Shenzhen, 518057, China
* Corresponding Authors: Haowei Hu. Email: ; Mu Du. Email:
Frontiers in Heat and Mass Transfer 2024, 22(4), 1071-1085. https://doi.org/10.32604/fhmt.2024.054218
Received 22 May 2024; Accepted 19 June 2024; Issue published 30 August 2024
Abstract
The self-driven behavior of droplets on a functionalized surface, coupled with wetting gradient and wedge patterns, is systematically investigated using molecular dynamics (MD) simulations. The effects of key factors, including wedge angle, wettability, and wetting gradient, on the droplet self-driving effect is revealed from the nanoscale. Results indicate that the maximum velocity of droplets on hydrophobic wedge-shaped surfaces increases with the wedge angle, accompanied by a rapid attenuation of driving force; however, the average velocity decreases with the increased wedge angle. Conversely, droplet movement on hydrophilic wedge-shaped surfaces follows the opposite trend, particularly in terms of average velocity compared to the hydrophobic case. Both wedge-shaped and composite gradient wedge-shaped surfaces are found to induce droplet motion, with droplets exhibiting higher speeds and distances on hydrophobic surfaces compared to hydrophilic surfaces, regardless of surface type. Importantly, the inclusion of wettability gradients significantly influences droplet motion, with hydrophobic composite gradient wedge-shaped surfaces showing considerable improvements in droplet speed and distance compared to their hydrophilic counterparts. By combining suitable wettability gradients with wedge-shaped surfaces, the limitations inherent in the wettability gradient range and wedge-shaped configuration can be mitigated, thereby enhancing droplet speed and distance. The findings presented in this paper offer valuable insights for the design of advanced functional surfaces tailored for manipulating droplets in real-world applications.Keywords
Nomenclature
| E | Interactions between water molecules (eV) |
| F | Driving force acting on the droplet (mN) |
| l | Chord length (m) |
| q | Atomic charge (e) |
| r | Atomic distance (Å) |
| Greek symbols | |
| β | Energy coefficient |
| γ | Interface tension (mN/m) |
| ε | Energy parameter |
| ε0 | Vacuum permittivity |
| θ | Static contact angle (°) |
| σ | Distance parameter |
| Subscripts | |
| 1 | Wedge-shaped surface |
| 2 | Wettability gradient surface |
| f | The front edge of the droplet |
| i,j | Relative atoms |
| LG | Liquid−gas |
| r | The rear edge of the droplet |
Self-driven droplet transport on a solid surface is a frequent natural occurrence, as illustrated by water droplets adhering to spider silk, which autonomously travel from the narrow to wide ends of its spindle knot [1,2]. Similarly, fog droplets captured by conical needles presented on cactus surfaces self-drive and move directionally towards the wide end of the needles [3,4]. Due to its energy-free operation, self-driven directional liquid transport has garnered considerable interest for various applications, such as condensers [5], fog collection [6,7], microfluidic devices [8,9], and so forth. Researchers, inspired by the phenomenon of liquid self-driven transport in nature, have created various biomimetic structures in an attempt to apply droplet self-driven transport to scientific research and industrial fields. Structural gradients [10–13] and wetting gradients [14–16] are key to enabling these structures to drive droplet motion without external energy input. The self-driven vehicle of droplets caused by wetting gradients was first proposed by Greenspan [17] and was studied in detail theoretically. Subsequently, in their experiments, Chaudhury et al. [18] were the first to observe the droplet transport process on surfaces with wetting gradients. Subramanian et al. [19] analyzed the sources of driving force involved in the movement of droplets driven by wetting gradient on solid surfaces and predicted the quasi-steady-state velocity of droplets under different wetting gradients. Chaudhury et al. [20] explored different mechanisms of droplet transport on solid surfaces and presented several techniques for creating wetting gradient surfaces. Huang et al. [21] investigated the behavior of self-propelled droplets and the role of precursor films in inducing the motion of static droplets. Zhang et al. [22] patterned a trapezoidal hydrophilic material onto a hydrophobic substrate, causing droplets to spontaneously spread from the narrow end of the trapezoid to the wider end. Khoo et al. [23] prepared triangular-shaped superhydrophobic substrates on superhydrophilic tracks on super-hydrophobic substrates with droplet spreading velocities of 50–400 mm/s. Ghosh et al. [24] presented a method for creating open microfluidic tracks using a wettability patterning technique, which could transport various liquid volumes on-chip, with applications in low-cost biomedical diagnostic devices. Feng et al. [25] conducted experiments to examine the impact of wettability gradients and triangular geometries on water condensation and transport, aiming to enhance the efficiency of water collection and storage.
Uncovering micro-mechanisms behind macro-performance drivers is essential to provide theoretical foundations for material preparation or structural processing. As a critical tool in modern scientific research, MD simulations play a pivotal role across materials science, physics, chemistry, biology, and environmental studies. Niu et al. [26] conducted simulations to explore how heat flux, surface wettability, and the size of neighboring droplets impact the nucleation and growth of droplets during the condensation process on solid surfaces. Hu et al. [27] simulated the condensation process of water vapor in a single nanopore with adjustable surface wettability, studied in detail the characteristics and dynamic behavior of water vapor adsorption and condensation in hydrophobic and hydrophilic nanopores, and quantitatively calculated the capillary pressure of hydrophobic nanopores with different sizes and surface wettability. MD simulations have also been used by researchers to study nanoscale droplet self-driven transport. Pu et al. [28] studied the growth and autonomous movement dynamics of individual condensed nanodroplets on nanostructured surfaces, uncovering the influence of Laplace pressure variation in initiating droplet detachment and self-propulsion. Guo et al. [29] employed the dissipative particle dynamics (DPD) approach to simulate and theoretically analyze droplet behavior on conical fibers with diverse cross-sectional geometries. They suggested a conical fiber featuring a tri-concave cross-section, which enhanced both the speed and displacement of droplets compared to traditional circular fibers. Subsequently, they proposed a strategy using conical grooves to achieve precise manipulation and autonomous motion control of nanodroplets [30]. Xu et al. [31] investigated the mechanism behind droplet movement on multi-gradient wedge surfaces and simulated how the gravity field influences self-driven droplet transport on a microscale. The findings revealed that as gravity increased, the average droplet speed initially rose and then declined, with this relationship following a nonlinear fitting curve.
Wang et al. [32] employed MD simulation to examine the impact of wedge angle and droplet size on the behavior of droplet movement on wedge-shaped surfaces, proposing various functional surface designs to control droplet movement. Mahmood et al. [33] utilized MD simulation to investigate the spontaneous propulsion of droplets due to wetting gradients, specifically the self-propulsion of water droplets on multi-gradient surfaces with varying surface energy parameters. They discovered that wedge-shaped surfaces facilitated the spontaneous propulsion of water droplets more effectively than parallel-shaped surfaces. Diewald et al. [34] applied both MD simulation and Phase Field (PF) simulation to analyze the movement of nanoscale droplets on surfaces with wetting gradients, comparing the outcomes of the two simulations. The findings indicated that for two droplets on distinct surfaces at different temperatures, the time evolution of the centroid and the droplets’ velocity were consistent between MD and PF simulations. Hu et al. [35] investigated the self-propulsion dynamics of nanosized water droplets (NWDs) on MoS2/graphene heterojunction surfaces using molecular dynamics simulations. The study reveals that single NWD moves at an average velocity of 5 m/s, resembling a locomotive towing a carriage, while double NWDs exhibit a gluttonous snake-like motion with velocities between 6.0 and 9.0 m/s due to hydrogen bonding interactions. Insights from their research could aid in designing and fabricating surfaces for applications requiring self-propelled nanoscale droplets. Potential applications include self-powering actuators, enhanced oil recovery, and drug delivery systems.
In current studies of droplet self-driven transportation, the self-driven effect of droplets on structured gradient surfaces is constrained by the shape of the structure, while on wetted gradient surfaces, it is limited by the range of wettability. Although previous studies have investigated the self-driven behavior of droplets on structural gradient surfaces, wettability gradient surfaces, and some composite gradient surfaces, there are still shortcomings in the research on the self-driven transport of droplets on nanoscale composite gradient wedge-shaped surfaces. This study employs MD simulation to examine the effects of wedge-shaped surfaces combined with wetting gradients on self-driven droplet transport. A surface integrating wedge-shaped structures and wetting gradients was designed. By simulating various surface parameters and wetting gradients, the study analyzed the speed and displacement distance of droplets, investigating the impact of different wedge angles, wettability levels, and wetting gradients on self-driven droplets. This research enhances the understanding of microscale self-driven droplet transport and aids in designing more efficient functional surfaces for directional droplet movement.
In this study, MD simulations are implemented with an open-source software Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [36]. The initial model of the simulated system is shown in Fig. 1. The simulated box is established with a size of 200 Å × 600 Å × 200 Å. Periodic boundary conditions are used in the x, y, and z directions. A spherical droplet with an initial diameter of 80 Å consisting of 8636 water molecules is located 3.5 Å above a surface composed of 92130 Face-Centered Cubic (FCC) arranged Cu atoms.

Figure 1: Models of droplet movement on different surfaces. (a) Wedge-shaped surface; (b) Composite gradient wedge-shaped surface
The water droplet is treated using the SPC/E model [37] with the SHAKE algorithm [38]. Water molecules are composed of an oxygen atom (−0.8476e) and two hydrogen atoms (+0.4328e) with an angle of 109.47° between them. The non-bonding interaction consists of van der Waals forces described by the 12-6LJ potential [39] and long-range Coulombic forces as follows:
E=4εij[(σijrij)12−(σijrij)6]+qiqj4πε0rij(1)
where εij=0.006734447 eV is the energy parameter of the LJ potential signifying the interaction intensity between particles, and σ=3.166 Å is the distance parameter of the LJ potential. qi and qj are the partial atomic charge of atom i and j, respectively, and ε0 is the vacuum permittivity.
The interaction between wall atoms and water molecules is also described by 12-6 LJ potential energy, and the corresponding parameters εij, σij are calculated according to the Lorentz-Bertholet mixing law as follows:
εij=β√εiεj(2)
σij=(σi+σj)2(3)
where εi and σi are the energy and scale parameters between the Cu atoms. εj and σj are the energy parameters and scale parameters between oxygen atoms. β is the energy coefficient of the interaction between wall atoms and water molecules.
To quantitatively represent the surface wettability of droplets at different energy coefficients, droplets on smooth Cu atomic walls at different β were simulated as shown in Fig. 2a. Before the droplet contacts the wall surface, The NVT (constant number of particles N, constant volume V, and continuous temperature T) ensemble is applied to the entire system. The system’s temperature was controlled to 300 K and stabilized using a Nose-Hoover thermostat [40]. The velocity equation was solved using the Verlet method. The Cu atoms were fixed at their original lattice positions to prevent vibration from changing the wall structure. After sufficient relaxation, the average density cloud map of the droplets after 0.5 ns was obtained, and the resulting contact angle was measured as a reference for surface wettability [41–43]. The results are presented graphically in Fig. 2b. The energy coefficient α between the wall atoms and water molecules ranged from 0.03 to 0.38. The corresponding contact angle changed from 167° to 10°, indicating a hydrophobic to hydrophilic range of wettability.

Figure 2: (a) Wetting behavior of droplets on a smooth plane; (b) The surface contact angle of droplets at different β
Similarly, at a system temperature of 300 K, the centroid of the initial droplet is located 3.5 Å above the apex of the wedge-shaped surface. The time step is 5 fs, running for 1,000,000 steps, with a total simulation duration of 5000 ps.
The model of the initial droplet on different surfaces is shown in Fig. 1, where Fig. 1a represents the wedge-shaped surface, and Fig. 1b represents the composite gradient wedge-shaped surface. The wedge angle α is set to 5°, 10°, 15°, and 20°. The gray and yellow areas represent weak wettability and strong wettability respectively. The wettability of different surfaces is characterized using the contact angle (θ), with the wedge-shaped surface divided into Group A (160°−100°), Group B (120°−60°), and Group C (80°−20°). On the composite gradient wedge-shaped surface, the wedge area is combined with multiple wettability gradients. The gray area represents weak wettability, and areas a, b, c, d represent wettability gradient areas with a surface contact angle difference of 10°, divided into Group AW (160°−130°−120°−110°−100°), Group BW (120°−90°−80°−70°−60°), and Group CW (80°−50°−40°−30°−20°).
The forces acting on the droplet on the wedge-shaped surface and the wettability gradient surface are shown in Fig. 3. The wedge structure of the wedge-shaped surface is the main source of driving force for the droplet. As shown in Fig. 3a, the driving force of the droplet on the wedge-shaped surface is influenced by the wedge angle, the wettability of the inner/outer areas, and the radius of the droplet [11]:
F1=l1γLG{(cosθ−cosθ0)+[cosθr(x)−cosθf(x)]}(4)
where l1 is the chord length. γLG denotes the liquid−gas interface tension. θ0 and θ denote the static contact angles in the superhydrophobic and wedge-shaped regions, respectively. θr(x) and θf(x) denote the maximum instant contact angles at the rear edge and front edge.

Figure 3: (a) Schematic diagram of droplet movement on the wedge-shaped surfaces; (b) Schematic diagram of droplet movement on the wetting gradient surface
On the wettability gradient surface, due to the traction of the unbalanced surface tension, the droplet moves towards the side with stronger wettability on the wettability gradient. As shown in Fig. 3b, this force can be represented by the difference in contact angles between the strong and weak wettability surfaces [44]:
F2=l2γLG{[cosθf−cosθf(t)]f−[cosθr−cosθr(t)]r}(5)
where l2 denote the contact length. γLG denote the liquid−gas interface tension. θf and θr denote the maximum instant contact angles at the front edge and rear edge, respectively. θf(t) and θr(t) are the dynamic contact angles at the front and rear edges, both of which are functions of the time t.
3.1 Movement of Droplets on Homogeneous Wedge-Shaped Surfaces
The aforementioned model was utilized to compute and compare the self-driven motion of water droplets on various wedge-shaped surfaces. As illustrated in Fig. 1a, the wettability of the outer side and the wedge-shaped area is categorized into Group A (160°−100°), Group B (120°−60°), and Group C (80°−20°), with the wedge angle α set at 5°, 10°, 15°, and 20°. Group A corresponds to hydrophobic-hydrophobic surfaces, Group B corresponds to hydrophobic-hydrophilic surfaces, and Group C corresponds to hydrophilic-hydrophilic surfaces. Upon contact with the surface, the droplet gradually spreads onto the wedge-shaped area. Due to the varying wettability of the inner and outer areas of the wedge, and the increasing width of the wedge in the direction of flow, the droplet spontaneously moves towards the wider end of the wedge. The study first analyzes the movement speed of the droplet in the x direction. As shown in Fig. 4, the results reveal that the wedge angle and wettability significantly impact the movement speed of the droplet. It can be observed that after the droplet begins to move, its speed sharply increases to a peak in the initial stage and then rapidly decreases. This is because the driving force received by the droplet rapidly increases in the initial stage and then decays as the center of mass of the droplet moves towards the wider end of the wedge. The second speed peak in Group A in Fig. 4a is due to the droplet moving to the rectangular area on the right in Fig. 1.

Figure 4: Velocity of a droplet moving in the x direction under different wedge angles and wettability. (a) α = 5°; (b) α = 10°; (c) α = 15°; (d) α = 20°
When considering Figs. 4 and 5, with consistent wetting properties, the peak velocity of droplets increases as the wedge angle enlarges, while the average velocity decreases with a larger wedge angle. As depicted in Fig. 5, the average velocity of Group A droplets declines with increasing wedge angle, whereas the average velocity of Group C droplets rises. However, for Group B, the average velocity initially rises and then falls with increasing wedge angle, with a turning point around 10°. This phenomenon occurs because the hydrophilic surface enhances the spreading capability of liquid droplets, maintaining a larger contact area with both the inner and outer regions of the wedge-shaped surface. Fig. 6 illustrates that the difference in contact angle between the leading and trailing edges of the droplet widens as the wedge angle increases, thus boosting the driving force on the droplet. Consequently, a larger wedge angle results in higher average velocity and displacement for droplets on hydrophilic surfaces. On the other hand, for hydrophobic surfaces, an increased wedge angle leads to a higher peak velocity initially due to a larger contact area with the inner side of the wedge, allowing the droplet to quickly move to the wider end. However, their driving force diminishes rapidly, causing a decrease in average velocity and an earlier cessation of movement. For Group B, a turning point around 10° is observed on the hydrophilic-hydrophobic wedge-shaped surface, leading to the fastest velocity.
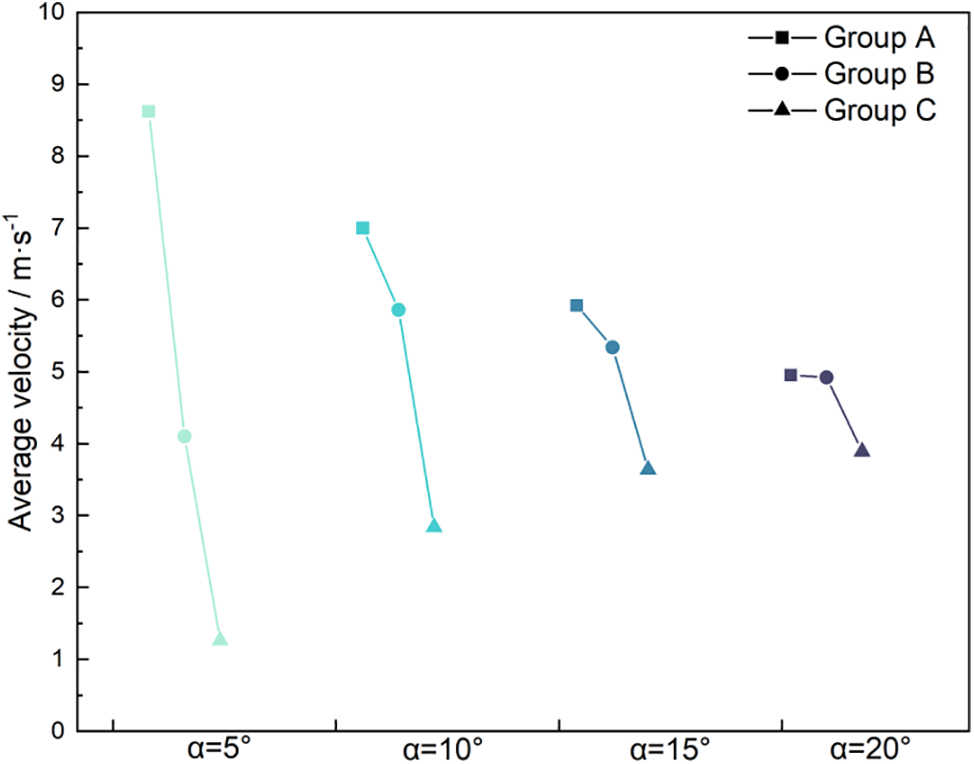
Figure 5: Average velocity of droplets at different wedge angles and wettability
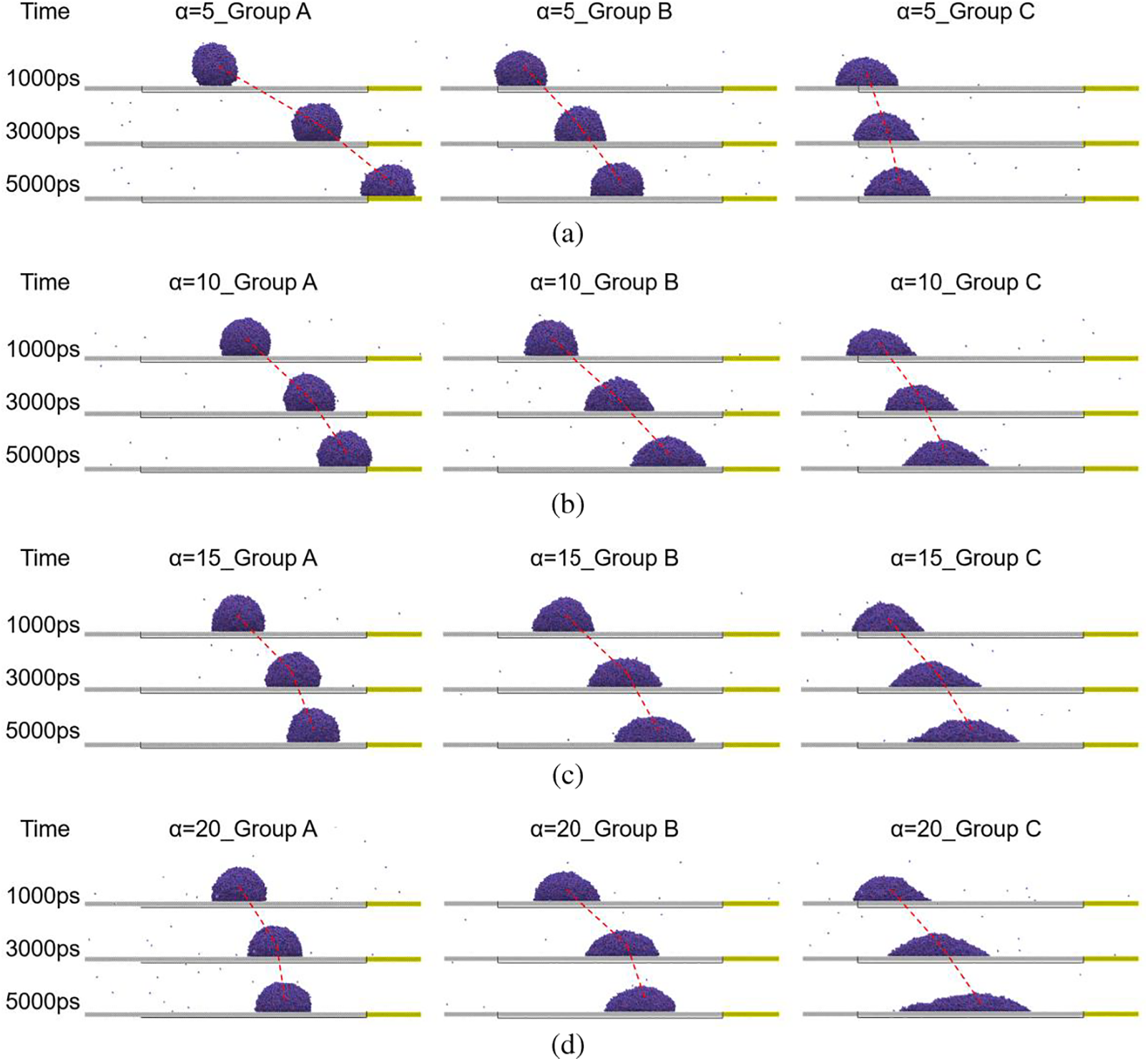
Figure 6: Snapshots of droplet at 1000, 3000 and 5000 ps on different wedge-shape surfaces, (a) α = 5°; (b) α = 10°; (c) α = 15°; (d) α = 20°
At a 5° wedge angle, significant variations in the average moving speed of droplets are observed among Groups A, B, and C, but this disparity diminishes as the wedge angle increases to 20°. As depicted in Fig. 4a, the speed of Group A droplets stabilizes within a certain range after reaching an initial peak at a 5° angle, while the speeds for Groups B and C decline towards zero, significantly slower than those of Group A. Conversely, Fig. 4d illustrates that the speeds for droplets in all groups sharply decline to near zero after peaking, suggesting that the droplets traverse only a short distance before nearly halting. Consequently, there is minimal difference in average speed and maximum displacement distance at a 20° wedge angle, as illustrated in Fig. 5. Although the average moving speed of droplets generally decreases with increasing wedge angles due to lower resistance on hydrophobic surfaces compared to hydrophilic ones, the speed and displacement of Group A droplets remain higher than those of Groups B and C at equivalent angles. This suggests that droplets on hydrophobic surfaces tend to move more easily and cover greater distances under similar conditions.
3.2 Movement of Droplets on Composite Gradient Wedge-Shaped Surfaces
To explore the combined influence of Laplace pressure differences and wettability gradients on droplet motion, researchers constructed a composite gradient wedge-shaped surface by integrating wedge-shaped patterns with gradients of wettability. Fig. 1b illustrates this wedge-shaped surface, highlighting four distinct levels of wettability gradient. Additionally, the contact angle at the terminal rectangular area aligns with that observed in the control group. The wettability gradient of each level increases by 10° from right to left. Group AW (160°−130°−120°−110°−100°) corresponds to the hydrophobic surface, Group BW (120°−90°−80°−70°−60°) corresponds to the hydrophobic-hydrophilic surface, and Group CW (80°−50°−40°−30°−20°) corresponds to the hydrophilic surface. The movement of droplets on different surfaces is compared and analyzed.
In Fig. 7, the fluctuations in the curve are due to the driving force generated by the differences in surface energy as the droplet crosses the boundaries of the wettability gradient. This results in a sudden increase in the droplet’s velocity. As the droplet continues across the boundary, the driving force rapidly diminishes, causing a swift decrease in its velocity. Fig. 7a demonstrates that the droplet on the composite gradient wedge-shaped surface takes a longer time to reach its peak speed in the initial stage than on the wedge-shaped surface. The droplet attains the peak speed while it is crossing the first wettability gradient, with a slightly lowered peak speed. The inset in Fig. 7 illustrates the position of the droplet at the first velocity peak for the group AW as it crosses the first wettability gradient. The speed of the droplet decreases more gently after it reaches the peak. The droplet experiences multiple accelerations due to the wettability gradient, which leads to significant speed fluctuations that are still visible after 2000 ps. Similarly, Fig. 7b shows the instantaneous velocity of the droplets in the group BW, Fig. 7c shows the instantaneous velocity of the droplets in the group CW, and Fig. 7d shows the instantaneous velocity of the droplets in the group DW.

Figure 7: The velocity of a droplet moving in the x direction on composite gradient wedge-shaped surfaces. (a) α = 5°; (b) α = 10°; (c) α = 15°; (d) α = 20°
As illustrated in Fig. 8, under varying wedge angles, the movement of droplets on the composite gradient wedge-shaped surface is significantly affected by surface wettability in comparison to the wedge-shaped surface alone. Each frame in Fig. 9 represents the displacement of the droplet over a 2000 ps interval, which also illustrates the self-driven effect of the droplet on different surfaces. The dashed lines in Fig. 9 connect the centroids of the droplets. The angles of these dashed lines indicate that the droplet’s movement is primarily concentrated in the early or later stages, reflecting the sustained motion capability of the droplet on different surfaces. The average velocity of droplets in Group CW resembles that of Group C, showing a gradual increase as the wedge angle becomes larger. However, the average velocity of droplets moving in Group CW decreases overall compared to Group C at all wedge angles. This indicates that the hydrophilic composite gradient wedge-shaped surface drives droplet movement less effectively than the wedge-shaped surface. This is due to the small wettability gradient difference on the composite gradient wedge-shaped surface, resulting in a smaller driving force for droplets on hydrophilic surfaces. In contrast, the average velocity of Group AW also decreases gradually with the increase of wedge angle like Group A. However, the average velocity of droplets moving in Group AW significantly improved compared to Group A. The small improvement in Group AW, when the wedge angle is 5°, is because the droplet has moved to the end of the model and cannot continue to move forward. This indicates that the hydrophobic composite gradient wedge-shaped surface drives droplet movement more effectively than the wedge-shaped surface. This is because the composite gradient wedge-shaped surface overcomes a significant disadvantage of the wedge-shaped surface under hydrophobic conditions and does not lose driving force due to the premature entry of droplets into the inner side of the wedge.
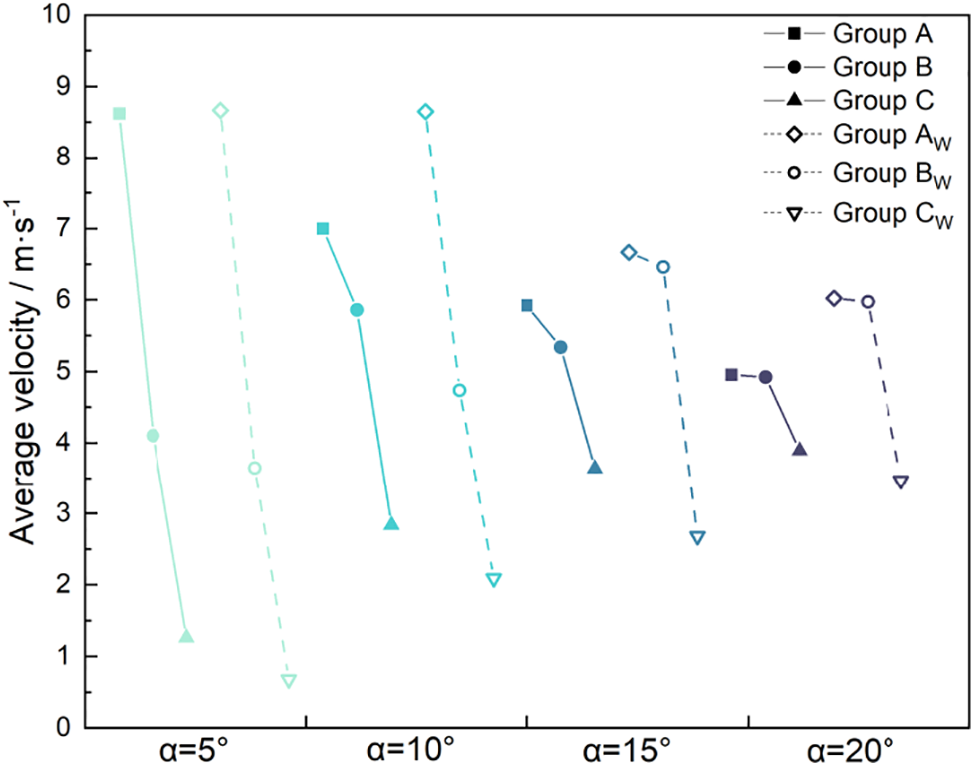
Figure 8: Average velocity of droplets on wedge-shaped surfaces and composite gradient wedge-shaped surfaces
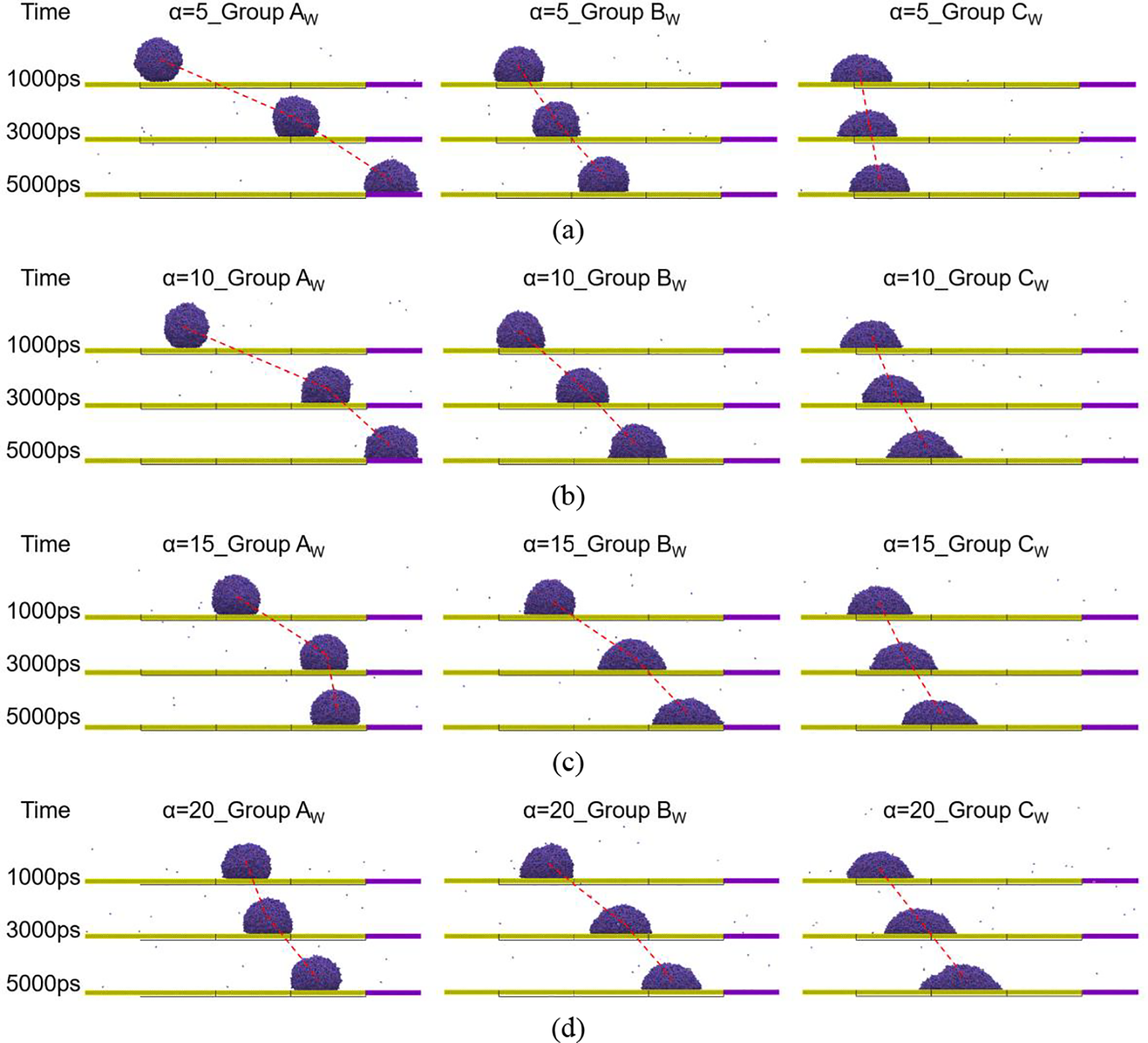
Figure 9: Snapshots of droplet at 1000, 3000 and 5000 ps on different composite gradient wedge-shaped surfaces, (a) α = 5°; (b) α = 10°; (c) α = 15°; (d) α = 20°
Due to the addition of a wettability gradient, although the peak velocity of droplets on composite gradient wedge-shaped surfaces decreases slightly, they can accelerate multiple times, greatly improving their ability to sustain movement. The average velocity of droplet movement in Group BW first increases and then decreases with increasing wedge angle, similar to Group B, but its peak value occurs near a 15° angle. When the wedge angle is 5° and 10°, the average velocity of droplet movement in Group BW is lower than in Group B. However, when the wedge angle is 15° and 20°, the average velocity of droplet movement in Group BW is higher than in Group B. This indicates an inflection point for average droplet movement on a hydrophobic-to-hydrophilic composite gradient wedge-shaped surface. The inflection point shifts to a higher wedge angle on a composite gradient wedge-shaped surface, causing droplets to move faster than on a wedge-shaped surface at 15° and 20°. Due to the combined effect of the wettability gradient and Laplace pressure difference, hydrophilic composite gradient wedge-shaped surfaces slightly reduce droplet movement ability. In contrast, hydrophobic composite gradient wedge-shaped surfaces can continue to accelerate after reaching their initial peak velocity, significantly increasing both maximum displacement distance and average velocity. Hydrophobic-to-hydrophilic composite gradient wedge-shaped surfaces exhibit optimal droplet movement near a 15° wedge angle.
Using the method of molecular dynamics simulation, the motion of nanoscale droplets on wedge-shaped surfaces and composite gradient wedge-shaped surfaces was studied. The effects of different wetting gradients and wedge angles on droplet velocity and displacement were compared. The results showed that on hydrophobic wedge-shaped surfaces, the velocity of droplets decreased with an increase in wedge angle, while on hydrophilic wedge-shaped surfaces, the velocity increased with an increase in wedge angle. On surfaces with both hydrophilic and hydrophobic regions, the droplet velocity first increased and then decreased with an increase in wedge angle, and a turning point occurred at around 10° of wedge angle. The introduction of the wetting gradient to the wedge-shaped surface resulted in a slight decrease in droplet motion capability on the hydrophilic composite gradient wedge-shaped surface. The hydrophobic-hydrophilic composite gradient wedge-shaped surface had a peak value of the average velocity of droplets at around 15° of wedge angle. A driving effect increase was observed for larger wedge angles (15°, 20°) compared to that of the typical wedge-shaped surface. The peak velocity of droplet motion slightly decreased on a hydrophobic composite gradient wedge-shaped surface; however, the average velocity and displacement distance increased significantly, resulting in the highest driving effect. Furthermore, the effect of driving droplets on the hydrophobic surface was always better than that on the hydrophilic surface on both surfaces. These results indicate that composite gradient wedge surfaces with specific wettability can significantly enhance the self-driving effect of droplets, enabling them to move faster and farther than single wedge surfaces.
Acknowledgement: The authors would like to sincerely thank Anhui Jianzhu University, Dalian Maritime University, and Shandong University for providing laboratory facilities support and financial support.
Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 52206073), the University Outstanding Youth Fund Project of Anhui Province (Nos. 2022AH020028 and 2022AH030037), the Natural Science Foundation of Anhui Province (Nos. 1908085QF292 and 2308085ME173), Anhui Province Outstanding Young Talents Support Program (No. gxyqZD2022058), Guangdong Basic and Applied Basic Research Foundation (Nos. 2024A1515011379 and 2023A1515110613).
Author Contributions: The authors confirm contribution to the paper as follows: funding acquisition, conceptualization, Haowei Hu; writing—original draft, data curation, Xinnuo Chen; methodology, Qi Wang, Qin Li; conceptualization, methodology, writing—review & editing, Dong Niu; investigation, writing—review & editing, Mu Du. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data can be provided on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zheng Y, Bai H, Huang Z, Tian X, Nie F, Zhao Y, et al. Directional water collection on wetted spider silk. Nature. 2010;463(7281):640–3. doi:10.1038/nature08729. [Google Scholar] [PubMed] [CrossRef]
2. Zhang S, Huang J, Chen Z, Lai Y. Bioinspired special wettability surfaces: from fundamental research to water harvesting applications. Small. 2017;13(3):1602992. doi:10.1002/smll.201602992. [Google Scholar] [PubMed] [CrossRef]
3. Ju J, Bai H, Zheng Y, Zhao T, Fang R, Jiang L. A multi-structural and multi-functional integrated fog collection system in cactus. Nat Commun. 2012;3(1):1247. doi:10.1038/ncomms2253. [Google Scholar] [PubMed] [CrossRef]
4. Fan B, Wu J, Gong G, Guo L. Biomimetic “cactus spine” with hierarchical groove structure for efficient fog collection. Adv Sci. 2015;2(7):1500047. doi:10.1002/advs.201500047. [Google Scholar] [PubMed] [CrossRef]
5. Park KC, Kim P, Grinthal A, He N, Weaver JC, Aizenberg J. Condensation on slippery asymmetric bumps. Nature. 2016;531(7592):78–82. doi:10.1038/nature16956. [Google Scholar] [PubMed] [CrossRef]
6. Chen H, Ran T, Gan Y, Zhou J, Zhang Y, Zhang D, et al. Ultrafast water harvesting and transport in hierarchical micro-channels. Nat Mater. 2018;17(10):935–42. doi:10.1038/s41563-018-0171-9. [Google Scholar] [PubMed] [CrossRef]
7. Chen Y, Zheng Y. Bioinspired micro-/nanostructure fibers with a water collecting property. Nanoscale. 2014;6(14):7703–14. doi:10.1039/c4nr02064b. [Google Scholar] [PubMed] [CrossRef]
8. Kai H, Toyosato R, Nishizawa M. Space-filling open microfluidic channels designed to collect water droplets. RSC Adv. 2018;8(29):15985–90. doi:10.1039/C8RA02655F. [Google Scholar] [PubMed] [CrossRef]
9. Hoseinpour B, Sarreshtehdari A. Lattice Boltzmann simulation of droplets manipulation generated in lab-on-chip (LOC) micro-fluidic T-junction. J Mol Liq. 2020;297:111736. doi:10.1016/j.molliq.2019.111736. [Google Scholar] [CrossRef]
10. Bai H, Tian X, Zheng Y, Ju J, Zhao Y, Jiang L. Direction controlled driving of tiny water drops on bioinspired artificial spider silks. Adv Mater. 2010;48(22):5521–5. doi:10.1002/adma.201003169. [Google Scholar] [PubMed] [CrossRef]
11. Lv C, Chen C, Chuang YC, Tseng FG, Yin Y, Grey F, et al. Substrate curvature gradient drives rapid droplet motion. Phys Rev Lett. 2014;113(2):026101. doi:10.1103/PhysRevLett.113.026101. [Google Scholar] [PubMed] [CrossRef]
12. Liu M, Yao Y, Li JJ, Peng ZL, Chen S. Directional sliding behavior of a water droplet on a wedge-shape patterned functional surface. J Phys Chem B. 2020;124(31):6905–12. doi:10.1021/acs.jpcb.0c02757. [Google Scholar] [PubMed] [CrossRef]
13. Guo L, Tang GH. Experimental study on directional motion of a single droplet on cactus spines. Int J Heat Mass Transf. 2015;84:198–202. doi:10.1016/j.ijheatmasstransfer.2014.12.072. [Google Scholar] [CrossRef]
14. Hou YP, Feng SL, Dai LM, Zheng YM. Droplet manipulation on wettable gradient surfaces with micro-/nano-hierarchical structure. Chem Mater. 2016;28(11):3625–9. doi:10.1021/acs.chemmater.6b01544. [Google Scholar] [CrossRef]
15. Lu Y, Shen Y, Tao J, Wu Z, Chen H, Jia Z, et al. Droplet directional movement on the homogeneously structured superhydrophobic surface with the gradient non-wettability. Langmuir. 2020;36(4):880–8. doi:10.1021/acs.langmuir.9b03411. [Google Scholar] [PubMed] [CrossRef]
16. Chakraborty M, Chowdhury A, Bhusan R, DasGupta S. Molecular dynamics study of thermally augmented nanodroplet motion on chemical energy induced wettability gradient surfaces. Langmuir. 2015;31(41):11260–8. doi:10.1021/acs.langmuir.5b03041. [Google Scholar] [PubMed] [CrossRef]
17. Greenspan H. On the motion of a small viscous droplet that wets a surface. J Fluid Mech. 1978;84(1):125–43. doi:10.1017/S0022112078000075. [Google Scholar] [CrossRef]
18. Chaudhury MK, Whitesides GM. How to make water run uphill. Science. 1992;256(5063):1539–41. doi:10.1126/science.256.5063.1539. [Google Scholar] [PubMed] [CrossRef]
19. Subramanian RS, Moumen N, McLaughlin JB. Motion of a drop on a solid surface due to a wettability gradient. Langmuir. 2005;21(25):11844–9. doi:10.1021/la051943i. [Google Scholar] [PubMed] [CrossRef]
20. Chaudhury MK, Chakrabarti A, Daniel S. Generation of motion of drops with interfacial contact. Langmuir. 2015;31(34):9266–81. doi:10.1021/la504925u. [Google Scholar] [PubMed] [CrossRef]
21. Huang H, Nuthalapati K, Sheng Y, Tsao H. Precursor film of self-propelled droplets: inducing motion of a static droplet. J Mol Liq. 2022;368:120729. doi:10.1016/j.molliq.2022.120729. [Google Scholar] [CrossRef]
22. Zhang J, Han Y. Shape-gradient composite surfaces: water droplets move uphill. Langmuir. 2007;23(11):6136–41. doi:10.1021/la063376k. [Google Scholar] [PubMed] [CrossRef]
23. Khoo HS, Tseng FG. Spontaneous high-speed transport of subnanoliter water droplet on gradient nanotextured surfaces. Appl Phys Lett. 2009;95(6):063108. doi:10.1063/1.3197574. [Google Scholar] [CrossRef]
24. Ghosh A, Ganguly R, Schutziusac TM, Megaridis CM. Wettability patterning for high-rate, pumpless fluid transport on open, non-planar microfluidic platforms. Lab Chip. 2014;14(9):1538–50. doi:10.1039/C3LC51406D. [Google Scholar] [PubMed] [CrossRef]
25. Feng W, Bhushan B. Multistep wettability gradient in bioinspired triangular patterns for water condensation and transport. J Colloid Interface Sci. 2020;560:866–73. doi:10.1016/j.jcis.2019.10.113. [Google Scholar] [PubMed] [CrossRef]
26. Niu D, Tang GH. Molecular dynamics simulation of droplet nucleation and growth on a rough surface: revealing the microscopic mechanism of the flooding mode. RSC Adv. 2018;8(43):24517–24. doi:10.1039/C8RA04003F. [Google Scholar] [PubMed] [CrossRef]
27. Hu HW, Li Q, Liu S, Fang TY. Molecular dynamics study on water vapor condensation and infiltration characteristics in nanopores with tunable wettability. Appl Surf Sci. 2019;494:249–58. doi:10.1016/j.apsusc.2019.07.132. [Google Scholar] [CrossRef]
28. Pu JH, Wang SK, Sun J, Wang W, Wang HS. Growth and self-jumping of single condensed droplet on nanostructured surfaces: a molecular dynamics simulation. J Mol Liq. 2021;340:116902. doi:10.1016/j.molliq.2021.116902. [Google Scholar] [CrossRef]
29. Guo L, Kumar S, Yang M, Tang GH, Liu Z. Role of the microridges on cactus spines. Nanoscale. 2022;14(2):525–33. doi:10.1039/D1NR05906H. [Google Scholar] [PubMed] [CrossRef]
30. Guo L, Sheng Q, Kumar S, Liu ZG, Tang GH. Lubricant-induced tunability of self-driving nanodroplets on conical grooves. J Mol Liq. 2023;373:121149. doi:10.1016/j.molliq.2022.121149. [Google Scholar] [CrossRef]
31. Xu B, Chen Z. Droplet movement on a composite wedge-shaped surface with multi-gradients and different gravitational field by molecular dynamics. Microgravity Sci Technol. 2018;30:571–9. doi:10.1007/s12217-018-9641-6. [Google Scholar] [CrossRef]
32. Wang S, Wang C, Peng Z, Chen SH. Moving behavior of nanodroplets on wedge-shaped functional surfaces. J Phys Chem C. 2019;123(3):1798–805. doi:10.1021/acs.jpcc.8b09831. [Google Scholar] [CrossRef]
33. Mahmood A, Chen S, Chen L, Chen C, Liu D, Weng D, et al. Spontaneous propulsion of a water nanodroplet induced by a wettability gradient: a molecular dynamics simulation study. Phys Chem Chem Phys. 2020;22(8):4805–14. doi:10.1039/C9CP06718C. [Google Scholar] [PubMed] [CrossRef]
34. Diewald F, Lautenschlaeger MP, Stephan S, Langenbach K, Kuhn C, Seckler S, et al. Molecular dynamics and phase field simulations of droplets on surfaces with wettability gradient. Comput Methods Appl Mech Eng. 2020;361:112773. doi:10.1016/j.cma.2019.112773. [Google Scholar] [CrossRef]
35. Hu C, Song XY, Cai JG, Chao L, Zeng N, Liu AJ, et al. Self-propulsion dynamics of nanosized water droplets on MoS2/graphene heterojunction surface: a molecular dynamics simulation study. Appl Surf Sci. 2022;596:153583. doi:10.1016/j.apsusc.2022.153583. [Google Scholar] [CrossRef]
36. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117(1):1–19. doi:10.1006/jcph.1995.1039. [Google Scholar] [CrossRef]
37. Berendsen HJC, Grigera JR, Straatsma TP. The missing term in effective pair potentials. J Phys Chem. 1987;91(24):6269–71. doi:10.1021/j100308a038. [Google Scholar] [CrossRef]
38. Ryckaer JP, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comput Phys. 1977;23(3):327–41. doi:10.1016/0021-9991(77)90098-5. [Google Scholar] [CrossRef]
39. Adams P, Henderson JR. Molecular dynamics simulations of wetting and drying in LJ models of solid-fluid interfaces in the presence of liquid-vapour coexistence. Mol Phys. 1991;73(6):1383–99. doi:10.1080/00268979100101991. [Google Scholar] [CrossRef]
40. Hoover WG. Canonical dynamics: equilibrium phase-space distributions. Phys Rev A. 1985;31(3):1695. doi:10.1103/PhysRevA.31.1695. [Google Scholar] [PubMed] [CrossRef]
41. Niu D, Tang GH. Static and dynamic behavior of water droplet on solid surfaces with pillar-type nanostructures from molecular dynamics simulation. Int J Heat Mass Transf. 2014;79:647–54. doi:10.1016/j.ijheatmasstransfer.2014.08.047. [Google Scholar] [CrossRef]
42. Niu D, Tang GH. The effect of surface wettability on water vapor condensation in nanoscale. Sci Rep. 2016;6(1):19192. doi:10.1038/srep19192. [Google Scholar] [PubMed] [CrossRef]
43. Sheng Q, Sun J, Wang Q, Wang W, Wang HS. On the onset of surface condensation: formation and transition mechanisms of condensation mode. Sci Rep. 2016;6(1):30764. doi:10.1038/srep30764. [Google Scholar] [PubMed] [CrossRef]
44. Liu M, Huang LY, Yao Y, Peng ZL, Chen SH. Dynamic behavior of a droplet across a hydrophobic and hydrophilic boundary. J Phys Chem C. 2019;123(38):23505–10. doi:10.1021/acs.jpcc.9b06323. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
