 Open Access
Open Access
ARTICLE
Enhanced Evaporation of Ternary Mixtures in Porous Medium with Microcolumn Configuration
1 Technology Center, China Tobacco Hunan Industrial Co., Ltd., Changsha, 410007, China
2 School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
3 School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai, 201418, China
* Corresponding Author: Zhenyu Liu. Email:
(This article belongs to the Special Issue: Fluid Flow, Heat and Mass Transfer within Novel Cooling Structures)
Frontiers in Heat and Mass Transfer 2024, 22(4), 997-1016. https://doi.org/10.32604/fhmt.2024.053592
Received 05 May 2024; Accepted 18 June 2024; Issue published 30 August 2024
Abstract
The high surface area of porous media enhances its efficacy for evaporative cooling, however, the evaporation of pure substances often encounters issues including local overheating and unstable heat transfer. To address these challenges, a volume of fluid (VOF) model integrated with a species transport model was developed to predict the evaporation processes of ternary mixtures (water, glycerol, and 1,2-propylene glycol) in porous ceramics in this study. It reveals that the synergistic effects of thermal conduction and convective heat transfer significantly influence the mixtures evaporation, causing the fluctuations in evaporation rates. The obtained result shows a significant increase in water evaporation rates with decreasing the microcolumn size. At a pore size of 30 μm and a porosity of 30%, an optimal balance between capillary forces and flow resistance yields a peak water release rate of 96.0%. Furthermore, decreasing the glycerol content from 70% to 60% enhances water release by 10.6%. The findings in this work propose the approaches to optimize evaporative cooling technologies by controlling the evaporation of mixtures in porous media.Keywords
Nomenclature
| Flow velocity | |
| Time | |
| Gravitational acceleration | |
| Surface tension | |
| Total energy | |
| Enthalpy source term | |
| Porosity resistance | |
| Temperature | |
| Enthalpy | |
| Mass source term | |
| Diffusion flux | |
| Stress-strain tensor | |
| Force term | |
| Pore size | |
| Gas-liquid interface curvature | |
| Evaporation/condensation relaxation coefficient | |
| Mass fraction | |
| Generating rate | |
| Mole fraction | |
| Mass diffusion coefficient | |
| Thermal diffusion coefficient | |
| Turbulent viscosity | |
| Greek Characters | |
| Volume fraction | |
| Porosity | |
| Density | |
| Surface tension coefficient | |
| Subscript | |
| Solid medium | |
| Fluid | |
| Component i | |
| Liquid | |
| Vapor | |
| Particle | |
| Saturation | |
| Superscript | |
| Enthalpy | |
Evaporative cooling, recognized as an environmentally friendly and energy-efficient technology, has been increasingly employed in cooling equipment [1,2], and HVAC (heat, ventilation, and air conditioning) systems [3]. This passive cooling technology not only offers a significant cost advantage but also avoids the use of ozone-depleting refrigerants, such as chlorofluorocarbons, making it a sustainable choice [4]. Studies have shown that HVAC systems account for about 50% of the total energy consumption in the building sector [5]. Therefore, optimizing evaporative cooling technology for an efficient energy management system should be crucial. One innovative approach, which utilizes a porous medium with a wicking capability to transport the working fluid, can eliminate the energy consumption for a mechanical pump system [6]. The inherent property of a porous medium can provide a large heat exchange surface area, which markedly enhances the evaporative cooling efficacy. Nonetheless, the evaporation performance within the porous medium is influenced by multiple parameters, including porosity, pore diameter, and physicochemical properties of porous surface [7–10].
Accordingly, extensive scholarly investigations have been conducted to elucidate the macroscopic evaporation process in porous medium with different approaches. Aboufoul et al. [11] investigated the evaporation dynamics of porous asphalt materials with porosity ranging from 15% to 29% through experimental and theoretical analysis. They fabricated the porous asphalts with various porosities utilizing 3D printing and found that the evaporation is influenced by the porosity, pore size, and connectivity. The larger pores weaken the capillary force and the water evaporation at the surface occurs during a relatively short period. The pore size was above 1.7 mm due to the limitations of 3D printing and observation techniques in their work, which cannot show the effect of small pore sizes on the capillary force. Zhang et al. [12] explored a double-layer porous medium interfacial evaporation system based on the theoretical approach. Their results indicated that, as the substrate porosity increases (from 0.1 to 0.9), both the evaporation rate and efficiency initially increase and then decrease, and the turning point is the porosity of 0.6. Huang et al. [13] conducted an experimental study of self-pumped evaporative cooling in a high-temperature wind tunnel. They achieved self-supplied coolant flow and evaporation on the porous surface, maintaining a stable temperature distribution. However, the evaporation process was mainly evaluated from the temperature measurement, and the details of the phase change process were not clearly observed in their study. The work of Liu et al. [14] developed a theoretical model that combines the effects of porous medium geometry and liquid evaporation on capillary penetration. They found that the penetration velocity and extent can be controlled by adjusting the evaporation rate and geometry. The trapezoid and hollow circular/square frustum were studied, and the investigation of the fluence of the cavity (microcolumn configuration) in the porous media needs further effort. Alberghini et al. [15] developed a comprehensive heat and mass transfer model, which can systematically simulate and characterize water wicking and evaporation in a porous medium. The water was used as the working fluid and the evaporation in woven PE textile was studied. The study of Guo et al. [6] found that the evaporative cooling effect is essential for accurately predicting the wicking behavior in a thin porous medium, especially under the local thermal non-equilibrium condition. The research of Nuske et al. [16] challenged the traditional understanding of multiphase and multicomponent flow in porous medium by relaxing the assumptions of local thermal and chemical equilibrium. Their model not only illustrated the impact of heat and mass transfer rates on evaporation rate but also confirmed the model’s convergence, providing a feasibility for simulating more complex systems. The above two studies showed the heat transfer between fluid and solid should be considered as the solid porous structure has a big pore size. The experimental and numerical work of Lu et al. [17] on the heat and mass transfer and fractal evaporative interfaces in porous medium further deepened the understanding of evaporation phenomena in porous medium. It found that both surface tension and pore distribution have an influence on the evaporative interfaces, so the porosity and pore size should be the important parameters to regulate the evaporation performance. Though extensive research has been conducted on the phase change mechanisms within porous media, the majority of studies have focused on the evaporation of pure substances. The evaporation of pure substances presents challenges of local overheating and unstable heat transfer. Consequently, utilizing mixtures can expand the temperature range for heat and mass transfer, alleviate intense localized boiling, decrease temperature gradients, and promote more uniform heat and mass transfer. However, the phase change mechanism of multicomponent fluid within porous media and its effect on diffusion and transport processes remain inadequately understood. Thus, the principles of heat and mass transfer of non-azeotropic mixtures in unsaturated porous media need further investigation.
In this study, the ternary mixtures of water, glycerol, and propylene glycol are utilized as the working fluid, and a phase change heat transfer model based on the VOF (Volume of Fluid) model and species transport model is established. The numerical simulation conducted with the established model not only analyzes the gas-liquid phase transition process in a porous medium but also reveals the dynamics of evaporation and the patterns of water release. Moreover, the prediction considers the impacts of macrostructure, pore structure, and the mass percentage of the ternary mixtures on the evaporation performance. The extensive analysis presents the key performance indicators, including the rates of water evaporation and water release, along with detailed visual representations of phase, temperature, and velocity distributions. This work provides new insights into the evaporation of mixtures in porous medium, which can contribute to the development and optimization of evaporative cooling devices.
For the permeation and phase transition processes of ternary mixtures in porous ceramics, the following assumptions are used to establish the mathematical model: (1) the thermophysical parameters of mixtures, the vapor generated by evaporation and the ceramics are assumed to be constant; (2) the ceramics are regarded as a homogeneous porous medium; (3) the constructed phase-transition heat-transfer model is governed by the heat-balance equations in the porous ceramics. To address the complex multi-component phase change flow in porous medium, a VOF (Volume of Fluid) model coupled with a component transport model is established, which not only enables the implementation of interface sharpening scheme, but also captures the diffusion phenomena of multi-components between different phases. Due to the frictional drag effect on the fluid caused by the complex pore structure in porous medium, the corresponding control equations (including mass, momentum and energy equations) need to be modified as follows [18]:
The energy equation in porous medium uses the heat balance as follows [19]:
where
where
The VOF method based on a volume tracking approach is used to simulate and capture the two-phase motion interface. By introducing the volume fraction (α), the morphology change of the two-phase fluid in the porous surface can be modeled more accurately. α = 0 means that the mesh is filled with gas phase; α = 1 means that the mesh is filled with liquid phase; 0 < α < 1 means that the mesh contains two-phase fluid. The volume transport equation is as follows [22]:
The surface tension at the control gas-liquid interface is obtained from the continuous surface force (CSF) model calculation [23]:
The curvature of the gas-liquid interface is calculated by the following equation [24]:
The mass transfer during the gas-liquid phase transition of a droplet is controlled by the Lee model of phase transition with the following equation [25]:
where
where
The vapor diffusion equation is as follows:
where
In this study, the phenomenon of evaporation of ternary mixtures in porous ceramics is investigated through the numerical simulations. As shown in Fig. 1a, the study object is simplified as a 10 mm × 10 mm × 5 mm three-dimensional cubic computational domain filled with the water/ propanetriol/propylene glycol ternary mixtures. Bottom heating is employed to provide the heat for the phase transition process of the mixtures within the pore structure, while the pressure outlet is provided at the top to ensure gas venting, and the sides are adiabatic walls.

Figure 1: Schematic diagram of porous ceramics: (a) physical model and computational domain, (b) different macrostructures
To delve deeper into the phase transition behaviors of ternary mixtures within porous ceramics, this study contemplates the impacts of macrostructure and pore structure (such as pore diameter and porosity) as well as component ratios on the phenomena of mixtures evaporation and water release. The macrostructural design focuses on the prospective effect of microcolumn configuration on the evaporation process. These microcolumns augment the area available for heat transfer and may significantly enhance capillary action, potentially facilitating the transport of liquids. Accordingly, three distinct structural designs are developed based on cavity and microcolumn dimensions to facilitate the evaluation (refer to Fig. 1b). Sample 1 comprises four cavities each with a side length of 3 mm, creating narrower microcolumns; Sample 2 features slightly smaller cavities with 2 mm sides, forming broader microcolumns; Sample 3, utilized as a contrast, includes neither cavities nor microcolumns. At the microstructural level, mixtures diffusive and permeative characteristics are adjusted by modifying the pore size and porosity of the porous ceramics, thus aiming to enhance the evaporation process. Concerning component concentrations, while maintaining propylene glycol at a 5% proportion, the variations in the ratios of water to glycerol are examined to assess the influence of component ratios on the evaporation characteristics of ternary mixtures in porous ceramics. Detailed computational details are presented in Table 1.

3.2 Boundary and Initial Conditions
Based on the control equations mentioned above, calculating the local three-dimensional flow and heat transfer characteristics in porous ceramics requires the establishment of boundary and initial conditions for numerical modeling. The specific conditions are as follows:
(1) Pressure Outlet Boundary: In the bottom heating process, there is no pumping behavior. The air surrounding the porous ceramics remains at atmospheric pressure. As such, the outlet is set to a constant pressure of 0 Pa, with all components of the exiting gas stream consisting of air recirculation.
(2) Porous Wall Boundary: The velocity at the porous walls is set to a no-slip condition, and a constant temperature heating boundary condition of 573 K.
(3) Initial Conditions: The initial phases of the porous ceramics are entirely liquid phase, with the ternary mixtures ratio of water, glycerol, and propylene glycol being 35:60:5 and later in the investigation of the effect of component concentration, the corresponding initial conditions are changed accordingly. The initial temperature and flow rate of the liquid phase are set to 300 K and 0 m·s−1, respectively.
In this study, a VOF and component transport coupled multi-component phase change heat transfer model is constructed to investigate the evaporation process of mixtures in a porous ceramic. The model is based on a pressure-based solver for transient simulation of the permeation and phase change process of the ternary mixtures with a gravitational acceleration of 9.81 m·s−2 acting in the negative direction of the y-axis. The adaptive time step (1 × 10−6 s~1 × 10−4 s) is set, and the implicit format is used to reduce the dependence of the simulation stability on the time step and to ensure the accuracy of the computation, which effectively improves the computational efficiency. The gas-liquid interface model is selected as the Sharp model. The first phase is set as the liquid phase (ternary water-glycerol-propylene glycol mixtures), and the second phase as the gas phase (water vapor-glycerol vapor-propylene glycol vapor-air mixtures). The surface tension is selected as the surface tension of the gas-liquid interface model. The first phase is set as liquid phase (ternary water-glycerol-propylene glycol mixtures) and the second phase is set as gas phase (water vapor-glycerol vapor-propylene glycol vapor-air mixtures). The surface tension model is set as the CSF (continuous surface force) model, and the surface tension coefficient is calculated according to the formula
3.4 Grid Independence Analysis
The mesh division of the three-dimensional model, as depicted in Fig. 2a, employs hexahedral elements, with localized mesh refinement at the bottom of the cavity to enhance the integrity of data transmission. To ensure the accuracy and reliability of the established numerical model, a grid independence analysis is conducted. Sample 1, which features unique macrostructural characteristics including four broad cavities and narrow microcolumns, is selected for this analysis. The model incorporates a porosity of 30% and a pore diameter of 30 micrometers, with the mass fraction percentages of water, glycerol, and propylene glycol set at 35:60:5, respectively. Three different mesh sizes are examined: 45,556, 84,583, and 204,494. Numerical simulations for this model are conducted using the commercial software Ansys Fluent 17.0. By comparing the obtained results, the mass losses of mixtures within the porous ceramics during the evaporation process under different mesh numbers are analyzed. Fig. 2b indicates that with an increase in mesh size, the deviation in the average evaporation rate of mixtures significantly decreases. This trend suggests that mesh refinement plays a crucial role in capturing the complex details of the evaporation process within the porous ceramics, but it also accompanies an increase in computational time and cost. After a comprehensive assessment of computational demands and simulation accuracy, a mesh count of 84,583 is determined to be the optimal choice. Figs. 2c–2eshow the 3D gas-phase profiles, temperature profiles, and velocity profiles under the 84,583 grids, respectively.

Figure 2: Grid independence analysis: (a) meshing detail, (b) mass loss of mixtures in different grids, (c) 3D gas phase profile, (d) temperature profile, (e) velocity profile
To illustrate the accurate reliability of the model, the evaporation model needs to be validated, and the classical D2 Law has been proposed in previous work to verify the validity of the model for single-component [27,28] or multi-component mixtures [29]. The solution satisfies the following relationship during the evaporation process:
A square computational domain is established in this study, as shown in Fig. 3, with all four sides set as pressure outlet boundaries. A droplet is initially suspended at the center of the computational domain with a starting velocity of 0 m/s and an initial temperature of 370 K. The ratio of the ternary mixtures (water: glycerol: propylene glycol) is 35:60:5. The surroundings are filled with superheated dry air at an initial temperature of 800 K. The variation curve of (d/d0)2 over time is calculated. It is observed that (d/d0)2 is linearly related to time, indicating that the constructed ternary component evaporation model conforms to the D2 Law and can be used for the subsequent evaporation process of ternary mixtures in porous ceramics.

Figure 3: Variation of volume of droplet over time
To evaluate the accuracy and reliability of the droplet model and numerical methods, this study compares the numerical results of droplet penetration and diffusion in porous media with previous research [30]. As shown in Fig. 4, H represents the penetration depth, R represents the diffusion radius, and R0 represents the initial radius. The results indicate that the curves from this study align well with the simulation data from the literature, demonstrating the validity of the numerical model.

Figure 4: Comparison and validation of droplet penetration models [30]: (a) variation of the ratio of penetration depth to initial radius with time, (b) variation of the ratio of diffusion radius to initial radius with time
To explore the numerical simulation of heat transfer characteristics during the evaporation of ternary mixtures, this study provides a comprehensive analysis of the evaporation behavior of a ternary system composed of water, propanetriol, and propylene glycol within porous ceramics. The complexity of the evaporation process is influenced by multiple factors, including the macrostructural configuration of the ceramic sample, the pore size and overall porosity, and the mass fractions of water, glycerol, and propylene glycol within the ternary mixtures.
4.1 Effect of Macrostructure on Evaporative Heat Transfer
The macro-structural features (particularly cavity dimensions and micropillar structure) play a significant role. The arrangement of cavities and interconnecting microcolumns within the ceramic matrix is crucial for modulating the evaporation dynamics and water release. This section delves into the effect of porous ceramics macrostructure on the evaporation efficacy and water release rate.
4.1.1 Gas-Liquid Phase Transition State in the Macroscopic Structure
Fig. 5 illustrates the gas-liquid phase transition in Sample 1, which has a cavity size of 3 mm3 × 3 mm3 × 3 mm3. The water: glycerol: propylene glycol ratio is 35:60:5, with a pore size of 30 μm and a porosity of 30%. Fig. 5a shows the temperature distribution cloud images within the porous ceramics over time. It can be observed that at the beginning of the phase transition process, the temperature at the bottom of the porous ceramics reaches 573 K, surpassing the boiling points of water (373 K), glycerol (563 K), and propylene glycol (458 K), with a certain degree of superheat. Consequently, the mixed liquid near the bottom undergoes phase transition first. Due to the low porosity and small pore size of the porous ceramics, nucleation is impeded, leading to the development of a smooth gas-liquid interface. Fig. 5b shows the gas phase distribution cloud images within the porous ceramics over time, where the clear delineation of the gas-liquid interface near the base of the sample is evident. As heating continues, the vapor accumulates in the lower regions of the porous ceramics. From 1 to 8 ms, the red regions in Fig. 5b continuously expand, indicating the spatial expansion of the gas phase. The accumulated vapor propels the gas-liquid interface upward continuously. Upon reaching the cavity bottom outlets at 20 ms, the vapor escapes through the interstices, causing a decrease in the internal pressure of the porous ceramics. This pressure difference induces compensatory air inflow into the interior of the porous ceramics (Fig. 5c). Consequently, throughout the entire process, a gas phase is maintained below the phase boundary, indicating a dynamic equilibrium between vapor efflux and air influx. While the vapor is expelled from the outlets, the high-temperature bottom of the porous ceramics continuously transfers heat into the interior through convection and heat conduction. Heating and evaporation persist, continuously generating more vapor in the upper part of the porous ceramics. The scope of the liquid phase transition progressively expands, with the fraction of the liquid phase concomitantly diminishing until evaporation is complete.
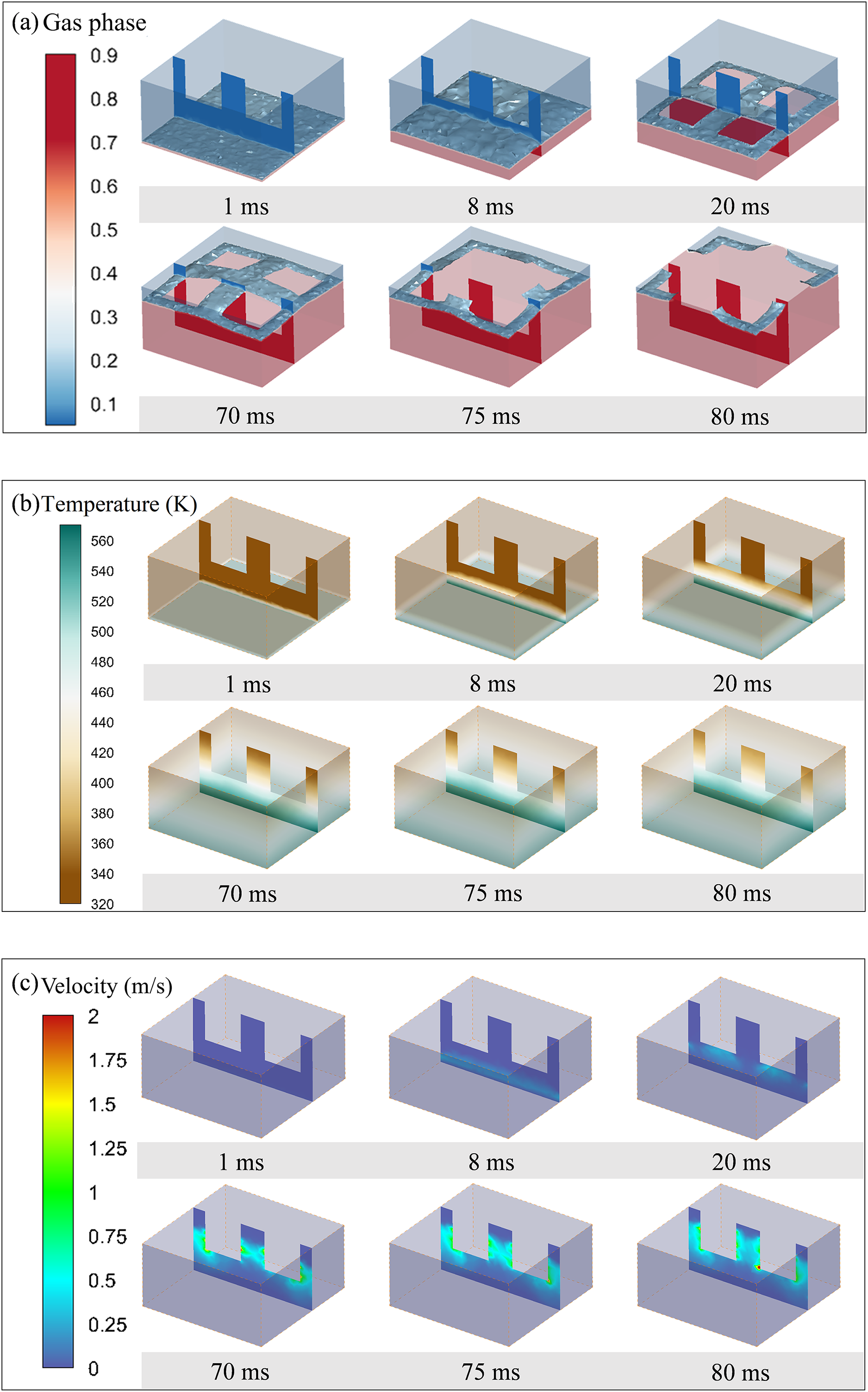
Figure 5: Simulation results for case 1: (a) gas phase distribution, (b) temperature distribution, (c) velocity distribution
4.1.2 Evaporation Behavior of Water in Macroscopic Structures
Fig. 6a shows the curves of the change in the residual mass of liquid water. For Sample 1 and Sample 2, it can be observed that as the evaporation proceeds, the mass of liquid water in the mixed liquid continues to decrease due to the continuous phase transition of liquid water into vapor. However, the evaporation rate of water also fluctuates over time.
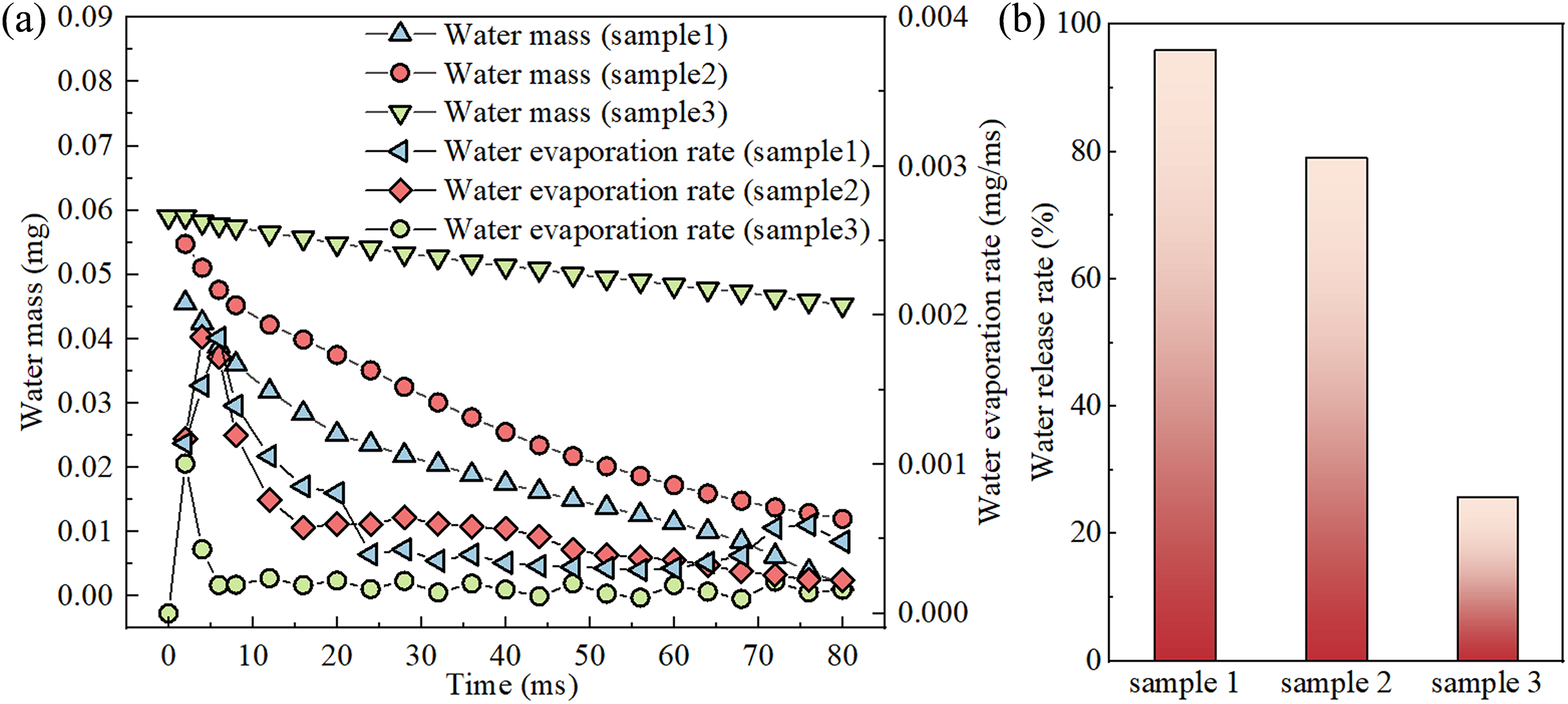
Figure 6: The effect of macrostructure on water evaporation behavior: (a) curves of the remaining mass of liquid water and the rate of water evaporation as a function of time for different samples, (b) water release rate at different samples
In the initial stage of evaporation (t = 0~1 ms), the temperature at the bottom of the porous ceramics rises rapidly, transferring the heat to the liquid phase filled inside, leading to the evaporation rate of the liquid phase being maintained at a high level. Subsequently, the intense phase transition generates steam that quickly adheres to the heating surface. Since the thermal conductivity of steam is lower than that of liquid, it leads to a reduction in the effective thermal conductivity of porous ceramics, negatively affecting the process of heat transfer from the bottom to the interior, causing the evaporation rate to gradually decrease.
When t = 8 ms, the vapor has completely covered the porous edge heating surface. In the subsequent time period of 8~20 ms, the water evaporation rates of the three samples drop sharply. This may be due to the fact that, before the mixed vapor reaches the outlet at the bottom of the cavity, the accumulation of steam gradually increases the pressure within the porous ceramics, which hinders the evaporation of the mixed liquid. Simultaneously, it can be observed that there is almost no flow of mixed vapor and mixed liquid within the porous ceramics, therefore, the contribution of convection to heat transfer can be neglected, and the evaporation of the mixed liquid is maintained solely by conduction. The range of steam only increases slowly.
At t = 20 ms, the water evaporation rate continues to decrease. By this time, a considerable amount of steam has accumulated at the bottom of porous ceramics and the liquid phase blocking the outlet at the cavity bottom has gradually evaporated, allowing a large volume of steam to overflow through the pores at the outlet. The pressure in the steam area gradually decreases and the flow velocity begins to increase. This process enhances the convective heat transfer between the high-temperature porous ceramics and the cool air at the outlet, resulting in the heat dissipation within the porous ceramics, further reducing the evaporation rate of the mixed liquid.
When t > 20 ms, the liquid at the lower part of the porous ceramics has been completely evaporated, leaving the remaining liquid to be evaporated at the upper part of the ceramic. Due to the inhomogeneity of local evaporation, the temperature decreases with increasing distance from the heated edge of the porous ceramics. Consequently, the evaporation rate of water from the upper part of the ceramic remains at a lower level and is almost constant.
In the advanced stages of evaporation (t = 70 ms), the central region of the porous ceramics undergoes a rapid phase transition, primarily due to the presence of the microcolumn structure that increases the heat transfer area of mixed liquid in the central region. This results in a pronounced gaseous region within the core of the structure. As the evaporation continues, the interface between gas and liquid propagates outward, causing the liquid regions to progressively retreat towards the four corners of the porous ceramics. During the diffusion of the gas-liquid interface, the thickness of liquid in the peripheral areas decreases, especially at the edges where the liquid forms thin films. This results in a reduction of thermal resistance, leading to a rapid evaporation phenomenon of these thin films, thereby increasing the evaporation rate. This is the reason for the peak in the evaporation rate around t = 70 ms.
When t > 75 ms, the thin liquid films rupture and disappear, isolating the liquid regions with steam, which further reduces the evaporation rate. The water evaporation rate trends of the three samples are consistent. However, the water evaporation rate of Sample 3 is lower than that of Sample 1 and Sample 2. There are three possible reasons for this phenomenon. (1) In porous ceramics lacking cavity and microcolumn structure, the pathways for vapor egress are significantly constricted, and it is difficult for vapor to be discharged from the interior of the material. Given that the thermal conductivity of vapor is inferior to that of liquid, this constraint further impedes the effective transfer of heat, resulting in a deceleration of the evaporation rate. (2) Moreover, the absence of a microcolumn structure prevents the use of capillary action to efficiently transport the liquid to the evaporation zone where the heat is concentrated, thus slowing down the evaporation process. As observed in Sample 1, the gas-liquid interface at the micro-pillar structures is meniscus, in contrast to the horizontal interface of Sample 3. This observation indicates that the presence of micro-pillar structures facilitates the occurrence of capillary phenomena. Given that the designed width of micro-pillars is less than 5 mm, the capillary action induced by surface tension is pronounced, which effectively enhances the upward transport of liquid and thus accelerates the evaporation from the liquid surface. Therefore, the design of micro-pillar structures plays a positive role in enhancing evaporation efficiency. (3) Compared to porous ceramics with cavities and microcolumn structure, the surface area of Sample 3 is relatively reduced, diminishing the area for evaporation and consequently decreasing the overall evaporation efficiency.
Fig. 6b shows the water release rates at t = 80 ms for different samples. Among them, sample 1 exhibits the highest water release rate at 96%, which is significantly higher than that of Sample 2 (79%) and Sample 3 (26%). This further illustrates that the design of cavities and micro-pillar structures is beneficial in enhancing the water evaporation and increasing the water release rate. Compared to Sample 2, Sample 1 has a similar structure but features a larger heat transfer area, which allows for a greater water evaporation within the same time period. Additionally, the micro-pillars in Sample 1 are narrower, which enhances the capillary action, making the water transport and evaporation more efficient. Considering the above factors, Sample 1 exhibits a higher water release rate.
Fig. 7 shows the mass fraction distribution of liquid water at t = 70 ms for different macrostructures. The water mass fraction distribution is consistent with the gas phase distribution diagram, which indicates that water is preferentially evaporated out during the evaporation of ternary mixtures because the water has a lower boiling point and viscosity.
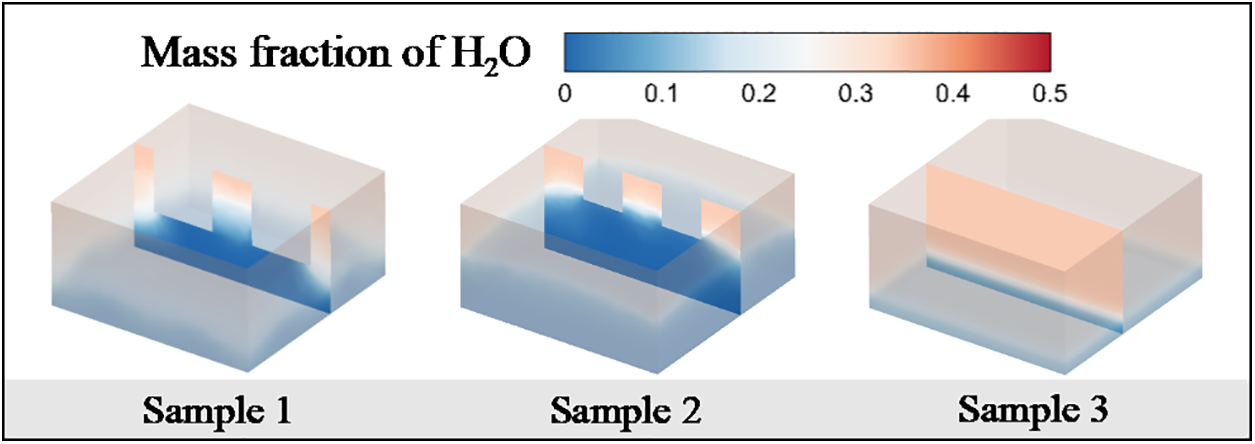
Figure 7: Distribution of water mass fraction for different macrostructures
4.2 Effect of Porosity on Evaporation Heat Transfer
For the evaporation of ternary mixtures in porous ceramics, the microstructural characteristics also impact the evaporation efficiency. The variations in pore size and porosity directly affect the diffusivity and permeability properties of the mixed liquid. Therefore, by precisely controlling the pore size and porosity, the evaporation performance of liquids in the porous ceramics can be enhanced.
Fig. 8a depicts the variation in residual water mass and evaporation rate over time under various porous configurations. It is evident that, during the initial phase of evaporation (0–70 ms), an increase in porosity and pore diameter correlates with the enhanced evaporation rates. This enhancement is attributed to the enlarged solid-liquid contact area resulting from increased pore dimensions, which effectively expands the heat transfer surface, thus augmenting the evaporation process. Additionally, the larger pore structures facilitate the gas-liquid phase transition of the mixtures, mitigating the adverse effects of vapor clogging and subsequent pressure increasing within the pores. In the later stages of evaporation (t > 70 ms), however, the evaporation rate associated with a 30 μm pore size exhibits a resurgence, surpassing that of the 40 μm one, consequently increasing the water release rate for 30 μm pores (Fig. 8b). These observations underscore the sensitivity of the fluid dynamics properties of mixtures in the porous ceramics to the interplay between capillary forces and resistance. While an increase in pore size may diminish the capillary action, a corresponding reduction in the coefficients of viscous and inertial resistance markedly decreases flow resistance. This diminution substantially enhances the convective heat transfer, thereby intensifying the gas-liquid phase transition process. Thus, it can be inferred that, relative to the diminishment of capillary action, a reduction in convective resistance more significantly promotes the evaporation process. Nonetheless, in the advanced stages of evaporation (t > 70 ms), the reduction in capillary action assumes a dominant role. This intricate interaction suggests that optimizing the overall efficiency of the evaporation process necessitates a balanced consideration of both convective resistance and capillary action.
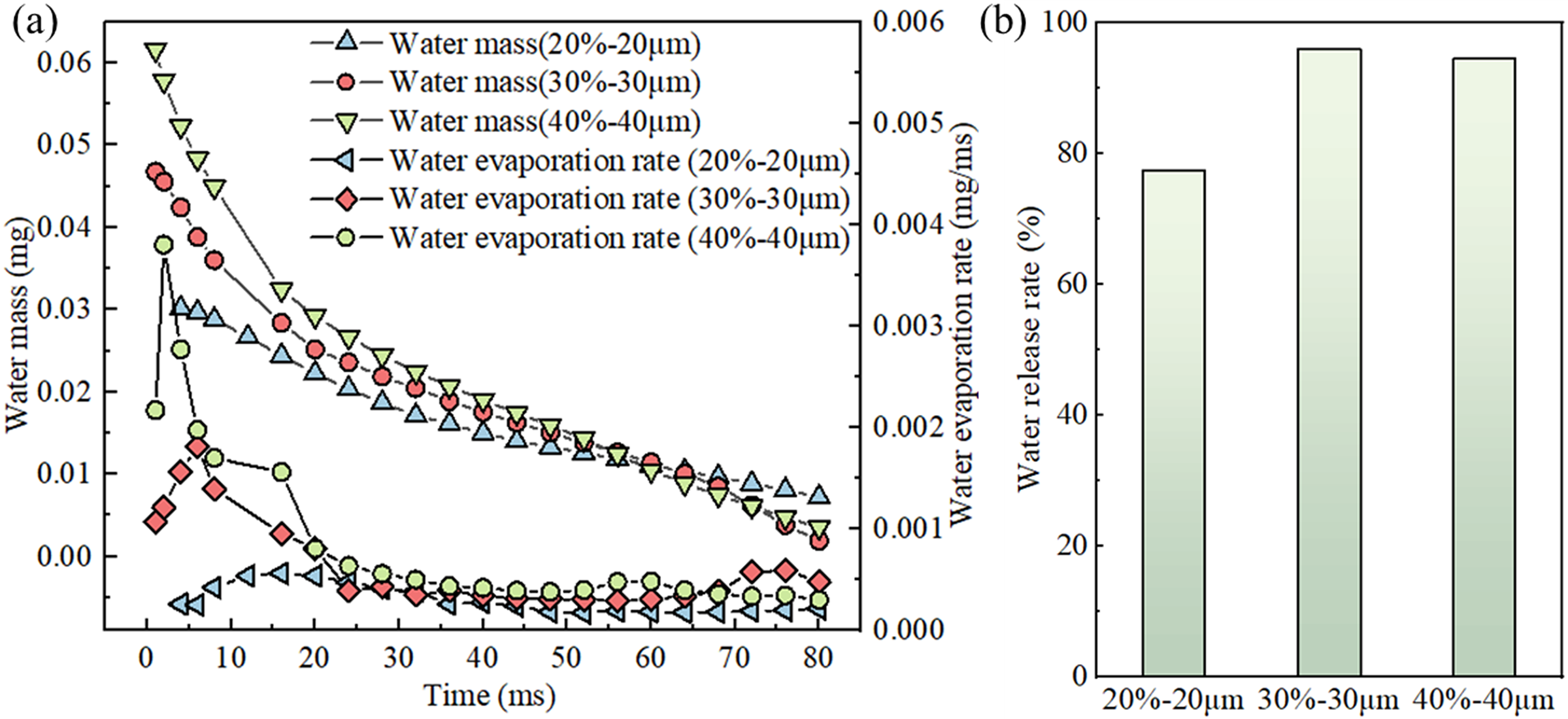
Figure 8: Effect of porosity on evaporative heat transfer: (a) curves of remaining mass of liquid water and rate of water evaporation as a function of time for different porosities, (b) water release rate at different porosity
Fig. 9 presents the mass fraction distribution of residual liquid water within the porous ceramics at t = 70 ms. In the case with 20% porosity and 20 μm pore diameter, there is a discernible demarcation between regions of high and low mass fractions, suggesting an inhomogeneous distribution and evaporation of water due to the constrained fluid dynamics within the pore space, leading to a localized evaporation phenomenon. In stark contrast, the 40% porosity and 40 μm pore diameter structure exhibits a more homogenized mass fraction distribution of water, indicating the facilitative effect of increased porosity and pore diameter on the uniform distribution and evaporation of water. This uniformity likely stems from the expanded flow space afforded by the larger pores, which permits the enhanced diffusion and evaporation, thereby maintaining a more consistent distribution of liquid water throughout the evaporation process.
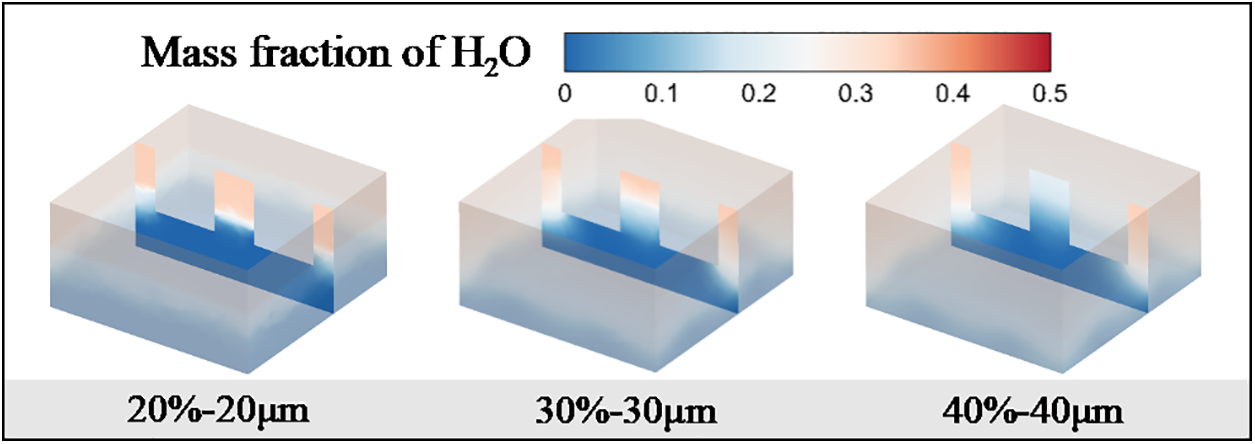
Figure 9: Distribution of water mass fraction at different pore sizes and porosities
4.3 Effect of Component Concentrations on Evaporation Heat Transfer
Fig. 10a displays the variations of residual mass of water and the evaporation rate within the liquid phase under different component concentrations. As the proportion of water in the mixed liquid increases and the proportion of glycerol decreases during the evaporation process, a marked decrease in the residual mass of water in the liquid phase is observed, alongside a significant enhancement in evaporation rate. This phenomenon occurs because the water with its lower boiling point evaporates more readily at an equivalent initial mass, resulting in a greater proportion of initial water leading to a larger mass of water vapor being evaporated, and leaving less residual liquid water. Additionally, the changes in the concentration of mixed liquid lead to alterations in the physical property parameters. The thermal conductivity and specific heat capacity of water are both higher than those of glycerol. In this study, the thermal diffusivity coefficient (

Figure 10: Effect of component concentrations on evaporative heat transfer: (a) curves of remaining mass of liquid water and rate of water evaporation as a function of time for different component concentrations, (b) water release rate at different component concentrations
Fig. 10b depicts the variations in water release rate at different component concentrations. Notably, increasing the initial proportion of liquid water from 25% to 35% results in an enhanced water release rate during evaporation. This enhancement is attributable to water’s lower boiling point compared to glycerol; thus, a higher water proportion leads to a reduced average boiling point of the mixture, decreasing the temperature required for the liquid-to-vapor transition and facilitating the escape of water molecules. However, further increasing the water proportion to 45% causes a decrease in water release rate. According to the formula for calculating the combined surface tension coefficient of mixtures, the increased proportion of water, which has a relatively high surface tension coefficient, raises the overall surface tension of mixed liquid. Higher surface tension leads the mixed liquid to minimize its surface area, enhancing the adhesion effect on the porous solid surfaces, resulting in greater residual water within the porous ceramics, thereby exhibiting a lower water release rate.
Fig. 11 shows the mass fraction distribution of the residual liquid water inside the porous ceramics for different initial component occupancies at t = 70 ms. According to the results, two different concentrations of 35% and 45% of initial water content do not show much difference in the evaporation process. However, at the concentration of 25:70:5, the mass fraction of liquid water is relatively low. It also indicates that evaporation is more easily achieved in mixed liquid with lower water content due to their low surface tension.
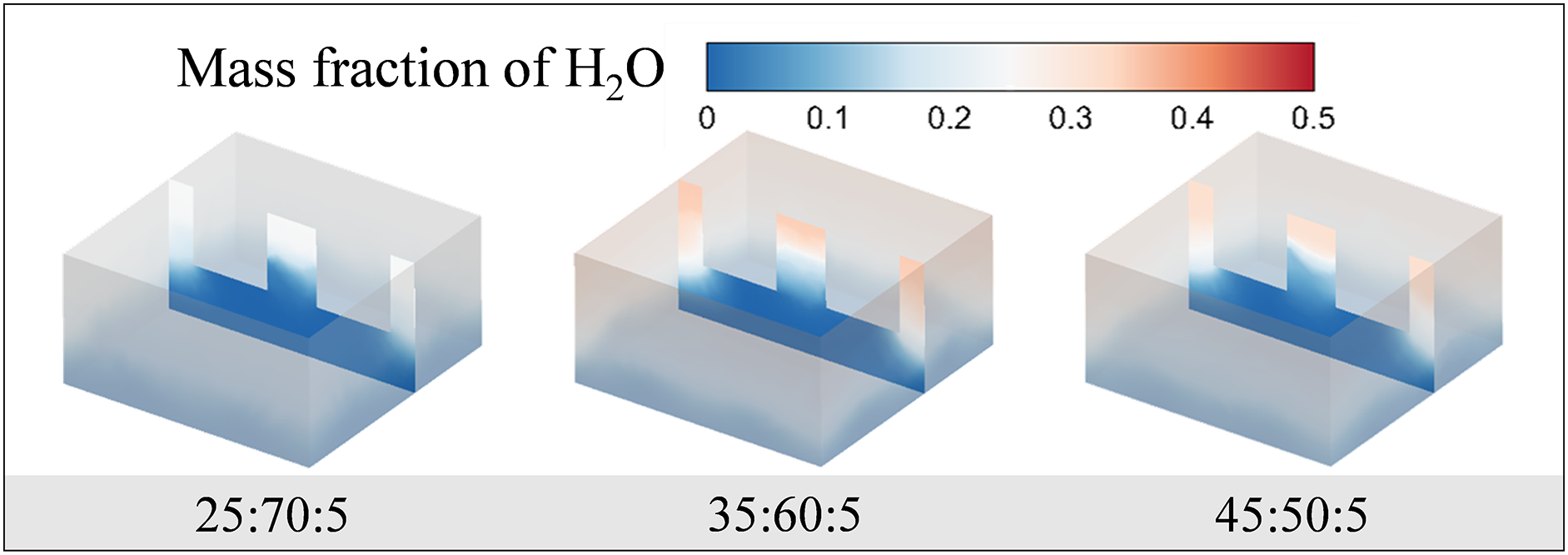
Figure 11: Distribution of water mass fraction at different component concentrations
In this study, a computational model for evaporative heat transfer of mixtures based on the VOF (Volume of Fluid) model coupled with the component transport model is established. The numerical simulations of the evaporation of ternary mixtures (water-glycerol-propylene glycol) within porous ceramics are conducted to investigate its evaporation mechanism and water release behavior. The main conclusions are as follows:
(1) The evaporative phase change process of mixed liquids within porous ceramics is influenced by the combined effects of heat conduction and convective heat transfer, resulting in the fluctuating evaporation rates. As the micro-column size decreases, both the evaporation rate and water release rate of water show an increasing trend.
(2) The porous ceramics with a high porosity and large pore diameter structures exhibit a higher water evaporation rate. Influenced by both capillary forces and flow resistance, the water release rate shows a significant increase followed by a slight decrease with increasing porosity and pore diameter.
(3) The comprehensive effects of thermal diffusion coefficient and surface tension coefficient lead to an effective increase in water evaporation rate due to the decrease in glycerol component in the mixed liquid, but the water release rate initially increases and then decreases.
This study provides a foundational understanding of the evaporation behavior of ternary mixtures within porous ceramics. Future research could explore more complex porous structures to optimize heat transfer performance. Additionally, incorporating advanced experimental techniques for validation could further enhance the reliability and applicability of the findings.
Acknowledgement: The authors would like to acknowledge the constructive remarks by worthy reviewers that led to this revised article.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Zhiguo Wang, Duo Ding, Zhenhai Pan, Zhenyu Liu; data collection: Bo Zhang, Peilin Cui; analysis and interpretation of results: Bo Zhang, Yunxie Huang; draft manuscript preparation: Bo Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that supports the findings of this study are available from the author upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Yang Y, Cui G, Lan CQ. Developments in evaporative cooling and enhanced evaporative cooling—A review. Renew Sustain Energy Rev. 2019;113:109230. doi:10.1016/j.rser.2019.06.037. [Google Scholar] [CrossRef]
2. Xuan YM, Xiao F, Niu XF, Huang X, Wang SW. Research and application of evaporative cooling in China: a review (I)–research. Renew Sustain Energy Rev. 2012;16(5):3535–46. [Google Scholar]
3. Ge G, Abdel-Salam MRH, Besant RW, Simonson CJ. Research and applications of liquid-to-air membrane energy exchangers in building HVAC systems at University of Saskatchewan: a review. Renew Sustain Energy Rev. 2013;26:464–79. doi:10.1016/j.rser.2013.04.022. [Google Scholar] [CrossRef]
4. Sultan M, El-Sharkawy II, Miyazaki T, Saha BB, Koyama S. An overview of solid desiccant dehumidification and air conditioning systems. Renew Sustain Energy Rev. 2015;46:16–29. doi:10.1016/j.rser.2015.02.038. [Google Scholar] [CrossRef]
5. Sajjad U, Abbas N, Hamid K, Abbas S, Hussain I, Ammar SM, et al. A review of recent advances in indirect evaporative cooling technology. Int Commun Heat Mass Transf. 2021;122:105140. doi:10.1016/j.icheatmasstransfer.2021.105140. [Google Scholar] [CrossRef]
6. Guo C, Guo W, Zhou Y, Huang T, Zhang P. Evaporative wicking in thin porous media. Int J Heat Mass Transf. 2023;216:124536. [Google Scholar]
7. Leu JS, Jang JY, Chou Y. Heat and mass transfer for liquid film evaporation along a vertical plate covered with a thin porous layer. Int J Heat Mass Transf. 2006;49(11–12):1937–45. [Google Scholar]
8. Unno N, K. Yuki, Inoue R, Kogo Y, Taniguchi J, Satake SI. Enhanced evaporation of porous materials with micropores and high porosity. J Therm Sci Technol. 2020;15:JTST0007. doi:10.1299/jtst.2020jtst0007. [Google Scholar] [CrossRef]
9. Wu H, Fang C, Wu R, Qiao R. Drying of porous media by concurrent drainage and evaporation: a pore network modeling study. Int J Heat Mass Transf. 2020;152:118718. doi:10.1016/j.ijheatmasstransfer.2019.118718. [Google Scholar] [CrossRef]
10. Gao B, Davarzani H, Helmig R, Smits KM. Experimental and numerical study of evaporation from wavy surfaces by coupling free flow and porous media flow. Water Resour Res. 2018;54(11):9096–117. [Google Scholar]
11. Aboufoul M, Shokri N, Saleh E, Tuck C, Garcia A. Dynamics of water evaporation from porous asphalt. Constr Build Mater. 2019;202:406–14. [Google Scholar]
12. Zhang Q, Sun X, Shen Y, Zhang Y, Cai Q, Deng W, et al. Establishing a transient model of double-layer porous media interfacial evaporation system to reveal the relationship between porous media parameters and evaporation performance. Appl Therm Eng. 2023;234:121311. doi:10.1016/j.applthermaleng.2023.121311. [Google Scholar] [CrossRef]
13. Huang G, Liao Z, Xu R, Zhu Y, Jiang PX. Self-pumping transpiration cooling with phase change for sintered porous plates. Appl Therm Eng. 2019;159:113870. doi:10.1016/j.applthermaleng.2019.113870. [Google Scholar] [CrossRef]
14. Liu M, Wu J, Gan Y, Hanaor DAH, Chen CQ. Tuning capillary penetration in porous media: combining geometrical and evaporation effects. Int J Heat Mass Transf. 2018;123:239–50. [Google Scholar]
15. Alberghini M, Boriskina SV, Asinari P, Fasano M. Characterisation and modelling of water wicking and evaporation in capillary porous media for passive and energy-efficient applications. Appl Therm Eng. 2022;208:118159. doi:10.1016/j.applthermaleng.2022.118159. [Google Scholar] [CrossRef]
16. Nuske P, Joekar-Niasar V, Helmig R. Non-equilibrium in multiphase multicomponent flow in porous media: an evaporation example. Int J Heat Mass Transf. 2014;74:128–42. doi:10.1016/j.ijheatmasstransfer.2014.03.011. [Google Scholar] [CrossRef]
17. Lu S, Zhu Q, Ying H. The effect of pore size distribution on the fractal evaporative interface in porous media. Appl Therm Eng. 2024;246:122960. [Google Scholar]
18. Faghri A, Zhang Y. Generalized governing equations for multiphase systems: averaging formulations. In: Transport phenomena in multiphase systems. Boston: Academic Press; 2006. p. 238–330. [Google Scholar]
19. Wang C, Beckermann C. A two-phase mixture model of liquid-gas flow and heat transfer in capillary porous media—I. Formulation. Int J Heat Mass Transf. 1993;36(11):2747–58. doi:10.1016/0017-9310(93)90094-M. [Google Scholar] [CrossRef]
20. Teng H, Zhao TS. An extension of Darcy’s law to non-Stokes flow in porous media. Chem Eng Sci. 2000;55(14):2727–35. [Google Scholar]
21. Yazdchi K, Luding S. Towards unified drag laws for inertial flow through fibrous materials. Chem Eng J. 2012;207–208:35–48. [Google Scholar]
22. Raeini AQ, Blunt MJ, Bijeljic B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J Comput Phys. 2012;231(17):5653–68. doi:10.1016/j.jcp.2012.04.011. [Google Scholar] [CrossRef]
23. Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. J Comput Phys. 1992;100(2):335–54. doi:10.1016/0021-9991(92)90240-Y. [Google Scholar] [CrossRef]
24. Ferrari A, Jimenez-Martinez J, Borgne TL, Méheust Y, Lunati I. Challenges in modeling unstable two-phase flow experiments in porous micromodels. Water Resour Res. 2015;51(3):1381–400. [Google Scholar]
25. Sun D, Xu J, Chen Q. Modeling of the evaporation and condensation phase-change problems with FLUENT. Numer Heat Transf Part B Fundam. 2014;66:326–42. doi:10.1080/10407790.2014.915681. [Google Scholar] [CrossRef]
26. Abdelwahid S, Malik MR, Tang H, Alfazazi A, Hernández-Pérez FE, Dally B, et al. Large eddy simulation of bluff-body turbulent hydrogen/nitrogen flames using principal component transport models with differential diffusion effects. Int J Hydrog Energy. 2024;71:174–83. doi:10.1016/j.ijhydene.2024.04.294. [Google Scholar] [CrossRef]
27. Law CK. Recent advances in droplet vaporization and combustion. Prog Energy Combust Sci. 1982;8(3):171–201. doi:10.1016/0360-1285(82)90011-9. [Google Scholar] [CrossRef]
28. Wang P, Sun G, Dong B, Chen L, Zhang X, Gong B. Lattice Boltzmann simulation of surface evaporation in porous media. Int Commun Heat Mass Transf. 2023;142:106609. [Google Scholar]
29. Zhang Z, Huang X, Xu J. Experiments and numerical simulation of n-decane/ethanol bi-component droplet evaporation. Molecules. 2023;28(5):2391. [Google Scholar] [PubMed]
30. Fu F, Li P, Wang K, Wu R. Numerical simulation of sessile droplet spreading and penetration on porous substrates. Langmuir. 2019;35(8):2917–24. doi:10.1021/acs.langmuir.8b03472. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools