Numerical Study of Temperature-Dependent Viscosity and Thermal Conductivity of Micropolar Ag–MgO Hybrid Nanofluid over a Rotating Vertical Cone

1  Introduction

Thermal properties of most base fluids used in industry are low and do not address the needs of recent technology. Nowadays, effective active heat transfer methods like ultrasonic vibration have been explored by Delouei et al. [1]. Another mechanism involves adding nanoparticles to the base fluid to improve heat transfer; this approach, discussed by Siavashi et al. [2], utilizes nanoparticles, known as nanofluids, to overcome this deficiency. At present, a widely explored research area for enhancing the thermal conductivity of base fluids is nanotechnology, as investigated by Izadi et al. [3]. The nanofluids have widespread applications in various engineering and industrial processes. Applications of this nature encompass cooling systems, heat exchangers, geothermal and solar energy systems, and biomedicine, particularly in the realm of targeted drug delivery, as highlighted by Siavashi et al. [2]. A considerable number of researchers have discussed the flows of nanofluid and its applications [2–7]. Akmal et al. [8] observed that the heat transfer rate increases as the values of the thermophoresis parameter increase. Zeeshan et al. [9] analyzed a convective MHD nanofluid water/ethylene glycol based flow towards a vertical cone. Hady et al. [10] reported a rapid reduction in heat transfer rates due to an increase in the nanofluid’s temperature and the solid volume fraction. Liu et al. [11] proposed a Pt/TiO2 nanocomposite for cancer-cell treatment because noble metal nanoparticles are supposed to enhance the photocatalytic activity of TiO2 nanoparticles. Some other significant studies for the reader’s interest can be found in [12–17].

Nanoparticles such as Cu, Ag, and Au are not readily available and are expensive. Additionally, unmodified particles of Cu, Ag, and Au may pose potential toxicity risks, as highlighted by Parveen et al. [18]. The availability, cost, and potential toxicity of the particles, especially for unmodified mono nanofluid particles, will impact the manufacturing cost of production and pose health risks. Researchers have established a novel generation of heat transfer fluid as an extension towards nanofluid technology. This involves two or more dilute suspensions of composite nanoparticles in a base fluid, giving rise to a new class of fluid called hybrid nanofluids, as discussed by Chahregh et al. [19]. These hybrid nanofluids overcome limitations and simultaneously enhance the physical and chemical properties of the materials involved. The investigation into the temperature-dependent viscosity and thermal conductivity of hybrid nanofluid over a rotating vertical cone is vital for advancing our understanding of nanofluid dynamics, optimizing industrial processes, and exploring the potential of nanotechnology in heat transfer applications.

The behaviour of a hybrid nanofluid composed of TiO2 and Ag in pure blood was studied by Chahregh et al. [19]. They reported the asymmetry of the channel, caused by different permeability at walls, significantly affects the nature of flow. A numerical investigation of the impact of magnetic field localization on the vortex generation in hybrid nanofluid flow studied by Ali et al. [20]. Many other investigations related to hybrid nanofluid have been published [21–23] to mention just a few.

It is known that many of the industrially and technologically important fluids are non-Newtonian fluids. In this article, a non-Newtonian micropolar fluid is considered. The most common type of non-Newtonian micropolar fluid is a fluid with a micro-structure that may consist of rigid, randomly oriented particles suspended in a viscous medium. MHD flow and heat transfer of carbon nanotube (CNTs/H2O) nanoparticles suspended in micropolar dusty fluid, considering thermal radiation, was studied by Ghadikolaei et al. [24]. In this study, they reported that the thermal boundary layer thickness increases with increasing volume fraction of nanoparticles. Sandeep et al. [25] reported that hybrid ferroliquid and thermal radiation play a significant role in stream and energy transport in their study of radiative MHD dusty-hybrid ferrofluids, taking Fe3O4 and CoFe2O4 as nanoparticles in kerosene/water-based liquids. Several research studies on the flow of micropolar hybrid nanoliquids have been analyzed in the relevant literature [26–28].

Motivated by the aforementioned works, the present study extends the work of Malik et al. [29]. This extension is not a simple one as the authors aim to address a hybrid nanofluid with spin gradient viscosity for a non-Newtonian micropolar fluid, an aspect that was not covered in their study. Furthermore, this extension addresses a gap not explored in classical fluid dynamics, as far as our knowledge extends. We examine the effects of volumetric nanofractions, micropolar, and viscous fluids and compare their impacts.

2  Mathematical Formulation of the Problem

Consider an inverted isothermal rotating cone with a semi-vertical angle of Θ∗ and time-dependent angular velocity of Ω. In this cone, a two-dimensional, incompressible, and unsteady magneto-micropolar hybrid nanofluid flow consisting of Ag−MgO with a variable viscosity of μhnf and thermal conductivity of khnf with a reference length of L is surrounded by a porous medium. Additionally, heat transfer is incorporated at the surface of the inverted cone in the presence of thermal radiation effects. Buoyancy forces are present due to temperature variations, with the assumption that the surface of the permeable cone is held at a variable temperature of T(x), where the temperature far away from the surface of the cone is denoted as T∞. The graphical representation of the flow model is illustrated in Fig. 1. Under these assumptions, the governing equations [29,30] for the boundary layer flow takes the form:

∂(xu)∂x+∂(xv)∂z=0,(1)

∂u∂t+u∂u∂x+w∂u∂z−v2x=1ρhnf∂∂z[(μhnf+κ)(∂u∂z)]+κ∂N∂z−νhnfK0u+g∗(βT)hnf(T−T∞)cos⁡Θ∗−σhnfB02ρhnfu,(2)

∂v∂t+u∂v∂x+w∂v∂z+uvx=1ρhnf∂∂z[(μhnf+κ)(∂v∂z)]+κ∂N∂z−νhnfK0v−σhnfB02ρhnfv,(3)

∂N∂t+u∂N∂x+w∂N∂z=γhnfρhnfj∂2N∂z2−κ(2N+∂u∂z),(4)

∂T∂t+u∂T∂x+w∂T∂z=1(ρCp)hnf∂∂z(khnf∂T∂z)−1(ρCp)hnf∂qr∂z,(5)

where qr=16T∞3σ∗3k∗(∂T∂z) [31], r=xcos⁡Θ∗ and, μhnf and khnf depend on temperature as defined [29]:

μhnf=μ0(1−Aθ(η)),khnf=k0(1+ζθ(η)).(6)

A<0 for gas and A>0 for liquid, A=χ(Tw−T∞) and ζ=−c(Tw−T∞), where χ and c are arbitrary constants. The initial and boundary conditions are given by:

t≤0,u=0,v=0,w=0,N=0,T=T0∀(x,y,z),(7a)

t>0,u=0,v=11−At∗Ωxsin⁡Θ∗,N=0,T=Tw,atz=0,(7b)

u→0,v→0,N→0,T→0,asz→∞,(7c)

where t∗=Ωtsin⁡Θ∗. All the values for the parameters Cp, K, ρ, β, σ, α are taken from Table 1. (Hiba et al. [32]).

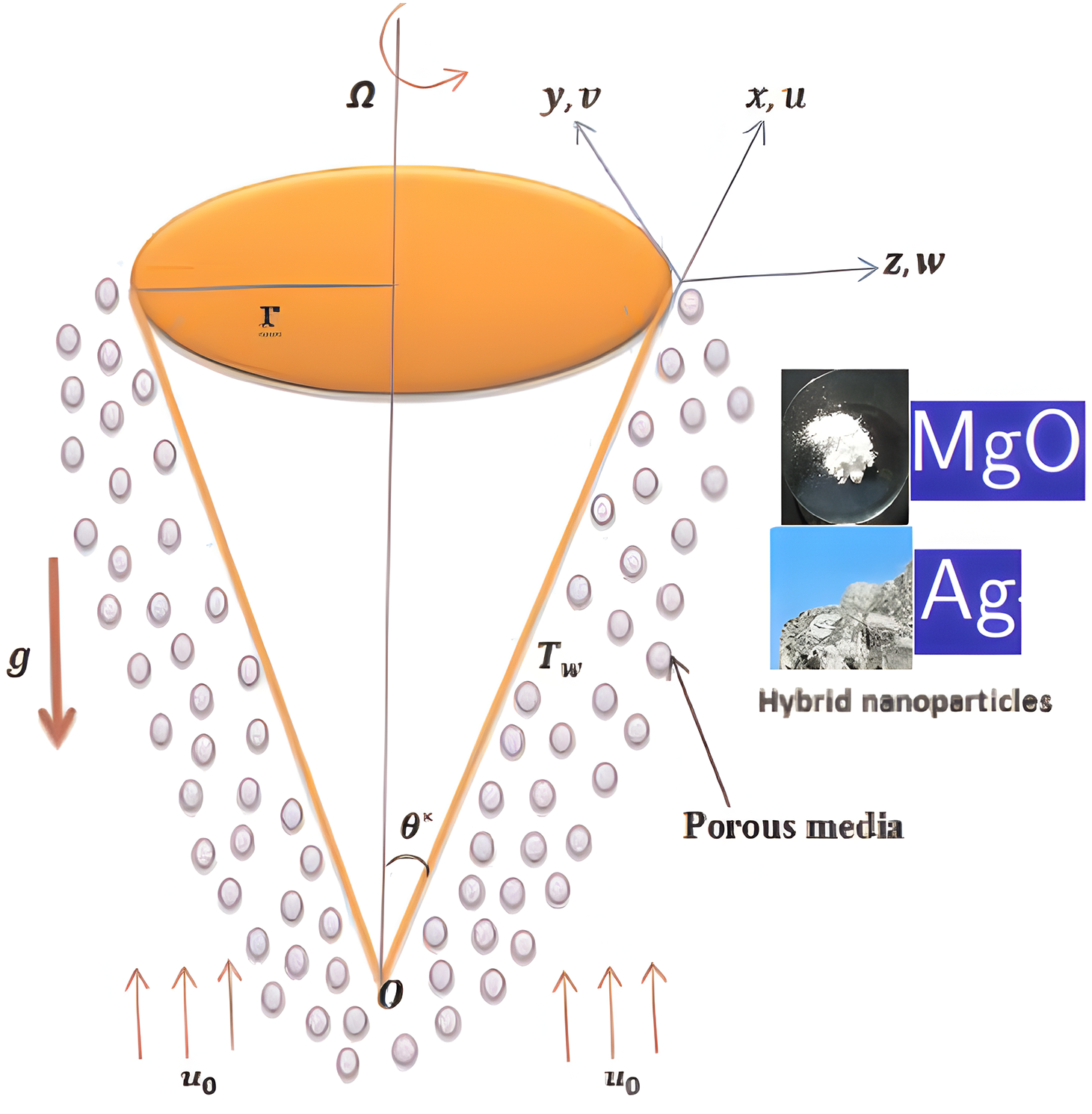
Figure 1: Geometry of the flow

According to Khan et al. [33], volume fraction, thermal conductivity, density, heat capacitance, thermal expansion coefficient, thermal conductivity and viscosity of the hybrid nanofluid, are defined by Eqs. (8)–(14), respectively:

ϕ=ϕAg+ϕMgO,(8)

αhnf=khnf(ρ)hnf,(9)

ρhnf=(1−ϕ)ρf+(ϕAg×ρAg+ϕMgO×ρMgO),(10)

(ρCp)hnf=(1−ϕ)(ρCp)f+(ϕAg×(ρCp)Ag+ϕMgO×(ρCp)MgO),(11)

(ρβ)hnf=(1−ϕ)(ρβ)f+(ϕAg×(ρβ)Ag+ϕMgO×(ρβ)MgO),(12)

khnfkbf=kMgO+2kbf+2ϕMgO(kMgO−kbf)kMgO+2kbf−ϕMgO(kMgO−kbf),kbfkf=kAg+2kf+2ϕAg(kAg−kf)kAg+2kf−ϕAg(kAg−kf)(13)

μhnf=μf(1−(ϕAg+ϕMgO))2.5.(14)

Using Eqs. (6), (8)–(14) and the transformations specified by [29]:

u=−Ωxsin⁡Θ∗2(1−At∗)f′(η),v=Ωxsin⁡Θ∗1−At∗g(η),w=(Ωxsin⁡Θ∗1−At∗)1/2f(η)N=x2(νfΩsin⁡Θ∗1−At∗)1/2ω(η),T=T∞+(Tw−T∞)θ(η),Tw−T∞=(T0−T∞)(1−At∗)xLη=(Ωsin⁡Θ∗ν0(1−At∗))1/2z,

the system of partial differential Eqs. (1)–(5) is transformed into ordinary differential Eqs. (15)–(18):

(1−Aθ+ϕ1K)f′′′−[Aθ′+K]f′′+ϕ1ϕ2[12f′2−ff′′−2g2−s(f′+η2f′′)−2ϕ4λθ]+ϕ2[Kω−Kpf′+ϕ3Mf′]=0,(15)

(1−Aθ+ϕ1K)g′′−[Aθ′+K]g′+ϕ1ϕ2[gf′−fg′−s(g+η2g′)]−ϕ2[Kpg+ϕ3Mg]=0,(16)

(1−Aθ+12ϕ1K)ω′′−[Aθ′+12K]ω′+ϕ1ϕ2[ωf′−fω′−s(ω+η2ω′)]−ϕ2KB(2ω−f′′)=0,(17)

khnfkf(1Pr)[(1+εθ+Rd)θ′′+εθ′2]+ϕ5[12θf′−fθ′−s(2θ+η2θ′)]=0,(18)

where

Gr=g∗(T0−T∞)L3νf2cos⁡Θ∗,ReL=ΩL2sin⁡Θ∗νf,λ=GrReL,K=κμf,B=νf(1−st∗)jΩsin⁡Θ∗,Rd=16σ∗T∞3L23k∗Gr1/2μf(ρCp)f,M=σfB02(1−st∗)Ωsin⁡Θ∗ρf,kp=νf(1−st∗)k0Ωsin⁡Θ∗,Pr=ν(ρCp)fkf,ϕ1=(1−ϕ)+ϕAg(ρAgρf)+ϕMgO(ρMgOρf),ϕ2=(1−ϕ)1/2,ϕ3=σhnfσf,ϕ4=(1−ϕ)+ϕAg((βt)Ag(βt)f)+ϕMgO((βt)MgO(βt)f),ϕ5=(1−ϕ)+ϕAg((ρCp)Ag(ρCp)f)+ϕMgO((ρCp)MgO(ρCp)f).

The nondimensional boundary conditions take the form:

f(0)=0,f′(0)=0,g(0)=1,ω(0)=0,θ(0)=1,(19a)

f′→0,g→0,ω→0,θ→0asη→∞.(19b)

The skin friction coefficient and local Nusselt number are defined as:

Cfx=2τxzρf(Ωxsin⁡Θ∗1−st∗)2,Cfy=−2τyzρf(Ωxsin⁡Θ∗1−st∗)2(20)

Nux=−xqwkf(Tw−T∞)(21)

where

τxz=μhnf(∂u∂z)z=0,τyz=μhnf(∂v∂z)z=0,qw=−xkf(Tw−T∞)[khnf∂T∂z+(qr)w]z=0z.

The corresponding non-dimensional form for Eqs. (20) and (21) are as follows:

CfxRex1/2=−[1ϕ2(1−Aθ)f′′(η)]η=0,CfyRex1/2=−[2ϕ2(1−Aθ)g′(η)]η=0(22)

NuxRex−1/2=−(khnfkf+Rd)θ′(0),(23)

where Rex=x2Ωsin⁡Θ∗νf(1−st∗) is the Reynolds number.

3  Numerical Method

Numerical solutions to the non-dimensionalized system of Eqs.(15)–(18) are obtained using the OGMDSQLM, proposed by Mkhatshwa [34]. The numerical solutions were generated through codes developed in MATLAB. The solution algorithm of this numerical method is based on numerical techniques namely QLM, spectral collocation, multidomain overlapping grid and Lagrange interpolation polynomials with Gauss-Lobatto-Chebyshev grid points. To implement the method, the integration domain, [0,η∞], is divided into finite overlapping subintervals of equal length, illustrated in Fig. 2. As shown in Fig. 2, the domain of integration is divided into p∈N|p>1 subintervals. Each subinterval is then discretized into a predefined number of collocation points, say Nη+1, where η denotes a space variable. The SQLM is then applied in each subinterval, with the approximate solution(s) of a previous subinterval set as starting values for SQLM iterations in the next interval. The incorporation of the overlapping phenomenon is achieved by permitting an iterative process within the current subinterval, wherein each iteration induces a displacement, denoted as a fixed step (η02−η01, as seen in Fig. 2). To obtain the solution of the nonlinear system of differential Eqs.(15)–(18) employing the overlapping grid multidomain spectral quasilinearization method, the algorithm is as follows: firstly, the division of the integration interval into overlapping subintervals, as illustrated in Fig. 2; subsequently, the application of QLM as proposed by Motsa et al. [35] to Eqs.(24)–(27) where l signifies a subinterval, and (r+1) denotes the current iteration level; further, the computation of derivatives at each subinterval collocation point through the utilization of the Chebyshev numerical differentiation matrix; and the employment of the pseudospectral collocation method at the boundaries (Eq. (34)). Ultimately, an iterative solution is obtained through the resolution of a matrix equation, as given by Eqs.(33) and (34), yielding the approximate solution.

a1,11,lfl,(r+1)′+a1,12,lfl,(r+1)′′+a1,13,lfl,(r+1)′′′+a1,10,lf+a1,41,lθl,(r+1)′+a1,40,lθl,(r+1)=R1,l(24)

a2,21,lgl,(r+1)′+a2,22,lgl,(r+1)′′+a2,41,lθl,(r+1)′+a2,40,lθ+a2,11,lfl,(r+1)′+a2,10,lfl,(r+1)=R2,l(25)

a3,31,lωl,(r+1)′+a3,32,lω′′l,(r+1)+a3,30,lωl,(r+1)+a3,41,lθ′+a3,40,lθl,(r+1)+a3,11,lfl,(r+1)′+a3,12,lfl,(r+1)′′+a3,10,lfl,(r+1)=R3,l(26)

a4,41,lθl,(r+1)′+a4,42,lθl,(r+1)′′+a4,40,lθl,(r+1)+a4,11,lf′+a4,10,lfl,(r+1)=R4,l(27)

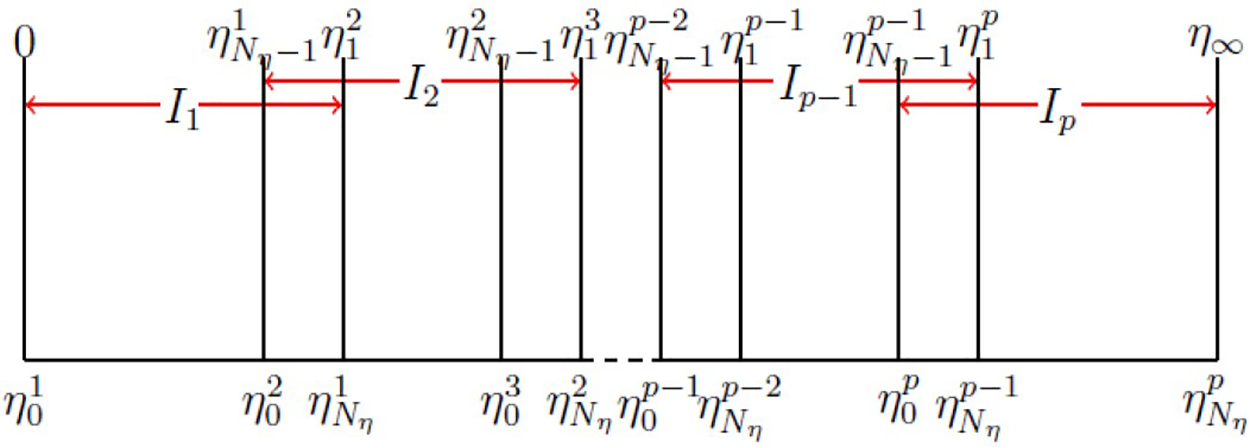
Figure 2: Overlapping grid, Mkhasthwa [34]

Using the SQLM method proposed by Motsa et al. [35], the coefficients of the unknowns are evaluated at the previous iteration level r (see Eqs.(28) and (29)).

a1,11,l=ϕ1ϕ2fl,r′−ϕ1ϕ2s−ϕ2Kp+ϕ2ϕ3M,a1,1(2,l)=−Aθl,r′−K−ϕ1ϕ2fl,r−ϕ1ϕ2sη2a1,13,l=1−Aθl,r+ϕ1K,a1,1(0,l)=−ϕ1ϕ2fl,r′′,a1,4(1,l)=−Afl,r′′,a1,40,l=−Afl,r′′′−2ϕ1ϕ2ϕ4Ka2,2(0,l)=ϕ1ϕ2fl,r′−ϕ1ϕ2s−ϕ2kp−ϕ2ϕ3M,a2,2(1,l)=−Aθl,r′−K−ϕ1ϕ2fl,r−ϕ1Φ2sη2a2,22,l=1−Aθl,r+ϕ1K,a2,2(0,l)=ϕ1ϕ2fl,r′−ϕ1ϕ2s−ϕ2Kp−ϕ2ϕ3M,a2,41,l=−Agl,r′,a2,4(0,l)=−Agl,r′′,a2,1(1,l)=ϕ1ϕ2gl,r,a2,10,l=−ϕ1ϕ2gl,r′,a3,3(1,l)=−Aθl,r′−0.5K−ϕ1ϕ2fl,r−ϕ1ϕ2η2,}(28)

a3,32,l=1−Aθl,r+0.5ϕ1K,a3,3(0,l)=ϕ1ϕ2fl,r′−ϕ1ϕ2s−2KBϕ2,a3,41,l=−Aωl,r′,a3,40,l=−Aωl,r′′,a3,1(1,l)=ϕ1ϕ2ωl,r,a3,40,l=−Aωl,r′′,a3,12,l=ϕ2KB,a3,1(0,l)=−ϕ1ϕ2ωl,r′,a4,4(1,l)=2εθl,r′KhnfKfPr−ϕ5fl,r−ϕ5sη2,a4,42,l=KhnfKfPr(1+ηθl,r+Rd),a4,40,l=KhnfKfPrηθl,r′′+0.5ϕ5fl,r′−2ϕ5s,a4,11,l=0.5ϕ5θl,r,a4,1(0,l)=−ϕ5θl,r′.}(29)

As mentioned earlier, the essence of the overlapping grid multidomain spectral quasilinearization is the slicing of the physical domain into a finite number of overlapping subintervals, the non-dimensional boundary conditions then become as written in Eq. (30).

f(0)l,(r+1)=0,f′(0)l,(r+1)=0,g(0)l,(r+1)=1,ω(0)l,(r+1)=0,θ(0)l,(r+1)=1,(30a)

fl,(r+1)′→0,gl,(r+1)→0,ωl,(r+1)→0,θl,(r+1)→0asη→∞.(30b)

The linearized system of Eqs.(24)–(27) can be written compactly as shown in system (31), where D is the Chebyshev numerical differentiation matrix, I is the identity matrix of dimension equal to the number of collocation points. Furthermore, the linearization coefficients, for example a1,1(1,l), are diagonal matrices of dimension equal to number of collocation points.

[a1,1(1,l)D1+a1,1(2,l)D2+a1,1(3,l)D3+a1,1(0,l)I]Fl,(r+1)+[a1,4(1,l)D+a1,4(0,l)I]Θl,(r+1)=R1,l,[a2,2(1,l)D+a2,2(2,l)D2+a2,2(0,l)I]Gl,(r+1)+[a2,4(1,l)D+a2,4(0,l)I]Θl,(r+1)+[a2,1(1,l)D+a2,1(0,l)I]Fl,(r+1)=R2,l,[a3,3(1,l)D+a3,3(2,l)D2+a3,3(0,l)I]Ωl,(r+1)+[a3,4(1,l)D+a3,4(0,l)I]Θl,(r+1)+[a3,1(1,l)D+a3,1(2,l)D2+a3,1(0,l)I]Fl,(r+1)=R3,l,[α4,4(1,l)D+α4,4(2,l)D2+α4,4(0,l)I]Θl,(r+1)+[α4,1(1,l)D+α4,1(0,l)I]Fl,(r+1)=R4,l.}(31)

The system of Eq. (31) can be represented in matrix from as system (32). The column vectors of unknowns at a subinterval and current iteration level are: Fr+1l, Gr+1l, Ωr+1l,Θr+1l.

[A11A12A13A14A21A22A23A24A31A32A33A34A41A42A43A44][Fr+1lGr+1lΩr+1lΘr+1l]=[R1lR2lR3lR4l](32)

where

A11=[a1,1(1,l)D+a1,1(2,l)D2+a1,1(3,l)D3+a1,1(0,l)I],A12=0,A13=0,A14=[a1,4(1,l)D+a1,4(0,l)I],A21=[a2,1(1,l)D+a2,1(0,l)I], A22=[a2,2(1,l)D2+a2,2(2,l)D+a2,2(0,l)I], A23=0,A24=[a2,4(1,l)D+a2,4(0,l)I],A31=a3,1(1,l)D2+a3,1(1,l)D+a3,l(0,l)l,A32=0,A33=[a3,3(1,l)D+a3,3(2,l)D2+a3,3(0,l)I],A34=[a3,4(1,l)D+a3,4(0,l)I],A41=[α4,1(1)D+α4,1(0)I],A42=0,A43=0,A44=[α4,4(1,l)D+α4,4(2,l)D2+α4,1(0,l)I].(33)

and 0 is a square matrix of zeros, also of dimension consistent with the number of collocation points in the computation.

Applying the pseudospectral method at the boundaries gives:

fr+1(zNη)=0,∑j=0NηDN,j fj,(r+1)=0,gr+1(zNη)=1,ωr+1(zNη)=0,θr+1(zNη)=1atη=0.∑j=0NηD0,jfj,(r+1)(z0)→0,gj,(r+1)(z0)→0,ωj,(r+1)(z0)→0,θj,(r+1)(z0)→0,asη→∞.}(34)

The OGMDSQLM leads to a sparse form of the coefficient matrix in system (32), which is expressed in its expanded form below, with the boundary conditions incorporated accordingly on the diagonal submatrices.

[D0,0D0,1D0,2……D0,N00……000……000……0A11A12A13A14DN,0DN,1DN,2……DN,N00……000……000……0000……100……000……000……0000……010……000……000……0A21A22A23A24000……000……100……000……0000……000……010……000……0A31A32A33A34000……000……000……100……0000……000……010……010……0A41A42A43A44000……000……000……000……1](35)

To begin the iterative search for approximate solutions, the following functions:

f0(η)=η2exp⁡(−η),g0(η)=exp⁡(−η),ω0(η)=ηexp⁡(−η)andθ0(η)=exp⁡(−η),(36)

that satisfy the boundary conditions are taken as approximate solutions.

4  Results and Discussion

To check the validity of the current numerical scheme, a comparison of the present values of skin friction and Nusselt number with those published in the literature by Malik et al. [29], Chamkha et al. [36] is presented in Table 2. Using the nanoparticle volume fractions of hybrid nanofluid consisting of portions of nano particles ϕAg=0.018 and ϕMgo=0.002, we examined the components of velocities, microrotation and temperature profile for selected parameters from the following respective ranges 0≤ε≤0.5, 0≤s≤0.5, 0≤B≤3, 0≤A≤2.5, 0≤M≤1, 0≤Rd≤1, 0≤K≤1, 0≤λ≤5 which lead to convergence and stable results. The following parametric values are used for the numerical computations: Pr=6.8, ε=0.2, s=0.2, B=2, A=0.02, M=0.5, K=0.6, λ=3. As the value of the nondimentional form K, of the coupling number κ approaches one the fluid is more micropolar whereas as it approaches zero the fluid becomes more viscous. Fig. 3a shows that with an increase in the value of the coupling number, the fluid becomes more micropolar, resulting in a primary velocity slowdown in the vicinity of the boundary at its peak. Conversely, a decrease in velocity for the secondary flow is observed, as depicted in Fig. 3b. Physically this is due the rotational effect of the flow, the main flow is retarded and the secondary flow increases. Also, it can be observed from Fig. 3b, that the hybrid nanofluid, ϕAg+ϕMgO, enhances the primary velocity than the mono-nanofluid ϕMgO. From Fig. 3b the reverse trend from the primary flow is observed throughout the flow medium. From Fig. 3c, it is observed that the hybrid nanoflid reduces the temperature compared to the mono-nanoflluid. This is because hybridizing appropriately chosen nanoparticles, the heat transfer of the particles in the medium increases. From the same figure it is seen micropolar fluids enhances the temperature. From Fig. 3d, the rotational effect in the fluid particles is observed by enhancing the micropolar parameter. When K=0, there is no rotation, and consequently, no flow for ω, indicating that the fluid behaves as a viscous fluid. Moreover, from the same graph, it is observed the rotational effect for hybrid nanofluid near the boundary is greater than that of the mono-nanofluid. This may be due to the higher viscosity for hybrid nanofluid than the mono nanofluid which warrants further investigation.

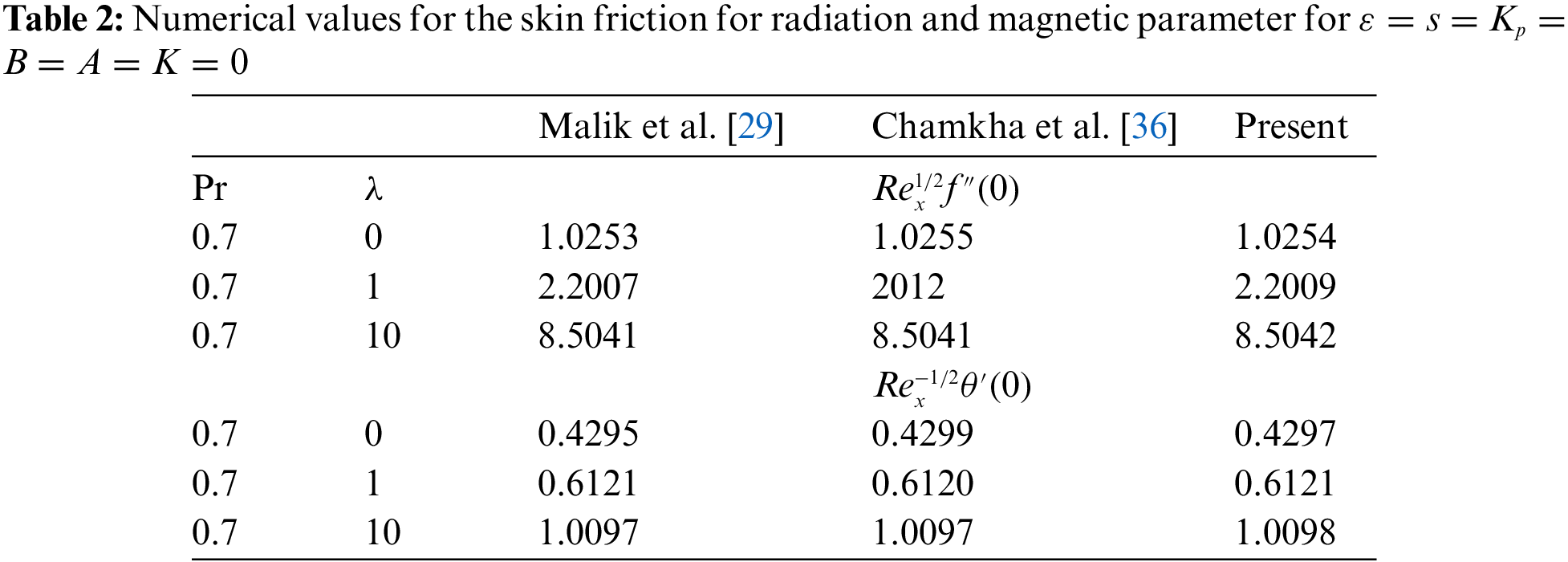
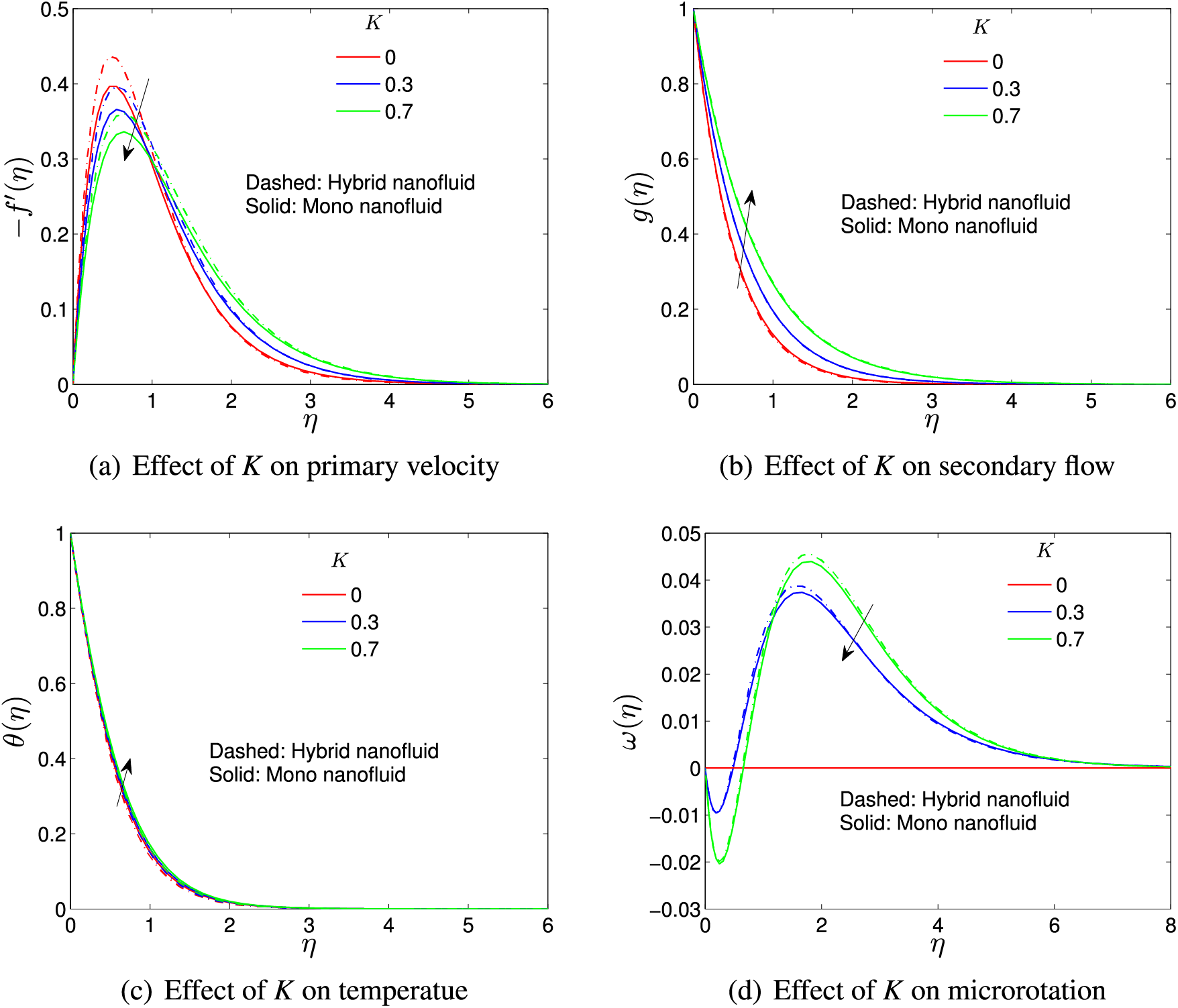
Figure 3: Coupling number effect

Fig. 4a shows that the smaller the variable viscosity parameter, the more the primary velocity diminishes. Physically, this implies that in the higher viscous region (near the boundary), the dominant force is buoyancy, and an increase in nanofluid concentration leads to an increase in velocity. The more hybrid nanofluid, the higher the thermal conductivity, which allows an increase in Brownian motion and, consequently, particle energy transfer. It is also interesting to note that away from the vicinity of the boundary, in the free stream region, the reverse effect is observed. However, it is evident from Fig. 4b that an increase in the variable viscosity parameter results in a decreasing effect on the secondary flow. This is because as the coupling number K increases, the fluid becomes more micropolar, and consequently, the particle sniping effect significantly retards the secondary flow. For the fractional volume of the hybrid nanofluid, ϕAg+ϕMgO, velocity is greater than the mon-nanofluid, ϕMgO, in both velocities. The influence of the variable viscosity parameter on temperature, presented in Fig. 4c, indicates that the higher the variable viscosity parameter, the lower the temperature. It is also noted that fractional volume hybrid nanofluid, ϕAg+ϕMgO, reduces the temperature than mon-nanofluid, ϕMgO. It is seen from the Fig. 4c that the temperature decreases with an increase in the variable viscosity parameter. It is also noted for fractional volume hybrid nanofluid, ϕAg+ϕMgO, temperature decreases compared to the mon-nanofluid, ϕMgO. This is because more nanoparticles are involved the thermal properties of the resulting mixture are improved and Brownian motions of nanoparticles increases leading to increase the viscosity in the medium. Fig. 4d describes the effect of variable viscosity on microrotation, the hybrid nanofluid fraction is higher than the mon-nanofluid in the region closer to the vicinity of the boundary.

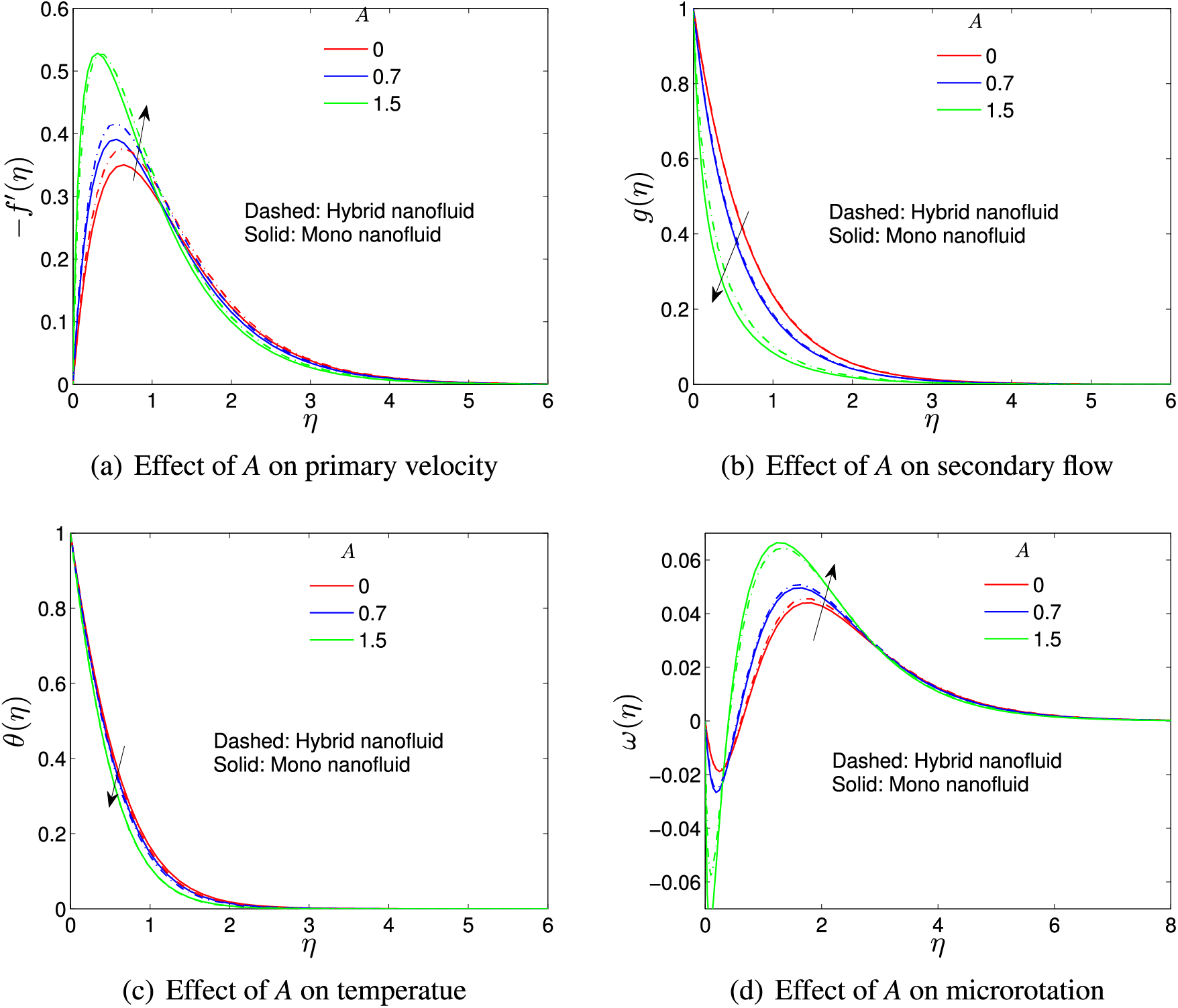
Figure 4: Variable viscosity parameter effect

Fig. 5a,b shows the impact of porosity parameter on both primary and secondary flows. It is clear from the figures that primary velocity decreases with an increase in the porosity parameter. The velocities of the hybrid nanofluid, ϕAg+ϕMgO, are enhanced as compared to the mono-nanofluid, ϕMgO. Physically increasing the value of k0, that is less pour in the flow medium, in Eq. (2), and hence decreasing the value of Kp in Eq. (15) causes the porous zone’s transparency to decrease and hence the velocity decreases. We can observe from these results hybrid nanofluid increase the flow velocities than the mono-nanofluid. The effect of Kp on temperature and microrotation as shown in Fig. 5c,d is similar to the effect of K in Fig. 3c,d.

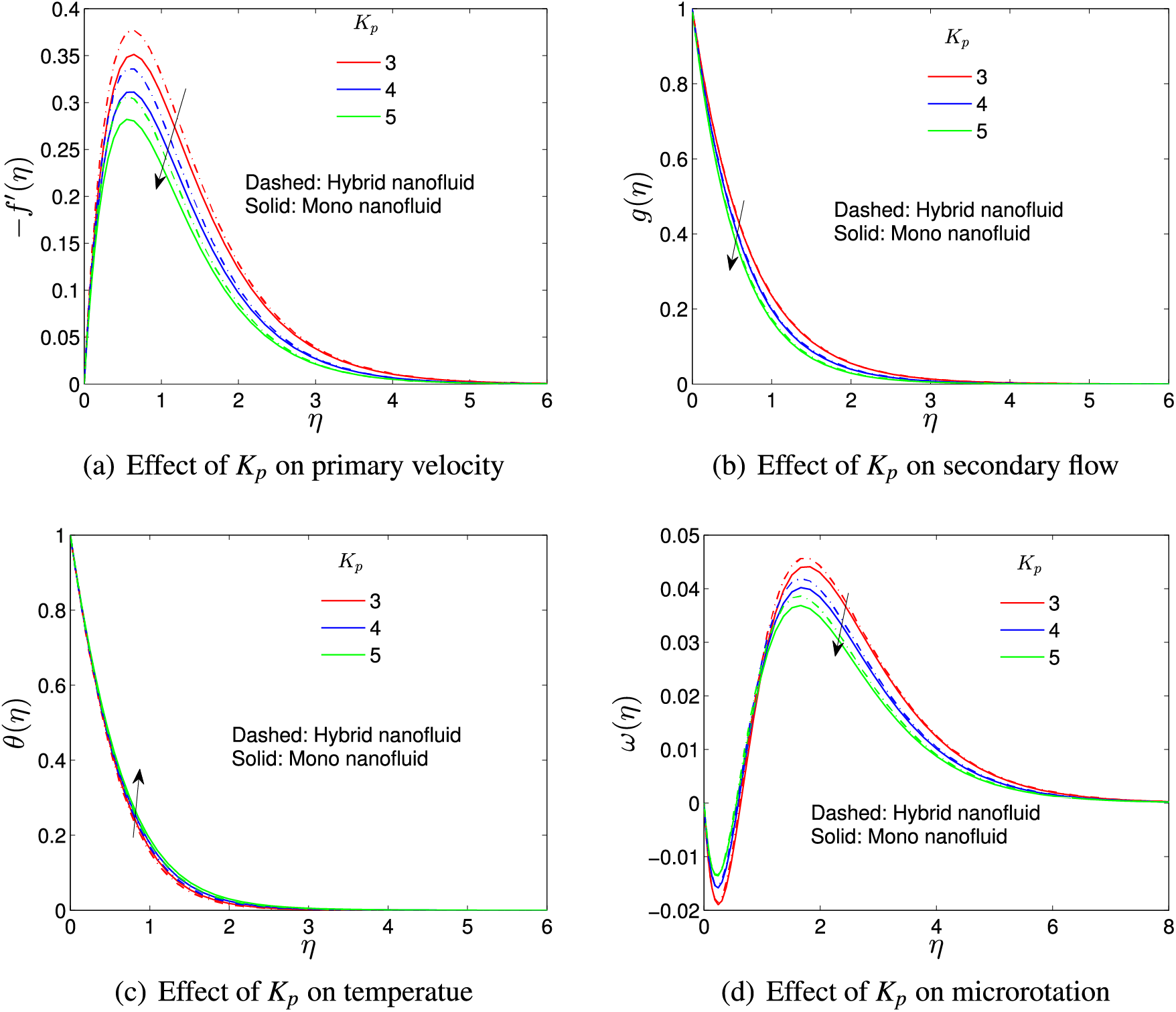
Figure 5: Porosity parameter effect

In Tables 3 and 4, the flow behaviour for different values of radiation and magnetic parameter on local sikin friction effect and Nusselt number are presented. The cases for mono-nanofluids Ag/water,MgO/water and hybrid nanofluid Ag−MgO/water are studied. It is observed that both the local skin friction and the Nusselt number increases with an increase in the radiation and magnetic parameters.

5  Conclusion

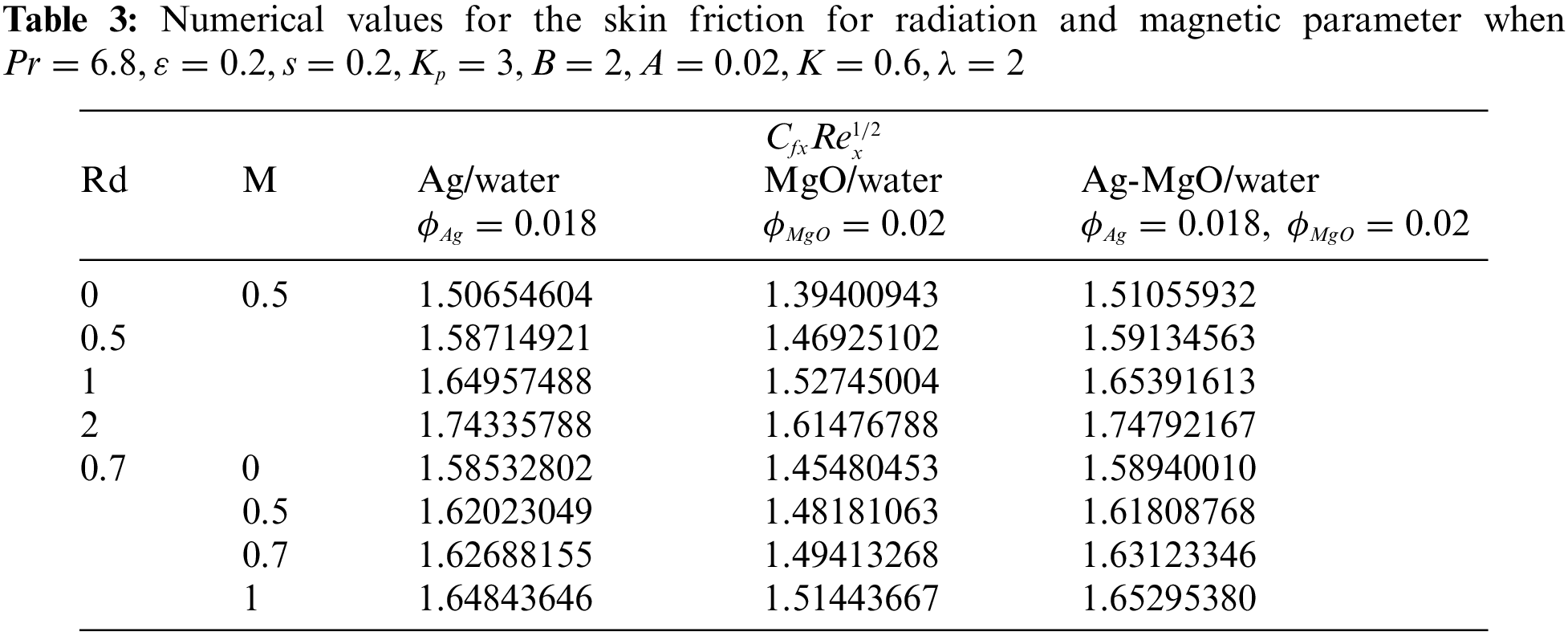
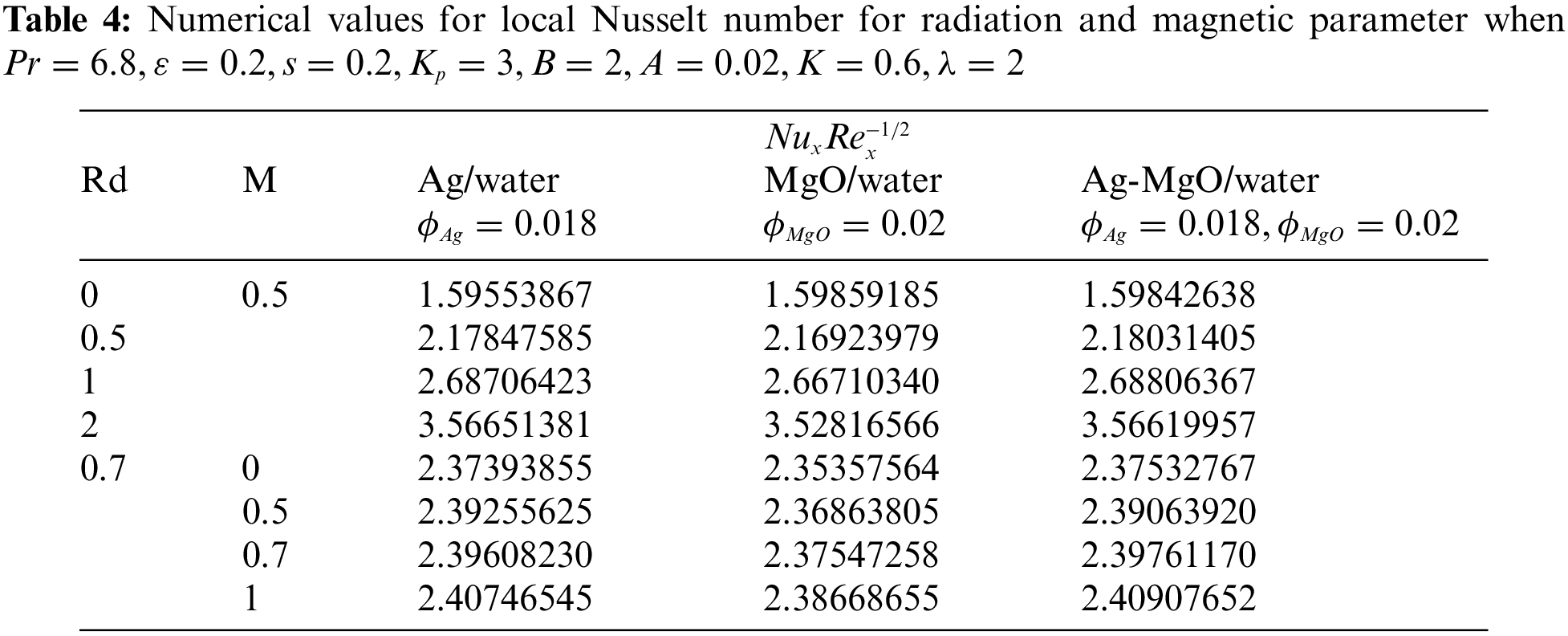
A numerical investigation for unsteady magneto micropolar Ag−MgO hybrid nanofluid flow on an inverted rotating cone is considered. The analysis is conducted in the presence of thermal radiation and uniform magnetic field in a porous media. Using appropriate transformations, the system of partial differential equations that models the problem is converted to a system of ordinary differential equations. These equations are then solved numerically using the overlapping grid multidomain spectral quasilinearization method. The velocities, microrotation and temperature profiles are examined graphically for prominent parameters. The main results are presented below:

•   Micropolar fluid assists the secondary flow and diminishes the main flow. The water hybrid nanofluid, ϕAg+ϕMgO, enhances the main flow whereas it decreases the secondary flow compared to the mono-nanofluid ϕMgO water.

•   The rotational effect for the hybrid nanofluid near the boundary is greater than that of the mono-nanofluid.

•   For the water hybrid nanofluid, ϕAg+ϕMgO, the variable viscosity parameter has a greater effect on velocity compared to the corresponding case of mono-nanofluid ϕMgO water.

•   The variable viscosity parameter reduces the temperature for the hybrid nanofluid, ϕAg+ϕMgO, compared to the mono-nanofluid ϕMgO water.

•   The porosity parameter decreases the main flow; however, the inclusion of the hybrid nanofluid ϕAg+ϕMgO can enhance velocity.

Acknowledgement: The authors would like to thank the anonymous reviewers for their valuable comments.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: conceptualisation: Mekonnen S. Ayano; writing original draft: Mekonnen S. Ayano; methodology, code writing: Thokozani N. Khumalo, Stephen T. Sikwila; Matlab code creation and validation: Mekonnen S. Ayano, Thokozani N. Khumalo, Stephen T. Sikwila; analysis and interpretation of results: Mekonnen S. Ayano, Stanford Shateyi; final manuscript preparation: Mekonnen S. Ayano, Stephen T. Sikwila; validation of results: Mekonnen S. Ayano, Stanford Shateyi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The readers can contact the corresponding author and request the Matlab codes used to generate the data.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Delouei A, Atashafrooz M, Hasan S, Karimnejad S. The thermal effects of multi-walled carbon nanotube concentration on an ultrasonic vibrating finned tube heat exchanger. Int Comm Heat Mass Trans. 2022;135:106098. [Google Scholar]

2. Siavashi M, Miri J, Seyed M. Numerical performance analysis of a counter-flow double-pipe heat exchanger with using nanofluid and both sides partly filled with porous media. J Therm Anal Calorim. 2018;135(2):1595–610. [Google Scholar]

3. Izadi A, Siavashi M, Xiong Q. Impingement jet hydrogen, air and Cu-H2O nanofluid cooling of a hot surface covered by porous media with non-uniform input jet velocity. Int J Hydrogen Energy. 2019;44(3015933–48. [Google Scholar]

4. Saleh H, Alali E, Ebaid A. Medical applications for the flow of carbon-nanotubes suspended nanofluids in the presence of convective condition using laplace transform. J Assoc Arab Univ Basic Appl Sci. 2017;24(1):206–12. [Google Scholar]

5. Wong KV, De Leon O. Applications of nanofluids: current and future. Adv Mech Eng. 2010;2:519659–70. [Google Scholar]

6. Mkhatshwa M, Motsa S, Ayano M, Sibanda P. MHD mixed convective nanofluid flow about a vertical slender cylinder using overlapping multi-domain spectral collocation approach. Case Stud Therm Eng. 2020;18:100598. doi:10.1016/j.csite.2020.100598. [Google Scholar] [CrossRef]

7. Thameem BH, Sivaraj R, Subramanyam RA, Chamkha AJ. SWCNH/diamond-ethylene glycol nanofluid flow over a wedge, plate and stagnation point with induced magnetic field and nonlinear radiation-solar energy application. Eur Phys J Spec Top. 2019;228(12):2531–51. doi:10.1140/epjst/e2019-900048-x. [Google Scholar] [CrossRef]

8. Akmal N, Sagheer M, Hussain S, Kamran A. Investigation of free convection in micropolar nanofluid with induced magnetic field. Eur Phys J Plus. 2019;134(5):179. doi:10.1140/epjp/i2019-12512-7. [Google Scholar] [CrossRef]

9. Zeeshan A, Ellahi R, Hassan M. Magnetohydrodynamic flow of water/ethylene glycol based nanofluids with natural convection through a porous medium. Eur Phys J Plus. 2014;129(12):123. doi:10.1140/epjp/i2014-14261-5. [Google Scholar] [CrossRef]

10. Hady FM, Ibrahim FS, Abdel-Gaied SM, Eid MR. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res Lett. 2012;7(1):26. doi:10.1186/1556-276X-7-229. [Google Scholar] [CrossRef]

11. Liu L, Miao P, Xu Y, Tian Z, Zou Z, Li G. Study of PT/TiO2 nanocomposite for cancer-cell treatment. J Photochem Photobiol B: Biol. 2010;98(3):207–10. doi:10.1016/j.jphotobiol.2010.01.005. [Google Scholar] [CrossRef]

12. Noghrehabadi A, Behseresht A, Ghalambaz M, Behseresht J. Natural-convection flow of nanofluids over vertical cone embedded in Non-Darcy porous media. J Thermophys Heat Trans. 2013;27(2):334–41. doi:10.2514/1.T3965. [Google Scholar] [CrossRef]

13. Sheikholeslami M, Gorji Bandpy M, Ellahi R, Hassan M, Soleimani S. Effects of mhd on cu-water nanofluid flow and heat transfer by means of CVFEM. J Magn Magn Mater. 2014;349(6):188–200. doi:10.1016/j.jmmm.2013.08.040. [Google Scholar] [CrossRef]

14. Afify AA. The effect of radiation on free convective flow and mass transfer past a vertical isothermal cone surface with chemical reaction in the presence of a transverse magnetic field. Can J Phys. 2004;82(6):447–58. doi:10.1139/p04-009. [Google Scholar] [CrossRef]

15. Makinde O, Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Therm Sci. 2011;50(7):1326–32. doi:10.1016/j.ijthermalsci.2011.02.019. [Google Scholar] [CrossRef]

16. Mehmood Z, Mehmood R, Iqbal Z. Numerical investigation of micropolar casson fluid over a stretching sheet with internal heating. Commun Theor Phys. 2017;67(4):443. doi:10.1088/0253-6102/67/4/443. [Google Scholar] [CrossRef]

17. El-Kabeir SMM, Abdou MM. Chemical reaction, heat and mass transfer on MHD flow over a vertical isothermal cone surface in micropolar fluids with heat generation/absorption. Appl Math Sci. 2007;1: 1663–74. [Google Scholar]