Analysis of Convective Heat Exchanges and Fluid Dynamics in the Air Gap of a Discoid Technology Rotary Machine

Dimensionless Numbers

1  Introduction

The cooling of wind turbine rotors represents a major challenge for a number of research projects, as well as the research carried out in [1,2] explored in depth the flow structure and heat exchange in a rotor-stator system for a better understanding. Reference [3] studied theoretically and experimentally the impact of an air inlet at the center of the stator on mass and heat transfer for different distances between the discs. The effect of the jet was to accelerate air renewal and disrupt the shear layer formed by disk rotation at this point, generating vortices at the jet exit. The work of [3,4] has also highlighted the effect of jet size and separation of the spray exit point from that of the impact surface on these heat transfer phenomena. Several studies have been carried out in similar configurations, including that of [5], who investigated the influence of gap ratio on heat transfer. In their study, they compared experimental results using k-ω SST turbulence to determine the deceleration point of the Nusselt coefficient (Nur) expression and the location of the second peak of a Nur distribution. Furthermore, reference [5] examined the location of the 2nd peak of the Nusselt profile, which describes the heat transfer distribution at the surface of the rotating disk. Their observations reveal that this second peak, corresponding to a further increase in heat transfer, is located at some distance from the jets. These results suggest that the interaction between the jets and the disc surface creates privileged zones where heat transfers are more intense. References [6,7] carried out a study of heat exchange inside a rotor equipped with a jet. They used thermographic imaging to measure the heat exchange coefficient along the rotor, varying parameters such as and flow rate. Their research indicated that, whatever the combination of flow parameters, the use of flow always improved heat exchange compared with the non-jet configuration. They also observed that the near-stop zone was highly dependent on flow rate. Similarly, at the outer radii of the rotor, the Nusselt number, which measures heat exchange, depends on both flow rate and Reynolds number. In their studies, references [6,8] have formulated relationships for the average Nusselt number, taking into account different ranges of ratio dimensions. These correlations make it possible to predict heat exchange in the rotor system as a function of flow conditions and geometric parameters this study was complemented by that of [9]. In this study, new calculations based on a Reynolds stress model were confronted with particle image velocimetry measurements and predictions from a k-ω SST model for a jet flow impacting a rotating disk in an unwrapped discoidal rotor-stator system. The results identified three distinct flow regions, characterized turbulence intensity, and found increased heat transfer in the jet-dominated region, with a notable influence of jet Reynolds number on heat transfer distribution. All these data were compared with the k-ω SST and RSM models of [9] in a similar geometry. The aim of this study is to numerically validate the experiments of [6,10], to propose a numerical model of two-jet cooling, and to analyze heat exchange and flow characteristics in a specific configuration using Ansys-Fluent [11] numerical simulation software, renowned for its accuracy in 3D modeling. To study flow and heat transfer, reference [12] numerically explored the effect of air friction heating on the rotor-stator micro-cavity at high speed, analyzing the influence of centrifugal force and spacing. Reference [13] analyzed the vortex flow and heat transfer properties of a rotor-stator cavity configuration. Reference [14] also numerically examined the heat transfer properties in the rotor-stator cavity using steady-state flow analysis. Kim et al. [15] conducted an experimental study of the central flow region of the rotor-stator disk cavity on a low-speed turbine test facility. Yang et al. [16] numerically and experimentally investigated the flow and heat transfer for a simplified rotor-stator pre-swirl system with the radial outflow.

2  Experimental Study

The experimental setup [6,10] shown in Figs. 1 and 2 features an aluminum stator with an outer radius of 310 mm. To study various configurations, we have the flexibility to adjust the spacing between the rotor and stator within a range of 3 to 50 mm, enabling us to obtain scaled spacings varying from G = 0.02 to G = 0.1. The stator is fitted with a fluorite window, enabling temperature to be measured on the rotor using infrared thermography. During operation, the stator disk is not subjected to any mechanical stress, but it is exposed to the thermal radiation emitted by the rotor. To regulate this radiative exchange, the stator surface is coated with a gray paint, whose emissivity is estimated at ϵs = 0.65 ± 0.03 by calibration. Two T-type thermocouples are positioned at radial distances of 0.05 and 0.3 m. Because infrared thermography is used to measure surface temperature, it is necessary to observe the rotor through the stator. In order not to attenuate the infrared signal emitted by the rotor and picked up by the camera, a quasi-infrared-transparent material is integrated into the stator, enabling a radius of the rotor to be observed. Fluorite, with its high transmission coefficient, is often the material of choice for such applications. A porthole made of two fluorite lamellae 145 mm × 20 mm in size, glued together, is chosen, defining the observable area of the disk between radii 0.02 and 0.31 m. To alter flows near the rotating disk and improve heat transfer to its surface, a jet is introduced. The stator is perforated by an eccentric opening of diameter D = 26 mm to allow the passage of a long cylindrical tube connected to a centrifugal fan, thus generating an eccentric jet. Influential parameters include the jet-related Reynolds number (Rej = UD/ϑjair), the adimensioned spacing (G = H/R = 0.02), and the average jet velocity (Uj) between 10 and 32 m/s, generating jet-related Reynolds numbers ranging from Rej=16×103 to Rej=55.46×103.

Figure 1: Experimental bench [6,9]

Figure 2: Illustration of the experimental device in rotor-stator configuration [6,9]

3  Modelling the Problem and Numerical Simulation

3.1 Geometric Model

Fig. 3 shows a complex configuration known as a rotor-stator system, used to study aerodynamic flows and heat transfer. The air is injected into the space using two cylindrical inlet tubes. The spacing between the two discs, also known as the rotor-stator spacing, is an essential parameter that is precisely adjusted within a range of 0.02 to 0.1. The air passes through two tubes before reaching the turning disc. These tubes perform a vital role in regulating the air flow, and preparing the flow before it reaches the rotating disc. In this context, the Reynolds numbers associated with the two air jets and the rotation are fundamental parameters for characterising the stream flow. The Reynolds number of the jet is determined by taking into account parameters such as the injected air flow, the air jet diameter and the kinematic viscosity of the air. The following factors can have a considerable impact on the dynamics of fluid flow in this particular system:

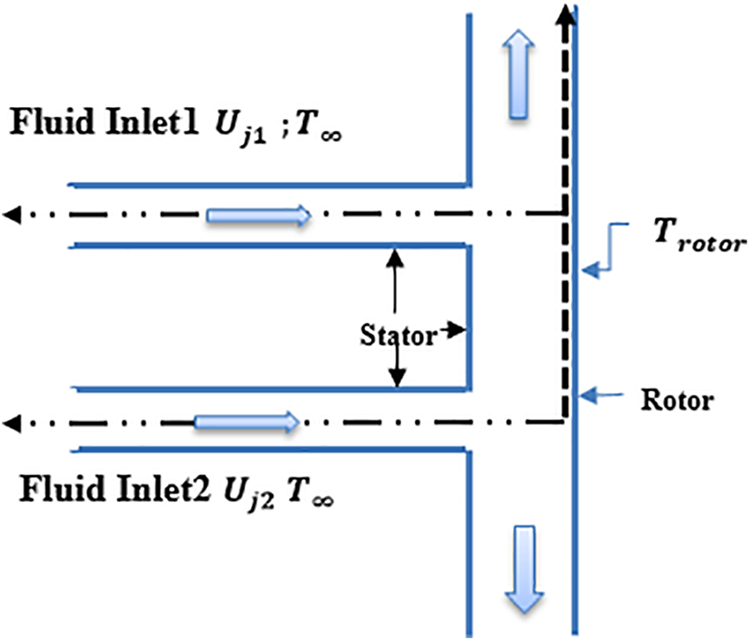
Figure 3: Rotor-stator configuration with two jets

•   Spacing between rotor and stator G=HRd

•   expression of reynolds number linked to the jet Rej=Uj×Dν

•   expression of rational Reynolds number Reω=ω×Rd2ν

3.2 Type of Meshing

Discrete transport equations refer to the mathematical equations that describe the behaviour of fluids in a system. In this context, these equations are solved on a computational domain, which is subdivided into numerous tetrahedral elements. The choice of a tetrahedral mesh (Fig. 4) has several advantages. Tetrahedral elements provide a better representation of the complex geometry of disc surfaces and offer greater flexibility for adjusting the mesh size. In the specific case of the spacing between two discs, it is crucial that the mesh is very fine. This means that the mesh size needs to be reduced around the walls in our tests in most cases in order to detect details and variations in the flow near the disc surfaces. In particular, it is important to have enough points in the boundary layer, which is the area where viscosity effects are dominant. To ensure an accurate representation of this limit layer, it is essential to ensure that the first layer of wall cells in the vertical orientation has a value of less than 5. Y+ is a dimensionless parameter used to characterise the resolution of the boundary layer, and a value of less than 5 guarantees an extremely precise reflection of the free flow regime in the vicinity of the walls. To achieve these objectives, it is necessary to adjust the mesh size according to the parameters that influence the flow, such that the air flow introduced, the spacing between the discs (G) and the rotor rotation speed. By modifying these parameters, it is important to adapt the mesh size accordingly to ensure adequate resolution of the boundary layer.

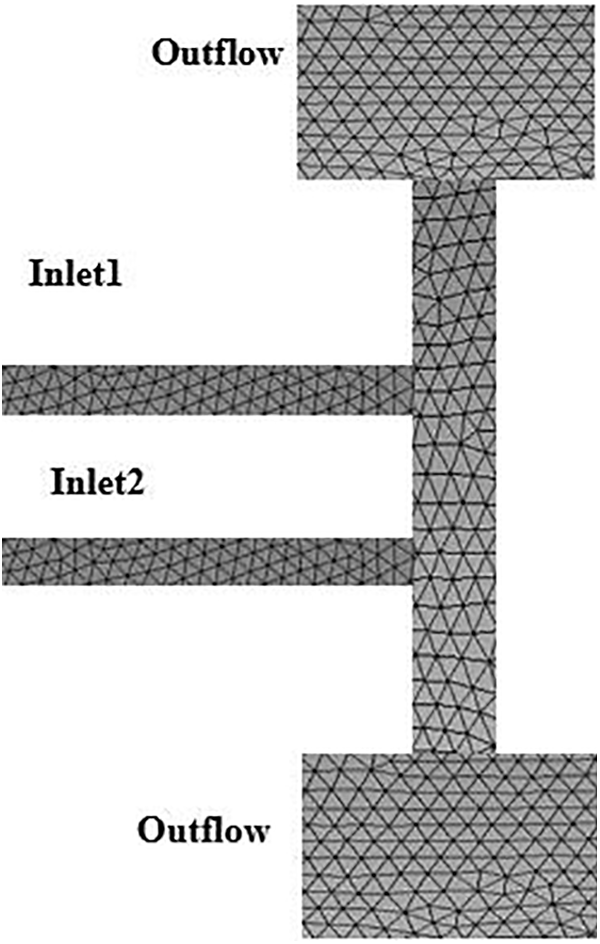
Figure 4: Study of the mesh structure with refinements close to the wall

Problem Boundary Specification defined as follows:

•   The flow characteristics are influenced by the velocities of the two jets, noted U1j and U2j.

•   While the temperatures T∞ are fixed in a prescribed manner.

•   On the walls, Ur=Uz=0, with the exception of the rotating walls, the tangential velocity is equal to Uθ=ω.r sur les parois tournantes et Uθ=0 hat on the fixed walls.

•   The fluid considered is air entering the cavity with a temperature T∞=20∘C.

•   Right Rotor Temperature Condition: Tr=80∘C.

3.3 Turbulence and Numerical Computation: Approaches and Methods

The Reynolds approach takes a statistical approach to exploring the characteristics of physical quantities. It subdivides these quantities into two distinct components: a mean value and a fluctuation. The Reynolds decomposition procedure is then used to integrate these two aspects into the Navier-Stokes flow equations. As far as the mean quantities are concerned, here are the equations derived from them:

u¯j∂u¯i∂xj=−1ρ∂p¯∂xi+ν∂2u¯i∂xj∂xj−∂(ui′uj′¯)∂xj(1)

uj¯∂T¯∂xj=−∂∂xj(λρcp∂T¯∂xj−T′uj′¯)(2)

where Rij=ui′uj′¯ and T′uj′¯ are called the terms relating to Reynolds constraints and turbulent heat transport. The number of unknowns in the problem then exceeds the number of equations available, and it becomes imperative to modelling turbulent tensors using turbulence models, in order to solve the problem consistently and establish a link between the fluctuating field and the mean field. For more details on turbulent flows and turbulence models [17], we encourage the reader to refer to Schiestel et al.’s book [18].

3.4 Simulating Turbulent Effects in Fluid Dynamics: RSM

Our approach is centred on a model using a 2nd order closure with a low Reynolds number derived from the model described by [19] and which is sensitive to the rotational effects described by [20]. The RSM model presented here offers an in-depth explanation of the flow field. Milan Đorđević et al. [21] has stated that RSM predictions are generally more accurate in the turbulent region. The general Reynolds tensor Rij is written as:

uj¯∂ui′uj′¯∂xj=Pij+Dij−εij+Oij+Ωij+Φij(3)

where Pij, Ωij, ϕij, εij, Oij simultaneously represent the following terms: The diffusion term, the pressure-deformation correction term and the dispersion term.

4  Results and Discussion

4.1 Streamlines

Fig. 5 shows a detailed graphical representation of the lines for different values of the rotation parameter. The area of the rotor and stator, delineated by solid lines, is clearly defined. At the core of this intricate configuration, two air jets converge toward the rotor, initiating the formation of a flow that radially propagates along the inner wall of the gap. When these two air jets come into contact, they generate a radial flow that is subsequently captured within a well-defined recirculation region. An interesting observation is that the size of this recirculation zone remains constant, irrespective of variations in the rotational Reynolds number. These findings align with the conclusions drawn from references [20,22], suggesting that the size of this recirculation zone primarily varies with the spacing parameter G. This stability in the dimension of the recirculation zone has significant implications for our overall understanding of the complex flows characterizing this specific configuration. These results underscore the importance of spacing parameter G as a key factor in the dynamics of flows and the convective transfer in the area under study.

Figure 5: Streamlines obtained for the 3 rotation rates for G = 0.02

For Reω=2.35×105 and beyond and r/Rd ratio of 0.62, the flow becomes centrifugal with streamlines parallel to the rotor. In cases of high rotation rates (Reω=4.02×105 and Reω=5.04×105) and at r/Rd values of 0.84 and 0.67, a large recirculation zone is observed near the stator, corresponding to an inflow of fluid from the outer region. Reference [22] noted the flow takes on a tangential orientation starting at r=0.186 and r=0.124 for a rotation rate of N=1.237 and N=2.47. For a Reynolds number and beyond an r/Rd ratio of 0.62, the flow takes on a centrifugal configuration with streamlines moving parallel to the rotor. In situations of high rotation rates (Reω=4.02×105 and Reω=5.04×105), at r/Rd points of 0.84 and 0.67, a large recirculation zone can be observed near the stator, corresponding to an intake of fluid from the outer region.

4.2 Velocity Mapping

Fig. 6 provides a detailed analysis of the radial mean velocity fields for different rotation values within our system. These data reveal significant variations in velocity near the impact points of the air jets, indicating a change in the direction of airflow at these specific locations. These variations are not random but result from the dynamic interaction between the air jets, the rotor, and the stator. When these jets interact with the rotor and stator, their trajectories undergo noticeable adjustments, resulting in velocity fluctuations. The negative velocities observed in the contours suggest regions where the airflow is moving in the opposite direction to the main flow direction. These regions may be associated with changes of direction or downshifts in the airflow, particularly near the edges of the rotor or stator. These negative velocities are often the result of phenomena such as air recirculation or vortex formation, which can significantly affect the overall flow dynamics and influence heat transfer in the system under study.

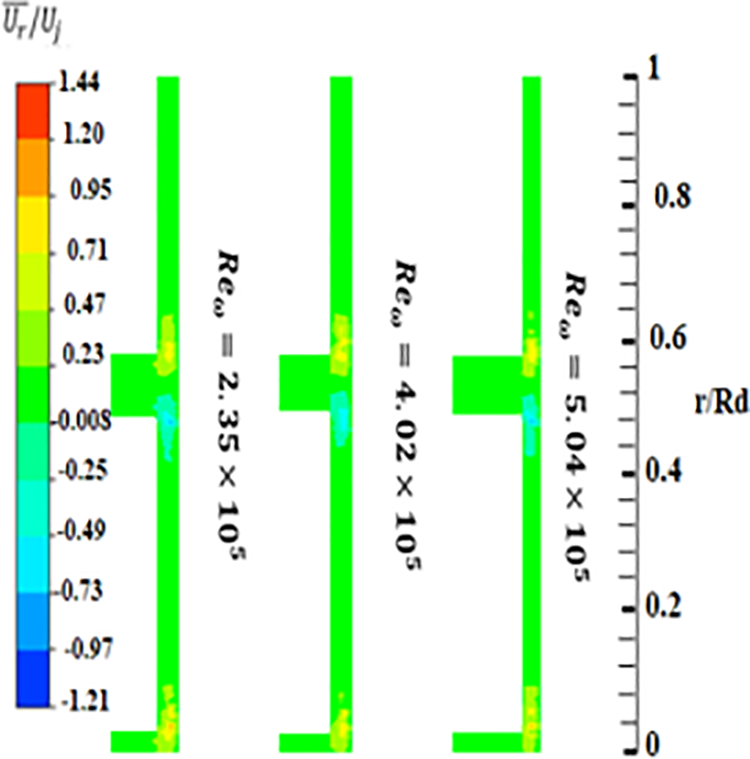
Figure 6: Radial mean velocity fields for G = 0.02, Rej=16×103

Fig. 7 of our study highlights the axis to axis distribution of radial and tangential velocities, considering non-zero rotation parameters, at three distinct positions for r/D (4.8, 5, 6.73, 6.92, 7.11). Examination of the characteristics of the radial and tangential velocity profiles enables us to identify different outflow structures. A stream with two clearly defined limiting levels, divided by a vigorously rotating, inviscid liquid, is categorized as a Batchelor [23] stream. Conversely, if the stream has only one boundary layer, with virtually zero tangential velocity at the distance of this boundary layer, it is referred to as a Stewartson [24] stream. These distinctions underline the variability of flow phenomena as a function of rotation parameters and positions in the configuration under consideration.

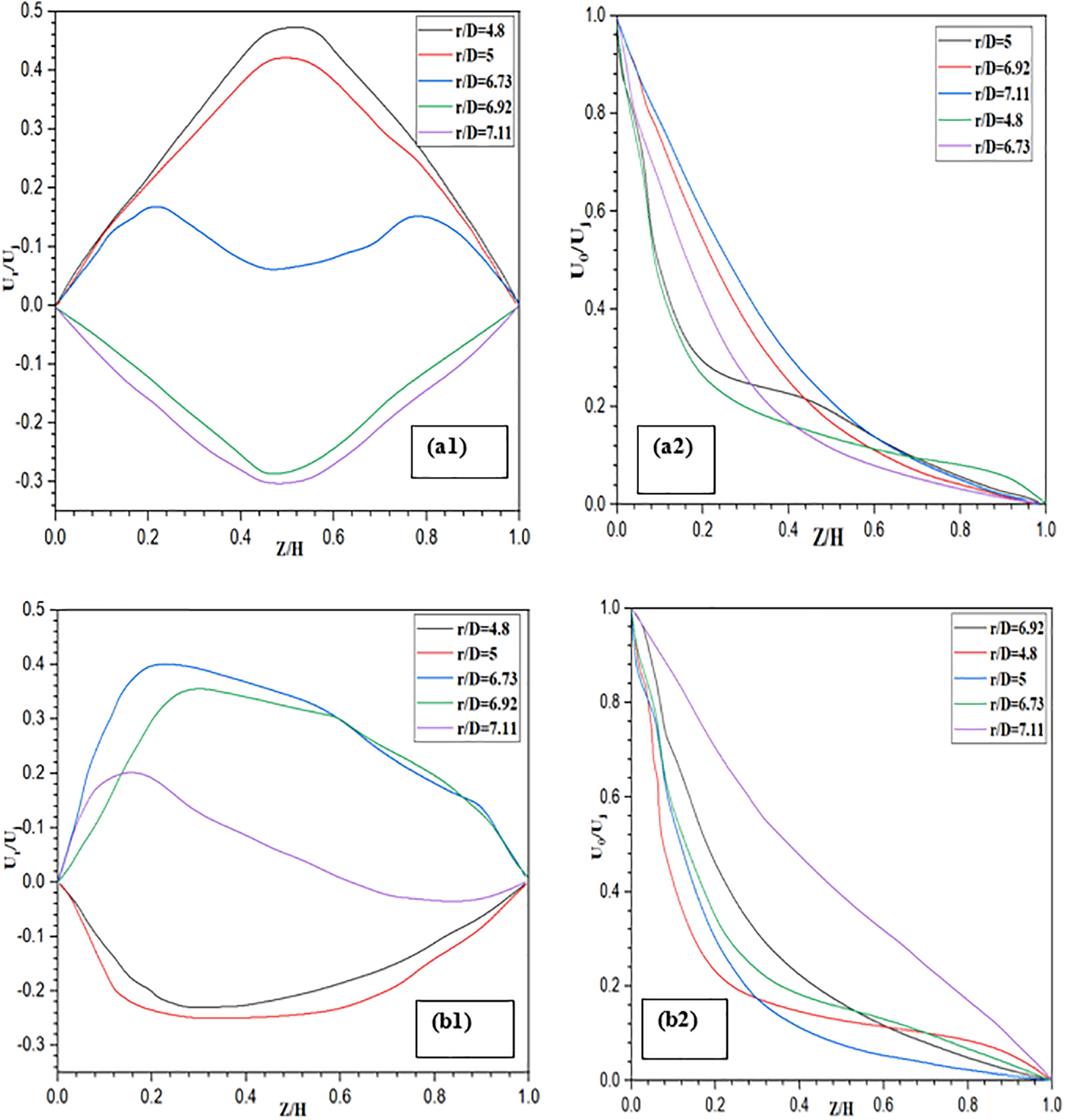
Figure 7: Analysis of the axial distribution of radial and tangential speeds in the air gap of a stator rotor for different radial positions

For Reω=2.35×105 and G=0.04 (see Fig. 7a1), the radial elements of the velocity, noted at various radial locations (r/D = 4.8, 5, 6.73, 6.92 and 7.11), show a parabolic profile similar to that obtained in the case of two parallel plates. The maximum peak of this magnitude is reached at the midpoint of the two disks for Z/H = 0.5. However, a negative radial velocity is observed for r/D = 6.92 and 7.11, corresponding to fluid re-entry. At r/D = 6.73, in the middle of the rotor between the two jets, a symmetrical radial velocity is observed.

Tangential velocity values (Fig. 7a2), which describe the flow in the vicinity of the rotor, are notably high. However, they gradually decrease with distance from the rotating disk in the direction normal to the rotor.

At the stator surface, characterized by Z/H = 1, these values ultimately reach zero. This development highlights a significant variation in flux within the system, with initially high tangential values near the rotor gradually declining to negligible values at the stator surface. At the stator surface, characterized by Z/H = 1, these values ultimately reach zero. This development highlights a significant variation in flux within the system, with initially high tangential values near the rotor gradually declining to negligible values at the stator surface.

Velocities in the circumferential direction are characterized by a single frontier zone close to the rotor. As one moves increasingly away from this boundary zone, the circumferential velocity decreases, finally reaching zero when Z/H = 1. The flow phenomena identified in this configuration are therefore similar to Stewartson-type [24].

4.3 Local and Medium Profiles of Nusselt

The analysis of heat exchange is based on a study of the local convection coefficient. Fig. 8 presents the variation in Nur for different values of the rotation parameter Reω=2.35×105, Reω=4.02×105 and Reω=5.04×105. For a constant jet Reynolds number of Rej=16×103 the evolution of the Nusselt number shows a significant variation along the disc. However, this variation shows a relatively low dependence on the number (Reω), particularly for small values (when r/D≤6.4). The local thermal convection coefficient distribution exhibits peaks at positions corresponding to r/D = 1.6, r/D = 5 and r/D = 6.6, suggesting high rates of heat transfer. This increase in heat transfer is that it results from increased Radial displacement within the boundary layer, particularly near the rotor, creating higher levels of shear stress. This increase in shear stress promotes more efficient heat transfer. When moving further from the point of impact and exceeding values of radius r/D ≥ 7.6, an increase in thermal convection coefficients is observed in relation to the parameters r and Reω in response to the increased influence of rotation. This observation can be attributed to a decline in radial in the vicinity of the stator and the expansion of the distance in the radical direction speed variation in the vicinity of the rotor. This leads to greater levels of the tangential deformation rate proximate to the rotor, which in turn promotes improved heat exchange in this region. In our study, an in-depth comparison of our results with those presented in reference works [6,25] reveals a significant observation related to the Nusselt number. Our meticulous analysis shows a remarkable constancy of the Nusselt number over the entire rotor surface. This observation conclusively suggests that our experimental configuration achieves full rotor cooling. The work of [6,25] played a crucial role in establishing a baseline for our study. The concordance of the results obtained reinforces the validity of our numerical approach. The observation of a constant Nusselt number underlines a homogeneous heat transfer over the rotor surface, highlighting the effectiveness of our experimental methodology. This stability of the Nusselt number can be attributed to a multitude of factors, including the specific design of the experimental set-up, the rigorously controlled operating conditions, as well as the specific thermal properties of the materials employed. In sum, our study makes a substantial contribution to the understanding of heat transfer in this particular configuration, confirming and extending the findings of previous work. These results provide a solid foundation for practical applications requiring optimal thermal management.

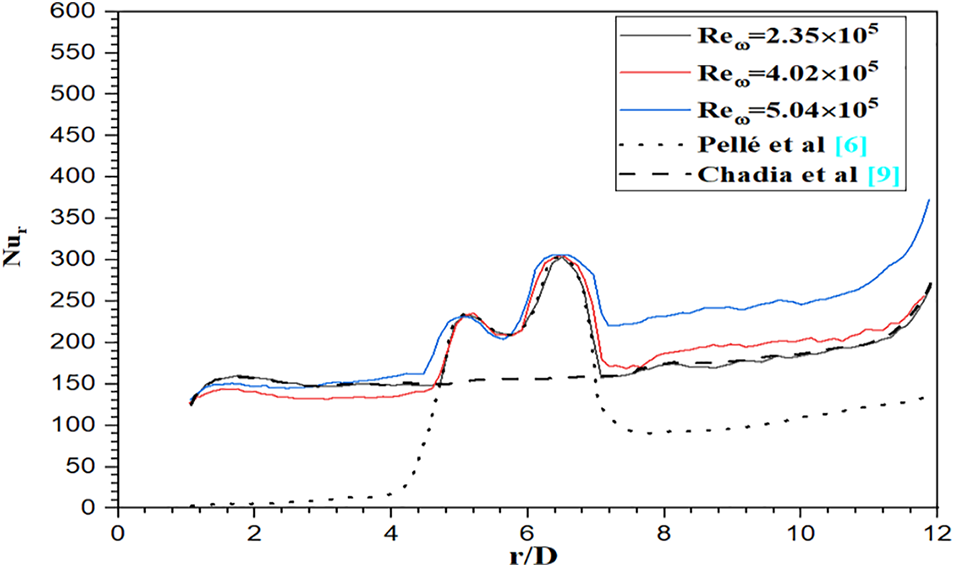
Figure 8: Local nusselt for Rej=16×103

In Fig. 9, keeping the rotational Reynolds number constant at Reω=5.04×105, we proceeded to vary the jet Reynolds number values, varying them from Rej=16×103 to 55.46×103. In the range of values where (r/D ≤ 4.4) is relatively low, it is essential to note that the introduction of air into the process has a significant impact on improving local heat transfer, this area is sensitive to variations in air flow, which is of crucial importance in optimising heat transfer. In the immediate vicinity of the interaction region, precisely when the value of r/D is in the range 4.4 to 6.8, the influence of the airflow becomes significant, creating a zone characterised by intensive heat transfer. This zone is characterised by fluctuations in the amplitude of heat transfer peaks, closely correlated with the jet’s relative Reynolds number, Rej. The study identified three well-defined zones, separated by characteristic radii. The first of these zones is a low-radius region (r/D ≤ 4.4) where heat transfer is relatively unaffected by rotational effects and airflow. The second zone, located near the point of impact, is mainly governed by the influence of the injected airflow, making it the main factor controlling heat transfers. Finally, the third zone, at the periphery, is characterised by the predominance of rotational effects in heat exchange.

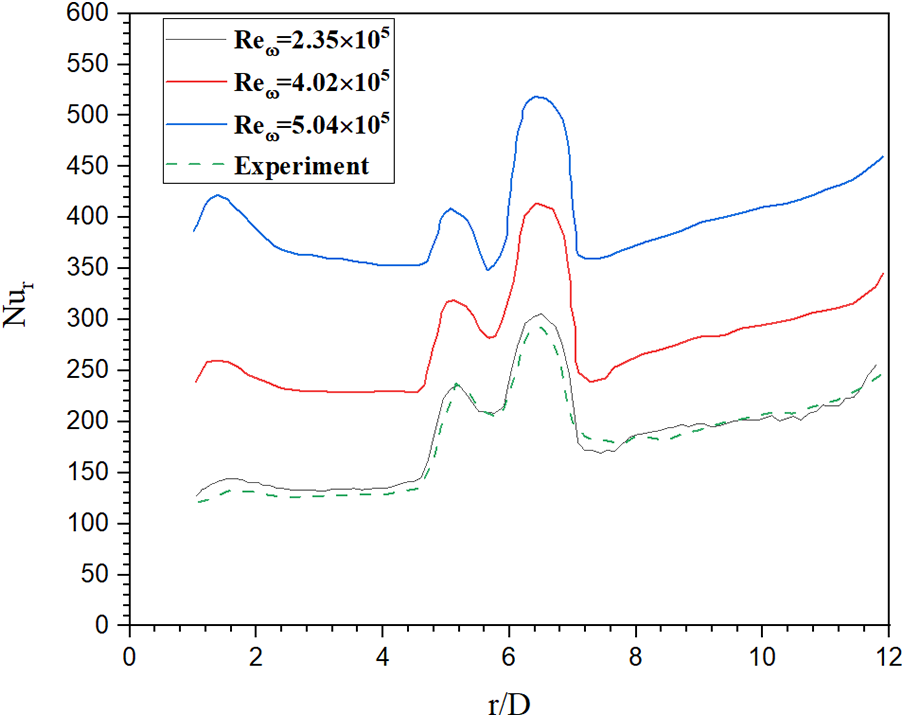
Figure 9: Nusselt local pour Reω=5.04×105, G = 0.04

The study, as shown in Fig. 10, focuses on the interaction between (Reω) and (Rej), and their impact on the average Nusselt number, a crucial indicator of heat transfer. The principal focus of this research is to increase our comprehension of the cooling mechanisms of the rotating disc and their repercussions on a global scale. The results reveal a clear trend: the mean Nusselt number increases proportionally with both Reω and Rej, a crucial relationship for assessing cooling efficiency. These findings at the global level confirm previous local observations, reinforcing our understanding of heat exchange. It is essential to note that increasing the flow of fresh air injected by the two jets has a direct impact on the overall cooling of the rotating disc, suggesting that airflow management can be an effective means of regulating the cooling process, with important practical implications for rotating systems.

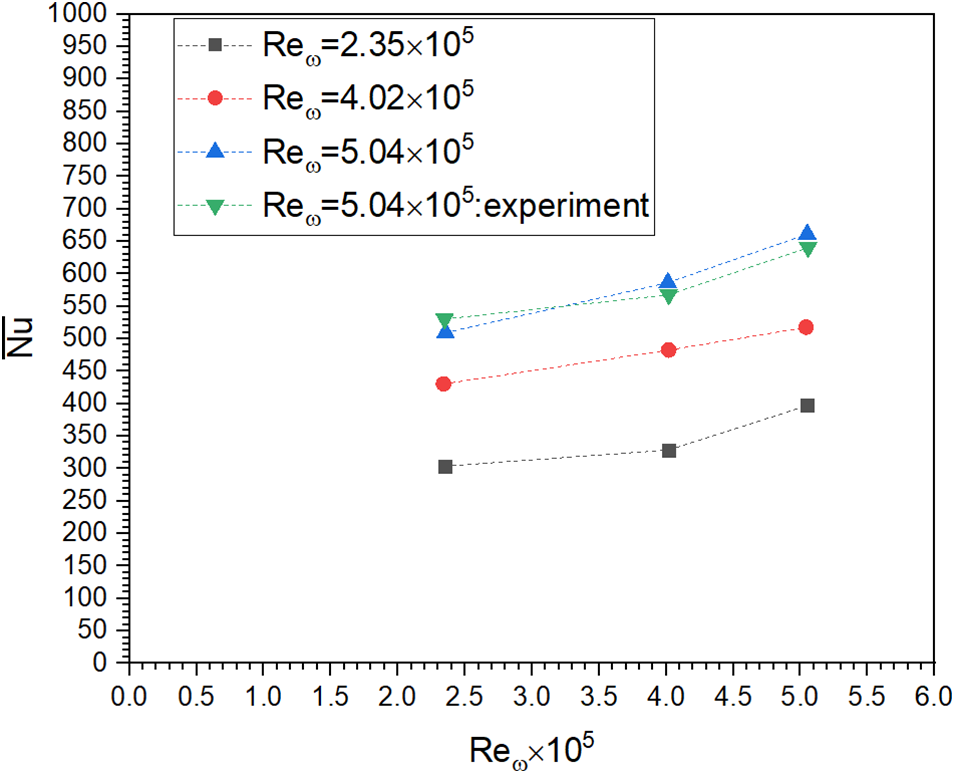
Figure 10: Average thermal convection coefficient in relation to Reω

5  Conclusion

In conclusion, this in-depth study investigated in detail the characteristics of the flow generated by the impact of two jets on a rotating disk, maintained at a constant temperature, using Ansys-Fluent simulation software. The results of this research clearly demonstrated the presence of two distinct recirculation zones in the flow, located close to the zone of impact of the jets on the disk. These zones are characterized by air recirculation phenomena and are of crucial importance for the heat exchange associated with this system. It is essential to note that heat transfer in this system is strongly influenced by the Reynolds number associated with the jets, covering a range from Rej=16×103 to 55.46×103. Substantial variations in Reynolds number have a direct impact on heat transfer performance, underlining its crucial role in this context. In addition, an essential parameter to take into account is the rotation number, which is linked to the rotation speed of the disc. The results indicate that heat transfer is also influenced by this variable, with rotational number values ranging from 2.35×105 to 5.04×105. In summary, this study provides valuable insights into the heat exchange mechanisms in this specific system, highlighting the significant impact of jet and rotation parameters on overall heat transfer performance. These findings offer important perspectives for the design and optimization of cooling systems in various industrial and technological applications, contributing to the advancement of sustainable energy generation technologies and thermal management practices.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the article as follows: conception of the analysis, data collection, analysis and writing of the article: Abdellatif El hannaoui; conception and realization of the analysis, revision of the article: Rachid Boutarfa; data collection: Chadia Haidar. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: There is no unavailable data in this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Boutarfa R, Harmand S. Local convective heat transfer for laminar and turbulent flow in a rotor-stator system. Exp Fluids. 2005;38(2):209–21. doi:10.1007/s00348-004-0900-5. [Google Scholar] [CrossRef]

2. Boutarfa R, Harmand S. Local convective heat exchanges and flow structure in a rotor-stator system. Int J Therm Sci. 2003;42(12):1129–43. doi:10.1016/S1290-0729(03)00092-9. [Google Scholar] [CrossRef]

3. Owen JM, Haynes CM, Bayley FJ. Heat transfer from an air-cooled rotating disk. Proc R Soc London A Math Phys Sci. 1974;336(1607):453–73. doi:10.1098/rspa.1974.0029. [Google Scholar] [CrossRef]

4. Chen SJW, Lee WT. Heat (mass) transfer between an impinging jet and a rotating disk. Am Soc Mech Eng. 1976;34(76):195–201. [Google Scholar]

5. Sagot B, Antonini G, Christgen A, Buron F. Jet impingement heat transfer on a flat plate at a constant wall temperature. Int J Therm Sci. 2008;47(12):1610–9. doi:10.1016/j.ijthermalsci.2007.10.020. [Google Scholar] [CrossRef]

6. Pellé J, Harmand S. Heat transfer study in a rotor-stator system air-gap with an axial inflow. Appl Therm Eng. 2009;29(8–9):1532–43. doi:10.1016/j.applthermaleng.2008.07.014. [Google Scholar] [CrossRef]

7. El Hannaoui A, Haidar C, Boutarfa R. Convective heat transfer in an air gap of a rotor-stator system subjected to a central jet. Int J Tech Phys Probl Eng. 2022;14(53):260–5. [Google Scholar]

8. Pellé J, Harmand S. Heat transfer measurements in an opened rotor-stator system air-gap. Exp Therm Fluid Sci. 2007;31(3):165–80. doi:10.1016/j.expthermflusci.2006.03.018. [Google Scholar] [CrossRef]

9. Poncet S, Nguyen D, Harmand S, Pellé J, Soghe RD, Bianchini C, et al. Turbulent impinging jet flow into an unshrouded rotor-stator system: hydrodynamics and heat transfer. Int J Heat Fluid Flow. 2013;44:719–34. doi:10.1016/j.ijheatfluidflow.2013.10.001. [Google Scholar] [CrossRef]

10. Haidar C, Boutarfa R, Harmand S. Fluid flow and convective heat transfer analysis on a rotor of wind turbine alternator with an impinging jet. Int J Renew Energy Res. 2019;9(3):1144–53. doi:10.20508/ijrer.v9i3.9471.g7692. [Google Scholar] [CrossRef]

11. ANSYS. CFD EXPERTS Simulate the Future. Available from: https://studylib.net/doc/27055621/fluent-beta-features-manual. [Accessed 2021]. [Google Scholar]

12. Liu J, Xu G, Zhao X, Dong B, Quan Y. Effect of windage heating on a micro high-speed rotor-stator cavity. Propuls Power Res. 2022;11(4):496–510. doi:10.1016/j.jppr.2022.03.006. [Google Scholar] [CrossRef]

13. Shi Y, Ding S, Liu P, Qiu T, Liu C, Qiu C, et al. Swirl flow and heat transfer in a rotor-stator cavity with consideration of the inlet seal thermal deformation effect. Aerospace. 2023;10(2):134. doi:10.3390/aerospace10020134. [Google Scholar] [CrossRef]

14. Liao G, Liu L, Zhang F, Jiaqiang E, Chen J. A comparison of numerical investigations on the flow and heat transfer characteristics in the rotor-stator cavity. Appl Therm Eng. 2019;162:114231. [Google Scholar]

15. Il Kim Y, Song SJ. Unsteady measurement of core penetration flow caused by rotating geometric non-axisymmetry in a turbine rotor-stator disc cavity. Exp Therm Fluid Sci. 2019;107:118–29. doi:10.1016/j.expthermflusci.2019.05.017. [Google Scholar] [CrossRef]

16. Yang X, Ren Z, Li X, Ren J. Flow and heat transfer characteristics in a pre-swirl rotor-stator cavity. Int J Therm Sci. 2022;172:107271. [Google Scholar]

17. Ibrahim MM, Kasem MM. Numerical thermal study of heat transfer enhancement in laminar-turbulent transition flow through absorber pipe of parabolic solar trough collector system. Front Heat Mass Transf. 2021;17:1–11. doi:10.5098/hmt.17.20. [Google Scholar] [CrossRef]

18. Elena L, Schiestel R. Turbulence modeling of rotating confined flows. Int J Heat Fluid Flow. 1996;17(3):283–9. doi:10.1016/0142-727X(96)00032-X. [Google Scholar] [CrossRef]

19. Launder BE, Tselepidakis DP. Application of a new second-moment closure to turbulent channel flow rotating in orthogonal mode. Int J Heat Fluid Flow. 1994;15(1):2–10. doi:10.1016/0142-727X(94)90025-6. [Google Scholar] [CrossRef]

20. Oguic R, Poncet S, Viazzo S. High-order direct numerical simulations of a turbulent round impinging jet onto a rotating heated disk in a highly confined cavity. Int J Heat Fluid Flow. 2016;61:366–78. doi:10.1016/j.ijheatfluidflow.2016.05.013. [Google Scholar] [CrossRef]

21. Milan Đorđević MV, Mančić M, Stefanović V. Numerical investigation of heat transfer in spirally coiled corrugated pipes: assessment of turbulence models. Therm Sci. 2023;1–13. doi:10.2298/TSCI230520184D. [Google Scholar] [CrossRef]

22. Nguyen TD, Pellé J, Harmand S, Poncet S. PIV measurements of an air jet impinging on an open rotor-stator system. Exp Fluids. 2012;53(2):401–12. doi:10.1007/s00348-012-1298-0. [Google Scholar] [CrossRef]

23. Batchelor BGK, College T. Note on a class of solutions of the Navier-stokes equations representing steady rotationally-symmetric flow. Quart J Mech Appl Math. 1951;4(1):29–41. doi:10.1093/qjmam/4.1.29. [Google Scholar] [CrossRef]

24. Stewartson K. On the flow between two rotating coaxial disks. Math Proc Cambridge Philos Soc. 1953;49(2):333–41. doi:10.1017/S0305004100028437. [Google Scholar] [CrossRef]

25. Haidar C, Boutarfa R, Sennoune M, Harmand S. Numerical and experimental study of flow and convective heat transfer on a rotor of a discoidal machine with eccentric impinging jet. J Therm Sci Eng Appl. 2020;12(2):1–11. doi:10.1115/1.4044207. [Google Scholar] [CrossRef]