Radiation Effect on Heat Transfer Analysis of MHD Flow of Upper Convected Maxwell Fluid between a Porous and a Moving Plate

1  Introduction

Due to its vast applications in science and technology, fluid in motion has become one of the most fascinating and challenging fields of study today. Moreover, numerous disciplines, including mechanical, aeronautical, and chemical engineering, are built upon the foundations of fluid mechanics. Advancements in the study of fluids directly impact applications in these domains. Archimedes formulated a famous law as Archimedes principle [1] while investigating fluid statics and buoyancy, which was the first study on fluids that can be traced back to 250 BC. Since then, almost all applied fields are based on fluid mechanics.

Based on Newton’s law of viscosity, the fluids are mainly classified into Newtonian and non-Newtonian fluids. This study stresses explicitly a non-Newtonian fluid categorized under rate type fluid known as Maxwell fluid [2]. This fluid model helps in the precise elucidation of the relaxation time effect. Due to their unique properties, Maxwell fluids have gained applications in designing and constructing hydraulic systems requiring high accuracy and precision control, designing shock absorbers, and developing lubrication. It has been considered one of the best choices for frictional vibration and reducing damping due to its ability to flow and deform under stress. Hence, Maxwell fluids have become essential in numerous engineering applications because of their reliability and versatility. Karra et al. [3] examined the behaviour of time-dependent Maxwell fluid flow that describes the visco-elastic material where the material moduli are pressure-dependent. Olsson et al. [4] analysed the constitute equation for a visco-elastic fluid in addition to continuity and momentum equations in a two-dimensional flow of a UCM fluid allowing artificial compressibility. The UCM fluid flow over a slowly moving rigid plate in an otherwise passive fluid was theoretically examined by Sadeghy et al. [5].

The study of fluid flow between two plates holds significant importance in fluid mechanics due to its wide-ranging industrial applications and influence on various scientific and technological fields. However, the analysis of non-Newtonian fluid flow between two plates presents a challenge to researchers due to its practical relevance and complex computational examination. Porous plate fluid flow finds extensive use in engineering and material science for designing and optimizing heat exchangers, filters, and lubrication systems. Choi et al. [6] have analysed the combined effects of visco-elasticity and inertia on a two-dimensional steady suction flow of an in-compressible UCM fluid through a porous channel. Ganesh et al. [7] analysed the unsteady laminar Stokes flow of viscous fluid between two plates placed parallelly with variable injection and suction at the walls. Numerous authors have studied the flow of Maxwell fluid in porous media [8–16].

The field of moving parallel plates with porosity is a significant area in the field of fluid flow. The concept has a variety of applications, including the production of thin films in the coating industry and the manufacturing of paper and textiles. Additionally, the movement of these plates can be used to control the flow of fluids, making it a valuable tool in developing fluid-based technologies. Overall, using moving parallel porous plates has proven to be a valuable technique with various applications in fluid mechanics. Yuan [17] investigated the two-dimensional steady-state laminar flow with moderate to high injection and suction velocity. Cox [18] analysed the similarity solution to the two-dimensional laminar flow of an incompressible viscous fluid in a single porous walled channel. Islam et al. [19] examined the flow of a homogeneous incompressible fluid being squeezed between porous infinite parallel plates approaching each other symmetrically. Several other researchers have also analysed the injection and suction effect on the squeezing flow [20–24].

The applications of MHD fluid flow are multifaceted and diverse. One of the most prominent applications of MHD is in the field of energy conversion, where electrical energy is obtained by converting thermal energy in MHD generators. MHD fluid flow is also employed in designing advanced propulsion systems for space travel and developing high-speed trains, where aerodynamic drag is reduced by MHD flow, whereas the efficiency is increased. MHD fluid flow is also used in the metallurgical industry to purify metals and in the chemical industry to produce high-purity chemicals. Additionally, in geophysics and astrophysics, MHD fluid flow is of significant importance as it provides insights into the behaviour of plasmas in space and the Earth’s magnetosphere. A viscous, incompressible fluid’s two-dimensional unsteady MHD flow through a porous media bounded by a moving upper plate and fixed lower plate was investigated by Hassanien et al. [25]. Barik et al. [26] studied the impact of injection and suction, and elasticity on the steady laminar MHD flow of a visco-elastic fluid through a porous pipe. Many researchers in the past have examined the impact of MHD on the fluid flow [27–33].

The field of heat transfer applications involving MHD fluid flow is a captivating area of study. It concerns the transfer of thermal energy between a solid surface and a fluid subject to the magnetic field. The presence of a magnetic field changes the fluid flow, leading to variations in the rate of heat transfer. This phenomenon has practical applications in several sectors, including MHD power production systems, heat exchanger design, and nuclear reactor design. It has gained increasing interest in recent years due to its potential to improve energy efficiency and reduce environmental impact. Kaviany [34] analysed the laminar flow between two porous plates parallel to each other placed at equal and constant temperatures, applying the Darcy effect for transport momentum. The MHD flow and heat transfer of a Maxwell fluid over an exponential stretching sheet through a porous media with variable thermal conductivity was numerically analysed by Singh et al. [35]. Further, Elbashbeshy et al. [36] analysed numerically the effect of heat transfer on the flow of Maxwell fluid over a stretching surface involving variable thickness in a porous media. Numerous other researchers have also analysed the MHD flow and heat transfer of fluid through porous channels [37–43].

The influence of radiation on MHD fluid flow has gained the attention of researchers due to its wide range of applications. Radiation alters the fluid flow and affects the heat transfer rate, which has potential uses in various industries, such as the creation of solar collectors, nuclear reactors, and space propulsion systems. Raptis et al. [44] numerically analysed the asymmetric steady flow of MHD fluid over a semi-infinite stationary plate subject to thermal radiation. The heat transfer was analysed by Hayat et al. [45] for a two-dimensional MHD flow through a channel of porous walls with thermal radiation. Mukhopadhyay et al. [46] numerically analysed the unsteady boundary layer flow of Maxwell fluid over a permeable surface that is continuously stretching subject to thermal radiation. Further, Elbashbeshy et al. [47] numerically studied the influence of thermal radiation on the heat transfer of Maxwell fluid flow over a stretching surface of variable thickness embedded in a porous media. Many authors in the literature have also analysed the impact of thermal radiation on fluid flow [48–50].

Once the given physical problem is formulated successfully, the fundamental equations of fluid flow must be solved with specific conditions. The fundamental equations cannot be solved using known analytical methods due to the non-linearity involved in the problem. However, numerical methods yield an approximate solution to these equations. A new class of mathematical tools known as the semi-analytical methods was introduced to overcome the difficulties encountered by researchers in solving these equations by numerical methods. One such semi-analytical method to solve a non-linear differential equation is the HPM. The HPM was proposed by He [51] in 1999. Further, He [52,53] demonstrated the efficiency and ease of employing HPM with the help of examples. Later, various other researchers implemented the concept of HPM to obtain a more approximate solution to the problems [54–58].

From the literature, it was observed that the MHD flow of UCM fluid between parallel plates has widespread applications in industrial and technical arenas. Moreover, the impact of thermal radiation on heat transfer analysis is employed in designing heat exchangers used in nuclear reactors and cooling high-power electronic devices. Conducting direct experiments can be laborious, expensive, and time-consuming. Thus, theoretical analysis of such models is extremely necessary so as to enhance the feasibility. The authors found that the theoretical analysis of the impact of thermal radiation on the UCM fluid flow is limited. Also, there is a need to analyse the flow and heat characteristics of the MHD flow of UCM fluid in the presence of thermal radiation under different geometries.

This study intends to theoretically analyse the impact of thermal radiation on the heat transfer of the MHD flow of a UCM fluid through plates placed parallel to each other. In the considered problem, the upper plate is impermeable and moves either towards or away from the lower plate, which is stationary and porous. This problem is approached by a semi-analytical method, specifically HPM, in order to obtain an approximate analytical solution. Moreover, this approach has several advantages in contrast to other mathematical techniques. The HPM solution is compared with the numerical solution obtained through the conventional finite difference method (FDM). This particular geometry has been mainly applicable in the metallurgy industry, specifically in the filtration of polymers. In the future, there is scope to further enrich this study by including activation energy, Brownian motion, Soret and Dufour effects. Also, the study can be further extended by experimenting with the fluid composition, which has wide applications in the industrial and engineering sectors.

2  Geometry and Formulation

Consider a two-dimensional MHD flow of a UCM fluid between a stationary porous lower plate and a moving upper plate at a distance h with temperature T1 and T2, respectively. Let Vh be the uniform velocity at which the top plate moves away or towards the fixed porous bottom plate, as shown in Fig. 1.

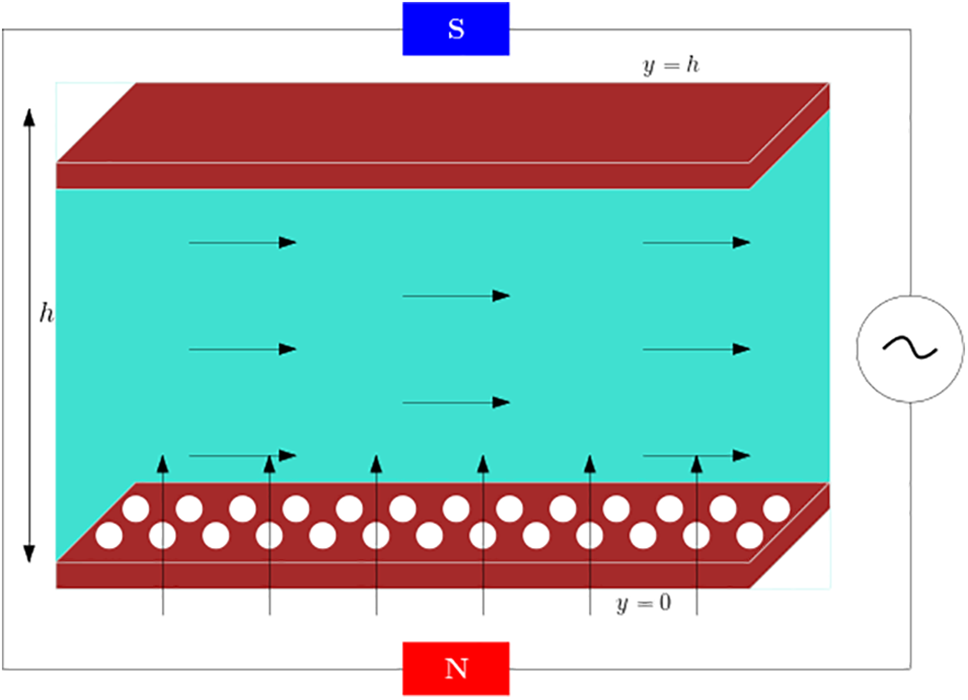
Figure 1: Flow geometry

The equations governing the MHD flow of UCM fluid in two-dimensions [45,59–61] are given by

∂u∂x+∂v∂y=0,(1)

u∂u∂x+v∂u∂y+λ[u2∂2u∂x2+v2∂2u∂y2+2uv∂2u∂x∂y]=ν∂2u∂y2−σB02ρ(u+λv∂u∂y)−ϕνku,(2)

ρCP(u∂T∂x+v∂T∂y)=k0∂2T∂y2−∂qrad∂y.(3)

The fluid’s density is represented by ρ, and its velocities in the x and y directions are represented by u and v, respectively. The relaxation time is given by λ, and the kinematic viscosity is represented by ν. The electrical conductivity is given by σ, while B0 represents the uniform magnetic field in the y direction. The porous medium’s permeability is represented by k, and its porosity is represented by ϕ. The thermal conductivity is represented by k0, while the specific heat capacity is given by CP. The temperature is represented by T, while the radiative heat flux is represented by qrad.

With the help of Rosseland approximation for radiation [62],

qrad=−4σ∗3k∗∂T4∂y.(4)

The mean absorption coefficient is represented as k∗ and σ∗ corresponds to the Stefan-Boltzmann constant. Taylor’s series expansion is performed around T1,

T4≅4T13T−3T14.(5)

The boundary conditions for the given problem are

u(x,0)=0,v(x,0)=AVh,u(x,0)=0,v(x,h)=Vh.(6)

By employing the following similarity transformations in Eq. (2).

X=xh,η=yhu=−VhXF ′(η)v=VhF(η),(7)

the momentum equation is transformed into

Fiv(η) −MRF ″(η)−MDe(F ′(η)F ″(η)+F(η)F ‴(η))−KF ″(η) +R[F ′(η)F ″(η)−F(η)F ‴(η)]+De[2F(η)(F ″(η))2+2(F ′(η))2F ″(η)−(F(η))2Fiv(η)]=0.(8)

The boundary conditions are thus transformed into

F(0)=A,F ′(0)=0,F(1)=1,F ′(1)=0.(9)

Similarly, using similarity transformation

θ(η)=T−T1T2−T1(10)

in Eq. (3), the energy equation transforms into

(1+43Rd)θ ″(η)−RPrF(η)θ ′(η)=0,(11)

θ(0)=0,θ(1)=1.(12)

The non-dimensional parameters R, M, De, K, Pr and Rd in Eqs. (8) and (11) representing Reynolds number, Deborah number, magnetic parameter, porosity parameter, Prandtl number and radiation parameter are given by

R=hVhν,De=λVh2ν,M=σB02hρVh,K=h2ϕρVh,Pr=CPμk0,Rd=4σ∗T13k0k∗.

3  Method of Solution

The considered problem is non-linear; hence, an analytical solution is difficult. Numerical and semi-analytical methods yield solution to this problem. In the current study, a semi-analytical method, HPM, is employed to obtain the solution based on which the velocity and temperature profiles are plotted. Also, the numerical values of the magnitude of skin friction coefficient and rate of heat transfer obtained by HPM are compared with a well-known numerical method, FDM.

3.1 Homotopy Perturbation Method

This study obtains fourth-order and second-order non-linear differential equations, representing the momentum and energy equations, respectively. Here, the model is mathematically analysed by employing HPM for the system of equations in the following manner:

Let D1 and D2 be the two differential operators of the unknown function g(η). Let the two known functions of the equations be denoted by g1(η) and g2(η). Thus, the considered model can be expressed as

Di[g(η)]−gi(η)=0.(13)

In HPM, the differential operator, Di is generally expressed as the sum of a linear and a non-linear part, that is

Di=Li+Ri,(14)

where Li is the linear part and Ri is the other part of Di.

Therefore, the homotopy equation for Eq. (13) is constructed by a wise choice of Li from Eqs. (8) and (11), and the initial guess v0 from the boundary conditions given in Eqs. (9) and (12) as mentioned below:

Hi(ξi,p)=(1−p)[Li(ξi,p)−Li(v0(η))]+p[Di(ξi,p)−gi(ξ)]=0,(15)

where i=1,2.

Assuming the solution of Eq. (15) in terms of power series,

ξ(η,p)=∑n=0∞pngn(η).(16)

Eq. (16) is the solution of the problem when p=1.

By employing the above mentioned scheme, the equations are solved to obtain the zeroth, first, second, and third order solution as given below:

F0=2Aη3−3Aη2+A−2η3+3η2,

F1 =1420(−200A3Deη9+900A3Deη8−1368A3Deη7+420A3Deη6+1008A3Deη5−1260A3Deη4 +656A3Deη3−156A3Deη2+48A2DeMη7−168A2DeMη6+126A2DeMη5+210A2DeMη4 −366A2DeMη3+150A2DeMη2+600A2Deη9−2700A2Deη8+4104A2Deη7−1596A2Deη6 −2016A2Deη5+2520A2Deη4−1128A2Deη3+216A2Deη2−24A2Rη7+84A2Rη6+⋯),

F2 =18408400(352000A5De2η15−1760000A4De2η15+3520000A3De2η15−3520000A2De2η15 +1760000ADe2η15−352000De2η15−2640000A5De2η14+13200000A4De2η14 −26400000A3De2η14+26400000A2De2η14−13200000ADe2η14+2640000De2η14+⋯),F3 =1570341772000(−15613189200De3+9435022128ADe3−4611552624A2De3−4221311472A3De3 −22475082672A4De3−16984778832A5De3+194020006320A6De3−139549113648A7De3 −2779228116De2K+2389920624ADe2K+3062988936A2De2K+5893338528A3De2K +11877902820A4De2K−20444922792A5De2K+115487358DeK2−224245980ADeK2+⋯),

θ0=η,

θ1=320(4Rd+3)(2APrRη5−5APrRη4+10APrRη2−7APrRη−2PrRη5+5PrRη4−3PrRη),

θ2=192400(4Rd+3)2(−3600A3DePrRη11+10800A2DePrRη11−10800ADePrRη11+3600DePrRη11 −4800A3DePrRRdη11+14400A2DePrRRdη11−14400ADePrRRdη11+4800DePrRRdη11 +19800A3DePrRη10−59400A2DePrRη10+59400ADePrRη10−19800DePrRη10+⋯),

θ3=18576568000(3+4Rd)3(302491584De2PrrR−142034472ADe2PrR−118048104A2De2PrR −164512296A3De2PrR−261151128A4De2PrR+383254416A5De2PrR+44735976DeKPrR −51505308ADeKPrR−58764852A2DeKPrR+65534184A3DeKPrR+306306K2PrR+⋯).

3.2 Finite Difference Method

FDM is a very well-established numerical method that is capable of solving a large class of non-linear differential equations. FDM discretizes the derivatives of flow variables using Taylor series expansion. This method is then applied to the differential form of the fundamental equations that govern the fluid flow. In this study, the FDM is employed to compare the results obtained through HPM. Hence, the numerical values of the magnitude of the skin friction coefficient and rate of heat transfer are also evaluated by this method.

4  Results and Discussion

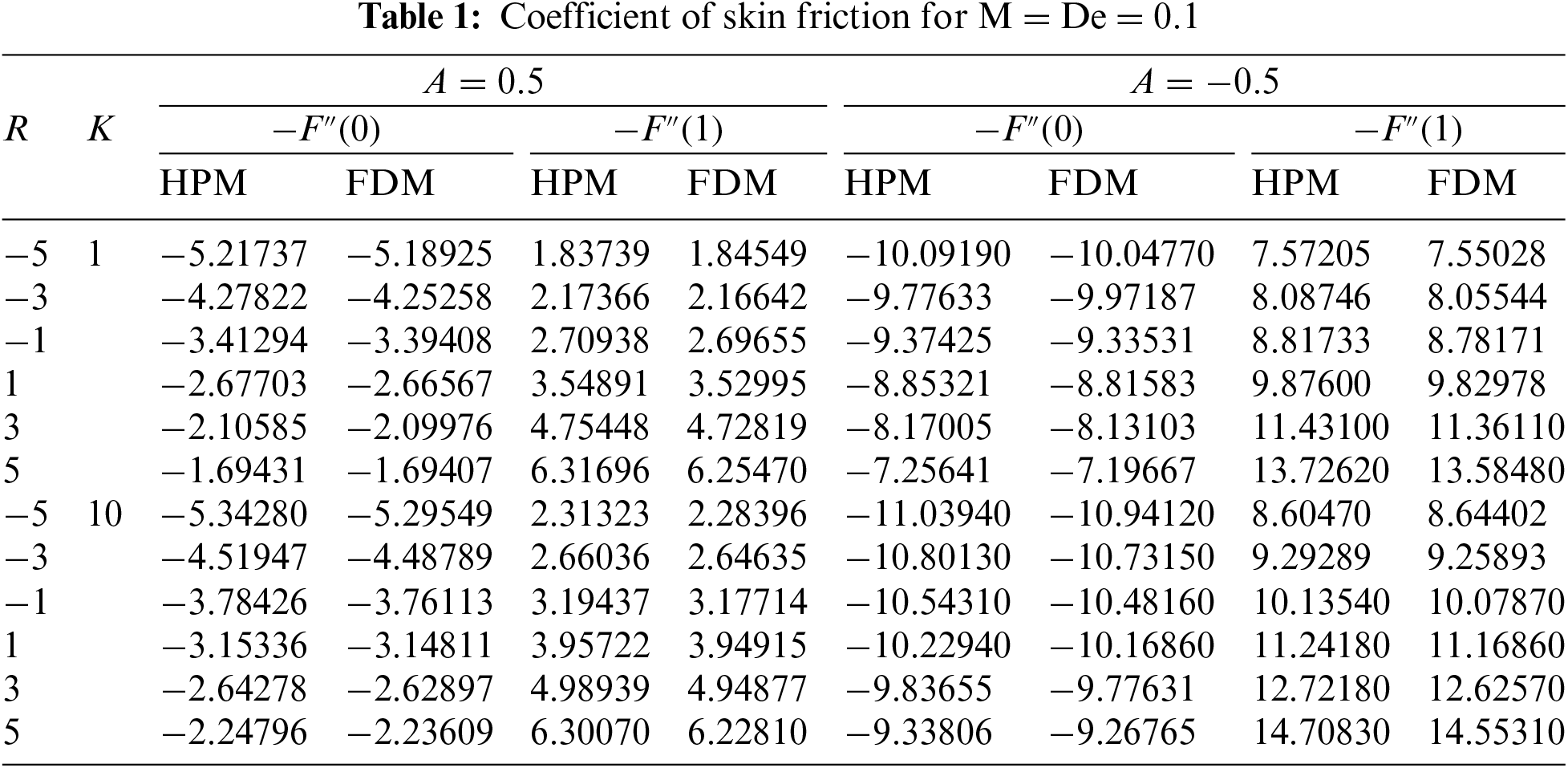
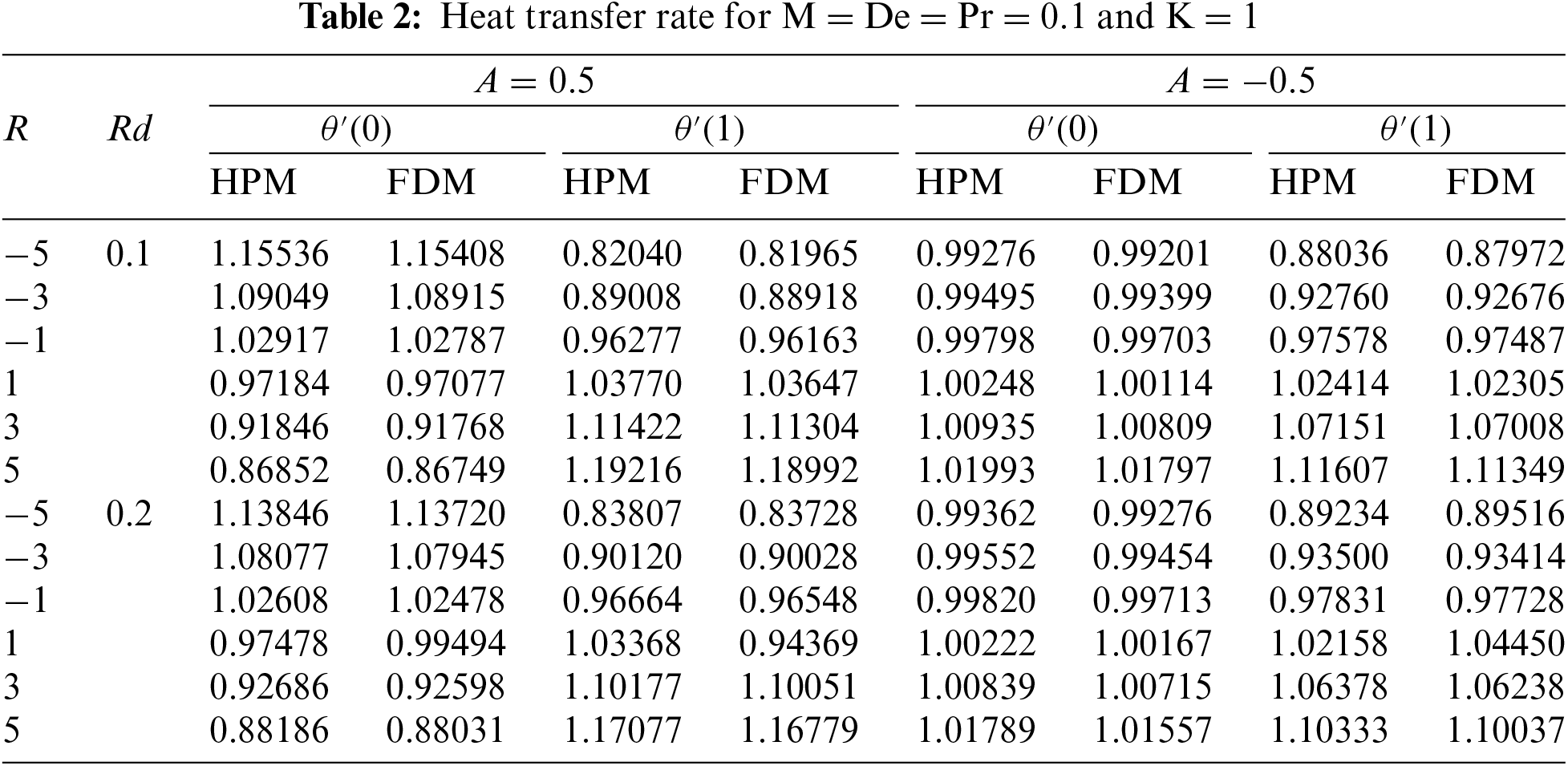
In this study, the impact of thermal radiation on the flow of two-dimensional magnetohydrodynamic UCM fluid that is squeezed between two parallel plates is investigated. The velocity and temporal fields for distinct values of the physical parameters obtained using HPM are illustrated in Figs. 2–15. Figs. 2 and 3 represent graphically the impact of the Reynolds number on the velocity profile for injection and suction, respectively. In the case of injection, the temporal distribution curve for the upper plate moving away and towards the lower is represented graphically in Figs. 4 and 15. The skin friction coefficient and heat transfer rate for both injection and suction are presented in Tables 1 and 2, respectively.

Figure 2: Velocity profile for varying R in case of injection with De = 0.1, K = 1, M = 0.1

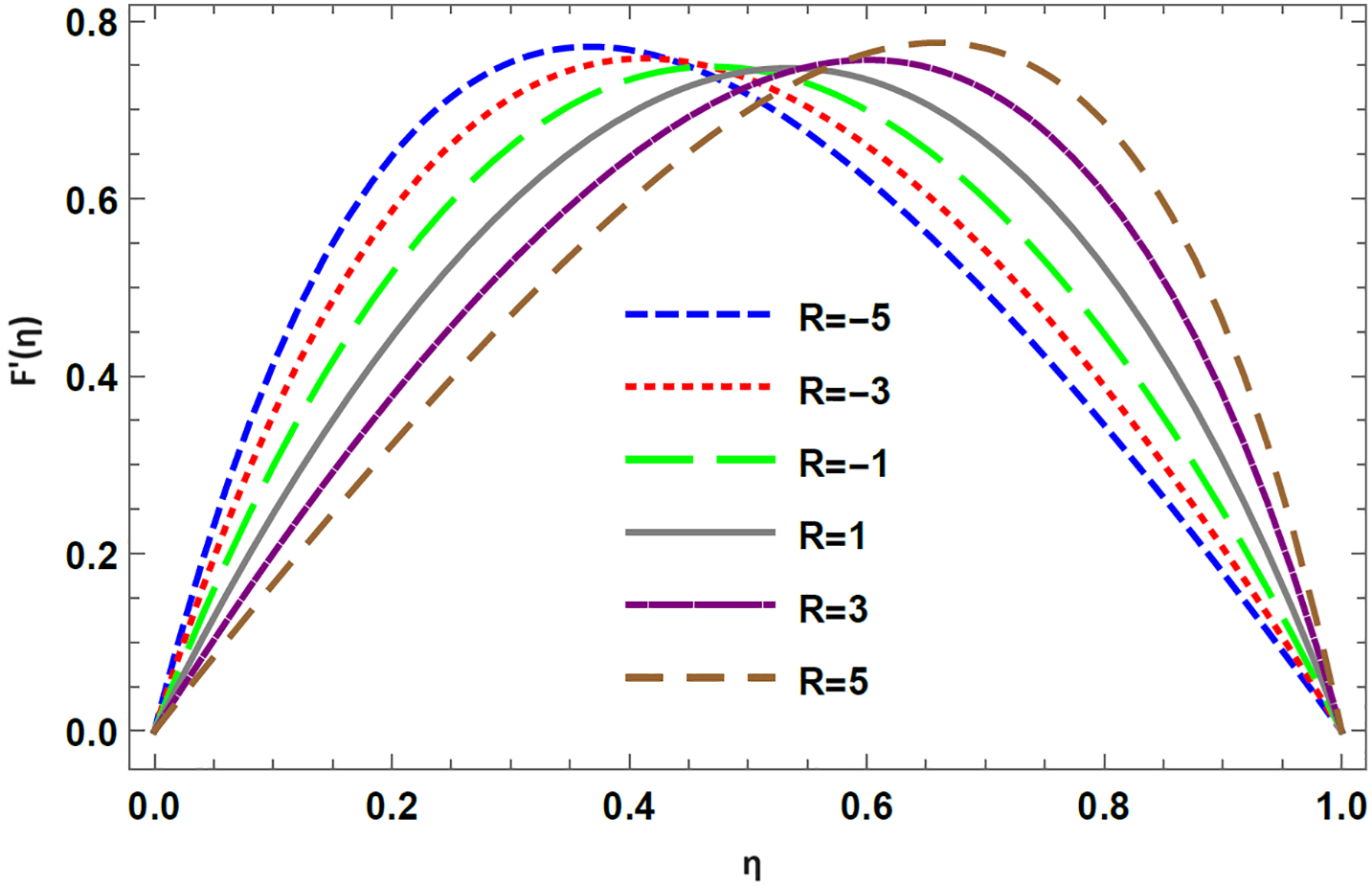
Figure 3: Velocity profile for varying R in case of suction with De = 0.1, K = 1, M = 0.1

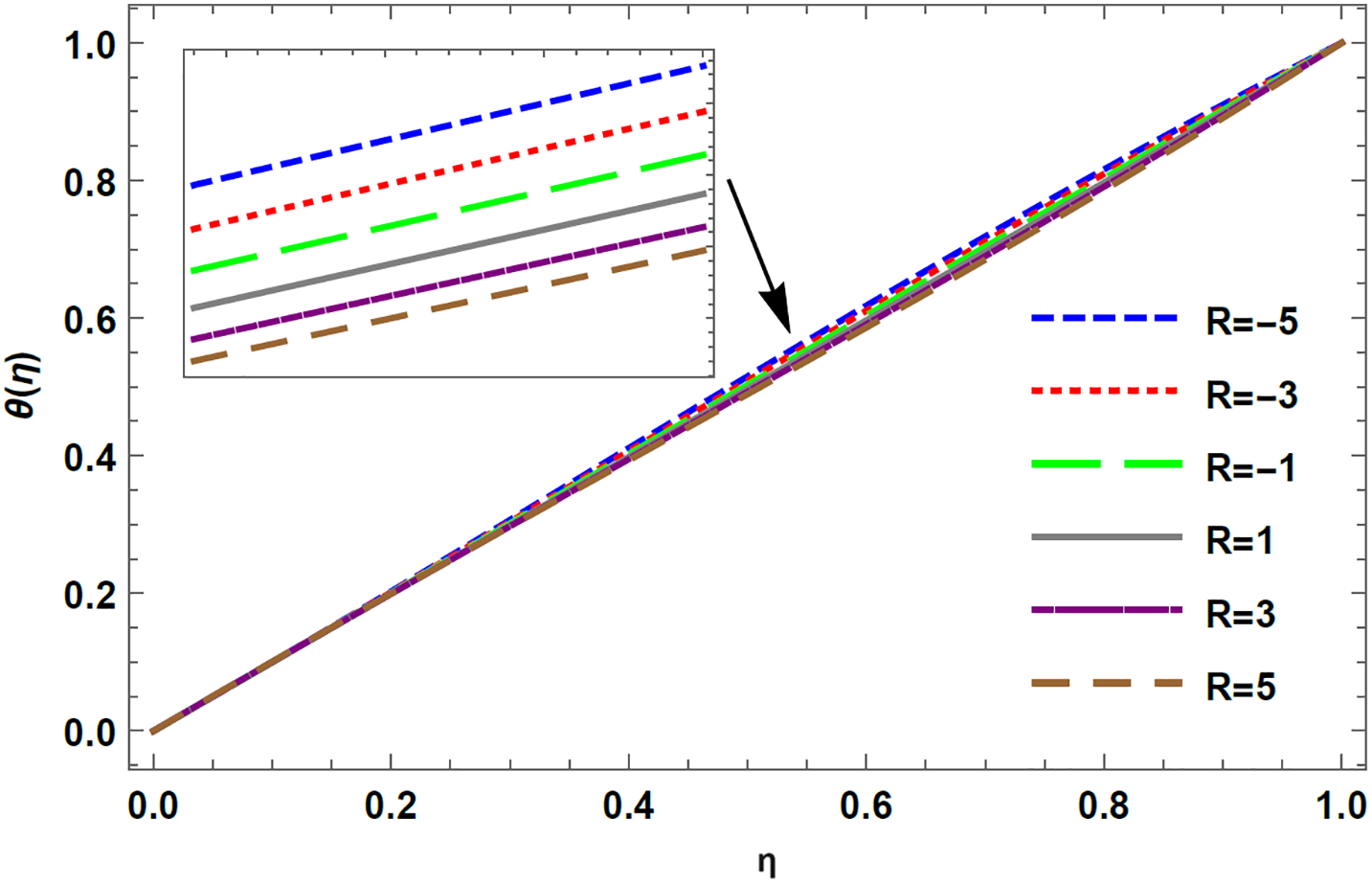
Figure 4: Temperature profile for varying R in case of injection with De = 0.1, K = 1, Rd = 0.1, Pr = 0.1, M = 0.1

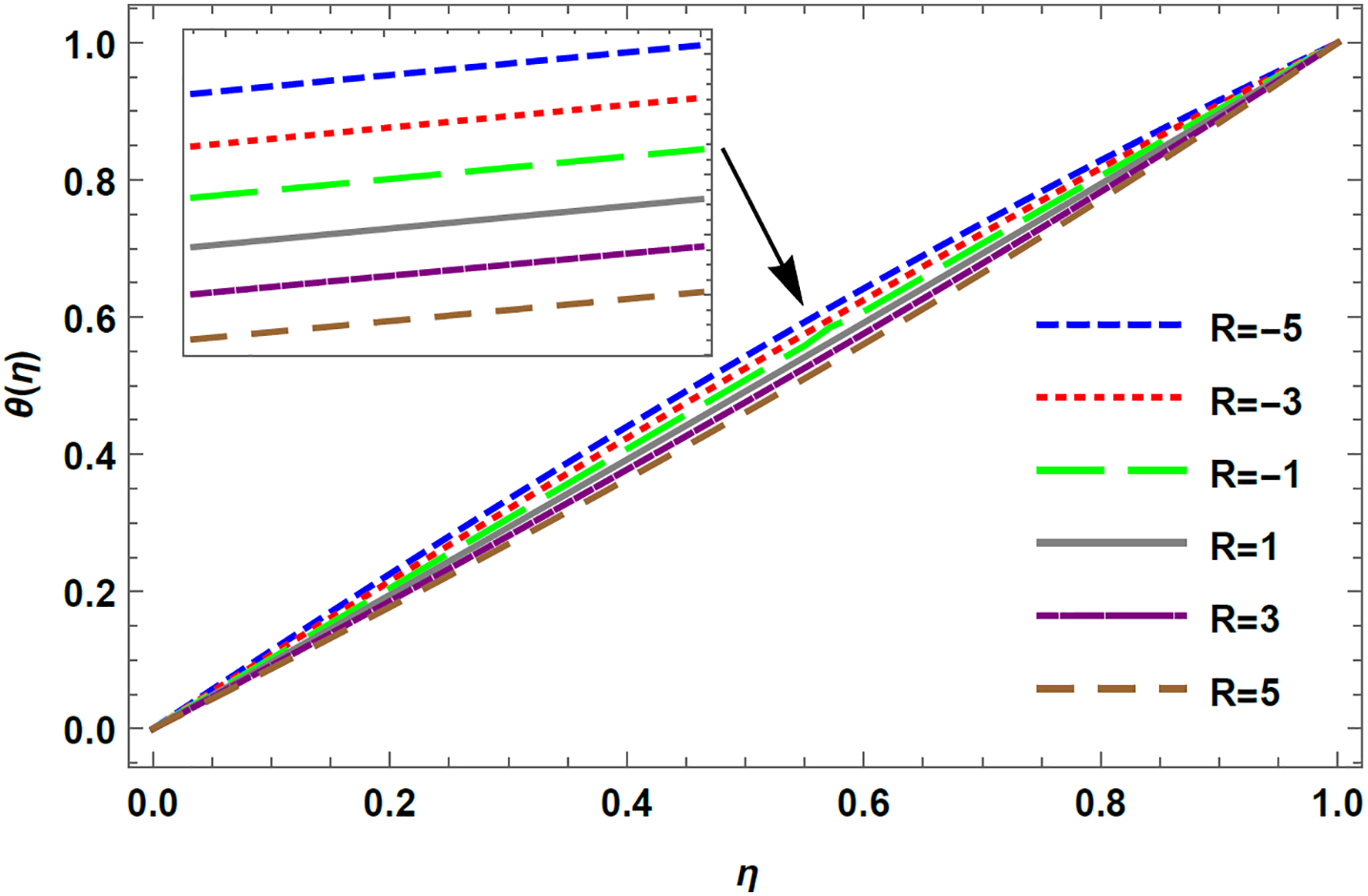
Figure 5: Temperature profile for varying R in case of suction with De = 0.1, K = 1, Rd = 0.1, Pr = 0.1, M = 0.1

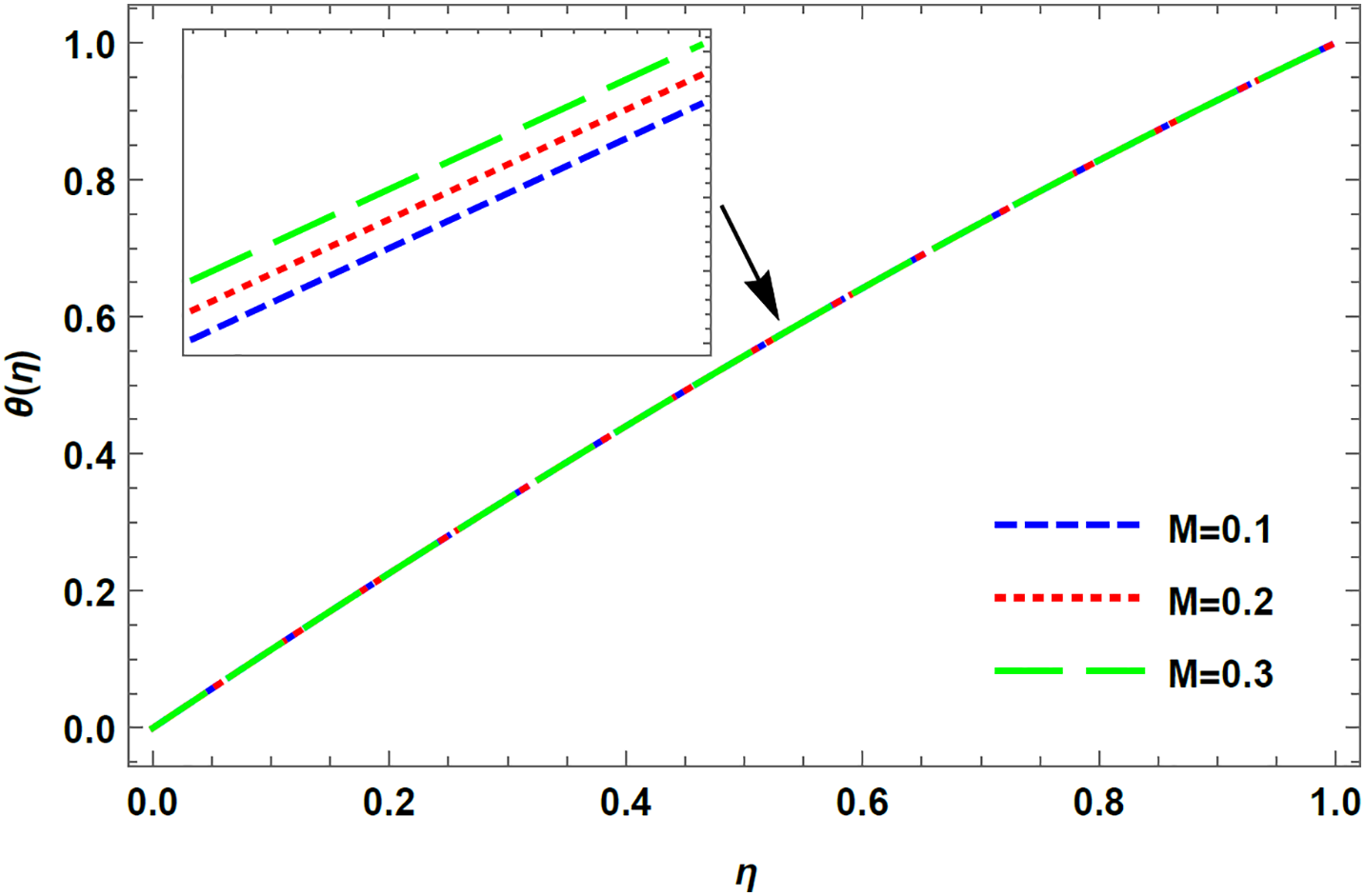
Figure 6: Temperature profile for varying M in case of injection, R = −5 with De = 0.1, K = 1, Rd = 0.1, Pr = 0.1

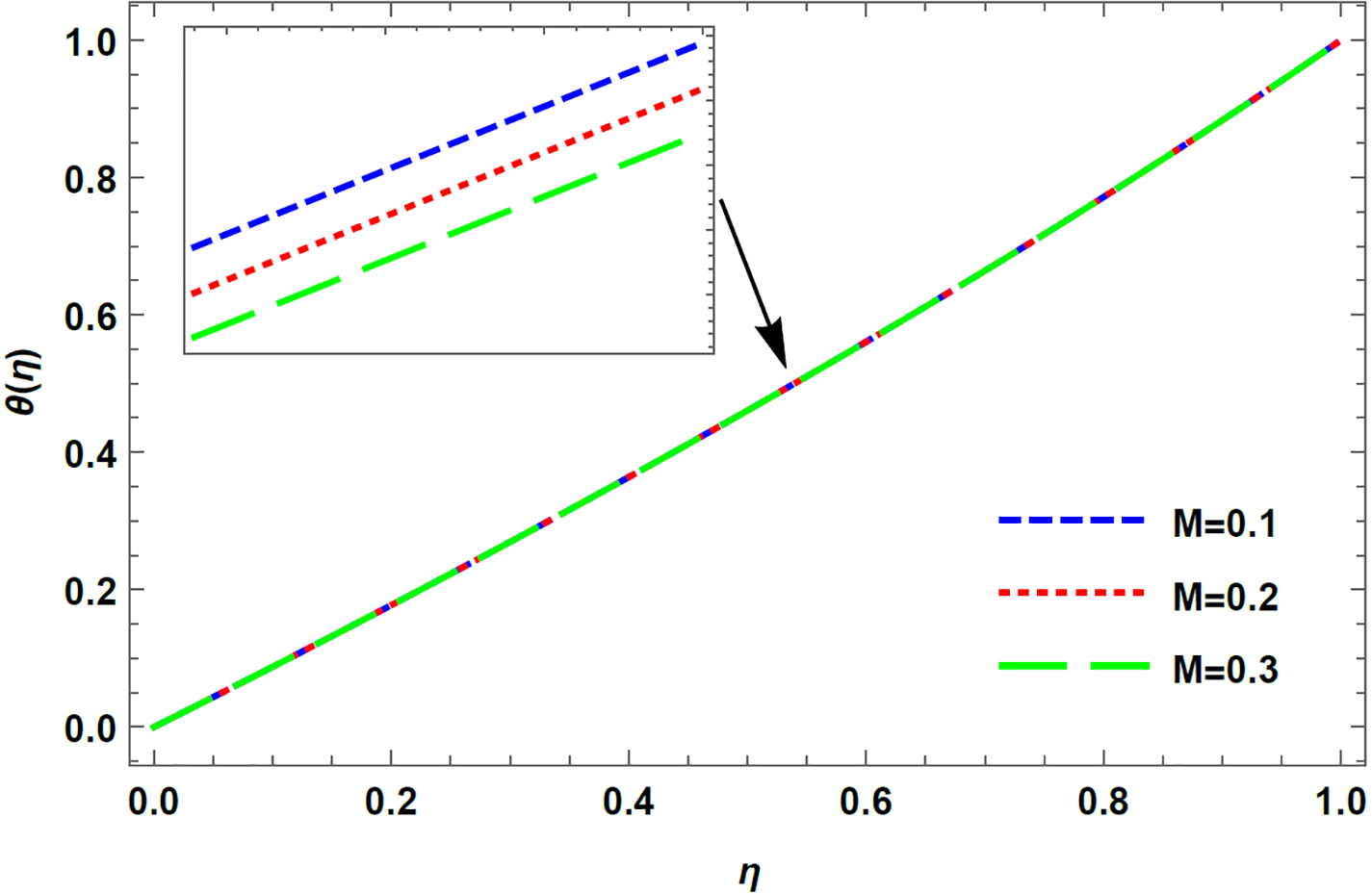
Figure 7: Temperature profile for varying M in case of injection, R = 5 with De = 0.1, K = 1, Rd = 0.1, Pr = 0.1

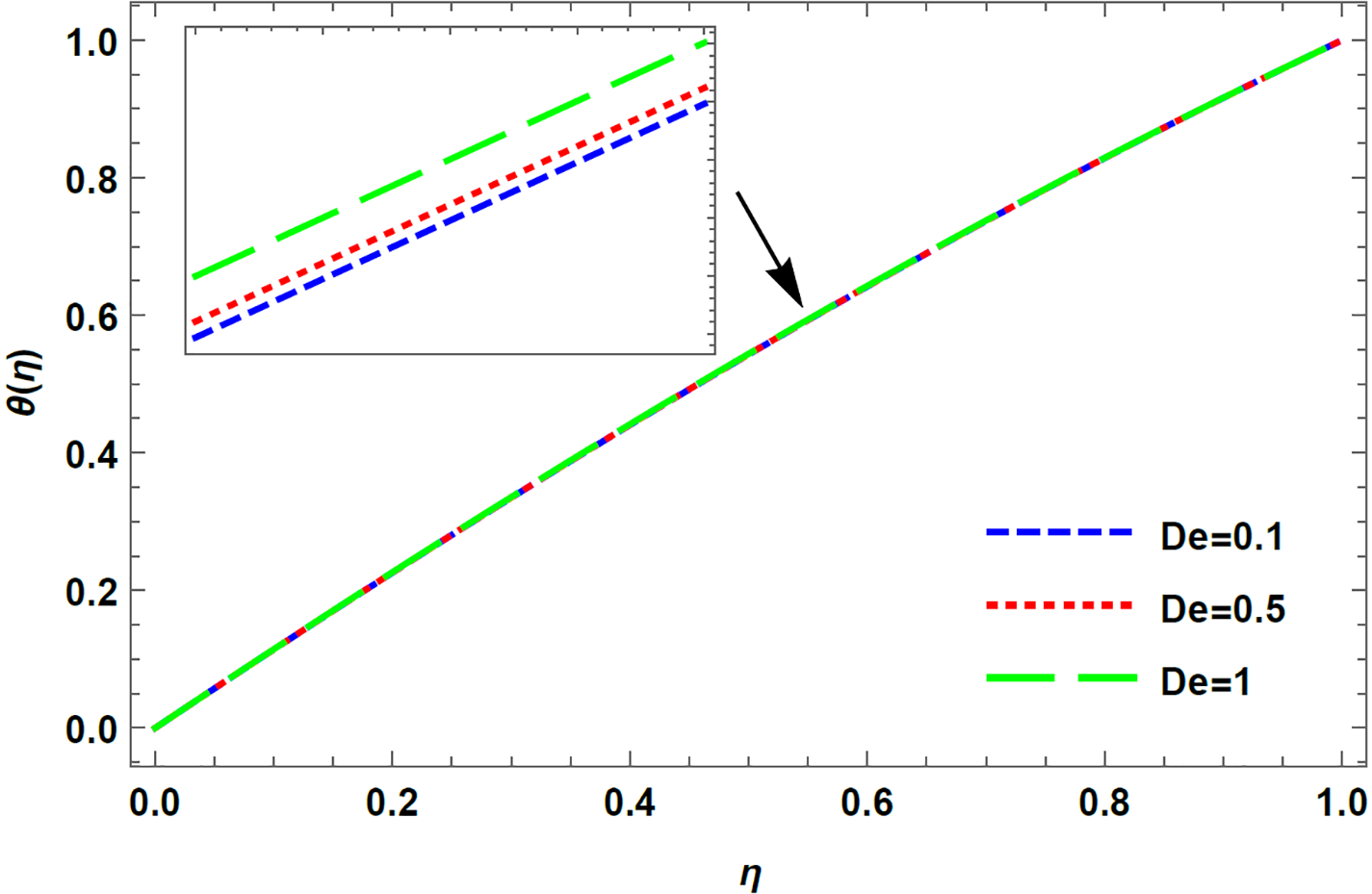
Figure 8: Temperature profile for varying De in case of injection, R = −5 with M = 0.1, K = 1, Rd = 0.1, Pr = 0.1

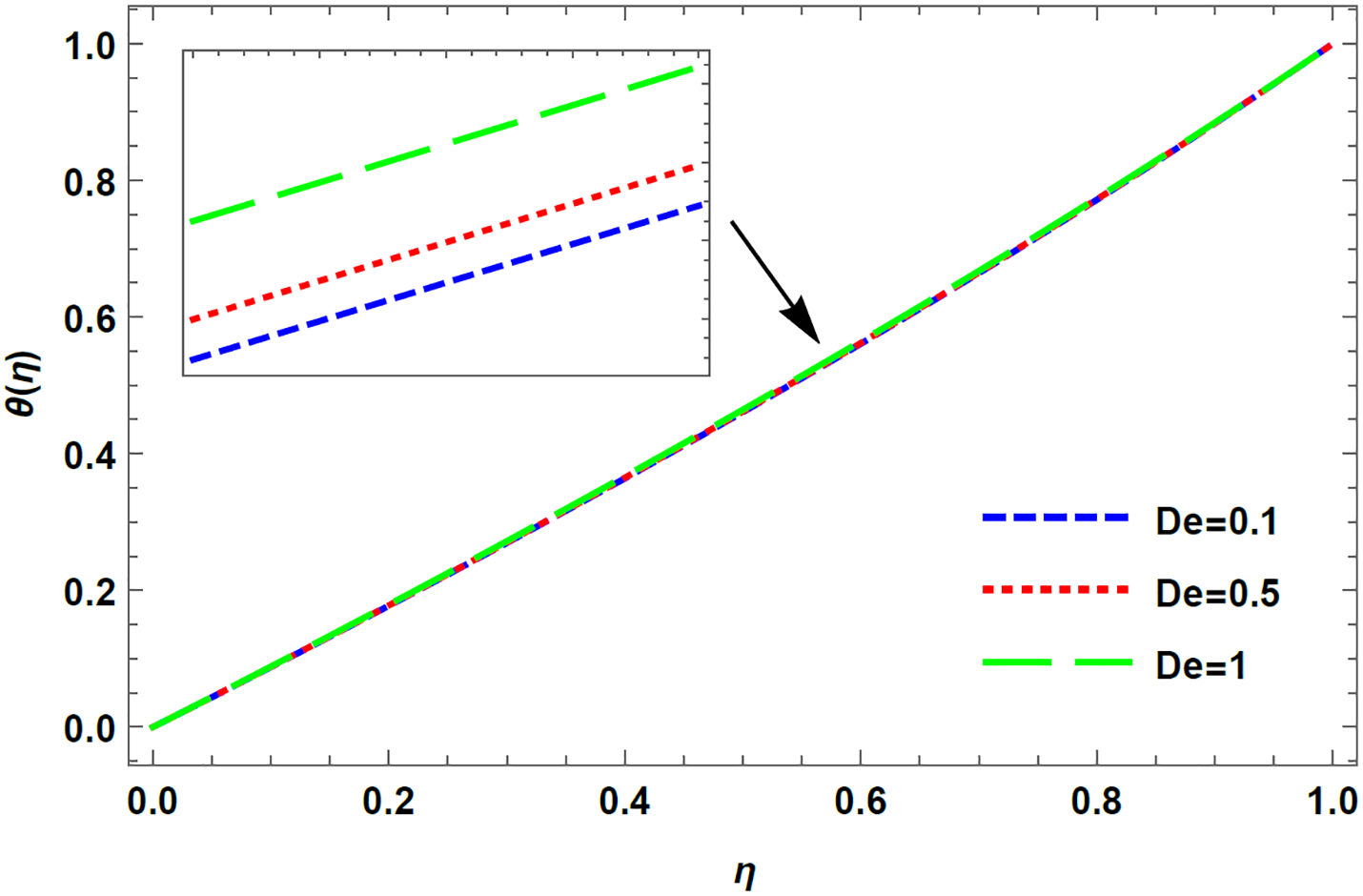
Figure 9: Temperature profile for varying De in case of injection, R = 5 with M = 0.1, K = 1, Rd = 0.1, Pr = 0.1

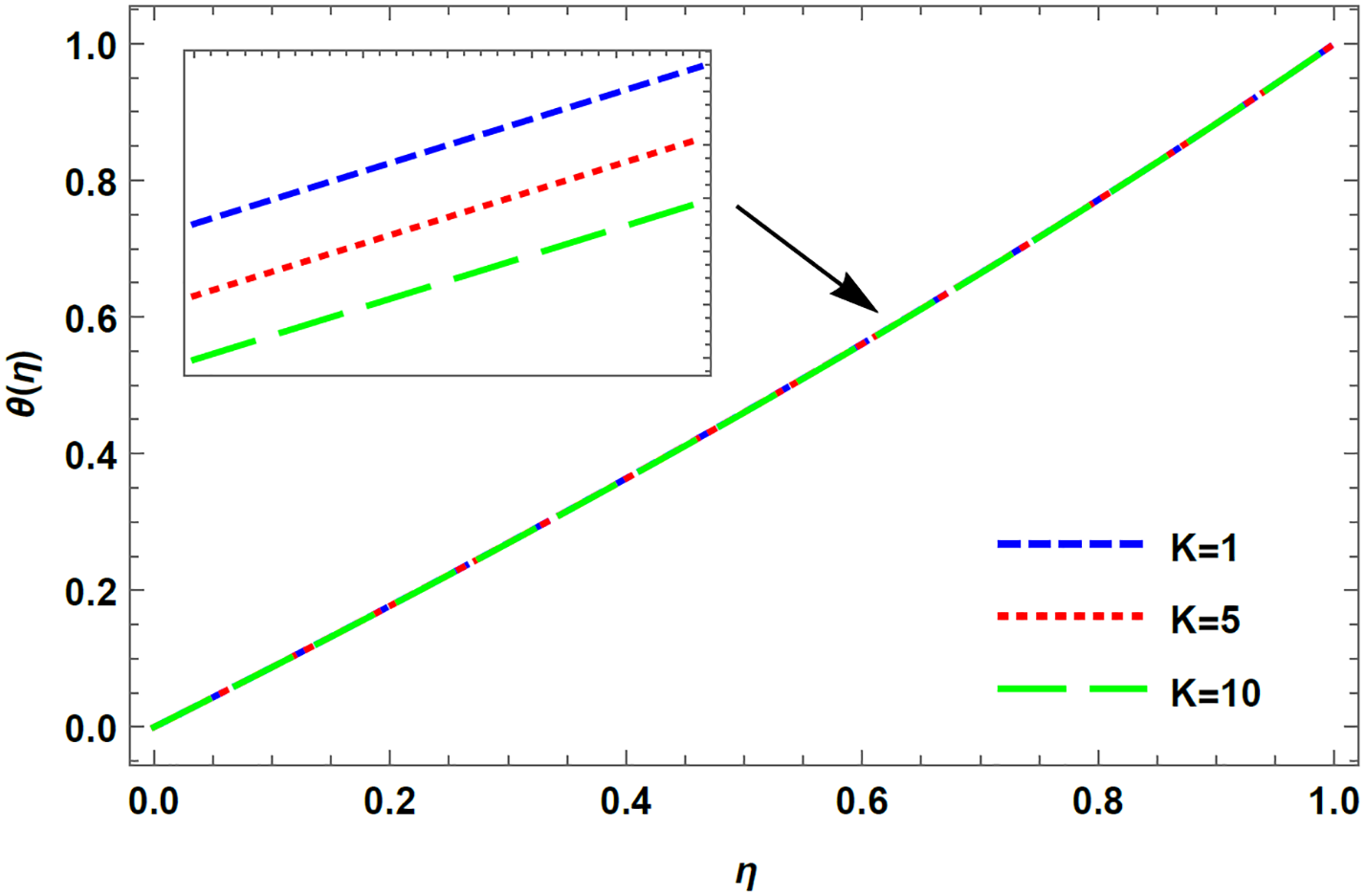
Figure 10: Temperature profile for varying K in case of injection, R = 5 with M = 0.1, De = 0.1, Rd = 0.1, Pr = 0.1

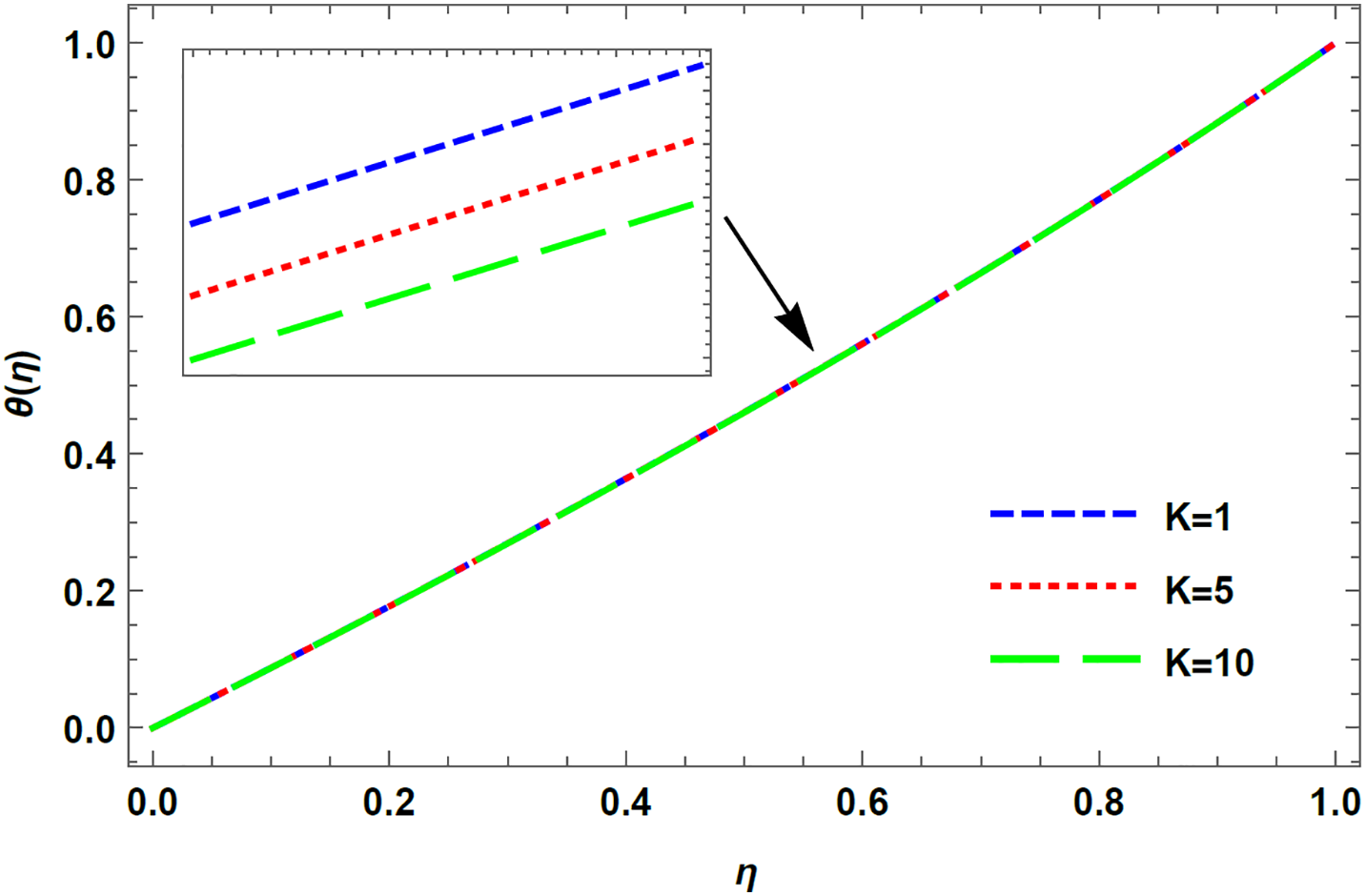
Figure 11: Temperature profile for varying K in case of injection, R = −5 with M = 0.1, De = 0.1, Rd = 0.1, Pr = 0.1

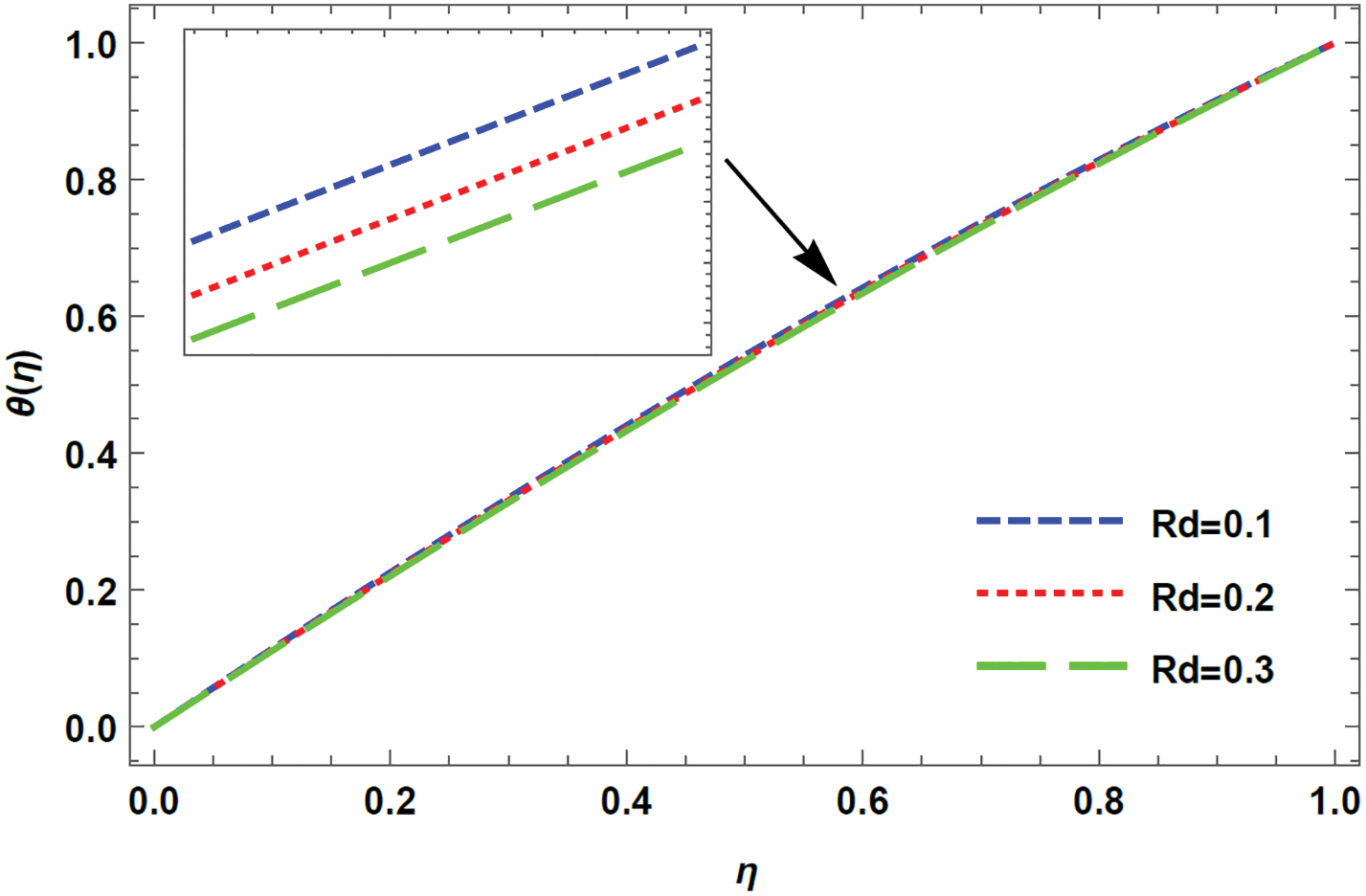
Figure 12: Temperature profile for varying Rd in case of injection, R = −5 with M = 0.1, De = 0.1, K = 1, Pr = 0.1

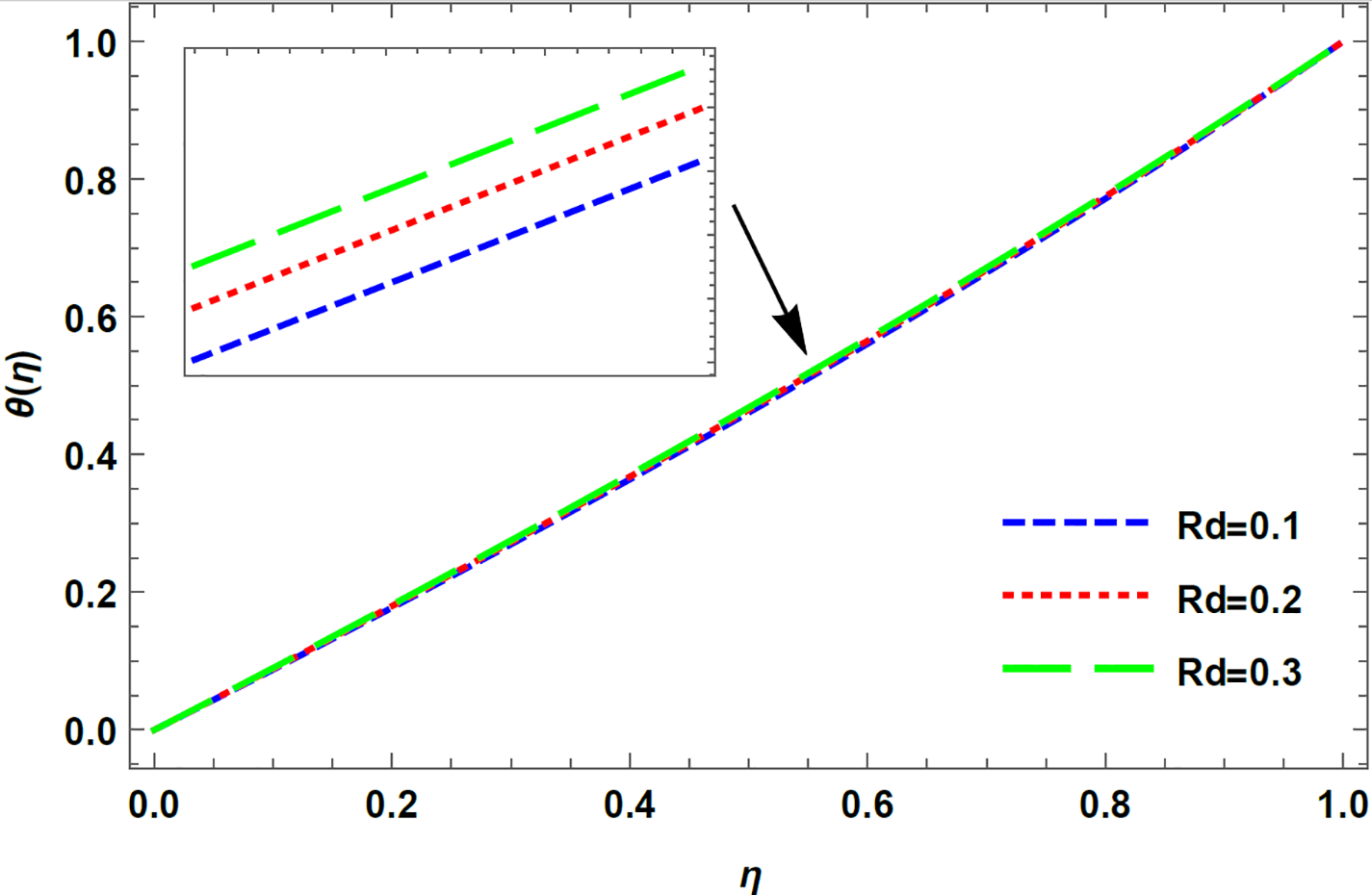
Figure 13: Temperature profile for varying Rd in case of injection, R = 5 with M = 0.1, De = 0.1, K = 1, Pr = 0.1

Figure 14: Temperature profile for varying Pr in case of injection, R = −5 with M = 0.1, De = 0.1, K = 1, Rd = 0.1

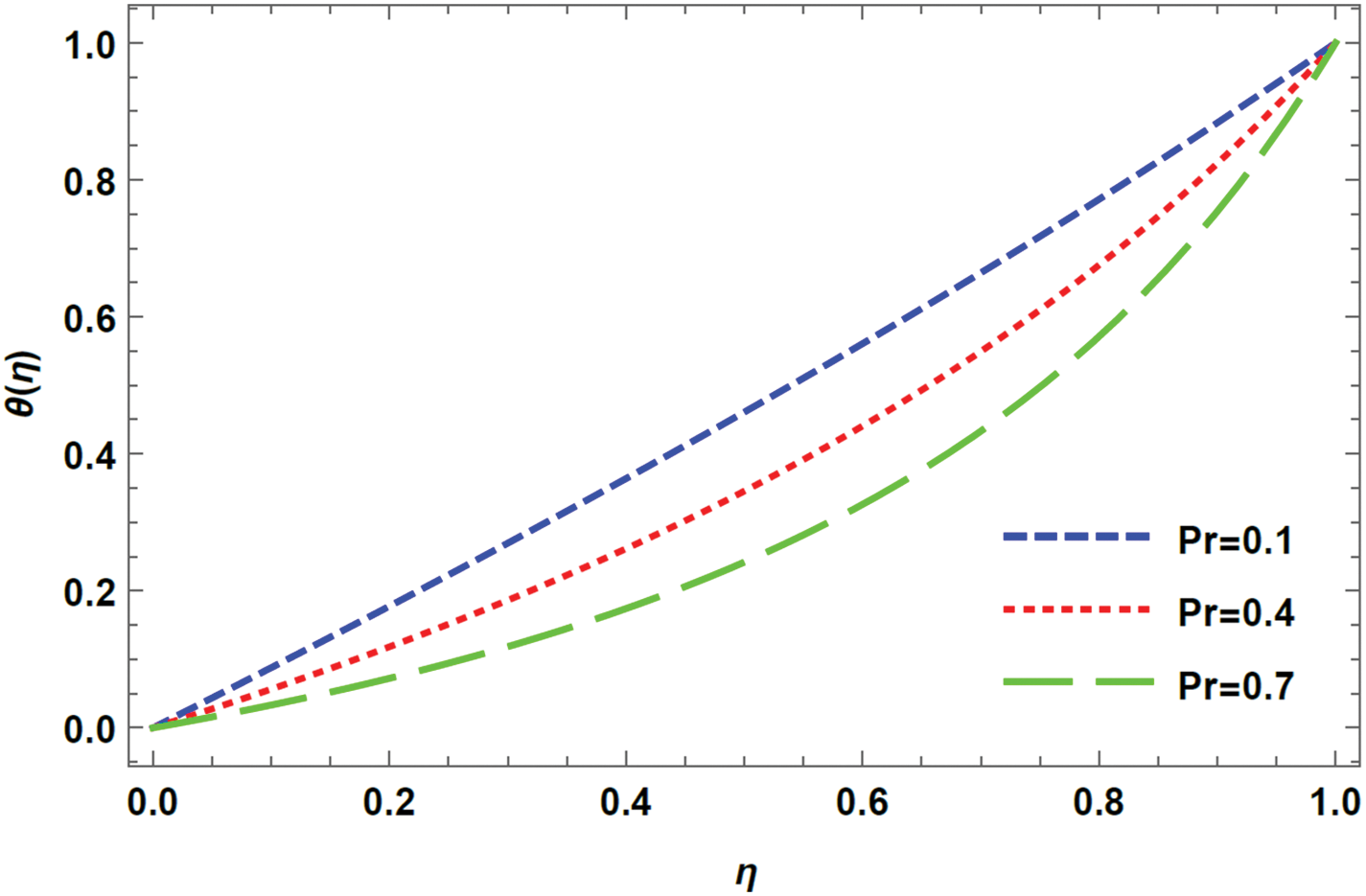
Figure 15: Temperature profile for varying Pr in case of injection, R = 5 with M = 0.1, De = 0.1, K = 1, Rd = 0.1

The impact of Reynolds number, R, on flow velocity in the injection case is illustrated in Fig. 2. As shown in the graph, F ′(η) increases in the first half when R increases, but it declines in the range 0.5≤η≤1. On the other hand, Fig. 3 demonstrates that the velocity F ′(η) decreases with an increment in R in the range 0≤η≤0.5, but it increases in the second half. Figs. 4 and 5 show the effect of R on temporal distribution for injection and suction, respectively. It is evident that θ(η) declines with an increment in R in both cases; that is, the temperature of the fluid reduces as the plates move closer in both injection and suction cases. The impact of the magnetic parameter on the temporal profile is illustrated in Figs. 6 and 7. As the strength of the applied magnetic field increases, a drag force known as the Lorentz force develops, causing the thermal boundary layer to become thinner in the case of plates moving away from each other. As a result, the flow is impeded, leading to a reduction in the magnitude of the temporal profile. Thus, as the plates move away from each other, the temperature of the flow declines with an increment in magnetic parameter, M, which is evident in Fig. 7. Whereas in the case of plates moving towards, an opposite trend is observed in Fig. 6.

When the Deborah number is small, the fluid exhibits characteristics of a viscous fluid, and the temperature of the flow remains relatively constant. On the other hand, in high Deborah number flows, the fluid behaves more like an elastic solid, and as a result, the deformation of the material causes the dissipation of energy, which leads to a significant increase in the temperature of the flow. It can be observed from Figs. 8 and 9 that an increment in Deborah number results in an increase of θ(η) for both plates moving towards and away from each other. The impact of the porosity parameter on the temporal profile is displayed in Figs. 10 and 11 as the upper plates move away and towards the stationary lower plate in the case of injection. It is evident that an increment in K results in an increase in θ(η) in both cases as the plates move away and towards each other. This is because as the porosity parameter increases, a larger amount of fluid is allowed to flow through the porous medium. This increases the velocity of the fluid flow, which in turn increases the viscous dissipation. Due to the increase in the viscous dissipation, the temporal profile of the UCM fluid gradually increases for both plates moving towards and apart in the case of injection. Moreover, a higher porosity parameter also allows for more heat transfer between the fluid and the plates, which further contributes to the increase in the temperature profile. Figs. 12 and 13 illustrate the impact of radiation parameter on the temperature profile. A fluid with high emissivity will absorb more radiation, thus resulting in an increased temperature, while a fluid with low emissivity will reflect more radiation, thereby decreasing the temperature. In the case of plates moving away from each other, the emissivity of the fluid decreases, resulting in a decrease of θ(η) with an increase in radiation parameter as demonstrated in Fig. 13. Whereas θ(η) increases with an increase in Rd as the emissivity increases when the plates move closer, as displayed in Fig. 12.

The Prandtl number determines the relationship between the momentum diffusivity of a fluid and its thermal diffusivity. A high Prandtl number indicates that the fluid has a low thermal diffusivity compared to its momentum diffusivity, resulting in a slower transfer of heat through the fluid than momentum. In contrast, a low Prandtl number signals that the fluid has a high thermal diffusivity relative to its momentum diffusivity, making it more capable of conducting heat than momentum. When the plates move apart, the transfer of momentum and heat between them decreases. This is because the gap between the plates increases, resulting in a reduction in the efficiency of the fluid flow to transport momentum and heat. As a result, both the momentum diffusivity and thermal diffusivity decrease, indicating a lower rate of transfer of momentum and heat. This is evident from Fig. 15 that θ(η) increases as the Prandtl number increases when plates move away from each other. In contrast, an opposite trend is observed when plates move closer to each other, as in Fig. 14.

The data presented in Table 1 indicates that a decrement in the porosity parameter at the upper plate and an increment in the porosity parameter at the bottom plate result in an increase in the skin friction coefficient magnitude when suction is applied. In contrast, an opposite behaviour is evident in the case of injection. In the case of suction, it was observed that an increment in Reynolds number results in a decrement of skin friction coefficient magnitude at the bottom plate, while an increase is observed at the top plate. However, for injection, whereas an increment in Reynolds number leads to a decrement in the skin friction coefficient magnitude at the upper plate and an increment at the bottom plate. Table 2 shows that for injection, an increment in Reynolds number, radiation parameter, and Prandtl number at the lower plate leads to an increase in the heat transfer rate. Conversely, an increase in these physical parameters at the upper plate results in a decrease in the heat transfer rate. However, when suction is applied, the opposite trend is observed.

5  Conclusion

The current article mainly focuses on the effect of thermal radiation on the MHD flow of a UCM fluid between parallel plates with an impermeable moving upper plate and stationary porous lower plate, specifically in the case of injection. The magnetic and radiative effects on the heat transfer of the UCM fluid flow are analysed with the help of HPM, leading to the following conclusions:

1.   The velocity and temperature fields of the flow increase with an increment in Reynolds number in case of injection and suction.

2.   In the case of injection, when the top plate moves away from the bottom one, an increment in the magnetic parameter and Prandtl number increases the temporal field.

3.   The temporal distribution increases with Deborah number for both top plates moving away and towards the bottom in case of injection.

4.   As the porosity parameter and the radiation parameter increases, the temporal profile retards for plates moving away from each other during injection.

5.   In the case of injection, the heat transfer rate at the bottom plate tends to increase as the Reynolds number, Prandtl number, and radiation parameter increase.

Acknowledgement: The authors are thankful to Manipal Academy of Higher Education (MAHE), Manipal for their support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: problem identification: Nityanand P. Pai; formulation and results: Devaki B.; analysis and interpretation of results: Sampath Kumar V. S.; draft manuscript preparation: Pareekshith G. Bhat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: There is no unavailable data in this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Archimedes (2009). On floating bodies, Book I. In: Heath, T. L. (Ed.The works of archimedes: Edited in modern notation with introductory chapters. Cambridge: Cambridge University Press. [Google Scholar]

2. Maxwell, J. C. (1867). On the dynamical theory of gases. Philosophical Transactions of the Royal Society of London, 157, 49–88. https://doi.org/10.1098/rstl.1867.0004. [Google Scholar] [CrossRef]

3. Karra, S., Prusa, V., Rajagopal, K. (2011). On maxwell fluids with relaxation time and viscosity depending on the pressure. International Journal of Non-Linear Mechanics, 46(6), 819–827. https://doi.org/10.1016/j.ijnonlinmec.2011.02.013 [Google Scholar] [CrossRef]

4. Olsson, F., Yström, J. (1993). Some properties of the upper convected maxwell model for viscoelastic fluid flow. Journal of Non-Newtonian Fluid Mechanics, 48(1), 125–145. https://doi.org/10.18869/acadpub.jafm.68.235.24939. [Google Scholar] [CrossRef]

5. Sadeghy, K., Najafi, A. H., Saffaripour, M. (2005). Sakiadis flow of an upper-convected maxwell fluid. International Journal of Non-Linear Mechanics, 40(9), 1220–1228. https://doi.org/10.1016/j.ijnonlinmec.2005.05.006 [Google Scholar] [CrossRef]

6. Choi, J. J., Rusak, Z., Tichy, J. A. (1999). Maxwell fluid suction flow in a channel. Journal of Non-Newtonian Fluid Mechanics, 85(2–3), 165–187. https://doi.org/10.1016/S0377-0257(98)00197-9 [Google Scholar] [CrossRef]

7. Ganesh, S., Krishnambal, S. (2007). Unsteady stokes flow of viscous fluid between two parallel porous plates. International Journal on Information Sciences and Computing, 1(1), 63–66. https://doi.org/10.18000/ijisac.50012 [Google Scholar] [CrossRef]

8. Haro, M. D., Rio, J. D., Whitaker, S. (1996). Flow of maxwell fluids in porous media. Transport in Porous Media, 25(2), 167–192. https://doi.org/10.1007/BF00135854 [Google Scholar] [CrossRef]

9. Hayat, T., Ali, N., Asghar, S. (2007). Hall effects on peristaltic flow of a maxwell fluid in a porous medium. Physics Letters A, 363(5–6), 397–403. https://doi.org/10.1016/j.physleta.2006.10.104 [Google Scholar] [CrossRef]

10. Kashyap, K. P., Ojjela, O., Das, S. K. (2019). Mhd slip flow of chemically reacting ucm fluid through a dilating channel with heat source/sink. Nonlinear Engineering, 8(1), 523–533. https://doi.org/10.1515/nleng-2018-0036 [Google Scholar] [CrossRef]

11. Kashyap, K. P., Ojjela, O., Das, S. K. (2019). Magnetohydrodynamic mixed convective flow of an upper convected maxwell fluid through variably permeable dilating channel with soret effect. Pramana, 92, 1–10. https://doi.org/10.1007/s12043-019-1732-4 [Google Scholar] [CrossRef]

12. Prasad, K. V., Hanumesh Vaidya, K., Vajravelu, B. S. S. (2020). Mhd flow of a ucm nanofluid in a permeable channel: Buongiorno’s model. International Journal of Applied and Computational Mathematics, 6(126), 1–19. https://doi.org/10.1007/s40819-020-00881-8 [Google Scholar] [CrossRef]

13. Shah, S., Hussain, S. (2021). Slip effect on mixed convective flow and heat transfer of magnetized ucm fluid through a porous medium in consequence of novel heat flux model. Results in Physics, 20, 103749. https://doi.org/10.1016/j.rinp.2020.103749 [Google Scholar] [CrossRef]

14. Fetecau, C., Vieru, D., Abbas, T., Ellahi, R. (2021). Analytical solutions of upper convected maxwell fluid with exponential dependence of viscosity under the influence of pressure. Mathematics, 9(334), 1–19. https://doi.org/10.3390/math9040334 [Google Scholar] [CrossRef]

15. Zeb, S., Ullah, Z., Urooj, H., Khan, I., Ganie, A. H. et al. (2023). Simultaneous features of mhd and radiation effects on the ucm viscoelastic fluid through a porous medium with slip conditions. Case Studies in Thermal Engineering, 45, 102847. https://doi.org/10.1016/j.csite.2023.102847 [Google Scholar] [CrossRef]

16. Zheng, Z., Chen, X., Yang, W. (2023). Squeeze flow of a maxwell fluid between a sphere and a plate. Physics of Fluids, 36(1), 013121. https://doi.org/10.1063/5.0185335 [Google Scholar] [CrossRef]

17. Yuan, S. W. (1956). Further investigation of laminar flow in channels with porous walls. Journal of Applied physics, 27(3), 267–269. https://doi.org/10.1016/S0376-7388(01)00546-4 [Google Scholar] [CrossRef]

18. Cox, S. M. (1991). Analysis of steady flow in a channel with one porous wall, or with accelerating walls. SIAM Journal on Applied Mathematics, 51(2), 429–438. https://doi.org/10.1137/0151021 [Google Scholar] [CrossRef]

19. Islam, S., Khan, H., Shah, I. A., Zaman, G. (2011). An axisymmetric squeezing fluid flow between the two infinite parallel plates in a porous medium channel. Mathematical Problems in Engineering, 2011, 1–10. https://doi.org/10.1155/2011/349803 [Google Scholar] [CrossRef]

20. Bujurke, N. M., Achar, P. K., Pai, N. P. (1995). Computer extended series for squeezing flow between plates. Fluid Dynamics Research, 16(2–3), 173–187. https://doi.org/10.1016/0169-5983(94)00058-8 [Google Scholar] [CrossRef]

21. Khan, U., Ahmed, N., Khan, S. I., Bano, S., Mohyud-din, S. T. (2014). Unsteady squeezing flow of a casson fluid between parallel plates. World Journal of Modelling and Simulation, 10(4), 308–319. https://doi.org/10.1016/j.jksus.2015.03.006 [Google Scholar] [CrossRef]

22. Sampath, K. V. S., Pai, N. P. (2018). Suction and injection effect on flow between two plates with reference to casson fluid model. Multidiscipline Modeling in Materials and Structures, 15(3), 559–574. https://doi.org/10.1108/MMMS-05-2018-0092 [Google Scholar] [CrossRef]

23. Abbas, Z., Hussain, S., Nadeem, A., Rauf, A. (2021). Non-newtonian fluid flow having fluid-partical interaction through porous zone in a channel with permeable walls. International Journal of Nonlinear Sciences and Numerical Simulations, 24(3), 1163–1175. https://doi.org/10.1515/ijnsns-2020-0213 [Google Scholar] [CrossRef]

24. Ashrafi, T. G., Hoseinzadeh, S., Sohani, A., Shahverdian, M. H. (2021). Applying homotopy perturbation method to provide ananalytical solution for newtonian fluid flow on a porousflat plate. Mathematical Methods in the Applied Sciences, 44(8), 7017–7030. https://doi.org/10.1002/mma.7238 [Google Scholar] [CrossRef]

25. Hassanien, I. A., Mansour, M. A. (1990). Unsteady magnetohydrodynamic flow through a porous medium between two infinite parallel plates. Astrophysics and Space Science, 163(2), 241–246. https://doi.org/10.1007/BF00655745 [Google Scholar] [CrossRef]

26. Barik, R. N., Dash, G. C., Rath, P. K. (2018). Steady laminar mhd flow of visco-elastic fluid through a porous pipe embedded in a porous medium. Alexandria Engineering Journal, 57(2), 973–982. https://doi.org/10.1016/j.aej.2017.01.025 [Google Scholar] [CrossRef]

27. Hayat, T., Fetecau, C., Sajid, M. (2008). On MHD transient flow of a maxwell fluid in a porous medium and rotating frame. Physics Letters A, 372(10), 1639–1644. https://doi.org/10.1016/j.physleta.2007.10.036 [Google Scholar] [CrossRef]

28. Nayak, M. K., Dash, G., Singh, L. (2014). Effect of chemical reaction on mhd flow of a visco-elastic fluid through porous medium. Journal of Applied Analysis and Computation, 4(4), 367–381. https://doi.org/10.11948/2014020 [Google Scholar] [CrossRef]

29. Khan, Z., Rasheed, H. U., Alkanhal, T. A., Ullah, M., Khan, I. et al. (2018). Effect of magnetic field and heat source on upper-convected-maxwell fluid in a porous channel. Open Physics, 16(1), 917–928. https://doi.org/10.1515/phys-2018-0113 [Google Scholar] [CrossRef]

30. Jamil, B., Anwar, M. S., Rasheed, A., Irfan, M. (2020). Mhd maxwell flow modeled by fractional derivatives with chemical reaction and thermal radiation. Chinese Journal of Physics, 67, 512–533. https://doi.org/10.1016/j.cjph.2020.08.012 [Google Scholar] [CrossRef]

31. Imtiaz, M. (2023). Impact of magnetohydrodynamics in bidirectional slip flow of maxwell fluid subject to stretching, radiation, and variable properties. Numerical Heat Transfer, Part A: Applications, 84(4), 1459–1476. https://doi.org/10.1080/10407782.2023.2176383 [Google Scholar] [CrossRef]

32. Sudarmozhi, K., Iranian, D., Khan, I. (2023). A steady flow of mhd maxwell viscoelastic fluid on a flat porous plate with the outcome of radiation and heat generation. Frontiers in Physics, 11, 1126662. https://doi.org/10.3389/fphy.2023.1126662 [Google Scholar] [CrossRef]

33. Sudarmozhi, K., Iranian, D., Alhazmi, H., Reddy, G. S., Khan, I. et al. (2024). Significance of heat generation in mhd channel flow of a maxwell fluid with heat suction and blowing effects. Case Studies in Thermal Engineering, 55, 104134. https://doi.org/10.1016/j.ijft.2023.100396 [Google Scholar] [CrossRef]

34. Kaviany, M. (1985). Laminar flow through a porous channel bounded by isothermal parallel plates. International Journal of Heat and Mass Transfer, 28(4), 851–858. https://doi.org/10.1016/0017-9310(85)90234-0 [Google Scholar] [CrossRef]

35. Singh, V., Agarwal, S. (2014). Mhd flow and heat transfer for maxwell fluid over an exponentially stretching sheet with variable thermal conductivity. Thermal Science, 18(2), 396–599. https://doi.org/10.2298/TSCI120530120S [Google Scholar] [CrossRef]

36. Elbashbeshy, E. M. A., Asker, H. G., Abdelgaber, K. M., Sayed, E. (2018). Heat transfer over a stretching surface with variable thickness embedded in porous medium in the presence of maxwell fluid. Journal of Applied Mechanical Engineering, 7(3), 1–10. https://doi.org/10.4172/2168-9873.1000307 [Google Scholar] [CrossRef]

37. Sinha, A. (2015). Mhd flow and heat transfer of a third order fluid in a porous channel with stretching wall: Application to hemodynamics. Alexandria Engineering Journal, 54(4), 1243–1252. https://doi.org/10.1016/j.aej.2015.06.00 [Google Scholar] [CrossRef]

38. Kim, S. K. (2020). Forced convected heat transfer for the fully-developed laminar flow of the cross fluid between parallel plates. Journal of Non-Newtonian Fluid Mechanics, 276, 104226. https://doi.org/10.1016/j.jnnfm.2019.104226 [Google Scholar] [CrossRef]

39. Krishna, M. V., Chamkha, A. J. (2020). Hall and ion slip effects on mhd rotating flow of elastico-viscous fluid through porous medium. International Journal Heat and Mass Transfer, 113, 104494. https://doi.org/10.1016/j.icheatmasstransfer.2020.104494 [Google Scholar] [CrossRef]

40. Na, W., Shah, N. A., Tlili, I., Siddique, I. (2020). Maxwell fluid flow between vertical plates with damped shear and thermal flux: Free convection. Chinese Journal of Physics, 65, 367–376. https://doi.org/10.1016/j.cjph.2020.03.005 [Google Scholar] [CrossRef]

41. Lahmar, S., Kezzar, M., Eid, M. R., Sari, M. R. (2020). Heat transfer of squeezing unsteady nanofluid flow under the effects of an inclined magnetic field and variable thermal conductivity. Physica A: Statistical Mechanics and its Applications, 540, 123138. https://doi.org/10.1016/j.physa.2019.123138 [Google Scholar] [CrossRef]

42. Sampath, K. V. S., Pai, N. P., Devaki, B. (2021). Analysis of mhd flow and heat transfer of laminar flow between porous disks. Frontiers in Heat and Mass Transfer, 16(3), 1–7. https://doi.org/10.5098/hmt.16.3 [Google Scholar] [CrossRef]

43. Hussain, S., Abbas, Z., Hasnain, J., Arslan, M. S., Ali, A. (2021). Thermally developed unsteady viscous nanofluid flow due to permeable channel with orthogonal motion of walls using beavers-joseph slip condition. Alexandria Engineering Journal, 60(2), 2335–2345. https://doi.org/10.1016/j.aej.2020.12.043 [Google Scholar] [CrossRef]

44. Raptis, A., Perdikis, C., Takhar, H. (2004). Effect of thermal radiation on mhd flow. Applied Mathematics and Computation, 153(3), 645–649. https://doi.org/10.1016/S0096-3003(03)00657-X [Google Scholar] [CrossRef]

45. Hayat, T., Sajjad, R., Abbas, Z., Sajid, M., Hendi, A. A. (2011). Radiation effects on mhd flow of maxwell fluid in a channel with porous medium. International Journal of Heat and Mass Transfer, 54(4), 854–862. https://doi.org/10.1016/j.ijheatmasstransfer.2010.09.069 [Google Scholar] [CrossRef]

46. Mukhopadhyay, S., Ranjan De, P., Layek, G. (2013). Heat transfer characteristics for the maxwell fluid flow past an unsteady stretching permeable surface embedded in a porous medium with thermal radiation. Journal of Applied Mechanics and Technical Physics, 54(3), 385–396. https://doi.org/10.1134/S0021894413030061 [Google Scholar] [CrossRef]

47. Elbashbeshy, E. M. A., Asker, H. G., Abdelgaber, K. M. (2019). Flow and heat transfer over a stretching surface with variable thickness in a maxwell fluid and porous medium with radiation. Thermal Science, 23(5), 3105–3116. https://doi.org/10.2298/TSCI170228146E [Google Scholar] [CrossRef]

48. Ibrahim, F. S., Hardy, F. M. (1990). Mixed convection-radiation interaction in boundary-layer flow over horizontal surfaces. Astrophysics and Space Science, 168(2), 263–276. https://doi.org/10.1007/BF00636872 [Google Scholar] [CrossRef]

49. Mansour, M. A. (1989). Radiative and free-convection effects on the oscillatory flow past a vertical plate. Astrophysics and Space Science, 166(2), 269–275. https://doi.org/10.1007/BF01094898 [Google Scholar] [CrossRef]

50. Bilal, M., Ramzan, M., Mehmood, Y., Alaoui, M. K., Chinram, R. (2021). An entropy optimization study of non-darcian magnetohydrodynamic williamson nanofluid with nonlinear thermal radiation over a stratified sheet. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 235(6), 1883–1894. https://doi.org/10.1177/09544089211027989 [Google Scholar] [CrossRef]

51. He, J. H. (1999). Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, 178(3), 257–262. https://doi.org/10.1016/S0045-7825(99)00018-3 [Google Scholar] [CrossRef]

52. He, J. H. (2000). A coupling method of a homotopy technique and a perturbation technique for non-linear problems. International Journal of Non-Linear Mechanics, 35(1), 37–43. https://doi.org/10.1016/S0020-7462(98)00085-7 [Google Scholar] [CrossRef]

53. He, J. H. (2003). Homotopy perturbation method: A new nonlinear analytical technique. Applied Mathematics and Computation, 135(1), 73–79. https://doi.org/10.1016/S0096-3003(01)00312-5 [Google Scholar] [CrossRef]

54. Babolian, E., Azizi, A., Saeidian, J. (2009). Some notes on using the homotopy perturbation method for solving time-dependent differential equations. Mathematical and Computer Modelling, 50(1–2), 213–224. https://doi.org/10.1016/j.mcm.2009.03.003 [Google Scholar] [CrossRef]

55. He, J. H., El-Dib, Y. O. (2020). Homotopy perturbation method for fangzhu oscillator. Journal of Mathematical Chemistry, 58, 2245–2253. https://doi.org/10.1002/mma.6384 [Google Scholar] [CrossRef]

56. Yu, D. N., He, J. H., Garcia, A. G. (2021). Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators. Journal of Low Frequency Noise, Vibration and Active Control, 38(3–4), 1540–1554. https://doi.org/10.1177/1461348419836344 [Google Scholar] [CrossRef]

57. Kashkari, B. S., El-Tantawy, S. A. (2021). Homotopy perturbation method for modeling electrostatic structures in collisional plasmas. The European Physical Journal Plus, 136(121), 1–23. https://doi.org/10.1029/2004RG000151 [Google Scholar] [CrossRef]

58. Pai, N. P., Sampath, K. V. S., Devaki, B. (2023). Heat transfer analysis of mhd casson fluid flow between two porous plates with different permeability. Frontiers in Heat and Mass Transfer, 20(30), 1–13. https://doi.org/10.5098/hmt.20.30 [Google Scholar] [CrossRef]

59. Mukhopadhyaya, S., Arifb, M. G., Pk, M. W. A. (2013). Effects of transpiration on unsteady mhd flow of an upper convected maxwell (UCM) fluid passing through a stretching surface in the presence of a first order chemical reaction. Chinese Physics B, 22(12), 124701. https://doi.org/10.1088/1674-1056/22/12/124701 [Google Scholar] [CrossRef]

60. Saleem, S., Awais, M., Nadeem, S., Sadeep, N., Mustafa, M. T. (2017). Theoretical analysis of upper-convected maxwell fluid flow with cattaneo-christov heat flux model. Chinese Journal of Physics, 55, 1615–1625. https://doi.org/10.1016/j.cjph.2017.04.005 [Google Scholar] [CrossRef]

61. Ahmad, S., Khan, M. N., Nadeem, S. (2021). Mathematical analysis of heat and mass transfer in a maxwell fluid with double stratification. Physica Scripta, 96, 025202. https://doi.org/10.1088/1402-4896/abcb2a [Google Scholar] [CrossRef]

62. Ali, M., Chen, T., Armaly, B. (1984). Natural convection-radiation interaction in boundary-layer flow over horizontal surfaces. AIAA Journal, 22(12), 1797–1803. https://doi.org/10.2514/3.8854 [Google Scholar] [CrossRef]