 Open Access
Open Access
ARTICLE
A Novel Numerical Method for Simulating Boiling Heat Transfer of Nanofluids
Low-Carbon Energy Institute, Ludong University, Yantai, 264025, China
* Corresponding Author: Yang Cao. Email:
(This article belongs to the Special Issue: Advances in Computational Thermo-Fluids and Nanofluids)
Frontiers in Heat and Mass Transfer 2024, 22(2), 583-595. https://doi.org/10.32604/fhmt.2024.049111
Received 28 December 2023; Accepted 13 March 2024; Issue published 20 May 2024
Abstract
In this paper, a new approach called the Eulerian species method was proposed for simulating the convective and/or boiling heat transfer of nanofluids. The movement of nanoparticles in nanofluids is tracked by the species transport equation, and the boiling process of nanofluids is computed by the Eulerian multiphase method coupled with the RPI boiling model. The validity of the species transport equation for simulating nanoparticles movement was verified by conducting a simulation of nanofluids convective heat transfer. Simulation results of boiling heat transfer of nanofluids were obtained by using the commercial CFD software ANSYS Fluent and compared with experimental data and results from another numerical method (Eulerian three-phase model). Good agreement with experimental data was achieved, and it was proved the Eulerian species method is better than the Eulerian three-phase model since it can give better simulation results with higher accuracy but needs fewer computation resources.Keywords
Nomenclature
| aif | Interfacial area per unit volume |
| Ab | The areas covered by bubbles |
| CD | Drag coefficient |
| CL | Lift coefficient |
| Dw | Bubble departure diameter |
| f | Bubble departure frequency |
| Fd | Drag force |
| FL | Lift force |
| FLUB | Wall lubrication force |
| Ftd,l | Turbulence dispersion force |
| Nw | Bubble nucleate site density |
| p | Pressure |
| q | Heat flux |
| T | Temperature |
| t | Time |
| u | Velocity |
| Ub | Fluid velocity near the wall |
| hc | Single-phase heat transfer coefficient |
| hfv | Latent heat |
| H | Enthalpy |
| DNP,m | Mass diffusion coefficient of the nanoparticles |
| DT,NP | Thermal diffusion coefficient |
| YNP | Mass fraction of the nanoparticles |
| SNP | Exogenous term of the nanoparticle component |
| JNP | Mass diffusion term |
| Greek Symbols | |
| Γ | Mass rate exchange between liquid and gas phases |
| ρ | Density |
| α | Volume fraction |
| µ | Dynamical viscosity |
| θ | Contact angle |
| Subscripts | |
| c | Convection |
| E | Evaporation |
| l | Liquid |
| g | Gas |
| Q | Quenching |
| w | Wall |
| sup | Superheat |
| sat | Saturation |
Enhancement of boiling heat transfer by modifying the physical properties of the working fluid has drawn considerable attention recently, and the application of nanofluids as the heat transfer medium is probably the most popular way and provides many opportunities to explore the new frontier but also poses great challenges in this research field [1]. Nanofluids, first reported and named by Choi et al. [2] in 1995, are a new kind of fluid composed of a base fluid and a small quantity of nano-sized particles that are uniformly and stably suspended in the base fluid and change the physical properties (e.g., thermal conductivity, viscosity) of the base fluid remarkably [3]. Nanofluids boiling, including pool boiling, flow boiling and jet impingement boiling, began to draw research interest in 2003 and has become an important research field [1]. The existing experimental investigations show much more cases of heat transfer enhancement than deterioration, the maximum enhancement is found in flow boiling of nanofluid with a 400% growth in heat transfer coefficient [4]. Although massive studies were conducted, there are still many issues unsolved about the nanofluids boiling heat transfer, so continuous long-term efforts need to be made, especially the numerical simulations and theoretical studies, because the experimental investigations account for about 95% of nanofluids boiling research so far [1].
Because of the co-existing of nanoparticles and vapor bubbles in the nanofluids when boiling occurs, it is quite complex to numerically simulate the boiling phenomena and heat transfer characteristic of nanofluids. It is simpler to simulate the convective heat transfer of nanofluids because there are no vapor bubbles generated by the boiling, and the numerical methods can be categorized as single-phase approach and two-phase approach, and the latter can be further divided into the Eulerian-Eulerian model and Lagrangian-Eulerian model. In the single-phase approach, the nanofluid is treated as a conventional single-phase (homogenous) fluid with the average physical properties of the particles and the base fluid by assuming the nanoparticles can be easily fluidized and the base fluid and particles are in thermal equilibrium and move with the same velocity [5]. In the two-phase approach, the nanoparticles and the base fluid are considered as two different phases with different velocities and temperatures; the movements of the solid particles and fluid must be solved, respectively, so it may get realistic results but need much more time and computation resources than the single-phase approach. Compared with the simulation of convective heat transfer of nanofluids, the boiling heat transfer simulation is more complicated, for one more phase must be computed, namely the vapor bubble phase generated by the boiling process, so the single-phase approach of nanofluids simulation will become a two-phase approach and the two-phases approach will become three-phases approach when the boiling heat transfer is simulated.
Abedini et al. [6,7] studied the subcooled flow boiling of Al2O3/water nanofluid using the two-phase mixture model (nanofluid liquid-vapor). The nanofluid was described as a single phase fluid with effective physical parameters, good agreement between their simulation and previously published experimental data was obtained, local flow characteristics of subcooled flow boiling such as axial volume fraction and distribution of temperature are well predicted. It was observed that the heat transfer coefficient for Al2O3/water nanofluid in subcooled flow boiling is higher than that of the base fluid and the heat transfer coefficient increases with increasing of the nanoparticles volume fraction. Li et al. [8] investigated the nucleate pool boiling of dilute water–silica nanofluid using the Eulerian–Eulerian two-fluid model. They developed correlations for active nucleate site density and bubble departure diameter in which the effect of wall wettability caused by nanoparticle deposition has been considered. A Comparison of numerical results against the pool boiling experimental data of pure water and dilute water–silica nanofluids demonstrated that the model accuracy was improved by including the effects of the improved surface wettability. However, the accuracy of the new model is still not satisfactory, which means further research is needed. The research conducted by Behroyana et al. [9] numerically investigated the heat transfer of nanofluids subcooled flow boiling using the Eulerian–Eulerian two-phase (liquid/nanofluid-vapor) model and the Eulerian–Lagrangian three-phases (liquid-vapor-particles) model, the changes on heating surface wettability induced by nanoparticles deposition was included in the cases via user defined functions (UDF) codes. The simulation results were compared between these two methods; for the heat transfer coefficient prediction, the Eulerian–Lagrangian three-phase model gives about 6% error, whereas the Eulerian–Eulerian model gives about 12% error when it is compared with Chen’s correlation. Heat transfer and the deposition of nanoparticles on heated walls were numerically investigated in a pool boiling flow on a single tube and four-tube bundle by Mostafa et al. [10]. The Eulerian-Eulerian two-phase approach was employed to model pool boiling, and the Lagrangian model was used to track the movement of the particles during the boiling process. New models are made through a user-defined function (UDF) for nucleation site density and bubble departure diameter to include the important effects of particles deposition and surface roughness. A good agreement is found that the percentage of deposition is dependent on the heat flux and particle concentration. Also, the heat transfer coefficient increases with expanding the horizontal distance between cylinders and then decreases to a fixed value.
In recent years, with the rapid development of the artificial intelligence, the machine learning and neural network have also used in the numerical study of the nanofluids research field [11]. The machine learning approaches were used to predict the physical properties (e.g., thermal conductivity [12,13], viscosity [14–16]) of nanofluids. The boiling heat transfer characteristic of nanofluids was also studied by the artificial intelligence methods [17], Artificial neural network and genetic algorithm were utilized to predict and optimize the boiling heat transfer coefficient as well as the wall superheat of the Fe3O4/water nanofluid at the atmospheric pressure on a precipitated surface by the nanofluid [18].
In general, the research on nanofluids heat transfer is still a hot topic in recent years. In this paper, an approach called Eulerian species method is proposed for simulating the convective and/or boiling heat transfer of nanofluids, where the species transport equation is solved to track the movement of the nanoparticles in the nanofluid. The Eulerian two-phase approach coupled with the RPI boiling model is used to compute the movements of the vapor phase and liquid phase of the nanofluids when the boiling process occurs. In the Eulerian species method, the nanofluid is treated as a homogenous liquid mixture consisting of the base fluid and the evenly distributed nanoparticles, which are considered as one species of the liquid mixture, so the nanoparticles are solved by the species transport equation.
2 Formulation of the Eulerian Species Model
2.1 The Basic Governing Equations
In this method, the boiling process of nanofluids is simulated by the Eulerian two-phase model coupled with the RPI boiling model. The basic governing equations, namely the Naiver-Stokes equations are solved for the nanofluids (liquid) and the boiling vapor phase, respectively, as follows:
The continuity equations for the nanofluids liquid and boiling vapor phase are:
∂ρ1,effα1∂t+∇⋅(ρ1α1→u1)=Γ1g(1)
∂ρgαg∂t+∇⋅(ρgαg→ug)=Γgl(2)
where the Γlg, Γgl are the mass rate exchanged between the nanofluids liquid and boiling vapor phases caused by the boiling process.
The momentum equations for the nanofluids liquid and boiling vapor phase are:
∂ρ1,eff α 1→u1∂t+∇⋅( ρ l,eff α 1→u1→u1)=− α 1∇p+ ρ l,eff α1→g+∇[ α1 μe1(∇→u1+(∇→u1)T)]+(Γlg→ug−Γgl→u1)+Flg(3)
∂ρgαg→ug∂t+∇⋅(ρgαg→ug→ug)=−αg∇p+ρgαg→g+∇[αgμg(∇→ug)]+(Γg1→u1−Γlg→ug)+Fgl(4)
where Fgl and Flg are the interfacial forces between the nanofluids liquid and the vapor phases and will be explained in Section 2.2.
The energy conservation equations for the nanofluids liquid and boiling vapor phase are:
∂ρ1,effα1H1∂t+∇⋅(ρ1,effα1→u1H1)=∇[α1ke1(∇T1)]+(Γg1H1−Γ1gHg)(5)
∂ρgαgHg∂t+∇⋅(ρgαg→ugHg)=∇[αgkg(∇Tg)]+(ΓlgHg−ΓglH1)(6)
In the method proposed in this paper, the nanoparticles are treated as a component of the nanofluid, like one species of a liquid mixture, such as the salt ions (Na+, Cl−) in the brine, so the species transport model is used for calculating the distribution and transportation of nanoparticles in nanofluid. The equations are as follows:
∂∂t(ρl,effYNP)+∇⋅(ρl,eff→vYNP)=−∇⋅→JNP+SNP(7)
Here the YNP is the mass fraction of the nanoparticles, SNP is the exogenous term of the nanoparticle component, and →JNP is the mass diffusion term. In the boiling process, there will be strong turbulence near the heating wall surface, so the influence of the liquid phase turbulence on the distribution of nanoparticles needs to be considered. In this equation, the diffusion of nanoparticles in the boiling turbulent flow is modeled using the following formula:
→JNP=−(ρDNP,m+μtSct)∇YNP−DT,NP∇TT(8)
where Sct is the turbulent Schmidt number, its value is 0.75, DNP,m is the mass diffusion coefficient of the nanoparticles, DT,NP is the thermal diffusion coefficient.
2.2 The Interfacial Force Model
The interaction forces at the interface between the nanofluid liquid and boiling vapor phases consist of the drag, lift force, turbulent dispersion force, wall lubrication force and virtual mass force, etc. Introduction of the forces is presented in following. The drag force correction model proposed by Ishii et al. [19] was adopted for the interphase exchange, since the wall boiling simulation is conducted:
Fd=18CDaifρl,eff|→ug−→u1|(→ug−→u1)(9)
CD=min(24Re(1+0.15Re0.75),23dp√σg|ρq−ρp|)(10)
where aif is the interfacial area per unit volume, and CD is the drag coefficient.
The lift force model uses the modified model proposed by Tomiyama [20]:
FL=αgρl,effCL(→ug−→u1)×(∇×→u1)(11)
where CL is the lift coefficient.
The wall lubrication force of the nucleated bubble boiling region adopts the wall lubrication force model proposed by Antal et al. [21]:
FLub=Cwρkαv|→ug−→u1|2→n(12)
Cw=max(0,Cw1dl+Cw2yw),Cw1=−0.01;Cw2=0.05(13)
The turbulence dispersion force adopts the modified model proposed by Bertodano [22]:
Ftd,l=−Ftd,g=CTDρl,effkl∇αg(14)
where CTD is a user-modifiable constant, the value of 0.1 is used in our simulation.
The RPI model developed by the Kurual et al. [23] is adopted as the boiling model, this model assumes that the total heat flux is partitioned into three components: heat flux due to convection ˙qc, heat flux due to surface quenching or transient conduction ˙qQ and that due to microlayer evaporation ˙qE.
˙qw=˙qc+˙qQ+˙qE(15)
Heat transfer due to turbulent convection ˙qc can be determined from [24]:
˙qc=hc(Tw−Tl)(1−Ab)(16)
where hc is the single-phase heat transfer coefficient; Tw, Tl are the wall and liquid temperature, respectively; and Ab are the areas covered by bubbles:
Ab=KNwπD2w4(17)
where K is the empirical constant.
When the liquid is in contact with a hot surface, heat is mainly transferred to the liquid through transient conduction. This part of the heat flow can be determined from:
˙qQ=2kl√πλltT(Tw−Tl)(18)
Heat transfer due to microlayer evaporation ˙qE can be determined from [25]:
˙qE=π6D3wNwρvhfvf(19)
where Dw is the bubble departure diameter, Nw is the nucleate site density, ρv is the evaporation phase density, hfv is the latent heat of evaporation, and f is the bubble departure frequency. f can be determined from Cole correlation [26]
f=1T=√4g(ρl−ρv)3pPlDw(20)
The nucleate site density can be corrected by the superheat of the surface, and can usually be calculated as [27]:
Nw=2101.8(Tw−Tsat)1.805(21)
The bubble departure diameter usually adopts the empirical correction formula proposed by Unal [28]:
Dw=2.4210−5p0.709(ab√φ)(22)
where
α=ΔTsup2ρghfv√ρsCpsksπ(23)
b={ΔTsup2(1−ρgρl)e(ΔTsub−12)ΔTsup≤3ΔTsup2(1−ρgρl)ΔTsup>3(24)
φ=max((UbU0)0.47,1.0)(25)
where Pl is the fluid pressure, ΔTsup is the superheat of the heating wall, ΔTsup=Tw−Tsat, hfv is the latent heat of evaporation, and Ub is the fluid velocity near the wall.
Since these correlations were originally developed for conventional fluids like water, the applicability of them is open to question. Due to the deposition of nanoparticles on the wall surface, it will affect the nucleate site density in the wall evaporation and boiling, thereby further affecting the bubble departure diameter. In this study, a modified model of nucleate site density proposed by Unal [28] was used:
Nw=1.206×104(1−cosθ)(Tw−Tsat)2.06(26)
where θ is the contact angle between the liquid and the heating wall surface, under the corrected nucleate site density, the corrected model of bubble departure diameter can be calculated according to the following formula:
Dw=0.629772+3cosθ−cosθ24[σg(ρl−ρg)]0.5(27)
In order to verify the proposed method for nanofluid simulation, in other words, to check the validity and accuracy of the species transport model for simulating the nanoparticles movements in nanofluids before it is used in the boiling simulation, the simulation of convective heat transfer (without boiling) of nanofluids in a channel was firstly conducted, since there is no boiling vapor phase in the simulation, so the simplified version of the proposed Eulerian species method was used.
The simulation results were verified by comparing with the experimental results from Zeinali et al. [29] as shown in Fig. 1. The nanofluid heat transfer experiments were conducted in a round channel with the length of 1 m and diameter 6 mm, constant wall temperature condition was used. The simulation was carried out according to the configuration of the experiments. Nusselt number as a function of Reynolds number (in the range 3000–8000) at various volume fractions (0.1%, 0.5%, 1%, 1.5%) were shown in the figures, as we can see, the simulation can reproduce the nanofluids convective heat transfer characteristic, a good agreement between the simulations and experiments was obtained, especially in the low volume fraction cases (0.1%, 0.5%). For larger volume fraction cases, good agreements were also obtained at high Re cases, the discrepancy at low Re cases, might be caused by nonuniform distribution and aggregation of the nanoparticles, which occurs easily at larger volume fraction and lower Re number cases. In general, the proposed new method can be used to simulating the nanofluids flow and convective heat transfer.
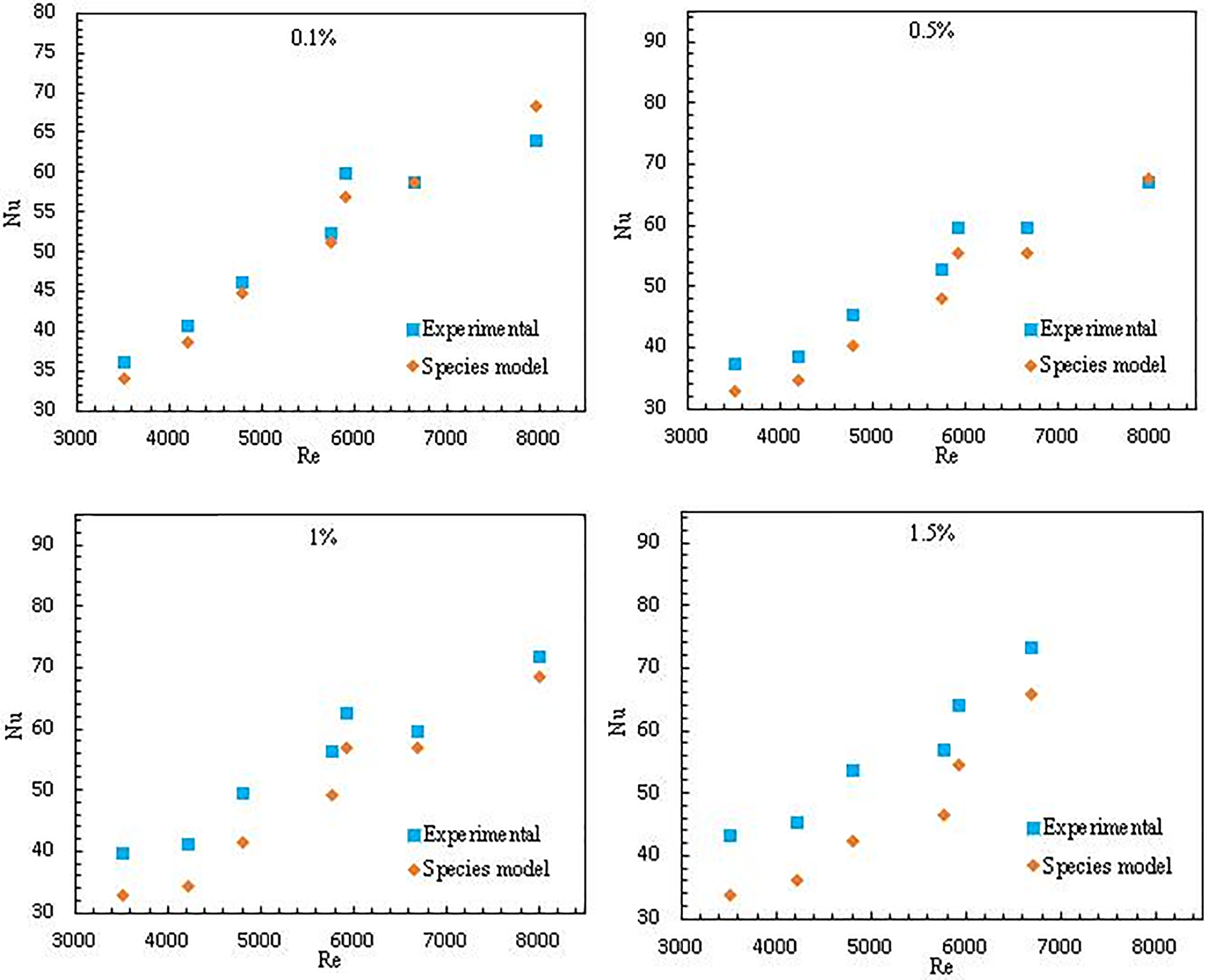
Figure 1: Comparison of nusselt number at different Re and volume fractions
Since the validity of the proposed new method applied in convective heat transfer simulation was confirmed, then this method was applied in the simulation of nanofluids boiling heat transfer for validity and accuracy verification. For comparison, the same simulation was also carried out by the Eulerian three-phases method, where the base fluid is regarded as a continuous phase, and the particles and the vapor bubbles are represented by two discrete phases, so three sets of governing equations were solved to get the movement of each phase, respectively, and the interfacial force models were set to be the same as those in the Eulerian species models. In order to compare with the experimental data, the simulation configuration was set to be identical to that of experiments conducted by Abedini et al. [30], the boiling heat transfer occurs in a circular channel with a length of 1000 mm and an inner diameter of 10 mm as illustrated in Fig. 2a, to get a high computation efficiency, the flow channel in the experiments was simplified to a 2D model in the simulation by using its feature of axial-symmetry as illustrated in Fig. 2b. The working fluid is set to be a nanofluid composed of TiO2 nanoparticles and pure water as the base fluid, which is the same with the experiments [30].
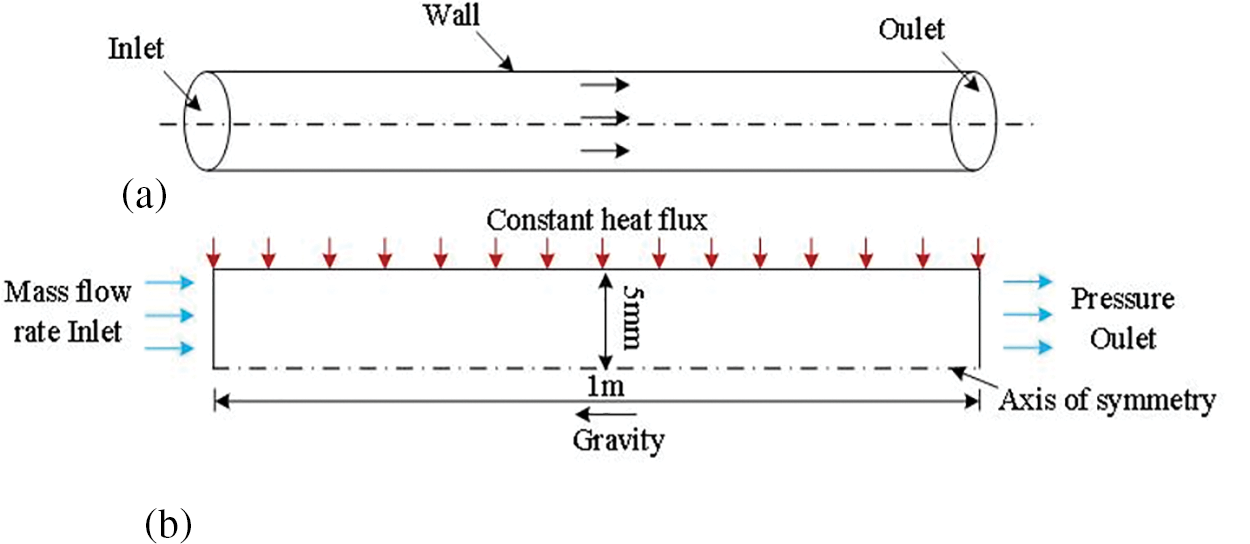
Figure 2: Configurations and boundary condition setup of the boiling simulation
The heat transfer coefficient at different position of the channel was given in Fig. 3, as can be seen, the Eulerian species method proposed in this paper can achieve very good agreement with the experimental data at both the 0.5% and 2.5% volume fractions (only experimental data at these two volume fractions were given in reference [30]), and it achieved better simulation results than the Eulerian three-phases method, especially for the positions near the exit of the channel, where the Eulerian three-phases method givers a large discrepancy from the experimental data. In Fig. 4, the wall temperature at various positions of the channel was given and the simulation results obtained from the two methods were very similar and both showed a good agreement with the experimental data, except the only data at position of 0.4 m in Fig. 4a, which might be caused by some unknown reasons. In Fig. 5, the heat transfer coefficient averaged over the whole channel was illustrated, the simulation results predicted by the Eulerian species method show a decrease tendency with the increase of the volume fraction of the nanoparticles, which is in accordance with the experimental data, however, the Eulerian three-phases method gives an opposite increase tendency.
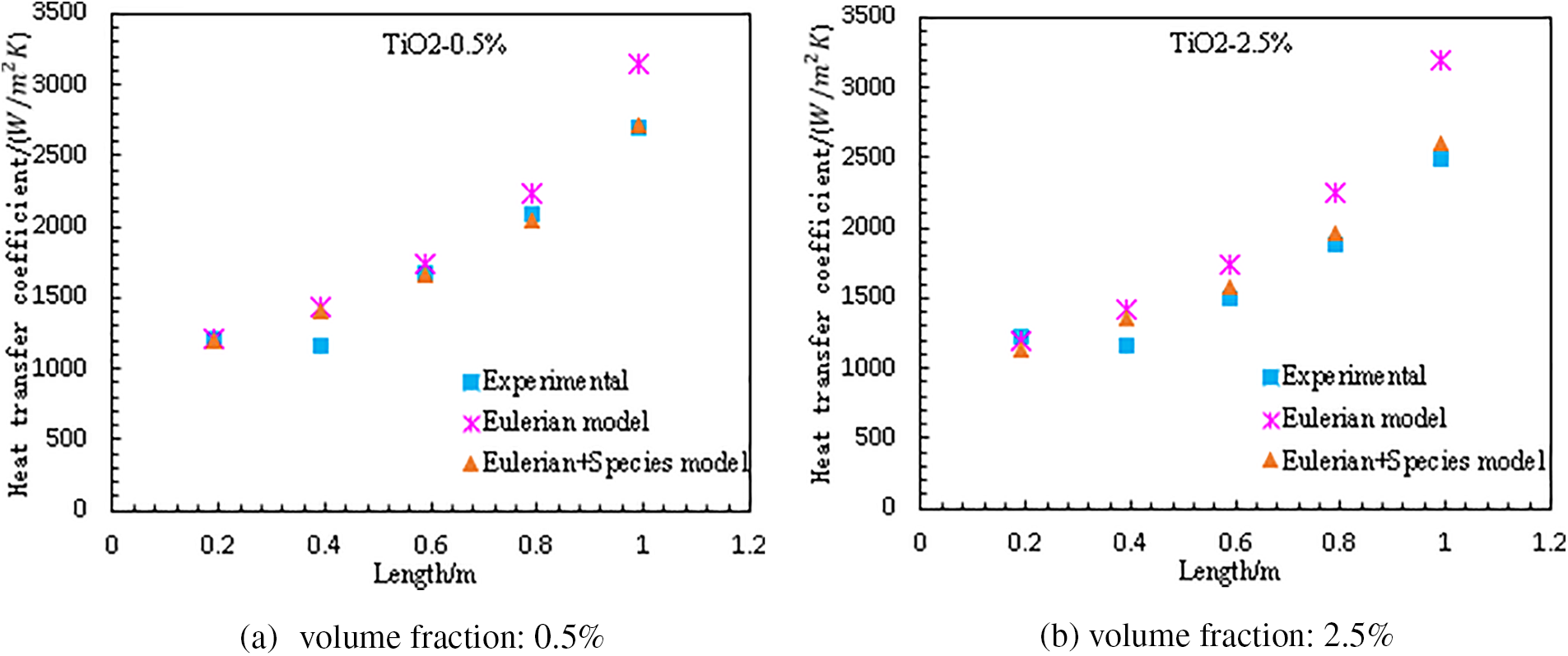
Figure 3: Heat transfer coefficient at different positions
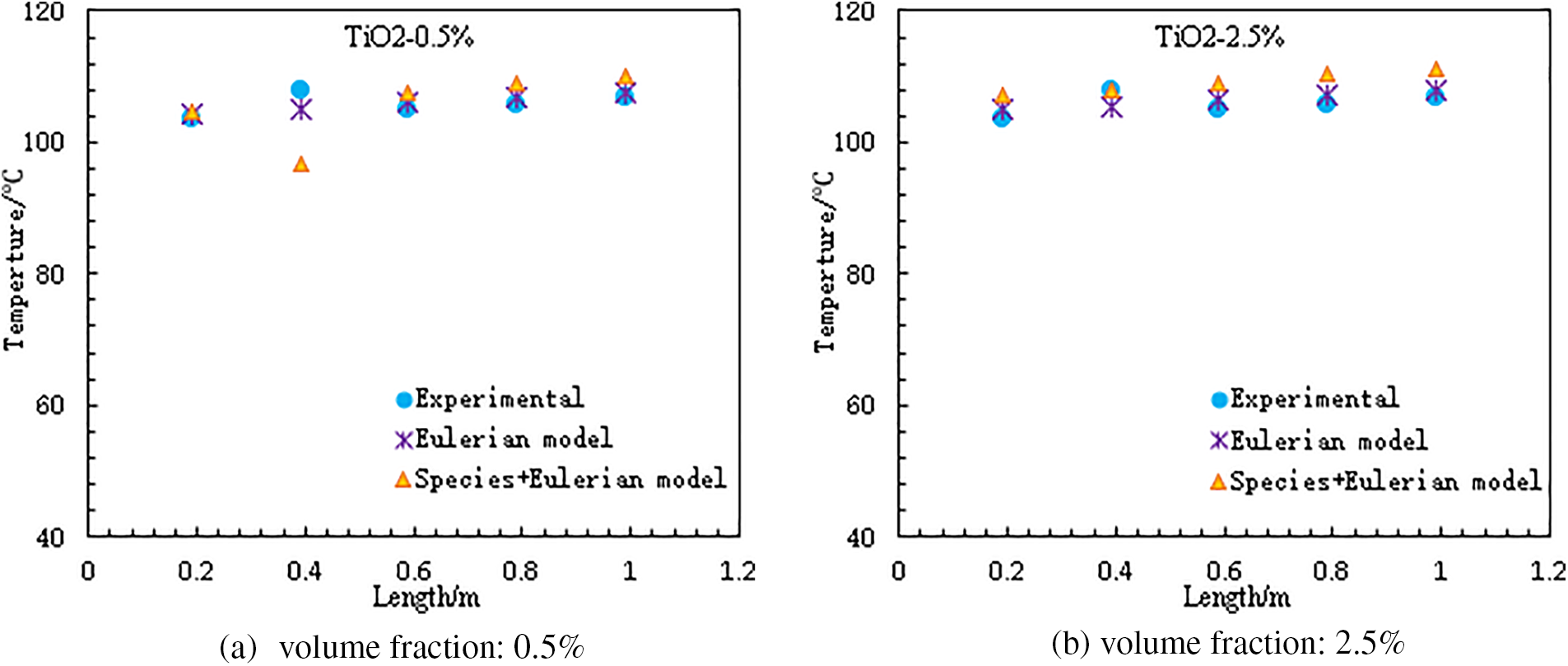
Figure 4: Wall temperature at different positions
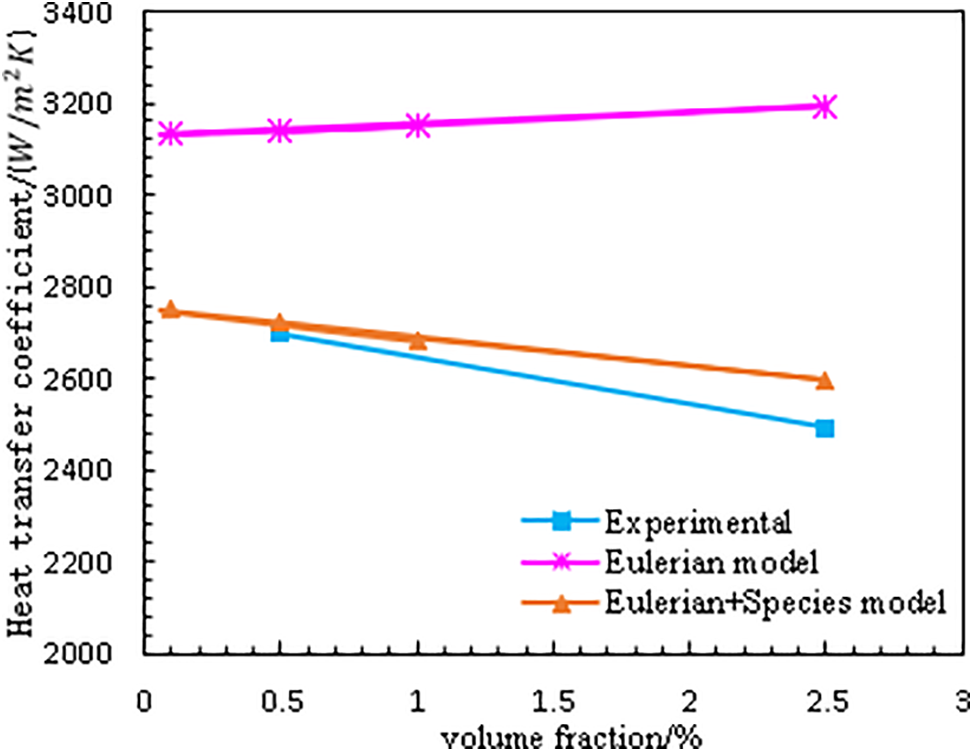
Figure 5: Average heat transfer coefficient at various volume fraction
In general, the new proposed Eulerian species method is better than the Eulerian three-phases method, because it not only can give more accurate results as discussed above, but also has a higher efficiency and needs less computation resources, since it solves only two sets of governing equations when the boiling heat transfer is simulated, instead of three sets of governing equations as needed in the Eulerian three-phases method. The validity of species transport equation for tracking the nanoparticle movement in the nanofluids were verified and can be explained by that the nanoparticles are treated as a component of the nanofluid, like one species of a liquid mixture.
A new method called the Eulerian species method was proposed for nanofluids boiling/convective heat transfer simulation; the species transport equation is used to track the movement of the nanoparticles based on the assumption that the nanoparticles are uniformly distributed in the nanofluids and can be treated as one species in a liquid mixture. Good agreements with experimental data are achieved for both the convective and boiling heat transfer of nanofluids. Compared with other methods available for nanofluids heat transfer simulation, this new method can provide good simulation results with a high accuracy but at a low computational cost.
Acknowledgement: The authors are grateful for the support of the Research Starting Program of Ludong University (Grant No. 221/20220045), and the valuable advice from Prof. Tomoaki Kunugi.
Funding Statement: This research is supported by the Research Starting Program of Ludong University (Grant No. 221/20220045).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Y. Cao; data collection: X. Meng; analysis and interpretation of results: Y. Cao; draft manuscript preparation: Y. Cao, X. Meng. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author, Y. Cao, upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Fang, X., Chen, Y., Zhang, H., Chen, W., Dong, A. et al. (2016). Heat transfer and critical heat flux of nanofluid boiling: A comprehensive review. Renewable and Sustainable Energy Reviews, 62, 924–940. https://doi.org/10.1016/j.rser.2016.05.047 [Google Scholar] [CrossRef]
2. Choi, S. U. S., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. American Society of Mechanical Engineers, Fluids Engineering Division, 231, 99–105. [Google Scholar]
3. Sheikholeslami, M., Ganji, D. D. (2016). Nanofluid convective heat transfer using semi analytical and numerical approaches: A review. Journal of the Taiwan Institute of Chemical Engineers, 65, 43–77. https://doi.org/10.1016/j.jtice.2016.05.014 [Google Scholar] [CrossRef]
4. Duursma, G., Sefiane, K., Dehaene, A., Harmand, S., Wang, Y. (2015). Flow and heat transfer of single- and two-phase boiling of nanofluids in microchannels. Heat Transfer Engineering, 36, 1252–1265. https://doi.org/10.1080/01457632.2014.994990 [Google Scholar] [CrossRef]
5. Vanakia, M., Ganesana, P., Mohammedb, H. A. (2016). Numerical study of convective heat transfer of nanofuids: A review. Renewable and Sustainable Energy Reviews, 54, 1212–1239. https://doi.org/10.1016/j.rser.2015.10.042 [Google Scholar] [CrossRef]
6. Abedini, E., Behzadmehr, A., Sarvari, S., Mansouri, S. (2013). Numerical investigation of subcooled flow boiling of a nanofluid. International Journal of Thermal and Science, 64, 232–239. https://doi.org/10.1016/j.ijthermalsci.2012.08.008 [Google Scholar] [CrossRef]
7. Ehsan, A., Taleb, Z., Hossein, R., Rasool, K., Masoud, A. (2017). Numerical investigation of vapor volume fraction in subcooled flow boiling of a nanofluid. Journal of Molecular Liquids, 238, 281–289. https://doi.org/10.1016/j.molliq.2017.04.120 [Google Scholar] [CrossRef]
8. Li, X., Li, K., Tu, J., Buongiorno, J. (2014). On two-fluid modeling of nucleate boiling of dilute nanofluids. International Journal of Heat and Mass Transfer, 69, 443–450. https://doi.org/10.1016/j.ijheatmasstransfer.2013.10.037 [Google Scholar] [CrossRef]
9. Behroyana, I., Ganesana, P., Heb, S., Sivasankaranc, S. (2018). CFD models comparative study on nanofluids subcooled flow boiling in a vertical pipe. Numerical Heat Transfer, Part A: Applications, 73, 55–74. https://doi.org/10.1080/10407782.2017.1420299 [Google Scholar] [CrossRef]
10. Mostafa, M., Mohsen, S., Josua, P. M. (2018). Exploration of nanofluid pool boiling and deposition on a horizontal cylinder in Eulerian and Lagrangian frames. International Journal of Heat and Mass Transfer, 125, 959–971. https://doi.org/10.1016/j.ijheatmasstransfer.2018.04.153 [Google Scholar] [CrossRef]
11. Bahiraei, M., Heshmatian, S., Moayedi, H. (2019). Artificial intelligence in the field of nanofluids: A review on applications and potential future directions. Powder Technology, 353, 276–301. https://doi.org/10.1016/j.powtec.2019.05.034 [Google Scholar] [CrossRef]
12. Mahdi, R., Mohammad, A. N., Mohammad, H. A., Giulio, L., Loan, P. (2019). A review on the applications of intelligence methods in predicting thermal conductivity of nanofluids. Journal of Thermal Analysis and Calorimetry, 138, 827–843. [Google Scholar]
13. Alhuyi, N. M., Ahmadi, M. H., Lorenzini, G., Maddah, H., Fahim, A. M. et al. (2018). Modeling thermal conductivity ratio of CuO/ethylene glycol nanofluid by using artificial neural network. Defect Diffus Forum, 388, 39–43. https://doi.org/10.4028/www.scientific.net/DDF.388 [Google Scholar] [CrossRef]
14. Mahdi, R., Mohammad, H. A., Mohammad, A. N., Milad, S., Lingen, C. (2019). A review on the utilized machine learning approaches for modelling the dynamic viscosity of nanofluids. Renewable and Sustainable Energy Reviews, 114, 109345. https://doi.org/10.1016/j.rser.2019.109345 [Google Scholar] [CrossRef]
15. Hemmat, E. M., Razi, P., Hajmohammad, M. H., Rostamian, S. H., Sarsam, W. S. et al. (2017). Optimization, modelling and accurate prediction of thermal conductivity and dynamic viscosity of stabilized ethylene glycol and water mixture Al2O3 nanofluids by NSGA-II using ANN. International Communications in Heat Mass Transfer, 82, 154–160. https://doi.org/10.1016/j.icheatmasstransfer.2016.08.015 [Google Scholar] [CrossRef]
16. Maddah, H., Aghayari, R., Ahmadi, M. H., Rahimzadeh, M., Ghasemi, N. (2018). Prediction and modelling of MWCNT/Carbon (60/40)/SAE 10W40/SAE 85W90(50/50) nanofluid viscosity using artificial neural network (ANN) and self-organizing map (SOM). Journal of Thermal Analysis and Calorimetry, 134, 2275–2286. https://doi.org/10.1007/s10973-018-7827-1 [Google Scholar] [CrossRef]
17. Ashutosh, P., Subrata, K. G. (2021). Surface qualitative analysis and ANN modelling for pool boiling heat transfer using Al2O3-water based nanofluids. Colloids and Surface A: Physicochemical and Engineering Aspects, 610, 125926. https://doi.org/10.1016/j.colsurfa.2020.125926 [Google Scholar] [CrossRef]
18. Yeping, P., Milad, B. G., Mohanmmad, N. A., Ali, A., Seyed, A. B. et al. (2021). Analysis of the effect of roughnrss and concentration of Fe3O4/water nanofluid on the boiling heat transfer using the artificial neural network: An experimental and numerical study. International Journal of Thermal Sciences, 163, 106863. https://doi.org/10.1016/j.ijthermalsci.2021.106863 [Google Scholar] [CrossRef]
19. Ishii, M., Zuber, N. (1979). Drag coefficient and relative velocity in bubbly, droplet or particle flows. AIChE Journal, 25(5), 843–855. https://doi.org/10.1002/aic.v25:5 [Google Scholar] [CrossRef]
20. Tomiyama, A. (1998). Struggle with computational bubble dynamics. Multiphase Science and Technology, 10(4), 369–405. https://doi.org/10.1615/MultScienTechn.v10.i4 [Google Scholar] [CrossRef]
21. Antal, S. P., Lahey Jr, R. T., Flaherty, J. E. (1991). Analysis of phase distribution in fully developed laminar bubbly two-phase flow. International Journal of Multiphase Flow, 17(5), 635–652. https://doi.org/10.1016/0301-9322(91)90029-3 [Google Scholar] [CrossRef]
22. Bertodano, M. L. D. (1992). Turbulent bubbly two-phase flow in a triangular duct. Proceedings of the NURETH-5, Salt Lake City, USA. [Google Scholar]
23. Kurul, N., Podowski, M. Z. (1991). On the modeling of multidimensional effects in boiling channels. Proceedings of the 27th National Heat Transfer Conference, Minneapolis, Minnesota, USA. [Google Scholar]
24. DelValle, V. H., Kenning, D. B. R. (1985). Subcooled flow boiling at high heat flux. International Journal of Heat and Mass Transfer, 28, 1907–1922. https://doi.org/10.1016/0017-9310(85)90213-3 [Google Scholar] [CrossRef]
25. Li, X., Chi, S., Cheng, P., Tu, J. (2014). Nucleate boiling of dilute nano fluids-mechanism exploring and modelling. International Journal of Thermal and Science, 84, 323–334. https://doi.org/10.1016/j.ijthermalsci.2014.05.021 [Google Scholar] [CrossRef]
26. Cole, R. (1960). A photographic study of pool boiling in the region of the critical heat flux. AIChE Journal, 6(4), 533–538. https://doi.org/10.1002/aic.v6:4 [Google Scholar] [CrossRef]
27. Lemmert, M. (1977). Influence of flow velocity on surface boiling heat transfer coefficient. New York, NY, USA: Academic Press and Hemisphere. [Google Scholar]
28. Unal, H. C. (1976). Maximum bubble diameter, maximum bubble growth time and bubble growth rate during subcooled nucleate flow boiling of water up to 17.7 MN/m2. International Journal of Heat and Mass Transfer, 19, 643–649. https://doi.org/10.1016/0017-9310(76)90047-8 [Google Scholar] [CrossRef]
29. Zeinali, S. H., Esfahany, M. N., Etemad, S. G. (2007). Experimental investigation of convective heat transfer of Al2O3/water nanofluid in circular tube. International Journal of Heat and Fluid Fow, 28, 203–210. https://doi.org/10.1016/j.ijheatfluidflow.2006.05.001 [Google Scholar] [CrossRef]
30. Abedini, E., Behzadmehr, A., Rajabnia, H., Sarvari, S. M. H., Mansouri, S. H. et al. (2013). Experimental investigation and comparison of subcooled flow boiling of TiO2 nanofluid in a vertical and horizontal tube. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 227(8), 1742–1753. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
