 Open Access
Open Access
ARTICLE
Computational Analysis of Selective Laser Sintering of Inconel 625
Department of Engineering Technology, Texas State University, San Marcos, TX, 78666, USA
* Corresponding Author: Bin Xiao. Email:
Frontiers in Heat and Mass Transfer 2024, 22(2), 417-432. https://doi.org/10.32604/fhmt.2024.048739
Received 17 December 2023; Accepted 14 February 2024; Issue published 20 May 2024
Abstract
A two-dimensional multi-physics finite element model is developed to simulate the Selective Laser Sintering (SLS) process using Inconel 625 powders. The validity of the developed model is first assessed by comparing its results with experimental data. Various factors such as phase transition, recoil pressure, surface tension, and the Marangoni force are considered. The study’s findings underscore that the morphology and thermal-fluid dynamics of the molten pool in the SLS process are predominantly shaped by the influence of the Marangoni force and recoil pressure acting on its surface. The recoil pressure at the front of the laser spot rises exponentially with temperature, making the liquid metal move downward, and creating a depression at the pool’s head. It also causes particles to splash from the pool’s rear edge. The study explores the influence of the backward Marangoni force, where high-temperature liquid flows from the front to the rear of the molten pool, creating a vortex and moving the pool in the rear. Process parameters like laser intensity, scan speed, and spot size were analyzed. The findings indicate that higher laser power lower scanning speed and laser beam spot size lead to increased width and depth of the molten pool.Keywords
In contrast to subtractive manufacturing, where an object is formed by removing material from a solid block until the final product is achieved, additive manufacturing (AM), commonly referred to as 3D printing, encompasses the production of three-dimensional objects through the layering of material, guided by 3D computer-aided design (CAD) [1–3]. Beyond facilitating the rapid and efficient creation of prototypes, AM technologies also make it possible to produce intricate geometries and shapes that would be challenging or unattainable through traditional subtractive and formative manufacturing methods. This capability empowers designers to innovate, leading to the development of products with distinctive features and enhanced performance [4–5]. Selective Laser Sintering (SLS) represents an AM technique that employs a high-power laser to selectively melt, and fuse powdered materials layer by layer. The outcome of this process is the creation of products known for their high accuracy and excellent mechanical properties. SLS stands out for its unique combination of material flexibility, part strength, design freedom, precision, and efficiency, rendering it a preferred choice in various industries, including medical, aerospace, automotive, and consumer goods [6–11].
The SLS process encompasses intricate physical phenomena, encompassing the absorption and melting of powder energy, convection within the molten pool, and powder evaporation. Nevertheless, the rapid melting and solidification on a micrometer scale poses a considerable challenge in monitoring the SLS process. Numerical analysis emerges as a potent tool capable of offering insights into the intricate thermofluidic interactions inherent in the SLS process, facilitating the optimization of process parameters and mitigating the occurrence of defects [12,13]. Criales et al. [14] established a numerically based approach to predict the 2-D temperature profile and melt pool geometry during the selective laser melting (SLM) of Inconel 625 metal powder. The study reveals that packing density (or porosity) significantly influences the temperature profile, with powder reflectivity having the greatest effect on the predicted peak temperature and melt pool geometry, followed by laser power and scanning speed. These findings offer a comprehensive understanding of the SLM process, addressing variables that are challenging to measure experimentally. Yaagoubi et al. [15] employed the three-dimensional element finite (EF) method using COMSOL Multiphysics software to explore the temperature dynamics in SLS process. The results indicate that the developed EF method adeptly captures the pronounced temperature gradients at the center of the laser spot on polyamide powders in the heat-affected zone. The study further delves into the impacts of physical properties and laser parameters. It is observed that within the polyamide 12 powder bed, temperature rises in tandem with both the increase in pre-heating temperature and the laser power used for sintering the polyamide powder bed. Gusarov et al. [16] proposed a model for coupled radiation transfer and thermal diffusion. Single line scanning of a laser beam over a thin layer of metallic powder placed on a dense substrate of the same material was studied. The layer is about 50 μm thick and the grain size is about 20 μm. The simulation results show that laser radiation can penetrate the powder through an open pore system until it reaches the substrate, creating a volumetric heat source. The melt pool formed around the laser beam contacts the substrate only at its central part. This complex shape of the melt surface can cause deformation driven by surface tension. The lateral parts of the melt pool are expected to detach from the neighboring powder, forming a rounded free surface with reduced surface energy.
The laser beam’s high power and energy density frequently result in material evaporation and consequent spatter formation, entailing the expulsion of molten materials and powder particles from the molten pool. Spatters in SLS processes tend to create uneven powder layers and printed layers, rendering SLS printed components susceptible to porosities, cracks, and fractures. Zhang et al. [17] have developed a machine learning-based method to extract and record metrics related to metal powder (MP) spattering using in-situ imaging data. The recorded spatter signatures disclose significant variations in spattering phenomena, particularly evident in the spatter count across different layers. The results suggest a robust correlation between spatter formation and various processing parameters, encompassing not only laser power and speed but also the hatching angle, essentially associated with gas flow. Under consistent conditions, a linear correlation model can be established between the spatter count and both laser power and scan speed, respectively. Moreover, Dogu et al. [18] conducted an extensive examination of both virgin and spatter Inconel 939 powders, exploring the impact of incorporating a specific amount of spatter powder on the quality of parts fabricated with the SLS process. Notable observations included color changes, the presence of Al2O3 oxide, pore formation, an increase in average particle size, and alterations in powder morphology in the spatter powder. Additionally, the spatter powder exhibited a higher average grain size and lower nano-hardness compared to the virgin powder. Introducing 10% by weight of spatter powder to the virgin powder resulted in reduced powder flowability. This addition had repercussions on the properties of the fabricated parts, leading to a decrease in relative density by approximately 0.3% and an increase in surface roughness by around 80.8%.
Because of its outstanding high-temperature strength, corrosion resistance, and fatigue resistance, Inconel 625, a nickel-based superalloy, is widely utilized in diverse industries such as aerospace, defense, and the chemical sector. Nevertheless, the SLS process of Inconel 625 presents challenges because of its high melting point and tendency to develop cracks and defects. It is crucial to control the microstructure during this process to guarantee the mechanical properties, dimensional accuracy, and performance of the final part [19–22]. Numerous studies have explored how factors like geometric parameters, operating conditions, and scanning patterns affect the mechanical properties of parts produced via SLS [23–25].
Currently, there is a scarcity of numerical models designed to explore the thermal and flow dynamics of the molten pool and keyhole, along with the morphological evolution and mechanisms of spatter formation in the SLS process of Inconel 625. Consequently, this study addresses this gap by developing a powder-scale model that meticulously examines the thermal fluid behavior and morphological evolution in the SLS process of Inconel 625.
In the SLS process, illustrated in Fig. 1 [26], a laser, guided by a lens, traverses cross-sections outlined in a 3D CAD file across the surface of a powder bed. Following the scanning of each cross-section, the powder bed descends by a layer’s thickness, a fresh layer of material is deposited on top, and the iterative process continues until the fabrication of the entire part is achieved. As depicted in Fig. 2 [27], when a laser beam impinges upon the surface of a thin powder layer, it triggers a sequence of intricate physical phenomena. These include the absorption of laser radiation by the powders, heat transfer during phase changes in the molten pool, solidification and melting, material spattering and evaporation, and fluid flow.
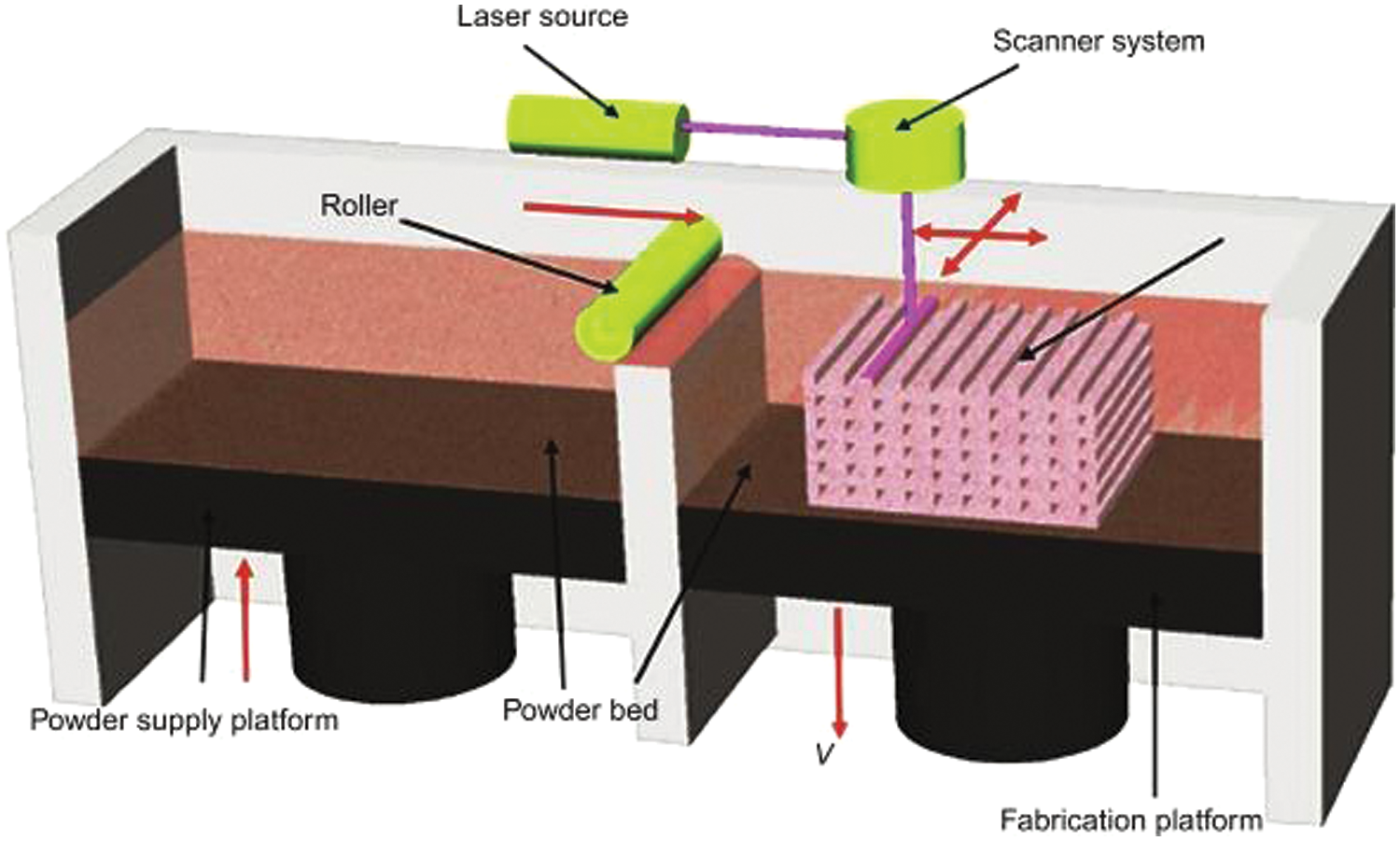
Figure 1: Schematic diagram of the SLS process [26]
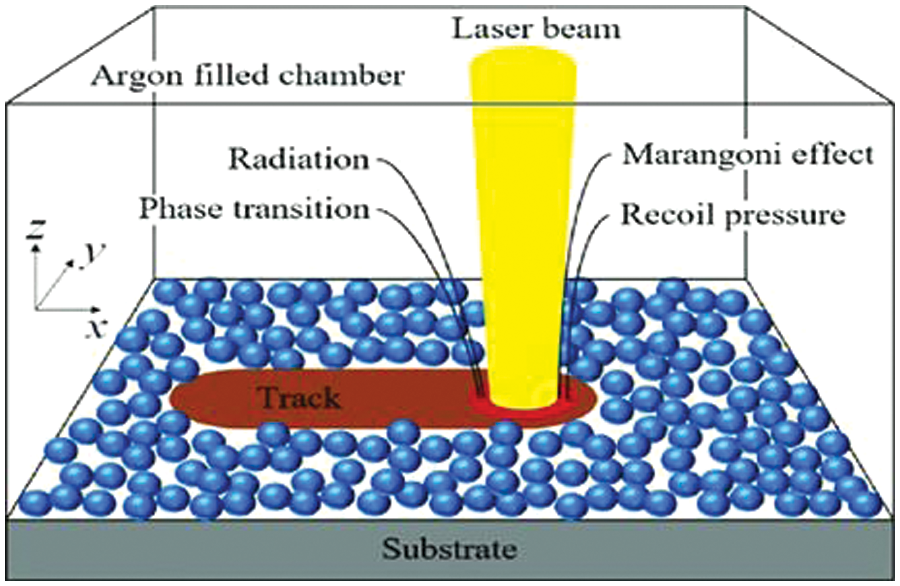
Figure 2: Physical phenomena in the SLS process [27]
The SLS process is simulated in this study through Computational Fluid Dynamics (CFD) and the Heat Transfer module within COMSOL Multiphysics. This model is specifically crafted to replicate the laser-powder interaction, enabling the prediction of thermal fluid behaviors and the morphological evolution of the molten pool. The simulation geometry comprises a layer of metal powder with a particle size of Dp = 10 μm positioned atop a solid base plate with a thickness of 80 μm. The ambient air surrounding the setup is held at a temperature of T∞ = 293.15 K. A Gaussian laser beam, characterized by a radius of R = 30 μm, is applied to irradiate the powder layer, utilizing a laser power of 150 W and a scanning speed of 1 m/s. The Gaussian laser beam employed in SLS exhibits an energy profile described by a Gaussian function, indicating a gradual decrease in laser intensity with increasing distance from the beam focus. To optimize computational efficiency, an adaptive finite element meshing method is employed, as illustrated in Fig. 3b. Proximity to the powders is designated with finer meshes, while areas farther away utilize coarser meshes.
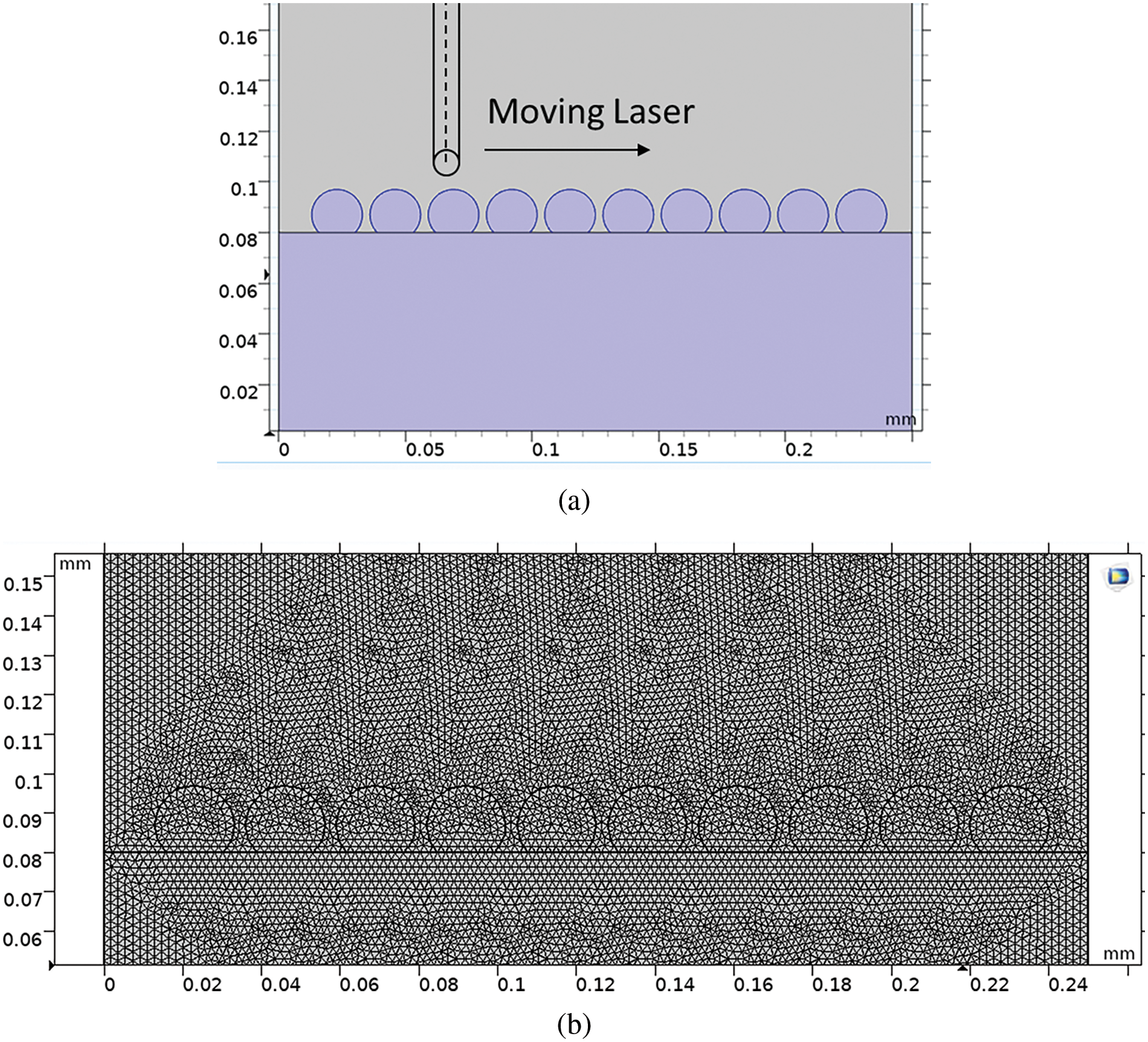
Figure 3: (a) Physical model and (b) finite element mesh of the SLS of Inconel 625
In Selective Laser Sintering (SLS), the powder-to-powder heat transfer occurs as a result of the focused laser energy interacting with the powdered material. Initially, a thin layer of powdered material is spread evenly across the building platform. As the laser scans the surface of the powder bed, it selectively absorbs the energy, causing localized heating.
The laser’s energy is absorbed by the powder particles, leading to a rapid temperature increase within the irradiated regions. This localized heating is essential for achieving the sintering temperature, causing the adjacent powder particles to fuse together. The heat transfer from the molten or semi-molten particles to the neighboring powder is facilitated by conduction.
Conduction in powder-to-powder heat transfer involves the transfer of thermal energy through direct contact between adjacent powder particles. As the temperature increases, the heat flows from the highly heated regions to the cooler surrounding areas. The success of this process relies on efficient heat transfer mechanisms to ensure uniform sintering throughout the powder bed.
Moreover, the powder bed acts as both a heat sink and a thermal insulator. The unexposed powder surrounding the laser-affected regions helps dissipate excess heat, preventing overheating and maintaining the structural integrity of the fabricated layers. Simultaneously, the powder bed prevents excessive heat loss to the surrounding environment, promoting efficient energy utilization.
The model simulates heat transfer by solving the time-dependent energy equation for temperature (T) within the fluid [28]:
∂ρCpT∂t+∇(ρuCpT)=∇(k∇T)−Q.(1)
where ρ is the powder density, Cp is the specific heat of the powder, and k is the thermal conductivity of the powder. The term ∇(ρuCpT) is the heat convection in the fluid due to the fluid flow and Q is the energy loss due to convection, radiation, fluid melt and evaporation and laser heat source. Expanding the heat loss term Q by plugging in Newton’s convection equation, radiation equation, the melting/evaporation heat loss, and the laser heat source, the energy equation becomes [28]:
∂ρCpT∂t+∇(ρuCpT)= ∇(k∇T)−∂ρΔHf∂t−∇(ρuΔHf)−[−k(∂T∂y) =−αPπR2exp(−(x−xi−Vt)2R2)+h(T−T∞)+σeε(T4−T4∞)+Qv] ×|→∇φ1|¯Cp¯ρCp1ρ1+Cp2ρ2(2)
where P is the laser power, α is the absorptance, R is the laser radius, xi is the initial position of the laser focal center and V is the scanning speed of the laser, h is the heat convection coefficient between the powders and their surroundings, and T∞ is the surrounding temperature. Qv=ΔHvJv is the evaporation heat loss caused by the evaporation mass flux, Jv=0.82Pv/√2πMRT, M is molecular mass and R is the gas constant. Pv is the recoil force induced by the evaporation at the surface of the molten pool and Pv=0.54pae(λKB(1T−1TB))→n. |→∇φ1| is the interface delta function of the volume fraction of metal (φ1) to smear out the volume fraction sudden jump between the metal phase and the air phase. Material properties at the interface are averaged by the term ¯Cp¯ρCp1ρ1+Cp2ρ2 in order to smear out the sudden jump between two phases.
Therefore, enhance the numerical convergence.
The model assumes that the lateral sides and the bottom surface of the computational domain are insulated, i.e., −k∇T=0. The initial condition is T(x,y)t=0=T∞.
The Navier-Stokes equation is used to solve the velocity field in the fluids [29]:
(∂u∂t)+∇(ρu×u)−∇p+∇{μ[∇u+∇uT]}+ρg[1−β(T−Tm]+FS(3)
where the ρg[1−β(T−Tm] is the buoyancy force term induced by the temperature dependency of density. FS are the source terms applied at the metal-air interface [29].
FS=∇tγ+Pv→n=∇t(γ0+dγdt(T−Tref))+Pv(4)
where ∇t(γ0+dγdt(T−Tref)) is the Marangoni force along the air-metal interface due to a gradient of the surface tension.
2.3 Physical Properties and Numerical Simulation
Eqs. (1)–(4) are addressed using the finite element method within COMSOL. Heat transfer dynamics are influenced by factors like laser beam spot size, laser power, scan speed, and powder material properties in Selective Laser Sintering, consequently impacting the quality and properties of the final sintered product. To explore this, multiple simulations are performed, comparing variations in scanning speed, laser beam spot size, and laser power. Tables 1 and 2 present the material properties for Inconel 625, details of the laser heat source model, and the associated process parameters.

Due to resource constraints, experimental comparisons with the simulation model were not conducted in this study. Instead, to validate the model’s accuracy, a simulation was performed to analyze the laser melting process of an Inconel 625 sheet exposed to a moving laser beam. The laser operates at a power level of 350 W, with the beam moving at a speed of 0.5 m/s, and the beam spot size of 0.18 mm. The simulated results are then compared to the experimental findings shown in Fig. 4b [32] under identical conditions. The comparison between the simulated and experimental results reveals differences in the width and depth of the melted region. Specifically, the disparities are −5.8% (0.96 mm in simulation vs. 1.02 mm in the experiment) for width and −4.5% (0.46 mm in simulation vs. 0.44 mm in the experiment) for depth. It is noteworthy that these discrepancies are deemed reasonable, considering the inherent uncertainties in experimental measurements and the theoretical assumptions made for certain high-temperature properties in the model due to the lack of experimental data.
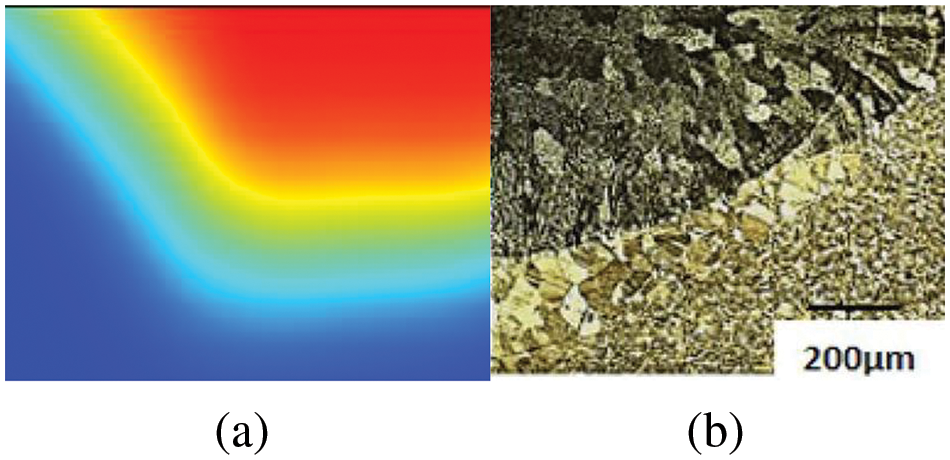
Figure 4: Comparison between (a) numerical (red: molten pool, red to blue: heat affected zone) and (b) experiment results (the solid curve represents the interface of the molten pool and the heat affected zone) [32]
Fig. 5 illustrates the temperature distribution at two distinct time points: 60 and 150 μs. In Fig. 5a, the laser beam is depicted irradiating the powder bed, leading to the melting and agglomeration of powders near the beam, forming a molten pool. As portrayed in Fig. 5b, as the laser progresses in the x-direction, more energy is transmitted to the powder bed, resulting in substrate melting. A rapid development of thermal gradients induces a Marangoni effect, causing fluid movement within the molten pool from the hot to cold regions and expanding the heat-affected zone. With the movement of the laser beam, the peak temperature also shifts accordingly.
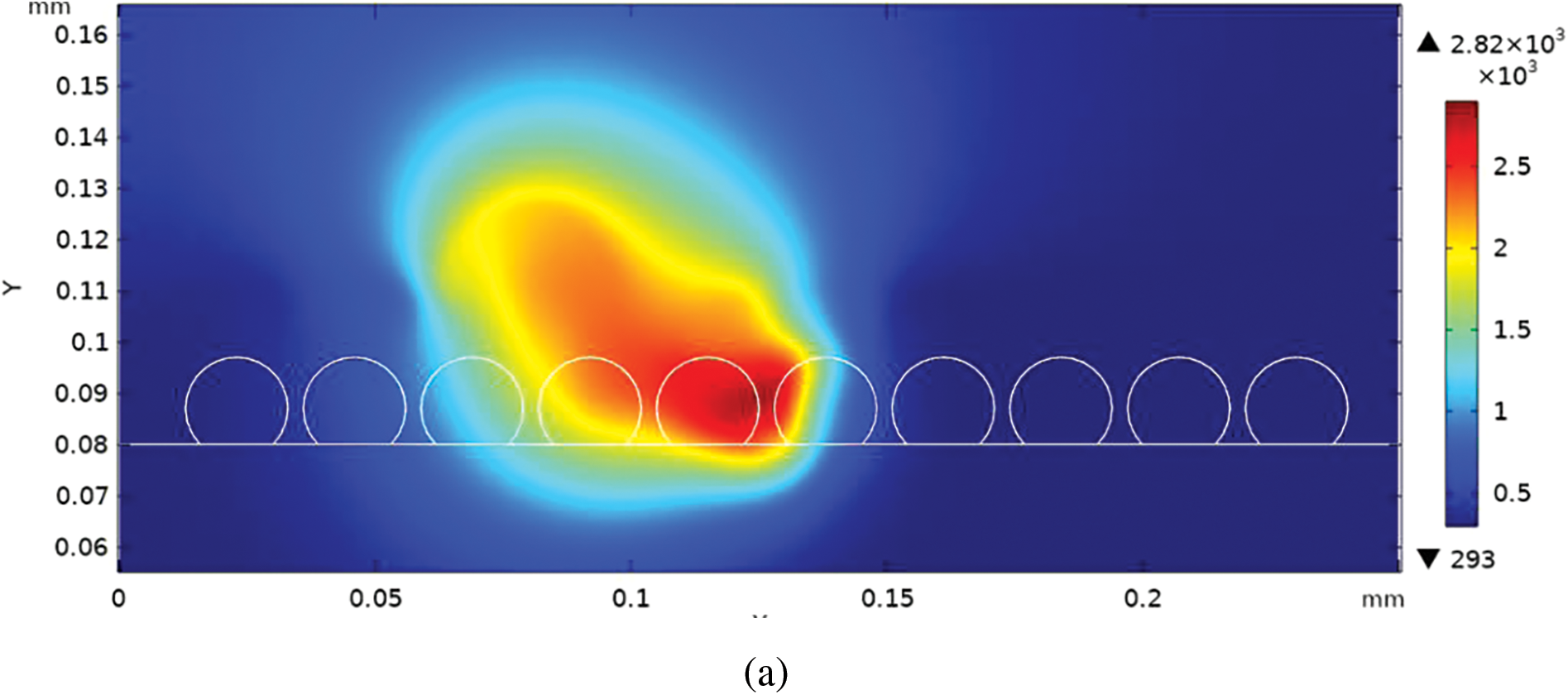
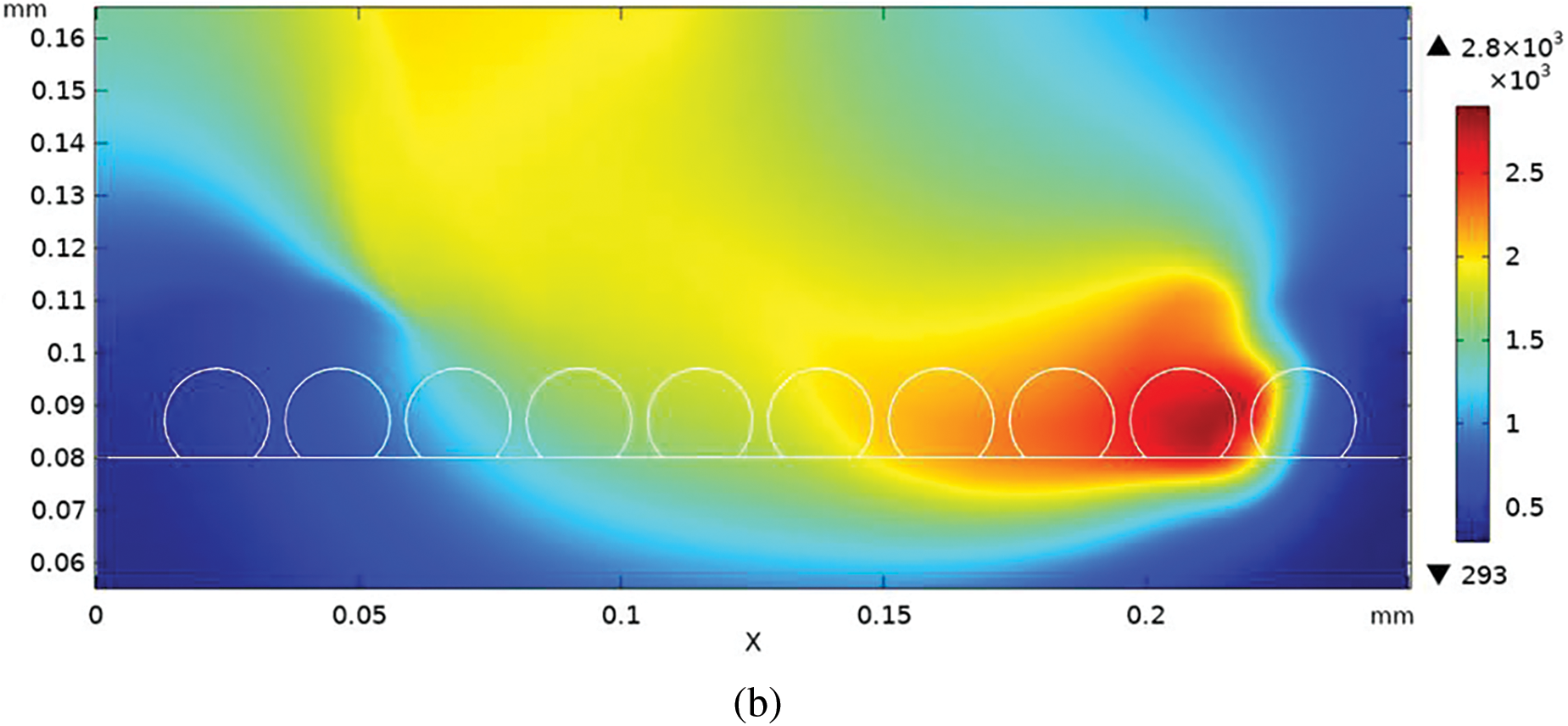
Figure 5: Temperature distribution at (a) 60 μs and (b) 150 μs
Fig. 6 illustrates the volume distribution at two distinct time points: 60 and 150 μs, employing a VOF (Volume of Fluid) method to capture the interface between the air phase and the metal phase. In this method, phases are discerned based on the volume fraction, ranging from 0 to 1. As depicted in Fig. 6a, a molten pool forms within microseconds of the laser interacting with the powder bed. Simultaneously, metal vapor rapidly emerges above the molten pool, exerting a recoil pressure on the pool surface. Inside the liquid, the rapid development of thermal gradients leads to Marangoni forces propelling the liquid from the hot region to the colder one. Fig. 6b demonstrates that both effects contribute to particle ejection, known as recoil-induced ejection from the molten pool. Once ejected, the hot particles descend back into the powder bed, cool down, and partially fuse with the solid material. Subsequent layer deposition results in solidified particles creating bumps, pores, and cavities on the part.
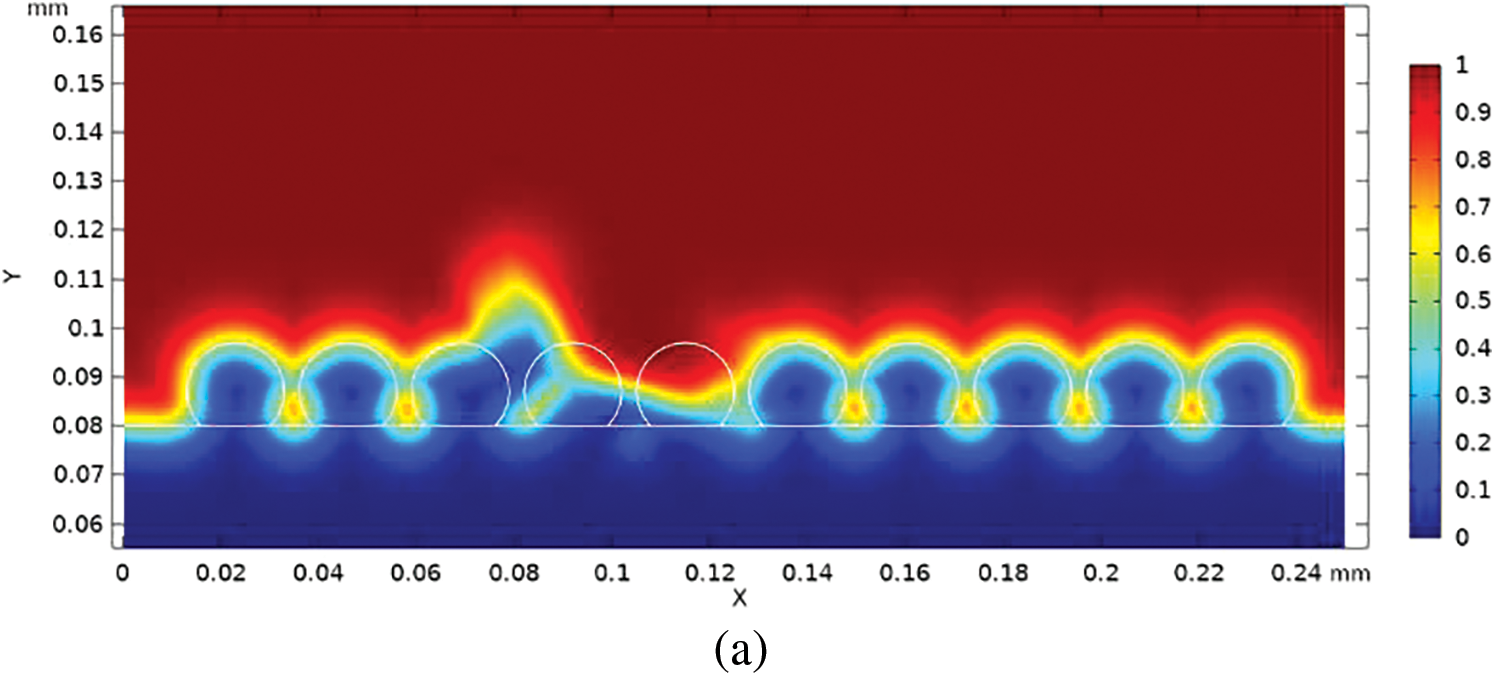
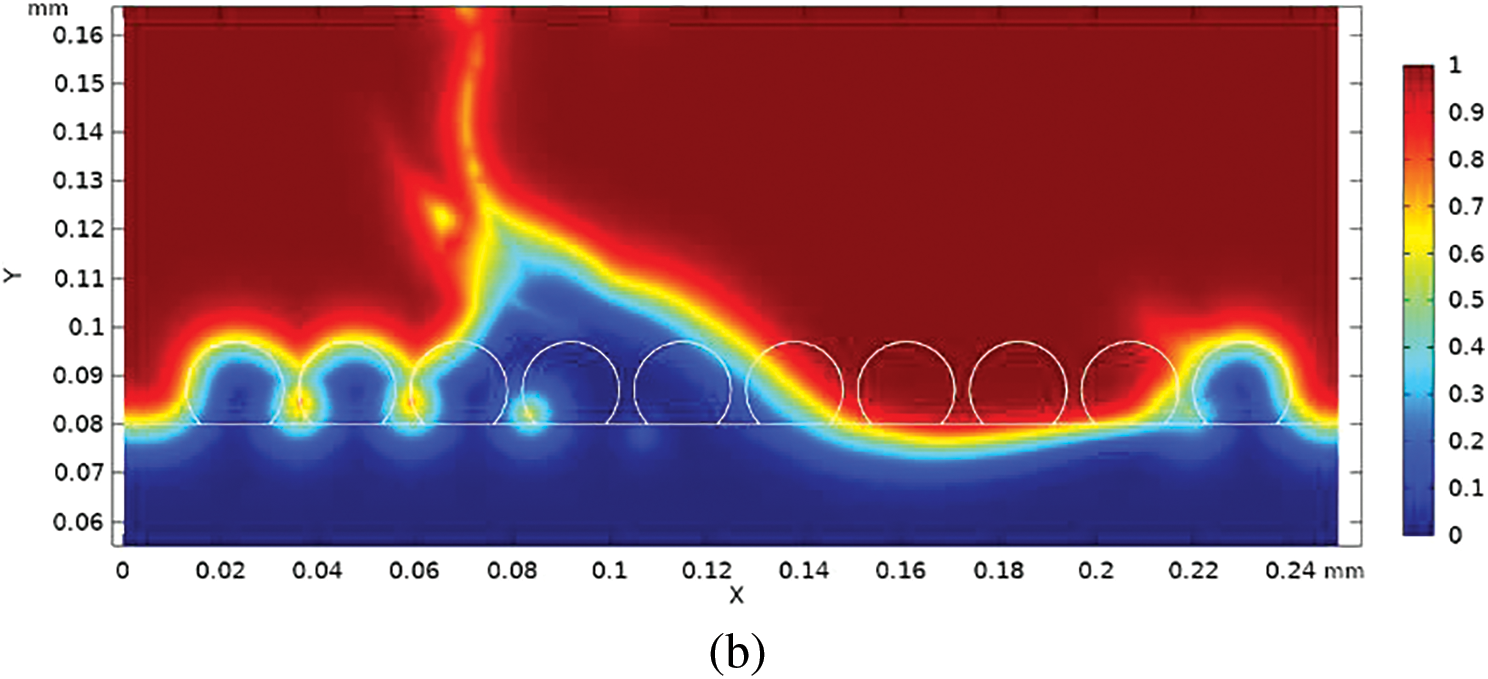
Figure 6: Volume fraction distribution at (a) 60 μs and (b) 150 μs
Fig. 7 illustrates the fluid flow distribution at two different time points: 60 and 150 μs. In Fig. 7a, lateral liquid flow is observed due to asymmetrical cooling in the transition region, which is caused by partially melted particles that remain in contact with the melt track and dissipate heat laterally. In Fig. 7b, the laser beam moves in the X direction, and as more powders receive energy, the surface tension pulls surface liquid towards the cold spot due to the Marangoni effect, biasing any lateral circulation. Additionally, as the temperature of the air near the hot zone rises, the density of the hot air becomes lighter, which drives the airflow upwards and generates buoyancy.
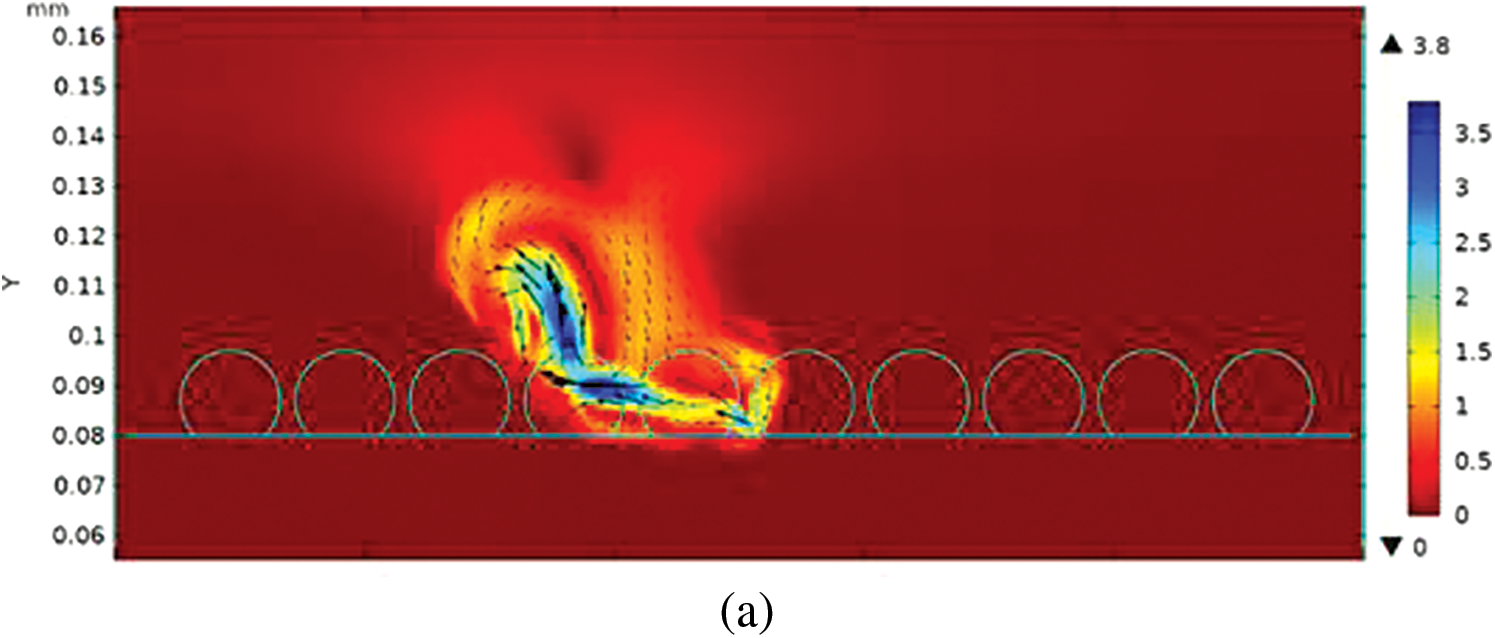
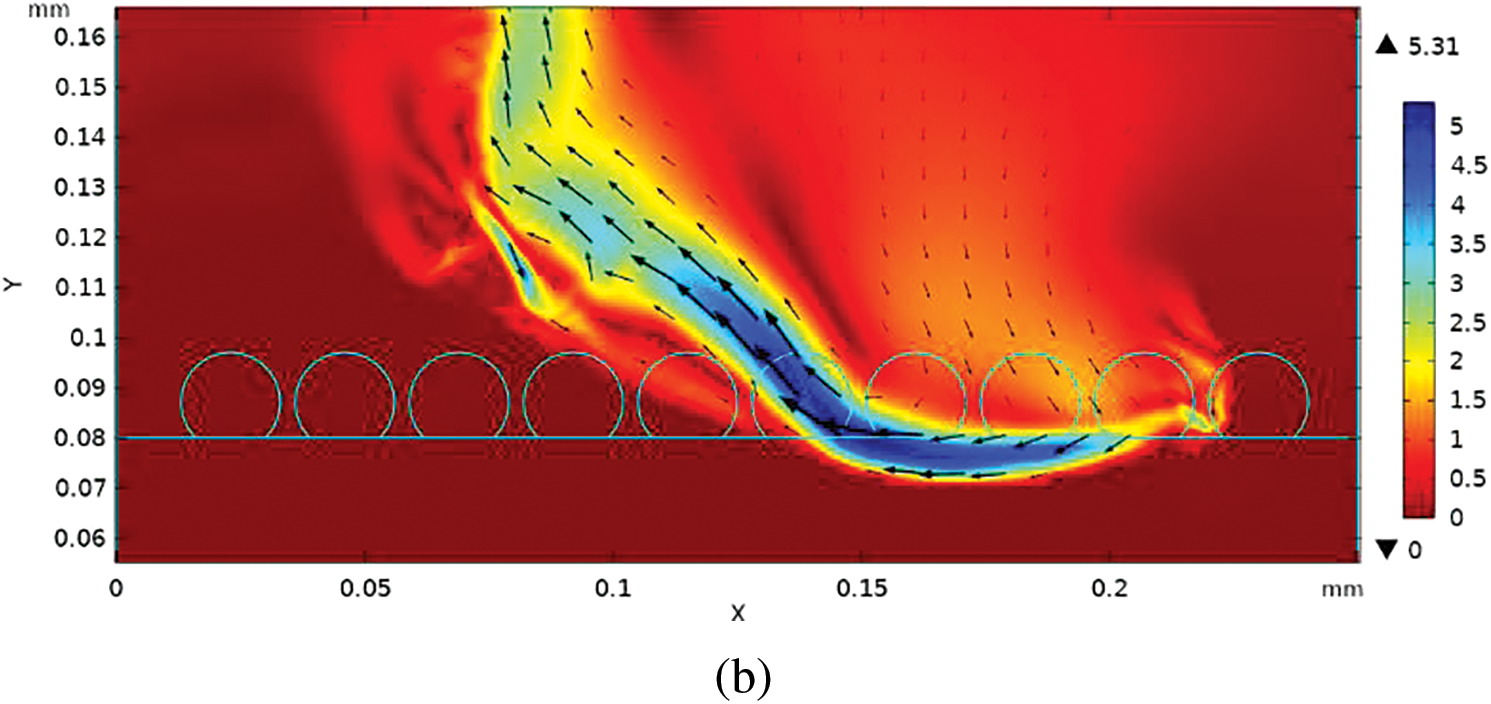
Figure 7: Fluid flow distribution at (a) 60 μs and (b) 150 μs
Fig. 8 illustrates the morphology of the molten pool at two distinct time points: 60 and 150 μs. As depicted in Fig. 8a, the laser induces heating in the vicinity of the laser spot, leading to the rapid melting of powders, followed by a subsequent subsidence that gives rise to the formation of an initial molten pool. In Fig. 8b, it is evident that with an increased delivery of energy to the powder bed, the molten pool undergoes rapid expansion, resulting in an augmentation of both its width and depth. The molten pool’s profile exhibits a subtle depression at the top, maintaining an overall smooth appearance. As the molten pool evolves in shape, it gradually takes on the form of a “U.” At the center of the molten pool, the top undergoes depression, attributed to the recoil force, while, notably, the left edge experiences significant elevation in the presented frame. The findings suggest that under lower laser powers, the predominant surface forces influencing the molten pool stem from surface tension, primarily facilitated through the Marangoni effect. Conversely, at higher laser power levels, the significance of recoil pressure becomes progressively more pronounced in shaping the behavior of the molten pool.
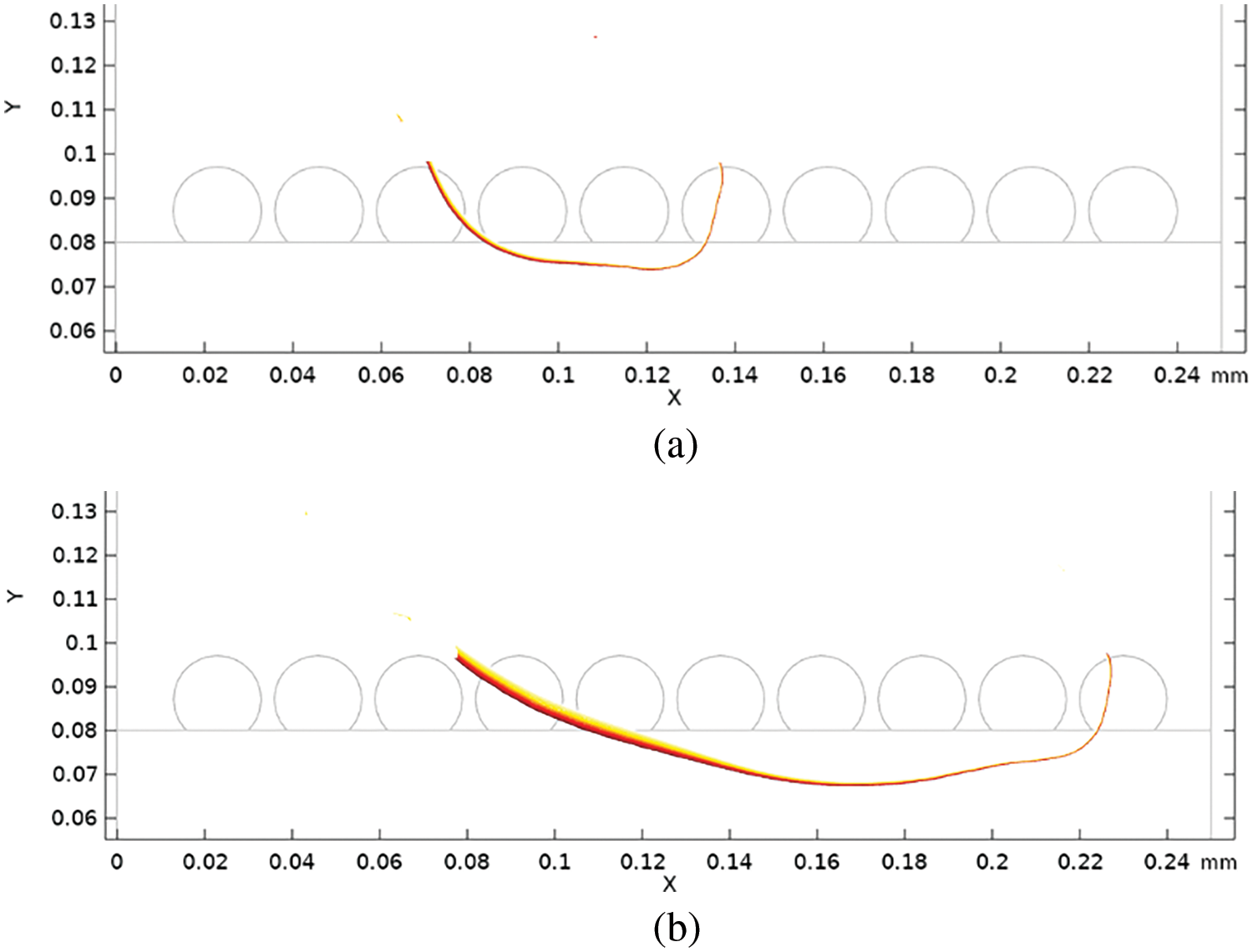
Figure 8: Morphology of the molten pool in the XY plane at (a) 60 μs and (b) 150 μs
Fig. 9 presents an analysis of the molten pool morphology, specifically focusing on width and depth at 150 μs, with a focus on the impact of process parameters. The plots within the figure illustrate how variations in laser power, beam spot size, and scanning speed of the laser beam influence the characteristics of the molten pool. As observed in Fig. 9, there is a noticeable correlation between laser power and the size of the molten pool, with an increase in laser power resulting in a larger molten pool. Conversely, the size of the molten pool diminishes with an increase in the beam spot size. Additionally, an increase in scan velocity is associated with a decrease in the size of the molten pool. The data in Fig. 9 further indicates that both the width and depth of the molten pool exhibit a roughly linear increase with higher laser power. This suggests a proportional relationship between these process parameters, highlighting how adjustments in laser power can directly influence the dimensions of the molten pool in a linear fashion. Contrastingly, there is a significant increase in both the width and depth of the molten pool when the beam size decreases. This phenomenon can be attributed to the exponential increase in laser intensity, as indicated by the term αP/(πR∧2)exp(−(x−x_i−Vt)∧2/R∧2) shown in Eq. (2). The relationship suggests that as the beam size decreases, the laser intensity experiences an exponential rise, resulting in a pronounced effect on the dimensions of the molten pool. Reducing the scanning speed has the effect of increasing the width of the molten pool. However, the corresponding increase in the depth of the molten pool is relatively insignificant. This indicates that changes in scanning speed primarily influence the lateral extent of the molten pool, with a less impact on its depth.
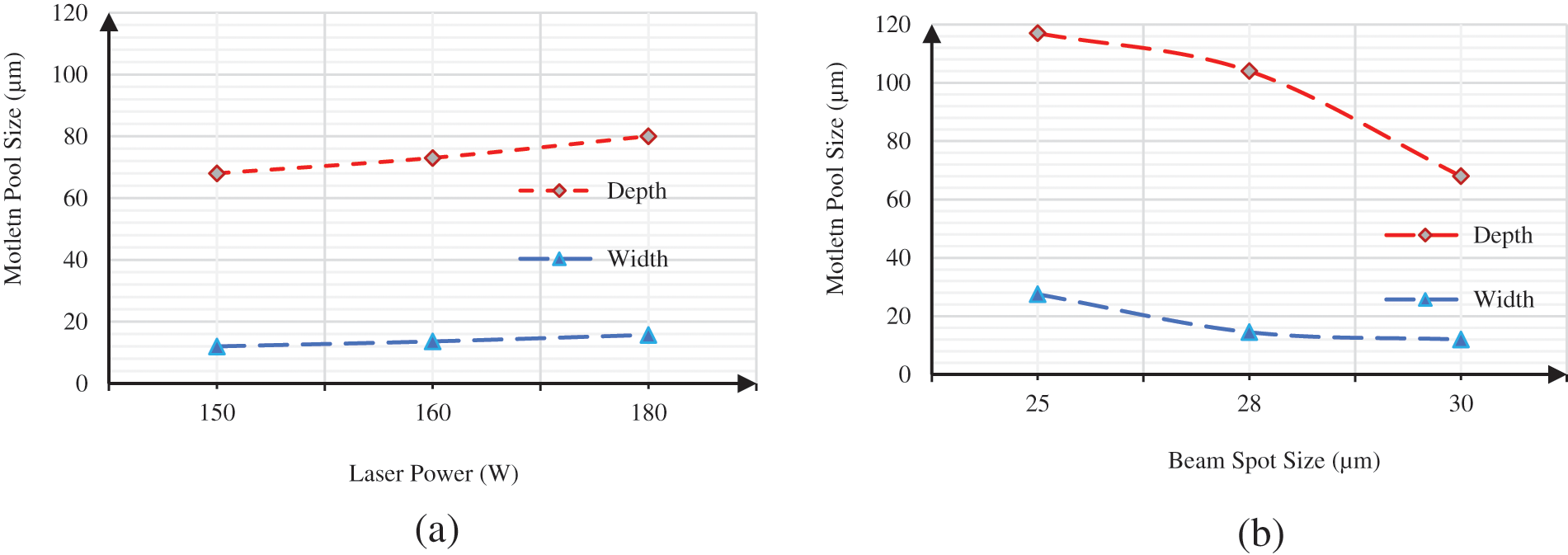
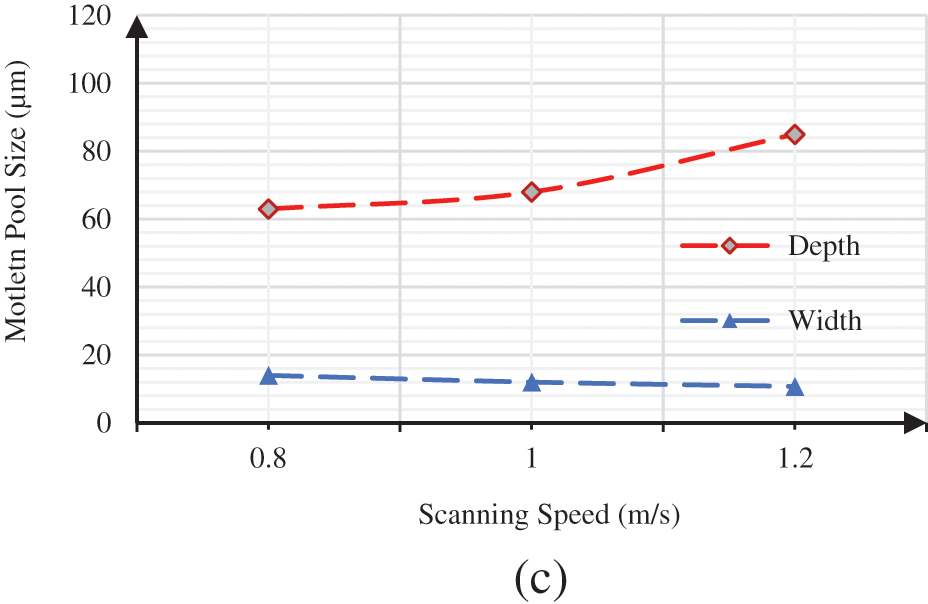
Figure 9: Parametric effect on the molten pool size
The paper introduces a two-dimensional, multi-physics finite element model designed to investigate the SLS process applied to Inconel 625 powders. The study employs numerical simulations to analyze and discern the influences of key process parameters on the sintering process. The conclusion drawn from the study emphasizes the significant roles played by recoil pressure and Marangoni force in shaping the thermal-fluid behaviors and influencing the growth of the molten pool in the SLS process. These two factors are underscored as key contributors to the observed phenomena in the investigated sintering process.
The first key factor influencing the molten pool is the recoil pressure generated at the front end of the laser spot. This pressure undergoes an exponential increase in relation to temperature, exerting a force that pushes the liquid metal downward to form a depression area at the head of the molten pool. Consequently, particles are generated and splashed from the rear edge of the molten pool due to the recoil pressure.
The second crucial factor influencing the molten pool is the backward Marangoni force. This force propels high-temperature liquid from the head of the molten pool towards the low-temperature liquid in the rear region. As a result, the molten pool experiences movement in the rear region, leading to the formation of a vortex. This phenomenon is a consequence of the interplay between temperature differentials and the Marangoni force within the molten pool.
The simulation findings additionally demonstrate that the molten pool size expands with higher laser power. Conversely, the molten pool size diminishes with an increase in beam spot size and/or an increase scan velocity.
To achieve a more comprehensive understanding of the thermal and fluid behaviors in the SLS process of Inconel 625, forthcoming efforts will focus on advancing the current two-dimensional model to a three-dimensional one. This advancement will facilitate a thorough examination, systematically exploring the separate and combined impacts of laser power, spot diameter, and scanning speed on molding the hydrodynamic characteristics of the molten pool. This upgraded model will consider the randomly distributed powders on the substrate, as well as the hatch spacing between adjacent laser tracks within a single layer. By incorporating these additional factors, the three-dimensional model aims to provide a more realistic and detailed representation of the SLS process for Inconel 625, contributing to a deeper insight into its thermal and fluid dynamics.
Acknowledgement: The authors would like to express their sincere gratitude to Dr. James Wilde at Texas State University for his support in this study.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Dr. Bin Xiao developed the models, conducted the simulations, and collected data. Dr. Byoung Hee You and Dr. Tongdan Jin contributed to result interpretation. All the authors collaborated on manuscript writing and revisions.
Availability of Data and Materials: The data that supports the findings of this study are available from the author upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Stavropoulos, P. (2023). Additive manufacturing: Design, processes, and applications. USA: Springer. [Google Scholar]
2. Zhou, K. (2023). Additive manufacturing: Materials, functionalities and applications. Switzerland: Springer. [Google Scholar]
3. Gade, S., Vagge, S., Rathod, M. (2023). A review on additive manufacturing-methods, materials, and its associated failures. Advances in Science & Technology Research Journal, 17(3), 40–63. https://doi.org/10.12913/22998624/163001 [Google Scholar] [CrossRef]
4. Guo, N., Leu, M. C. (2009). Additive manufacturing: Technology, applications and research needs. Frontiers of Mechanical Engineering, 8, 215–243. https://doi.org/10.1007/s11465-013-0248-8 [Google Scholar] [CrossRef]
5. Li, N., Khan, S., Chen, S., Aiyiti, W., Zhou, J. et al. (2023). Promising new horizons in medicine: Medical advancements with nanocomposite manufacturing via 3D printing. Polymers, 15(20), 4122. https://doi.org/10.3390/polym15204122 [Google Scholar] [PubMed] [CrossRef]
6. Mierzejewska, Z. A., Markowicz, W. (2015). Selective laser sintering–binding mechanism and assistance in medical applications. Advances in Materials Science, 15(3), 5–16. https://doi.org/10.1515/adms-2015-0011 [Google Scholar] [CrossRef]
7. Yan, C., Shi, Y., Li, Z., Wen, S., Wei, Q. (2021). Selective laser sintering additive manufacturing technology. USA: Elsevier. [Google Scholar]
8. Ameen, W., Ghaleb, A. M., Alatefi, M., Alkhalefah, H., Alahmari, A. (2018). An overview of selective laser sintering and melting research using bibliometric. Virtual and Physical Prototyping, 13(4), 282–291. https://doi.org/10.1080/17452759.2018.1489973 [Google Scholar] [CrossRef]
9. de Andrade, G. A., Vazquez, R., Pagano, D. J., Mascheroni, J. M. (2019). Design and implementation of a backstepping controller for regulating temperature in 3D printers based on selective laser sintering. IEEE 58th Conference on Decision and Control (CDC), pp. 1183–1188. Nice, France. [Google Scholar]
10. Storch, S., Nellessen, D., Schaefer, G., Reiter, R. (2003). Selective laser sintering: Qualifying analysis of metal-based powder systems for automotive applications. Rapid Prototyping Journal, 9(4), 240–251. https://doi.org/10.1108/13552540310489622 [Google Scholar] [CrossRef]
11. Pilipović, A., Brajlih, T., Drstvenšek, I. (2018). Influence of processing parameters on tensile properties of SLS polymer product. Polymers, 10(11), 1208. https://doi.org/10.3390/polym10111208 [Google Scholar] [PubMed] [CrossRef]
12. Xiao, B., Zhang, Y. (2007). Marangoni and buoyancy effects on direct metal laser sintering with a moving laser beam. Numerical Heat Transfer, Part A: Applications, 51(8), 715–733. https://doi.org/10.1080/10407780600968593 [Google Scholar] [CrossRef]
13. Acherjee, B., Kuar, A. S., Mitra, S., Misra, D. (2012). Effect of carbon black on temperature field and weld profile during laser transmission welding of polymers: A FEM study. Optics & Laser Technology, 44(3), 514–521. https://doi.org/10.1016/j.optlastec.2011.08.008 [Google Scholar] [CrossRef]
14. Criales, L., Arısoy, Y., Özel, T. (2018). Sensitivity analysis of material and process parameters in finite element modeling of selective laser melting of Inconel 625. The International Journal of Advanced Manufacturing Technology, 86(9–12), 2653–2666. https://doi.org/10.1007/s00170-015-8329-y [Google Scholar] [CrossRef]
15. Yaagoubi, H., Abouchadi, H., Janan, M. T. (2021). Numerical simulation of heat transfer in the selective laser sintering process of Polyamide12. Energy Reports, 7, 189–199. https://doi.org/10.1016/j.egyr.2021.08.089 [Google Scholar] [CrossRef]
16. Gusarov, A. V., Yadroitsev, I., Bertrand, P. H., Smurov, I. (2009). Model of radiation and heat transfer in laser-powder interaction zone at selective laser melting. Journal of Heat Transfer, 131, 035303. https://doi.org/10.1115/1.3109245 [Google Scholar] [CrossRef]
17. Zhang, H., Vallabh, C. K. P., Zhao, X. (2023). Influence of spattering on in-process layer surface roughness during laser powder bed fusion. Journal of Manufacturing Processes, 104, 289–306. https://doi.org/10.1016/j.jmapro.2023.08.058 [Google Scholar] [CrossRef]
18. Dogu, M. N., Mussatto, A., Yalçın, M. A., Ozer, S., Davut, K. et al. (2023). A comprehensive characterization of the effect of spatter powder on IN939 parts fabricated by laser powder bed fusion. Materials & Design, 235, 112406. https://doi.org/10.1016/j.matdes.2023.112406 [Google Scholar] [CrossRef]
19. Zhang, M., Zhu, Z., Zhang, L., Gao, M., Gao, J. et al. (2023). Understanding microstructure evolution and corrosion behavior of wire arc cladding Inconel 625 superalloy by thermodynamic approaches. Journal of Alloys and Compounds, 947, 169530. https://doi.org/10.1016/j.jallcom.2023.169530 [Google Scholar] [CrossRef]
20. Zhong, C., Ren, X., Fu, K., Luan, B. (2023). Effect of thermal aging on the microstructure and mechanical properties of Inconel 625 superalloy fabricated by high-speed laser metal deposition. Metallurgical and Materials Transactions B, 544, 2723–2736. https://doi.org/10.2139/ssrn.4387480 [Google Scholar] [CrossRef]
21. Hong, M., Wang, S., Sun, W., Geng, Z., Xin, J. et al. (2022). Effect of welding speed on microstructure and mechanical properties of selective laser melting Inconel 625 alloy laser welded joint. Journal of Materials Research and Technology, 19, 2093–2103. https://doi.org/10.1016/j.msea.2021.141507 [Google Scholar] [CrossRef]
22. Bon, D., Cavalcante, T., Thiesen, A., Santos, H., Gutjahr, J. et al. (2024). Effect of stress relief and solubilization heat treatments on laser additive manufactured Inconel 625: Microstructure and properties. The International Journal of Advanced Manufacturing Technology, 130(9–10), 4919–4931. https://doi.org/10.1007/s00170-024-12967-4 [Google Scholar] [CrossRef]
23. Banerjee, A., Rossin, J., He, M. R., Musinski, W. D., Shade, P. A. et al. (2023). Decoupling build orientation-induced geometric and texture effects on the mechanical response of additively manufactured IN625 thin-walled elements. Materials Science and Engineering: A, 870, 144826. https://doi.org/10.1016/j.msea.2023.144826 [Google Scholar] [CrossRef]
24. Ren, D., Xue, Z., Jiang, Y., Hu, X., Zhang, Y. (2020). Influence of single tensile overload on fatigue crack propagation behavior of the selective laser melting Inconel 625 superalloy. Engineering Fracture Mechanics, 239, 107305. https://doi.org/10.1016/j.engfracmech.2020.107305 [Google Scholar] [CrossRef]
25. Wang, L., Wei, Q. S., Shi, Y. S., Liu, J. H., He, W. T. (2011). Experimental investigation into the single-track of selective laser melting of IN625. Advanced Materials Research, 233(1), 2844–2848. https://doi.org/10.4028/www.scientific.net/AMR.233-235.2844 [Google Scholar] [CrossRef]
26. Wang, X., Jiang, M., Zhou, Z., Gou, J., Hui, D. (2017). 3D printing of polymer matrix composites: A review and prospective. Composites Part B, 110, 442–458. https://doi.org/10.1016/j.compositesb.2016.11.034 [Google Scholar] [CrossRef]
27. He, Q., Xia, H., Liu, J., Ao, X., Lin, S. (2020). Modeling and numerical studies of selective laser melting: Multiphase flow, solidification and heat transfer. Materials and Design, 196, 109115. https://doi.org/10.1016/j.matdes.2020.109115 [Google Scholar] [CrossRef]
28. Panwisawas, C., Perumal, B., Ward, R. M., Turner, N., Turner, R. P. et al. (2017). Keyhole formation and thermal fluid flow-induced porosity during laser fusion welding in titanium alloys: Experimental and modelling. Acta Materialia, 126, 251–262. https://doi.org/10.1016/j.actamat.2016.12.062 [Google Scholar] [CrossRef]
29. Khairallah, S. A., Anderson, A. T., Rubenchik, A., King, W. E. (2016). Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Materialia, 108, 36–45. https://doi.org/10.1016/j.actamat.2016.02.014 [Google Scholar] [CrossRef]
30. ASM Aerospace Specification Metals Inc. (2013). Special metals Inconel Alloy 625. https://asm.matweb.com/search/SpecificMaterial.asp?bassnum=NINC33 (accessed on 25/01/2023). [Google Scholar]
31. High Temp Metals (2015). Inconel 625 Technical Data. https://www.hightempmetals.com/techdata/hitempInconel625data.php (accessed on 23/01/2023). [Google Scholar]
32. Tlili, I., Baleanu, D., Sajadi, S. M., Ghaemi, F., Fagiry, M. A. (2022). Numerical and experimental analysis of temperature distribution and melt flow in fiber laser welding of Inconel 625. The International Journal of Advanced Manufacturing Technology, 121, 765–784. https://doi.org/10.1007/s00170-022-09329-3 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF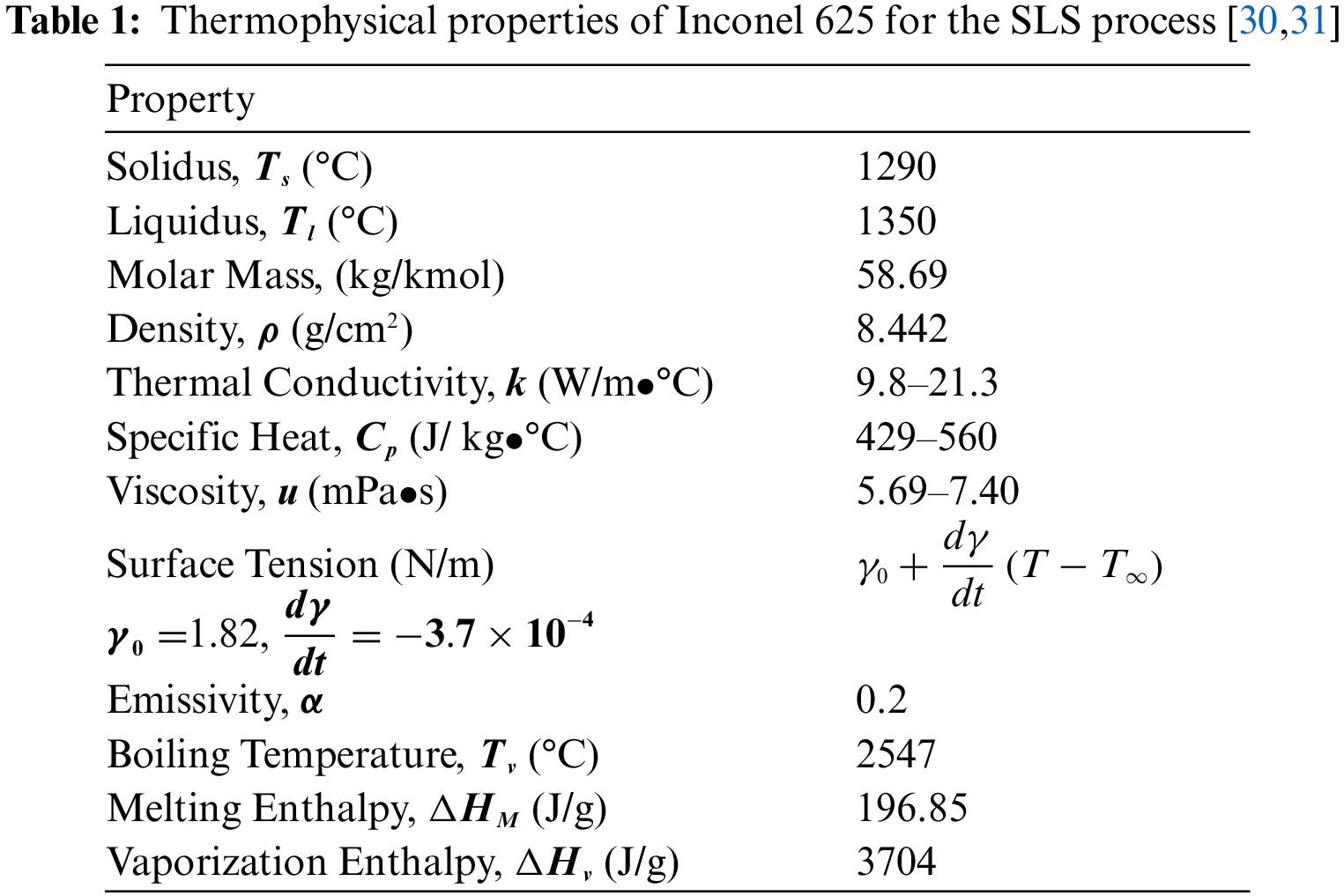
 Downloads
Downloads
 Citation Tools
Citation Tools
