 Open Access
Open Access
ARTICLE
Numerical Examination of a Cavity Containing Nanofluid with an Upper Oscillating Wall and Baffle
1 Middle Technical University, Technical Engineering College, Baghdad, Iraq
2 Department of Biomedical Engineering, University of Technology, Baghdad, Iraq
3 Department of Electromechanical Engineering, University of Technology, Baghdad, Iraq
* Corresponding Author: Akram H. Abed. Email:
(This article belongs to the Special Issue: Computational and Numerical Advances in Heat Transfer: Models and Methods I)
Frontiers in Heat and Mass Transfer 2024, 22(2), 557-581. https://doi.org/10.32604/fhmt.2024.047814
Received 18 November 2023; Accepted 25 January 2024; Issue published 20 May 2024
Abstract
The cavity with lid-driven is greatly used in mixing, coating, and drying applications and is a substantial issue in the study of thermal performance rate and fluid field. A numerical approach is presented to study the thermal distribution and passage of fluid in a lid-driven cavity with an upper oscillating surface and an attached baffle. The walls of a cavity at the left and right were maintained at 350 and 293 K, respectively. The upper oscillating surface was equipped with a variable height to baffle to increase the convection of the three kinds of TiO, AlO, and CuO nanofluids with various of 0.4, 0.8, and 0.4, 0.8, and 1.2 vol. % in volume fractions. It was found that using a baffle attached to the oscillating upper surface of the cavity will lead to improving the distribution of vorticity in the cavity and increase the stream in the cavity. Also, increasing the baffle height, oscillating velocity, and volume fraction of nanoparticles contributes to enhancing the Nusselt number values by 50% for increasing baffle height from h = 0.1 to 0.1. Also, the Nu improved by 20% for increasing oscillating velocity from w = 05 to 20 rad/s and by 12% for using AlO nanofluid instead of TiO at = 0.8 vol. %.Keywords
Nomenclature
| Cp | Nanofluids specific heat (J.kg−1.K−1) |
| L | Channel height (m) |
| H | Height of the cavity (m) |
| W | Width of the cavity (m) |
| h | Baffle height, m |
| ω | Angular velocity of moving wall (rad/s) |
| k | Nanofluids thermal conductivity (W/m.K) |
| P | Pressure (Pa) |
| q | Applied heat flux (W/m2) |
| T | Temperature (K) |
| u | Axial velocity (m/s) |
| v | Transverse velocity (m/s) |
| x, y | Cartesian coordinates |
| Nu | Nusselt number |
| T | Nanofluids Temperature (K) |
| U, V | Velocity components Dimensionless in x, y directions |
| X, Y | Dimensionless Cartesian coordinates |
| u, v | Components of Velocity in x, y directions (m/s) |
| Vpa | Nanoparticle volume |
| Vnf | Nanofluid volume |
| Greeg Symbols | |
| μ | Dynamic viscosity (Pa s) |
| θ | Dimensionless temperature |
| ρ | Density (kg/m2) |
| v | Kinematics viscosity (m2/s) |
| ∆ | Difference |
| Nanoparticle volume fraction | |
| Subscribe | |
| nf | Nanofluid |
| F | Fluid |
| p | Solid nanoparticle |
Since it is relevant to industrial flows and the effectiveness of heat transfer, flow within a cavity where the lid is in motion, oscillating back and forth, has been researched throughout time by Zhu et al. [1]. When the lid of the cavity oscillates horizontally, a Stokes layer develops with a pair of primary vortices, one rotating clockwise and the other counterclockwise during the oscillation cycle of the upper wall, which will indicate the oscillatory lid-driven cavity flows. Square cavities feature complex vortex dynamics due to the generation and growth of corner vortices that interact with the primary vortices as a result of flow separation [2,3].
The possibility of using a cavity with a viscometer utilizing oscillating lid-driven flow, which was explored in a preliminary study [4], motivated further investigation into the steadiness of the 2D flow. When compared to steady lid-controlled cavity flows, lid-controlled flow with two-dimensional oscillations dynamics are Extra complicated [5]. The poor thermal conductivity is the fundamental drawback of classical base fluids that are employed in the process of thermal energy exchange applications, like water, oil, and ethylene glycol in comparison to modified nanofluids. Modified nanofluids refer to a blend of base fluids and nanoparticles that are nano-sized and possess superior thermal conductivity [6]. Numerous numerical analyses of a fluid with high viscosity in square cavities were conducted. The top sliding wall, which performs sinusoidal oscillations, is what propels the flows. Different general settings are used to obtain the results of two key physical factors; examples include the (Re) and the non-dimensional oscillation rate of the lid [7]. Using Lattice Boltzmann model of a 2D two-phase, Hu et al. [8] conducted experimental testing of heat transfer rate of a nanofluid consisting of Al2O3 particles dispersed in water within a square cavity. Pourmahmoud et al. [9] investigated the influence of laminar mixed convection that steady temperature is maintained for the vertical walls, but with some variability, and the bottom and top horizontal surfaces are thermally insulated. Jmai et al. [10] explored a square hollow container with a lid on both sides that was used in an experiment involving a partially heated Cu-water nanofluid. The type of fluid flow observed was laminar mixed convection. Minea et al. [11] examined ZnO-water nanofluid with less common heat transfer in a confined enclosure. By using the entropy production that revealed a decline as the Rayleigh number rises. In a study by Goqo et al. [12], the flow of nanofluid in cavity filled with a was investigated. The cavity was filled with a porous media and unprotected to an external magnetic. Except for the top, the hollow surfaces remain stationary. The upright surfaces of the cavity do not allow heat changed and the temperature of the bottom wall remains constant. Shah et al. [13] used CVFEM to model the 2D flow of a hybrid nanofluid with non-Darcy behavior. via undulating by using entropy optimization. Wong et al. [14] carried out numerical research for an unstable 2D incompressible fluid with laminar flow. It is seen that the cavity flow’s viscous heating dissipates into the surrounding air. Aun et al. [15] conducted both experimental and numerical analyses to inspect the associated heat rate with convection inside an enclosure containing a vertically heated block and baffles. They conducted the impact of various factors, such as (q), (Re), baffle width, and baffle arrangement, on the heat transfer features and flow phenomena in the area of enclosure. In a study by Al-Farhany et al. [16], numerical simulations were conducted to investigate enclosure-based natural convection with Cu/water nanofluids. The simulations also accounted for the presence of baffles with bottom blocks. Alsabery et al. [17] studied the mixing convection in the lid-driven enclosure has a wavy shape and contains a nanofluid as well as a substantial heat source was explored. Investigations are conducted into how adding nanoparticles to the base flow affects the velocity, temperature, and concentration field. Shehata et al. [18] used a computational analysis to scrutinize the belongings of nanofluids to a square lid-driven cavity to enhance hydro-magnet mixed convection. Similarly, Pordanjani et al. [19] detected how a field of magnetic exaggerated the Al2O3/water nanofluid’s natural convection in the cavity with sinusoidal of the distribution of wall temperature and isothermal barriers at Ri = 0.001. The findings demonstrated that the Nu increased in proportion to the nanoparticles volume fraction of 6% nanoparticles, the Nu jumped by 9.04% over the base fluid. Zheng et al. [20] studied the effects of radiation and the entropy creation on the natural of Al2O3 nanofluid in a titled cavity. The left wall of the cage has a circular quadrant at a hot temperature of Th. According to the statistics, there is a 160% and 40% increase in Nu when Ra is increased and Ha is decreased. Befalls as a result of raising Ra and lowering Ha. The maximal generation of entropy rises by 288% and 39%, respectively, when the Ra and Ha are increased. The largest average Nu and total entropy generation happen at a 30° inclination angle. Berrahil et al. [21] presented a numerical investigation of the natural convection of Al2O3 nanofluid’s in a vertical annulus that is differentially heated and subjected to a uniform magnetic field is done by. They established an internal Nu rises once more after falling until it reaches a volume fraction of 0.05. The impact of nanopowder shape on irreversibilities and natural convection in water/alumina nanofluids was examined by Yan et al. [22]. Furthermore, a multi-walled carbon nanotube-iron oxide (MWCNTFe3O4) hybrid nanofluid MHD nano liquid convective flow in an oddly shaped cavity was designated by the Al-Kouz et al. [23]. The cavity interior and exterior limitations are reserved in an isothermal state. The periodic field magnetic effects on the free convection and entropy production of a Fe3O4 nanofluid in a square enclosure were explored by Mehryan et al. [24]. Morever, Izadi et al. [25] studied the set of governing equations pertinent to the current circumstance by using the FEM. The findings demonstrate that the Nusselt number of porous material of the two phases flow grasses. For applications including oscillators and non-destructive testing, the vibration examination of carbon nanotubes (CNTs) are valuable. Hussain [26] investigated the characteristics of vibration of CNT by using a nonlocal elasticity shell model. Hussain et al. [27] investigated the impact natural vibrations by boundary conditions on the of (SWCNTs) by using shell dynamical equations and wave propagation approach (WPA) to govern the vibrations of carbon nanotubes. Rashed et al.’s [28] investigation of heat transfer via a downstream annulus in a laminar flow zone employed water as the working fluid. An inner circular pipe and an exterior twisted square duct made up the annulus. For the laminar flow system with a low Reynolds number, the Navier-Stokes equations were numerically solved using a three-dimensional model. The impact of an oscillating thin plate with varying inclination angles on the Al2O3-water nanofluid flow and heat transfer performance was examined numerically by Jehhef et al. [29]. The next work uses COMSOL Multiphysics 5.4 to develop techniques for creating fluid-structure interactions through the effect of an Al2O3-water nanofluid at 0.1–1.0 vol. % volume fraction upon the thin plate. Finally, In the presence of a triangular rib, Jehhef et al. [30] investigated the mixed convection between two parallel plates of a vertical channel. On the heated wall, six triangular rib heat-generating components were spaced evenly apart.
All the above literature works concentrated on the heat transfer in lid-driven without moving baffle, but the current simulation study absorbed on outcome of attached baffle of moving wall on enhancement of the heat transfer and fluid flow in lid-driven. Thus, goal of this study is to evaluate the impacts of attaching baffles with various heights to the upper cavity with lid-driven for three types of nanofluids. A numerical simulation was created to characterize the hydrodynamics and heat transfer behavior in a 2D cavity. The influences of baffle height, oscillating velocity, and volume fraction of nanoparticle concentration have been investigated to achieve high thermal efficiency as compared to the cavity without an attached baffle. This particular study is important due to adding the effect of the baffle attached to the oscillation upper wall on the mixed convection inside the cavity.
After conducting a thorough review of the literature, Minea et al. [11] studied the thermal behavior of a less commonly used nanofluid, ZnO-water nanofluid, in context of natural convection heat transfer inside a closed rectangular hollow. The present study adopted this well-established benchmark as a case study for validation purposes. To solve the equations of governing, the authors employed a (CFD) that is identical to the algorithm implemented in ANSYS-Fluent. The schematic of the problem descriptions of the square cavity that has an upper oscillating wall with and without baffle can be seen in Fig. 1. The fluid used for the present work is a nanofluid consisting of water and alumina nanoparticles at 0.4, 0.8, and 1.2 vol. % volume concentrations. The thermal equilibrium assumption is made of the water and nanoparticles and there is no relative motion between them. The cavity’s left wall is consistently maintained at a constant high temperature (Th), while the right wall is consistently kept at a constant low temperature (Tc). The lower wall is considered a stationary and insulation surface but the upper wall is moved at constant sine wave angular velocity. Some of the assumptions were considered as follows:

Figure 1: Schematics for the problem under consideration
1) Conservation equations of 2D form.
2) Incompressible Steady state fluid flow.
3) Nanofluids flow in the cavity have been considered turbulent.
4) Nanofluids thermos-physical properties are assessed at an average fluid temperature.
5) Heat transfer by conduction is neglected.
6) Radiation heat transfer in the model is neglected.
In the present work, it is presumed that the thermophysical characteristics of the nanofluid remain unchanged, except for density fluctuations that are estimated using the Boussinesq model. ANSYS-Fluent is employed to develop a two-dimensional model for heat and fluid flow within the enclosure, taking into account forced convective laminar heat transfer and steady-state incompressible fluid flow boundary. The equations that govern this particular type of flow are the time-independent equations of Navier-Stokes, which describe steady viscous, incompressible laminar flow in two dimensions. The given equations that are suitable can be expressed as:
The equation that describes the conservation of mass is:
x-direction momentum conservation formula:
y-direction momentum conservation formula:
Energy conservation formula:
The thermal diffusivity (αnf), representing the measure of thermal inertia, is determined by the following calculation:
The formula for calculating αnf involves the fluid thermal conductivity (knf) measured in W/m K, the density (ρnf) expressed in kg/m3, and the (Cpnf) of the nanofluid in J/kg.K. A greater magnitude of αnf signifies efficient heat transfer and a nanofluid with enhanced thermal conductivity. The temperature variable is represented as T. While using the Boussinesq Approximation, density variations are a function of reference density, temperature, and a coefficient of thermal expansion.
where appears in the x-momentum equation and links it by incorporating the equation of energy. In this context, ∆T = Th − Tc represents the difference temperature between the hot and cold walls.
In the numerical work, the enclosed cavity is simulated in 2-dimensional modeling. The main goal is to investigate the rate of heat transfer and fluid flow profile of various volume fractions of Al2O3-water nanofluid. A constant temperature of 350 K is maintained for the hot temperature, while the cold wall is fixed at 293 K. To replicate the impact of nanoparticles, the Tiwari-Das model [31] is utilized, enabling simulation of various metallic nanoparticles and their concentrations (volume fraction). Since the particles are extremely small, ANSYS-Fluent implements this method as a “one-phase flow” modification. In ANSYS-Fluent, a nanofluid is defined as a novel fluid that possesses unique characteristics such as density, viscosity, thermal conductivity, and specific heat. These properties are derived from a base fluid and determined by the type and concentration (volume fraction) of nanoparticles present. The estimation of the volume fraction can be accomplished using the following method:
The viscosity that effectively characterizes the dynamic behavior of a nanofluid can be expressed using Brinkman’s formula [32].
The estimation of the nanofluid effective density can also be derived using Pak et al. [33].
The determination of the coefficient of thermal expansion for the nanofluid can be achieved by:
The nanofluid specific heat was given by Xuan et al. [34].
To ascertain the nanofluid’s effective thermal conductivity by employing the Maxwell-Garnet relation, specifically for spherical nanoparticles [35,36].
One possible approach for defining the local Rayleigh number involves the comparison between thermal buoyancy and viscous hydrodynamic force, and can be expressed as follows:
The Nusselt number is given by:
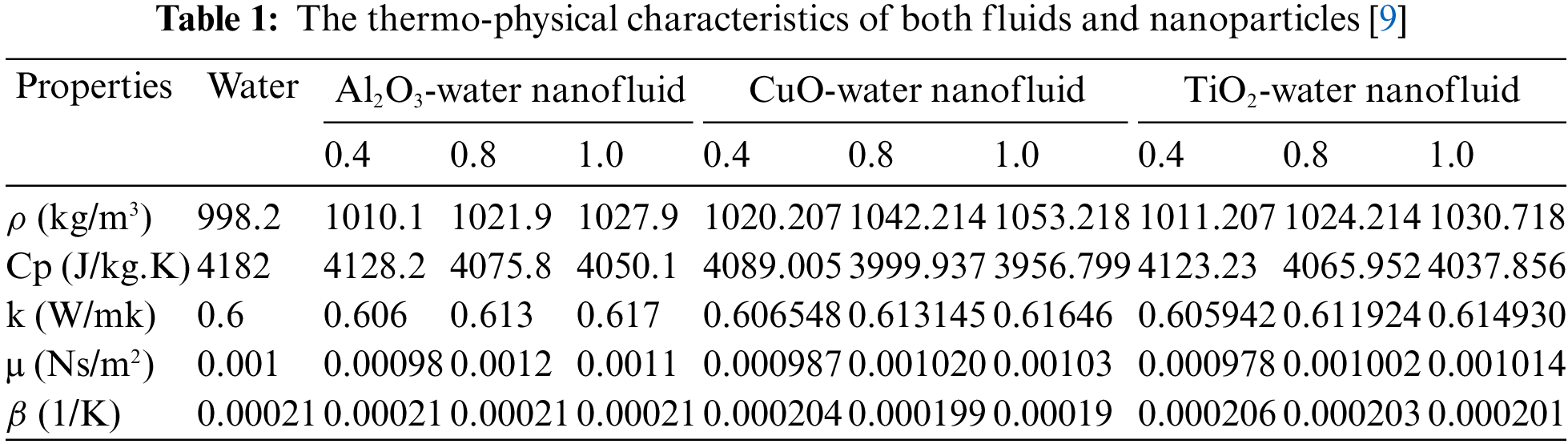
In the provided equation, the symbol ‘g’ corresponds to the acceleration due to gravity, ‘y’ represents the coordinate, ‘h’ signifies the convective heat transfer coefficient, H denotes the height of the enclosure, and ‘w’ represents the heat flux rate calculated in ANSYS-Fluent. For this study, Table 1 presents the thermophysical properties of pure water and the nanofluid at a temperature of 298 K.
The thermal boundary conditions depicted in Fig. 2 are applied as described:

Figure 2: Geometry distribution and boundary conditions
The left wall: stationary with constant of temperature, T = 350 K.
The right wall remains stationary and maintains a constant temperature of 293 K.
The bottom walls are adiabatic and remain stationary.
The upper wall: oscillating moving wall with Adiabatic.
Fig. 2 illustrates the geometrical arrangements of the upper wall, which oscillates on one side and is utilized in the current numerical analysis. The first case involves the upper lid being stationary with zero velocity obstruction (U = 0). In the second case, the upper lid exhibits a constant velocity, denoted as U = Uo. In the third case, the upper lid without the baffle oscillates solely with a velocity of U = Uo cos (ωt), as depicted in Fig. 2a. In the fourth case, the upper lid with baffle oscillates with a velocity of U = Uo cos (ωt), as shown in Fig. 2b. However, the remaining walls are stationary. In this context, U represents the magnitude of the lid’s velocity, which is fixed according to Re expressed as:
where W represents the cavity width, and vnf denotes the viscosity of the nanofluid. The value of U is associated with the Mach number and should be sufficiently low to ensure the incompressibility of the fluid. As U influences the Reynolds number (Re), an increase in Re indicates a larger oscillation amplitude. This study aims to examine the variations in flow modes under antiparallel and parallel oscillating wall motions by systematically adjusting the parameters (Re and ω) across a wide range of values (see Table 2). For simplicity, the average angular frequency ω– has been normalized following the approach of Iwatsu et al. [7].
The highest and lowest values of St are determined as follows:
The oscillation period T, presented in Table 2, is calculated as follows:
In the numerical simulation, the sum is not expected to be zero, but it should gradually decrease with each iteration. The residual serves as an indicator of the extent of deviation in the solution of a specific transport equation. Monitoring the average residual associated with each transport equation helps determine the convergence of the solution. In this simulation, approximately 500 iterations are required to achieve a final solution, with the residuals often decreasing by several orders of magnitude as listed in Table 3. As previously described, the ANSYS-Fluent residual print plot indicated convergence, and the grid dependency investigation was performed by progressively refining the model’s mesh until the results reached a stable state, as demonstrated in Fig. 3. The near-wall clustering cell is given by a y+<1 near baffle with growth ratio of 1.06. To assess the mesh sensitivity, the heat transfer coefficient profile along the heated left wall was computed and plotted against the number of nodes. The mesh with the size of 62500 or 350 × 350 is selected in present modeling as shown in Fig. 4.

Figure 3: Grid dependency analysis
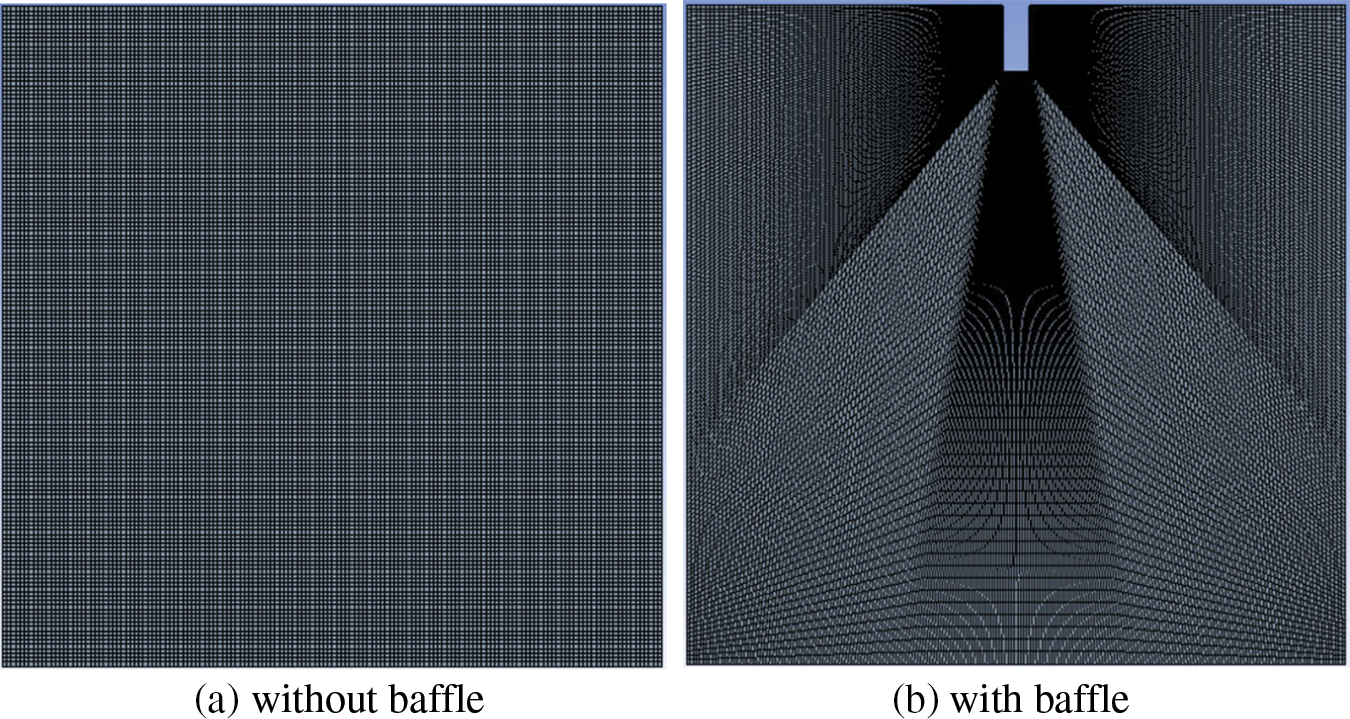
Figure 4: Computational domain mesh of the square cavity model
Convergence can face obstacles due to several factors, including a high volume of computational cells, excessively cautious under-relaxation factors, and intricate flow physics. Determining if a solution has truly converged can also pose challenges. The upcoming sections will delve into various numerical controls and modeling techniques that can be employed to improve convergence and uphold stability, as illustrated in Fig. 5. The method of solution can be direct or iterative. Furthermore, some control parameters are employed to control the method’s convergence, stability, and accuracy. For the momentum and energy variables was used, and Semi-Implicit Method for Pressure Linked Equations (SIMPLIE) is used to couple the interaction between pressure and velocity. The tolerance for continuity and velocity was set to (1 × 10−6) while the tolerance for energy was set to (1 × 10−8).
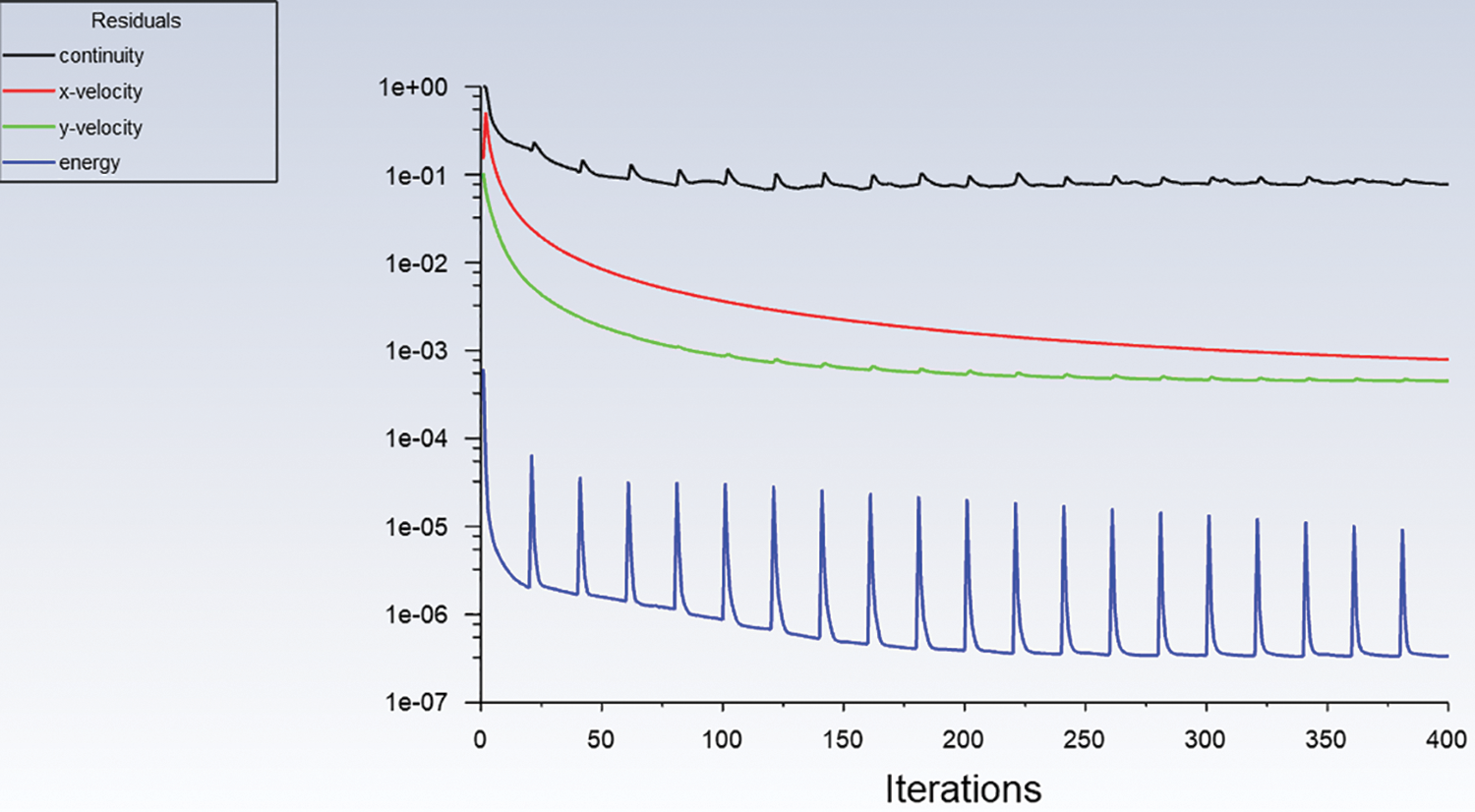
Figure 5: Convergence of computational model
2.7 Validation with Previous Studies
To validate the accurateness of the ANSYS-Fluent model in simulating mixed convection within a cavity containing Al2O3-water nanofluid at a Rayleigh number of 104, a comparison was conducted with a study conducted by Minea et al. [11]. Outcomes of this comparison presented in Fig. 6. Although replicating exact values proved challenging, the stream function and temperature contour patterns were compared. The ANSYS-Fluent simulation was found to agree with the Minea et al. [11] results, as evidenced by the similarities in the stream function and temperature contour patterns. To further establish confidence in the model, additional tests were performed. With confidence established in the simulations, more complex geometries can be explored. Also, to validate the numerical recent data with experimental data results of Shehata et al. [18], Fig. 7 displays a good arrangement of the results in profile and trent of the Nusselt number.
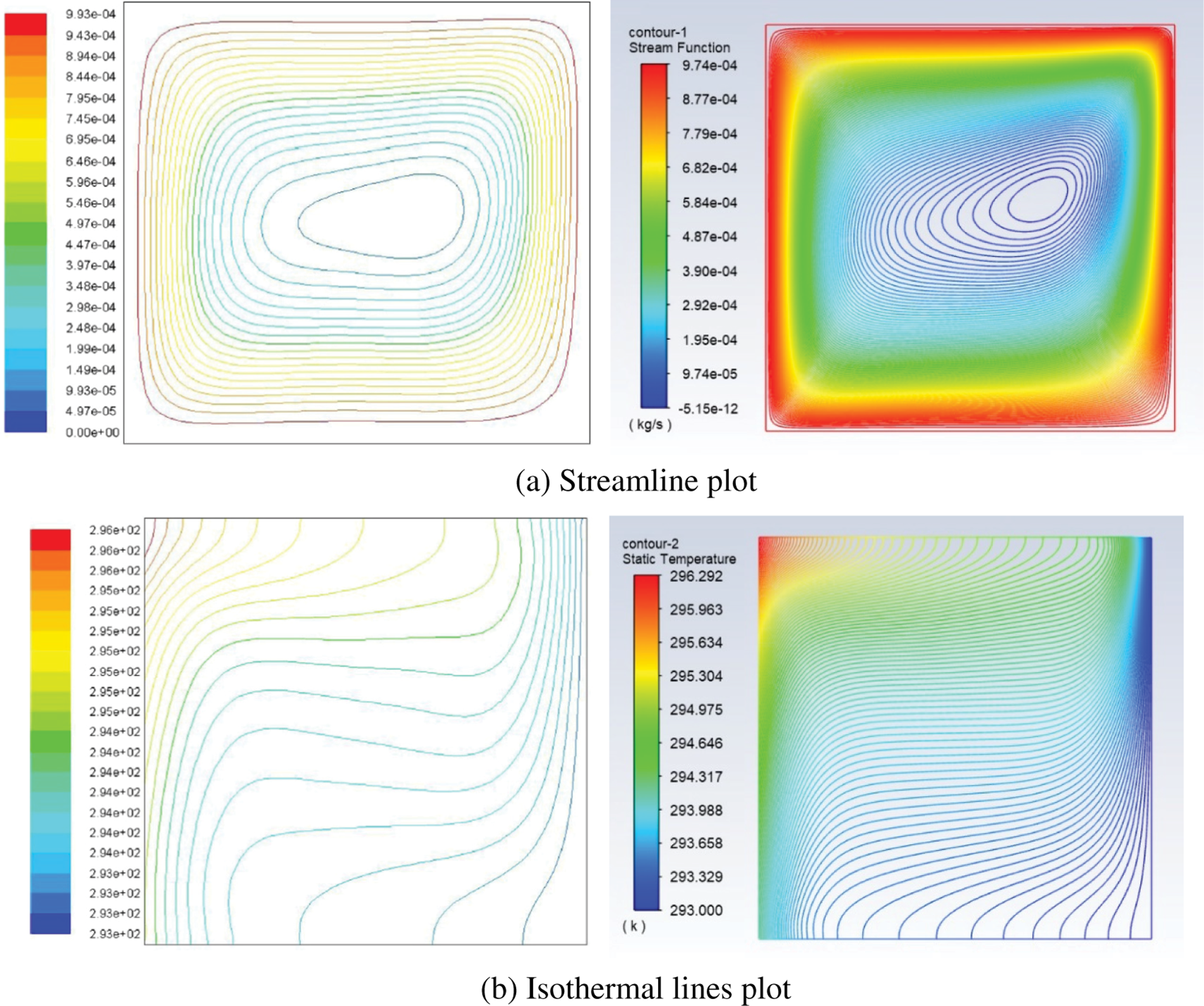
Figure 6: Streamline and isothermal lines contours for water for Minea et al. [11] (left) present study (right), with a Rayleigh number of 104
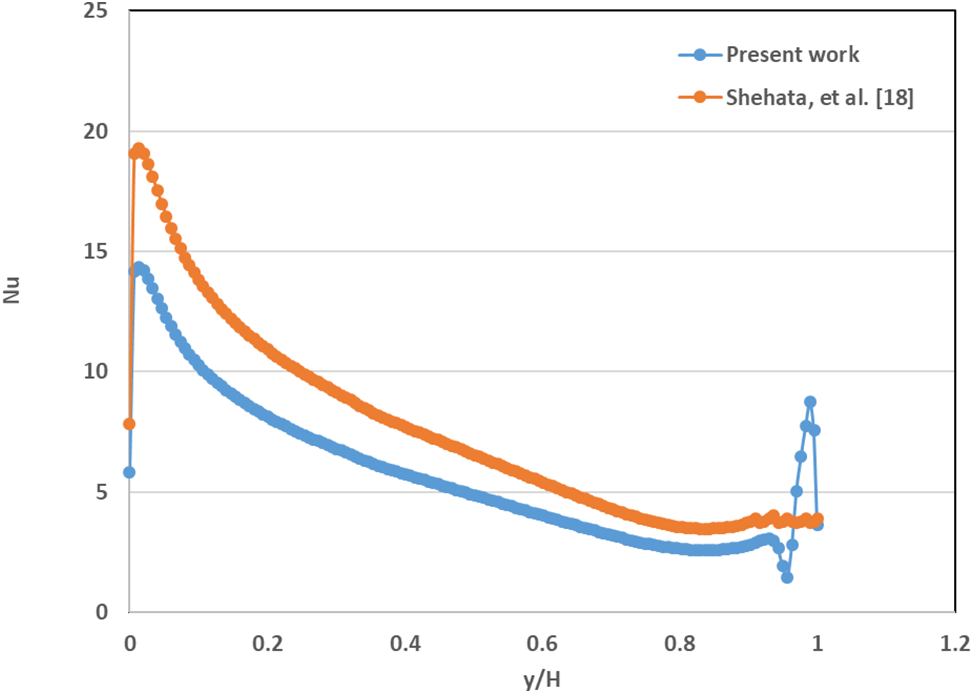
Figure 7: Streamline and isothermal lines contours for water for Shehata et al. [18] (left) present study (right), with a Rayleigh number of 104
Present numerical results work regarding effect of the oscillating upper wall of the enclosed cavity filled with nanofluid are presented with the aid of plots for streamlining and isothermal lines. In this study, the following parameter is investigated numerically as three values of upper wall velocity u = 0.5, 1.0, and 1.5 without oscillating, four baffle height to cavity height ratios of h* = hb/H = 0.1, 0.15, 0.2 and 0.25, and five oscillating velocities π/2.5, π/5, π/7.5 and π/10.
3.1 Effect of Uniform Velocity
To study the effect of upper wall velocity without baffle, Fig. 8 displays the ANSYS Fluent results of the effect of uniform velocity on the isothermal and streamlines function. The figure shows the outcomes obtained from different uniform velocity models used to create temperature contours for water inside an enclosure with an aspect ratio of 1 (AR = H/W = 1) and a Rayleigh number of 104, the volume fraction of the water was set to a low value of 0%. The outcomes showed that increasing the velocity of the top wall will impact the profile of the isothermal line and stream function lines as compared with the zero-uniform velocity. As a result, the increasing uniform velocity from u = 0 to 0.5 primes a decrease in the temperature from 339 to 326 K in the upper zone, due to pushing the heated zone towered the cold surface. Also, the results display an increase of the maximum stream function near the upper wall by about 0.085 kg/s when increasing uniform velocity from 0 to 0.5 m/s.
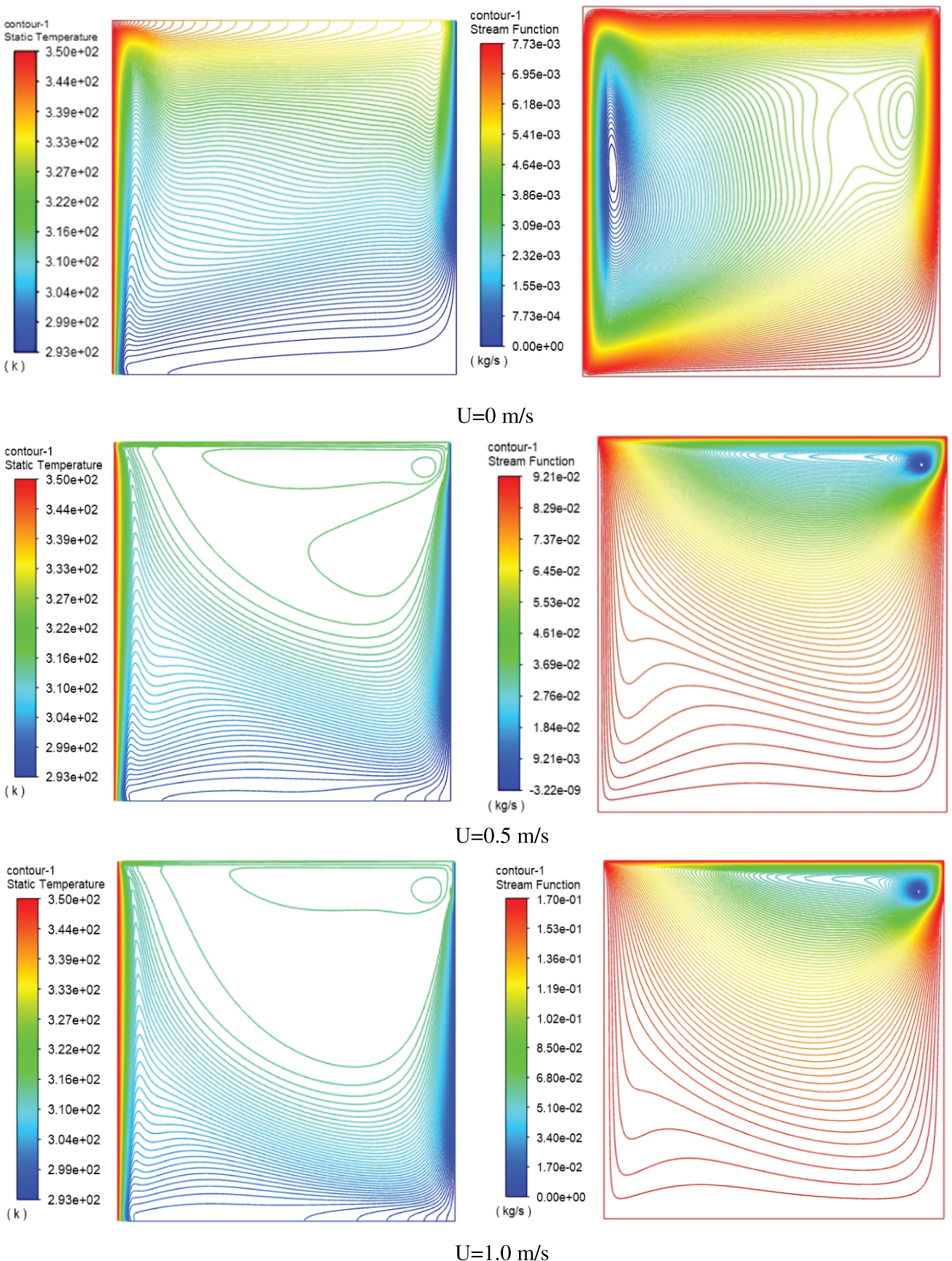
Figure 8: Isotherms (left) and Streamlines (right) for water inside square cavity with stationary and moving top wall
The results in numerical form regarding the influence of the ratio of the height of the baffle to the height of the cavity on the isothermal and streamlines function are depicted in Fig. 9 which displays the results with different baffle height ratios for generating isothermal contour of water with a low volume fraction of 0% and Ra = 104. The results specified that attaching the baffle to the oscillating upper surface of the enclosed cavity will induce flow within the cavity and enhance the vorticity of the water and this will lead to mixing the hot and cold layers inside the cavity. Also, the outcomes indicated that increasing the baffle height has a considerable effect on the profile of the isothermal line and stream function lines as compared with the smooth upper wall (h* = 0) case. As a result, the increasing baffle height from h* = 0.1 to 0.15 leads to increasing the heated zones that are oriented towards the cold side and this increases the heating process along the cold surface. In the top zone, due to pushing the heated zone towered the cold wall. However, the results showed the intensity of the vorticity of the center streamlines the function and it will separate into two strong vorticities caused by the baffle.
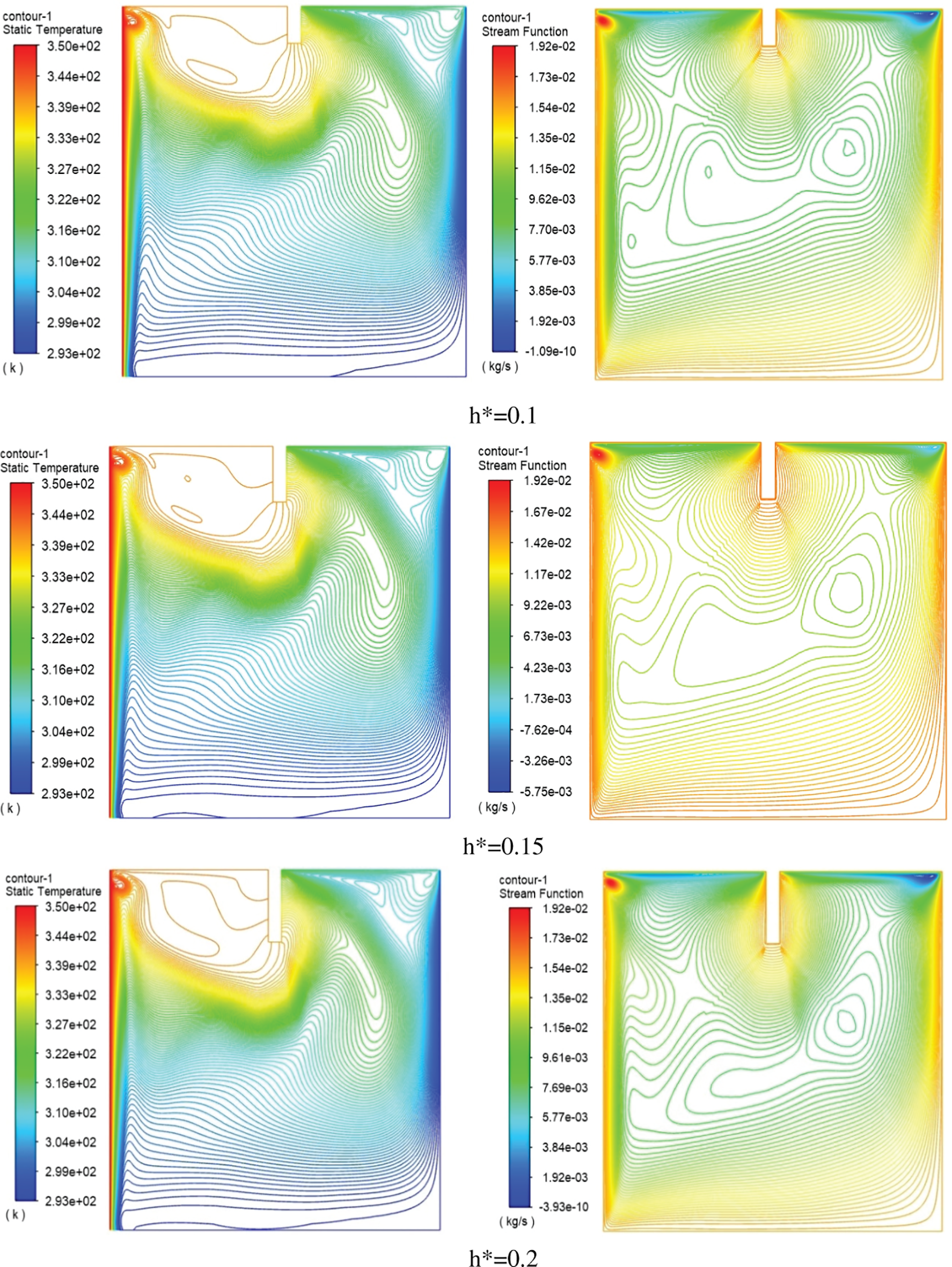
Figure 9: Isotherms (left) and Streamlines (right) for water inside square cavity with rectangular baffle along moving top wall with various hight
3.3 Effect of Oscillating Velocity
The impact of increasing the upper wall velocity is illustrated in Fig. 10 at a constant baffle height of h* = 0.15. The results showed that increasing the oscillating velocity from ω = 5 to 15 caused to increase in the heated and cold fluids inside the enclosing cavity due to increasing velocity of the nanofluid neighboring the upper oscillation wall. Furthermore, elevating oscillating velocity leads to increasing the streamline function in the upper zone of the cavity due to the oscillating motion of the fluids in this region.
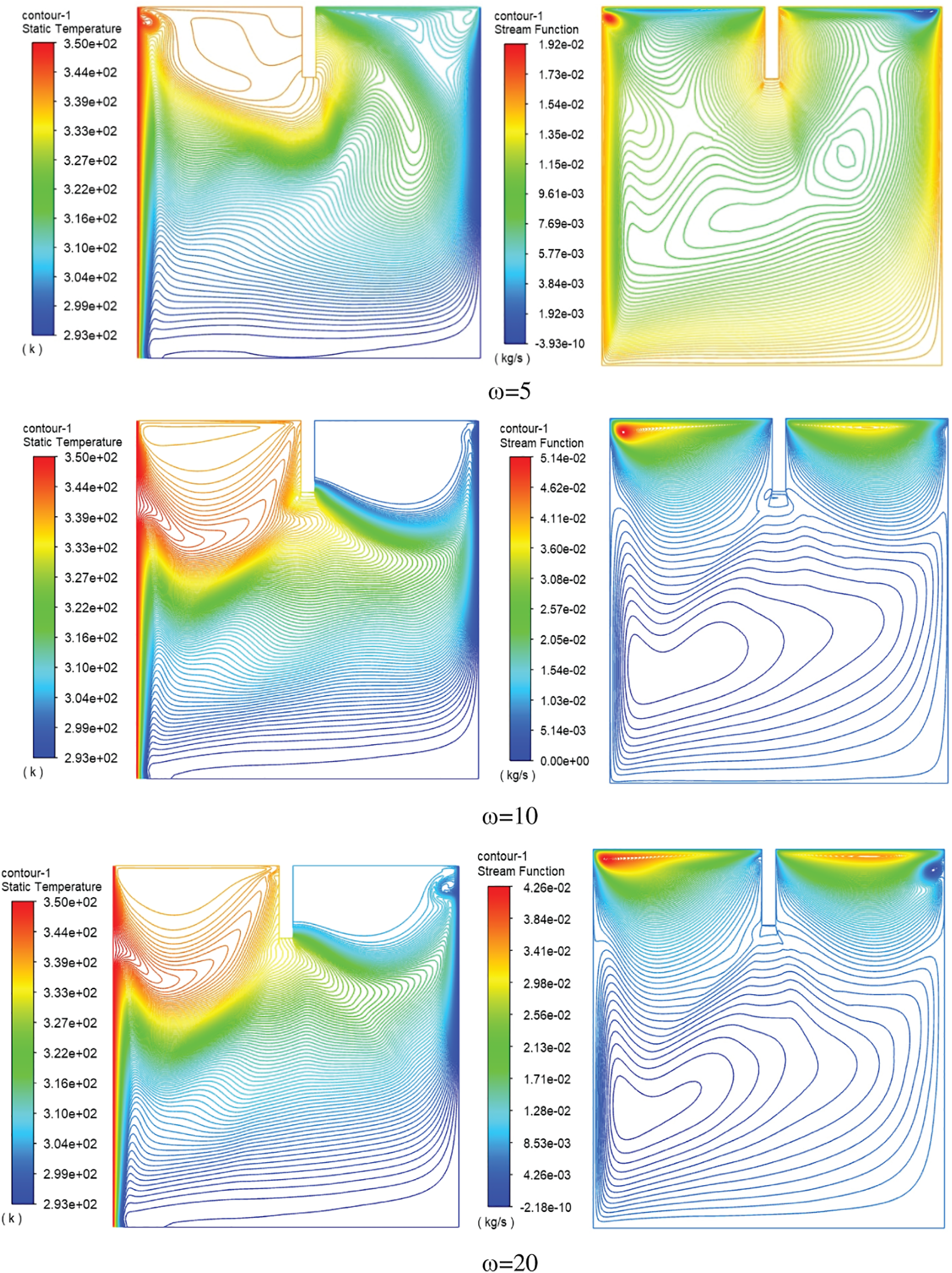
Figure 10: Isotherms (left) and Streamlines (right) for water inside square cavity with rectangular baffle along moving top wall with various oscillation velocities
3.4 Effect of Using Nanofluids
Nanofluids are a mixture of water and metal particles that are used to enhance the water’s thermal properties. In the present study, three categories of fluid suspensions containing nanoparticles were employed (Al2O3, TiO2, and CuO-water nanofluids) with three nanoparticle concentrations of (0.4, 0.8, and 1.0 vol. %). Isotherms (left) and Streamlines (right) for Al2O3, CuO, and TiO2-water in a cavity with a rectangular baffle along the moving top wall plotted in Figs. 11–13, respectively.
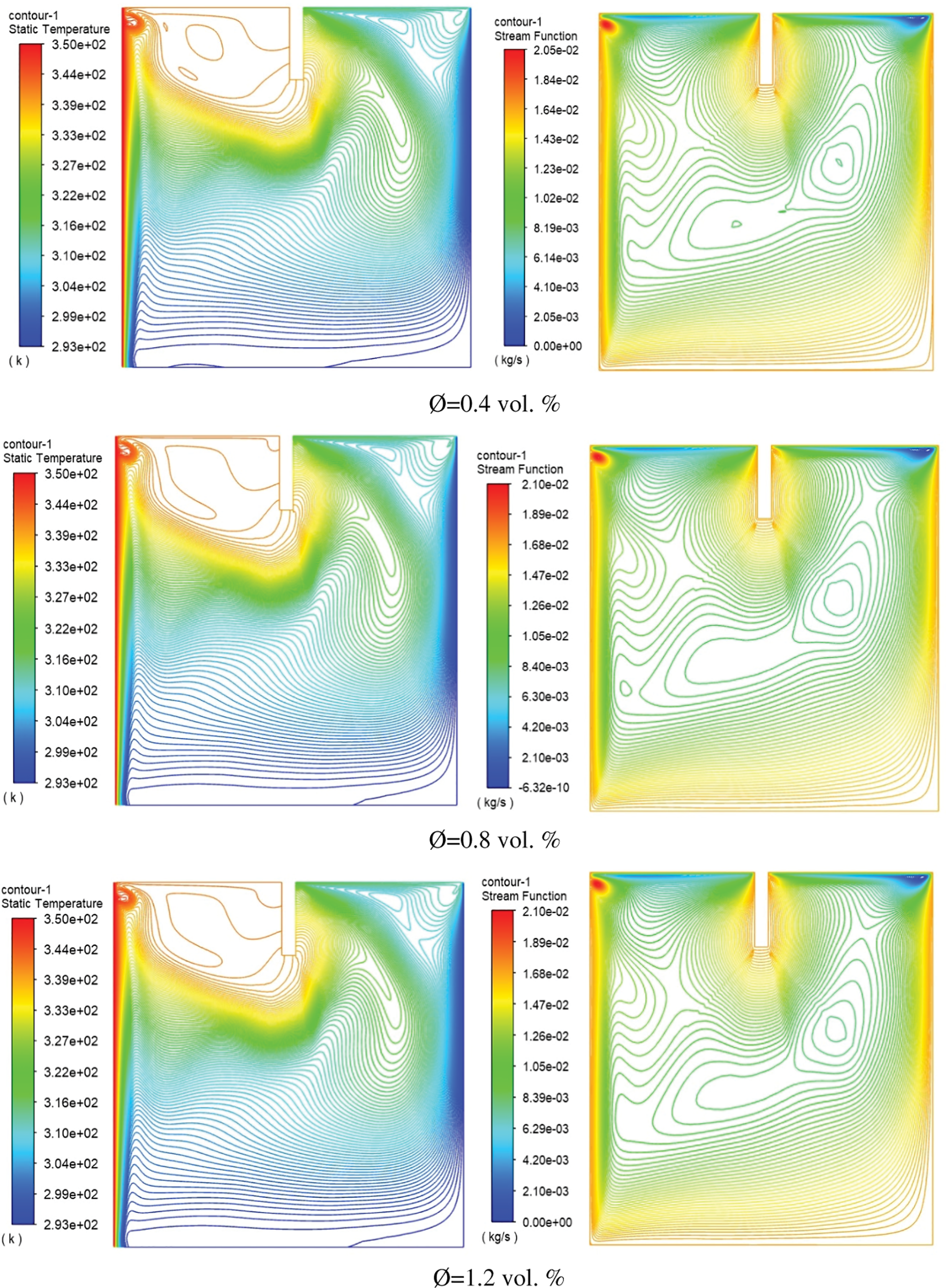
Figure 11: Isotherms (left) and Streamlines (right) for Al2O3-water nanofluid inside square cavity with rectangular baffle along moving top wall with oscillation
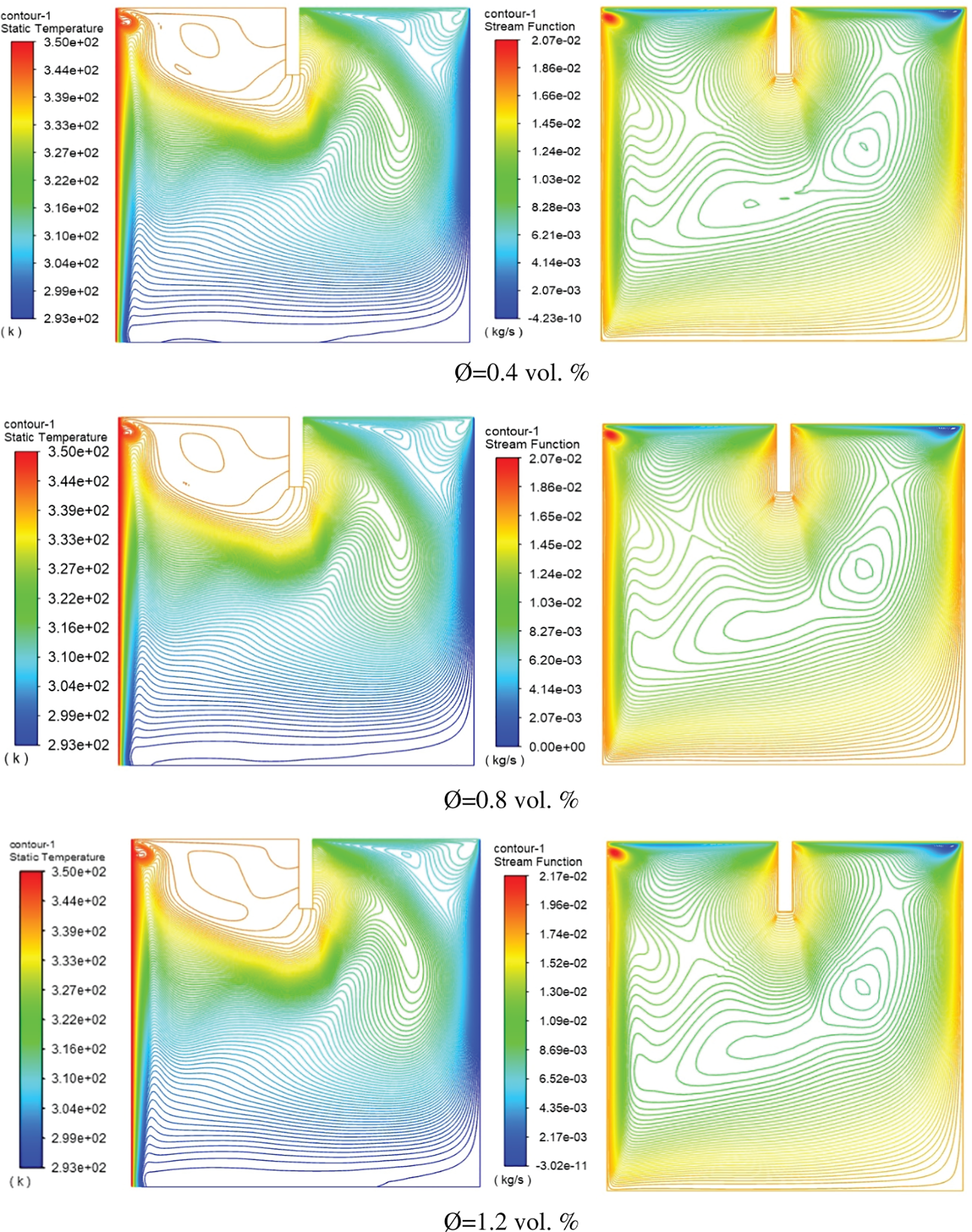
Figure 12: Isotherms (left) and Streamlines (right) for CuO-water nanofluid inside square cavity with rectangular baffle along moving top
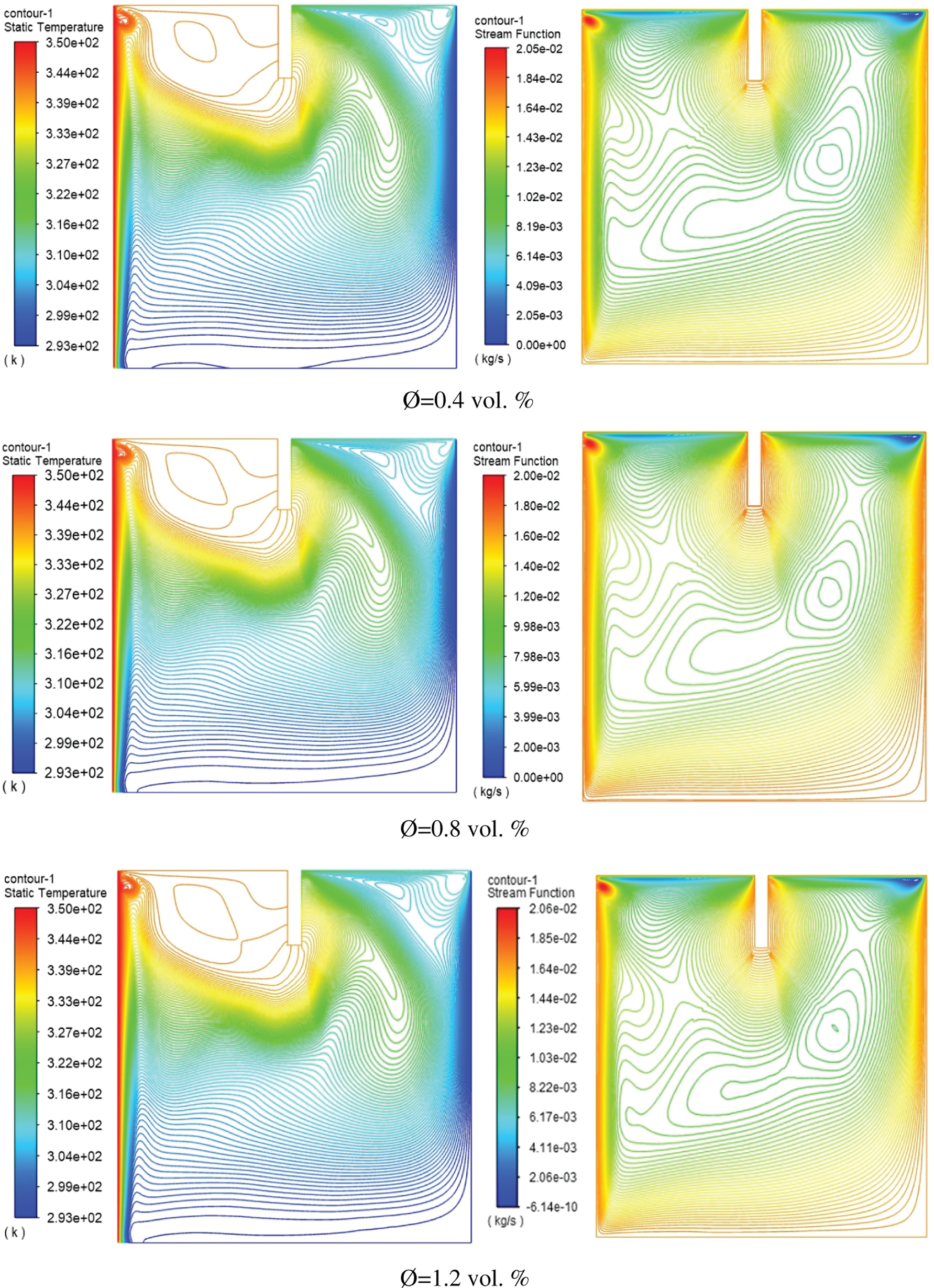
Figure 13: Isotherms (left) and Streamlines (right) for TiO2-water nanofluid inside square cavity with rectangular baffle along moving top wall
In general, the figures demonstrated that the effect of using different nanofluids will lead to creating a small vorticity within the area situated between the baffle and the heated wall and lead to increasing the rate of thermal exchange between the heated and cold wall. Using CuO–water nanofluid instead of Al2O3 will lead to increasing the maximum stream function from 2.05e–02 to 2.07e–02 because of the low viscosity of the fluid used later. Furthermore, for volume fraction increasing from 0.4 to 1.2 vol. %, the temperature isothermal profile will be changed and the heated plume will increase toward the cold surfaces. The stream function increased from 2.05 × 10−2 to 2.10 × 10−2 when increasing the fraction of volume from 0.4 to 0.8 vol. %. Fig. 14 displays the effect of changes in baffle height on the distribution of y-velocity distribution sideways the cavity centerline (x/W = 0.5). The figure explains that increasing the baffle height ratio will impact the velocity profile, especially near the oscillating upper wall. The maximum y-velocity found in the case of h* = 0.25 due to increasing the baffle height led to reaching the central axis of the enclosed cavity. Moreover, the impact of increasing the oscillating velocity (w) on the centerline y-velocity is plotted in Fig. 15. The consequences presented that more oscillating of fluid around centerline due to increasing the oscillation velocity. And the maximum inversed velocity was about (−0.0006 m/s) at an oscillating velocity of (w = 20).
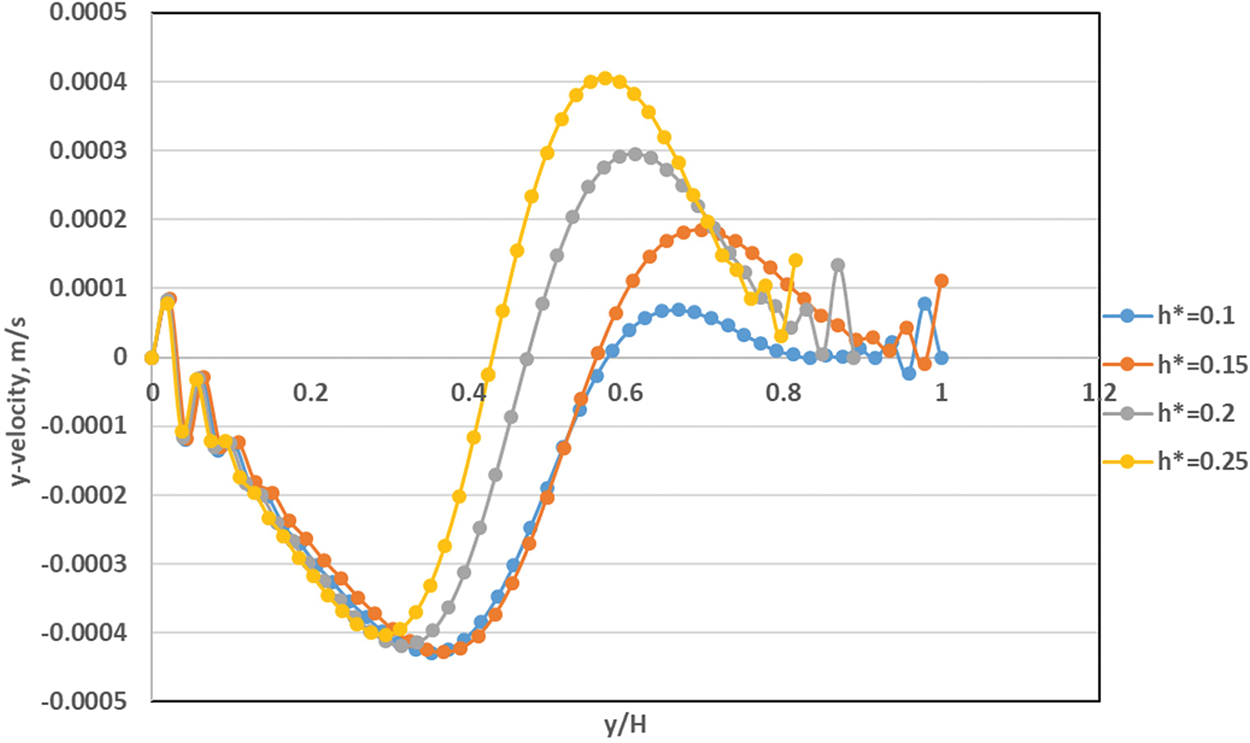
Figure 14: Variation of y-velocity for different baffle height ratios for Al2O3-water nanofluid inside square cavity with rectangular baffle along moving top wall
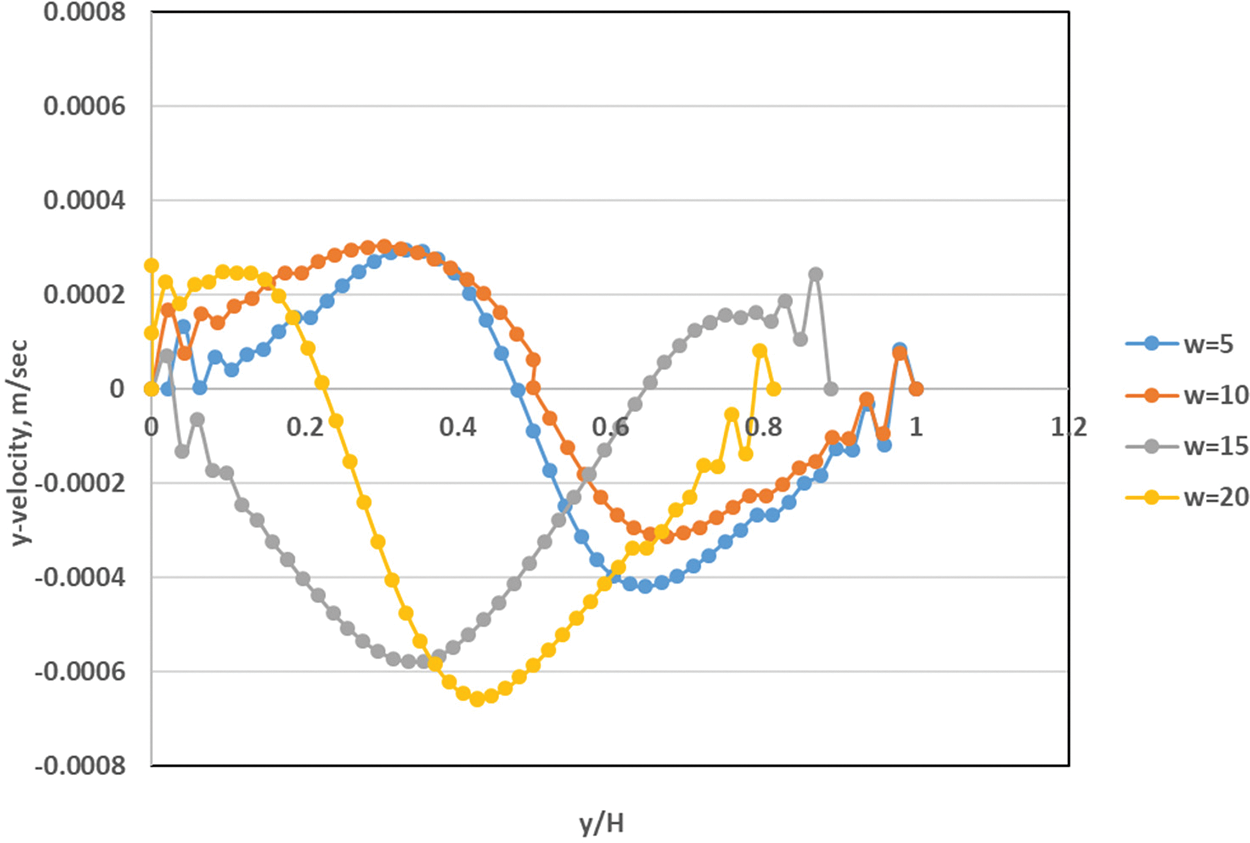
Figure 15: Variation of y-velocity for different oscillating velocities for Al2O3-water nanofluid inside square cavity with rectangular baffle along moving top wall
The chief of present study focus is to examine the effects of the attached baffle upon the upper oscillating wall in the enclosed cavity on the improvement in convective heat transfer by utilizing three types of nanofluids. Figs. 16–18 present the effect of baffle height ratio, oscillating velocity, and concentration of nanoparticles, respectively, on the Nu. The outcomes indicated that augmenting the baffle height ratio increased the Nu adjacent to the bottom wall. This will lead to the rise of nanofluid momentum and thermal behavior rate along the oscillating top oscillation wall leading to increasing moving of fluid near the upper wall of the lid-driven. Also, The Nusselt number value exhibited an increase as the the oscillation velocity near the oscillating upper wall by about 60% when applying an oscillating velocity of (w = 20). Moreover, using different nanofluids with three volumes of the fraction of (0.4, 0.8, and 1.2 vol. %) will prime to increasing the Nu values along the left surface by about (10%), (7%) and (5%) when using the nanofluid of (nanofluids of Al2O3, CuO and TiO2-water) at volume fraction of (Ø = 1.2 vol. %) instead of using water at nanoparticles concentration of (Ø = 0.0 vol. %). The highest value of Nusselt number is obtain in Al2O3–water nanofluids outstanding for increasing the nanofluids thermal conductivity.
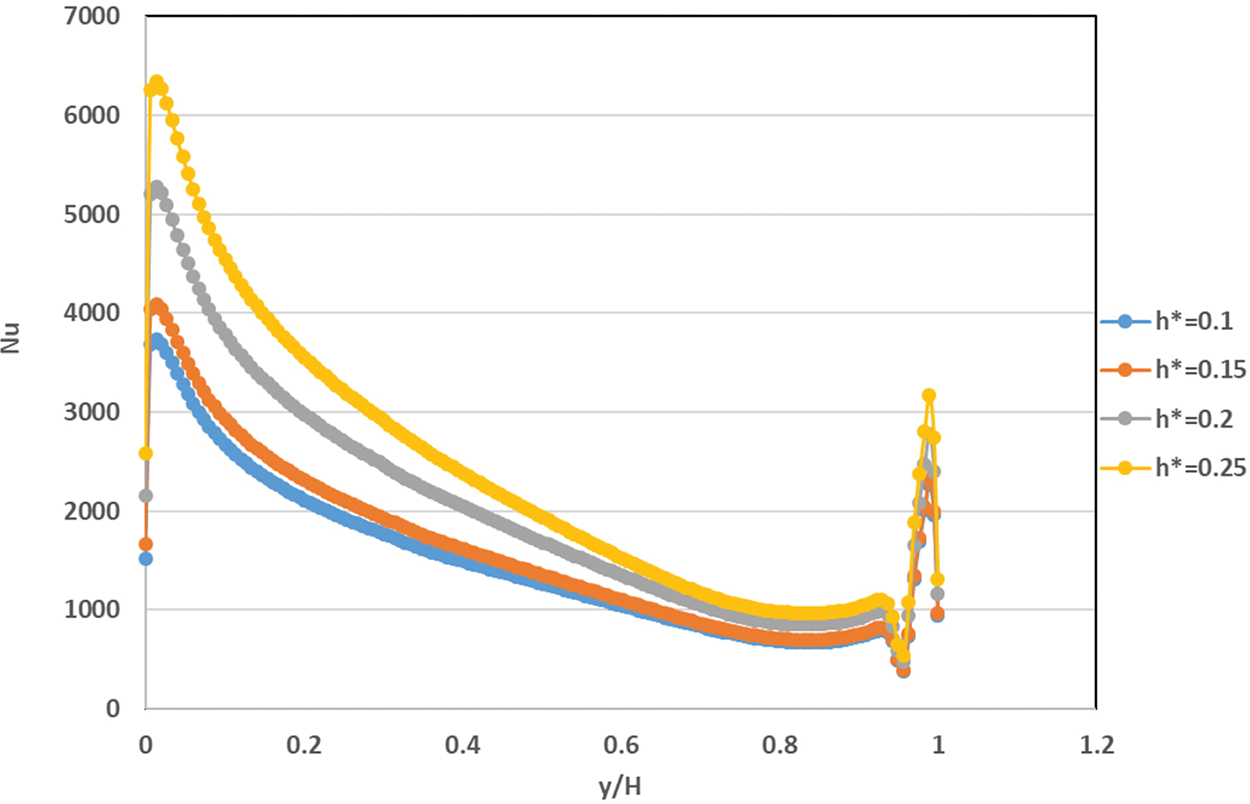
Figure 16: Variations in the Nusselt number for various baffle height ratios for Al2O3-water nanofluid inside square cavity with rectangular baffle along moving top wall
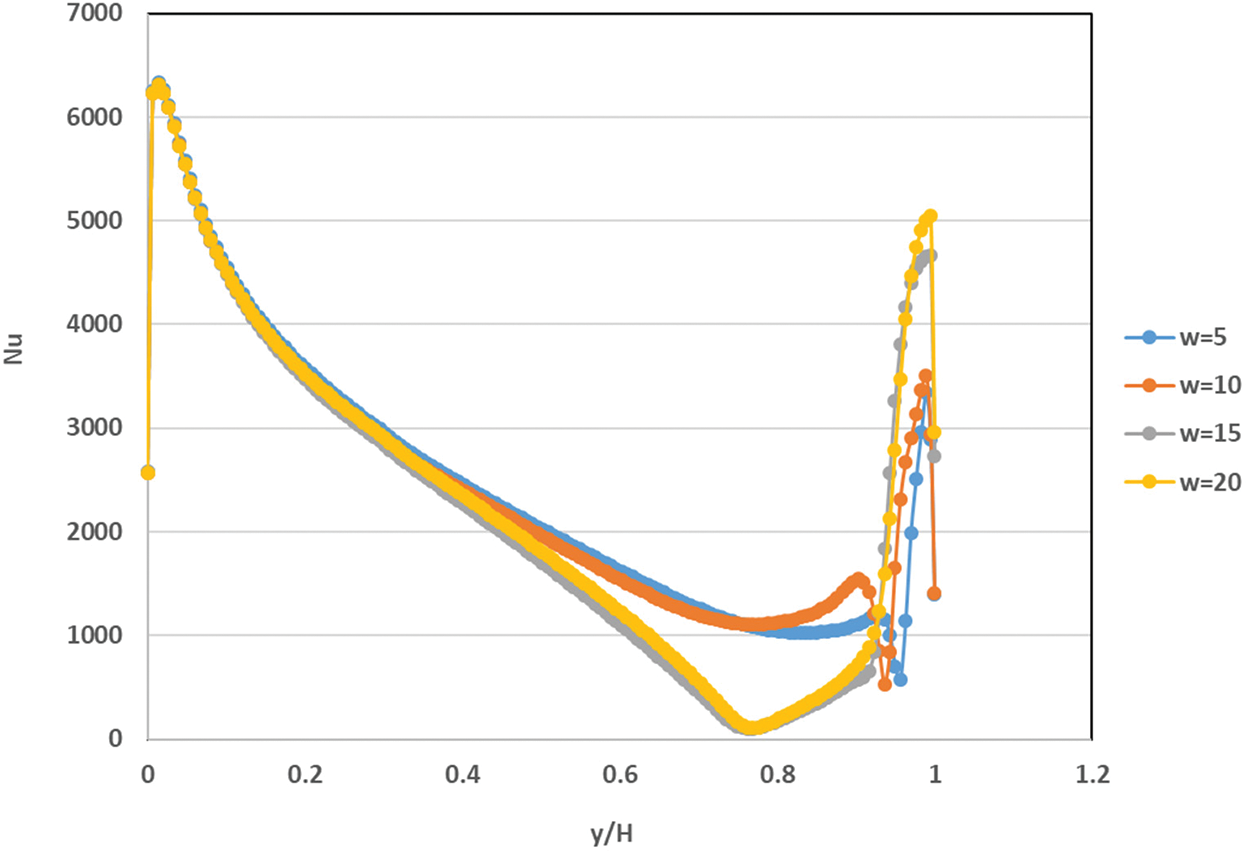
Figure 17: Variations in the Nusselt number for various oscillating velocity for Al2O3-water nanofluid inside the cavity with rectangular baffle along moving top wall
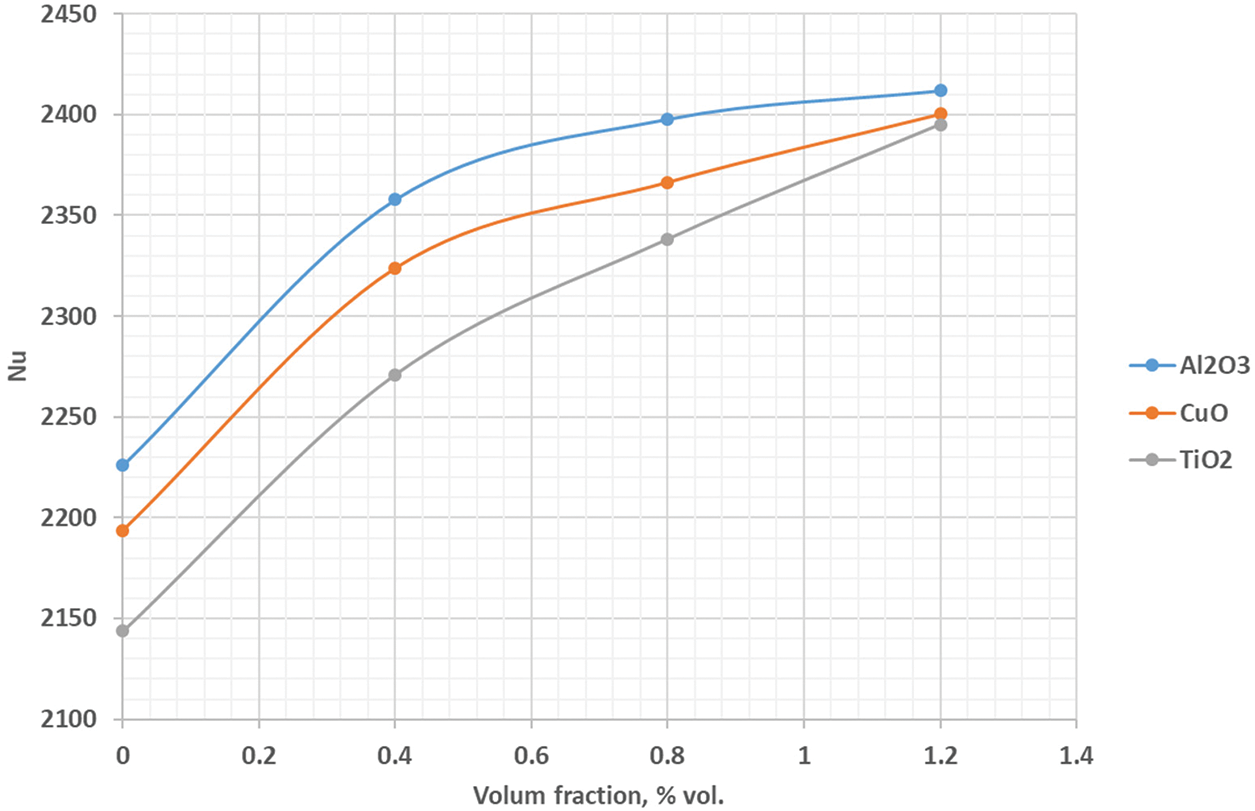
Figure 18: The influence of different nanofluids on the Nu inside the cavity with rectangular baffle along moving top wall
The study of thermal behavior and nanofluid flow by forced convection in a square cavity with an oscillating upper surface with an attached baffle at a variable height ratio (h*) was presented numerically. Different concentrations of nanoparticles (Al2O3, CuO, and TiO2) are used to fill the cavity with nanofluids. The numerical method is employed for numerical simulation. The current study describes the dependence of the thermal behavior and nanofluids flow field performance in an upper-sided oscillating lid-driven cavity concerning the parameters (h*, Re,
Acknowledgement: The authors gratefully acknowledge the Middle Technical University and University of Technology-Iraq for supporting this work.
Funding Statement: The authors received no specific funding for this work.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kadhum Audaa Jehhef, Ali J. Ali, Akram H. Abed; analysis and interpretation of results: Kadhum Audaa Jehhef, Salah H. Abid Aun, Ali J. Ali; draft manuscript preparation: Kadhum Audaa Jehhef, Salah H. Abid Aun, Akram H. Abed; revising the manuscript critically for important intellectual content: Ali J. Ali, Salah H. Abid Aun; approval of the version of the manuscript to be published: Ali J. Ali, Akram H. Abed.
Availability of Data and Materials: The data supporting the findings of this study are available from the corresponding author (Akram H. Abed) on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhu, J., Holmedal, L. E., Wang, H., Myrhaug, D. (2020). Vortex dynamics and flow patterns in a two-dimensional oscillatory lid-driven rectangular cavity. European Journal of Mechanics-B/Fluids, 79, 255–266. https://doi.org/10.1016/j.euromechflu.2019.09.013 [Google Scholar] [CrossRef]
2. Soh, W. Y., Goodrich, J. W. (1988). Unsteady solution of incompressible Navier-Stokes equations. Journal of Computational Physics, 79(1), 113–134. https://doi.org/10.1016/0021-9991(88)90007-1 [Google Scholar] [CrossRef]
3. Jehhef, K. A., Ali, A. J. (2021). Numerical investigation of interaction between saccular abdominal aortic aneurysms and arterial bifurcations. International Journal Bioautomation, 25(3), 209–224. https://doi.org/10.7546/ijba [Google Scholar] [CrossRef]
4. Vogel, M. J., Hirsa, A. H., Lopez, J. M. (2003). Spatio-temporal dynamics of a periodically driven cavity flow. Journal of Fluid Mechanics, 478, 197–226. https://doi.org/10.1017/S002211200200349X [Google Scholar] [CrossRef]
5. Ghia, U. G., Ghia, K. N., Shin, C. T. (1982). High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. Journal of Computational Physics, 48(3), 387–411. https://doi.org/10.1016/0021-9991(82)90058-4 [Google Scholar] [CrossRef]
6. Godson, L., Raja, B., Lal, D. M., Wongwises, S. A. (2010). Enhancement of heat transfer using nanofluids—An overview. Renewable and Sustainable Energy Reviews, 14(2), 629–641. https://doi.org/10.1016/j.rser.2009.10.004 [Google Scholar] [CrossRef]
7. Iwatsu, R., Hyun, J. M., Kuwahara, K. (1992). Numerical simulation of flows driven by a torsionally oscillating lid in a square cavity. Journal of Fluids Engineering, 114(2), 143–151. https://doi.org/10.1115/1.2910008 [Google Scholar] [CrossRef]
8. Hu, Y., He, Y., Qi, C., Jiang, B., Schlaberg, H. I. (2014). Experimental and numerical study of natural convection in a square enclosure filled with nanofluid. International Journal of Heat and Mass Transfer, 78, 380–392. https://doi.org/10.1016/j.ijheatmasstransfer.2014.07.001 [Google Scholar] [CrossRef]
9. Pourmahmoud, N., Ghafouri, A., Mirzaee, I. (2015). Numerical study of mixed convection heat transfer in lid-driven cavity utilizing nanofluid: Effect of type and model of nanofluid. Thermal Science, 19(5), 1575–1590. https://doi.org/10.2298/TSCI120718053P [Google Scholar] [CrossRef]
10. Jmai, R., Ben-Beya, B., Lili, T. (2016). Numerical analysis of mixed convection at various walls speed ratios in two-sided lid-driven cavity partially heated and filled with nanofluid. Journal of Molecular Liquids, 221, 691–713. https://doi.org/10.1016/j.molliq.2016.05.076 [Google Scholar] [CrossRef]
11. Minea, A. A., Lorenzini, G. (2017). A numerical study on ZnO based nanofluids behavior on natural convection. International Journal of Heat and Mass Transfer, 114, 286–296. https://doi.org/10.1016/j.ijheatmasstransfer.2017.06.069 [Google Scholar] [CrossRef]
12. Goqo, S. P., Mondal, H., Sibanda, P., Motsa, S. S. (2019). A multivariate spectral quasilinearisation method for entropy generation in a square cavity filled with porous medium saturated by nanofluid. Case Studies in Thermal Engineering, 14, 100415. https://doi.org/10.1016/j.csite.2019.100415 [Google Scholar] [CrossRef]
13. Shah, Z., Sheikholeslami, M., Kumam, P. (2020). Influence of nanoparticles inclusion into water on convective magneto hydrodynamic flow with heat transfer and entropy generation through permeable domain. Case Studies in Thermal Engineering, 21, 100732. https://doi.org/10.1016/j.csite.2020.100732 [Google Scholar] [CrossRef]
14. Wong, H. F., Ahmad, N., Siri, Z., Noor, N. M. (2021). Viscous heating and cooling process in a mixed convection cavity with free-slip effect. Case Studies in Thermal Engineering, 28, 101349. https://doi.org/10.1016/j.csite.2021.101349 [Google Scholar] [CrossRef]
15. Aun, S. H. A., Ghadhban, S. A., Jehhef, K. A. (2021). Experimental and numerical investigation of convection heat transfer in an enclosure with a vertical heated block and baffles. Journal of Thermal Engineering, 7(3), 367–386. https://doi.org/10.18186/thermal.878156 [Google Scholar] [CrossRef]
16. Al-Farhany, K., Al-Muhja, B., Ali, F., Khan, U., Zaib, A. et al. (2022). The baffle length effects on the natural convection in nanofluid-filled square enclosure with sinusoidal temperature. Molecules, 27(14), 4445. https://doi.org/10.3390/molecules27144445 [Google Scholar] [PubMed] [CrossRef]
17. Alsabery, A. I., Vaezi, M., Tayebi, T., Hashim, I., Ghalambaz, M. et al. (2022). Nanofluid mixed convection inside wavy cavity with heat source: A non-homogeneous study. Case Studies in Thermal Engineering, 34, 102049. https://doi.org/10.1016/j.csite.2022.102049 [Google Scholar] [CrossRef]
18. Shehata, A. I., Dawood, M. M. K., Amer, M., William, M. A. (2023). Enhancement of mixed convection in a lid driven enclosure based on magnetic field presence with nanofluid. Advances in Mechanical Engineering, 15(2). https://doi.org/10.1177/16878132231157184 [Google Scholar] [CrossRef]
19. Pordanjani, A. H., Jahanbakhshi, A., Nadooshan, A. A., Afrand, M. (2018). Effect of two isothermal obstacles on the natural convection of nanofluid in the presence of magnetic field inside an enclosure with sinusoidal wall temperature distribution. International Journal of Heat and Mass Transfer, 121, 565–578. https://doi.org/10.1016/j.ijheatmasstransfer.2018.01.019 [Google Scholar] [CrossRef]
20. Zheng, Y., Yaghoubi, S., Dezfulizadeh, A., Aghakhani, S., Karimipour, A. et al. (2020). Free convection/radiation and entropy generation analyses for nanofluid of inclined square enclosure with uniform magnetic field. Journal of Thermal Analysis and Calorimetry, 141(1), 635–648. https://doi.org/10.1007/s10973-020-09497-y [Google Scholar] [CrossRef]
21. Berrahil, F., Filali, A., Abid, C., Benissaad, S., Bessaih, R. et al. (2021). Numerical investigation on natural convection of Al2O3/water nanofluid with variable properties in an annular enclosure under magnetic field. International Communications in Heat and Mass Transfer, 126, 105408. https://doi.org/10.1016/j.icheatmasstransfer.2021.105408 [Google Scholar] [CrossRef]
22. Yan, S. R., Pordanjani, A. H., Aghakhani, S., Goldanlou, A. S., Afrand, M. (2020). Effect of nano powder shapes on natural convection of nanofluids inside a square enclosure in presence of fins with different shapes and magnetic field effect. Advanced Powder Technology, 31(7), 2759–2777. https://doi.org/10.1016/j.apt.2020.05.009 [Google Scholar] [CrossRef]
23. Al-Kouz, W., Aissa, A., Koulali, A., Jamshed, W., Moria, H. et al. (2021). MHD darcy-forchheimer nanofluid flow and entropy optimization in an odd-shaped enclosure filled with a (MWCNT-Fe3O4/water) using galerkin finite element analysis. Scientific Reports, 11(1), 22635. https://doi.org/10.1038/s41598-021-02047 [Google Scholar] [CrossRef]
24. Mehryan, S. M., Izadi, M., Chamkha, A. J., Sheremet, M. A. (2018). Natural convection and entropy generation of a ferrofluid in a square enclosure under the effect of a horizontal periodic magnetic field. Journal of Molecular Liquids, 263, 510–525. https://doi.org/10.1016/j.molliq.2018.04.119 [Google Scholar] [CrossRef]
25. Izadi, M., Mohebbi, R., Sajjadi, H., Delouei, A. A. (2019). LTNE modeling of Magneto-Ferro natural convection inside a porous enclosure exposed to nonuniform magnetic field. Physica A: Statistical Mechanics and its Applications, 535, 122394. https://doi.org/10.1016/j.physa.2019.122394 [Google Scholar] [CrossRef]
26. Hussain, M., Vasu, B.,Chamkha, A. J. (2023). A review study of numerical simulation of lid-driven cavity flow with nanofluids. Journal of Nanofluids, 12, 589–604. https://doi.org/10.1166/jon.2023.1930 [Google Scholar] [CrossRef]
27. Hussain, M., Naeem, M. N. (2017). Vibration analysis of single-walled carbon nanotubes using wave propagation approach. Mechanical Sciences, 8(1), 155–164. https://doi.org/10.5194/ms-8-155-2017 [Google Scholar] [CrossRef]
28. Rashed, M. K., Jehhef, K. A., Badawy, F. A. (2022). Numerical study on thermal performance of water flow in a twisted duct heat exchanger. International Journal of Applied Mechanics and Engineering, 27(2), 199–216. https://doi.org/10.2478/ijame-2022-0028 [Google Scholar] [CrossRef]
29. Jehhef, K. A., Rasheed, M. K., Siba, M. A. (2023). Numerical simulation of the oscillating thin plate impact on nanofluids flow in channel. Chemical Industry and Chemical Engineering Quarterly, 30(2), 123–133. [Google Scholar]
30. Jehhef, K. A., Badawy, F. A., Hussein, A. A. (2021). Thermal performance enhancement of the mixed convection between two parallel plates by using triangular ribs. International Journal of Applied Mechanics and Engineering, 26(2), 11–30. https://doi.org/10.2478/ijame-2021-0017 [Google Scholar] [CrossRef]
31. Tiwari, R. K., Das, M. K. (2007). Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of Heat and Mass Transfer, 50(9–10), 2002–2018. [Google Scholar]
32. Brinkman, H. C. (1952). The viscosity of concentrated suspensions and solutions. The Journal of Chemical Physics, 20(4), 571. https://doi.org/10.1063/1.1700493 [Google Scholar] [CrossRef]
33. Pak, B. C., Cho, Y. I. (1998). Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Experimental Heat Transfer, 11(2), 151–170. https://doi.org/10.1080/08916159808946559 [Google Scholar] [CrossRef]
34. Xuan, Y., Roetzel, W. (2000). Conceptions for heat transfer correlation of nanofluids. International Journal of Heat and Mass Transfer, 43(19), 3701–3707. https://doi.org/10.1016/S0017-9310(99)00369-5 [Google Scholar] [CrossRef]
35. Maı̈ga, S. E. B., Nguyen, C. T., Galanis, N., Roy, G. (2004). Heat transfer behaviours of nanofluids in a uniformly heated tube. Superlattices and Microstructures, 35(3–6), 543–557. [Google Scholar]
36. Maxwell, J. C. (1873). A treatise on electricity and magnetism, vol. 1. Oxford University, UK: Clarendon Press. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools