Cross-Diffusion Effects on an MHD Williamson Nanofluid Flow Past a Nonlinear Stretching Sheet Immersed in a Permeable Medium

Nomenclature

1  Introduction

Newton’s law of viscosity, which asserts that shear stress and shear rate must be inversely proportional, is infringed by non-Newtonian fluids. The viscosity of non-Newtonian fluids fluctuates with the rate of shear or shear stress. This demonstrates that the fluid’s resistance to flow varies depending on the conditions under which it flows. There are several types of non-Newtonian fluids, each with its distinct flow characteristics such as pseudoplastic fluids-toothpaste, ketchup, paints, dilatant fluids-a mixture of cornstarch and water, often called oobleck, Bingham plastic fluids-drilling muds, visco-elastic fluids-slime, polymer solutions, and human mucus. Magnetohydrodynamics (MHD) is an integrative discipline dedicated to investigating the properties of conducting fluids in the context of magnetic fields by combining fluid dynamics with electromagnetic concepts. It has several applications ranging from astronomy to engineering. Raju et al. [1] examined the flow of a chemically reacting fluid via an inclined vertical permeable moving plate in an unsteady MHD fluid flow. Many more studies have been drawn to this field of study [2,3].

In recognition of its many potential applications in industry, the boundary layer flow of such fluids is gaining prominence. The Naiver-Stokes equations alone are insufficient for determining and enhancing the rheological properties of materials. One of the most elegant non-Newtonian techniques for circumventing this hindrance is the Williamson fluid flow model (WFFM). The WFFM is based on a power-law relationship between the shear stress (τ) and the shear rate (γ˙) as of the form τ=η0(γ˙)n. The power-law index (n) determines the degree of shear-thinning or shear-thickening behavior. For n<1, the fluid exhibits shear-thinning, while for n>1, it exhibits shear-thinning. The consistency index (η0) represents the fluid’s resistance to flow and is related to the viscosity of the fluid at low shear rates. The viscosity of the Williamson fluid is not constant but depends on the shear rate. As the shear rate increases, the viscosity decreases for shear-thinning behavior. The WFFM can capture both shear-thinning and shear-thickening behavior by adjusting n, which finds applications in various engineering processes, particularly those involving non-Newtonian fluids with shear-thinning behavior. This versatility makes it suitable for describing a wide range of non-Newtonian fluids that exhibit different rheological behaviors under varying flow conditions. The WFFM is primarily empirical and is based on fitting experimental data. It is not derived from fundamental principles but rather formulated to provide a mathematical description of observed shear-rate-dependent viscosity. The mathematical form of the WFFM is relatively simple, making it easy to use and interpret. This simplicity facilitates analytical solutions and is advantageous for applications where computational efficiency is essential. Examples include polymer processing, food manufacturing, and pharmaceutical production. Nadeem et al. [4] investigated the Williamson fluid flow (WWF) over a stretching sheet. Megahed [5] examined the effects of viscous dissipation and thermal radiation of the WFF due to a nonlinear stretching sheet. Bibi et al. [6] analyzed numerically the heat transfer in the presence of an MHD WFF through a permeable stretching sheet. Salahuddin et al. [7] explored the Cattaneo-Christov heat and mass transfer analysis of dissipated Williamson fluid with double stratification.

Nanofluids possess several characteristics that make them suitable for various industrial applications which include enhanced thermal conductivity, increased heat transfer efficiency, improved lubrication and wear resistance, stability and suspension of nanoparticles, tailored properties by selecting different nanoparticles and base fluids, compatibility with existing systems and potential for multi-functionality. The use of nanofluids in industrial applications offers several advantages due to the unique properties of nanoparticles at the nanoscale. Some key industrial applications of nanofluids are heat transfer and cooling systems, lubrication and wear resistance, oil and gas extraction, aerospace and rocket propulsion, solar thermal energy, electronic cooling, and biomedical applications, etc.

When nanoparticles are incorporated into the Williamson base fluid, their properties change, leading to improved heat transmission and other desired features. Williamson nanofluid flow (WNFF) has an extensive scope of industrial applications, encompassing heat transfer improvement, electronics cooling, solar thermal systems, lubrication and machining, biomedical applications, and so on. Nadeem et al. [8] illustrated the heat transfer analysis of a WNFF. Bhatti et al. [9] investigated the combined implications of thermo-diffusion and heat radiation on a porous stretched sheet filled with WNFF. Reddy et al. [10] investigated the MHD WNFF over a stretched sheet with variable thickness and diverse thermal conductivity to transfer mass and heat in the presence of radiation. Mabood et al. [11] used a finite difference approach to explore the MHD WNFF on a perpetually shifting heated surface to study the impacts of thermal radiation and heat source. Mebarek-Oudina et al. [12] analyzed the hydromagnetic flow of magnetite-water nanofluid utilizing an adapted Buongiorno model. Ramesh et al. [13] illustrated the computational analysis of the magnetic properties of a radiative nano Carreau fluid flow in a microchannel. Abbas et al. [14] explored the effects of heat generation and viscous dissipation of an MHD WNFF past a nonlinear stretching sheet immersed in a porous medium. Plenty of scholars enlightened their study on this globally vital problem in such a captivating manner [15–24].

Because of their unusual mechanical properties, nonlinear stretching sheets, also known as nonlinearly elastic membranes or nonlinearly deformable surfaces, offer a wide range of lucrative uses. A nonlinear stretching sheet is a mathematical model that describes the behavior of a stretching sheet or surface when the tension or stretching force is not exactly proportional to the displacement. This simulation is frequently employed for researching fluid dynamics and heat transport in a range of engineering processes. Das [25] addressed the partial slip of the boundary layer flow of a nanofluid at an ordained surface temperature across a nonlinear stretching sheet (NLSS). Bilal et al. [26] collaborated to detect the MHD 3D boundary layer flow of a Williamson fluid confined by a bidirectional nonlinear stretched membrane (NLSS). Abo-Dahab et al. [27] investigated the effect of suction/injection on an MHD Casson nanofluid flow over NLSS in a heated porous medium. The study carried out by Hayat et al. [28] explored the magnetohydrodynamic (MHD) boundary layer flow of Powell-Eyring nanofluid across a nonlinear stretching sheet with varying thickness. Qayyam et al. [29] sought an MHD third-grade nanofluid across a nonlinear stretching material that differed by thickness with effects of the heat radiation and chemical reaction. It has a broad spectrum of usages in industry, including stretching electronics, packing and wrapping, energy harvesting, robotics, and soft robotics. In recent decades, many more investigations have explored fascinatingly on this research area [30–36].

The implications of Soret and Dufour are two important transfers of mass and heat mechanisms in hydraulic systems. The Soret effect, popularly referred to as thermal diffusion, lays out how a species’ concentration in a mixture affects temperature dispersion. The Dufour effect, formerly referred to as thermal diffusion of momentum, is an aberration that stresses mass flow in the direction of a temperature gradient when there is a disparity in temperature in a fluid system. Hayat et al. [37] apparent the heat and mass transfer through natural convection to detect the impacts of the chemical reaction, Soret and dufour effects from vertical surfaces in a permeable medium. In the inclusion of magnetic nanoparticles, Postelnicu et al. [38] inquired about the effects of Soret and Dufour over fluid flow on a vertically stretched sheet due to multiple slips. Seid et al. [39] focused on the oscillatory flow of an elevated stress fluid due to a stretchy curved surface along the cross-diffusion impacts. Chemical engineering, combustion, isotope separation, biological sciences, geophysics, and energy conversion benefit substantially from the cross-diffusion effects. Understanding and accounting for these effects in relevant systems allow for improved process design, optimization, and performance research works [40–46].

The motivation for this study was gathered by studying the literature work existing in the references [4–6,14,27] to do the research on the WNFF. The novelty of this research work is to investigate the impacts of the cross-diffusions (Soret and Dufour effects) of an MHD Williamson nanofluid flow past a nonlinearly stretched sheet immersed in a permeable medium. A comprehensive examination of prior research that was published recognizes that no such attempt has ever been made, even though the current study’s range of views and phenomena may be anticipated to result in unusually dynamic interactions across disciplines. The subsequent section goes over the fluid flow model, flow regime, solution strategy, and results display.

2  Fundamental Formulation of the Williamson Fluid Flow

The corresponding equations of continuity and momentum associated with an incompressible Williamson fluid flow are provided using the references [4,6,8] as follows:

divV=0(1)

ρdVdt=divS+ρb(2)

where b is the specific body force vector, V is the velocity, S is the Cauchy stress tensor, ρ is the density and ddt denotes the material time derivative. The Williamson fluid flow model’s structural equations have been established as

S=−pI+τ,(3)

where

τ=[μ∞+μ0−μ∞1−Γγ˙]A1(4)

Here S is the Cauchy stress tensor, p is the pressure, I is the identity vector, τ is an extra tensor, μ∞ is the high shear rate, μ0 is the low-rate shear, Γ is a positive time constant, γ˙ is a shear rate and A1 is the first Rivlin-Ericksen tensor. The shear rate γ˙ is formally defined as

γ˙=∑i∑jγ˙ijγ˙ji=Π2(5)

where

Π=tr(A1)2,(6)

called the strain tensor of the second invariant and the case μ∞=0 is taken into account only and Γγ˙<1. Then the extra tensor evolves into

τ=[μ01−Γγ˙]A1(7)

Using binomial series expansion:

τ=μ0(1+Γγ˙)A1(8)

Also, γ˙=[(∂u∂x)2+12(∂u∂y+∂v∂x)2+(∂v∂y)2]12 and the elements of the extra tensor are represented as

τxx=2μ0(1+Γγ˙)(∂u∂x);τxy=τyx=μ0(1+Γγ˙)(∂u∂y+∂v∂x)

τyy=2μ0(1+Γγ˙)(∂v∂y)and τxz=τyz=τzx=τzz=τzy=0

The component form of the equations of continuity and momentum is represented as

ux+vy=0(9)

ρ(uux+vuy)=−px+∂∂x(τxx)+∂∂y(τxy)(10)

ρ(uvx+vvy)=−py+∂∂x(τyx)+∂∂y(τyy),(11)

3  Mathematical Formulation

The current study examines the characteristics of a two-dimensional, viscous, and incompressible Williamson nanofluid flow past a nonlinear stretching sheet in the region (y>0) with a varying velocity distribution uw(x)=axn. The wall temperature distribution is defined as Tw=T∞+Axn where A>0, T∞ denotes ambient fluid temperature and C∞ is the ambient nanoparticle concentration. Variable magnetic field of intensity B(x)=B0xn−12 is applied in the transverse direction to the fluid flow. The electrical field is omitted whereas the induced magnetic field is disregarded by assuming a low magnetic Reynolds number. The flow direction is along x-axis and the y-axis is normal to the flow. The external magnetic field and the impacts of Soret and Dufour are taken into account. Fig. 1 depicts the physical interpretation of Williamson nanofluid flow.

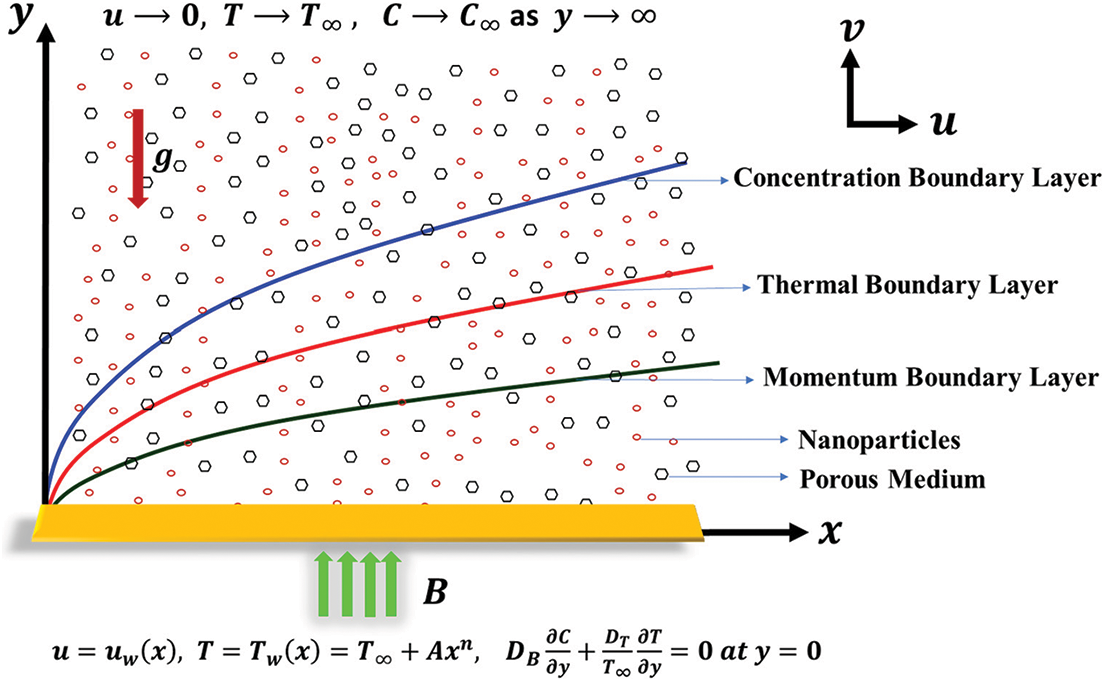
Figure 1: Physical interpretation of the fluid flow

The governing nonlinear partial differential equations of the considered fluid flow phenomena using the references [14,27] are given as

∂u∂x+∂v∂y=0(12)

u∂u∂x+v∂u∂y=ν∂2u∂y2+2νΓ∂u∂y∂2u∂y2−σB2(x)ρu−ν(uk)(13)

u∂T∂x+v∂T∂y=α∂2T∂y2+τ[DB∂T∂y∂C∂y+DTT∞(∂T∂y)2]+DmkTcscp∂2C∂y2(14)

u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2+DmkTTm∂2T∂y2(15)

The pertinent boundary conditions for the defined fluid flow are given as

At y=0:u=uw(x)=axn,v=0,T=Tw(x)=T∞+Axn,DB∂C∂y+DTT∞∂T∂y=0As y⟶∞:u⟶0,T⟶T∞,C⟶C∞}(16)

where u and v are the velocities along x and y directions, B(x)=B0xn−12 is the intensity of the variable magnetic field, τ=(ρC)P(ρC)f is the ratio of effective heat capacity, ν is the kinematic viscosity, α is the thermal diffusivity, k is the porous medium permeability, DT is the thermophoresis coefficient, ρ is the fluid’s density, and DB is the Brownian diffusion coefficient, σ is the electrical conductivity, n is the nonlinear stretching sheet index, Tw is the wall temperature, T∞ is the free stream temperature, Cw is the wall concentration, and C∞ is the free stream concentration.

The following similarity variable transformations [27] are executed to switch the nonlinear PDEs (12) to (15) along their boundary conditions (16) to nonlinear ODEs:

η=aνxn−12y;u=axnf′(η);v=−axn−12νa(n+12f(η)+n−12ηf′(η))

θ(η)=T−T∞Tw−T∞;ϕ(η)=C−C∞Cw−C∞(17)

where θ(η) is the temperature and ϕ(η) is the concentration functions of η, respectively.

After applying the above similarity transformations for the Eqs. (12) to (15), Eq. (12) satisfied identically; the transformed ODEs are provided below in the Eqs. (18) to (20):

f‴+(n+12)ff″−nf′2+Wef′′f‴−(M+K)f′=0(18)

1Prθ″+(n+12)fθ′−nf′θ+Nbθ′ϕ′+Ntθ′2+Duϕ″=0(19)

ϕ″+(n+12)Scfϕ′+(NtNb)θ″+Srθ″=0(20)

The corresponding boundary conditions (16) for the proposed fluid flow becomes

At η=0:f=0,f′=1,θ=1,Nbϕ′+Ntθ′=0As η⟶∞:f′⟶0,ϕ⟶0,θ⟶0}(21)

In the Eqs. (18) to (21), the parameters are defined as Williamson nanofluid parameter We=2Γa32x3n−12ν, magnetic parameter M=σB02aρ, porous parameter K=νakxn−1, Prandtl number Pr=να, Schmidt number Sc=νDB, Brownian motion parameter Nb=τDB(Cw−C∞)ν, thermophoresis parameter Nt=τDT(Tw−T∞)T∞, Dufour parameter Du=DmkTνcscp(Cw−C∞)(Tw−T∞), Soret number Sr=DmkT(Tw−T∞)DBTm(Cw−C∞). We encountered after assessing that the parameters We and K are functions of x. To solve such a circumstance, which yields a non-similar solution to our current problem, we need to non-dimensionalize We with n=13 and K with n=1. As a result, the relevant parameters will become We=2Γa32ν and K=νak.

For the practical study, introducing the new quantities called the skin friction coefficient Cf, the Nusselt number Nux and the Sherwood number Shx, which are interpreted as [14,27]

Cf=τwρuw2,Nux=xqwk(Tw−T∞),Shx=xqmDB(Cw−C∞),

where the wall shear stress τw=μ[(1+Γ2∂u∂y)∂u∂y]y=0, the heat flux qw=−k[∂T∂y]y=0and the mass flux qm=−DB[∂C∂y]y=0. Using the similarity variable transformation in (17), the above Cf,Nux and Shx are transformed as follows:

ReCf=f″(0)[1+Wef″(0)],Nux=−Reθ′(0),Shx=−Reϕ′(0)(22)

where Re=uwxν is the Reynolds number.

4  Solution Methodology

The system of interconnected differential Eqs. (18)–(20) presents a significant analytical obstacle, necessitating the utilization of a numerical approach for resolution. Although numerous numerical methods are available, the Runge Kutta Fehlberg-45 method proves to be particularly efficient when dealing with first-order first-value problems. Therefore, we have chosen to tackle Eqs. (18)–(20) and the corresponding boundary conditions (21) using the shooting technique in conjunction with the RKF-45 scheme. The Newton-Raphson method has been used for initial guesses. The resulting outcomes are subsequently verified by employing the MATHEMATICA-12.0. The procedure for implementing the RKF-45 method and the shooting strategy is outlined in Fig. 2. The fundamental procedures implicated in the conversion of the specified predicament into an initial value problem (IVP) of the first-order can be delineated as follows:

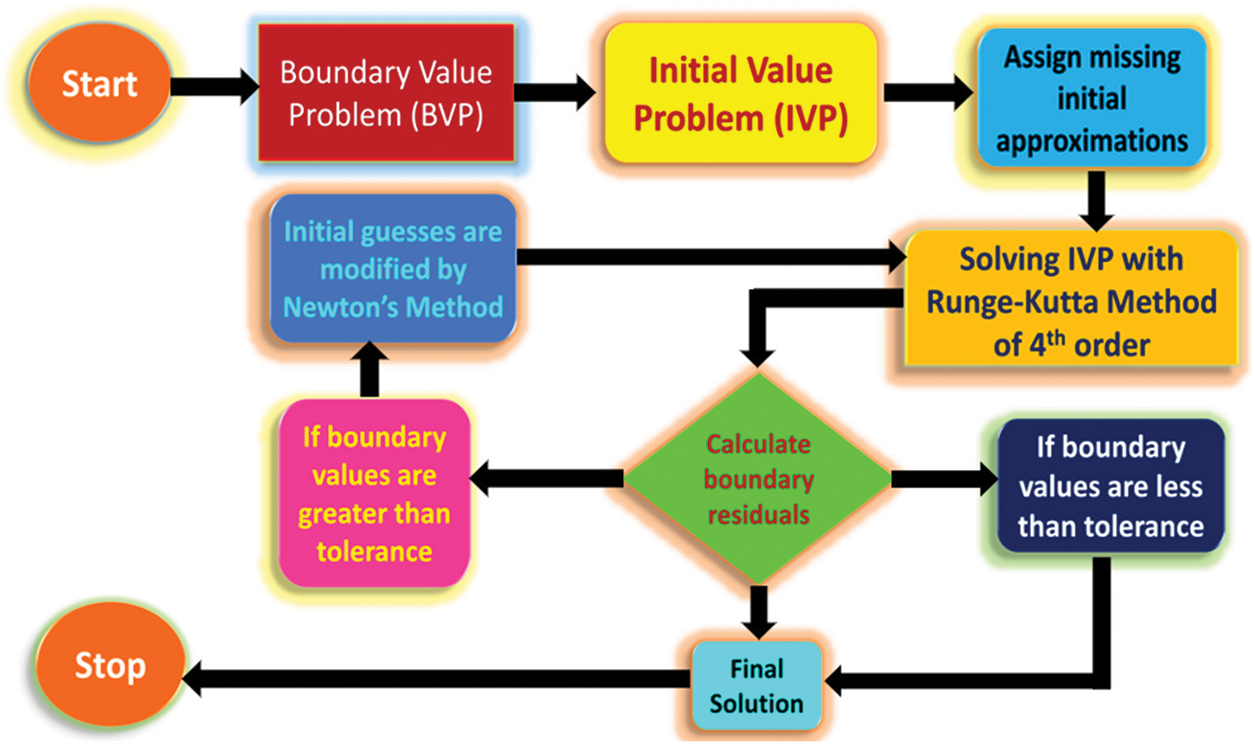
Figure 2: The flow chart for the shooting method

Eqs. (18)–(20) are converted into a system of ODEs by taking the following substitutions:

y1=f,y2=f′,y3=f″ and y4=θ,y5=θ′,y6=ϕ,y7=ϕ′

The formulated initial value problem is given by

y1′=f′=y2(23)

y2′=f″=y3(24)

y3′=−(n+12)y1y3+ny22−Wey3y3′+(M+K)y2(25)

y4′=θ′=y5(26)

y6′=ϕ′=y7(27)

y5′=−Pr(n+12)y1y5+nPry2y4−PrNby5y7−PrNty52−PrDuy7′(28)

y7′=−(n+12)Scy1y7−(NtNb)y5′−Sry5′(29)

The initial conditions are given as

y1(0)=0,y2(0)=1,y3(0)=f″(0)=ε1,y4(0)=1,y5(0)=θ′(0)=ε2,y6(0)=ϕ(0)=ε3,y7(0)=−(NtNb)y5(0)}(30)

The intricate and non-linear differential Eqs. (23)–(29) are efficiently addressed through the robust method of fourth-fifth order RKF. By attaining remarkable convergence, the numerical outcomes exhibit boundary residuals falling below the error threshold of 10−6, facilitated by a step size of Δη=0.001. Commencing with initial approximations (30) along with the unknown values ε1,ε2,ε3 (initial guesses), the Newton method enhances the calculations, persistently iterating with unwavering determination until the desired level of convergence is achieved.

5  Results and Discussion

This section portrays the flow characteristics encountered throughout the flow regime for the computations of the velocity profiles f′(η), temperature profiles θ(η), and mass concentration profiles ϕ(η), for various flow parameters namely Williamson nanofluid parameter We, magnetic parameter M, porous parameter K, Schmidt number Sc, Brownian motion parameter Nb, Prandtl number Pr, Dufour parameter Du, thermophoresis parameter Nt, and Soret number Sr that influence the flow characteristics. Using the strategy of the Runge-Kutta 4th order approach along with the shooting technique, the solution set for the pertinent flow model is accomplished. Asymptotically, the estimated outcomes fulfill the stated boundary conditions, emphasizing the exactitude of the achieved solutions. The limitations of the defined fluid flow problem for the convergence region are 0≤M,K≤0.5,0≤n≤2.5,0≤We≤4.5,0≤Pr≤1.45,0≤Nt≤3.0,0≤Sr≤0.7,0≤Nt,Sc,Du≤0.4. For each of the physical factors stated above, all of the research results are deployed as follows.

Fig. 3a depicts the effects of the Williamson parameter We on the velocity field f′(η), where it proves that f′(η) upsurges as We drops. It is worth noting that the Williamson parameter is the ratio of relaxation time to the retardation time. By dropping the values of We, the retardation time rises, causing fluid particles to take less time to return to their original position, causing viscosity to get lower and hence, the velocity of the fluid escalates.

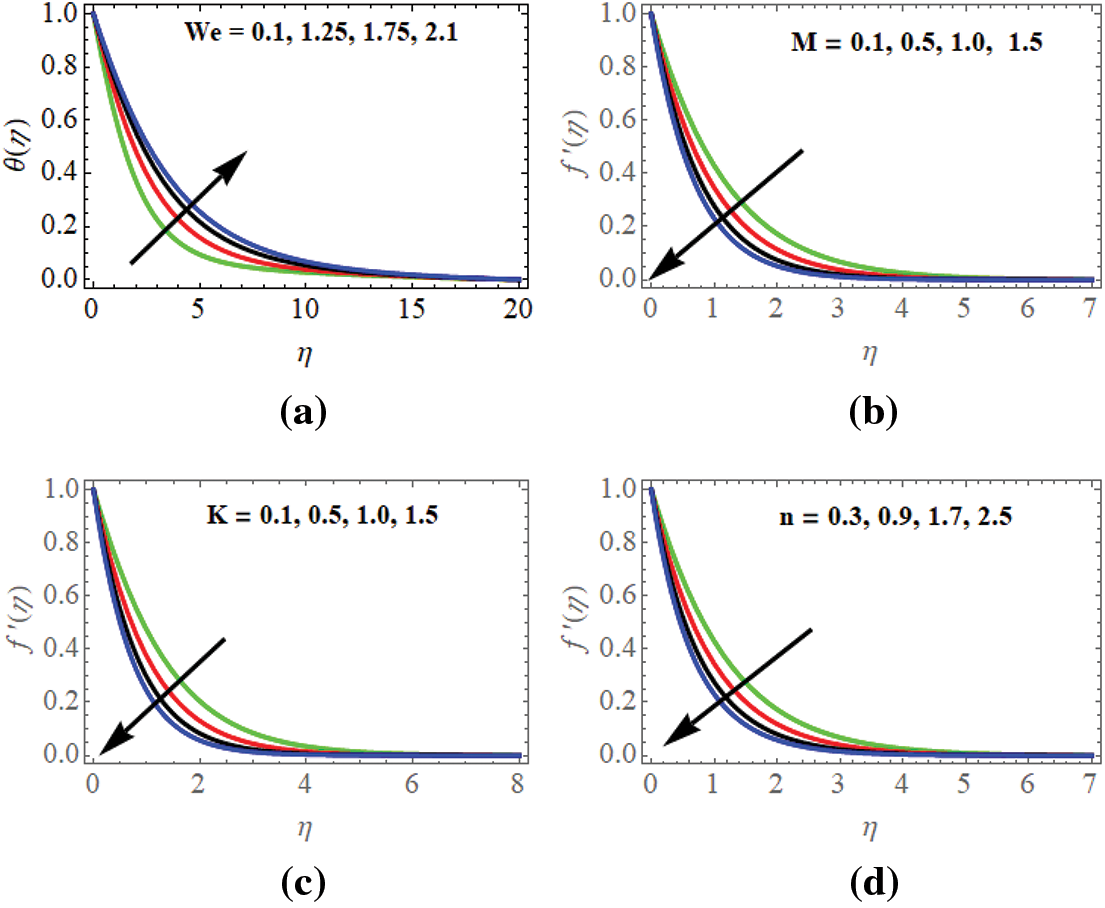
Figure 3: (a) Velocity profiles w.r.t We. (b) Velocity profiles w.r.t M. (c) Velocity profiles w.r.t K. (d) Velocity profiles w.r.t n

The detrimental impact of the magnetic parameter M on the velocity profiles f′(η) of the nanofluid flow is seen in Fig. 3b. It illustrates that f′(η) gradually shrinks as M value elevates. The timing coincidence was driven about by the relativistic force (Lorentz force), which originates from the induced magnetic field in the nanofluid flow. As a result, both the fluid’s velocity and the thickness of the boundary layer will monotonically diminish.

Fig. 3c illustrates the ramifications of the porosity parameter K on the velocity profiles f′(η). The velocity field decelerates as the values of K rise. When K escalates, it indicates an increase in the resistance offered by the porous medium to the flow of the nanofluid. Higher porosity or lower permeability leads to more obstacles and hindrances for the fluid to navigate through the porous structure. The increased resistance implies that it requires more force to push the fluid through the porous medium. The fluid velocity decreases as a consequence because the applied force or pressure gradient is not as effective in overcoming the enhanced resistance. Fig. 3d depicts the effect of the nonlinear stretching sheet index n on f′(η). The graphic approach elaborates that a boost in n triggers a fall in f′(η). Enhanced values of n indicate an increased rate of stretching of the sheet. The sheet imparts more motion to the fluid, creating a stronger driving force for the flow. The escalated stretching of the sheet creates a stronger adverse pressure gradient along the surface, which leads to slowing down the fluid flow near the surface. The boundary layer, which is the region of the flow near the surface where viscous effects dominate, becomes thinner as n elevates. The reduced thickness of the boundary layer contributes to lower fluid velocities within that layer. The stretching sheet induces shear stress at the fluid-solid interface. As the stretching effect intensifies, the shear stress increases, leading to a more significant slowing down of the fluid.

In addition, we can see in Fig. 4a that when the Williamson parameter We evolves, the fluid’s temperature profiles θ(η) gradually flourish, causing a diminution in relaxation time, and allowing the fluid to drift more elastically. Moreover, the viscosity of the fluid increases as the Williamson parameter increases, affecting the temperature profile of the fluid. The temperature profile of the fluid rises as the viscosity of the fluid rises. This is because fluid viscosity is directly related to the rate of heat transmission in the fluid. As a result, elevating the Williamson parameter induces a boost in the fluid’s viscosity, which leads to an enhancement in the fluid’s temperature profile.

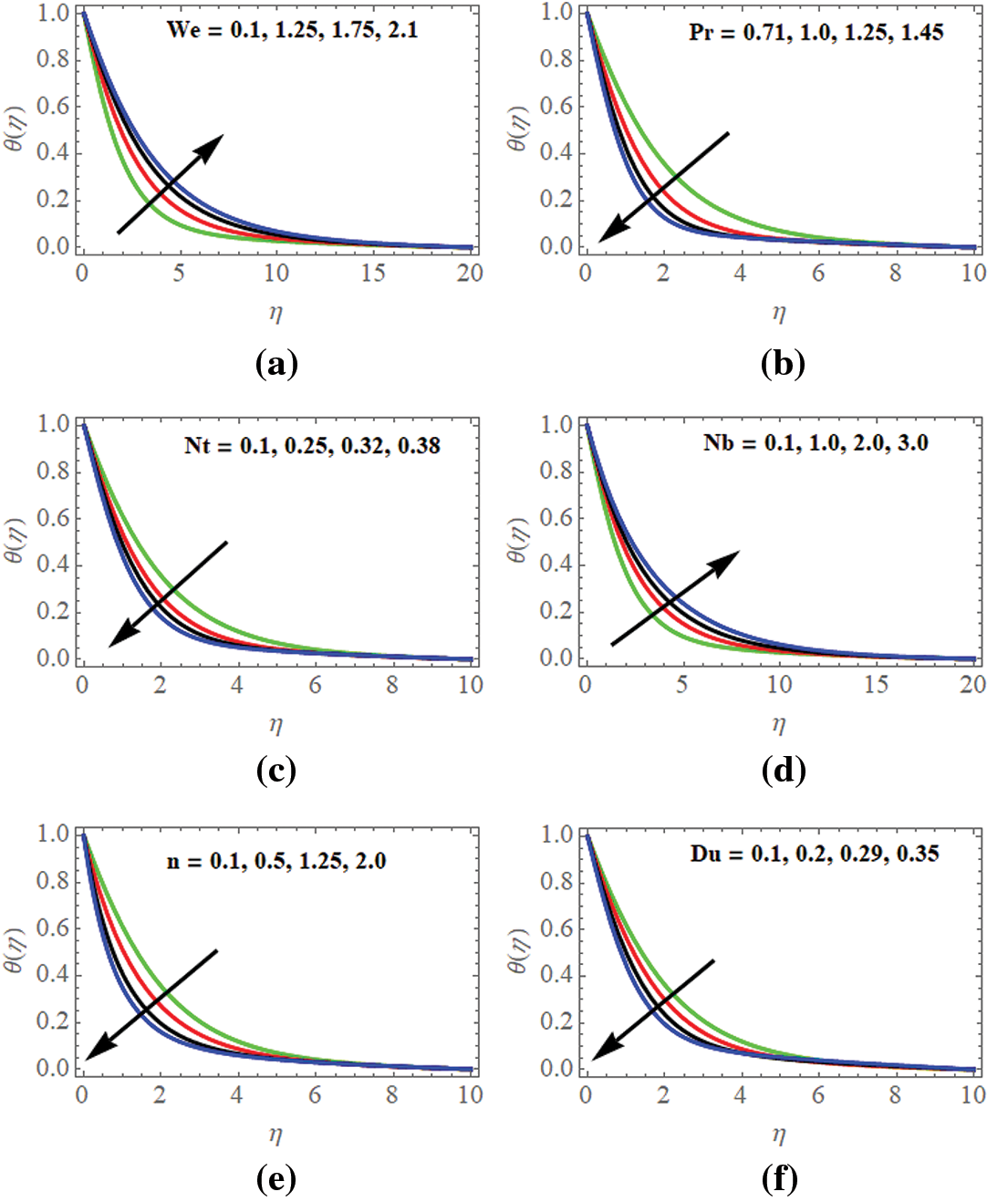
Figure 4: (a) Temperature profiles w.r.t We. (b) Temperature profiles w.r.t Pr. (c) Temperature profiles w.r.t Nt. (d) Temperature profiles w.r.t Nb. (e) Temperature profiles w.r.t n. (f) Temperature profiles w.r.t Du

In Fig. 4b, the temperature profiles θ(η) fall as the Prandtl number Pr broadens. The Prandtl number is defined as the ratio of momentum diffusivity (kinematic viscosity) to thermal diffusivity. Boosting of Pr values means that thermal diffusivity becomes relatively more significant compared to momentum diffusivity. In such a scenario, temperature gradients within the fluid tend to reduce because heat is conducted more efficiently than momentum is diffused. It also leads to thinner thermal boundary layers, which results in temperature variation within the boundary layer being reduced.

Fig. 4c illuminates that the thermophoresis parameter Nt increases gradually, and the nanofluid particles have a monotonic decrease in temperature profiles θ(η). This scenario happens as the particles move towards colder regions, they experience enhanced heat transfer with the surrounding fluid. The colder fluid extracts heat from the particles more efficiently, resulting in a decrease in the particle’s temperature. Essentially, the stronger thermophoretic force pulls the particles towards the colder regions, where they lose thermal energy to the fluid, leading to their temperature decrease.

Fig. 4d deploys that the effect of the temperature profiles θ(η) vs. Brownian motion parameter Nb. It is worth noting that there is a gradual enhancement in the temperature profiles of the nanofluid particles as the values of Nb increase, which results in increased thermal energy to both the fluid molecules and the suspended nanoparticles. This increased thermal energy translates into greater kinetic energy, leading to more frequent and energetic collisions between the nanoparticles and the fluid molecules.

Fig. 4e portrays the temperature profiles θ(η) for various values of the nonlinear stretching sheet index n. As n escalates the stretching effect intensifies, which leads to an enhanced flow velocity near the surface. Such a scenario boosts the heat transfer away from the surface and hence, there is a drop in temperature profiles of the nanofluid flow. As the stretching of the surface increases, the fluid particles are subjected to higher shear stresses, resulting in improved mixing and better dispersion of nanoparticles throughout the fluid. This wider distribution optimizes the thermal conductivity and hence, the heat transfer capabilities of the nanofluid. As a result, the waning temperature profiles θ(η) illustrate that the nanofluid successfully transfers heat away from the surface and re-distributes it throughout the fluid.

Fig. 4f describes the temperature profiles concerning the Dufour parameter Du. Notice that as the values of Du upsurge, the temperature profiles decrease. This effect is due to the enhanced thermal diffusion which causes more heat to be transferred away from the surface through diffusion. Such diffusion of heat reduces the temperature gradient near the surface which results in a gradual decline in temperature profiles θ(η).

Fig. 5a illustrates the scenario of the concentration profiles ϕ(η) vs. the Soret parameter Sr. For monotonical elevation of the Sr values, the concentration profiles ϕ(η) also enhances. Due to this impact, the nanofluid particles are migrated from higher to lower temperature regions. The presence of nanoparticles in a nanofluid enhances the Soret effect due to their influence on thermal conductivity and diffusivity. The nanoparticles can affect both the thermal properties and the mass diffusion properties of the fluid. The enhanced mass concentration profiles ϕ(η) indicates that the nanofluid exhibits intensified transfer characteristics of mass due to the Soret effect, the combined effects of diffusion and convection.

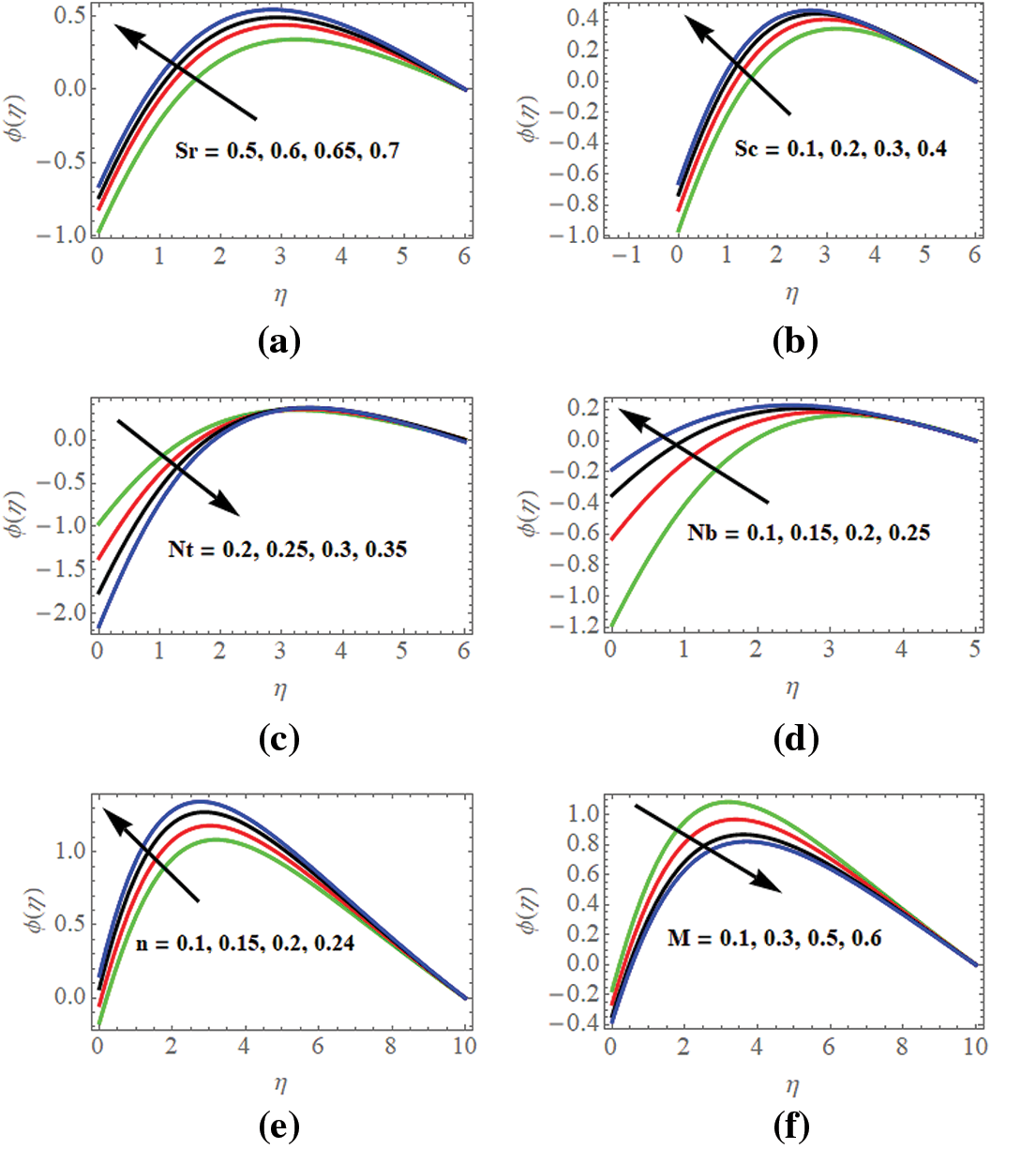
Figure 5: (a) Concentration profiles w.r.t Sr. (b) Concentration profiles w.r.t Sc. (c) Effect of ϕ(η)vs.Nt. (d) Effect of ϕ(η)vs.Nb. (e) Effect of ϕ(η)vs.n. (f) Effect of ϕ(η)vs.M

Fig. 5b depicts that as the Schmidt number Sc intensifies, the concentration profiles ϕ(η) are gradually rising. The physical significance of the parameter Sc represents to characterize the relative importance of momentum diffusion (viscous forces) to mass diffusion (diffusion of a solute) in a fluid. When the values of Sc escalate, that is, diffusivity dominates viscosity, the concentration profiles ϕ(η) become sharper such that the nanoparticles tend to concentrate in the concentration boundary layer region (as shown in Fig. 1) of the fluid. The concentration gradient becomes steeper, indicating that concentration intensifies more along the flow direction because the diffusivity of the nanoparticles is relatively higher when compared to the diffusivity of the momentum, allowing the nanoparticles to diffuse less and retain a more concentrated form.

Fig. 5c exhibits the nonlinear behavior of the concentration profiles ϕ(η) for a gradual rise in the Thermophoresis parameter Nt because the thermophoretic force does not increase linearly withNt. Enhancing the values of Nt, leads to stronger thermophoretic forces acting on the nanoparticles, resulting in enhanced particle accumulation in hotter regions, reduced dispersion in colder regions, possible nonlinear concentration gradients, and more pronounced boundary layer effects.

Fig. 5d explores the behavior of concentration profiles ϕ(η) concerning Brownian motion parameter Nb. Brownian motion is a stochastic process resulting from the continuous bombardment of nanoparticles by fluid molecules. It leads to the random dispersion of nanoparticles throughout the fluid. Escalating the values of Nb indicates an enhancement in the intensity of Brownian motion within the nanofluid. Brownian motion influences the effective properties of nanofluids, such as thermal conductivity and viscosity. The increased Brownian motion promotes the dispersion of nanoparticles over a larger volume, contributing to higher concentrations across the flow field.

Fig. 5e deploys that the concentration profiles ϕ(η) are increasing as the stretching sheet index rises. Boosting the values of n leads to more rapid stretching of the sheet. This results in an increase in the fluid flow velocity near the surface. With higher flow velocities, there will be enhanced fluid mixing and convective transport of the nanoparticles. Due to the convective transport, the nanoparticles near the stretching sheet will experience higher rates of diffusion and dispersion, which can lead to up surged penetration of nanoparticles into the fluid. Consequently, the concentration of nanoparticles near the stretching sheet will rise as n elevates. Fig. 5f explores that as the Magnetic parameter M rises, the concentration profiles ϕ(η) are declines. That is, when M is increased, the intensity of the applied magnetic field upsurges, which exerts a stronger force on the nanoparticles in the nanofluid. The nanoparticles move towards areas with stronger magnetic fields due to the driving impact of this magnetic force. The concentration of the nanoparticles in other areas of the nanofluid will drop as they travel towards areas with stronger magnetic fields because they tend to congregate there. This phenomenon can be utilized in various applications such as magnetic separation, drug delivery systems, and targeted therapy, where controlling the concentration and distribution of nanoparticles within a fluid is essential.

The local skin coefficient values prominence when the graph is displayed over the Williamson parameter We vs. the magnetic parameter M, as seen in Fig. 6a. This evidence shows that the magnetic field, not viscous forces, is the most significant feature controlling the friction coefficient. This might happen because the flow dynamics are being more strongly impacted by the magnetic field, boosting the drag or resistance between the fluid and the surface. This behavior might be seen in real-world settings when a strong magnetic field is given to a fluid flow, potentially increasing friction and drag by making the fluid interact more strongly with the surface. This may have repercussions for a variety of technological applications, including flow control devices or magnetohydrodynamic (MHD) propulsion systems.

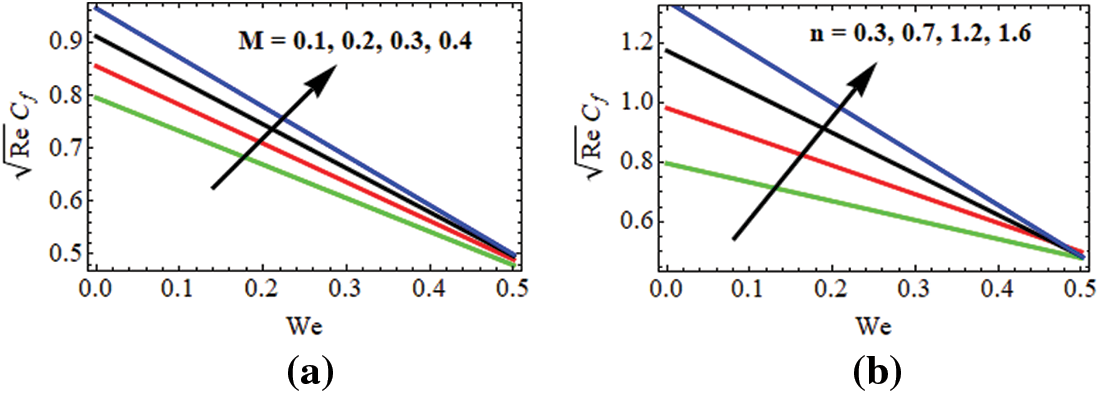
Figure 6: (a) Effect of M on CfxRe against We. (b) Effect of n on CfxRe against We

Prioritizing the local skin coefficient values over the Williamson parameter when the graph is shown as shown in Fig. 6b, We contrasted with the nonlinear stretching sheet index n. The stretching effect caused by a greater value of n might thin the boundary layer close to the surface, corresponding to this influence. Higher local skin friction coefficient values might be the result of stronger velocity gradients and shear stresses that are brought on by a thinner boundary layer. Practically, this behavior may be seen in situations where a stretched surface interferes with the fluid flow across it (such as during manufacturing operations, heat transfer applications, or boundary layer control). More noticeable stretching effects and, as a result, a greater collision between the fluid and the surface, which would increase friction and drag, might arise from an increase in the stretching sheet index n.

In Table 1, the current investigation is compared to previous research that was published to validate the existing numerical solution. It draws attention to that current and past findings are in good harmony. The present findings are validated due to the top-notch agreement between the results and their interpretation. Tables 2a–2d provide the computational values of the mass transfer rate (local Sherwood number) for the Schmidt parameter Sc, Soret number Sr, nonlinear stretching sheet index n, and Thermophoresis parameter Nt. The tabular values show that for increasing values of Sc,Sr,n, and Nt, the local Sherwood number fluctuates from lower to higher values gradually.

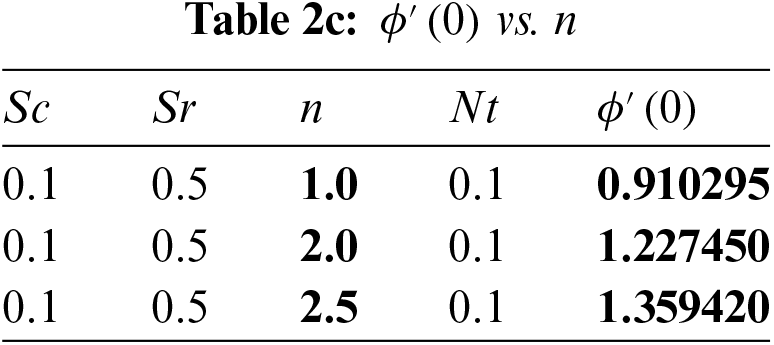
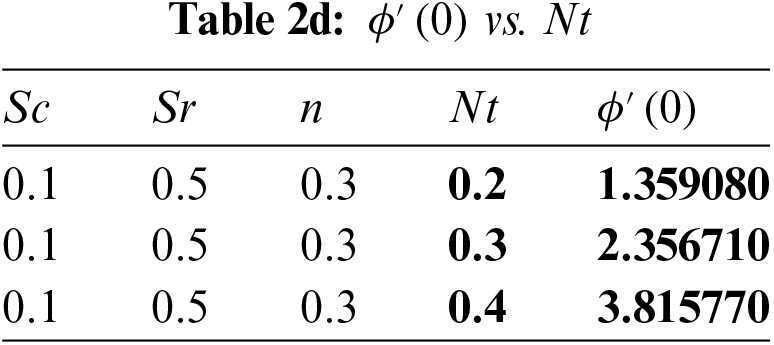
The values of local Sherwood number (−ShxRe) for parameters Sc,Sr,n and Nt are tabulated in the following Tables 2a–2d with initial values We=0.01,M=0.1,K=0.1,n=0.3,Pr=0.71,Nb=0.1,Nt=0.1,Du=0.2,Sc=0.1,Sr=0.5.

6  Conclusion

The problem of the 2D-steady, viscous, and incompressible MHD heat and mass transfer of a Williamson nanofluid flow past a nonlinear stretching sheet immersed in a porous medium with the Soret and Dufour effects was investigated. Using appropriate similarity variable transformations, the nonlinear PDEs were altered into nonlinear ODEs and then solved numerically using the RKF-45 method along with the shooting technique. The impact of various physical parameters on concentration, velocity, and temperature profiles is deployed through graphs. From the present investigation, the following conclusions could be drawn:

•   Boosting the magnetic, Williamson, porosity, and stretching sheet index parameters, the velocity of the fluid flow decreases.

•   The temperature is enhanced as the Williamson and Brownian motion parameters upsurge, but it decreases as the Prandtl, thermophoresis, stretching sheet index, and Dufour parameters escalate.

•   The concentration distribution decreases as the thermophoresis and magnetic parameters upsurge but it escalates as the Soret, Schmidt, Brownian motion, and stretching sheet index parameters increase.

•   Skin friction coefficient boosted as the stretching sheet index and magnetic parameters enhanced against the Williamson parameter.

•   The findings from this study have been contrasted with earlier findings on local Nusselt numbers, which show substantial support and endorse the existing approach’s validity.

•   The numerical values of the local Sherwood number gradually increase as the Schmidt, Soret, stretching sheet index, and thermophoresis parameters are upsurged.

Future Research Study: In the future, we will study different non-Newtonian nanofluids for this study along with different physical effects.

Acknowledgement: No acknowledgement.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection, analysis and interpretation of results, draft manuscript preparation: R. Madan Kumar, R. Srinivasa Raju, F. Mebarek-Oudina, M. Anil Kumar, N. Vamsi Krishna. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data are available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Raju, R. S. K., Reddy, M. A., Anil Kumar, G. J., Rama, M., Reddy Gorla, S. (2020). Unsteady magnetohydrodynamic chemically reacting fluid flow past an inclined vertical permeable moving plate. International Journal of Fluid Mechanics Research, 47(3), 191–215. [Google Scholar]

2. Srinivasa Raju, R., Anitha, G., Jithender Reddy, G. (2017). Analytical and numerical investigation of heat and mass transfer effects on magnetohydrodynamic natural convective flow past a vertical porous plate. Journal of Heat and Mass Transfer Research, 4, 117–133. [Google Scholar]

3. Raju, R. S. (2017). Application of finite element method to mhd mixed convection chemically reacting flow past a vertical porous plate with cross diffusion and biot number effects. American Journal of Heat and Mass Transfer, 4(3), 53–74. https://doi.org/10.7726/ajhmt.2017.1009 [Google Scholar] [CrossRef]

4. Nadeem, S., Hussain, S. T., Lee, C. (2013). Flow of a Williamson fluid over a stretching sheet. Brazilian Journal of Chemical Engineering, 30, 619–625. [Google Scholar]

5. Megahed, A. M. (2019). Williamson fluid flow due to a nonlinearly stretching sheet with viscous dissipation and thermal radiation. Journal of the Egyptian Mathematical Society, 27(1), 1–10. [Google Scholar]

6. Bibi, M., Malik, M. Y., Tahir, M. (2018). Numerical study of unsteady Williamson fluid flow and heat transfer in the presence of MHD through a permeable stretching surface. The European Physical Journal Plus, 133, 1–15. [Google Scholar]

7. Salahuddin, T., Iqbal, M. A., Bano, A., Awais, M., Muhammad, S. (2023). Cattaneo-Christov heat and mass transmission of dissipated Williamson fluid with double stratification. Alexandria Engineering Journal, 80, 553–558. https://doi.org/10.1016/j.aej.2023.09.012 [Google Scholar] [CrossRef]

8. Nadeem, S., Hussain, S. T. (2014). Flow and heat transfer analysis of Williamson nanofluid. Applied Nanoscience, 4, 1005–1012. [Google Scholar]

9. Bhatti, M. M., Rashidi, M. M. (2016). Effects of thermo-diffusion and thermal radiation on Williamson nanofluid over a porous shrinking/stretching sheet. Journal of Molecular Liquids, 221, 567–573. https://doi.org/10.1016/J.MOLLIQ.2016.05.049 [Google Scholar] [CrossRef]

10. Reddy, C. S., Naikoti, K., Rashidi, M. M. (2017). MHD flow and heat transfer characteristics of Williamson nanofluid over a stretching sheet with variable thickness and variable thermal conductivity. Transactions of A. Razmadze Mathematical Institute, 171(2), 195–211. https://doi.org/10.1016/J.TRMI.2017.02.004 [Google Scholar] [CrossRef]

11. Mabood, F., Ibrahim, S. M., Lorenzini, G., Lorenzini, E. (2017). Radiation effects on Williamson nanofluid flow over a heated surface with magnetohydrodynamics. International Journal of Heat and Technology, 35, 196–204. https://doi.org/10.18280/IJHT.350126 [Google Scholar] [CrossRef]

12. Mebarek-Oudina, F., Preeti, S. A. S., Vaidya, H., Lewis, R. W., Areekara, S. et al. (2024). Hydromagnetic flow of magnetite-water nano-fluid utilizing adapted Buongiorno model. International Journal of Modern Physics B, 38(1), 2450003. https://doi.org/10.1142/S0217979224500036 [Google Scholar] [CrossRef]

13. Ramesh, K., Mebarek-Oudina, F., Ismail, A. I., Jaiswal, B. R., Warke, A. S. et al. (2023). Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sciencia Iranica, 30(2), 376–390. [Google Scholar]

14. Abbas, A., Jeelani, M. B., Alnahdi, A. S., Ilyas, A. (2022). MHD Williamson nanofluid fluid flow and heat transfer past a non-linear stretching sheet implanted in a porous medium: Effects of heat generation and viscous dissipation. Processes, 10(6), 221. https://doi.org/10.3390/pr10061221 [Google Scholar] [CrossRef]

15. Bouselsal, M., Mebarek-Oudina, F., Biswas, N., Ismail, A. I. (2023). Heat transfer enhancement using Al2O3 -MWCNT hybrid-nanofluid inside a tube/shell heat exchanger with different tube shapes. Micromachines, 14(5), 1072. https://doi.org/10.3390/mi14051072 [Google Scholar] [PubMed] [CrossRef]

16. Mebarek-Oudina, F., Chabani, I. (2023). Review on nano enhanced PCMs: Insight on nePCM application in thermal management/storage systems. Energies, 16(3), 1066. https://doi.org/10.3390/en16031066 [Google Scholar] [CrossRef]

17. Wang, F., Asjad, M. I., Rehman, S. U., Ali, B., Hussain, S. et al. (2021). MHD Williamson nanofluid flow over a slender elastic sheet of irregular thickness in the presence of bioconvection. Nanomaterials, 11(9), 2297. https://doi.org/10.3390/NANO11092297 [Google Scholar] [PubMed] [CrossRef]

18. Loganathan, P., Sangeetha, S. (2022). Effect of Williamson parameter on Cu-water Williamson nanofluid over a vertical plate. International Communications in Heat and Mass Transfer, 137, 106273. https://doi.org/10.1016/J.ICHEATMASSTRANSFER.2022.106273 [Google Scholar] [CrossRef]

19. Ibrahim, W., Gamachu, D. (2019). Nonlinear convection flow of Williamson nanofluid past a radially stretching surface. AIP Advances, 9(8), 085026. https://doi.org/10.1063/1.5113688 [Google Scholar] [CrossRef]

20. Sridhar, W., Vijaya Lakshmi, G., Al-Farhany, K., Ganesh, G. R. (2021). MHD Williamson nanofluid across a permeable medium past an extended sheet with constant and irregular thickness. Heat Transfer, 50(8), 8134–8154. https://doi.org/10.1002/HTJ.22270 [Google Scholar] [CrossRef]

21. Shawky, H. M., Eldabe, N. T. M., Kamel, K. A., Abd-Aziz, E. A. (2019). MHD flow with heat and mass transfer of Williamson nanofluid over stretching sheet through porous medium. Microsystem Technologies, 25(4), 1155–1169. https://doi.org/10.1007/S00542-018-4081-1 [Google Scholar] [CrossRef]

22. Gupta, S., Kumar, D., Singh, J. (2020). Analytical study for MHD flow of Williamson nanofluid with the effects of variable thickness, nonlinear thermal radiation and improved Fourier’s and Fick’s Laws. SN Applied Sciences, 2(3), 438. https://doi.org/10.1007/S42452-020-1995-X [Google Scholar] [CrossRef]

23. Ahmed, K., Akbar, T. (2021). Numerical investigation of magnetohydrodynamics Williamson nanofluid flow over an exponentially stretching surface. Advances in Mechanical Engineering, 13(5). https://doi.org/10.1177/16878140211019875 [Google Scholar] [CrossRef]

24. Qureshi, M. A. (2021). Numerical simulation of heat transfer flow subject to mhd of williamson nanofluid with thermal radiation. Symmetry, 13(1), 1–22. https://doi.org/10.3390/SYM13010010 [Google Scholar] [CrossRef]

25. Das, K. (2015). Nanofluid flow over a non-linear permeable stretching sheet with partial slip. Journal of the Egyptian Mathematical Society, 23(2), 451–456. https://doi.org/10.1016/j.joems.2014.06.014 [Google Scholar] [CrossRef]

26. Bilal, S., Khalil-ur-Rehman, M., Malik, M. Y., Hussain, A., Khan, M. (2017). Effects of temperature dependent conductivity and absorptive/generative heat transfer on MHD three-dimensional flow of Williamson fluid due to bidirectional non-linear stretching surface. Results of Physics, 7, 204–212. https://doi.org/10.1016/j.rinp.2016.11.063 [Google Scholar] [CrossRef]

27. Abo-Dahab, S. M., Abdelhafez, M. A., Mebarek-Oudina, F., Bilal, S. M. (2021). MHD Casson nanofluid flow over nonlinearly heated porous medium in presence of extending surface effect with suction/injection. Indian Journal of Physics, 95, 2703–2717. https://doi.org/10.1007/s12648-020-01923-z [Google Scholar] [CrossRef]

28. Hayat, T., Ullah, I., Alsaedi, A., Farooq, M. (2017). MHD flow of Powell-Eyring nanofluid over a non-linear stretching sheet with variable thickness. Results of Physics, 7, 189–196. https://doi.org/10.1016/j.rinp.2016.12.008 [Google Scholar] [CrossRef]

29. Qayyum, S., Hayat, T., Alsaedi, A. (2017). Chemical reaction and heat generation/absorption aspects in MHD nonlinear convective flow of third grade nanofluid over a nonlinear stretching sheet with variable thickness. Results of Physics, 7, 2752–2761. https://doi.org/10.1016/j.rinp.2017.07.043 [Google Scholar] [CrossRef]

30. Ahmed, K., McCash, L. B., Akbar, T., Nadeem, S. (2022). Effective similarity variables for the computations of MHD flow of Williamson nanofluid over a non-linear stretching surface. Processes, 10(6), 1119. https://doi.org/10.3390/pr10061119 [Google Scholar] [CrossRef]

31. Khan, M., Malik, M. Y., Salahuddin, T., Hussian, A. (2018). Heat and mass transfer of Williamson nanofluid flow yield by an inclined Lorentz force over a nonlinear stretching sheet. Results of Physics, 8, 862–868. https://doi.org/10.1016/j.rinp.2018.01.005 [Google Scholar] [CrossRef]

32. Seth, G. S., Bhattacharyya, A., Kumar, R., Chamkha, A. J. (2018). Entropy generation in hydromagnetic nanofluid flow over a non-linear stretching sheet with Navier’s velocity slip and convective heat transfer. Physics of Fluids, 30(12), 122003. https://doi.org/10.1063/1.5054099 [Google Scholar] [CrossRef]

33. Rasool, G., Shafiq, A., Khalique, C. M., Zhang, T. (2019). Magnetohydrodynamic Darcy-Forchheimer nanofluid flow over a nonlinear stretching sheet. Physica Scripta, 94(10), 105221. https://doi.org/10.1088/1402-4896/ab18c8 [Google Scholar] [CrossRef]

34. Jafar, A. B., Shafie, S., Ullah, I. (2020). MHD radiative nanofluid flow induced by a nonlinear stretching sheet in a porous medium. Heliyon, 6(6), E04201. https://doi.org/10.1016/j.heliyon.2020.e04201 [Google Scholar] [PubMed] [CrossRef]

35. Prasannakumara, B. C., Gireesha, B. J., Krishnamurthy, M. R., Ganesh Kumar, K. (2017). MHD flow and nonlinear radiative heat transfer of Sisko nanofluid over a nonlinear stretching sheet. Informatics in Medicine Unlocked, 9123–9132. https://doi.org/10.1016/j.imu.2017.07.006 [Google Scholar] [CrossRef]

36. Makinde, O. D., Mabood, F., Ibrahim, M. S. (2018). Chemically reacting on MHD boundary-layer flow of nanofluids over a non-linear stretching sheet with heat source/sink and thermal radiation. Thermal Science, 22(1), 495–506. https://doi.org/10.2298/tsci151003284m [Google Scholar] [CrossRef]

37. Hayat, T., Rashid, M., Alsaedi, A., Ahmad, B. (2018). Flow of nanofluid by nonlinear stretching velocity. Results of Physics, 81104–81109. https://doi.org/10.1016/j.rinp.2017.12.014 [Google Scholar] [CrossRef]

38. Postelnicu, A. (2007). Influence of chemical reaction on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Heat and Mass Transfer/Waerme-und Stoffuebertragung, 43(6), 595–602. https://doi.org/10.1007/S00231-006-0132-8/FIGURES/15 [Google Scholar] [CrossRef]

39. Seid, E., Haile, E., Walelign, T. (2022). Multiple slip, Soret and Dufour effects in fluid flow near a vertical stretching sheet in the presence of magnetic nanoparticles. International Journal of Thermofluids, 13, 100136. https://doi.org/10.1016/J.IJFT.2022.100136 [Google Scholar] [CrossRef]

40. Imran, M., Naveed, M., Abbas, Z. (2023). Dynamics of Soret and Dufour effects on oscillatory flow of couple stress fluid due to stretchable curved surface. Research Article Advances in Mechanical Engineering, 2, 1–18. https://doi.org/10.1177/16878132231156742 [Google Scholar] [CrossRef]

41. Vafai, K., Khan, A. A., Fatima, G., Sait, S. M., Ellahi, R. (2021). Dufour, Soret and radiation effects with magnetic dipole on Powell-Eyring fluid flow over a stretching sheet. International Journal of Numerical Methods & Heat Fluid Flow, 31(4), 1085–1103. https://doi.org/10.1108/HFF-06-2020-0328 [Google Scholar] [CrossRef]

42. Makinde, O. D. (2011). On MHD mixed convection with soret and dufour effects past a vertical plate embedded in a porous medium. Latin American Applied Research, 41(1), 63–68. [Google Scholar]

43. Makinde, O. D., Olanrewaju, P. O. (2011). Mixed convection with soret and dufour effects unsteady mixed convection with soret and dufour effects past a porous plate moving through a binary mixture of chemically reacting fluid. Chemical Engineering Communications, 1989, 920–938. https://doi.org/10.1080/00986445.2011.545296 [Google Scholar] [CrossRef]

44. Partha, M. K., Murthy, P. V. S. N., Sekhar, G. P. R. (2006). Soret and Dufour effects in a non-darcy porous medium. Journal of Heat Transfer, 128(6), 605–610. https://doi.org/10.1115/1.2188512 [Google Scholar] [CrossRef]

45. Mortimer, R. G., Eyring, H. (1980). Elementary transition state theory of the Soret and Dufour effects. Proceedings of the National Academy of Sciences of the United States of America, 77(4), 1728–1731. https://doi.org/10.1073/PNAS.77.4.1728 [Google Scholar] [PubMed] [CrossRef]

46. Dharmaiah, G., Mebarek-Oudina, F., Balamurugan, K. S., Vedavathi, N. (2024). Numerical analysis of the magnetic dipole effect on a radiative ferromagnetic liquid flowing over a porous stretched sheet. Fluid Dynamics & Materials Processing, 20(2), 293–310. https://doi.org/10.32604/fdmp.2023.030325 [Google Scholar] [CrossRef]

47. Reddy Gorla, R. S., Sidawi, I. (1994). Free convection on a vertical stretching surface with suction and blowing. Applied Scientific Research, 52, 247–257. [Google Scholar]