 Open Access
Open Access
ARTICLE
Energy and Exergy Analysis of Pyramid-Type Solar Still Coupled with Magnetic and Electrical Effects by Using Matlab Simulation
1 Air Conditioning Engineering Department, Faculty of Engineering, Warith Al-Anbiyaa University, Baghdad, Iraq
2 Mechanical Engineering Department, University of Technology, Baghdad, Iraq
3 Control and Systems Engineering Department, University of Technology, Baghdad, Iraq
4 Mechanical Engineering Department, Faculty of Engineering, Kafrelsheikh University, Kafrelsheikh, Egypt
* Corresponding Author: Karrar A. Hammoodi. Email:
(This article belongs to the Special Issue: Passive Heat Transfer Enhancement for Single Phase and Multi-Phase Flows)
Frontiers in Heat and Mass Transfer 2024, 22(1), 217-262. https://doi.org/10.32604/fhmt.2024.047329
Received 02 November 2023; Accepted 04 December 2023; Issue published 21 March 2024
Abstract
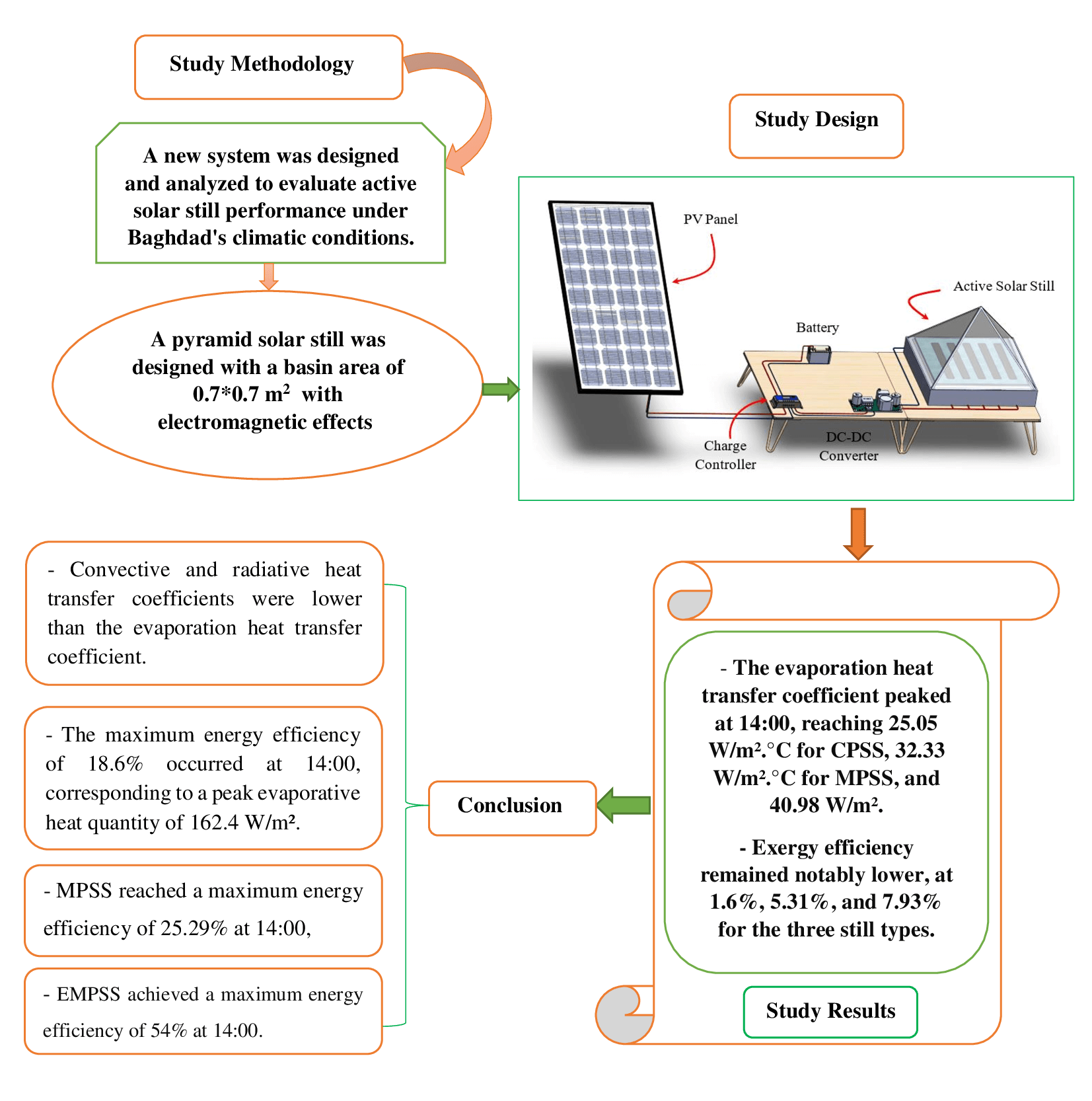
In the face of an escalating global water crisis, countries worldwide grapple with the crippling effects of scarcity, jeopardizing economic progress and hindering societal advancement. Solar energy emerges as a beacon of hope, offering a sustainable and environmentally friendly solution to desalination. Solar distillation technology, harnessing the power of the sun, transforms seawater into freshwater, expanding the availability of this precious resource. Optimizing solar still performance under specific climatic conditions and evaluating different configurations is crucial for practical implementation and widespread adoption of solar energy. In this study, we conducted theoretical investigations on three distinct solar still configurations to evaluate their performance under Baghdad’s climatic conditions. The solar stills analyzed include the passive solar still, the modified solar still coupled with a magnetic field, and the modified solar still coupled with both magnetic and electrical fields. The results proved that the evaporation heat transfer coefficient peaked at 14:00, reaching 25.05 W/m2.°C for the convention pyramid solar still (CPSS), 32.33 W/m2.°C for the magnetic pyramid solar still (MPSS), and 40.98 W/m2.°C for elecro-magnetic pyramid solar still (EMPSS), highlighting their efficiency in converting solar energy to vapor. However, exergy efficiency remained notably lower, at 1.6%, 5.31%, and 7.93% for the three still types, even as energy efficiency reached its maximum of 18.6% at 14:00 with a corresponding peak evaporative heat of 162.4 W/m2.Graphic Abstract
Keywords
Nomenclature
| Subscript | |
| Symbol | Definition |
| a | Ambient |
| b | Basin |
| C | Cell |
| c | Convection |
| cond. | Conduction |
| e | Evaporation |
| eff. | Effective |
| ele. | Electric |
| fg | Latent heat of evaporation |
| g | Glass |
| i | Initial |
| ins. | Insulation |
| L | Light |
| mg | Magnetic |
| mp | Maximum power point |
| oc | Open circut |
| p | Pressure |
| r | Radiation |
| ref. | Reference condition |
| s | Sky |
| sc | Short circut |
| t | Total |
| th. | Theoretical |
| w | Water |
| Latin Symbols | |
| Symbol | Definition units |
| Area m2 | |
| Basin area m2 | |
| Glass area m2 | |
| a | Ideality factor |
| B | Width m |
| Constant | |
| Specific heat at constant pressure J/kg.K | |
| Diameter m | |
| dp | Dew point temperature °C |
| E | Energy W |
| Gravitational acceleration m/s2 | |
| H | Hight m |
| Heat transfer coefficient W/m2.°C | |
| Current A | |
| Light current A | |
| Reverse saturation current A | |
| Tilt solar radiation W/m2 | |
| Thermal conductivity W/m.°C | |
| Length m | |
| Insulation thickness m | |
| Mass kg | |
| Mass flow rate kg/s | |
| Productivity kg/m2 | |
| N | Number of solar cells |
| P | Pressure Pa |
| Prandtl number | |
| Heat transfer W/m2 | |
| Loss heat transfer W/m2 | |
| Heat flux W/m2 | |
| R | Resistance Ω |
| Temperature K°C | |
| t | Time sec |
| Overall heat transfer coefficient W/m2.°C | |
| Volt V | |
| Velocity, speed m/s | |
| W | Work N.m |
| Thickness m | |
| Greek symbols | |
| Symbol | Definition units |
| Thermal diffusivity m2/s | |
| Thermal expansion coefficient K-1 | |
| Emissivity | |
| Semiconductor band gap energy | |
| Efficiency % | |
| Voltage temperature coefficient V/°C | |
| Dynamic viscosity kg/m.s | |
| Kinematic viscosity m2/s | |
| Density kg/m3 | |
| Δ | Difference |
| Transmissivity | |
| Stefan-Boltzmann constant | |
| Thermal efficiency | |
| Current temperature coefficient A/°C | |
| Density kg/m3 | |
| Abbreviations | |
| Symbol | Definition |
| 3D | Three dimension |
| CSS | Conventional solar stills |
| CPSS | Conventional pyramid solar stills |
| EDR | Electrodialysis reversal |
| EMPSS | Elecro-magnetic pyramid solar still |
| EX | Exergy |
| HDH | Humidification-Dehumidification |
| HTC | Heat transfer coefficient |
| MD | Membrane distillation |
| MED | Multi-effect desalination |
| MSF | Multi stage flash |
| MPSS | Magnetic pyramid solar still |
| mT | milli teslla |
| MVC | Mechanical vapor compression |
| PV | Photovoltaic |
| PSS | Pyramid solar still |
| RO | Reverse osmosis |
| SD | Solar distillation |
| WHO | World Health Organization |
Authors in today’s world, one of the greatest challenges we face is water scarcity, which threatens global economic development [1]. Projections indicate that by 2025, a third of the world’s population could confront severe water shortages [2,3]. While our planet is mostly covered in water, approximately 97% of it is salty and unsuitable for direct consumption or most agricultural purposes [4–6]. This scarcity issue is compounded by the energy crisis, characterized by the high cost, environmental damage, and pollution associated with the current heavy reliance on fossil fuels. Addressing these dual challenges necessitates innovative and sustainable solutions to ensure the well-being of our planet and its inhabitants [7,8].
In many developing nations, access to safe drinking water remains a significant challenge. Even in regions with abundant water resources, such as numerous rivers, only a fraction of urban residents, around 40%, enjoy reliable access to potable water [9]. For those residing in rural areas, deserts, or specific urban neighborhoods, access to clean water is even scarcer [10].
Addressing this global challenge involves deploying high-performance distillation plants or considering individual distillation systems for households [11]. Traditional distillation plants typically rely on a substantial quantity of fossil fuels, which has adverse environmental consequences [4,12–14]. Consequently, distillation systems leveraging renewable energy sources, particularly solar energy, are strongly recommended for their environmental friendliness [15,16].
Many regions worldwide, including those with abundant sunlight, can harness solar energy effectively for desalination. Peak solar intensity can reach impressive levels, such as 1250 W/m2 during the peak of summer [17]. Various techniques are available to desalinate non-potable water and produce clean drinking water. Conventional methods, like multi-stage flash (MSF), reverse osmosis (RO), multi-effect distillation (MED), and electrodialysis (ED), have become less favored due to their high costs and environmental impact. As a result, there is a growing emphasis on utilizing solar energy as an alternative and environmentally friendly energy source [18].
Solar distillation offers a viable approach to treating saltwater. Passive solar stills, where solar radiation directly impacts the distillation basin, are commonly used for this purpose [19]. These stills typically consist of a water basin, a tube for introducing saline water, a transparent cover, and channels for collecting distilled water [20]. Various designs, including single-slope, double-slope, and pyramid solar stills, provide flexibility and efficiency [21]. By introducing external energy sources like solar collectors, reflectors, or solar trackers, passive solar stills can be further optimized for performance [22,23].
In solar distillation, sunlight is utilized to evaporate water, leaving impurities and salt behind. The resulting vapor is then condensed to produce freshwater. However, solar distillation typically yields limited amounts of freshwater compared to alternative purification methods [24–28].
To cost-effectively address this challenge, harnessing solar energy for water purification has emerged as a compelling option. Solar stills, which are simple and user-friendly devices, offer an environmentally responsive solution for converting saline water into drinkable water. One of their primary advantages is their low fabrication cost. Nevertheless, they do suffer from low productivity.
To overcome this productivity limitation, researchers have explored various techniques to enhance the performance of both active and passive solar stills [29]. These methods include modifying the distiller’s shape, adding components to increase the water’s temperature, and other innovative approaches [30,31]. These methods include cooling the glass cover with continuously flowing water or intermittent water flow [32,33]. Wind speed also plays a role, as increased air movement enhances convective heat transfer from the cover to the atmosphere, thereby boosting condensation and evaporation rates, and ultimately, production [34].
Researchers have developed various types of solar stills to increase productivity. These include solar stills with integrated solar collectors [35–37], those with condensers, low-pressure solar stills, systems with heat recycling, differently configured stills, multi-stage/multi-effect solar stills, models with heat storage, and hybrid solar still/photovoltaic (PV) systems [38–41]. Despite these innovations, solar distillates are not yet commercially viable due to their limited production capacity. To address this, researchers have investigated the use of phase change materials (PCMs) with high latent heat capacity to absorb and store energy [42–45]. Additionally, some studies have examined graded solar stills and simple solar distillers equipped with a single basin and PCM for energy storage. Continuing distillation after sunset has been shown to increase productivity by utilizing the stored energy. Maintaining a substantial temperature difference between the water and the cooler glass cover has also been found to be beneficial [46]. Other Researchers has shown that magnetic fields have a substantial impact on water evaporation rates [47–51]. Consequently, the application of magnetic fields stands out as one of the most influential and contemporary techniques for enhancing the productivity of solar stills [52].
While numerous studies have investigated various technologies worldwide, there has been limited research specifically focused on the integrated coupling of magnetic and electrical effects [53]. This study aims to provide a comprehensive understanding of the potential advantages of integrating both magnetic and electrical fields into pyramidal distillers and their influence on vaporization processes and overall productivity [54]. The theoretical investigation involves a detailed energy and exergy analysis conducted using Matlab Simulink, 2021.
In this research, a pyramid-type solar distiller was constructed and examined under the conditions of Baghdad, Iraq, with the incorporation of both magnetic and electrical fields. The pyramid-shaped solar still was designed with a textured surface to enhance the evaporation area and improve solar radiation absorption, ultimately leading to increased production. Notably, unlike conventional solar stills, this pyramid still featured glass on all sides, eliminating issues related to shadowing [29,55,56].
By incorporating these innovative techniques, this paper contributes significantly to the originality of research in this field. It offers valuable insights into the combined effects of magnetic and electrical fields in pyramidal distillers and highlights the potential for optimizing distillation processes to enhance productivity.
3 Description of the Physical Model
A solar still is a device designed to produce fresh, drinkable water by harnessing solar energy and emulating the natural hydrological cycle. It operates by allowing solar energy to pass through a transparent glass cover, which initiates the evaporation of water in the basin through the greenhouse effect. Subsequently, the water vapor condenses on the inner side of the glass cover and is collected via a trough, as depicted in Fig. 1. The entire testing setup was assumed to be situated in Baghdad, at a latitude of 33.3°N, a longitude of 44.5°E, and an elevation of 33 m above sea level. The critical components of a solar still include:
• The basin: This container holds and contains the raw water.
• The basin liner: The base of the basin acts as an absorber plate, collecting solar energy. It is typically painted black to maximize absorptivity.
• A transparent glass cover: Placed atop the solar still, it permits solar rays to pass through while simultaneously serving as a condenser.
• A collecting trough: A small channel designed to gather the fresh water produced during condensation.
• Additional components: These may include a water tank, pipes, fittings, and a water leveling system.
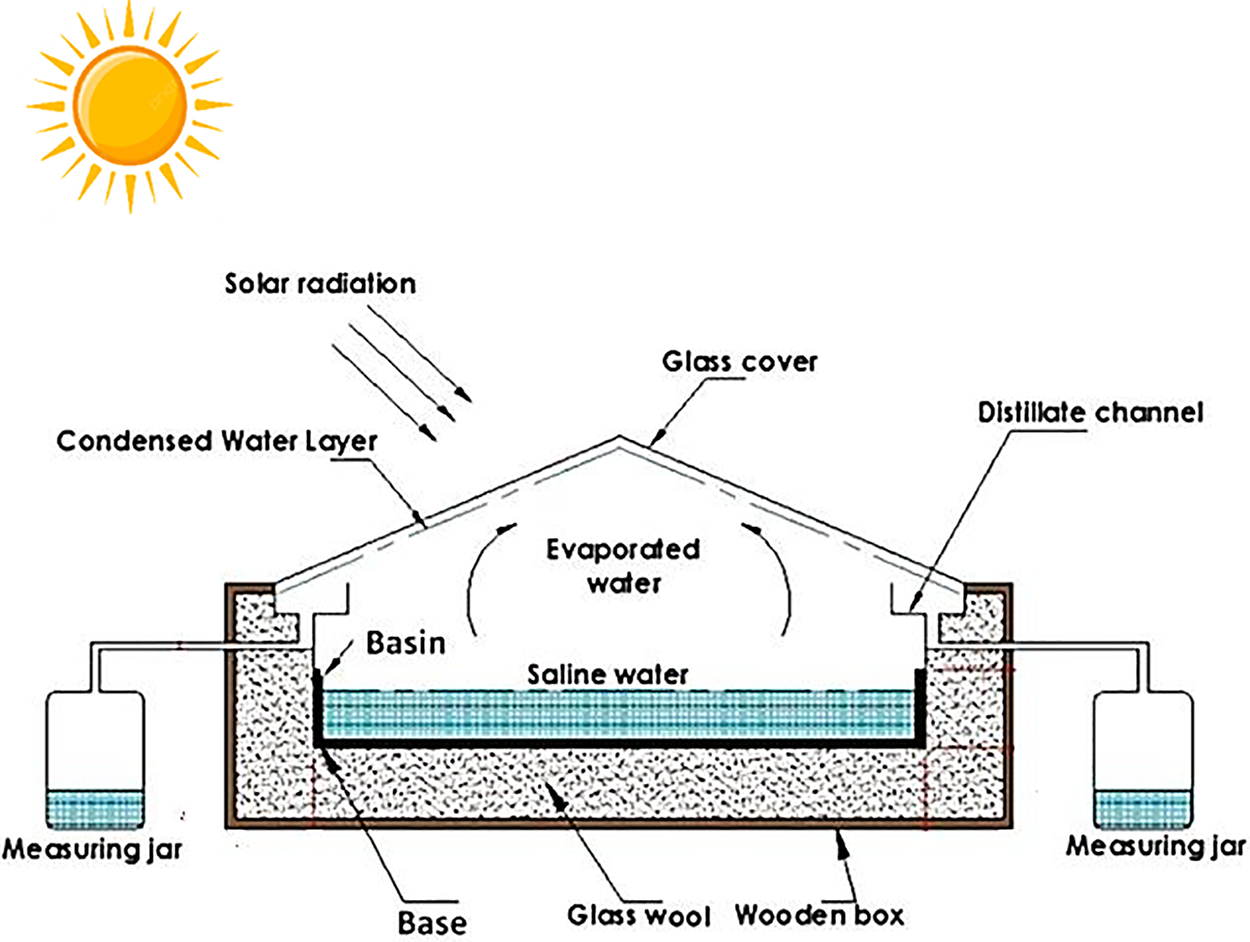
Figure 1: Schematic view of the CPSS
In the subsequent sections, detailed explanations of the energy balance equations and heat transfer mechanisms governing the operation of the solar still will be presented.
4 Heat Transfer Mechanisms in a Solar Distiller
The concurrent transfer in heat and mass occurring within a solar still is the basic mechanism for water evaporating and condensing stages. The process of heat transfer, internally or externally, happens in the still depending on its flow of thermal energy inside or outside the system. Regarding the internal process, it is usually the engine for evaporating the raw water and transferring its vapor, leaving behind all the sorts of impurities inside the basin of the solar still. The external process, in contrast, is in charge of the yielding the fresh water by condensing its vapor. Both of these principal heat transfer processes will be described in the following two subsections [57].
During this process, significant heat transfer occurs within the confined space between the water surface in the basin and the inner surface of the glass cover of the solar still. This heat transfer encompasses three distinct mechanisms: evaporation, convection, and radiation processes taking place within the solar still.
4.1.1 Convection Heat Transfer
The heat transfer mechanism in this process is quite complex, involving two stages: thermal conduction and fluid motion. It depends largely on the properties of the solid surfaces (such as their roughness and geometry) and the properties of the water and air. In a typical solar distiller, this heat transfer occurs between the water in the basin and the inner surface of the glass cover, facilitated by the moist air between them, driven by differences in temperature.
The rate of convective heat transfer within this enclosed space can be denoted as (
where, (
On the other side, the saturation vapor pressures at water temperature (Tw) and at the temperature for top glass cover’s internal face (Tg) stated in the preceding equation can be estimated as follows [58]:
Radiation is the fastest heat transfer mechanism and can occur in gases, liquids, and solids. It is not significantly affected by a vacuum and can even occur between two substances separated by a colder medium. In solar distillation, heat is transferred by radiation between the water in the distiller and the inner side of the glass cover. The rate of this heat transfer depends largely on the view factor between these two surfaces. For a solar still with a single basin and a single slope, this view factor is usually considered as unity. The heat transfer by radiation (
For this equation, the part
In addition, the effective emittance (εeff) of the preceding equation can be computed by the following empirical relationship:
4.1.3 Evaporation Heat Transfer
Evaporation is a process where water transforms into water vapor at the boundary between the liquid water and the vapor phase when the vapor pressure becomes lower than the diffusion pressure of water at a specific temperature. The rate of evaporative heat transfer
where,
The entire rate of internal heat energy transfer between raw water and basin inside glass cover is, as a result, computed as the total effects of all the three kinds of heat transport variations-by convection (
The total rate of heat energy internally transferred can be alternatively computed as a function of the overall coefficient of internal heat transfer and temperatures of both salty water and the inner face of the glass cover, as illustrated in the following formula:
For the above equation the value of the overall internal heat transfer coefficient transfer (
Energy transfer in a solar still involves three distinct processes: convection, conduction, and radiation, each occurring independently. This process accounts for the loss of thermal energy from the solar still to the surrounding environment. In a typical solar still unit, we consider three components.
The heat energy is externally transported from the outside glass cover’s surface to the atmosphere by the aid of both processes of radiation and convection. The rate of heat loss due to convection from external surface of the glass cover to the outside is calculated as follows [61]:
where,
Thermal energy lost by the radiation from the external part of the glass cover to the outside ambient can be quantified using this expression:
Or:
where,
Different models are available for the effective sky temperature
where,
or it is calculated as:
Eqs. (20) and (21) are applied for moist climate only. Eq. (19) is adopted when dew point temperature or relative humidity is available; otherwise, Eq. (20) is used.
The overall collective effect of heat energy loss by radiation (
Similarly, it is also can be written in terms of the entire top-loss heat transfer coefficient, and the temperatures of the ambient air and the top glass cover external part [65]:
Moreover, the coefficient of overall heat loss (top) (
The coefficient of overall heat energy loss (top) can additionally be quantified depending of wind velocity of wind (v) as follows Tiwari et al. [66]:
It is observed that thermal energy is dissipated from the water and basin liner to the surroundings via the insulation material through three heat transfer mechanisms: radiation, conduction, and convection. These three processes of heat energy transfer within the solar desalination unit are expressed as follows:
● The rate of energy transfer due to convection can incorporate the brackish water and basin liner; it is calculated using this relationship [66]:
where,
● Conductive heat transferability occurring between bottom of basin and the outside atmosphere through the insulating material can be quantified as follows [66]:
where, the overall coefficient of heat transfer (
where, Li is the insulation material thickness (m), Ki is the insulation material thermal conductivity (W/m2.K) and
The schematic diagram, depicted in Fig. 2, illustrates the interactions among the different components of a solar still. The heat transfer between each component is comparable in nature to the current flow within an electrical circuit. The presented electrical analogy diagram offers a simplified depiction of the intricate heat transfer mechanisms occurring within a solar still. This facilitates a visual and intuitive comprehension of the variables that influence the rates of water evaporation and heat transfer efficacy.

Figure 2: Electrical analogy model for heat transfer in a solar still
To effectively develop any system, theoretical thermal modeling is a crucial starting point. This process helps in various ways, such as determining key design parameters, exploring system improvements, testing its capabilities before full-scale implementation, and assessing its performance compared to existing alternatives. In the case of solar stills, their performance is typically predicted based on factors like efficiency and daily yield. Despite the apparent simplicity of solar stills, their theoretical analysis is too intricate. There are two fundamental approaches to thermal modeling:
• Energy analysis: This method employs the first law of thermodynamics (1st law energy efficiency) to understand and optimize energy usage.
• Exergy analysis: It utilizes the second law of thermodynamics (second law energy efficiency) to analyze the quality of energy transfer within the system.
Both approaches are essential for comprehensively evaluating and improving thermal systems.
In this section, we will discuss the assumptions and limitations of our models, outlining the potential sources of uncertainty and how they might impact the robustness of our theoretical predictions. We believe this approach will provide readers with a clearer understanding of the theoretical uncertainties associated with our work.
Many assumptions were made to simplify the mathematical model for the case under study, such that energy and exergy equations were solved by Matlab programming. In order to evaluate the important stills component temperatures and other factors, the following main assumptions are considered in the theoretical analysis [58,67,68]:
1. The system is under quasi steady-state regime during day time.
2. Water vapor is an ideal gas.
3. There are no temperature gradients in all the components of distiller.
4. No stratification in the water mass.
5. Constant depth for the water inside the basin.
6. Film condensation happens along the basin glass cover.
7. Heat loss is neglected.
8. Neglect the conduction resistance of glass cover.
9. The solar still is entirely sealed, meaning there are no leaks or openings.
10. The temperature gradient across the thickness of the glass cover and water depth is considered negligible.
11. The physical properties of water are assumed to remain constant even with varying temperatures.
12. The surface areas of the water and the basin are equal.
For a standard thermal system, relevant theoretical equations can be developed based on the energy balance relationships of several parts of the system. The typical components of classical solar still include saline water, a basin, and a top glass cover.
5.2 Conservation of Energy Equations of Solar Still System
Solar radiation, when it strikes a surface, interacts in various ways depending on the material. For instance, in the case of a glass cover, most of the solar radiation is transmitted through it, but some is absorbed and reflected (see Table 1). The transmitted radiation is then absorbed by the saline water in the still, with a small amount of heat being lost through the bottom and sides of the basin. The heat transfer processes within each component of the system are illustrated in Figs. 3–6, while all the modes of heat transfer loss are summarized in Fig. 7. Furthermore, Figs. 8 and 9 illustrate schematic diagrams of the proposed system with a magnetic field alone and with both magnetic and electrical effects, respectively.


Figure 3: Heat balance of the glass cover in the passive solar still (CPSS)

Figure 4: Heat balance of the basin in the passive solar still (CPSS)

Figure 5: Heat balance of water in the passive solar still (CPSS)

Figure 6: Heat balance of water in the active solar sill (EMPSS)

Figure 7: Heat loss modes in the solar still system
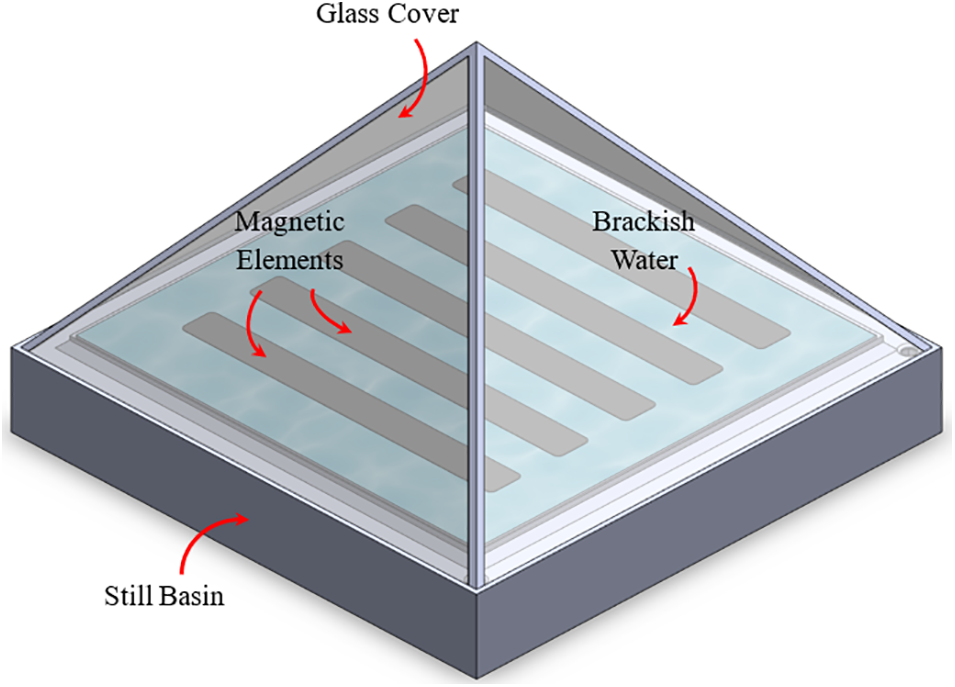
Figure 8: 3D representation of an active pyramid solar still incorporates magnetic field (MPSS)

Figure 9: 3D representation of a magnetic pyramid solar still incorporates electric and magnetic field (EMPSS)
According to the first law of thermodynamics, energy cannot be created or destroyed but can only change forms. This principle can be expressed theoretically as follows [58]:
Or, in the time rate form:
By applying the assumptions outlined in Section 5.1 to each component of the system, we can derive energy balance equations for these components, as detailed below. This research involved the use of two different types of solar stills for comparative analysis:
• Conventional pyramid solar still (CPSS).
• Pyramid solar still with magnetic effect (MPSS).
• Pyramid solar still with electrical field effect (EPSS).
• Pyramid solar still with both magnetic and electrical field effect (EMPSS).
Each of these parts has been analyzed individually, taking into account the type and number of heat sources, as follows.
5.2.1 Conventional Pyramid Solar Still (CPSS)
In order to analyze the solar still system, each component of the solar still must be analyzed individually as follow:
Conservation of Energy of the Glass Cover
The conservation of energy equations of the glass cover can be obtained using the general Eq. (30), but neglect the terms of work and energy rate as follows [68]:
As follows:

where,
In heat flux form (q =
where,
Conservation of Energy of the Basin
Using Eq. (30) when

where,
Conservation of Energy of Saline Water
It is agreed that the sum of solar-based heat energy absorbed by the salty water and the heat energy obtained from still basin by convection is equal to the sum of energy kept in water and the total heat lost to inside surface of glass cover.
Using Eq. (30) when

Using Eqs. (35) and (38), and rearranged the above equations in order to evaluate the temperatures of glass cover and still basin as follows [68]:
To evaluate the water temperature of the passive solar still, substitute the above Eqs. (44) and (45), in Eq. (43), result:
where,
Calculating the sky temperature from equation of (20) and using calculus method to solve the Eq. (48), so by integrating Eq. (48) and apply initial conditions; at t = 0, Twi = Tw, resulting Eq. (49) bellow, which used to calculate the water temperature in the still as follows:
5.2.2 Pyramid Solar Still with Magnetic Effect (MPSS)
Using the same procedure in the conventional pyramid solar still analysis but take into account the effect of magnetic field addition to the system. The theoretical analysis of the glass cover and water are the same as in the passive solar still, and the updated conservation equation for the energy of the basin is [69]:
The above expression can be rearranged as follows:
where,
The final temperature of magnetic element is:
5.2.3 Pyramid Solar Still with Electrical Effect (EPSS)
The electric field effect can be produced by applying a potential difference across the saline water surface using an external power source. The electric field intensity can be controlled by varying the applied potential difference and the distance between the electrodes. Using the same procedure as in the conventional pyramid solar still analysis, but accounting for the effect of the system’s addition of an electrical field, the theoretical analysis of the glass cover and basin is still the same as in the passive solar system, but the equation for saline water is updated to:
where,
In this study, we employ the parameters of the I-V (current-voltage) model to compute the electrical characteristics of the PV/T (photovoltaic/thermal) panel. The model and its reference parameters are based on the work of Yazdanpanahi et al. [70].
The four parameters of this model, which are series resistance (Rs), light current (IL), reverse saturation current (IO), and ideality factor (a), were calculated using the following equations [70]:
The subscript ‘ref’ indicates the value of these parameters under reference conditions (Tc,ref = 25°C, Iref = 1000 W/m2). The values of Voc, Vmp, Isc, and Imp under these reference conditions are typically provided by PV module manufacturers [70].
To calculate the electrical parameters under actual operating conditions (Gc, Tc), a set of translation equations enables the determination of electrical parameters for specific real-world operating conditions, accounting for changes in temperature (Tc) and solar radiation (Gc).
5.2.4 Pyramid Solar Still with Both Magnetic and Electric Field Effect (EMPSS)
Using the same procedure as the conventional pyramid solar still analysis, but considering the influence of magnetic and electric fields on the system, the theoretical analysis of the glass cover remains the same as in the passive solar still (Eq. (35)), and the energy conservation equations for the water and basin remain consistent with Eqs. (51) and (55) mentioned earlier.
5.3.1 Theoretical Distillate Yield
Solar still production rate can be evaluated either hourly or daily, so the production of solar still each hour can be calculated as follows:
The value of
where,
5.3.2 The Efficiency of the Solar Still
Instantaneous energy efficiency is given by the following relationship [71]:
Exergy, often called available work, represents the maximum usable work attainable when a system reaches equilibrium with its surroundings, typically a heat reservoir. It signifies a system’s potential to do useful work as it aligns with its environment. When equilibrium is reached, exergy becomes zero, indicating no further work can be extracted.
In the design and analysis of systems, principles like mass and energy conservation, along with the second law of thermodynamics, can be applied to understand and optimize energy use. Exergy encompasses physical, potential, and kinetic energy. Often, potential and kinetic components are negligible unless there are substantial energy changes.
Exergy happened due to irreversibility and can be given in the following relation [72]:
Exergy destroyed = Exergy input − Exergy accumulation − Exergy output (useful and/or losses).
To simplify the calculations, we have omitted the consideration of exergy accumulation, which encompasses heat capacity contributions from the glass cover, metal basin, and insulation materials integrated into the system.
● Exergy of glass cover
The general exergy equation of the glass cover [73]:
where,
In addition, exergy of solar radiation
where Ta is the temperature of the environment, i.e., temperature (K) of the atmosphere outside the solar still and Tsun is the temperature of the sun (6000 K for the present analysis).
● Exergy of water mass
The general exergy equation of the water mass is presented as follows [75]:
Additionally:
where,
● Exergy of the basin
The general exergy equation of the glass cover present as follows [75]:
● Instantaneous exergy efficiency
The exergy efficiency of the system may be defined as the exergy of the output to the exergy of the input [76]:
where,
By substitute, the Eqs. (82) and (91) into the Eq. (90) result:
Eq. (92) can also be written in the following form:
● Global exergy efficiency of passive solar still.
Global exergy efficiency (O exergy efficiency) is derived above in this thesis can be written in terms of exergy losses (irreversibility of components of solar still) and effective absorptance as follows [73,75]:
Exergy Balance in Solar Still Coupled with Magnets Field
In the case of a solar still coupled with a magnet field only, the exergy analysis in the glass cover and water mass is similar to the method followed in the passive solar still (Eqs. (77) and (83)) but the exergy destruction in the basin with block magnets is estimated by:
Here,
Exergy Balance in Solar Still Coupled with Both Magnetic and Electrical Field
In the case of a solar still coupled with magnets and an electrical field, the exergy analysis in the glass cover is similar to the method followed in the passive solar still (Eq. (83)), and the additional exergy obtained by the magnet field will be added to the basin liner in equation (Eq. (98)). Furthermore, the additional energy obtained by the electrical field will be added to the water mass, and the exergy balance of the water is given by:
Exele. = the rate of electrical exergy
Global Exergy Efficiency of Active Solar Still
The use of magnetic and electrical fields in an active solar still can increase the efficiency of the system by increasing the rate of evaporation. The magnetic field can be used to induce a Lorentz force on the liquid, which can increase the rate of evaporation by enhancing the heat and mass transfer. The electrical field can be used to control the direction of the charged particles in the liquid, which can also increase the rate of evaporation.
By continuously updating Eq. (96) to account for each specific effect and substituting Eq. (95) accordingly, it becomes possible to compute the overall exergy efficiency of an active solar still. Specifically, this can be done for scenarios involving a magnetic field alone and for scenarios involving both magnetic and electrical fields. The relevant equations for these calculations are provided in Eqs. (101) and (102), respectively.
6.1 Numerical Calculations Algorithm
Experimental work provides valuable data under specific conditions, but for a deeper exploration of diverse parameters, numerical methods prove beneficial. Numerical solutions efficiently calculate results, ensuring precision and ease of use. In this theoretical study, a computational model is used to investigate the influence of magnetic and electrical fields on solar still systems. It assesses distillate yield, temperature profiles, and heat transfer coefficients. The computer program solves a set of energy equations to perform this analysis. The computer program is specifically designed to solve a set of energy equations as follows:
• Eq. (35): This equation describes the energy balance of the glass cover in the solar still.
• Eq. (38): This equation pertains to the energy balance of the basin liner within the solar still.
• Eq. (43): This equation addresses the energy balance of the water mass present in the solar still.
• Eq. (51): This equation represents a conservation equation for the energy of the basin in the solar still, considering magnetic effects only.
• Eq. (55): This equation deals with the energy balance of the water mass within the solar still when coupled with an electrical field.
These equations result in three temperature equations, which are solved using an explicit method. The computational process starts with the initial solution of the energy equation, with values for all other variables evaluated. Temperature and thermo physical properties are then updated through iterative energy equation solving. This iteration cycle continues until all designated time steps are completed. This computational approach offers a robust method for comprehensively studying the impact of different parameters on solar still system performance. It allows for precise simulations and provides a deep understanding of the system’s behavior.
6.2 Computer Program Description
A dedicated computer program was developed to execute the numerical solution process as described earlier. The initial phase of this solution process begins with establishing the initial temperatures of the system components, which include the glass cover, water, and basin liner. These initial temperature values are estimated from available data.
Subsequently, the program calculates temperature-dependent thermo physical properties such as thermal conductivity, specific latent heat of vaporization, thermal diffusivity, coefficient of thermal expansively, density, saturation pressure at initial temperatures, and absorption factors. Finally, the program computes heat transfer coefficients and utilizes them to determine the temperatures of each component, as well as new rates of water evaporation, updating the previous values as necessary.
An engineering software program was employed to solve the energy equation, leading to a crucial insight: the energy equation can be effectively solved to determine the temperature profile 𝑇= (t). This computational program was developed using Matlab, operating on Windows 10, Matlab version R2021b to solve the system of equations by using the design factors were described the solar still, as given in the Tables 1–3 are listed below. These data depend on the properties of the various still components as utilized in the theoretical analyses conducted by Kadhum et al. [75–78]. A typical dialog box showing part of the program is presented in Fig. 10.



Figure 10: A dialog box showing part of the calculations was written in Matlab
The program’s structure has been designed to evaluate the thermal performance of both passive and active solar stills, as illustrated in Fig. 11. These flowcharts outline the logical sequence of operations within the computer programs. In both cases, the programs are created to assess vital parameters such as energy and exergy efficiencies for each type of solar still. These programs include explanatory comments, denoted by green text, which clarify the logic and objectives of the program. Furthermore, they incorporate mathematical expressions that represent the system’s equations, allowing for the calculation of various performance metrics.


Figure 11: Flow chart of the active solar still
Solar distillation technology is a really cool and promising solution in the search for sustainable and effective water desalination methods! However, it is really important to optimize its performance for widespread adoption. This study explores a detailed comparison between the theoretical results of evaporative heat transfer coefficients found in the study and the experimental findings of well-known researchers. This comparative exploration is a great way to understand how consistent and reliable the outcomes of this work are in the context of solar distillation.
The present study’s theoretical results for evaporative heat transfer coefficients were compared with the experimental findings of various other researchers. These researchers included Dunkle [79], Panchal et al. [80], and Kadhum et al. [75].
Fig. 12 displays the comparison, illustrating that the behavior of the evaporative heat transfer coefficients in the present work closely resembles that of Dunkle [79], Panchal et al. [80], and Kadhum et al. [75]. During solar distillation at a water depth of 1.5 cm on May 2022. The general trends and patterns of evaporative heat transfer coefficients in the present work align well with the earlier studies, indicating consistent behavior during solar distillation. However, it should be noted that there are differences in the numerical values of the heat transfer coefficients obtained in each study.

Figure 12: The comparison of evaporative heat transfer coefficients for the presented model of a passive solar still with other researchers
These discrepancies in values can be attributed to variations in the hypotheses adopted and the specific weather conditions prevailing during the experiments conducted by different researchers. For a more comprehensive understanding of these variations, refer to Table 4, where detailed information about this parameter. The comparative insights not only contribute to affirming the robustness of the present study but also shed light on potential refinements in solar distillation processes. The implications of these findings extend to the practical implementation of solar distillation systems and beckon further research into nuanced aspects of this critical water purification method. In essence, this comparative analysis acts as a cornerstone for advancing our comprehension of solar distillation dynamics, bridging theory and practice for more effective and sustainable water desalination methods.

8 Numerical Results and Discussion
In this section, we present and analyze the theoretical outcomes obtained from our computational model. These outcomes involve energy and exergy analyses, providing valuable insights into the overall system performance. The energy and exergy analyses aid in comprehending the individual contributions of system components and identifying areas with potential for improvement. Through an examination of energy and exergy flows, we can pinpoint efficiency levels and areas for optimization within the system. Furthermore, we assess the system’s performance, considering key parameters such as energy and exergy efficiency. To validate the robustness of our theoretical models, we conduct a comparative discussion of our results with those proposed by other researchers.
This result presents a comprehensive analysis of the energy performance of passive and modified solar stills. Through various figures, we examine the thermal behavior under different operating conditions, focusing on the impact of integrating electrical and magnetic fields. Detailed discussions provide valuable insights into system performance, highlighting the effectiveness of the integrated approach and the influence of parameters like magnetic field intensity and electrical strength. This enhances our understanding of the improved performance of active solar stills compared to passive ones.
8.1.1 Heat Transfer Coefficients
Figs. 13 to 15 illustrate the hourly variations in theoretical heat transfer coefficients from water in the basin to the glass cover for three types of solar stills: passive, solar coupled with a magnetic field, and solar coupled with both magnetic and electrical fields. The evaporation heat transfer coefficient gradually increases, reaching peak values at 14:00 h (25.05, 32.33, and 40.98 W/m2.°C for the three types, respectively). Subsequently, the evaporation coefficient decreases for all types.

Figure 13: Hourly variation of heat transfer coefficients (evaporative, convective and radiative) of CPSS at depth of water (1.5 cm)

Figure 14: Hourly variation of heat transfer coefficients (evaporative, convective and radiative) of MPSS with (810 mT) magnetic fields

Figure 15: Hourly variation of heat transfer coefficients (evaporative, convective and radiative) of EMPSS with (810 mT & 24 V)
Both convective and radiative heat transfer coefficients are significantly smaller compared to the evaporation coefficient. The maximum convective heat transfer coefficients are (3.58, 4.09, and 4.76 W/m2.°C) for the three types, respectively. Correspondingly, the radiative heat transfer coefficients are (6.55, 6.71, and 6.95 W/m2.°C), respectively. Notably, the theoretical patterns of heat transfer coefficients exhibit similarity among the three types of solar stills.
Figs. 16 to 18 present the hourly variations of theoretical evaporation, convection, and radiation heat transfer coefficients from the water in the basin to the glass cover in three types of solar stills: passive solar still, solar still coupled with a magnetic field, and solar still coupled with both magnetic and electrical fields.

Figure 16: Hourly variation of evaporative heat transfer coefficients of three types of solar stills at depth of water (1.5 cm)

Figure 17: Hourly variation of convective heat transfer coefficients of three types of solar still at depth of water (1.5 cm)

Figure 18: Hourly variation of radiative heat transfer coefficients of three types of solar still at depth of water (1.5 cm)
The analysis reveals a consistent trend across the three types, with heat transfer coefficients gradually increasing until they peak at 14:00, after which they start to decline. It is noteworthy that the simulated results are influenced by the initial values, including a magnetic field intensity of 810 mT and an electrical current intensity of 24 V. As a result, solar stills integrated with a magnetic field and both magnetic and electrical fields demonstrate slightly higher heat transfer coefficients compared to passive solar stills, with a marginal increase of a few percent.
Figs. 19 to 22 showcase the hourly variations in temperatures of the glass cover, ambient surroundings, and saline water for three distinct solar still configurations: a passive solar still, a solar still coupled with a magnetic field, and a solar still coupled with both magnetic and electrical fields. The data was collected through a simulation program, reflecting a typical May month dataset with a water depth of 1.5 cm. The simulations employed a magnetic field intensity of 810 mT and an electrical current intensity of 24 V.

Figure 19: Hourly variation of water, glass cover and ambient temperatures for CPSS at depth of water (1.5 cm)

Figure 20: Hourly variation of water, glass cover and ambient temperatures of MPSS with 810 mT magnetic fields at depth of water (1.5 cm)

Figure 21: Hourly variation of water, glass cover and ambient temperatures of EMPSS with (810 mT & 24 V) at depth of water (1.5 cm)

Figure 22: Hourly variation of water temperatures of three types of solar still at depth of water (1.5 cm)
The temperature trends show consistent patterns for all three types of solar stills. Initially, the temperatures rise gradually due to the increasing intensity of solar radiation until they reach their maximum values after 13:00. Subsequently, the temperatures start to decrease as solar radiation decreases. The daylight hours can be divided into three intervals:
• The first interval (from 8:00 to 11:00) shows insignificant hourly temperature variation due to the low intensity of solar radiation.
• The second interval (from 11:00 to 14:00) displays relatively high temperature variations because of the high solar radiation intensity.
• The third interval after 14:00 exhibits a decrease in solar radiation and, consequently, a decrease in temperatures.
Results show the temperature of the water inside the basin was observed to be higher than the temperature of the glass cover or the external environment in the solar still system. This difference can be attributed to four main factors:
• Greenhouse Effect: The glass cover acts as a greenhouse, trapping solar energy inside the basin and preventing its escape. This leads to enhanced heating of the water, resulting in higher temperatures.
• Direct Solar Radiation: The water inside the basin receives direct solar radiation, providing a direct and efficient source of heat. In contrast, the glass cover and external surfaces may partially reflect or transmit solar radiation, leading to a lesser heating effect.
• Thermal Insulation: The glass cover and external surfaces act as thermal insulators, reducing heat loss from the basin to the surrounding environment. This helps maintain higher temperatures inside the basin.
• Electrical and Magnetic Fields: The presence of electrical and magnetic fields can also play a role in increasing the temperature inside the basin. These fields can stimulate particle movement and enhance the evaporation process, leading to higher temperatures in the water.
These factors boost solar still efficiency by creating a temperature difference between the basin water and the glass cover or the surrounding environment. The analysis demonstrates a consistent behavior between solar radiation and temperature, enhancing our understanding of solar still performance under varying solar radiation levels. This underscores a distinct correlation between solar radiation and temperature fluctuations.
Figs. 23 to 26 depict the average hourly exergy rate variation of three different solar still configurations: CPSS, MPSS coupled with a magnetic field of 810 mT, and EMPSS coupled with both magnetic and electrical fields (810 mT & 24 V).

Figure 23: Hourly variation of exergy rate for CPSS at depth of water (1.5 cm)

Figure 24: Hourly variation of exergy rate for MPSS with 810 mT magnetic fields at depth of water (1.5 cm)

Figure 25: Hourly variation of exergy rate for EMPSS with (810 mT & 24 V) at depth of water (1.5 cm)

Figure 26: Hourly variation of exergy rate of three types of solar still at depth of water (1.5 cm)
In the case of the passive solar still, the exergy associated with evaporation heat transfer between water and the glass cover starts at 0 W/m2 at 8:00 and gradually increases, reaching its maximum value of 21.47 W/m2 at 14:00. On the other hand, the solar still coupled with a magnetic field exhibits a similar trend, starting with 0 W/m2 at 8:00 and reaching a higher maximum value of 47.98 W/m2 at 14:00. Likewise, the solar still coupled with both magnetic and electrical fields follows the same pattern, with exergy associated with evaporation heat transfer starting at 0 W/m2 at 8:00 and reaching the highest value of 63.35 W/m2 at 14:00.
The exergy linked to radiation heat transfer between water and the glass cover, as well as the exergy associated with convection heat transfer, consistently remained at low levels across all three solar still configurations. These results underscore the substantial influence of increased solar radiation, magnetic field intensity, and electrical intensity on exergy rates. The internal energy provided by these factors serves as the driving force for the solar still’s operation. Consequently, any escalation in these energy inputs elevates the water temperature within the system, leading to a higher level of evaporative exergy. This heightened evaporation significantly contributes to the enhanced distillation productivity achieved in the integrated solar stills.
Figs. 27 to 30 illustrate the variations of instantaneous exergy and energy efficiencies for three types of solar stills: passive solar still, solar still coupled with a magnetic field of 810 mT, and solar still coupled with both magnetic and electrical fields (810 mT & 24 V).

Figure 27: Hourly variation of overall instantaneous energy and exergy efficiencies for CPSS at depth of water (1.5 cm)

Figure 28: Hourly variation of overall instantaneous energy and exergy efficiencies for MPSS with 810 mT magnetic fields at depth of water (1.5 cm)

Figure 29: Hourly variation of overall instantaneous energy and exergy efficiencies for EMPSS with (810 mT & 24 V) at depth of water (1.5 cm)

Figure 30: Hourly variation of overall instantaneous energy efficiencies for three types of solar still at depth of water (1.5 cm)
It is evident from these figures that the exergy efficiency is significantly lower than the energy efficiency, with values of (1.6%, 5.31%, and 7.93%) for the three aforementioned types of solar stills, respectively. This difference can be attributed to the relatively small quantities of available energy and exergy associated with the heat evaporation process.
In CPSS, as shown in Fig. 19, the brackish water temperature fluctuates between (19.8°C) and peaks at (57°C) around 14:00. The highest energy efficiency, at (18.6%), aligns with the maximum evaporative heat quantity of (162.4 W/m2) also observed at 14:00. Simultaneously, the corresponding exergy efficiency reaches its peak of (1.6%) at the highest exergy value of (16.75 W/m2) achieved at 14:00.
In MPSS, shown in Fig. 20, the brackish water temperature varies from (22.4°C) and reaches its maximum of (59.3°C) at 14:00. The maximum energy efficiency of (25.29%) corresponds to the peak quantity of evaporative heat (390.21 W/m2) at 14:00. The corresponding maximum exergy efficiency is (5.31%) at its peak exergy value of (28.44 W/m2) achieved at 14:00.
For EMPSS, as presented in Fig. 21, the brackish water temperature varies from (31.3°C) and reaches its maximum of (62.6°C) at 14:00. The maximum energy efficiency of (54%) corresponds to the peak quantity of evaporative heat (720.8 W/m2) at 14:00. The corresponding maximum exergy efficiency is (7.93%) at its peak exergy value of (44.47 W/m2) achieved at 14:00. These results highlight the differences in energy and exergy efficiencies among the three types of solar stills, indicating the potential advantages of employing magnetic and electrical fields to enhance the overall efficiency of the solar stills.
Table 4 presents a comparative analysis between our current findings and previous research outcomes. This assessment aims to gauge the enhanced efficiency of the solar distiller after implementing the proposed modifications. Solar stills integrated with magnetic and electromagnetic effects exhibited significantly superior performance compared to the models discussed in earlier publications.
The present work conducted theoretical investigations on three solar still configurations, namely the passive solar still, the modified solar still coupled with a magnetic field, and the modified solar still coupled with both magnetic and electrical fields, all under the climatic conditions of May in Baghdad. The objective of the study was to gain a comprehensive understanding of the operational dynamics and performance of these configurations under the recommended conditions, thereby offering valuable insights into their prospective uses. The specific findings and conclusions drawn from our theoretical analysis are:
1. The evaporation heat transfer coefficient exhibited a gradual increase, peaking at 14:00, with values of 25.05, 32.33, and 40.98 W/m2.°C for CPSS, MPSS, and EMPSS solar stills, respectively.
2. Convective and radiative heat transfer coefficients were lower than the evaporation heat transfer coefficient.
3. The increase in water temperature inside the basin was influenced by multiple factors, including the greenhouse effect of the glass cover, direct solar radiation, thermal insulation, and the presence of electrical and magnetic fields.
4. Exergy efficiency was found to be significantly lower than energy efficiency, with values of 1.6%, 5.31%, and 7.93% for the three types of solar stills.
5. The maximum energy efficiency of 18.6% occurred at 14:00, corresponding to a peak evaporative heat quantity of 162.4 W/m2. The corresponding maximum exergy efficiency of 1.6% was also achieved at this time.
6. The solar still coupled with a magnetic field reached a maximum energy efficiency of 25.29% at 14:00, coinciding with a peak evaporative heat quantity of 390.21 W/m2. The corresponding maximum exergy efficiency was 5.31% at the peak exergy value of 28.44 W/m2.
7. The solar still coupled with both magnetic and electrical fields achieved a maximum energy efficiency of 54% at 14:00, aligning with a peak evaporative heat quantity of 720.8 W/m2. The corresponding maximum exergy efficiency was 7.93% at this time.
10 Recommendations and Future Scope
The results and findings clearly show that the new design has improved productivity. The following factors are suggested to be studied in the future because of their important advantages. The following points are recommended for further study:
1. Considering the use of magnetic fields in combination with other desalination techniques, such as reverse osmosis or electrodialysis. This could lead to even more efficient and productive desalination systems.
2. Exploring alternative materials: Consider exploring alternative materials for the solar still basin that can better retain and amplify the magnetic field. The choice of materials may significantly influence the overall efficiency and productivity of the system.
3. Incorporating heat storage: Exploring the integration of heat storage systems to store excess thermal energy during peak sunlight hours. This stored heat could be utilized during periods of low solar radiation, enhancing system efficiency and productivity.
4. Enhancing heat transfer mechanisms: Investigating additional methods to improve heat transfer mechanisms within the solar still. Enhancements could include the use of advanced wicking materials, surface coatings, or improved thermal insulation.
5. Comparative studies: Conducting comparative studies with other advanced desalination technologies, such as reverse osmosis and multi-effect distillation, to evaluate the competitiveness of the integrated solar still system in terms of efficiency, cost, and environmental impact.
6. The use of a reflector is very important to increase the thermal flux entering the solar still as a result of increasing its productivity.
Acknowledgement: The authors extend their thanks to the University of Warith Al-Anbiyaa, Karbala, Iraq, for financial support for this study.
Funding Statement: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Author Contributions: Study conception and design: Karrar A. Hammoodi, Hayder A. Dhahad; data collection, Wissam H. Alawee and Z. M. Omara; draft manuscript preparation, analysis and interpretation of results. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest: All authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Singh, A. K. (2021). An inclusive study on new conceptual designs of passive solar desalting systems. Heliyon, 7(2), E05793. https://doi.org/10.1016/j.heliyon.2020.e05793 [Google Scholar] [PubMed] [CrossRef]
2. Katekar, V. P., Deshmukh, S. S. (2020). A review of the use of phase change materials on performance of solar stills. Journal of Energy Storage, 30, 101398. https://doi.org/10.1016/j.est.2020.101398 [Google Scholar] [CrossRef]
3. Zhang, Y., Sivakumar, M., Yang, S., Enever, K., Ramezanianpour, M. (2018). Application of solar energy in water treatment processes: A review. Desalination, 428, 116–145. https://doi.org/10.1016/j.desal.2017.11.020 [Google Scholar] [CrossRef]
4. Hammoodi, K. A., Dhahad, H. A., Alawee, W. H., Omara, Z. M., Essa, F. et al. (2023). Improving the performance of a pyramid solar still using different wick materials and reflectors in Iraq. Desalination and Water Treatment, 285, 1–10. https://doi.org/10.5004/dwt.2023.29226 [Google Scholar] [CrossRef]
5. Essa, F. A., Abdullah, A. S., Omara, Z. (2023). Enhancement of pyramid solar distiller performance using thermal storage material. Journal of Contemporary Technology and Applied Engineering, 2(1), 56–64. https://doi.org/10.21608/JCTAE.2023.233154.1016 [Google Scholar] [CrossRef]
6. Kavitha, S., Nagarajan, M., Sengottaiyan, S. (2023). Regenerative effect of pyramid solar still with incorporation of nickel oxide particles in the basin. Environmental Progress & Sustainable Energy, 42(3), e14051. https://doi.org/10.1002/ep.14051. [Google Scholar] [CrossRef]
7. Yuanlei, S., Hammoodi, K. A., Sajadi, S. M., Rashid, F. L., Li, Z. et al. (2024). The effect of initial conditions (temperature and pressure) on combustion of Fe-coated-aluminum hydride nanoparticles using the molecular dynamics approach. Case Studies in Thermal Engineering, 53, 103901. https://doi.org/10.1016/j.csite.2023.103901. [Google Scholar] [CrossRef]
8. Naji, D., Al, D., Kadim, M., Alkanany, N., Hammoodi, K. A. (2023). Revue des Composites et des Matériaux Avancés. Journal of Composite and Advanced Materials Improving the Mechanical Properties of the Air-Conditioning Pipe Using Composite Materials, 33(2), 103–109. https://doi.org/10.3389/fenrg.2021.754546 [Google Scholar] [CrossRef]
9. Castellanos H. G., Aryanfar Y., Hammoodi K. A., Ghriss O., Keçebaşet A., et al. Evaluation of the energy and exergy of a trans-critical CO2 cycle driven by a double flash geothermal power plant. Environmental Progress & Sustainable Energy, 2024, https://doi.org/10.1002/ep.14370 [Google Scholar] [CrossRef]
10. Marghany, M., Hasab, H. A., Mansor, S., Bin Mohamed Shariff, A. R. (2016). Developing hydrological model for water quality in Iraq marshes zone using Landsat-TM. IOP Conference Series: Earth and Environmental Science, 37(1), 6–11. https://doi.org/10.1088/1755-1315/37/1/012073 [Google Scholar] [CrossRef]
11. Rghif, Y., Colarossi, D., Principi, P. (2023). Salt gradient solar pond as a thermal energy storage system: A review from current gaps to future prospects. Journal of Energy Storage, 61, 106776. https://doi.org/10.1016/j.est.2023.106776 [Google Scholar] [CrossRef]
12. Basem, A., Hammoodi, K. A., Al-Tajer, A. M., Mohsen, A. M., Omar, I. (2022). A numerical investigation of the increase in heat transfer in a half-cylindrical container filled with phase change copper rods. Case Studies in Thermal Engineering, 40, 102512. https://doi.org/10.1016/j.csite.2022.102512 [Google Scholar] [CrossRef]
13. Fadhil, N. A., Hammoodi, K. A., Jassim, L., Al-Asadi, H. A., Habeeb, L. J. (2023). Multiphysics analysis for fluid-structure interaction of blood biological flow inside three-dimensional artery. Curved and Layered Structures, 10(1), 20220187. https://doi.org/10.18280/mmep.090229 [Google Scholar] [CrossRef]
14. Fadhil, N. A., Hammoodi, K. A., Jassim, L., Al-Asadi, H. A., Habeeb, L. J. (2023). Multiphysics analysis for fluid–structure interaction of blood biological flow inside three-dimensional artery. Curved and Layered Structures, 10(1), 20220187. [Google Scholar]
15. World Health Organization (2010). Joint monitoring programme for water supply and sanitation: Report on intercountry workshop, Jakarta, Indonesia, No. SEA-EH-563. WHO Regional Office for South-East Asia. [Google Scholar]
16. Alawee, W. H., Abdullah, A. S., Suha, A. M., Hayder, A. D., Omara, Z. M. et al. (2022). Augmenting the distillate yield of cords pyramid distiller with baffles within compartments. Journal of Cleaner Production, 356, 131761. https://doi.org/10.1016/j.jclepro.2022.131761 [Google Scholar] [CrossRef]
17. Kazem, H. A., Chaichan, M. T. (2012). Status and future prospects of renewable energy in Iraq. Renewable and Sustainable Energy Reviews, 16, 6007–6012. https://doi.org/10.1016/j.rser.2012.03.058 [Google Scholar] [CrossRef]
18. Mousa, H., Naser, J., Gujarathi, A. M., Al-Sawafi, S. (2019). Experimental study and analysis of solar still desalination using phase change materials. Journal of Energy Storage, 26, 100959. https://doi.org/10.1016/j.est.2019.100959 [Google Scholar] [CrossRef]
19. Mohan, I., Yadav, S., Panchal, H., Brahmbhatt, S. (2019). A review on solar still: A simple desalination technology to obtain potable water. International Journal of Ambient Energy, 40(3), 335–342. https://doi.org/10.1080/01430750.2017.1393776 [Google Scholar] [CrossRef]
20. Durkaieswaran, P., Murugavel, K. K. (2015). Various special designs of single basin passive solar still—a review. Renewable and Sustainable Energy Reviews, 49, 1048–1060. https://doi.org/10.1016/j.rser.2015.04.111 [Google Scholar] [CrossRef]
21. Singh, A. K., Gautam, S. (2022). Optimum techno-eco performance requisites for vacuum annulus tube collector-assisted double-slope solar desaltification unit integrated modified parabolic concentrator. Environmental Science and Pollution Research, 29, 34379–34405. https://doi.org/10.1007/s11356-021-18426-x [Google Scholar] [PubMed] [CrossRef]
22. Daneshmand, S., Vini, M. H., Mohammad Sajadim, S., Mouthanna, A., Jasim, D. J. et al. (2023). Numerical and experimental investigations of mechanical, tribological, and electrical properties of laminated Bi-metal Al/SiC/Ni composites. Materials Today Communications, 37, 107355. [Google Scholar]
23. Sun, C., Fares, M. N., Sajadi, S. M., Li, Z., Jasim, D. J. et al. (2024). Numerical examination of exergy performance of a hybrid solar system equipped with a sheet-and-sinusoidal tube collector: Developing a predictive function using artificial neural network. Case Studies in Thermal Engineering, 53, 103828. [Google Scholar]
24. Omara, Z. M., Alawee, W. H., Mohammed, S. A., Dhahad, H. A., Abdullah, A. S. et al. (2022). Experimental study on the performance of pyramid solar still with novel convex and dish absorbers and wick materials. Journal of Cleaner Production, 373, 133835. https://doi.org/10.1016/j.jclepro.2022.133835 [Google Scholar] [CrossRef]
25. Hussen, H. M., Younes, M. M., Alawee, W. H., Abdullah, A. S., Mohammed, S. A. et al. (2023). An experimental comparison study between four different designs of solar stills. Case Studies in Thermal Engineering, 44, 102841. https://doi.org/10.1016/j.csite.2023.102841 [Google Scholar] [CrossRef]
26. Essa, F. A., Alawee, W. H., Abdullah, A. S., Aljaghtham, M., Mohammed, S. A. et al. (2022). Augmenting the performance of pyramid distiller via conical absorbing surface, reflectors, condenser, and thermal storing material. Journal of Energy Storage, 55, 105597. https://doi.org/10.1016/j.est.2022.105597 [Google Scholar] [CrossRef]
27. Abdullah, A. S., Alawee, W. H., Mohammed, S., Majdi, A., Omara, Z. et al. (2023). Utilizing a single slope solar still with copper heating coil, external condenser, phase change material, along with internal and external reflectors—Experimental study. Journal of Energy Storage, 63, 106899. https://doi.org/10.1016/j.est.2023.106899 [Google Scholar] [CrossRef]
28. Abdullah, A. S., Alawee, W. H., Mohammed, S. A., Majdi, A., Omara, Z. M. et al. (2023). Increasing the productivity of modified cords pyramid solar still using electric heater and various wick materials. Process Safety and Environmental Protection, 169, 169–176. https://doi.org/10.1016/j.psep.2022.11.016 [Google Scholar] [CrossRef]
29. Hammoodi, K. A., Dhahad, H. A., Alawee, W. H., Omara, Z. M. (2023). A detailed review of the factors impacting pyramid type solar still performance. Alexandria Engineering Journal, 66, 123–154. https://doi.org/10.1016/j.aej.2022.12.006 [Google Scholar] [CrossRef]
30. Guo, Z. (2020). A review on heat transfer enhancement with nanofluids. Journal of Enhanced Heat Transfer, 27(1), 1–70. https://doi.org/10.1615/JEnhHeatTransf.2019031575 [Google Scholar] [CrossRef]
31. Asdrubali, F., D’Alessandro, F., Schiavoni, S. (2015). A review of unconventional sustainable building insulation materials. Sustainable Materials and Technologies, 4, 1–17. https://doi.org/10.1016/j.susmat.2015.05.002 [Google Scholar] [CrossRef]
32. Nagarajan, P. K., El-Agouz, S. A., Arunkumar, T., Sathyamurthy, R. (2017). Effect of forced cover cooling technique on a triangular pyramid solar still. International Journal of Ambient Energy, 38(6), 597–604. https://doi.org/10.1080/01430750.2016.1159609 [Google Scholar] [CrossRef]
33. Abdullah, A. S. (2013). Improving the performance of stepped solar still. Desalination, 319, 60–65. https://doi.org/10.1016/j.desal.2013.04.003 [Google Scholar] [CrossRef]
34. Abdulsahib, A. D., Hammoodi, K. A. A., Omar, I., Murad, M. E., Flayyih, M. A. (2022). An analysis of how different forms of heated bodies affect thermal conductivity inside a nanofluid square domain. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 98(1), 104–115. https://doi.org/10.37934/arfmts.98.1.105116 [Google Scholar] [CrossRef]
35. Hegazy, A. A. (2001). Effect of dust accumulation on solar transmittance through glass covers of plate-type collectors. Renewable Energy, 22(4), 525–540. https://doi.org/10.1016/S0960-1481(00)00093-8 [Google Scholar] [CrossRef]
36. El-Nashar, A. M. (1994). The effect of dust accumulation on the performance of evacuated tube collectors. Solar Energy, 53(1), 105–115. https://doi.org/10.1016/S0038-092X(94)90610-6 [Google Scholar] [CrossRef]
37. Montes, M. J., Abánades, A., Martínez-Val, J. M., Valdés, M. (2009). Solar multiple optimization for a solar-only thermal power plant, using oil as heat transfer fluid in the parabolic trough collectors. Solar Energy, 83(12), 2165–2176. https://doi.org/10.1016/j.solener.2009.08.010 [Google Scholar] [CrossRef]
38. Cura, D., Yilmaz, M., Koten, H., Senthilraja, S., Awad, M. M. (2022). Evaluation of the technical and economic aspects of solar photovoltaic plants under different climate conditions and feed-in tariff. Sustainable Cities and Society, 80, 103804. https://doi.org/10.1016/j.scs.2022.103804 [Google Scholar] [CrossRef]
39. Riahi, A., Ali, A. B. H., Fadhel, A., Guizani, A., Balghouthi, M. (2020). Performance investigation of a concentrating photovoltaic thermal hybrid solar system combined with thermoelectric generators. Energy Conversion and Management, 205, 112377. https://doi.org/10.1016/j.enconman.2019.112377 [Google Scholar] [CrossRef]
40. Kabeel, A. E., Hamed, M. H., Omara, Z. M. (2012). Augmentation of the basin type solar still using photovoltaic powered turbulence system. Desalination and Water Treatment, 48(1–3), 182–190. https://doi.org/10.1080/19443994.2012.698811 [Google Scholar] [CrossRef]
41. Elbar, A., Refat, A., Hassan, H. (2020). An experimental work on the performance of new integration of photovoltaic panel with solar still in semi-arid climate conditions. Renewable Energy, 146, 1429–1443. https://doi.org/10.1016/j.renene.2019.07.069 [Google Scholar] [CrossRef]
42. Shahsavar, A., Afrand, M., Kalbasi, R., Aghakhani, S., Bakhsheshi-Rad, H. R. et al. (2023). A comprehensive review on the application of nanofluids and PCMs in solar thermal collectors: Energy, exergy, economic, and environmental analyses. Journal of the Taiwan Institute of Chemical Engineers, 104856. https://doi.org/10.1016/j.jtice.2023.104856 [Google Scholar] [CrossRef]
43. Jamil, H., Alam, M., Sanjayan, J. (2019). Thermal performance of hollow-core slab ventilation system with macro-encapsulated phase-change materials in supply air duct. Buildings, 9(2), 51. https://doi.org/10.3390/buildings9020051 [Google Scholar] [CrossRef]
44. Safaei, M. R., Goshayeshi, H. R., Chaer, I. (2002). Solar still efficiency enhancement by using graphene oxide/paraffin nano-PCM. Energies, 12(10), 2002. https://doi.org/10.3390/en12102002 [Google Scholar] [CrossRef]
45. Alawee, W. H., Essa, F. A., Mohammed, S. A., Dhahad, H. A., Abdullah, A. S. et al. (2021). Improving the performance of pyramid solar distiller using dangled cords of various wick materials: Novel working mechanism of wick. Case Studies in Thermal Engineering, 28, 101550. https://doi.org/10.1016/j.csite.2021.101550 [Google Scholar] [CrossRef]
46. Kabeel, A. E., Abdelgaied, M. (2020). Enhancement of pyramid-shaped solar stills performance using a high thermal conductivity absorber plate and cooling the glass cover. Renewable Energy, 146, 769–775. https://doi.org/10.1016/j.renene.2019.07.020 [Google Scholar] [CrossRef]
47. Alawee, W. H., Essa, F. A., Mohammed, S. A., Dhahad, H. A., Abdullah, A. S. et al. (2021). Improving the performance of pyramid solar distiller using dangled cords of various wick materials: novel working mechanism of wick. Case Studies in Thermal Engineering, 28, 101550. https://doi.org/10.1016/j.csite.2021.101550 [Google Scholar] [CrossRef]
48. Kaviti, A. K., Ram, A. S., Thakur, A. K. Influence of fully submerged permanent magnets in the evaluation of heat transfer and performance analysis of single slope glass solar still. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 236(1), 109–123. https://doi.org/10.1080/01430750.2020.1722746 [Google Scholar] [CrossRef]
49. Wang, Y., Wei, H., Li, Z. (2018). Effect of magnetic field on the physical properties of water. Results in Physics, 8, 262–267. https://doi.org/10.1016/j.rinp.2017.12.022 [Google Scholar] [CrossRef]
50. Alawee, W. H., Hammoodi, K. A., Dhahad, H., Dhahad, Z., Omara, F. E. et al. (2023). Effects of magnetic field on the performance of solar distillers: A review study. Engineering and Technology Journal, 41(1), 121–131. [Google Scholar]
51. Szcześ, A., Chibowski, E., Rzeźnik, E. (2020). Magnetic field effect on water surface tension in aspect of glass and mica wettability. Colloids and Interfaces, 4(3), 37. https://doi.org/10.3390/colloids4030037 [Google Scholar] [CrossRef]
52. Hammoodi, K. A., Dhahad, H. A., Alawee, W. H., Amro, M. I., Omara, Z. M. et al. (2023). Experimental study on pyramid solar distiller performance with applying magnet field under various operating conditions. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 45(4), 11410–11423. https://doi.org/10.1080/15567036.2023.2258081 [Google Scholar] [CrossRef]
53. Kadim, A. M., Hammoodi, K. A., Salih, G. S. (2018). Fabrication of hybrid QDOLEDs from core/shell/shell QDs and conductive organic polymers. Nano Hybrids and Composites, 22, 11–22. [Google Scholar]
54. Aich W., Hammoodi K.A., Mostafa L., Saraswat M., Shawabkeh A. et al. Techno-economic and life cycle analysis of two different hydrogen production processes from excavated waste under plasma gasification. Process Safety and Environmental Protection, 184, 1158–1176. [Google Scholar]
55. Hammoodi, K. A., Dhahad, H. A., Alawee, W. H., Omara, Z. M., Yusaf, T. (2023). Pyramid solar distillers: A comprehensive review of recent techniques. Results in Engineering, 18, 101157. https://doi.org/10.1016/j.rineng.2023.101157 [Google Scholar] [CrossRef]
56. Angappan, G., Pandiaraj, S., Panchal, H., Kathiresan, T., Ather, D. et al. (2022). An extensive review of performance enhancement techniques for pyramid solar still for solar thermal applications. Desalination, 532, 115692. https://doi.org/10.1016/j.desal.2022.115692 [Google Scholar] [CrossRef]
57. Elango, C., Gunasekaran, N., Sampathkumar, K. (2015). Thermal models of solar still—a comprehensive review. Renewable and Sustainable Energy Reviews, 47, 856–911. https://doi.org/10.1016/j.rser.2015.03.054 [Google Scholar] [CrossRef]
58. Mohammed, R. H., Askalany, A. A. (2019). Productivity improvements of adsorption desalination systems. Solar Desalination Technology, 325–357. https://doi.org/10.1007/978-981-13-6887-5_15 [Google Scholar] [CrossRef]
59. Rabbi, H. M. F., Sahin, A. Z. (2021). Performance improvement of solar still by using hybrid nanofluids. Journal of Thermal Analysis and Calorimetry, 143, 1345–1360. https://doi.org/10.1007/s10973-020-10155-6 [Google Scholar] [CrossRef]
60. Jobrane, M., Kopmeier, A., Kahn, A., Cauchie, H. M., Kharroubi, A. et al. (2022). Theoretical and experimental investigation on a novel design of wick type solar still for sustainable freshwater production. Applied Thermal Engineering, 200, 117648. https://doi.org/10.1016/j.applthermaleng.2021.117648 [Google Scholar] [CrossRef]
61. Nayi, K. H., Modi, K. V. (2018). Pyramid solar still: A comprehensive review. Renewable and Sustainable Energy Reviews, 81, 136–148. https://doi.org/10.1016/j.rser.2017.07.004 [Google Scholar] [CrossRef]
62. Deceased, J. A. D., Beckman, W. A. (2013). Thermal processes solar engineering. Solar Energy Laboratory, The University of Wisconsin-Madison, John Wiley & Sons. [Google Scholar]
63. Radwan, S. M., Hassanain, A. A., Abu-Zeid, M. A. (2009). Single slope solar still for sea water distillation. World Applied Sciences Journal, 7(4), 485–497. https://doi.org/10.13140/RG.2.2.35804.59525 [Google Scholar] [CrossRef]
64. Haruna, I. U., Yerima, M., Pukuma, A. D., Sambo, I. I. (2014). Experimental investigation of the performance of basin type single-slope solar still. International Journal of Scientific & Technology Research, 3(3), 169–174. [Google Scholar]
65. Ashok Kumar Singh, R. K. Y., Mishra, D., Prasad, R., Gupta, L. K., Kumar, P. (2020). Active solar distillation technology: A wide overview. Desalination, 493, 114652. https://doi.org/10.1016/j.desal.2020.114652 [Google Scholar] [CrossRef]
66. Tiwari, G. N., Sahota, L. (2017). Advanced solar-distillation systems: basic principles, thermal modeling, and its application. Springer. [Google Scholar]
67. Sampathkumar, K., Arjunan, T. V., Senthilkumar, P. (2011). Single basin solar still coupled with evacuated tubes-thermal modeling and experimental validation. International Energy Journal, 12(1), 53–66. [Google Scholar]
68. Hussein, A. A., Jassim, N. A. (2022). Experimental investigation of solar still with separate condenser coupled. Materials Today: Proceedings, 60, 1611–1622. [Google Scholar]
69. Dhivagar, R., Mohanraj, M., Raj, P., Gopidesi, R. K. (2021). Thermodynamic analysis of single slope solar still using graphite plates and block magnets at seasonal climatic conditions. Water Science and Technology, 84(10–11), 2635–2651. https://doi.org/10.2166/wst.2021.156 [Google Scholar] [PubMed] [CrossRef]
70. Yazdanpanahi, J., Sarhaddi, F., Adeli, M. M. (2015). Experimental investigation of exergy efficiency of a solar photovoltaic thermal (PVT) water collector based on exergy losses. Solar Energy, 118, 197–208. https://doi.org/10.1016/j.solener.2015.04.038 [Google Scholar] [CrossRef]
71. Ranjan, K. R., Kaushik, S. C., Panwar, N. L. (2016). Energy and exergy analysis of passive solar distillation systems. International Journal of Low-Carbon Technologies, 11(2), 211–221. https://doi.org/10.1093/ijlct/ctt069 [Google Scholar] [CrossRef]
72. Zhang, Y., Hammoodi, K. A., Sajadi, S. M., Li, Z., Jasim, D. J. et al. (2023). Obtaining an accurate prediction model for viscosity of a new nano-lubricant containing multi-walled carbon Nanotube-Titanium dioxide nanoparticles with oil SAE50. Tribology International, 191, 109185. [Google Scholar]
73. Vaithilingam, S., Esakkimuthu, G. S. (2015). Energy and exergy analysis of single slope passive solar still: An experimental investigation. Desalination and Water Treatment, 55(6), 1433–1444. https://doi.org/10.1080/19443994.2014.928794 [Google Scholar] [CrossRef]
74. Ataee, S., Ameri, M. (2015). Energy and exergy analysis of all-glass evacuated solar collector tubes with coaxial fluid conduit. Solar Energy, 118, 575–591. https://doi.org/10.1016/j.solener.2015.06.019 [Google Scholar] [CrossRef]
75. Kadhum, N. A., Jassim, N. A., Lateef, K. H. (2020). Thermal modeling of solar still coupled with heat pipes and experimental validation. Journal of Engineering, 26(6), 172–192. [Google Scholar]
76. Elsheikh, A., Hammoodi, K. A., Ibrahim, A., Mourad, A. H. I., Fujii, M. et al. (2023). Augmentation and evaluation of solar still performance: A comprehensive review. Desalination, 117239. [Google Scholar]
77. Sathyamurthy, R., Nagarajan, P. K., Vijayakumar, D. (2016). Experimental validation of fresh water production using triangular pyramid solar still with PCM storage. International Journal of Engineering Research in Africa, 20, 51–58. https://doi.org/10.4028/www.scientific.net/JERA.20.51 [Google Scholar] [CrossRef]
78. Hedayati-Mehdiabadi, E., Sarhaddi, F., Sobhnamayan, F. (2020). Exergy performance evaluation of a basin-type double-slope solar still equipped with phase-change material and PV/T collector. Renewable Energy, 145, 2409–2425. https://doi.org/10.1016/j.renene.2019.07.160 [Google Scholar] [CrossRef]
79. Dunkle, R. V. (1961). Solar water distillation: The roof type still and a multiple effect diffusion still. Proceedings of the International Heat Transfer Conference, vol. 5. USA, University of Colorado. [Google Scholar]
80. Panchal, H. N., Shah, P. K. (2012). Effect of varying glass cover thickness on performance of solar still: In a winter climate conditions. International Journal of Renewable Energy Research, 1(4), 212–223. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools