 Open Access
Open Access
ARTICLE
Comparative Numerical Analysis of Heat and Mass Transfer Characteristics in Sisko Al2O3-Eg and TiO2-Eg Fluids on a Stretched Surface
1 Department of Humanities and Science, Ravindra College of Engineering for Women, Kurnool, Andhra Pradesh, 518002, India
2 Department of Mechanical Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, Andhra Pradesh, 522302, India
3 Department of Biological and Agricultural Engineering, Faculty of Engineering, Universiti Putra Malaysia, Serdang, Selangor, 43400, Malaysia
4 Department of Mechanical Engineering, ANURAG Engineering College (Autonomous) in Kodad, Telangana, 508206, India
5 Department of Mechanical Engineering, CVR College of Engineering, Ibrahimpatnam, Telangana, 501510, India
6 Faculty of Engineering, Kuwait College of Science & Technology, Doha District, 35004, Kuwait
7 Department of Mathematics, G Pulla Reddy College of Engineering College (Autonomous), Kurnool, 518002, India
* Corresponding Author: Abhishek Dasore. Email:
Frontiers in Heat and Mass Transfer 2024, 22(1), 79-105. https://doi.org/10.32604/fhmt.2024.046891
Received 18 October 2023; Accepted 13 December 2023; Issue published 21 March 2024
Abstract
In the current research, a thorough examination unfolds concerning the attributes of magnetohydrodynamic (MHD) boundary layer flow and heat transfer inherent to nanoliquids derived from Sisko Al2O3-Eg and TiO2-Eg compositions. Such nanoliquids are subjected to an extending surface. Consideration is duly given to slip boundary conditions, as well as the effects stemming from variable viscosity and variable thermal conductivity. The analytical approach applied involves the application of suitable similarity transformations. These conversions serve to transform the initial set of complex nonlinear partial differential equations into a more manageable assembly of ordinary differential equations. Through the utilization of the FEM, these reformulated equations are solved, considering the specified boundary conditions. The outcomes attained are graphically depicted by means of plots and tables. These visual aids facilitate a comprehensive exploration of how diverse parameters exert influence over the distributions of velocity, temperature, and concentration. Furthermore, detailed scrutiny is directed towards the fluctuations characterizing pivotal parameters, viz., Nusselt number, skin-friction coefficient, and Sherwood number. It is identified that the Nusselt number showcases a diminishing trend coinciding with increasing values of the volume fraction parameter (ϕ). This trend remains consistent regardless of whether the nanoliquid under consideration is Al2O3-Eg or TiO2-Eg based. In contrast, both the skin-friction coefficient and Sherwood number assume lower values as the volume fraction parameter (ϕ) escalates. This pattern remains congruent across both classifications of nanoliquids. The findings of the study impart valuable insights into the complex interplay governing the characteristics of HMT pertaining to Sisko Al2O3-Eg and TiO2-Eg nanoliquids along an extending surface.Graphic Abstract

Keywords
Nomenclature
| B0 | Magnetic field strength |
| B | Sisko fluid parameter |
| B2 | Variable thermal viscosity |
| B3 | Variable thermal conductivity |
| Shx | Sherwood number |
| Cf | Skin-friction coefficient |
| Cr | Chemical reaction parameter |
| Dm | Mean fluid concentration |
| f(η) | Dimensionless stream function |
| FEM | Finite element method |
| G | Vertical velocity |
| Jw | Wall mass flux, Jw |
| K | Permeability parameter, H/m |
| M | Magnetic parameter |
| Nux | Nusselt number |
| ODE | Ordinary differential equations |
| PDE | Partial differential equations |
| Pr | Prandtl number |
| qr | Radiative heat flux, W/m2 |
| R | Radiation parameter |
| Raa | Rayleigh number |
| V0 | Suction parameter |
| Electrical conductivity | |
| Stream function | |
| Fluid viscosity, Pa.s |
At present, providing efficient thermal fluids for heat transfer and cooling purposes, particularly in engineering practice, has become increasingly challenging. Therefore, it remains a significant undertaking for researchers. Various approaches can be employed to enhance heat transfer. The thermal conductivity of any nanofluid is affected by the type, size, and shape of the nanoparticles involved. The primary purpose of nanoliquids is to enhance the thermal conductivity within heat transfer fluids. Generally, nanoliquids are created by suspending nanoparticles in base fluids such as water, oil, kerosene, and so on. Nanoliquids represent the cutting edge of technological advancement in this field. The extensive practical implications of nanotechnology have sparked enthusiasm across various technological and industrial domains. These span sectors like information technology, power generation, ecological studies, healthcare, national security, food integrity, and transportation.
Several research studies have contributed to these advancements. Tasawar et al. [1] conducted a classical study on the rotating disk problem, while Ramesh et al. [2] explored the anomalous thermal behavior between two rotating disks. Choi et al. [3] investigated the enhancement of thermal conductivity in nanotube suspensions. Sheremet et al. [4] discussed the influence of a constant magnetic field on mixed convection in a trapezoidal cavity filled with Cu-water nanofluid. Hassan et al. [5] focused on the combined effects of heat and mass transfer (HMT), as well as the impact of thermal radiation, in the flow of sisko nanofluid with gold nanoparticles using blood as the base fluid. These studies contribute to our understanding and application of nanotechnology in improving heat transfer and fluid dynamics in various systems.
In the domain of computational investigation, Sheremet et al. [6] performed research to explore the impact of Brownian diffusion and thermophoresis on natural convection within a water-based nanofluid, constrained within two triangular cavities. The remaining walls of the cavities were maintained at a low constant temperature, while the top and bottom walls were kept at a high constant temperature. Furthermore, Sheremet et al. [7] conducted numerical scrutiny of heat transfer during steady-state free convection within a right-angled triangular porous enclosure that was occupied by a nanofluid, using the Buongiorno model. An evaluation of statistical patterns pertaining to free convection heat conveyance within a parallelogram-shaped enclosure with porous media was specifically undertaken, focusing on Cu-water nanoliquids [8]. Moreover, the utilization of the fifth-order Runge-Kutta-Fehlberg technique in conjunction with a shooting method is deployed to explore the impacts of a consistent magnetic field and nonlinear thermal radiation on the transfer of mass and heat within the flow of Sisko nanofluid over an extending surface [9,10]. These numerical studies contribute to the understanding of heat transfer phenomena in various complex systems and environments.
Convective boundary conditions and thermal radiation were harnessed by Jyothi et al. [11] to explore the characteristics of flow and heat transfer involving single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) positioned amidst two rotating discs. The investigation encompassed diverse combinations of rotating and stretching velocities. Hashim et al. [12] developed a new model to examine the intricacies of HMT in the flow of Carreau nanoliquids. Hayat et al. [13] studied the three-dimensional Darcy-Forchheimer flow of Carreau nanofluid with a convectively heated surface, considering zero nanoparticles mass flux conditions. Raju et al. [14] investigated the flow of nanofluid over a bidirectional stretching surface in a porous medium, incorporating thermal radiation and the effects of non-uniform heat source/sink along with magnetohydrodynamics (MHD) and the Sisko ferro model. Reddy et al. [15] conducted a numerical analysis of HMT in single-phase nanofluid scenarios over rotating cylinders, considering the Cattaneo-Christov heat flux and slip effects. These studies contribute to our understanding of heat transfer phenomena and fluid dynamics in various nanofluid systems under different boundary conditions.
An experimental exploration into the heat transfer and flow attributes of nanoliquids containing multi-walled carbon nanotubes (MWCNTs) within a double-pipe heat exchanger was carried out by Moradi et al. [16]. Hashim et al. [17] engaged in numerical investigation of the HMT characteristics of Williamson nanofluid over a wedge geometry, accounting for temporal variations. Sreedevi et al. [18] delved into the analysis of HMT within a vertical cone, incorporating both single- and multi-wall carbon nanotubes, and incorporating convective boundary conditions. Li et al. [19] analyzed HMT in magnetohydrodynamic (MHD) Williamson nanofluid over an exponentially porous stretching surface, noting the effects of thermophoresis and Brownian motion parameters on heat transmission rate. Veera et al. [20] investigated MHD fluid flow of nanoliquids through a vertically traveling absorbent plate in the existence of radiation absorption. Azmi et al. [21] examined heat transmission and friction concerns in the turbulent flow of titanium oxide (TiO2) and aluminum oxide (Al2O3) nanoliquids within a tube. An artificial neural network (ANN) framework was introduced by Ahmadloo et al. [22] to anticipate the thermal conductivity ratio of diverse nanoliquids concerning the base fluid. This prediction model takes input variables like the nature of nanoparticles and the base fluid into consideration. Investigation into the interplay of heat and mass transfer within an unsteady chemically reactive boundary layer flow was undertaken by Prashar et al. [23]. This study focused on a ZnO-MWCNTs/ethylene glycol hybrid nanoliquid and encompassed the incorporation of a non-Newtonian flow model alongside Arrhenius activation energy effects. The impact of nanoparticle migration on the convective heat transfer coefficient within nanoliquids based on Al2O3-EG/water was subject to experimental inquiry by Choi et al. [24]. Nabil et al. [25] conducted empirical research into the heat transfer and friction factor of nanoliquids containing TiO2-SiO2, in conjunction with an H2O:EG mixture. Maddah et al. [26] experimentally examined the heat exchanger performance using Al2O3-TiO2 hybrid nanofluid in the presence of thermal radiation. Urmi et al. [27] discussed the thermophysical properties of 40% EG-based TiO2-Al2O3 hybrid nanoliquids and highlighted the improved thermal conductivity and low viscosity of hybrid nanoliquids for realistic heat transfer applications. Yıldız et al. [28] evaluated the efficacy of heat transfer within an Al2O3-SiO2/H2O hybrid nanofluid, additionally contrasting theoretical and experimental models for thermal conductivity. Several researchers [29–31] have undertaken investigations into the heat transfer attributes of diverse fluids, while considering a range of geometries.
This paper focuses on the analysis of HMT characteristics of MHD Sisko nanoliquid over a stretching sheet, with a specific emphasis on comparing Al2O3-Eg and TiO2-Eg nanoliquids. The study takes into account slip conditions and radiation effects. It is noteworthy that this topic has not been previously addressed, making this analysis novel and unique. The outcomes of this study bear immediate relevance in numerous domains, notably in the blending of lubricants, food products, and the fusion of plasma with lubricants and moisturizers.
Under consideration is a stretching sheet characterized by velocities, viz.,
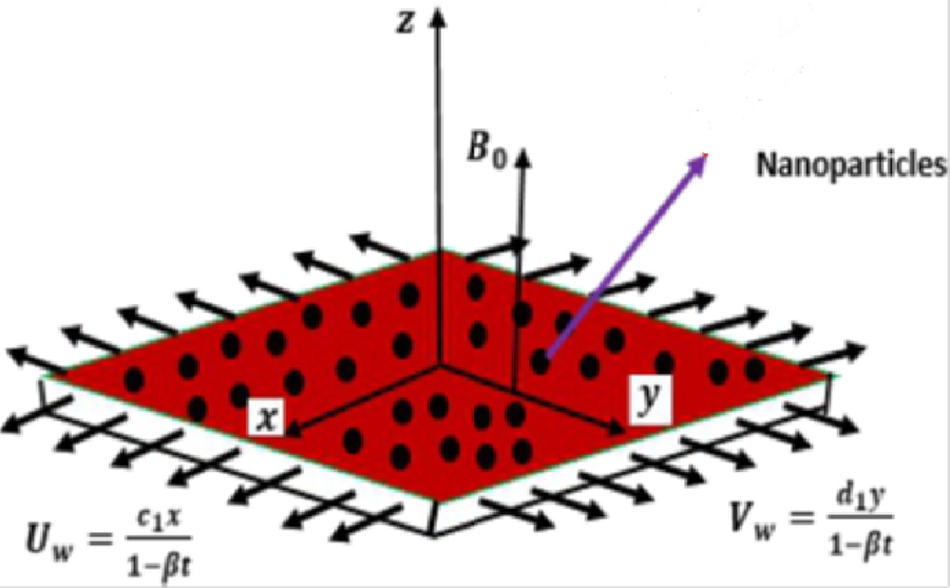
Figure 1: Physical explanation and cartesian geometry of the problem
The related boundary situations are
at
at
To reorganize the mathematical analysis of the problem, we introduce the following similarity transformations:
The nanoliquid’s dynamic viscosity
Through the utilization of the Rosseland approximation to model radiation effects, the radiative heat flux,
Assuming that the temperature variations within the flow result in an approximation of the
Disregarding terms of higher order in above Eq. (11) past the linear degree in
Thus, substituting Eq. (12) into Eq. (10), we get
Utilizing Eqs. (8), (9), and (13), the controlling non-linear partial differential Eqs.(1)–(5), in conjunction with the boundary constraints (6) and (7), are simplified to
The renovated boundary conditions are
where, main denotes ordinary differentiation with respect to
The skin-friction coefficients in the x and y directions, as well as the local Nusselt number (
The afore mentioned in the form of non–dimensional variables are
3 Numerical Method of Solution
The numerical technique known as the finite element method (FEM) [28–30] is utilized for the computation of Eqs. (14)–(17) in conjunction with boundary conditions (18). In contrast to alternative numerical approaches, FEM is recognized as a sophisticated method for precisely and effectively solving both partial and ordinary differential equations.
FEM proves highly adept at resolving both regular and partial differential equations. This technique functions by partitioning the complete domain into smaller units referred to as “finite elements,” each possessing bounded dimensions as depicted in Fig. 2. This approach is especially fitting for tackling integral equations spanning diverse domains, including heat conduction, fluid dynamics, chemical engineering, electrical networks, and other branches of engineering science.
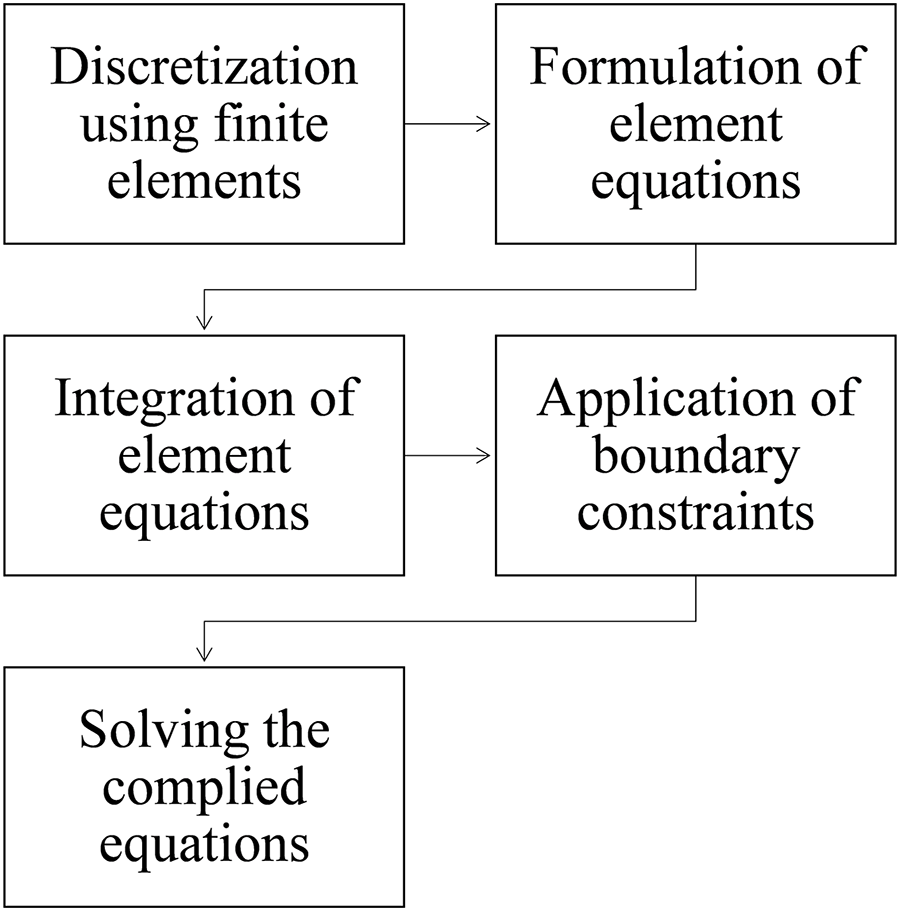
Figure 2: Stages in FEM
Choosing appropriate form functions to approximate real functions is a pivotal consideration. When tackling the solution of a system of non-linear ordinary differential Eqs. (14)–(17) coupled with boundary conditions (18), the first assumption is that.
The Eqs. (14) to (17) then reduces to
The boundary conditions take the form
The variational formulation corresponding to Eqs. (19) to (24) across a standard linear element
here
3.3 Finite Element Formulation
Upon incorporating finite element approximations of the specified kind into the above-mentioned equations, the finite element model can be generated.
with,
where
The resulting finite element representation of the formulated equations is as follows:
where
The comparison of sisko Al2O3-Eg and TiO2-Eg numerical resolutions of nanoliquids flow over a stretching sheet in the existence of MHD, were exemplified for various values of the related parameters and results were exposed graphically as well as in tabular form. The influence of the volume fraction parameter (ϕ) on the thickness of the hydrodynamic boundary layer, thermal boundary layer, and concentration boundary layer is depicted in the study of both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids using Figs. 3–5. It is identified that a rise in the value of (ϕ) tends to a fall in the radial velocity and temperature profiles. This reduction is more pronounced in the case of TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid. However, the concentration profiles exhibit an inverted behavior.
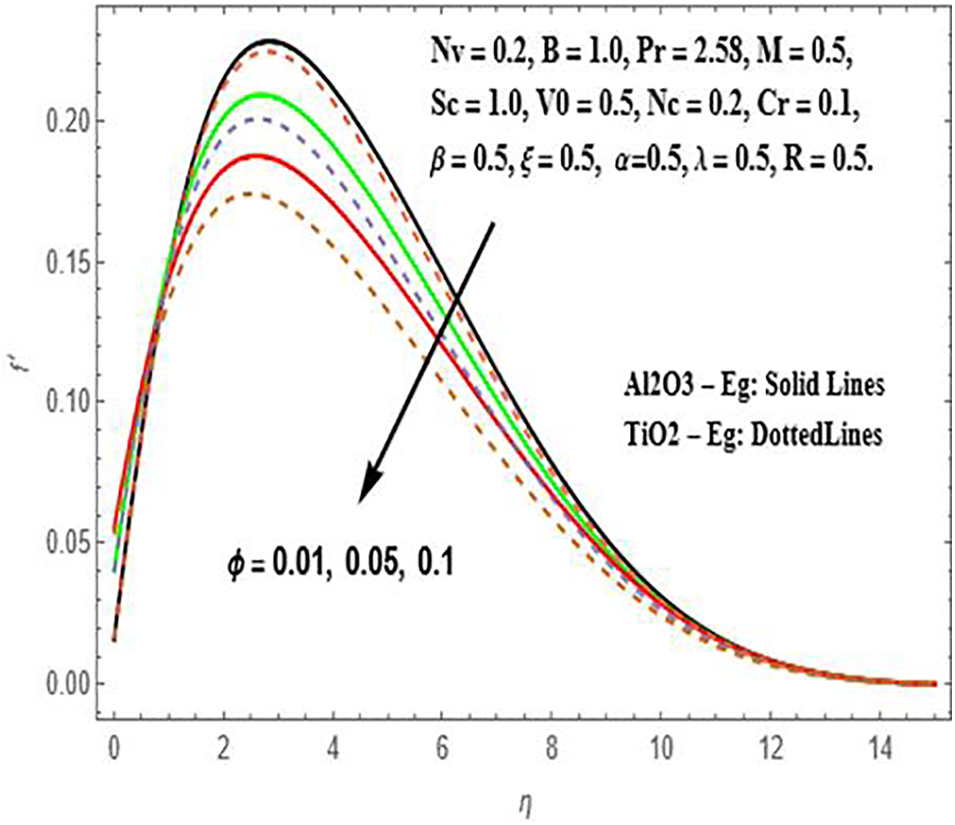
Figure 3: Illustration of
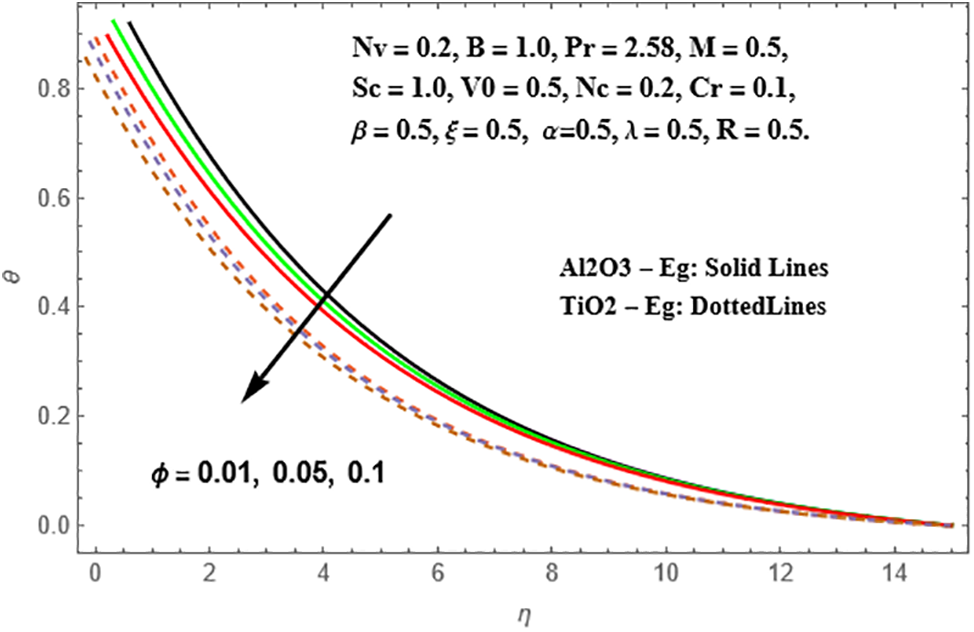
Figure 4: Representation of θ against ϕ
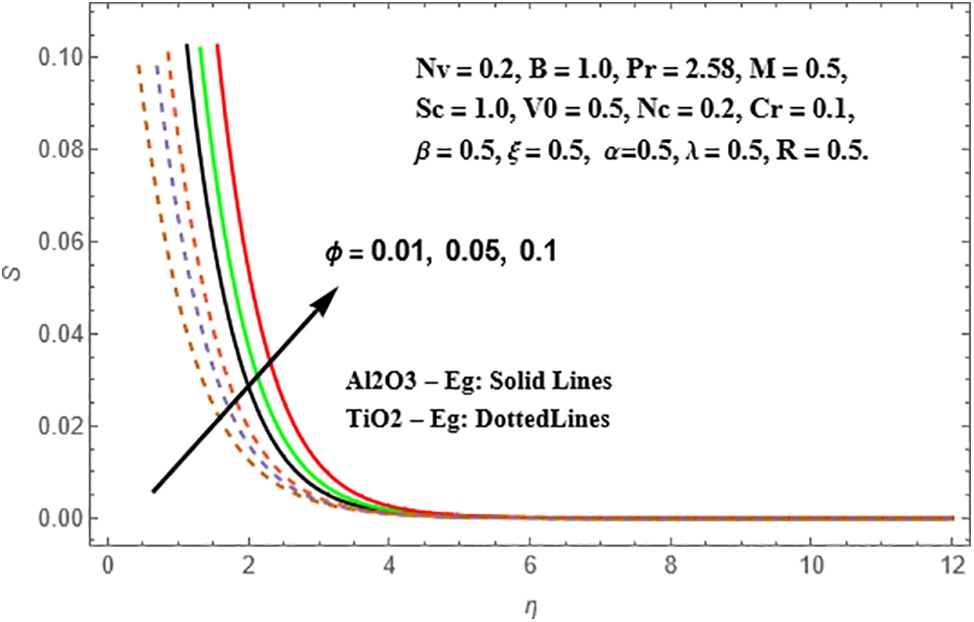
Figure 5: Variation of S against ϕ
The impact of the magnetic parameter (M) on the radial velocity, temperature, and concentration profiles of Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids is illustrated in Figs. 6–8. The radial velocity profile exhibits a rise with higher values of (M) for both nanoliquids, with TiO₂-Eg nanofluid showing a more significant enhancement compared to Al₂O₃-Eg nanofluid. On the other hand, the temperature profiles deteriorate for both Al₂O₃-Eg and TiO₂-Eg nanoliquids as (M) increases. This reduction is more pronounced in TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid. A similar decline is observed in the concentration profiles, with Al₂O₃-Eg nanofluid exhibiting a higher decrease than TiO₂-Eg nanofluid.
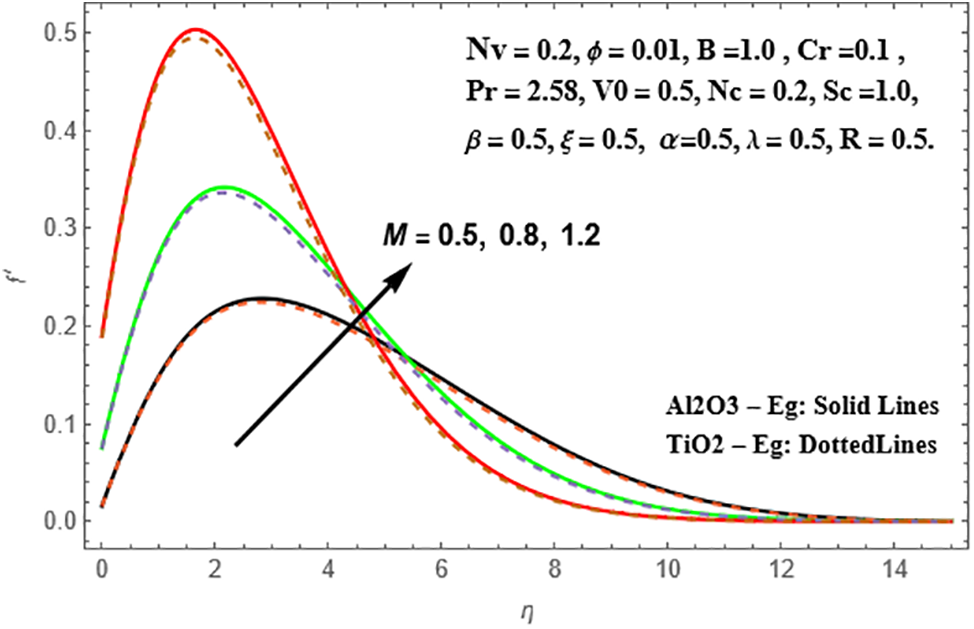
Figure 6: Illustration of
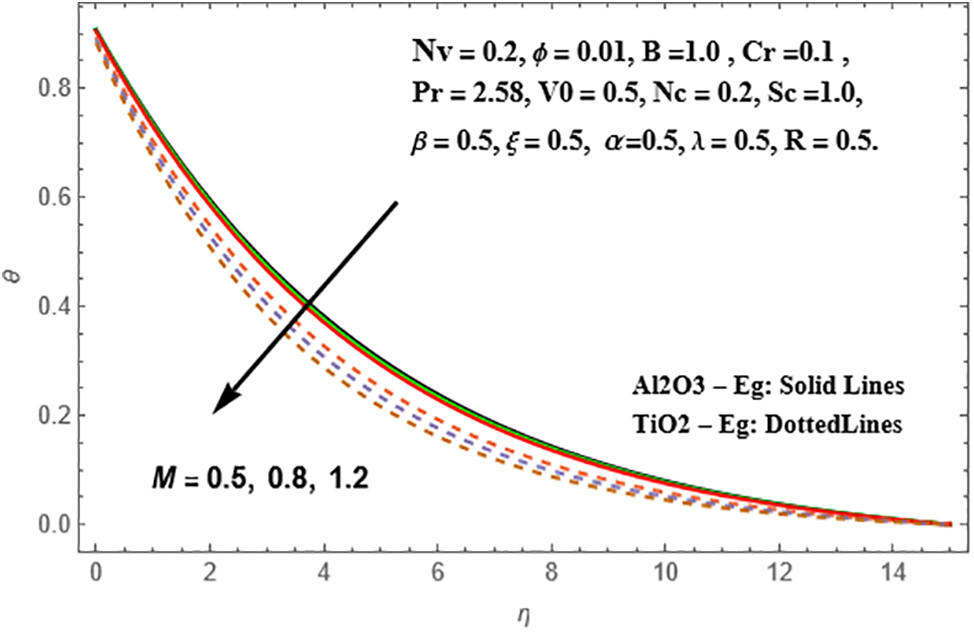
Figure 7: Presentation of θ against M
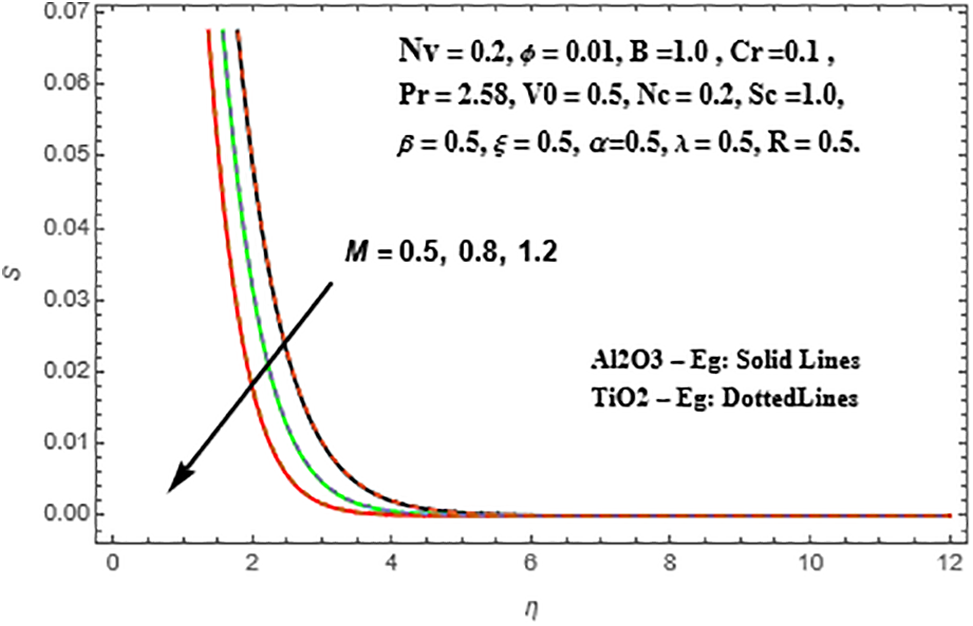
Figure 8: Variation of S against M
The effects of the Siskofluid parameter (B) on the radial velocity, temperature, and concentration profiles of Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids are depicted in Figs. 9–11. In both nanoliquids, an increase in (B) leads to an increase in the radial velocity profiles. The temperature profiles, on the other hand, decrease with higher values of (B) for both Al₂O₃-Eg and TiO₂-Eg nanoliquids. This phenomenon is more pronounced in TiO₂-Eg-based nanofluid. Conversely, the concentration profiles increase with escalating values of (B). This accumulation trend is more significant in Al₂O₃-Eg nanofluid compared to TiO₂-Eg-based nanofluid.
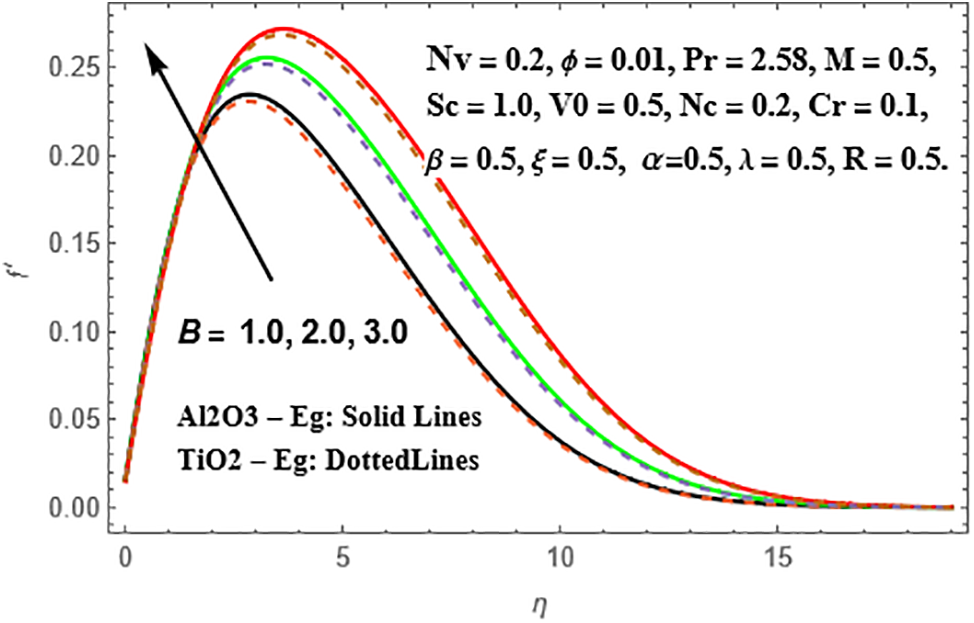
Figure 9: Variation of
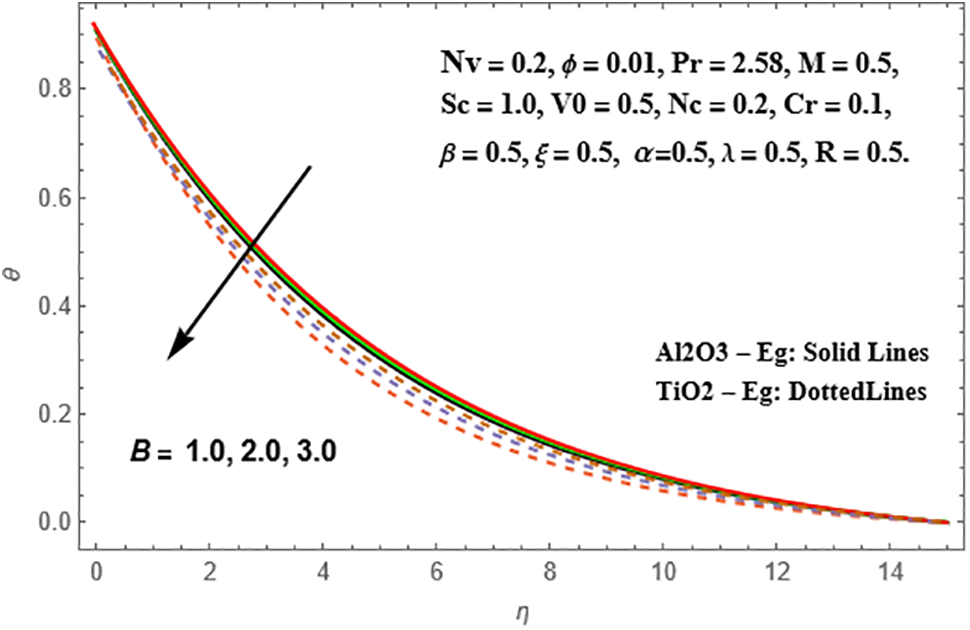
Figure 10: Variation of θ against B
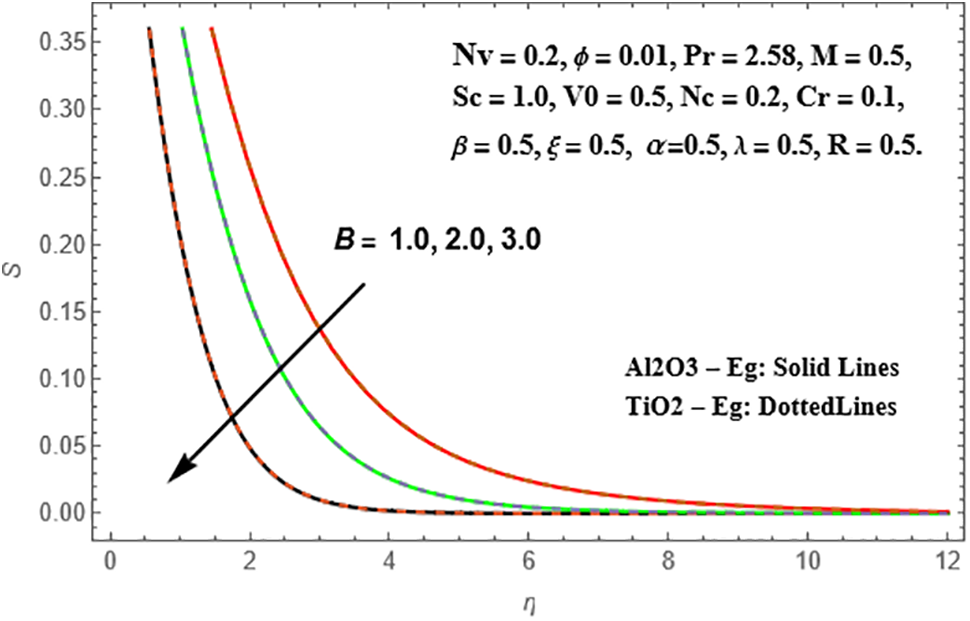
Figure 11: Variation of S against B
Figs. 12 and 13 illustrate the effects of the Prandtl number (Pr) on the enhancements of radial velocity and temperature profiles in Sisko Al₂O₃-Eg and TiO₂-Eg based nanoliquids. The radial velocity exhibits an increase with increasing values of Pr, and it is observed that this increase is more pronounced in TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid. The same trend is observed in the temperature profiles as well.
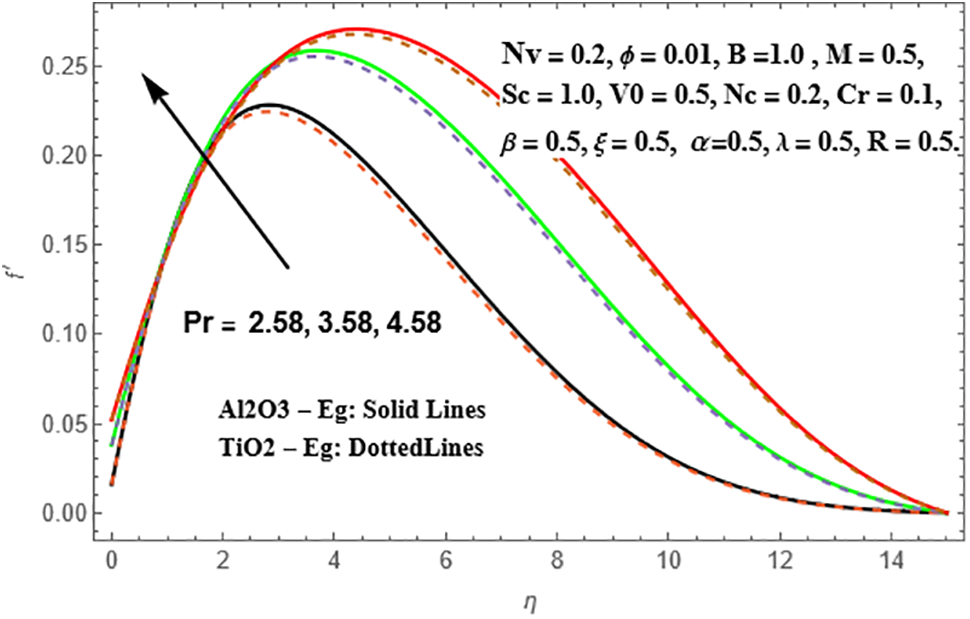
Figure 12: Variation of
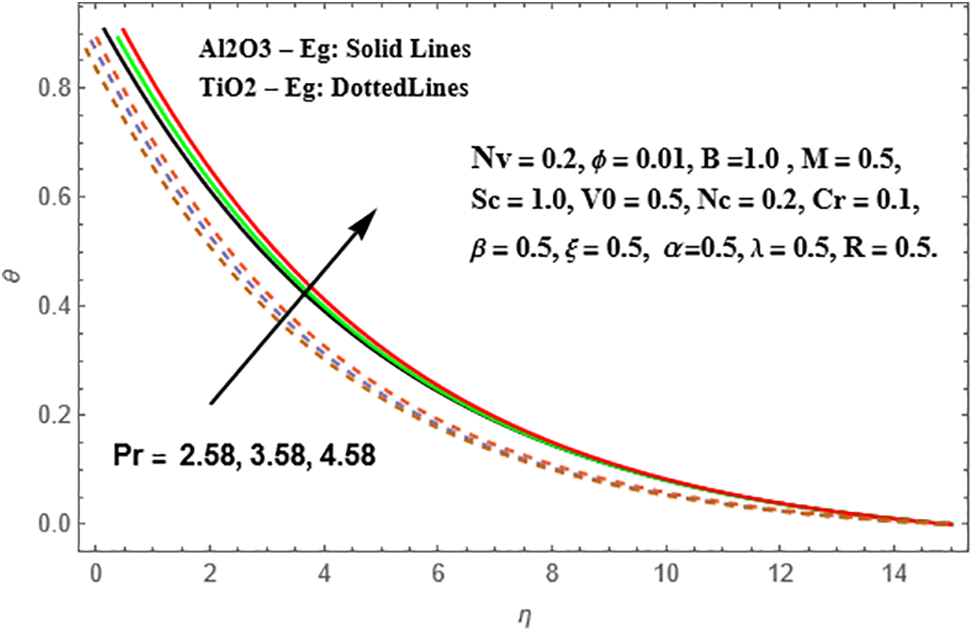
Figure 13: Illustration of θ against Pr
From the observations in Figs. 14and 15, it is evident that the profiles of radial velocity and temperature intensify in both Sisko Al₂O₃-Eg and TiO₂-Eg based nanoliquids as the Schmidt number (Sc) increases. Moreover, this enhancement is more significant in TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid. As for the chemical reaction parameter (Cr). Figs. 16 and 17 showcase the influence of the chemical reaction parameter (Cr) on the radial velocity and concentration distributions in Sisko Al₂O₃-Eg and TiO₂-Eg based nanoliquids. It is observed that the reduction in both nanoliquids is slightly more pronounced in TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid in terms of the concentration distributions.
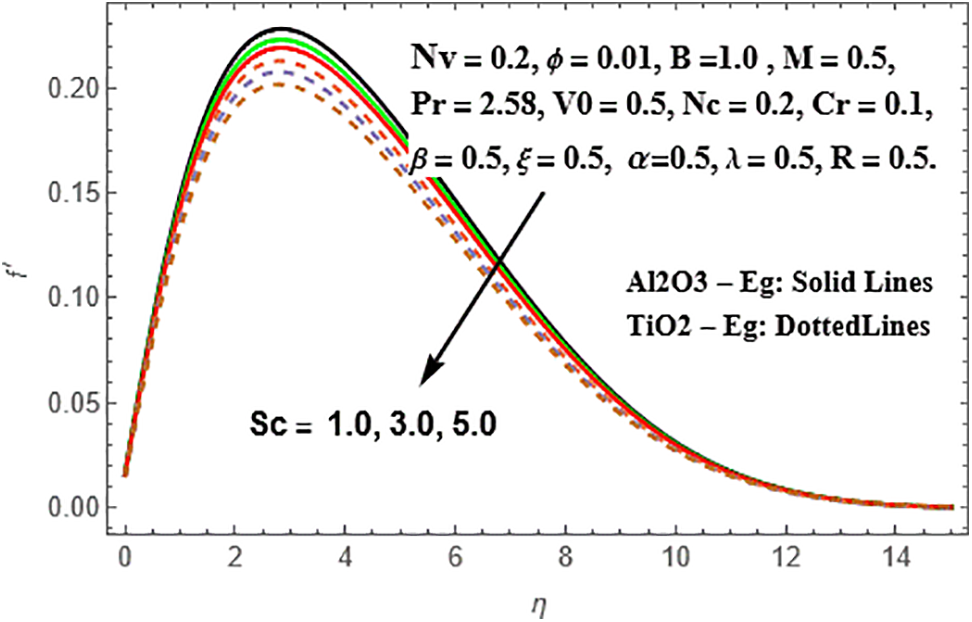
Figure 14: Variation of
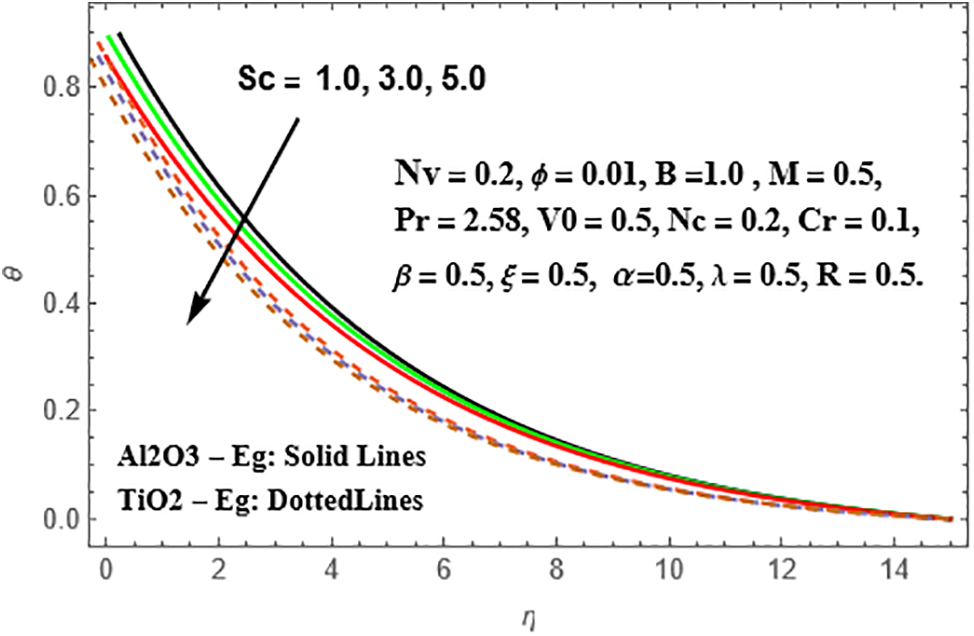
Figure 15: Variation of θ against Sc
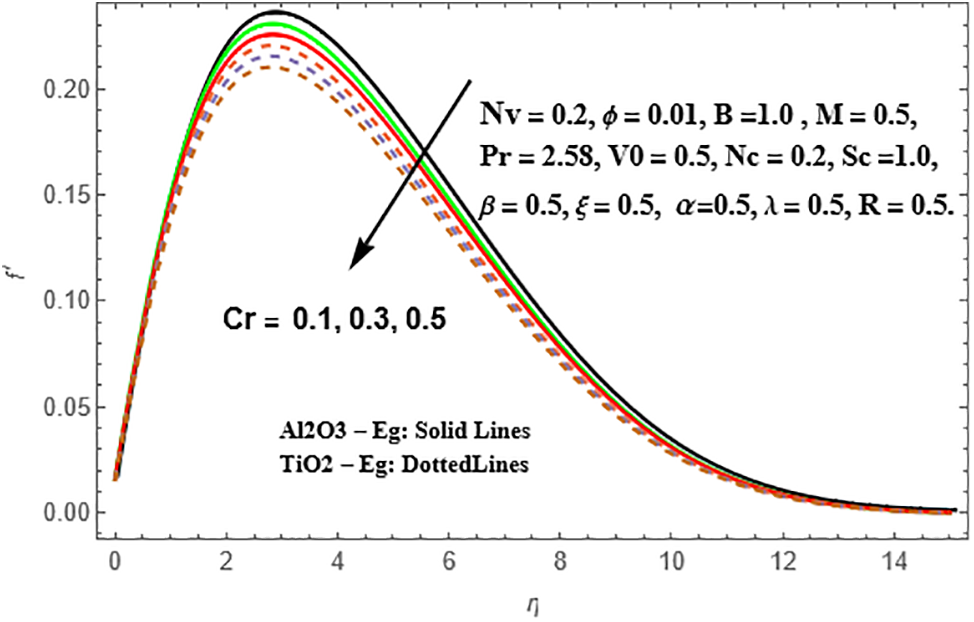
Figure 16: Variation of
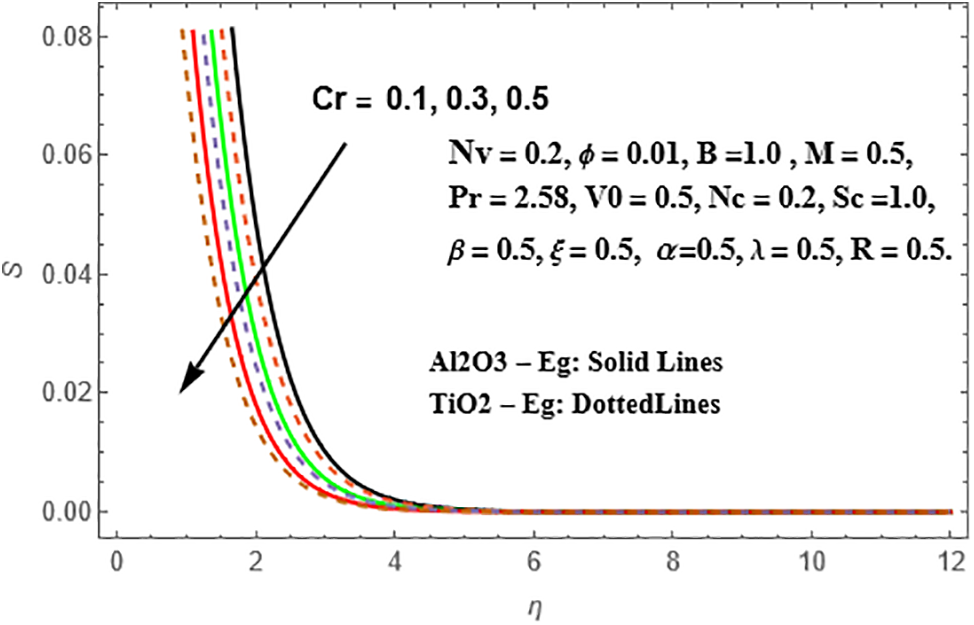
Figure 17: Illustration of
Figs. 18 and 19 depict the variations in radial velocity and temperature profiles for different values of the Reynolds number (R) in both Sisko Al₂O₃-Eg and TiO₂-Eg based nanoliquids. It is observed that as the values of R increase, there is a decrease in the radial distributions for both nanoliquids. Furthermore, this decrease is more pronounced in TiO₂-Eg nanofluid compared to Al₂O₃-Eg nanofluid.
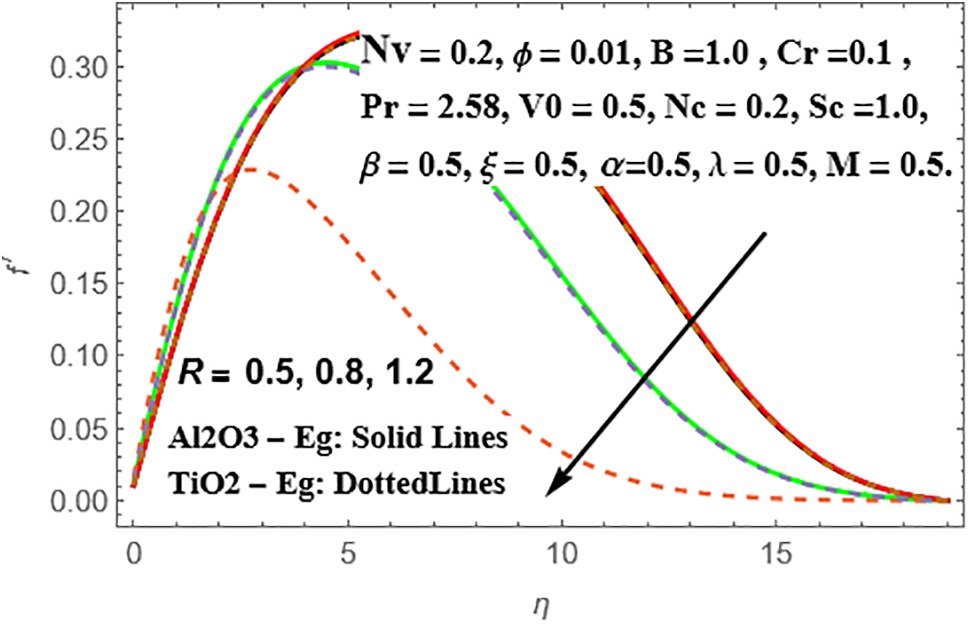
Figure 18: Variation of
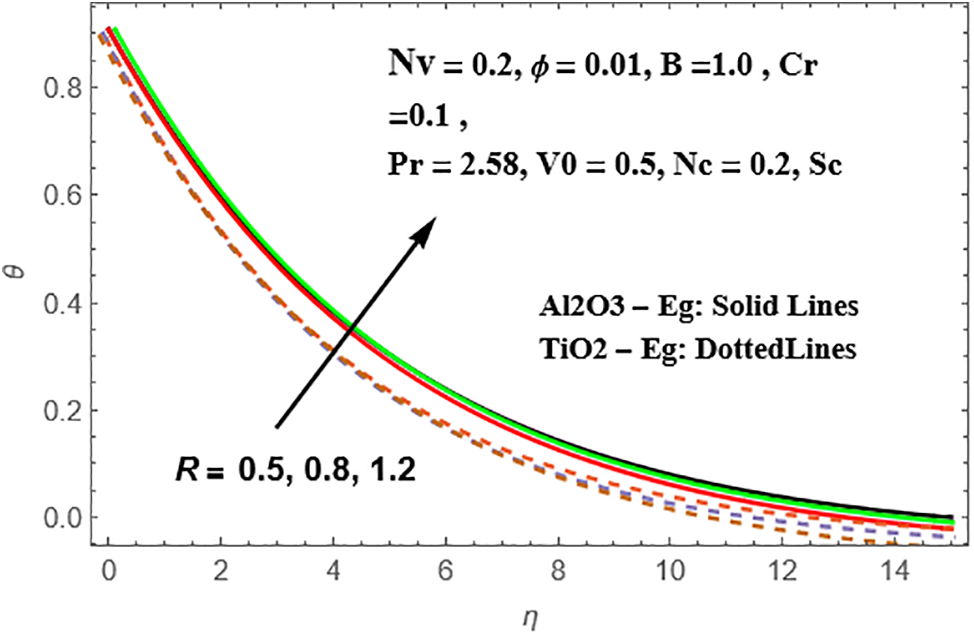
Figure 19: Variation of
In Fig. 19, it is observed that the temperature variations are significant in both nanoliquids, with TiO₂-Eg nanofluid exhibiting higher scatterings compared to Al₂O₃-Eg nanofluid. Figs. 20–22 present the radial velocity, temperature, and concentration variations for different values of the nanoparticle volume fraction (Nv) in Sisko Al₂O₃-Eg and TiO₂-Eg based nanoliquids. As the values of Nv increase, the radial velocity intensifies in both nanoliquids. This intensification is more pronounced in TiO₂-Eg based nanofluid compared to Al₂O₃-Eg based nanofluid. The temperature variations also increase with higher values of Nv, and this increment is more significant in TiO₂-Eg based nanofluid compared to Al₂O₃-Eg based nanofluid. Additionally, there is a reversed pattern in the concentration distributions, where Al₂O₃-Eg based nanofluid shows more significant changes compared to TiO₂-Eg based nanofluid.
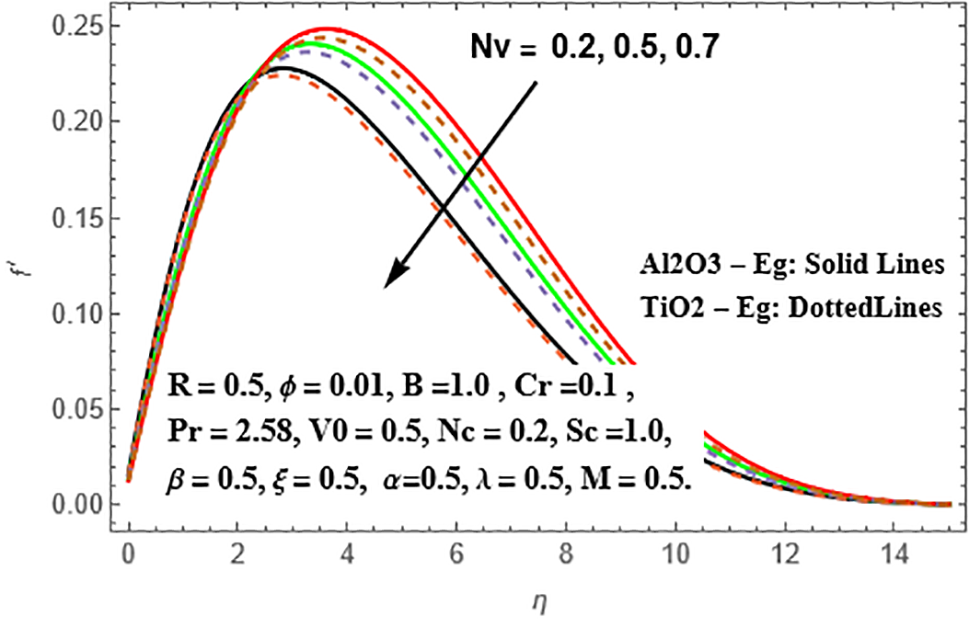
Figure 20: Variation of
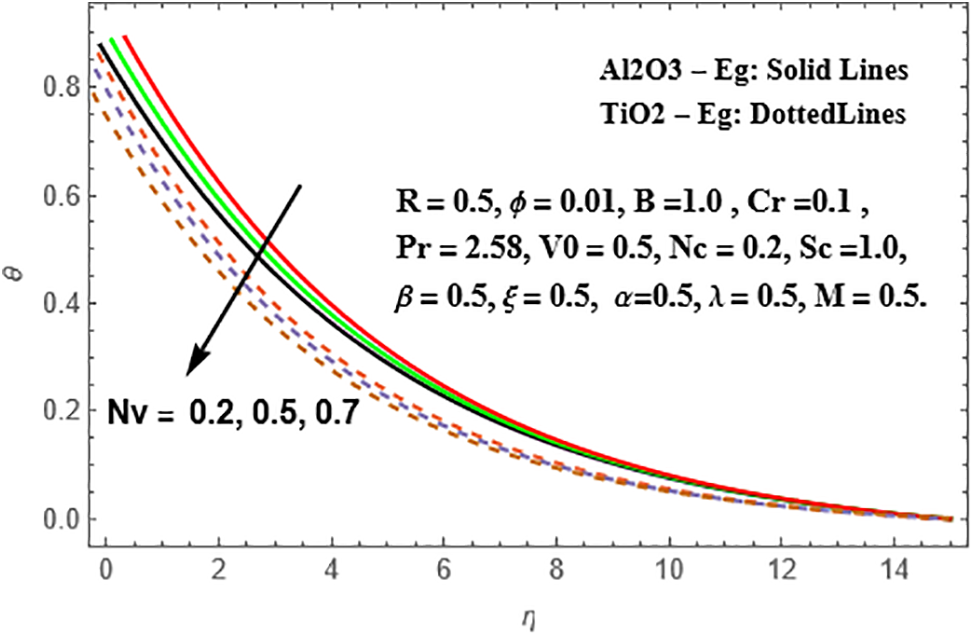
Figure 21: Variation of
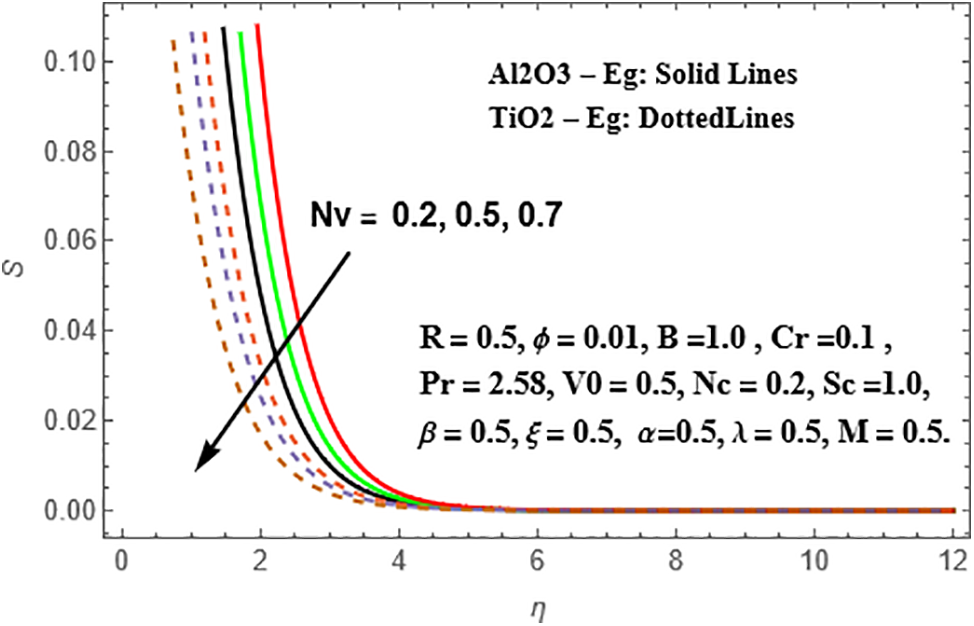
Figure 22: Variation of S against
The radial velocity distributions for different values of Nc are examined in Fig. 23 for both nano liquids, revealing an observed dropout phenomenon. Interestingly, it is observed that the dropout is more pronounced in the
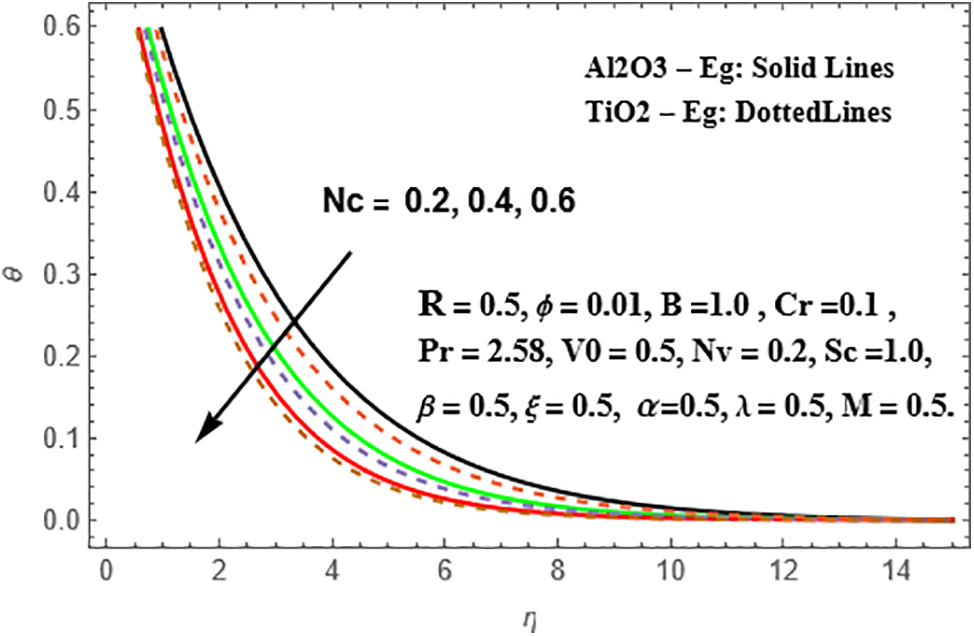
Figure 23: Variation of
Figs. 24–26 present the disparities in radial velocity, temperature, and concentration patterns for different suction parameter values

Figure 24: Variation of
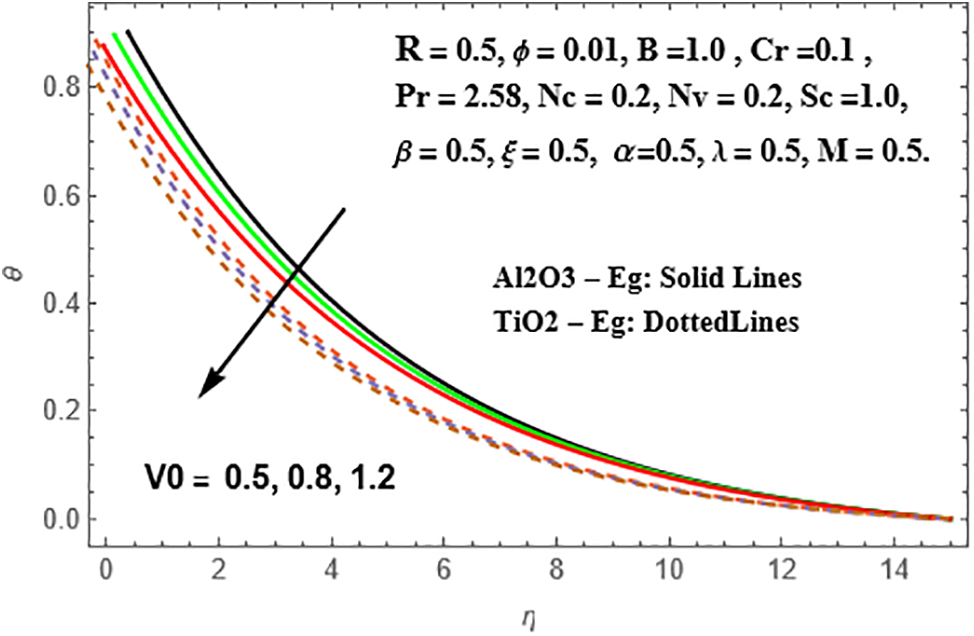
Figure 25: Variation of
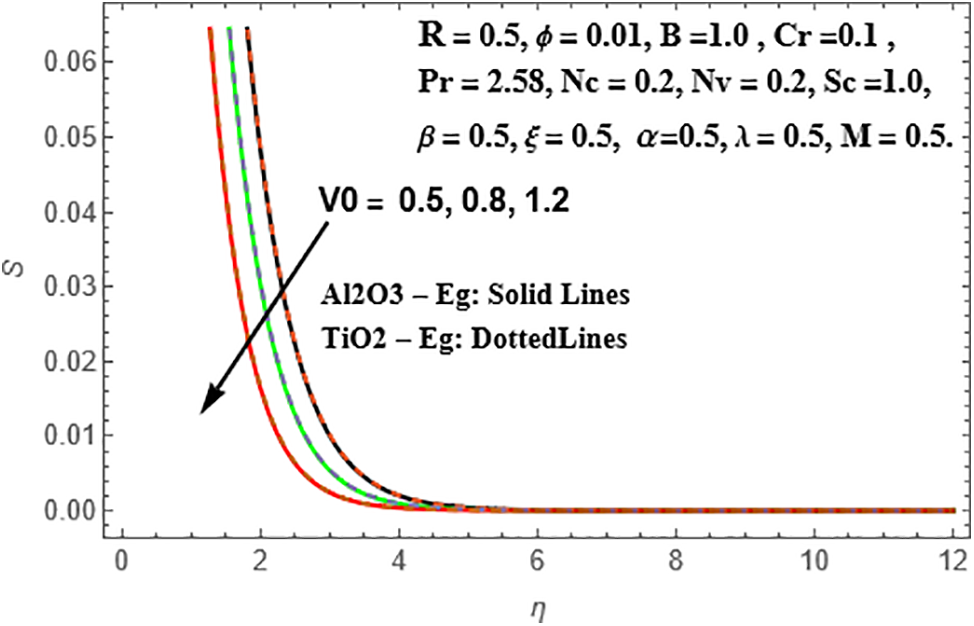
Figure 26: Variation of S against
The influence of the viscosity ratio parameter (α) on radial velocity patterns and concentration amplifications is examined for both Sisko
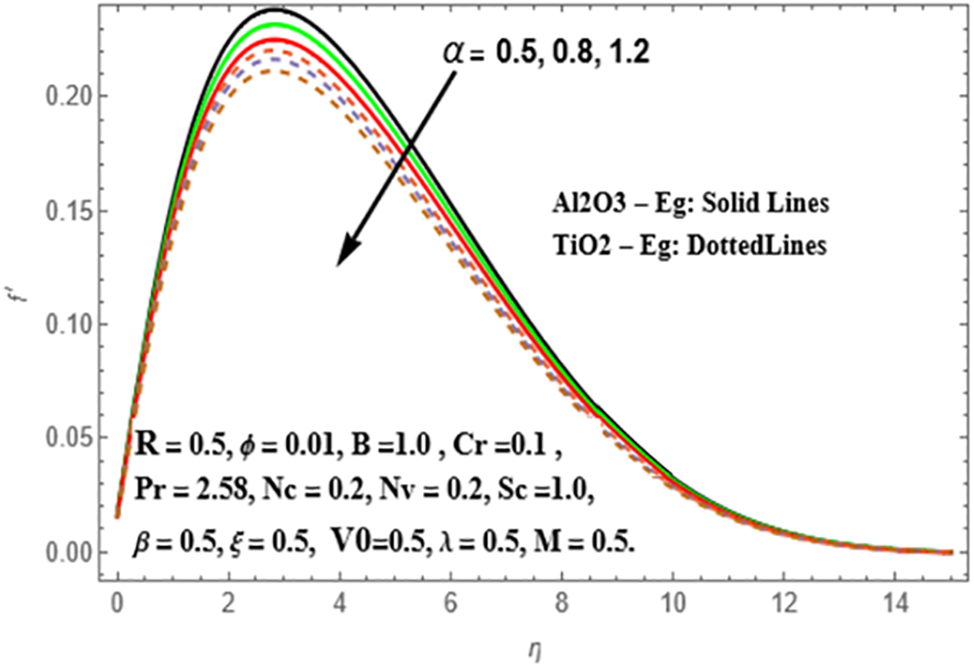
Figure 27: Variation of
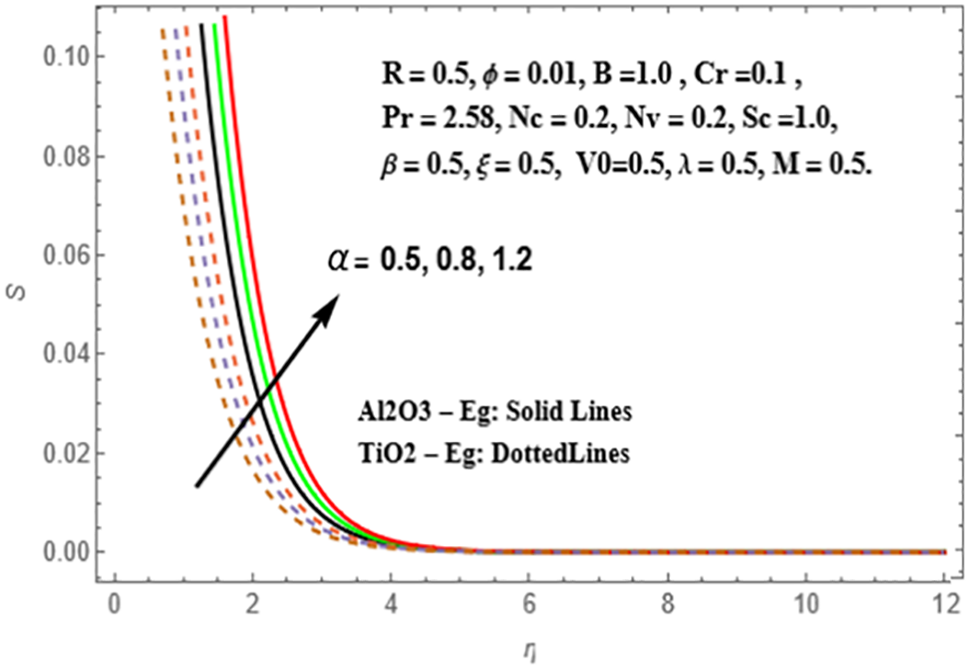
Figure 28: Variation of S against
Fig. 29 demonstrates that the radial velocity of Sisko

Figure 29: Variation of
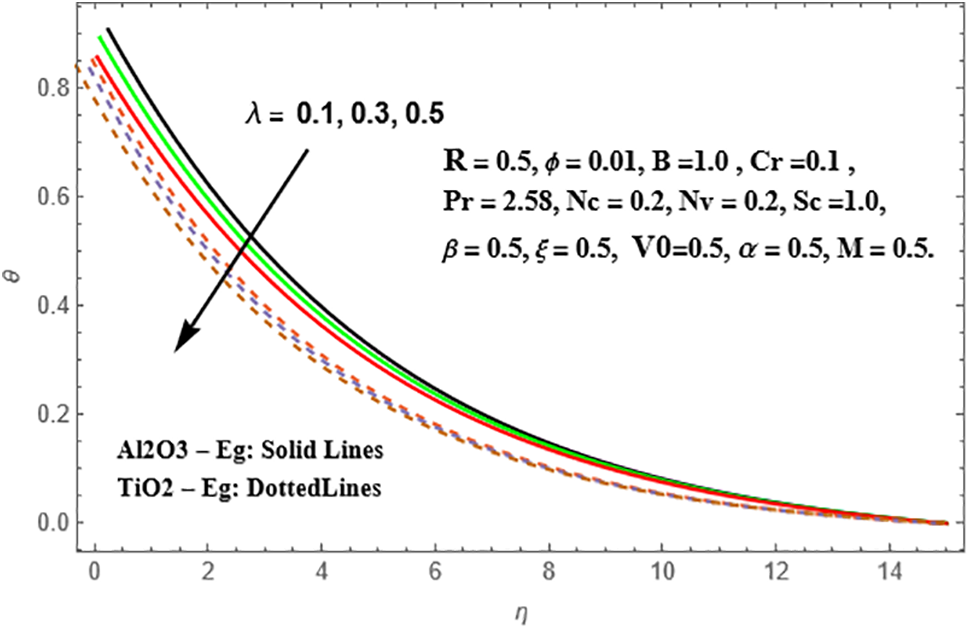
Figure 30: Change of
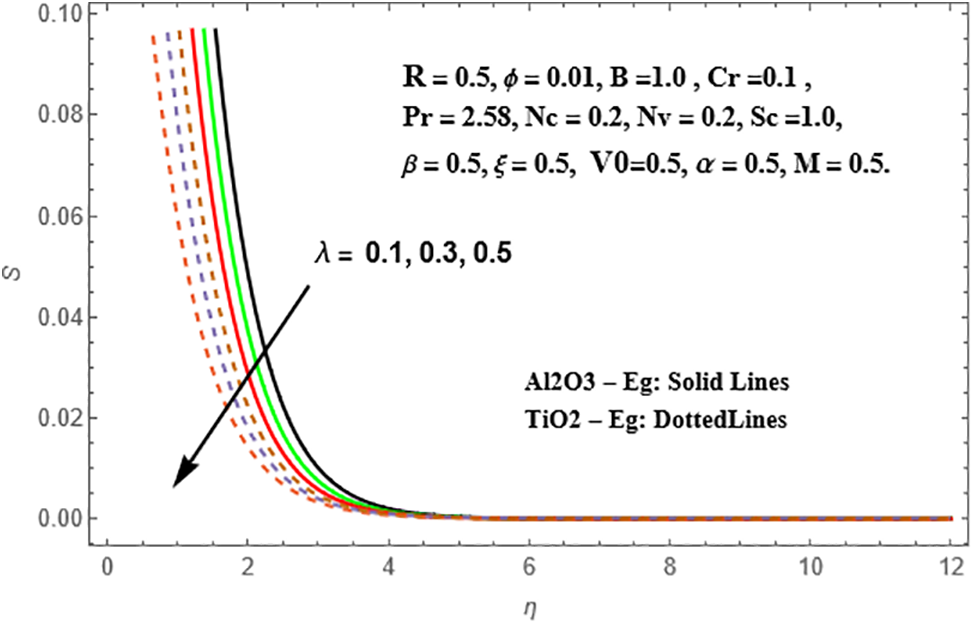
Figure 31: Presentation of S against λ
The impact of the temperature slip parameter (β) on temperature distributions is illustrated in Fig. 32, revealing a decrease in fluid temperature as the values of (β) increase. This temperature reduction is more pronounced in
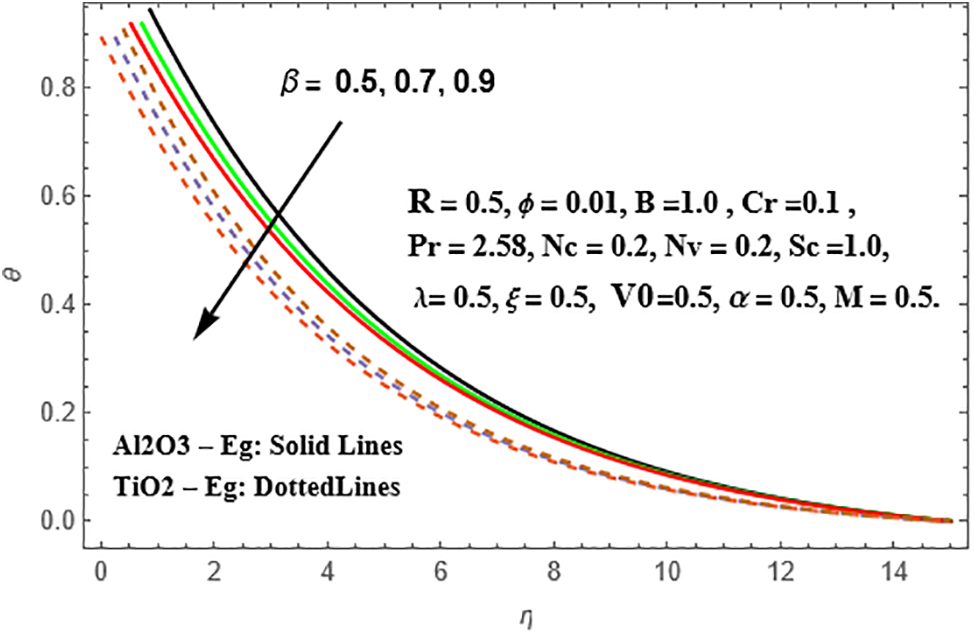
Figure 32: Presentation of θ against
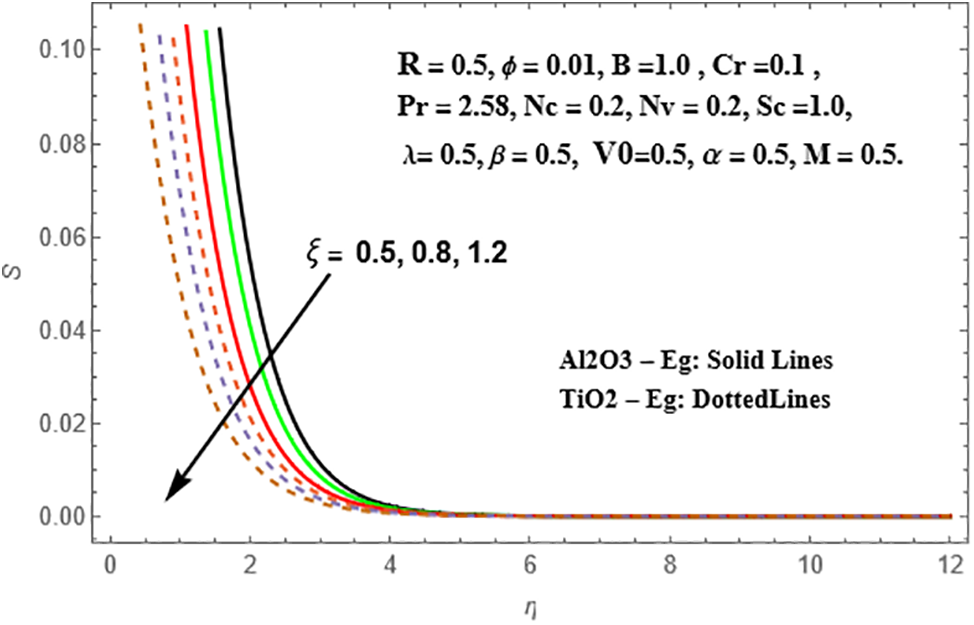
Figure 33: Variation of S against
Additionally, discussions and graphs have been developed for all non-dimensional parameters found in the physical phenomena of Sisko Al2 O3-Eg and TiO2-Eg-based nanoliquids. Efforts were made to present exclusively novel findings obtained from Mathematica 10.4. The non-dimensional parameters include volume fraction (ϕ), magnitude, V0, Nc, Nv, Sc, and others
The statistical data pertaining to the Skin friction, local Nusselt number, and local Sherwood number for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids has been calculated and presented in Tables 2 and 3. Analysis of Table 2 reveals a consistent decrease in the numerical values of the skin-friction coefficient, Nusselt number, and Sherwood number for both Sisko Al₂O₃-Eg and TiO₂-Eg cases as the parameter (𝜙) increases. The impact of (M) on the dimensionless rates of velocity shows an increase along the x-direction and an increase along the y-direction, while rates of temperature and mass exhibit a slight depreciation, as indicated in Table 2. Moreover, as the values of (Pr) increase, there is a notable decline in the skin-friction coefficient, Nusselt number, and Sherwood number for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids.
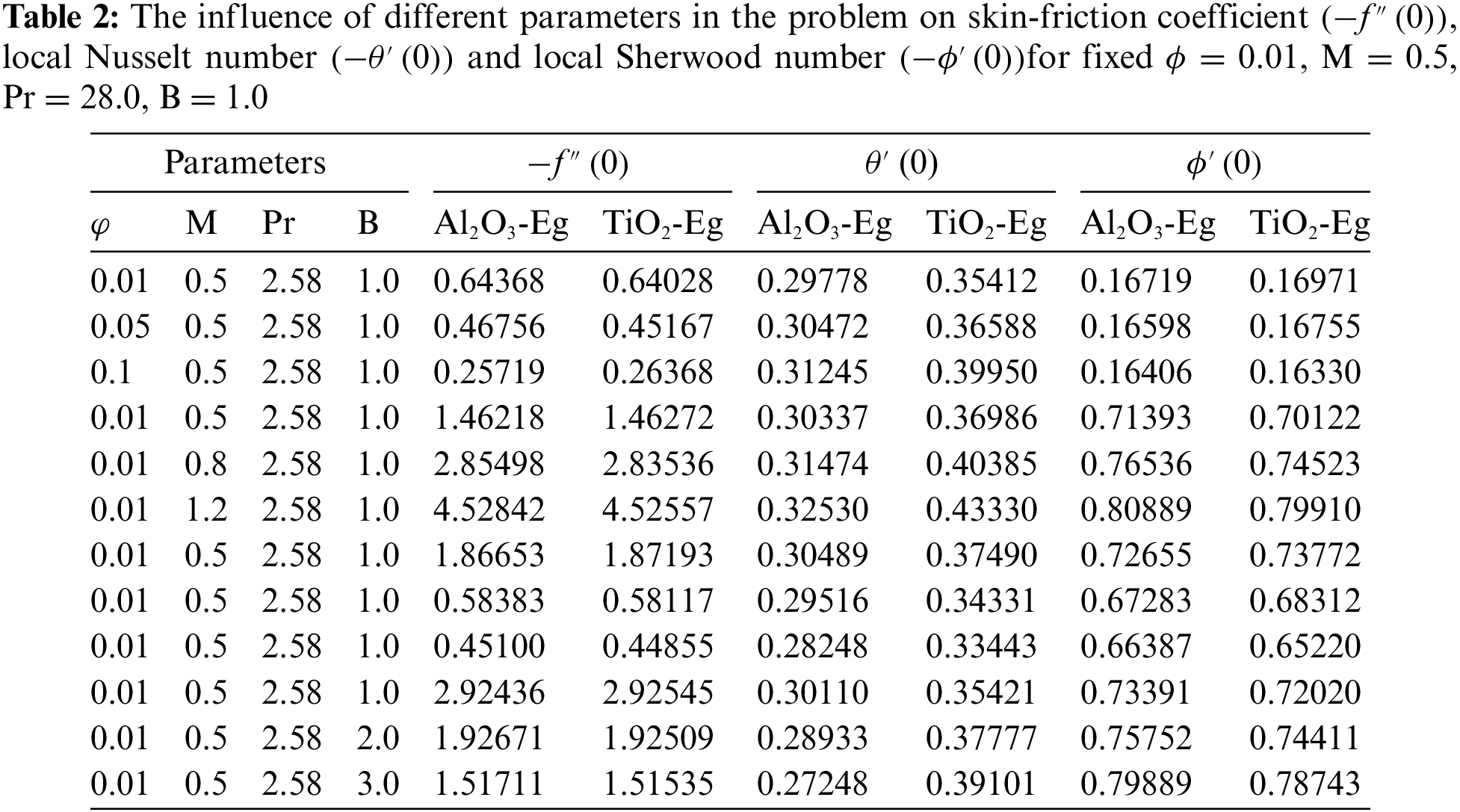
Furthermore, in Table 2, it is evident that the values of the skin-friction coefficient decrease with an increase in (B) for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids. The Nusselt number decreases for the Sisko Al₂O₃-Eg nanofluid but increases for the TiO₂-Eg nanofluid. However, the Sherwood number shows an escalation for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids.
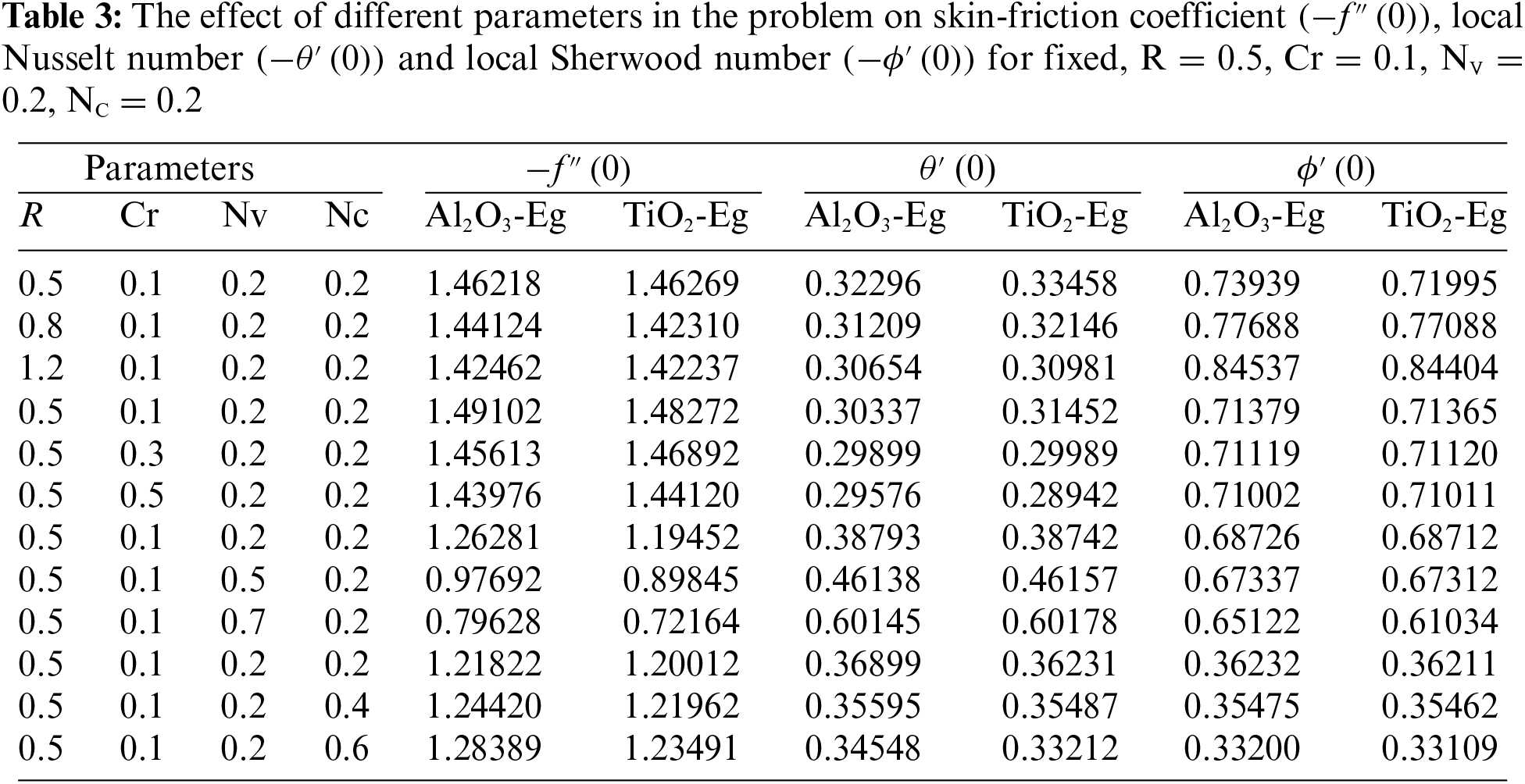
Table 3 illustrates the dimensionless rates of velocity upsurges along the x-direction and their deterioration along the y-direction for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids. In these cases, the Nusselt number and skin-friction coefficient values decrease, while the Sherwood number values increase across various values of (R). Notably, there is a decreasing trend observed in the rates of velocity and mass transfer for higher values of (Nv), while the rate of heat transfer increases with (Nv) for both Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids. Furthermore, the skin-friction coefficient values rise with increasing values of (Nc) for both nanoliquids. Conversely, the Nusselt number and Sherwood number values decrease with increasing (Nc) for both cases of Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids. These findings align closely with previously published results [30–32].
The present study employs FEM to computationally solve nonlinear PDEs, transformed into ODEs using appropriate similarity transformations. Investigating variable thermal conductivity and viscosity effects on MHD boundary layer flow, HMT in Sisko Al₂O₃-Eg and TiO₂-Eg nanoliquids over a stretching surface with slip boundary conditions, several key conclusions emerge. An increase in the volume fraction of nanoparticles (ϕ) corresponds to elevated non-dimensional heat transfer rates, suggesting an enhancement in heat transfer efficiency due to nanoparticle attributes. Additionally, higher Sisko parameter (B) values correlate with reduced temperature profiles within nanoliquids. Moreover, amplified magnitudes of the parameter characterizing variable thermal conductivity (Nc) induce temperature reductions in the fluid region, showcasing the influence of variable thermal conductivity on temperature distributions. Furthermore, augmenting the parameter for variable viscosity (Nv) leads to decreased velocities within Sisko nanoliquids. These findings significantly contribute to understanding nanoliquid behavior and potentially find applications in various engineering and industrial processes.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: conceived and designed the analysis, collected the data, performed the analysis, and wrote the paper: K. Jyothi; conceived and designed the analysis, draft manuscript prepared: Abhishek Dasore; revised the article: R. Ganapati, Sk. Mohammad Shareef, Ali J. Chamka, V. Raghavendra Prasad. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: There is no unavailable data in this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Tasawar, H., Madiha, R., Muhammad, I. K., Ahmed, A. (2018). Melting heat transfer and induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Results in Physics, 9, 1618–1630. [Google Scholar]
2. Ramesh, C. A., Vijay, K. S. (1972). On the heat transfer between two rotating disks. International Journal of HMT, 15(11), 2119–2132. [Google Scholar]
3. Choi, S. U. S., Zhang, Z. G., Yu, W., Lockwood, F. E., Grulke, E. A. (2001). Anomalous thermal conductivity enhancement in nanotube suspensions. Applied Physics Letter, 79(14), 2252–2254. [Google Scholar]
4. Sheremet, M. A., Pop, I. (2015). Natural convection in a horizontal cylindrical annulus filled with a porous medium saturated by a nanofluid using Tiwari and Das’ nanofluid model. The European Physical Journal Plus, 130, 107. [Google Scholar]
5. Hassan, W., Umar, F., Taseer, M., Umair, M. (2022). Importance of shape factor in Sisko nanofluid flow considering gold nanoparticles. Alexandria Engineering Journal, 61(5), 3665–3672. [Google Scholar]
6. Sheremet, M. A., Revnic, C., Pop, I. (2017). Natural convective heat transfer through two entrapped triangular cavities filled with a nanofluid: Buongiorno’s mathematical model. International Journal of Mechanical Sciences., 133, 484–494. [Google Scholar]
7. Sheremet, M. A., Pop, I. (2015). Free convection in a triangular cavity filled with a porous medium saturated by a nanofluid: Buongiorno’s mathematical model. International Journal of Numerical Methods for Heat & Fluid Flow, 25(5), 1138–1161. [Google Scholar]
8. Reddy, K. J., Madhusudhana Reddy, N. P., Konijeti, R. K., Dasore, A. (2018). Numerical investigation of chemical reaction and heat source on radiating MHD stagnation point flow of carreau nanofluid with suction/injection. Defect and Diffusion Forum, 388, 171–189. [Google Scholar]
9. Raghunath, K., Charankumar, G., Dasore, A., Logesh, K. M., Laxmaiah, G. et al. (2023). Influence of MHD mixed convection flow for maxwell nanofluid through a vertical cone with porous material in the existence of variable heat conductivity and diffusion. Case Studies in Thermal Engineering, 44, 102875. [Google Scholar]
10. Dasore, A., Tarun, P., Ramakrishna, K., Naveen, P. (2020). Convective hot air-drying kinetics of red beetroot in thin layers. Frontiers in Heat and Mass Transfer, 14, 1–8. https://doi.org/10.5098/hmt.14.23 [Google Scholar] [CrossRef]
11. Jyothi, K., Sudarsana, R. P., Suryanarayana, R. M. (2018). Influence of magnetic field and thermal radiation on convective flow of SWCNTs-water and MWCNTs-water nanofluid between rotating stretchable disks with convective boundary conditions. Powder Technology, 331, 326–337. [Google Scholar]
12. Hashim Khan, M. (2016). A revised model to analyse the HMT mechanisms in the flow of Carreau nanofluids. International Journal of HMT, 103, 291–297. [Google Scholar]
13. Hayat, T., Aziza, A., Muhammad, T., Alsaedi, A. (2018). An optimal analysis for Darcy-Forchheimer 3D flow of carreau nanofluid with convectively heated surface. Results in Physics, 9, 598–608. [Google Scholar]
14. Raju, C. S. K., Sandeep, N. (2015). HMT in 3D Non-Newtonian nano and ferro fluids over a bidirectional stretching surface. International Journal of Engineering Research in Africa, 21, 33–51. [Google Scholar]
15. Reddy, P. S., Sreedevi, P., Chamkha, A. J. (2021). HMT analysis of nanofluid flow over swirling cylinder with Cattaneo-Christov heat flux. Journal of Thermal Analysis and Calorimetry, 147(4), 3453–3468. [Google Scholar]
16. Moradi, A., Toghraie, D., Isfahani, A. H. M., Hosseinian, A. (2019). An experimental study on MWCNT-water nanofluids flow and heat transfer in double-pipe heat exchanger using porous media. Journal of Thermal Analysis and Calorimetry, 137(5), 1797–1807. [Google Scholar]
17. Hashim Khan, M., Hamid, A. (2018). Numerical investigation on time-dependent flow of Williamson nanofluid along with HMT characteristics past a wedge geometry. International Journal of HMT, 118, 480–491. [Google Scholar]
18. Sreedevi, P., Reddy, P. S., Chamkha, A. J. (2018). Magneto-hydrodynamics HMT analysis of single and multi-wall carbon nanotubes over vertical cone with convective boundary condition. International Journal of Mechanical Sciences, 135, 646–655. [Google Scholar]
19. Li, X. Y., Alshbool, M. H., Lv, Y. P., Khan, I., Khan, M. R. et al. (2021). HMT in MHD Williamson nanofluid flow over an exponentially porous stretching surface. Case Studies in Thermal Engineering, 26, 100975. [Google Scholar]
20. Veera, K. M., Ameer, A. N., Chamkha, A. J. (2021). Radiation absorption on MHD convective flow of nanofluids through vertically travelling absorbent plate. Ain Shams Engineering Journal, 12(3), 3043–3056. [Google Scholar]
21. Azmi, W. H., Abdul Hamid, K., Usri, N. A., Mamat, R., Mohamad, M. S. (2016). Heat transfer and friction factor of water and ethylene glycol mixture based TiO2 and Al2O3 nanofluids under turbulent flow. International Communications in HMT, 76, 24–32. [Google Scholar]
22. Ahmadloo, E., Azizi, S. (2016). Prediction of thermal conductivity of various nanofluids using artificial neural network. International Communications in HMT, 74, 69–75. [Google Scholar]
23. Prashar, P., Ojjela, O. (2021). Numerical investigation of ZnO-MWCNTs/ethylene glycol hybrid nanofluid flow with activation energy. Indian Journal of Physics, 96(7), 2079–2092. [Google Scholar]
24. Choi, T. J., Park, M. S., Kim, S. H., Jang, S. P. (2021). Experimental study on the effect of nanoparticle migration on the convective heat transfer coefficient of EG/water-based Al2O3 nanofluids. International Journal of HMT, 169, 120903. [Google Scholar]
25. Nabil, M. F., Azmi, W. H., Hamid, K. A., Mamat, R. (2018). Experimental investigation of heat transfer and friction factor of TiO2-SiO2 nanofluids in water: Ethylene glycol mixture. International Journal of HMT, 124, 1361–1369. [Google Scholar]
26. Maddah, H., Aghayari, R., Mirzaee, M., Ahmadi, M. H., Sadeghzadeh, M. et al. (2018). Factorial experimental design for the thermal performance of a double pipe heat exchanger using Al2O3-TiO2 hybrid nanofluid. International Communications in HMT, 97, 92–102. [Google Scholar]
27. Urmi, W. T., Rahman, M. M., Hamzah, W. A. W. (2020). An experimental investigation on the thermophysical properties of 40% ethylene glycol based TiO2-Al2O3 hybrid nanofluids. International Communications in HMT, 116, 104663. [Google Scholar]
28. Yıldız, C., Arıcı, M., Karabay, H. (2019). Comparison of a theoretical and experimental thermal conductivity model on the heat transfer performance of Al2O3-SiO2/water hybrid-nanofluid. International Journal of HMT, 140, 598–605. [Google Scholar]
29. Rajak, U., Nashine, P., Chaurasiya, P. K., Verma, T. N., Pathak, K. K. et al. (2022). Correction: The effects on performance and emission characteristics of DI engine fuelled with CeO2 nanoparticles addition in diesel/tyre pyrolysis oil blends. Environment Development and Sustainability. https://doi.org/10.1007/s10668-022-02431-2 [Google Scholar] [CrossRef]
30. Zaman, A., Khan, A. A. (2022). Unsteady biomedical investigation of nano-fluid flow via a bent stenosed blood vessel (with aneurysm) using the Sisko model. Waves in Random and Complex Media. https://doi.org/10.1080/17455030.2022.2123972 [Google Scholar] [CrossRef]
31. Dasore, A., Ramakrishna, K., Chaitanya, Rajak, U. (2021). Numerical analysis of thermal energy storage systems using novel composite phase change materials. Materials Today: Proceedings, 47, 6332–6335. [Google Scholar]
32. Khan, A. A., Zafar, S., Kanwal, A. (2021). Effect of relaxation and retardation times on dusty Jeffrey fluid in a curved channel with peristalsis. Advances in Mechanical Engineering, 13(6), 1–10. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools