 Open Access
Open Access
ARTICLE
Effects of Viscous Dissipation and Periodic Heat Flux on MHD Free Convection Channel Flow with Heat Generation
Robotics and Artificial Intelligence Engineering Department, Faculty of Engineering, Al-Ahliyya Amman University, Amman, 19328, Jordan
* Corresponding Author: Mustafa Abdullah. Email:
(This article belongs to the Special Issue: Computational and Numerical Advances in Heat Transfer: Models and Methods I)
Frontiers in Heat and Mass Transfer 2024, 22(1), 141-156. https://doi.org/10.32604/fhmt.2024.046788
Received 15 October 2023; Accepted 08 December 2023; Issue published 21 March 2024
Abstract
This study investigates the influence of periodic heat flux and viscous dissipation on magnetohydrodynamic (MHD) flow through a vertical channel with heat generation. A theoretical approach is employed. The channel is exposed to a perpendicular magnetic field, while one side experiences a periodic heat flow, and the other side undergoes a periodic temperature variation. Numerical solutions for the governing partial differential equations are obtained using a finite difference approach, complemented by an eigenfunction expansion method for analytical solutions. Visualizations and discussions illustrate how different variables affect the flow velocity and temperature fields. This offers comprehensive insights into MHD flow behavior and its interactions with the magnetic field, heat flux, viscous dissipation, and heat generation. The findings hold significance for engineering applications concerning fluid dynamics and heat transfer, offering valuable knowledge in this field. The study concludes that the transient velocity and temperature profiles exhibit periodic patterns under periodic heat flow conditions. A temperature reduction is observed with an increase in the wall temperature phase angle. In contrast, an increase in the heat flux phase angle values raises the temperature values.Keywords
Nomenclature
| δ1,2, ψ1,2 | Separation variables |
| λ1,2 | Separation constants |
| υ | Kinematic viscosity |
| ρ | Density |
| σ | Electrical conductivity |
| Frequency of heat flux oscillation | |
| Frequency of wall temperature oscillation | |
| ωh | Frequency of nondimensional heat flux oscillation |
| ωT | Frequency of nondimensional temperature oscillation |
| B0 | Magnetic flux density |
| Cp | Specific heat |
| g | Gravitational acceleration |
| Gr | Grashof number |
| K | Thermal conductivity |
| M | Dimensionless magnetic parameter |
| Pr | Prandtl number |
| q | Heat flux at the wall |
| Q0 | Heat generation coefficient |
| S | Dimensionless heat generating parameter |
| T* | Temperature |
| T | Dimensionless temperature |
| Tw | Wall temperature |
| T∞ | Free stream temperature |
| t* | Time |
| t | Dimensionless time |
| u* | Velocity |
| u | Dimensionless velocity |
| x*, y* | Cartesian coordinates |
| x, y | Dimensionless coordinates |
Over the past few decades, numerous researchers have presented studies on magnetohydrodynamics (MHD) fluid flow and heat transfer, owing to its significance. The field of MHD offers a diverse range of engineering applications, including MHD pumps, power generators, cooling systems, petroleum industries, reactors, accelerators, and various other domains. The impact of factors such as viscous dissipation, heat generation, and nonuniform heat flux on flow and thermal behavior has been extensively explored in separate studies across various MHD systems and scenarios.
Among the investigations conducted, particular attention has been given to understanding the effects of viscous dissipation on magnetohydrodynamic fluid flow systems. In a study by Barletta et al. [1], forced and natural flow was investigated in a vertical channel The flow was assumed to be laminar, parallel, and fully developed with adiabatic and isothermal walls. Jha et al. [2] studied the effect of viscous dissipation on the free convective fully developed flow of an incompressible viscous fluid between two infinite vertical parallel plates, considering periodic temperature on the boundaries. Meanwhile, Dessie et al. [3] examined the influence of variable viscosity on magnetohydrodynamic flow and heat transfer past a stretching sheet. the effects of viscous dissipation and porous medium were considered. Raju et al. [4] studied the effects of viscous dissipation and joule heating on an MHD convective flow in a porous medium down a horizontal channel. A uniform transverse magnetic field was applied in a rotational system. The effects of viscous dissipation and Joule heating on MHD free-convective flow near a stretching isothermal vertical sheet are studied by Jaber [5]. A uniform transverse magnetic field with variable properties was considered to control the flow. Additionally, Kishan et al. [6] examined the combined effect of viscous and ohmic dissipations on transient, laminar and fully developed flow in a vertical rectangular duct, taking into account the heat source/sink effects. The viscous dissipation effect of a porous medium fluid flow over an isothermal vertical flat plate is examined numerically by Duwairi [7]. In his study, the coefficient of thermal diffusivity was considered as the sum of molecular diffusivity and the dispersion thermal diffusivity due to mechanical dispersion. Furthermore, Swain et al. [8] illustrated MHD flow and heat transfer of a Newtonian fluid past a stretching sheet embedded in a porous matrix. More recent studies such as that of Ajibade et al. [9] explored the effects of magnetic field, and viscous dissipation on an electrically conducting incompressible fluid passing through a vertical porous channel. Moreover, Munira et al. [10] studied the MHD free convection fluid flow with heat generation and viscous dissipation effects.
Previous research papers have already shed light on the behavior of MHD flow with respect to heat generation. For instance, Mamun et al. [11] investigated the effects of viscous dissipation, and heat generation on free MHD flow past a vertical flat plate in the presence of conduction. Muthtamilselvan et al. [12] numerically explored the impact of variable heat generation/absorption on transient boundary layer flow past a vertical stretching porous surface, with an applied uniform magnetic field. Meanwhile, Ajibade et al. [13] studied the effect of radiation absorption on transient MHD flow in a vertical channel filled with porous materials. The influence of radiation absorption, heat source, and chemical reaction is considered. The unsteady MHD natural convection flow of a viscous fluid past an infinite vertical plate was studied by Shah et al. [14] considering ramped temperature and heat source. Venkateswarlu et al. [15] studied the hydromagnetic free convection flow in a vertical micro-channel, taking into account the presence of heat generation, viscous dissipation, and velocity slip effects. The effect of thermal radiation and heat generation on steady hydromagnetic fully developed free convection flow in a vertical micro channel with porous medium was studied by Ponna et al. [16]. Additionally, Ali et al. [17] studied the dusty fluid flow between two parallel plates, considering heat generation and Newtonian heating. Upreti et al. [18] studied the effect of the shape factor on magnetized Casson nanofluid flow through an elongated sheet with a non-uniform heat source/sink.
Engineering applications involving fluid and heat transfer with periodic wall heat flux have attracted significant interest, particularly in the analysis of heat exchangers and cooling tubes. Zniber et al. [19] conducted an analytical study on MHD flow through a channel considering periodic heat flux. The research demonstrated that increasing the heat flux frequency will increase the heat transfer between the wall and the fluid for all values of parameters. Another investigation by Das et al. [20] studied the effect of radiation and alternating heat flux on MHD free convective flow of a fluid over a vertical permeable plate with a uniform magnetic field. Abdullah et al. [21] used a numerical finite difference method to study the influence of periodic magnetic field and periodic heat flux on MHD flow through a porous medium between two parallel plates.
By reviewing previous studies, there has been no work that studied MHD flow and thermal behavior through a channel considering viscous dissipation and periodic heat flow. This study examines the convective MHD flow between vertical parallel plates, considering viscous dissipation and heat generation. A uniform transverse magnetic field is applied perpendicular to the channel. A periodic temperature and periodic wall heat flux are considered to control the fluid behavior. The governing equations are solved numerically and analytically, and the results are compared with each other.
In this study, the impact of periodic wall heat flux on a transient laminar fully developed flow that passes through a vertical channel consisting of parallel plates is investigated. The channel is represented in Fig. 1 and the fluid is assumed to be viscous and incompressible.
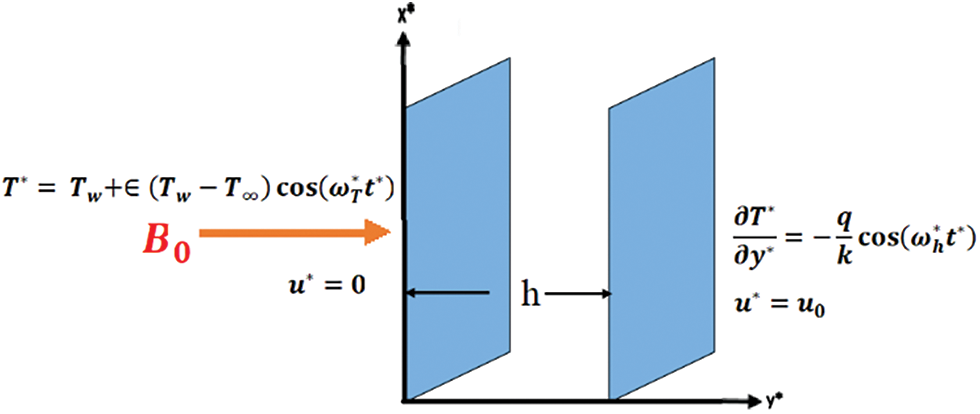
Figure 1: Physical model description
Initially, it is assumed that the fluid and channel walls are both stationary and have the same temperature of T∞. After time zero, one plate is kept stationary and periodically heated, while the other moves at a constant velocity and has a periodic heat flux.
A free convective laminar flow with a uniform transverse magnetic field B0 is considered. The governing equations for transient momentum and energy include viscous dissipation and heat generation effects, using the Boussinesq approximation [22] are:
The initial and boundary conditions considered are:
Next, the following dimensionless variables are introduced:
By utilizing the aforementioned dimensionless quantities, the governing equations can be expressed in a dimensionless form.
And the corresponding initial and boundary conditions are:
In this work, the governing momentum and energy equations are coupled and non-linear and their boundary conditions are nonhomogeneous. Hence a numerical Finite difference method is used to solve the problem by using the Crank Nicolson technique with Thomas algorithm. The technique is fully implicit that is both stable and convergent.
The forward difference method for time discretization and the central difference method for spatial discretization are used to convert the partial derivatives into finite difference equations. The derivatives in the momentum equations can be performed as:
Similarly, for the energy equation:
Here, “i” and “n” are used as index variables for special and time indexing, respectively, and Δt represents the time step size while Δy represents the space step size.
By applying the above forms of the derivatives, the resulting dimensionless governing equations Eqs. (5) and (6) are:
The implicit form of the equations can be written as:
Using the previous equations, a tri-diagonal matrix representing the algebraic equations for all values of y can be formed. The equations are evaluated at each point in the y domain with a step size of Δy = 0.001. The Thomas algorithm is then used to solve the resulting system of algebraic equations at each time with Δt = 0.01.
The numerical solution has been validated by comparing it with the analytical solution for specific scenarios. The eigenfunction expansion method is used to solve both the momentum and energy equations.
A constant heat flux with constant wall temperature and negligible Ec and S parameters are used to solve the energy equation analytically.
The corresponding boundary conditions are:
When
The eigenfunction expansion method requires transforming the boundary conditions into linear and homogeneous equations. Therefore, the following variable is introduced:
Therefore, the energy equation will be:
Below are the corresponding boundary conditions:
When
Let
By substituting the function H(y, t) and its derivatives into Eqs. (11) and (12), the eigenvalue problem can be obtained.
The solution of the eigenvalue problem is:
And the eigenvalues are:
where n = 1, 2, 3,......, ∞.
The solution of the time dependent function δ(t) is:
Hence the solution of H(y, t) is as follows:
By utilizing the condition
the coefficient
Finally, the dimensionless temperature has been solved using the following solution:
To solve the momentum equation analytically, the Grashof number is neglected (Gr = 0).
The boundary conditions are:
A new variable is introduced to transform non-homogeneous boundary conditions into homogeneous.
The momentum equation can be expressed as follows:
And the boundary conditions become:
Initially, we will solve the homogeneous part of Eq. (21).
The problem can be solved using separation of variables method.
The problem of finding eigenvalues will be:
The solution of
And the corresponding eigenvalues are:
The solution to the nonhomogeneous Eq. (21) that satisfies the time-dependent variable is:
Then the solution of Eq. (21) is:
Then, the final solution is reached:
This study analyzes flow and thermal behavior of a viscous, incompressible fluid through a vertical channel, accounting for the impact of viscous dissipation and periodic heat flux. The momentum and energy equations are solved using the numerical Crank-Nicolson method. The results are verified through analytical solutions, assuming uniform wall temperature and heat flux, and negligible Grashof and Eckert numbers.
Graphs are presented to illustrate the impact of various variables on velocities and temperatures. In this study, the following values of parameters are considered for numerical calculations: Gr = 2, M = 2, Pr = 0.71, S = 0.2, Ec = 1. Fig. 2 demonstrates the influence of the Grashof number on velocity, indicating that the velocity increases with a higher Grashof number. This is because the Grashof number represents the ratio of thermal buoyancy force to viscous force, and so as the Grashof number increases, buoyancy dominates and the thermal buoyancy force tends to induce much flow in the boundary layer, while viscosity dominates when the buoyant force decreases. In Fig. 3, the effect of the magnetic field parameter (M) is shown. As M increases, the flow slows down. The reason for this is that when a transverse magnetic field is applied, a force called Lorentz force will arise, which resists the flow and thus reduces its speed. This means that increasing M leads to an increase in the thickness of the momentum boundary layer.
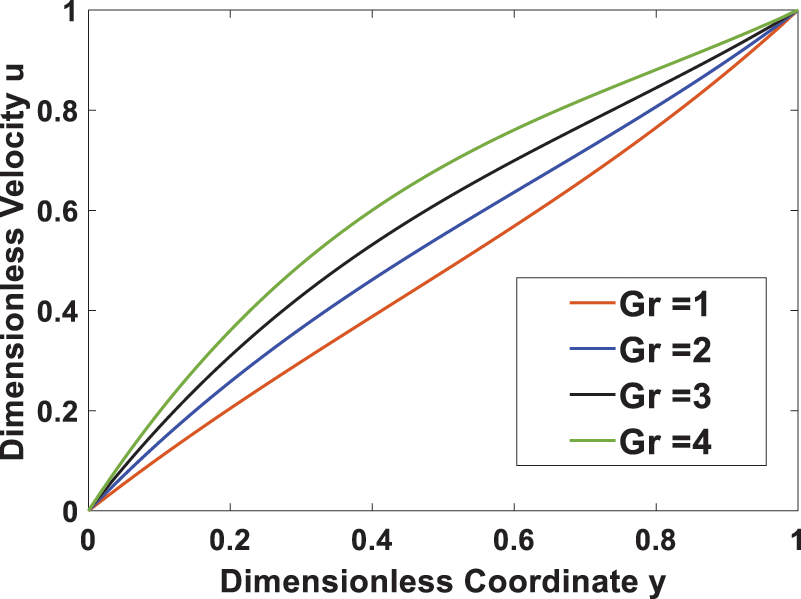
Figure 2: Effect of Grashof number Gr on the velocity
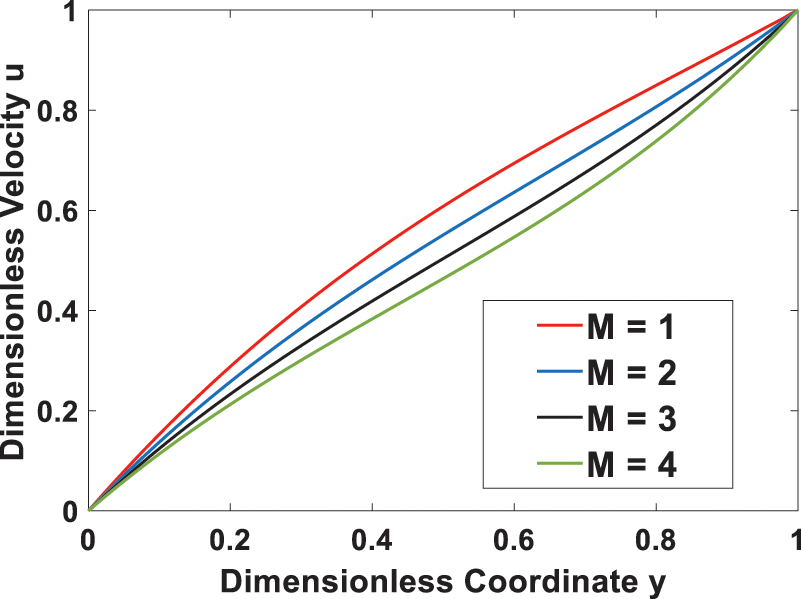
Figure 3: Effect of magnetic parameter M on the velocity
Figs. 4 and 5 display the effect of the Prandtl number on velocity and temperature fields, respectively. An increase in the Prandtl number results in an enhanced velocity profile due to increased viscous diffusivity or decreased thermal diffusivity. Additionally, Fig. 5 shows that a higher Prandtl number reduces the diffusion of heat generated due to viscous dissipation, which results in a lower energy transfer capability, leading to an increased temperature profile. It is also noted that when Pr = 7, the temperature rises until it reaches a maximum at y = 0.2 and then decreases in the remaining region.
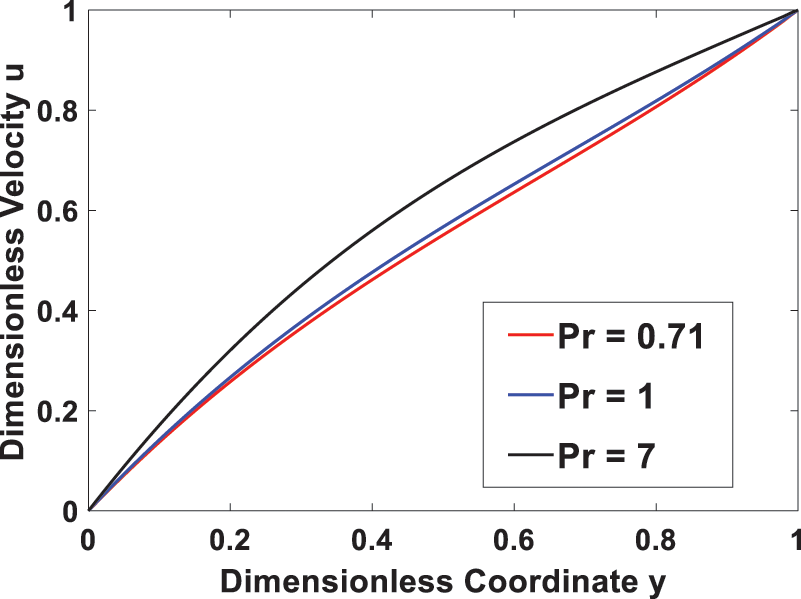
Figure 4: Effect of Prandtl number Pr on the velocity
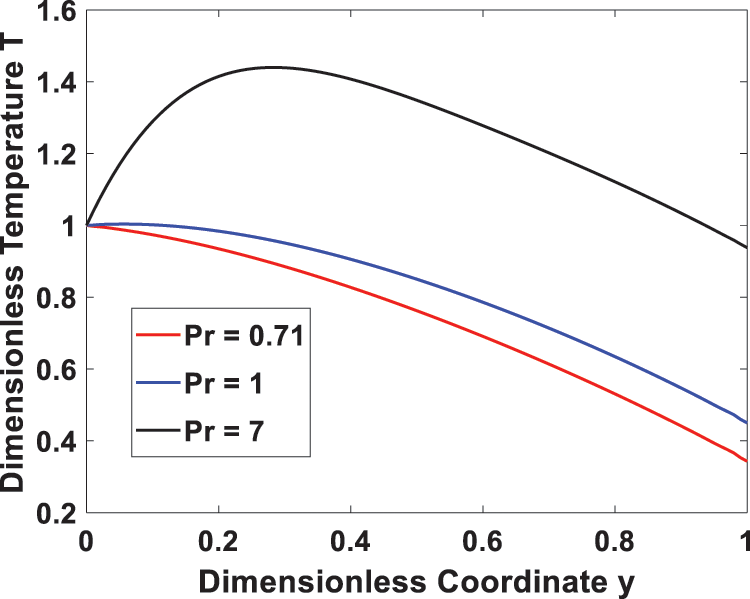
Figure 5: Effect of Prandtl number Pr on the temperature
Figs. 6 and 7 show how the velocity and temperature profiles are affected by the Eckert number (Ec), respectively. An increase in Ec due to increased viscous dissipation raises both the velocity and temperature of the system. This occurs because of shear stress within the fluid, which leads to an increase in the thermal energy stored in the fluid with an increase in viscosity dissipation. Fig. 8 depicts the temperature profile for different values of the heat generating parameter (S), indicating that increasing S leads to higher temperature values due to increased heat generation. Increased heat generation strengthens the convection current and thus reduces the density of the fluid, leading to a rise in temperature.
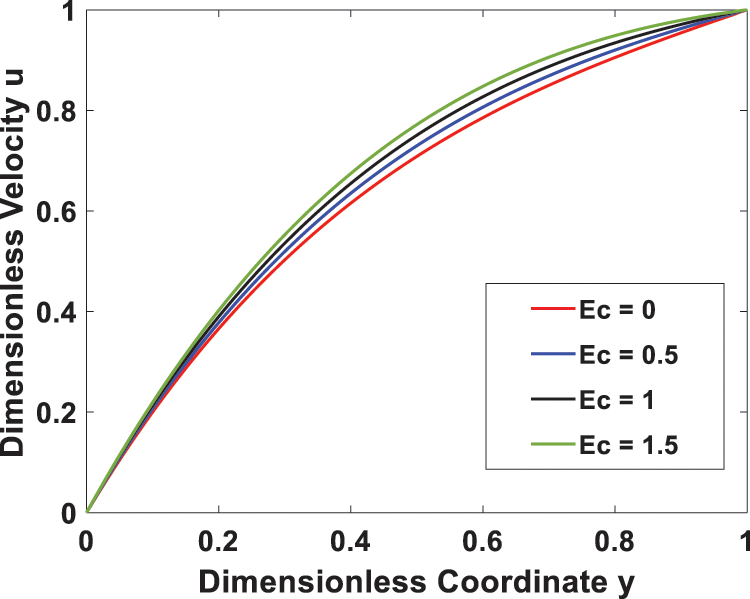
Figure 6: Effect of Eckert number Ec on the velocity
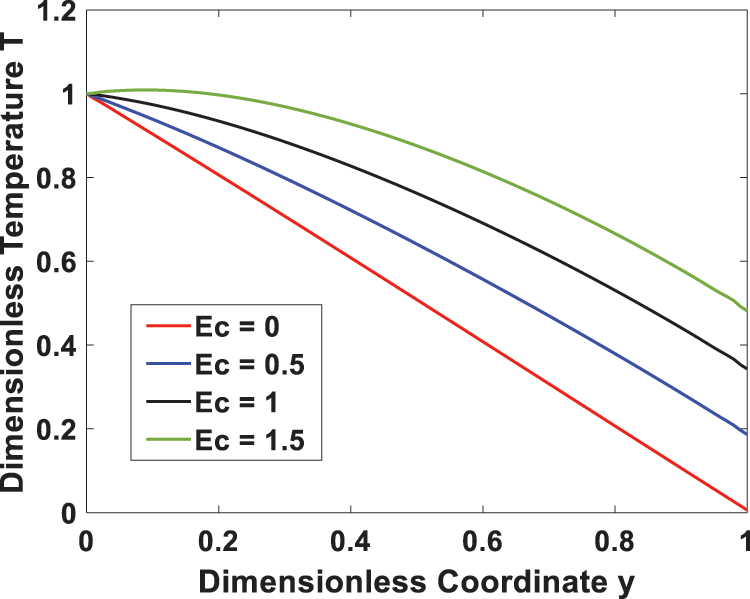
Figure 7: Effect of Eckert number Ec on the temperature
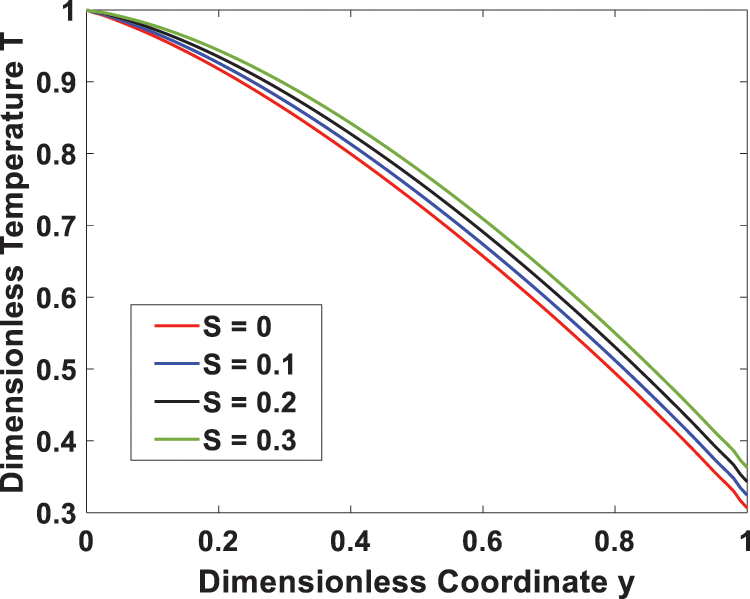
Figure 8: Effect of heat generating parameter S on the temperature
Furthermore, Fig. 9 investigates the effect of the time-periodic heat flux on transient temperature. It is seen that the temperature profile has a periodic behavior, and the amplitude decreases as the heat flux frequency rises. In Figs. 10 and 11, the transient flow and temperature behaviors at different locations are shown. A rise in the time-periodic velocity and temperature profiles was observed as we approached the right channel wall. The effect of wall temperature and heat flux phase angles on the temperature profile is represented in Figs. 12 and 13, it is observed that the temperature increases with an increase in heat flux phase angle, while it decreases with an increase of wall temperature phase angle.
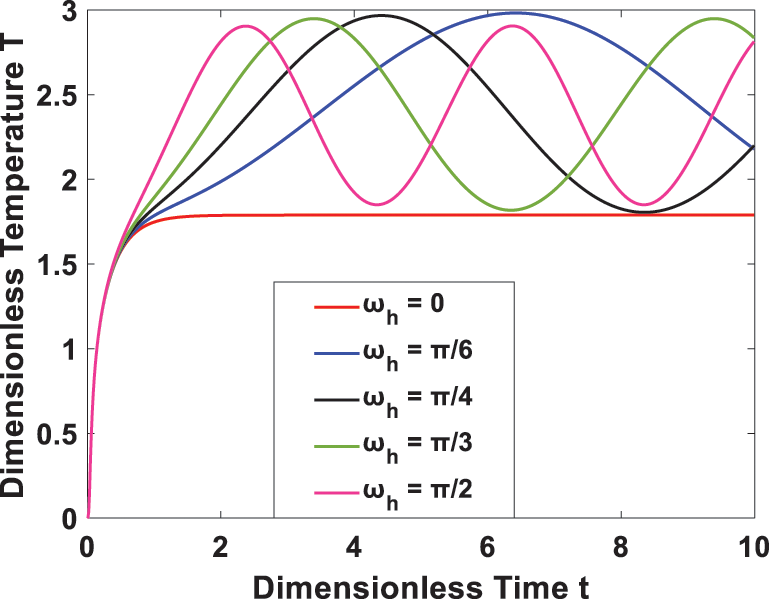
Figure 9: Effect of heat flux frequency on transient temperature
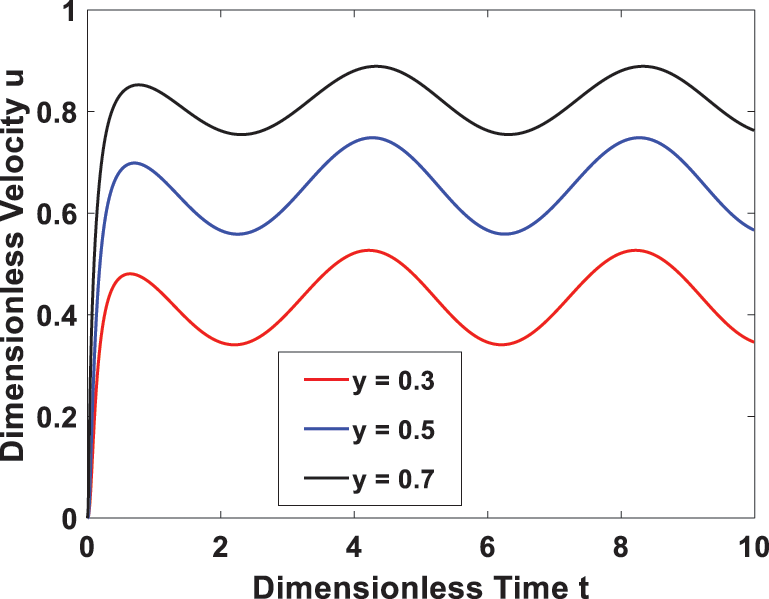
Figure 10: Transient velocity at different locations
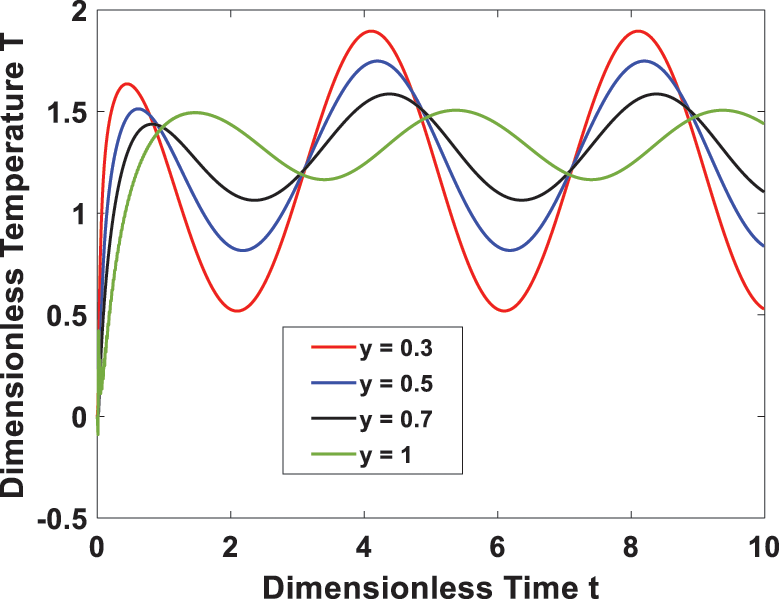
Figure 11: Transient temperature at different locations
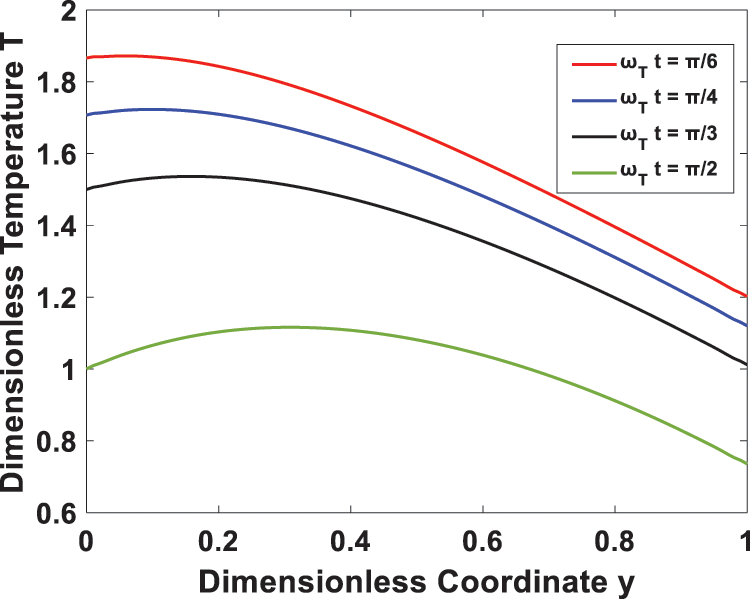
Figure 12: Effect of phase angle ωTt on the temperature
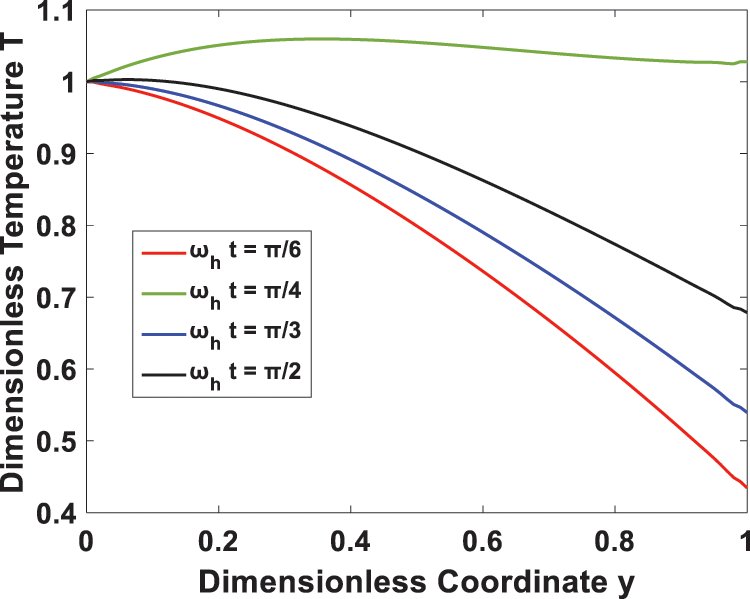
Figure 13: Effect of phase angle ωht on the temperature
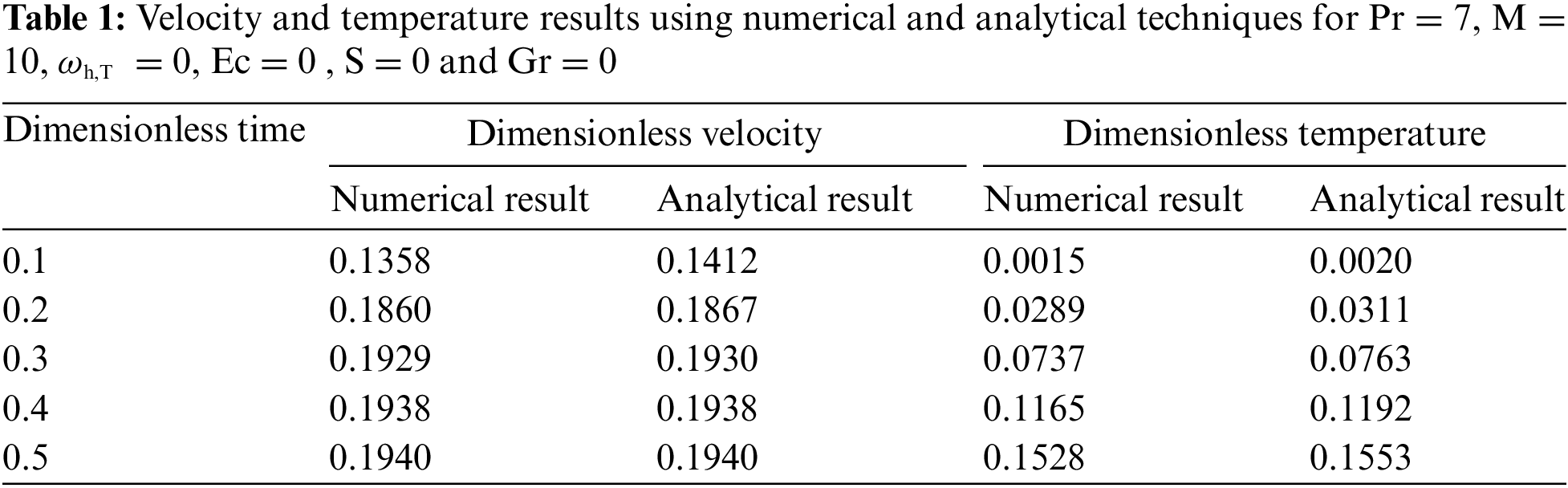
A comparison between the accuracy of the numerical results and the results using analytical procedure for special cases is presented in Table 1 and excellent agreement is found.
This work examines the temperature distribution and fluid velocity via a vertical channel affected by viscous dissipation and periodic heat flow. A completely implicit numerical approach was used to solve the dimensionless governing partial differential equations computationally. The numerical solution was proved and validated by solving a particular case analytically using eigenfunction expansion method. The influence of several physical variables are presented graphically. Thus, it is determined that:
1. The fluid’s Grashof number, Prandtl number, Eckert number, or heat source must all be raised in order for the fluid’s velocity and temperature to increase.
2. As the magnetic field’s intensity increases, the fluid's velocity falls.
3. The transient velocity and temperature profiles show periodic patterns of behaviour when a periodic heat flux is applied.
4. A rise in the wall temperature angle phase difference is correlated with a decrease in temperature, but a rise in the heat flux phase shift values results in an increase in temperature.
Acknowledgement: Not applicable.
Funding Statement: The author received no specific funding for this study.
Author Contributions: A single author prepared this study.
Availability of Data and Materials: The data are available from the corresponding author upon request.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
References
1. Barletta, A., Celli, M. (2008). Mixed convection MHD flow in a vertical channel: Effects of Joule heating and viscous dissipation. International Journal of Heat and Mass Transfer, 51(25–26), 6110–6117. [Google Scholar]
2. Jha, B. K., Ajibade, A. O. (2012). Effect of viscous dissipation on natural convection flow between vertical parallel plates with time-periodic boundary conditions. Communications in Nonlinear Science and Numerical Simulation, 17(4), 1576–1587. [Google Scholar]
3. Dessie, H., Kishan, N. (2014). MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Engineering Journal, 5(3), 967–977. [Google Scholar]
4. Raju, K. V. S., Sudhakar Reddy, T., Raju, M. C., Satya Narayana, P. V., Venkataramana, S. (2014). MHD convective flow through porous medium in a horizontal channel with insulated and impermeable bottom wall in the presence of viscous dissipation and Joule heating. Ain Shams Engineering Journal, 5(2), 543–551. [Google Scholar]
5. Jaber, K. K. (2014). Effects of viscous dissipation and Joule heating on MHD flow of a fluid with variable properties past astretching vertical plate. European Scientific Journal, 10(33), 383–393. [Google Scholar]
6. Kishan, N., Shekar, B. C. (2015). Finite element analysis of fully developed unsteady MHD convection flow in a vertical rectangular duct with viscous dissipation and heat source/sink. Journal of Applied Science and Engineering, 18(2), 143–152. [Google Scholar]
7. Duwairi, H. M. (2016). Thermal dispersion effects on convection heat transfer in porous media with viscous dissipation. International Journal of Heat and Technology, 34(2), 207–212. [Google Scholar]
8. Swain, B. K., Parida, B. C., Kar, S., Senapati, N. (2020). Viscous dissipation and joule heating effect on MHD flow and heat transfer past a stretching sheet embedded in a porous medium. Heliyon, 6(10), 1–8. [Google Scholar]
9. Ajibade, A. O., Umar, A. M., Kabir, T. M. (2021). An analytical study on effects of viscous dissipation and suction/injection on a steady mhd natural convection couette flow of heat generating/absorbing fluid. Advances in Mechanical Engineering, 13(5), 1–12. [Google Scholar]
10. Munira, S., Sarker, S. P. K., Alam, M. M. (2022). MHD and heat generation along a vertical flat plate with variable viscosity and viscous dissipation: A numerical solution. International Journal of Mathematics and Statistics Studies, 10(4), 78–94. [Google Scholar]
11. Mamun, A. A., Chowdhury, Z. R., Azim, M. A., Molla, M. M. (2008). MHD-conjugate heat transfer analysis for a vertical flat plate in presence of viscous dissipation and heat generation. International Communications in Heat and Mass Transfer, 35(10), 1275–1280. [Google Scholar]
12. Muthtamilselvan, M., Prakash, D., Doh, D. H. (2014). Effect of non-uniform heat generation on unsteady MHD flow over a vertical stretching surface with variable thermal conductivity. Journal of Mechanics, 30(2), 199–208. [Google Scholar]
13. Ajibade, A. O., Umar, A. M. (2016). Effect of chemical reaction and radiation absorption on the unsteady MHD free convection Couette flow in a vertical channel filled with porous materials. Afrika Matematika, 27, 201–213. [Google Scholar]
14. Shah, N. A., Zafar, A. A., Akhtar, S. (2018). General solution for MHD-free convection flow over a vertical plate with ramped wall temperature and chemical reaction. Arabian Journal of Mathematics, 7, 49–60. [Google Scholar]
15. Venkateswarlu, M., Prameela, M., Makinde, O. D. (2019). Influence of heat generation and viscous dissipation on hydromagnetic fully developed natural convection flow in a vertical micro-channel. Journal of Nanofluids, 8(7), 1506–1516. [Google Scholar]
16. Ponna, B., Malapati, V. (2021). Influence of heat generation and thermal radiation on MHD flow in a vertical micro-porous-channel in the presence of viscous dissipation. Mapana Journal of Sciences, 20(2), 27–58. [Google Scholar]
17. Ali, F., Ali, G., Khan, A., Khan, I., Eldin, E. T. et al. (2023). Effects of Newtonian heating and heat generation on magnetohydrodynamics dusty fluid flow between two parallel plates. Frontiers in Materials, 10, 1120963. [Google Scholar]
18. Upreti, H., Mishra, S. R., Kumar Pandey, A., Joshi, N., Joshi, B. P. (2023). Diversified role of fuzzified particle concentration on Casson gold-blood nanofluid flow through an elongating sheet for different shape nanoparticles. Journal of Taibah University for Science, 17(1), 2254465. [Google Scholar]
19. Zniber, K., Oubarra, A., Lahjomri, J. (2005). Analytical solution to the problem of heat transfer in an MHD flow inside a channel with prescribed sinusoidal wall heat flux. Energy Conversion and Management, 46(7–8), 1147–1163. [Google Scholar]
20. Das, S., Guchhait, S. K., Jana, R. N. (2013). Radiation effects on MHD free convective flow past an oscillating vertical porous plate with periodic heat flux. International Journal of Computer Applications, 65(3), 28–35. [Google Scholar]
21. Abdullah, M., Owida, H. A. (2023). Transient MHD flow between parallel plates with influence of periodic magnetic field and periodic heat flux. Mathematical Modelling of Engineering Problems, 10(2), 558–564. [Google Scholar]
22. Shao, Z., Shah, N. A., Tlili, I., Afzal, U., Khan, M. S. (2019). Hydromagnetic free convection flow of viscous fluid between vertical parallel plates with damped thermal and mass fluxes. Alexandria Engineering Journal, 58(3), 989–1000. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools