 Open Access
Open Access
ARTICLE
Steady Natural Convection from a Vertical Hot Plate with Variable Radiation
1 Department of Mechanical Engineering, Universitas Sriwijaya, Indralaya, 50662, Indonesia
2 Department of Engineering Science, Universitas Sriwijaya, Palembang, 30139, Indonesia
* Corresponding Author: Kaprawi Sahim. Email:
Frontiers in Heat and Mass Transfer 2024, 22(1), 305-315. https://doi.org/10.32604/fhmt.2023.041882
Received 10 May 2023; Accepted 07 July 2023; Issue published 21 March 2024
Abstract
The natural convection from a vertical hot plate with radiation and constant flux is studied numerically to know the velocity and temperature distribution characteristics over a vertical hot plate. The governing equations of the natural convection in two-dimension are solved with the implicit finite difference method, whereas the discretized equations are solved with the iterative relaxation method. The results show that the velocity and the temperature increase along the vertical wall. The influence of the radiation parameter in the boundary layer is significant in increasing the velocity and temperature profiles. The velocity profiles increase with the increase of the radiation parameter. The temperature profiles near the wall plate parallel each other due to the constant heat flux applied to the wall. The influence of the radiation parameter is significant either in velocity or temperature characteristics. At the same time, the effect of the Prandtl number greater than 0.71 is not sensitive to the velocity and temperature variations elsewhere.Keywords
Nomenclature
| Cp | Specific heat (J/kg·K) |
| g | Gravitation (m/s2) |
| Gr | Grashoff number |
| k | Thermal conductivity (W/m·K) |
| L | Plate length (m) |
| m | Number of mesh points in x direction |
| n | Number of mesh points in y direction |
| Pr | Prandtl number |
| qr | Surface heat flux (W/m2) |
| R | Dimensionless radiation parameter |
| T | Temperature (K) |
| u, v | Velocity parallel and normal to the vertical plate, respectively (m/s) |
| U, V | Dimensionless velocity parallel and normal to the vertical plate, respectively |
| x, y | Coordinates parallel and normal to the vertical plate, respectively (m) |
| X and Y | Dimensionless coordinates are parallel and normal to the vertical plate, respectively |
| Greek Symbols | |
| μ | Absolute viscosity (kg/m·s) |
| δ | Boundary layer thickness (m) |
| τ | Dimensionless shear stress |
| τo | Shear stress (kg/m·s2) |
| ρ | Density (kg/m3) |
| θ | Dimensionless temperature |
| υ | Kinematic viscosity (m2/s) |
| σ | Stefan-Boltzmann constant (W/m2·K4) |
| Subscripts | |
| I | Discretized the point in the x direction |
| j | Discretized point in y direction |
| w | Condition at the wall |
| ∞ | Ambient environment |
The study about the heating and cooling of the engineering apparatus has been conducted continuously by researchers for a long time. Many types of engineering equipment have a process of natural convection, such as electronic components, solar collectors, heaters, and heat exchangers. The integrated circuit of an electronic device is one of the types of approach or application of this study. A surface of a vertical plate is maintained in still fluid at a temperature higher or lower than that of the fluid; a layer of fluid adjacent to the surface gets heated or cooled. A higher surface temperature is supplied with a heat source coming from the internal of the plate. The decrease and increase in the heat flux from a vertical plate will also decrease and increase the heat transfer coefficient, as shown by Teymourtash et al. [1], using the finite difference method to solve the convection problem. In their studies, they applied the finite difference method in solving the governing equation of convection. Furthermore, Singh et al. [2] calculated the heat transfer performance of free convection across a heated vertical tube wall. Cao et al. [3] studied the effect of a gas flow with slip and radiation on natural convection along a heated vertical plate. Ferdows et al. [4] used micropolar fluid as a medium for natural convection along a vertical plate to know the effect of the magnetic fields and heat generation on convective parameters. Pantokratoras [5] introduced the non-linear thermal radiation parameter in natural convection along a vertical plate with a constant temperature. Al-Farhany et al. [6] investigated the heat transfer performance of nanofluid’s natural convection in a tall enclosure where the vertical left-sided wall is heated partially with constant temperature while the other sides are insulated. The study of the heat transfer characteristics of natural convection in vertical plate arrays has been given by Wong et al. [7]. The experimental work of Kaneda et al. [8] gives the effect of the magnet in natural convection in a duct where one of the duct walls was heated partially. The influence of natural convection radiation over a cone’s vertical wavy frustum is explored numerically. The experimental investigation of heat transfer in unsteady natural convection across a vertical plate is carried out [9]. The influence of thermal radiation in free nanofluid convection over a vertical isothermal plate has been explored analytically by Fetecau et al. [10]. The effect of radiation and magnetic field on free convection from stretched vertical flat plate has been given analytically by Gnaneswara Reddy [11]. Chandra Reddy et al. used the finite difference in solving the governing equation of natural convection of nanofluid [12]. The rate of heat transfer of nanofluid fluid convection over a vertical plate in a two-dimension problem is presented numerically by Uddin et al. [13]. In this case, they used the finite difference method. Molla et al. [14] have presented the flow characteristics due to the free convection of two-dimension over a vertical plate with sinusoidal surface temperature in which the finite difference method has been used to obtain the fluid parameters. The effect of the Prandtl number on the temperature distribution of convection fluid over a moving vertical plate with heat generation is significant [15,16]. In an accelerated vertical plate, the thermal radiation in natural convection tends to accelerate the fluid velocity, and the higher radiation parameter values raise the surface heat transfer, as Kumar et al. showed [17]. In a constantly moving plate in free convection, an increase in thermal radiation increases the fluid velocity and temperature profiles [18]. Thermal radiation tends to reduce fluid velocity and temperature for flow along an accelerated infinite vertical plate with ramped plate temperature [19]. The unsteady free convection over a vertical plate with varying heat flux dan for low Prandtl number was presented by [20]. A study of an accelerating vertical plate in a thermally stratified fluid flow in viscous dissipation was investigated numerically by Goud et al. [21]. The investigation of the combined effects of thermophoretic motion and thermal radiation on steady, viscous, incompressible, and two-dimensional mixed convection flow of optically dense grey fluid was explored by Abbas et al. [22]. The influence of the Prandtl number and the radiation on temperature profiles for unsteady free convection was presented by Ramalingeswara Rao et al. [23]. Experimentally examined the influence of radiative heat transfer from a heated vertical plate in the air [24]. The combined impact of thermal radiation and chemical reaction on MHD-free convective heat and mass transfer effects of the nanofluid has been investigated by Arulmozhi et al. [25]. Yasin et al. [26] investigated a numerical solution of ferrofluid’s mixed convection boundary layer flow at the stagnation point on a vertical flat plate. Abdullah et al. [27] have contributed periodic heat flux at the wall surface in the energy equation studied to know the effect of heat generation and thermal radiation on the free convection flow and heat transfer past a vertical plate.
From the literature surveys, the steady natural convection along a vertical hot with variable radiation and constant surface heat flux needs to be investigated using the finite difference method since this method is straightforward, has good accuracy, and is suitable for more complicated problems which can solve at least two-dimension problems. In this case, the effect of the plate length may also influence the fluid performance parameters in the boundary layer of the natural flow since the study is conducted in a two-dimensional case. We have extended the work of Mamun et al. [28] with the novelty of considering the radiation term in the energy equation. We have also extended the work of Yildiz et al. [29] with the novelty of introducing the term of the Prandtl in the governing equation. In the case of Yildiz’s work, they used commercial software to find the convection variables.
2 Formulation of Natural Convection
The Boussinesq approximation is used to characterize the buoyancy effects of fluid flow due to temperature changes. The two-dimensional equation of continuity, momentum, and energy for natural convection of incompressible flow steady state condition has the following form:
with boundary conditions as follows:
The sketch of the physical problem is described in Fig. 1. The x-axis is taken along the vertical plate with the origin at the bottom end, which is the plate’s leading edge, and the y-axis is perpendicular to the plate. The plate is heated at constant flux, and the radiation heat parameter qr diffuses perpendicular to the plate surface. The fluid adjacent to the surface moves vertically due to the buoyancy effect, which makes the hydrodynamic boundary layer δu, thermal boundary layer δt, and thermal expansion represented by coefficient β. u and v are the velocity components in the x and y axes, respectively.

Figure 1: Natural convection over a vertical hot plate
The radiation heat flux can be simplified using the Rosseland diffusion approximation, which is valid for an optically thick, isotropically scattering medium [30]:
where βr is the extinction coefficient and σ stefan Boltman parameter.
The Eq. (5) is then substituted into Eq. (3), and it becomes the following equation:
The dimensionless quantities are the following expressions:
Gr is the Grashoff number, g is gravitation acceleration, L is plate length, and Pr is the Prandtl number.
By applying the above dimensionless variables, the dimensionless form of the governing equations of (1)–(3) are
where
Introducing the following heat flux parameter:
Then, the boundary conditions of the Eq. (4) become
The above dimensionless equations are coupled and are solved under the boundary conditions given in Eq. (11) and are solved with numerical methods. These equations are discretized using the finite-difference method in which the backward finite difference is applied to x terms and the central finite difference in y terms. Then the Eqs. (7)–(9) change in a discretized system that is a linearized system of the equations, shown by Eqs. (12)–(14). The variables with subscript i are to be solved, and previous calculations or boundary conditions know subscript i−1. The discretized equations are solved with the implicit procedures since the implicit method is stable unconditionally. On the boundary condition, the velocity values are all zeros; the temperatures are zero at far from the wall, and unknown temperature values at the wall. Therefore, we use the iterative method to solve these equations. In this linearized system of equations, the choice of ΔX small enough compared to ΔY.
where
The fluid velocity normal to the surface is calculated from the Eq. (7):
Starting from i =1, then Ui,j is given initial values for
Fig. 2 shows the velocity profiles for X and Pr ≈ 0.71 values, which correspond to air and the radiation parameter R = 2. For Pr = 15, different X and R = 2, the velocity profiles are represented by Fig. 3. The comparison of both figures shows that profiles are similar except for X = 0.2 in Fig. 3. It observed that the peak values are slightly different which for Pr = 0.71 it is higher for X > 0.6. However, it is lower for X < 0.6. This may be due to the difference in specific heat and viscosity of the fluid. The liquid means a high Prandtl number (Pr = 15) and absorbs the heat faster than the gas (Pr = 0.71), but the liquid has slow motion due to the shear stress among the molecules. The profiles have a significant variation in the vertical direction where the maximum differences are at the peak values of every distance X. The discrepancies get smaller the further away from the wall, and the curves go to zero at Y ≈ 8. It is essential to observe the velocities at the boundary layer where zero velocities occur to a narrow region of about Y ≈ 8. It means the boundary layer thickness develops very slowly in the vertical direction. The velocities increase near the wall increase quickly and reach their maximum value of about Y ≈ 1.2. The position of maximum velocities shifted slightly with an increase in X. This may be due to the increase in the shear stress at the wall, and the velocity is zero at the wall since there is no slip. It is also observed that the more the X value increases, the higher the velocity.

Figure 2: Velocity profiles for different X and Pr = 0.71

Figure 3: Velocity profiles for different X and Pr = 15
The velocity profiles for variation in the radiation parameter and, for X = 0.8 and Pr = 0.71, are shown in Fig. 4. It can be seen that profiles are similar for all radiation parameter values. However, their values are significantly different, which increases with the radiation increase. The position of the maximum values occurs at the same distance from the wall of Y ≈ 1.4. The radiation influences the fluid velocity in natural convection, which is indicated by the velocity increase when the radiation parameter increases. The increase in radiation parameters does not seem to change the boundary layer thickness. In the case of R = 0 that it corresponds to the condition in which the radiation does not influence the natural convection. The energy is transferred from molecule to molecule through collision. Many molecules with raised kinetic energy are carried away by the flow and are replaced by colder fluid, resulting in increased energy transfer rates, making the fluid velocities higher.

Figure 4: Velocity profiles for different R
The velocity profiles for X = 1 and Pr = 15 is represented in Fig. 5. It seems that the velocity decreases with the increasing the Prandtl number since the velocity profiles for R = 2 and X = 1 in Fig. 4 is smaller than that of in Fig. 2 for the exact value of R and X. We can see from the figure that the peak value of the velocity is about 0.9 for Pr = 0.71 and 0.8 for Pr = 15. The velocity profiles without radiation or R = 0 and Pr =15 are lower than those for Pr = 0.71. The decrease of the velocities with the increase in the Prandtl number is caused by the retarding of flow at the wall due to shearing stress, which increases viscosity. The increasing Prandtl number does not change the boundary layer thickness much.
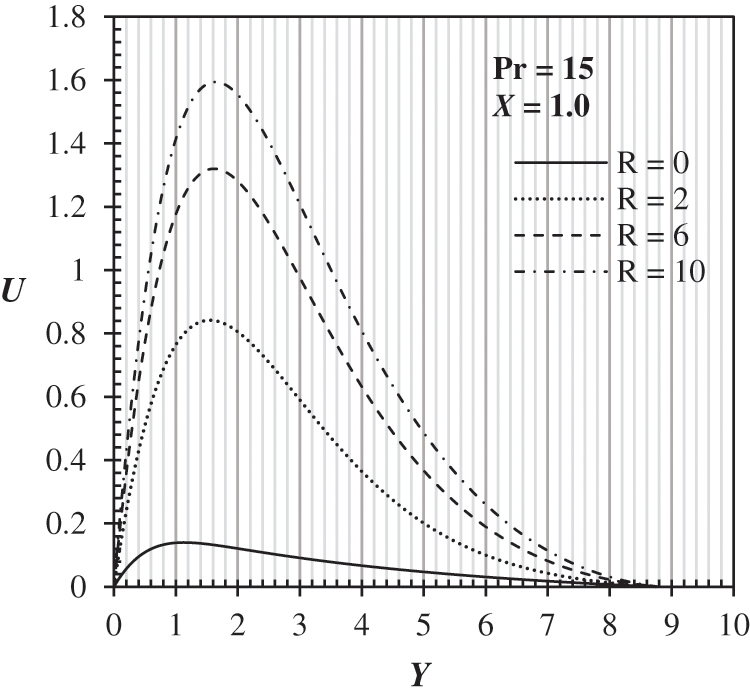
Figure 5: Velocity profiles for different R and Pr = 15
The Effect of all Prandtl numbers 0.71 to 40 is presented in Fig. 6 for R = 2 and X = 0.8. It can be observed that the curves coincide with each other for Pr ≤ 7 since the velocity distributions are influenced by the temperatures as shown by the Eq. (8), in which the temperature is further influenced by the Prandtl number shown in Eq. (9). For Y < 2.5 the velocity profile for Pr = 0.71 is higher than the profile for Pr ≥ 7 since the Effect of shearing stress is higher for the liquid phase. When Y > 2.5, the velocity profile is lower for higher Pr ≥ 7, and it may be caused by the capacity of liquid to absorb heat which is higher than gas or Pr = 0.71, so the buoyancy effect is higher.

Figure 6: Velocity profiles for different Pr
The Effect of the radiation parameter on the shear stress at the plate surface is drawn in Fig. 7 for Pr = 15. It can be observed that the shear stress rises quickly for X ≤ 0.2 and slowly after X ≈ 2. The zero shear stress at X = 0 is due to no fluid flow before the leading edge.

Figure 7: Shear stress for different R
The temperature profile in the boundary layer is given in Fig. 8 for Pr = 0.71 and R = 2. In contrast, for Pr = 0.71 and R = 6 is presented in Fig. 9 the velocity profiles seem similar. However, the difference is in the values and the boundary layer thickness in which the smaller values for lower radiation parameters. The higher R’s velocity is due to much of the heat energy being absorbed by fluids. The temperature profiles are similar to each other, but a significant variation in different values of X is observed. The temperature distributions of the wall are the highest, and then the temperatures decrease rapidly with the increase of X, in which the maximum limit of X = 1. The curves go down to zero at the boundary layer, with a value of Y ≈ 8.5. Near the wall, the rise of the temperatures decreases with the constant increase of the X. The essential characteristics of the profile temperature near the wall seem to be linear and parallel since the heat flux is constant along the vertical plate as prescribed by the boundary condition of the equation. When the radiation is applied to natural convection, its Effect on the temperature variation is significant, as shown by Fig. 10 for Pr = 0.71 since the radiation parameter R in Eq. (9) is sensitive to temperature variations. The velocities vary linearly with the increase in Y near the wall of all radiation parameters ranging from 0 to 10. If no radiation occurs, R = 0, the zero velocity far from the wall is found at Y ≈ 2.5, and this location increases with the increase in the radiation parameter.
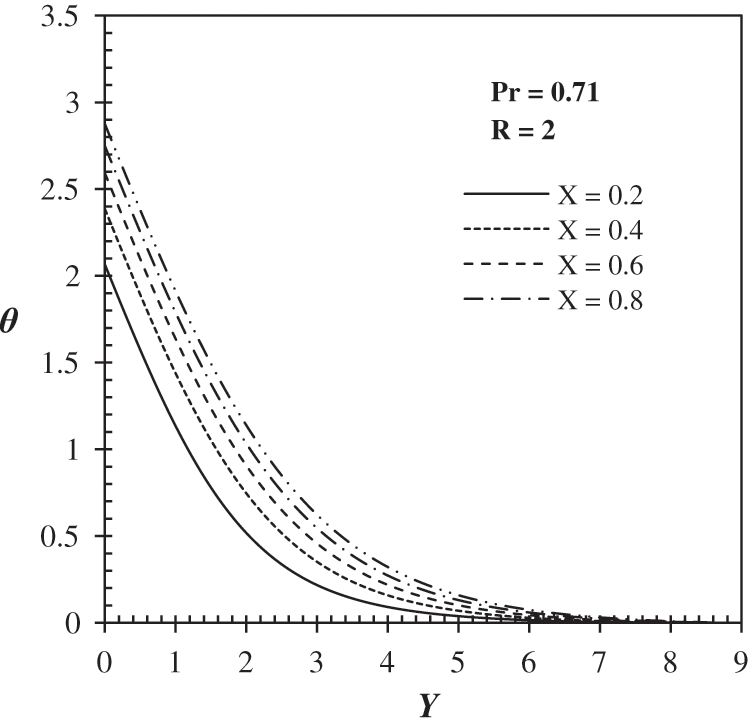
Figure 8: Temperature profiles for different X and R = 2
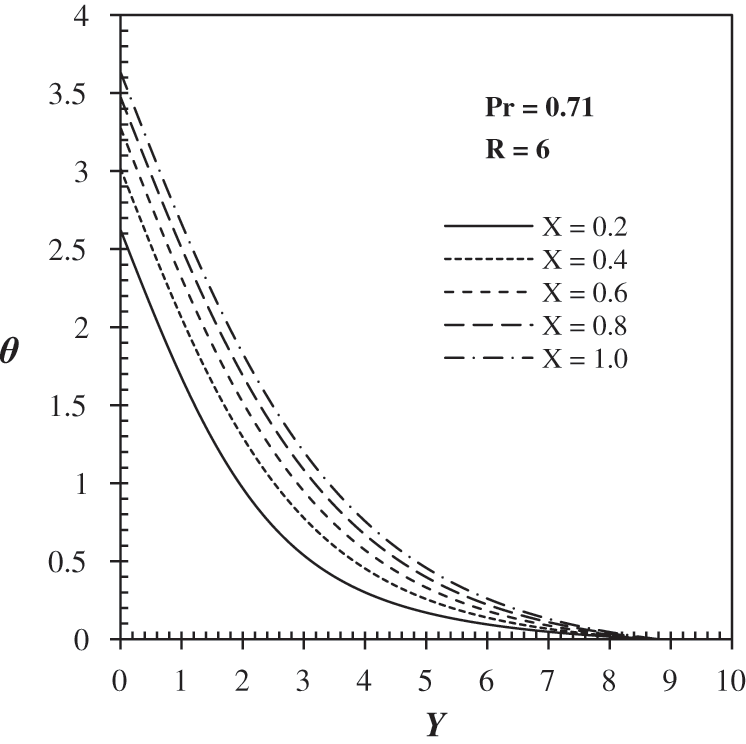
Figure 9: Temperature profiles for different X and R = 6

Figure 10: Temperature profiles for different R
The influence of the Prandtl number on the temperature profiles is presented in Fig. 11, plotted for R = 6 and X = 0.8. The effect of Pr is minimal since the curves are coincided and closely parallel. These are due to the term 1/Pr being much smaller than the term of R in Eq. (9). In this case, the higher the value of the Prandtl number, the smaller the 1/Pr since Pr is the denominator in this term. Although the curves coincide together with each other, we can observe that the velocity decreases with the increase in the Prandtl number.

Figure 11: Temperature profiles for different Pr
The Effect of the radiation and Prandtl number on the natural convection of vertical plates has been explored numerically with the implicit finite difference method. The velocity and temperature distribution profiles depend strongly on radiation parameters and the location along the plate. In contrast, the Prandtl number does not affect these profiles much at the plate’s exact location. The study of two-dimensions conditions of natural convection allows us to obtain more details of hydrodynamic and thermal characteristics of natural convection along the vertical heated plate with constant heat flux.
Acknowledgement: The authors are grateful and sincerely thank the editors and anonymous referees for carefully reading the manuscript and giving valuable comments and suggestions to improve the paper.
Funding Statement: The authors received no funding for this study.
Author Contributions: The authors confirm their contribution to the paper as follows: Introduction study: Dewi Puspitasari and Diah Kusuma Pratiwi; Numerical computation, analysis of results and interpretation: Kaprawi Sahim and Pramadhony. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The main data as the result of the numerical calculations are presented in the form of the presented figures.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Teymourtash, A. R., Rezaei Khonakdar, D., Raveshi, M. R. (2013). Natural convection on a vertical plate with variable heat flux in supercritical fluids. The Journal of Supercritical Fluids, 74, 115–127. [Google Scholar]
2. Singh, J., Singh, C. (2021). Computational analysis of convective heat transfer across a vertical tube. FME Transactions, 49(4), 932–940. [Google Scholar]
3. Cao, K., Baker, J. (2015). Non-continuum effects on natural convection-radiation boundary layer flow from a heated vertical plate. International Journal of Heat and Mass Transfer, 90, 26–33. [Google Scholar]
4. Ferdows, M., Liu, D. (2018). Natural convective flow of a magneto-micropolar fluid along a vertical plate. Propulsion and Power Research, 7(1), 43–51. [Google Scholar]
5. Pantokratoras, A. (2014). Natural convection along a vertical isothermal plate with linear and non-linear Rosseland thermal radiation. International Journal of Thermal Sciences, 84, 151–157. [Google Scholar]
6. Al-Farhany, K., Al-Dawody, M. F., Hamzah, D. A., Hamza, N. H. (2020). Numerical study of nanofluid natural convection in a partially heated tall enclosure. IOP Conference Series: Materials Science and Engineering, 928, 022137. [Google Scholar]
7. Wong, S. C., Chu, S. H., Ai, M. H. (2018). Revisit on natural convection from vertical isothermal plate arrays II—3-D plume buoyancy effects. International Journal of Thermal Sciences, 126, 205–217. [Google Scholar]
8. Kaneda, M., Nazato, K., Fujiwara, H., Wada, K., Suga, K. (2019). Effect of magnetic field on natural convection inside a partially-heated vertical duct: Experimental study. International Journal of Heat and Mass Transfer, 132, 1231–1238. [Google Scholar]
9. Schaub, M., Kriegel, M., Brandt, S. (2019). Experimental investigation of heat transfer by unsteady natural convection at a vertical flat plate. International Journal of Heat and Mass Transfer, 136, 1186–1198. [Google Scholar]
10. Fetecau, C., Vieru, D., Azhar, W. A. (2017). Natural convection flow of fractional nanofluids over an isothermal vertical plate with thermal radiation. Applied Sciences, 7(3), 247. [Google Scholar]
11. Gnaneswara Reddy, M. (2014). Influence of thermal radiation, viscous dissipation and hall current on MHD convection flow over a stretched vertical flat plate. Ain Shams Engineering Journal, 5(1), 169–175. [Google Scholar]
12. Chandra Reddy, P., Raju, M. C., Raju, G. S. S., Varma, S. V. K. (2016). Free convective magneto-nanofluid flow past a moving vertical plate in the presence of radiation and thermal diffusion. Frontiers in Heat and Mass Transfer, 7(1), 1–11. [Google Scholar]
13. Uddin, Z., Harmand, S. (2013). Natural convection heat transfer of nanofluids along a vertical plate embedded in porous medium. Nanoscale Research Letters, 8(1), 1–19. [Google Scholar]
14. Molla, M. M., Saha, S. C., Hossain, M. A. (2011). Radiation effect on free convection laminar flow along a vertical flat plate with streamwise sinusoidal surface temperature. Mathematical and Compututer Modelling, 53(5), 1310–1319. [Google Scholar]
15. Chiranjeevi, B., Valsamy, P., Vidyasagar, G. (2021). Radiation absorption on MHD free convective laminar flow over a moving vertical porous plate, viscous dissipation and chemical reaction with suction under the influence of transverses magnetic field. Materials Today: Proceedings, 42(3), 1559–1569. [Google Scholar]
16. Prameela, M., Gangadhar, K., Reddy, G. J. (2022). MHD free convective non-Newtonian Casson fluid flow over an oscillating vertical plate. Partial Differential Equations in Applied Mathematics, 5, 100366. [Google Scholar]
17. Kumar, M. A., Reddy, Y. D., Goud, B. S., Rao, V. S. (2021). Effects of soret, dufour, hall current and rotation on MHD natural convective heat and mass transfer flow past an accelerated vertical plate through a porous medium. International Journal of Thermofluids, 9, 100061. [Google Scholar]
18. Abu Zeid, M., Ali, K. K., Shaalan, M. A., Raslan, K. R. (2019). Numerical study of thermal radiation and mass transfer effects on free convection flow over a moving vertical porous plate using cubic B-spline collocation method. Journal of the Egyptian Mathematical Society, 27(36), 1–17. [Google Scholar]
19. Dharmendra Reddy, Y., Shankar Goud, B., Anil Kumar, M. (2021). Radiation and heat absorption effects on an unsteady MHD boundary layer flow along an accelerated infinite vertical plate with ramped plate temperature in the existence of slip condition. Partial Differential Equations in Applied Mathematics, 4, 100166. [Google Scholar]
20. Lin, W., Armfield, S. W., Khatamifar, M. (2021). Scalings for unsteady natural convection boundary layer under time-varying heating flux in a small Prandtl number fluid. Case Studies in Thermal Engineering, 27, 101351. [Google Scholar]
21. Goud, B. S., Srilatha, P., Mahendra, D., Srinivasulu, T., Dharmendra Reddy, Y. (2023). Thermal radiation effect on thermostatically stratified MHD fluid flow through an accelerated vertical porous plate with viscous dissipation impact. Partial Differential Equations in Applied Mathematics, 7, 100488. [Google Scholar]
22. Abbas, A., Ashraf, M., Chamkha, A. J. (2021). Combined effects of thermal radiation and thermophoretic motion on mixed convection boundary layer flow. Alexandria Engineering Journal, 60(3), 3243–3252. [Google Scholar]
23. Ramalingeswara Rao, S., Vidyasagar, G., Deekshitulu, G. V. S. R. (2019). Unsteady MHD free convection Casson fluid flow past an exponentially accelerated infinite vertical porous plate through porous medium in the presence of radiation absorption with heat generation/absorption. Materials Today: Proceedings, 42, 1608–1616. [Google Scholar]
24. Ryms, M., Lewandowski, W. M. (2021). Evaluating the influence of radiative heat flux on convective heat transfer from a vertical plate in the air using an improved heating plate. International Journal of Heat and Mass Transfer, 173, 121232. [Google Scholar]
25. Arulmozhi, S., Sukkiramathi, K., Santra, S. S., Edwan, R., Fernandez-Gamiz, U. et al. (2022). Heat and mass transfer analysis of radiative and chemical reactive effects on MHD nanofluid over an infinite moving vertical plate. Results in Engineering, 14, 100394. [Google Scholar]
26. Yasin, S. H. M., Mohamed, M. K. A., Ismail, Z., Salleh, M. Z. (2022). Magnetite water-based ferrofluid flow and convection heat transfer on a vertical flat plate: Mathematical and statistical modeling. Case Studies Thermal Engineering, 40, 102516. [Google Scholar]
27. Abdullah, M. R., Alghazawi, O. K., Al-Ayyad, M. (2019). Effect of Non-uniform heat source and radiation effect on a transient MHD flow past a vertical moving plate with inclined magnetic field and periodic heat flux. Engineering Technology & Applied Science Research, 9(4), 4361–4366. [Google Scholar]
28. Mamun, A. A., Chowdhury, Z. R., Azim, M. A., Maleque, M. A. (2008). Conjugate heat transfer for a vertical flat plate with heat generation effect. Nonlinear Analysis: Modeling and Control, 13(2), 213–223. [Google Scholar]
29. Yildiz, S., Başaran, B. (2019). Investigation of natural convection heat transfer along a uniformly heated vertical plate. Arabian Journal for Science and Engineering, 44(2), 1685–1696. [Google Scholar]
30. Modest, M. F., Mazumder, S. (2013). Radiative heat transfer, 3rd edition. Oxford, UK: Cathleen Sether. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools