 Open Access
Open Access
ARTICLE
Study of Double Diffusivity and Heat Conducting Phenomena under the Casson Nanofluid Flowing through a Vertical Peristaltic Tube
1 Department of Mathematics, University of Gujrat, Gujrat, 50700, Pakistan
2 Faculty of Engineering, Future University in Egypt, New Cairo, Egypt
3 Department of Mathematics, College of Science, Qassim University, Buraydah, 51452, Saudi Arabia
* Corresponding Author: Azad Hussain. Email:
(This article belongs to the Special Issue: Computational and Numerical Advances in Heat Transfer: Models and Methods I)
Frontiers in Heat and Mass Transfer 2023, 21, 563-590. https://doi.org/10.32604/fhmt.2023.042818
Received 13 June 2023; Accepted 17 August 2023; Issue published 30 November 2023
Abstract
The current article discusses the peristaltic flow of the Casson fluid model with implications for double diffusivity, radiative flux, variable conductivity and viscosity. This study offers a thorough understanding of the functioning and illnesses of embryological organs, renal systems, respiratory tracts, etc., that may be useful to medical professionals and researchers. The main purpose of the study is to evaluate the consequences of double diffusivity on the peristaltic flow of nanofluid. By implementing the appropriate transformation, the governed differential equations of momentum, temperature, concentration and double diffusivity are worked out numerically. The lowest Reynolds number and highest wavelength are used. The ramifications of pertinent parameters on the velocity field, heat, chemical reaction rate and double diffusivity are discussed by plotting the graphs using the bvp4c technique. Our analysis shows that solutal and thermal Grashof numbers enhance the motion of fluid flow over the pumping area of the peristaltic boundary. The activation energy and Lewis number indicate the opposite impact on concentration distribution. Due to variations in thermophoresis and the Brownian parameter, the heating process slows during the pumping section and accelerates during the free pumping section. The graph of double diffusivity initially goes upward by escalating Dufour and Brownian parameters and then moves down over the right sinusoidal geometry.Keywords
Nomenclature
| Symbols | Description |
| Left amplitude of the wave | |
| Right amplitude of the wave | |
| Concentration rate | |
| Coefficient of diffusivity | |
| Left wall restriction | |
| Right wall restriction | |
| Width of channel | |
| Temperature rate | |
| Phase shift | |
| Pressure | |
| Wavelength | |
| Velocity components | |
| Cartesian coordinates | |
| Casson fluid parameter | |
| Casson stress tensor | |
| Boltzmann constant | |
| Stefan-Boltzmann number | |
| Double diffusivity rate | |
| Gravitational acceleration | |
| Radiative heat flux | |
| Rate of chemical reaction | |
| Radiation parameter | |
| Reynolds number | |
| Wave number | |
| Thermophoresis parameter | |
| Brownian motion | |
| Dufour diffusivity parameter | |
| Solutal Grashof number | |
| Thermal Grashof number | |
| Nanofluid Grashof number | |
| Nanofluid Lewis number | |
| Lewis number | |
| Stream function | |
| Pre-exponential factor | |
| Power Law Index | |
| Conductivity parameter | |
| First Rivlin–Erickson tensor | |
| Conductivity parameter | |
| Thermal property of fluid | |
| Viscosity at zero shear rates | |
| Prandtl number | |
| Activation energy | |
| Constant chemical reaction rate |
In many of the medical processes, such as the instruments which are used for the treatment and determining the disease of the heart and lungs, peristalsis phenomena is used. Many contemporary mechanical machines are built on the peristaltic pumping principle for the movement of fluids. For instance, during cardiopulmonary bypass, a machine temporarily replaces the function of the heart and lungs to maintain the flow of blood and oxygen to the body during surgery. Most of the scientists were attracted to the phenomenon of peristalsis, after the work of T.W Latham. The peristaltic movement of viscous fluid in the present studies has been discussed with non-identical characteristics of transfer of mass and heat, symmetric and axisymmetric channels, correspondence variation and so on. In fluid dynamics, fluids are classified as non-Newtonian and Newtonian according to time-dependent, shear thinning and shear thickening characteristics. For Newtonian and non-Newtonian fluids different models are available, i.e., the Casson fluid model, Buongiorno, Jeffery and Williamson models, etc., to design ways for more research to get knowledge about the concealed properties of fluids.
The thermal radiative system has abundant applications in thermal industrial and engineering processes. Right now, solar energy, like solar photovoltaic to produce electricity, and passive designs to absorb solar radiation for heating and cooling, is used for business and home appliances. Therefore, scholars divert toward research to modify solar technologies to make life effortless. Akbar et al. [1] studied the entropy generation in a tube filled with a viscous Cu-water nanofluid flowing peristaltically. Their investigation aims to examine the creation of entropy in the context of various physical characteristics. Their task is based on the inquiry of entropy in the peristaltic fluid transport phenomenon. The effects of peristaltic phenomena on the analysis of entropy generation in the electro-osmosis modulated peristaltic flow of the Eyring-Powell fluid were investigated by Mabood et al. [2]. Kotnurkar et al. [3] have examined the effects of joule heating and electro-osmosis on the peristaltic transport of hyperbolic tangent fluid through a permeable forum in an endoscope. Kotnurkar et al. [4] also analyzed the impact of thermal jump and magnetic field on the peristaltic motion of Jeffrey fluid with silver nanoparticles in the eccentric annulus. They concluded that the Jeffrey fluid has a lower temperature and momentum than the Jeffrey nanofluid. These results are beneficial to evaluate the fluid flow features and speed of the syringe’s injection at the time of cancer treatment, the removal of artery blockage and slowing down the bleeding throughout the surgery. Farooq et al. [5] elaborated on the peristaltic movement of Williamson blood flow with the consideration of the solar mimetic system. Rashid et al. [6] examined peristaltic phenomena by utilizing the MHD effects on Williamson fluid in a curved channel. Also, the theoretical investigation of blood flow through peristaltic arteries containing migrating gyrotactic bacteria and nanoparticles has been scrutinized by Hussain et al. [7]. The interesting aspect of their research is to examine the flow of blood while highlighting the effects of the solar mimetic system, MHD consequences and tangent hyperbolic model.
Many researchers are focused on the fluid with double diffusivity in peristaltic flow as it has much more significance in medical as well as in engineering like double immune diffusion to identify antibodies and antigens. Information about the magneto-tangent hyperbolic nanofluid double in a non-uniform channel with diffusivity convection under peristaltic flow has been explored by Saeed et al. [8]. Akbar et al. [9] have explored their work on peristalsis with double diffusivity convection along with thermophoresis and Brownian movement. The effect of double diffusivity and convection has been elaborated by Akram et al. [10], in the peristaltic pumping of magneto Sisko nanofluids in a non-uniform inclined channel. Under the impact of the magnetic field, thermal radiation and porous medium scholars named Shivappa Kotnurkar et al. [11] have studied the double diffusivity phenomena on peristalsis flow of nanofluid. Their research work has potential in engineering, biomedical and industrial applications. Akram et al. [12] have analyzed how Powell–Eyring nanofluids in a non-uniform channel are affected by double-diffusivity convection. Akram et al. [13] have done their research on hybrid double-diffusivity convection and induced magnetic field effects on peristaltic waves of Oldroyd 4-constant nanofluids in the non-uniform channel. Tangent hyperbolic fluid with mixed convection has been explored by Ibrahim et al. [14]. They want to talk about the influences of the combination of natural and forced convection flow of nanoparticles. Chu et al. [15] have examined research for the characteristics of thermal radiation, heat generation, and the impact of convective boundary conditions through a duct using the Rabinowitsch fluid. Javid et al. [16] studied the combined effects of the electric and magnetic field on the transportation of viscous fluid via the non-uniform curved channel due to the intricate structure of metachronal waves.
Moreover, peristalsis is very momentous under the effect of the magnetic field in the magneto-therapy, cancer therapy and arterial flow. We can magnetize our fluids by applying a strong external magnetic field. We can change the properties of fluids by appropriately utilizing the magnetic field. Akram et al. [17] have explored the peristaltic pumping of Prandtl nanofluids in a magnetic field and non-uniform inclined channel. The advantage of their work includes pharmacodynamic pumps and designed encouragement for gastrointestinal motility. Tanveer et al. [18] have scrutinized the advantages of a porous medium by modifying Darcy’s law for Sisko fluid in peristaltic movement. Parida et al. [19] have also studied the magnetic effect over a permeable shrinking sheet. Tripathi et al. [20] theoretically studied the electro-kinetic peristaltic pumping of nanofluids with heat and mass transfer. Eldabe et al. [21] have explored the peristaltic motion of Williamson nanofluids through a non-Darcy porous medium. Ali et al. [22] have examined electromagnetism for nano-blood considering the Jeffery fluid model through the peristaltic channel. Das et al. [23] have explicated how both electrohydrodynamics and magnetohydrodynamics affect the peristaltic flow of hybrid fluid in which water is a base fluid.
Casson fluid model discriminates the non-Newtonian behavior of the fluid, also extensively utilizes for modeling the flow of blood in tapered arteries. We should have the knowledge that the generalized non-Newtonian model namely the Casson model was first proposed by Oka [24] as a special case for the study of properties of flow in an elastic tube. Jayaraman et al. [25] globalized Oka’s work and explored how Casson fluid applies to artificial lungs. Khan et al. [26] have done their research on non-Newtonian Casson fluid across a permeable medium through a stretching surface. Saravana et al. [27] explored the effect of an aligned magnetic field and cross-diffusion on the Casson fluid. Also, the peristaltic flow of Jaffery nanofluid was examined by Reddy et al. [28] to explore the impact of Brownian and thermophoresis movement on MHD flow. It elaborates that the unique characteristics of nanofluids make them potentially important in mass and heat transfer phenomena happening in industrial and medical processes including pharmaceutical processes, hybrid engines, microelectronics, refrigerators, chillers and so on. The effects of Soret and Dufour on the free convective flow of Casson fluid across a nonlinearly elongating sheet embedded in a porous medium have been studied by Biswal et al. [29]. Reddy et al. [30] have scrutinized how in an inclined skew channel, the electro-osmotic of couple stress fluids greatly under the authority of Debye length. Reddy et al. [31] also inspected the features of the transfer of heat by thermal radiation on Casson fluid and concluded the result about the effect of certain parameters on temperature, velocity and coefficient of skin friction. Kotnurkar et al. [32] have elaborated the non-Newtonian peristaltic movement of Casson fluid of hydro-magnetics immerse with chemical reaction.
In the present article, we explored the Casson fluid flow on peristalsis geometry with the involvement of double diffusivity, activation energy, variable viscosity and conductivity. An infinite viscosity at a zero rate of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear are all characteristics of the shear-thinning liquid known as Casson fluid. Basic equations like the equation of continuity, the momentum equation, the chemical and heat equations and the equation of double diffusivity are generalized. Then, after applying a suitable transformation, we make them dimensionless using various parameters. The effects of various factors are elaborated through graphs utilizing the MATLAB bvp4c technique. The findings presented here should provide reasonably accurate theoretical estimates for a variety of potential fluid mechanical flow controlling parameters associated with peristaltic blood transport. Our investigation is unique because of the involvement of double diffusivity in the peristaltic flow of Casson fluid. In fluid mechanics, double diffusivity is the mechanism by which convection occurs for two distinct density gradients. as it is significant in the identification of antigens and antibodies. Normal breathing depends on the diffusion of gases across the respiratory membrane. Our research work is significant as the double diffusivity is also useful for the uplifting of nutrients and the vertical transmission of salt and heat in oceans. The work's novelty lies in its scientific investigation of the effects of double-diffusive convection on the peristaltically flowing Casson fluid. Our work may be helpful for the industry's transportation of corrosive fluids, sanitary fluid transport, and the movement of hazardous fluids in nuclear reactors. For the concentration discussion, a pre-exponential component represents a chemical reaction that occurs close to the esophageal wall surfaces. Even though our work has significant applications in numerous disciplines, including medicine, we have not detected any drawbacks in the future. Until now, no research has been conducted on peristaltic flow with the combined effects of heat radiating flux, activation energy and the double diffusion process for the Casson fluid model.
2 Mathematical Modeling of Peristaltic Motion
In this segment mathematical model for the two-dimensional peristaltic flow of Casson fluid is evaluated. Beneficial to determine the consequences of mimetic solar radiation and speed up of chemical reaction; activation energy and Rosseland's estimation are also encompassed here. Fig. 1 embellishes the distinctive geometry of the contemporary model under particular situations. Geometry shows that the nanofluid is flowing in a vertical downward direction along with a solar radiative effect.
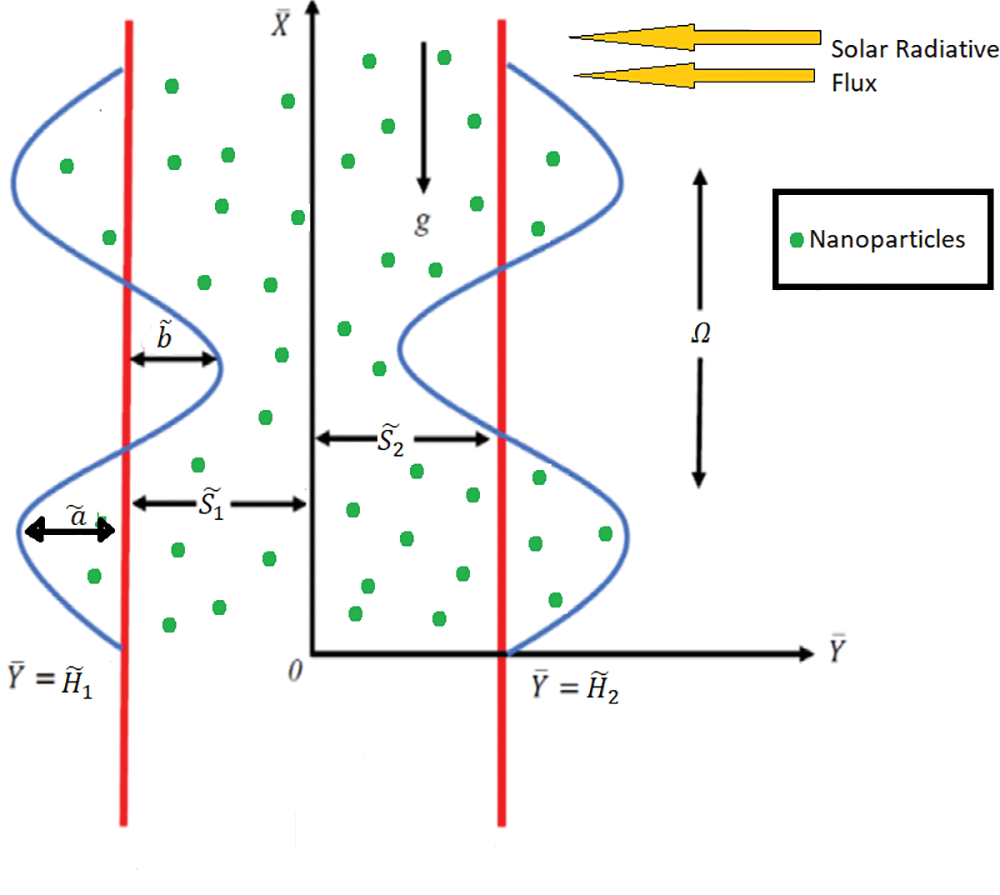
Figure 1: Geometrical structure of peristaltic motion
The wall boundaries are defined as [33]
Here
Solar heat flux plays a remarkable role in the absorption and ejection of energy, therefore we obtain it by applying Rosseland’s approximation [34],
In the above equation,
In the above equations of variable viscosity and conductivity the parameters
Here the exponential term is denoted by
The mathematical modeling of incompressible Casson fluid is defined as follows:
In the above expression, the
By utilizing the fundamental equations of continuity, temperature, momentum, double diffusivity and concentration rate, the following formulations in terms of (
Continuity equation:
Y-component of momentum equation:
Temperature equation:
Concentration equation:
The equation for Double diffusivity:
where the mass density of nanoparticles is shown by
After applying the transformation, the system moves from static to peristaltic movement, i.e.,
After transformation we get
Continuity equation:
Temperature equation:
Concentration equation:
The equation for Double diffusivity:
Now to convert the above equations into dimensionless bodywork, we use the following parameters:
Therefore above Eqs. (17)–(22) become as in form of strain function.
In the above equations, the involved parameters
After solving the cooperative equations from Eqs. (23)–(27) with the presumption of long wavelength and low Reynolds number (i.e.,
By partially differentiating Eq. (31) with respect to ‘y’ and did some changings in the above equations, we obtain
Initial and boundary conditions [5] are given as
here,
The numerical technique bvp4c will be utilized, to get the consequences of generalized non-linear differential Eqs. (36)–(40). Therefore, we explore the graphical analysis, in such an extent they give the premier results of our progressive material. Taking
Applying these substitutions on set of Eqs. (36) to (40), we get
In this segment, we explain the graphical representation of generalized partial differential equation. In order to investigate their graphical results, we use bvp4c technique, which is adopted by many researchers to solve the partial differential equation. We discuss the effect of various parameters on the velocity profile, temperature, concentration, and double diffusivity characteristics, such as Prandtl number, thermal Grashof number, nanoparticle Grashof number, thermophoresis and Brownian diffusion parameter, Dufour diffusion, thermal diffusion and radiating flux parameter, etc.
Figs. 2–6 represent the consequences of different parameters on velocity of Casson nanofluid model over the peristaltic arterial wall. The fluid velocity is an essential parameter to characterize the mechanism of momentum and heat transfer through internal flows. In 1896, Franz Grashof was introduced Grashof parameter, which is named after him. This is a very important dimensionless variable in analyzing natural or free convection. Grashof number is the ratio of buoyancy force to viscous hydrodynamic force. Generally, the velocity profile raised with enlarging the values of solutal Grashof number
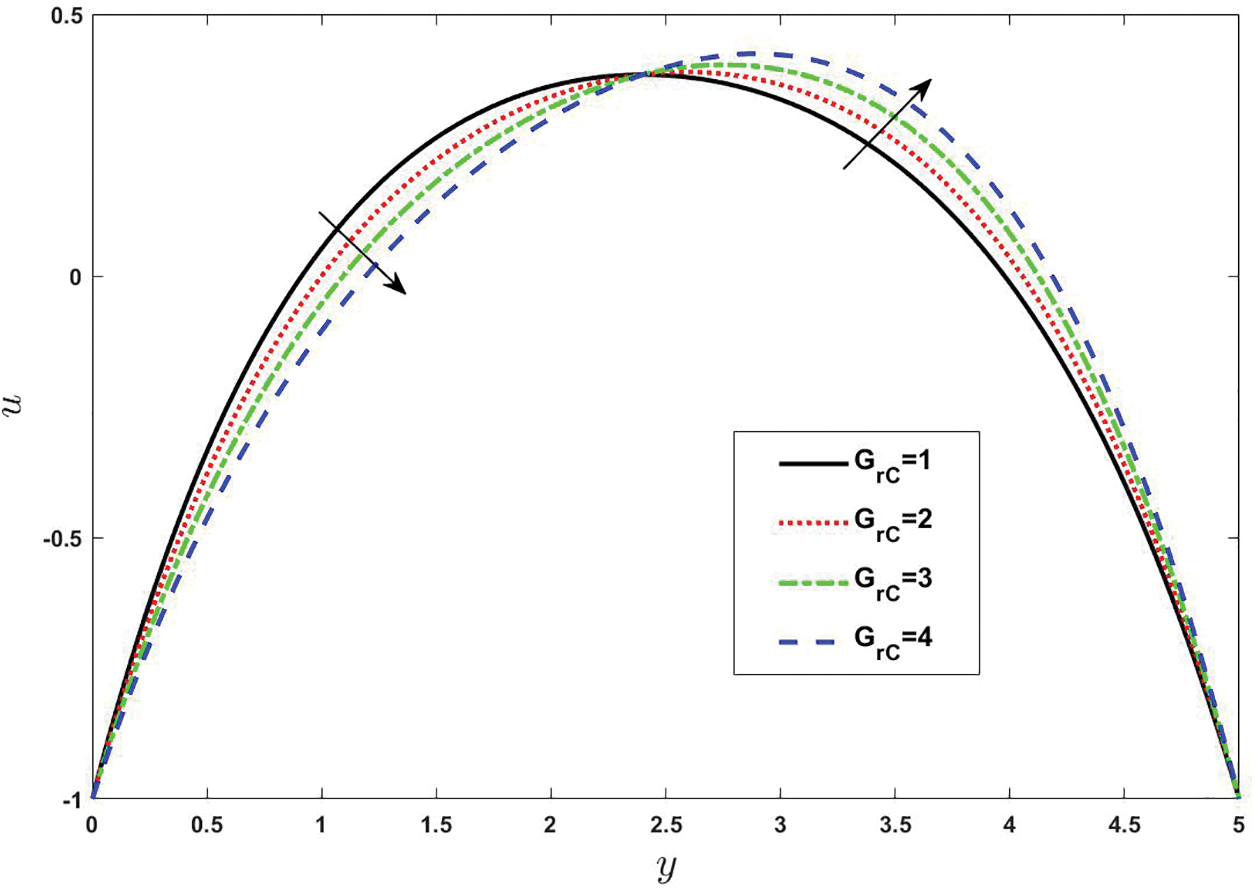
Figure 2: Effect of various values of Solutal Grashof on velocity. Other fixed values are:
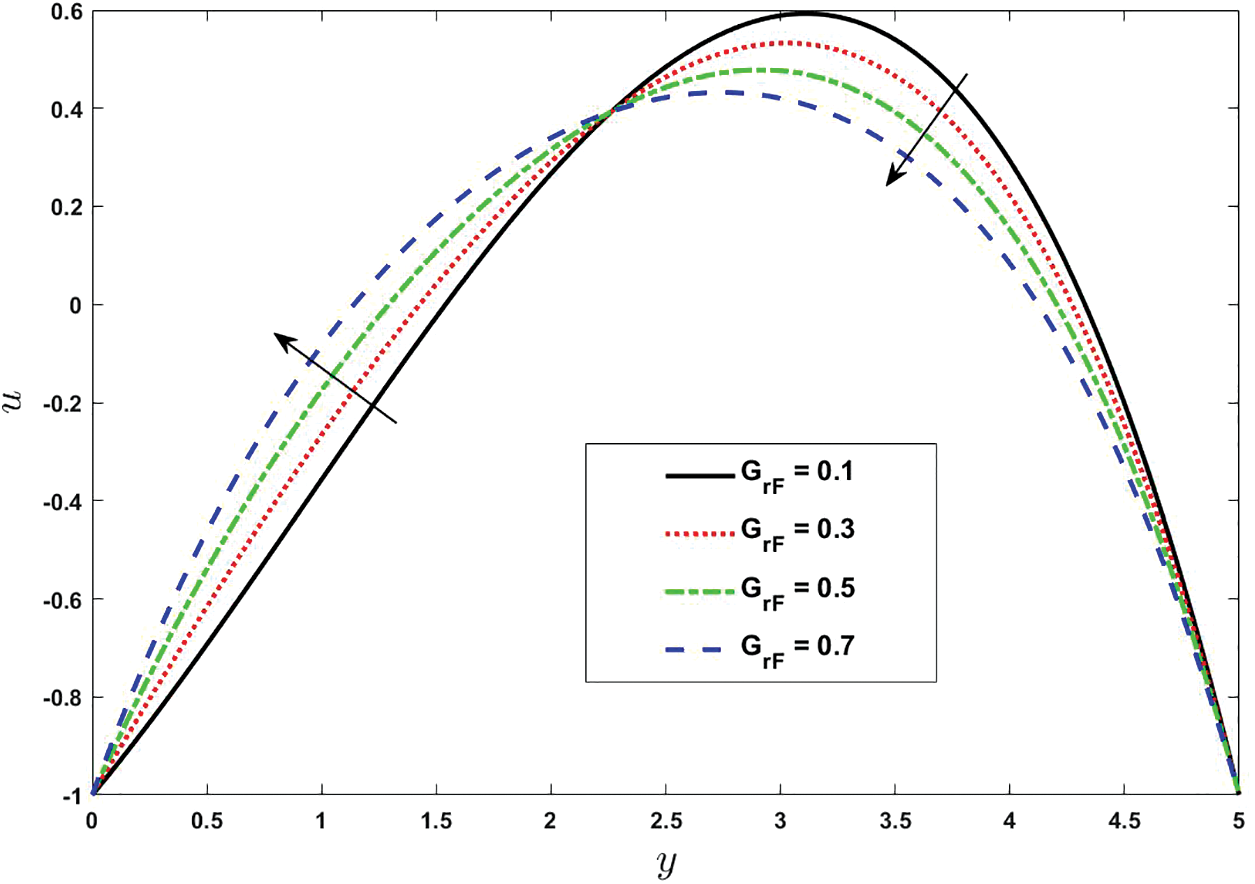
Figure 3: Effect of various values of nanoparticle Grashof on velocity. Other fixed values are:
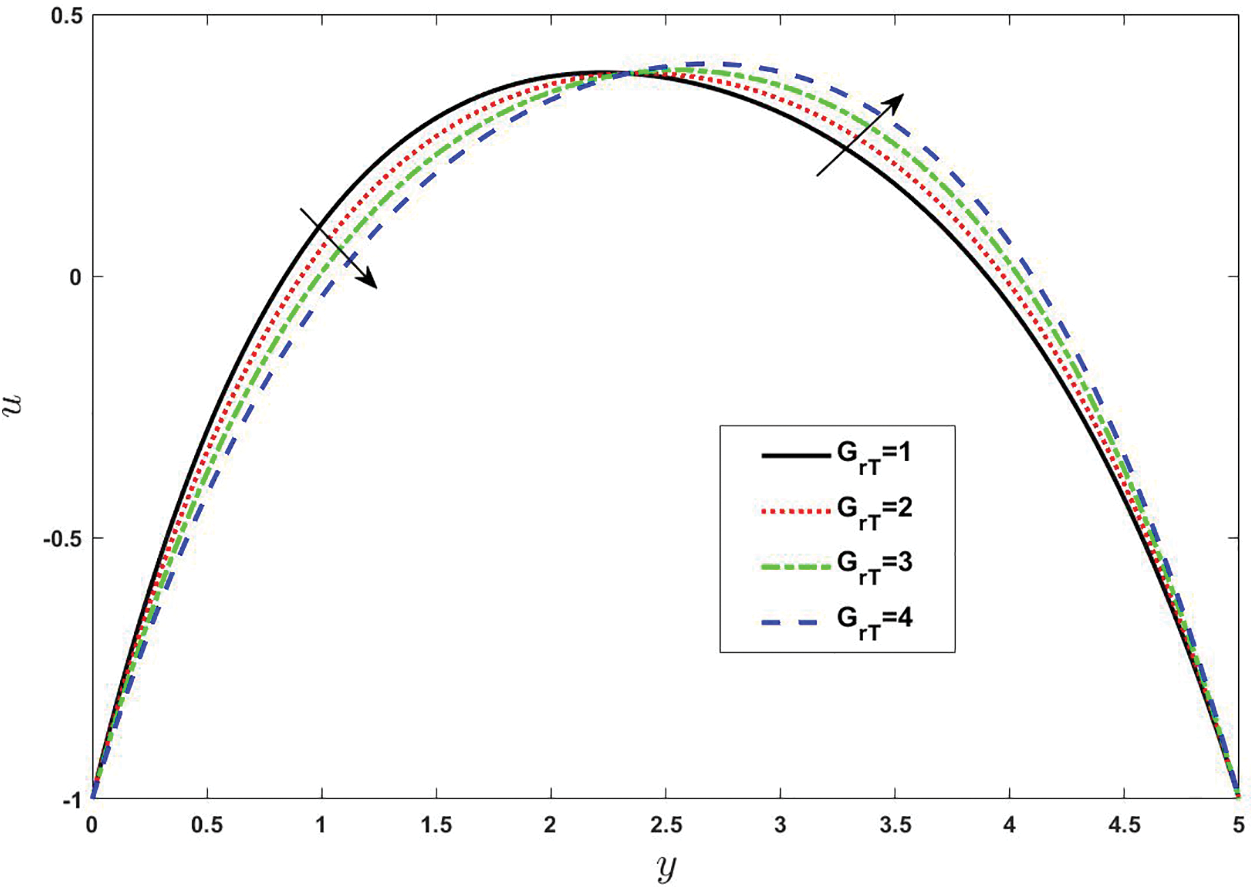
Figure 4: Effect of various values of Thermal Grashof number on velocity. Other fixed values are:
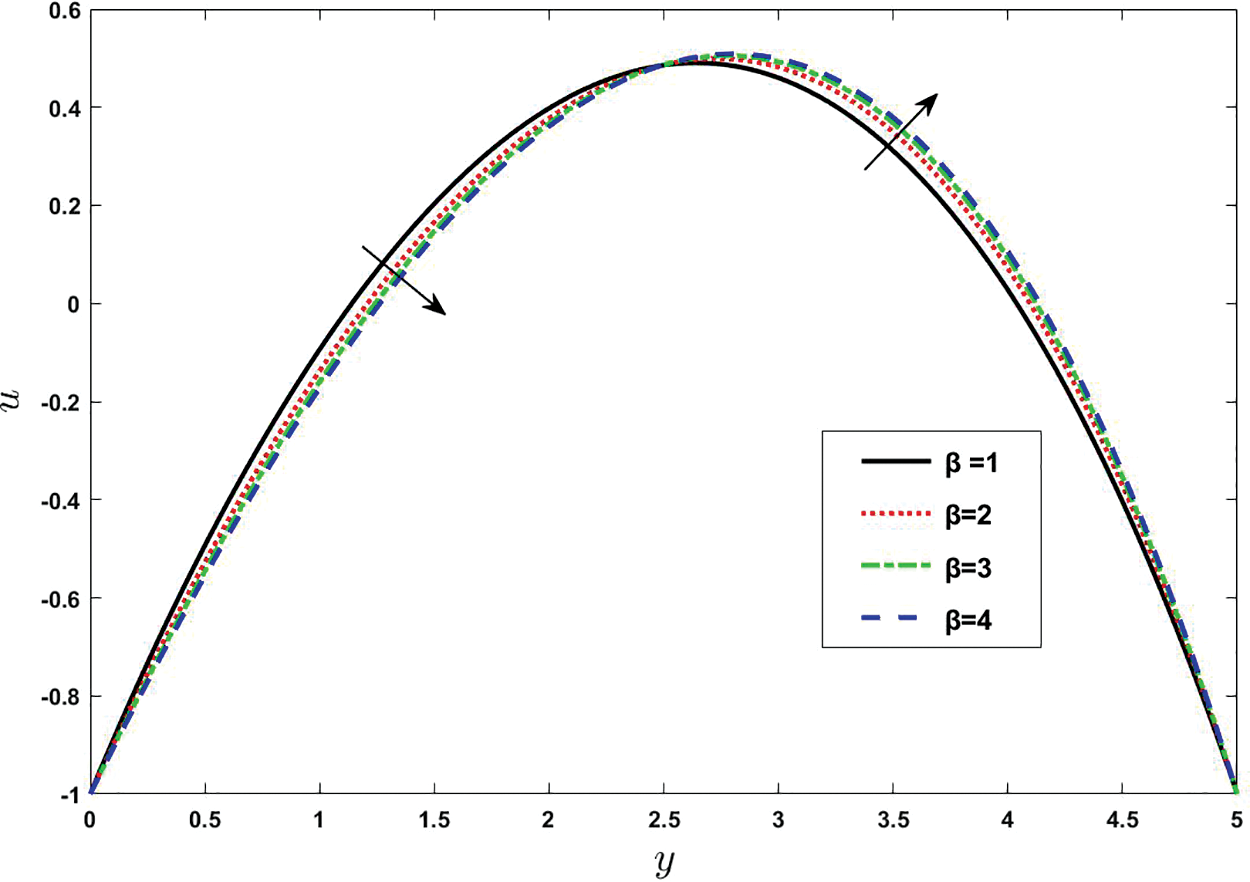
Figure 5: Effect of various values of Casson fluid parameter
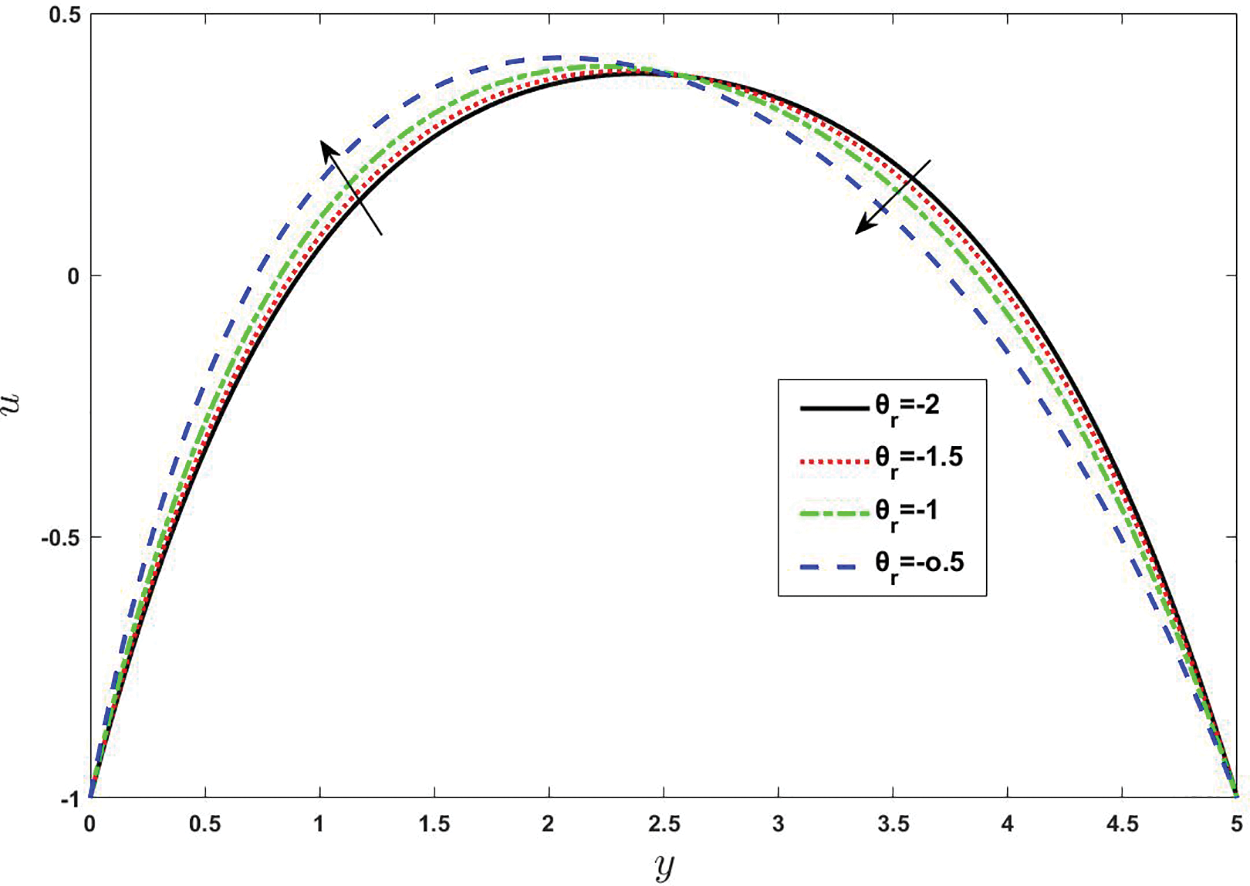
Figure 6: Effect of various values of viscosity parameter on velocity. Other fixed values are:
The temperature greatly affects our body as the blood flowing through your veins and arteries causes you to emit heat. Your circulatory system intensifies its attempts to dissipate heat to cool you down on a hot day. Your heart may pump two to four times as much blood per minute as it does on a cold day because it beats quicker and works harder. Figs. 7–12 exhibit the particular features of temperature distribution under the variation of Prandtl number, Brownian diffusion parameter, Thermophoresis diffusion parameter, Dufour parameter and thermal radiation. Temperature is one of the leading physical factors in the habitat of living things. It is the measure of the general rate of incidental motion of atoms and molecules, the particles move fast as the temperature rises. Fig. 7 presents that how the temperature is affected by distinct values of the Brownian diffusion parameter
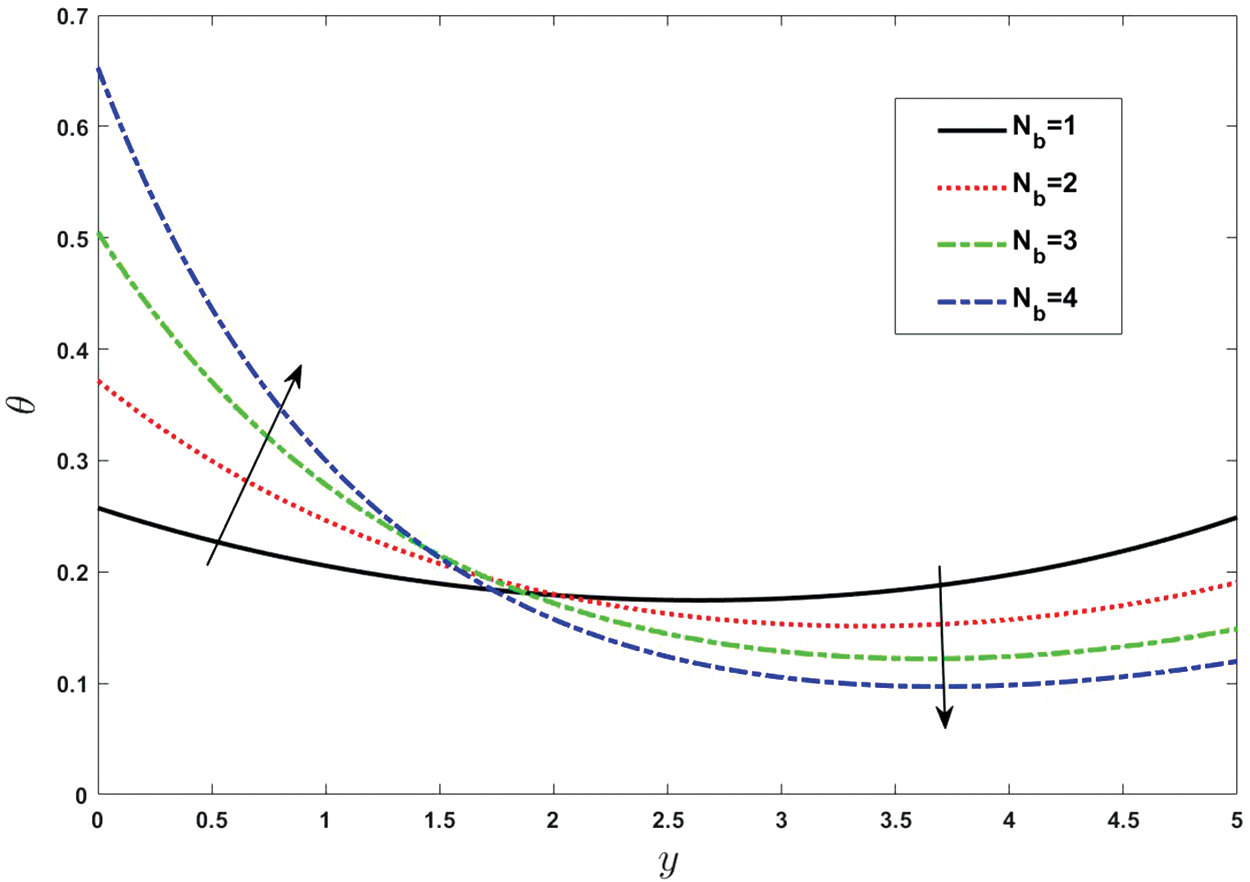
Figure 7: Effect of various values of Brownian diffusion parameter on temperature. Other fixed values are:
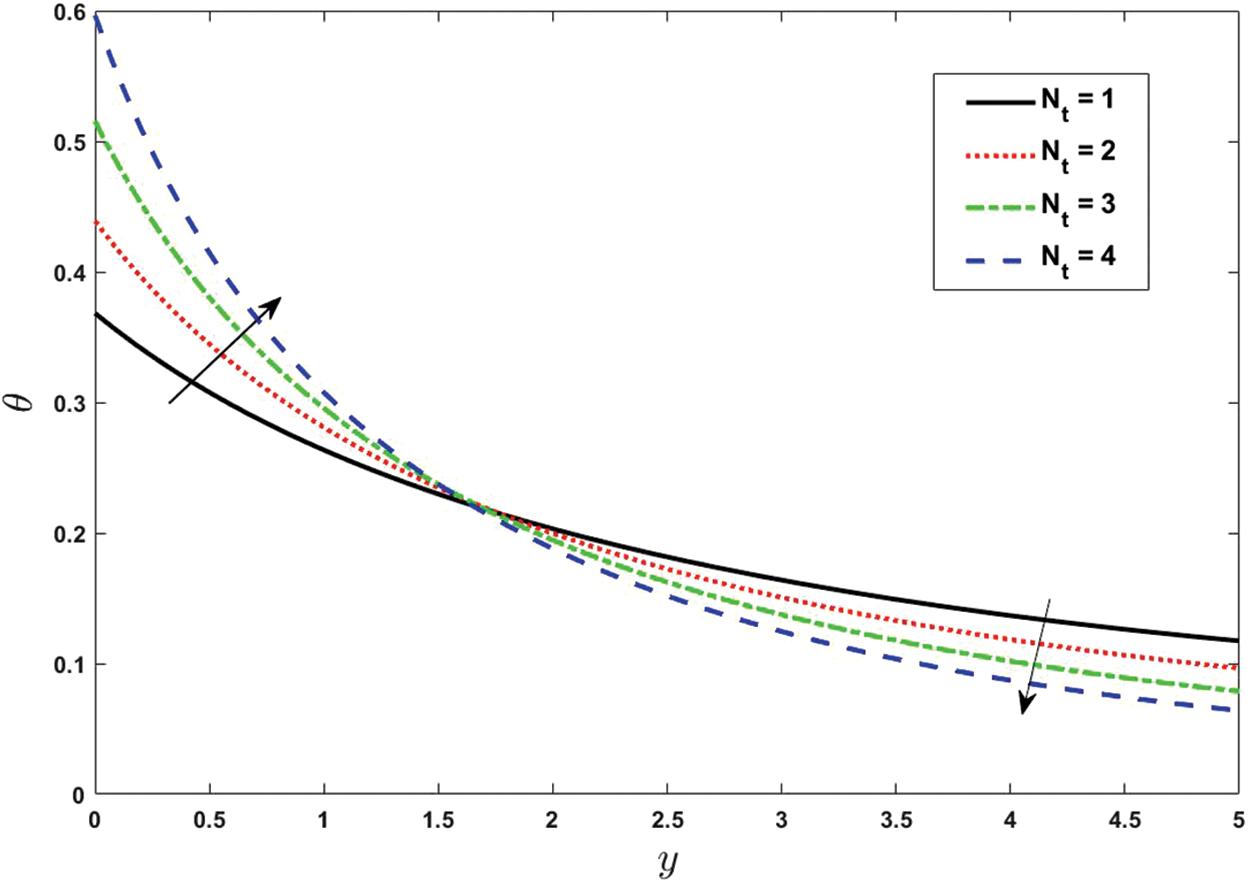
Figure 8: Effect of various values of Thermophoresis diffusion parameter on temperature. Other fixed values are:
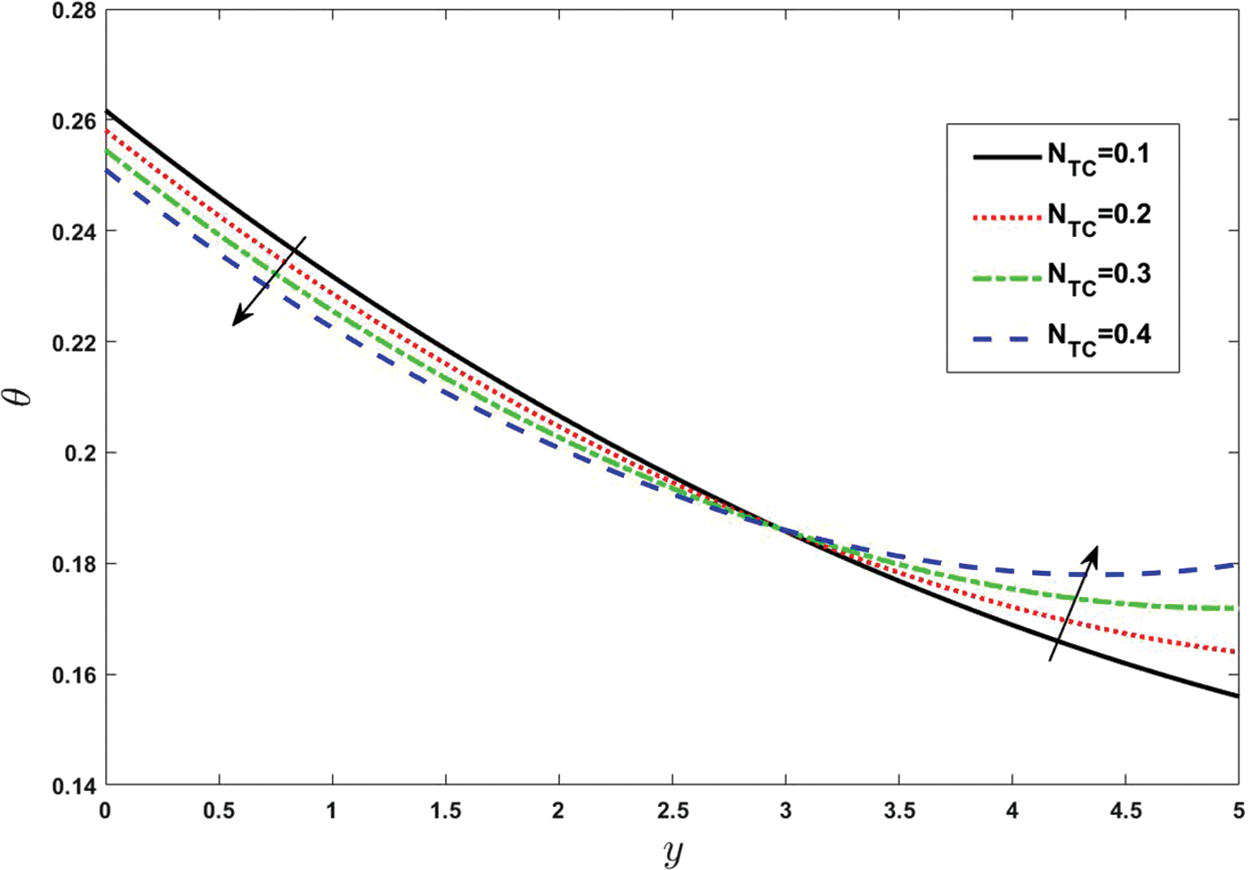
Figure 9: Effect of various values of Dufour parameter on temperature. Other fixed values are:
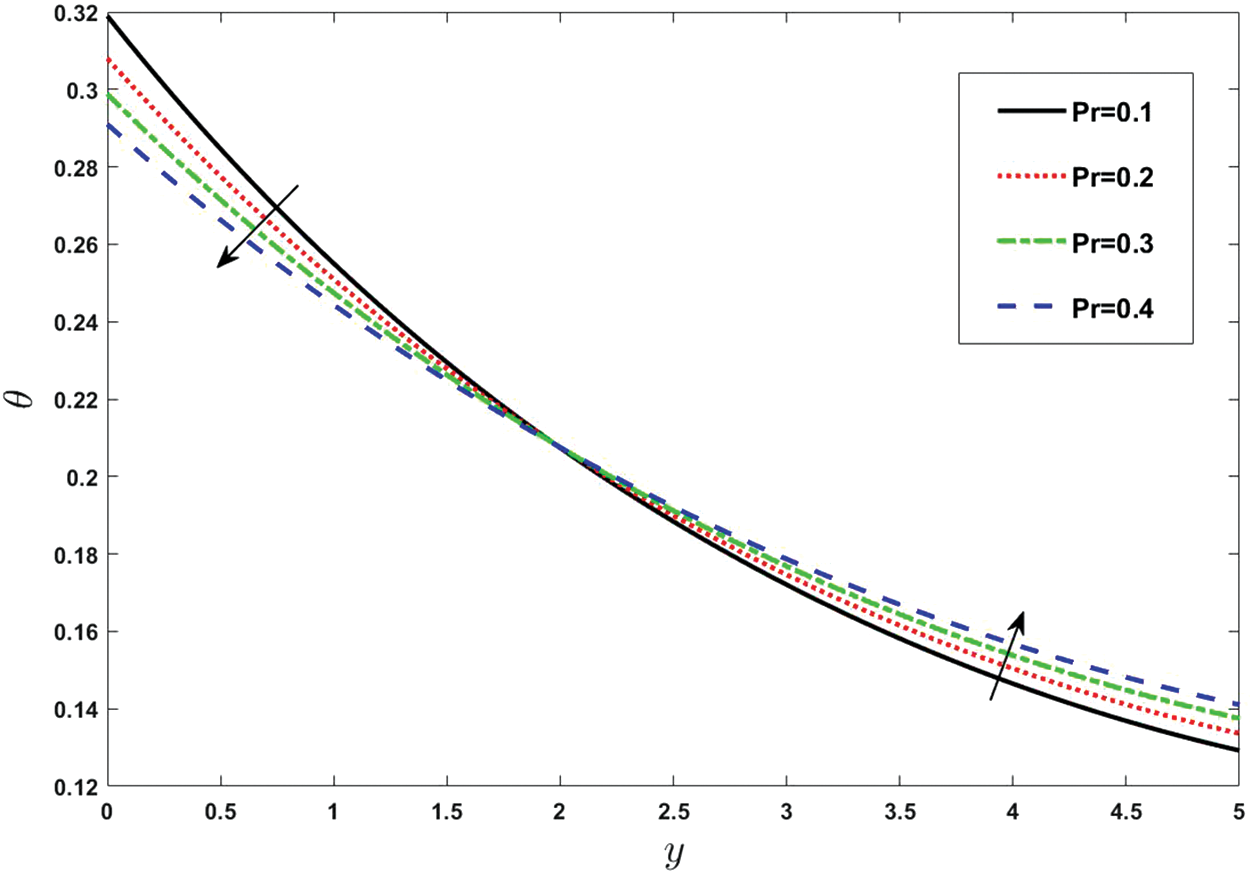
Figure 10: Effect of various values of Prandtl number on temperature. Other fixed values are:
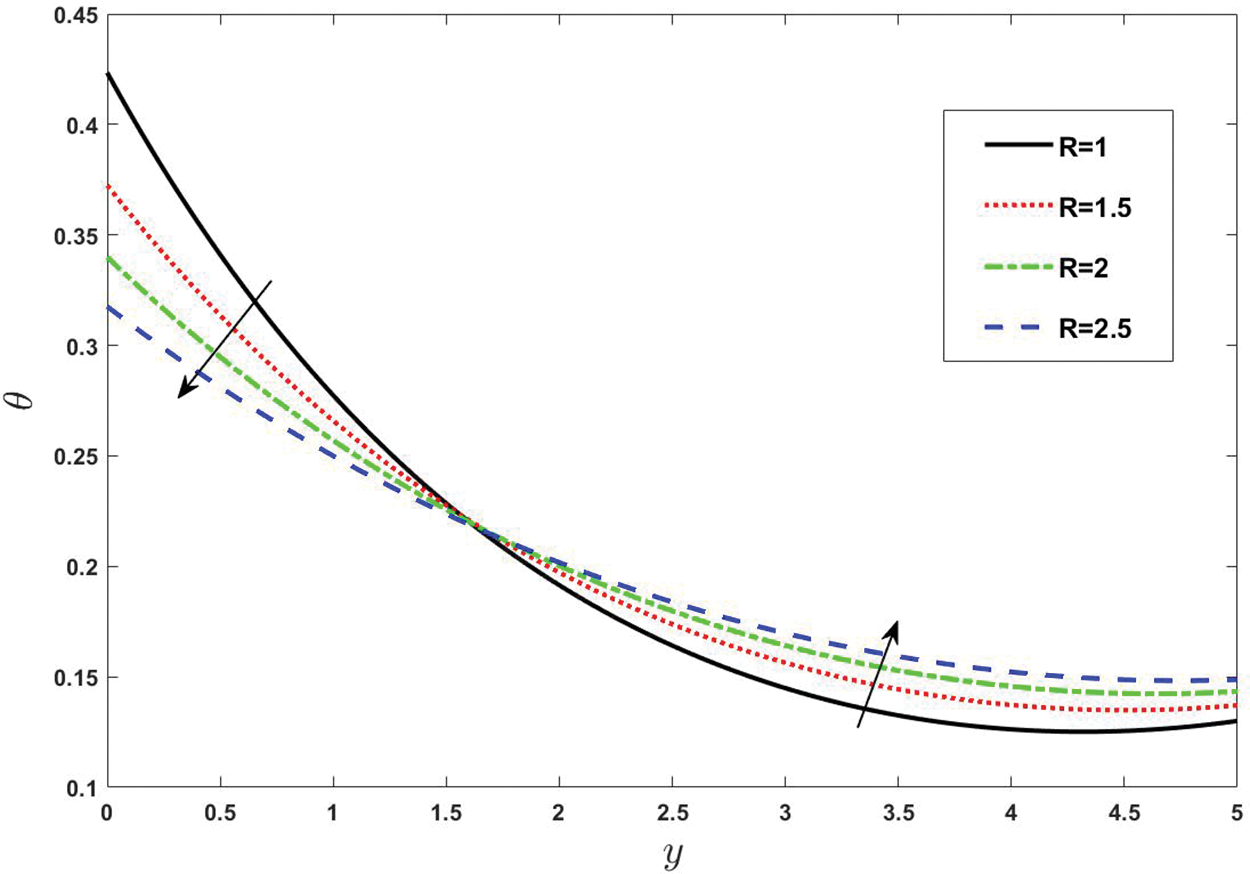
Figure 11: Effect of various values of thermal radiation on temperature. Other fixed values are:
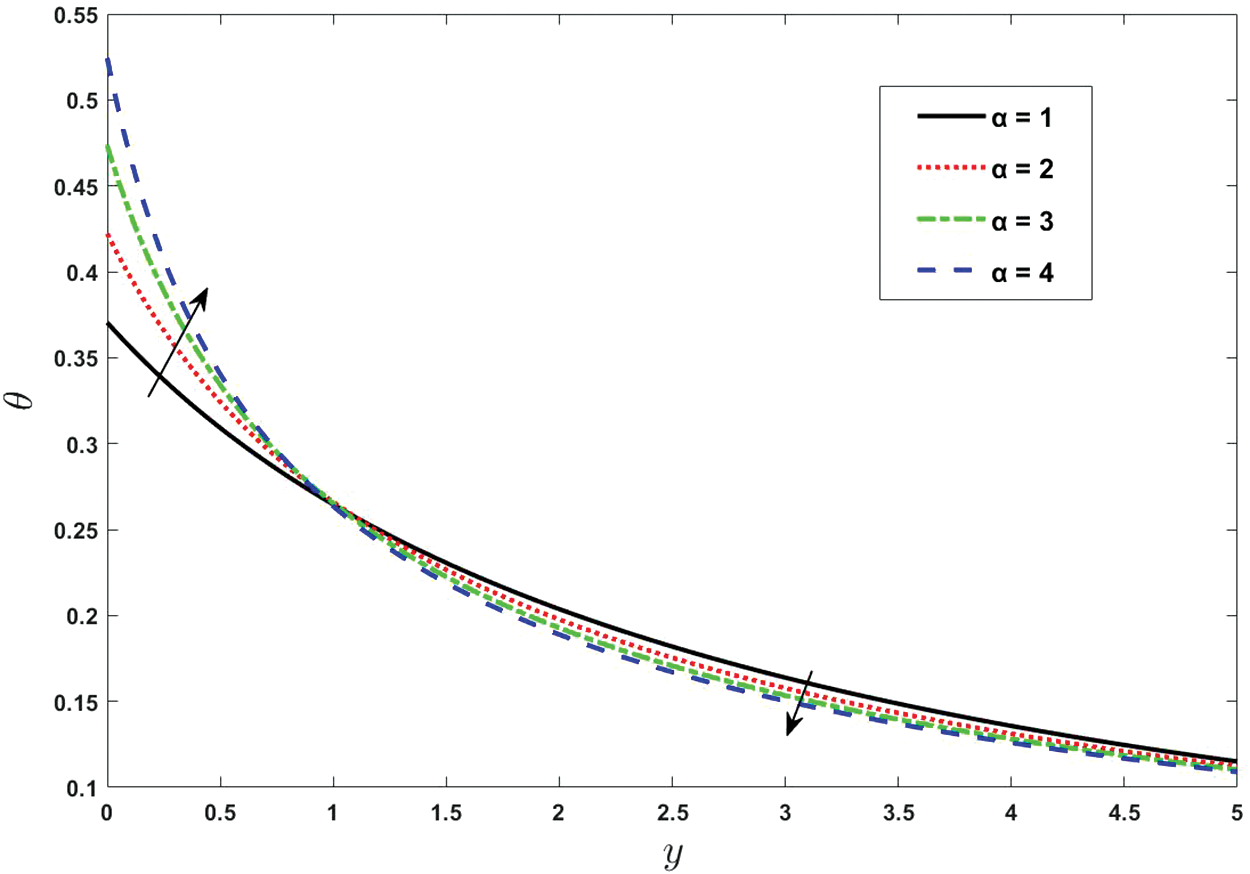
Figure 12: Effect of various values of conductivity parameter on temperature. Other fixed values are:
The effect of different parameters on concentration is shown graphically in Figs. 13–18. Concentration is the quantity of solute present in a solution and it is important to know about the stoichiometry of reactants in chemical reactions. Firstly, in Fig. 13, the influence of the diffusivity parameter is described. The diffusion parameter is one of the most important parameters for the genuine classification of rehabilitation procedures, which are based on solvent. It can be seen that concentration increases with increases in the diffusivity parameter
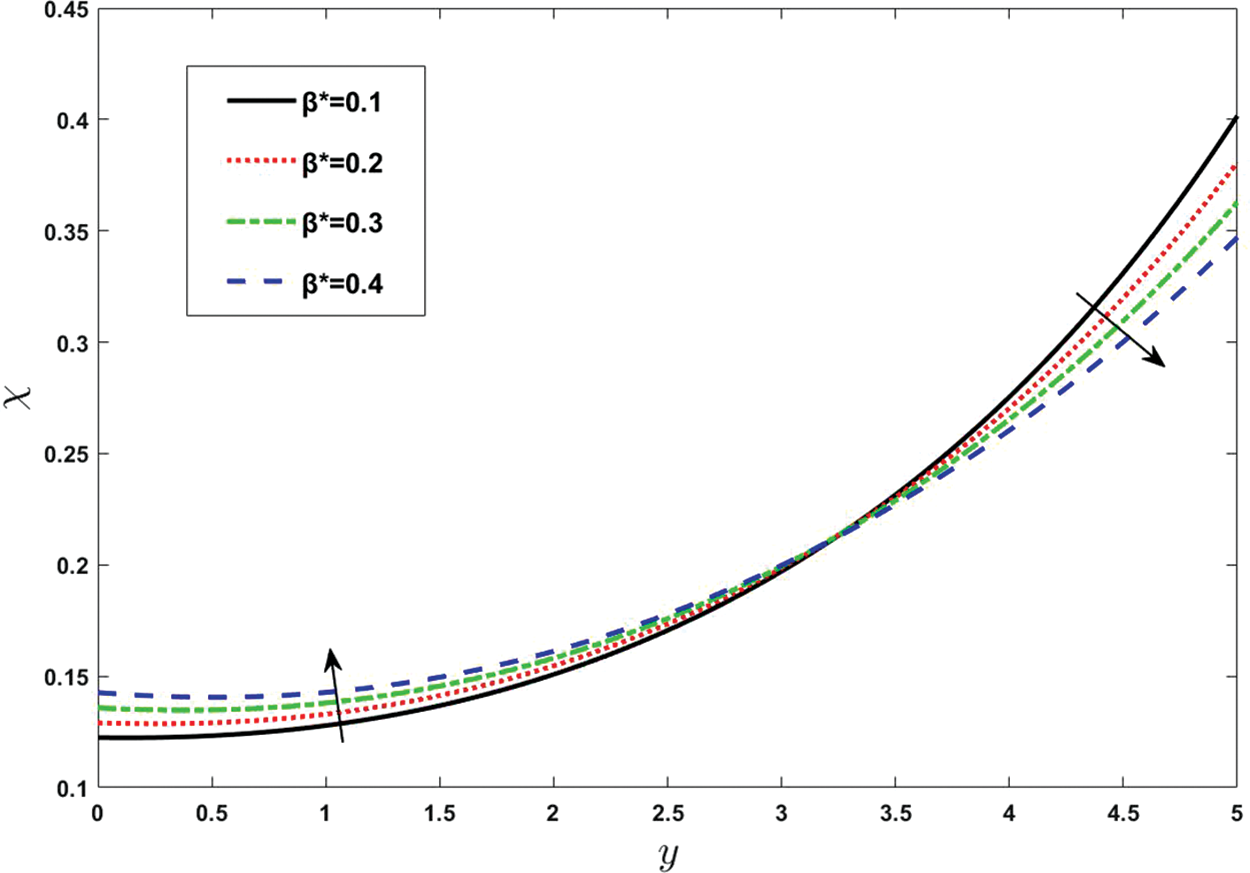
Figure 13: Effect of various values of
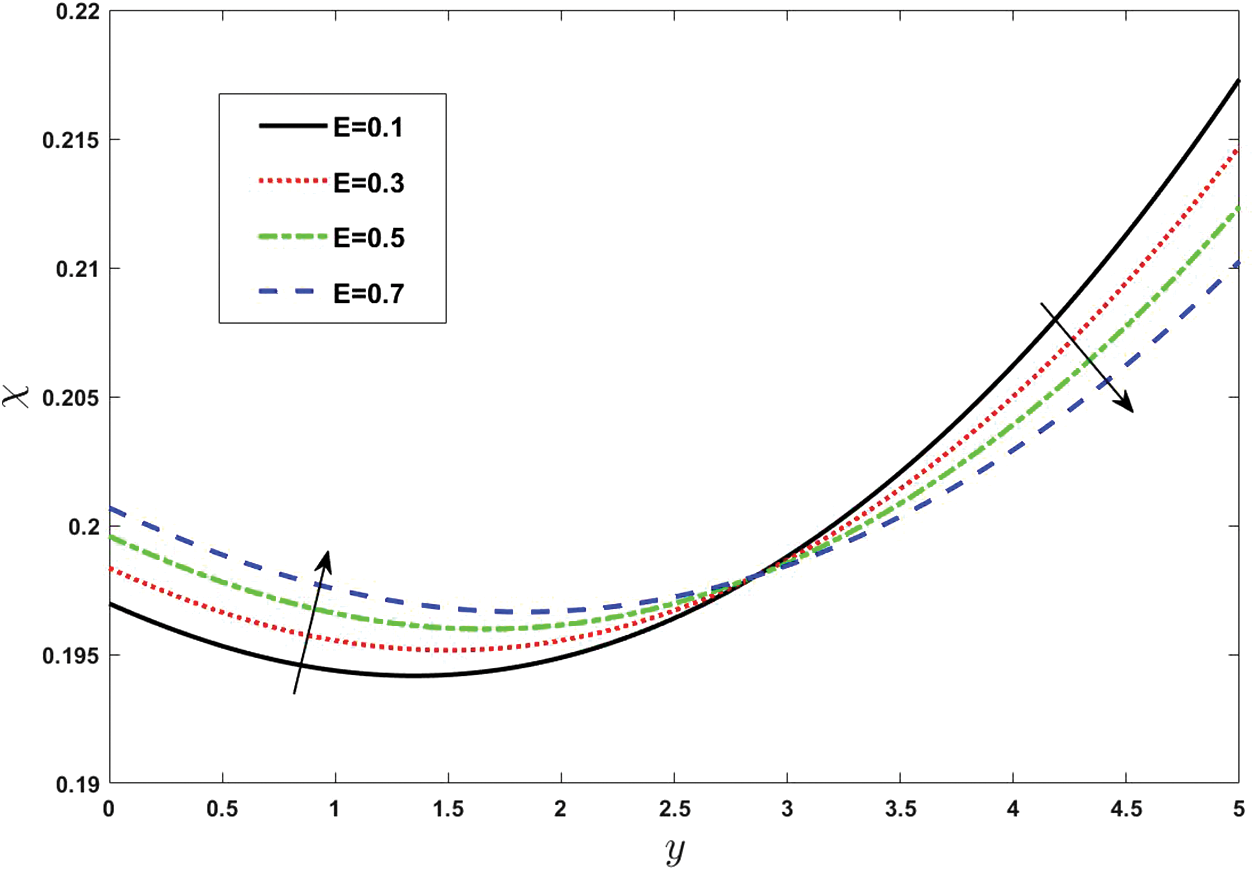
Figure 14: Effect of various values of activation energy
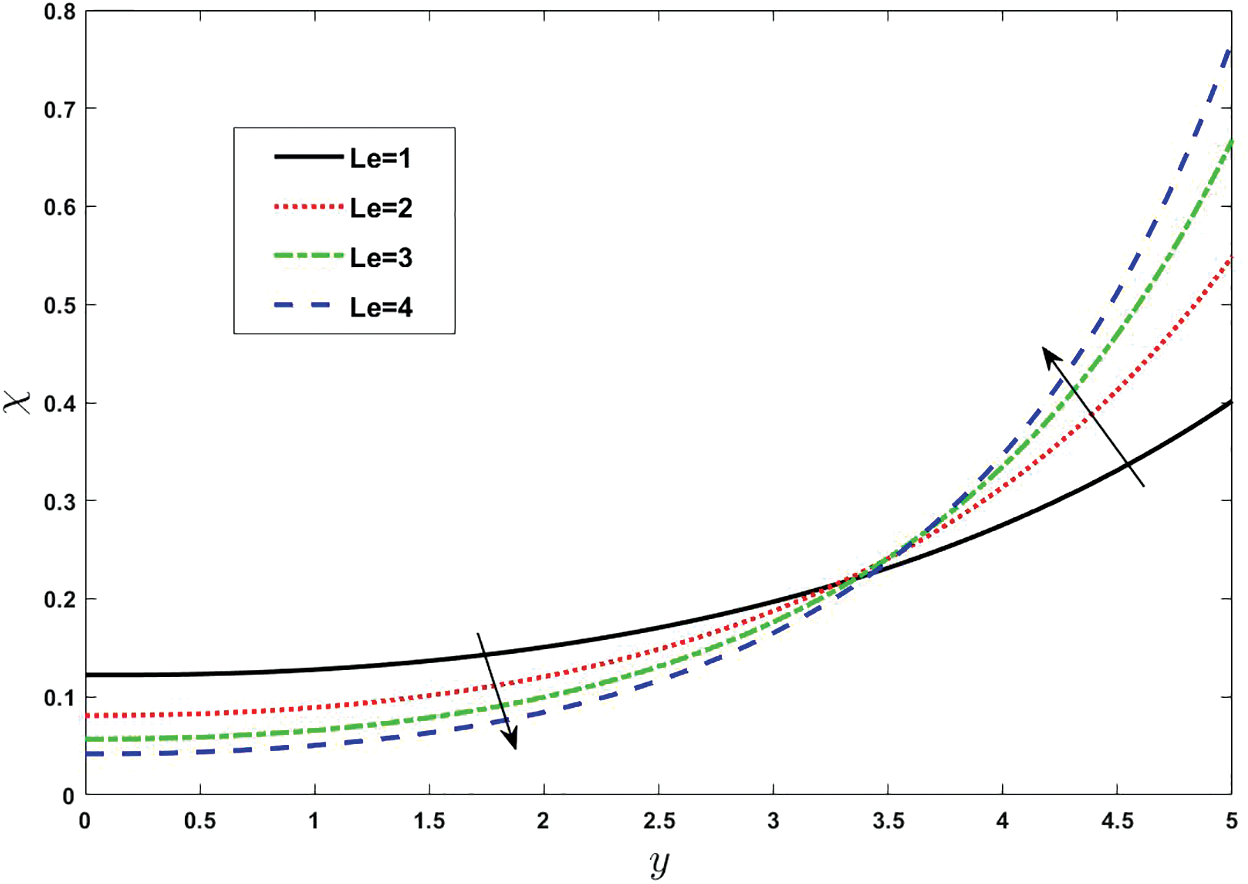
Figure 15: Effect of various values of Lewis number on concentration. Other fixed values are:
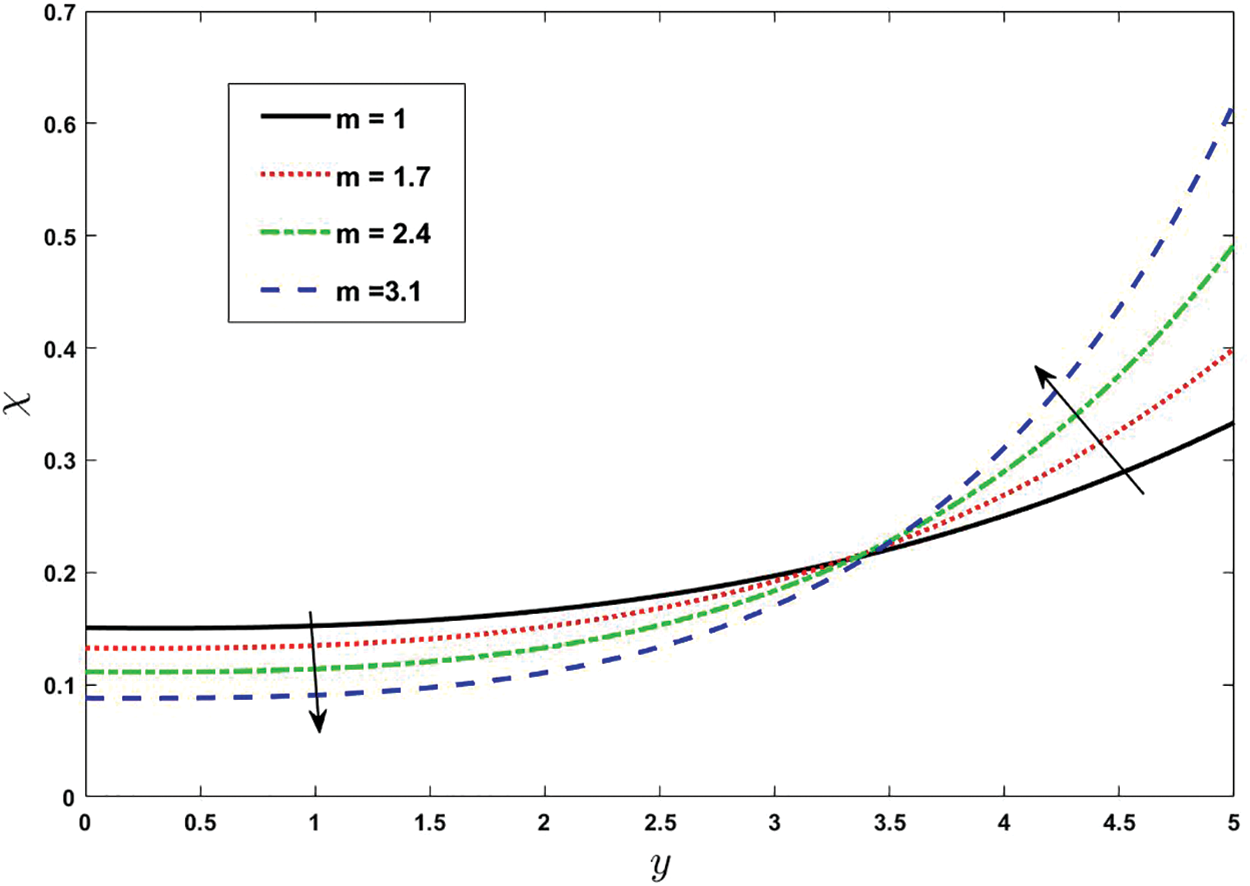
Figure 16: Effect of various values of m on concentration. Other fixed values are:
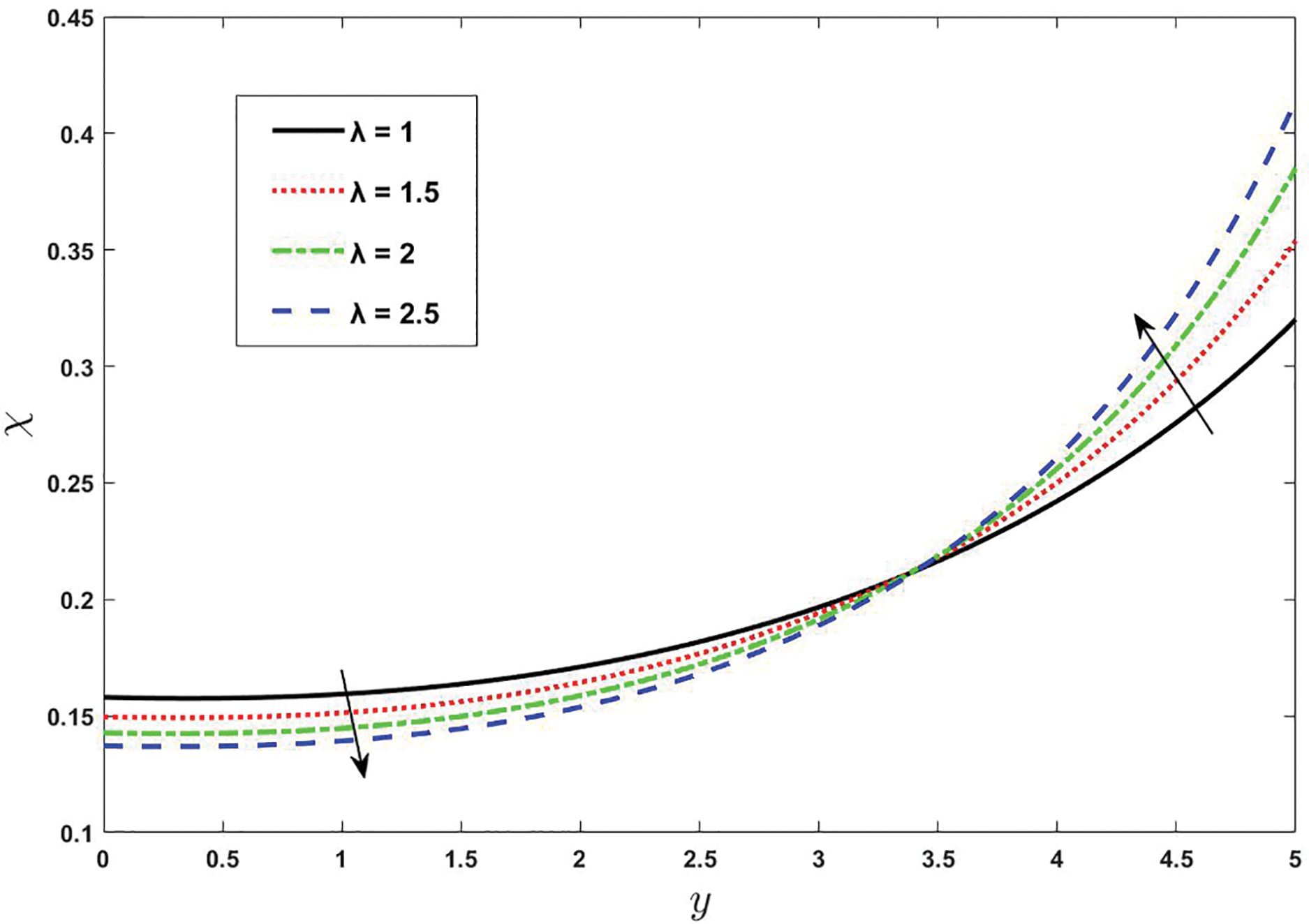
Figure 17: Effect of various values of
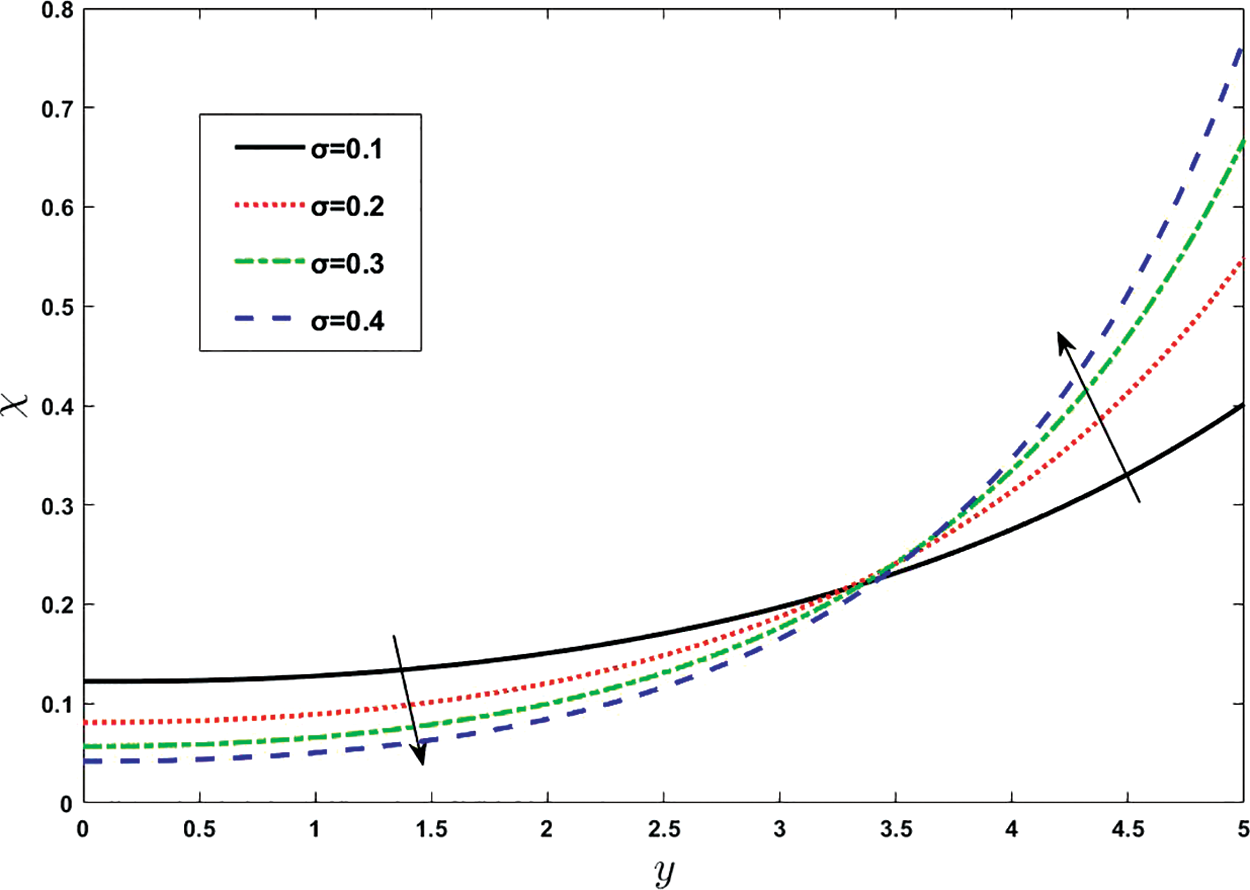
Figure 18: Effect of various values of
4.4 Double Diffusivity Convection
To demonstrate the impacts of pertinent physical quantities on the double diffusion convection process, they are plotted from Figs. 19 to 24. Double-diffusive convection (DDC) is a term used to describe buoyancy-driven convection flows in which the fluid density is dependent on two scalar components. Since the density of salt water is influenced by both temperature and salinity, the ocean is the most pertinent terrestrial habitat where DDC occurs. Double diffusion has been studied in laboratories as it is quite easy to set up and investigate the observations of distinct fluxes, while the definite measurements of various fluxes are very difficult to prescribe. Diffusion is very significant in medical sciences and for cells it is so valuable because it enables them to acquire the beneficial materials they need to obtain energy and expand, making it possible for them to dispose of waste. Fig. 19 depicts the double diffusivity by varying the Brownian diffusion parameter
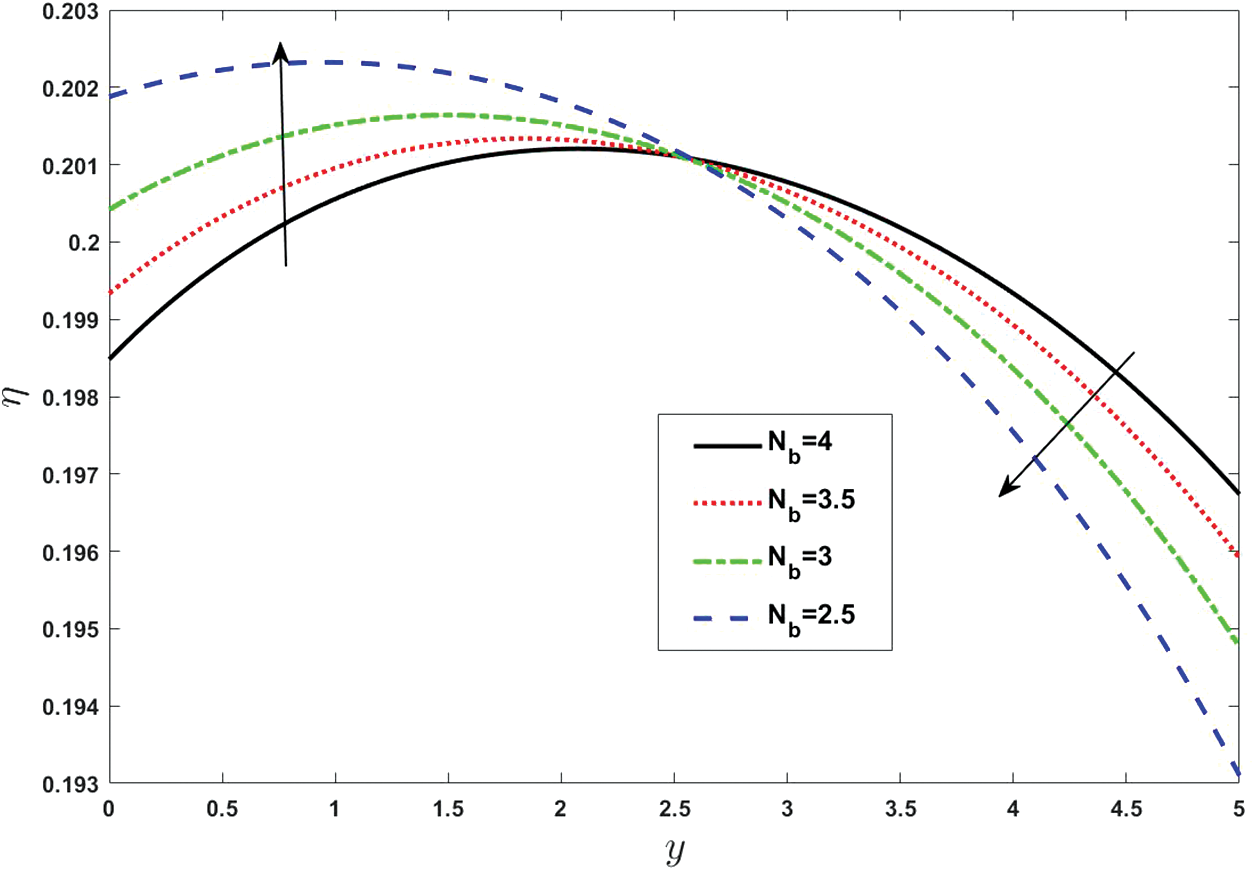
Figure 19: Effect of various values of Brownian diffusion parameter on double diffusivity. Other fixed values are:
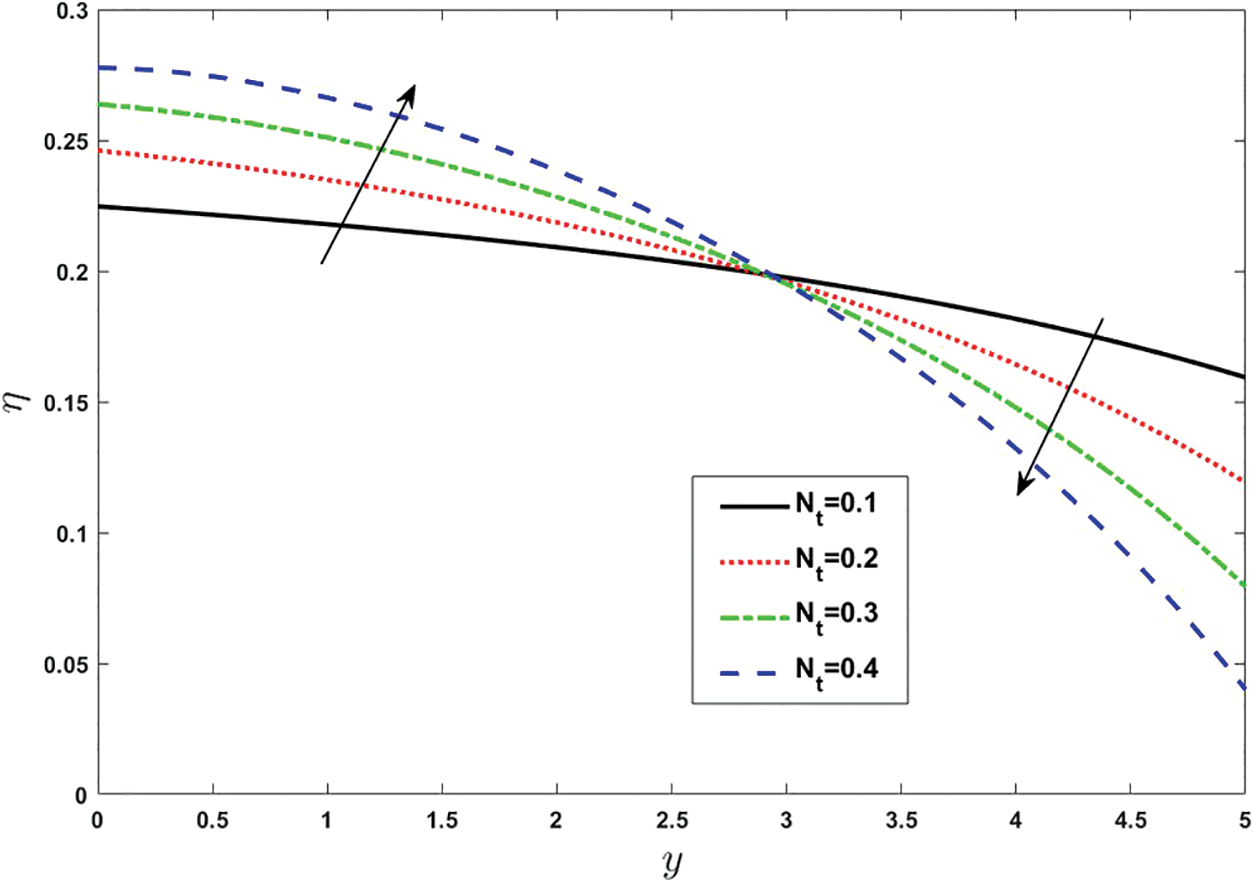
Figure 20: Effect of various values of Thermophoresis parameter on double diffusivity. Other fixed values are:
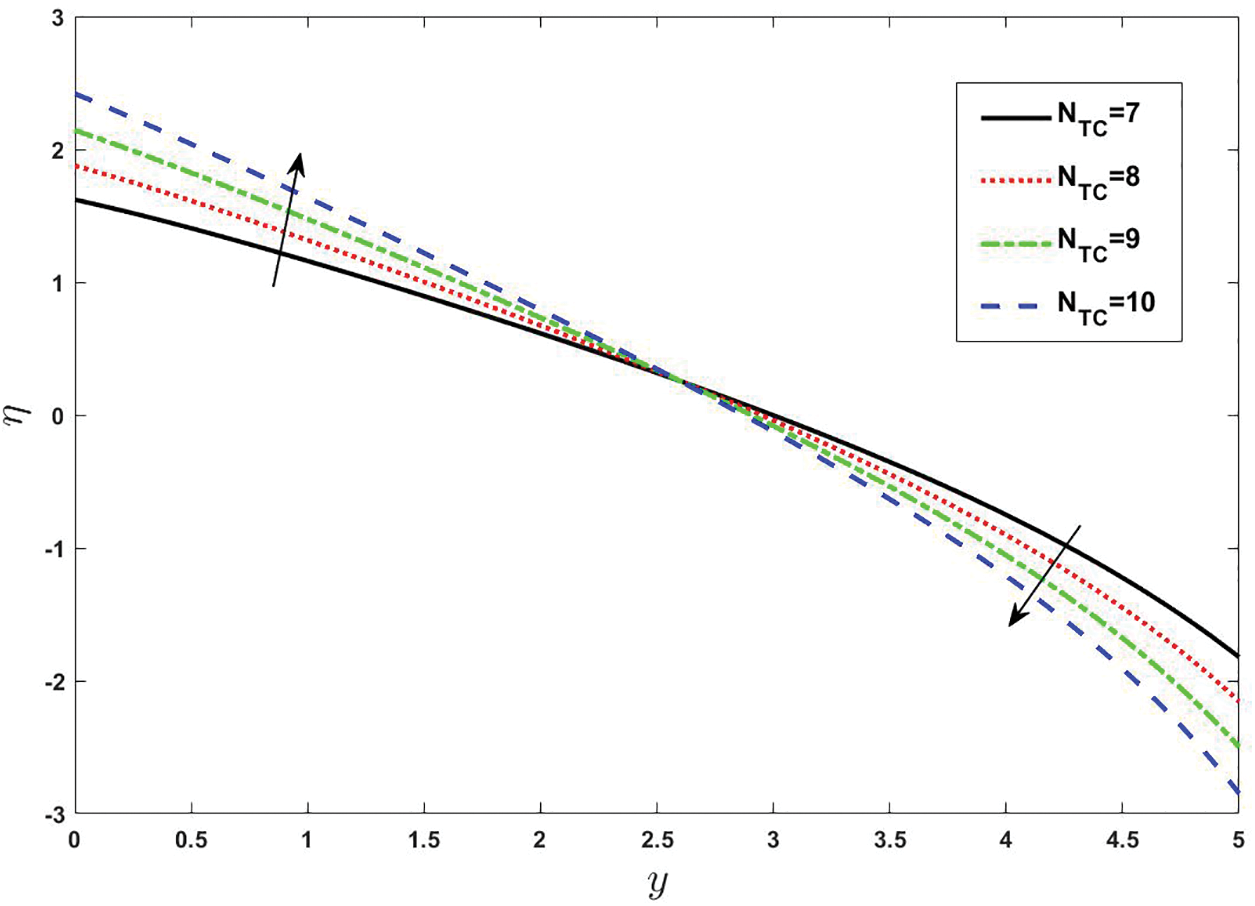
Figure 21: Effect of various values of Dufour parameter on double diffusivity. Other fixed values are:
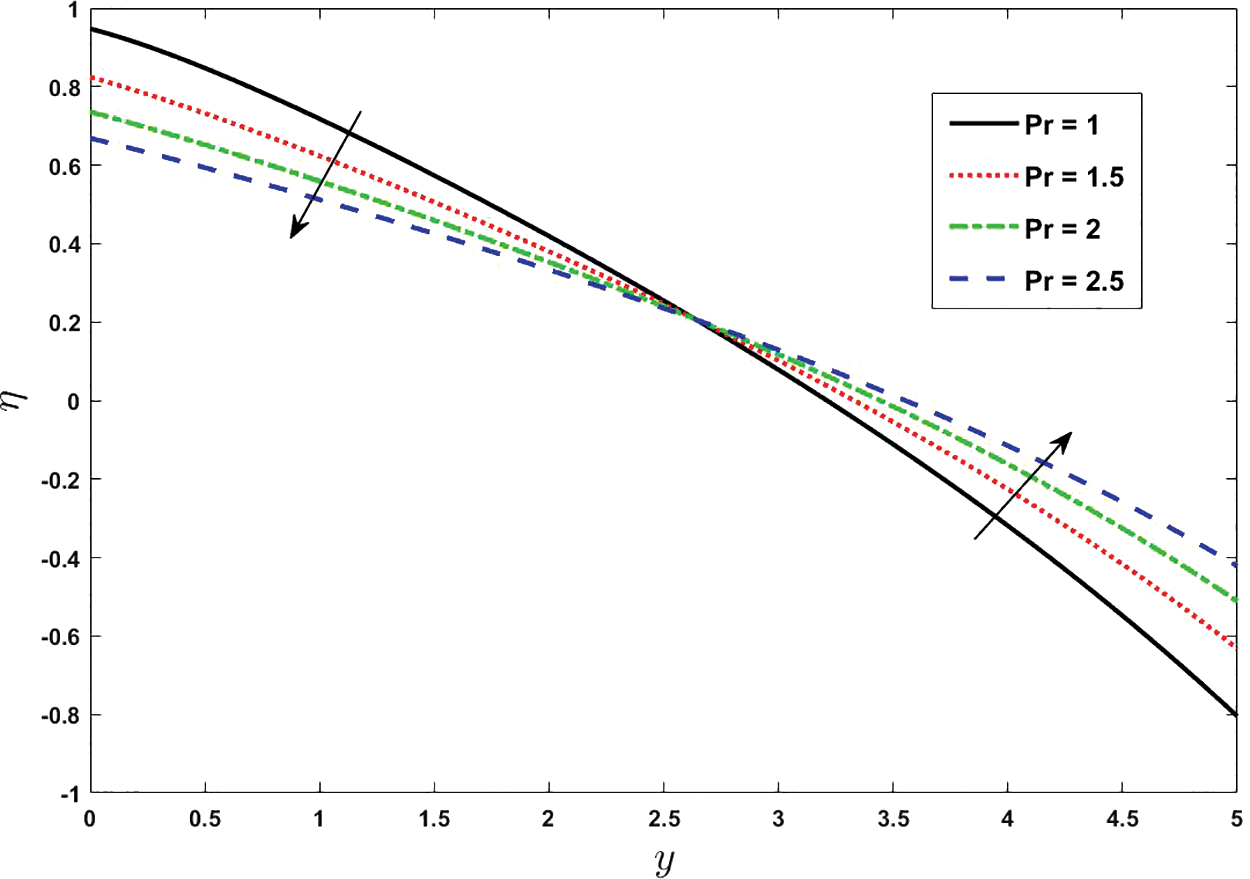
Figure 22: Effect of various values of Prandtl number on double diffusivity. Other fixed values are:
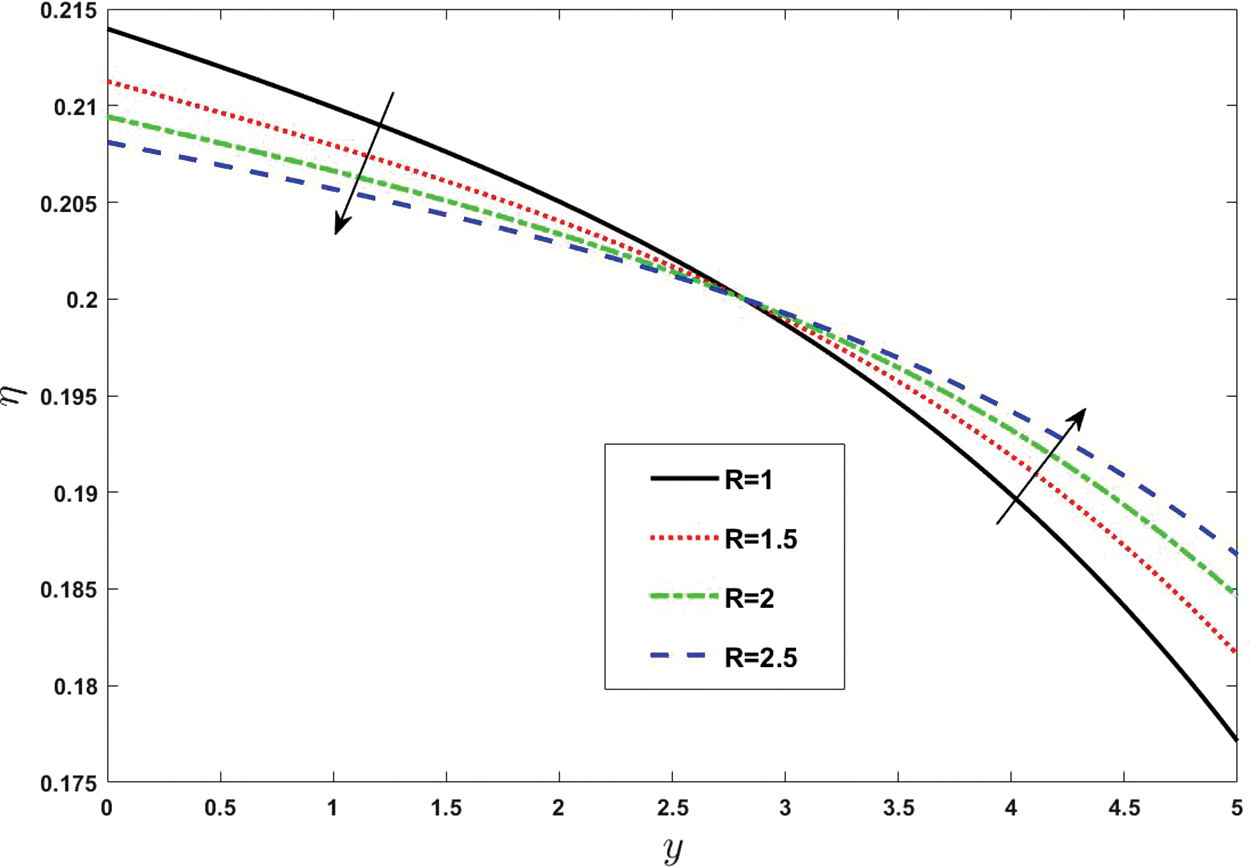
Figure 23: Effect of various values of radiation parameter on double diffusivity. Other fixed values are:
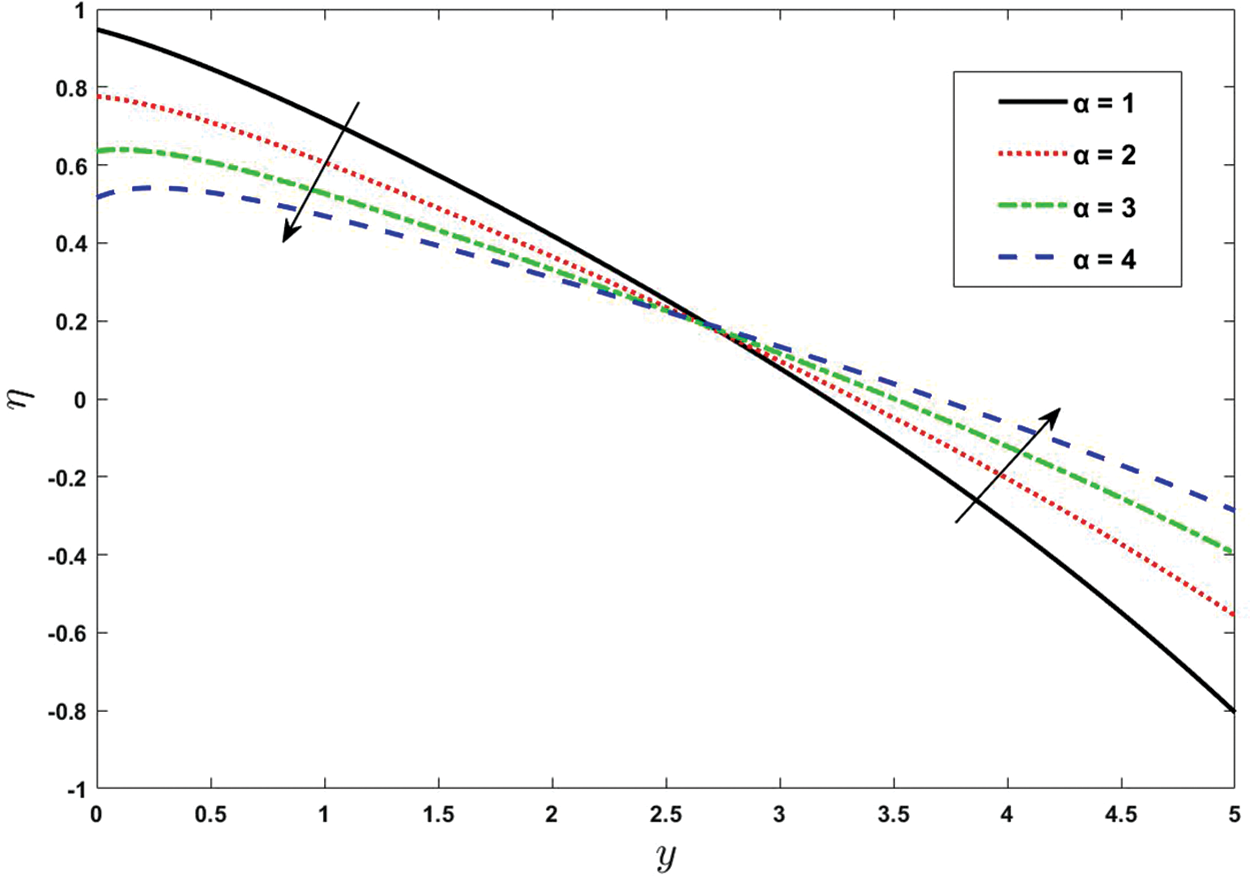
Figure 24: Effect of various values of thermal conductivity
The current analysis divulges the phenomena of the flow of the Casson fluid model through peristaltic motion. Low Reynolds number and high wavelength have been considered for the description of the influence of wall features. By sketching the graphs of velocity, temperature, concentration and double diffusivity, the physical characteristics of relevant quantities are investigated. The basic effort of this article is to discuss the features of double diffusivity, which has vast applications in medicine as well as engineering. We summarize our findings as follows:
• By elevating the viscosity parameter, the velocity of blood nanomaterial falls off in the free pumping part.
• Velocity of fluid enhances with the increase of solutal Grashof number and nanofluid Grashof number while the behavior is opposite for thermal Grashof number.
• It is clear that velocity travels in a parabolic path toward the center of the sinusoidal channel but exhibits mixed behavior closer to the wall limits due to the asymmetrical design of the walls.
• Activation energy lowers the concentration of nanoparticles and facilitates the efficient dispersion of medication administration through blood flow.
• By enhancing the Brownian and thermophoresis motions, the temperature of blood flow is raised.
• As the radiative heat flux parameter increases, the temperature contour of the free pumping and co-pumping portions steams.
• The temperature amplifies by surging the value of the Brownian motion parameter because different nanoparticles have different values for
• The activation energy amplifies the heating phenomenon because higher activation energies result in higher molecular kinetic energies and lots of molecular collisions produce a lot of heat.
• Activation energy initially enhances the concentration profile, but as the concentrated nanoparticles enter the free pumping part of the peristaltic tube, the concentration drops abruptly.
• It is concluded that as the thermal conductivity increases, double diffusivity also increases and then there is a great motion created between the particles.
• Initially double diffusivity declines by enlarging the value of thermal heat flux and then raised in the zone
• The results for the concentration profile are more strong for the Casson fluid model than the Williamson model [5].
• The novelty of this manuscript is that it discloses the spotlight effects of double diffusivity on the peristaltic flow of Casson fluid in a vertical channel.
• In the future, we may extend our work on the peristalsis by taking more suitable model also for the effect of MHD, electro-osmosis and may also be done for hybrid nanofluid.
Acknowledgement: I am grateful to all of those with whom I have had the pleasure to work during this and other related projects.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Azad Hussain: Conceptualization, Supervision, Methodology, Software, Visualization, Validation. Naila Farooq: Data Curation, Writing—Original Draft, Investigation, Validation, Review. Ayesha Saddiqa: Editing and Writing. Ahmad M Hassan; Revised, Design and Implementation. Abdulkafi Mohammed Saeed: Review and Editing. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Authors agree to make data and materials supporting the results or analyses presented in their paper available upon reasonable request.
Conflicts of Interest: On behalf of all authors, the corresponding author states that there is no conflict of interest.
References
1. Akbar, N. S., Butt, A. W. (2017). Entropy generation analysis for the peristaltic flow of Cu-water nanofluid in a tube with viscous dissipation. Journal of Hydrodynamics, 29(1), 135–143. [Google Scholar]
2. Mabood, F., Farooq, W., Abbasi, A. (2022). Entropy generation analysis in the electro-osmosis-modulated peristaltic flow of Eyring-Powell fluid. Journal of Thermal Analysis and Calorimetry, 147(5), 3815–3830. [Google Scholar]
3. Kotnurkar, A. S., Talawar, V. T. (2022). Impact of electroosmosis and joule heating effects on peristaltic transport with thermal radiation of hyperbolic tangent fluid through a porous media in an endoscope. Partial Differential Equations in Applied Mathematics, 5, 100340. [Google Scholar]
4. Kotnurkar, A. S., Talawar, V. T. (2022). Influence of thermal jump and inclined magnetic field on peristaltic transport of Jeffrey fluid with silver nanoparticle in the eccentric annulus. Heliyon, 8(9), e10543. [Google Scholar] [PubMed]
5. Farooq, N., Hussain, A. (2022). Peristaltic analysis of Williamson blood flow model with solar biomimetic pump. International Communications in Heat and Mass Transfer, 138, 106305. [Google Scholar]
6. Rashid, M., Ansar, K., Nadeem, S. (2020). Effects of induced magnetic field for peristaltic flow of Williamson fluid in a curved channel. Physica A: Statistical Mechanics and its Applications, 553, 123979. [Google Scholar]
7. Hussain, A., Farooq, N. (2023). Gyrotactic micro-organisms swimming under the hyperbolic tangent blood nano material and solar biomimetic system over the Esophagus. International Communications in Heat and Mass Transfer, 141, 106579. [Google Scholar]
8. Saeed, K., Akram, S., Ahmad, A., Athar, M., Razia, A. et al. (2022). Impact of slip boundaries on double diffusivity convection in an asymmetric channel with magneto-tangent hyperbolic nanofluid with peristaltic flow. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 103, e202100338. [Google Scholar]
9. Akbar, N. S., Habib, M. B. (2019). Peristaltic pumping with double diffusive natural convective nanofluid in a lopsided channel with accounting thermophoresis and Brownian moment. Microsystem Technologies, 25(4), 1217–1226. [Google Scholar]
10. Akram, S., Athar, M., Saeed, K., Razia, A. (2021). Crossbreed impact of double-diffusivity convection on peristaltic pumping of magneto sisko nanofluids in non-uniform inclined channel: A bio-nanoengineering model. Science Progress, 104(3). https://doi.org/10.1177/00368504211033677 [Google Scholar] [PubMed] [CrossRef]
11. Shivappa Kotnurkar, A., Giddaiah, S. (2020). Double diffusion on peristaltic flow of nanofluid under the influences of magnetic field, porous medium, and thermal radiation. Engineering Reports, 2(2), e12111. [Google Scholar]
12. Akram, S., Athar, M., Saeed, K., Umair, M. Y. (2021). Double-diffusivity convection on Powell-Eyring nanofluids in non-uniform inclined channel under the impact of peristaltic propulsion and induced magnetic field. The European Physical Journal Plus, 136(5), 1–14. [Google Scholar]
13. Akram, S., Athar, M., Saeed, K., Razia, A., Muhammad, T. et al. (2022). Hybrid double-diffusivity convection and induced magnetic field effects on peristaltic waves of Oldroyd 4-constant nanofluids in non-uniform channel. Alexandria Engineering Journal, 65, 786–796. [Google Scholar]
14. Ibrahim, W., Gizewu, T. (2019). Tangent hyperbolic nanofluid with mixed convection flow: An application of improved Fourier and Fick’s diffusion model. Heat Transfer—Asian Research, 48(8), 4217–4239. [Google Scholar]
15. Chu, Y. M., Nazeer, M., Khan, M. I., Hussain, F., Rafi, H. et al. (2021). Combined impacts of heat source/sink, radiative heat flux, temperature dependent thermal conductivity on forced convective Rabinowitsch fluid. International Communications in Heat and Mass Transfer, 120, 105011. [Google Scholar]
16. Javid, K., Riaz, M., Chu, Y. M., Khan, M. I., Khan, S. U. et al. (2021). Peristaltic activity for electro-kinetic complex driven cilia transportation through a non-uniform channel. Computer Methods and Programs in Biomedicine, 200, 105926. [Google Scholar] [PubMed]
17. Akram, S., Athar, M., Saeed, K. (2021). Hybrid impact of thermal and concentration convection on peristaltic pumping of Prandtl nanofluids in non-uniform inclined channel and magnetic field. Case Studies in Thermal Engineering, 25, 100965. [Google Scholar]
18. Tanveer, A., Hayat, T., Alsaedi, A., Ahmad, B. (2017). On modified Darcy’s law utilization in peristalsis of Sisko fluid. Journal of Molecular Liquids, 236, 290–297. [Google Scholar]
19. Parida, S. K., Swain, K. (2023). Magnetohydrodynamics stagnation point flow and heat transfer over a non-isothermal permeable shrinking sheet with variable surface temperature. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 103, e202100241. [Google Scholar]
20. Tripathi, D., Sharma, A., Bég, O. A. (2017). Electrothermal transport of nanofluids via peristaltic pumping in a finite micro-channel: Effects of joule heating and helmholtz-smoluchowski velocity. International Journal of Heat and Mass Transfer, 111, 138–149. [Google Scholar]
21. Eldabe, N., Abo-Seida, O. M., Abo Seliem, A. A., Elshekhipy, A. A., Hegazy, N. (2018). Magnetohydrodynamic peristaltic flow of Williamson nanofluid with heat and mass transfer through a non-Darcy porous medium. Microsystem Technologies, 24(9), 3751–3776. [Google Scholar]
22. Ali, A., Barman, A., Das, S. (2022). Electromagnetic phenomena in cilia actuated peristaltic transport of hybrid nano-blood with Jeffrey model through an artery sustaining regnant magnetic field. Waves in Random and Complex Media, 1–32. https://doi.org/10.1080/17455030.2022.2072533 [Google Scholar] [CrossRef]
23. Das, S., Barman, B. (2022). Ramification of hall and ion-slip currents on electro-osmosis of ionic hybrid nanofluid in a peristaltic microchannel. BioNanoScience, 12(3), 957–978. [Google Scholar]
24. Oka, S. (1971). An approach to α unified theory of the flow behavior of time-independent non-Newtonian suspensions. Japanese Journal of Applied Physics, 10(3), 287. [Google Scholar]
25. Jayaraman, G., Lautier, A., Hung, B. M., Jarry, G., Laurent, D. (1981). Numerical scheme for modelling oxygen transfer in tubular oxygenators. Medical and Biological Engineering and Computing, 19(5), 524–534. [Google Scholar] [PubMed]
26. Khan, K. A., Jamil, F., Ali, J., Khan, I., Ahmed, N. et al. (2022). Analytical simulation of heat and mass transmission in casson fluid flow across a stretching surface. Mathematical Problems in Engineering, 2022, 1–11. [Google Scholar]
27. Saravana, R., Sailaja, M., Reddy, R. H. (2019). Effect of aligned magnetic field on Casson fluid flow over a stretched surface of non-uniform thickness. Nonlinear Engineering, 8(1), 283–292. [Google Scholar]
28. Reddy, K. V., Reddy, M. G., Makinde, O. D. (2019). Thermophoresis and Brownian motion effects on magnetohydrodynamics electro-osmotic Jeffrey nanofluid peristaltic flow in asymmetric rotating microchannel. Journal of Nanofluids, 8(2), 349–358. [Google Scholar]
29. Biswal, M. M., Swain, K., Dash, G. C., Ojha, K. (2023). Study of radiative magneto-non-Newtonian fluid flow over a nonlinearly elongating sheet with Soret and Dufour effects. Numerical Heat Transfer, Part A: Applications, 83(4), 331–342. [Google Scholar]
30. Reddy, K. V., Reddy, M. G., Makinde, O. D. (2021). Heat and mass transfer of a peristaltic electro-osmotic flow of a couple stress fluid through an inclined asymmetric channel with effects of thermal radiation and chemical reaction. Periodica Polytechnica Mechanical Engineering, 65(2), 151–162. [Google Scholar]
31. Reddy, K. V., Reddy, G. V. R. (2022). Outlining the impact of melting on Mhd Casson fluid flow past a stretching sheet in a porous medium with radiation. Biointerface Research in Applied Chemistry, 13, 1–14. [Google Scholar]
32. Kotnurkar, A., Hadapad, C. (2021). Magnetohydrodynamic peristaltic transport of Casson fluid embedded with chemical reaction in an asymmetrical permeable conduit. Journal of New Results in Science, 10(3), 98–113. [Google Scholar]
33. Kothandapani, M., Prakash, J. (2015). Effect of radiation and magnetic field on peristaltic transport of nanofluids through a porous space in a tapered asymmetric channel. Journal of Magnetism and Magnetic Materials, 378, 152–163. [Google Scholar]
34. Rosseland, S. (1931). Astrophysik und atom-theoretische Grundlagen, pp. 41–44. Berlin: Springer-Verlag. [Google Scholar]
35. El-Hawary, H. M., Mahmoud, M. A., Abdel-Rahman, R. G., Elfeshawey, A. S. (2013). Similarity analysis for effects of variable diffusivity and heat generation/absorption on heat and mass transfer for a MHD stagnation-point flow of a convective viscoelastic fluid over a stretching sheet with a slip velocity. Mathematical Problems in Engineering, 2013, 1–11. [Google Scholar]
36. Khan, M., Salahuddin, T., Malik, M. Y., Khan, F. (2019). Arrhenius activation in MHD radiative Maxwell nanoliquid flow along with transformed internal energy. The European Physical Journal Plus, 134(5), 198. [Google Scholar]
37. Salahuddin, T., Bashir, A. M., Khan, M., Elmasry, Y. (2021). Activation energy study for peristaltically driven divergent flow with radiation effect. Case Studies in Thermal Engineering, 27, 101172. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools