MHD (SWCNTS + MWCNTS)/H₂O-Based Williamson Hybrid Nanouids Flow Past Exponential Shrinking Sheet in Porous Medium

Nomenclature

1  Introduction

Nanofluid played a vital role in industrial and automotive applications. It is widely used as the radiator coolant, brake fluid and as a smart fluid in battery devices. Nanofluid is also applied as a coolant medium at a nuclear reactors, geothermal power, tire plant as well as in very small electronic applications such as microchip coolers [1].

Historically, the term nanofluid has first been coined by Choi et al. [2] to express the term nanofluid (nanoparticles fluid suspension). The nano size (<100 nm) solid particles in the fluid later known as the nanoparticles are usually made from metal or oxide. Metal nanoparticles such as zinc Zn, copper Cu and silver Ag are popular because of their high in thermal conductivities [3–5]. On the other side, these metal nanoparticles are high in density and thus promoted high friction between fluid and surface which cause corrosion. Furthermore, it is expensive. Meanwhile, the oxide nanoparticles are cheap and economical to be produced in mass production, but the oxide nanoparticles have low thermal conductivities. Increasing the percentage of nanoparticles in the fluid may increase the thermal behavior performance, but too many nanoparticles in the fluid will promote clogging.

Hybrid nanofluids can be considered as a new generation of Nanofluids. It is a very new idea. This is the composition of two variant types of dispersed nanoparticles in base fluids. This phenomenon have tale features that might make them helpful in many heat transfer organizations, like microelectronics, components of energy, pharmaceutical equipment, half breed powdered engines, engine cooling, car warming Administration, home cooler, chiller, thermal exchanger, atomic reactor coolant, grinding machinery, space innovation [6]. Sundar et al. [7] have proposed a thorough process for generating hybrid nanofluids, including their advantages and disadvantages. Waini et al. [8] have investigated the stretching and contracting of a sheet-induced hybrid nanofluid created by adding copper nanoparticles to an Al2O3/water nanofluid. To explore the impact of thermal radiation, chemical reaction, suction, and slip condition on the heat and mass transfer of an unsteady MHD flow across a stretched surface, researchers Sreedevi et al. [9] have combined both carbon nanotubes and silver nanoparticles in the base fluid (water). The influence of radiation and suction on the dynamics of an MHD hybrid nanofluid moving through a stretching sheet has been studied by Yashkun et al. [10].

With the rising era of graphene, the carbon nanotube (CNT) seems to be the alternative for the high-density issue of metal nanoparticles while providing better thermal conductivity than oxide nanoparticles. Anuar et al. [11] studied the stability analysis of flow and heat transfer of carbon nanotubes over a moving plate. The heat transfer capabilities between the single (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) nanoparticles in water as a based fluid are numerically examined. Next, Hayat et al. [12] investigated the carbon nanotube effects represented by SWCNTs and MWCNTs nanoparticles in the melting heat transfer over an impermeable stretchable surface in a nanofluid. Zaki et al. [13] concluded that the presence of SWCNTs nanoparticles in the Cu/water nanofluid so-called SWCNTs-Cu/water hybrid nanofluid dramatically raised the surface temperature and the heat transfer coefficient. Recently, Idrees et al. [14] studied the 3D rotational flow and heat transfer dynamics of a hybrid (SWCNT-MWCNT) nanofluid.

Considering the stretching/shrinking sheet in industrial processes, the heat transfer rate on the stretching/shrinking components plays an important factor in the quality of the product produces. Since half a century ago, the investigation of convection flow past a stretching/shrinking sheet has attracted the researcher’s attention [15]. The investigation evolved by including various physical external forces on a fluid flow such as the magnetic effects, the thermal radiation effects, the chemical reaction, the viscous dissipation, the heat generation/absorption and the permeability effects [16–20]. Recently, the bio-convection and activation energy across of Prandtl nanofluid flow on a stretching cylinder has been investigated by Shah et al. [21].

The study flows on a stretching sheet then are extended by considering the industrial fluid such as the Maxwell fluid, the Williamson hybrid ferrofluid, the micropolar nanofluid, the second-grade nanofluid, the Casson nanofluid and the viscoelastic nanofluid as recently studied by [22–28].

Motivated by the above literature, the present study investigates the carbon nanotube Williamson hybrid nanofluid flow on an exponentially stretching sheet with MHD effects. The SWCNTs and MWCNTs nanoparticles are taken as the hybrid particles. Such investigation has never been done before, so the reported result in this study is new. This research will be answering whether the blended carbon nanotube performs better than the single carbon nanotube nanofluid and the effects of the magnetic, shrinking surface, and the porosity in the fluid on the fluid flow and heat transfer performance.

2  Mathematical Formulations

Consider a steady 2-dimensional Williamson hybrid nanofluid boundary layer flow with single (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) nanoparticles with water H2O as a based-fluid on an exponentially shrinking sheet. The porous surface is considered, with variable wall mass suction/injection applied through it. Fig. 1 shows a physical representation of this situation. Physical model of the fluid flow can be modelled to a basic equation for motion and energy distribution are as follows [28]:

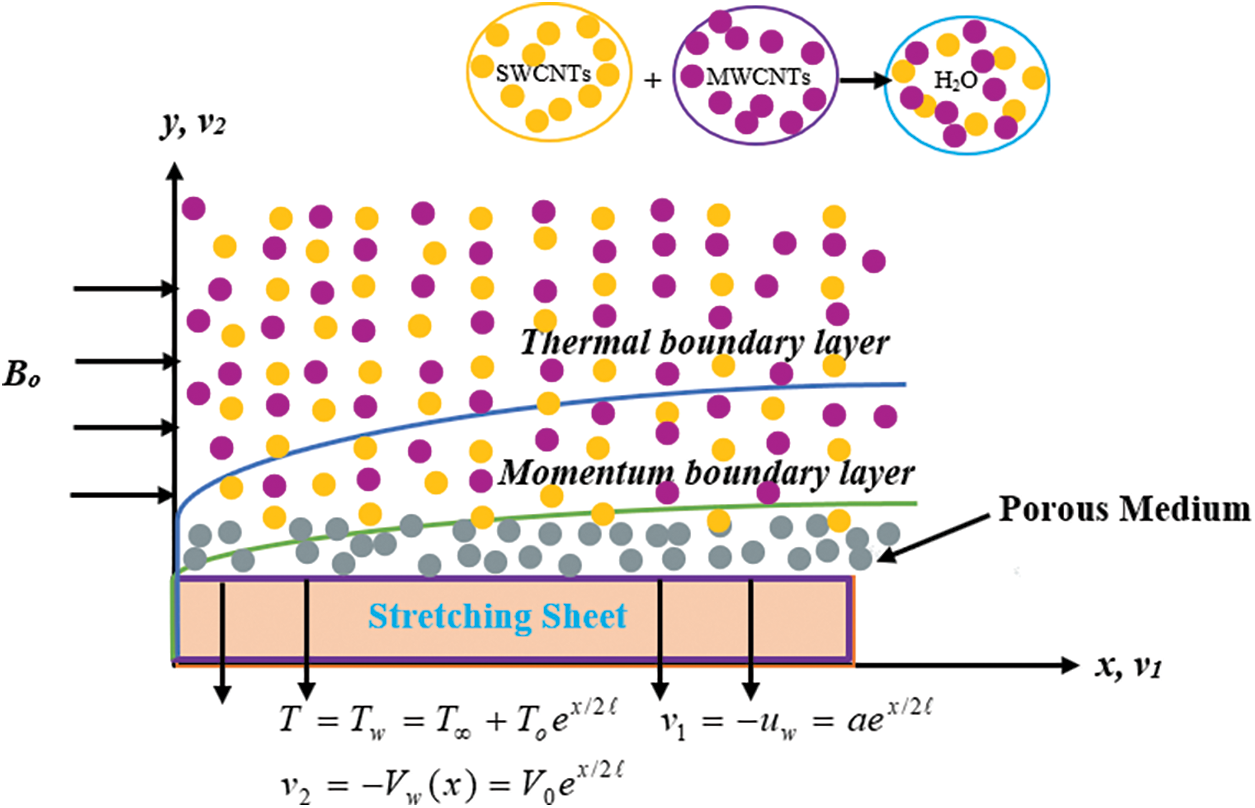
Figure 1: Physical geometry of the fluid flow

∂v1∂x+∂v2∂y=0,(1)

v1∂v1∂x+v2∂v1∂y=μhnfρhnf(∂2u1∂y2−v1k∗)−σhnfρhnfB02v1+2Γ∂v1∂y∂2v1∂y2,(2)

v1∂T∂x+v2∂T∂y=khnf(ρCP)hnf∂2T∂y2,(3)

subjected to

v1=−uw(x)=aex/2ℓ,v2=−Vw(x)=V0ex/2ℓT=Tw=T∞+Toex/2ℓaty=0,v1→0,T→T∞asy→∞,(4)

where v1 and v2 denotes respectively velocity components along x- and y-directions, k=ko/ex/2ℓ gives variable permeability of porous medium with ko being a non-negative constant, T represents temperature of hybrid nanofluid, uw=aex/2ℓ is variable shrinking velocity with a being positive constant having dimension ℓT−1. Next, Vw=V0ex/2ℓ is variable velocity of suction/injection, To and ℓ denote reference temperature and length. Furthermore, (ρhnf),(μhnf), (σhnf),(khnf), and (ρcp)hnf are the density, dynamic viscosity, electrical conductivity, thermal conductivity and heat capacity of hybrid nanofluid, respectively, which are defined as [29]

ρhnf=(1−χSW)[(1−χMW)ρf+χSWρSW]+χMWρMW,μhnf=μf(1−χSW)2.5(1−χMW)2.5,(ρcp)hnf=(1−χMW)[(1−χSW)(ρcp)f+χSW(ρcp)SW]+χGO(ρcp)GO,khnfkbf=(kMW+2kbf)−2χMW(kbf−kMW)(kMW+2kbf)+χMW(kbf−kMW),

where

kbfkf=(kSW+2kf)−2χSW(kf−kSW)(kSW+2kf)+χSW(kf−kSW),αhnf=khnf(ρcp)hnf,

σhnfσf=1+3[χSWσSW+χMWσMWσf−(χSW+χMW)][χSWσSW+χMWσMWσf+2]−[χSWσSW+χMWσMWσf−(χSW+χMW)].

Note that the properties related to base fluid, the SWCNTs and MWCNTs nanoparticles are denoted with subscript f,SW and MW. Next, the continuity Eq. (1) is satisfied with the introduction of the stream function Ψ so that v1=∂Ψ∂y and v2=−∂Ψ∂x. To simply, the dependent variable in Eqs. (2) and (3) can be reduced. It is introduced the following self-similar transformations:

v1=aex/ℓF′(η),v2=−avf2ℓ(F(η)+ηF′(η)),θ(η)=T−T∞Tw−T∞,η=yex/2ℓa2ℓvf.(5)

Using Eq. (5), the Eqs. (2) and (3) can be expressed in the form of self-similar nonlinear equations as follows:

P1P2(F‴−KF′)+FF″−2(F′)2−P3P2MF′+WeF″F‴=0,(6)

P4θ″+Pr(Fθ′−F′θ)=0,(7)

where K=2ℓvfak∗ is the permeability parameter, Pr=vf(ρCp)fkf is the Prandtl number.

We=x2Γa3vf is the Weissenberg number and M=(σfB02aρf) is the magnetic parameter. Also

P1=1(1−χSW)2.5(1−χMW)2.5,P2=(1−χSW)[(1−χMW)ρf+χSWρSW]+χMWρMW,P3=1+3[χSWσSW+χMWσMWσf−(χSW+χMW)][χSWσSW+χMWσMWσf+2]−[χSWσSW+χMWσMWσf−(χSW+χMW)],P4=khnf/kbf(1−χMW)[(1−χSW)(ρcp)f+χSW(ρcp)SW/(ρcp)f]+χMW(ρcp)MW/(ρcp)f.

The boundary conditions in Eq. (4) is reduced to the following forms:

F=S,F′=−1,θ=1,atη=0,F′→0,θ→0,asη→∞.(8)

Here, S=V02ℓ/avf is the wall mass transfer parameter, The physical quantities interested in this study are the local skin friction coefficient Cf and the Nusselt number Nu which can be expressed as [28]

Cf=τ¯xρhnfUw2,Nu=xq¯wkf(Tw−T∞),(9)

where

τ¯x=μhnf(∂v1∂y)y=0,q¯w=−khnf(∂T∂y)y=0.(10)

Using the definitions described above then the Cf and Nu are reduced as

ReCf=K1K2[F″(0)+We(F″(0))2],NuRe=−khnfkfθ′(0).(11)

with Re=xavf where Re is the local Reynolds number.

3  Numerical Simulation

The transformed ordinary differential Eqs. (6) and (7) with the boundary conditions (8) were solved numerically considering the water-based Williamson nanofluid SWCNTs/H2O and the water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O. Results from the study are presented in a graphic and tabular format, with a focus on the model’s mathematical components and their effects on velocity, temperature, and physical interest quantities. This study used the numerical technique from bvp4c function in MATLAB. bvp4c is the finite difference code implements the well-known three-stage Lobatto IIIA formula. Named after Rehuel Lobatto, this method is a collocation formula as Runge-Kutta method and provides a fourth-order accurate uniformly results. Related works that implements the bvp4c method included [30,31] and recently by [32,33].

To use this approach, the transformed ordinary differential equations are converted into the system of 1st order differential equations, which is followed as

{y1=F,y2=F′,y3=F″,yya=F‴,y4=θ,y5=θ′,yyb=θ″(12)

with

yya=[1/((P1P2)−Wey3)][(P1P2)Ky2+2y22+(P3P2)My2](13)

yyb=−(PrP4)[y1y5−y2y4].(14)

Corresponding boundary condition are converted as

{ y1(0)−Sy2(0)+1y2(∞){ y4(0)−1y4(∞)(15)

The resulting transformation above with the suitable IVP are coded into MATLAB software to compute numerically, see Fig. 2.

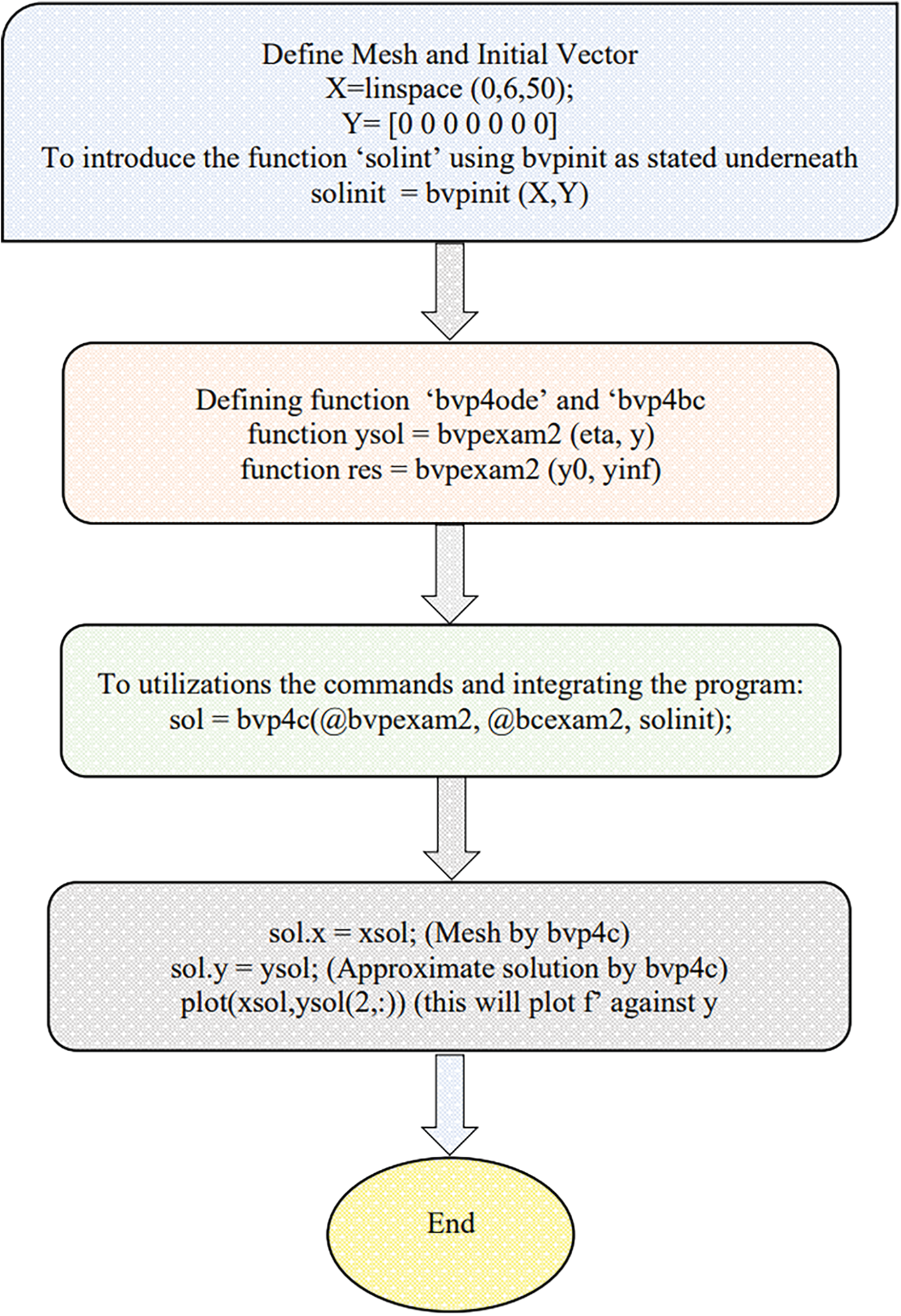
Figure 2: Flow chart of bvp4c method

4  Results and Discussion

The transformed ordinary differential Eqs. (6) and (7) with boundary conditions (8) were solved numerically using the BVP4C function in MATLAB software. The numerical computation considers the changes of pertinent parameters such as the permeability parameter K, the magnetic parameter M, the Williamson parameter We, the nanoparticle volume fractions of SWCNTs χSW and MWCNTs nanoparticles χMW, respectively and the wall mass transfer parameter S in the fluid flow. Further, the Prandtl number Pr is taken as 7 considering the Pr values for water. Table 1 shows the thermos-physical properties of water as a based fluid with carbon nanotube nanoparticles.

The effects of fluid parameters on the reduced skin friction coefficient ReCf is tabulated in Table 2. From Table 2, it is found that the increase in magnetic parameter M, the permeability parameter K, the nanoparticle volume fractions of MWCNTs χMW and the wall mass transfer parameter S results in enhanced friction between the fluid and the plate surface. This is physically realistic due to the effects of M and K attracting the fluid particle or giving the suction effects towards the plate surface which contributing extra force from fluid to a surface thus increased friction. Meanwhile, the increase in Williamson parameter We have reduced the skin friction coefficient. Crossing Table 2, it is concluded that, the water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O produced high in ReCfvalues compared to the water-based Williamson nanofluid SWCNTs/H2O.

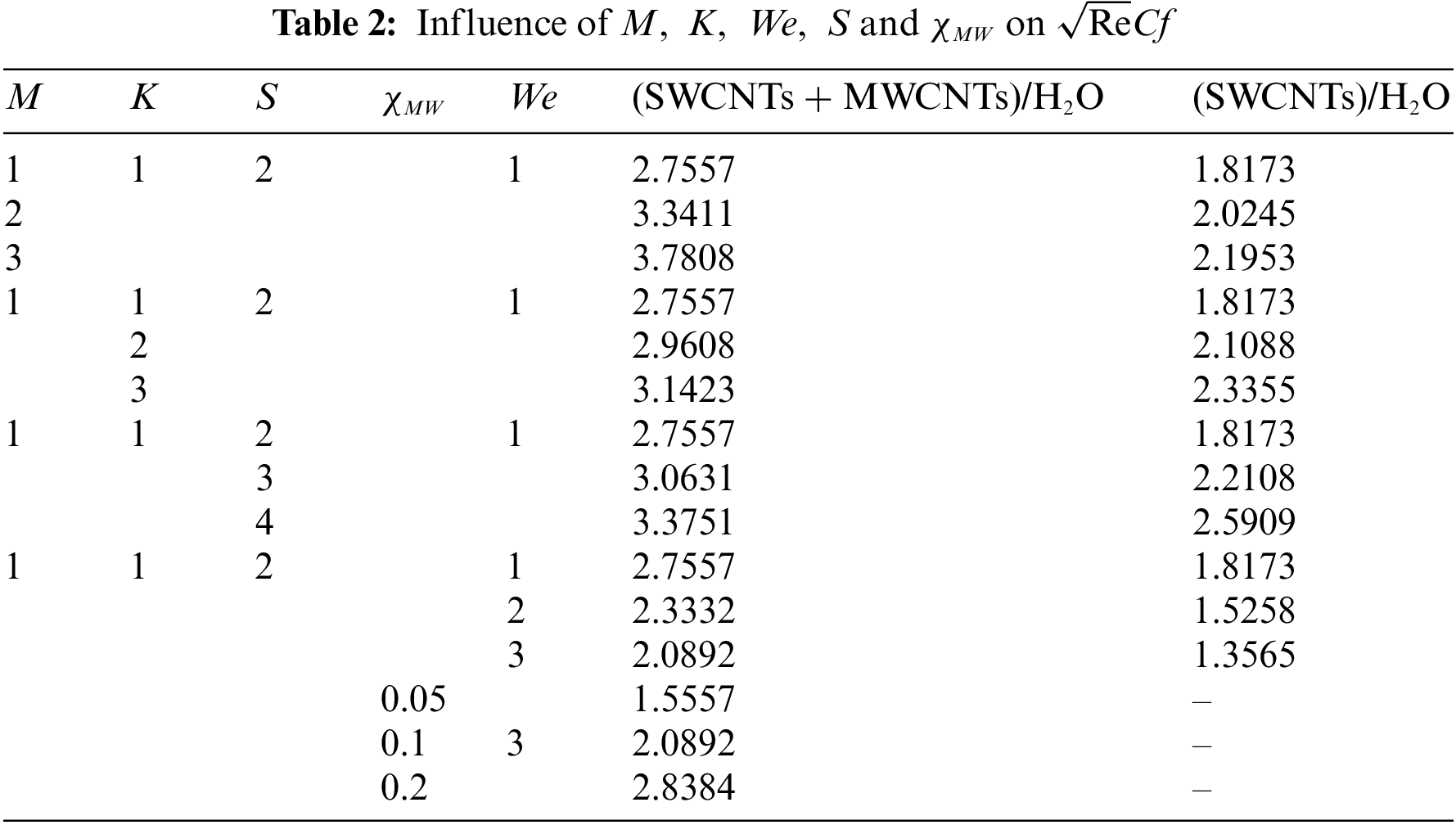
Table 3 tabulated the effects of fluid parameters on the reduced Nusselt number Nu/Rex. It is suggested that a small increment on Nu/Rex was found as M and K increased. On the other hand, the increase in S has boosting the values of Nu/Rex drastically. Physically the suction effect produced by the wall mass transfer parameter S reduced the fluid particle, providing the convection process between the fluid and plate surface occurs effectively thus boosted the reduced Nusselt number Nu/Rex. Meanwhile, the increase in Williamson parameter We and χMW has slightly reduced the values of Nu/Rex. Comparing the performance between the nanofluid, the water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O has lower in Nu/Rex values compared to the water-based Williamson nanofluid SWCNTs/H2O. Physically, carbon nanotube nanoparticles have high thermal conductivity properties. The increase in carbon nanotube nanoparticles in the fluid has enhanced the fluid thermal conductivity, thus raising the fluid conductive properties, therefore reducing the convective heat transfer capabilities of the fluid.

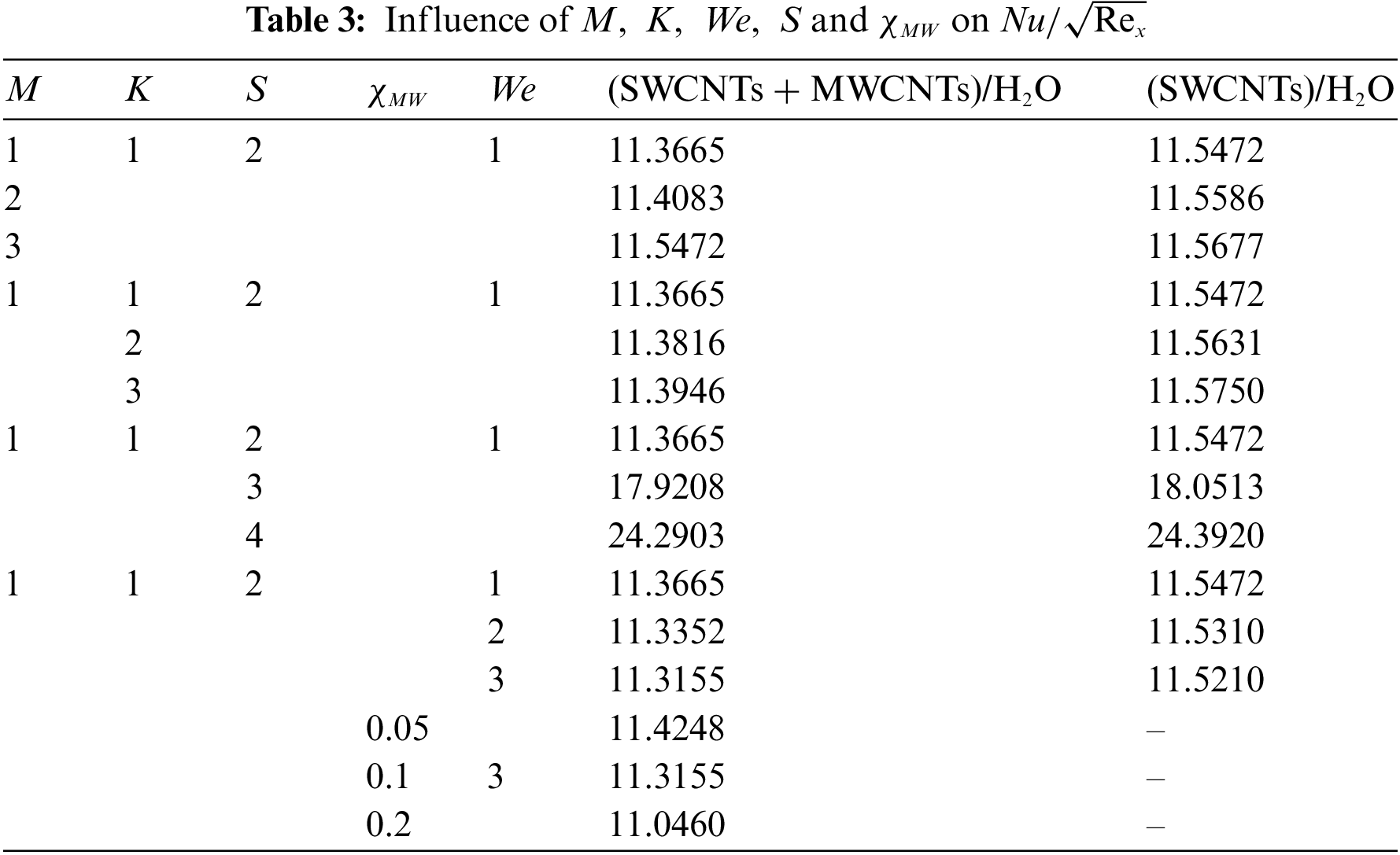
In discussing the fluid flow behavior across the boundary layer, Figs. 3–7 are illustrated. From Figs. 3 and 5, it is found that the increase of M, K and S has slightly increased the fluid flow velocity while reducing the velocity boundary layer thickness. The reduction in the thickness of the boundary layer physically leads to the increase in velocity gradient which derives to the increase in skin friction coefficient as found in Table 2. The same pattern occurs in Fig. 7 where the increase in χMW results in an increase in velocity distribution while reducing the boundary layer thickness. The increase in χMW enhanced the fluid momentum thus speeds up the fluid flow velocity. This outcome is agreed by the fluid comparison achieved in Figs. 3–6 where the water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O has higher fluid flow velocity as well as the skin friction coefficient compared to the water-based Williamson nanofluid SWCNTs/H2O. Meanwhile, the Williamson parameter We gives negative effects on the fluid flow. As seen in Fig. 6, it is found that the velocity distribution decreases as the We increases.

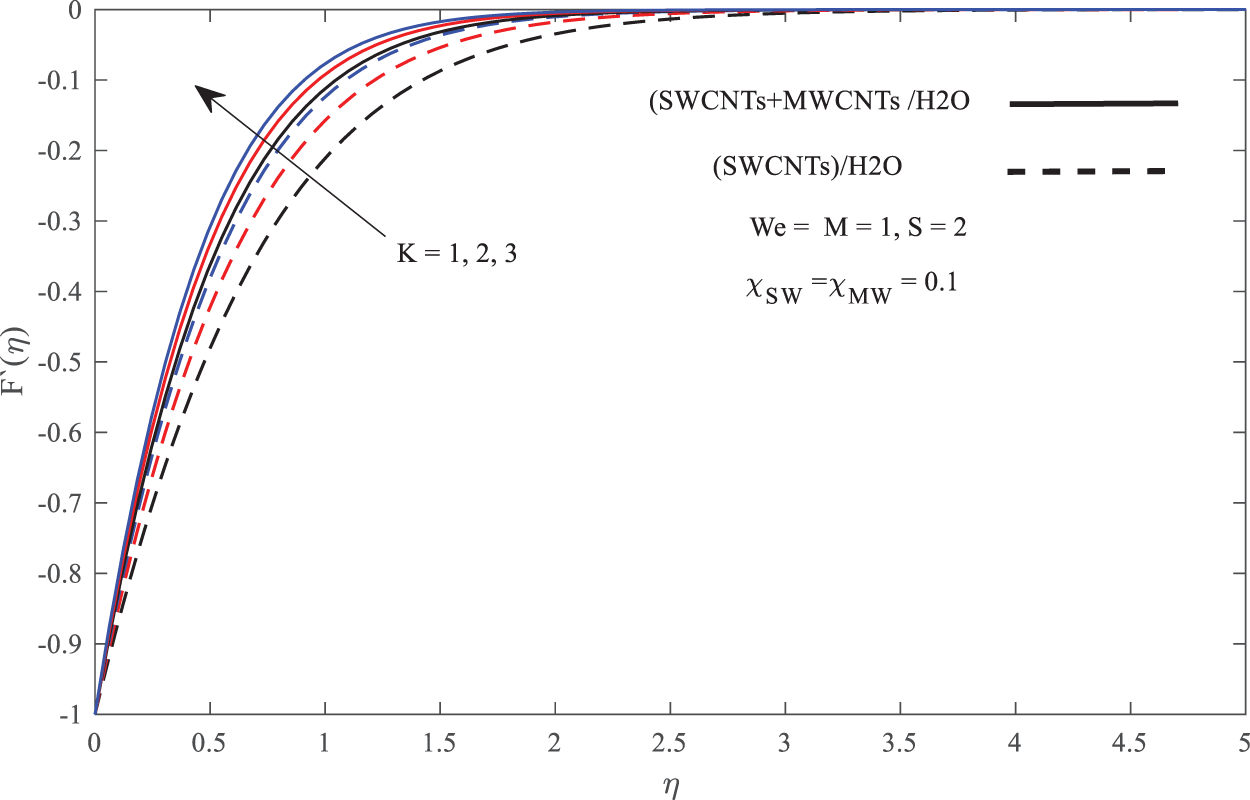
Figure 3: Influence of K on velocity profiles F′(η)

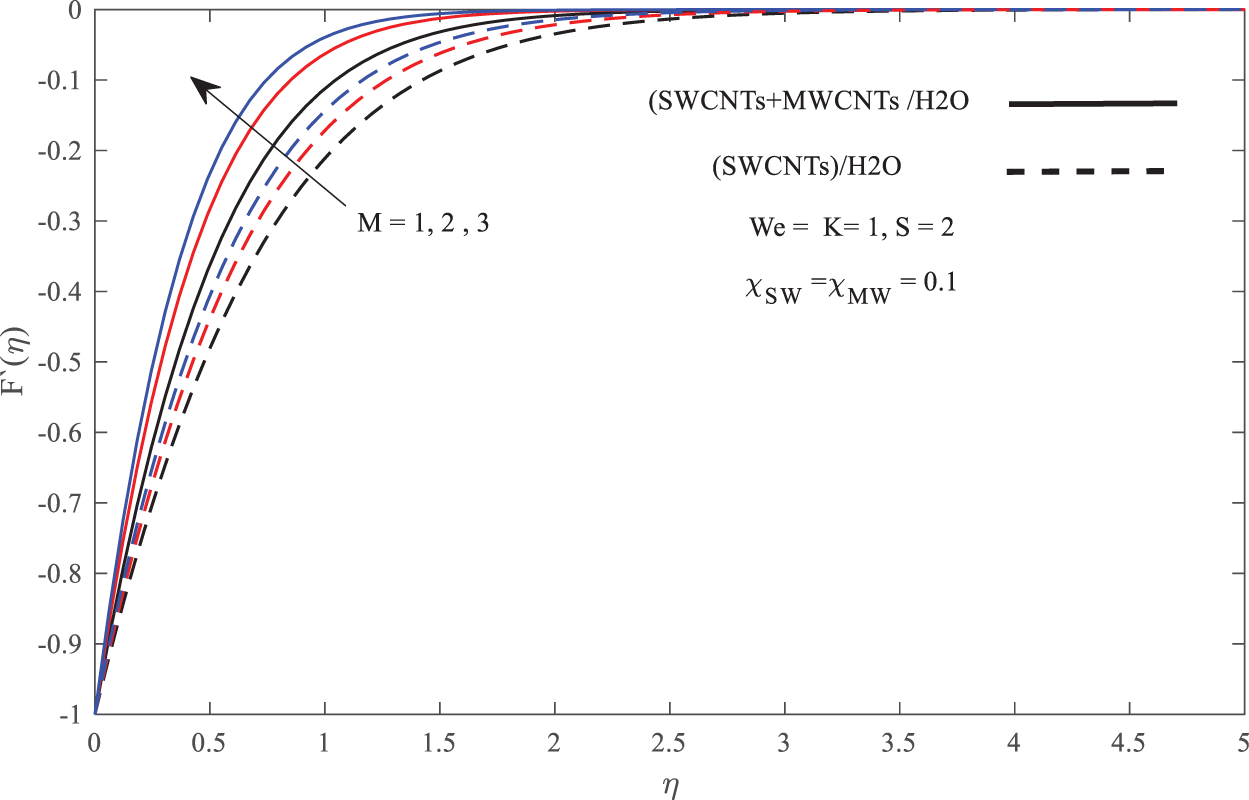
Figure 4: Influence of M on velocity profiles F′(η)

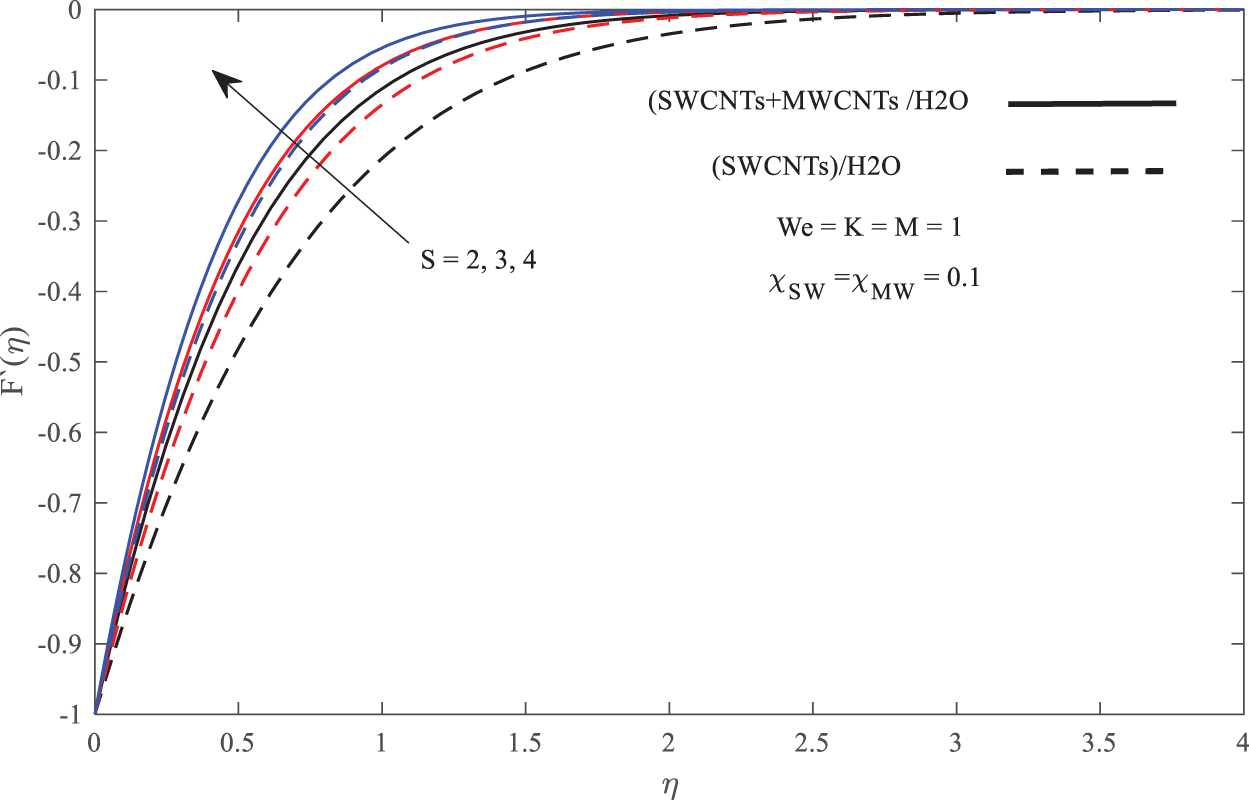
Figure 5: Influence of S on velocity profiles F′(η)

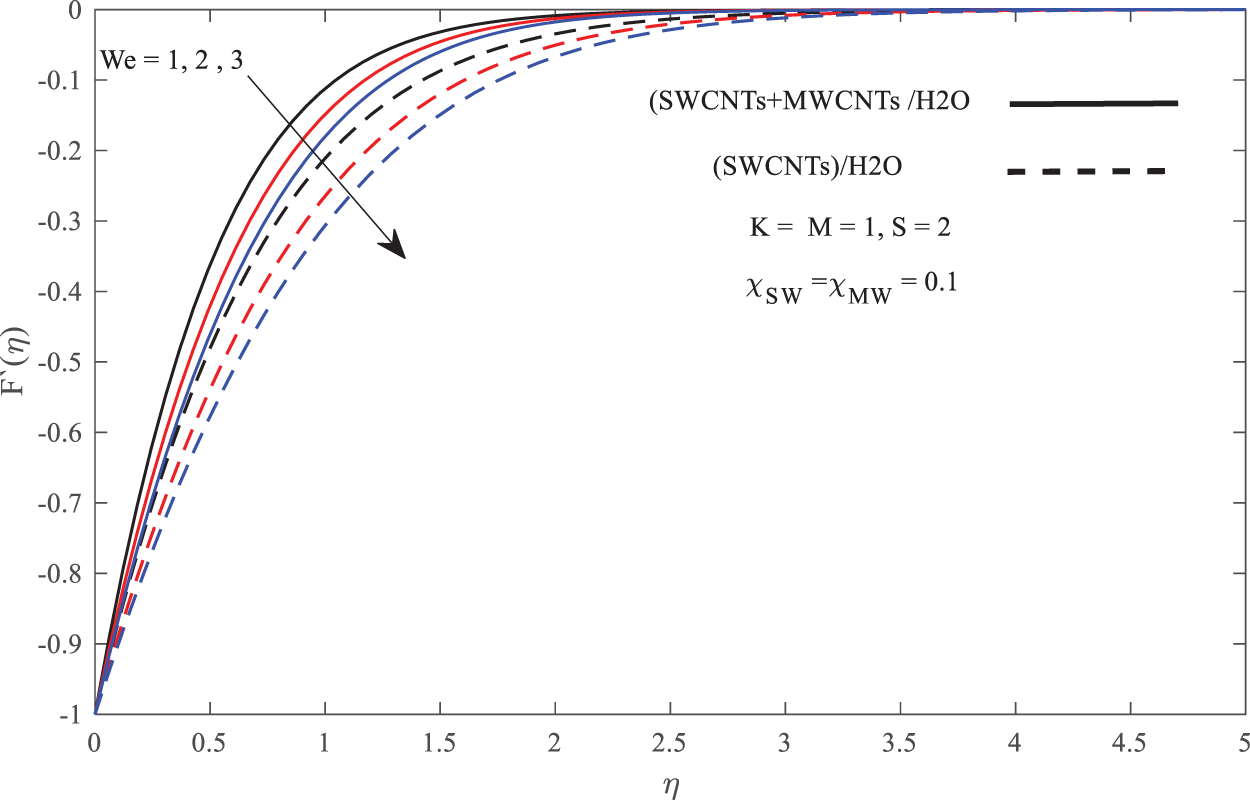
Figure 6: Influence of We on velocity profiles F′(η)

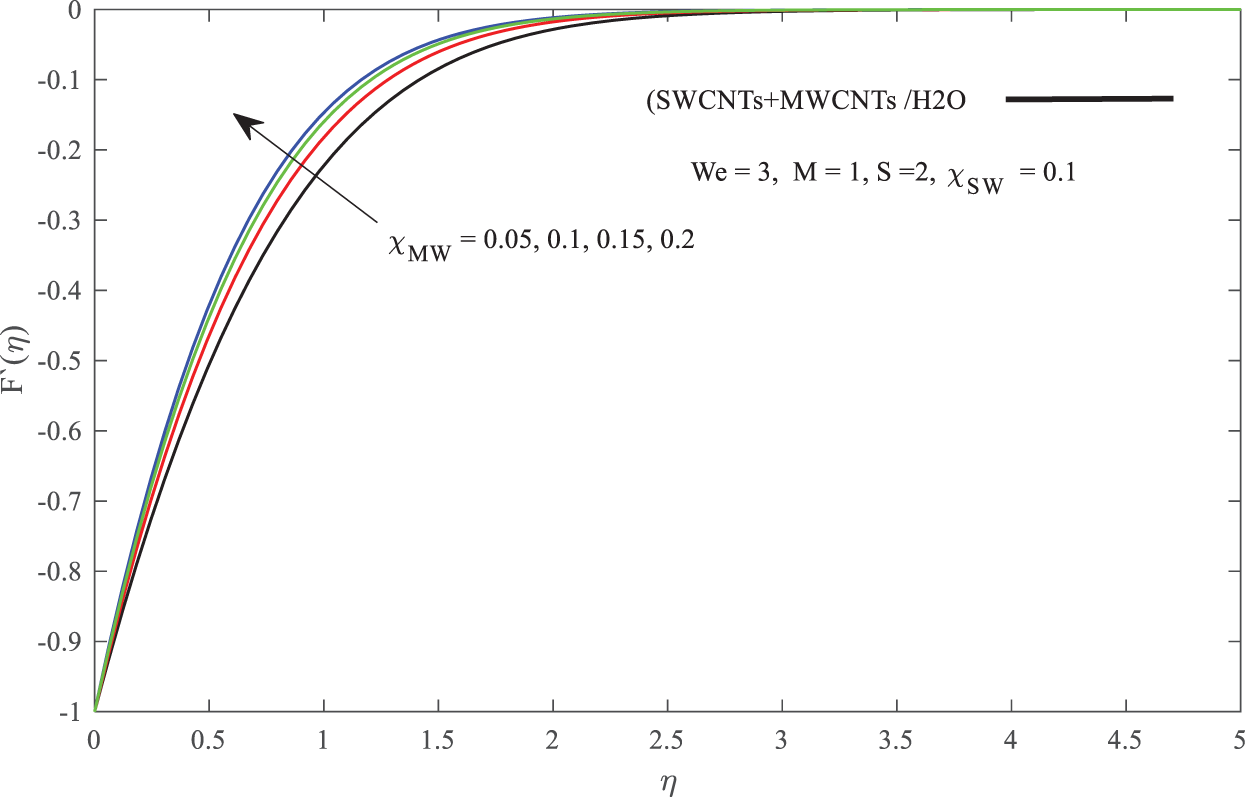
Figure 7: Influence of χMW on velocity profiles F′(η)

Lastly, Figs. 8 and 9 depicted the temperature profiles θ(η) for different values of S and χMW, respectively. From Fig. 8, it is observed that the increase in S results in a reduction in the thermal boundary layer thickness. This implies shortening the depth for the fluid with wall temperature to achieve the stream temperature outside the boundary layer. Shortening the thickness refers to the increase in the temperature gradient, thus physically reflecting the increase in Nusselt number as supported by Table 3. Meanwhile, the increase in χMW in Fig. 8 has widened the thermal boundary layer thickness as well as the temperature distributions. This is realistic because the increase in χMW leads to an increase in nanofluid thermal conductivities, thus enhancing the fluid thermal capabilities. The comparison between the temperature distributions for the water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O and the water-based Williamson nanofluid SWCNTs/H2O are shown in Fig. 8. It is clearly shown the advantages of high χSW and χMW in the fluid enhanced temperature and its thermal boundary layer thickness.

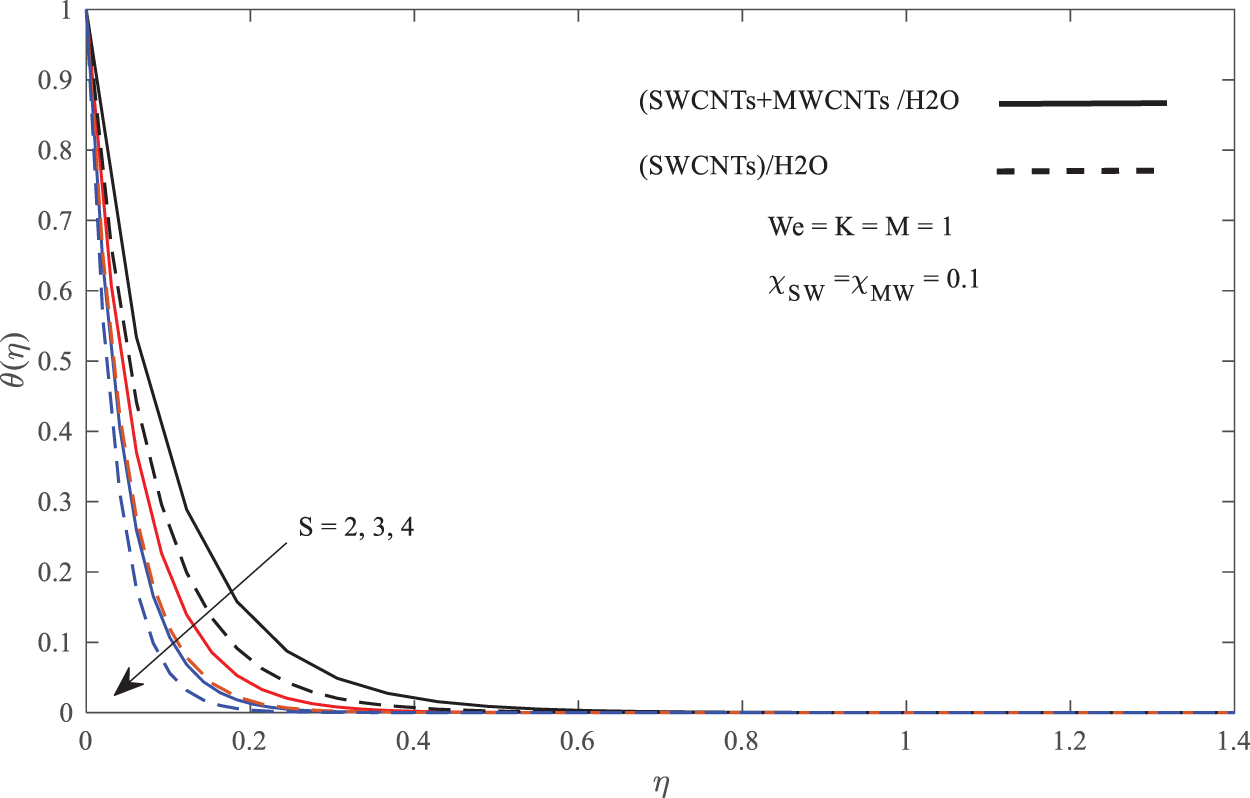
Figure 8: Influence of S on temperature profiles θ(η)

Figure 9: Influence of χMW on temperature profiles θ(η)

.

5  Conclusions

The study on the flow and heat transfer of porous Williamson hybrid nanofluid on an exponentially shrinking sheet with magnetohydrodynamic (MHD) effects are numerically studied. The influence of the fluid parameters such as the permeability parameter K, the magnetic parameter M, the Williamson parameter We, the nanoparticle volume fractions of SWCNTs χSW and MWCNTs nanoparticles χMW, respectively and the wall mass transfer parameter S on the fluid flow and heat transfer characteristic are analyzed and discussed. In conclusion, it is found that:

•   The increase in M, K, χMW, and S has promoted the increase in skin friction coefficient while We do the contrary.

•   The small increase has been recorded on a Nusselt number as M and K increase.

•   S played an important role as it increased may boost the values of Nusselt number drastically. Meanwhile, the Nusselt number reduced with the increase of We and χMW.

•   The water-based Williamson hybrid nanofluid (SWCNTs + MWCNTs)/H2O has a lower Nusselt number compared to the water-based Williamson nanofluid SWCNTs/H2O. This might be explained by the increase in fluid thermal conductivity in the fluid thus increasing the domination of conduction over the convection heat flow.

•   The increase in magnetic paramater in SWCNTs + MCWNTs hybrid nanofluid results to the increase of 72.2% on skin friction compared to SWCNT nanofluid.

We note that this analysis may be extended for the Jeffrey fluid, Oldroyd-B fluid and other non-Newtonian fluids.

Acknowledgement: Authors are grateful to acknowledge the Ajloun National University for providing the facilities support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Alkasasbeh T. H Formal Analysis, Investigation, and Methodology; Software and Validation; Muhammad K. A. M Writing—Review and Editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this paper can be requested from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wong, K. V., de Leon, O. (2010). Applications of nanofluids: Current and future. Advances in Mechanical Engineering, 2, 519659. [Google Scholar]

2. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. IL, USA: Argonne National Lab. [Google Scholar]

3. Aladdin, N. A. L., Bachok, N., Pop, I. (2020). Cu-Al2O3/water hybrid nanofluid flow over a permeable moving surface in presence of hydromagnetic and suction effects. Alexandria Engineering Journal, 59(2), 657–666. [Google Scholar]

4. Zainal, N. A., Nazar, R., Naganthran, K., Pop, I. (2021). MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. International Journal of Numerical Methods for Heat & Fluid Flow, 31(3), 858–879. [Google Scholar]

5. Prasad, P. D., Kumar, R. K., Varma, S. (2018). Heat and mass transfer analysis for the MHD flow of nanofluid with radiation absorption. Ain Shams Engineering Journal, 9(4), 801–813. [Google Scholar]

6. Lee, C., Choi, K., Leavitt, R., Eastman, L. (1995). Infrared hot-electron transistor with a narrow bandpass filter for high temperature operation. Applied Physics Letters, 66(1), 90–102. [Google Scholar]

7. Sundar, L. S., Sharma, K. V., Singh, M. K., Sousa, A. (2017). Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor–A review. Renewable and Sustainable Energy Reviews, 68, 185–198. [Google Scholar]

8. Waini, I., Ishak, A., Pop, I. (2019). Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. International Journal of Heat and Mass Transfer, 136, 288–297. [Google Scholar]

9. Sreedevi, P., Sudarsana, R. P., Chamkha, A. (2020). Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Applied Sciences, 2(7), 1222–12237. [Google Scholar]

10. Yashkun, U., Zaimi, K., Bakar, N. A. A., Ishak, A., Pop, I. (2020). MHD hybrid nanofluid flow over a permeable stretching/shrinking sheet with thermal radiation effect. International Journal of Numerical Methods for Heat & Fluid Flow, 31(3), 1014–1031. [Google Scholar]

11. Anuar, N., Bachok, N., Pop, I. (2018). A stability analysis of solutions in boundary layer flow and heat transfer of carbon nanotubes over a moving plate with slip effect. Energies, 11(12), 3243. [Google Scholar]

12. Hayat, T., Muhammad, K., Alsaedi, A., Asghar, S. (2018). Numerical study for melting heat transfer and homogeneous-heterogeneous reactions in flow involving carbon nanotubes. Results in Physics, 8, 415–421. [Google Scholar]

13. Zaki, A. M. M., Mohammad, N. F., Soid, S. K., Mohamed, M. K. A., Jusoh, R. (2021). Effects of heat generation/absorption on a stagnation point flow past a stretching sheet carbon nanotube water-based hybrid nanofluid with newtonian heating. Malaysian Journal of Applied Sciences, 6(2), 34–47. [Google Scholar]

14. Idrees, M., Shah, S. A. A., Ahmad, B., Ali, B., Mahmood, I. (2022). New insights into the heat transfer dynamics of a hybrid (SWCNT-MWCNT) nanofluid: A case of 3D rotational flow. International Communications in Heat and Mass Transfer, 138, 106311. [Google Scholar]

15. Crane, L. J. (1970). Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP, 21, 645–647. [Google Scholar]

16. Sulochana, C., Sandeep, N. (2016). Stagnation point flow and heat transfer behavior of Cu-water nanofluid towards horizontal and exponentially stretching/shrinking cylinders. Applied Nanoscience, 6, 451–459. [Google Scholar]

17. Raju, R. S., Reddy, G. J., Rao, J. A., Rashidi, M., Gorla, R. S. R. (2016). Retracted: Analytical and numerical study of unsteady MHD free convection flow over an exponentially moving vertical plate with heat absorption. International Journal of Thermal Sciences, 107, 303–315. [Google Scholar]

18. Jusoh, R., Nazar, R., Pop, I. (2019). Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. Journal of Heat Transfer, 141(1), 1–10. [Google Scholar]

19. Alkasasbeh, H. T., Abu-Ghurra, S., Alzgool, H. A. (2019). Similarity solution of heat transfer for the upper-convected Maxwell casson fluid over a stretching/shrinking sheet with thermal radiation. JP Journal of Heat and Mass Transfer, 16, 1–17. [Google Scholar]

20. Zokri, S. M., Arifin, N. S., Mohamed, M. K. A., Salleh, M. Z., Kasim, A. R. M. et al. (2017). Influence of radiation and viscous dissipation on magnetohydrodynamic Jeffrey fluid over a stretching sheet with convective boundary conditions. Malaysian Journal of Fundamental and Applied Sciences, 13(3), 279–284. [Google Scholar]

21. Shah, S. A. A., Ahammad, N. A., Ali, B., Guedri, K., Awan, A. U. et al. (2022). Significance of bio-convection, MHD, thermal radiation and activation energy across Prandtl nanofluid flow: A case of stretching cylinder. International Communications in Heat and Mass Transfer, 137, 106299. [Google Scholar]

22. Narayana, P. V., Babu, D. H., Babu, M. S. (2019). Numerical study of a Jeffrey fluid over a porous stretching sheet with heat source/sink. International Journal of Fluid Mechanics Research, 46(2), 187–197. [Google Scholar]

23. Alwawi, F. A., Alkasasbeh, H. T., Rashad, A., Idris, R. (2020). MHD natural convection of sodium alginate casson nanofluid over a solid sphere. Results in Physics, 16, 102818. [Google Scholar]

24. Alazwari, M. A., Abu-Hamdeh, N. H., Goodarzi, M. (2021). Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical keller-box scheme. Mathematics, 9(20), 2563. [Google Scholar]

25. Kumar, R. N., Jyothi, A., Alhumade, H., Gowda, R. P., Alam, M. M. et al. (2021). Impact of magnetic dipole on thermophoretic particle deposition in the flow of Maxwell fluid over a stretching sheet. Journal of Molecular Liquids, 334, 116494. [Google Scholar]

26. Swalmeh, M. Z., Alkasasbeh, H. T., Hussanan, A., Nguyen, T. T., Mamat, M. (2022). Microstructure and inertial effects on natural convection micropolar nanofluid flow about a solid sphere. International Journal of Ambient Energy, 43(1), 666–677. [Google Scholar]

27. Zokri, S. M., Arifin, N. S., Yusof, Z. M., Sukri, N. M., Kasim, A. R. M. et al. (2022). Carboxymethyl cellulose based second grade nanofluid around a horizontal circular cylinder. CFD Letters, 14(11), 119–128. [Google Scholar]

28. Wan, R. W., Mohamed, M. K. A., Sarif, N., Mohammad, N. F., Soid, S. K. (2022). Blood conveying ferroparticle flow on a stagnation point over a stretching sheet: Non-Newtonian Williamson hybrid ferrofluid. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 97(2), 175–185. [Google Scholar]

29. Devi, S. U., Devi, S. P. A. (2017). Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. Journal of the Nigerian Mathematical Society, 36(2), 419–433. [Google Scholar]

30. Jusoh, R., Nazar, R., Pop, I. (2019). Magnetohydrodynamic boundary layer flow and heat transfer of nanofluids past a bidirectional exponential permeable stretching/shrinking sheet with viscous dissipation effect. Journal of Heat Transfer, 141(1), 012406. [Google Scholar]

31. Jamaludin, A., Naganthran, K., Nazar, R., Pop, I. (2020). Thermal radiation and MHD effects in the mixed convection flow of Fe3O4-water ferrofluid towards a nonlinearly moving surface. Processes, 8(1), 95. [Google Scholar]

32. Bing, K. Y., Jusoh, R., Salleh, M. Z., Hisyam, A. M., Zainuddin, N. (2023). Magnetohydrodynamics flow of Ag-TiO2 hybrid nanofluid over a permeable wedge with thermal radiation and viscous dissipation. Journal of Magnetism and Magnetic Materials, 565, 170284. [Google Scholar]

33. Yap, B. K., Rahimah, J., Salleh, M. Z., Mohd, H. A., Nooraini, Z. (2022). Magnetohydrodynamics Ag-Fe3O4-ethylene glycol hybrid nanofluid flow and heat transfer with thermal radiation. CFD Letters, 14(11), 88–101. [Google Scholar]