 Open Access
Open Access
ARTICLE
Numerical Investigation Thermal Performance of Solar Air Heater Using Different Angle V-Grooved of Corrugated Absorber Plate
Engineering Technical College of Mosul, Northern Technical University, Mosul, 41001, Iraq
* Corresponding Author: Ayad S. Abedalh. Email:
Frontiers in Heat and Mass Transfer 2023, 21, 227-243. https://doi.org/10.32604/fhmt.2023.041777
Received 05 May 2023; Accepted 08 June 2023; Issue published 30 November 2023
Abstract
Solar energy, a renewable resource, can be harnessed instead of fossil fuels to generate power and heat. One effective method for converting solar energy into heat is through a solar air heating (SAH) system. The theoretical investigation focused on the thermal performance of various V-groove angles on a corrugated absorber plate. The researchers maintained the exterior dimensions and constraints of the absorber plate while increasing its surface area by using a corrugated absorber surface. For the simulation, three different V-groove angles were employed: 45°, 30°, and 15°. The temperature and air flow rate into the system had been set at 30°C and 0.15 m/s, respectively four various solar radiation intensities have been examined for each of the variables. The governing equations associated with the standard design, including the turbulent kinetic energy (k) and dissipation rates model (ε), were solved using the ANSYS 2020 R2 program. The results indicated that Utilizing corrugated absorber plates resulted in a rise in the Nusselt number., surpassing the performance of flat plate absorbers. Among the different configurations, the V-grooved 45° plate demonstrated the best results under the same conditions. Furthermore, it was observed that the efficiency values improved with increasing solar irradiance. The investigation also showed that the employing of V-grooved 45°, V-grooved 30°, and V-grooved 15° absorbers led to efficiency improvements of about 20.8%, 26.3%, and 36.14%, respectively, when compared to a flat plate at a solar irradiation of 900 W/m2.Graphic Abstract
Keywords
Nomenclature
| Ac | Collector absorber area (m2 |
| Aduct | Cross-sectional area of the round duct (m2) |
| Cp | Specific heat (J/kg.K) |
| dduct | Duct diameter (m) |
| Dh | Hydraulic diameter (m) |
| h | The heat transfer coefficient (W/m2.K) |
| hr | The heat transfer coefficient radiation (W/m2.K) |
| I | Intensity solar radiation (W/m2) |
| K | The thermal conductivity (W/m.K) |
| m | Mass flow of air (kg/s) |
| Qu | Energy gained (W) |
| Re | Reynolds number |
| Ta | Ambient air temperature (°C) |
| Tap | Temperature of absorber plate surface (°C) |
| Tbase | Bottom plate temperature (°C) |
| Tc | Temperature of cover (°C) |
| Tf | Fluid Temperature of fluid (°C) |
| Ti | Inlet air temperature (°C) |
| To | Outlet air temperature (°C) |
| U | Overall heat loss coefficient (W/m2.K) |
| Va | Air velocity (m/s) |
| Greek Symbols | |
| εp | Emittance of absorber plate |
| εc | Emittance of glass cover |
| σ | Stephen-Boltzman constant |
| α | Solar absorptance of collector plate |
| η | Thermal efficiency |
| τ | Solar transmittance of glazing |
| μ | Air viscosity (m2/s) |
A solar air heater (SAH) is a device that warms the air using the sun’s rays. The SAH is made up of one or more glass covers, an absorber plate, one or more airflow channels, and insulation for the solar collector’s sidewalls and bottom. The initial and ongoing costs of these systems are quite low. To keep it clean, all that needs to be done is to wipe the transparent cover. SAH is a fantastic option when low to medium heating temperatures are required. Additional applications include drying crops, desalinating water, and heating structures [1–3].
Gao et al. [4] numerically investigated the convective heat transport in U-corrugated solar collectors. According to the results, the height ratio must be more than two, while the geometric ratio must be bigger than one, and the inclination angle must be lower than 40° to effectively reduce heat loss via natural convection. Liu et al. [5] studied the influence of corrugated and V-groove absorber plates on thermal efficiency at various the mass flow rate per unit area the SAH, ranging of 0.002 to 0.5 kg/m2. The findings revealed that the corrugated SAH is more efficient than the V-groove SAH in terms of efficiency by 7%. This improvement might be attributed to improved turbulence in the airflow duct. Three models were used by Fudholi et al. [6] studied the influence of corrugated and V-groove absorber plates on thermal efficiency at various mass flow per unit area of the SAH, ranging from 0.002 to 0.5 kg/m2. The findings revealed that the corrugated SAH is more efficient than the V-groove SAH in terms of efficiency by 7%. This improvement might be attributed to improved turbulence in the airflow duct.
Bhandari et al. [7] conducted a comparative investigation of the efficiency of several types of flat plate SAHs. To conduct the entire analysis, a MATLAB software code was developed. The efficiency of SAHs was examined in relation to flow rates, inlet air temperature, and solar irradiance intensity. The three types of SAHs utilized for the analysis are traditional SAH, double glass SPSAH, and DPSAH with inner fins. The results show that for the same mass flow rate, the double-pass finned SAH has the maximum efficiency. It was also noted that as the mass flow rate increases, the values of the mean absorber plate temperature (Tpm) and air temperature outlet decrease. Metwally et al. [8] evaluated a corrugated channel collector and five more common layouts. With a flow rate of 0.01 to 0.1 kg/s and 950 W/m2 of solar radiation, the results showed that the efficiency was improved by 15%–43% over other standard collectors. They indicated that the corrugated duct SAH could be considered an enhanced design valued similarly to common types. Hedayatizadeh et al. [9] investigated a mathematical model of a glazed DPSAH with a V-corrugated absorber plate. They projected the effects of a V-corrugated plate on exergy loss for a glazed DPSAH. With the results of the available literature, the computational predictions were validated. Additionally, it was observed that increased efficiency reached 6.27% with an air flow rate of 0.005 kg/s, a collector area of 1.76 m2, a corrugation height of 0.0122 m, and a gap of 0.0023 m between both covers. A corrugated absorber collector outperforms a polyethylene plate collector in terms of thermal performance. When forced convection is used, the average efficiency is 77%. V-corrugated heating solar air systems using phase-change substance (PCS) were found to be the most efficient heaters at night, both with and without an insulated cover by Shalaby et al. [10]. Fahmi et al. [11] investigated various solar collector systems with triangular longitudinal fins affixed to the surface of the absorber under various environmental circumstances. The statistics show a steady increase in temperature differentials up to noon, followed by a steady reduction up to dusk. The greatest temperature differential and the highest level of efficiency were attained at the fourth kind, or 20.6°C. Sudhakar et al. [12] conducted an experimental investigation of a solar air heater with and without spherical-shaped capsules of phase-change material and with an inclined plate. Paraffin wax was used as a storage heat substance and compared with a normal air heater. The thermal efficiency without spherical capsules was 31%, with spherical capsules was 39%, and with an inclined plate was 43%. The efficiency for capsules was 42.2% for an inclined plate and 40% for a horizontal plate with spherical capsules. Hai et al. [13] analyzed the effectiveness of a solar air heater that uses inclined impinging jets on an absorber plate and has nozzles placed in parallel and crossing orientations. Numerical analysis was used to examine the effectiveness of the solar air heater that used inclined impinging jets on an absorber plate. The turbulent flow within the channel was simulated using the RNG k-model. The hydraulic and thermal behavior of the jet solar air heater was studied in relation to a number of geometric and operational parameters. The results showed that the proposed design performed better than the traditional unimproved solar air heater in terms of the Nusselt number and thermo-hydraulic performance parameter. Jet impingement produced a Nusselt number that was up to 4.26 times higher than a smooth duct solar air heater. Increasing the streamwise and spanwise pitch ratios resulted in a rise in the Nusselt number with just a slight impact on the friction factor.
Hassan et al. [14] conducted an experimental investigation of the energy and exergy evaluation on a newly designed nabla-shaped tubular solar air heater (∇ TSAH). The objective was to assess the performance and efficiency of the (∇ TSAH) through energy and exergy analysis. The study was conducted in hot climate conditions in Upper Egypt, with a mass flow rate range of 0.018–0.081 kg/s. The findings show that the tubular solar air heater in the shape of a (∇ TSAH) outperforms the traditional flat plate solar air heater (OTSAH). The TSAH displays higher output air temperature, energy gain, energy efficiency, exergy efficiency, and thermo-hydraulic efficiency, with lower top losses. The TSAH increases the exit air temperature by approximately 13.5°C for single pass (SP) and 5°C for double pass (DP) configurations compared to the OTSAH. The TSAH also exhibits higher energy efficiency and exergy efficiency compared to the flat plate solar air heater (FSAH).
Borah et al. [15] conducted an experimental investigation on a solar air heater using a modified absorber plate with square obstructions and threaded pin fins. The aim of the study was to investigate the performance and efficiency of this design. The results of this study indicate that the modified absorber plate outperforms the conventional flat absorber plate in a solar air heater. The enhanced absorber plate resulted in an increase of about 9% in the solar air heater’s exit temperature. The energetic efficiency showed improvement with the relevant settings. By utilizing the redesigned absorber plate, significant enhancements in useful energy obtained and energy efficiency were achieved for a fixed air flow rate of 0.0094 kg/s, with improvements of 28.81% and 23.59%, respectively, particularly at a higher collector tilt angle of 35°. Similar reports suggest that energy efficiency will increase by 30% under the same conditions. Moreover, the implementation of the redesigned absorber plate reduces energy destruction by approximately 10% due to the greater angle of collector tilt and airflow rate. The projected energy payback period for the system with the improved absorber plate is estimated to be 1.42 years. Additionally, it results in a decrease of 32.98 kg/year in CO2 emissions compared to the CO2 mitigation value of 333.33 tons over a system life of 30 years. Nishidh et al. [16] numerically analyzed the effects of suction and blowing on the fluid flow and heat transfer properties of a solar air heater. The objective was to investigate the impact of various strategies on the system’s performance. Computational fluid dynamics (CFD) was used to study the influence of suction and blowing on the fluid flow and heat transfer characteristics of a solar air heater. The ANSYS Fluent software, based on a finite volume method, was employed to calculate the field variables. The channel dimensions were set at a length of 1000 mm, width of 500 mm, confinement height of 25 mm, and transition length of 1000 mm. Among the various cases examined, it was observed that blowing exhibited superior efficiency compared to suction. The maximum efficiency achieved was 42.35% at a mass flow rate of 0.05 kg/s. These results indicate that blowing has a more favorable impact on the performance of the solar air heater in terms of fluid flow and heat transfer characteristics.
This study aims to numerically analyze the performance of a flat plate solar air heater (SAH) with different shapes of absorber plates. Ordinary smooth plates and corrugated plates with three different angles of V-grooves (45°, 30°, and 15°) will be employed to increase the heat transfer area. The thermal performance of the solar air heater will be evaluated when the air flows separately over and under these types of plates, ultimately leading to improved collector efficiency. The study will be conducted using the latest version of the ANSYS Fluent Workbench 2020 R2 software. Various parameters will be examined and discussed to determine the optimal thermal efficiency of the solar heater using absorber plates with different V-Groove angles. The study will analyze the velocity, temperature, and Nusselt number of the exit air inside the solar air heater channel and compare them with those obtained using flat plates.
The equations for mass, momentum, and energy conservation (Navier-Stokes equations), which explain fluid movement and heat, are as follows: These equations explain the following types of turbulent and incompressible flow. To simplify the numerical case, the following assumptions were made:
1. The airflow was assumed to be steady-state and incompressible.
2. Heat transfer by conduction in the absorber wall was neglected.
3. Three-dimensional conservation equations were used to describe the flow and heat transfer.
4. Turbulent airflow was considered within the channel.
5. All properties, such as density and viscosity, were evaluated based on the average temperature.
Mass conservation [17]
Momentum conservation [18]
• x-direction (u-momentum)
• y-direction (v-momentum)
Energy equation [19]
The turbulent dissipation rate equation (
Turbulent kinetic energy [20]
Dissipation rate (
where:
where “
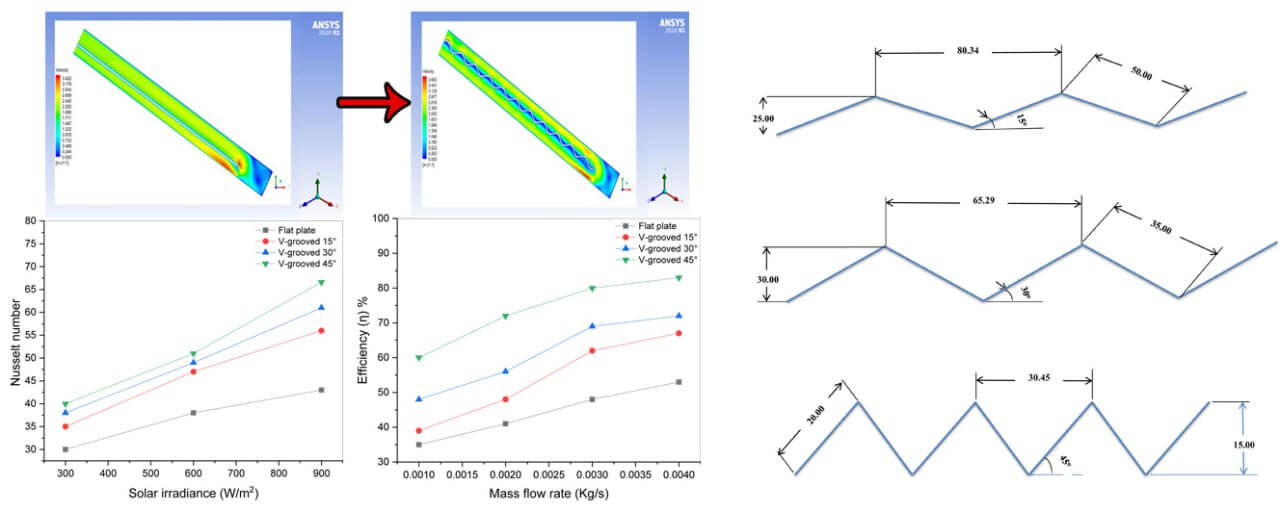
The configurations chosen for the model under testing are shown in Fig. 1. The present simulation made use of absorbers with V-grooved 45°, V-grooved 30°, and V-grooved 15°. All variants utilized the same selective black surface.


Figure 1: Three angles of corrugated solar air absorbers
This study investigated the parameters of forced heat transfer in a dual-flow solar air heater, focusing on various Reynolds numbers along the top channel. Finite-volume grids were generated throughout the entire geometric domain to determine these parameters. The construction of each geometry and mesh generation were simplified using SOLIDWORKS 2018 software, while mesh files were developed using ANSYS Fluent Workbench 2020 R2. A tetrahedral mesh consisting of 4,345,152 nodes in the three-dimensional directions was employed to model the air space. Fig. 2 presents a section of the mesh of the dual-flow solar air heater.

Figure 2: Computational domain mesh of the dual-flow SAH cavity model
The mathematical equations of the thermal balance of the dual-flow SAH are [24]
For the cover collector
For the upper stream
For absorber plate
Thermal perfomace is defined as the ratio of energy gained to total incident solar irradiance [25]
The energy gained is given by
Air mass flow rate
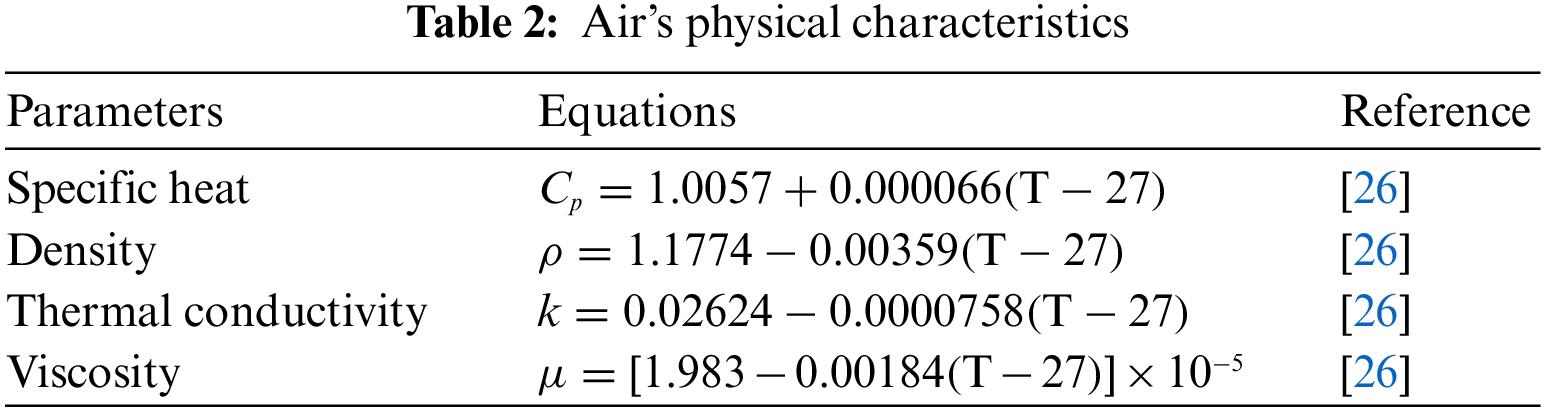
Air’s physical characteristics are expected to fluctuate linearly with temperature and are regulated by the following relationships in Table 2 below:
The hydraulic diameter and Reynolds number are expressed as follows [27,28]:
Here (W) stands for the collector width in meters, and d for the channel depth (m). The modified Grashof number evaluates the buoyant force to viscous force ratio in the presence of constant heat flux [29,30].
The Rayleigh number in the current investigation has been (
The equation below states that the Nusselt’s number is a function of both the Rayleigh and Prandtl [31,32]:
In this study, the ANSYS Fluent program was employed to conduct a numerical analysis of the surface design of an air solar absorber. The simulation included four different types of absorbers: flat plate, V-grooved 45°, V-grooved 30°, and V-grooved 15°. The numerical results presented in Table 3 indicated that, compared to the flat plate absorber under the same solar irradiance and time, the average outlet temperature exhibited an increase of 19.8% for the V-grooved 45° absorber, 14.3% for the V-grooved 30° absorber, and 7.8% for the V-grooved 15° absorber.
Furthermore, it was observed that the V-grooved 45° model outperformed the other models in terms of enhancing heat transfer from the heated absorber to the airflow in the air solar heater, especially with increasing solar irradiance. This improvement was attributed to the increased momentum of the airflow within the channel, which was evident in the higher exit velocity of the hot air.
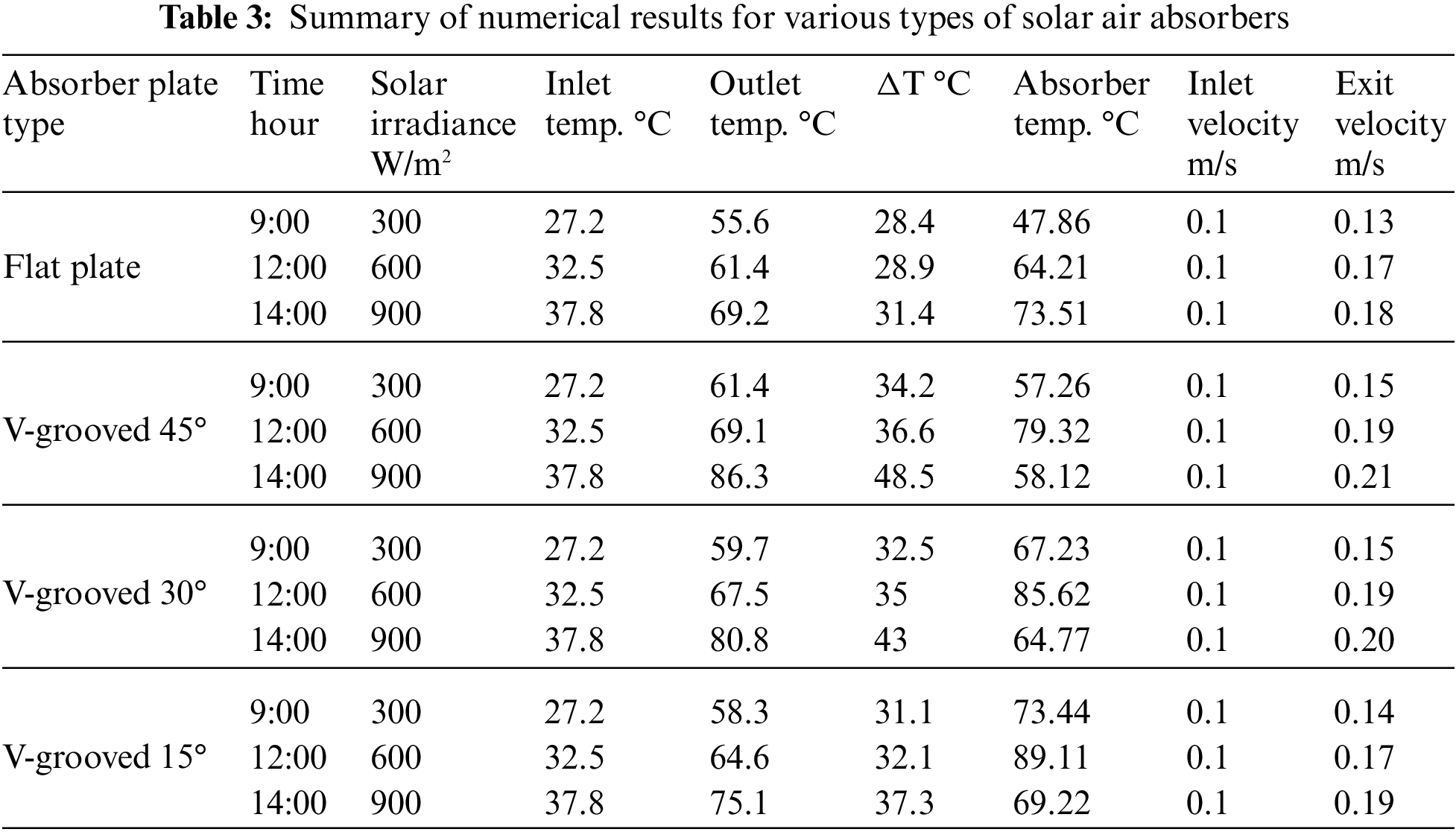
Fig. 3 illustrates the efficiency (η) at varied mass flow rates of 0.001, 0.002, 0.003, and 0.004 kg/s for different types of solar air heaters: flat plate, V-grooved 45°, V-grooved 30°, and V-grooved 15° absorbers. At a solar irradiance of 900 W/m² and with the time set at 16:00, it was observed that the efficiency of the V-grooved 45° corrugated absorber was higher than that of the flat plate, V-grooved 30°, and V-grooved 15° absorbers when considering the parallel flow direction, as indicated in Fig. 3. This difference in efficiency can be attributed to the fact that the air flowing completely around the V-grooved 45° absorber plate creates more turbulence, leading to an improved heat transfer coefficient.

Figure 3: The efficiency vs. mass flow rates at the time 16:00 with Solar irradiance 900 w/m2
Additionally, Fig. 4 demonstrates the impact of solar irradiance on the efficiency (η) of the various absorber types: flat plate, V-grooved 45°, V-grooved 30°, and V-grooved 15°. It was observed that the efficiency values increased with higher solar irradiance. Furthermore, the use of 45°, 30°, and V-grooved 15° absorbers resulted in efficiency improvements of approximately 20.8%, 26.3%, and 36.14%, respectively, compared to the flat plate absorber at a solar irradiance of 900 W/m². Fig. 5 illustrates the variation in energy gained with the hour of the day for the four different absorber plate types. The energy gained started at its lowest value at 09:00 and gradually increased until reaching its peak at 16:00. Moreover, it was demonstrated that the amount of energy gained is directly related to the mass flow rate. As the mass flow rate increased, the energy gained also increased. This is because a higher airflow rate leads to lower operating temperatures for the solar air heater. Among the four types of dual-flow solar air heaters, the V-grooved 45° absorber achieved the maximum energy gained at 16:00, with 210 W at a mass flow rate of 0.004 kg/s. In comparison, the energy gained for V-grooved 30°, V-grooved 15°, and flat plate absorbers at the same mass flow rate was 190, 170, and 140 W, respectively.
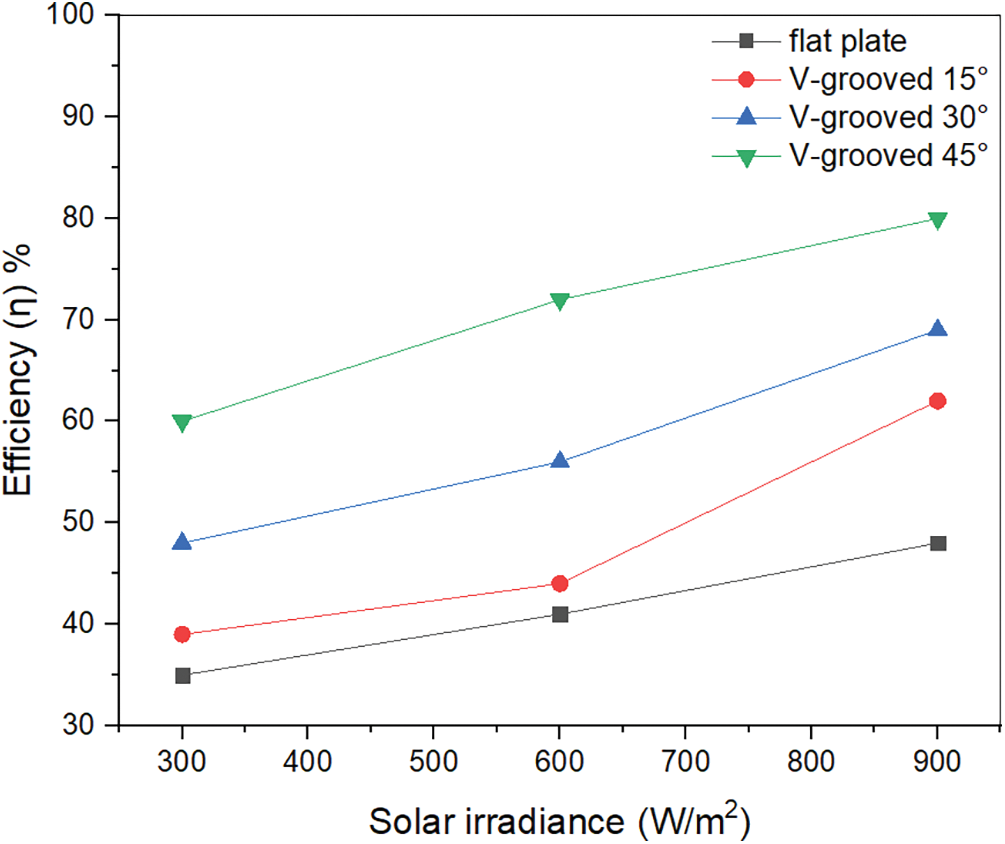
Figure 4: The efficiency vs. solar irradiance at the time 16:00 and mass flow rate 0.004 kg/s
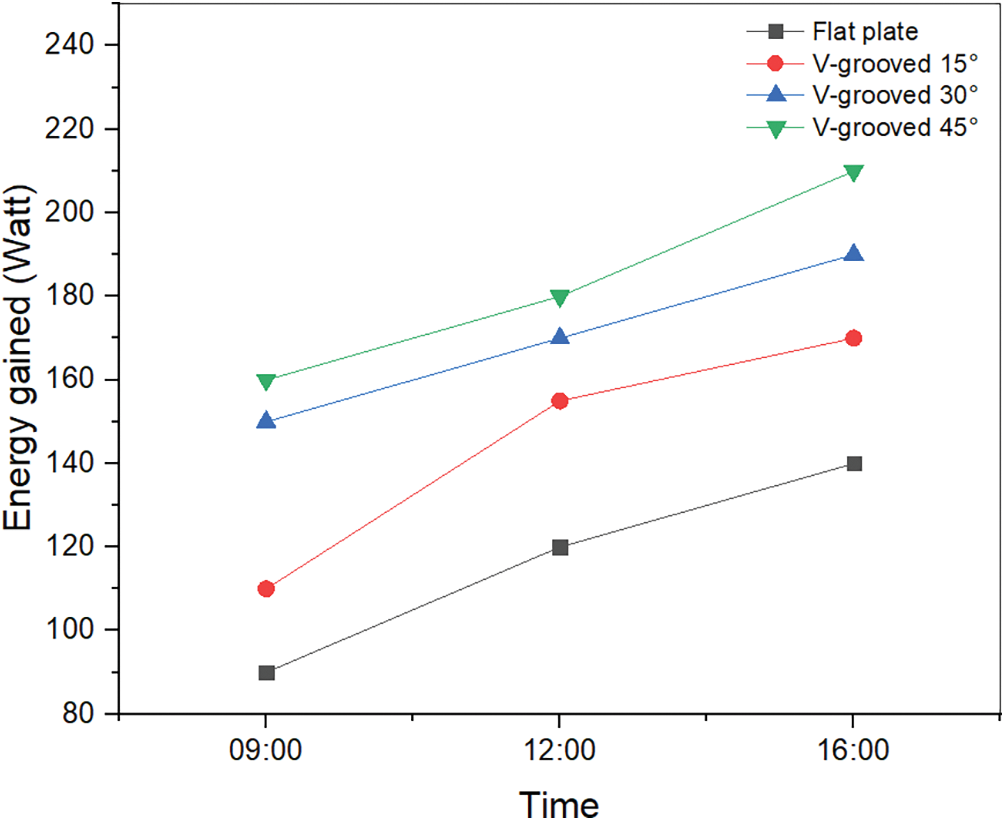
Figure 5: The energy gained vs. hour of day at four different absorber plate
The numerical Nusselt number calculated for all absorber plate types is presented in Fig. 6. It was found that using a V-grooved 45° plate absorber in the solar air heater enhanced the Nusselt number by 35.4% compared to the flat plate absorber under the same simulation conditions of 900 W/m². The V-grooved 30° plate absorber showed a 29.5% improvement, while the V-grooved 15° plate absorber exhibited a 23.2% improvement compared to the flat plate absorber.
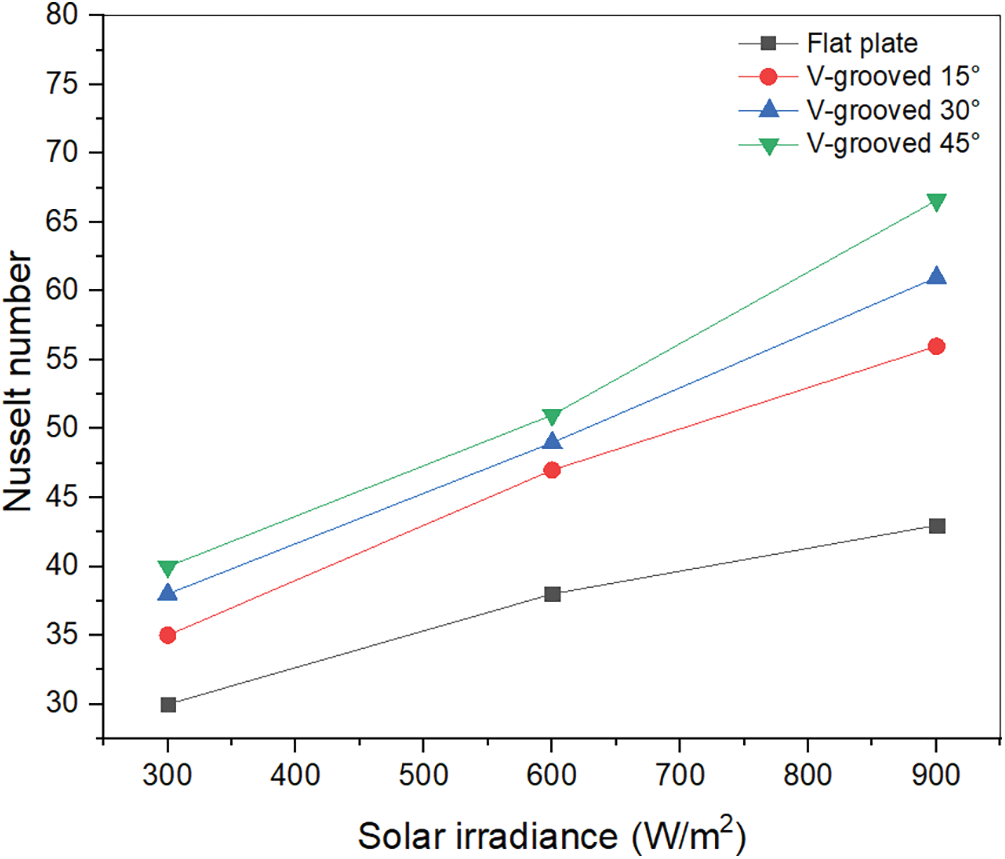
Figure 6: Variation of Nusselt number with solar radiation intensity
In the numerical study, a flat plate absorber was used in the dual-flow solar air heater at different times, as shown in Fig. 7. The results were presented in terms of pressure, temperature, and velocity. Fig. 6 displays the pressure contours in the flat plate dual-flow solar air heater at an air mass flow rate of 0.004 kg/s. The outcomes show that under the same circumstances, increasing the air mass flow rate causes a greater pressure drop. The top zone of the solar heater contains the highest pressure area. The data further demonstrated that while the maximum temperature increased as the day progressed, it reduced with increasing air mass flow rate. The top channel of the solar air heater was where the maximum velocity was found, and it rose together with the air mass flow rate and the lengthening of the day.


Figure 7: Pressure, temperature and velocity contours of flat absorber plate at the time 16:00 with Solar irradiance 900 W/m2
Fig. 8 presents the pressure distribution results, indicating that the utilization of a V-grooved 45° plate in a parallel direction to airflow increased the pressure from 0.15 to 9.8 Pa at the air flow rate of 0.004 kg/s and at 16:00. The maximum temperature decreased from 98.4°C to 46.5°C when utilizing the V-grooved 45° plate in parallel direction to airflow at an airflow rate of 0.004 kg/s and at 16:00. Additionally, the maximum velocity for the V-grooved 45° plate in parallel direction to airflow was found to be 3.38 m/s, compared to max. velocity of 0.47 m/s for the flat plate absorber at an airflow rate of 0.004 kg/s. This increase in velocity is a result of enhanced airflow momentum due to the utilization of the V-grooved 45° plate in parallel direction to airflow.


Figure 8: Pressure, temperature and velocity contours in the V-grooved 45° absorber plate at the time 16:00 with solar irradiance 900 W/m2
Finally, it was observed that the maximum absorber temperature was concentrated in the upper region of the V-grooved 45° plate in parallel direction to airflow. This increase in temperature can be attributed to the projection of solar radiation in these regions, as compared to the flat plate absorber. The thermal performance of the present dual-flow SAH at a mass flow rate (0.004 kg/s) was compared to previous studies by Hameed et al. [33]. Fig. 9 shows that the agreement with previous work is quite good.
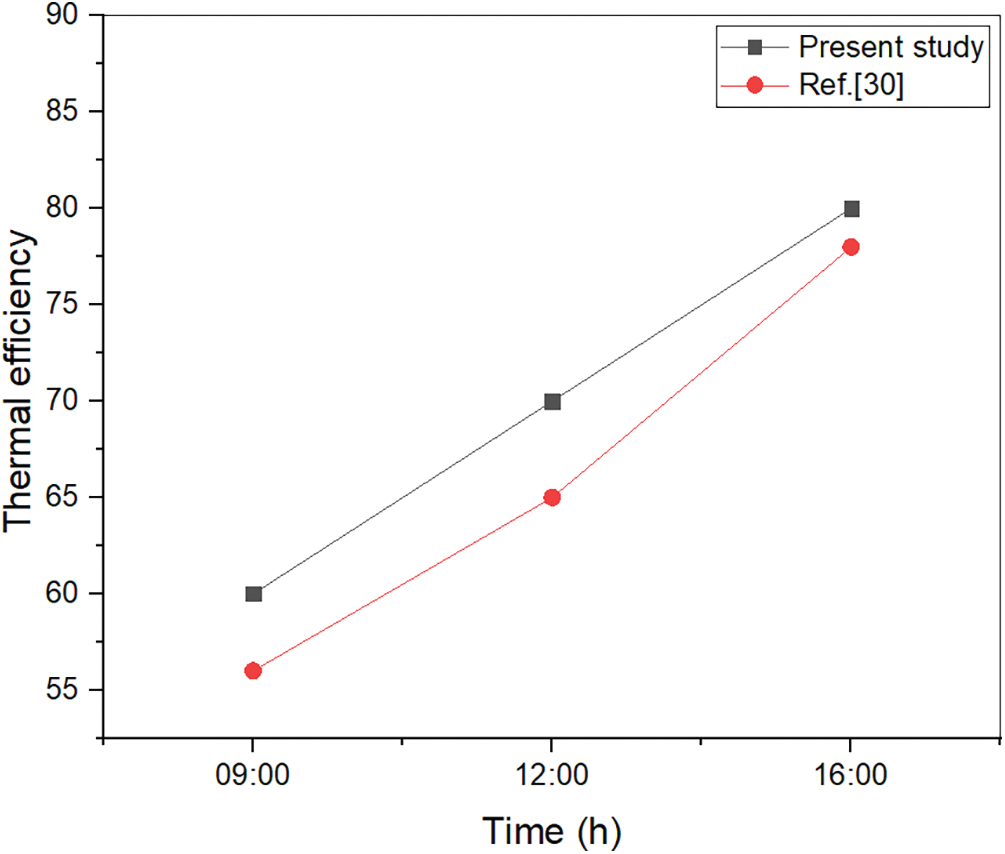
Figure 9: Validation of the thermal efficiency of the dual-flow SAH at a mass flow rate (0.004 kg/s)
The study of forced convection heat transfer inside the channel of the air solar heater with four types of the corrugated plate of air solar heater absorber was presented numerically.
1. The effect of four models of solar air absorbers was studied numerically: V-grooved 45°, V-grooved 30°, V-grooved 15°, and Flat plate absorbers.
2. The study investigated the impact of air mass flow rates ranging from 0.001 to 0.004 kg/s on thermal efficiency, absorber plate temperature, and outlet air temperature.
3. Results indicated that the V-grooved 45° corrugated absorber plate was more effective in enhancing heat transmission compared to the flat plate solar air heaters.
4. Increasing the mass flow rates of air improved the thermal performance of the absorber plates by generating more turbulence, thereby enhancing heat transfer.
5. When the solar irradiation is 900 W/m2 and the mass flow rate is 0.004 kg/s,, the average thermal efficiency of the dual-flow solar air heater increased by 20.8%, 26.3%, and 36.14% compared to the flat plate for the V-grooved 45°, V-grooved 30°, and V-grooved 15° models, respectively.
6. The V-grooved 45° corrugated absorber plate exhibited a 35.4% increase in Nusselt number compared to the flat plate absorber under the same simulation conditions of 900 W/m2.
7. The maximum energy gained per hour for the four studied models (V-grooved 45°, V-grooved 30°, V-grooved 15°, and flat plate) at a mass flow rate of 0.0046 kg/s and at 16:00 h were 210, 190, 170, and 140 W, respectively.
8. There is a direct relationship between mass flow rate and energy gained, meaning that increasing the mass flow rate leads to an increase in the amount of energy gained.
Acknowledgement: The researchers are very thankful of the cooperation provided by the Northern Technical University laboratories team during the execution of the study.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Abedalh; data collection: Mohammed; analysis and interpretation of results: Abedalh, Mohammed; draft manuscript preparation: Abedalh. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: In order to access the data used in the study, readers can contacting the corresponding author (ayad.selman@ntu.edu.iq).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kalogirou, S. A. (2004). Solar thermal collectors and applications. Progress in Energy and Combustion Science, 30(3), 231–295. [Google Scholar]
2. Abedalh, A. S., Yasin, N. J., Ameen, H. A. (2021). Thermal performance of HAVC system using heat pipe heat exchanger. Journal of Mechanical Engineering Research and Developments, 44(2), 336–344. [Google Scholar]
3. Shaalan, Z. A., Abedalh, A. S., Hamadalla, M. W. (2021). Heat pump performance enhancement by using a nanofluids (experimental study). Journal of Mechanical Engineering Research and Developments, 44(2), 1–9. [Google Scholar]
4. Gao, W., Lin, W., Lu, E. (2000). Numerical study on natural convection inside the channel between the flat-plate cover and sine-wave absorber of a cross-corrugated solar air heater. Energy Conversion and Management, 41(2), 145–151. [Google Scholar]
5. Liu, T., Lin, W., Gao, W., Xia, C. (2007). A comparative study of the thermal performances of cross-corrugated and v-groove solar air collectors. International Journal of Green Energy, 4(4), 427–451. [Google Scholar]
6. Fudholi, A., Sopian, K., Ruslan, M. H., Othman, M., Yahya, M. (2011). Thermal efficiency of double pass solar collector with longitudinal fins absorbers. American Journal of Applied Sciences, 8(3), 254–260. [Google Scholar]
7. Bhandari, D., Singh, D. S. (2012). Performance analysis of flat plate solar air collectors with and without fins. International Journal of Engineering Research & Technology, 1(6), 1–25. [Google Scholar]
8. Metwally, M. N., Abou-Ziyan, H. Z., El-Leathy, A. M. (1997). Performance of advanced corrugated-duct solar air collector compared with five conventional designs. Renewable Energy, 10(4), 519–537. [Google Scholar]
9. Hedayatizadeh, M., Sarhaddi, F., Safavinejad, A., Ranjbar, F., Chaji, H. (2016). Exergy loss-based efficiency optimization of a double-pass/glazed v-corrugated plate solar air heater. Energy, 94(8), 799–810. [Google Scholar]
10. Shalaby, S. M., Khalil, A., Kabeel, A. E., Zayed, M. E. (2018). Improvement of the thermal performance of the v-corrugated plate solar air heater with PCM by using insulated upper cover during night. IEEE International Conference on Smart Energy Grid Engineering (SEGE), pp. 346–350. New York, USA. [Google Scholar]
11. Fahmi M. S., Khalil W. H., Shareef A. J. (2020). Energy and exergy analysis of a finned-plate double pass solar air heater with different arrangement. Journal of Power and Energy Engineering, 8(10), 1–17. [Google Scholar]
12. Sudhakar, P., Cheralathan, M. (2021). Encapsulated PCM based double pass solar air heater: A comparative experimental study. Chemical Engineering Communications, 208(6), 788–800. [Google Scholar]
13. Hai, T., Mansir, I. B., Alshuraiaan, B., Abed, A. M., Ali, H. E. et al. (2023). Numerical investigation on the performance of a solar air heater using inclined impinging jets on absorber plate with parallel and crossing orientation of nozzles. Case Studies in Thermal Engineering, 45, 102913. [Google Scholar]
14. Hassan, H., Osman, O. O., Abdelmoez, M. N., Abo-Elfadl, S. (2023). Energy and exergy evaluation of new design nabla shaped tubular solar air heater (∇ TSAHExperimental investigation. Energy, 276, 127451. [Google Scholar]
15. Borah, P. P., Pathak, K. K., Gupta, A., Roy, S., Das, B. (2023). Experimental study of a solar air heater with modified absorber plate through square obstacles with threaded pin fins. Applied Thermal Engineering, 228(11), 120544. [Google Scholar]
16. Nishidh, N. B., Deepakkumar, R. (2023). Numerical investigation of suction and blowing effects on fluid flow and heat transfer characteristics of solar air heater. Materials Today Proceedings, 72(6), 2846–2853. [Google Scholar]
17. Abdallah, A. S., Yasin, N. J., Ameen, H. A. (2022). Thermal performance enhancement of heat pipe heat exchanger in the air-conditioning system by using nanofluid. Frontiers in Heat and Mass Transfer, 18(10), 1–7. [Google Scholar]
18. Govindaraj, N., Singh, A., Shukla, P. (2022). Fluid flow and heat transfer over a stretching sheet with temperature dependent prandtl number and viscosity. Frontiers in Heat and Mass Transfer, 15(1), 1–8. [Google Scholar]
19. Bejan, A., Kraus, A. D. (2003). Heat transfer handbook. New York: J. Wiley. [Google Scholar]
20. Gatski, T. B., Hussaini, M. Y., Lumley, J. L. (1996). Simulation and modeling of turbulent flows. USA: Oxford University Press. [Google Scholar]
21. Matsuno T., Lee J. S., Shimizu M., Kim S. H., Pang I. C. (2006). Measurements of the turbulent energy dissipation rate ɛ and an evaluation of the dispersion process of the Changjiang Diluted Water in the East China sea. Journal of Geophysical Research, 111(11), C11S09. [Google Scholar]
22. Ferrari, R., Wunsch, C. (2009). Ocean circulation kinetic energy: Reservoirs, sources, and sinks. Annual Review of Fluid Mechanics, 41(1), 253–282. [Google Scholar]
23.Yousef, B. A., Adam, N. M. (2008). Performance analysis for flat plate collector with and without porous media. Journal of Energy in Southern Africa, 19(4), 32–42. [Google Scholar]
24. Abdullah, A. S., Abou Al-sood, M. M., Omara, Z. M., Bek, M. A., Kabeel, A. E. (2018). Performance evaluation of a new counter flow double pass solar air heater with turbulators. Solar Energy, 173, 398–406. [Google Scholar]
25. Alaskari, M., Rasham, A. (2018). Thermal analysis of double-pass solar air collector with different materials of absorber plate and different dimensions of air channels. International Journal of Science and Research, 6, 901–908. [Google Scholar]
26. Pérez, Á. D. D., Romero, R. R., Durán, E. D., Montaño, P. R., Bernal, R. A. et al. (2011). The mastoid osteoma, an incidental feature? Acta Otorrinolaringologica (English Edition), 62(2), 140–143. [Google Scholar]
27. Abedalh, A. S., Shaalan, Z. A., Saleh Yassien, H. N. (2021). Mixed convective of hybrid nanofluids flow in a backward-facing step. Case Studies in Thermal Engineering, 25(6), 100868. [Google Scholar]
28. Kumar, A., Sreenivaslu, G., Rao, P. S. R., Vinod, K. D. T., Pattanaik, A. (2019). Experimental investigation on performance of solar air heaters with thermal storage. International Journal of Renewable Energy and its Commercialization, 5(1), 37–46. [Google Scholar]
29. Kumar, N., Tyagi, A., Yadav, T., Prakash, O., Singh, V. et al. (2019). Heat transfer analysis of flat plate air collector. IOP Conference Series: Materials Science and Engineering, 691(1), 012075. [Google Scholar]
30. Alam, T., Kim, M. H. (2016). Numerical study on thermal hydraulic performance improvement in solar air heater duct with semi ellipse shaped obstacles. Energy, 112, 588–598. [Google Scholar]
31. Gilani, S. E., Al-Kayiem, H. H., Woldemicheal, D. E., Gilani, S. I. (2017). Performance enhancement of free convective solar air heater by pin protrusions on the absorber. Solar Energy, 151(7), 173–185. [Google Scholar]
32. Dissa, A. O., Ouoba, S., Bathiebo, D., Koulidiati, J. (2016). A study of a solar air collector with a mixed ‘porous’ and ‘non-porous’ composite absorber. Solar Energy, 129(5), 156–174. [Google Scholar]
33. Hameed, H., Azeez, H., Saeed, M. (2021). Performance of a new model of air heating system: Experimental investigation. Journal of Mechanical Engineering Research and Developments, 44(5), 420–432. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools