 Open Access
Open Access
REVIEW
Use of Statistical Tools for Comparison between Different Analytical and Semi-Empirical Models of the Bleve Fireball
1 Materials, Energy, Acoustics Team (MEAT), High School of Technology-Salé, Mohammed V University in Rabat,
Rabat, 10051, Morocco
2 Forensic Institute of the Royal Gendarmerie, Rabat, Morocco
3 Department of Mathematics, Faculty of Sciences, Ibn Tofail University, Kenitra City, Morocco
* Corresponding Authors: Abderraouf Guelzim. Email: ; Anas Mbarki. Email:
,
Frontiers in Heat and Mass Transfer 2023, 21, 125-140. https://doi.org/10.32604/fhmt.2023.041832
Received 08 May 2023; Accepted 12 July 2023; Issue published 30 November 2023
Abstract
The Bleve is an explosion involving both the rapid vaporization of liquid and the rapid expansion of vapor in a vessel. The loss of containment results in a large fireball if the stored chemical is flammable. In order to predict the damage generated by a Bleve, several authors propose analytical or semi-empirical correlations, which consist in predicting the diameter and the lifetime of the fireballs according to the quantity of fuel. These models are based on previous experience, which makes their validity arbitrary in relation to the initial conditions and the nature of the product concerned. The article delves into uncertainty analysis associated with analytical and semi-empirical models of the BLEVE fireball. It could explore how uncertainties in input data, and the choice of a more or less inappropriate model, propagate into the model results. Statistical techniques such as global sensitivity analysis or uncertainty analysis are employed to quantify these uncertainties. In this paper, an attempt is made to evaluate and select reasonable models available in the literature for characterizing fireballs and their consequences. Correlations were analyzed using statistical methods and BLEVE data (experimental and estimated data by correlation) to determine the residual sum of squares (RSS) and average absolute deviation (AAD). Analysis revealed that the Center for Chemical Process Safety (CCPS), the TNO (Netherlands Organization for Applied Scientific Research), and the Gayle model revealed a high degree of satisfaction between the experimental and estimated data through correlation.Graphic Abstract
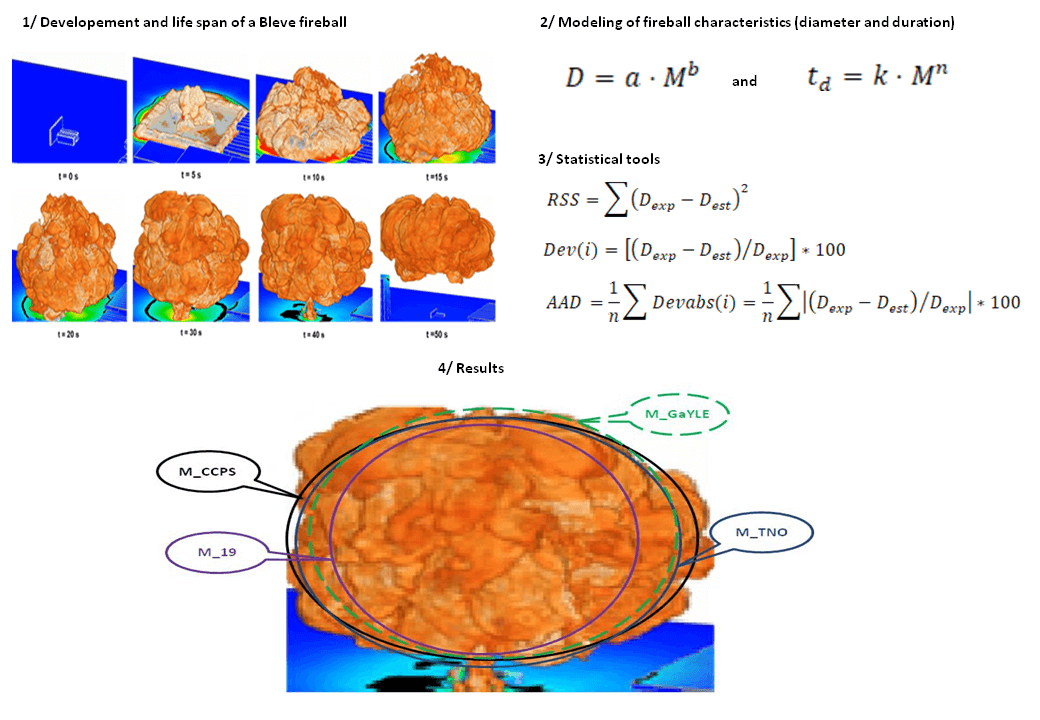
Keywords
Nomenclature
| C | Heat capacity (J/m3·K) |
| cp | Specific heat (J/kg·K) |
| h | Latent heat of phase change (J/kg) |
| k | Thermal conductivity (W/m·K) |
| M | Molar mass (kg/kmol) |
| q″ | Heat flux (W/m2) |
| R | Reflectivity |
| Rg | Specific gas constant (J/kg·K) |
| t | Time (s) |
| T | Temperature (K) |
| u | Interfacial velocity (m/s) |
| x | Coordinate (m) |
| ε | Total emissivity |
| ρ | Density (kg/m3) |
| σ | Stefan–Boltzmann constant (W/m2·K4) |
Industrial facilities involving chemical products or processes are subject to significant accident risks. A boiling expanding liquid explosion (BLEVE) is one of the most catastrophic accidents that can occur on a storage site for flammable products or superheated liquefied gas under pressure following the total or partial loss (complete burst or crack) of the containment.
To predict the thermal and mechanical consequences as well as the concentrations of gases or vapors generated by a BLEVE, and therefore to provide the most suitable operational response, several authors have proposed analytical or semi-empirical correlations for the determination of the diameter and the lifetime of the fireballs as a function of the mass of fuel [1–3].
Among the authors who have tried to solve the problem of choosing the appropriate model [4–7], we find K. Satyanarayana, who conducted a statistical study to compare 16 different correlations between fireball diameter and duration. The comparison of fireball characteristics according to their modes of generation by Dorofeev et al. [3], as well as the proposal of appropriate models for certain types of fuels. Abbasi and Abbasi who have made a synthesis of the mechanism, causes, consequences and modelling, empirical and analytical correlations of estimation of diameter D and duration t of the fireball.
This article attempts to evaluate and select reasonable models available in the literature to characterize fireballs and their consequences. Correlations were analysed using statistical methods and BLEVE data (experimental and correlation-estimated data) to determine the residual sum of squares (RSS) and mean absolute deviation (AAD).
A literature review was carried out in the field of prevention and modeling of risks, generated by the thermal effects of Bleve fireballs, using search motors such as Google Scholar and scientific databases such as Wiley, IEEE Xplore, Scopus and Web of Science, setting the chronological search interval between 1980 and 2023. The search string included terms such as “Bleve thermal effect”, “Bleve fireball” and “radiative heat flux”. As a result of this first search, 45 full-text articles in English were found. Then, a snowball sampling was applied to the references of these articles. And 125 new full text articles in English were found.
The final selection of articles was made on the basis of the authors’ choices of inclusion by unanimity, according to the following criteria: modeling of the fireball, modeling of the radiative flux, dimensional and temporal characteristics of the fireball, consequences of the total loss of a hydrocarbon storage tank, identification and classification of the models used for the characterization of the fireball (analytical model, semi-empirical correlation, …) and the results of the experimental campaigns carried out for the understanding of the phenomenon. Prismatic diagram of Fig. 1.

Figure 1: Literature review Prisma flowchart
The analysis of the 45 documents constituting the literature review allowed us to group together the different analytical and semi-empirical models that exist.
This part will be divided into two parts (modeling the Bleve fireball and the synthesis of the different models characterizing the fireball), in order to simplify the presentation of the results obtained.
3.1 Modeling the BLEVE Fireball
The origin of the fireball formation starts with the release of the flammable vapor from the storage tank when it breaks. The volume of the ignited combustible vapor increases and expands, due to the turbulence and entrainment of the ambient air inside the cloud, creating a combustible mixture (fuel-air) and producing a wake [8–11]. The size and duration of the fireball depends on the mass of fuel consumed inside the fireball. The quasi-instantaneous nature of the phenomenon leaves us with two assumptions:
• The amount of mass ejected upon rupture of the storage tank is the total flammable content in the tank prior to rupture;
• At the moment of rupture and due to the temperature of the boiling liquid, a portion of the fuel ignites immediately (isentropic ignition fraction), while the other portion will form fine droplets which will vaporize as they fall;
• During the formation phase some of the steam dissipates and forms a puddle on the ground, which will burn like a pool fire.
In the case of the BLEVE the total mass contained in the storage tank is consumed in the fireball. Then, the fireball will quickly reach its maximum diameter by rising from the ground level, until reaching the maximum height and then extinguish [3].
Regarding the prediction of the radiation intensity of a Bleve fireball, it lies in the modeling and determination of the following factors [12]:
• The duration of the fireball;
• The diameter of the fireball;
• The surface emissive power of the fireball;
• The geometric view factor;
• The atmospheric transmittance.
The fireball’s characteristics modeling can be conducted from two perspectives, static or dynamic.
The fireball behaves as a static event and does not take into consideration the time evolution, time being expressed by a function of the gas mass. The fireball is characterized by a constant size, by a radiant heat emission at a constant rate, and it is located at a fixed position with respect to the ground level [13–17].
The characteristics of the fireball (diameter, elevation, duration and radiation) are a function of the fuel mass M and can be written as follows [2,3,18–20]:
• Fireball Shape
The models treat the fireball as a sphere for most of its life.
• Fireball Diameter
The fireball momentarily reaches its most extreme diameter and retains that same measurement throughout its life. The diameter of the fireball is calculated using an equation of the following form, which relates the mass of fuel in the fireball to the maximum diameter [14,15,21–24].
• Fireball Duration
Fireball duration correlates the duration or life of the fireball with the mass of fuel used in the fireball [14,15,21–24].
• Surface Emissive Power
The formulas used to calculate surface emissivity (SEP) typically relate the pressure in the vessel at the time it bursts (its rupture) to SEP. The following equation is proposed by Roberts [25] to predict the fraction of the total accessible thermal energy radiated by the fireball.
Once you have calculated the fraction of radiated heat, you can move on to the next step. The surface emissivity of a fireball is calculated using the following formula [14,21,23,26]:
where Hc is the heat of combustion of the fuel in kJ/kg,
M · Hc is the total amount of heat energy available, kJ,
π · D² is the surface area of the spherical fireball, m².
A direct relationship between surface emissivity and storage tank burst pressure is valid for burst pressures that do not exceed 2 MPa (~300 psi) [14].
• The thermal flux
The heat flux intensity (Ith) received by a target is given by the following equation [21,27,28]:
• The thermal dose
The thermal dose is the exposure to thermal radiation during a certain period of time that coincides with the lifetime of the fireball or a fraction of that time. It depends on two variables, the intensity of the heat flux received and the duration of exposure [15,29]. The thermal dose is expressed as follows:
where teff is the persons exposure time to heat flux.
Dynamic modeling uses the same formulations as static models, but taking into account the temporal evolution (time factor), based on a comparison with experimental results. Two dynamic models are used (Martinsen & Marx et Roberts) [30,31]. These models assume that the fireball reaches its maximum diameter at the end of the first third of its duration, and then remains constant until its extinction [32].
• Fireball Duration
The burning time of the fireball is given by the following equation [33]:
• Fireball Diameter and Location
During the early stages of a fireball’s life, the dynamic model treats it as a sphere whose diameter increases with time while remaining tangent to the slope.
During the first third of the fireball’s lifetime, the diameter of the fireball tends to reach its maximum. It is at this point that the fireball rises into the air and maintains its diameter until it disappears [29,34]. The formulation of the diameter of a fireball is given by the following system:
where D(t) is in m, M is in kg, and t is in sec.
The height of the center of the fireball also depends on the time factor. The center of the fireball rises at a steady rate from its take-off position to three times that position [24], during the last two thirds of the fireball duration [29]. The formulation of the height of the center of the fireball is given by the following system:
• Surface Emissive Power
The thermal radiation emitted from the surface of the fireball is time dependent. The flux emitted at the surface of the fireball is considered to be constant during the growth period, and then is assumed to decrease linearly from its maximum value to zero during the last two thirds of the fireball duration. The following system gives the formulation of the emissivity of the surface [15,32]:
The radiant heat fraction (fh) is calculated as follows [25]:
• The thermal flux
The intensity of the thermal flux (Ith) received by a target is given by the following equation [35]:
• The thermal dose
The physical injuries caused by a fireball BLEVE are determined by the thermal dose (Idose), which is the integral of the intensity of the heat flow during the duration of the fireball:
3.2 Synthesis of the Different Models Characterizing the Fireball
Experiments have been conducted and analyzed over the years to arrive at empirical and semi-analytical relationships of fireball size and duration as a function of fuel weight consumed (Eqs. (1) and (2)). These models are exponential relationships based on the flammable mass consumed.
To analyze and compare them, we use the statistical tool. Based on the following measurements, the calculation of the sum of squares of the residuals (SSR), the deviation Dev(i), the absolute deviation Devabs(i), the percentage of the average of the absolute deviation (AAD), which indicates how close the calculated values are to the experimental values, and the (Bias) indicates the distribution of the experimental values on either side of the calculated values [22], which we translate into the following formulas:
where Dexp is the diameter measured during an experiment or accident; and Dest is the diameter estimated by the listed estimation models.
The different models identified in our study are summarized in Table 1.
The model that gives the lowest sum of squares of the residuals between experimental and estimated values (RSS), the lowest mean of the absolute deviation and the lowest bias is the most representative model.
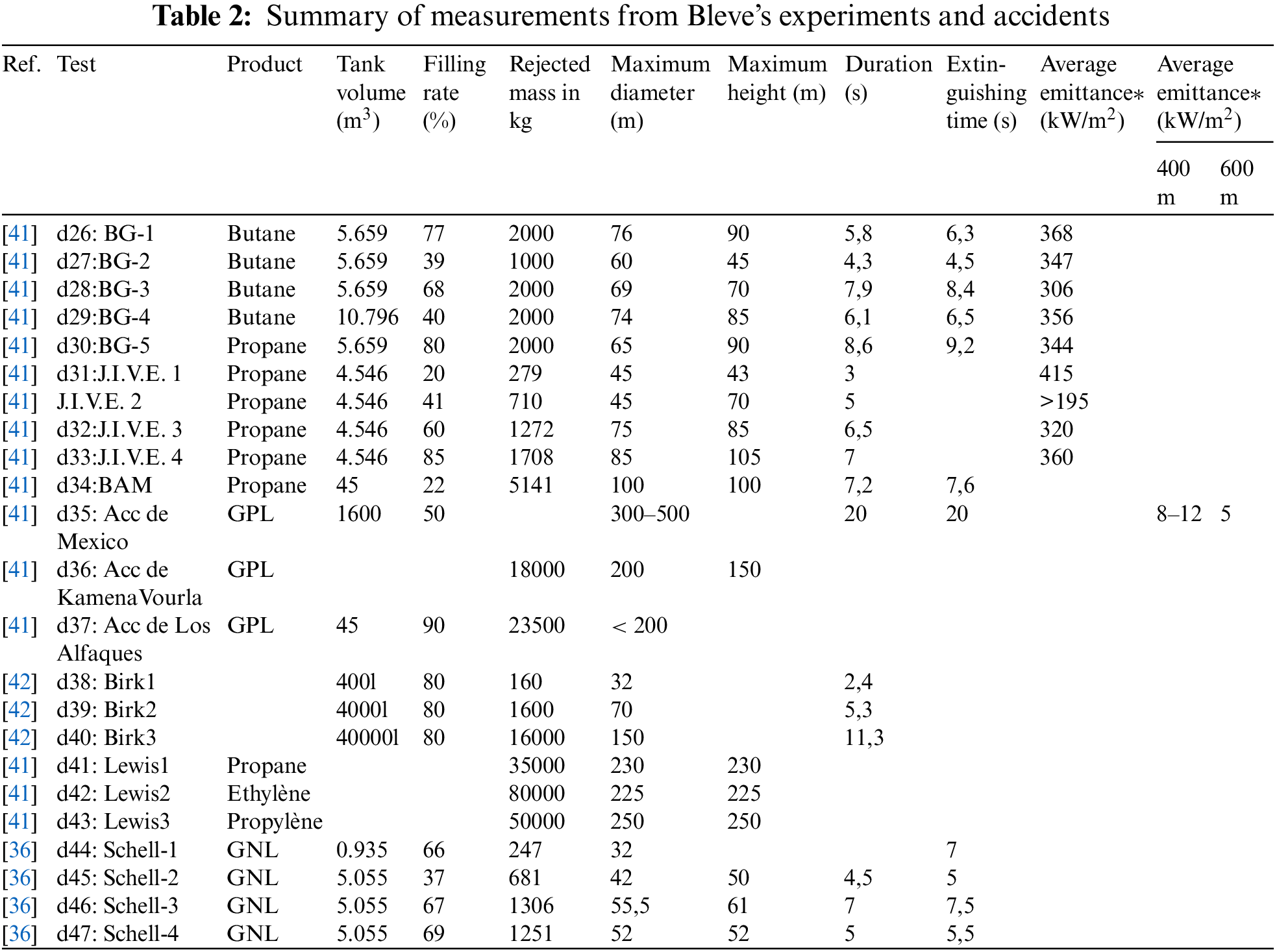
In the same way, the results of the different experiments carried out have been grouped together as well as the conclusions of some accidents that have already occurred in Table 2.
The number of models that we have listed since our literature review amounts to 31 static models and one dynamic model.
A double reading of the results grouped in Table 3, informs us on the following comparison conclusion:
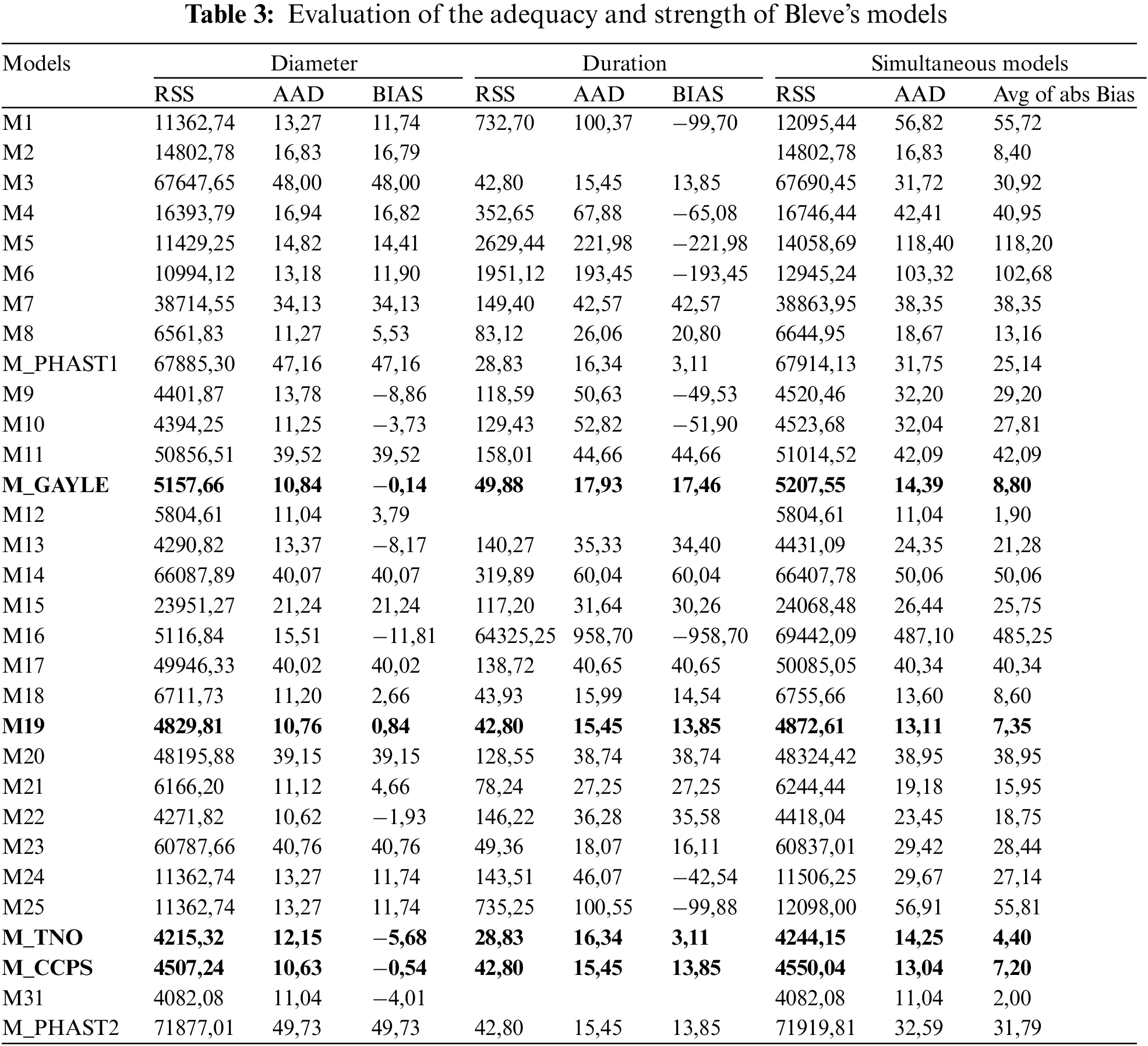
1/ If we classify the models of the fireball diameters, according to the values of the lowest RSS, AAD and the Biais of distribution indices, we find that the ranking of strength and adequacy between estimated model and measured values is as follows: models M22, M_CCPS, M19, M_GAYLE, M31, M10, M_TNO, M13, M9 and M16 show the lowest values respectively and their scores are of the same magnitudes, so they can be described as very strong models.
2/ Models M_CCPS, M19, M3, M_PHAST2, M18, M_TNO, M_PHAST1, M_GAYLE, M23, and M21, respectively, showed the lowest RSS, AAD and the Biais of distribution indices, and ranked as the best estimates of Bleve duration.
3/ If we filter the RSS, AAD and Bias of distribution indices values for diameter and duration simultaneously for each model, we manage to include the M_CCPS, M19, M_TNO and M_GAYLE models. The M_CCPS model gives a satisfactory agreement between the predicted and reported data of the fireball diameter and Bleve duration, compared to the other models. The M19 model proposed by Lihou and Maund, the M_TNO model and the M_Galye model are as good as the M_CCPS model, and can be selected for the prediction and estimation of the maximum diameter and duration of Bleve.
4/ The Martinsen and Marx model is a dynamic model that takes into account the dynamic evolution of the fireball over time, as well as the different phases through which the fireball passes. This model at the end of the expansion phase coincides with the values proposed by the CCPS model, which gives it a great ability to predict the maximum values of diameter and duration.
The results of the calculation of RSS and AAD indices are shown in Table 3.
To demonstrate the validity of the empirical and analytical equations modeling the defining characteristics of the thermal effects of the fireball, we have drawn a cluster of fireball diameters (Fig. 2) using the 31 statistical models already listed in Table 1, and comparing them to the experimental measurements in Table 3. It can be seen that as the mass of fuel involved increases, the diameter of the fireball grows exponentially for the entire cluster.

Figure 2: Beam of fireball diameter as function of the fuel weight
The values of the measurements of the maximum diameters of the fireballs taken during the different experiments listed in Table 2, coincide with the graphs of the four models (M_CCPS, M19, M_TNO and M_GAYLE) that we found the most suitable for the estimation of the dimensions of the fireball through the calculation of the residues’ squares sums, the average of the absolute deviation and the bias of distribution.
Similarly, a graphical representation of the Bleve duration beam was plotted in Fig. 3, calculated on the basis of the statistical models in Table 1, and by comparing the experimental measurements in Table 2. The Bleve duration varies positively with the mass of the fuel involved, the more the mass increases, the more the Bleve duration extends for the whole beam. In addition, the experimental measurements coincide with the graphs of the four models (M_CCPS, M19, M_TNO and M_GAYLE) that we found best suited for estimating the dimensions of the fireball.

Figure 3: Beam of fireball duration as function of the fuel weight
This study was conducted to identify the theory of modeling the thermal effects of the Bleve fireball, to explore the possibilities of understanding and predicting its effects. The literature suggests a large number of static and dynamic semi-analytical correlation models and relationships that provide a wide choice for users. The formulation of this large number of relationships is due to the number of experiments performed on different types of fuels and products (LPG, LNG, Diesel, Flammable liquid, Hydrocarbons, 1,1 difluoroethane, propane, propylene, butane, rocket fuel, …).
Nevertheless, many authors have opted for the use of some models more than others, namely the Gayle, CCPS (Center for Chemical Process Safety of the American Institute of Chemical Engineers) and TNO (The Netherlands Organization of Applied Scientific Research) models which give very satisfactory prediction and estimation results [22], as well as a great adequacy and explanation of the experimental measurement results [22]. However, the thermodynamic nature and the physico-chemical properties of the studied product play a major role in the choice of the appropriate model as for LNG, Diesel and DBTP [1,8,23,36,43].
Through this literature review, which defines the state of the art and the progress of scientific research in this field, the following deductions and conclusions have been obtained:
1. The heat released by the fireball is characterized by the emission of an intense thermal flux [21];
2. The empirical correlation gives a constant estimate of the heat flux over time, which is not representative of the evolution of the fireball [21];
3. The radiation model of the “solid flame”, the fire is idealized as a simple geometric shape (cylinder, cone, sphere, …) emitting thermal radiation from its sides [32,44];
4. The solid flame model requires the estimation of the diameter and height of the geometric shape, as well as the emissive power by its surface [32,44];
5. The influence of the weight of the liquid contained in the storage tank at the time of its release and the burst pressure, on the diameter, duration and intensity of the thermal radiation of the BLEVE fireball [26,45];
6. The evolution of the thermal dose is proportional to the evolution of the quantity of fuel and the burst pressure [26,45];
7. The intensity of the radiative flux is significantly reduced with increasing distance from the center of the fireball [26,45];
8. Selecting the appropriate model for each fuel type improves simulation predictions [36];
9. Existing models are only valid for a single BLEVE and fireball event scenario. Therefore, characterization of multiple BLEVEs and fireballs requires appropriate estimation of an equivalent mass that actually contributes to the overall hazard;
10. The modeling strategy of the radiative effects allowed to evaluate the possible damages during a Bleve phenomenon, to anticipate the minimization and the damping of the consequences and the establishment of industrial safety;
11. The evacuation of individuals is influenced by the short duration of the fireball, its ascent and the formation of updrafts, which creates a powerful airflow in a horizontal direction from the outside to the inside.
This paper presents a systematic review of the methods used in the literature for modeling the radiative flux, the characteristics and dimensions of the fireball generated during a Bleve phenomenon. Analytical methods that are based on suggested semi-analytical and empirical correlations have shown their usefulness in prediction and estimation, thus the adequacy of the models with the experimental data could be determined. Among the mathematical models, the CCPS, M19 (Lihou and Maund), TNO and Gayle models are the best to use.
Regarding diameter modeling, the RSS shows that the best-fitting model is the TNO model with an RSS equal to 4215 and an AAD of 12%, followed by the CCPS, M19 and Gayle models with values of 4507, 4829 and 5017 for the RSS and 10.6%, 10.7% and 10.8% for the AAD, respectively. Similarly, for the modeling of Bleve lifespan, the best-fitting model is the TNO model with an RSS equal to 28.8 and an AAD of 16.3%, followed by the CCPS, M19 and Gayle models with values of 42.8, 42.8 and 49.8 for the RSS and 15.45%, 15.45% and 17.9% for the AAD, respectively. The combination of the two models' parameters respects the same order of relevance.
Clearly, the importance of this work comes from its ability to select the most effective models, which combines simplicity and precision, since it brings together all existing models and confronts them with a large number of empirical results from experimental campaigns and reports of accidents that have already occurred. Compared with a similar study in 1991, which compared 11 models with data from a single experiment.
The studied models are based on two perceptions: source point and solid flame. However, they do not take into consideration the real shape of the fireball which does not have an ideal geometrical form, but rather, similar to a mushroom (superposition of a sphere and a cylinder). At the same time, they fail to take into account the time factor, which is the main determinant of the evolution of the geometric shape of the cloud of flaming vapor, through the phases it goes through during its existence.
It is imperative to point out that this work being one of the first steps of a larger project, several future perspectives are possible:
(i) This work is the first step of a project aiming at improving the existing models;
(ii) The analysis of existing models will allow us to develop basic techniques and tools for the determination of effect distances and lethality, which will be characterized by ease of use and the replacement of calculation and estimation models by graphic abacuses;
(iii) The realization of a new dynamic modeling approach, which will focus on the true shape of the fireball.
Acknowledgement: None.
Funding Statement: This work was not supported by any organism or institute.
Author Contributions: All the authors contributed equally to the study and analysis carried out in this article, they also contributed to the French writing of the article and the validation of its content. The first author of the article also contributed to the translation of the article into English.
Availability of Data and Materials: All data, equation and formula used in this article are available from the public data repository at web site in reference.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Blankenhagel, P., Wehrstedt, K. D., Mishra, K. B., Steinbach, J. (2017). Fireballs as a possible hazard scenario of organic peroxides in steel drums. Conference: 5 Magdeburger Brand-und Explosionsschutztage, Magdeburg, Germany. [Google Scholar]
2. Mishra, K. B., Wehrstedt, K. D., Krebs, H. (2015). Boiling liquid expanding vapour explosion (BLEVE) of peroxy-fuels: Experiments and computational fluid dynamics (CFD) simulation. Energy Procedia, 66, 149–152. https://doi.org/10.1016/J.EGYPRO.2015.02.082 [Google Scholar] [CrossRef]
3. Dorofeev, S. B., Sidorov, V. P., Efimenko, A. A., Kochurko, M. S., Kuznetsov, B. B. et al. (1995). Fireballs from deflagration and detonation of heterogeneous fuel-rich clouds. Fire Safety Journal, 25(4), 323–336. https://doi.org/10.1016/0379-7112(96)00008-2 [Google Scholar] [CrossRef]
4. Prugh, R. W. (1994). Quantitative evaluation of fireball hazards. Process Safety Progress, 13(2), 83–91. https://doi.org/10.1002/PRS.680130211 [Google Scholar] [CrossRef]
5. Makhviladze, G., Roberts, J., Yakush, S. (2000). Modelling and scaling of fireballs from single- and two-phase hydrocarbon releases. Fire Safety Science, 6, 1125–1136. https://doi.org/10.3801/IAFSS.FSS.6-1125 [Google Scholar] [CrossRef]
6. Roberts, T., Gosse, A., Hawksworth, S. (2000). Thermal radiation from fireballs on failure of liquefied petroleum gas storage vessels. Process Safety and Environmental Protection, 78(3), 184–192. https://doi.org/10.1205/095758200530628 [Google Scholar] [CrossRef]
7. Center for Chemical Process Safety (2010). Guidelines for vapor cloud explosion, pressure vessel burst, BLEVE, and flash fire hazards, 2nd edition. The American Institute of Chemical Engineers. [Google Scholar]
8. Mbarki, A., Ettahir, A., Guelzim, A. (2022). Determination of the thermal lethality distances generated by the radiative flux emitted by the Di-Tert-Butyl Peroxide (DTBP, C8H18O2) Fireball: Use of characteristic curves. IOP Conference Series: Earth and Environmental Science, 1050(1), 012018. https://doi.org/10.1088/1755-1315/1050/1/012018 [Google Scholar] [CrossRef]
9. Mbarki, A., Ettahir, A., Guelzim, A. (2022). Delineation of the thermal effect zones generated by the radiation emitted by the fireball of an LPG BLEVE, using the characteristic curves of Lee’s Poinpt source model. International Review of Mechanical Engineering, 16(5), 222–229. https://doi.org/10.15866/ireme.v16i5.21945 [Google Scholar] [CrossRef]
10. Vukelic, G., Vizentin, G., Bozic, Z., Rukavina, L. (2021). Failure analysis of a ruptured compressor pressure vessel. Procedia Structural Integrity, 31(8), 28–32. https://doi.org/10.1016/j.prostr.2021.03.006 [Google Scholar] [CrossRef]
11. Chae, C. K., Lee, J. H., Chae, S. B., Kim, Y. G., Han, S. T. (2020). Development of a tool for predicting the occurrence time of BLEVE in sSmall LPG storage tanks. Journal of the Korean Society of Safety, 35(4), 74–83. https://doi.org/10.14346/JKOSOS.2020.35.4.74 [Google Scholar] [CrossRef]
12. Sauerwein, B. (2019). Simplified estimations of the heat radiation and blast effects of selected hazardous events (Master Thesis). Montanuniversitaet Leoben. [Google Scholar]
13. Dhurandher, B. K., Kumar, R., Dhiman, A. (2015). Impact assessment of thermal radiation hazard from LPG fireball. Procedia Earth and Planetary Science, 11, 499–506. https://doi.org/10.1016/J.PROEPS.2015.06.050 [Google Scholar] [CrossRef]
14. Planas, E., Casal, J. (2016). 21 BLEVE-Fireball. In: Handbook of combustion. New Jersey: John Wiley and Sons. https://doi.org/10.1002/9783527628148.HOC093 [Google Scholar] [CrossRef]
15. Papazoglou, I. A., Aneziris, O. N. (1999). Uncertainty quantification in the health consequences of the boiling liquid expanding vapour explosion phenomenon. Journal of Hazardous Materials, 67(3), 217–235. https://doi.org/10.1016/S0304-3894(99)00041-2 [Google Scholar] [PubMed] [CrossRef]
16. Wang, Y., Gu, X., Xia, L., Pan, Y., Ni, Y. et al. (2020). Hazard analysis on LPG fireball of road tanker BLEVE based on CFD simulation. Journal of Loss Prevention in the Process Industries, 68(3), 104319. https://doi.org/10.1016/j.jlp.2020.104319 [Google Scholar] [CrossRef]
17. Shafiq, U., Shariff, A. M., Babar, M., Babar, A., Abulhassan, A. et al. (2020). A review on modeling and simulation of blowdown from pressurized vessels and pipelines. Process Safety and Environmental Protection, 133, 104–123. https://doi.org/10.1016/j.psep.2019.10.035 [Google Scholar] [CrossRef]
18. Cabeza-Lainez, J. M., Salguero-Andújar, F., Rodríguez-Cunill, I. (2022). Prevention of hazards induced by a radiation fireball through computational geometry and parametric design. Mathematics, 10(3), 387. https://doi.org/10.3390/math10030387 [Google Scholar] [CrossRef]
19. Shelke, A. V., Wen, J. X. (2021). The burning characteristics and flame evolution of hydrocarbon and hydrogen flash fires. Proceedings of the Combustion Institute, 38(3), 4699–4708. https://doi.org/10.1016/j.proci.2020.05.013 [Google Scholar] [CrossRef]
20. Biswas, S. K., Mathur, U., Hazra, S. K. (2021). Fundamentals of process safety engineering, 1st edition. Boca Raton: CRC Press. https://doi.org/10.1201/9781003107873 [Google Scholar] [CrossRef]
21. Sellami, I., Manescau, B., Chetehouna, K., de Izarra, C., Nait-Said, R. et al. (2018). BLEVE fireball modeling using fire dynamics simulator (FDS) in an Algerian gas industry. Journal of Loss Prevention in the Process Industries, 54, 69–84. https://doi.org/10.1016/J.JLP.2018.02.010 [Google Scholar] [CrossRef]
22. Satyanarayana, K., Borah, M., Rao, P. G. (1991). Prediction of thermal hazards from fireballs. Journal of Loss Prevention in the Process Industries, 4(5), 344–347. https://doi.org/10.1016/0950-4230(91)80048-Y [Google Scholar] [CrossRef]
23. Blankenhagel, P., Wehrstedt, K. D., Xu, S., Bhushan, K. M., Steinbach, J. (2017). A new model for organic peroxide fireballs. Journal of Loss Prevention in the Process Industries, 50(3), 237–242. https://doi.org/10.1016/J.JLP.2017.10.002 [Google Scholar] [CrossRef]
24. Chen, M., Li, H., Li, P., Ouyang, D., Weng, J. et al. (2020). Fireball modeling and thermal hazards analysis of leaked 1,1-difluoroethane in fluorine chemical industry based on FDS. Journal of Thermal Analysis and Calorimetry, 146(1), 355–366. https://doi.org/10.1007/S10973-020-09951-X [Google Scholar] [CrossRef]
25. Roberts, A. F. (1981). Thermal radiation hazards from releases of LPG from pressurised storage. Fire Safety Journal, 4(3), 197–212. https://doi.org/10.1016/0379-7112(81)90018-7 [Google Scholar] [CrossRef]
26. Sellami, I., Nait-Said, R., Chetehouna, K., Izarra, C., Zidani, F. (2018). Quantitative consequence analysis using Sedov-Taylor blast wave model. Part II: Case study in an Algerian gas industry. Process Safety and Environmental Protection, 116, 771–779. https://doi.org/10.1016/J.PSEP.2018.02.003 [Google Scholar] [CrossRef]
27. Johnson, D. M., Pekalski, A., Tam, V. H. Y., Bassam, A. B., Hoorelbeke, P. et al. (2020). Interpretation of damage caused by a vapor cloud explosion. Process Safety Progress, 39(2), e12106. https://doi.org/10.1002/prs.12106 [Google Scholar] [CrossRef]
28. Heymes, F., Eyssette, R., Lauret, P., Hoorelbeke, P. (2020). An experimental study of water BLEVE. Process Safety and Environmental Protection, 141(5), 49–60. https://doi.org/10.1016/j.psep.2020.04.029 [Google Scholar] [CrossRef]
29. Skřínská, M., Skřínský, J., Sluka, V., Sencik, J., Maly, S. et al. (2014). Mathematical models for the prediction of heat flux from fire balls. WSEAS Transactions on Heat and Mass Transfer, 9, 252–543. [Google Scholar]
30. Eckhoff, R. K. (2014). Boiling liquid expanding vapour explosions (BLEVEsA brief review. Journal of Loss Prevention in the Process Industries, 32(6), 30–43. https://doi.org/10.1016/j.jlp.2014.06.008 [Google Scholar] [CrossRef]
31. Gillet, M., Perez, L., Autrique, L. (2019). A model based predictive tool for fire safety intumescent coatings design. Fire Safety Journal, 110(3), 102908. https://doi.org/10.1016/j.firesaf.2019.102908 [Google Scholar] [CrossRef]
32. Mbarki, A., Ettahir, A., Guelzim, A. (2023). Comparative study of radiative flux from mushroom BLEVE model. In: Agarwal, R. K. (Ed.Recent advances in manufacturing engineering and processes, pp. 135–146. Singapore: Springer Nature. [Google Scholar]
33. Martinsen, W. E., Marx, J. D., By, P. (1999). An improved model for the prediction of radiant heat from fireballs quest an improved model for the prediction of radiant heat from fireballs. International Conference and Workshop on Modeling Consequences of Accidental Releases of Hazardous Materials, San Francisco, California. [Google Scholar]
34. Bonilla, J. M., Àgueda, A., Muñoz, M. A., Vílchez, J. A., Planas, E. et al. (2019). Thermal radiation model for dynamic fireballs with shadowing. Process Safety and Environmental Protection, 128(3), 372–384. https://doi.org/10.1016/j.psep.2019.05.029 [Google Scholar] [CrossRef]
35. Baker, Q. A., Pierorazio, A. J., Woodward, J. L., Tang, M. J. (2011). Update of CCPS book “Guidelines to evaluating vapor cloud explosion, pressure vessel burst, BLEVE and flash fire hazards”. Process Safety Progress, 30(3), 296–300. https://doi.org/10.1002/prs.10447 [Google Scholar] [CrossRef]
36. Betteridge, S., Phillips, L. (2015). Large scale pressurised LNG BLEVE experiments. Symposium Series No 160. Edinburgh, UK. https://www.icheme.org/media/8502/xxv-paper-35.pdf [Google Scholar]
37. Abbasi, T., Abbasi, S. A. (2007). The boiling liquid expanding vapour explosion (BLEVEMechanism, consequence assessment, management. Journal of Hazardous Materials, 141(3), 489–519. https://doi.org/10.1016/j.jhazmat.2006.09.056 [Google Scholar] [PubMed] [CrossRef]
38. Hadef, H., Djebabra, M., Boufades, D., Belmazouzi, Y. (2021). Domino effect analysis at a gas facility: Application at a storage facility. Materialstoday: Proceedings. https://doi.org/10.1016/J.MATPR.2021.05.612 [Google Scholar] [CrossRef]
39. Prugh, R. W. (1994). Quantitative evaluation of fireball hazards. Process Safety Progress, 13, 83–91. https://doi.org/10.1002/(ISSN)1547-5913 [Google Scholar] [CrossRef]
40. Xian, T., Fang, L. (2011). Hazards and prevention of BLEVE. Proceedings of the Second International Conference on Innovations in Bio-Inspired Computing and Applications, IBICA 2011, pp. 261–263. Shenzhen, China. https://doi.org/10.1109/IBICA.2011.68 [Google Scholar] [CrossRef]
41. INERIS (2017). OMEGA 5-Le BLEVE: Phenomenologie et modelisation des effets thermiques. Rapport. INERIS. https://primarisk.ineris.fr/node/996 [Google Scholar]
42. Birk, A. M. (1995). The BLEVE: An update and reexamination of response strategies. Prevention preparedness and response to major industrial accidents involving hazardous substances. Proceedings Major Industrial Accidents Council of Canada (MIACC), pp. 469–494. Ontario, Canada. [Google Scholar]
43. Mbarki, A., Boned, C., Guelzim, A., Ettahir, A. (2022). Performance of the corresponding states model of dual-reference on the determination of viscosity according to the pressure of pure hydrocarbons. International Review of Mechanical Engineering (IREME), 16(8), 420–433. https://doi.org/10.15866/ireme.v16i8.22073 [Google Scholar] [CrossRef]
44. Yang, S., Zhang, Y., Wu, H. (2012). Comparison and validation of thermal radiation models for hydrocarbon jet fire and fireball. Applied Mechanics and Materials, 204–208, 3503–3512. https://doi.org/10.4028/WWW.SCIENTIFIC.NET/AMM.204-208.3503 [Google Scholar] [CrossRef]
45. Zhang, Q. X., Liang, D. (2013). Thermal radiation and impact assessment of the LNG BLEVE fireball. Procedia Engineering, 52(4), 602–606. https://doi.org/10.1016/j.proeng.2013.02.192 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF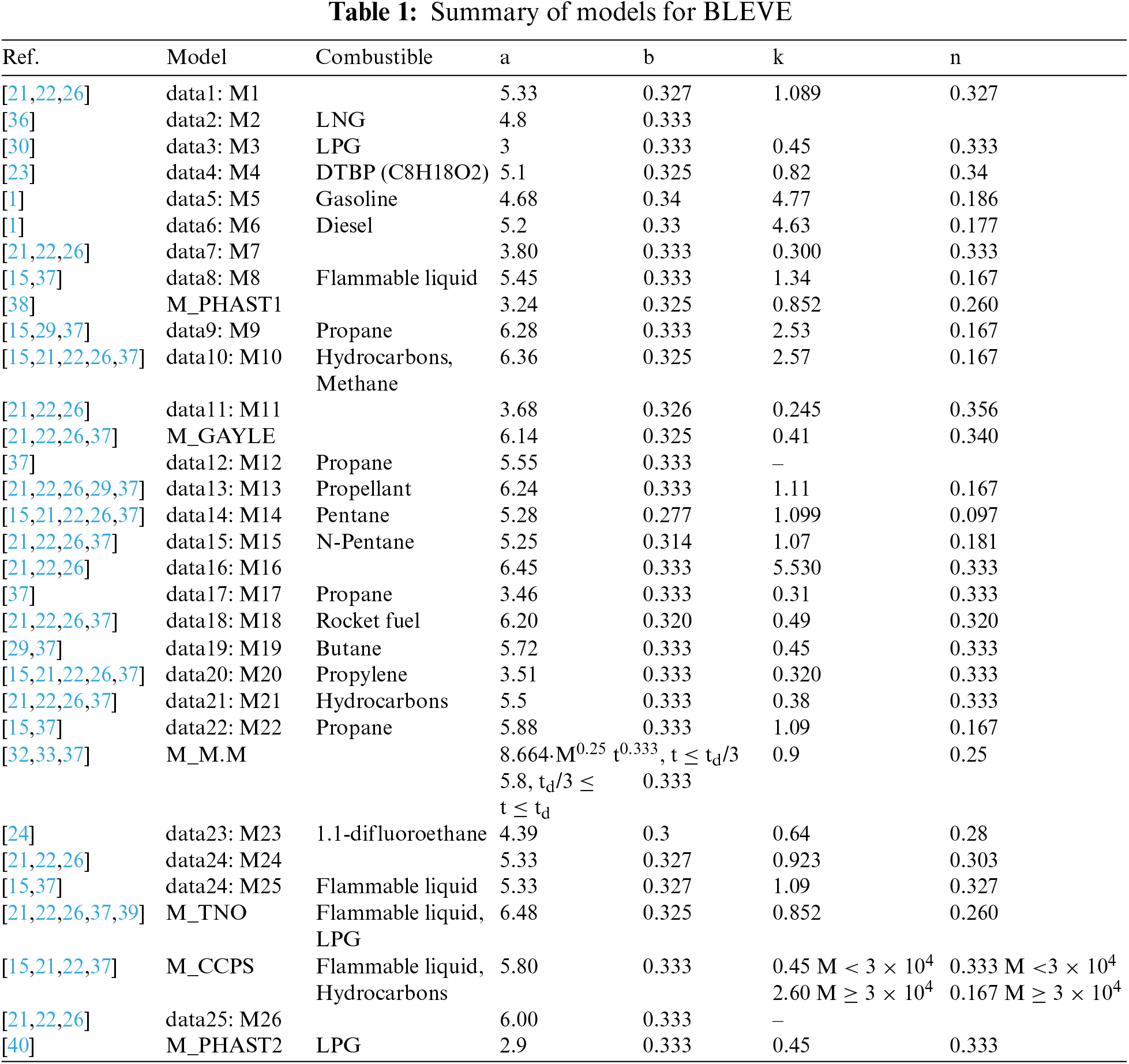
 Downloads
Downloads
 Citation Tools
Citation Tools