Numerical Examination of Free Convection Flow of Casson Ternary Hybrid Nanofluid across Magnetized Stretching Sheet Impacted by Newtonian Heating

Nomenclature

1  Introduction

In fluid dynamics, the models that relate shear stress to shear rate with a linear relationship are insufficient to describe the behavior of complicated fluids; however they are particularly helpful in this field. Models that are common in use to describe the rheological behavior of such fluids are based on Casson model, which is firstly presented in 1959 by Casson [1]. There are two crucial parameters included in the model: The Casson yield stress, which represents the minimal stress needed to onset the flow, and Casson viscosity, which reflects the fluid’s resistance to deformation once it has started flow. In recent years, this model has received attention due to its numerous applications. For example, simulation of fluid flows of drilling fluids and the behavior of inks and paints in printing sectors. In the literature, different numerical studies have investigated the flow behavior of the Casson fluid, highlighting its potential applications in various fields. The study by Hazarika et al. [2] investigated numerically the behavior of a steady MHD micropolar Casson fluid and its heat transfer characteristics as it flowed over a spherical object. They reported that the micropolar factor increases the temperature, while Casson factor decreases it. These results could be used in applications of tissue engineering and bioengineering. A recent numerical study presented by Gireesha et al. [3] analyzed the impact of chemical reactions, a magnetic field, and a space-dependent energy source on the thermal behavior of Casson liquid moving across a curved stretch sheet. Their findings indicated that the increase of the Casson factor is resulted in substantial flow profile variations. Moreover, the study reported that temperature is an increasing function in terms of thermal Biot number, while concentration is an increasing function in terms of concentration Biot number. A study by Nagaraja et al. [4] carried out the flow and melting energy transport across a stretching sheet for a magneto dusty Casson fluid, focusing on the Cattaneo-Christov heat flux model. They found that, elevating the Casson parameter raises the Nusselt number and reduces the drag force. More comprehensive studies can be found in [5,6].

Nanoparticles have emerged as promising materials for enhancing heat transport owing to their distinctive characteristics, which include a high surface area to volume ratio, tunable size and shape, and relatively high thermal conductivity. When dispersed in a fluid, nanoparticles can increase the thermal conductivity of the original liquid, leading to improve heat transport performance. The first known study to introduce the use of nanoparticles for enhancing energy transport was conducted by Choi et al. in 1995 [7]. They proposed the concept of nanofluids, which are fluids containing nanoparticles. In their seminal paper, Choi and Eastman demonstrated that the inclusion of nanosolids in an original fluid could dramatically improve its thermal conductivity, thereby supporting its thermal performance. Their work sparked a lot of interest in the scientific community, and studies continued, confirming that the use of these unique nanoparticles in energy transport applications has the potential to improve heat efficiency and reduce costs in various industries [8–10]. Their work still inspires researchers to explore the potential of nanoparticles and optimizing them to enhance the process of energy transport. Hybrid nanoparticles have emerged as a promising approach for enhancing the heat transfer of fluids in various engineering applications. By combining two or more types of nanosolids in a single liquid, a hybrid nanoliquid is obtained with unique thermal and rheological properties. Indeed, this will enhance thermal conductivity and stability and reduce agglomeration compared to mono-nanofluids. Additionally, hybrid nanoparticles can alter rheological properties, such as viscosity and density, affecting fluid flow patterns and heat transfer rates [11–16]. However, for further enhancement of the performance of nanoliquids, researchers have developed the third generation of nanoliquids, known as ternary hybrid nanoliquid. It consists of three different kinds of nanosolids dispersed in a fluid and offer superior energy transport properties compared to their mono and hybrid nanoparticle counterparts [17–20]. The thermal capabilities of these ternary hybrid nanofluids have been scrutinized through a multitude of numerical investigations. Manjunatha et al. [21] explored the convective energy transport characteristics of ternary nanofluids passing over a stretching sheet. Their research revealed that the thermal conductivity of the ternary nanofluid surpasses that of the hybrid nanofluid, highlighting the enhanced heat transfer capabilities of the ternary nanofluid. In their numerical study, Algehyne et al. [22] delved the behavior of ternary hybrid nanoliquid flowing over a stretched permeable surface. By employing a pseudoplastic model and the Darcy-Forchheimer relation, they uncovered significant enhancements in velocity, energy transport rate, and thermal conductivity, varying as much as 11.73%, 32%, and 61%, depending on the type of nanocomposite used. Guedri et al. [23] carried out a computational analysis to examine the flow of a tri-hybrid nanofluid across a stretching sheet subjected to Joule heating and viscous dissipation. They observed that the magnetic factor and electric field had a considerable effect on fluid flow, and these factors supported the Bejan number and reduced the production of entropy in the system. Related research can be seen in references [24–33].

Numerous industrial and engineering heat-transmitting operations critically rely on fluid movement over a stretching sheet. In the polymer industry, film casting involves stretching a polymer sheet while simultaneously cooling it with fluid flow to prevent overheating and maintain its desired properties. Similarly, in the glass industry, fluid flow is utilized to deftly control the cooling rate of stretched molten glass sheets, ensuring they meet precise thickness and smoothness standards. Wire drawing also benefits from fluid flow to cool wires during stretching, which improves their surface finish for use in electrical and construction applications. On the other hand, fluid flow is employed to regulate the drying rate of stretched paper sheets, resulting in desirable properties such as strength, thickness, and smoothness which is an essential process in paper production and manufacturing. By ensuring that stretching sheets meet stringent industry standards, fluid flow plays an indispensable role in elevating the quality of industrial processes. On the other hand, the interaction between magnetic fields and conductive fluids, such as plasma and liquid metals, in the context of heat transfer through fluids, or what is known as magnetic hydrodynamics (MHD), can have a significant impact on fluid flow patterns and heat transfer rates. In the presence of a magnetic field, the motion of a conductive fluid can be affected by the Lorentz force, which arises from the interaction between the magnetic field and the current in the fluid. This force can cause movement of fluid in different ways than it would in the absence of a magnetic field. MHD has numerous applications in heat transfer through fluids, ranging from the design of fusion reactors, where its effects can play an important role in determining the efficiency of energy transfer between the plasma and the reactor walls, to the cooling of nuclear reactors by improving the rate of heat transfer between the coolant and the reactor walls. This is important to prevent overheating and maintain safe operating conditions. MHD can also be used in many industrial processes, such as metal casting and crystal growth, to improve heat transfer efficiency and control the flow of a conductive liquid. In the presence of these enormous applications of fluid flow through a stretched plate under the influence of a magnetic field, wide numerical studies have tackled this problem in an attempt to improve the thermal performance of these fluids as well as gain a deep understanding of the factors affecting that performance. Sohail et al. [34] examined the role of tri-hybrid nanosolids in a mixture of pseudo-plastic liquids over a 2D porous stretched surface. Fatima et al. [35] conducted a study to examine the convective heat transport in hydromagnetic H2O nanoliquid, H2O hybrid nanoliquid, and H2O tri hybrid nanoliquid flow while subjecting it to the influence of Cattaneo-Christov heat flux and nonlinear thermal radiation over a stretching sheet [36]. The impact of Hall current and thermal radiation on the movement of magnetohydrodynamic liquid carrying tiny particles across a nonlinear stretching surface was investigated by Ali et al. [37].

The investigation focuses on the numerical analysis of Casson fluid behavior, considering the non-Newtonian characteristics inherent in many real-world fluids. This aspect is of paramount importance as it allows for a more accurate representation of the fluid flow and heat transfer phenomena encountered in practical engineering applications. The study incorporates a ternary hybrid nanofluid composition, comprising a mixture of three distinct nanoparticles. This aspect introduces a new dimension to the research as it explores the synergistic effects of multiple nanoparticles on the convective heat transfer characteristics of the fluid. The examination of such complex nanofluid compositions holds significant potential for advancing the understanding and optimization of heat transfer processes in various industrial domains. Moreover, the investigation accounts for the influence of a magnetic field on the fluid flow, thus incorporating magnetohydrodynamic effects. The inclusion of the magnetic field as a governing parameter is crucial, as it allows for the analysis of the coupled interactions between fluid flow, heat transfer, and the magnetic field. Understanding these interactions is vital for the design and optimization of magnetohydrodynamically-driven systems, with applications in areas such as energy conversion and thermal management. Lastly, the study investigates the impact of Newtonian heating, which introduces an additional heat source to the system. By considering this aspect, the research contributes to a deeper understanding of convective heat transfer phenomena in the presence of Newtonian heating, which has practical implications for a wide range of industrial processes. The outcomes of this research endeavor are anticipated to enhance the fundamental knowledge base and pave the way for advancements in the design and optimization of heat transfer systems in various engineering applications. More specifically, the current investigation can be summarized via the following questions:

1. How do the governing equations for Casson tri-hybrid nanoliquid, under magnetic field, models produce in the presence of unsteady free convection flow over a stretching sheet?

2. How can a mathematical formulation for the problem of MHD Casson tri-hybrid nanoliquid be introduced over a stretching sheet?

3. How do the MHD Casson tri-hybrid nanoliquid models compare with the previously investigated natural heat and mass transfer flow problems?

4. How do analysis of the numerical results that can be gained from the influences of MHD Casson tri-hybrid parameters on the heat transfer and physical quantities?

5. How does the heat transfer demeanor of the employed nanoparticles that are suspended in the based fluid under the impact of considered parameters?

2  Mathematical Formulation

In this study, a two dimensional natural convection boundary layer flow is investigated. The physical model under consideration is a stretching sheet with an incompressible magnetohydrodynamic Casson ternary hybrid nanofluid with a Newtonian heating on the boundaries. Two types of Casson ternary hybrid nanofluid are taken into account. The first type is ternary hybrid nanofluid compositions Al2O3-CuO-Ag and Al2O3-CuO-Cu nanoparticles, and the second type is a hybrid nanofluid composition Al2O3-CuO. Magnetic field β02 intensity is employed, and it varies the orientation of the ternary hybrid nanofluid flow. Additionally, the ternary hybrid nanofluids acquire a characteristic through the Casson environment. The Cartesian frame is chosen in such a way that the fluid flow in the x-direction, which is gauged over in the horizontal direction of the stretching sheet. Also, the y-axis is the distance orthogonal on the considered stretching sheet, as displayed in Fig. 1. The form of Newtonian heating is applied to the wall. In the energy equation, the viscous dissipation effect was assumed to be neglected. The influence of magnetic, electrical conductivity, Casson, and nanoparticle volume fraction are included in the momentum equation.

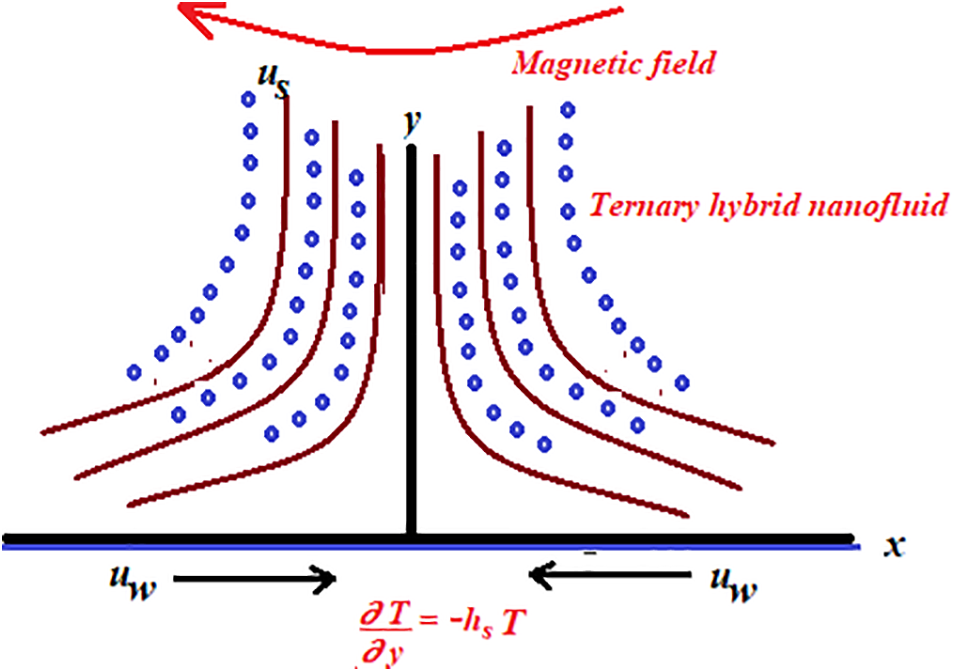
Figure 1: Physical model and coordinate system

The rheological property of Casson fluid is given as follows (see Casson [1]):

τij={2(μβ+Py2π)eij,π>πi2(μβ+Py2πc)eij,π<πi,(1)

Here, the symbol Py is dfined the yield stress of the fluid. πc, μβ are called critical value of this product based and the plastic dynamic viscosity of the non-Newtonian model, respectively. π=eijeij,eij is the component of the deformation rate.

In the state of the Casson fluid, case π>πc, we get:

μ=μβ+Py2π,(2)

where Py=μβ2π/β. Then we get:

μρ=μβρ+[1+1β],(3)

Upon all the above regarding, the ternary hybrid nanofluids model, regarding magnetic, and Casson impacts, the governing equations, namely (continuity, momentum, and thermal) can be established as [38–42]:

∂u∂x+∂v∂y=0,(4)

u∂u∂x+v∂v∂x=vTHnf(1+1β)∂2u∂y2−σTHnfρTHnfB02u,(5)

u∂T∂x+v∂T∂y=KTHnf(ρCP)THnf∂2T∂y2,(6)

according to Newtonian heating (NH) boundary conditions, according to Newtonian heating (NH) boundary conditions, can be written as [42]:

u=uw=ax,v=0,T=−hs∂T(x)∂y,at y=0

u→0, T→T∞ as y→∞(7)

T is referred to the temperature; u and v are symbolized as the velocity components which depend on the x and y directions. β02 is the magnetic field strength, hs and ρs are heat transfer parameter, thermal expansion coefficient, and density of nanoparticles, respectively. ρf, vf, β are density, kinematic viscosity, and Casson parameter, respectively. αTHnf, ρTHnf, (ρcp)HTnf, μTHnf, kTHnf and σTHnf are thermal diffusivity, density, heat capacity, viscosity, thermal conductivity, and electrical conductivity of ternary hybrid nanofluid, respectively, and they are given in Table 1, where χ1, χ2, and χ3 are defined the nanoparticle volume fraction parameter refer to Al2O3, CuO, and Ag or Cu, respectively. μf, kf and σnf are viscosity, thermal and electrical conductivity, respectively of base fluid.

Substitute Eqs. (7) and (8) and the resultant properties in Table 1 into Eqs. (4)–(6), we get the following partial differential equations:

ρfρthnf[1(1−χ1)2.5(1−χ2)2.5(1−χ3)2.5](1+1β)f‴(η)+f(η)f″(η)−(f′(η))2

−ρfρthnfσthnfσfMf′(η)=0,(9)

1Pr(kthnf/kf(1−χ1)[(1−χ2)[(1−χ3)+χ3(ρcp)3(ρcp)f]+χ2(ρcp)2(ρcp)f]+χ1(ρcp)1(ρcp)f)(θ″(η))+f(η)θ′(η)=0,(10)

and the boundary conditions

f(0)=0,f′(0)=1,θ′(0)=−Hs−θ(0),at η=0,f′(η)→0,θ(η)→0 at η→∞,(11)

where Pr=vfkf, M=σfB02e2ρfvthnf, Hs=(vfa)1/2hs are the Prandtl number, magnetic parameter, the conjugate parameter, respectively. It is worth noting that Newtonian heating is ruled by a non-dimensional conjugate parameter, which has a minimum value of 0 (insulated wall) to ∞ (wall temperature remains constant). Furthermore, the position with Newtonian heating occurs in what is usually termed conjugate convection flow, where the heat is provided to the convective fluid via a bounding surface with a finite heat capacity. This composition happens in numerous necessary engineering machines, for example in heat exchangers where the conduction in the convection significantly impacts solid tube wall in the fluid flowing over it.

Due to engineering purposes, the local skin friction coefficient Cf and the Nusselt number Nu of the current model can be expressed as

Cf=τwρuw2,

Nu=xqwk(Tw−T∞),(12)

where τw and qw correspond to shear stress and heat flux on the plane of the wall, and are given by

qw=kTHnf∂T∂y,τw=μTHnf(∂u∂y)at y=0,(13)

As a result, the local skin friction coefficient and Nusselt number become

Cf=Re−12[1(1−χ1)2.5(1−χ2)2.5(1−χ3)2.5](1+1β)f″(0),

Nu=Re12kTHnfkf(θ′(0)),(14)

where Re=ax2vf is the local Reynolds number.

3  Numerical Method and Accuracy

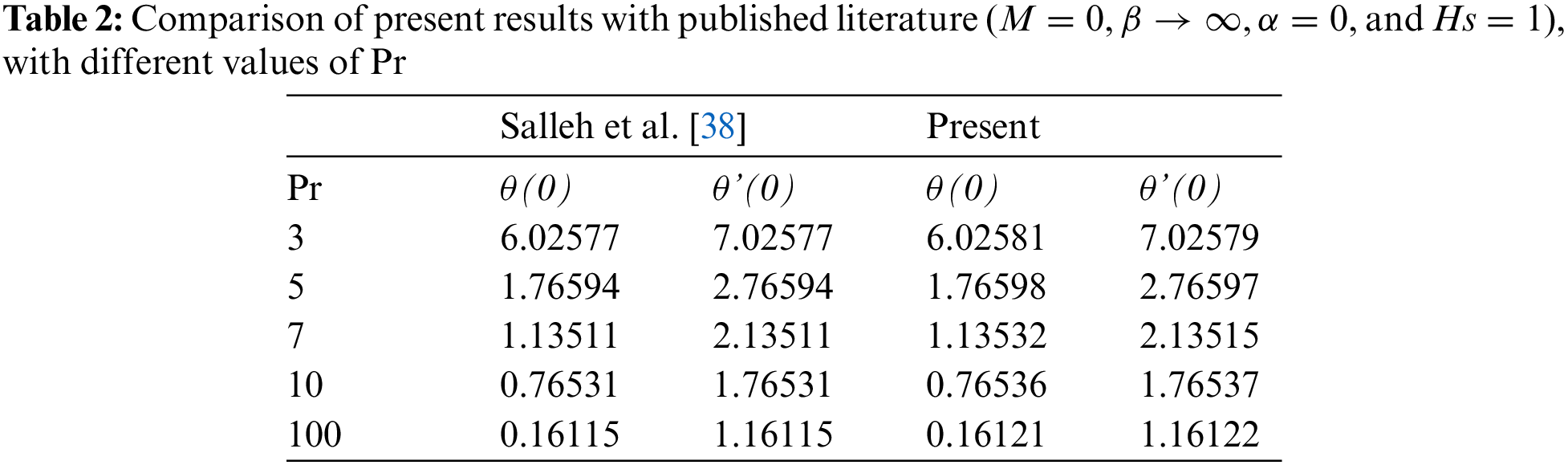
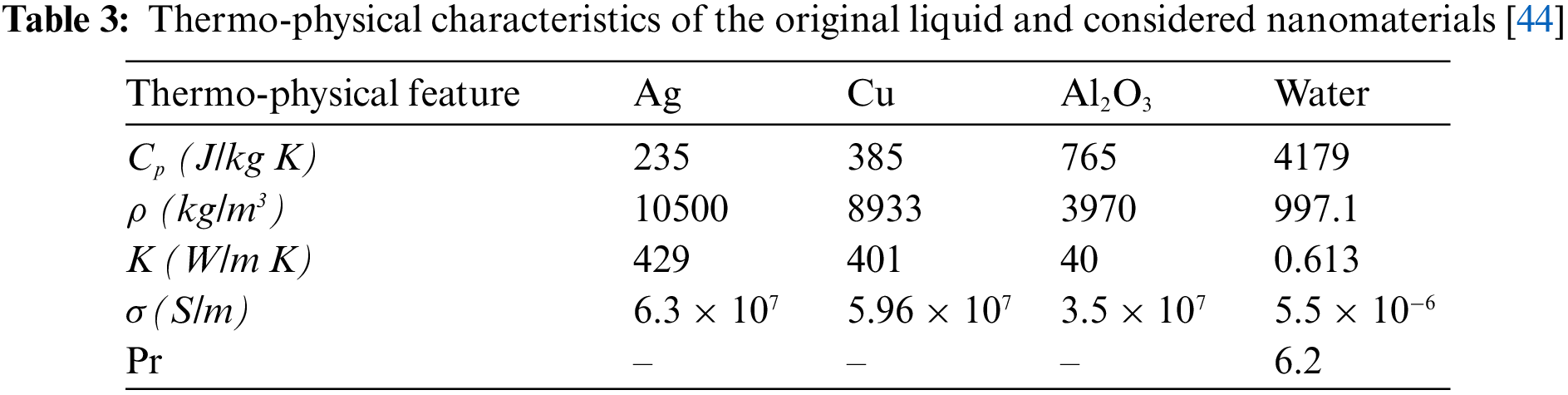
The generated equations obtained in previous section, are solved numerically using Kellar-box scheme. This numerical method relies on steps and methods as follows: Reducing equations with high order partial derivative to the first order using finite difference method. Then the resultant equations are centered using centering method, which gives the difference equations. In third step, the gained difference equations are linearized using Newton’s method, consequently, the linear system is solved by the block tridiagonal elimination technique. Lastly, the resulting system is coded via MATLAB software and we compare results with relevant literature. An excellent agreement was found between the present results and the literature. The comparison is presented in Table 2. Table 3 displays the thermos-physical properties of utilized nanoparticles and base fluid.

Briefly, the mathematical formulations and the Keller box method numerical method can be summarized as a flow chart of research methodology, Fig. 2 as follows [45]:

Figure 2: Flow chart of research methodology

4  Results and Discussions

Graphical impersonations of the influences of different important parameters on physical collections, regarding heat transfer, are offered in Figs. 3–9. The conduct of Casson ternary hybrid nanofluid outcoming from the effect of these parameters is also debated and analyzed. The impacts of Casson β, nanoparticle volume fraction α, which is defined as α=χ1=χ2=χ3, conjugate Hs, and magnetic M parameters have been taken into this investigation, in which their domains are 0.3 ≤ Hs ≤ 3, 1 ≤ β ≤ 9, 0.01≤ α ≤ 0.03, and 0.1 ≤ M ≤ 4. The conjugate parameter impresses on temperature profiles of ternary hybrid nanofluids while stabilizing the values of the nanoparticle volume fraction α = 0.02, Casson parameter β = 3, and M = 0.5 as constant values, as clarified in Fig. 3. As the conjugate values are raised, the ternary hybrid nanofluid temperature is boosted. This can be attributed to the improved thermal contact and enhanced thermal conductivity between the stretching sheet and the ternary hybrid nanofluid. As a result, the heat generated by the Newtonian heating source is more efficiently transferred to the ternary hybrid nanofluid, leading to an increase in its temperature. Besides that, when the impacts of the conjugate parameter were employed on the velocity profiles, it was found that the velocity profiles did not respond. This is due to Eq. (5), where the parameter affects only the temperature terms, and does not affect the velocity profiles. Therefore, their figures were not included. From Fig. 4, it can be noted that the temperature profiles of the ternary hybrid nanofluid are getting down by the increase in the Casson parameter values. The repression in the nanofluid temperature occurs because the increment in the Casson parameter progresses the viscosity of the nanofluids, and this performs a rise in the nanofluid’s opposition to temperature, that way decreasing the temperature profiles. Fig. 5 explains the magnitude to which magnetic parameter condensation impacts the temperature profiles of nanofluids while fixing the values of other parameters. It is noted that temperature profile amounts turn down as raise the values of the magnetic parameters. Decreasing occurs due to the limitation in the flow of the fluid resulting from an increment of the magnetic field intensity. Also, Fig. 6 describes the changes in temperature profiles for different values of the nanoparticle volume fraction parameter at Hs = 0.8, β = 3, and M = 0.5. Clearly, growing the values of this parameter supports the increase in the temperature profile. As the volume fraction of nanoparticle is raised, the number of nanoparticles per unit volume increases. This leads to an increase in the total surface area available for heat transfer within the original fluid. The tri-hybrid nanoparticles have high thermal conductivity, and as they are embedded in the original fluid, they enhance the overall thermal conductivity of the original fluid. This increased thermal conductivity facilitates a more efficient transfer of heat from the stretching sheet to the tri-hybrid nanofluid, raising its temperature. Now, we direct our alertness to the investigation of graphical outcomes that supply the velocity profile variations. As both β and α increase, the fluid velocity increases, and the curves become more betterment pointing to the raise of velocity profiles, as shown in Figs. 7 and 8. In the opposite behavior, Fig. 9, the velocity profiles decrease when the magnetic parameter increases. A magnetic field’s presence can induce magneto-hydrodynamic (MHD) effects on the fluid flow. The Lorentz force is one of the primary impacts of MHD. The Lorentz force acts perpendicular to both the magnetic field direction and the fluid velocity. An augmentation in the magnetic parameter corresponds to a heightened intensity of the applied magnetic field, leading to the Lorentz force becoming dominant and tending to oppose the fluid motion. As visible in all presented figures, the comparisons between the compositions (ternary hybrid nanofluids, hybrid nanofluids) are considered. Interestingly, the ternary hybrid nanofluid, formed of water with Al2O3-CuO-(Ag or Cu) had higher temperature and velocity profiles compared with the hybrid nanofluid containing water and Al2O3-CuO under the Casson, magnetic, nanoparticle volume fraction parameters effects. Additionally, two ternary hybrid nanofluids are compared as physical comparisons. Where it is found that the Al2O3-CuO-Ag/water has higher temperature profiles than Al2O3-CuO-Cu/water, but the opposite case happens, the velocity profiles for Al2O3-CuO-Cu/water are higher than Al2O3-CuO-Ag/water, as shown in the all figures included.

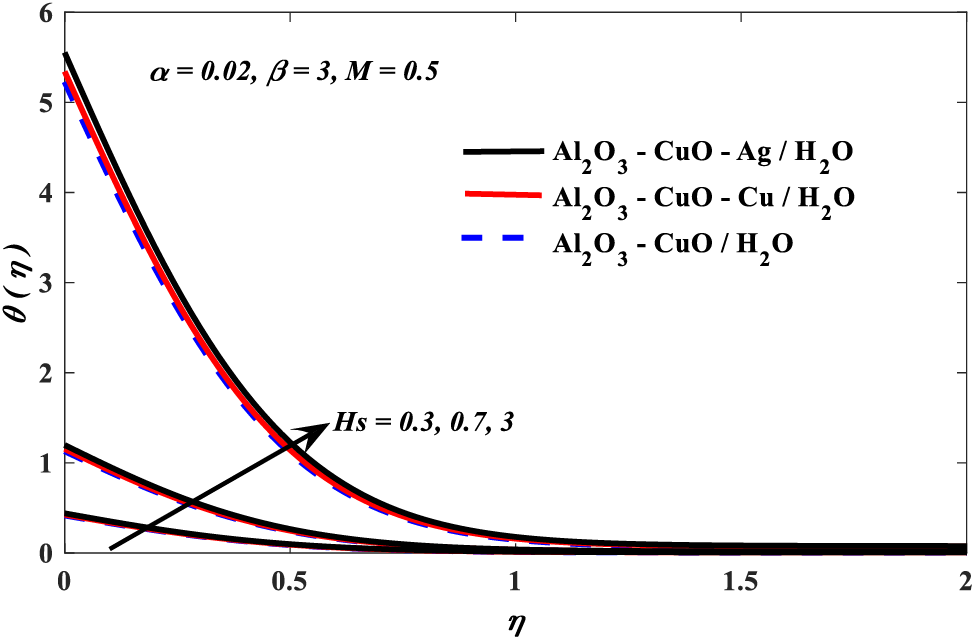
Figure 3: Conjugate parameter vs. temperature profiles

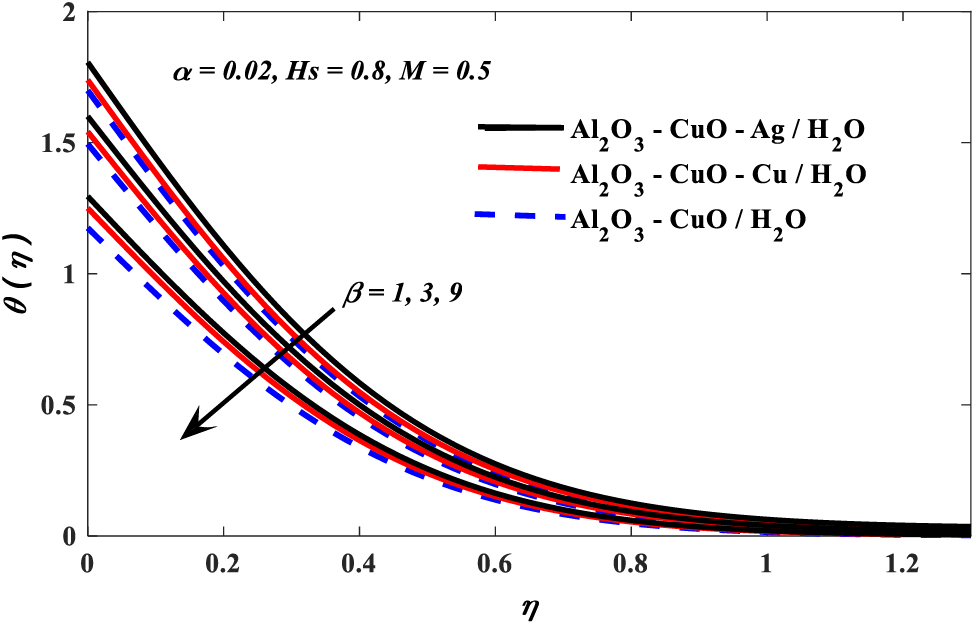
Figure 4: Casson parameter vs. temperature profiles

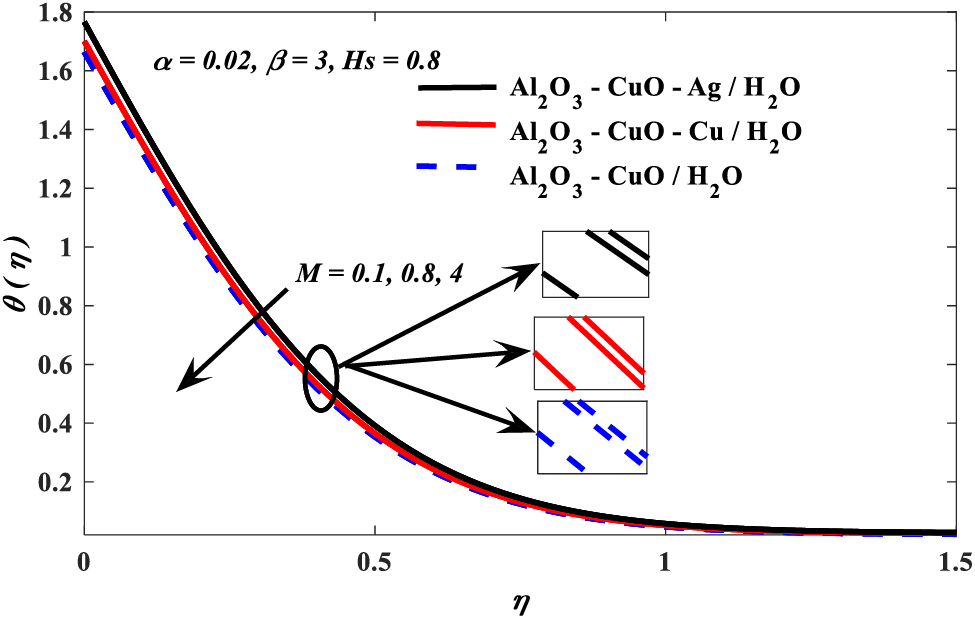
Figure 5: Magnetic parameter vs. temperature profiles

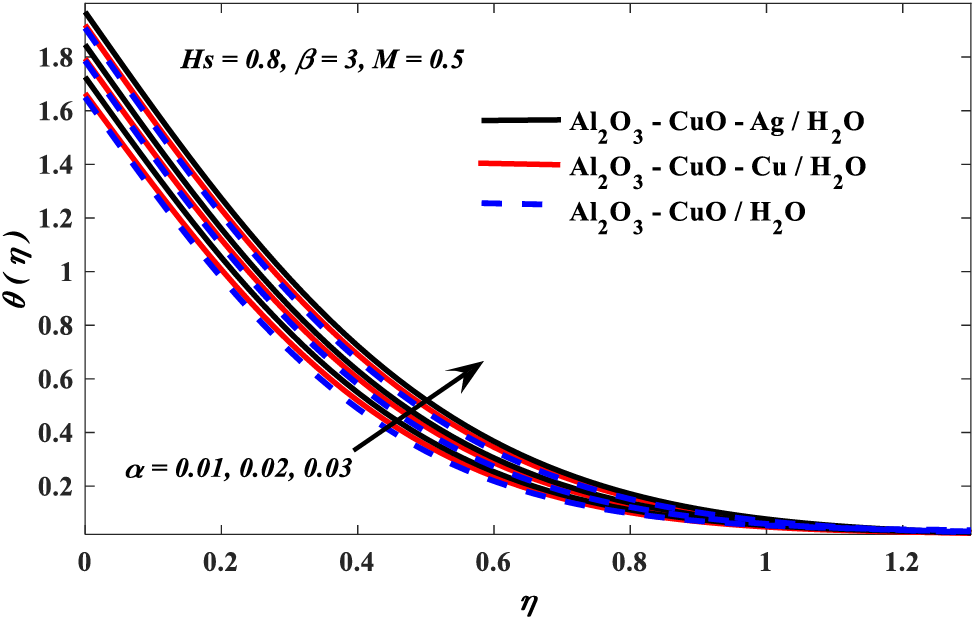
Figure 6: Nanoparticle volume fraction parameter vs. temperature profiles

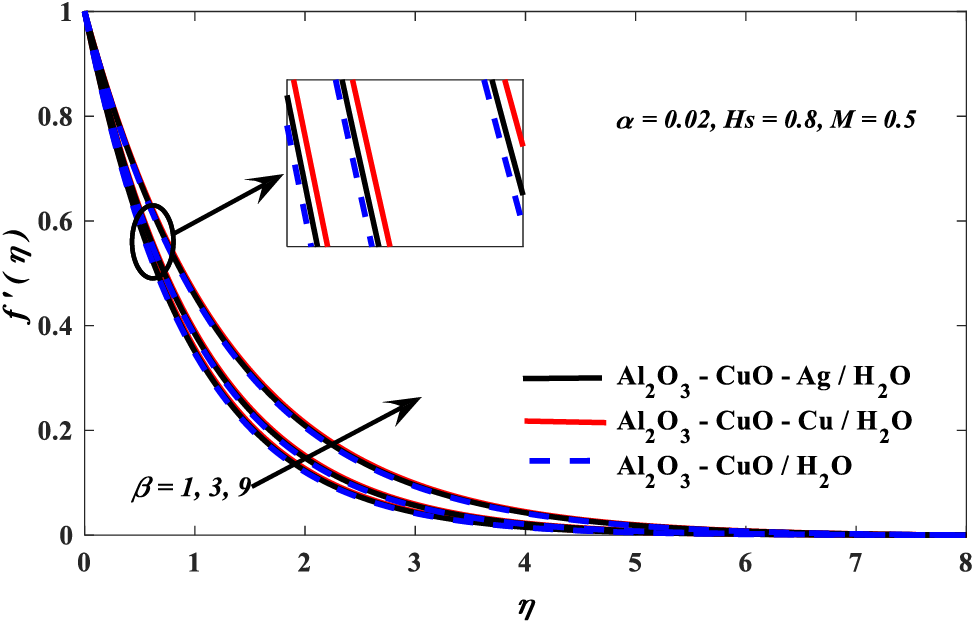
Figure 7: Casson fraction parameter vs. velocity profiles

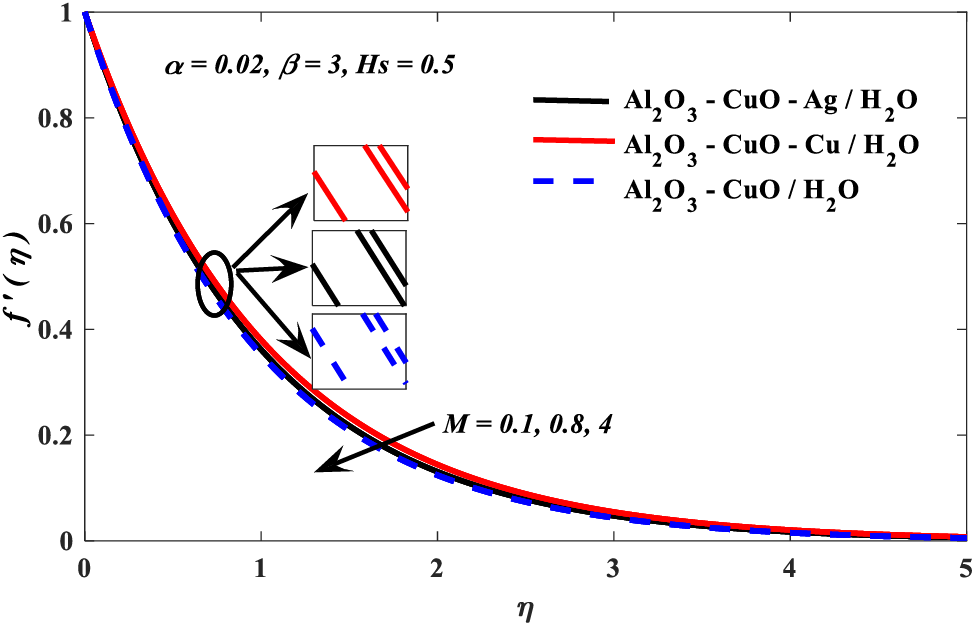
Figure 8: Magnetic parameter vs. velocity profiles

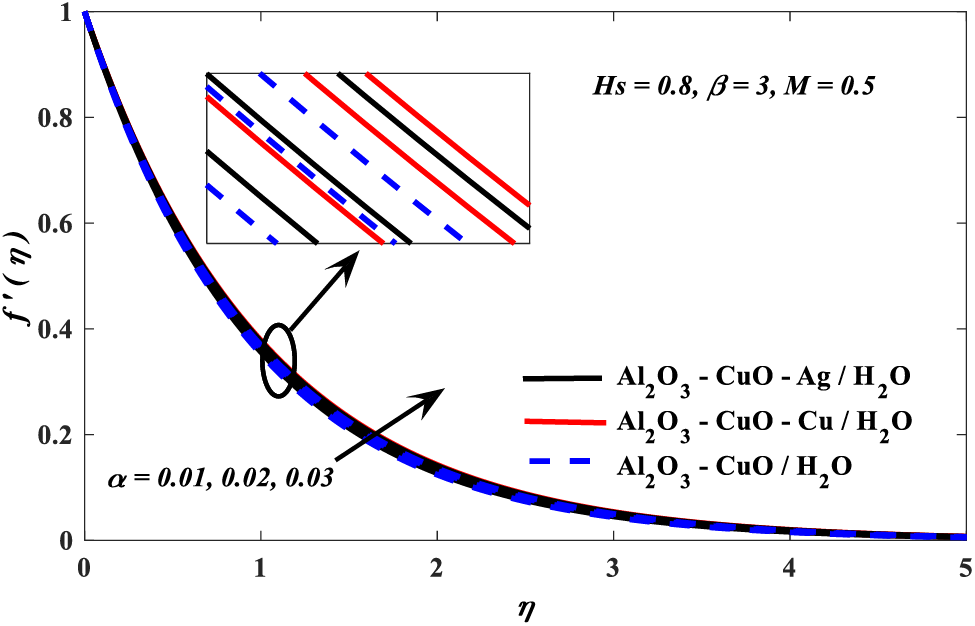
Figure 9: Nanoparticle volume fraction parameter vs. temperature profiles

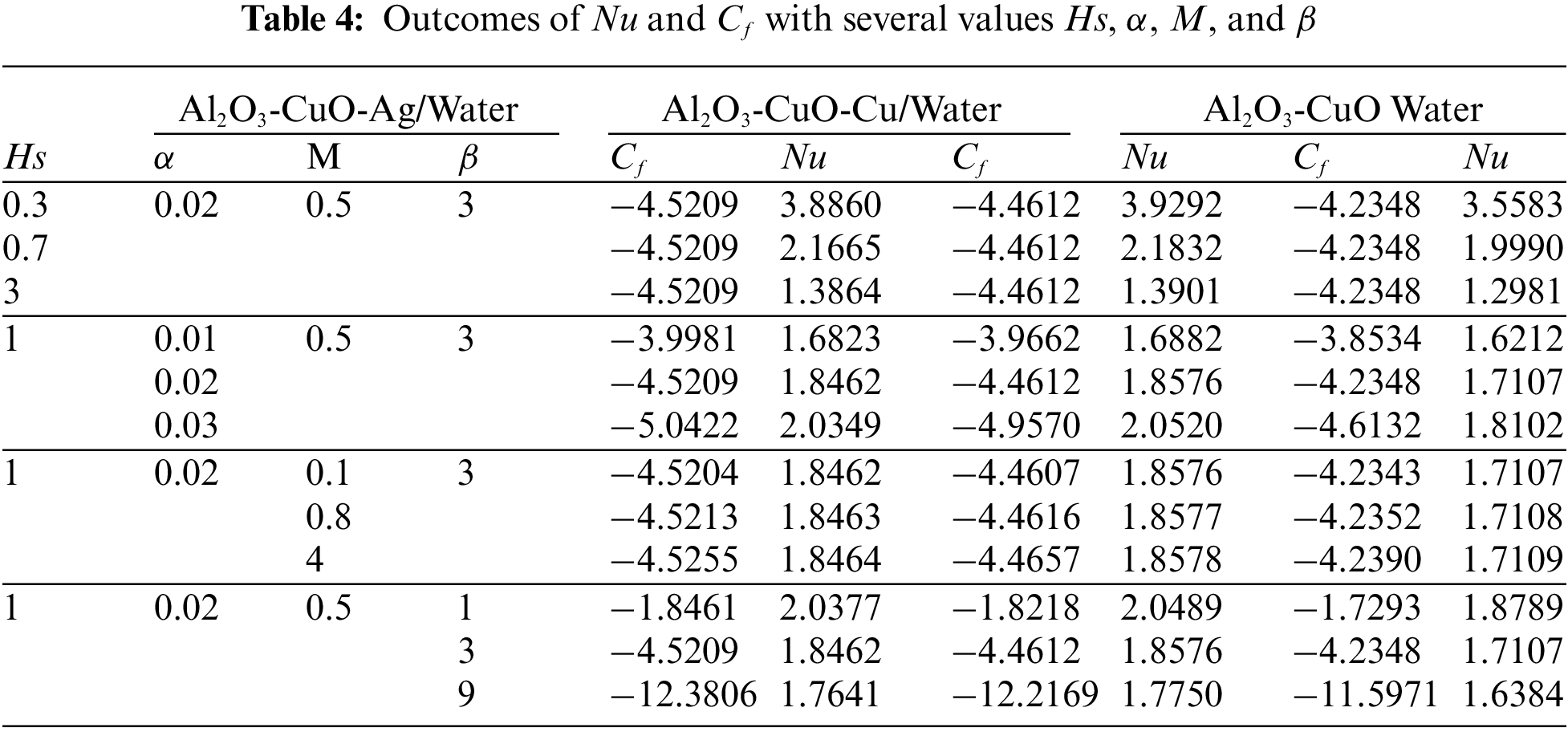
Table 4 displays the influences of Hs, α, M, and β on the local skin friction coefficient and local Nusselt number, respectively. It is observed that the Nu distribution is changed at the variation of all utilized parameters values, in this study. Moreover, the local Nusselt number decreases with the increasing values of both Hs and β. On the contrary, when the other parameters, α, M, are increased, Nu values are decreased. Besides that, it is noticed that the Cf distribution is unaffected by the conjugate parameter Hs, because there is no effect of this parameter in equation number 20. On the other hand, Cf is influenced by the other parameters, α, M, and β. We get that the growth in the parameters (α, M, and β), leads to the rate of local skin friction being reduced. Likewise, it is observed that the ternary hybrid nanofluids have the highest Nu values than the hybrid nanofluids, with different values of employed parameters, Hs, α, M, and β. But it is noticed that the ternary hybrid nanofluids have the lowest Cf values than the hybrid nanofluids, at the move of these parameters. Additionally, Al2O3-CuO-Ag/water has a lower Cf and higher Nu than Al2O3-CuO-Cu/water.

5  Conclusions

This investigation aimed to supply the research gap, which includes the impacts of ternary hybrid nanofluids with the magnetic fields, and subject to Newtonian heating boundary conditions, in the presence of natural convection. The current study developed a mathematical model (governing equations) and used mathematical techniques to convert these equations to partial differential equations (PDEs). Moreover, these PDEs have been successfully solved by the Keller box method, programmed the resulting linear system, and discussed the resulting numerical outcomes. Consequently, we acquired new results which were compared with previous literature. So, it can contribute this consideration to establishing coming studies. Relying on that, this study has outlined the following conclusions:

1.    Temperature profiles drop with increased values of the Casson and magnetic parameters, whereas it is boosted when the increment of values of nanoparticle volume fraction and conjugate parameters.

2.    Velocity profile escalated with the Casson and nanoparticle volume fraction parameters, but it diminishes due to the growing values of the magnetic parameter.

3.    The decrement of the local skin friction coefficient was evaluated with increased Casson, magnetic, and nanoparticle volume parameters, but did not affect with conjugate parameter.

4.    The decrement of the local skin friction coefficient was evaluated with increased Casson, magnetic, and nanoparticle volume parameters, but did not affect with conjugate parameter. On the hand, the values of the Nusselt number increased by increasing the nanoparticle volume fraction and magnetic parameters but decreased due to an increase in conjugate and Casson parameters.

5.    Local Nusselt number creates better values for ternary hybrid nanofluids compared with the hybrid nanofluid. Likewise, temperature profiles for Al2O3-CuO-Ag/Water (ternary hybrid nanofluids) are higher values than Al2O3-CuO-Cu/Water.

6.    Based on this study, we can take into consideration some future studies. The current problem can be developed in future research using more physical influences, such as thermal radiation, chemical reactions, viscous dissipation, and joule heating impacts, as well as it can also develop to comprise ternary hybrid nanofluids with viscous dissipation and Joule heating impacts. On the other hand, it can utilize other boundary conditions; such as convective boundary conditions, constant heat flux, etc.

Acknowledgement: The authors happily thank the Center for Graduate Studies Management, Al-Hussein Bin Talal University, Ma’an, Jordan, for the financial support through Voting No. (93/2023) for this research.

Funding Statement: This research was funded by the Center for Graduate Studies Management, Al-Hussein Bin Talal University through Voting No. (93/2023).

Author Contributions: The authors confirm their contribution to the paper as follows: construct the mathematical formulations, discussions, investigation: Mohammed Z. Swalmeh, Wejdan Mesa’adeen; write literature, review, editing: Firas A. Alwawi; methodology, software: A. A. Altawallbeh; resourcing, writing original draft: Feras M. Al Faqih, Ahmad M. Awajan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Casson, N. (1959). Flow equation for pigment-oil suspensions of the printing ink-type. Rheology of Disperse Systems, 2, 84–104. [Google Scholar]

2. Hazarika, S., Ahmed, S. (2020). Steady magnetohydrodynamic micropolar Casson fluid of Brownian motion over a solid sphere with thermophoretic and Buoyancy forces: Numerical analysis. Journal of Nanofluids, 9(4), 336–345. [Google Scholar]

3. Gireesha, B. J., Shankaralingappa, B. M., Prasannakumar, B. C., Nagaraja, B. (2022). MHD flow and melting heat transfer of dusty Casson fluid over a stretching sheet with Cattaneo-Christov heat flux model. International Journal of Ambient Energy, 43(1), 2931–2939. [Google Scholar]

4. Nagaraja, B., Gireesha, B. J. (2021). Exponential space-dependent heat generation impact on MHD convective flow of Casson fluid over a curved stretching sheet with chemical reaction. Journal of Thermal Analysis and Calorimetry, 143, 4071–4079. [Google Scholar]

5. Abbasi, A., Khan, S. U., Al-Khaled, K., Khan, M. I., Farooq, W. et al. (2022). Thermal prospective of Casson nano-materials in radiative binary reactive flow near oblique stagnation point flow with activation energy applications. Chemical Physics Letters, 786, 139172. [Google Scholar]

6. Ahmad, I., Qureshi, N., Al-Khaled, K., Aziz, S., Chammam, W. et al. (2021). Magnetohydrodynamic time dependent 3-D simulations for Casson nano-material configured by unsteady stretched surface with thermal radiation and chemical reaction aspects. Journal of Nanofluids, 10(2), 232–245. [Google Scholar]

7. Choi, S. U. S., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. No. ANL/MSD/CP-84938; CONF-951135-29. Argonne, IL, USA: Argonne National Lab (ANL). [Google Scholar]

8. Pordanjani, A. H., Aghakhani, S., Afrand, M., Mahmoudi, B., Mahian, O. et al. (2019). An updated review on application of nanofluids in heat exchangers for saving energy. Energy Conversion and Management, 198, 111886. [Google Scholar]

9. Wong, K. V., De Leon, O. (2010). Applications of nanofluids: Current and future. Advances in Mechanical Engineering, 2, 519659. [Google Scholar]

10. Okonkwo, E. C., Wole-Osho, I., Almanassra, I. W., Abdullatif, Y. M., Al-Ansari, T. (2021). An updated review of nanofluids in various heat transfer devices. Journal of Thermal Analysis and Calorimetry, 145, 2817–2872. [Google Scholar]

11. Leong, K., Ahmad, K. K., Ong, H. C., Ghazali, M., Baharum, A. (2017). Synthesis and thermal conductivity characteristic of hybrid nanofluids–a review. Renewable and Sustainable Energy Review, 75, 868–878. [Google Scholar]

12. Muneeshwaran, M., Srinivasan, G., Muthukumar, P., Wang, C. C. (2021). Role of hybrid-nanofluid in heat transfer enhancement-A review. International Communications of Heat and Mass Transfer, 125, 105341. [Google Scholar]

13. Turcu, R., Darabont, A., Nan, A., Aldea, N., Macovei, D. et al. (2006). New polypyrrole-multiwall carbon nanotubes hybrid materials. Journal of Optoelectronics and Advanced Materials, 8, 643–647. [Google Scholar]

14. Suresh, S., Venkitaraj, K., Selvakumar, P., Chandrasekar, M. (2011). Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 388, 41–48. [Google Scholar]

15. Baghbanzadeh, M., Rashidi, A., Rashtchian, D., Lotfi, R., Amrollahi, A. (2012). Synthesis of spherical silica/multiwall carbon nanotubes hybrid nanostructures and investigation of thermal conductivity of related nanofluids. Thermochimica Acta, 549, 87–94. [Google Scholar]

16. Swalmeh, M. Z., Alwawi, F. A., Kausar, M. S., Ibrahim, M. A. H., Hamarsheh, A. S. et al. (2023). Numerical simulation on energy transfer enhancement of a Williamson ferrofluid subjected to thermal radiation and a magnetic field using hybrid ultrafine particles. Scientific Reports, 13, 3176. [Google Scholar] [PubMed]

17. Adun, H., Kavaz, D., Dagbasi, M. (2021). Review of ternary hybrid nanofluid: Synthesis, stability, thermophysical properties, heat transfer applications, and environmental effects. Journal of Cleaner Production, 328, 129525. [Google Scholar]

18. Rekha Sahoo, R. (2021). Effect of various shape and nanoparticle concentration based ternary hybrid nanofluid coolant on the thermal performance for automotive radiator. Heat and Mass Transfer, 57, 873–887. [Google Scholar]

19. Kumar, V., Sahoo, R. R. (2021). Experimental and numerical study on cooling system waste heat recovery for engine air preheating by ternary hybrid nanofluid. Journal of Enhanced Heat Transfer, 28(4), 1–29. [Google Scholar]

20. Dezfulizadeh, A., Aghaei, A., Hassani Joshaghani, A., Najafizadeh, M. M. (2022). Exergy efficiency of a novel heat exchanger under MHD effects filled with water-based Cu-SiO2-MWCNT ternary hybrid nanofluid based on empirical data. Journal of Thermal Analysis Calorimetry, 147, 4781–4804. [Google Scholar]

21. Manjunatha, S., Puneeth, V., Gireesha, B. J., Chamkha, A. (2022). Theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. Journal of Applied and Computational Mechanics, 8(4), 1279–1286. [Google Scholar]

22. Algehyne, E. A., Alrihieli, H. F., Bilal, M., Saeed, A., Weera, W. (2022). Numerical approach toward ternary hybrid nanofluid flow using variable diffusion and non-Fourier’s concept. ACS Omega, 7(33), 29380–29390. [Google Scholar] [PubMed]

23. Guedri, K., Khan, A., Gul, T., Mukhtar, S., Alghamdi, W. et al. (2022). Thermally dissipative flow and Entropy analysis for electromagnetic trihybrid nanofluid flow past a stretching surface. ACS Omega, 7(37), 33432–33442. [Google Scholar] [PubMed]

24. Shi, Q. H., Hamid, A., Khan, M. I., Kumar, R. N., Gowda, R. P. et al. (2021). Numerical study of bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy. Scientific Reports, 11(1), 16030. [Google Scholar] [PubMed]

25. Jakeer, S., Reddy, S. R. R., Rashad, A. M., Rupa, M. L., Manjula, C. (2023). Nonlinear analysis of Darcy-Forchheimer flow in EMHD ternary hybrid nanofluid (Cu-CNT-Ti/water) with radiation effect. Forces in Mechanics, 10, 100177. [Google Scholar]

26. Hasnain, J., Abid, N. (2023). Numerical investigation for thermal growth in water and engine oil-based ternary nanofluid using three different shaped nanoparticles over a linear and nonlinear stretching sheet. Numerical Heat Transfer, Part A: Applications, 83(12), 1365–1376. [Google Scholar]

27. Qadan, H., Alkasasbeh, H., Yaseen, N., Sawalmeh, M. Z., ALKhalafat, S. (2019). A Theoretical study of steady MHD mixed convection heat transfer flow for a horizontal circular cylinder embedded in a micropolar casson fluid with thermal radiation. Journal of Computational Applied Mechanics, 50(1), 165–173. [Google Scholar]

28. Swalmeh, M. Z., Alkasasbeh, H. T., Hussanan, A., Mamat, M. (2019). Influence of micro-rotation and micro-inertia on nanofluid flow over a heated horizontal circular cylinder with free convection. Theoretical and Applied Mechanics, 46(2), 125–145. [Google Scholar]

29. Alzgool, H. A., Alkasasbeh, H. T., Abu-ghurra, S., Al-houri, Z., Swalmeh, M. Z. (2019). Numerical solution of heat transfer in MHD mixed convection flow micropolar Casson fluid about solid sphere with radiation effect. International Journal of Engineering Research and Technology, 12(4), 519–529. [Google Scholar]

30. Alsabery, A. I., Yazdi, M. H., Altawallbeh, A. A., Hashim, I. (2019). Effects of nonhomogeneous nanofluid model on convective heat transfer in partially heated square cavity with conducting solid block. Journal of Thermal Analysis and Calorimetry, 136, 1489–1514. [Google Scholar]

31. Arshad, M., Hassan, A. (2022). A numerical study on the hybrid nanofluid flow between a permeable rotating system. The European Physical Journal Plus, 137(10), 1126. [Google Scholar]

32. Arshad, M., Hassan, A., Haider, Q., Alharbi, F. M., Alsubaie, N. et al. (2022). Rotating hybrid nanofluid flow with chemical reaction and thermal radiation between parallel plates. Nanomaterials, 12(23), 4177. [Google Scholar] [PubMed]

33. Altawallbeh, A. A., Hashim, I., Bhadauria, B. S. (2019). Magneto-double diffusive convection in a viscoelastic fluid saturated porous layer with internal heat source. AIP Conference Proceedings, 2116, 030015. [Google Scholar]

34. Sohail, M., El-Zahar, E. R., Mousa, A. A. A., Nazir, U., Althobaiti, S. et al. (2022). Finite element analysis for ternary hybrid nanoparticles on thermal enhancement in pseudo-plastic liquid through porous stretching sheet. Scientific Reports, 12(1), 9219. [Google Scholar] [PubMed]

35. Fatima, N., Hasnain, J., Abid, N., Lashin, M. M., Eldin, S. M. (2023). Aspects of Cattaneo-Christov heat flux in nonlinear radiative ternary, hybrid, and single mass diffusion past stretching surface; A comparative study. Case Studies in Thermal Engineering, 43, 102776. [Google Scholar]

36. Elsebaee, F. A. A., Bilal, M., Mahmoud, S. R., Balubaid, M., Shuaib, M. et al. (2023). Motile micro-organism based trihybrid nanofluid flow with an application of magnetic effect across a slender stretching sheet: Numerical approach. AIP Advances, 13(3), 035237. [Google Scholar]

37. Ali, M. Y., Reza-E-Rabbi, S., Rasel, M. M. H., Ahmmed, S. F. (2023). Combined impacts of thermoelectric and radiation on hydromagnetic nanofluid flow over a nonlinear stretching sheet. Partial Differential Equations in Applied Mathematics, 7, 100500. [Google Scholar]

38. Salleh, M. Z., Nazar, R., Pop, I. (2010). Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. Journal of the Taiwan Institute of Chemical Engineers, 41(6), 651–655. [Google Scholar]

39. Abbas, W., Bani-Fwaz, M. Z., Asogwa, K. K. (2023). Thermal efficiency of radiated tetrahybrid nanofluid [(Al2O3-CuO-TiO2-Ag)/water]tetra under permeability effects over vertically aligned cylinder subject to magnetic field and combined convection. Science Progress, 106(1), 00368504221149797. [Google Scholar] [PubMed]

40. Alwawi, F. A., Swalmeh, M. Z., Hamarsheh, A. S. (2023). Computational simulation and parametric analysis of the effectiveness of ternary nano-composites in improving magneto-micropolar liquid heat transport performance. Symmetry, 15(2), 429. [Google Scholar]

41. Altawallbeh, A. A., Saeid, N. H., Hashim, I. (2013). Magnetic field effect on natural convection in a porous cavity heating from below and salting from side. Advances in Mechanical Engineering, 5, 183079. [Google Scholar]

42. Alkasasbeh, H., Swalmeh, M., Bani Saeed, H., Al Faqih, F., Talafha, A. (2020). Investigation on CNTs-water and human blood based Casson nanofluid flow over a stretching sheet under impact of magnetic field. Frontiers in Heat and Mass Transfer, 14, 1–7. https://doi.org/10.1016/j.est.2021.103009 [Google Scholar] [CrossRef]

43. Hou, E., Wang, F., Nazir, U., Sohail, M., Jabbar, N. et al. (2022). Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines, 13(2), 201. [Google Scholar] [PubMed]

44. Mutuku-Njane, W. N. (2014). Analysis of hydromagnetic boundary layer flow and heat transfer of nanofluids (Doctoral dissertation). Cape Peninsula University of Technology, South Africa. [Google Scholar]

45. Cebeci, T., Bradshaw, P. (2012). Physical and computational aspects of convective heat transfer. Springer Science and Business Media. [Google Scholar]