 Open Access
Open Access
ARTICLE
Effect of Surface Tension on the Dynamics of an Oscillating Interface in a Vertical Slotted Channel
1 Laboratory of Vibrational Hydromechanics, Perm State Humanitarian Pedagogical University, Perm, 614000, Russia
2 Department of Applied Physics, Perm National Research Polytechnic University, Perm, 614990, Russia
* Corresponding Author: Veronika Dyakova. Email:
(This article belongs to the Special Issue: Non-Equilibrium Processes in Continuous Media)
Fluid Dynamics & Materials Processing 2025, 21(3), 493-508. https://doi.org/10.32604/fdmp.2025.060577
Received 05 November 2024; Accepted 22 January 2025; Issue published 01 April 2025
Abstract
An experimental investigation of the dynamics of the interface between two low-viscosity fluids with high density contrast oscillating in a fixed vertical slotted channel has been conducted. It has been found that as the amplitude of the liquid column oscillations increases, parametric oscillations of the interface are excited in the form of a standing wave located in the channel plane. In particular, depending on the interfacial tension, the standing waves have a frequency equal to that of liquid piston oscillations (harmonic response), or half of the frequency of oscillations of the liquid column in the channel (subharmonic response). The detected type of instability has a gravitational-capillary nature and is analogous to Faraday waves. The analysis of the overcritical dynamics of wave oscillations indicates that interfacial tension plays a crucial role in determining the type of parametric instability. At high interfacial tension, only synchronous (harmonic) wave modes are observed, and the threshold of the wave excitation is determined by the amplitude of piston oscillations of the liquid column. In this case, the oscillation acceleration does not play a role and has a small value in the threshold of the synchronous mode response. In the case of weak surface tension, subharmonic oscillations are observed. The threshold for the development of these oscillations is determined by the dimensionless acceleration of the oscillating liquid column and remains almost constant with variations in the dimensionless frequency of oscillations. At moderate values of interfacial tension (in the region of moderate dimensionless frequencies), a synchronous wave mode emerges in the stability threshold of the oscillating interface. As the dimensionless acceleration is increased further, a subharmonic mode is excited. The growth of subharmonic oscillations occurs against the background of harmonic wave oscillations, with the oscillations of the interface representing a combination of two standing waves.Keywords
The dynamics of multiphase systems in oscillating force fields is currently a topic of great scientific and practical interest. This interest is motivated by the prevalence of multiphase systems in both natural and engineered contexts. Specific attention is given to the generation and suppression of various types of instabilities at interfaces between media in containers of different geometry. The dynamics of the interface depends on the properties of the contacting phases, the geometry of the containers, and the nature of the external influence. If a two-liquid system is selected for use as a multiphase system, the observed dynamics will be largely dependent on how the fluids are moving within the container. In slotted channels, Hele-Shaw cells, which in laboratory experiments serve as the prototype for porous media, the viscous interaction of oscillating fluids with channel walls is dependent on the dimensionless oscillation frequency ω = Ω d2/ν, where Ω = 2πf is the radian frequency of the fluid oscillations, d is the channel thickness, ν is the kinematic viscosity.
In the case of fluids with a high viscosity contrast (ω1 ~ 1, ω2 >> 1), the Saffman-Taylor instability can occur when a high-viscosity fluid is displaced by a low-viscosity one. This instability manifests as the penetration of low-viscosity “fingers” into the viscous fluid [1,2]. The Saffman-Taylor instability can occur at the interface of immiscible and miscible fluids. In the case of immiscible fluids, the scale of the instability is determined by surface tension [3,4]. In the context of miscible fluids, the wave number of perturbations is attributed to the combined effects of molecular and hydrodynamic diffusion, which are influenced by the joint action of convection (destabilization) and dissipation (stabilization) [5,6]. In [7–9], a novel type of oscillatory finger instability which takes place within a fraction of the oscillation cycle was documented. The oscillatory viscous fingering in rectangular, conical, and cylindrical cells has been experimentally studied in [7–9], respectively. These studies show that the different character of motion of fluids of different viscosities in a slotted channel (viscous/non-viscous oscillations) is the primary cause of this phenomenon. The studies also relate to the case of extremely high viscosity contrast (ω1 ~ 1, ω2 >> 1), with one of the fluids making viscous oscillations in accordance with Darcy’s law and the other making non-viscous oscillations. It should be noted that in instances where the dimensionless frequencies are relatively similar in magnitude, the Saffman-Taylor oscillatory instability does not occur.
It is of particular interest to consider the limiting case of ω1 >> 1, ω2 >> 1, in which flows of both fluids are inviscid, and inertial effects may be observed due to contrasting densities. The excitation of standing waves at the interface between two fluids of different densities in the presence of piston oscillations in a vertical slotted channel was experimentally found in [10,11]. Excitation of harmonic waves (when the frequency of oscillations coincides with that of the liquid column) and subharmonic waves with a frequency of half that of the oscillations were observed. The present study is designed to clarify the nature of this difference and the role of surface tension. The paper presents the findings of a research study examining the effect of varying surface tension on the dynamics of oscillating fluids. The phenomenon under investigation is new but has common roots with the known and systematically studied phenomenon of parametric oscillations of the interface in a cavity which is known as Faraday waves.
In this context, it is worthwhile to consider a brief description of Faraday waves. The phenomenon of wave excitation at the interface between fluids in cavities undergoing vertical harmonic oscillations has been documented in detail in [12–14]. This type of instability is known in the literature as “Faraday waves”, a term inspired by Faraday’s initial observations of standing waves on the surface of mercury [15,16]. Initially, the phenomenon of standing waves, or ripples, was observed at the free surface of fluids. Subsequent research efforts were directed toward the examination of the interface dynamics of a pair of fluids within containers under harmonic vertical oscillations [17] and Faraday waves in non-Newtonian fluids [18,19]. It is possible to excite a standing wave characterized by oscillations at a frequency synchronous with that of an external force (a harmonic response) [10,20,21] or a wave with a frequency that is a multiple of the external frequency (a subharmonic response) [22,23]. Faraday ripples are manifested in the formation of gravity-capillary standing waves at the interface of fluids under the effect of an oscillating force field, typically of an inertial nature. The dispersion relation for gravity-capillary waves developing at the interface between low-viscosity fluids of different densities in an infinite container undergoing vertical oscillations is presented in [24]. A dispersion relation that takes into account energy dissipation in viscous boundary layers that emerge near the interface is presented in [25]. Nevertheless, for the low-viscosity fluids under consideration in this paper, the impact of the supplementary term derived in [25] is insignificant and does not result in a prominent effect on the interface dynamics.
In contrast, interfacial tension is a crucial factor affecting the dynamics of the interface between fluids. Recently, it was demonstrated the importance of the out-of-plane curvature, whose contribution has been neglected so far in the literature [26].
The proximity of the side walls in slotted channels can have a considerable impact on the oscillating fluid surface profile [27]. New theoretical and experimental data on the effect of capillary forces including dissipation in Stokes boundary layers on the excitation of Faraday ripples at the free surface of the fluid in a vertical Hele-Shaw cell subjected to vertical oscillations are presented in [28]. The study demonstrates that incorporating the out-of-plane interface curvature and dissipation in the boundary layers near the cell side walls results in an increase in the stability threshold and frequency detuning while the natural frequencies of the wave oscillations are shifted downward.
In contrast with the classical formulation, which describes the development of Faraday waves at the interface between fluids in an oscillating cavity, the present study examines the dynamics of the interface oscillating in a fixed vertical slotted channel. The objective of the study is to investigate the threshold and overcritical dynamics of the interface between two fluids, with a particular focus on the effect of surface tension, and to determine the control parameters of the problem.
To the best of the authors’ knowledge, this is the first study of the influence of tension at the interface between two fluids on a new phenomenon—the oscillatory excitation of a parametric wave at the interface between two low-viscosity fluids in a narrow gap. It is found that an increase in interfacial tension leads to transition from subharmonic waves to harmonic ones, existing simultaneously at the intermediate values of interfacial tension. The applied interest of the conducted research lies in the possibility of oscillatory control of the interphase boundary in slot channels in order to intensify heat and mass transfer.
The dynamics of an oscillating interface between two low-viscosity immiscible fluids of different densities in a vertical flat slotted channel is experimentally investigated. The experiments are conducted within a rectangular channel with dimensions of width L = 7.5 cm, height H = 11.5 cm, and gap width d = 0.23 cm (Fig. 1). The experiments are conducted with three pairs of fluids with different surface tension coefficients. All experiments were carried out at an ambient temperature of 23 ± 1°C. The characteristics of the fluids at this temperature are given in Table 1.
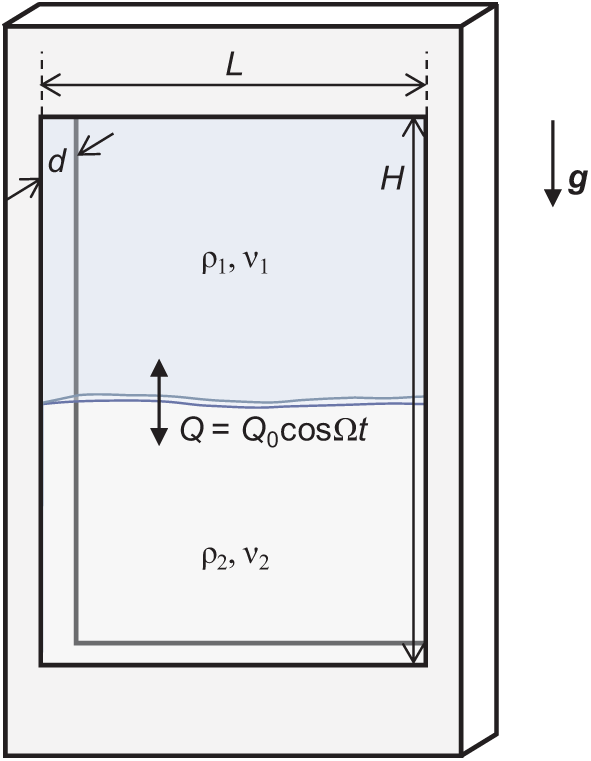
Figure 1: Sketch of the slotted channel
The channel is filled with a pair of fluids, with their interface positioned at the mid-height level of the slotted channel. The denser fluid (Fluorinert FC-40) is located in the lower part of the channel while the less dense fluid (water, water with the addition of a surfactant, silicone oil PMS-0.65) is located in the upper part. The fluid-filled channel is connected to a hydraulic circuit that provides oscillatory motion of the interface due to harmonic changes in the flow rate of the fluid pumped through the channel. The oscillating motion of the liquid in a closed circuit is set by a push-pull pump. The volume of fluid pumped through the channel varies by the law Q = Q0 cos Ωt, where Q0 is the amplitude of the pumped fluid volume, Ω = 2πf is the radian frequency. To ensure uniform piston oscillations of the liquids in the gap, pressure equalization of the pumped liquids at the upper and lower ends of the channel is provided by special expansion chambers. A detailed description of the hydraulic circuit and the cavity construction can be found in [9].
Let us briefly review the experiment technique which is similar to that used in reference [11]. In the absence of oscillations, the denser fluid occupies a stable position in the lower part of the channel while the less dense fluid occupies the upper part. The interface between the fluids remains undisturbed and horizontal. The digital generator ZETLab is used to set the frequency of oscillations with an accuracy 0.01 Hz and to increase the amplitude of fluid oscillations in a stepwise manner. The oscillation frequency f varies within the range of 2–14 Hz while the peak-to-peak displacement Δl of the liquid column ranges from 0 to 1 cm. The latter is measured with an accuracy 0.1 mm by the oscillation peak-to-peak displacement of light-scattering particles which visualize the piston oscillations of the liquid column outside the viscous boundary layers at a distance of approximately 4 cm from the interface. The oscillating interface is recorded at each step of the experiment through the transparent channel wall using a FUJIFILM X-E4 camera at 120 fps. The video sequence is converted into a series of photos for further image processing.
To obtain contrast images of the interface, the slotted channel is illuminated with a green laser or a collimated white light source mounted behind the slotted channel. In the experiments conducted with fluid pairs #1 and #2 (see Table 1), light-scattering particles with a diameter of 40 μm and a density of 1.02 g/cm3 were added to the upper fluid to visualize the currents that arise near the interface. Blue food coloring is added to the less dense fluid in the experiments conducted with Fluorinert FC-40 and water (#3 in Table 1).
When the channel is vertical, the interface and the liquid column oscillate vertically. At small amplitudes of fluid oscillations, the interface oscillates symmetrically with respect to the initial position undergoing a shift to the upper fluid and lower one at the same distance. The interface is observed to be horizontal and undisturbed. Once a critical value of the oscillation amplitude is reached, the interface becomes unstable to the excitation of parametric oscillations. The interface oscillates at a frequency equal to that of the piston oscillations of the liquid column (synchronous response) or at a frequency that is half that of the oscillations of the liquid column (subharmonic response). The observed instability is a novel phenomenon. In contrast with the classical scenario, we consider an oscillating interface in a fixed slotted channel.
A synchronous response is observed in experiments conducted with the fluid pair Fluorinert-water whose interfacial tension coefficient is σ = 51 mN/m (Fig. 2). To ensure the clarity of the experimental results, the width of all photos of the interface presented in the paper is aligned with the width of the slotted channel (L = 7.45 cm). A harmonic standing wave is excited at the oscillating interface in a threshold manner synchronized with the piston oscillations of the liquid column. The excitation of instability is soft and is believed to occur when the contact line undergoes a disruption marking the transition from meniscus to piston oscillations. The profile of the interface in the phases of its maximum displacement into the upper and lower fluid at increasing piston oscillation amplitude is illustrated in Fig. 2. It can be noted that the shape of the interphase boundary depends on the phase of the oscillatory process. In the phase of maximum displacement of the interface into the upper liquid (Fig. 2a,c,e), the interface profile can be described as a series of peaks, with a constant distance between neighboring peaks. In the opposite phase of the oscillatory process, when the interface is maximally shifted downward (Fig. 2b,d,f), the shape of the standing wave also changes to the opposite.

Figure 2: Profile of the Fluorinert-water interface in the phases of its maximum displacement to the upper (a, c, e) and lower (b, d, f) fluids: Δl = 0.22 cm (a, b), Δl = 0.24 cm (c, d), Δl = 0.31 cm (e, f); σ = 51 mN/m, f = 5.40 Hz
The spatial wave period λ (the distance between neighboring standing wave peaks) is significantly greater than the channel thickness and is dependent upon the frequency of the fluid oscillations. An increase in the amplitude of piston oscillations results in an increase in the amplitude of the interface oscillations in the peaks of the standing wave while the spatial period λ remains almost unchanged. No evidence of hysteresis is found. A detailed description of the technique for determining the instability threshold is given in [10].
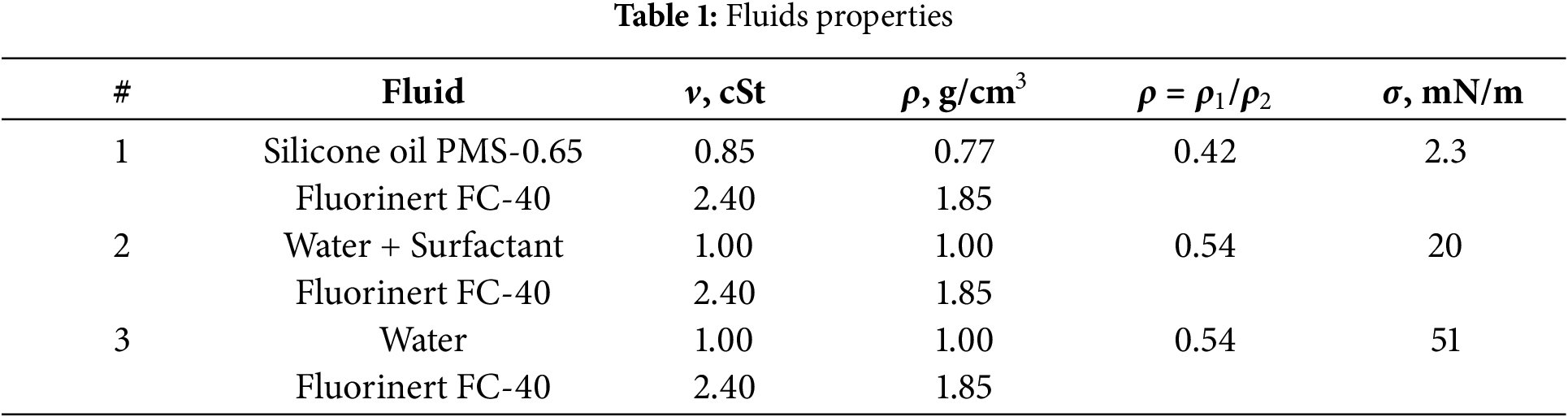
Experiments with the fluid pair Fluorinert-silicone oil (surface tension coefficient σ = 2.3 mN/m) demonstrate a subharmonic response, as described in [11]. Once the critical value of the amplitude of piston oscillations is reached, a standing wave forms at the interface. This frequency is precisely half that of the fluid oscillations in the slotted channel (Fig. 3). In the maximum displacement phase, the interface takes the form of a sinusoid. Through a period of piston oscillations of the liquid, the hills and troughs of the wave are reversed. The excitation of the standing wave with a hysteresis is observed at small amplitudes of liquid column oscillations.
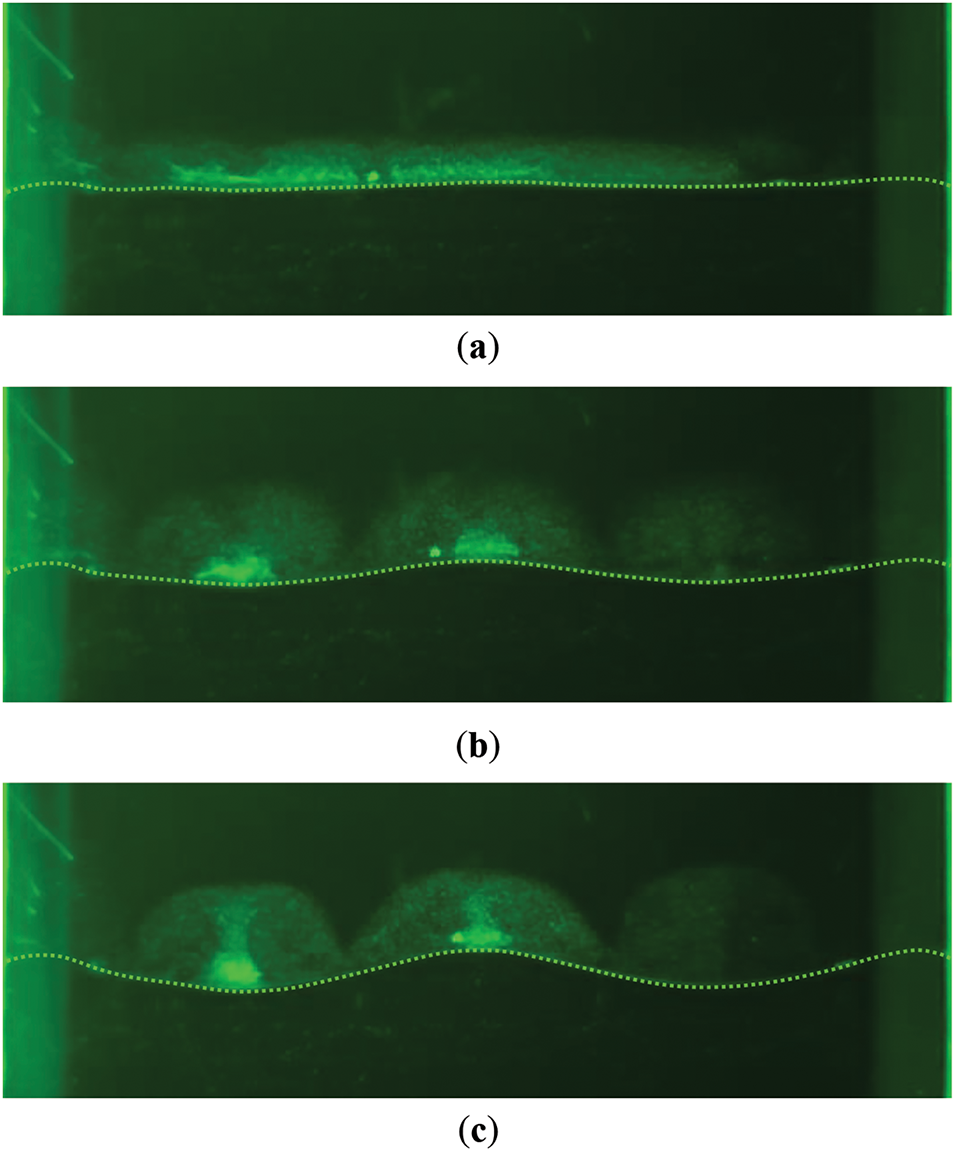
Figure 3: Photos of the interface between Fluorinert and silicone oil PMS-0.65 in the phase of maximum upward displacement of the interface at different amplitudes of piston oscillations: Δl = 0.25, 0.26 and 0.31 cm (a–c), σ = 2.3 mN/m, f = 7.75 Hz
Fig. 3 shows the profile of the interface in the phase of its maximum displacement into the upper fluid. Fig. 3 illustrates that an increase in the amplitude of piston oscillations at a definite oscillation frequency results in an augmented height of the standing wave peaks while the number of peaks remains unaltered. An increase in the oscillation frequency results in an increase in the number of peaks which in turn leads to a decrease in the standing wave length λ. The change in standing wave length with frequency occurs in a discrete manner. It is revealed that the number of standing wave wavelengths m, fitted along the width of the channel, adjusts to its width. For this pair of fluids (#1 in Table 1), waves with m = 1.5–6.5 are experimentally detected. Notably, there are standing wave displacement antinodes on the cavity narrow side walls in all experiments. A similar configuration of standing wave nodes and antinodes was identified in the study of classical Faraday waves in slotted channels of finite width [29]. Parametric oscillations result in the excitation of the time-averaged flows in the vicinity of the oscillating interface. These flows take the form of a system of counter-rotating vortices with their rotation axes oriented perpendicular to the cell plane. The photos (Fig. 3) show the tracer particles suspended near the interface illuminated by the green laser.
In experiments with a pair of fluids whose surface tension coefficient has an intermediate value σ = 20 mN/m (Fluorinert-water with surfactant), both synchronous and subharmonic oscillations are identified (Fig. 4). With an increase in the amplitude of the oscillations of the liquid column, instability manifests itself in the threshold occurrence of a harmonic standing wave that performs synchronous oscillations with the column: Fig. 4 shows the profile of the interphase boundary in opposite phases of liquid column oscillations Ωt = 0 (Fig. 4a) and Ωt = π (Fig. 4b). It is evident that after half an oscillation cycle, in addition to the interface displacement, the phase of the standing wave becomes reversed. As the amplitude increases, a threshold is reached where subharmonic oscillations of the interface are excited at a frequency that is half that of the external forced oscillations (Fig. 4c–f).
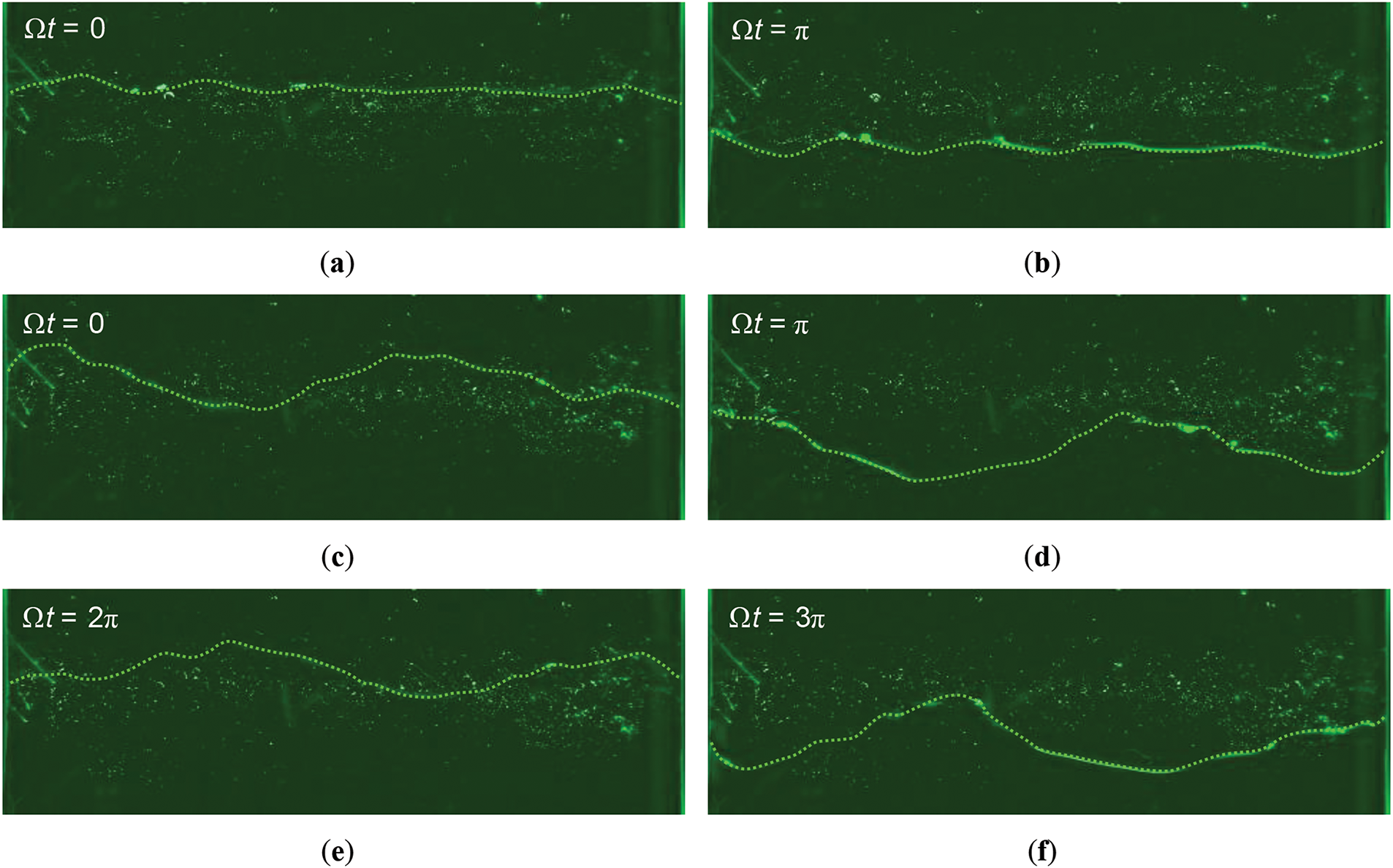
Figure 4: Synchronous (harmonic) (a, b) and subharmonic (c–f) wavy oscillations of the interface between Fluorinert and water with surfactant at different phases of the oscillation cycle: Δl = 0.61 (a, b) and 0.76 cm (c–f), σ = 20 mN/m, f = 8.00 Hz
Fig. 4c–f illustrates the evolution of the oscillating interface over time in the supercritical region. Here, the phase in which the fluid and the interface are maximally shifted upward is selected as the zero phase of the oscillation cycle (Fig. 4с). During the first part of the oscillation cycle, the curved interface maintains its shape and moves downward into the lower fluid (Fig. 4d). During the second part of the oscillation cycle of the fluid, the phase of the standing wave oscillations is reversed (Fig. 4e). During the second cycle of the liquid column oscillation, the dynamics of the interface is preserved (Fig. 4e,f), and the standing wave returns to its original shape and position as in Fig. 4c. The data demonstrate that the wave length λ increases significantly in the presence of subharmonic oscillations. At the threshold of subharmonic oscillations, their amplitude is high, and the subharmonic mode is the dominant phenomenon, though it does not entirely suppress the synchronous mode. Fig. 4c–f illustrates that the synchronous mode manifests as small-scale patterns against the background of large-scale patterns induced by subharmonic oscillations. Fig. 5 illustrates the transition from synchronous interface oscillations to subharmonic oscillations, accompanied by a notable increase in the standing wave length with rising amplitude of oscillations at a fixed frequency of piston oscillations. Hereinafter, the error bars of the measured parameters are not shown in the graphs if they are smaller than the symbols. Our findings indicate that in both synchronous and subharmonic modes, the amplitude of the standing wave increases with the amplitude of the fluid oscillation at a fixed frequency while the wavelength remains unchanged. The letters in Fig. 5 correspond to photos (a) and (c) in Fig. 4. No evidence of hysteresis is observed in the dependence of the standing wave length on the amplitude of piston oscillations.
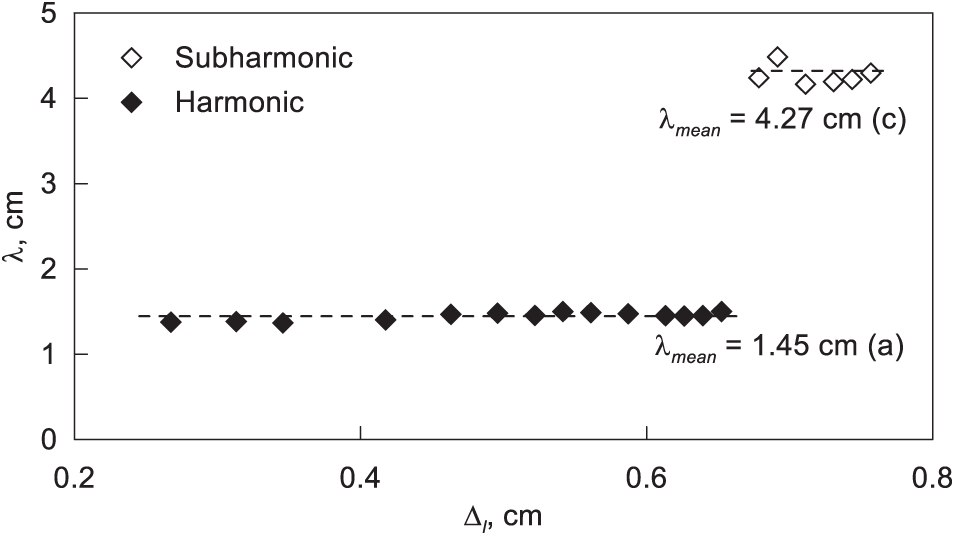
Figure 5: Dependence of the standing wave length λ on the amplitude of piston oscillations Δl of the interface between Fluorinert and water with surfactant at f = 8.00 Hz. The letters correspond to photos (a, c) in Fig. 4
As mentioned above, for both synchronous and subharmonic responses, the excitation of the standing wave occurs in a threshold manner. Furthermore, it is demonstrated that synchronous oscillations of the interface can be induced by fluid oscillations at amplitudes that are relatively small. It is presumed that the threshold of the wave is related to the disruption of the contact line and the transition from meniscus to piston oscillations.
Fig. 6 illustrates the dependence of the threshold value of the peak-to-peak displacement Δl on the oscillation frequency for three pairs of fluids. It can be observed that at the threshold of synchronous mode excitation, Δl is independent of frequency and takes a constant value of 0.16 ± 0.03 cm across the entire frequency range studied for the two pairs of fluids (dashed line in Fig. 6). In contrast to the soft excitation of synchronous oscillations, subharmonic mode excitation in the case of σ = 20 mN/m has finite-amplitude character.
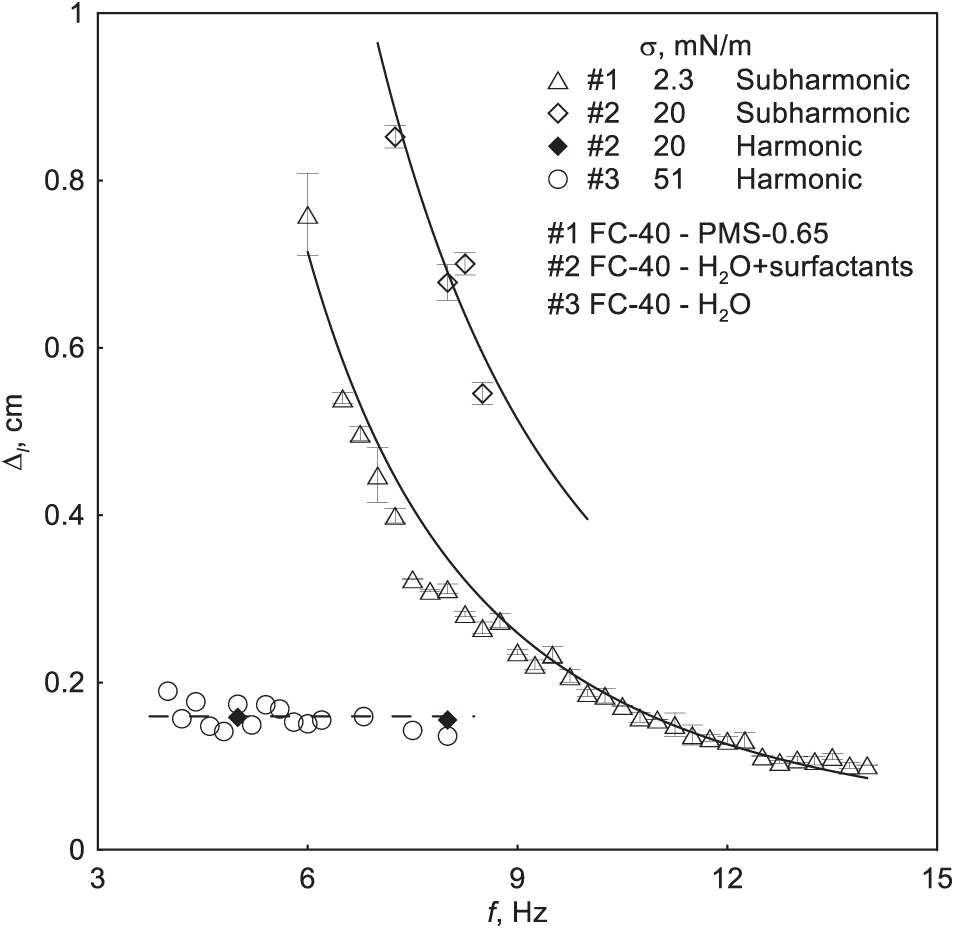
Figure 6: Dependence of the threshold value of the fluid peak-to-peak displacement Δl on the oscillation frequency f. The solid lines correspond to the law Δl ~ f−2.5; the dashed line corresponds to Δl = 0.16 cm
The critical value of the fluid peak-to-peak displacement at σ = 2.3 mN/m [11] decreases monotonically with increasing oscillation frequency (Fig. 6). The solid lines on the graph correspond to the law Δl ~ f −2.5. The physical meaning of the obtained dependence is that the threshold is determined by the oscillatory acceleration, which decreases with frequency according to the law Δl f 2 ~ f −0.5. Note that the wave-length of the excited wave decreases with frequency. It is in agreement with the classical case of vibration excitation of Faraday ripples [17], when the vibration acceleration is decisive. In this scenario, finite-amplitude excitation is observed only in the low-frequency range. For frequencies above 8 Hz, the soft excitation of oscillations without hysteresis is revealed (see [11]).
In the overcritical region, a change in the oscillation frequency of the liquid column results in a change in the number of peaks and, consequently, a change in the standing wave length. As the frequency of oscillation increases, the standing wave length decreases in a discrete manner (Fig. 7). In other words, there are narrow ranges of frequencies at which the wavelength remains unchanged. This discrete transition from one number of waves m to another also affects the threshold of instability onset, as demonstrated by the step-like dependence of the peak-to-peak displacement on the oscillation frequency in the threshold of parametric oscillations excitation (Fig. 6). The findings indicate that the synchronous and subharmonic oscillations of the interface are of gravity-capillary nature.
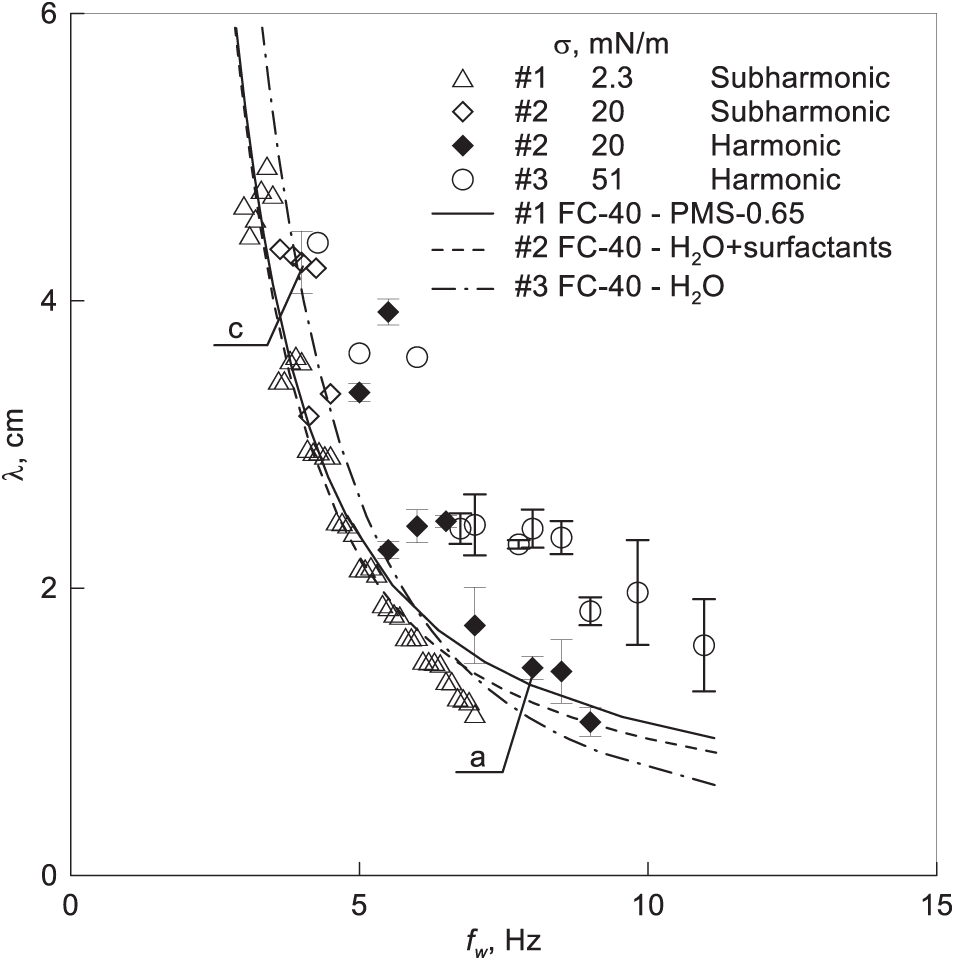
Figure 7: Dependence of the standing wave length λ on the wave oscillation frequency fw in experiments with pairs of fluids with different surface tensions. Letters correspond to photos (a, c) in Fig. 4
The classical example of such waves are Faraday waves [15,16]. The dispersion relation for gravity-capillary waves that are generated at the interface between two low-viscosity immiscible fluids of different densities in a deep channel, in the absence of side walls, is as follows [24]:
Ω2w=gkρ1−ρ2ρ1+ρ2+σk3ρ1+ρ2,Ω2w=gkρ1−ρ2ρ1+ρ2+σk3ρ1+ρ2,(1)
where k ≡ 2π/λ is the wavenumber, Ωw is the radian frequency of the wave oscillations (Ωw = Ω for the synchronous response; Ωw = Ω/2 for the subharmonic response). Fig. 7 presents a comparison between the experimental data on the standing wave length and the theoretical model proposed by Benjamin et al. [24]. The graph illustrates the results of standing wave length measurements as a function of the wave oscillation frequency in the context of both synchronous and subharmonic responses. The lines on the graph correspond to the dispersion relation (1), calculated for three different pairs of working fluids, considering their characteristics.
The results of experiments demonstrate that one of the parameters that govern the instability of the oscillating interface in the slotted channel is the surface tension σ. An increase in the surface tension has a stabilizing effect preventing the excitation of subharmonic oscillations. Instead, synchronous wave oscillations develop at the threshold of instability. Synchronous wave oscillations are gravity-capillary waves analogous to Faraday waves which oscillate at the frequency of the external force.
If the capillary wavelength λcap=√2σ/g(ρ1−ρ2)λcap=√2σ/g(ρ1−ρ2) is selected as the unit of length and the parameter √λcap/g√λcap/g is selected as the unit of time, then the dispersion relation (1) will take the following form:
Ω∗2=k∗+12k∗3Ω∗2=k∗+12k∗3(2)
here, Ω∗≡Ωw√λcap/AgΩ∗≡Ωw√λcap/Ag, A≡(ρ1−ρ2)/(ρ1+ρ2)A≡(ρ1−ρ2)/(ρ1+ρ2) is the Atwood number, k∗≡2πλcap/λk∗≡2πλcap/λ is the dimensionless wavenumber. A comparison of experimental data with the classical dispersion relation for the oscillations of the interface between inviscid fluids [24] is presented in Fig. 8. The qualitative agreement between the experimental data and the theoretical model suggests that the oscillations of the interface can be classified as gravity-capillary waves. The subharmonic oscillations are observed at small dimensionless frequencies Ω* (small wave numbers k*) corresponding to gravitational waves when the surface tension is negligible. By contrast, synchronous standing waves appear in the capillary wave region (large values of Ω* and k*).
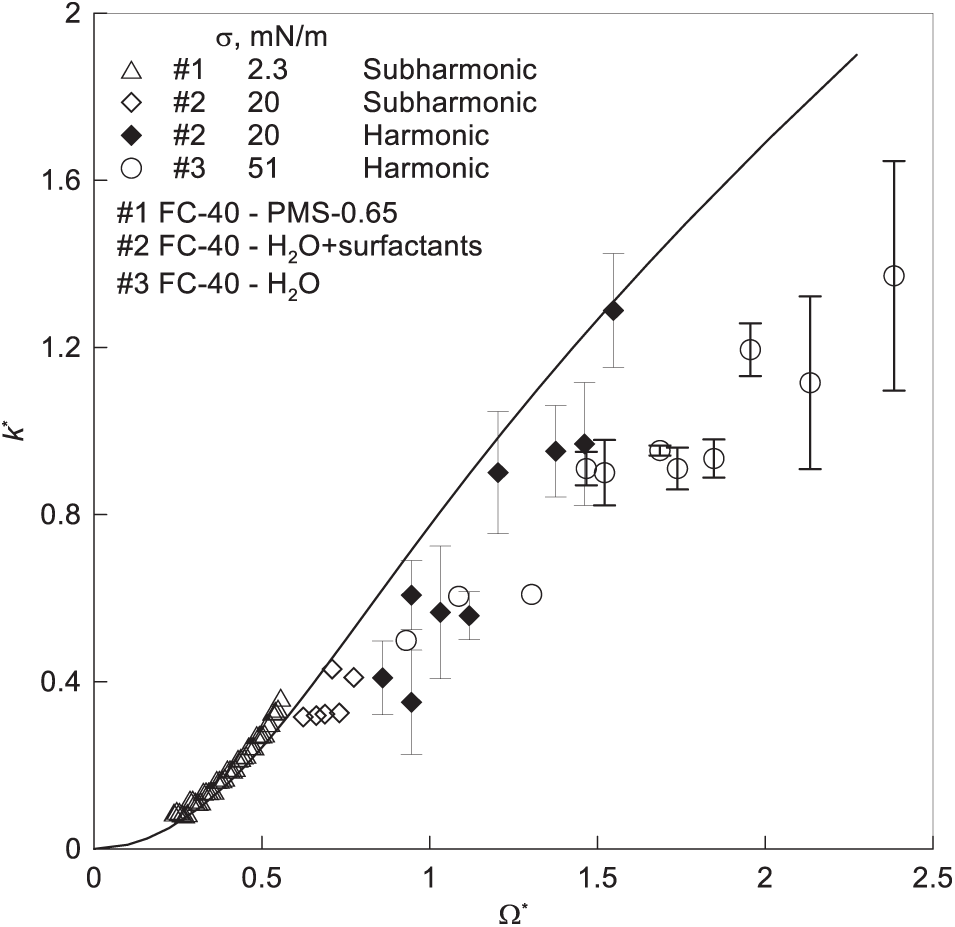
Figure 8: Dependence of the dimensionless wave number k* on the dimensionless frequency Ω* in experiments with various fluid pairs
The results of the experimental investigation are in good agreement with the theoretical data for the pair of low-viscosity fluids in the case of low surface tension σ = 2.3 mN/m (Fig. 8). An increase in the surface tension to σ = 20 mN/m results in not only a shift of experimental data to the region of large dimensionless frequencies but also a notable reduction in the wave number of the observed waves (in this instance, synchronous) in comparison to the theoretical curve. The gap between the experimental data and the theoretical predictions widens as the interfacial tension increases up to σ = 51 mN/m in the region of high dimensionless frequencies where capillary effects are significant (Fig. 8).
In the case of synchronous interface oscillations, experimental wavelengths differ from the predictions of the theory [24] which can be explained by the qualitative difference between the problem under consideration and the case of an infinite interface. It is important to note that even in the approximation of inviscid fluid oscillations, the contact lines on the channel walls begin to play a significant role. In the classical problem concerning inviscid gravity-capillary waves in a channel of finite width, the effect of capillary forces at the contact line between the fluid and the side walls of the slotted channel is not considered. It is commonly accepted that the contact angle between the fluids and the channel wall is 90° (see for example reference [30]). In this context, it is of interest to study the excitation of wave oscillations at the interface in a Hele-Shaw cell in the classical setting whereby the instability is initiated at the static interface by an oscillating force field.
Recent research studies [26,27,31,32] concentrated on the experimental and theoretical investigation of the fluid interface dynamics in vibrating Hele-Shaw cells. The theoretical model [24] assumes that the fluid motion in the channel obeys Darcy’s law which allows us to use a two-dimensional formulation of the problem after averaging over the thickness of the Hele-Shaw layer. This does not meet the specified criteria for the present research. This approach fails to consider the impact of the contact angle on the profile of the interface as well as the thickness (δ=√2ν/Ωδ=√2ν/Ω << d) of the Stokes boundary layers that occur in the vicinity of the slotted channel sidewalls. While the aforementioned results are not directly applicable to the present research, the cited studies suggest that considering dissipation and additional curvature of the interface in the plane perpendicular to the side walls of the slotted channel results in a transformation of the dispersion relation and a notable reduction of the wave number. It could be reasonably assumed that the observed decrease in the wave number of the standing wave and the transition from synchronous to subharmonic wave oscillations at an increase in the surface tension is explained by this phenomenon.
The experimental results indicate that the peak-to-peak displacement of the piston oscillations plays a pivotal role in the emergence of instability. Fig. 9 illustrates experimental results in the dimensionless parameter plane Ω*, Γ, where Γ = blΩ2/g is the dimensionless oscillatory acceleration, bl = Δl/2 is the amplitude of piston oscillations, and g is the acceleration of gravity. In the region of small dimensionless frequencies, where the dimensionless acceleration Γ monotonically decreases with increasing dimensionless frequency Ω*, the development of a subharmonic mode is observed (region I in Fig. 9). In the region Ω* > 0.8, the development of a synchronous mode of oscillations is observed. The threshold dimensionless acceleration Γ increases with increasing Ω* (region II in Fig. 9) due to the fact that the excitation threshold is characterized by a constant value of the liquid column oscillation amplitude (Fig. 6). The upper boundary of the region II is a result of the finite range of amplitudes of fluid oscillations. Of particular interest in the graph are the data obtained for the fluid pair #2. At small dimensionless accelerations, a synchronous wave mode develops (filled rhombuses in Fig. 9), and a transition from synchronous to subharmonic mode is observed with increasing dimensionless acceleration (empty rhombuses in Fig. 9). The dimensionless acceleration Ω* in the dispersion relation [24] is calculated through the oscillation frequency of the wave Ωw. Consequently, the transition is accompanied by a shift to the region of lower frequencies Ω*. As illustrated in Fig. 9, the threshold value of Γ is observed to be higher in the case of σ = 20 mN/m than in the case of σ = 2.3 mN/m. This phenomenon can be understood not only in terms of the development of subharmonic oscillations against the background of synchronous oscillations but also due to the effect of surface tension. As shown in [11], the stability threshold increases with increasing out-of-plane curvature and strengthening of capillary effects in the plane perpendicular to the side walls of the channel.
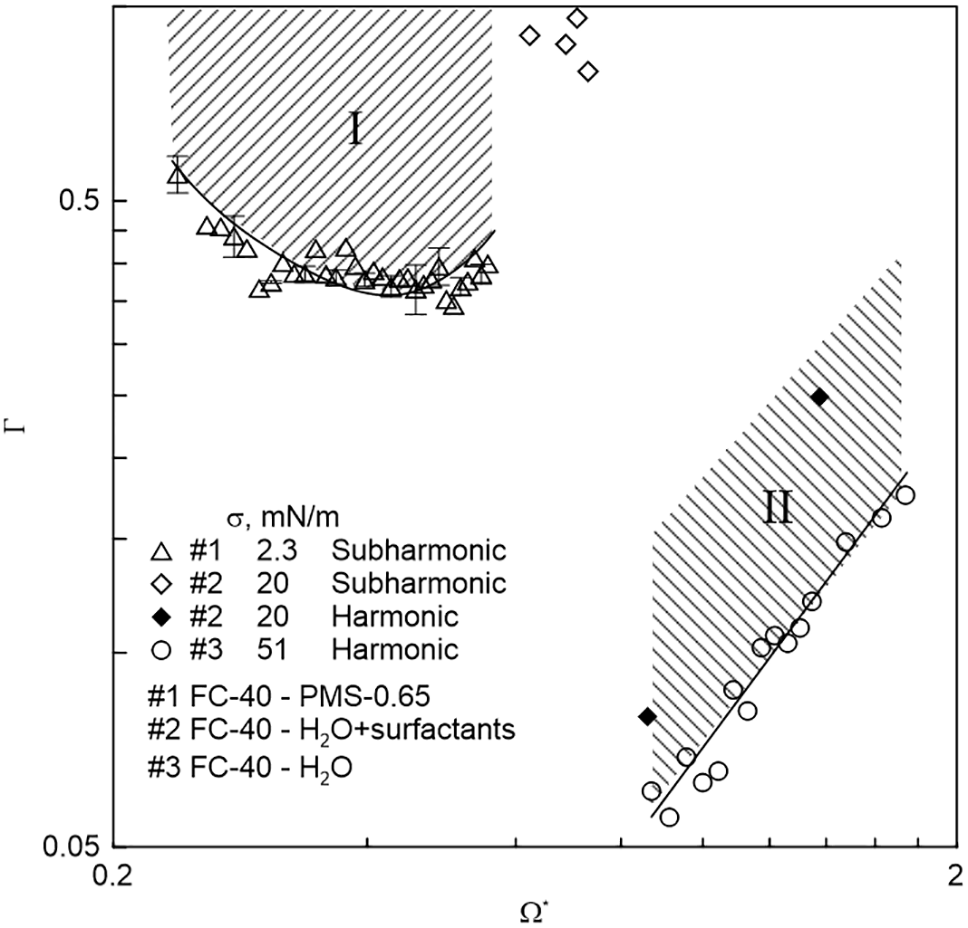
Figure 9: Dependence of the critical dimensionless oscillatory acceleration Γ on the dimensionless frequency Ω*
It should be noted that currently the attention of scientists is drawn to the influence of vibrations on different systems with interfaces [33,34] as well of various complicating factors on the behavior of the interphase boundary (including the wave dynamics): rotation, temperature nonuniformity, rheological properties of liquids, electric field and shear stresses [35,36]. The latter are important in applied terms. The influence of these factors on the new type of instability studied in the work could be a promising task.
A systematic experimental investigation of the oscillatory dynamics of the interface between two low-viscosity fluids of different densities oscillating in a normal direction relative to the interface within a vertical slotted channel is conducted. In the case of small oscillation amplitudes, the interface remains horizontal. It is demonstrated that an increase in the oscillation amplitude results in the threshold excitation of parametric oscillations of the interface in the form of a standing wave in the plane of the channel. The excitation of oscillations is observed at a frequency equal to that of the piston oscillations of the liquid column (synchronous response) or at a frequency that is twice less than the frequency of the liquid column oscillations (subharmonic response). The detected type of instability is gravity-capillary. The wavelength-frequency dependence is only qualitatively consistent with the classical dispersion relation for low-viscosity fluids in a wide and deep basin. The impact of sidewalls coupled with the unique shape of the interface which oscillates in the form of a tongue with an almost fixed contact line results in a reduction in the natural frequency of oscillations. The excitation thresholds of standing waves and their overcritical dynamics are analyzed for three pairs of fluids with different surface tension coefficients. It is demonstrated that the surface tension plays a pivotal role. In experiments conducted with fluids whose surface tension is relatively high, only a synchronous wave mode (Ωw = Ω) is observed. The instability develops when the contact line is disrupted and the transition from the meniscus to piston oscillations occurs. In experiments conducted with a pair of fluids with a relatively low surface tension, subharmonic oscillations are observed (Ωw = Ω/2). In the region of dimensionless frequencies Ω* > 0.8, at moderate values of interfacial tension (σ = 20 mN/m), a synchronous wave mode develops at the stability threshold. However, a further increase in dimensionless acceleration results in a transition from synchronous to subharmonic mode. The development of subharmonic oscillations occurs against the background of a synchronous standing wave, and the interface oscillations are a superposition of two standing waves.
The article presents the results of first study of the influence of tension at the interface between two liquids on a new phenomenon—the oscillatory excitation of parametric waves at the interface between two liquids in vertical slotted channels. It is found that, an increase in interfacial tension leads to transition from subharmonic waves to harmonic ones. At the intermediate values of interfacial tension, both harmonic and subharmonic waves manifest themselves simultaneously. The discovered phenomenon has important practical significance, in particular, in terms of intensifying heat and mass transfer in a two-fluid system in slotted channels, and requires further investigation.
Acknowledgement: The authors are grateful to Dr. Denis Polezhaev for fruitful discussions.
Funding Statement: The research was supported by the Ministry of Education of the Russian Federation (Project No. 1023032300071-6-2.3.1).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Victor Kozlov; data collection: Olga Vlasova, Veronika Dyakova; analysis and interpretation of results: Victor Kozlov, Olga Vlasova, Veronika Dyakova; draft manuscript preparation: Victor Kozlov, Olga Vlasova, Veronika Dyakova. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Abbreviations
| A | Atwood number |
| bl | Amplitude of piston oscillations, cm |
| d | Channel thickness, cm |
| f | Oscillation frequency, Hz |
| fw | Frequency of the wave interface oscillations, Hz |
| g | Acceleration of gravity, cm/s2 |
| H | Channel height, cm |
| k | Wave number, 1/cm |
| k* | Dimensionless wave number |
| L | Channel width, cm |
| m | Number of standing wavelengths fitting across the channel width |
| t | Time, s |
| Q | Volume of liquid pumped through a channel, cm3 |
| Q0 | Amplitude value of pumped liquid volume, cm3 |
| Γ | Dimensionless oscillation acceleration |
| δ | The Stokes boundary layer thickness, cm |
| Δl | Peak-to-peak displacement of the piston fluid oscillations, cm |
| λ | Wavelength, cm |
| λcap | Capillary wavelength, cm |
| ν | Kinematic viscosity of the fluids, cSt |
| ρ | Fluid relative density |
| ρ1 | Density of the less dense fluid, g/cm3 |
| ρ2 | Density of the denser fluid, g/cm3 |
| ρ3 | Density of light-scattering particles, g/cm3 |
| σ | Surface tension, mN/m |
| ω | Dimensionless frequency of oscillations |
| Ω | Radian frequency liquid column oscillations, 1/s |
| Ωw | Radian frequency of the standing wave oscillations, 1/s |
| Ω* | Dimensionless radian frequency of wave oscillations |
References
1. Saffman PG. Viscous fingering in hele-shaw cells. J Fluid Mech. 1986;173:73–94. doi:10.1017/S0022112086001088. [Google Scholar] [CrossRef]
2. Saffman PG, Taylor GI. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc R Soc Lond Ser A. 1958;245(1242):312–29. doi:10.1098/rspa.1958.0085. [Google Scholar] [CrossRef]
3. Chuoke RL, van Meurs P, van der Poel C. The instability of slow, immiscible, viscous liquid-liquid displacements in permeable media. Trans AIME. 1959;216(1):188–94. doi:10.2118/1141-G. [Google Scholar] [CrossRef]
4. Park CW, Homsy GM. Two-phase displacement in hele shaw cells: theory. J Fluid Mech. 1984;139:291–308. doi:10.1017/S0022112084000367. [Google Scholar] [CrossRef]
5. Yuan Q, Zhou X, Wang J, Zeng F, Knorr KD, Imran M. Control of viscous fingering and mixing in miscible displacements with time-dependent rates. AlChE J. 2019;65(1):360–71. doi:10.1002/aic.16359. [Google Scholar] [CrossRef]
6. Keable D, Jones A, Krevor S, Muggeridge A, Jackson SJ. The effect of viscosity ratio and peclet number on miscible viscous fingering in a hele-shaw cell: a combined numerical and experimental study. Transp Porous Medium. 2022;143(1):23–45. doi:10.1007/s11242-022-01778-4. [Google Scholar] [CrossRef]
7. Kozlov V, Vlasova O. Oscillatory dynamics of immiscible liquids with high viscosity contrast in a rectangular Hele-Shaw channel. Phys Fluids. 2022;34(3):032121. doi:10.1063/5.0084363. [Google Scholar] [CrossRef]
8. Subbotin S, Karpunin I, Kurysheva D, Kozlov V. Effect of the density ratio on the oscillatory Saffman-Taylor instability in vertical conical Hele-Shaw cell. Phys Fluids. 2023;35(9):093102. doi:10.1063/5.0162264. [Google Scholar] [CrossRef]
9. Kozlov V, Karpunin I, Kozlov N. Finger instability of oscillating liquid-liquid interface in radial Hele-Shaw cell. Phys Fluids. 2020;32(10):102102. doi:10.1063/5.0018541. [Google Scholar] [CrossRef]
10. Kozlov VG, Vlasova OA, Dyakova VV. Stability of the interface of liquids oscillating in a vertical flat channel. Interfacial Phenom Heat Transf. 2024;12(1):15–25. doi:10.1615/InterfacPhenomHeatTransfer.2023049906. [Google Scholar] [CrossRef]
11. Kozlov V, Vlasova O, Dyakova V. Oscillatory excitation of Faraday waves on the interface of immiscible fluids in a slotted channel. Phys Fluids. 2024;36(10):102117. doi:10.1063/5.0230721. [Google Scholar] [CrossRef]
12. Miles J, Henderson D. Parametrically forced surface waves. Annu Rev Fluid Mech. 1990;22(1):143–65. doi:10.1146/annurev.fl.22.010190.001043. [Google Scholar] [CrossRef]
13. Muller HW, Friedrich R, Papathanassiou D. Theoretical and experimental investigations of the Faraday instability. In: Busse FH, Muller SC, editors. Evolution of spontaneous structures in dissipative continuous systems. Berlin/Heidelberg, Germany: Springer; 1998. p. 230–65. [Google Scholar]
14. Ibrahim RA. Recent advances in physics of fluid parametric sloshing and related problems. J Fluids Eng. 2015;137(9):090801. doi:10.1115/1.4029544. [Google Scholar] [CrossRef]
15. Faraday M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Proc R Soc Lond. 1837;3:49–51. doi:10.1098/rspl.1830.0024. [Google Scholar] [CrossRef]
16. Faraday MI. On the forms and states assumed by fluids in contact with vibrating elastic surfaces. Phil Trans R Soc Lond. 1831;121:319–40. [Google Scholar]
17. Lyubimov DV, Lyubimova TP, Cherepanov AA. Dynamics of interfaces in vibration fields. Moscow, Russia: FizMatLit. 2003 (In Russian). [Google Scholar]
18. Huo Q, Wang X. Faraday instability of non-Newtonian fluids under low-frequency vertical harmonic vibration. Phys of Fluids. 2022;34(9):094107. doi:10.1063/5.0108295. [Google Scholar] [CrossRef]
19. Varges PR, Azevedo PE, Fonseca BS, de Souza Mendes PR, Naccache MF, Martins AL. Immiscible liquid-liquid displacement flows in a Hele-Shaw cell including shear thinning effects. Phys Fluids. 2020;32(1):013105. doi:10.1063/1.5133054. [Google Scholar] [CrossRef]
20. Mathiessen L. Akustische Versuche, die Klieinsten Transversalivellen der Flussigkeiten Betreffend (Acoustic experiments concerning the smallest transverse waves in liquids). Ann Phys. 1868;134:107–17. [Google Scholar]
21. Mathiessen L. Uber die transversal-schwingungen tonender tropfbarer und elastisher flussigkeiten (on the transverse vibrations of ringing low-viscosity and elastic liquids). Ann Phys. 1870;141:375–93. [Google Scholar]
22. Rayleigh L. On the crispations of fluid resting upon a vibrating support. Lond Edinb Dubl Phil Mag. 1883;16(97):50–8. doi:10.1080/14786448308627392. [Google Scholar] [CrossRef]
23. Rayleigh L. On the maintenance of vibrations by forces of double frequency, and on the propagation of waves through a medium endowed with a periodic structure. Lond Edinb Dubl Phil Mag. 1887;24(147):145–59. doi:10.1080/14786448708628074. [Google Scholar] [CrossRef]
24. Benjamin TB, Ursell FJ. The stability of the plane free surface of a liquid in vertical periodic motion. Proc R Soc Lond Ser A. 1954;225(1163):505–15. doi:10.1098/rspa.1954.0218. [Google Scholar] [CrossRef]
25. Kumar K, Tuckerman LS. Parametric instability of the interface between two fluids. J Fluid Mech. 1994;279:49–68. doi:10.1017/S0022112094003812. [Google Scholar] [CrossRef]
26. Li J, Li X, Liao S. Stability and hysteresis of Faraday waves in hele-shaw cells. J Fluid Mech. 2019;871:694–716. doi:10.1017/jfm.2019.335. [Google Scholar] [CrossRef]
27. Li X, Li J, Li X, Liao S, Chen C. Effect of width on the properties of Faraday waves in Hele-Shaw cells. Sci China Phys Mech Astron. 2019;62(7):974711. doi:10.1007/s11433-018-9335-6. [Google Scholar] [CrossRef]
28. Bongarzone A, Jouron B, Viola F, Gallaire F. A revised gap-averaged Floquet analysis of Faraday waves in Hele-Shaw cells. J Fluid Mech. 2023;977:A45. doi:10.1017/jfm.2023.986. [Google Scholar] [CrossRef]
29. Liu D, Jiang X, Lin P. Numerical simulation of interfacial resonant Faraday waves between two immiscible liquids. Phys Fluids. 2024;36(2):022123. doi:10.1063/5.0190392. [Google Scholar] [CrossRef]
30. Lamb H. Hydrodynamics. Cambridge, UK: Cambridge University Press; 1924. [Google Scholar]
31. Li J, Li X, Chen K, Xie B, Liao S. Faraday waves in a hele-shaw cell. Phys Fluids. 2018;30(4):042106. doi:10.1063/1.5022424. [Google Scholar] [CrossRef]
32. Truzzolillo D, Cipelletti L. Hydrodynamic instabilities in miscible fluids. J Phys Condens Matter. 2018;30(3):033001. doi:10.1088/1361-648X/aa9eaa. [Google Scholar] [PubMed] [CrossRef]
33. Lyubimova T, Garicheva Y, Ivantsov A. The behavior of a gas bubble in a square cavity filled with a viscous liquid undergoing vibrations. Fluid Dyn Mater Process. 2024;20(11):2417–29. doi:10.32604/fdmp.2024.052391. [Google Scholar] [CrossRef]
34. Zimasova A, Kozlov V, Kozlov N. Stability of a viscous liquid film in a rotating cylindrical cavity under angular vibrations. Fluid Dyn Mater Process. 2024;20(12):2693–707. doi:10.32604/fdmp.2024.052398. [Google Scholar] [CrossRef]
35. Yadav D, Awasthi M, Kumar A, Dutt N. Swirling capillary instability of Rivlin–Ericksen liquid with heat transfer and axial electric field. Physics. 2024;6(2):828–44. doi:10.3390/physics6020051. [Google Scholar] [CrossRef]
36. Srija R, Singh AK, Awasthi MK, Yadav D. Impact of swirling on capillary instability of Walter’s B viscoelastic fluid-viscous fluid interface with heat and mass transfer. Proc Inst Mech Eng Part C J Mech Eng Sci. 2024;238(11):5359–68. doi:10.1177/09544062231213186. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
