 Open Access
Open Access
ARTICLE
Enhanced Boiling Heat Transfer in Water Pools with Perforated Copper Beads and Sodium Dodecyl Sulfate Surfactant
1 Faulty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming, 650093, China
2 State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization, Kunming University of Science and Technology, Kunming, 650093, China
3 Yuxi Cigarette Factory, Hongta Tobacco (Group) Co., Ltd., Yuxi, 653100, China
* Corresponding Author: Jianxin Xu. Email:
Fluid Dynamics & Materials Processing 2025, 21(2), 325-349. https://doi.org/10.32604/fdmp.2024.057496
Received 19 August 2024; Accepted 05 November 2024; Issue published 06 March 2025
Abstract
In modern engineering, enhancing boiling heat transfer efficiency is crucial for optimizing energy use and several industrial processes involving different types of materials. This study explores the enhancement of pool boiling heat transfer potentially induced by combining perforated copper particles on a heated surface with a sodium dodecyl sulfate (SDS) surfactant in saturated deionized water. Experiments were conducted at standard atmospheric pressure, with heat flux ranging from 20 to 100 kW/m2. The heating surface, positioned below the layer of freely moving copper beads, allowed the particle layer to shift due to liquid convection and steam nucleation. The study reports on the influence of copper bead diameter (2, 3, 4, and 5 mm), particle quantity, arrangement, and SDS concentration (20, 200, and 500 ppm). It is shown that the combination of 5 mm particles and a 500 ppm SDS concentration can yield a remarkable 139% improvement in heat transfer efficiency. As demonstrated by direct flow visualization, bubble formation occurs primarily in the gaps between the particles and the heated surface, with the presence of SDS reducing bubble size and accelerating bubble detachment.Graphic Abstract

Keywords
Nomenclature
| Heat transfer surface area on the back of the heating plate (m2) | |
| Voltage (V) | |
| Heat transfer coefficient (W/m2K) | |
| Current (A) | |
| Heat flux (W/m2K) | |
| Temperature (K) | |
| Bubble departure frequency | |
| Time | |
| Average pore diameter (hydraulic diameter) (m) | |
| Copper particles inner diameter (m) | |
| Copper particle diameter (m) | |
| Heat transfer coefficients for containers with copper particles (W/m2K) | |
| Heat transfer coefficients for copper-free particle containers (W/m2K) | |
| Permeability (m2) | |
| Copper bead mass (g) | |
| Water mass (g) | |
| Hydraulic radius (m) | |
| Packing particle volume (m3) | |
| Packing particle surface area (m2) | |
| Mean wall temperature (K) | |
| Saturated temperature (K) | |
| Mean wall superheat ( = Tw-Ts) (K) | |
| Porosity of the dispersed copper porous insert inner tube | |
| Rohsenow’s constant | |
| Surface tension of liquids (N/m) |
With the advancement of electronic and electromechanical system performance, there is an increasingly urgent demand for heat transfer efficiency. In this context, pool boiling enhanced heat transfer plays a crucial role as an important technology. Nucleate boiling, with its characteristics of small temperature differences and high heat transfer coefficients, is widely applied in the thermal management of high-performance microprocessors, industrial engines, reactors, factories, and other fields [1]. The efficiency of heat transfer in the boiling nucleate zone is heavily impacted by the dynamics of bubble formation, expansion, merging, and detachment, which are in turn highly affected by the characteristics of the surface. In pool boiling processes, to enhance the heat transfer coefficient, two main techniques are commonly employed: surface modification techniques and fluid modification techniques. As summarized by Webb [2] in the literature, surface treatment techniques and surfactant addition techniques.
In surface modification techniques, various methods can be employed to alter the morphology of the heating surface, including manufacturing multiscale surfaces [3–5], chemical etching and heat treatment [6,7], electroplating [8], porous structures [9,10], microcavities/ribs [11–15], and particles [16,17], among others. Structured surfaces have been found to be a prevalent method for improving the efficiency of boiling heat transfer. Structured coverings play a role in enhancing both the heat transmission surface area and the density of nucleation sites. Additionally, they provide unique pathways for liquid-vapor movement and have a positive impact on bubble dynamics, thereby improving heat transfer efficiency.
The heat transmission performance during the entire boiling process is greatly influenced by the surface modification treatment of the heating surface. As an illustration, Benjamin et al. [18] achieved varying surface roughness on stainless steel and aluminum surfaces by using different grades of sandpaper for polishing. They then investigated the impact of surface-liquid interaction on boiling incidents, specifically on nucleation site density and heat flux. Surtaev et al. [19] conducted an experimental study on pool boiling heat transfer using two coolants, water and liquid nitrogen, on capillary porous coatings under atmospheric pressure. Unique capillary porous coatings with varying thicknesses (400–1390 μm), morphologies, and high porosities (up to 60%) were fabricated using directed plasma spraying technology. The research indicated that the use of capillary porous coatings can significantly enhance heat transfer performance: during boiling with liquid nitrogen, the heat transfer enhancement reached up to 4 times, while in water boiling, the enhancement was as high as 3.5 times in low heat flux regions. Additionally, Joseph et al. [20] conducted an experimental study on the effect of nano-copper oxide (nano-CuO) coatings on the enhancement of pool boiling heat transfer on 316 LN stainless steel. The coatings were prepared using the sol-gel dip-coating technique. The results showed that the boiling heat transfer coefficient of the CuO coated surface, fabricated by the sol-gel method, increased by up to 30% compared to the uncoated surface. da Silva Vilaronga et al. [21] examined how several porous microstructured materials affect the heat transfer of deionized water during pool boiling. It was discovered that using porous copper microchannels with thicknesses less than the capillary length of the working fluid helped to detach bubbles, which in turn improved heat transfer. All of these investigations highlight the substantial influence of modifying the heating surface on the performance of heat transfer, despite the intricate and expensive nature of current fabrication methods. Therefore, some studies have attempted to find simpler fabrication processes for modified surfaces. As an illustration, Kim et al. [22] examined the impact of unbound copper particles on the process of transferring heat through nucleate boiling and the density at which critical heat flow occurs. The experimental findings demonstrated that the presence of microscale-free particles significantly facilitated the formation of bubbles, hence increasing the heat transfer coefficient during nucleate boiling. Observations of enhanced nucleate boiling heat transfer and critical heat flux (CHF) were made by carefully choosing the size and number of particles. Wen et al. [23] conducted tests on pool nucleate boiling utilizing porous copper beads as an improved porous medium in saturated deionized degassed water. The findings demonstrated that unbound particles possess notable benefits in the process of transferring heat through boiling. Yang et al. [24] conducted an experiment where they joined copper foam blocks together to create a layer of copper foam. They then examined how the heat transfer ability of the foam layer was affected by factors such as the number of pores, thickness, and temperature of the liquid in the pool. Compared to conventional surfaces, the boiling onset temperature significantly decreased with the copper foam cover layer, and the heat transfer coefficient was two to three times higher than that of conventional surfaces. Gheitaghy et al. [25] conducted an experimental study on the pool boiling heat transfer performance of copper-based mesoscopic channels, microstructured porous coatings, and their combinations. The results indicated that integrating microporous copper on the surface of microchannels could effectively enhance boiling performance. Compared to a flat surface, the critical heat flux (CHF) achieved was 170 W/cm2 (an increase of 2.1 times), and the heat transfer coefficient (HTC) was 23.5 W/cm2K (an increase of 3.9 times). These investigations highlight the significant influence of modifying the heating surface on the performance of heat transfer while also suggesting easier techniques for fabricating it.
When surfactants are present in the working fluid, the unique structure of surfactant molecules with hydrophilic heads and hydrophobic tails causes them to aggregate and adsorb at the interface, significantly altering the dynamics of bubbles, and thereby affecting heat transfer characteristics. For example, Gouda et al. [26] conducted pool boiling experiments to investigate the heat transfer efficiency of a solution containing a biosurfactant called rhamnolipid. The results demonstrated a 200% increase in the heat transfer coefficient when compared to pure water. In addition, Hu et al. [27] examined the correlation between surfactant adsorption and bubble behavior. They also created a model to explain the excessive adsorption of surfactants at the interface between liquid and gas, as well as the surface tension of surfactant solutions in water. By conducting experiments using ionic surfactants like The element sodium Dodecyl Sulfate (SDS) and non-ionizing surfactants like Triton X-114, researchers discovered that at low heat flux levels, the additional adsorption and surface tension had minimal impact on heat flux. However, at high heat flux levels, the excess adsorption decreased and the surface tension increased significantly. Li et al. [28] examined the heat transfer coefficient (HTC) and crucial heat flux (CHF) of Sodium Dodecyl Sulfate (SDS) surfactant solutions at various concentrations and subcooling settings through pool boiling. The researchers discovered that subcooling had minimal impact on natural convection in pool boiling, but had a considerable influence on nucleate boiling. Additionally, they observed that temperature overshoot events were more prominent in SDS solutions compared to deionized water. Wen et al. [29] studied the boiling performance of aqueous solutions containing four quaternary ammonium cationic surfactants. The surfactants used were Decyltrimethylammonium bromide (DeTAB), Dodecyltrimethylammonium bromide (DoTAB), Tetradecyltrimethylammonium bromide (MTAB), and Cetyltrimethylammonium bromide (CTAB). The experiments were conducted on a copper heater at various concentrations, both with and without the application of an electric field. The experimental findings demonstrate that surfactant solutions in water substantially increase the heat transfer coefficient in comparison to pure water, with the highest relative enhancement of the HTC reaching 209.3%. Furthermore, Etedali et al. [30] investigated the pool boiling heat transfer of a nanofluid composed of deionized water (DI water), silica (SiO2) nanoparticles, and additives (such as Ps20, CTAB, and SLS) on a copper surface, studying its performance under different nanofluid concentrations at atmospheric pressure. The results indicated that the boiling heat transfer of DI water enhanced when surfactants were added compared to DI water alone. Yang et al. [31] examined the precise impacts of surfactants on the characteristics of boiling nucleate heat transfer in pure water. The researchers discovered that Tween20 demonstrated exceptional improvement in boiling performance by increasing the number of nucleation sites. In contrast, Span20 only showed boiling enhancement benefits at low concentrations. Nevertheless, the combination of Tween20 and Span20 greatly intensified the negative impact of Span20 on boiling performance, rendering it inappropriate for the preparation of fluids intended for increased boiling heat transfer. These papers highlight the substantial influence of surfactants on the efficiency of heat transmission during boiling and present specific experimental findings to substantiate this perspective.
Based on literature research, it can be inferred that currently, single-enhancement heat transfer techniques are quite comprehensive, including surface modification techniques and fluid modification techniques. Both of these techniques play a positive role in enhancing heat transfer. However, research on these two techniques in pool boiling is mostly conducted separately, with only a few studies mentioning the combined improvement of pool boiling heat transfer rates by these two techniques. Wen et al. [32] were pioneers in investigating the simultaneous use of surface alteration and fluid modification techniques in boiling studies. Wen et al. [32] conducted a study on the impact of surface wettability on the pool boiling behavior of surfactants (specifically, 95% Sodium Dodecyl Sulfate, Triton X-100, and Octadecylamine) utilizing deionized water and acetone as the liquids being tested, all under atmospheric pressure. The results showed that Triton X-100 exhibited better heat transfer performance than SDS on rough surfaces. Similarly, Gouda et al. [33] investigated the combined effect of structured surfaces (segmented fin surface and uniform cross-sectional surface) and rhamnolipid biosurfactant on enhancing pool boiling heat transfer rates. The results showed that the segmented fin surface exhibited better heat transfer performance, with a 200% increase in heat transfer coefficient. Additionally, Li et al. [34] investigated pool boiling experiments using copper surfaces with different levels of roughness immersed in Sodium Dodecyl Sulfate (SDS) solutions. They found that increasing the SDS concentration improved heat transfer. Meanwhile, Jia et al. [35] investigated the combined impact of wire-cut groove surfaces and surfactants (SDS) on pool boiling heat transfer. The findings indicated that the SDS solution demonstrated excellent heat transfer capabilities at low and moderate levels of heat flux. Additionally, the combination with the grooved surface had a synergistic impact, further improving heat transfer performance. This led to a significant maximum increase in the heat transfer coefficient, reaching approximately 238%. These works offer valuable references and insights for investigating the integration of surface modification and fluid modification approaches to improve pool boiling heat transfer rates.
To summarize, the simultaneous use of surface modification and fluid modification techniques can greatly improve the rates at which heat is transferred during pool boiling. This study aims to investigate the combined effect of perforated free copper beads and Sodium Dodecyl Sulfate surfactant in pool boiling. Our objective is to investigate the impact of surfactant concentration and free particles on the pool boiling heat transfer process, as well as the characteristics of bubble behavior. We will analyze factors such as the concentration of SDS, weight, size, and number of free particles, along with heat flux density. Additionally, we also examine the enhanced mechanism of boiling heat transfer inside the liq-uid-saturated particle sphere.
2 Experiment Apparatus and Procedure
2.1 Experimental Apparatus and Procedure
The experimental setup, as shown in Fig. 1, mainly consists of three main parts: the heating system, the data acquisition and processing system, and the boiling chamber. A ceramic flat plate heater is welded to the back of the boiling heating surface, driven directly by an AC power supply and regulated by a transformer to provide heat flux. The boiling heating surface is a square body with dimensions of 50 × 50 mm2 and a thickness of 5 mm. Copper is chosen as the material for the boiling surface due to its excellent thermal conductivity. There are six channels on the boiling heating surface, each having a diameter of 0.5 mm2. These channels are used to position six T-type thermocouples, as depicted in Fig. 2. The thermocouple signals are collected by an SHSIWI TS-16A multi-channel data processor and analyzed, then stored in a computer. The boiling chamber is custom-made from organic quartz glass for experimental observation. Located in the uppermost part of the boiling chamber is a copper metal cover used to condense steam. This cover features two ventilation holes that are connected to the steam condensation cycle mechanism. Temperature sensors are employed to measure the temperature of the boiling liquid. Experiments were performed at standard atmospheric pressure to ensure reproducible conditions. The boiling chamber is filled with ultra-pure deionized water, which has been pre-heated to its saturation temperature in a separate container. After being subjected to a drying process, the surfactant is measured using a highly accurate balance to create solutions with concentrations of 50, 200, and 500 ppm. This is achieved by combining 5, 200, and 500 mg of the surfactant with ultra-pure deionized water, respectively. Prior to the experiment, the interior surface of the boiling chamber is thoroughly washed many times using surfactant solutions with identical concentrations. For the selection of SDS concentrations (20, 200 and 500 ppm), we referred to the valid range of surfactant concentrations in Wen et al. [32] to ensure that the heat transfer effects from low to high concentrations were covered.
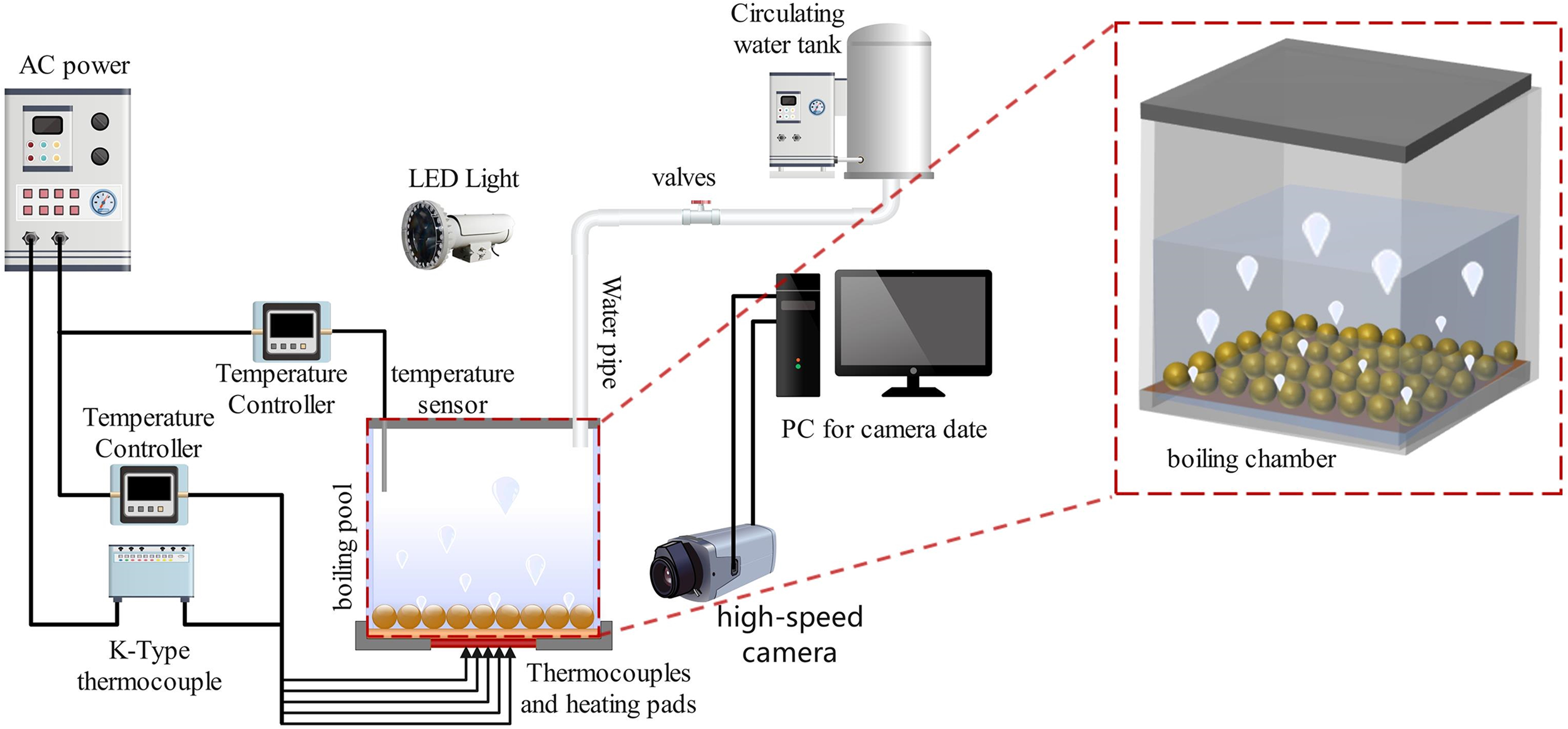
Figure 1: Experimental setup diagram

Figure 2: Schematic of thermocouple distribution and photo of copper bead under test
Fig. 1 depicts the schematic diagram of the setup for the experiments and test container used in this study. The test container is constructed from organic glass and has a diameter of 100 mm and a height of 200 mm. The top cover is equipped with a polytetrafluoroethylene rectangular sealing ring and a spiral auxiliary heater (manufacturer: CHINTA) to ensure that the test liquid remains in a pre-boiling state at saturated temperature. During the experiment, some of the generated steam condenses on the top copper metal cover and gravity flows back into the boiling pool liquid area. The remaining steam, which has not condensed in time, passes through the top vents and enters the steam circulation condensation device, then is re-fed back into the pool. To minimize heat loss, the interior of the boiling chamber is coated with transparent insulation material. Test copper beads are placed on the heating surface, with an average diameter of 2–5 mm. The choice of copper particle diameters (2, 3, 4 and 5 mm) was based on the experience of Wen et al. [23] in heat transfer studies with porous materials, with the aim of evaluating the effect of particle size on the boiling heat transfer performance while ensuring that the particles could maintain good fluidity and free movement in the liquid. Deionized water and pre-prepared SDS solutions are introduced into the test container individually, and heat is applied through the bottom heating plate. The heating plate is made of a 50 mm × 50 mm ceramic rectangular piece, with its edges bonded and fixed by high-temperature resistant insulation adhesive. Considering the contact impedance between the heating surface and the ceramic heating pad, this factor may affect heat transfer efficiency. We finely polished the copper heating surface to ensure that the ceramic heating pad fits tightly against it, and the ceramic heating surface was bonded to the copper heating surface using strong insulating adhesive to improve surface roughness and ensure good contact. Additionally, we applied thermal paste at the joint, which helps to further reduce thermal resistance and improve heat transfer efficiency, thereby minimizing contact impedance. To further reduce heat loss, we used foam insulation on the backside of the heating plate and the boiling surface. The power supply for the heating plate and auxiliary heater is controlled by an AC regulated power supply (Manufacturer: SHXISHO, 300 V/10 A). The test procedures were carried out at atmospheric pressure conditions, utilizing ultra-pure deionized water as the boiling medium. A thermocouple was positioned at the uppermost part of the container to gauge the temperature of the liquid undergoing boiling. Six holes, each with a diameter of 0.5 mm, were drilled into the bottom plate of the container to facilitate the placement of six thermocouples located on the rear of the heating plate. MTWISE utilized calibrated stainless steel thermocouples (Type E) to accurately monitor the temperatures of both the backside of the test heating plate and the water pool. Data was recorded by a multi-channel data acquisition system (manufacturer: SHSIWI; model: TS-16A). The readings of the thermocouples on the heating surface were averaged to obtain the wall temperature. Before being installed, the thermocouples underwent calibration using a constant temperature oil bath, After calibrating the thermocouples, we immersed them in ethanol cleaner for a few minutes to soften any grease. Then, we gently wiped the surface of the thermocouples with a cotton swab soaked in the cleaner and finally rinsed them with deionized water to remove the cleaner and any remaining grease. After that, we dried the thermocouple surfaces with a soft cloth to ensure they were completely dry. This process effectively ensures the accuracy of the thermocouples, avoiding any contamination from grease that could affect the measurement results, thereby guaranteeing an overall accuracy of ±0.2°C. The experimental approach involves vigorously boiling the liquid in the pool at the start of each run using a plate-type ceramic heater for a duration of 1 h. This process is done to remove gas from the test liquid. We conducted concentration measurements both before and after degassing. The concentration of the solution was determined using UV-Vis spectrophotometry to confirm that there was no significant change in SDS concentration. During the degassing process, we maintained constant stirring and temperature, which helped ensure the uniformity of the solution and minimized the loss or decomposition of SDS, thereby reducing any impact on the SDS concentration. The experimental system was initiated without any power supply. Subsequently, the pool was gradually heated at a low intensity until it reached its maximum temperature. The voltage of the heater was regulated by systematically raising the power supplied to the test area, in increments of five to ten volts, until the boiling process initiated. Steady state was defined as the period of time when the difference between the temperature detected by the thermocouple on the wall and the temperature of the liquid pool was within a range of ±0.5°C. After the liquid pool reached a stable boiling state for 10 min, data recording was performed, including heater voltage, liquid pool temperature, and temperature on the heating plate.
We then applied heat to the plate surface and conducted joint tests with different concentrations of SDS and various sizes of porous copper particles. The experimental steps are as follows: We uniformly distributed the selected perforated copper particles (with diameters of 2, 3, 4, and 5 mm) on the heating surface according to a predetermined quantity, ensuring appropriate spacing between the particles to allow for fluid convection and free movement of steam. Next, we poured the prepared SDS solution, made with degassed deionized water, into the boiling chamber to the corresponding scale. Once ready, we turned on the heating device and set the initial heat flux (20 kW/m2), maintaining it for a certain period to reach steady state, while recording the initial temperatures of the liquid and heating surface. Subsequently, as we increased the heat flux (to 30, 50 kW/m2, and so on), we maintained stability at each heat flux for a designated time, recording temperature changes and boiling behavior. At each heat flux level, we observed the boiling behavior of the liquid and documented the characteristics of vapor nucleation and liquid convection. After each set of experiments, we performed a cleaning of the experimental equipment for 5 min. This cleaning procedure mainly included the following steps: using an SDS-water mixture to clean the cavity and heating surface for approximately 3 min to ensure thorough removal of dirt and deposits. Then, we rinsed the cleaned surfaces with deionized water for about 2 min to ensure all SDS residues were sufficiently removed. During the cleaning and rinsing process, we continuously monitored the cleanliness of the cavity and heating surface to verify whether the desired results were achieved. If necessary, we performed multiple rinses to ensure the surface was completely clean. To ensure the accuracy of the experiments, we adopted a systematic approach to standardize the cleaning process and recorded the time spent on each step, allowing for reproducibility in subsequent experiments. All under saturated circumstances. The study captured the actions of bubbles by employing a high-speed camera (FHAGILEDEVICE, model 5F01-M). This allowed for the determination of heat flux, wall superheat, and heat transfer coefficient. During the experimental process, we conducted multiple repeat experiments to evaluate the heat transfer performance under different combinations of conditions. This process helped us ensure the reliability of the data and, to some extent, eliminate random errors. Comprehensive data on bulk copper porous particles are shown in Figs. 1 and 2. The beads were placed in the test container, and the physical characteristics and dimensions of the porous copper beads are summarized in Table 1. In this study, the outer diameter of the dispersed porous copper samples was used as follows: Dc = 5 mm (Experiment ID 1), Dc = 4 mm (Experiment ID 2), Dc = 3 mm (Experiment ID 3), Dc = 2 mm (Experiment ID 4). In addition, a smooth surface indicates that the test container (Experiment ID 5) does not contain any beads. The density method was employed to determine the porosity of the four samples. The average pore diameter is calculated based on the equivalent diameter, which is equal to four the hydraulic radius of the tubes found in the dispersed metal permeable beads. The hydraulic radius is calculated by dividing the total volume of void spaces within the tube filled with porous beads by the total surface area of the solid. Wen et al. [23] provided the equation for determining the average pore diameter, also known as hydraulic diameter:
(1)
where
(2)
and(3)

Darcy’s law can be utilized to compute permeability. Nevertheless, in order to streamline the computation of permeability in this work, a simplified formula from Reference [23] was utilized.
(4)
where is the porosity and Dc is the particle size of the dispersed beads.
2.2 Data Deduction and Uncertainty Analysis
The heat flux supplied to the heater can be determined by calculating the product of the voltage U and current I.
(5)
In this context, the symbol q denotes the rate of heat transfer, whereas A indicates the surface area of the heating plate.
During the experiment, the multi-channel data acquisition system simultaneously recorded the signals from six thermocouples. As shown in Fig. 3, the typical variation of temperature signals between two adjacent points on the heating surface over time was captured. The temperature distribution on the boiling surface exhibits clear unevenness, with a temperature disparity of approximately 2°C between sites A and B. Even at the same point, significant temperature fluctuations over time are observed. The calculation of heat transfer coefficients takes into account the average temperature, i.e.,
(6)
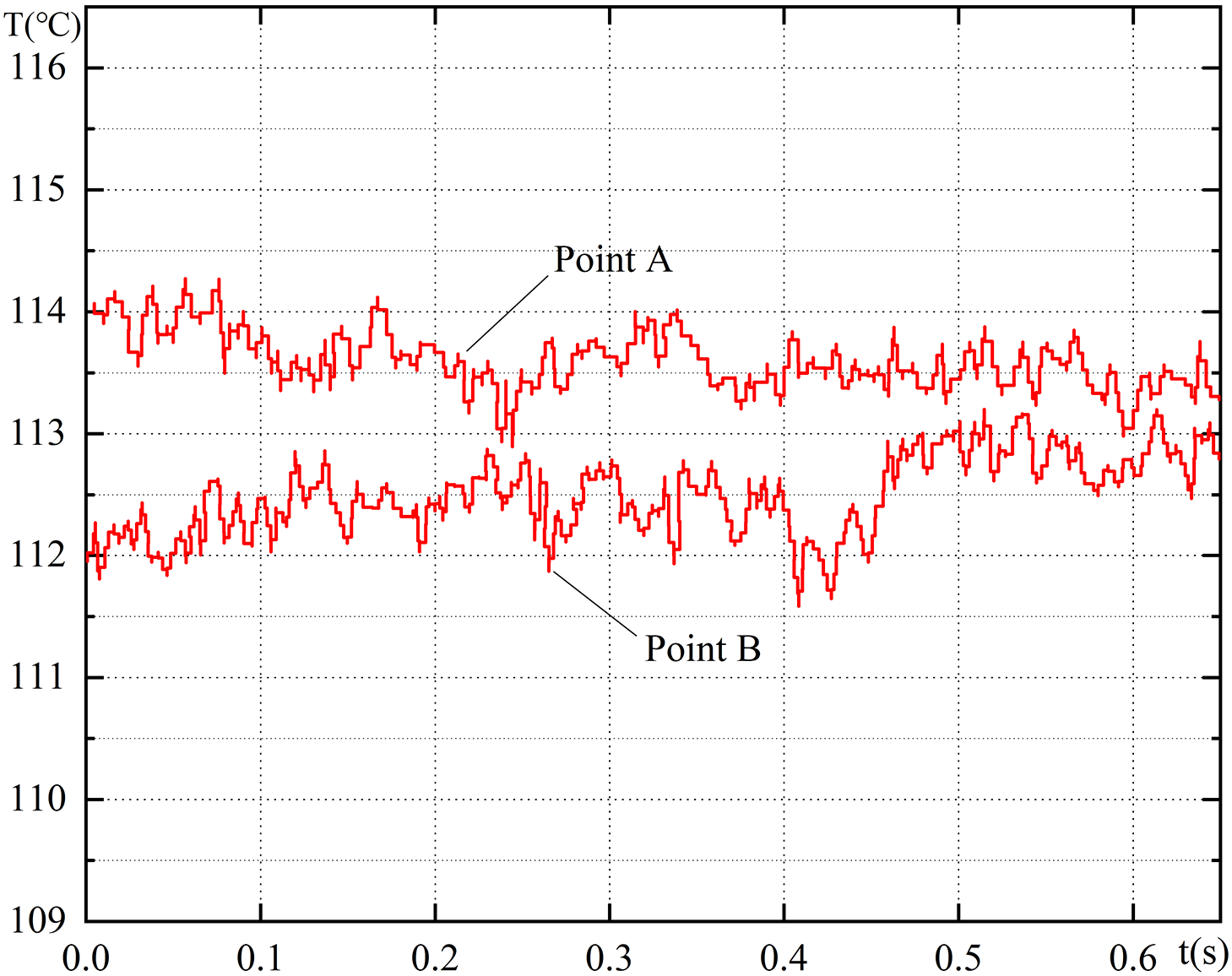
Figure 3: Temperature signals of two points
Using the one-dimensional conduction equation to calculate the boiling surface temperature.
(7)
Here, b represents the thickness of the heating plate. The superheat and the average boiling heat transfer coefficient are defined as follows:
(8)
(9)
In the experiments, the experimental data were fitted with Rohsenow to obtain the constant Csf and the measured experimental data were compared to verify the accuracy of the experimental results. If the trend of the experimental data agrees with the theoretical predictions, then the model is applicable to the boiling conditions under study. In Eq. (10), h0 is boiling heat transfer coefficient (W/m2 K), Csf is Rohsenow’s constant, σ is the surface tension of the liquid (N/m), ΔTw is temperature difference between the temperature of the heated surface and the saturation temperature of the liquid (K), and L is the length of the heated surface (m).
(10)
The K-type thermocouples utilized in the experiment were supplied by the MTWISE firm and had a precision of 0.1 K. The measurement uncertainties for voltage (U) and current (I) were 1.0 V and 0.05 A, respectively. In our study, we maintained the heat flux at (q = 20 kW/m2), (q = 30 kW/m2), and (q = 60 kW/m2) by adjusting the voltage of the AC controller. The thermal losses in the cavity, connectors, and cables were calculated based on the uncertainty of heat transfer [23]. We placed six temperature sensors at the bottom of the copper heating surface to record the average temperature at the surface’s base, while the temperature at the top of the heating surface was obtained by measuring the temperature of the copper heating surface. The temperature of the upper part of the copper heating surface was provided by a temperature sensor installed at the bottom of the boiling heating surface. We calculated the heat transfer from the heating pad to the upper part of the copper heating surface based on one-dimensional steady-state conduction, and the heating surface was insulated with multilayer insulation cotton on the outside of the boiling chamber. Additionally, we used multilayer insulation foam on the outside of the chamber to insulate the heating surface and accounted for radiative heat loss as well as thermal losses from the connectors and cables within the uncertainty range of the heat transfer calculations. After taking into account all relevant aspects, the total level of uncertainty in the heat flow for the current experiment is ±5.3%, while the uncertainty in the coefficient of heat transfer is ±8.3%.
The heat flux, wall superheat, and heat transfer coefficient examined are also provided in convective effects in the concave cavity geometry greatly diminish the observed wall superheat.
In Table 2, along with their respective range and measurement uncertainty, the uncertainty associated with the measured heat flow has been calculated to be ±2.5% at the maximum heat flux and grows to ±5.3% at the lowest possible heat flux. Convective effects in the concave cavity geometry greatly diminish the observed wall superheat.

In our experimental study, we explored the synergistic improvement of pool boiling heat transfer by placing perforated copper particles and adding sodium dodecyl sulfate (SDS) surfactant. Selecting an appropriate data analysis model is crucial in this context. The model comparison primarily involves artificial neural networks (ANN). ANNs can capture complex nonlinear relationships and are highly adaptable due to their multilayer structure, making them well-suited for modeling intricate heat transfer phenomena. However, they require a large amount of training data to avoid overfitting and exhibit poor interpretability, making it difficult to clearly explain how different parameters affect the heat transfer mechanism. Support vector machines (SVM) perform well in high-dimensional problems and can achieve good performance on smaller datasets compared to ANN. Particularly in cases where the data is not linearly separable, SVMs are highly effective through the use of kernel functions. However, they are relatively sensitive to parameter selection and need careful tuning. Additionally, they may be vulnerable to outliers, which is critical in experiments where conditions vary significantly. Gaussian process regression (GPR) offers a probabilistic model that estimates prediction uncertainty, which is particularly useful in experimental scenarios with high noise and variability. However, as the amount of data increases, the computational cost of GPR can become high, and it may not scale well for very large datasets. Each model has unique advantages and limitations in specific application contexts. In our experiments, we investigated the impact of the following variables on boiling heat transfer performance: copper particle diameters (2, 3, 4, and 5 mm), particle quantities (varying numbers of copper particles), particle layering (different arrangements of particles), and SDS concentrations (20, 200, and 500 ppm). Our analysis found that the random forest (RF) model was particularly effective. RF can delve into the influence of various input parameters on heat transfer rates, providing reliable interpretability and feature importance analysis. For example, the RF model revealed the significant effect of particle diameter on boiling heat transfer performance while indicating how to choose appropriate particle sizes to enhance heat transfer efficiency. Furthermore, through the feature importance analysis of the RF model, we could quantify the role of SDS concentration under different experimental conditions, guiding the selection of optimal concentrations for practical applications. Our experiments and data analysis demonstrate that the synergistic effect of perforated copper particles and SDS can significantly enhance pool boiling heat transfer performance. Utilizing the random forest model for data analysis not only helps us understand the key parameters influencing heat transfer efficiency but also provides a solid theoretical basis for future research and practical applications. This research outcome will serve as an important reference for the development and optimization of cooling technologies.
3.2 Effect of Surfactant Solution Concentration on Boiling Heat Transfer
The experimental observations indicate that the addition of the surfactant SDS in a particle-free container results in uniform nucleation and rapid growth of bubbles on the copper surface. This leads to a decrease in bubble detachment diameter and an increase in detachment frequency. This is because when SDS molecules are present in the aqueous solution, the hydrophobic alkyl chains tend to aggregate at the liquid surface, while the hydrophilic sulfate ions are oriented towards the water phase. This configuration limits the contact between the hydrophobic component and the water, resulting in a decrease in the surface tension of the liquid. As a result, the energy required for the formation and detachment of bubbles is reduced. The experimental observations indicated that by subjecting the liquid to saturation boiling under a thermal flux of 60 kW/m2 and maintaining it at that state for 10 min, a subsequent analysis of the recorded data, as depicted in Fig. 4, revealed a consistent rise in the boiling heat transfer coefficient upon the introduction of SDS. High-speed camera recordings of bubble behavior, as analyzed in Fig. 5, showed that the bubble detachment rate in saturated pure water was 29 ms. After the addition of the surfactant, the bubble detachment rate decreased to 26 ms. With the SDS concentration increasing to 500 ppm, the bubble detachment rate further decreased to 16 ms. Compared to pure water boiling, the bubble detachment rate decreased by 13 ms. Table 3 presents the calculated percentage enhancement of heat transfer coefficient (HTC) on a particle-free surface using different concentrations of SDS solution. The molecular principle, seen in Fig. 6, demonstrates that the existence of surfactants decreases the energy required for the creation of bubbles on the liquid surface, leading to an augmentation in the rate at which bubbles are formed. At the same time, when bubbles detach from the liquid surface, surfactants can reduce the adhesion between the bubbles and the liquid surface, making it easier for the bubbles to detach from the surface. Therefore, compared to pure deionized water, bubbles in a liquid containing SDS exhibit a faster growth rate of uniform nucleation on the copper surface, resulting in smaller bubble detachment diameters and higher detachment frequencies. However, this enhancement does not continue to increase with the concentration of the surfactant. Elevated levels of surfactants can generate a durable layer of foam on the surface of a liquid, impeding the creation and separation of bubbles. As a result, the bubbles remain on the surface for an extended period, which ultimately decreases the efficiency of heat transfer.
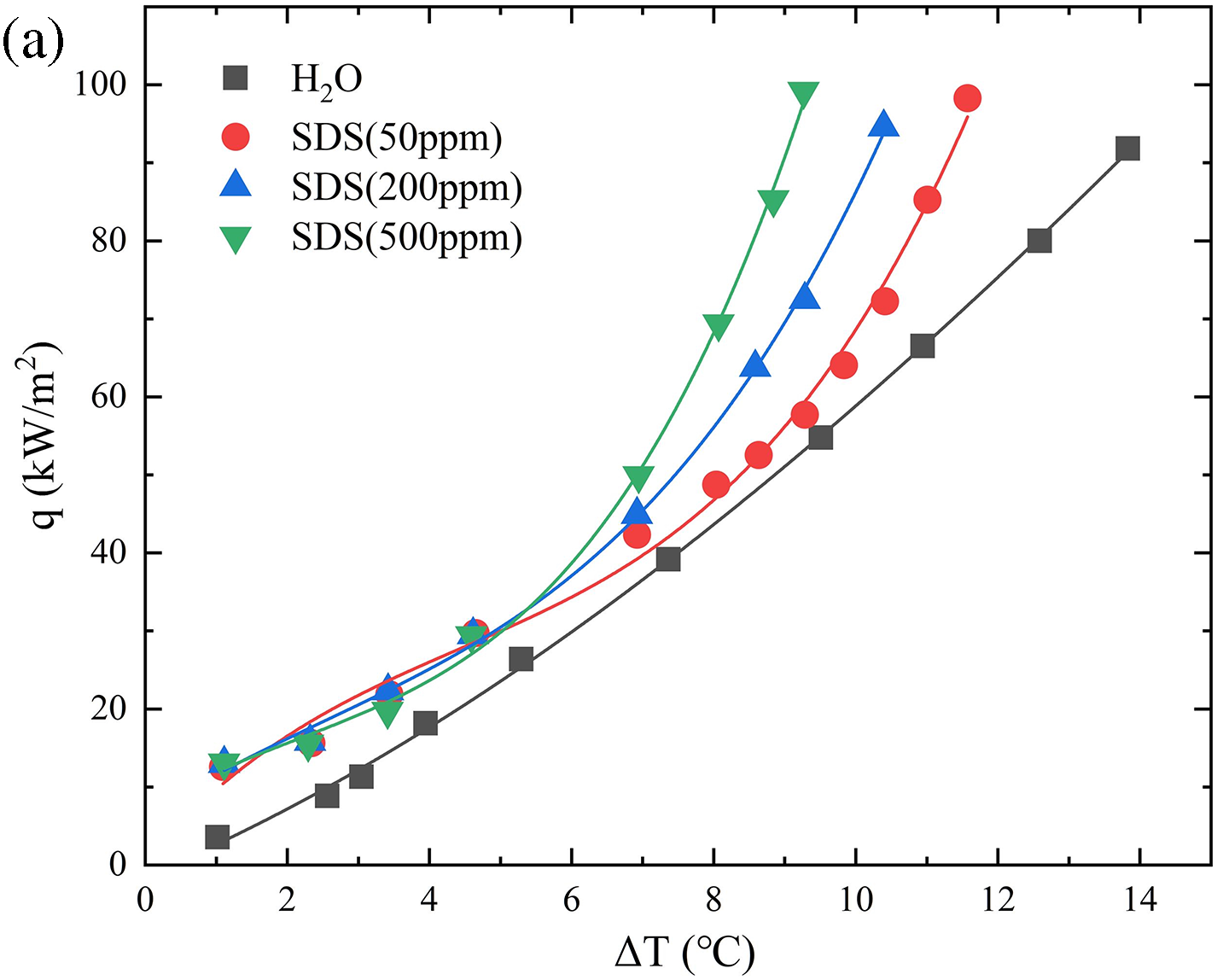
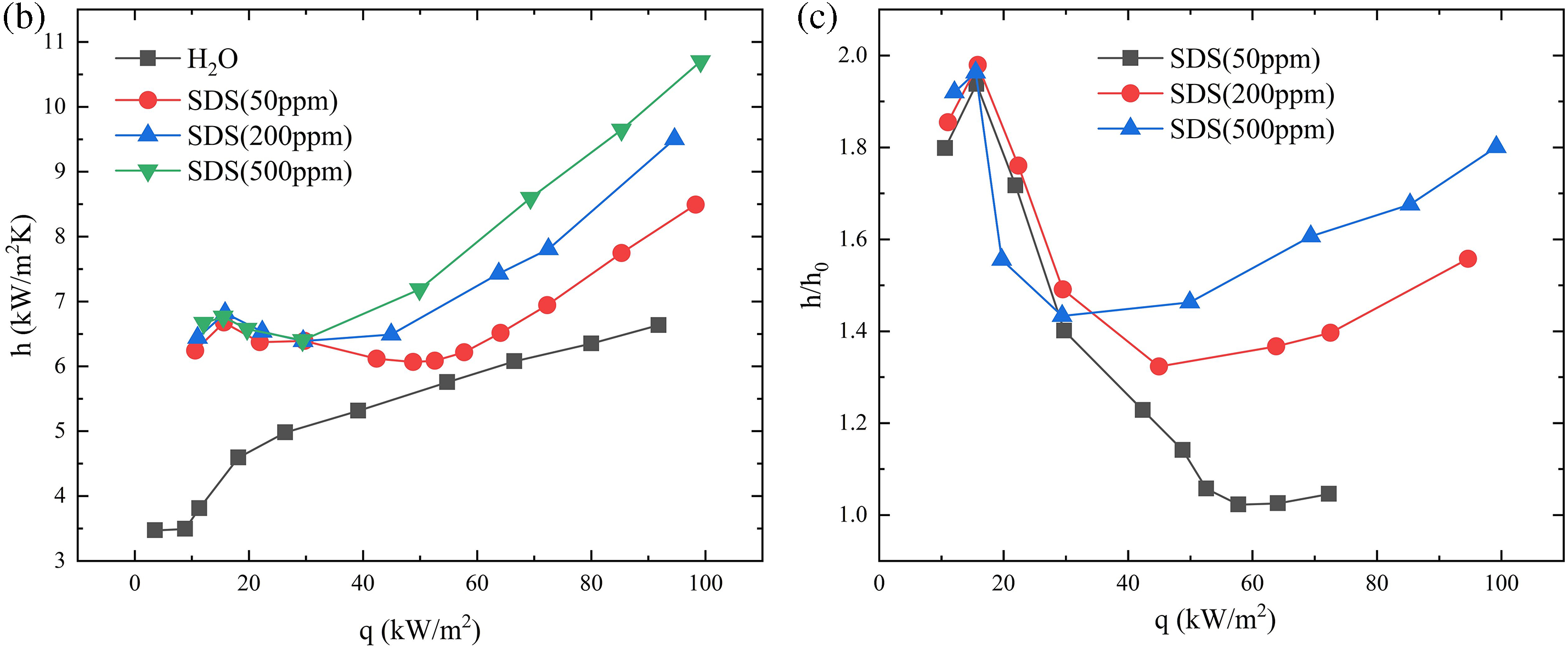
Figure 4: SDS surfactant concentration effect, SDS concentration on boiling curve (a), SDS concentration on heat transfer coefficient (b), SDS concentration on heat transfer enhancement rate (c)

Figure 5: High-speed visualization images of bubble nucleation and dissipation in nucleate boiling state: (a1) Bubble nucleation on a flat surface at 60 kW/m2; (a2) Bubble detachment on a flat surface at 60 kW/m2; (b1) Bubble nucleation on a flat surface with 50 ppm SDS at 60 kW/m2; (b2) Bubble detachment on a flat surface with 50 ppm SDS at 60 kW/m2; (c1) Bubble nucleation on a flat surface with 200 ppm SDS at 60 kW/m2; (c2) Bubble detachment on a flat surface with 200 ppm SDS at 60 kW/m2; (d1) Bubble nucleation on a flat surface with 500 ppm SDS at 60 kW/m2; (d2) Bubble detachment on a flat surface with 500 ppm SDS at 60 kW/m2


Figure 6: Schematic diagram of surfactant and vapor bubble interaction. Adapted with permission from Reference [26], Copyright © 2024, Published by Elsevier
3.3 Enhanced Nucleate Boiling Heat Transfer by Free Particles
In order to ensure consistency in the experimental setup, a test container free of any particulates (used as the testing sample plate) was taken as a baseline reference, and comparisons were made using the well-known Rohsenow correlation. The experimental data fit well with the Rohsenow constant Csf = 0.0103. Fig. 7 presents a typical comparison of the heat transfer coefficients and heat transfer rates on a horizontal plate. It can be observed that for heat fluxes q ≤ 100 kW/m2, the current experimental results align closely with the predicted data obtained from the Rohsenow correlation, showing trends similar to those reported in relevant literature [11], as well as those by Yang et al. [24] and Wen et al. [23]. This information clearly indicates that the experimental method employed is effective. The results demonstrate that the experimental data exhibit similar trends to those reported in the literature, with the observed deviations averaging around 5.3%. This can be attributed to uncertainties in the experimental setup and the correlations used.

Figure 7: Comparison of the results of the smooth heated plane test with the fitted data of Rohsenow and the experimental results given in the literature by Wen and Ho [11], Wen and Jang [23] and Yang et al. [24]
The test container, which is see-through, is filled with copper beads that have little holes or spaces in them. Flow visualization allows for the observation of phase transition behavior inside the structure of the bead packing. A container filled with beads and water is heated from the bottom using a heating unit. Zoom-capable imaging equipment, capable of acquiring up to 1000 frames per second, is used to visualize the boiling behavior at the bead packing structure. Hence, the acquired data, encompassing the arrangement of bubble interfaces, the dynamic behavior of bubbles, and the processes of interfacial transport, continues to offer significant empirical evidence for comprehending phenomena and physical causes.
Fig. 8 depicts high-speed images of boiling with 2–5 mm porous particles under a thermal flux of 60 kW/m2. When 2 mm particles are introduced, relatively small and frequent bubbles are generated. As the size of the injected particles rises, the size of the bubbles also increases progressively, resulting in the simultaneous presence and merging of bubbles, albeit with a significantly lower frequency of separation. This is because initially, there is a significant temperature gradient on the heating surface, causing the liquid to quickly heat up to the boiling point and form small bubbles. As time progresses, the temperature around the liquid gradually increases, requiring a higher degree of superheat for bubble formation, thus resulting in larger bubble sizes. However, the frequency of bubble detachment may decrease because the higher degree of superheat slows down the rate of new bubble formation. The coexistence and aggregation of bubbles result from factors such as liquid flow, bubble convection, and mutual attraction. Particles in boiling processes oscillate, and because of the buoyancy of vapor bubbles, they stay in contact with the surface that is heated and consistently create nucleation sites. Fig. 8 illustrates that when exposed to a heat flow of 60 kW/m2, vapor bubbles are observed to first appear at the sharp edges of the particles, then grow in size and detach from the surface. The primary mechanism for the enhanced heat transfer coefficient, as compared to polished surfaces, is the formation of strong vapor bubbles due to the presence of millimeter-scale free particles in water.

Figure 8: (a–d) represent the high-speed visualization of the bubbles about to leave under saturated boiling with 60 kW/m2 heat flux of 2, 3, 4, and 5 mm porous copper particles, respectively
3.4 Enhanced Nuclear State Boiling by Combined Free Particle SDS
3.4.1 Effect of Free Particle Size
In order to examine the impact of the size of porous particles that are not confined on the improvement of heat transfer during boiling in water, an investigation was conducted on copper particles with sizes ranging from 2 mm to 5 mm. Every experiment entailed the application of particles to the heating surface to ensure the presence of evenly distributed nucleation sites. In order to assess the impact of particle size on the boiling curve in water, a series of experiments were conducted. The experiments involved using particles of different sizes: 5 mm (Experiment 1), 4 mm (Experiment 2), 3 mm (Experiment 3), 2 mm (Experiment 4), and no particles (Experiment 5). The mass concentrations of the particles were kept consistent (mc/mw) throughout the experiments. In addition, 500 parts per million (ppm) of SDS were introduced into each experimental container to examine the synergistic impact of free porous particles and SDS on the improvement of nucleate boiling in water. Fig. 8 displays the outcomes of the boiling curves using various sizes of loose copper beads and the collective impact of SDS. Fig. 9 depicts a phenomenon known as partial nucleate boiling, in which the transport of heat can be affected by variations in the size of particles. Boiling heat transfer begins when the temperature of the wall (ΔT) is just above zero. Heat transmission takes place by natural convection in a fluid that is in a single phase. When the temperature difference (ΔT) exceeds around 1.0°C, little vapor bubbles become visible on the surface of the test plate. These bubbles subsequently separate from the surface and ascend. Exactly. This is the early stage of boiling. As the value of q increases, both the quantity and size of the bubbles increase. An increasing amount of foam is being seen. Certain bubbles coalesce to create larger bubbles, resulting in an increased occupation of surface area by vapor bubbles. Turbulent motion is observed in the liquid during this phase, and as bubbles detach from the heated surface, cooler liquid takes their place, enhancing the transfer of heat from the surface being tested. Fig. 7 displays the results observed during the nucleate boiling phase in the water pool. This also confirms the modifications to the bubble, as depicted in Figs. 10 and 11.

Figure 9: Indicates the effect of particle size on boiling heat transfer with the coordinated addition of particles of different sizes (2, 3, 4 and 5) at SDS concentration (500 ppm). Effect of particle size on boiling curve (a), effect of particle size on heat transfer coefficient (b), effect of particle size on heat transfer enhancement (c)

Figure 10: High speed comparison images of 5 mm free porous particles saturated with and without 500 ppm SDS solution over a heat flux range of 20 to 100 kW/m2

Figure 11: High-speed visualization of particle flow for different experimental numbers (1, 2, 3, 4, and 5) at q = 60 kW/m2
Fig. 10 displays high-speed pictures of 5 mm porous particles in a free state, both with and without the inclusion of 500 ppm SDS, with heat fluxes varying from 20 to 100 kW/m2. In the top diagram of Fig. 10, it can be observed that with increasing heat flux, there is a continuous generation of nucleation sites. The lower diagram in Fig. 10 demonstrates more pronounced nucleate boiling in comparison to the upper image due to the presence of SDS, which leads to the formation of vapor bubbles that are sufficiently massive to cover the entire particle. In the bottom diagram, with the addition of SDS, it can be observed that there are more bubbles on the heating surface, the bubbles are fuller, and their diameters are larger. When particles oscillate on the heating surface due to the buoyancy of vapor bubbles, their contact with the heating surface is maintained, thus enhancing the detachment rate of bubbles. The boiling nucleus heat transfer phenomenon is visualized at high speeds as the heat flow increases. From Fig. 10 (on the left), it is evident that bubbles ascend from the internal pore locations of the permeable material when q = 20 kW/m2. As the heat flux increases to 30 kW/m2 (Fig. 10, middle), an increasing number of nucleation sites are activated in the narrow gap region, which refers to the small space between the copper beads and the heating surface. In Fig. 10 (right) (q = 60 kW/m2), at higher heat fluxes, the number of active nucleation sites becomes significantly higher. Bubbles start to merge with each other, and a completely different path of steam escape seems to come into play. The influence of heat flux and bead-filling circumstances on the number of active places for nucleation-generating bubbles is evident in Figs. 10 and 11.
3.4.2 Effect of the Number of Free Particle Layers
In order to examine the impact of the number of layers of porous particles on heat transmission during boiling, we performed a series of experiments where we added successive layers of copper beads onto the heating surface of the boiling vessel. Fig. 12 depicts the nucleate boiling properties of water in Test 1, showcasing the presence of 1, 2, and 3 layers of copper beads. Typically, a higher quantity of particle layers leads to a reduction in the frequency of nucleate boiling. Moreover, it is evident that when the temperature increases, there is a simultaneous increase in both the dimensions of vapor bubbles and the quantity of nucleation sites. As the number of particle layers increases, the frequency at which bubbles detach at each nucleation site drops. Furthermore, Fig. 13 exhibits high-speed images of pool boiling that were detected by flow visualization in Experiments 1, 2, 3, 4, and 5. These tests were conducted at a constant heat flux of q = 60 kW/m2. These photos demonstrate that when the heat flux is constant, the size of the vapor bubbles increases as the particle size increases, while the density of nucleation sites drops. In comparison to a flat surface lacking copper particles, this structure has the ability to produce smaller vapor bubbles. These bubbles are then stimulated to develop actively, resulting in a decrease in the initial boiling surface superheat (ΔT). In addition, any bubbles that occur on the heating surface will expand within the spaces between the copper beads. Heat is transported both from the wall to the bubbles and from the particles to the bubbles. If the boiling point of the liquid is less than that of the fragments, as is frequently observed, the rate of bubble formation will be higher. This enhances boiling heat transfer and can be considered a fin effect. Overall, in this study, we found that there is not a strong correlation between the boiling curve and the number of particle layers. This phenomenon can be attributed to the fact that as the number of particle layers rises, the thermal conductivity also increases. However, the increase in particle layers simultaneously results in higher flow resistance due to the impact on bubbles and liquid. This restricts the release of steam and the replenishment of liquid. Table 4 calculates the percentage increase in heat transfer coefficient (HTC) for 5 mm particles at different layers under the condition of a 500 ppm SDS solution. As the number of layers increases, the percentage enhancement in heat transfer decreases, which also corroborates our previous findings.
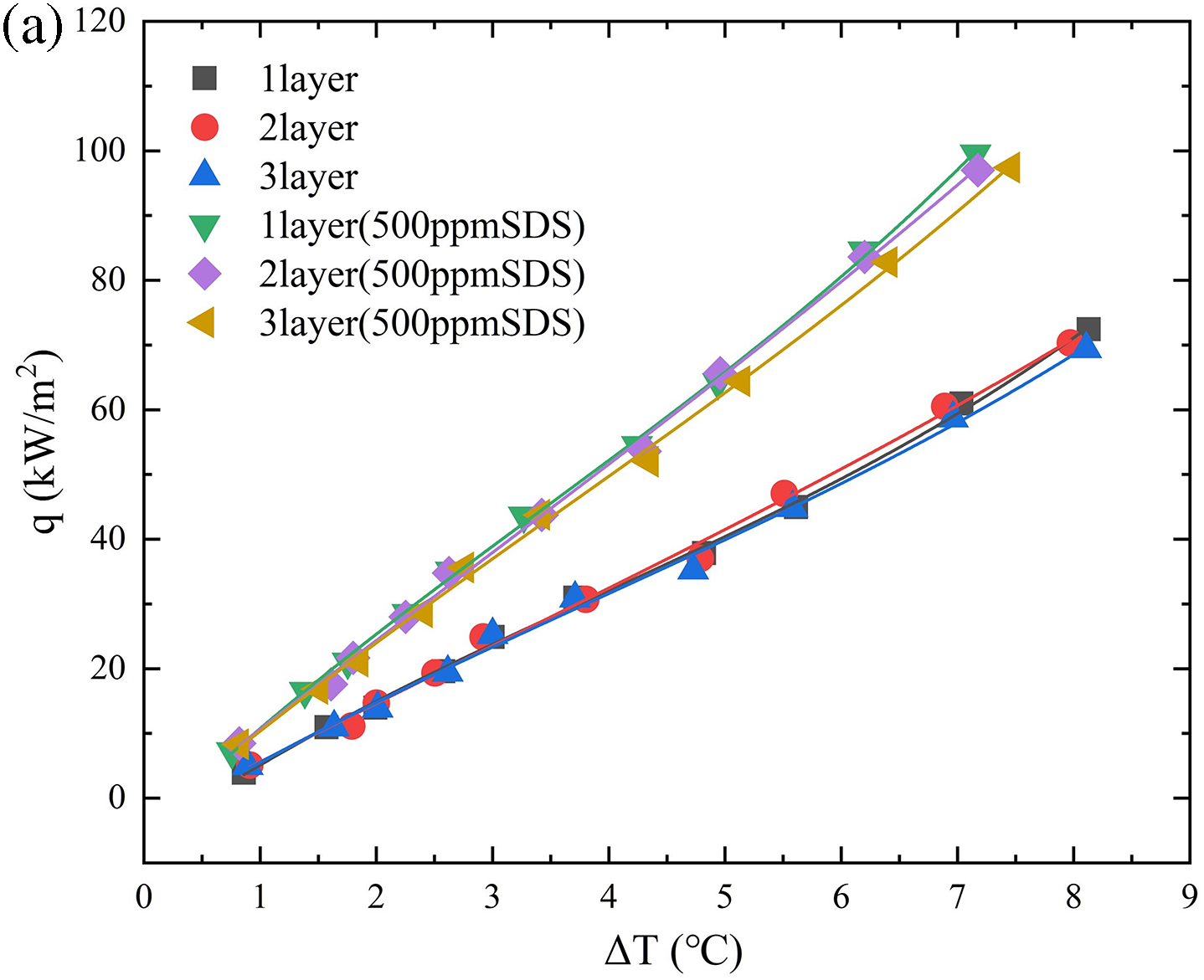
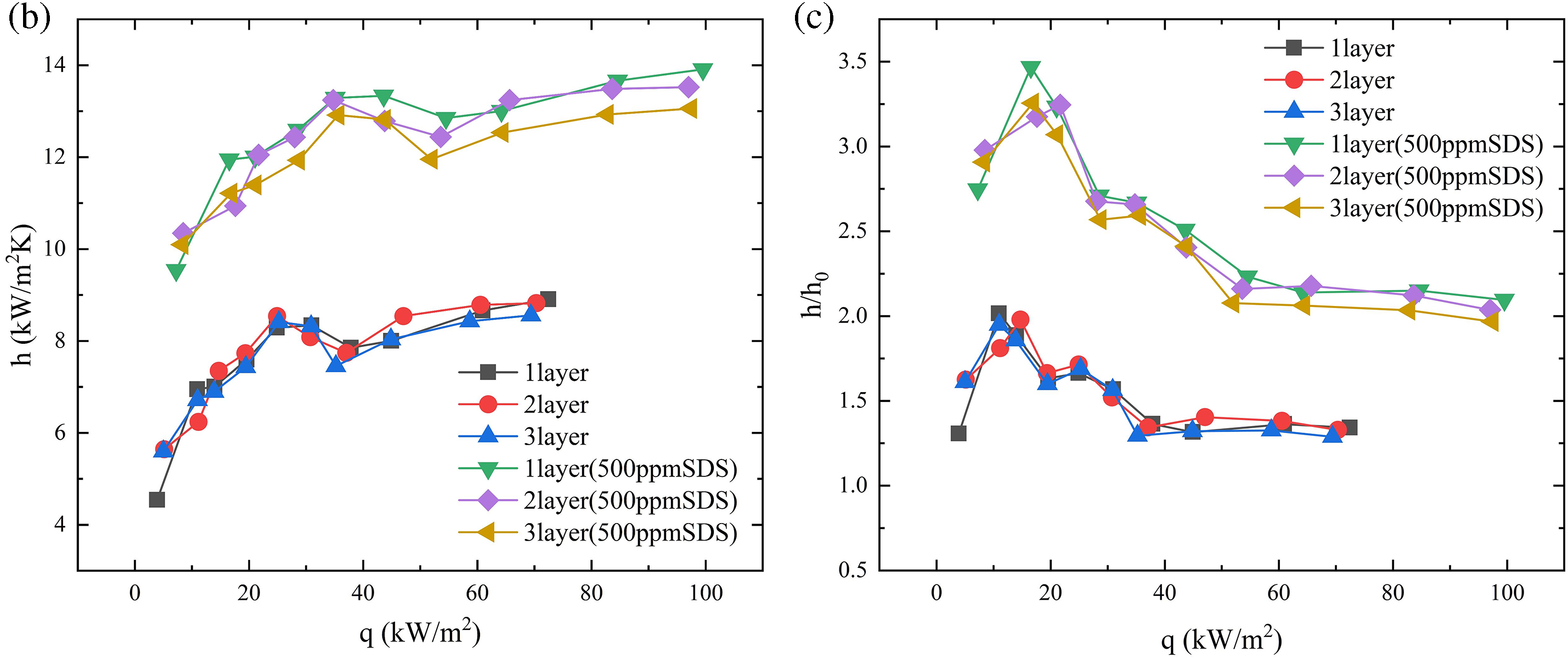
Figure 12: Effect of number of layers of 5 mm porous particles with SDS (500 ppm) on heat transfer coefficient, effect of number of layers of particles on boiling curve (a), effect of number of layers of particles on heat transfer coefficient (b), effect of number of layers of particles on heat transfer enhancement (c)

Figure 13: High-speed visualization of 5 mm copper bead particles at q = 60 kW/m2 saturated condition with different number of layers (1, 2 and 3)

3.5 Comparison of Heat Transfer Coefficients
Fig. 9 illustrates the boiling curves on the surface of free porous particles with a concentration of 500 ppm SDS surfactant. Observing the images, the curve shifts to the left, indicating that the boiling performance on the surface of free porous particles with SDS surfactant is better compared to a smooth surface. Furthermore, the initiation of nuclear boiling occurs at an earlier stage on the surface of unencumbered permeable particles compared to flat surfaces, and the amount of heat transferred is greater on the face of porous particles than on smooth surfaces. Consequently, the combination of the SDS surfactant solution and the structured heating surface results in enhanced heat transfer efficiency.
Fig. 14 depicts the heat transfer efficiency (HTC) on the test surfaces of porous particles treated with an SDS surfactant solution. The trend of HTC on surfaces of different particle sizes remains consistent as the boiling fluid changes from deionized water to one containing SDS surfactant. With increasing particle size, the HTC gradually increases, with the surface of 5 mm particles achieving nearly 139% enhancement. The rise in HTC can be attributed to the cumulative impact of the surface area of unbound porous particles and the SDS surfactant solution. The surface of free porous particles contains a greater number of nucleation sites compared to a flat surface. This is because the presence of sharp edges on the particles provides active nucleation sites, which in turn reduces the temperature required for heterogeneous nucleation. Therefore, compared to a flat surface, a structured surface can achieve a higher HTC. Additionally, low-surface-tension fluids can stimulate additional nucleation by reducing the critical cavity radius by approximately 50%. As a result, fluids with SDS surfactant solution observed approximately 20–30 times more nucleation compared to pure water. Additionally, when using SDS surfactant solution, a very low wall thickness is required to activate the nucleation cavities on the surface of free porous particles. Due to the low surface tension of the SDS surfactant solution, the surface tension acting on the vapor bubble decreases, overcoming buoyancy. Therefore, once the bubble nucleates, it detaches, and the frequency of vapor bubble detachment from the heater surface is higher than with pure water. This results in disruptions in the boundary layer of heat in close proximity to the surface of the heater, which hinders the growth of the wall thickness. Additionally, the surface of free porous particles provides nearly 2.5 times the heat transfer surface area compared to a flat surface, and its bubble dynamics are significantly enhanced, resulting in an enhancement of HTC.

Figure 14: Effect of heat flux on heat transfer coefficient and heat transfer enhancement for different particle sizes at SDS (500 ppm), effect of different conditions on heat transfer coefficient (a), effect of different conditions on heat transfer enhancement (b)
Table 5: We summarize the percentage enhancement in heat transfer coefficient (HTC) for different combinations of porous particle surfaces under the condition of a 500 ppm SDS solution. Specifically, when using 5 mm particles, the combined boiling heat transfer performance improved by 139% compared to the smooth surface without particles. Additionally, when compared to the experiments with porous particles conducted by Wen et al. [23], the overall enhancement in heat transfer efficiency increased by 10% after adding the surfactant solution. This demonstrates a significant improvement in heat transfer efficiency.

This study investigates an enhanced boiling technique based on the combination of free porous particles and SDS surfactant in ultra-pure deionized water as the working fluid. The experimental results indicate that the presence of loose metal particles on the heating surface enhances boiling heat transfer by creating active nucleation sites. The study encompassed a series of experiments that involved pool boiling in water that was saturated, deionized, and de-gassed. Additionally, flat plate studies were undertaken to validate the impact of porous particles on heat transmission. Uniform cleaning and aging protocols were implemented on all test specimens prior to experimentation. To summarize, this study utilized an optimum experimental design and a methodical approach. As a result, the following findings can be made:
1. The addition of perforated copper particles to the heated surface, along with the inclusion of Sodium Dodecyl Sulfate (SDS) surfactant, can greatly improve the efficiency of pool boiling heat transfer.
2. The flow visualization data suggest that the bubbles primarily originate in the gaps between the tiny particles and the surface that is heated. SDS addition decreases the size of bubbles when they detach and increases the frequency at which they detach.
3. Partial boiling of nucleates occurs when the transfer of heat is influenced by variations in the size of particles.
4. The notable enhancement in heat transfer coefficient observed in containers containing copper beads, as opposed to those without any beads, can be attributed to the presence of porous particles within the containers. These particles offer a greater number of nucleation sites and heat transfer area in comparison to the containers without beads.
5. The findings demonstrate a notable benefit in the process of transferring heat through boiling when utilizing a mixture of unobstructed particles and SDS surfactant. The boiling heat transfer effect is significantly enhanced in containers with 5 mm particles and a 500 ppm SDS concentration, resulting in a heat transfer boost of 139%.
6. In this investigation, the relationship between the boiling curve and the particle layers is not significant. This could be attributed to the correlation between the number of metal bead layers and the thermal conductivity, where an increase in the former leads to an increase in the latter. Nevertheless, the presence of flow resistance caused by bubbles and liquid is responsible for an escalation in the quantity of copper bead layers, resulting in heightened flow resistance. Consequently, this hinders the escape of vapor and the replenishment of liquid.
Acknowledgement: We acknowledged the support of the National Natural Science Foundation of China, National Key Research and Development Plan Project and supported by Yunnan Major Scientific and Technological Projects; this work is supported by Research on Development and Application of Complete Set of Technology for Extraction of Aromatic Substances from Tobacco Waste-Research on Pyrolysis Process Technology.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Project No. 52166004), the National Key Research and Development Program of China (Project No. 2022YFC3902000), the Major Science and Technology Special Project of Yunnan Province (Project Nos. 202202AG050007; 202202AG050002), and the Research on the Development of Complete Sets of Technology for Extraction of Aromatic Substances from Tobacco Waste and Its Application, Applied Research-Pyrolysis Process Technology Research (2023QT01).
Author Contributions: Pengcheng Cai: Survey, methodology, data organization, validation, writing—original manuscript. Teng Li: Investigation, writing—original manuscript. Jianxin Xu: Supervision, writing—review and editing. Xiaobo Li: Supervision, writing—review and editing. Zhiqiang Li: Methodology, data organization. Zhiwen Xu: Validation. Hua Wang: Supervision, guidance. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets generated and analyzed during the current study are not publicly available due to confidentiality request by the party providing the data but are available from the corresponding author on reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. You SM, Simon TW, Bar-Cohen A. A technique for enhancing boiling heat transfer with application to cooling of electronic equipment. In: Proceedings Intersociety Conference on Thermal Phenomena in Electronic Systems, 1992 Feb 05–08; Austin, TX, USA: IEEE; p. 66–73. doi:10.1109/itherm.1992.187742 [Google Scholar] [CrossRef]
2. Webb RL. The evolution of enhanced surface geometries for nucleate boiling. Heat Transf Eng. 1981;2(3-4):46–69. doi:10.1080/01457638108962760. [Google Scholar] [CrossRef]
3. Khalaf-Allah RA, Mohamed SM, Saeed E, Tolan M. Augmentation of water pool boiling heat transfer using heating surfaces fabricated by multi passive techniques. Appl Therm Eng. 2023;219(7):119693. doi:10.1016/j.applthermaleng.2022.119693. [Google Scholar] [CrossRef]
4. Bergles AE, Chyu MC. Characteristics of nucleate pool boiling from porous metallic coatings. J Heat Transfer. 1982;104(2):279–85. doi:10.1115/1.3245084. [Google Scholar] [CrossRef]
5. Al Omari SAB, Elnajjar E. An experimental study on enhancing cooling rates of low thermal conductivity fluids using liquid metals. Fluid Dyn Mater Process. 2013;9:91–109. doi:10.3970/fdmp.2013.009.091. [Google Scholar] [CrossRef]
6. Sen P, Kalita S, Sen D, Das S, Das AK. Pool boiling heat transfer on a micro-structured copper oxide surface with varying wettability. Chem Eng Technol. 2022;45(5):808–16. doi:10.1002/ceat.202100558. [Google Scholar] [CrossRef]
7. Sen P, Kalita S, Sen D, Das AK, Saha BB. Pool boiling heat transfer and bubble dynamics of modified copper micro-structured surfaces. Int Commun Heat Mass Transf. 2022;134(10):106039. doi:10.1016/j.icheatmasstransfer.2022.106039. [Google Scholar] [CrossRef]
8. Haji A, Moghadasi H, Saffari H. Enhanced boiling heat transfer efficiency through the simultaneous use of electrospray and photolithography methods: an experimental study and correlation. Therm Sci Eng Prog. 2023;38(3):101661. doi:10.1016/j.tsep.2023.101661. [Google Scholar] [CrossRef]
9. Liu H, Zhang C, Wang J, Zhang L. Critical heat flux enhancement using composite porous structure produced by selective laser melting. Appl Therm Eng. 2021;197:117396. doi:10.1016/j.applthermaleng.2021.117396. [Google Scholar] [CrossRef]
10. Liter SG, Kaviany M. CHF enhancement by modulated porous-layer coating. In: Proceedings of the ASME International Mechanical Engineering Congress and Exposition (IMECENew Orleans, LA, USA, 1998; p. 165–73. doi:10.1115/IMECE1998-0593. [Google Scholar] [CrossRef]
11. Wen MY, Ho CY. Pool boiling heat transfer of deionized and degassed water in vertical/horizontal V-shaped geometries. Heat Mass Transf. 2003;39:729–36. doi:10.1007/s00231-002-0358-z. [Google Scholar] [CrossRef]
12. Liu B, Yang X, Li Q, Chang H, Qiu Y. Enhanced pool boiling on composite microstructured surfaces with microcavities on micro-pin-fins. Int Commun Heat Mass Transf. 2022;138(3):106350. doi:10.1016/j.icheatmasstransfer.2022.106350. [Google Scholar] [CrossRef]
13. Ustinov A, Ustinov V, Mitrovic J. Pool boiling heat transfer of tandem tubes provided with the novel microstructures. Int J Heat Fluid Flow. 2011;32(4):777–84. doi:10.1016/j.ijheatfluidflow.2011.04.001. [Google Scholar] [CrossRef]
14. Gao Z, Hong S, Dang C. An experimental investigation of subcooled pool boiling on downward-facing surfaces with microchannels. Appl Therm Eng. 2023;226(4):120283. doi:10.1016/j.applthermaleng.2023.120283. [Google Scholar] [CrossRef]
15. Huang CW, Srikanth V, Kuznetsov AV. The evolution of turbulent micro-vortices and their effect on convection heat transfer in porous media. J Fluid Mech. 2022;942:1–38. doi:10.1017/jfm.2022.291. [Google Scholar] [CrossRef]
16. Searle M, Emerson P, Crockett J, Maynes D. Influence of microstructure geometry on pool boiling at superhydrophobic surfaces. Int J Heat Mass Transf. 2018;127(12):772–83. doi:10.1016/j.ijheatmasstransfer.2018.07.044. [Google Scholar] [CrossRef]
17. Gouda RK, Pathak M, Khan MK. Pool boiling heat transfer characteristics of a biosurfactant particle deposited heating surface. Int J Heat Mass Transf. 2020;163(4):120455. doi:10.1016/j.ijheatmasstransfer.2020.120455. [Google Scholar] [CrossRef]
18. Benjamin RJ, Balakrishnan AR. Nucleation site density in pool boiling of saturated pure liquids: effect of surface microroughness and surface and liquid physical properties. Exp Therm Fluid Sci. 1997;15(1):32–42. doi:10.1016/S0894-1777(96)00168-9. [Google Scholar] [CrossRef]
19. Surtaev A, Kuznetsov D, Serdyukov V, Pavlenko A, Kalita V, Komlev D, et al. Structured capillary-porous coatings for enhancement of heat transfer at pool boiling. Appl Therm Eng. 2018;133(1):532–42. doi:10.1016/j.applthermaleng.2018.01.051. [Google Scholar] [CrossRef]
20. Joseph A, Mohan S, Sujith Kumar CS, Mathew A, Thomas S, Vishnu BR, et al. An experimental investigation on pool boiling heat transfer enhancement using sol-gel derived nano-CuO porous coating. Exp Therm Fluid Sci. 2019;103(6–7):37–50. doi:10.1016/j.expthermflusci.2018.12.033. [Google Scholar] [CrossRef]
21. da Silva Vilaronga AG, Manetti LL, Gajghate SS, de Oliveira JD, Cardoso EM. The effect of metal foam fins on pool boiling of DI-water. Exp Therm Fluid Sci. 2024;154:111151. doi:10.1016/j.expthermflusci.2024.111151. [Google Scholar] [CrossRef]
22. Kim TY, Weibel JA, Garimella SV. A free-particles-based technique for boiling heat transfer enhancement in a wetting liquid. Int J Heat Mass Transf. 2014;71(5):808–17. doi:10.1016/j.ijheatmasstransfer.2013.12.070. [Google Scholar] [CrossRef]
23. Wen MY, Jang KJ, Ho CY. Pool boiling heat transfer of deionized and degassed water in packed-perforated copper beads. Heat Mass Transf. 2016;52(11):2447–57. doi:10.1007/s00231-016-1756-y. [Google Scholar] [CrossRef]
24. Yang Y, Ji X, Xu J. Pool boiling heat transfer on copper foam covers with water as working fluid. Int J Therm Sci. 2010;49(7):1227–37. doi:10.1016/j.ijthermalsci.2010.01.013. [Google Scholar] [CrossRef]
25. Gheitaghy AM, Saffari H, Mohebbi M. Investigation pool boiling heat transfer in U-shaped mesochannel with electrodeposited porous coating. Exp Therm Fluid Sci. 2016;76:87–97. doi:10.1016/j.expthermflusci.2016.03.011. [Google Scholar] [CrossRef]
26. Gouda RK, Pathak M, Khan MK. A biosurfactant as prospective additive for pool boiling heat transfer enhancement. Int J Heat Mass Transf. 2020;150(8):119292. doi:10.1016/j.ijheatmasstransfer.2019.119292. [Google Scholar] [CrossRef]
27. Hu ZC, Liu XY, Wang Q. Calculation and analysis of excess adsorption and surface tension of aqueous surfactant solutions under pool boiling conditions. Int J Heat Mass Transf. 2022;185(2):122416. doi:10.1016/j.ijheatmasstransfer.2021.122416. [Google Scholar] [CrossRef]
28. Li X, Fang X, Guo Y, Yang P, He Z. Experimental study on subcooled pool boiling heat transfer of sodium dodecyl sulfate surfactant solution. Phys Fluids. 2023;35(2):4028. doi:10.1063/5.0138370. [Google Scholar] [CrossRef]
29. Wen T, Luo J, Jia K, Lu L. Pool boiling heat transfer enhancement of aqueous solution with quaternary ammonium cationic surfactants on copper surface. Int J Heat Mass Transf. 2022;190(5):122761. doi:10.1016/j.ijheatmasstransfer.2022.122761. [Google Scholar] [CrossRef]
30. Etedali S, Afrand M, Abdollahi A. Effect of different surfactants on the pool boiling heat transfer of SiO2/deionized water nanofluid on a copper surface. Int J Therm Sci. 2019;145(4):105977. doi:10.1016/j.ijthermalsci.2019.105977. [Google Scholar] [CrossRef]
31. Yang Z, Yao Y, Wu H. Effects of surfactants on subcooled pool boiling characteristics: an experimental study. Int J Heat Mass Transf. 2022;199:123419. doi:10.1016/j.ijheatmasstransfer.2022.123419. [Google Scholar] [CrossRef]
32. Wen DS, Wang BX. Effects of surface wettability on nucleate pool boiling heat transfer for surfactant solutions. Int J Heat Mass Transf. 2002;45(8):1739–47. doi:10.1016/S0017-9310(01)00251-4. [Google Scholar] [CrossRef]
33. Gouda RK, Ranjan A, Pathak M, Khan MK. Combined effect of structured surface and biosurfactant in pool boiling heat transfer enhancement. Int J Heat Mass Transf. 2024;221(3):125102. doi:10.1016/j.ijheatmasstransfer.2023.125102. [Google Scholar] [CrossRef]
34. Li B, Zheng J, Dang C, Kang Y, Jia H. Experimental investigation on bubble dynamic behaviors in pool boiling of surfactant solutions. Int J Therm Sci. 2024;198(3):108858. doi:10.1016/j.ijthermalsci.2023.108858. [Google Scholar] [CrossRef]
35. Jia H, Xu L, Xiao X, Zhong K. Study on boiling heat transfer of surfactant solution on grooved surface. Int J Heat Mass Transf. 2021;181(1):121876. doi:10.1016/j.ijheatmasstransfer.2021.121876. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
