Vibrational Suspension of Two Cylinders in a Rotating Liquid-Filled Cavity with a Time-Varying Rotation Rate

Nomenclature

1  Introduction

Many researchers give attention to the problems of vibrational hydromechanics, studying the effect of oscillating force fields on systems containing phase inclusions. The dynamics of free phase inclusions in the fluid, as well as the averaged forces acting on them, are of interest in such studies. An example of the effect of an averaged vibrational force on a phase inclusion in an inviscid fluid is its attraction/repulsion to/from a solid wall. The direction of the averaged force is determined by the distance to the wall at high dimensionless frequencies. The force of attraction is due to the fact that the fluid in the gap between the body and the wall flows at a higher velocity than on the other side of the body, which leads to a decrease in pressure in the gap (Bernoulli’s law) [1]. The attractive force replaces the repulsive force at the viscous interaction distance, which is determined by the thickness of the viscous Stokes layer. The action of the repulsive force is limited by the thickness of the viscous boundary layer, within which the fluid motion is viscous. On the opposite side, the flow around the cylinder is a potential oscillating flow, which leads to an inhomogeneity of the averaged pressure near the body [2]. A better understanding of the vibrational dynamics of inclusions in fluids allows the creation of means to control vibrational processes in fluids. This field of research is of interest for the development of methods for the redistribution of phase inclusions in fluids (e.g., cleaning contaminants from the boundary fluid layer).

Numerous theoretical and experimental studies have been conducted on the attraction and repulsion forces acting on inclusions of different shapes (sphere/cylinder) and densities at high dimensionless frequencies. Thus, a theoretical description of the averaged attractive force acting on cylindrical and spherical bodies that oscillate at high frequency and small amplitude is given in [3–5]. Namely, Lyubimov and co-authors studied the oscillatory motion of a cylinder at an arbitrary distance from the cavity wall at high dimensionless frequencies and determined the conditions under which an oscillating body with a density higher (lower) than that of the fluid floats (sinks) [5]. The results of theoretical and experimental studies of the repulsive vibrational force acting on a cylinder in a cavity under translational oscillations are presented in [6]. It is shown that the repulsive force is manifested at the viscous interaction distance between the oscillating cylinder and the wall. Schipitsyn et al. demonstrated that the vibrational lift force depends on the amplitude and frequency of oscillations as well as on the fluid density [7]. It is found that the magnitude of the averaged lift force decreases with increasing dimensionless amplitude.

Detailed experimental and theoretical studies of phase inclusions enable the determination of universal laws that describe their dynamics. This, in turn, allows the control of the distribution of inclusions in the fluid. This direction is significant for various technological processes including wastewater treatment and enhanced oil recovery. An overview of studies and developments in dynamic filtration across various technological applications is given in [8]. There is a commercial VSEP (Vibratory Shear Enhanced Process) technological process which is based on the generation of high shear at the surface of the filter membrane. This causes bodies and foulants to detach from the membrane surface, increasing the permeability of the membrane pores. In contrast to the studies described above, this process occurs at low non-dimensional frequencies.

The effect of the averaged vibrational force is evident in microgravity. The effect of g-jitter (spacecraft oscillations) on fine particles suspended in a fluid cell was studied in [9]. It is found that the vibrational force shifts from attraction to repulsion as the fluid viscosity increases. Additionally, the effect of vibrational force grows with increasing oscillation frequency and amplitude. Liang and colleagues employed numerical modeling to investigate bubble dynamics in the vicinity of a wall under microgravity conditions relevant to material processing, such as crystal growth in space [10]. It is demonstrated that the fluid viscosity and the distance between the bubble and the wall are crucial parameters in determining the direction of the vibrational force. The recent paper presents the research project T-PAOLA (Thermovibrationally-driven Particle self-Assembly and Ordering mechanisms in Low Gravity) [11]. The primary aim of the project is to investigate the occurrence of new dispersed-phase self-organization phenomena driven by the application of vibrations. The paper provides a detailed description of the space hardware and software, the experiment protocol, the ground tests and procedures, and all the adaptations that had to be implemented to overcome many technological and physical issues.

The inclusion motion is determined by the interaction with other inclusions, too. Two issues are considered: (a) bodies are suspended and streamlined by an oscillating fluid flow [12–14]; (b) one of the bodies oscillates under the action of an external force while the second body and the fluid remain stationary at a significant distance from the oscillating body [3,15,16]. Note that the interaction between two bodies is influenced by the direction of the body oscillations. When oscillations are directed along the axis connecting the centers of two suspended cylinders, a repulsive force occurs. On the contrary, when oscillations are perpendicular to this axis, the cylinders are attracted. When discussing the dynamics of several bodies, the phenomenon of flow-induced vibration (FIV) is of great interest to scientists due to its significance in offshore and ocean engineering applications. Various aspects of FIV have been studied including the mutual arrangement of cylinders [17,18], the distance between cylinders [19,20], the cylinders’ shape [21–23] as well as the steady and unsteady forces acting on cylinders [24,25]. The reduction of vibrations caused by the flow around a tandem of cylinders is one of the most important research topics for the safety of various facilities (underwater pipelines, pipe arrays in heat exchangers, chimneys, and bridge abutments).

This work presents an experimental study of the dynamics of two cylinders near the wall of an unevenly rotating horizontal cylindrical cavity filled with fluid. This paper is part of a series of works devoted to the study of the dynamics of a single cylinder in a rotating cavity and the measurement of the averaged lift force [26–28]. Previous research has shown that a cylinder experiences an averaged repulsive force in a cylindrical cavity undergoing modulated rotation. In this case, the non-dimensional lift force increases almost linearly with the dimensionless frequency of oscillations.

2  Experimental Setup

The paper examines the effect of lift force acting on two free cylinders 1 and 2 in an unevenly rotating horizontal cylindrical cavity 3 (Fig. 1). The cylinders are made of plastic ( ρS=1.05 g/cm3) rods and have similar length l=58 mm and diameter d=4.3 mm. The cylinders are marked with a straight line running through the center of one end wall to track their rotation. The transparent Plexiglas cylindrical cavity has the following dimensions: radius R=30 mm and length L=74 mm. The cavity is filled with silicone oil of viscosity of ν=0.2 St or 1.0 St and density ρL of 0.95 or 0.99 g/cm3, respectively. The cylinders’ relative density varies within a range of 1.06–1.10. The low relative density of the cylinders allows us to reduce the average effect of gravity on the cylinders to a negligible value [26].

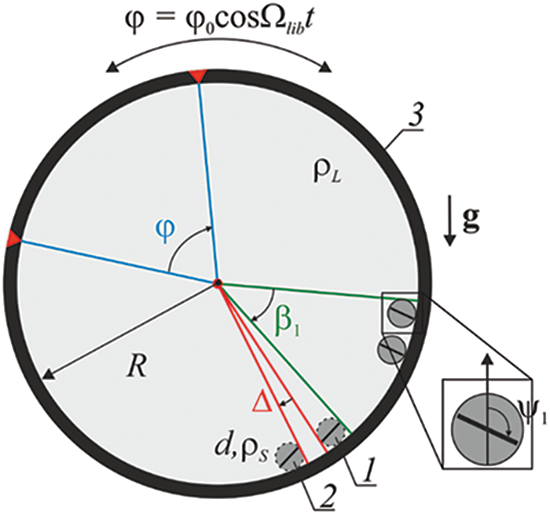
Figure 1: Scheme of the experimental setup and scheme indicating the measured parameters

The cavity filled with fluid and containing cylinders rotates about a horizontal axis according to the law Ω=Ωrot(1+εcos⁡Ωlibt) . Here, Ωlib=2πflib is the radian frequency of modulation, Ωrot=2πfrot is the mean value of angular velocity, and ε=φ0Ωlib/ΩlibΩrotΩrot is the amplitude of the angular velocity modulation. The cavity 1 is rotated by stepper motor 2 (Fig. 2). The motor is controlled by SMD 4.2 type driver 3 and power supply 4. The ZetLab 210 module 5 and a personal computer are used to control and change the rotation parameters. A more detailed design of the experimental setup is presented in [27].

Figure 2: Scheme of the experimental setup

The modulated rotation of the cavity can be considered as the sum of uniform rotation and rotational oscillations. The dynamics of two cylinders is studied in a reference frame that rotates uniformly at a rate of frot . In this frame of reference, the cavity undergoes azimuthal oscillations according to the law φ=φ0cos⁡Ωlibt . In experiments, the rotation rate frot varies in the range of 3–4 rps, and the frequency flib varies in the range of 2–16 Hz. During the experiment, the modulation amplitude ε increases step by step at fixed frequencies frot and flib . The dynamics of two cylinders is recorded at each step of the experiment using a high-speed camera positioned in front of the cavity. The recorded video is converted into a number of frames to measure the azimuthal coordinates of the cavity φ and the cylinders β , the angle ψ of the cylinders’ rotation about their axis, the angular distance between two cylinders Δ , and the gap thickness h (Fig. 1). We use subscripts 1 and 2 to distinguish the quantities related to each of the cylinders.

3  Experimental Results

At the beginning of the experiment, the cavity is rotated to a speed frot at which the cylinders are pressed against the wall of the cavity by centrifugal force (Fig. 3a). As the cavity rotates uniformly, the cylinders are positioned close to each other. Then, the modulation of the rotation rate with the frequency flib and amplitude ε is activated. The cylinders begin to oscillate in the azimuthal direction due to viscous interaction with the cylindrical wall of the unevenly rotating cavity. The amplitude β0 of the cylinders’ oscillations increases linearly with the amplitude φ0 of the cavity oscillations (Fig. 3b). Here, filled symbols indicate the amplitude of the cylinder 1 oscillations while empty symbols indicate the amplitude of the cylinder 2 oscillations.

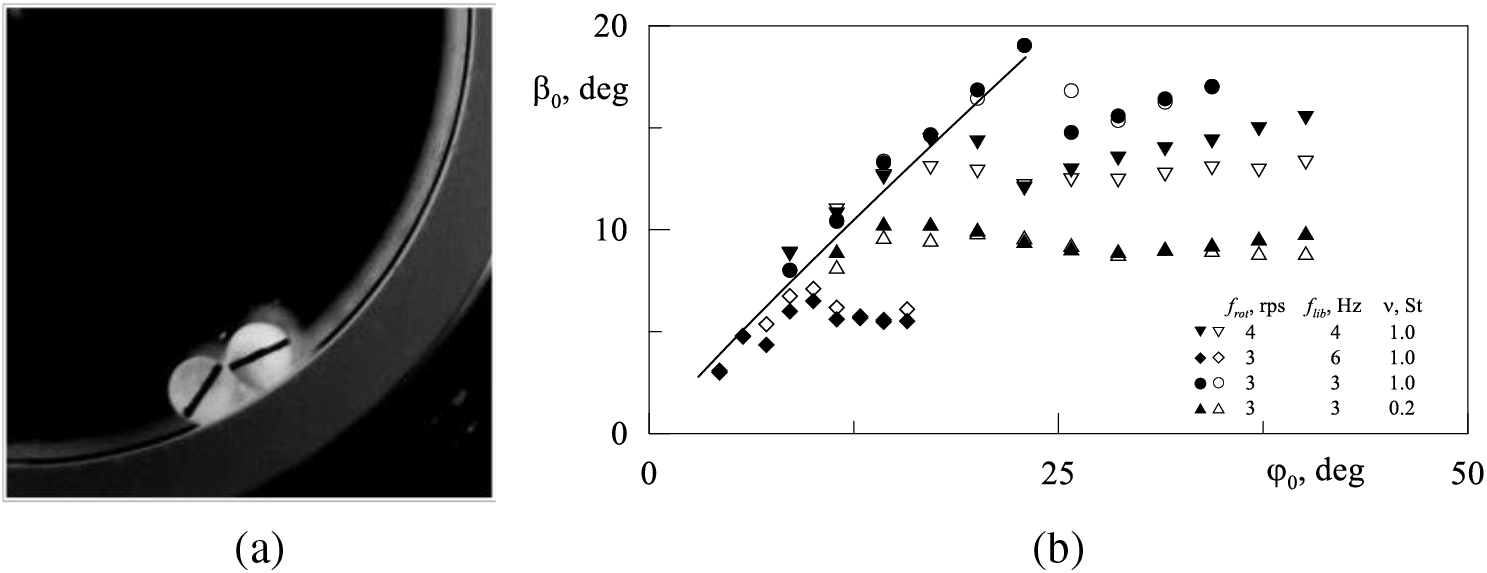
Figure 3: (a) Photograph of two cylinders located near the cavity wall at frot=4 rps, flib=4 Hz, ε=0 , ν=1.0 St; (b) dependence of the amplitude of azimuthal oscillations of two cylinders on the amplitude of the cavity oscillations

The oscillatory dynamics of a pair of cylinders will be analyzed with reference to the dynamics of a single spherical and single cylindrical body, as presented in [26–28]. This will enable us to identify the impact of an increase in the number of bodies on their oscillatory dynamics. It is evident that the amplitude of azimuthal oscillations grows linearly only up to the threshold value of φ0 (the threshold value of φ0 increases as the frequency of oscillation decreases flib ). When the threshold value of φ0 is reached, the amplitude β0 decreases abruptly. As φ0 is further increased, the amplitude β0 continues to increase linearly, but the dependence of β0 on φ0 weakens. A similar dependence β0(φ0) was previously obtained for a single cylindrical body [26,28]. Note that the dependence of β0(φ0) is the same for both cylinders for a fixed value of flib . The break in the graph is explained by the detachment of the cylinders from the cavity wall and further transition to the suspended state (Fig. 4a).

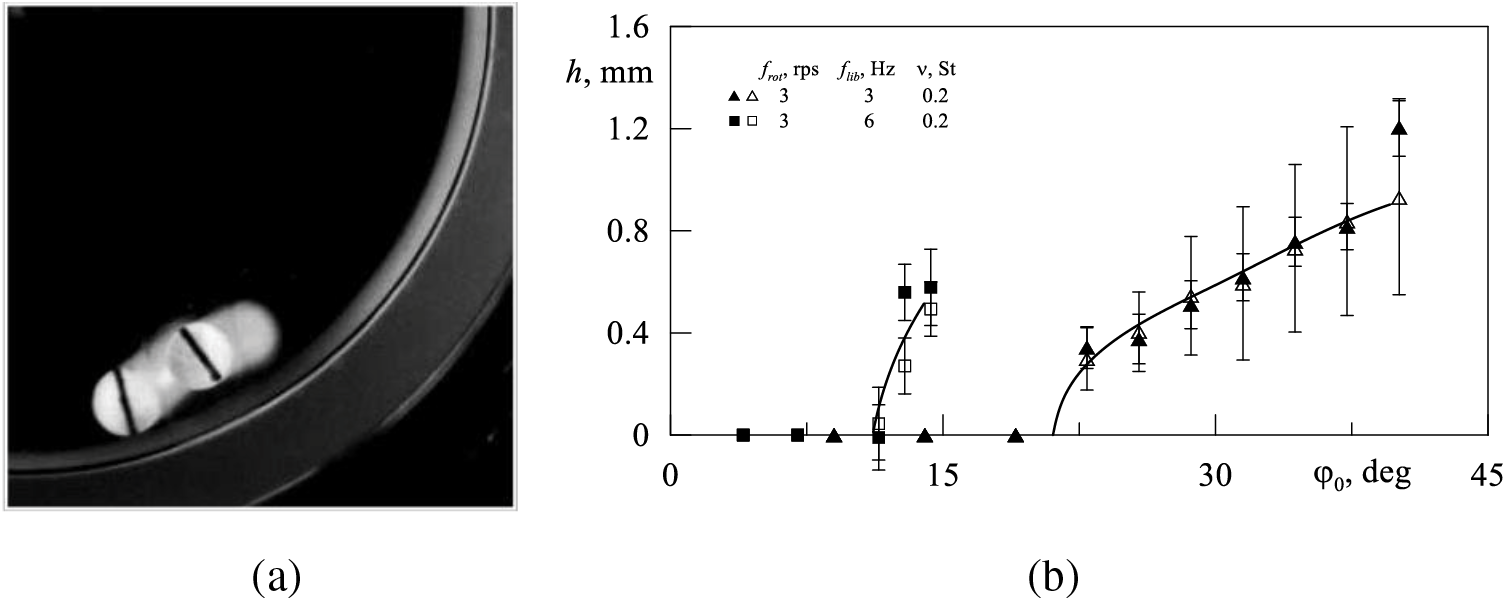
Figure 4: (a) Photo of the suspended cylinders at frot=4 rps, flib=4 Hz, ε=0.75 , ν=1.0 St; (b) dependence of the gap width h on the amplitude of the azimuthal oscillations of the cavity

The transition to the suspended state occurs at the threshold value of φ0 (Fig. 4b). As the frequency of oscillation flib increases, the threshold value of φ0 decreases. So, the gap width between the cylinders and the cavity wall is equal to zero at small amplitudes of azimuthal oscillations of the cavity. The gap h increases monotonically with increasing φ0 . Note that unlike the case of a single cylinder studied in [26,28] a pair of suspended cylinders undergo both radial and azimuthal oscillations. The plot displays the average distance between the cylinders and the cavity wall during its azimuthal oscillations. One can find that the amplitude of radial oscillations increases with φ0 . Error bars indicate the deviation from the mean.

Experiments conducted over a wide range of modulation parameters show that, in addition to azimuthal oscillations, the cylinders undergo rotational oscillations about their axis. These oscillations are caused by the viscous interaction between the cylinders and the oscillating wall. The amplitude of rotational oscillations of the cylinders ψ0 grows linearly with φ0 (Fig. 5a). One can find that the experimental data are consistent with each other within the range of investigated parameters. The linear dependence of ψ0 on φ0 indicates that viscous interaction plays a crucial role in the dynamics of cylinders. A similar dependence was obtained for a single cylinder and a sphere oscillating near the wall due to viscous interaction with the one [26,28]. Note that the detachment of the cylinders from the cavity wall does not affect the dependence of ψ0 on φ0 . This is because in the suspended state, the cylinder remains within a viscous Stokes boundary layer of thickness δ=(2ν/2νΩlibΩlib) which ensures its rotation about its axis. The experimental data deviate from the linear law only at large supercriticality. Let us examine experimental data indicated by the red oval in Fig. 5а. Fig. 5b displays the trajectory of the cylinders in this experiment ( frot=4 rps, flib=4 Hz, ε=0.70 , ν=1.0 St). As previously mentioned, the cylinders undergo radial oscillations while moving along the cavity wall.

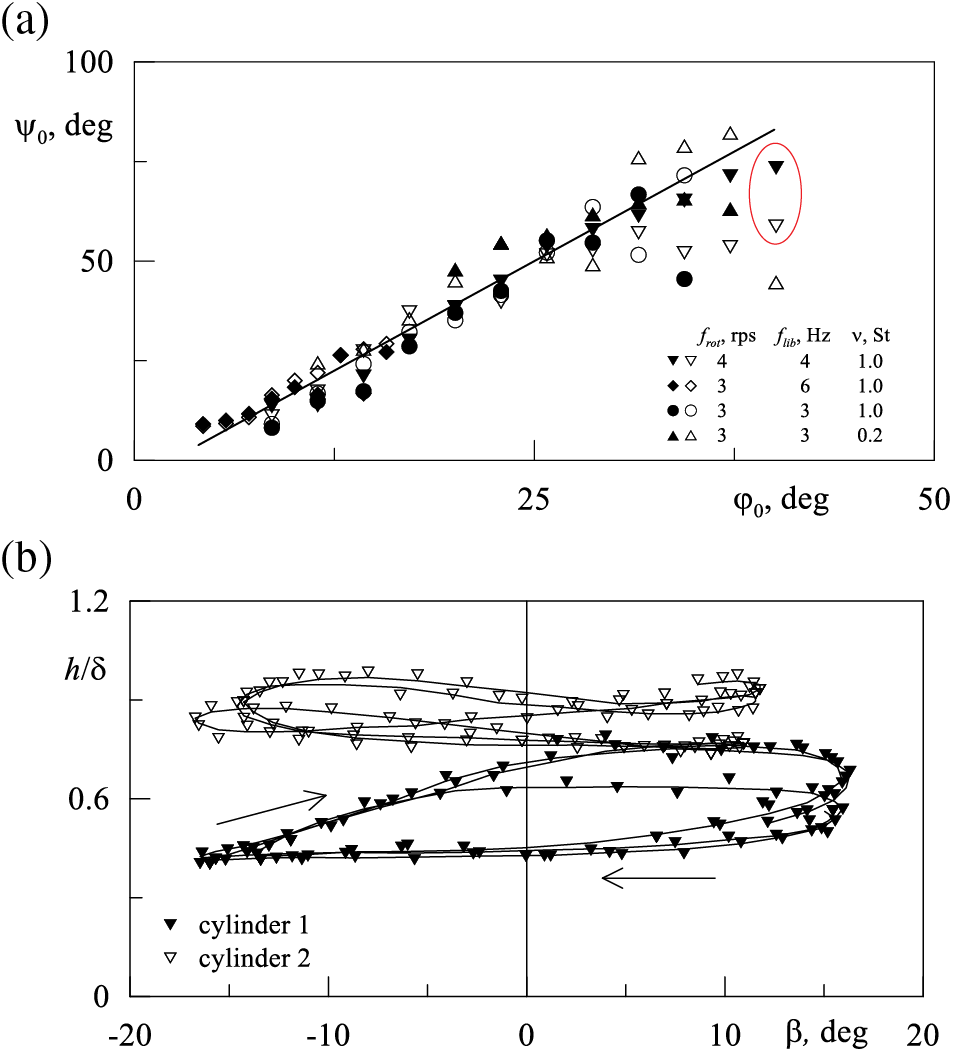
Figure 5: (a) Dependence of the amplitude of the cylinder rotational oscillations on the amplitude of the cavity oscillations and (b) trajectories of two cylinders ( frot=4 rps, flib=4 Hz, ε=0.70 , ν=1.0 St)

It is evident that cylinder 1 undergoes radial oscillations within the Stokes boundary layer ( h/hδδ < 1 ). Therefore, the amplitude of the rotational oscillations is determined by the amplitude of the cavity oscillations: The experimental point (filled inverted triangle in Fig. 5a) is in agreement with the linear law. At the same time, cylinder 2 is outside the boundary layer for a portion of the oscillation period ( h/hδδ > 1 ). This weakens the viscous interaction with the oscillating cavity wall and reduces the amplitude ψ0 of rotational oscillations of the cylinder (empty inverted triangle in Fig. 5а).

In addition to the detachment of two cylinders from the cavity wall, we reveal the repulsive force between cylinders first described in [13]. At the beginning of the experiment, the cylinders are placed next to each other (Fig. 3а). At small amplitudes of cavity oscillations, the cylinders move side by side along the cavity wall. As the amplitude of azimuthal oscillations of the cavity increases, an angular gap with a value of Δ appears between the cylinders (Fig. 4а). The value of the distance Δ increases as the value of φ0 increases (Fig. 6). Note that the distance Δ varies during the oscillation cycle: the cylinders move closer together in the extreme positions, and the distance between the cylinders becomes maximum in the mid-position. Error bars on the graph indicate the deviation from the mean value of Δ . It is evident that although the cylinders tend to converge during the oscillation cycle, the gap between the cylinders is maintained. The symbols at Δ < 0 can be attributed to measurement error caused by parallax resulting from the axial displacement of the cylinders relative to each other. It can be seen that the gap between the cylinders occurs in a threshold manner. The threshold value of Δ decreases as the libration frequency increases in experiments with fluid of the same viscosity. This requires further research.

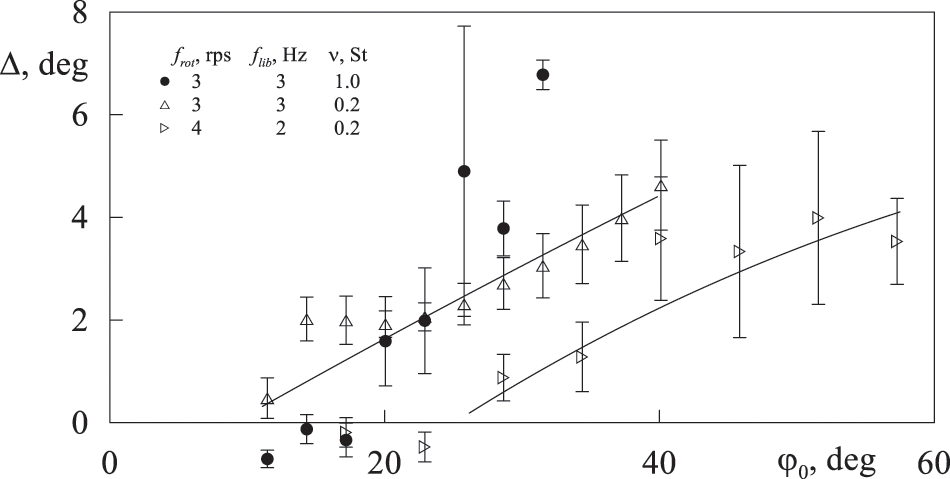
Figure 6: Scheme of the experimental setup and scheme indicating the measured parameters

The detachment of the cylinders from the cavity wall is caused by an average vibrational lift force, the description of which is given in [29]. The lift force is associated with the asymmetry of the flow velocity distribution near the oscillating cylinder. The oscillatory flow between the cylinders and the wall is viscous while on the opposite side of the cylinders the flow is potential. This results in a pressure gradient away from the cavity wall.

It has been demonstrated in previous experiments with bodies of various shapes (sphere, cylinder, plate) that the repulsive (lift) force acts at a distance comparable to the thickness of the Stokes boundary layer [30–32]. In this study, the cylinders detach from the cavity wall at a distance of approximately δ , too (Fig. 5b). The method of quasi-stationary suspension of the body in the static field of centrifugal force is used to measure the average vibrational lift force (Fig. 7а). The formula F∗=πd(ρ−1)φ02/πd(ρ−1)φ022ε2β02(R−d/d22)2ε2β02(R−d/d22) determines the non-dimensional lift force calculated by the velocity amplitude of tangential oscillations of the cylinder center of mass. This formula was initially presented in the experimental work [28] for the case of a single cylinder oscillating in the vicinity of a wall. In addition, the authors derived a formula for the force acting on an oscillating spherical body. Earlier, researchers measured the lift force acting on a single body (sphere, cylinder) that oscillates due to viscous interaction with the oscillating cavity wall [28,29]. It is revealed that the value of F∗ does not change with the distance to the cavity wall. It is hypothesized that the amplitude of the body oscillations, rather than its distance to the cavity wall, is the major factor affecting the lift force. A similar effect is observed when a pair of cylinders oscillates in the fluid near the wall. Fig. 7b illustrates the relationship between the non-dimensional lift force and the non-dimensional gap width. Since the cylinders undergo both azimuthal and radial oscillations, the average value of h is used. One can find that the magnitude of the non-dimensional lift force remains unaffected by the distance to the cavity wall. Note that the lift force increases as the non-dimensional frequency ω=Ωlibd2/Ωlibd24ν4ν increases. This is due to the fact that the thickness of the Stokes layer decreases with increasing ω . This leads to an increase in the fraction of the cylinder surface that is in contact with the inviscid fluid flow which is responsible for the generation of the lift force.

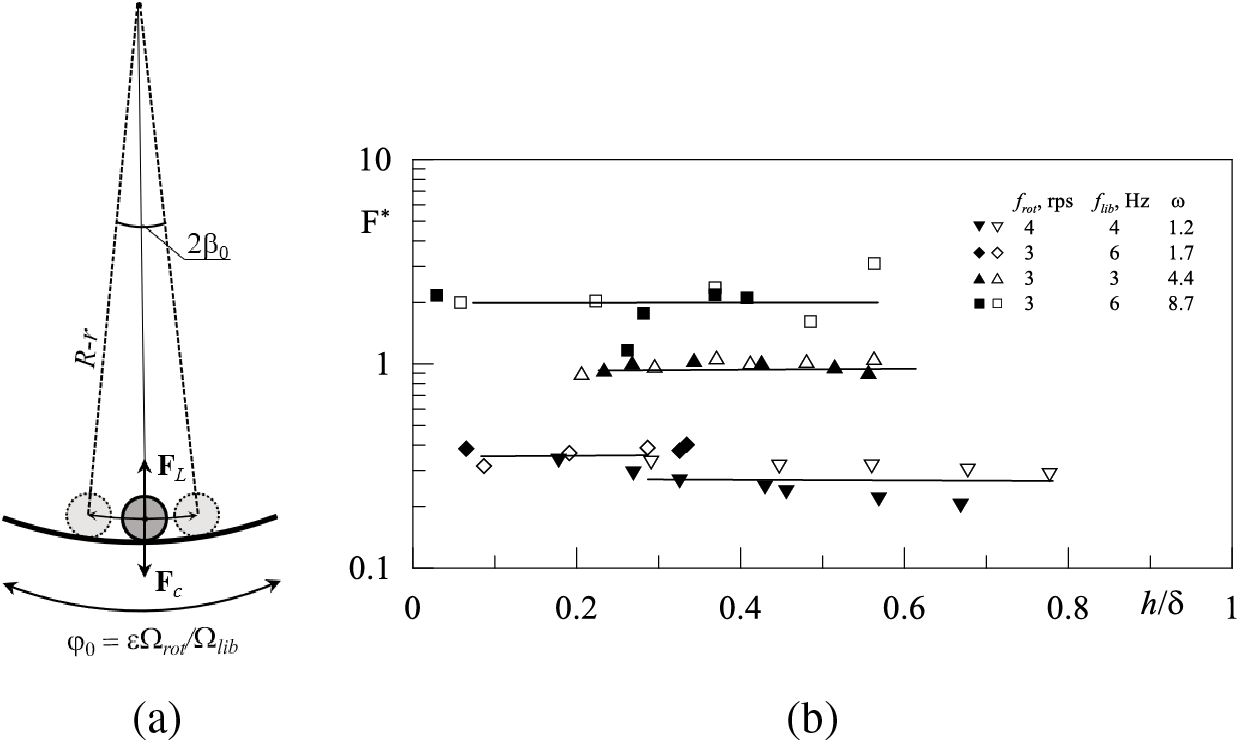
Figure 7: (a) Forces acting on the cylinder relative to a uniformly rotating frame of reference; (b) dependence of the non-dimensional lift force on the non-dimensional gap width between the cylinder and the cavity wall

As discussed above, the magnitude of the lift force depends on the non-dimensional frequency. When a body undergoes inertial oscillations in a cavity, the lift force increases with frequency in the limit of low frequencies [6,30,31]. Also, the dependence of F∗ on ω weakens or disappears completely in the limit of high non-dimensional frequencies. However, in the case of a cylinder oscillating due to viscous interaction with an oscillating wall, a nearly linear increase in the value of F∗ with ω is found in a wide range of non-dimensional frequencies [27,28]. When a pair of cylinders oscillates near a solid wall, a similar dependence of F∗ on ω is found (Fig. 8). Here, the results obtained in experiments with a single cylinder are illustrated by filled symbols, while data obtained in experiments with a pair of cylinders are represented by symbols. It is evident that new experimental data are in satisfactory agreement with data obtained in previous studies. This indicates that the presence of the second cylinder does not affect the magnitude of the lift force. It can be concluded that an increase in the number of bodies in the oscillating cavity does not result in qualitative or quantitative changes in the generation of the lift force. This is likely due to the fact that the case of close densities between the bodies and the surrounding fluid is being considered. In this case, the amplitude of oscillations of the bodies and the lift force are determined by the viscous interaction with the oscillating wall. The cylinders do not affect the oscillatory motion of each other.

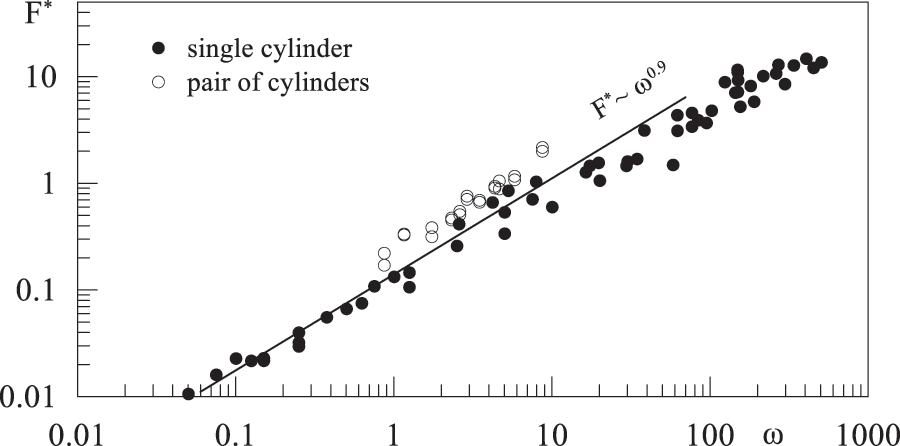
Figure 8: Dependence of the non-dimensional lift force on the non-dimensional oscillation frequency

4  Conclusion

The average vibrational lift force acting on a pair of cylinders in a fluid near the wall of a non-uniformly rotating cylindrical cavity is experimentally studied. It is shown that the cylinders oscillate relative to the cavity due to the viscous interaction with the wall and transit to the suspended state when the threshold amplitude of oscillations is reached. The transition of a body into a suspended state is the result of the action of a vibrational lift force. The lift force can only occur if the body oscillates relative to the surrounding fluid and a portion of the body is immersed in the viscous boundary layer to provide viscous interaction with the oscillating cavity wall. As with the single-cylinder experiments, the lift force is calculated by the velocity amplitude of the azimuthal oscillations of two cylinders. It is revealed that the lift force is independent of the gap width but depends on the non-dimensional frequency. A comparison of new experimental data with the data obtained previously for the case of a single cylinder indicates that the addition of a second cylinder does not affect the magnitude of the vibrational lift force. It is suggested that increasing the number of bodies in an oscillating cavity does not lead to qualitative and quantitative changes in the generation of the vibrational lift force. The effect of repulsion may be useful in regulating heat transfer and enhancing fluid mixing in multiphase flows. This may be of particular importance under conditions of reduced gravity.

Acknowledgement: The author is grateful to Professor Victor Kozlov for fruitful discussions.

Funding Statement: The study was financially supported by the Russian Science Foundation (Grant No. 22-71-00081).

Author Contributions: All the work done by the corresponding author.

Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Saadatmand M, Kawaji M, Hu HH. Vibration-induced attraction of a particle towards a wall in microgravity—The mechanism of attraction force. Microgravity Sci Technol. 2012;24:53–64. doi:10.1007/s12217-011-9291-4. [Google Scholar] [CrossRef]

2. Saadatmand M, Kawaji M. Mechanism of vibration-induced repulsion force on a particle in a viscous fluid cell. Phys Rev E. 2013;88(2):23019. doi:10.1103/PhysRevE.88.023019. [Google Scholar] [PubMed] [CrossRef]

3. Sennitskii VL. Motion of a sphere in fluid caused by vibrations of another sphere. J Appl Mech Tech Phys. 1986;27(4):501–5. doi:10.1007/BF00910190. [Google Scholar] [CrossRef]

4. Lugovtsov BA, Sennitskiy VL. Motion of body in vibrating fluid. USSR Rept Eng Equip JPRS UEQ. 1987;289(2):68. [Google Scholar]

5. Lyubimov DV, Lyubimova TP, Cherepanov AA. On a motion of solid body in a vibrating fluid. In: Convective Flows; 1987. p. 61–70 (In Russian). [Google Scholar]

6. Ivanova AA, Kozlov VG, Shchipitsyn VD. Lift force acting on a cylindrical body in a fluid near the boundary of a cavity performing translational vibrations. J Appl Mech Tech Phys. 2014;55(5):773–80. doi:10.1134/S002189441405006X. [Google Scholar] [CrossRef]

7. Schipitsyn VD, Kozlov VG. Oscillatory and steady dynamics of a cylindrical body near the border of vibrating cavity filled with liquid. Microgravity Sci Technol. 2018;30(1–2):103–12. doi:10.1007/s12217-017-9583-4. [Google Scholar] [CrossRef]

8. Cheng M, Xie X, Schmitz P, Fillaudeau L. Extensive review about industrial and laboratory dynamic filtration modules: scientific production, configurations and performances. Sep Purif Technol. 2021;265:118293. doi:10.1016/j.seppur.2020.118293. [Google Scholar] [CrossRef]

9. Saadatmand M, Kawaji M. Effect of viscosity on vibration-induced motion of a spherical particle suspended in a fluid cell. Microgravity Sci Technol. 2010;22(3):433–40. doi:10.1007/s12217-010-9189-6. [Google Scholar] [CrossRef]

10. Liang R, Liang D, Yan F, Liao Z, Duan G. Bubble motion near a wall under microgravity: existence of attractive and repulsive forces. Microgravity Sci Technol. 2011;23:79–88. doi:10.1007/s12217-010-9238-1. [Google Scholar] [CrossRef]

11. Lappa M, Burel T, Kerr M, Crewdson G, Boaro A, Capobianchi P, et al. Particle vibration, an instrument to study particle accumulation structures on board the international space station. Microgravity Sci Technol. 2022;34(33):1–12. doi:10.1007/s12217-022-09939-2. [Google Scholar] [CrossRef]

12. Zapryanov Z, Kozhoukharova Z, Iordanova A. On the hydrodynamic interaction of two circular cylinders oscillating in a viscous fluid. Zeitschrift für angewandte Mathematik und Physik ZAMP. 1988;39:204–20. doi:10.1007/BF00945766. [Google Scholar] [CrossRef]

13. Lyubimova T, Lyubimov D, Shardin M. The interaction of rigid cylinders in a low Reynolds number pulsational flow. Microgravity Sci Technol. 2011;23:305–9. doi:10.1007/s12217-010-9252-3. [Google Scholar] [CrossRef]

14. Pyatigorskaya OS, Sennitskii VL. Motion of solid particles in an oscillating liquid. J Appl Mech Tech Phys. 2013;54:404–7. doi:10.1134/S0021894413030085. [Google Scholar] [CrossRef]

15. Pyatigorskaya OS, Sennitskii VL. Motion of a sphere in a liquid caused by vibrations of another sphere. J Appl Mech Tech Phys. 2004;45:542–5. doi:10.1023/B:JAMT.0000030331.35411.2e. [Google Scholar] [CrossRef]

16. Al-Hatmi MM, Purnama A. On the motion of two microspheres in a stokes flow driven by an external oscillator field. Int J Math Math Sci. 2021;2021:1–9. doi:10.1155/2021/9211272. [Google Scholar] [CrossRef]

17. Gao Y, Yang B, Zhu H, Peng G, Zhang Z, Pan G. Flow induced vibration of two rigidly connected circular cylinders in different arrangements at a low Reynolds number. Ocean Eng. 2020;217:107741. doi:10.1016/j.oceaneng.2020.107741. [Google Scholar] [CrossRef]

18. Ali MH, Munir A, Zhao M. Numerical investigation of flow across three co-rotating cylinders in side-by-side arrangement. Phys Fluids. 2023;35(11):113601. doi:10.1063/5.0176585. [Google Scholar] [CrossRef]

19. Pereira PT, Cenci F, Fujarra ALC. Transverse displacement phase analysis on 2DOF FIV of rigid cylinders in tandem configurations. J Mar Sci Technol. 2020;25(4):1217–27. doi:10.1007/s00773-020-00710-z. [Google Scholar] [CrossRef]

20. Neumeister RF, Petry AP, Möller SV. Experimental analysis of the space ratio influence on the excitation frequencies of one and two cylinders free to vibrate in tandem arrangement. Vibration. 2022;5(4):770–91. doi:10.3390/vibration5040045. [Google Scholar] [CrossRef]

21. Nepali R, Ping H, Han Z, Zhou D, Yang H, Tu J, et al. Two-degree-of-freedom vortex-induced vibrations of two square cylinders in tandem arrangement at low Reynolds numbers. J Fluid Struct. 2020;97:102991. doi:10.1016/j.jfluidstructs.2020.102991. [Google Scholar] [CrossRef]

22. Kumar D, Sourav K. Vortex-induced vibrations of tandem diamond cylinders: a novel lock-in behavior. Int J Mech Sci. 2023;255:108463. doi:10.1016/j.ijmecsci.2023.108463. [Google Scholar] [CrossRef]

23. Badri Ghomizad M, Yamakawa M. Transverse vortex-induced vibration of two elliptic cylinders in tandem: effects of spacing. Phys Fluids. 2023;35(11):117114. doi:10.1063/5.0169835. [Google Scholar] [CrossRef]

24. Chen W, Ji C, Xu D, Zhang Z. Vortex-induced vibrations of two inline circular cylinders in proximity to a stationary wall. J Fluid Struct. 2020;94:102958. doi:10.1016/j.jfluidstructs.2020.102958. [Google Scholar] [CrossRef]

25. Schewe G, van Hinsberg NP, Jacobs M. Investigation of the steady and unsteady forces acting on a pair of circular cylinders in crossflow up to ultra-high Reynolds numbers. Exp Fluids. 2021;62(8):176. doi:10.1007/s00348-021-03268-7. [Google Scholar] [CrossRef]

26. Vlasova OA, Kozlov VG, Kozlov NV. Lift force acting on a heavy solid in a rotating liquid-filled cavity with a time-varying rotation rate. J Appl Mech Tech Phys. 2018;59:219–28. doi:10.1134/S0021894418020050. [Google Scholar] [CrossRef]

27. Vlasova OA, Karpunin IE, Solomennikov MN. Lift force acting on a heavy cylinder and a steady flow in an unevenly rotating container. Microgravity Sci Technol. 2020;32:889–96. doi:10.1007/s12217-020-09817-9. [Google Scholar] [CrossRef]

28. Vlasova OA, Kozlov VG. Experimental study of the solid motion in the vicinity of the wall in an oscillating cavity. Microgravity Sci Technol. 2023;35(4):38. doi:10.1007/s12217-023-10062-z. [Google Scholar] [CrossRef]

29. Ivanova AA, Kozlov VG. Lift force acting on body in liquid in the vicinity of boundary executing tangential oscillations. Microgravity Sci Technol. 2014;26(3):179–87. doi:10.1007/s12217-014-9394-9. [Google Scholar] [CrossRef]

30. Ivanova AA, Kozlov VG, Kuzaev AF. Vibrational lift force acting on a body in a fluid near a solid surface. Dokl Phys. 2005;50(6):311–4. doi:10.1134/1.1958123. [Google Scholar] [CrossRef]

31. Ivanova AA, Kozlov VG, Shchipitsyn VD. A light cylinder under horizontal vibration in a cavity filled with a fluid. Fluid Dyn. 2010;45(6):889–97. doi:10.1134/S0015462810060062. [Google Scholar] [CrossRef]

32. Kozlov V, Vlasova O. The repulsion of flat body from the wall of vibrating container filled with liquid. Microgravity Sci Technol. 2015;27:297–303. doi:10.1007/s12217-015-9460-y. [Google Scholar] [CrossRef]