Natural Convection of a Power-Law Nanofluid in a Square Cavity with a Vertical Fin

Nomenclature

1  Introduction

Free convection heat transfer in square enclosures is largely used in numerous engineering applications such as heat exchangers, buildings, built-in-storage solar collectors and thermal management of electronics [1]. Researchers have expressed significant concern regarding the enhancement of heat transfer in free convection due to its inherently low heat transfer coefficient. Consequently, they actively explored diverse techniques and concepts to improve the heat transfer in this process. One of those techniques that researchers frequently focus on is adding nanoparticles to the conventional working fluid. The addition of nanoparticles enhances the thermophysical properties of the base fluid, particularly thermal conductivity, a pivotal parameter that improves the heat transfer mechanisms [2–6]. Therefore, the single-phase model was largely employed due to its simplicity and computational efficiency, making it suitable for diluting nanofluids with low nanoparticle concentrations. However, its simplicity may lead to inaccuracies, as it oversimplifies complex nanofluid behavior and neglects nanoparticle interactions [7]. The two-phase model, initiated in 2006 by Buongiorno, offered a deeper insight into the movement of nanoparticles into the base fluid. Alsabery et al. [8] have concluded in their review that the high computational cost of the two-phase models has limited the adoption of the model of single-phase among researchers. As a result, only 19% of nanofluid studies have opted for the two-phase approach.

Some analytical and numerical investigations have been performed on free convection through nanofluids in cavities of different shapes [9–13]. These studies have investigated the impact of altering the nanoparticle’s volume fraction at various Rayleigh numbers (Ra) on heat transfer.

Houda Jalali [14] have explored enhanced heat transfer in Al2O3−water nanofluid through nanoparticle addition. They have carried out a numerical study of a square enclosure, revealing optimal conditions for heat transfer improvement. They have proposed precise correlations for thermal conductivity and viscosity on the basis of experimental outcomes. They have identified the minimum value of temperature (40°C) and the diameter limit (45–50 nm) for enhanced heat transmission. Ma et al. [15,16] have numerically investigated the natural convection of TiO2 and Al2O3−H2O nanofluids inside a U-shaped enclosure featuring a heated obstacle. It was demonstrated that an increase in the Ra and the nanoparticles volume fraction ( φ ) led to a higher Num on the obstacle sides, irrespective of the aspect ratio. At lower Ra , nanoparticles had a greater impact on the improvement of the heat transfer in slender cavities compared to larger ones. Moreover, when the diameters of nanoparticles are equal, Al2O3 nanoparticles are more effective than TiO2 ones in enhancing heat transfer. Faraz et al. [17] have conducted a study on convective heat transfer through Cu−water nanofluid within a hexagonal cavity with an internal square. Their research focused on how the heat transfer characteristics are affected by the placement of the active sections of the side walls and the nanoparticles volume fraction. Their parametric investigation revealed that increasing the volume fraction of Cu nanoparticles led to enhanced heat transfer within the cavity.

While most studies have concentrated on free convection heat transfer for Newtonian fluids within cavities, the influence of non-Newtonian behavior exhibited by nanofluids on free convection heat transport remains less explored. Some studies have employed a comparative analysis to investigate the free convection heat transfer characteristics between Newtonian and non-Newtonian behaviors. Turan et al. [18] considered the free convection phenomenon in a square enclosure exposed to heat flux at the sidewalls, focusing on power-law fluids and Newtonian fluids. For both power-law and Newtonian fluids, heat transfer increased with rising Ra values. Nevertheless, at the same Ra, shear-thinning fluids with n < 1 exhibited greater heat transfer rates compared to both Newtonian fluids and dilatant behavior with n > 1 . These obtained results are confirmed by several researchers [19–22].

Several published studies have proved that the presence of the fin in cavities introduces an additional heat transfer surface, leading to improved convective heat transfer. Elatar et al. [23] have numerically investigated the laminar free convection in a square differentially heated enclosure with one simple horizontal fin fixed to the heated wall. The study has revealed that the effectiveness of the fin has increased with its length. Saravanan et al. [24] have numerically analyzed the free convection inside an enclosure with a heated plate, considering thermal radiation effects. In the cases of the absence of emissivity, it has been well documented in the literature that the heat transfer is significantly improved when the fin is both longer and vertical. These same results were obtained also by Mahalakshmi et al. [25].

In the constantly changing field of heat transfer involving fluid flow through nanoparticles inside cavities, there have been notable advancements in recent years. Islam et al. [26] analyzed copper-water nanofluid convective flow through a prismatic cavity under two different temperature boundary conditions, aiming to visualize temperature flow and identify the most efficient temperature change path. Khan et al. [27] studied TiO2−H2O nanofluid free convection heat transfer inside a square enclosure with partly active sidewalls employing Finite Element Method (FEM). Saha et al. [28] conducted a numerical study of MHD free convective heat transfer and fluid flow inside a square cavity containing Al2O3−H2O nanofluid. The cavity features a wavy top wall and a vertically attached, hot single fin in the center of the bottom side. The upper wavy side is considered cold, while the bottom, left, and right sides were thermally isolated. Al2O3 nanoparticles possess a high thermal conductivity, and Cu nanoparticles exhibit both high specific heat capacity and thermal conductivity, while TiO2 nanoparticles possess a high surface area. They also exhibit other advantages that make them versatile for numerous applications. Additionally, alumina nanoparticles are chemically inert, non-toxic, and widely available. Furthermore, titania nanoparticles are known for their photocatalytic properties and UV-blocking capabilities. And copper nanoparticles are recognized for their chemical stability and their ability to work effectively with numerous HTF and materials. However, despite the existing literature, there is still a research gap that needs to be further investigated in order to fully understand the non-Newtonian flow behavior in a square enclosure with a hot central fin.

The current study introduces several novel contributions to the area of fluid flow and thermal transfer. The study begins by examining the power-law nanofluids behavior, capturing specifics of shear-thinning (pseudo-plastic behavior) and shear-thickening (dilatant behavior) fluids in a square cavity having a heated central vertical fin, utilizing the finite element method; offering a fresh perspective as it examines a geometry that has received limited attention in previous research. The rheological response of non-Newtonian nanofluids in this configuration allowed us to further control the fin-induced heat transfer enhancement. This is particularly significant due to its involvement in various practical and industrial applications, including thermal management of electronic components, nuclear reactors, heat exchangers and float glass production, among others. Moreover, the inclusion of changing Rayleigh numbers ( Ra ), nanoparticle volume fractions ( φ ), power-law index ( n ), and fin dimensions ( Ar ) presents a parametric study that improves the understanding of Newtonian and non-Newtonian nanofluid behavior across diverse conditions. Additionally, a comparison is conducted among three types of nanoparticles with the primary objective of augmenting convective heat transfer. This investigation allows for a thorough analysis of the effects of these parameters on convective heat transport, particularly by evaluating their effects on the mean Nusselt number ( Num ). Through pinpointing the areas in the cavity that demonstrate the largest Num, the study offers important insights into achieving the optimum of heat transfer efficiency in nanofluidic systems.

2  Modelling and Mathematical Formulation

The square cavity Fig. 1 is enclosed by two vertical walls cooled to a temperature of Tc and two horizontal walls that are adiabatic. A heated fin with dimensionless variable length (Ar=bL=0.3,  0.5,  and 0.7) is vertically positioned at the cavity’s midpoint, kept at an elevated temperature Th . The enclosure contains water-based nanofluid incorporating nanoparticles of Al2O3 , TiO2 , or Cu , assumed as a laminar and incompressible Boussinesq power law model, with a Prandtl number ( Pr ) set at 6.2. Assuming thermal stability between the water-based fluid and nanoparticles, with no slip occurring due to their thermophysical properties as listed in Table 1. Under these conditions and according to the nanofluid model suggested by Tiwari et al. [29,30], continuity, momentum, and energy equations, in laminar incompressible nanofluid may be expressed in their nondimensional form for the numerical solution as follows [24,27,28,31,32]:

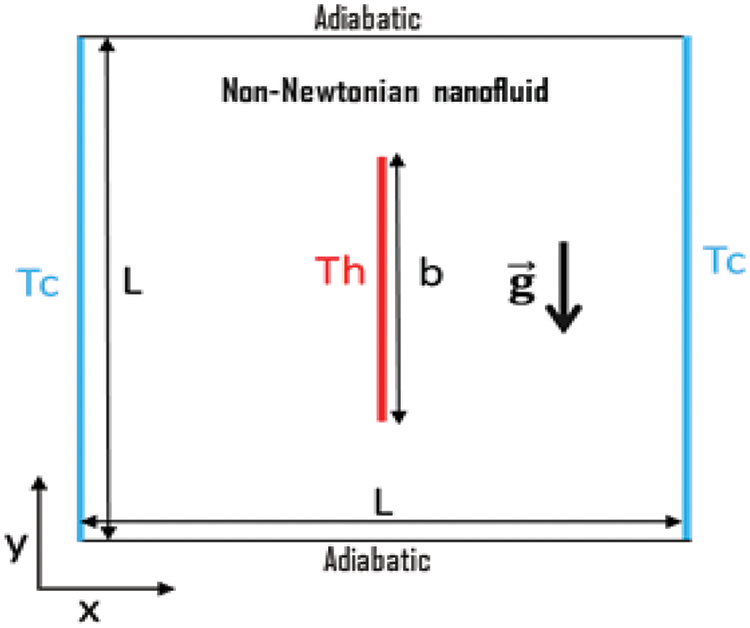
Figure 1: Some functions of x

Dimensionless variables can be linked to dimensional ones through [19,28]:

X=xL,  Y=yL,  U=u(αfL)Ra,  V=v(αfL)Ra,  P=pρ(αfL)2Ra,  Θ=T−TcTh−Tc   (5)

Dimensionless Rayleigh ( Ra ) and Prandtl ( Pr ) numbers are expressed below [27,33]:

Ra=ρfgβfL3(Th−Tc)μeff αf,  Pr = μeffρf αf  (6)

The thermo-physical characteristics of the nanofluid are determined using conventional models reported in the literature [34,35] as follows:

ρnf=(1−φ)ρf+φρp  (7)

(ρCp)nf=(1−φ)(ρCp)f+φ(ρCp)p (8)

(ρβ)nf=(1−φ)(ρβ)f+φ(ρβ)p  (9)

The nonofluid’s density, specific heat, thermal expansion coefficient, and thermal diffusivity are represented by ρ , cp , β , and α , respectively. The nanoparticle volume fraction is denominated by φ , while the subscripts nf , f , and p correspond to the nanofluid, base fluid, and nanoparticle, respectively. The Hamilton-Crosser model [36] was employed to determine the effective thermal conductivity of the spherically shaped nanofluid, this model has been adopted by many researchers [19,37,38]:

knf=kf[(kp+2kf)−2φ(kf−kp)(kp+2kf)+φ(kf−kp)]  (10)

The Brinkman model was used to calculate the effective dynamic viscosity of the nanofluid μnf [35,39]:

μnf=μeff(1−φ)2.5  (11)

The non-Newtonian fluid inside the cavity obeys the Ostwald-de Waele power law model, based on the shear stress tensor:

τxx=2μnf∂u∂x  (12)

τyy=2μnf∂v∂y  (13)

τxy=τyx=μnf(∂u∂y+ ∂v∂x)  (14)

where μeff could be defined as follows:

μeff=M{2[(∂u∂x)2+ (∂v∂y)2]+ ( ∂v∂x+∂u∂y)2}n−12  (15)

The effective viscosity ( μeff ) and consistency index ( M ) are not intrinsic fluid properties; however, they are related to the fluid shear rate. The power-law index ( n ) is employed to describe the non-Newtonian fluid attitude. Newtonian fluids are identified when n equals 1, while non-Newtonian fluids are specified when n is different from 1. When n is less than 1, the non-Newtonian nanofluid behaves as a shear-thinning fluid, where its apparent viscosity reduces with rising the shear rate. However, when n is greater than 1, the non-Newtonian nanofluid behaves as a shear-thickening fluid, where its apparent viscosity rises with an increasing in shear rate.

μeff¯=M{2[(∂U∂X)2+ (∂V∂Y)2]+ ( ∂V∂X+∂U∂Y)2}n−12  (16)

The problem’s boundary conditions, when dimensionless, are presented below:

{ U=V=0,∂Θ∂Y=0Horizontal wallsU=V=0,Θ=Θc=0Vertical wallsU=V=0,Θ=Θc=0At the fin(17)

Some relationships are conducted to clarify how Rayleigh number, Prandtl number, and power-law index influence the Nusselt number for the model of power-law fluids [18].

Nu∼h.Lknf∼Lδth or Nu∼Lδf(Ra, Pr, n) (18)

where the hydrodynamic and thermal boundary-layer thicknesses, δ and δth , are related by this expression: δ/δth∼f(Ra, Pr, n) in which f(Ra, Pr, n) denotes a function of Rayleigh number, Prandtl number, and power-law index. A positive correlation with increasing Prandtl number is expected.

The average Nusselt number is expressed by:

Nu¯∼(Ra2−nPr−n)12(n+1)f(Ra, Pr, n) when Nu¯ > 1  (19)

3  Numerical Methodology and Validation

Numerical solutions for the Eqs. (1)–(4), considering the initial and boundary conditions (17), were computed employing COMSOL, a partial differential equations (PDEs) solver that utilizes the Galerkin weighted residual finite element approach is adapted. The flow is laminar and the fluid is assumed to be incompressible. The computational domain was subdivided to triangular elements, and various orders of triangular Lagrange finite elements were employed to represent the various flow variables throughout the computational domain. To handle the non-linear terms present in momentum equations, Newton iterative method was employed for simplifications.

The stream function equation is solved using the Poisson’s equation:

∂2ψ∂X2+∂2ψ∂Y2=∂U∂Y−∂V∂X  (20)

Multiple sensitivity grid tests were performed to assess the adequacy of the scheme of mesh and ensure that the outcomes are not influenced by the grid used. The default settings of COMSOL for pre-defined mesh sizes are employed as below in Table 2.

The extra fine grid type of 16,630 elements is chosen to accurately resolve the governing equations and the local-average heat transfer.

To verify the numerical outcomes accuracy found in the current investigation, a comparison was conducted between quantitative results (mean Nusselt number and the maximum of streamlines) and qualitative aspects (isotherms and streamlines behaviors) (as illustrated in Fig. 2 of the current work) with those reported by Brinkman et al. [39] for a differentially heated enclosure without a fin, both in the presence and absence of magnetic fields (which are not presented here). The results of the current study align well with those of Ghasemi et al. with the highest deviation observed at 1.96% for Ra=107 and Ha=30 .

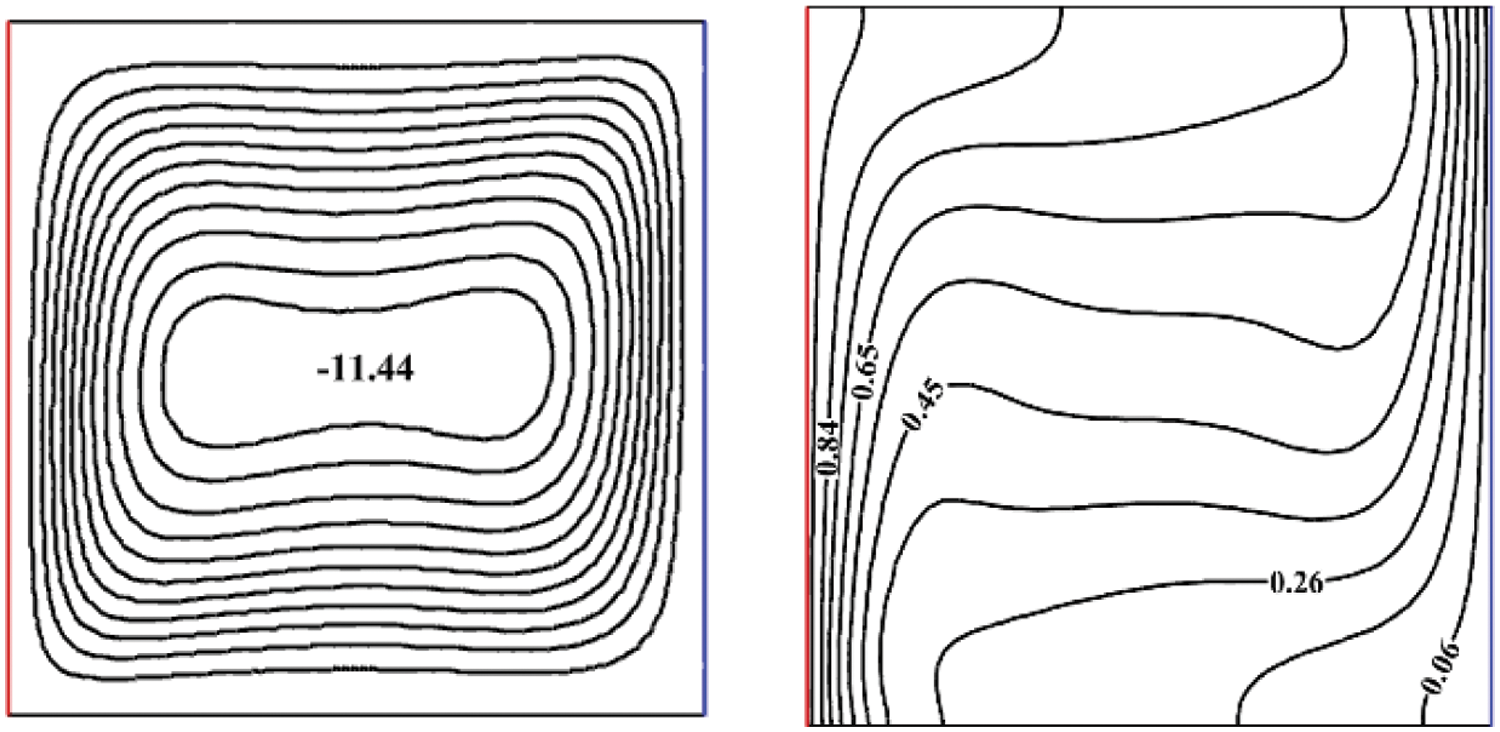
Figure 2: Streamlines (left) and the isotherms (right) of the current study for a=105 , φ = 0.03 , n=1 , Pr=6.2 and Ha=0

Furthermore, another comparison of the Num is made among the current work and the one of Turan et al. [18] for various n and Ra , at φ = 0 and Pr=100 is represented in Table 3. The results agree well with those of Turan et al. [18], for the highest error of no more than 0.61% recorded for Ra=106  and n=0.6.

4  Results and Discussion

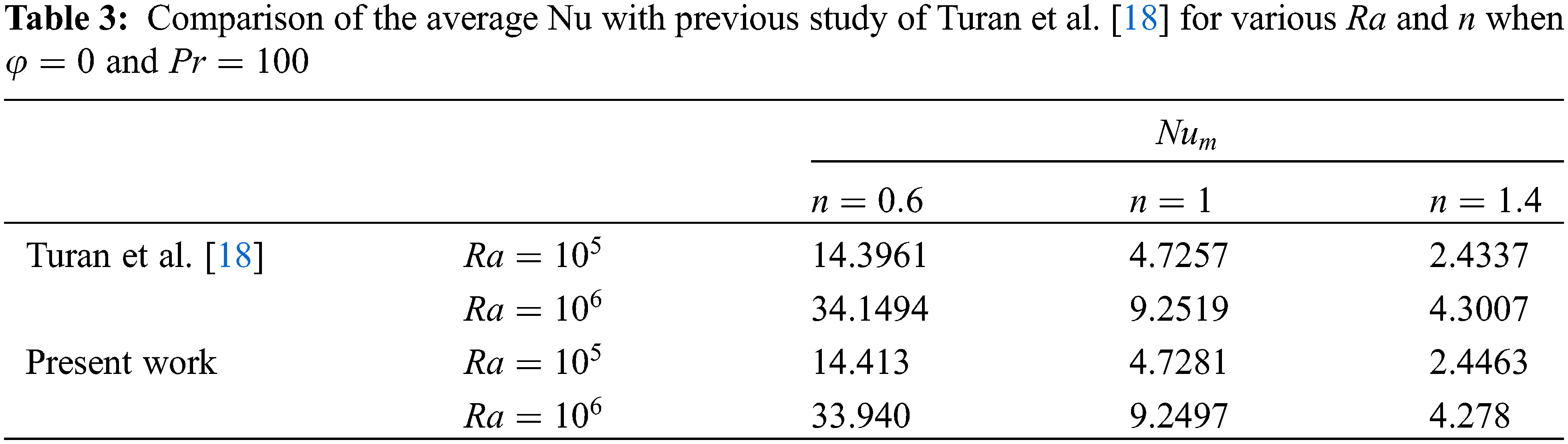
Fig. 3 illustrates the changes of the mean Nusselt number ( Num ) with the volume fraction ( φ ) of TiO2, Al2O3, and Cu nanoparticles, considering various values of Rayleigh number ( Ra ) and power-law index ( n ). The examination of this figures shows that for all nanoparticles types, the mean Nusselt number has an upward trend as the nanoparticle volume fraction increases, this trend can be caused by the fact that raising this parameter enhances the thermal fluid conductivity, thereby resulting in an improvement in the energy transported by the nanofluid. Additionally, it also improves with the rise in ( Ra ) and a decrease in the ( n ). This reduction results in an amplification of the heat flux magnitude at the vertical walls.

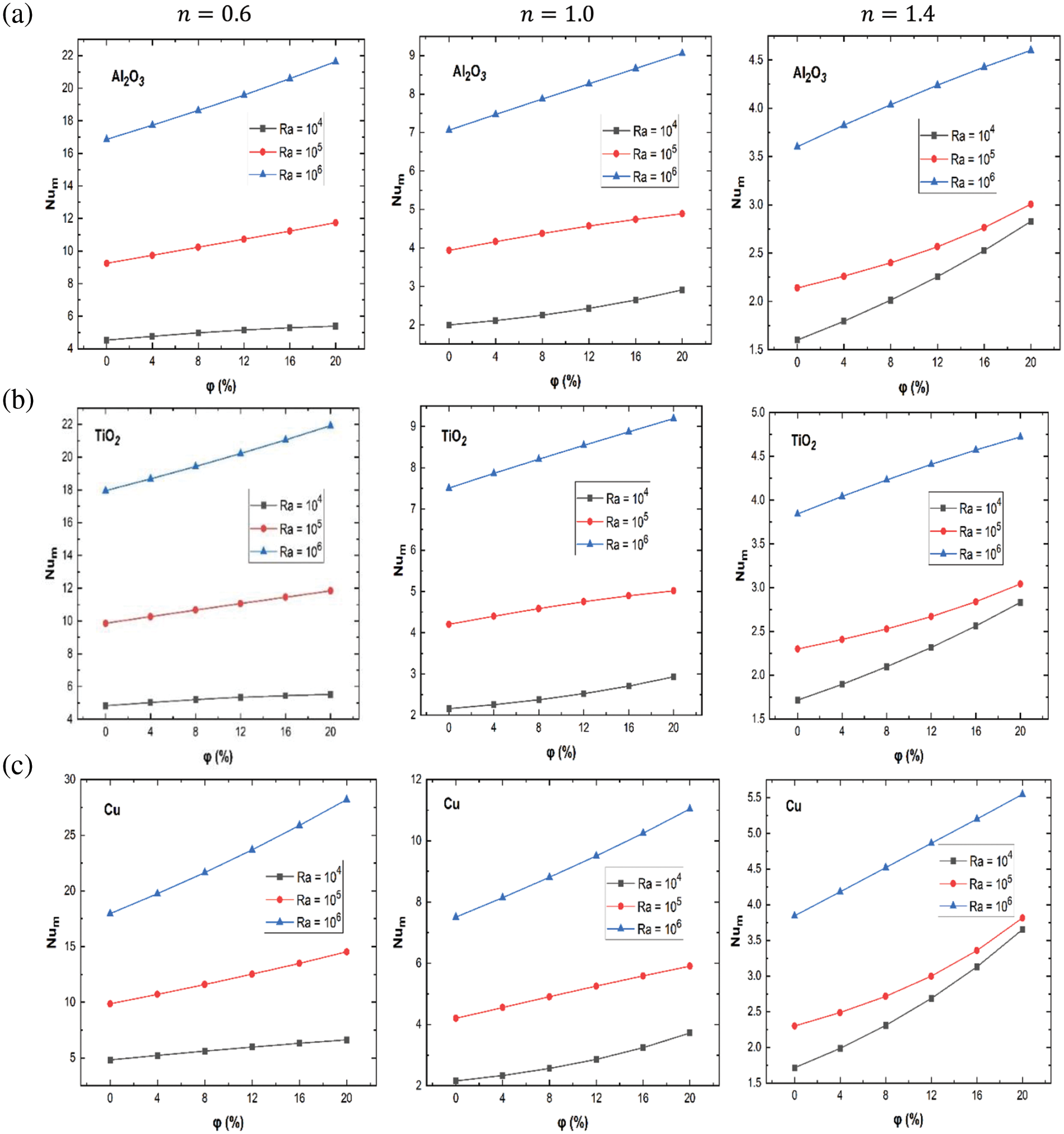
Figure 3: The Num number at φ and n : (a) Al2O3 , (b) TiO2 and (c) Cu nanoparticles

In fact, for shear-thinning nanofluids ( n=0.6 ), such as Al2O3, TiO2, and Cu , these fluids exhibit the highest Nusselt numbers. This is attributed to their apparent viscosity, which reduces as the shear rate rises. Consequently, the fluid becomes less resistant to flow, leading to enhanced convective heat transfer. Moreover, the synergistic effect of shear-thinning behavior and an increased nanoparticle volume fraction further contribute to the overall improvement in convective heat transfer efficiency. However, for shear-thickening nanofluids ( n=1.4 ), where viscosity increases under shear stress, the inhibitory effect on fluid mobility tends to suppress convective heat transfer efficiency, as shown evidence by the lowest average Nusselt numbers. This rheological behavior creates a challenging scenario for heat transport enhancement. Particularly noteworthy is the observation that, at a relatively low Ra=104 , the addition of Al2O3, TiO2, and Cu nanoparticles have a more significant impact. In this scenario, the altered viscosity and flow patterns induced by these nanoparticles appear to overcome the inhibitory effect imposed by shear-thickening behavior, leading to a more favorable convective heat transfer outcome.

For Newtonian fluid case behavior ( n=1 ), characterized by constant viscosity irrespective of applied stress or shear rate, the average Nusselt numbers reach 9 for Al2O3 and TiO2 and 11 for Cu . These results emphasize the notable impact of Cu nanoparticles in enhancing convective heat transfer, surpassing the improvements achieved with the Al2O3 and TiO2. However, Cu falls behind shear-thinning fluids while outperforming shear-thickening ones in terms of the enhancement of heat transfer.

Remarkably, the most substantial rise in the mean Nusselt number with varying volume fractions of Al2O3, TiO2, and Cu nanoparticles is observed at a high Ra=106 , with Cu showing the most significant increase of 3.5. This observation underscores the heightened effectiveness of Cu nanoparticles in enhancing convective heat transfer, particularly under conditions of elevated thermal gradients and fluid motion. These findings highlight Cu’s potential for applications requiring efficient performance of heat transfer, particularly at elevated values of Ra .

The most pronounced impact of nanoparticles on heat transport is evident at a power law index ( n=0.6 and Ra=106 ) for all three sorts of nanoparticles. This specific combination of rheological behavior and high thermal gradients results in the most substantial improvement in convective heat transfer efficiency. The findings suggest that, under these conditions, the synergistic effects of shear-thinning behavior and the nanoparticles presence contribute significantly to improving the heat transfer in the system.

The observations depicted in Fig. 4 underscore the significant influence of fluid rheology, particularly the transition from shear-thinning to the behavior of shear-thickening. This transition is associated with a decrease in ( Num ), showing a reducing in convective heat transfer efficiency. Notably, among the nanoparticles, TiO2 demonstrates the most pronounced effect of ( n ) on ( Num ). Furthermore, Fig. 4 highlights that the nanoparticles addition has a positive impact on the average Nu , contributing to enhanced convective heat transfer. Furthermore, the nanoparticle volume fractions of Cu exhibit a more pronounced impact on the Nu compared with those of Al2O3 and TiO2, as evident in Figs. 5 and 6. This distinction becomes more pronounced when the nanofluids exhibit shear-thinning behavior. In Fig. 6, all nanofluids display similar behavior at various Ra , however, it was found that Cu provided the highest heat transport compared to the other considered nanofluids.

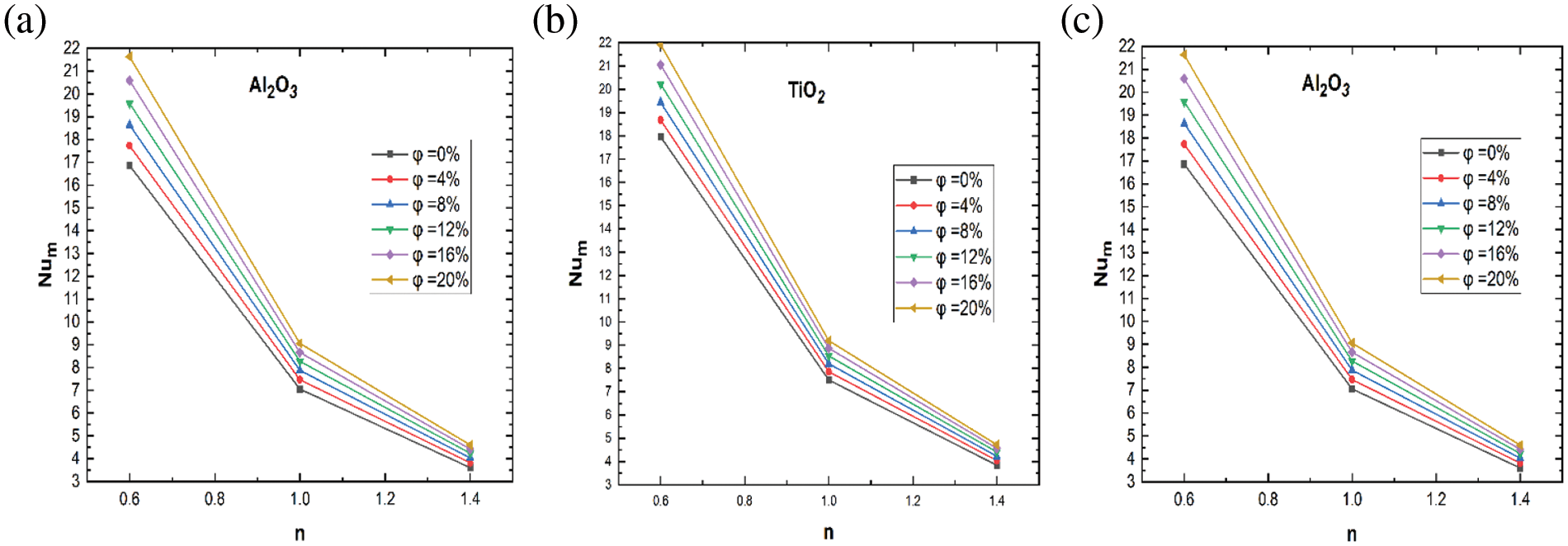
Figure 4: The Num number at n and φ for Ra=106 : (a) Al2O3– water, (b) TiO2 – water and (c) Cu – water nanofluids

Figure 5: Influence of nanoparticles on the Num number for varied φ , at fixed Ra=106and n=0.6

Figure 6: Effect of nanoparticles on the Numnumber at different Ra, at fixed φ=0.04and n=0.6

Fig. 7 provides a visual representation of the circulation of liquid and thermal transmission in Cu – water nanofluids at Ra=106 and φ=0.2 . This specific set of conditions corresponds to the previously observed most significant heat transfer enhancement. The outcomes are presented to analyze the combined influence of the power-law ( 0.6≤n≤1.4 ) index and the dimensions of the fin on heat transfer, as depicted through streamlines and isotherms. These visualizations aim to offer insights into the intricate fluid dynamics and thermal distribution within the device under varying rheological behaviors and fin geometries.

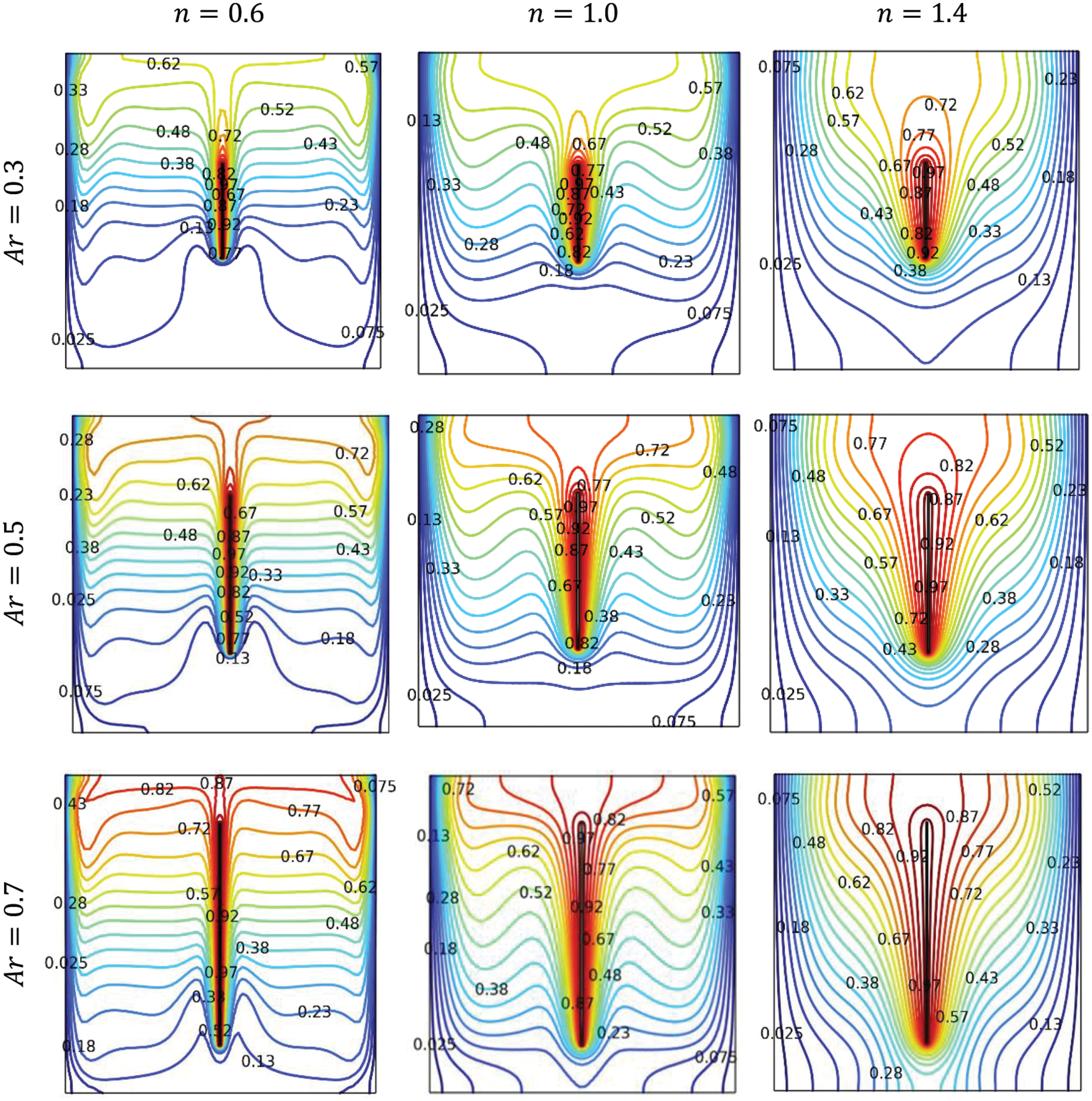
Figure 7: Isotherms at various n , Ar for Ra=106 , φ=0.2 , and Cu−water nanofluid

It is apparent from Fig. 8 that as the n value increases (decreases), the intensity ψmax decreases (increases) because of a decrease (increase) in convective transport strength relative to the resistance from the viscous flow. It is important to highlight that in the case of pseudoplastic or shear-thinning behavior, their reduced viscosity at higher shear rates allow for better flow and mixing within the fluid. This enhanced flow can facilitate the dissipation of heat from hot regions to cooler regions, resulting in a more uniform temperature distribution. This aspect underscores the favorable effect of shear-thinning heat transfer behavior, providing insights into the fluid dynamics that contribute to the observed heat transfer enhancements in the system.

Figure 8: Streamlines at various n , Ar for Ra=106 , φ=0.2 , and Cu−water nanofluid

The presence of the fin, serving as a heat source, induces the formation of temperature stratification zones on both sides of the heat-generating region. As the power law index reduces, the distribution of isotherms becomes increasingly curved in a horizontal manner. This curvature is a consequence of the intensified strength of convection. The result for higher values of n demonstrates a reducing in the circulation of convective flow and the emergence of a heat conduction-driven way within the proximity of the walls. Consequently, one may observe less effective cavity cooling from the vertical walls. This observation highlights the intricate interplay between fluid dynamics, heat conduction, and the index of power law, influencing the total heat transport characteristics within the system.

The observation notes that the streamlines intensity represented by ψmax raises with the enlargement of the fin dimension. This indicates a more vigorous and intensified flow within the cavity. A more intense flow, can contribute to a highly efficient exchange of heat among the fluid and the surfaces of the cavity.

It should be emphasized that the presence of the fin and its vertical positioning at the center significantly increases the rate of heat transport in the enclosure. This finding is in line with the research of Saravanan et al. [24] in the context of pure convection, where they compared the horizontal and vertical positions. This improvement of heat transfer is facilitated by the rise of the area surface provided by the fin, allowing for more contact between the fin and the surrounding fluid.

The influence of the fin’s dimensions and the index of power law on heat transport is more apparent in the results found in terms of Num shown in Fig. 9. This parameter increases with the rising of the Cu nanoparticle volume fractions, enlargement of the fin dimension and a lower value of the index power law ( n ). The shear-thinning nanofluid at Ar=0.7 exhibits the highest Num , accentuating the most important enhancement of heat transfer.

Figure 9: Num number at various φ , Ar , n , at Ra=106 , for Cu – water nanofluid

Fig. 10 shows that, at a constant Ra=106 and φ= 0.04 , the Num reduces with a higher index of power law ( n ) and smaller fin dimension ( Ar ). The impact of the fin’s dimension is more pronounced for shear-thinning nanofluids compared to Newtonian and even more so compared to shear-thickening nanofluids. The highest Nu is seen for shear-thinning nanofluid n=0.6 and Ar=0.7 , this combination yields the most efficient convective heat transfer under the specified conditions. These findings emphasize the significance of both rheological properties and fin geometry in influencing heat transfer efficiency within the cavity.

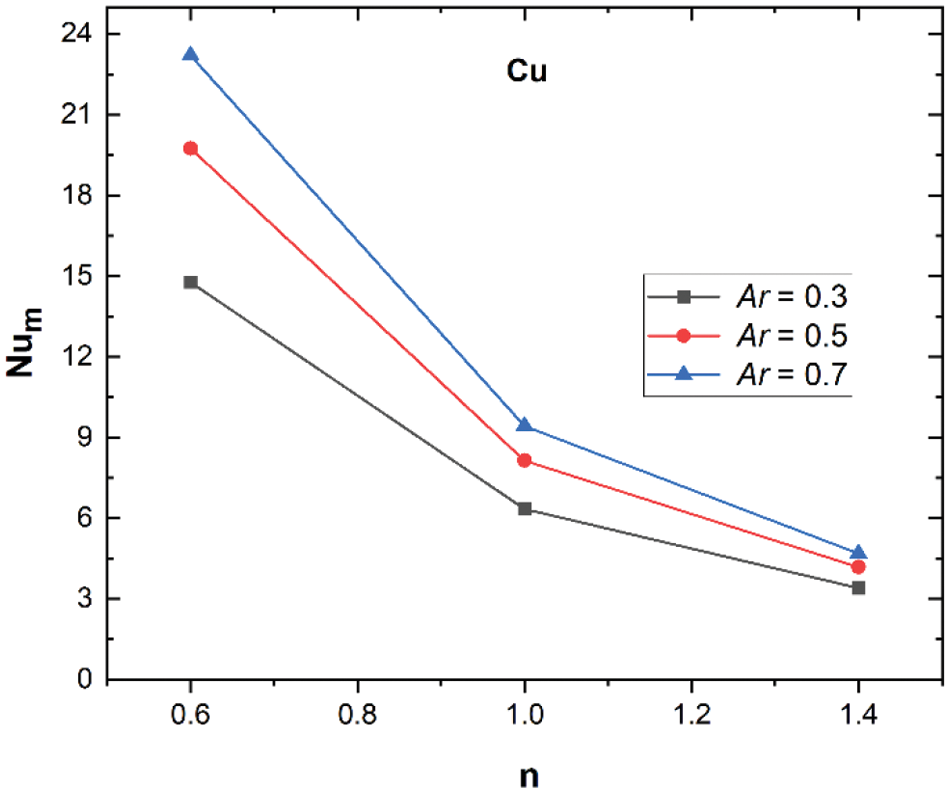
Figure 10: Num number at various n , Ar , at Ra=106 , φ= 0.04 for Cu−water nanofluid

5  Conclusions

In the current study, heat transfer by free convection for Al2O3 , TiO2 and Cu−H2O power-law nanofluid in a square enclosure with the presence of a vertical fin was carried out. This study covered the relevant parameters within the following ranges: the index of power-law ( n=0.6−1.4 ), Ra=104 −106 , the volume fractions (“φ” = 0%–20% ) and the dimensions of the fin ( Ar= 0.3, 0.5, 0.7 ).

The following outcomes have been concluded:

•   For shear-thinning Al2O3 , TiO2 and Cu nanofluids ( n = 0.6 ) demonstrate the highest Nusselt numbers.

•   In the shear-thickening rheological behavior, adding Al2O3 , TiO2 and Cu nanoparticles have a more significant effect at Ra=104  .

•   For Newtonian fluid behavior ( n = 1 ), it has been conducted that Cu nanoparticles have a notable impact on enhancing the heat transfer by convective compared with other nanoparticles, demonstrating the most substantial increase of 3.5, at Ra=106 

•   The most significant impact of nanoparticles adding on the heat transfer is recorded at n = 0.6 for Ra=106 for Al2O3 , TiO2 and Cu .

•   The Cu ’s nanoparticles provided the highest heat transfer compared with the and nanoparticles.

•   The impact of the fin’s dimension is more pronounced for shear-thinning nanofluids compared to Newtonian and even more so compared to shear-thickening nanofluids. The highest Num is observed for nanofluid shear-thinning of n = 0.6 and Ar = 0.7 .

In summary, the improvement of heat transport in the square enclosure is represented by the increment of the Num . It enhances with the decrease for index of power law, which speeds up the flow because of the reduction of the viscosity of the fluid, the increase of Ra which causes the change of the heat transport mechanism from conductive to convective, the rise of nanoparticles volume fractions and the enlargement of the vertical fin.

Acknowledgement: The authors gratefully acknowledge the LERMAB laboratory for fostering an enabling environment for this research and facilitating the first author’s participation in the conference in Italy. Special thanks are also due to Amina Sabeur (LSIM, UST d’Oran) and Dang Mao Nguyen (LERMAB, Université de Lorraine) for their valuable comments aimed at improving this paper. Additionally, the authors thank Mahmoud Eissa for his assistance with plagiarism-related matters.

Funding Statement: This research has received financial support by Campus France within the framework of the PHC-Maghreb 45990SH Project. The first author also receives support from the Tunisian Republic Ministry of Higher Education and Scientific Research for a part of her stay in France. We also acknowledge CRTEn for providing her some flight tickets.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Amira M’hadbi, Haïkel Ben Hamed; numerical validation: Amira M’hadbi, Khalid Chtaibi; data collection: Amira M’hadbi; analysis and interpretation of results: Amira M’hadbi, Mohammed El Ganaoui, Amenallah Guizani; draft manuscript preparation: Amira M’hadbi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Should a request be made for data used in the study, the authors will endeavor to make the information available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Baïri A, Zarco-Pernia E, de María MG. A review on natural convection in enclosures for engineering applications. The particular case of the parallelogrammic diode cavity. Appl Therm Eng. 2014 Feb 05;63(1):304–22. doi:10.1016/j.applthermaleng.2013.10.065. [Google Scholar] [CrossRef]

2. Sundar LS, Farooky MH, Sarada SN, Singh MK. Experimental thermal conductivity of ethylene glycol and water mixture based low volume concentration of Al2O3 and CuO nanofluids. Int Commun Heat Mass Transf. 2013;41:41–6. doi:10.1016/j.icheatmasstransfer.2012.11.004. [Google Scholar] [CrossRef]

3. Lomascolo M, Colangelo G, Milanese M, de Risi A. Review of heat transfer in nanofluids: conductive, convective and radiative experimental results. Renew Sustain Energ Rev. 2015;43:1182–98. doi:10.1016/j.rser.2014.11.086. [Google Scholar] [CrossRef]

4. Ali B, Naqvi RA, Ali L, Abdal S, Hussain S. A comparative description on time-dependent rotating magnetic transport of a water base liquid H2O with hybrid nano-materials Al2O3-Cu and Al2O3-TiO2 over an extending sheet using Buongiorno model: finite element approach. Chin J Phys. 2021;70:125–39. doi:10.1016/j.cjph.2020.12.022. [Google Scholar] [CrossRef]

5. Islam MS, Islam S, Siddiki MNAA. Numerical simulation with sensitivity analysis of MHD natural convection using Cu-TiO2-H2O hybrid nanofluids. Int J Thermofluids. 2023;20:100509. doi:10.1016/j.ijft.2023.100509. [Google Scholar] [CrossRef]

6. Rajesh V, Öztop HF. Heat transfer in a non-isothermal walled square closed space filled with ternary hybrid nanofluids. Chem Phys. 2024;577:112133. doi:10.1016/j.chemphys.2023.112133. [Google Scholar] [CrossRef]

7. Abouali O, Ahmadi G. Computer simulations of natural convection of single phase nanofluids in simple enclosures: a critical review. Appl Therm Eng. 2012;36:1–13. doi:10.1016/j.applthermaleng.2011.11.065. [Google Scholar] [CrossRef]

8. Alsabery AI, Abosinnee AS, Al-Hadraawy SK, Ismael MA, Fteiti MA, Hashim I, et al. Convection heat transfer in enclosures with inner bodies: a review on single and two-phase nanofluid models. Renew Sustain Energ Rev. 2023;183:113424. doi:10.1016/j.rser.2023.113424. [Google Scholar] [CrossRef]

9. Snoussi L, Chouikh R, Ouerfelli N, Guizani A. Numerical simulation of heat transfer enhancement for natural convection in a cubical enclosure filled with Al2O3/water and Ag/water nanofluids. Phys Chem Liquids. 2016;54(6):703–16. doi:10.1080/00319104.2016.1149173. [Google Scholar] [CrossRef]

10. Bendaraa A, Charafi MM, Hasnaoui A. Numerical study of natural convection in a differentially heated square cavity filled with nanofluid in the presence of fins attached to walls in different locations. Phys Fluids. 2019 May;31(5):052003. doi:10.1063/1.5091709. [Google Scholar] [CrossRef]

11. Motlagh SY, Soltanipour H. Natural convection of Al2O3-water nanofluid in an inclined cavity using Buongiorno’s two-phase model. Int J Therm Sci. 2017;111:310–20. doi:10.1016/j.ijthermalsci.2016.08.022. [Google Scholar] [CrossRef]

12. Chtaibi K, Amahmid A, Dahani Y, Hasnaoui M, Hamed HB. Natural convection in a diamond-shaped receiving cavity heated from the bottom corner and filled with Fe3O4-H2O nanofluid in the presence of thermal radiation. Heat Transf Res. 2023;54(13):39–64. doi:10.1615/HeatTransRes.2023046669. [Google Scholar] [CrossRef]

13. Benzema M, Benkahla YK, Boudiaf A, Ouyahia SE, Ganaoui MEl. Magnetic field impact on nanofluid convective flow in a vented trapezoidal cavity using buongiorno’s mathematical model. EPJ Appl Phys. 2019;88(1):11101. doi:10.1051/epjap/2019190239. [Google Scholar] [CrossRef]

14. Houda Jalali HA. Analysis of the influence of viscosity and thermal conductivity on heat transfer by Al2O3-water nanofluid. Fluid Dyn Mater Proc. 2019;15(3):253–70. doi:10.32604/fdmp.2019.03896. [Google Scholar] [CrossRef]

15. Ma Y, Mohebbi R, Rashidi MM, Yang Z. Simulation of nanofluid natural convection in a U-shaped cavity equipped by a heating obstacle: effect of cavity’s aspect ratio. J Taiwan Inst Chem Eng. 2018;93:263–76. doi:10.1016/j.jtice.2018.07.026. [Google Scholar] [CrossRef]

16. Aleem M, Asjad MI, Shaheen A, Khan I. MHD influence on different water based nanofluids (TiO2, Al2O3, CuO) in porous medium with chemical reaction and newtonian heating. Chaos Solitons Fractals. 2020;130:109437. doi:10.1016/j.chaos.2019.109437. [Google Scholar] [CrossRef]

17. Faraz N, Nisar MS, Khan Y, Hussain A, Iqbal K. Natural convection of Cu-H2O nanofluid inside hexagonal enclosure fitted with a square cavity with a non-uniformly heated wall(s). Results Phys. 2023 Aug;51:106648. doi:10.1016/J.RINP.2023.106648. [Google Scholar] [CrossRef]

18. Turan O, Sachdeva A, Chakraborty N, Poole RJ. Laminar natural convection of power-law fluids in a square enclosure with differentially heated side walls subjected to constant temperatures. J Nonnewton Fluid Mech.Sep 2011;166(17–18):1049–63. doi:10.1016/j.jnnfm.2011.06.003. [Google Scholar] [CrossRef]

19. Acharya S, Dash SK. Natural convection in a cavity with undulated walls filled with water-based non-Newtonian power-law CuO-water nanofluid under the influence of the external magnetic field. Numeri Heat Transf A Appl. 2019;76(7):552–75. doi:10.1080/10407782.2019.1644898. [Google Scholar] [CrossRef]

20. Ali FH, Hamzah HK, Egab K, Arıcı M, Shahsavar A. Non-Newtonian nanofluid natural convection in a U-shaped cavity under magnetic field. Int J Mech Sci. Nov 2020;186:105887. doi:10.1016/j.ijmecsci.2020.105887. [Google Scholar] [CrossRef]

21. Parvin S, Roy NC, Saha LK. Natural convective non-Newtonian nanofluid flow in a wavy-shaped enclosure with a heated elliptic obstacle. Heliyon. 2023 Jun;9(6):e16579. doi:10.1016/j.heliyon.2023.e16579. [Google Scholar] [PubMed] [CrossRef]

22. Jain S, Bhargava R. Natural convection flow on a bent wavy vertical enclosure filled with power-law nanofluid simulated by element free galerkin method. Math Comput Simul. 2023;205:970–86. doi:10.1016/j.matcom.2022.10.033. [Google Scholar] [CrossRef]

23. Elatar A, Teamah MA, Hassab MA. Numerical study of laminar natural convection inside square enclosure with single horizontal fin. Int J Therm Sci. 2016;99:41–51. doi:10.1016/j.ijthermalsci.2015.08.003. [Google Scholar] [CrossRef]

24. Saravanan S, Sivaraj C. Coupled thermal radiation and natural convection heat transfer in a cavity with a heated plate inside. Int J Heat Fluid Flow. 2013 Apr;40:54–64. doi:10.1016/j.ijheatfluidflow.2013.01.007. [Google Scholar] [CrossRef]

25. Mahalakshmi T, Nithyadevi N, Oztop HF, Abu-Hamdeh N. Natural convective heat transfer of Ag-water nanofluid flow inside enclosure with center heater and bottom heat source. Chin J Phys. 2018;56(4):1497–507. doi:10.1016/j.cjph.2018.06.006. [Google Scholar] [CrossRef]

26. Islam T, Alam MN, Asjad MI, Parveen N, Chu YM. Heatline visualization of MHD natural convection heat transfer of nanofluid in a prismatic enclosure. Sci Rep. 2021;11(1):10972. doi:10.1038/s41598-021-89814-z. [Google Scholar] [PubMed] [CrossRef]

27. Khan SA, et al. Computational analysis of natural convection with water based nanofluid in a square cavity with partially active side walls: applications to thermal storage. J Mol Liq. 2023;382:122003. doi:10.1016/j.molliq.2023.122003. [Google Scholar] [CrossRef]

28. Saha T, Islam T, Yeasmin S, Parveen N. Thermal influence of heated fin on MHD natural convection flow of nanofluids inside a wavy square cavity. Int J Thermofluids. 2023;18:100338. doi:10.1016/j.ijft.2023.100338. [Google Scholar] [CrossRef]

29. Tiwari RK, Das MK. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Transf. 2007;50(9):2002–18. doi:10.1016/j.ijheatmasstransfer.2006.09.034. [Google Scholar] [CrossRef]

30. Aghamajidi M, Yazdi M, Dinarvand S, Pop I. Tiwari-Das nanofluid model for magnetohydrodynamics (MHD) natural-convective flow of a nanofluid adjacent to a spinning down-pointing vertical cone. Propulsion Power Res. 2018;7(1):78–90. doi:10.1016/j.jppr.2018.02.002. [Google Scholar] [CrossRef]

31. Alsabery AI, Chamkha AJ, Saleh H, Hashim I. Transient natural convective heat transfer in a trapezoidal cavity filled with non-Newtonian nanofluid with sinusoidal boundary conditions on both sidewalls. Powder Technol. Feb 2017;308:214–34. doi:10.1016/j.powtec.2016.12.025. [Google Scholar] [CrossRef]

32. Kumar A, Sinha MK. Buoyancy driven flow through a square enclosure. Mater Today Proc. 2022;56:2780–4. doi:10.1016/j.matpr.2021.10.091. [Google Scholar] [CrossRef]

33. Almensoury MF, Hashim AS, Hamzah HK, Ali FH. Numerical investigation of natural convection of a non-Newtonian nanofluid in an F-shaped porous cavity. Heat Transfer. 2021;50(3):2403–26. doi:10.1002/htj.21984. [Google Scholar] [CrossRef]

34. Xuan Y, Roetzel W. Conceptions for heat transfer correlation of nanofluids. Int J Heat Mass Transf. 2000;43(19):3701–7. doi:10.1016/S0017-9310(99)00369-5. [Google Scholar] [CrossRef]

35. Dinarvand S, Behrouz M, Ahmadi S, Ghasemi P, Noeiaghdam S, Fernandez-Gamiz U. Mixed convection of thermomicropolar AgNPs-GrNPs nanofluid: an application of mass-based hybrid nanofluid model. Case Stud Therm Eng. 2023;49:103224. doi:10.1016/j.csite.2023.103224. [Google Scholar] [CrossRef]

36. Hamilton RL, Crosser OK. Thermal conductivity of heterogeneous two-component systems. Ind Eng Chem Fundam. 1962;1(3):187–91. doi:10.1021/i160003a005. [Google Scholar] [CrossRef]

37. Ho CJ, Chen MW, Li ZW. Numerical simulation of natural convection of nanofluid in a square enclosure: effects due to uncertainties of viscosity and thermal conductivity. Int J Heat Mass Transf. Aug 2008;51(17–18):4506–16. doi:10.1016/j.ijheatmasstransfer.2007.12.019. [Google Scholar] [CrossRef]

38. Ghasemi B, Aminossadati SM, Raisi A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int J Therm Sci. Sep 2011;50(9):1748–56. doi:10.1016/j.ijthermalsci.2011.04.010. [Google Scholar] [CrossRef]

39. Brinkman HC. The viscosity of concentrated suspensions and solutions. J Chem Phys. Dec 2004;20(4):571. doi:10.1063/1.1700493. [Google Scholar] [CrossRef]

40. Dutta S, Goswami N, Biswas AK, Pati S. Numerical investigation of magnetohydrodynamic natural convection heat transfer and entropy generation in a rhombic enclosure filled with Cu-water nanofluid. Int J Heat Mass Transf. 2019;136:777–98. doi:10.1016/j.ijheatmasstransfer.2019.03.024. [Google Scholar] [CrossRef]