 Open Access
Open Access
ARTICLE
Three-Dimensional Convection in an Inclined Porous Layer Subjected to a Vertical Temperature Gradient
1 Computational Fluid Dynamics Laboratory, Institute of Continuous Media Mechanics UB RAS, Perm, 614068, Russia
2 Theoretical Physics Department, Perm State University, Perm, 614990, Russia
* Corresponding Author: Ivan Shubenkov. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(9), 1957-1970. https://doi.org/10.32604/fdmp.2024.050167
Received 29 January 2024; Accepted 15 April 2024; Issue published 23 August 2024
Abstract
In this paper, we study the onset and development of three-dimensional convection in a tilted porous layer saturated with a liquid. The layer is subjected to a gravitational field and a strictly vertical temperature gradient. Typically, problems of thermal convection in tilted porous media saturated with a liquid are studied by assuming constant different temperatures at the boundaries of the layer, which prevent these systems from supporting conductive (non-convective) states. The boundary conditions considered in the present work allow a conductive state and are representative of typical geological applications. In an earlier work, we carried out a linear stability analysis of the conductive state. It was shown that at any layer tilt angles, the most dangerous type of disturbances are longitudinal rolls. Moreover, a non-zero velocity component exists in -direction. In the present work, three-dimensional non-linear convection regimes are studied. The original three-dimensional problem is reduced to two-dimensional one with an analytical expression for the velocity -component . It is shown that the critical Rayleigh number values obtained through numerical solutions of the obtained 2D problem by a finite difference method for different layer inclination angles, are in a good agreement with those predicted by the linear theory. The number of convective rolls realized in nonlinear calculations also fits the linear theory predictions for a given cavity geometry. Calculations carried out at low supercriticalities show that a direct bifurcation takes place. With increasing supercriticality, no transitions to other convective regimes are detected. The situation studied in this problem can be observed in oil-bearing rock formations under the influence of a geothermal temperature gradient, where the ensuing fluid convection can affect the distribution of oil throughout the layer.Graphic Abstract
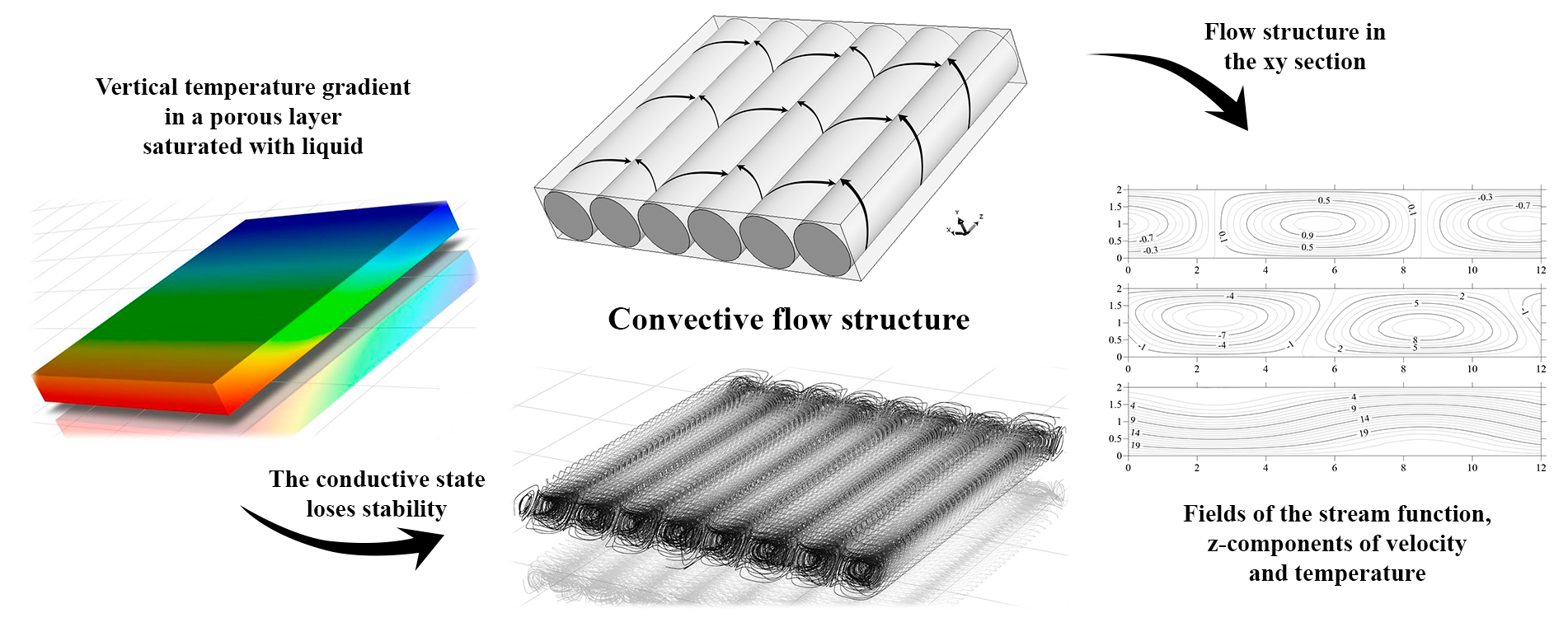
Keywords
Lyubimov [1] studied stationary two-dimensional convection in a closed porous cavity with perfectly conductive boundaries. The cavity was heated from below. It was found that stationary flows and their stability in a horizontal layer are the same for both a porous layer and a liquid layer in a non-porous medium. But if the liquid layer is tilted relative to the horizon, then differences appear between the porous and non-porous layers.
Tilted porous layer convection often arouses interest when it comes to the exploitation of geothermal reservoirs and groundwater flows [2]. In industrial applications, it is possible to increase the efficiency of heat exchangers by tilting them at some angle to the horizon, thereby causing tilted layer convection [3]. Other important areas are pollutant transport, oil production and food processing [4,5]. Convection in a porous layer is considered in the literature [6].
Gershuni et al. [7] investigated the stability of the conductive state of a tilted layer of liquid under the influence of a vertical temperature gradient. Two-dimensional disturbances were studied. It was found that, depending on the layer tilt angle, the most dangerous disturbances can be cellular (non-zero wave number) or longwave (zero wave number). Accordingly, there is a critical angle at which one type of instability passes into another.
Weber [8] carried out a linear investigation of tilted porous layer convection. It was assumed that the layer is limited by impermeable, perfectly conductive solid boundaries. The boundaries have different temperatures. Along each boundary the temperature is constant. In this case, the temperature gradient is not vertical, therefore a non-convective state is impossible. For any arbitrarily small temperature difference between the boundaries of the layers, a stationary plane-parallel convective flow arises. It is shown that the wave vector of the most dangerous type of disturbances is perpendicular to the velocity vectors of the base flow (longitudinal rolls).
Bories et al. [9] experimentally investigated the same problem. It has been found that at layer tilt angles less than approximately 15°, the flow has the form of hexagonal cells. This can be explained by nonlinear effects such as the dependence of thermal diffusivity and viscosity on temperature [10,11] or changes in average temperature [12]. At large tilt angles, the disturbances become two-dimensional with the axes of the rolls corresponding to the longitudinal rolls.
Various experiments indicate that during natural convection in a porous layer with large lateral dimensions, there are different flow configurations, which are determined by the layer tilt angle, the Rayleigh number, and the layer spatial configuration. Caltigirone et al. [13] used linear stability theory and three-dimensional numerical modeling to study these flows. It was found that theoretical prediction of flow structures observed in the experiment is possible.
Rees et al. [14] carried out a linear analysis of the stability of Darcy–Boussinesq convection in a tilted porous layer. Only disturbances with axes perpendicular to the velocity vectors of the base flow (transverse rolls) were considered. As in [8], it was assumed that the boundaries of the layer are impermeable and constant temperatures are maintained on them, different for the upper and lower boundaries. It was found that transverse rolls exist only up to a layer tilt angle of
Arora et al. [15] studied the nonlinear stability of natural convection in a tilted layer of liquid that has a uniform internal source (or, on the contrary, a sink) of heat, while a constant temperature is maintained at the boundaries of the layer. It has been established that the stability region is significantly determined by the layer tilt angle and the value of the Prandtl number. The most unstable orientation of the layer to arbitrary perturbations is vertical.
Storesletten et al. [16] studied the occurrence of convection in a tilted porous layer which is heated internally by a uniform distribution of heat sources. The linear stability of the basic parallel flow and the influence of layer tilt angle, internal heat generation and anisotropy on it were studied. It has been established that when convection occurs, the convective motion significantly depends on the anisotropy of the layer (
In the mentioned works, problems were studied in which a conductive (non-convective) state is impossible. The conductive state is possible only in the case of a temperature distribution at the boundaries of the layer corresponding to a strictly vertical temperature gradient. Situations with boundary conditions of this type can occur when it comes to geological applications [17]. For example, in oil-bearing rock formations, which are a porous medium, vertical temperature gradients can arise.
Kolesnikov et al. [18] studied tilted porous layer convection. A strictly vertical temperature gradient is maintained at the boundaries of the layer. Two-dimensional disturbances were studied. A linear analysis of the stability of the conductive state was carried out. It was found that for a vertical layer, the instability is long-wave, but for any other layer orientation, cellular disturbances are the most dangerous, although long-wave instability also exists for them.
Lyubimova et al. [19] considered the same problem, but stability to three-dimensional disturbances was studied. It was found that the most dangerous type of disturbances are longitudinal rolls (rolls with axes directed along the layer and perpendicular to the axis relative to which the layer is tilted). At the layer tilt angle
In the present work, the onset and development of longitudinal convection rolls in a tilted porous layer saturated with liquid under a vertical temperature gradient is studied numerically. We study three-dimensional non-linear convection regimes arising after the conductive (non-convective) state loses stability. The three-dimensional problem is reduced to a two-dimensional one with analytical expression for
Let us consider an infinitely long tilted porous layer saturated with liquid. Fig. 1 shows a layer infinite along the
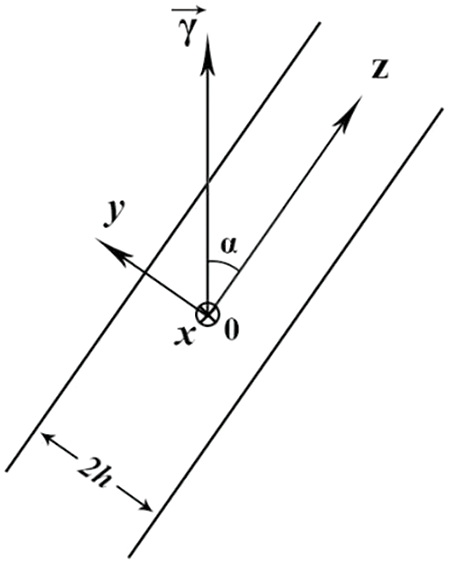
Figure 1: Geometry of the problem
To describe thermal convection in a porous layer saturated with liquid, the Darcy-Boussinesq model will be used [20]:
Here
At the boundaries of the layer, impermeability conditions and a temperature distribution corresponding to a strictly vertical temperature gradient are set:
The problem formulated above admits a solution corresponding to the conductive state:
Introduce the values
Here,
3 Reducing a Three-Dimensional Problem Statement to a Two-Dimensional One
Fig. 2 shows a cell of an infinitely extended layer, in which the structure of the convective flows that we are considering is schematically shown. We consider convective rolls whose axes are perpendicular to the axis relative to which the layer is tilted (longitudinal rolls).
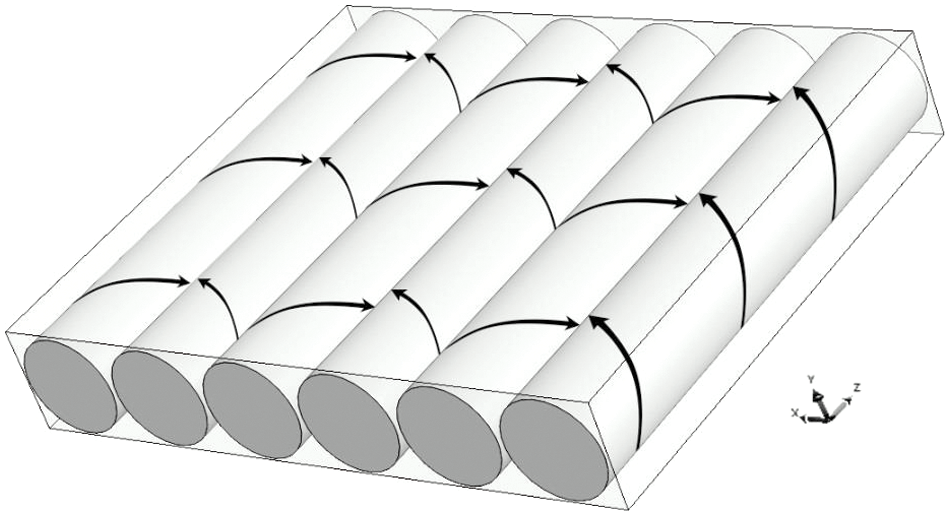
Figure 2: Schematic structure of flow in a cell of an infinitely extended layer
Let us consider nonlinear convection regimes in a region representing a cross-section of a cell of an infinitely extended layer (Fig. 3).
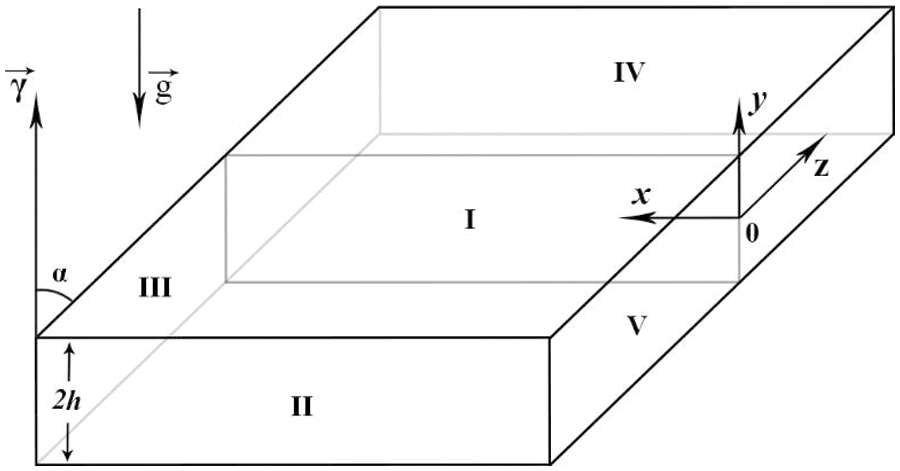
Figure 3: Cell of an infinitely extended layer (I–section under investigation; II and IV–infinitely extended boundaries; III and V–periodic boundaries; boundaries parallel to the
Let us rewrite Eq. (3), highlighting the part in temperature corresponding to the vertical temperature gradient
The boundary conditions have the form:
Applying the
and applying the
Taking into account (8), the energy Eq. (5) is rewritten as:
As was shown in [19], the most dangerous in this problem at any layer tilt angle are longitudinal disturbances (
For
Now apply the
For
Eqs. (11) and (13) have a joint solution:
The function
Thus, the boundary conditions have the form:
and periodicity conditions at the lateral boundaries.
The transformation we propose allows us to reduce a three-dimensional problem to a two-dimensional one and obtain an analytical expression for the z-component of velocity. This significantly simplifies the problem and allows for a comprehensive numerical study of the behavior of the system for various parameters.
4 Nonlinear Three-Dimensional Convective Regimes
To solve the problem (8), (9), (17), the finite difference method was used. An explicit scheme of second order accuracy in spatial variables was used. The grid was used with square cells and a spatial step of 1/30. Table 1 presents data from a grid sensitivity study. As can be seen from the table, the grid resolution used in the calculations makes it possible to calculate the critical Rayleigh number with high accuracy and is sufficient for modeling the flow structures that are realized in this problem for the studied system parameters. The main calculations were carried out for a cavity with an aspect ratio of 6 × 1 (
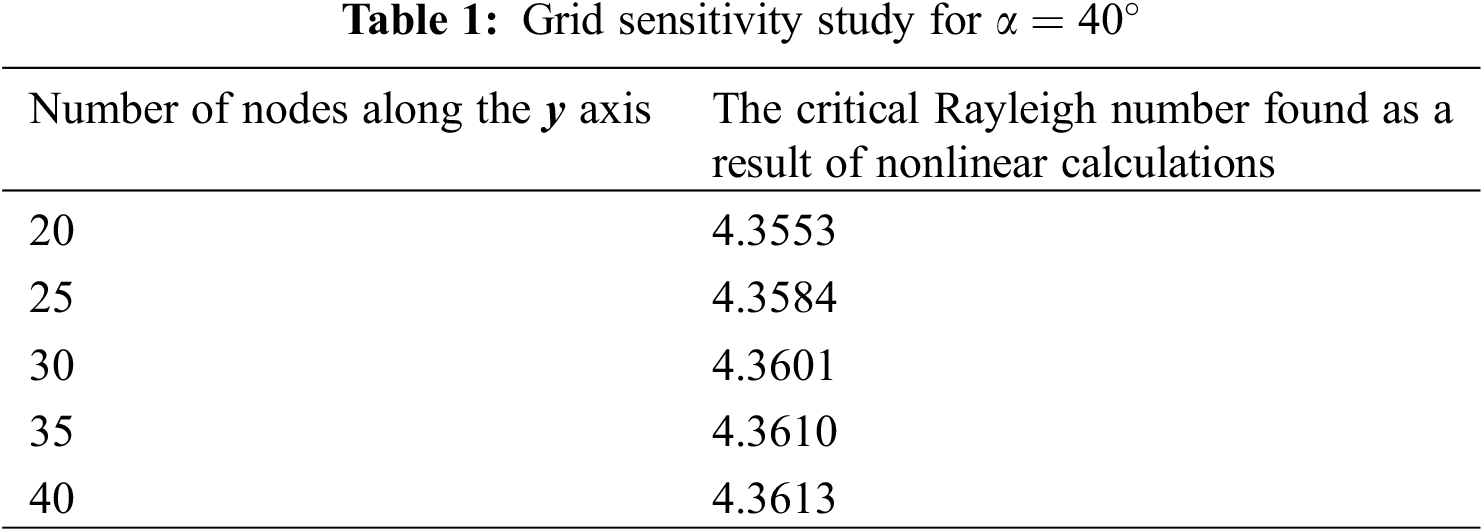
Fig. 4 shows the dependence of the critical

Figure 4: Dependence of the critical Rayleigh number on the layer tilt angle (dashed curve–linear theory, solid curve–data of nonlinear calculations)
Figs. 5 and 6 show the dependences of the integral characteristics of the flow

Figure 5: Dependency

Figure 6: Dependency
Fig. 7 shows the dependence of the wave number on the layer tilt angle, found as a result of linear calculations (solid curve). In nonlinear calculations, when using periodic conditions on the lateral boundaries, it is possible to implement convective modes only with an integer number of wavelengths, i.e., an even number of vortices. As calculations have shown, at layer tilt angles

Figure 7: Dependence of the critical wave number on the layer tilt angle (solid curve–linear theory for an infinitely extended cavity, dots–data from nonlinear calculations)
Figs. 8–10 show the fields of the stream function
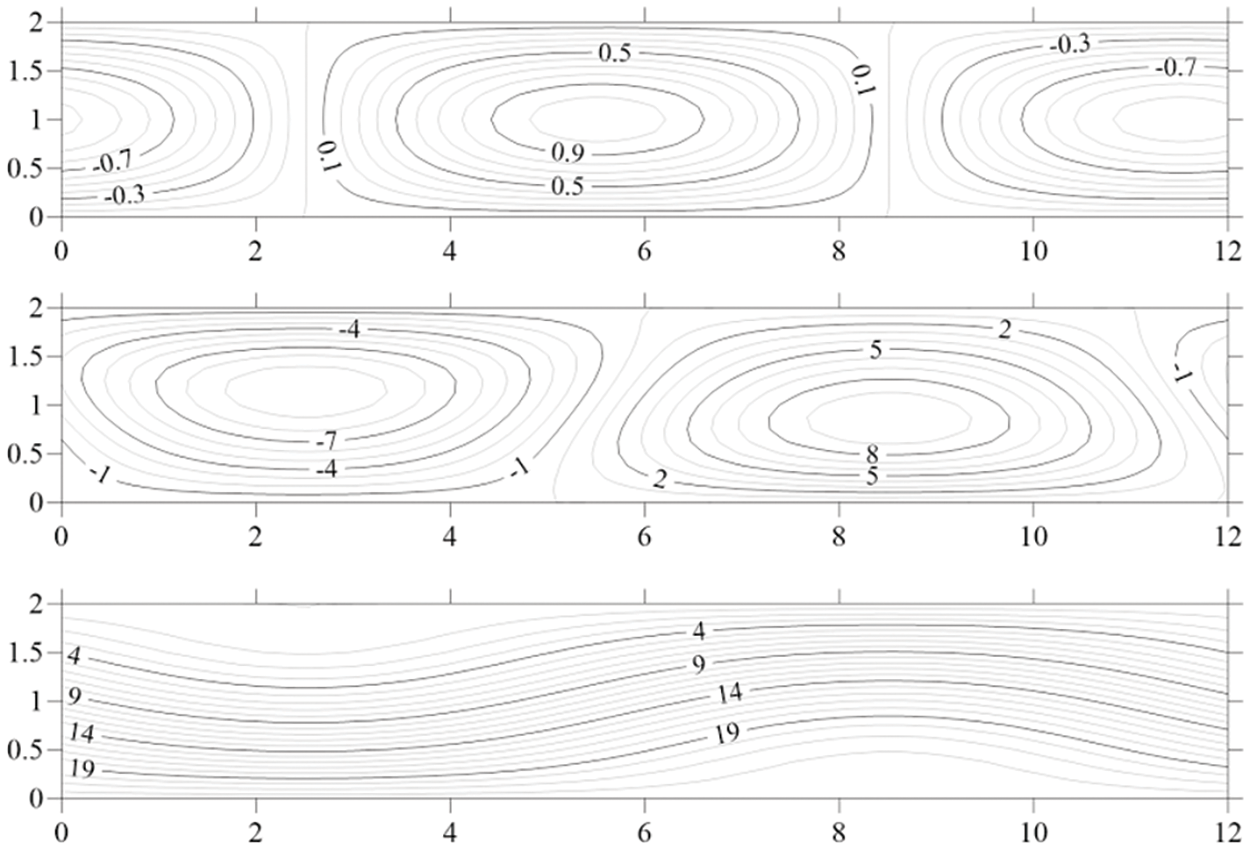
Figure 8: Fields of

Figure 9: Fields of

Figure 10: Fields of
The fields of the temperature components
As can be seen from Figs. 8–10, with increasing layer tilt angle, the temperature gradient increases, and the influence of convective flows on the temperature distribution in the section under consideration weakens.
Calculations were also carried out for a cavity with an aspect ratio of 10 × 1 and also using solid impermeable thermally insulated side boundaries. Fig. 11 shows the fields of the stream function

Figure 11: Fields of
For a cavity with solid lateral boundaries, the maximum wavelength of disturbances should correspond to one vortex for the entire cavity. As can be seen from Fig. 12, under such boundary conditions, most of the cavity is actually occupied by one vortex, but along with it, small side vortices are realized at the side boundaries, the direction of rotation of which is opposite to the direction of rotation of the main vortex.
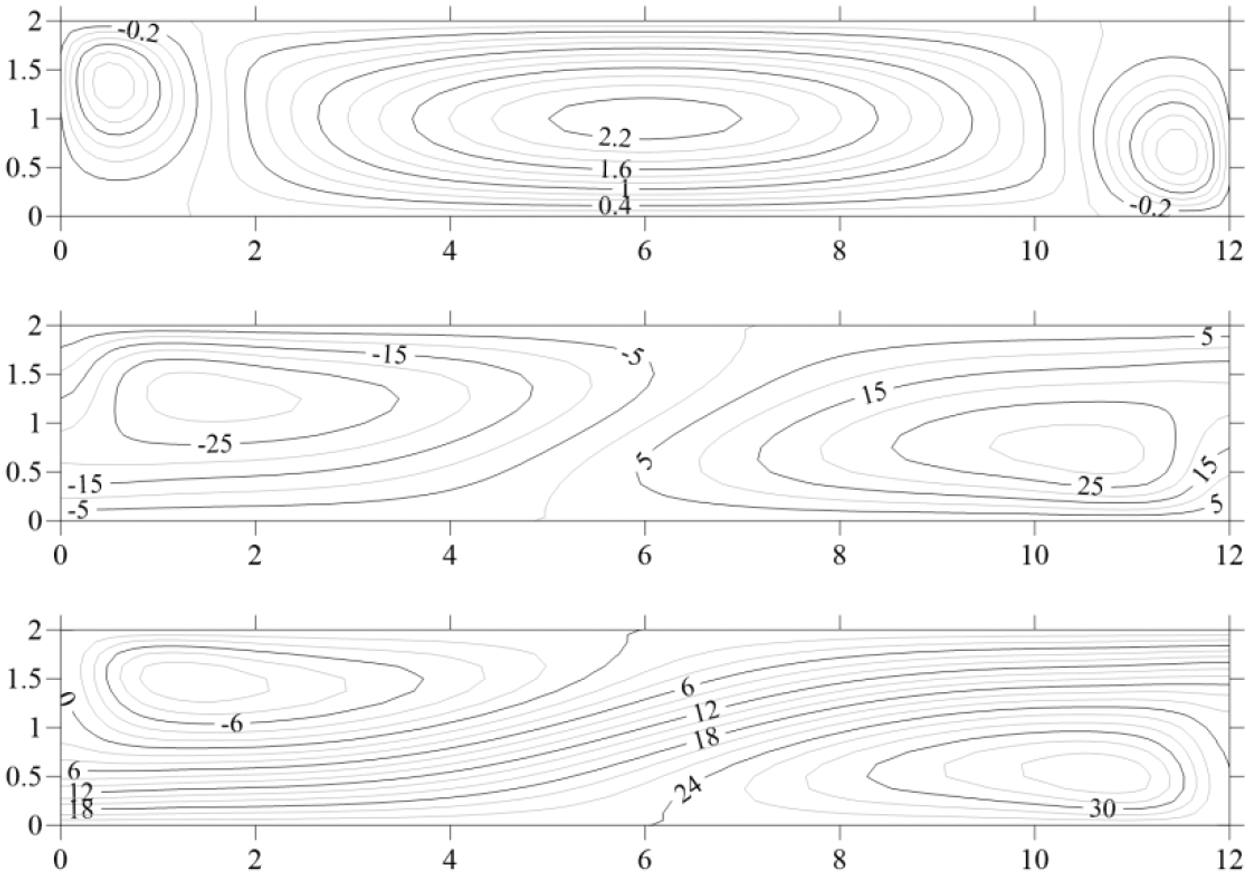
Figure 12: Fields of
At layer tilt angles corresponding to multicellular convection, no side vortices are formed at the layer boundaries and the realized number of vortices corresponds to the linear theory. In particular, Fig. 13 shows the fields of the stream function

Figure 13: Fields of
In calculations for various layer tilt angles at high supercriticalities, no transitions to other convective regimes were revealed, in addition to the main one predicted by the linear theory. However, with increasing supercriticality, the shape of the convective rolls may be somewhat distorted. The relative dimensions of the rolls may also change (Fig. 14). The higher the

Figure 14: Fields of
1) The onset and development of longwave and multicellular longitudinal convection rolls in a tilted porous layer saturated with liquid under a strictly vertical temperature gradient have been studied numerically.
2) The three-dimensional problem is reduced to two-dimensional one with analytical expression for z-component of the velocity
3) The number of rolls (wave number) realized in nonlinear calculations corresponds to the linear theory [19].
4) The values of the critical Rayleigh number obtained in nonlinear calculations for different layer tilt angles correspond with good accuracy to the values predicted by linear theory [19].
5) As a result of nonlinear calculations, the structure of the velocity field
6) Calculations carried out at low supercriticalities showed that at all layer tilt angles, direct bifurcation takes place.
7) No transitions to other convective regimes with increasing supercriticality were found.
Acknowledgement: The authors would like to thank the respected reviewers for their valuable suggestions for improving the quality of the manuscript.
Funding Statement: This work was carried out with financial support from the Ministry of Science and Higher Education of the Russian Federation (Topic No. 121031700169-1).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Lyubimova T.; data collection: Shubenkov I., Sadilov E.; analysis and interpretation of results: Shubenkov I., Lyubimova T.; draft manuscript preparation: Shubenkov I., Lyubimova T. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data is available upon request to the corresponding author.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lyubimov DV. Convective motions in a porous medium heated from below. J App Mech Tech Phys. 1975;16:257–61. doi:10.1007/BF00858924. [Google Scholar] [CrossRef]
2. Matta A. Thermal convection in an inclined porous layer with effect of heat source. In: Srinivasacharya D, Reddy K, editors. Numerical heat transfer and fluid flow. Singapore: Springer; 2019. p. 47–54. doi:10.1007/978-981-13-1903-7_7. [Google Scholar] [CrossRef]
3. Arora M, Singh J, Bajaj R. Nonlinear stability of natural convection in an inclined fluid layer. Int J Appl Comput Math. 2020;6:21. doi:10.1007/s40819-020-0780-2. [Google Scholar] [CrossRef]
4. Bendrichi G, Shemilt LW. Mass transfer in horizontal flow channels with thermal gradients. Can J Chem Eng. 1997;75:1067–74. doi:10.1002/cjce.5450750609. [Google Scholar] [CrossRef]
5. Chen X, Li AG. An experimental study on particle deposition above near-wall heat source. Build Environ. 2014;81:139–49. doi:10.1016/j.buildenv.2014.06.020. [Google Scholar] [CrossRef]
6. Narasimhan A. Essentials of heat and fluid flow in porous media. Cham: Springer; 2023. p. 1–242. doi:10.1007/978-3-030-99865-3. [Google Scholar] [CrossRef]
7. Gershuni GZ, Zhukhovitskii EM. Convective stability of incompressible fluids. 1st ed. Jerusalem: Keter Publishing House; 1976. p. 1–330 (In Russian). [Google Scholar]
8. Weber JE. Thermal convection in a tilted porous layer. Int J Heat Mass Transf. 1975;18:474–5. [Google Scholar]
9. Bories S, Combarnous M. Natural convection in a sloping porous layer. J Fluid Mech. 1973;57:63–79. doi:10.1017/S0022112073001023. [Google Scholar] [CrossRef]
10. Palm E. On the tendency towards hexagonal cells in steady convection. J Fluid Mech. 1960;8:183–92. doi:10.1017/S0022112060000530. [Google Scholar] [CrossRef]
11. Busse FH. The stability of finite amplitude convection and its relation to an extremum principle. J Fluid Mech. 1967;30:625. doi:10.1017/S0022112067001661. [Google Scholar] [CrossRef]
12. Krishnamurti R. Finite amplitude convection with changing mean temperature. Part 1. Theory. J Fluid Mech. 1968;33:445–55. doi:10.1017/S0022112068001436. [Google Scholar] [CrossRef]
13. Caltagirone JP, Bories S. Solutions and stability criteria of natural convective flow in an inclined porous layer. J Fluid Mech. 1985;155:267–87. doi:10.1017/S002211208500180X. [Google Scholar] [CrossRef]
14. Rees DAS, Bassom AP. The onset of Darcy-Benard convection in an inclined layer heated from below. Acta Mech. 2000;144:103–18. doi:10.1007/BF01181831. [Google Scholar] [CrossRef]
15. Arora M, Bajaj R. Global stability of natural convection in internally heated inclined fluid layer. J Eng Math. 2021;128:7. doi:10.1007/s10665-021-10127-1. [Google Scholar] [CrossRef]
16. Storesletten Leiv, Rees D.Andrew S. Onset of convection in an inclined anisotropic porous layer with internal heat generation. Fluids. 2019;4(2):75. doi:10.3390/fluids4020075. [Google Scholar] [CrossRef]
17. Simmons CT, Kuznetsov AV, Nield DA. Effect of strong heterogeneity on the onset of convection in a porous medium: importance of spatial dimensionality and geologic controls. Water Resour Res. 2010;46:W09539. doi:10.1029/2009WR008606. [Google Scholar] [CrossRef]
18. Kolesnikov AK, Lyubimov DV. On the convective instability of a liquid in an inclined layer of a porous medium. J App Mech Tech Phys. 1973;14:400–4. doi:10.1007/BF00850957. [Google Scholar] [CrossRef]
19. Lyubimova TP, Muratov ID, Shubenkov IS. Onset and nonlinear regimes of convection in an inclined porous layer subject to a vertical temperature gradient. Phys Fluids. 2022;34:094114. doi:10.1063/5.0104575. [Google Scholar] [CrossRef]
20. Nield DA, Bejan A. Convection in porous media. 1st ed. New York: Springer; 2006. p. 1–640. doi:10.1007/978-1-4614-5541-7 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools