Open Access

ARTICLE

Three-Dimensional Convection in an Inclined Porous Layer Subjected to a Vertical Temperature Gradient

Ivan Shubenkov^1,2,*, Tatyana Lyubimova^1,2, Evgeny Sadilov¹

1 Computational Fluid Dynamics Laboratory, Institute of Continuous Media Mechanics UB RAS, Perm, 614068, Russia
2 Theoretical Physics Department, Perm State University, Perm, 614990, Russia

* Corresponding Author: Ivan Shubenkov. Email:

(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)

Fluid Dynamics & Materials Processing 2024, 20(9), 1957-1970. https://doi.org/10.32604/fdmp.2024.050167

Received 29 January 2024; Accepted 15 April 2024; Issue published 23 August 2024

Abstract

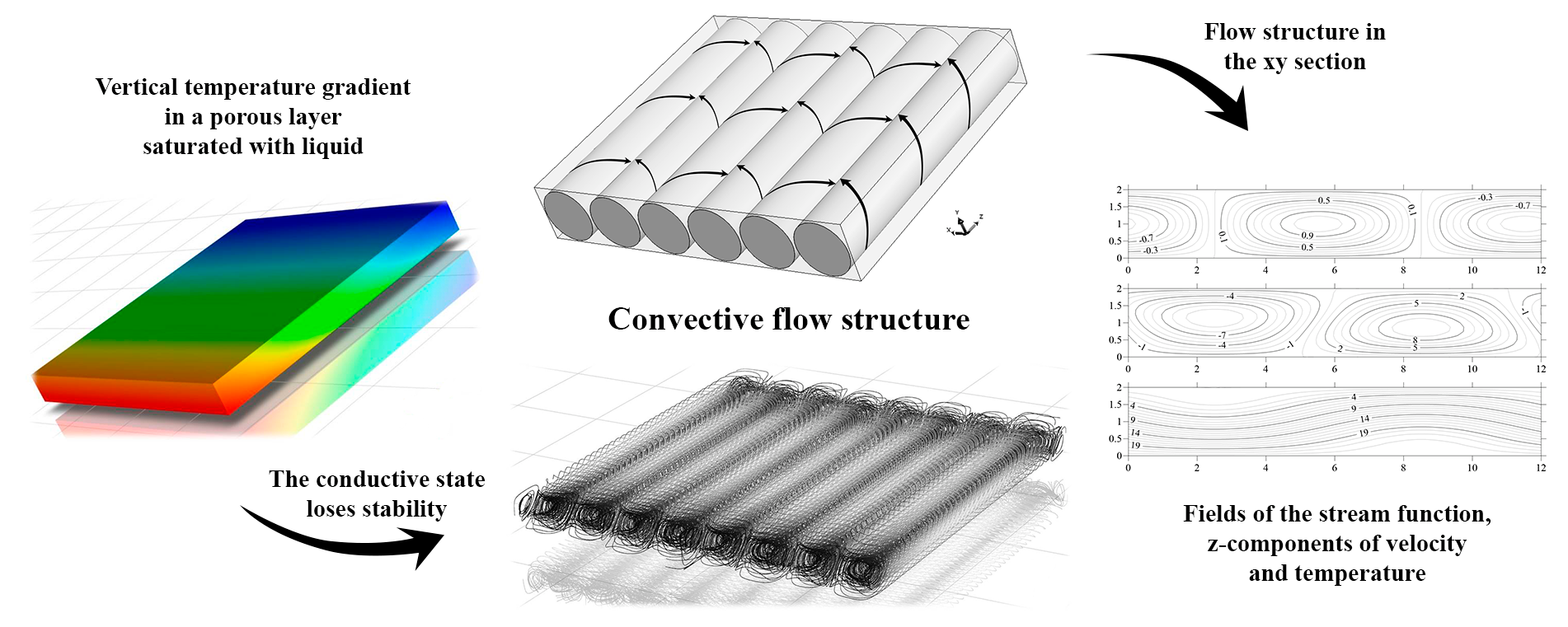
In this paper, we study the onset and development of three-dimensional convection in a tilted porous layer saturated with a liquid. The layer is subjected to a gravitational field and a strictly vertical temperature gradient. Typically, problems of thermal convection in tilted porous media saturated with a liquid are studied by assuming constant different temperatures at the boundaries of the layer, which prevent these systems from supporting conductive (non-convective) states. The boundary conditions considered in the present work allow a conductive state and are representative of typical geological applications. In an earlier work, we carried out a linear stability analysis of the conductive state. It was shown that at any layer tilt angles, the most dangerous type of disturbances are longitudinal rolls. Moreover, a non-zero velocity component exists in -direction. In the present work, three-dimensional non-linear convection regimes are studied. The original three-dimensional problem is reduced to two-dimensional one with an analytical expression for the velocity -component . It is shown that the critical Rayleigh number values obtained through numerical solutions of the obtained 2D problem by a finite difference method for different layer inclination angles, are in a good agreement with those predicted by the linear theory. The number of convective rolls realized in nonlinear calculations also fits the linear theory predictions for a given cavity geometry. Calculations carried out at low supercriticalities show that a direct bifurcation takes place. With increasing supercriticality, no transitions to other convective regimes are detected. The situation studied in this problem can be observed in oil-bearing rock formations under the influence of a geothermal temperature gradient, where the ensuing fluid convection can affect the distribution of oil throughout the layer.

---

Graphic Abstract

---

Keywords

---