 Open Access
Open Access
ARTICLE
Experimental Study of Liquid Metal Flow for the Development of a Contact-Less Control Technique
Laboratory of Technological Hydrodynamics, Institute of Continuous Media Mechanics of the Ural Branch of Russian Academy of Science (ICMM UB RAS), Perm, 614018, Russia
* Corresponding Author: Aleksandr Poluyanov. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(7), 1553-1563. https://doi.org/10.32604/fdmp.2024.050165
Received 29 January 2024; Accepted 21 March 2024; Issue published 23 July 2024
Abstract
The article presents an experimental study on the flow of an eutectic gallium alloy in a cylindrical cell, which is placed in an alternating magnetic field. The magnetic field is generated by a coil connected to an alternating current source. The coil is located at a fixed height in such a way that its plane is perpendicular to the gravity vector, which in turn is parallel to the axis of the cylinder. The position of the cylinder can vary in height with respect to the coil. The forced flow of the considered electrically conductive liquid is generated due to the action of the localized electromagnetic force. It is assumed that under the action of the alternating magnetic field, the liquid is heated uniformly, and the resulting heat is quickly absorbed by the forced flow, so that liquid free convection can be neglected. The experiment is carried out using an ultrasonic Doppler anemometer. One transducer is installed in the axially located cylinder sluice and the other transducer is placed in the near-wall region. According to the results, a velocity profile, corresponding to a two-tori flow pattern can be hardly obtained in the low frequency range of the power supply. However, this is possible in the high frequency range. The average velocity profiles depend essentially on the location of the coil relative to the cell. The spectral analysis of velocity signals shows that the amplitude of the velocity pulsations is comparable to the average value of the flow velocity. Such experimental results and their verification through comparison with numerical calculations are intended to support the development of new methods for reducing the intensity of vortex flows during the electromagnetic separation of impurities through an electromagnetic induction mechanism (able to produce an electromotive force that displaces particles).Graphic Abstract
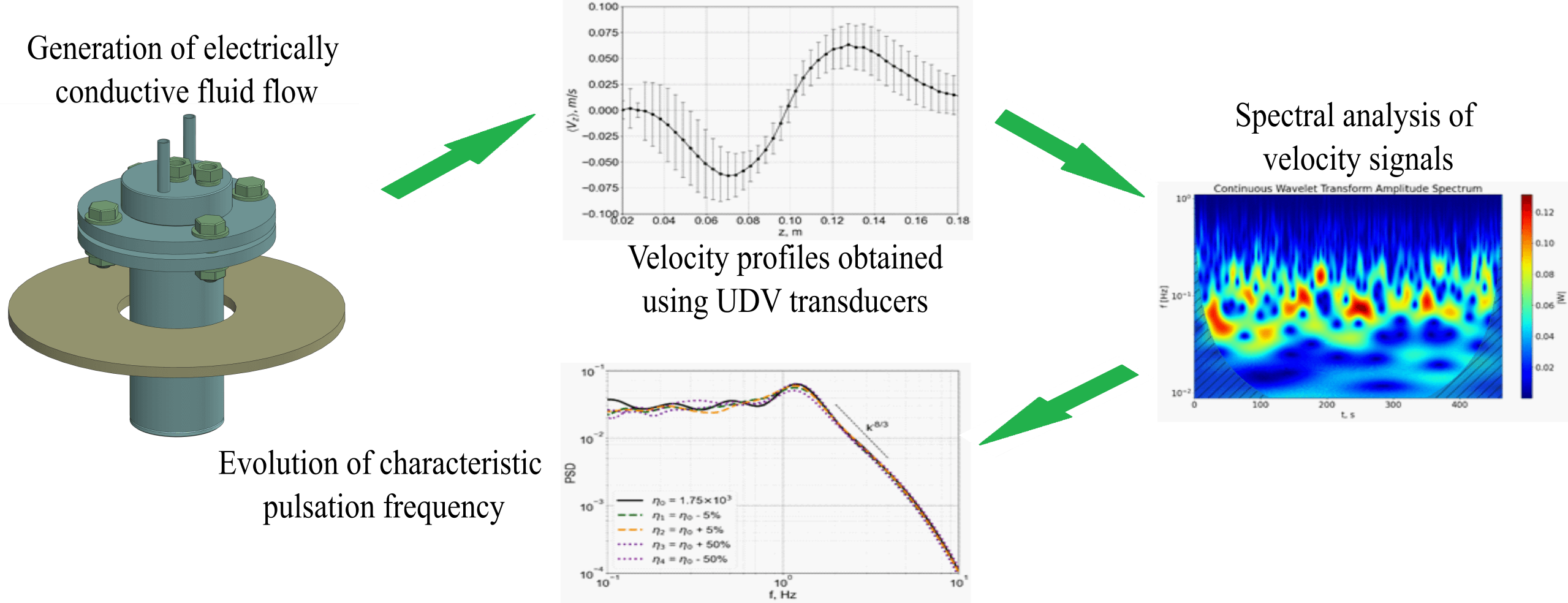
Keywords
Nomenclature
| | Magnetic field (T) |
| | Frequency of velocity pulsations (Hz) |
| | Coil frequency (Hz) |
| | Electromagnetic (pinch) force (N/m3) |
| | Height of cylindrical cell (m) |
| | Hartmann number |
| | Coil current (A) |
| | Power spectrum density of velocity signal |
| | Radius of cylindrical cell (m) |
| | Reynolds number |
| | Coil voltage (V) |
| | Axial component of velocity (m/s) |
| | Radial coordinate (m) |
| | Axial coordinate (m) |
| Greek Symbols | |
| | Kinematic viscosity (m2/s) |
| | Dynamic viscosity (kg/ms) |
| | Density (kg/m3) |
| | Electrical conductance (Si/m) |
The study of processes occurring in liquid metals and their alloys provides a framework for further development of metallurgical technologies. Liquid metal is considered to be the best heat-carrying medium for cooling systems of fast neutron nuclear reactors and fusion power plants. The experimental investigation of some metals, having the highest usage in industry, is extremely difficult due to their high temperature, chemical aggressiveness and environmental hazards in a molten state. Examples of such metals are aluminum, lead, magnesium, sodium, and their alloys. Determination of the physical properties of metal alloys in a molten state is a primary problem of materials science. Property measurement can be useful in determining the composition of alloys or multiphase media. Understanding of the chemical and physical properties of metals is also crucial for correct mathematical modeling of processes occurring in melts. In this case, direct measurements are either impossible or give results of low reliability. Therefore, the way out is to use methods of indirect determination of properties by measuring the characteristics of processes, for example, hydrodynamic ones. In this paper, we attempted to develop a methodology for predicting some physical properties of an electrically conductive medium in a molten state. This technique involves the generation of a liquid metal flow and the measurement of its properties. It relies on the fact that the flow demonstrates features, for example, pulsations, the parameters of which can be associated with the properties of a liquid medium. Due to the difficulties of working with melts mentioned above, the technique should be non-contact, and the cell with the melt should have a simple shape, for example, a cylindrical one.
Due to the fact that liquid metals and alloys conduct electric current, the hydrodynamic process can be initiated by electromagnetic forces. In this case, it is most reasonable to use a widespread configuration, which is a cylindrical cell filled with liquid metal. The cell is placed coaxially in a solenoid that generates an alternating magnetic field. In plasma physics, the described configuration is called the “azimuthal pinch”. In practice, this configuration and its variants are widely used in induction furnaces [1], electromagnetic pumps [2,3], and stirrers [4–6]. As a rule, metallurgical production deals with multiphase media, for example, liquid metals with desirable or undesirable impurities. Therefore, one should take into account the fact that the electromagnetic force and the resulting vortex flow produce a selective action on the multiphase media, which consists of components with different properties [7,8]. This principle of operation underlies electromagnetic separators [9,10], which extract impurities from melts. Another important area of metallurgy is the removal of impurities from liquid metals. Actually, there are two mechanisms for generating electromagnetic forces: conduction [8–11] and induction [12–14] mechanisms. The disadvantage of the conduction mechanism is the current supply to the cell subjected to high temperatures. The induction mechanism does not have such a disadvantage, but instead, it can generate a vortex stirring flow, the influence of which needs to be reduced. The behavior of the liquid metal flow in the above configuration is studied in detail in the context of induction melting problems [15–18], where the height of the cell is less than the height of the solenoid. Paper [19] numerically studies natural convection in an inclined cylinder placed in an alternating magnetic field. The numerical calculations were performed for a wide range of Hartmann numbers. Flow pulsations lead to fluctuations of the impurity distribution field [20], which plays an important role in the separation process.
The above considerations explain our interest in the magnetohydrodynamic processes occurring in this configuration. The ultimate goal of our study is to create a non-contact technique for effective control of the properties of a conducting melt. Despite the above-mentioned active research in this field, little attention was paid to the establishment of links between the properties of the medium and the features of its hydrodynamic characteristics. Our previous studies were devoted to numerical modeling of magnetohydrodynamic processes [21] in a configuration with a short solenoid [22]. The main finding of the work [21] is the detection of flow pulsations and the investigation of their characteristics. The results of the numerical study allowed us to obtain the dependence of the Reynolds number and the characteristic frequency of velocity pulsations on the force parameter, which is equal to a squared value of the Hartmann number. In this regard, the question arises as to whether the selected pulsation frequency will really appear in the experiment. This is what targeted our efforts in conducting the experiment described in the article. It is impossible to perform experiments with conducting media commonly used in industry due to the above-mentioned reasons. Therefore, as a model medium, we used eutectic gallium alloy. It is a liquid alloy at room temperature, which does not pose a hazard to laboratory studies. The objectives of the study are as follows: to conduct an experiment with a liquid metal to confirm the possibility of detecting velocity pulsations and determining the characteristic frequency; to obtain characteristics of oscillatory flow regimes caused by the action of an alternating magnetic field of a short solenoid. The obtained results are expected to facilitate further development of the non-contact technique for controlling the properties of molten alloys, which is of considerable importance for materials science.
2 Experimental System and Methods
The experimental setup and the experimental scheme shown in Figs. 1 and 2 include a cylindrical cell 1. The cell of height H = 0.2 m, outer radius R = 0.038 m, and wall thickness 0.004 m is made of stainless steel. height H = 0.2 m, outer radius R = 0.038 m, wall thickness 0.004 m. The cell is filled with a eutectic gallium alloy with a melting point of 17°C and the following characteristics: Ga – 87.5%, Sn – 10.5%, Zn – 2%.
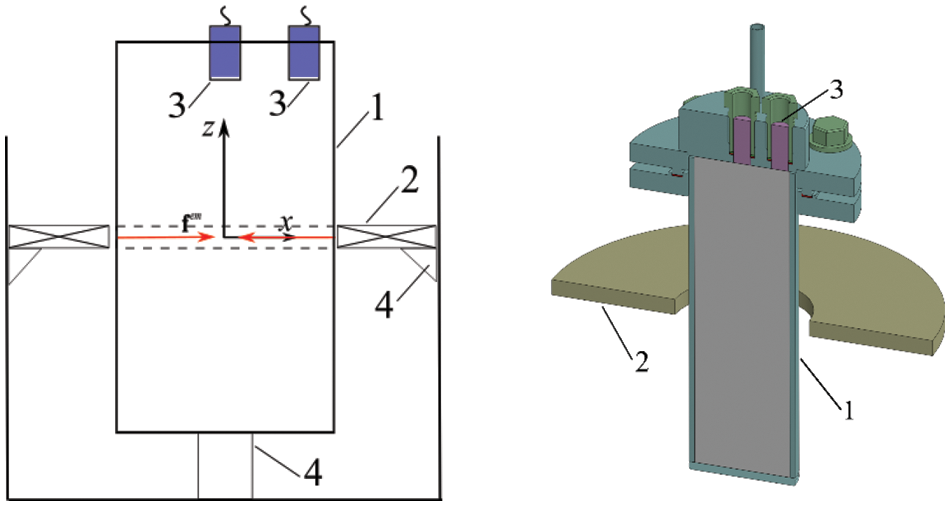
Figure 1: Scheme of experiment: 1-cylindrical cell, 2-coil, 3-ultrasonic transducers, 4-positioning system

Figure 2: Experimental setup
In the experiment, an ultrasonic Doppler velocimeter (UDV) Dop-5000, Signal Processing, Switzerland was used to measure the flow velocity of an electrically conductive medium in a non-contact way. Two ultrasonic transducers are inserted into gateway 3 on the upper surface of the cell. One transducer is placed on the axis of the cell, and the other transducer is located in the near –wall region. Such location of transducers is due to the fact that the large-scale structures can be observed in the central region of the cell, while the near-wall region is under the influence of the skin effect. The use of the Thorlabs positioning system makes it possible to locate the coil in such a way that the position of the cell relative to the coil can be readily changed if necessary. In Fig. 1, the positioning system is marked 4. It should be noted that the location of the coil relative to the cylinder has a significant effect on the topology of the magnetic field. For this reason, the experiments were carried out in compliance with the requirement of maximal alignment and strict verticality of working elements.
The ultrasonic Doppler velocimeter (UDV) allows non-contact measurements in optically opaque medium, in which visual detection of physical effects is impossible. The principle of the UDV operation is the emission of high-frequency ultrasonic pulses and registration of the echo reflected from the moving particles of the medium [26,28–30]. Transducers that consist of piezoelectric elements serve as pulse sources. The UDV makes it possible to measure only the vertical component of the flow velocity of a conducting liquid. The UDV parameter settings were so selected that the pulse frequency of each of the two transducers was 4 MHz. Both transducers were connected to a multiplexer. The polling rate of each transducer was 8.8 Hz. According to Nyquist’s theorem, the value of the velocity pulsation frequency that can be reliably determined is no more than 4.4 Hz.
An important feature of the measurements is the presence of particles capable of reflecting high-frequency pulses. Such function is performed by gallium oxides, which are formed in the liquid metal upon contact with air during the filling process. Note however, that an excessive amount of oxides significantly impedes correct velocity measurements. Moreover, the main requirement for successful measurements is the absence of a solid phase of the eutectic alloy, which crystallizes at ambient temperature. In the experiment, the gallium alloy contained in the cell was in a liquid phase.
A short coil generates an alternating magnetic field, which induces a vortex electric current in the liquid metal. The interaction of the eddy current with its own magnetic field produces a pinching electromagnetic force
Due to the presence of an eddy current the liquid metal in the cell is subjected to local heating, which initiates a thermo-gravitational convective flow in the melt. It is expected that its velocity will be considerably smaller than the velocity of the flow driven by the electromagnetic force. In article [34], the convection of liquid sodium in a cylindrical cell was studied experimentally. It was found that the velocity of large-scale circulation was 0.06 m/s. To achieve this velocity, it is essential that the temperature difference between the ends of the cylinder should be 30
One of the main issues of any experiment is the accuracy of measurements. The coil current was measured with an accuracy of ± 0.5 A. It is possible to measure the induction of the magnetic field B for a given value of the coil current. The accuracy of distance measurement was ±2 mm. The accuracy of velocity measurement using the UDV was ± 2 mm/s. It should be noted that the UDV has a lower measurement limit of approximately 5 mm/s. Magnetic field measurements were carried out using the LakeShore 460 3-Channel Gaussmeter in the root-mean-square (RMS) mode of operation. The Hall sensor, whose operation is based on the like-named effect, was placed in the gap between the coil and the cell.
In order to generalize and analyze the results, we introduced a dimensionless parameter, which is the Hartmann number
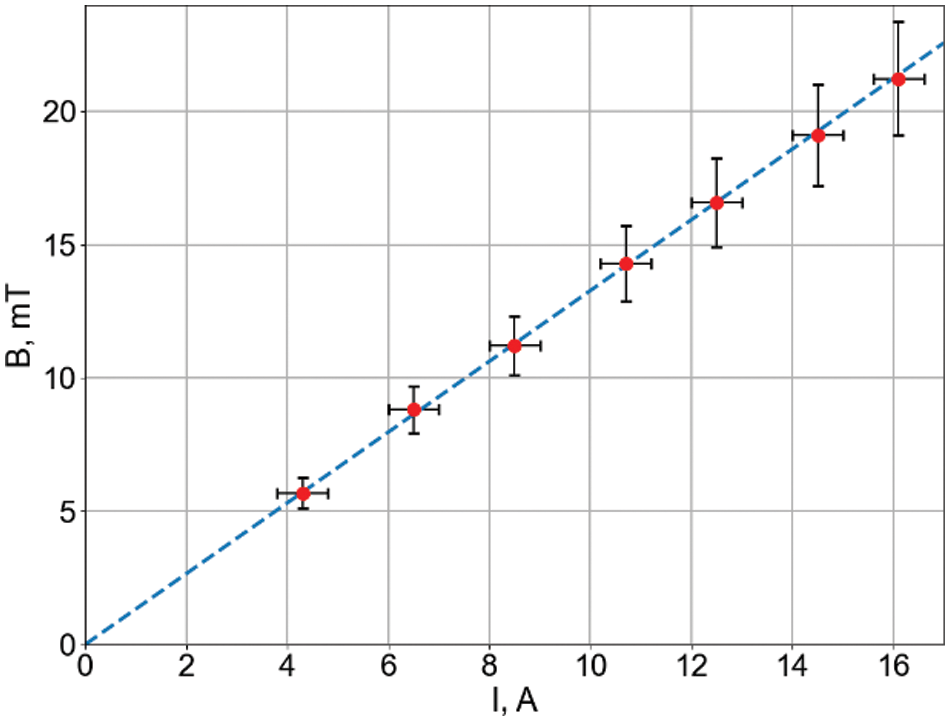
Figure 3: Dependence of the magnetic field on the current
The result of the UDV transducer measurement polling is an output file, containing information about the spatial-temporal distribution of the vertical velocity component, which is directed along the emitted beam. The results of a series of measurements obtained with UDV were processed in the Matlab and Python environments. The UDV registers the values of the vertical velocity component and logs them in the file at regular intervals. The results of data processing showed that in this experiment the pulsations of velocity of the conducting liquid are observed. This is illustrated by vertical lines on the average velocity profile (Fig. 4a), which are indicative of strong pulsations in the fluid flow.
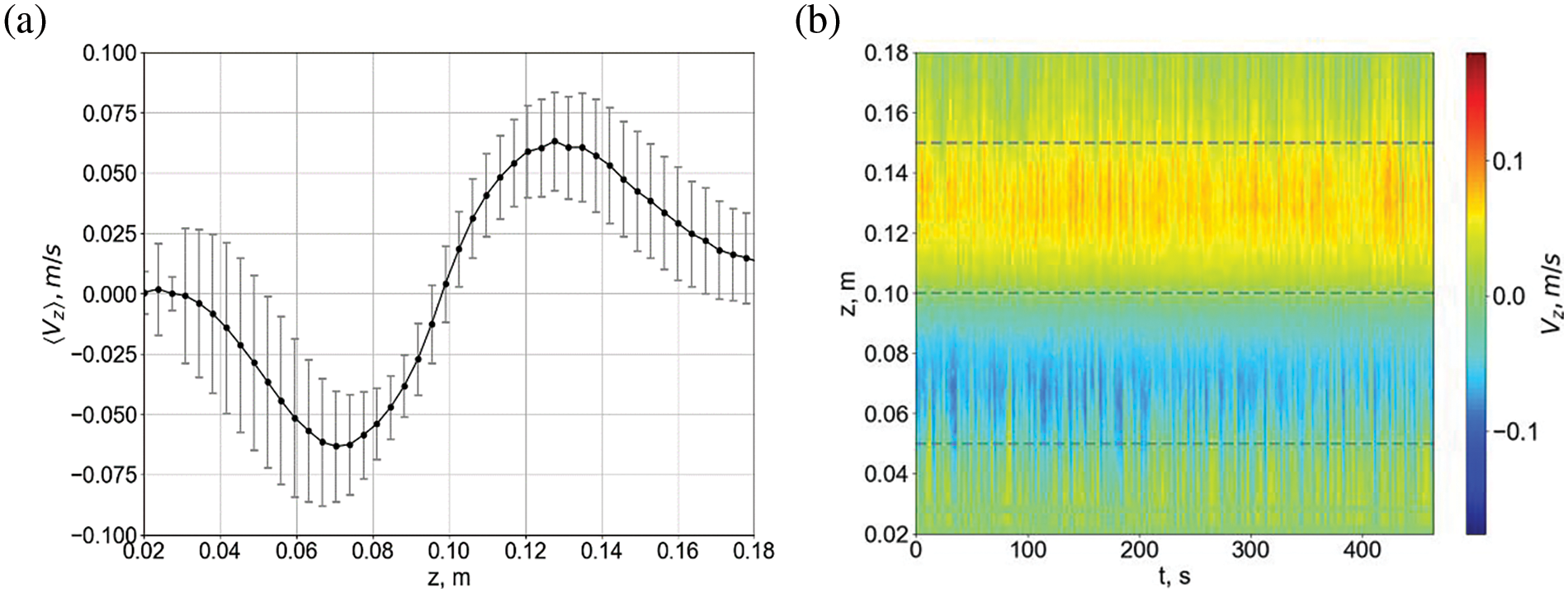
Figure 4: The average velocity profile located along the central UDV transducer–at the left, and profiles of the vertical velocity component located along the central UDV transducer–at the right
An important step in getting the required information is the analysis of one-dimensional signals. The oscillatory behavior of velocity was studied based on the plotting of the velocity signals at the specified points inside the region. The most suitable points were selected based on the analysis of velocity profile diagrams. In the diagram (Fig. 4b), the velocity profiles obtained at each time step are sequentially placed on a given segment. Such profiles are built only for the vertical velocity component
Fig. 5a shows the dependence of the Reynolds number on the current strength. The Reynolds number
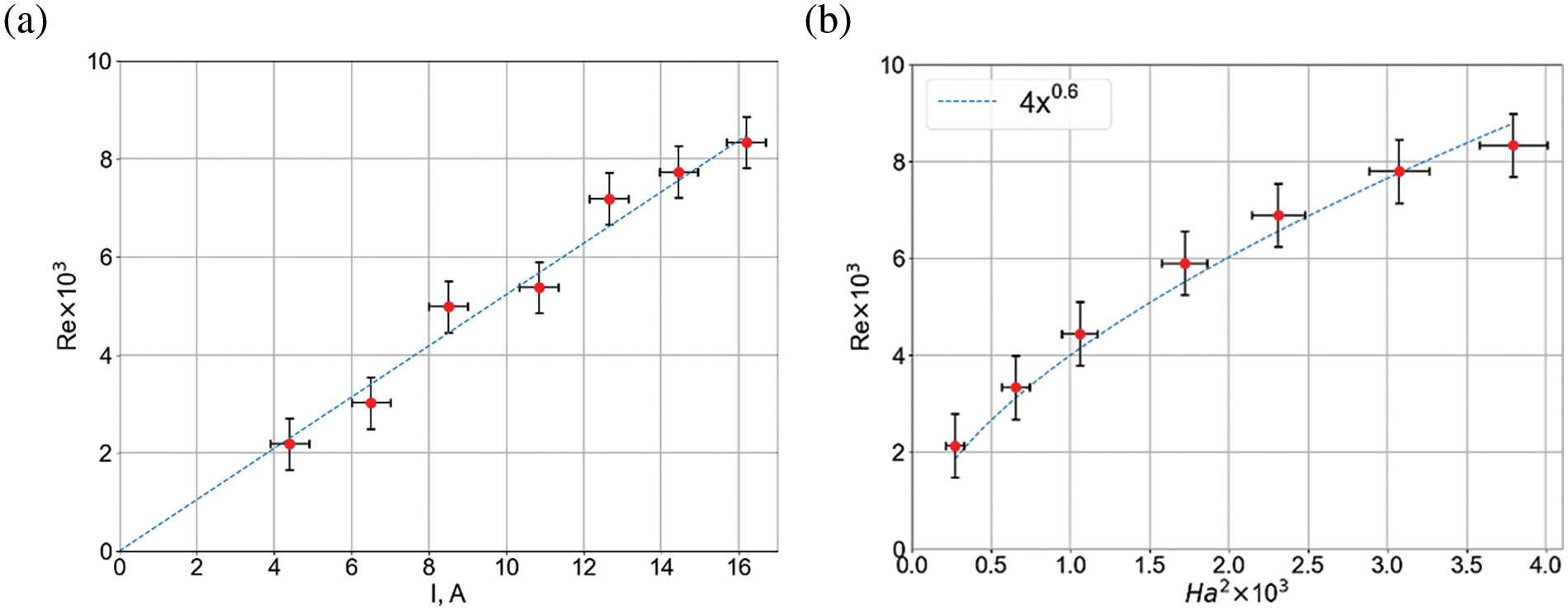
Figure 5: Dependence of the Reynolds number on the current (a), and dependence of the Reynolds number on the square of the Hartmann number (b)
The basic requirement in the experimental study is the symmetry of the configuration, the alignment of the magnetic field with the cell, and the horizontal position of the coil. The dependences of the average velocity profiles on the location of the cell and the coil were obtained (Fig. 6) by performing the following procedure. Initially, the coil was fixed at a height of 0.393 m. Then, the cell was raised with a step of 0.01 m relative to the coil. According to the location of the average velocity profile, the curve shown in green and corresponding to the position of the coil at a height of 0.413 m best fits the configuration of the system, in which the center of the cell coincides with the center of the coil. It can be concluded that the green curve intersects the horizontal line corresponding to the value of the average velocity
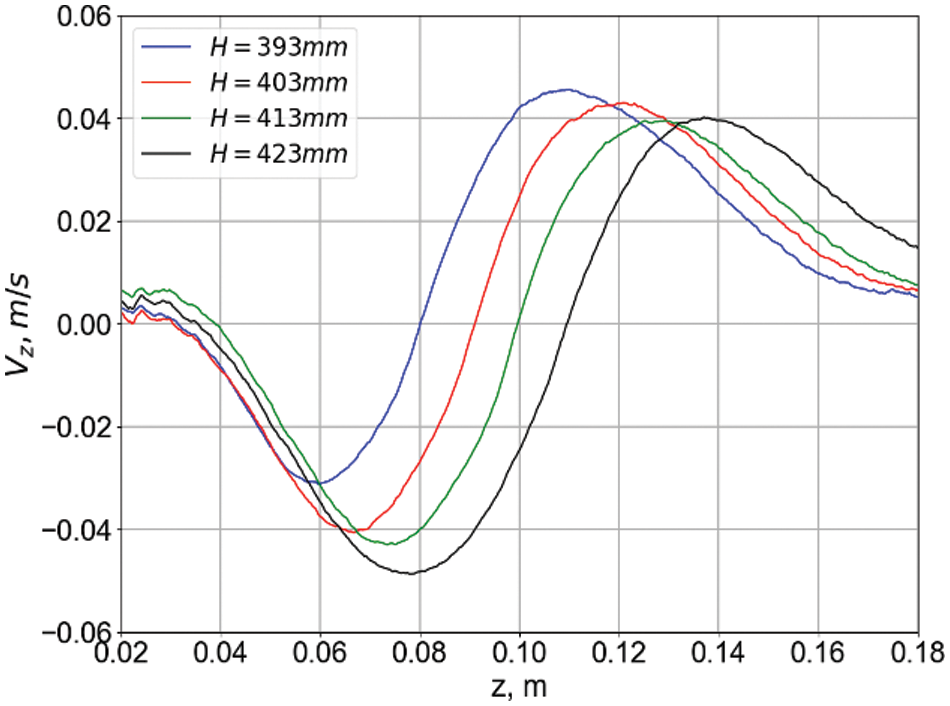
Figure 6: Dependence of the average velocity profile on the location of the cell
The characteristic frequency of velocity pulsations was determined by constructing the Fourier spectra at the three specified points located along the selected velocity profile. Velocity pulsations were generally irregular in nature. The spectral composition of the velocity signal at a point in space varied with time. The characteristic pulsation frequencies were also determined by the Wavelet analysis [37]. In this case, the complex Morlet wavelet was used. Wavelet spectrograms (Fig. 7a) allowed us to detect time variation in the oscillation structure in the case of complex spectral composition. In Fig. 7b, the Fourier spectra are denoted by solid lines, and the dotted lines are the integral wavelet spectra of velocity signals at the same points in space. The results show that the characteristic frequency of 0.1 Hz is detected along the central profile at the top of the cell.
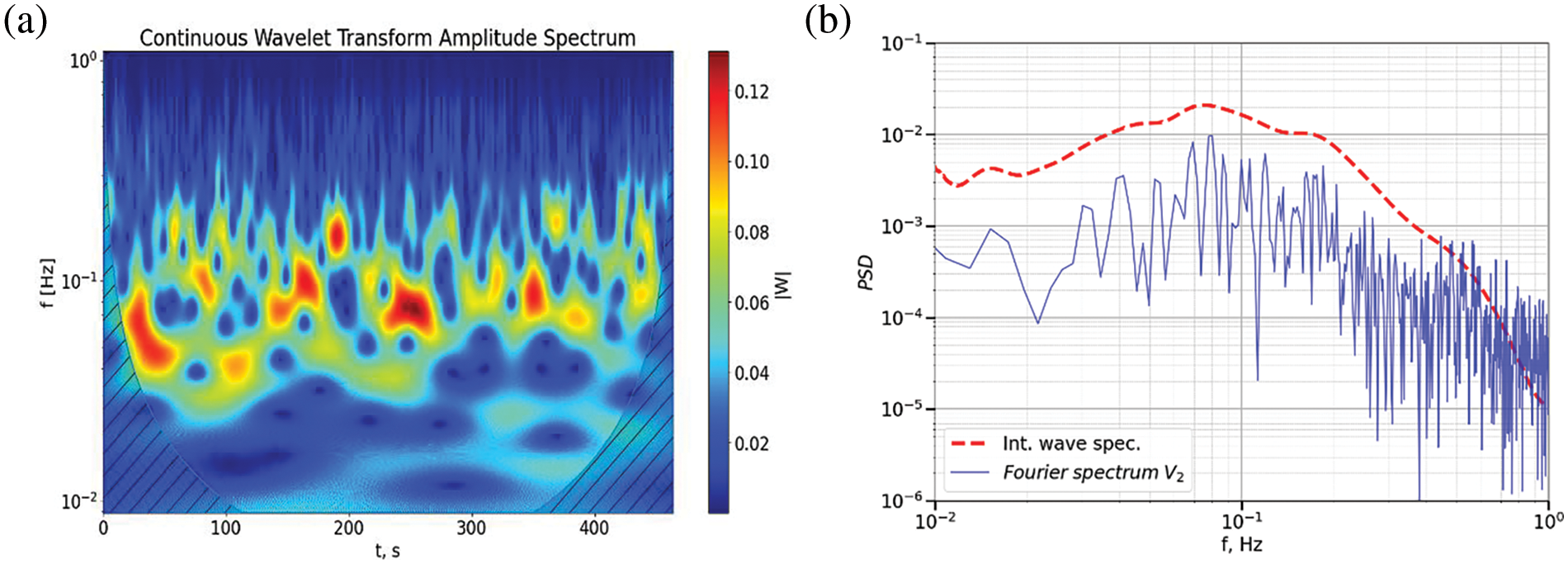
Figure 7: The wavelet spectrogram–at the left, and the Fourier spectrum–at the right, of the signals of the vertical velocity component for the central profile. The results are presented for parameter values: I = 10.84 A, U = 100.5 V,
(1) In this study, we experimentally investigated the flow of liquid metal, which occurs under the action of an alternating magnetic field of a short solenoid in a cylindrical cell. The use of an ultrasonic Doppler anemometer made it possible to measure the evolution of the vertical component of the flow velocity at different values of parameters, characterizing the intensity of the electromagnetic force. Measurements and analysis showed that the average flow is in the form of two tori. The maximum value of the average flow velocity was 0.05 m/s at the current strength of 16.2 A, voltage 150 V, and the frequency of the source
(2) The conducted experiments revealed the existence of velocity pulsations against the background of an average flow. Spectral analysis confirmed the presence of a dedicated frequency of about 0.1 Hz in the spectra. In this case, the use of the wavelet analysis for determining the dedicated frequency is more appropriate than the Fourier analysis, which is apparently due to the fact that frequency oscillations are of a non-harmonic nature and exist in the form of irregular pulsations. This is clearly seen in the wavelet diagrams. In this case, the wavelet analysis allows us to determine the frequency range, in which the detected frequency of oscillations occurs. The estimation can be made using the average value of the frequency in this interval. It should be noted that the allocated frequency cannot be determined at all points. However, the presence of even one point, at which this oscillation frequency can be determined, generates researchers’ interest in this technique.
(3) Pulsations of the flow velocity are caused by the oscillations of a large eddy circulation, consisting of two tori. Spectral analysis makes it possible to detect the allocated frequency of these pulsations. However, in the range of the parameters being considered, it does not reveal the pronounced dependence of the allocated frequency on the power parameter or the frequency of coil current in contrast to work [21]. Probably, the reason is the insufficient magnitude of the electromagnetic force, as was mentioned above. Nevertheless, the obtained finding can actually form the basis of the method for studying the properties of a liquid medium. The technique is based on recording the frequency of pulsations of a large eddy circulation in a cylindrical cell with an electrically conductive liquid medium. The value of the electrical conductivity of the medium can be found by comparing the results of frequency measurements with calculations. This will allow us to estimate the relative change in the properties of the medium. This raises the question of why exactly the value of electrical conductivity is so important. Impurities in liquids can be in a dissolved and undissolved state. At high fluid flow rates, in a turbulent regime, the dissolved impurity has a greater effect on the electrical conductivity as compared to viscosity. Preliminary calculations in the framework of the mathematical model proposed in [21] showed that the change in viscosity has little effect on the location of the velocity pulsation maximum (Fig. 8). Direct measurements of electrical conductivity cause considerable difficulties, and is even dangerous when dealing with such media as liquid aluminum and sodium. The methodology we are developing based on the results of our study is aimed at overcoming these difficulties. The appearance of suspended impurities in the initially pure molten metal has an impact on the average electrical conductivity of the medium causing its variation. In turn, this leads to a change in the allocated oscillation frequency of the large eddy circulation. The proposed technique will allow tracing these frequency variations. The technique can be implemented as an express test of the properties of molten metal samples. In our future studies, we intend to complete the development of this technique.
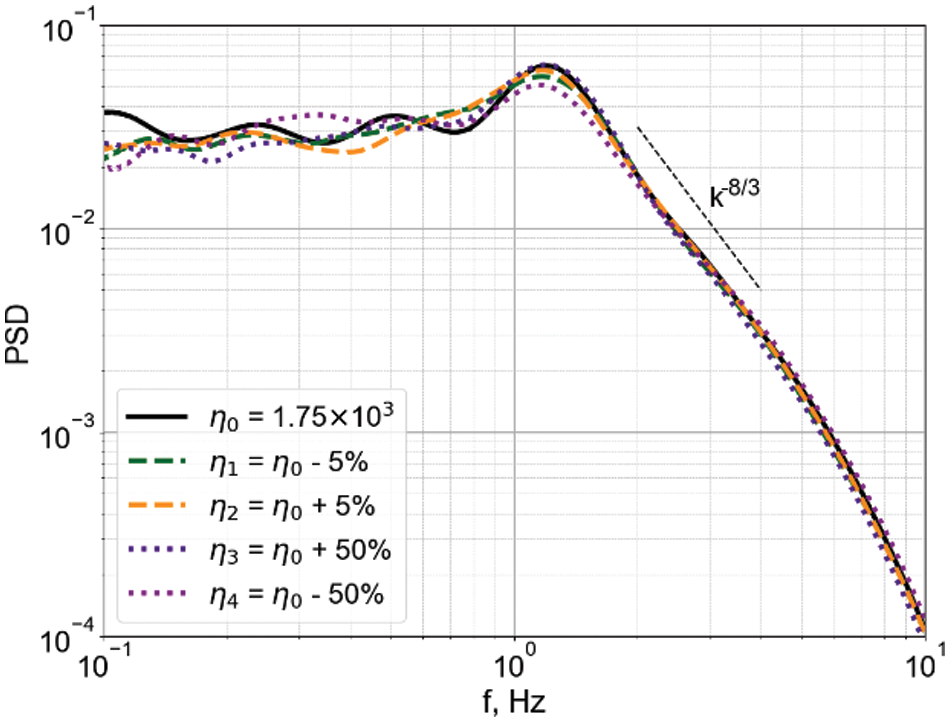
Figure 8: Fourier spectra of signals of the vertical velocity component for the side profile. The dependence of the characteristic frequency on the dynamic viscosity
Acknowledgement: The authors express their gratitude to the researchers of the Laboratory of Technological Hydrodynamics of the ICMM UB RAS, V.A. Yeltischev and A.D. Mamykin for their help in preparing for the experiment. We sincerely thank anonymous reviewers for their constructive comments which led to serious improvement of the manuscript.
Funding Statement: This research was supported by Russian Science Foundation Grant RSF-22-19-20106 (https://rscf.ru/project/22-19-20106/).
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: I. Kolesnichenko; data collection: A. Poluyanov, I. Kolesnichenko; analysis and interpretation of results: A. Poluyanov, I. Kolesnichenko; draft manuscript preparation: A. Poluyanov. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data acquired during this study are available from the corresponding author upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Tarapore ED, Evans JW. Fluid velocities in induction melting furnaces: Part I. Theory and laboratory experiments. Metalurgical Trans B. 1976;7:343–51. doi:https://doi.org/10.1007/BF02652704. [Google Scholar] [CrossRef]
2. Poitout S, Branco P. Theoretical modeling and experimental tests of an electromagnetic fluid transportation system driven by a linear induction motor. IEEE Trans Magn. 2006;42(9):2133–51. doi:https://doi.org/10.1109/TMAG.2006.880396. [Google Scholar] [CrossRef]
3. Kolesnichenko IV, Khalilov RI. Extremum in the dependence of the head generated by electromagnetic pump of liquid metal on feeding current frequency. Comp Continuum Mech. 2022;15:495–506 (In Russian). doi:https://doi.org/10.7242/1999-6691/2022.15.4.38. [Google Scholar] [CrossRef]
4. Moffatt HK. Electromagnetic stirring. Phys Fluids A: Fluid Dyn. 1991;3(5):1336–43. doi:https://doi.org/10.1063/1.858062. [Google Scholar] [CrossRef]
5. Wang X, Wang S, Zhang L, Sridhar S, Conejo A, Liu X. Analysis on the deflection angle of columnar dendrites of continuous casting steel billets under the influence of mold electromagnetic stirring. Metall Mater Trans A. 2016;47:5496–509. doi:https://doi.org/10.1007/s11661-016-3695-0. [Google Scholar] [CrossRef]
6. Timofeev V, Pervukhin M, Vinter E, Sergeev N. Behavior of non-conducting particles in molten aluminium cast into electromagnetic molds. Magnetohydrodynamics. 2020;56(4):459–72. doi:https://doi.org/10.22364/mhd. [Google Scholar] [CrossRef]
7. El-Kaddah N, Patel AD, Natarajan TT. The electromagnetic filtration of molten aluminum using an induced-current separator. JOM. 1995;47:46–9. doi:https://doi.org/10.1007/BF03221176. [Google Scholar] [CrossRef]
8. Makarov S, Ludwig R, Apelian D. Electromagnetic separation techniques in metal casting. I. Conventional methods. IEEE Trans Magn. 2000;36(4):2015–21. doi:https://doi.org/10.1109/20.875303. [Google Scholar] [CrossRef]
9. Losev G, Mamykin A, Kolesnichenko I. Model of electromagnetic purification of liquid metal. Magnetohydrodynamics. 2021;57(1):73–84. doi:https://doi.org/10.22364/mhd. [Google Scholar] [CrossRef]
10. Xu Z, Li T, Zhou Y. Continuous removal of nonmetallic inclusions from aluminum melts by means of stationary electromagnetic field and DC current. Metall Mater Trans A. 2007;38(5):1104–10. doi:https://doi.org/10.1007/s11661-007-9149-y. [Google Scholar] [CrossRef]
11. Jiang Y. A new processing method for the nonlinear signals produced by electromagnetic flowmeters in conditions of pipe partial filling. Fluid Dyn Mater Propcess. 2021;17(4):759–72. doi:https://doi.org/10.32604/fdmp.2021.014470 [Google Scholar] [CrossRef]
12. Taniguchi S, Brimacombe J. Application of pinch force to the separation of inclusion particles from liquid steel. ISIJ Int. 1994;34(9):722–31. doi:https://doi.org/10.2355/isijinternational.34.722. [Google Scholar] [CrossRef]
13. Zhang B, Ren Z, Wu J. Continuous electromagnetic separation of inclusion from aluminum melt using alternating current. T Nonferr Metal Soc. 2006;16(1):33–8. [Google Scholar]
14. Shu D, Sun B, Li K, Wang J, Zhou Y. Effects of secondary flow on the electromagnetic separation of inclusions from aluminum melt in a square channel by a solenoid. ISIJ Int. 2002;42(11):1241–50. doi:https://doi.org/10.2355/isijinternational.42.1241. [Google Scholar] [CrossRef]
15. Stiller J, Koal K, Nagel W, Pal J, Cramer A. Liquid metal flows driven by rotating and traveling magnetic fields. Eur Phys J Spec Topics. 2013;220:111–22. doi:https://doi.org/10.1140/epjst/e2013-01801-8 [Google Scholar] [CrossRef]
16. Cramer A, Galindo V, Zennaro M. Frequency dependence of an alternating magnetic field driven flow. Magnetohydrodynamics. 2015;51(1):133–48. doi:https://doi.org/10.22364/mhd. [Google Scholar] [CrossRef]
17. Nikulin IL, Perminov AV. The mathematical model of nickel melt convection in the induction melting. The solving of the magnetic subproblem. PNRPU Mech Bul. 2013;3:193–209 (In Russian). [Google Scholar]
18. Nikulin IL, Perminov AV. Mathematical model of the processes of heat and mass transfer and diffusion of the magnetic field in an induction furnace. J Engineering Phys Thermophys. 2016;89(2):397–409. doi:https://doi.org/10.1007/s10891-016-1389-5. [Google Scholar] [CrossRef]
19. Mebarek-Oudina F, Bessaih R, Mahanthesh B, Chamkha AJ, Raza J. Magneto-thermal-convection stability in an inclined cylindrical annulus filled with a molten metal. Int J Numer Methods Heat Fluid Flow. 2020;31(4):1172–89. [Google Scholar]
20. Ščepanskis M, Jakovičs A, Baake E, Nacke B. Analysis of the oscillating behaviour of solid inclusions in induction crucible furnaces. Magnetohydrodynamics. 2012;48(4):677–86. doi:https://doi.org/10.22364/mhd. [Google Scholar] [CrossRef]
21. Poluyanov AO, Kolesnichenko IV. Oscillations of the liquid metal flow generated in a cylindrical cell by an alternating magnetic field. Comp Continuum Mech. 2024 (In Russian). doi:https://doi.org/10.7242/1999-669112024.17.1.3. [Google Scholar] [CrossRef]
22. Statra Y, Fawaz S, Menana H, Douine B. Experimental electromagnetic characterization of high temperature superconductors coils located in proximity to electromagnetically active materials. Fluid Dyn Mater Process. 2022;18(5):1529–37. doi:https://doi.org/10.32604/fdmp.2022.021827. [Google Scholar] [PubMed] [CrossRef]
23. Zikanov O, Belyaev I, Listratov Y, Frick P, Razuvanov N, Sviridov V. Mixed convection in pipe and duct flows with strong magnetic fields. App Mech Rev. 2021;73(1):010801. doi:https://doi.org/10.1115/1.4049833. [Google Scholar] [CrossRef]
24. Dobosz A, Plevachuk Y, Sklyarchuk V, Sokoliuk B, Gancarc T. Thermophysical properties of the liquid Ga-Sn-Zn eutectic alloy. Fluid Ph Equilib. 2018;465:1–9. doi:https://doi.org/10.1016/j.fluid.2018.03.001. [Google Scholar] [CrossRef]
25. King EM, Aurnou JM. Turbulent convection in liquid metal with and without rotation. P Natl Acad Sci USA. 2013;110(17):6688–93. doi:https://doi.org/10.1073/pnas.1217553110. [Google Scholar] [PubMed] [CrossRef]
26. Losev G, Kolesnichenko I. The influence of the waveguide on the quality of measurements with ultrasonic Doppler velocimetry. Flow Meas Instrum. 2020;75:101786. doi:https://doi.org/10.1016/j.flowmeasinst.2020.101786. [Google Scholar] [CrossRef]
27. Losev G, Kolesnichenko I. Structure of MHD vortex flows in a thin layer of liquid metal. Magnetohydrodynamics. 2019;55(1):97–106. [Google Scholar]
28. Liu K, Stefani F, Weber N, Weier T, Li BW. Numerical and experimental investigation of electro-vortex flow in a cylindrical container. Magnetohydrodynamics. 2020;56(1):27–42. doi:https://doi.org/10.22364/mhd. [Google Scholar] [CrossRef]
29. Zürner T, Schindler F, Vogt T, Eckert S, Schumacher J. Combined measurement of velocity and temperature in liquid metal convection. J Fluid Mech. 2019;876:1108–28. doi:https://doi.org/10.1017/jfm.2019.556. [Google Scholar] [CrossRef]
30. Franke S, Räbiger D, Galindo V, Zhang Y, Eckert S. Investigations of electrically driven liquid metal flows using an ultrasound Doppler flow mapping system. Flow Meas Instrum. 2016;48:64–73. doi:https://doi.org/10.1016/j.flowmeasinst.2015.09.004. [Google Scholar] [CrossRef]
31. Sarma M, Grants I, Herrmannsdörfer T, Gerbeth G. Contactless generation of cavitation in high temperature liquid metals and its impact on particle dispersion in solidified iron and steel samples. J Mater Proc Tech. 2021;291:117041. doi:https://doi.org/10.1016/j.jmatprotec.2021.117041. [Google Scholar] [CrossRef]
32. He Y, Tang J, Kalantar-Zadeh K, Dickey MD, Wang X. Noncontact rotation, levitation, and acceleration of flowing liquid metal wires. P Natl Acad Sci USA. 2022;119(6):e2117535119. doi:https://doi.org/10.1073/pnas.2117535119. [Google Scholar] [PubMed] [CrossRef]
33. Nikulin IL, Perminov AV. Simulation of the averaged flow of a metal melt in an alternating magnetic field with variable amplitude and frequency. J Eng Phys Thermophys. 2020;93(3):556–66. doi:https://doi.org/10.1007/s10891-020-02153-0. [Google Scholar] [CrossRef]
34. Zwirner L, Khalilov R, Kolesnichenko I, Mamykin A, Mandrykin S, Pavlinov A, et al. The influence of the cell inclination on the heat transport and large-scale circulation in liquid metal convection. J Fluid Mech. 2020;884:A18. doi:https://doi.org/10.1017/jfm.2019.935. [Google Scholar] [CrossRef]
35. Herreman W, Benard S, Nore C, Personnettaz P, Cappanera L, Guermond JL. Solutal buoyancy and electro-vortex flow in liquid metal batteries. Phys Rev Fluids. 2020;5:074501. doi:https://doi.org/10.1103/PhysRevFluids.5.074501. [Google Scholar] [CrossRef]
36. Wondrak T, Sieger M, Mitra R, Schindler F, Stefani F, Vogt T, et al. Three-dimensional flow structures in turbulent Rayleigh-Bénard convection at low Prandtl number Pr = 0.03. J Fluid Mech. 2023;974:A48. doi:https://doi.org/10.1017/jfm.2023.794. [Google Scholar] [CrossRef]
37. Frik PG, Sokoloff DD, Stepanov RA. Wavelets for the space-time structure analysis of physical fields. Phys Usp. 2022;65(1):62–89. doi:https://doi.org/10.3367/UFNe.2020.10.038859. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools