Open Access

ARTICLE

Numerical Analysis of Permeability of Functionally Graded Scaffolds

Dmitry Bratsun^*, Natalia Elenskaya, Ramil Siraev, Mikhail Tashkinov

Laboratory of Mechanics of Biocompatible Materials and Devices, Perm National Research Polytechnic University, Perm, 614990, Russia

* Corresponding Author: Dmitry Bratsun. Email:

(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)

Fluid Dynamics & Materials Processing 2024, 20(7), 1463-1479. https://doi.org/10.32604/fdmp.2024.047928

Received 22 November 2023; Accepted 29 December 2023; Issue published 23 July 2024

Abstract

In this work, we numerically study the hydrodynamic permeability of new-generation artificial porous materials used as scaffolds for cell growth in a perfusion bioreactor. We consider two popular solid matrix designs based on triply periodic minimal surfaces, the Schwarz P (primitive) and D (diamond) surfaces, which enable the creation of materials with controlled porosity gradients. The latter property is crucial for regulating the shear stress field in the pores of the scaffold, which makes it possible to control the intensity of cell growth. The permeability of functionally graded materials is studied within the framework of both a microscopic approach based on the Navier-Stokes equation and an averaged description of the liquid filtration through a porous medium based on the equations of the Darcy or Forchheimer models. We calculate the permeability coefficients for both types of solid matrices formed by Schwarz surfaces, study their properties concerning forward and reverse fluid flows, and determine the ranges of Reynolds number for which the description within the Darcy or Forchheimer model is applicable. Finally, we obtain a shear stress field that varies along the sample, demonstrating the ability to tune spatially the rate of tissue growth.

---

Graphic Abstract

---

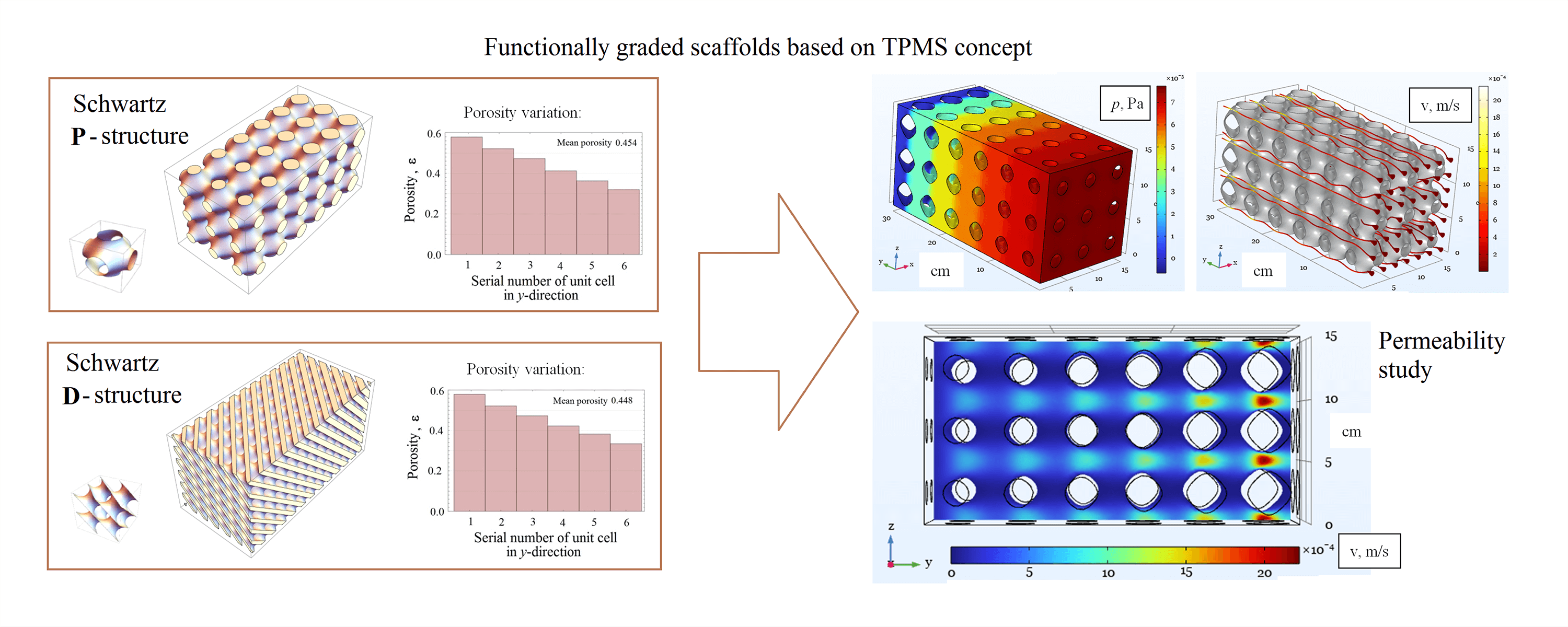
Keywords

---