Experimental Investigation of Wave–Current Loads on a Bridge Shuttle-Shaped Cap–Pile Foundation

1  Introduction

In recent decades, a growing number of coastal regions worldwide have witnessed the construction of sea-crossing bridges. These bridges typically feature a substantial cap–pile group foundation, which plays a crucial role in their design and construction due to the harsh maritime conditions involving strong waves and currents in deep sea areas (Hallowell et al. [1–3]). The complex geometry of the composite structure, consisting of the cap and the pile group, coupled with intricate interactions among waves, currents, and the structure, pose challenges in accurately estimating the wave-current loads. Therefore, accurately predicting and analyzing the wave–current loads and the hydrodynamic effects on the cap–pile foundation is crucial for achieving a better design and safer construction.

The cap–pile foundation of a sea-crossing bridge typically consists of a composite structure, comprising a large-size cap and multiple small-size piles. Due to the significant disparity in sizes, the calculation of wave-current forces requires separate theoretical approaches. The assumption can be made that the diameter of a single pile relative to the wavelength is typically small, indicating minimal influence on the wave field. The Morison Equation is a classical method for evaluating the wave forces on a slender pile [4], and the key lies in selecting an appropriate wave theory and hydrodynamic coefficients (drag coefficient CD and inertial coefficient CM). Further validation and expansion of the Morison Equation have been conducted by Lighthill [5], and Moberg [6] through flume model experiments and analyses of cylinders with small diameters. Deng et al. [7] improved upon the Morison Equation for assessing non-linear wave forces on a cylinder by both model experiments and numerical simulations.

The spacing between piles in the pile group is small, resulting in significant interactions such as interference and shielding. Consequently, accurately and comprehensively analyzing wave-current loads on pile groups becomes challenging due to the highly complex pile group effect. As a solution, a series of experiments were conducted to develop practical evaluation methods. Shiravani et al. [8] examined the impact of cylinder arrays on wave diffraction and resulting wave forces. Bonakdar et al. [9] summarized the wave action on the pile groups based on extensive scaled model tests of single piles and small-scale pile groups, proposing a new hybrid model to estimate the effect coefficient of the pile group.

Sea-crossing bridges typically have large caps that generate scattering effects. The Morison Equation is inadequate for estimating the wave forces on the cap, as it does not account for wave diffraction near the structure. Instead, an analytical solution based on linear diffraction theory, developed by MacCamy and Fuchs, is commonly used to estimate the wave forces and moments on large circular cylinders [10]. The predictions of this method have been validated by experiments conducted on large circular cylinders subjected to regular waves by Chakrabarti et al. [11–13]. Iuppa et al. [14] conducted experiments to measure the fluctuating pressure and force caused by diffracted waves on the surface of a large circular cylinder. Additionally, Serinaldi et al. [15], and Seiffert et al. [16] studied wave-deck interactions through experiments and computations, proposing probabilistic models for maximum load estimation. The interaction between the incident wave field and a structure is intensified in the presence of currents, resulting in the generation of a complex diffracted wave–current field around the structure [17]. Furthermore, the size and shape of caps vary across different projects. Several researchers have investigated wave forces and wave–current forces on large structures. Based on model tests, Xu et al. [18] compared the variations in horizontal and vertical wave forces on caps at different depths and under varying wave conditions. Jeong et al. [19] measured the enhancement effect of the shoal on the long-term non-linear diffraction wave force of three-type specially shaped cylindrical foundations used in wind turbines. Kang et al. [20] examined the hydrodynamic coefficients of a dumbbell-shaped cofferdam under the combination of waves and currents. They varied the wave height and period, current velocity, and the incident direction of flow through experiments and numerical simulations. The results indicated that the hydrodynamic coefficient was strongly correlated with the sinusoidal value of the incident angle of flow. Wei et al. [21,22] conducted a model experiment on a large round-ended caisson foundation and determined that the wave–current–induced base shear force was approximately equal to the sum of the corresponding wave-induced and current-induced base shear forces. In engineering design, the wave force on the cap is typically calculated using linear diffraction theory, while the current force is calculated determined by the resistance formula. The wave–current load on the cap is then obtained by combining these forces, as has been reported by Mei et al. [23]. The wave load on the pile group is calculated using the Morison Equation. To obtain the overall wave-current load on the foundation, the wave–current loads on the pile group and the cap are added together, as demonstrated by Pan et al. [24].

However, the aforementioned methods fail to accurately represent the combine action of waves and the currents on the cap–pile group, leading to significant deviations from experimental data [25]. Deng et al. [26] conducted numerical modeling to analyze the impact of the cap on wave forces on the pile group. They concluded that the cap primarily affects the wave forces on piles located close to its front. Moreover, the ratios of the inline length and submerged depth of the cap to the wavelength were found to significantly influence on the effect coefficient of pile group.

Chen et al. [27] conducted numerical simulations to analyze the wave forces acting on a high-rise pile–cap structure. The results revealed that the maximum horizontal wave force on all piles with the cap increased by 30% compared to those without the cap. Similarly, the horizontal wave force on the cap with piles increased by 15%. These findings indicate that the conventional Morison Equation and diffraction theory underestimate the wave loads on both the piles and the cap in this scenario.

The design wave–current loads on the foundation of the sea-crossing bridge are primarily obtained by laboratory experiments. Liu et al. [28] conducted experiments on a scaled model of the pile–cap foundation of a bridge. They discovered that the wave loads increased in relation to both wave height and period. Furthermore, they observed that the trends in load variations under the combined action of waves and currents were similar to those under wave-only conditions. In a separate study, Liu et al. [29] analyzed the variation in the effect coefficient of pile group under the combined action of waves and currents based on model experiments on a cap–pile foundation for an offshore wind farm. They also discussed the impact of the cap on wave loads on the pile group under regular wave conditions.

A comprehensive review of the literature reveals the intricate nature of the wave–current loads on the cap–pile group structure, making accurate analysis challenging. The methods employed to estimate the loads on the cap–pile group in engineering also possess limitations, leading to uncertain results. Prior investigations have primarily assumed conventional wave and current conditions in this regard, with limited exploration of the loads on deep-water foundations of sea-crossing bridges under the combined action of intense waves and currents. However, with advancements in construction technology and the increasing necessity for sea-crossing bridges in deep waters, these foundations are subjected to harsh environment characterized by strong waves and currents. Consequently, the wave–current loads under the combined actions of these factors have become the dominant load in the design of sea-crossing bridge foundations [30].

To enhance adaptability to the deep-water environment characterized by waves and currents, the foundation of the main tower of a sea-crossing bridge incorporates a combined structure comprising a novel shuttle-shaped cap and 18 piles, with each pile having a diameter of 6.3 m (Fig. 1). However, there is limited understanding regarding the hydrodynamic load characteristics on the shuttle-shaped cap-pile foundation under the combined effects of waves and currents, which hampers structural design considerations and the development of an effective construction plan.

Figure 1: Shuttle-shaped cap-pile group foundation

This study utilizes a prototype of the aforementioned shuttle-shaped cap-pile group foundation to investigate the wave-current forces acting in three different directions (inline, transverse, and vertical). A model of the foundation was constructed, allowing for the measurement of inline, transverse, and vertical forces on the foundation at three distinct water depths. The variations in the forces on the foundation were then analyzed according to significant wave height and period, current velocity, incident flow direction, and water level. Furthermore, a comparative analysis was conducted to examine the characteristics of wave forces and wave–current forces, with a particular emphasis on the wave-current forces induced by strong waves and currents. The conclusions are expected to enhance the understanding of evaluating the wave–current loads on large shuttle-shaped cap–pile foundations and assist in their optimization design.

2  Experimental Design and Setup

2.1 Model of Shuttle-Shaped Cap–Pile Foundation

The wave flume used in the experiments was 75 m in length, 1.8 m in width, and 2 m in depth, and the maximum allowable operating depth of water was 1.5 m. As is shown in Fig. 2, a hydraulic piston-type wave generator installed on one side of the flume could generate one-way waves. On the other side, an efficient absorber beach was installed to minimize wave reflections. With an inlet and an outlet at the bottom of both ends, uniform currents could be generated by the circulation pump system.

Figure 2: Schematic diagram of wave flume (unit: m)

The prototype was a shuttle-shaped cap–pile foundation for the main tower of a sea-crossing bridge. The main feature of the foundation was its large shuttle-shaped cap, with dimensions of 68 m × 46.4 m × 10 m (length × width × height). Additionally, the pile group was densely arranged, with the pile center distance (11~12.6 m) ≤2 times of the pile diameter. The pile group consisted of 18 piles, each with a diameter of 6.3 m, and the distance between the bottom of the cap and the seabed was 54 m. In consideration of navigation safety, the cap was designed to remain partially submerged at both the highest and the lowest water levels, with a draft of 6 m under normal conditions. To account for the size of the flume, wave and current conditions, and the capacity of the measuring instrument, a test model at a 1:125 scale (model/prototype) was designed based on geometric similarity and Froude’s similarity criterion. The theoretical relationship between the model and the prototype is outlined in Table 1. The model was constructed using plexiglass, and its dimensions are shown in Fig. 3, with additional details provided in Table 2.

Figure 3: Shuttle-shaped cap-pile group model (unit: cm)

The test model was installed on a rigid steel frame (Fig. 4a), positioned approximately 35 m from the wave generator. Fig. 4b shows the installation diagram, perpendicular to the wave propagation direction. The fixed base, three-component force sensor, adapter clamp, and shuttle-shaped cap–pile group were connected by high-strength bolts to ensure the model mounting rigidity. The top of the cap was equipped with four M8 bolts to securely hold the model in place, while the adapter clamp had bolt-mounting holes spaced 22.5° apart. To prevent any interference from the ground, the bottom of the pile group was maintained 1 cm above the ground of the flume, thus ensuring accurate force measurements.

Figure 4: Installation diagram of shuttle-shaped cap-pile group model (unit: cm)

2.2 Testing Conditions

The flow field conditions for wave-only, current-only, and combined wave and current scenarios were simulated to evaluate the loads and their respective development trends on the shuttle-shaped cap–pile foundation. The water depth and the waves and currents conditions adopted in the experiment were derived from recorded data of the water channel.

The water depth at the bridge site was 60 m under normal conditions, with the highest and lowest tidal levels occurring over a 100-year return period as 3.5 and −2.6 m, respectively. For the experiments, three water depths (i.e., d = 47.0, 49.0 and 52.0 cm) were selected. The simulated water levels are depicted in Fig. 4b.

The wave heights corresponding to cumulative frequencies of 1% and 13% were 7.80 and 5.32 m, respectively, over a 100-year return period, with an average wave period of 10.4 s. Then, a JONSWAP spectrum was generated, featuring significant wave heights (Hs) of 5.32 and 3.54 m, as well as peak periods (Tp) of 12.6 and 9.5 s. In order to gain a deeper understanding of the dynamic loads acting upon the shuttle-shaped cap–pile foundation in response to long-period waves, peak periods Tp of 16 and 19.5 s were incorporated. To maintain consistency, a geometric scaling of 1:125 was applied following Froude’s similarity criterion. The corresponding relation between the model and the prototype regarding wave parameters is presented in Table 3.

Under the current-only conditions, uniform currents with velocities (U ) of 1.1, 2.2, and 3.3 m/s were devised for the experiment, based on the design current velocity (U) of 3.3 m/s over a 100-year return period. For the combined actions of random waves propagating in the same direction as the currents, two scenarios were considered: random waves with Hs = 3.54 m and Tp = 9.5 s, and Hs = 5.32 m and Tp = 12.6 s were combined with currents with velocities U = 1.1, 2.2, and 3.3 m/s. The parameters of the waves and currents for both the model and prototype are displayed in Table 4. In addition, the simulation included three different incident angles (i.e., θ = 0°, 22.5°, 45°) for waves and wave currents, achieved by adjusting the mounting hole of M8 bolts, as shown in Fig. 3a.

2.3 Operation Mode of Wave and Current Conditions

This experiment adopted the same method applied by Kang et al. [20] for generating wave and the current conditions. For the wave-only conditions, random waves were generated by the reciprocal motion of the wave generator. For the current-only conditions, uniform currents were generated by adjusting the flow rate of the circulation pump system until a stable current velocity was achieved. For the wave–current interaction conditions, the current-only condition was initially established, and then the wave generator was activated using the same control parameters as in the wave-only condition. The measurements of wave–current forces on the model were conducted when both the waves and currents remained sufficiently stable.

2.4 Instrumentation and Data Sampling

In this study, three instruments were utilized for measurements: wave gauges, Acoustic Doppler Velocimetry (ADV) and a three-component force sensor. To capture the distribution of the wave field, six capacitance-type wave gauges (WG1~WG6) were arranged at different locations inside the flume, as shown in Fig. 2a. The wave gauges featured a length of 30 cm, a resolution of 0.1 mm, accuracy within ±0.3%, and a sampling frequency of 200 Hz. Specifically, WG1 was positioned 4.5 m upstream of the model to measure the incident waves, WG2 and WG3, WG5and WG6 were placed to record fluctuations around the model, while WG4 served the purpose of assessing waves at the same horizontal location outside the center area of the model.

An ADV (CM1) was positioned 6.5 m upstream of the model to measure the current velocity, as shown in Fig. 2a. The ADV system boasted an accuracy of 0.5% and operated at a sampling frequency of 100 Hz.

The forces acting on the model were measured by the three-component force sensor FC3D80, which was installed as shown in Fig. 4b. The calibrated sensor possessed the following performance-related characteristics: Fx and Fy were within a range of ±150 N, with a resolution of 0.015 N; while Fz was within a range of ±300 N, with a resolution of 0.03 N. The three-component force sensor had a sampling frequency of 200 Hz. Fx represented the inline force, consistent with the direction of the bridge; Fy represented the transverse force, perpendicular to the direction of the bridge; and Fz represented the vertical force.

All wave gauges, the ADV, and the three-component force sensor were calibrated prior to the experiment. The experiment was repeated three times for each set of conditions, and the resulting average value was utilized to minimize random error and improve accuracy.

Before the installation of the shuttle-shaped cap–pile group model, calibration tests were conducted separately for random waves and only currents. Furthermore, the variations in the significant wave height were measured under the combined actions of random waves and currents. The significant values of wave heights, wave forces and wave–current forces were determined by averaging the first third of the maximum crest or trough values of the time series of the measured data, as follows:

xis=3N∑i=1N/3⁡xi (1)

where xis represents the significant wave height Hs or the significant wave/wave–current force Fiws/Fiwcs , xi is the time series of the measurement data, and N is the number of data items.

2.5 The Blockage Effect

The ratio of the transverse dimension D of the model to the width B of the water flume is defined as the blocking ratio D/B. Due to limitations in the experimental setup, the blockage ratio for this study is approximately 0.2. According to the test conditions outlined in Tables 2 and 3, the corresponding Reynolds number is high (Re = 2.5 × 104~1.5 × 105). For the flow around a circular cylinder, Zdravkovich [31] noted that for high Reynolds numbers, when D/B < 0.1, the blockage effect can be ignored as it has minimal impact. However, when 0.1 < D/B < 0.6, the blockage effect slightly affects fluid flow; When D/B > 0.6, the blockage ratio becomes a control parameter, leading to a complete alteration of the flow pattern around the cylinder. Studies by Liu [32] showed that, with a blockage ratio of 0.2 and 0.05, the variation pattern of the wake vortex remained largely unchanged, with negligible impact from the wall surface. Additionally, when the blockage ratio did not exceed 0.2, the variations in the hydrodynamic coefficients CD and CL were relatively smooth. Griffith et al. [33] and Yang et al. [34] similarly suggested that the blockage effect has a minimal impact on flow when the blockage ratio D/B ≤ 0.2, warranting it being disregarded. Moreover, Al Mashan et al. [35] successfully obtained reasonable experimental results using a blockage ratio of D/B > 0.4 in an offshore platform model experiment. Therefore, in this study, the D/B is approximately 0.2 for most cases, implying that the blockage effect has an insignificant influence on the hydrodynamic loads on the shuttle-shaped cap–pile group foundation. Thus, subsequent analysis will not take the blockage effect into consideration.

3  Random Wave Field in the Currents

The experimental parameters are detailed in Tables 3 and 4. The analysis of test results for the wave surface at d = 49 cm is presented as follows:

3.1 Calibrating of Random Waves and Changes under the Influence of Currents

The representative time series of wave elevations for water depth d = 49 cm with random waves Hs = 2.8 cm and Tp = 0.85 s, and Hs = 4.3 cm and Tp = 1.13 s, both with and without the current, are presented in Figs. 5a and 5b. Comparisons between the measured and the target spectrums of the random waves are also shown.

Figure 5: Time series for surface elevations of random wave and random wave with current, and the comparison of spectrums

The measured spectrum for the random waves alone was in alignment with the target spectrum, which verified the accuracy of the simulated random waves. Furthermore, the time series of wave elevations clearly indicates that the influence of the current primarily manifests as a reduction in wave amplitude, which became more pronounced with increasing current velocity. Interestingly, the peak spectral S(ωm) exhibits a significant decrease with an increase in the current velocity, while the peak frequency ωm was nearly unaffected. Specifically, the peak spectral for Hs = 2.8 cm and Tp = 0.85 s decreased by 21.4% under a current velocity of U = 0.1 m/s, while the peak spectral for Hs = 4.3 cm and Tp = 1.13 s decreased by 48.3% under a current velocity of U = 0.3 m/s.

3.2 Influence of Current on the Significant Wave Height

Li et al. [36] conducted research on wave deformations under the influence of current, revealing that random waves can be regarded as a linear superposition of several simple harmonic waves based on the conservation principle of wave flux and the linear superposition principle of stationary random processes. For waves in deep water, the estimation of the current-affected significant wave height can still be achieved through the evaluation method applied to wave height under regular wave–current interaction. Therefore, the transformation of the wave height Hs is defined as follows:

HsHs0=(1−UC)0.5(Lp0Lp)0.5(A0A)0.5(1+UC2−AA)0.5 (2)

A0=1+2k0dsinh2k0d (3)

A=1+2kdsinh2kd (4)

where Hs , Lp , k , and A are the current-affected significant wave height, the wavelength corresponding to the peak wave period, wave number and wave energy transmissivity, respectively. Hs0 , Lp0 , and k0 are the significant wave height, the wavelength corresponding to the peak wave period, wave number and wave energy transmissivity in still water, respectively. U is the current velocity, C is the wave celerity in the current, and d is the water depth.

Fig. 6 presents a comparison of significant wave heights between the measured data and the theoretical values under the combined actions of random waves with Hs0 = 2.8 cm and Tp = 0.85 s, as well as Hs0 = 4.3 cm and Tp = 1.13 s, and currents with velocities ranging from U = 0 to 0.3 m/s. It is observed that when the relative current velocity U/c0≥ 0.18, the significant wave height experiences a reduction of 35.5% for Hs0 = 2.8 cm and 28% for Hs0 = 4.3 cm, indicating that higher current velocities have a greater impact on wave heights. Additionally, the influence of the current on the significant wave height becomes more pronounced as the initial wave height becomes smaller.

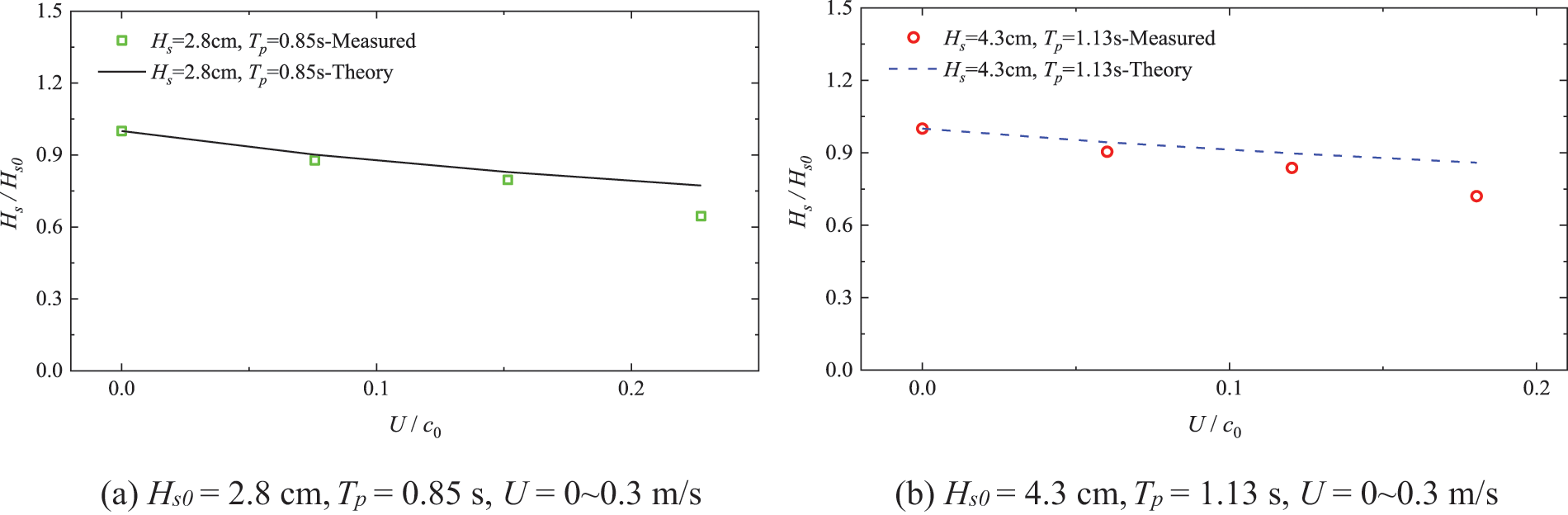
Figure 6: Comparison of significant wave heights between the measured data and the theoretical solutions with different current velocities (d = 49.0 cm)

The comparison of the data demonstrates that in deep water, the variation trend of significant wave heights aligns with the theoretical solution when considering changes in the current velocity, particularly within the range of U/c0= 0~0.15. However, as the current velocity surpasses U/c0≥ 0.18, the reduction trend in significant wave height intensifies, leading to an increased discrepancy between the measurements and the theoretical solution. This is primarily attributed to the amplification of non-linearity in the random wave field due to higher velocities, which is not accounted for in Eq. (2) as it ignores frequency changes caused by current effects. However, it should be noted that the condition U/c0≥ 0.18 applied in the experiments corresponded to an extreme case with an actual current velocity of 3.3 m/s. On the other hand, U/c0= 0~0.15 encompasses a wider range of typical sea conditions. Therefore, Eq. (2) remains applicable for calculating significant wave heights under the combined action of conventional random waves and currents.

4  Experimental Results and Discussion

4.1 Significant Wave Forces on the Shuttle-Shaped Cap–Pile Group

4.1.1 Time Series of Typical Wave Force

The wave forces acting on the shuttle-shaped cap–pile group were measured under wave-only actions. Figs. 7a~7i illustrate the wave forces in three directions (i.e., inline ( Fx ), transverse ( Fy ), and vertical ( Fz )) for random wave of Hs  = 4.3 cm, Tp = 1.13 s, with incident angle θ = 0° at three different water levels (i.e., d = 47, 49, 52 cm). Notably, Figs. 7d–7f show that the amplitude of the transverse force ( Fy ) increased as the water level rose. On the other hand, Figs. 7g–7i show that the downward force component of the vertical force ( Fz ) increased significantly with the water level, while the uplifting force component gradually decreased. Additionally, Fig. 7 suggests that the inline force Fx was considerably smaller than 10% of Fy and Fz . This finding highlights the need for a more thorough examination of the transverse and vertical wave forces on this deep-water foundation under the wave-only conditions.

Figure 7: Wave force time series in three directions (x, y and z) on the model for Hs = 4.3 cm, Tp = 1.13 s, θ = 0°

4.1.2 Significant Wave Forces

The study investigated the effects of wave incident directions and water depth on significant wave forces over a wide range of relative wavelengths (i.e., the longitudinal length of the cap/wavelength, Dy / LP ). Fig. 8 illustrates the variations in dimensionless significant forces ( Fyws/(ρgHA) and Fzws/(ρgHA) ) as Dy / LP changed from 0.16 to 0.49 at water depth of 47.0, 49.0, 52.0 cm, for Hs = 2.8 and 4.3 cm. The wavelength LP corresponding to the peak spectral period TP and water depth d could be estimated by the Dispersion equation (i.e., Eq. (5)):

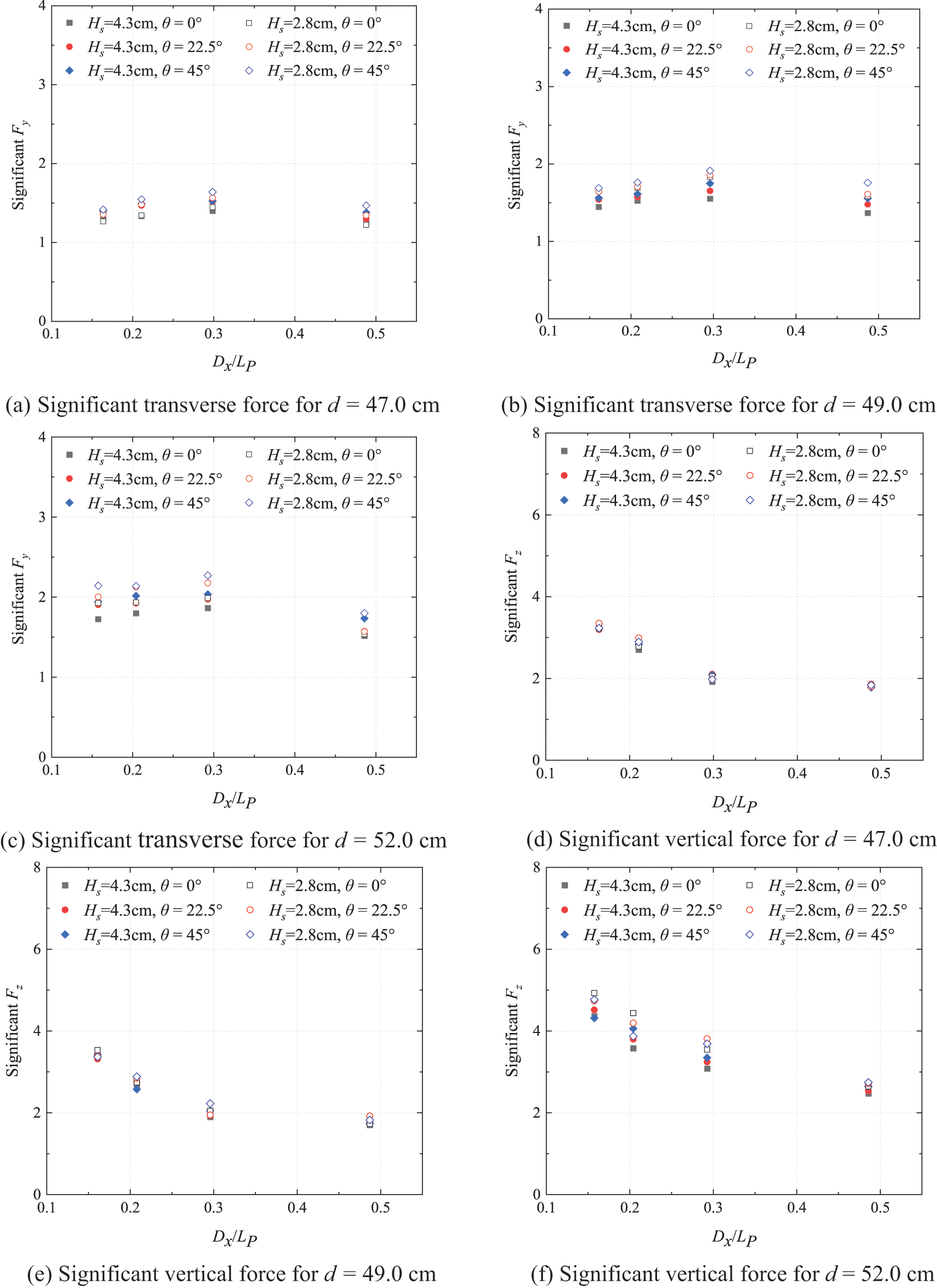
Figure 8: Significant transverse and vertical wave forces with respect to relative wavelength for different water depth and incident angles for Hs = 2.8 and 4.3 cm

LP=gTP22πtanh2πdLP (5)

Figs. 8a~8c reveal that the transverse significant wave force Fyws was greater for waves with longer periods ( Dy / LP = 0.16–0.29) and decreased significantly at Dy / LP = 0.49 for all three water depths. This decrease was attributed to the significant phase lag during the wave movement from the model’s leading edge to the trailing edge. For Dy / LP = 0.49, the wave phases at the leading and trailing edges of the model were nearly opposite in direction. As a result of the wave propagation characteristics, the horizontal waves at these two positions acted in opposing directions, leading to a subtractive effect on the wave force. In the range of Dy / LP from 0.16 to 0.29, the phases at the leading and trailing edges of the model were similar, and the directions of the horizontal wave were identical. Consequently, the wave force was superimposed.

The incident direction of the wave exerts a certain influence on the transverse significant wave force. On one hand, a larger incident angle θ results in a greater water-blocking area for the structure. On the other hand, as shown in Fig. 3, the relatively dense arrangement of the pile group causes the forward piles to shield the rear piles due to the wave diffractions. Simultaneously, within the range of incident angles θ from 0° to 45°, the angle between the geometric connection of the front and rear piles and the wave propagation increases. thereby weakening the shielding effect. Additionally, the projected length of the model in the wave propagation direction decreases, leading to a decrease in phase lag. The combined effect of these factors causes the transverse wave force to increase with the incident angle. Moreover, the difference in transverse significant wave force slightly increases with the relative wavelength under the three wave incidence angles. For most wave conditions, when the incident angle was 45° or 0°, the difference in Fyws is approximately 10%. However, for random waves with Hs = 4.3 cm, the difference in Fyws reaches its maximum value of 14.15% at θ = 45° or 0° when d = 52.0 cm and Dy / LP = 0.49.

For the same wave conditions, the transverse significant wave force increases with the water level. In particular, for the case of Hs = 4.3 cm, Dx / LP = 0.29, θ = 45°, and d = 52.0 cm, Fyws/(ρgHA) reached its maximum value of 2.035, which was 33.4% higher than that when d = 47.0 cm.

Figs. 8d~8f illustrate that the vertical significant wave force Fzws/(ρgHA) of the model gradually decreases with an increasing relative wavelength Dy / LP . Statistically, analysis was conducted on the values of Fzws/(ρgHA) at three water depths and three incident angles. Dy / LP varied from 0.16 to 0.49, and on average, Fzws/(ρgHA) exhibited a decrease by 82.5% for d = 47.0, 49.0, 52.0 cm, and θ = 0°, 22.5°, and 45°. This phenomenon occurs because a larger relative wavelength Dy / LP , leads to a larger phase lag between the leading and trailing edges of the model. As a result, the uniformity of the vertical wave pressure at each position of the model diminishes, consequently causing a decrease in the vertical wave force.

The incidence angle has minimal effect on the vertical significant wave force Fzws . For Hs = 4.3 cm, the difference in Fzws minimal the three incident angles were less than 10%.

The water level has a significant impact on the vertical significant wave force Fzws/(ρgHA) . Data comparison shows that the values of Fzws/(ρgHA) for each value of Dy / LP are relatively close to each other for d = 47.0 and 49.0 cm. However, Fzws/(ρgHA) for d = 52.0 cm was significantly higher than those for d = 47.0 and 49.0 cm. For Hs = 4.3 cm and Tp = 1.13 s, the average values of Fzws/(ρgHA) are 2.038 and 1.959 for d = 47.0 and 49.0 cm, respectively. In contrast, the average value of Fzws/(ρgHA) for d = 52.0 cm is 3.224, which is 58.2% and 64.5% higher than those for d = 47.0 and 49.0 cm, respectively. The main reason for this disparity is that for d = 52.0 cm, the static water level closely approached the top surface of the cap, resulting in prominent overtopping in wave propagation. In other words, when the wave crest interacted with the cap, it crossed the top surface, causing water to exert downward pressure on it and leading to a significant increase in the downward wave force. However, for d = 47.0 and 49.0 cm, the wave crest did not surpass the top surface of the cap, thus precluding any downward pressure. Consequently, the vertical behaviors of the waves at d = 47.0 and 49.0 cm were similar, resulting in comparable values and trends in vertical wave forces.

The above analyses indicate that the combination of a long wave and a high tide results in the transverse and vertical wave loads being the primary design loads on the shuttle-shaped cap–pile group.

4.2 Significant Wave–Current Forces on the Shuttle-Shaped Cap–Pile Group

4.2.1 Times Series of Typical Wave–Current Forces

The forces acting on the shuttle-shaped cap–pile group, including inline ( Fx ), transverse ( Fy ), and vertical ( Fz ), exhibited notable differences when subjected to the combined influence of random waves and currents as opposed to random waves alone. Fig. 9 showcases the typical time series and frequency spectra of forces under specific conditions: wave-only, current-only, and wave-current. The measurements were conducted under Hs = 4.3 cm, Tp = 1.13 s, and U = 0.1 and 0.3 m/s, with θ fixed at 0°, and d = 47.0, 49.0, and 52.0 cm.

The forward amplitudes of the transverse forces exhibit a significant increase with high current velocity, while their reverse amplitudes decrease rapidly. Conversely, low-velocity currents have minimal effect on the transverse force, as shown in Figs. 9a~9f. When the current velocity is U = 0.1 m/s, the time series Fy and the spectrum S(ω)Fy of the transverse forces under wave–current actions closely resemble those under the wave-only condition. The forward and reverse amplitudes of the transverse forces are similar, with a mean value close to zero. However, when the velocity increases to U = 0.3 m/s, the characteristics of the time series of the transverse forces under wave–current action undergo noticeable changes. The forward amplitudes exhibit a significant increase, while the reverse amplitudes decrease rapidly. The mean values of these forces approach that of the current-only conditions, around 5~6 N at all three water levels. Spectral analyses indicated that even with an increase in current velocity, the peak spectral frequency ( ωmy ) of the transverse force caused by wave–current action remains close to that of the wave-only condition. This suggests that the frequency of wave action on the structure is not significantly altered by the current. However, the peak values of S(ω)Fy decrease, primarily due to a reduction in the wave height influenced by the current. This finding aligns with the analysis of the effects of the current on the waves in Section 3.

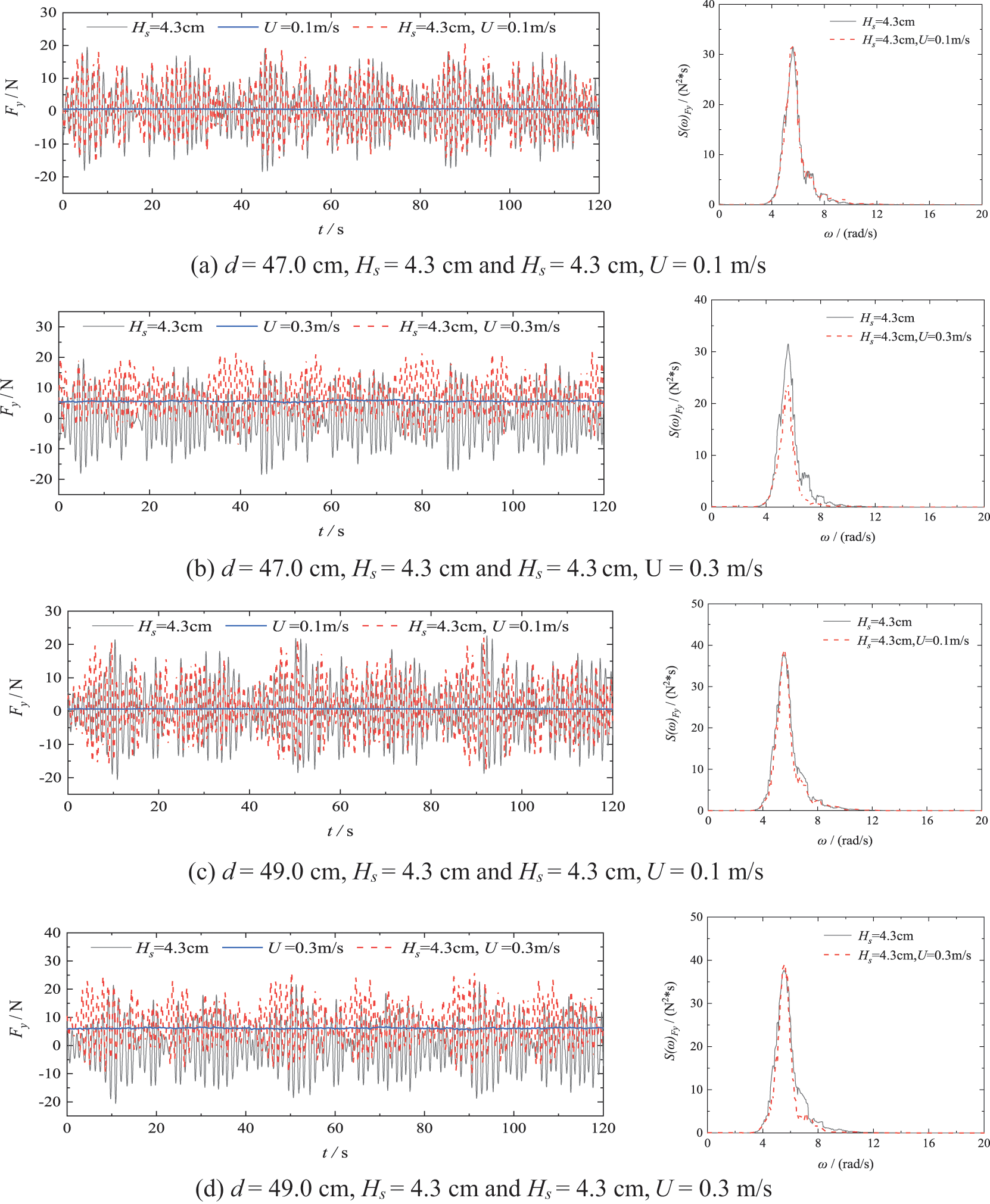
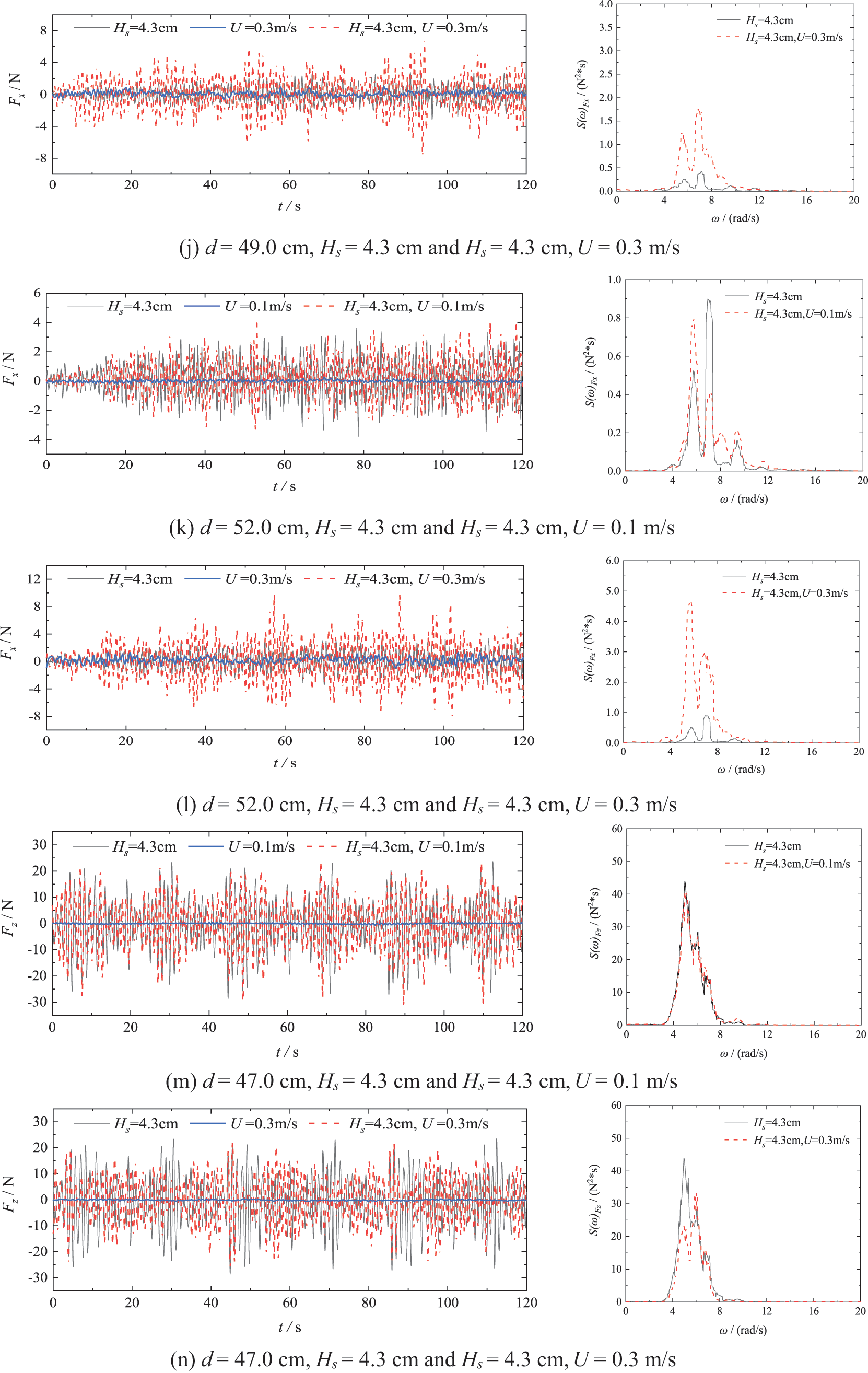
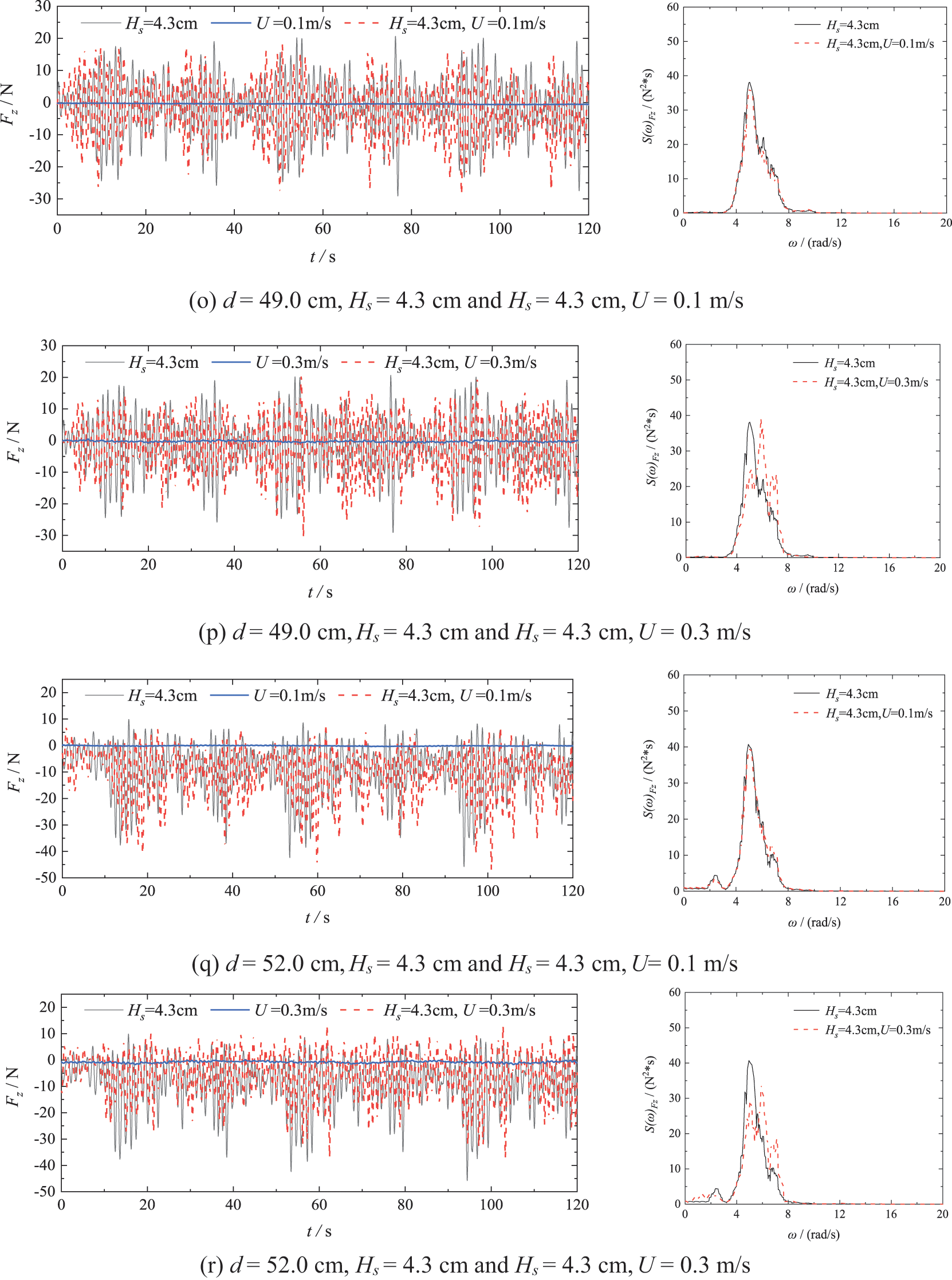
Figure 9: Time series and spectrums for forces in three directions (x, y and z) on the model driven by random waves, currents, and random waves combine with currents

The amplitude of the inline force Fx increases significantly when subjected to the combined action of random waves and high current velocity, as shown in Figs. 9g~9l. Specifically, when the current velocity reaches U = 0.3 m/s, the amplitudes of inline forces under the combined wave–current actions are more than three times greater than those under the wave-only actions. In the spectral analysis, it is observed that the peak values of S(ω)Fx under wave-current actions, with Hs = 4.3 cm and U = 0.3 m/s, are 4–5 times higher than those observed under wave-only actions. Moreover, under the wave-current action, the shape of the peak of S(ω)Fx changes and the frequency extends slightly towards higher frequencies.

The amplitude of the vertical force Fz slightly decreases in the presence of high-velocity currents. As shown in Figs. 9m~9r, similar to the transverse forces Fy , the time series of the vertical forces Fz and their spectrum S(ω)Fz are very close to those under wave-only actions when the current velocity is low, such as U = 0.1 m/s. However, when the current velocity reaches U = 0.3 m/s, the amplitude of Fz under the wave-current action decreases compared to that under wave-only action. Additionally, the peak values of S(ω)Fz decreases and the peak spectral frequency ωmz slightly shifts to a higher frequency.

The effects of the water level on forces in all three directions during wave-current actions are found to be similar to those under wave-only actions. With consistent parameters for waves and currents, the amplitude of the transverse forces increases as the water level rose. Notably, the amplitude of the downward vertical forces experiences a noticeable increase with rising water level, while the amplitudes of the uplift forces gradually decrease. However, the water level does not noticeably affect the amplitude of the inline forces.

In general, a high-velocity current results in significantly higher inline and transverse forces on the shuttle-shaped cap–pile group under wave–current actions compared to wave-only actions. In particular, the amplitude of the inline force increases several times.

4.2.2 Significant Wave–Current Forces

The study investigated the impact of the structure orientation and the water depth on significant wave–current forces over a wide range of relative velocities (U/c). Fig. 10 demonstrates the variations in dimensionless significant forces (i.e., inline ( Fxwcs/(ρgHA) ), transverse ( Fywcs/(ρgHA) ), and vertical ( Fzwcs/(ρgHA) )) as U ranges from 0 to 0.3 m/s (equivalent to U/c = 0 to 0.18 for Hs = 4.3 cm and Tp = 1.13 s, and U/c = 0 to 0.22 for Hs = 2.8 cm and Tp = 0.85 s) at the three water levels (i.e., d  = 47.0, 49.0, and 52.0 cm).

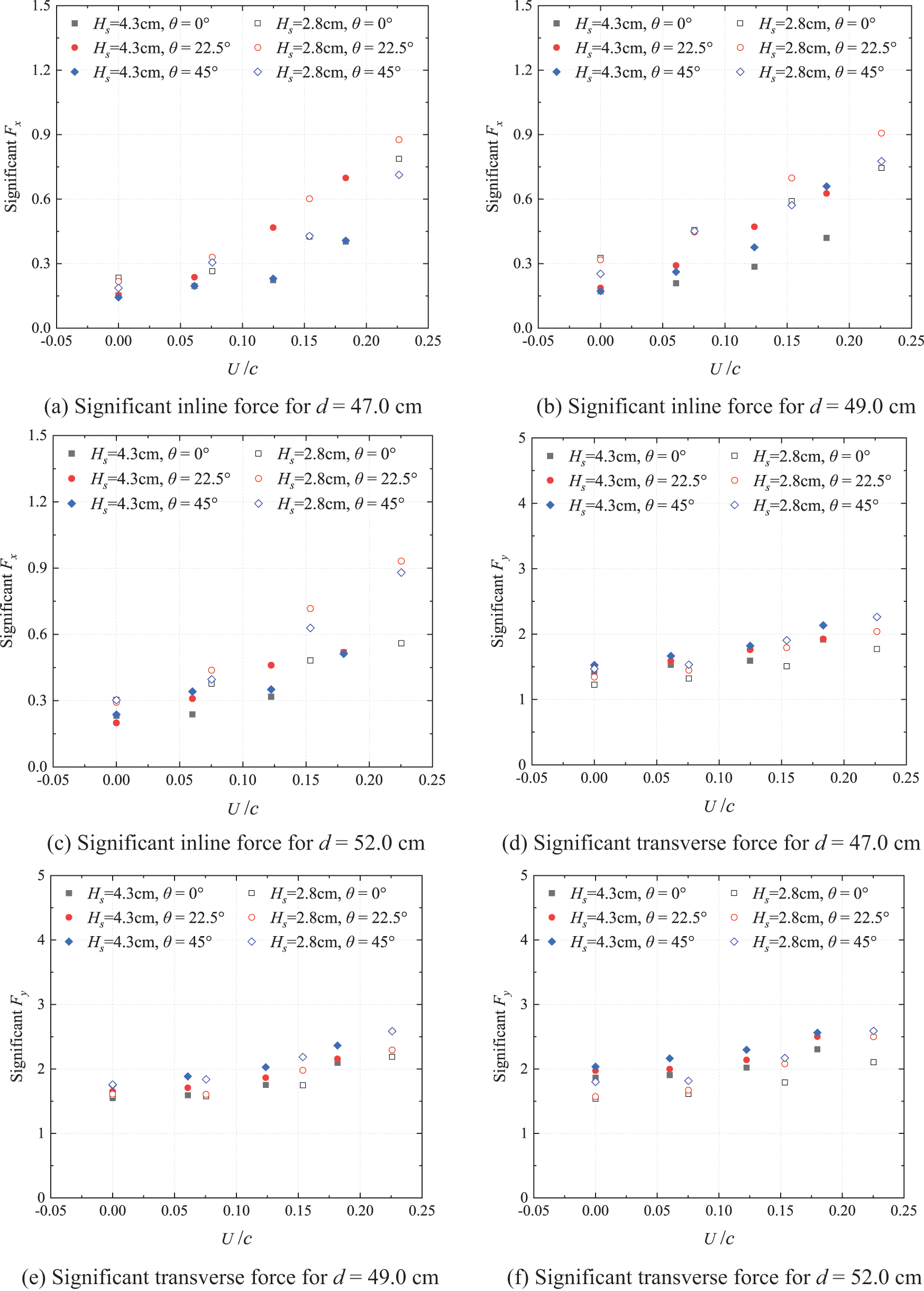
Figure 10: Significant inline, transverse and vertical wave-current forces with respect to relative velocity for different water depth and orientation for Hs = 2.8 and 4.3 cm

Figs. 10d~10f reveal the rapid increase in the transverse significant wave-current force Fywcs for the model as the current velocity rises. It is evident that the impact of current on the transverse wave force is more pronounced for lower wave heights compared to higher ones. For Hs = 2.8 and 4.3 cm with d = 47.0, 49.0, and 52.0 cm, Fywcs/(ρgHA) demonstrates an accelerated increase as U varies from 0 to 0.3 m/s. Furthermore, the values of Fywcs/(ρgHA) under wave–current actions with U = 0.1 m/s closely resemble those of Fxws under the wave-only actions. However, when the current velocity reaches 0.3 m/s for Hs = 2.8 and 4.3 cm, Fywcs/(ρgHA) increased by more than 40% and 25%, respectively, compared to Fyws/(ρgHA) . Additionally, the differences in the values of Fywcs/(ρgHA) for various wave-current incident angles ( θ = 0°, 22.5°, and 45°) grow with increasing U. Similarly, resembling the behavior observed when only waves act on the structure, Fywcs/(ρgHA) gradually rises as θ increases from 0° to 45°. This phenomenon primarily arises from the conversion of the incident angle, leading to an increased wave–current interaction area, diminished shielding effect and phase lag. Under the same wave and the current conditions, Fywcs/(ρgHA) increases with the water level. When the water level closely approaches the top surface of the cap, with the maximum wave-current incidence angle and the current velocity (i.e., d = 52 cm. θ = 45°, and U = 0.3 m/s), the peak values of Fywcs/(ρgHA) for Hs = 2.8 and 4.3 cm amount to 2.589 and 2.558, respectively.

The impact of high-velocity currents on inline wave–current forces is found to be significant. As shown in Figs. 10a~10c, the combination of random waves with heights Hs = 2.8 and 4.3 cm, and current with velocities ranging from U = 0 to 0.3 m/s, results in a gradual increase in significant inline wave–current force across all water levels. For d = 47.0, Hs = 4.3 cm, U = 0.3 m/s, and θ = 22.5°, the maximum value of Fxwcs/(ρgHA) is 0.699, which is 4.6 times greater than Fxws/(ρgHA) . For most wave–current actions with U = 0.3 m/s, Fxwcs / Fxws exceeds 2.5. In the case of waves combined with U = 0.1 m/s, the effect of incident flow directions on Fxwcs was negligible, as their values at all incident angles remain similar. However, when waves combined with U = 0.2 or 0.3 m/s, noticeable variations in Fxwcs/(ρgHA) are observed across different incident angles. Additionally, the water level does not appear to have a significant impact on the significant inline wave–current forces.

The significant vertical wave-current force undergoes a reduction to some extent due to the influence of high-velocity current, which is significantly affected by the water level. Figs. 10g~10i demonstrate that, for water levels in the middle of the cap (i.e., d = 47 and 49 cm), the significant vertical wave–current force Fzwcs/(ρgHA) changed slowly for Hs = 2.8 and 4.3 cm as U varies from 0 to 0.2 m/s. However, Fzwcs/(ρgHA) decreases rapidly when the current velocity further increases to U= 0.3 m/s. When the water level is close to the top surface of the cap (i.e., d = 52 cm), Fzwcs/(ρgHA) changed slowly for Hs = 2.8 and 4.3 cm as U varies from 0 to 0.1 m/s. However, the rate of reduction of Fzwcs/(ρgHA) increases noticeably when the current velocity further increases to U = 0.2 and 0.3 m/s. At all three water levels, Fzwcs is consistently smaller than Fzws for all cases. Additionally, Fzwcs/(ρgHA) reaches its minimum values for Hs = 2.8 and 4.3 cm with U = 0.3 m/s. The differences in Fzwcs/(ρgHA) at the three incident angles do not significantly increase with increasing current velocity. Furthermore, for the same wave-current actions, the measured values of Fzwcs at d = 52 cm are greater than those at d = 47 cm and d = 49 cm. The measured values of Fzwcs are similar at d = 47 cm and d = 49 cm, resembling the cases when only the waves act on the structure. Similarly to the wave-only conditions, at d = 52 cm, the static water level is near the top surface of the cap, and prominent overtopping occurred in the wave–current propagation, resulting in a significant increase in the downward vertical force.

The experimental results demonstrate the necessity of considering the influence of current in evaluating the design loads of the shuttle-shaped cap–pile foundation. Moreover, wave height, current velocity, incidence flow direction and water level at the bridge site are significantly determinants of wave–current loads of the foundation. To accurately evaluate and optimize the wave–current forces acting on the bridge foundation, all the aforementioned factors must be carefully taken into account during the design process. These experimental results serve as a valuable reference for the design of the cap–pile foundation.

4.3 Comparison with Simple Methods of Estimating Significant Wave–Current Forces

In practice applications, the wave-only transverse force and current-only transverse force are commonly linearly summed to estimate the wave–current transverse force on the deep-water foundation, as presented by Mei et al. [23] and Pan et al. [24]. In this section, we examined the disparities between the measured significant transverse wave–current forces ( Fywcs ) and the linear summation of the measured significant transverse wave forces ( Fyws ) and the current forces ( Fyc ) acting on the shuttle-shaped cap–pile foundation.

Figs. 9a~9f illustrate the slight fluctuations observed in the measured current forces under the current-only actions. The current force ( Fyc ) represents the mean value of the time series. Table 5 presents the ratio between the significant transverse wave–current forces ( Fywcs ) and the linear summation of the significant transverse wave forces ( Fyws ) and current forces ( Fyc ). The disparities between Fywcs and ( Fyws+Fyc ) are influenced by the significant wave height Hs , current velocity U , and incident angle θ. As U varies from 0.1 to 0.3 m/s, the mean values of Fywcs /( Fyws+Fyc ) decreases from 0.95 to 0.82 for Hs = 2.8 cm and from 0.99 to 0.89 for 4.3 cm, respectively. The difference between Fywcs and ( Fyws+Fyc ) gradually increased with higher current velocities. For Hs = 2.8 cm and U = 0.3 m/s, the mean values of Fywcs /( Fyws+Fyc ) are 0.84, 0.81, and 0.80 at θ = 0°, 22.5°, and 45°, respectively. For Hs = 4.3 cm and U = 0.3 m/s, the mean values are 0.95, 0.86, and 0.87, respectively. The differences between Fywcs and ( Fyws+Fyc ) are more pronounced for lower wave heights compared to higher wave heights. Furthermore, the differences between Fywcs and ( Fyws+Fyc ) are more prominent at incident angles of θ = 22.5° and 45° than at θ = 0°.

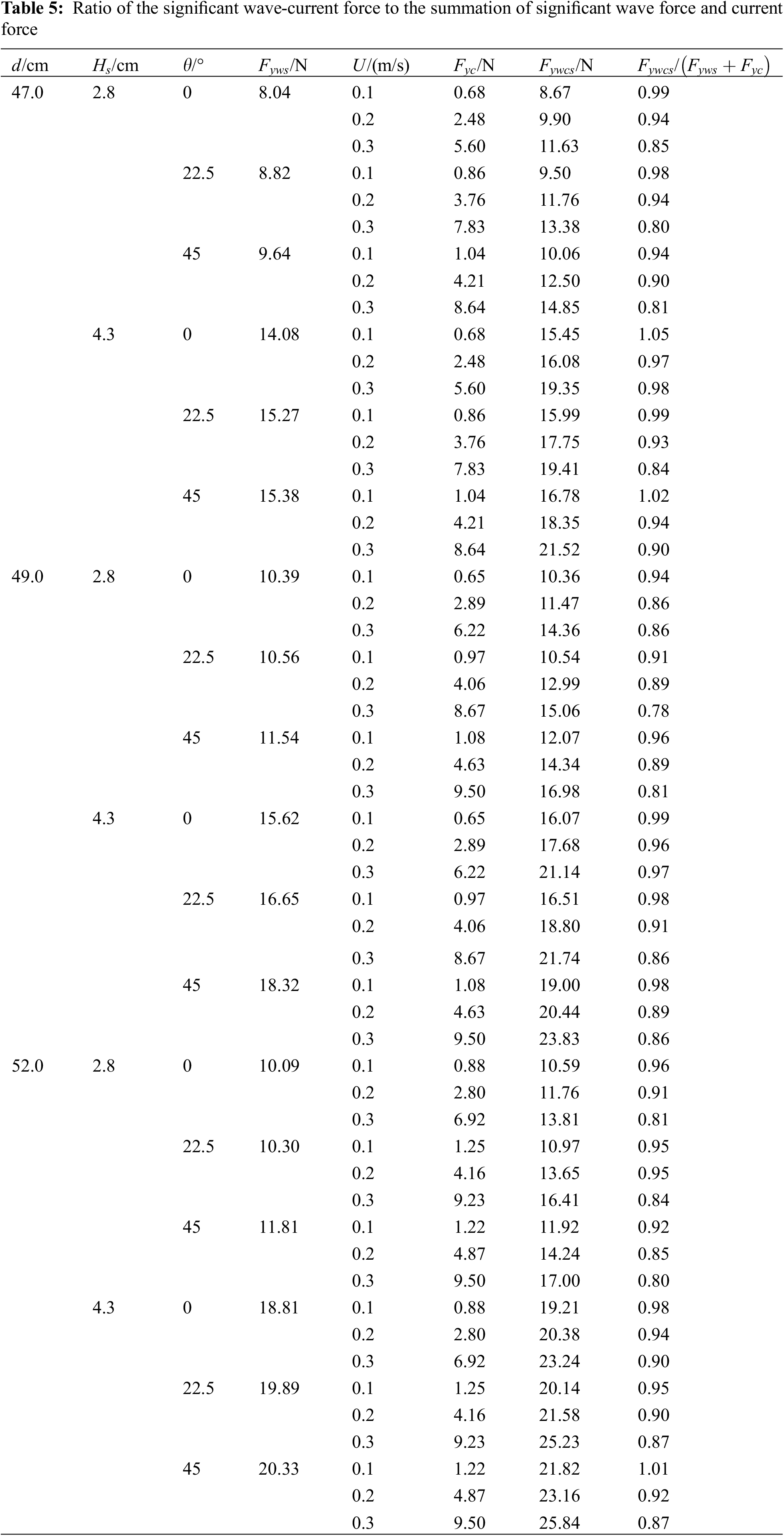
The findings suggest that for high waves with low velocities, the significant transverse wave–current force is approximately equal to the combined linear sum of the significant transverse wave force and the current force. However, due to non-linear wave–current interactions, the linear summation of the significant transverse wave force and the current force overestimate the actual significant transverse wave–current force acting on the shuttle-shaped cap–pile foundation in the majority of wave–current scenarios. In practice, relying on this simple superposition method to estimate wave–current forces on deep-water foundations may result in unnecessary waste of resources and financial burden. Conducting precise model experiments of wave-current interaction provides a more accurate and dependable approach to evaluating the wave-current load on such structures.

5  Conclusions

This study experimentally investigated the effects of random waves and random wave–currents on a model of a shuttle-shaped cap–pile deep-water foundation for a sea-crossing bridge. The study measured the inline, transverse, and vertical forces generated by these interactions at various water levels and incident angles. The following conclusions can be drawn:

Under the random wave-only conditions, the shuttle-shaped cap–pile deep-water foundation primarily experienced transverse and vertical wave forces. When the relative wavelength Dy / LP was small, the increase in Dy / LP led to increased wave steepness, horizontal fluctuation energy, and a decrease in the transmission coefficient. This resulted in an increased transverse force on the structure. Conversely, when Dy / LP was large, the phase lag caused by diffraction effects rapidly expanded, significantly reducing the transverse force. Moreover, the phase lag increased with Dy / LP , leading to a downward trend in vertical force.

The tests conducted under the combined actions of waves and currents revealed that an increase in relative current velocity resulted in higher inline and transverse forces on the structure. Notably, the transverse force showed a significant increase under the combinations of strong waves and currents, in contrast to the scenario where waves acted alone.

In actual engineering design for large deepwater foundations, the combination of high tide, strong waves, and strong currents emerged as the key control load condition. The shuttle-shaped cap–pile foundation experienced the most significant hydrodynamic load in this scenario, with the peak values of inline and transverse wave-current forces. These findings provide vital insights for the design of large deepwater foundation structures.

Under high water level conditions, the hydrodynamic load of the shuttle-shaped cap–pile foundation was even more significant. For the same wave conditions, the transverse wave force and vertical wave force under high water level conditions increase by more than 30% and 50%, respectively, compared to low water level conditions.

The impact of wave-current incidence angle on the hydrodynamic loads of the foundation was relatively limited. When θ varied from 0° to 45°, the changes in the transverse and vertical force values were approximately 10%.

Furthermore, the study indicates that the linear summation wave-only and current-only forces would overestimate the actual significant transverse wave-current forces acting on the shuttle-shaped cap–pile foundation in most wave-current combined cases. Hence, this calculation approach is not a reasonable method for estimating wave-current forces, particularly under combined actions of waves and stronger currents.

Acknowledgement: This model test was conducted in the Laboratory of Offshore Engineering at Zhejiang University of Technology.

Funding Statement: This study was supported by the Major Special Science and Technology Project of “Ningbo Science and Technology Innovation 2025” (Grant No. 2019B10076), Natural Science Foundation of Zhejiang Province (No. LY23E080001).

Author Contributions: Conceptualization, Zhongda Lyu; Data curation, Chenkai Hong; Formal analysis, Lei Wang; Funding acquisition, Zhongda Lyu and Fei Wang; Methodology, Chenkai Hong; Project administration, Zhuo Zhao; Resources, Zhongda Lyu and Zhuo Zhao; Validation, Fei Wang and Lei Wang; Writing–original draft, Chenkai Hong; Writing–review & editing, Zhongda Lyu. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The data supporting this study have been provided within this paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Hallowell S, Myers AT, Arwade SR. Variability of breaking wave characteristics and impact loads on offshore wind turbines supported by monopiles. Wind Energy. 2016;19(2):301–12. [Google Scholar]

2. Jameel M, Oyejobi DO, Siddiqui NA, Ramli Sulong NH. Nonlinear dynamic response of tension leg platform under environmental loads. KSCE J Civ Eng. 2017;21(3):1022–30. [Google Scholar]

3. Akiyama M, Frangopol DM, Arai M, Koshimura S. Reliability of bridges under tsunami hazards: emphasis on the 2011 Tohoku-oki earthquake. Earthq Spectra. 2013;29:295–314. [Google Scholar]

4. Morison JR, O’Brien MP, Johnson JW, Schaaf SA. The force exerted by surface waves on piles. J Petro Tec. 1950;2(5):149–54. [Google Scholar]

5. Lighthill J. Waves and hydrodynamic loading. In: Proceedings of the Second International Conference on the Behaviour of Offshore Structures, 1979; London, UK. p. 1–40. [Google Scholar]

6. Moberg G. Wave forces on a vertical slender cylinder; 1988. London. Available from: https://www.proquest.com/docview/2395197306?pq-origsite=wos&accountid=28172&sourcetype=Dissertations%20&%20Theses. [Accessed 2023]. [Google Scholar]

7. Deng Y, Tian X, Li X. Study on nonlinear characteristics of freak-wave forces with different wave steepness. China Ocean Eng. 2019;33(5):608–17. [Google Scholar]

8. Shiravani G, Sadeghi K. Diffraction of water waves with arrays of vertical cylinders. Tehran: ICOPMAS; 2008. [Google Scholar]

9. Bonakdar L, Oumeraci H, Etemad-Shahidi A. Wave load formulae for prediction of wave-induced forces on a slender pile within pile groups. Coastal Eng. 2015;102:49–68. [Google Scholar]

10. MacCamy R, Fuchs R. Wave forces on piles: a diffraction theory. U.S. Army Corps of Engineers Beach Erosion Board, Technical Memorandum No. 69, Washington DC, USA; 1954. Available from: https://www.semanticscholar.org/paper/Wave-forces-on-piles%3A-a-diffraction-theory-Ahmy-Cupy/cc2be94af8d14f2646c54946e5d797fce3a88c36. [Accessed 2023]. [Google Scholar]

11. Chakrabarti SK, Tam WA. Gross and wave load on a large vertical cylinder—theory and experiment. In: Proceedings of Offshore Technology Conference, 1973; Dallas, USA. [Google Scholar]

12. Neelamani S, Sundar V, Vendhan CP. Dynamic pressure distribution on a cylinder due to wave diffraction. Ocean Eng. 1989;16(4):343–53. [Google Scholar]

13. Sundar V, Neelamani S, Vendhan CP. Diffracted wave field and dynamic pressures around a vertical cylinder. Ocean Eng. 1990;17(1–2):125–54. [Google Scholar]

14. Iuppa C, Carlo L, Foti E, Faraci C. Calibration of CFD numerical model for the analysis of a combined caisson. Water. 2021;13(20):2862. [Google Scholar]

15. Serinaldi F, Cuomo G. Characterizing impulsive wave-in-deck loads on coastal bridges by probabilistic models of impact maxima and rise times. Coast Eng. 2011;58:908–26. [Google Scholar]

16. Seiffert B, Hayatdavoodi M, Ertekin RC. Experiments and computations of solitary-wave forces on a coastal-bridge deck. Part I: flat plate. Coast Eng. 2014;88:194–209. [Google Scholar]

17. Miles J, Martin T, Goddard L. Current and wave effects around windfarm monopile foundations. Coastal Eng. 2017;121:167–78. [Google Scholar]

18. Xu B, Wei K, Qin S, Hong J. Experimental study of wave loads on elevated pile cap of pile group foundation for sea-crossing bridges. Ocean Eng. 2020;197:106896. [Google Scholar]

19. Jeong YJ, Park MS, Kim J, Song SH. Wave force characteristics of large-sized offshore wind support structures to sea levels and wave conditions. Appl Sci. 2019;9(9):1855. [Google Scholar]

20. Kang A, Zhu B, Lin P, Ju J, Zhang D. Experimental and numerical study of wave-current interactions with a dumbbell-shaped bridge cofferdam. Ocean Eng. 2020;210:107433. [Google Scholar]

21. Wei C, Zhou D, Ou J. Experimental study of the hydrodynamic responses of a bridge tower to waves and wave currents. J Waterw Port Coast. 2017;143(3):4017002. [Google Scholar]

22. Wei C, Zhou D, Ou J. Wave and wave-current actions on a bridge tower: an experimental study. Adv Struct Eng. 2019;22(6):1467–78. [Google Scholar]

23. Mei D, Liu QJ, Hu Y, Wang D. Study of calculation methods and composite coefficient of wave-current forces for sea-crossing bridge pile caps and implementation. World Bridges. 2017;45:51–5 (In Chinese). [Google Scholar]

24. Pan JN, Wang DT, Wang XG, Nie F. Wave-current force on bridge foundation. In: Proceedings of the 7th International Conference on Asian and Pacific Coasts, 2013; Makassar, Indonesia: Hasanuddin University Press. p. 549–54. [Google Scholar]

25. Chakrabarti SK, Tam WA. Interaction of waves with large vertical cylinder. J. Ship Res. 1975;19:23–33. [Google Scholar]

26. Deng L, Yang W, Li Q, Li A. CFD investigation of the cap effects on wave loads on piles for the pile-cap foundation. Ocean Eng. 2019;183:249–61. [Google Scholar]

27. Chen L, Zhou J, Wang X, Wang Z. Nonlinear wave loads on high-rise pile cap structures in the Donghai bridge wind farm. Int J Offshore Polar. 2018;28(3):263–71. [Google Scholar]

28. Liu M, Liu H, Ma J, Ge L, Chen H. Experimental study of the wave load on the main pier of Huangmaohai bridge under wave-current coupling effect. IOP Conf Ser Earth Environ Sci. 2021;621(1):012155. [Google Scholar]

29. Liu H, Wang B, Xue L, He Y. Recent progress in wave-current loads on foundation structure with piles and cap. Appl Math Mech. 2013;37:1098–1109. [Google Scholar]

30. Wei K, Qin S, Zhao W, Zhu B, Xu G. State-of-the-art review of bridge hydrodynamics in 2020. J Civ Environ Eng. 2021;43:31–42 (In Chinese). [Google Scholar]

31. Zdravkovich MM. Flow around circular cylinders: volume 2: applications. London, UK: Oxford University Press; 1997. [Google Scholar]

32. Liu L. Research on computing method of wave-current force on sea-crossing bridge substructures (Ph.D. Dissertation). Southwest Jiaotong University: China; 2017. [Google Scholar]

33. Griffith MD, Leontini J, Thompson MC, Hourigan K. Vortex shedding and three-dimensional behaviour of flow past a cylinder confined in a channel. J Fluid Struct. 2011;27(5):855–60. [Google Scholar]

34. Yang H, Yang W, Li Q, Kou J. Experimental investigation of current forces on floating cylinder during the sinking process. Ocean Eng. 2019;178:134–44. [Google Scholar]

35. Al Mashan N, Neelamani S, Al-Houti D. Experimental investigations on wave impact pressures under the deck and global wave forces and moments on offshore jacket platform for partial and full green water conditions. Ocean Eng. 2021;234:109324. [Google Scholar]

36. Li YC, Teng B. Wave action on maritime structures. China: China Ocean Press; 2015. p. 127–167 (In Chinese). [Google Scholar]