Oscillatory Dynamics of a Spherical Solid in a Liquid in an Axisymmetric Variable Cross Section Channel

Nomenclature

1  Introduction

In the field of developing and studying energy-efficient technologies, there is a need to develop new methods for enhancing mass exchange processes between different types of phase inclusions and their environment. The study of flows excited by fluid oscillations in channels of variable cross section or wavy (sinusoidal) profile is relevant for controlling heat and mass transfer in porous media [1–4]. A variable cross section channel, also known as a variable shape channel, is a hydraulic system designed to efficiently transport liquid, gas or other media. The main characteristic of this type of channel is the gradual variation of its cross section along its length. This allows optimum flow conditions to be achieved, including control of velocity, pressure and other hydrodynamic parameters. This design improves the efficiency of liquid or gas transport. The internal flows become more laminar and flow resistance is reduced by gradually changing the shape of the channel. In addition, the variable cross section channel has a wide range of applications. It can be used in various industries, including power generation, chemical, oil and gas, and hydraulic engineering. Due to its flexibility and adaptability, such a system can be successfully applied to solve a wide range of engineering problems.

The problem of bubble or agglomeration float-up in vertical straight columns is a common issue. Recent studies [5,6] have analyzed typical flow regimes in bubble columns. However, research has shown that channels with a curved shape are more effective in improving inclusion dynamics. The dynamics of homogeneous and heterogeneous hydrodynamic systems in flat and axisymmetric channels of variable cross section are widely studied. The object of study is often either a liquid flow or a gas phase inclusion in the liquid. The papers [7–10] examine the dynamics of gas phase inclusions in channels with varying cross-sections, both theoretically and experimentally. It is demonstrated that the shape of the channel significantly impacts the oscillations of the phase inclusion boundary, suggesting the potential for efficient mass transfer. Papers [11–14] provide a comprehensive literature review and detailed analysis of the method of intensifying fluid mixing processes through pulsations and vibrations in the presence of constant non-zero flow in the channel. The works described focus on the dynamics of hydrodynamic systems in channels with a fixed profile. However, it is worth noting that there are works that consider channels with a changing profile over time. Peristaltic pumping refers to the movement of fluid, particles or suspension in a tube caused by waves of contraction in the channel’s wall. These systems are of significant interest due to their practical applications in physiological and technological processes. The papers [15–17] examine the dynamics of solid particles in such a system and how the transport of the solid particle depends upon its diameter, frequency of peristaltic waves on the walls, Reynolds number and its initial placement in the channel. The intensification of mass transfer processes in channels with peristaltic wall dynamics and in models of porous media is a widely studied topic [18,19]. However, there is a lack of experimental consideration of the dynamics of inclusions, both deformable (liquid) and solid boundary, in oscillating fluid flow in channels of variable cross section. The literature lacks sufficient representation of theoretical and experimental studies on the dynamics of phase inclusions in an oscillating fluid flow with zero mean flow rate.

There are several methods for the generation of intense averaged flows. For example, intense fluid oscillations can be generated by rotational oscillations of the cavity [20] or by oscillations of the elastic cavity walls [21]. In both cases, fluid oscillations lead to averaged flows that can significantly intensify mass transfer in the system. In the region of medium and low frequencies, the generation of averaged flows is found, the intensity of which decreases with decreasing dimensionless vibration frequency. It is shown that at high dimensionless frequencies the experimental results are in agreement with theoretical estimates. In [22], the flow in a two-dimensional symmetric channel with wavy walls is studied experimentally with periodic variation of the fluid pumping as a function of the dimensionless frequency. It is found that the fluid oscillations lead to the excitation of the stationary flow in the form of a system of transverse waves. It is shown that, in the low-frequency limit (for viscous fluid fluctuations), they can be used to describe steady-state flows (and hence mass transfer phenomena) excited by fluid fluctuations in porous media, which are a system of interconnected pores–channels of different cross section. This modelling approach is fully applicable to axisymmetric channels with periodically varying radius. A channel of variable cross section is a system of interconnected pores that represent the gaps between the substance forming the ‘skeleton’ of the porous medium [23,24]. In the given formulation and geometry, Darcy’s law is applicable. The results of previous studies [25] have shown that the structures and intensity of averaged flows in an axisymmetric channel of variable cross section under oscillating fluid flow in the channel excite the averaged flow in the form of a system of toroidal vortex flows. The direction of the flows and their flow rate are determined by the pulsating Reynolds number and the dimensionless frequency. These dimensionless complexes are determined by the values of the characteristic amplitudes of the fluid vibrations, the kinematic viscosity of the fluid and the cavity size.

In the present work, the problem of the dynamics of a spherical body in an oscillating fluid flow in a channel of variable cross section, depending on the amplitude and frequency of the oscillations of the fluid column, is considered experimentally. The oscillating motion of the liquid column has an effect on a heavy body moving freely in a vertical channel. The forces acting on a body immersed in a fluid, along with the averaged vibrational forces and flows, combine to produce various effects. This study considers a spherical body as a model of a particle that can oscillate in a fluid, and a channel of variable cross section as a model of a porous medium. The practical applicability of this study is in the field of vibratory hydromechanics, heat and mass transfer, phase transitions, and transfer processes, as well as in the development and design of equipment for these processes.

2  Experimental Setup and Methodology

The experimental setup (Fig. 1) is a closed hydraulic circuit, which includes a system of periodic pumping of liquid and an experimental cuvette with technological units. Experimental cuvette 1 is a plexiglas parallelepiped with a length of L=225 mm and a square cross section of 40×40 mm2. The cuvette is made of two symmetrical halves in which grooves of variable depth are milled along the long side. The channel’s cross-section shape is described by the following expression R=10.6+4.4cos⁡(0.15x) mm. High precision of manufacturing on a numerically controlled machine while assembling the two halves with bolts allows to organize an axisymmetric channel of variable cross section. The radial dimensions of the narrow and wide sections of the channel are R1=6.2 mm and R2=15.0 mm, respectively. Along the length of the channel there are 5 symmetrical segments with spatial period λ=42.0 mm. Fig. 1 shows a natural view of the part of the channel with the body (in the red frame) and an indication of the direction of the gravity field vector and the y -coordinate system. The experimental study involves studying the motion of the phase inclusion in a vertical channel during fluid oscillations. Thus, systems are needed to ensure the insertion, launching and collecting of the phase inclusion. The insertion and launching unit 2 consists of a metal branch at 45°, a ball valve and a plexiglas cube with a cylindrical channel, in the middle part of which a rotating ring with a mesh is placed. The valve allows an inclusion to be inserted into the channel and provides tightness. The configuration of the cube with a mesh overlapping the channel allows the body to be held in front of the channel and the oscillating flow rate of the liquid to be adjusted. When the required frequency and amplitude of fluid oscillation is set, the ring with the mesh is rotated and the spherical body begins to move, entering the variable cross section channel. As the body passes through the channel, it is collected at the bottom of the cuvette by the collection unit 3. In the angled deflection channel, a mesh cylinder is installed across the fluid flow, deflecting the spherical body away from the channel. The collection unit eliminates the possibility of system and liquid flow blockage. Spherical bodies accumulate in the outlet and it is possible to carry out a number of experiments without disassembly of the setup. The cuvette complete with assemblies is connected to pump 4 by means of hydraulic circuit 5.

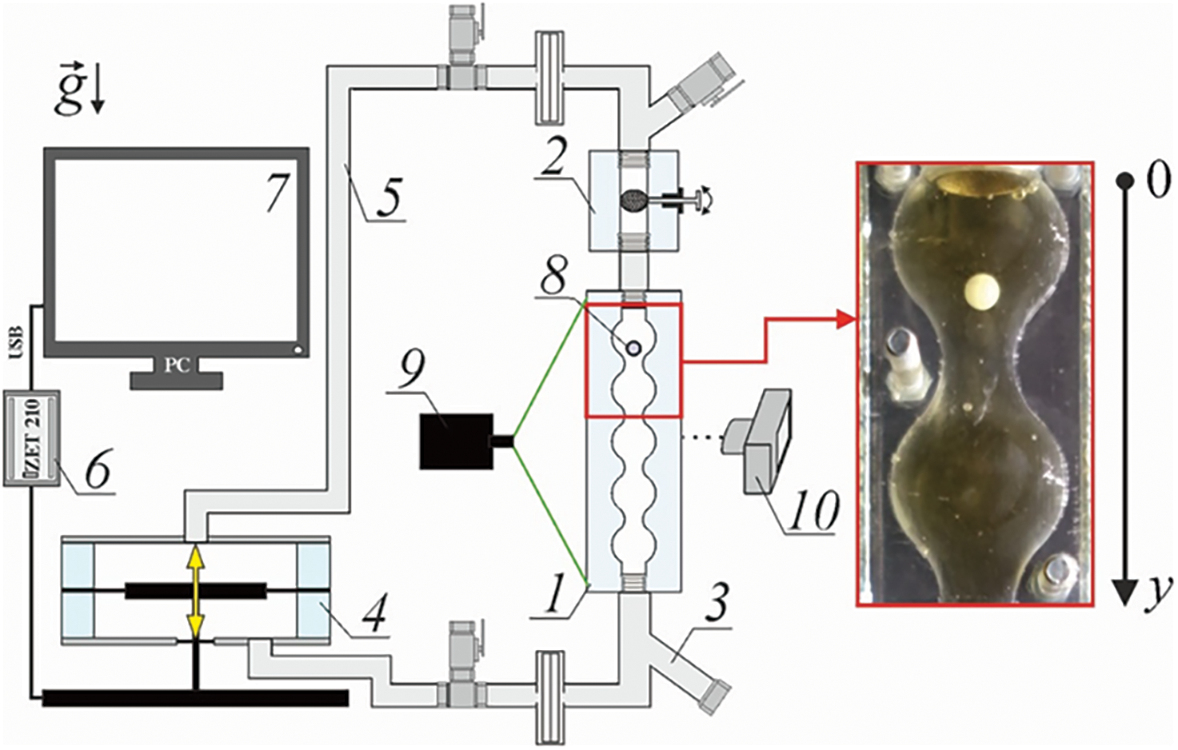
Figure 1: Scheme of the experimental setup (side view)

Pump 4 consists of two independent, immiscible circuits separated by an elastic membrane. Vibrations transmitted to the membrane by the vibration stand cause oscillations of the fluid in the hydraulic circuit 5. The pump based on the “push-pull” principle provides a harmonic change in the volume of liquid pumped in the closed hydraulic circuit according to the law Q∼cos⁡Ωvibt , where Ωvib=2πfvib . The electrodynamic vibration stand is controlled by the Zet 210 digital generator 6 via a personal computer 7. A detailed description of the working principle and design of the hydraulic pump is given in [26]. The oscillation frequency fvib is set by the generator and can be varied in the range of 4−10 Hz. The volume of the oscillating liquid is adjusted by changing the amplitude of the oscillations of the electrodynamic vibration table, which is rigidly connected to the membrane. In the experiments, the amplitude b of the fluid oscillations is determined by measuring the oscillation range of the visualization particles suspended in the working fluid. In the study region of dimensionless frequencies, the flow in the channel is viscous. Measurements are made in a wide cross section of the working channel where the fluid oscillations are close to the piston oscillations. This means that the amplitude of fluid oscillations (flow rate) is constant in the wide part of the channel. During the oscillation of the fluid, the particles suspended in it make uniform oscillations relative to their average position. The amplitude of fluid oscillations is small compared to the inhomogeneity of the wall relief. The maximum amplitude of the fluid oscillations is measured at the channel axis.

The phase inclusion 8 is a solid ball made of polyoxymethylene (POM) with a diameter of dS=6.0,8.0mm and a density of ρS=1.380 g/cm3. Depending on the density of the working fluid relative to the density of the phase inclusion ρ=(ρS−ρL)/ρL , the latter can either ‘sink’ or ‘float’ in the channel. In the experiments, a water-glycerol solution with a density of ρL=1.295 g/cm3 and a viscosity of νL=27.3 cSt is used as the working fluid. The density of the working fluid can be varied by dissolving sodium iodide NaI in different mass concentrations. In the present work, the relative density is ρ=(ρS−ρL)/ρL=0.07 and the body sinks in the liquid. Spherical body was externally loaded (through a ball valve from insertion and launching unit 2) into the channel before each new experiment.

In the experiments investigates both the dynamics of phase inclusion and the structure of flows excited by fluid and body oscillations in a channel of variable cross section. Plastic tracer particles of average size dP=60 µm and an average density of ρP=1.040 g/cm3 are used to visualize the fluid motion in the channel. A 2 millimeter KLM-532/h-1000 continuous laser 9 is used to create a laser sheet in the plane of which the structure of the flow is investigated. The optical axis of the cameras 10 is always perpendicular to the flat outer edge of the axisymmetric channel. The construction of the cuvette and the close refractive index values of the plexiglas and the working fluid minimise optical distortion at the curved edge of the channel. Video registration of the particle tracer position is performed using the Optronis CamRecord CL600x2 high speed camera, which is fixed in the laboratory reference frame. Video registration of the phase inclusion position in the axisymmetric channel is performed using a Fujifilm X-E4 camera with a frame rate of 60 to 120 frames per second. The specialized software ImageJ was used for frame-by-frame processing of the experiments.

3  Experimental Results

The dynamics of a spherical phase inclusion in an axisymmetric vertical channel of variable cross section in the absence of vibrations consists in moving along the channel in the gravity field. Fig. 2 shows the y -coordinate variation of the center of mass of the spherical body with time. The axis is directed downwards along the direction of motion of the body (see in Fig. 1). The body sinks in the liquid, but because the profile of the channel is curved, a deviation of the points from the linear law can be observed. This is directly related to the shape of the channel and the size of the body. In the narrow part of the channel, the diametral dimension is around 12 mm and the diameters of the bodies are 6 and 8 mm. Thus, the relative size of the phase inclusion to the channel size appears to be significant and, approaching the narrowing of the channel, the body slows down slightly. The movement can be characterized as peristaltic. However, in general, the body moves uniformly in the liquid along the channel axis.

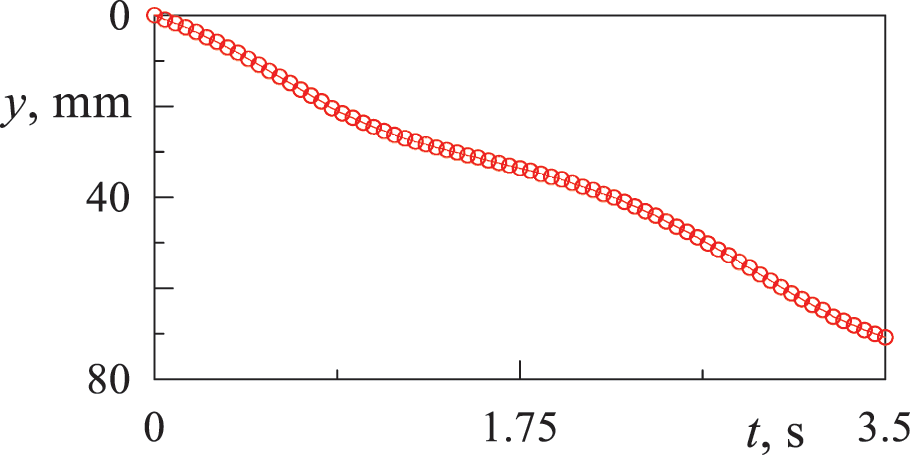
Figure 2: Time dependence of the y -coordinate of the center of phase inclusion dS=6 mm, while moving in the gravitational field without vibrations

When the fluid in the channel oscillates at a given frequency, the dynamics of the body depends on several physical phenomena: the generated fluid flow and the thickness of the Stokes boundary layer. The velocity of the fluid flows is significant because of the large amplitude of the oscillations. The viscous boundary layer δ=2νL/2νLΩΩvib (where Ωvib=2πfvib is the radian frequency of fluid oscillation) is a region of viscous fluid flow of small transverse thickness formed directly at the curved channel wall. The interaction of a body with a viscous boundary layer largely determines the dynamics of the body. For oscillations with a frequency of fvib=4−10 Hz, the thickness of the Stokes boundary layer δ is nearly 1.5−0.9 mm. The dynamics of the body is due to the action of gravity and averaged vibration forces on it. Since the density of the body is greater than the density of the fluid and it is sinking, the body moves along the axis of the channel at a certain average speed as the fluid in the channel oscillates. However, as the amplitude of the fluid oscillations increased at a fixed frequency, an interesting effect was found: the effect of phase inclusion held by the oscillating flow in a variable cross section channel is observed at certain threshold amplitude b of the fluid oscillations.

The body-holding effect is observed after a sufficient liquid velocity (amplitude of oscillation) is reached when the liquid oscillates in the variable cross section channel. In this case, the spherical phase inclusion “hangs” near the constriction of the channel (Fig. 3). The spherical body is held by the oscillating fluid flow and oscillates relative to its mean position (Fig. 3a) with the frequency of the oscillations of the fluid column. The thickness of the layer, as was mentioned early, is significant, and when the body is near the narrowing of the channel, this contributes to the observed body-holding effect and prevents the body from passing into the next pore of the channel. In Fig. 3b the values obtained in the experiment are marked: the reference point of the inclusion position, the coordinate y0 , relative to which the observed oscillations are registered; the coordinates of the extreme upper y1 and lower y2 positions of the center of mass of the spherical body. It can be assumed that the oscillations of the liquid column in the channel generate an averaged lifting force acting on the body, which occupies a quasi-stationary position in one of the cells of the vertical channel.

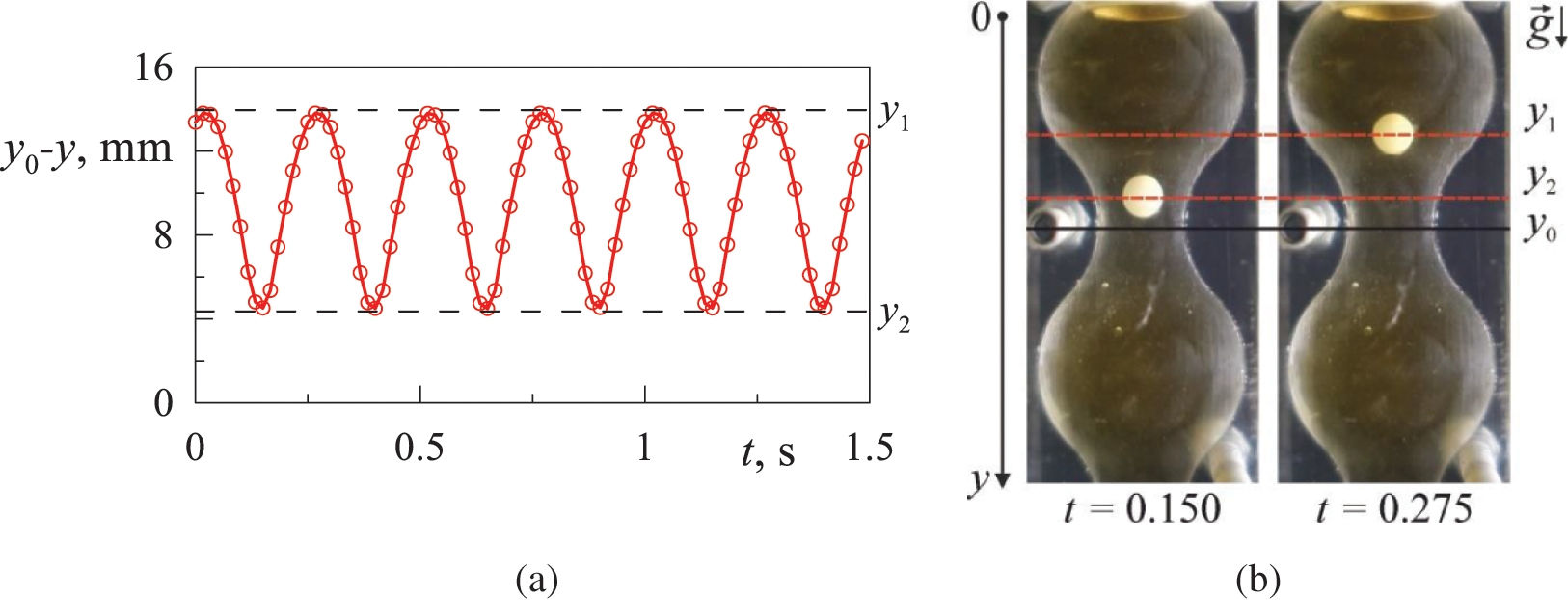
Figure 3: Oscillatory dynamics of a phase inclusion dS=6 mm: dependence of the y -coordinate of the position of the phase inclusion center on time (a) and photos of the relative position (b) for fluid oscillations with a frequency of fvib=4 Hz and an amplitude of b=2.10 mm

Fig. 4a shows the dependence of the y -coordinate of the center of mass of a solid spherical body on its mean position with respect to the zero coordinate (see Fig. 3b) with vibration frequency. The suspended state of the body, i.e., above the threshold of the occurrence of the effect, is being considered. The graph shows the coordinate points of the extreme positions of the center of the spherical body as the amplitude of the fluid oscillations b increases.

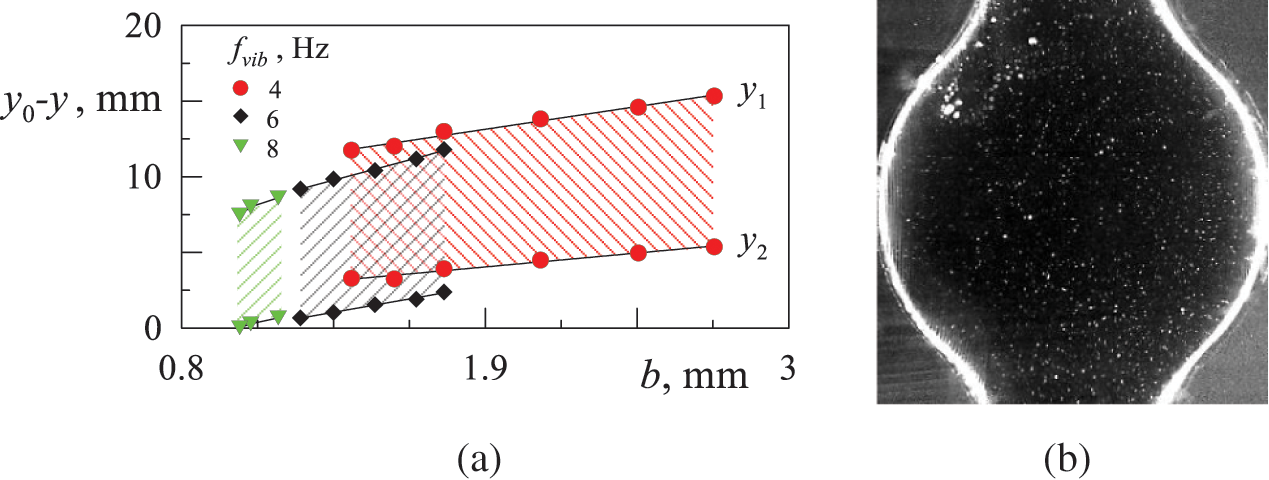
Figure 4: Dependence of the y-coordinate of the centre of mass of a solid spherical body dS = 6 mm on its mean position with respect to the zero coordinate y0 (a) with vibration frequency. Photograph of a channel segment with visualizer particles suspended in the fluid (b)

The amplitude of the oscillations of the fluid at a given frequency is determined by the spread of the visualizer particles suspended in the fluid in the wide part of the channel (Fig. 4b). The visualizer particles are visible in the plane of the laser sheet cutting the channel along its axis. From the graph it is possible to determine the amplitude of the body oscillation, the dependence of the coordinate of the average position of the body on fvib and b . As the frequency of fluid oscillation increases, the amplitude of both fluid and body oscillation decreases. In this case, the body is oscillating at the frequency of the liquid column. As the amplitude of the fluid oscillation increases, the amplitude of the body oscillation proportionally increases. As the amplitude b of the liquid oscillations decreases at a fixed fvib , the “floating” body approaches the region of maximum channel narrowing y0 . Upon reaching region y0 and oscillating relative to the reference point, the body is carried by the fluid flow to the next segment and moves down the channel.

The amplitude of a body’s oscillations relative to its mean position characterizes its dynamics. With a gradual increase in the amplitude of the fluid oscillations b , the amplitude of the body oscillations, defined as AS=(y1−y2)/(y1−y2)22 , increases (Fig. 5). The graph shows the experimental results for the body’s quasi-equilibrium suspension during its oscillations. For the given system and frequency range, it is possible to maintain the body in a quasi-stationary suspended state once the threshold amplitude b is reached. As the vibration amplitude of the fluid column decreases, the body’s own density, which are greater than those of the fluid, cause the body to approach the narrow part of the channel, at which point it can no longer be held by the flows and the averaged vibration force. For different fvib and dS one can see the uniform dynamics of the change in amplitude of the body vibration with increasing of b . The amplitude of the body’s response to the fluid vibrations is determined by the curvature and shape of the channel. This in turn is determined by the difference in the amplitude of the fluid vibrations between the wide and narrow parts of the channel. An interesting effect found in the experiments is the possibility of controlling the relative position of the phase inclusion. By gradually reducing the amplitude of the fluid oscillations (flow rate), it is possible to move the phase inclusion to any of the following channel cells. After reaching the required relative position along the channel, by successively increasing the amplitude of the fluid oscillation, it is possible to achieve the effect of holding the oscillating phase inclusion in a particular part of the channel with a variable cross section.

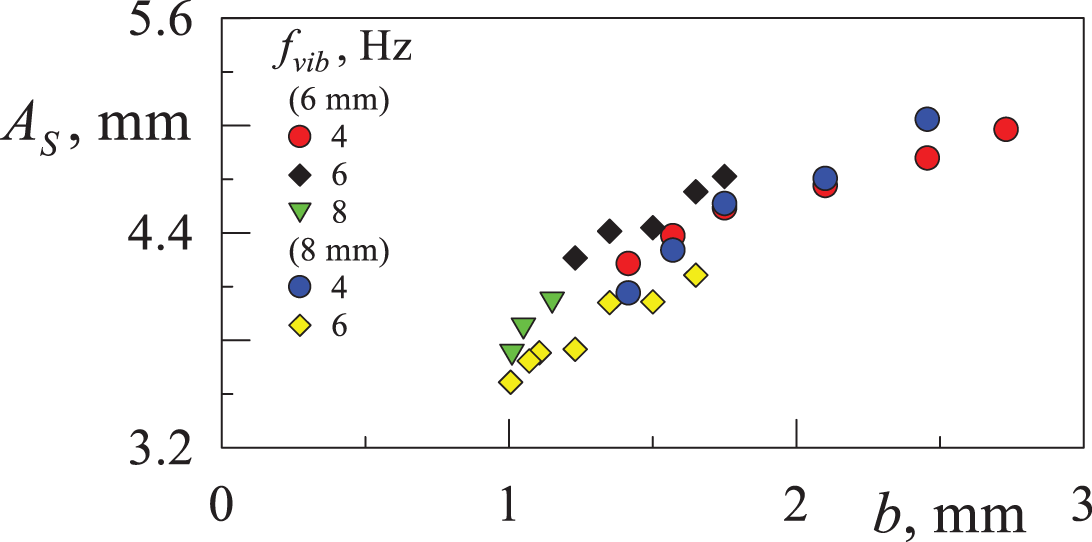
Figure 5: Dependence of the amplitude of the phase inclusion oscillation on the amplitude of the fluid oscillation at different frequencies of the fluid column oscillation

The threshold effect of holding a heavy phase inclusion relative to the oscillations of the working fluid is observed. The threshold value of the amplitude of body oscillations is defined as the mean value of the amplitude of the body when the effect of holding occurs and the amplitude of the body at the moment of collapse of the quasi-equilibrium state. The amplitude of body oscillations at the threshold of the ‘suspended’ state effect, against the background of its oscillations, depends on the frequency fvib and size dS of the body. Fig. 6 shows that as the frequency increases, the holdup is observed at a smaller amplitude of the body oscillations, which is directly related to the amplitude of the fluid oscillations. A similar dependence can be observed for bodies of different sizes. However, for a larger body, oscillating at the same frequency, the amplitude of oscillations is smaller when the holding effect occurs.

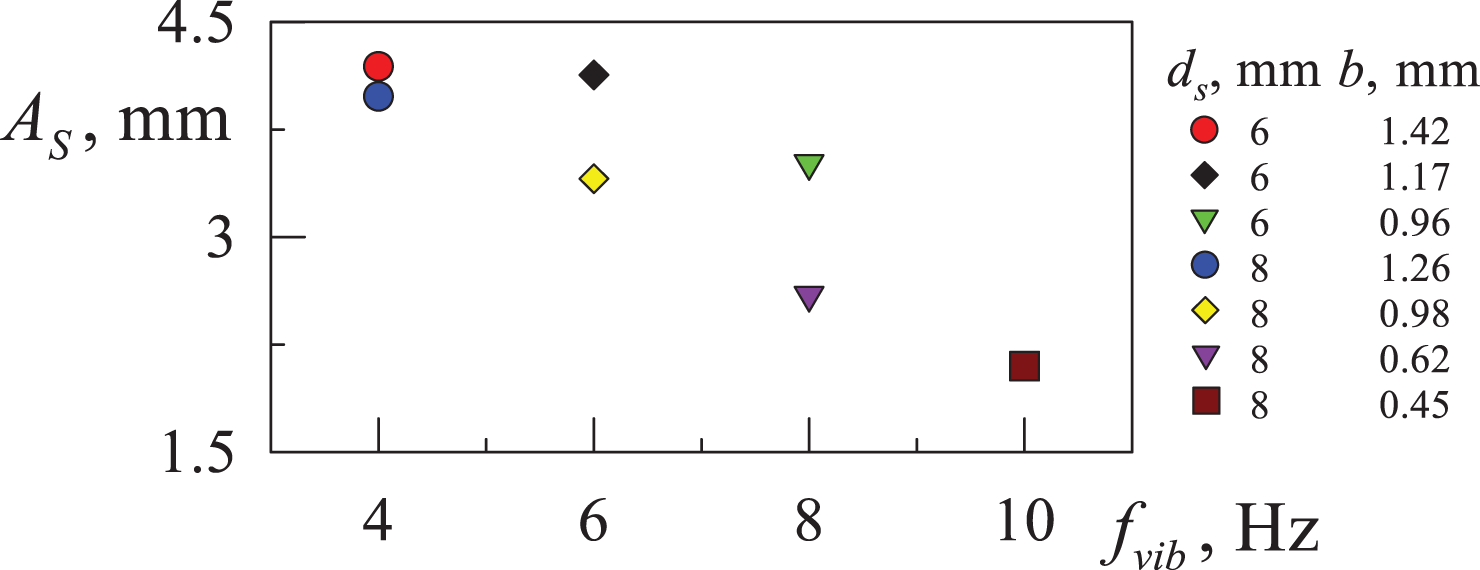
Figure 6: Dependence of the threshold value of the amplitude of body oscillations on the fvib

Periodic changes in the flow rate of the fluid pumped through the channel result in the generation of average flows in each of the channel cells. The earlier experimental study of averaged flows excited by fluid oscillations in an axisymmetric channel whose cross section varies periodically with the longitudinal coordinate [25] has shown that the parameter determining the structure and intensity of the averaged flows is a dimensionless frequency ω . The dimensionless frequency ω=ΩvibR12/ΩvibR12νLνL is determined by the ratio of the characteristic size of the channel (in a narrow part, where δ is significant) to the viscous Stokes boundary layer δ near the wall. In order to determine whether the position of the channel (vertical) and the presence of phase inclusion change the dynamics, the structure of the fluid flows was determined qualitatively. The position of the visualizer particles was video recorded by cutting the channel along its axis with the plane of the laser sheet. The structure of the flows generated by the oscillation of the liquid column was obtained by superimposing the frames of the video recording taken after one period. The visualizer particles, which move over a period of time, leave traces. In the above photographs of the channel with and without a body (Figs. 7a and 7b) obtained in the experiments, the averaged fluid motion along the channel axis is directed from a narrow region of segments to a wide one. The flow structure observed in Fig. 7c for the dimensionless frequency (equal to ω=35−88 in this study) is qualitatively consistent with the findings of a previous study [25].

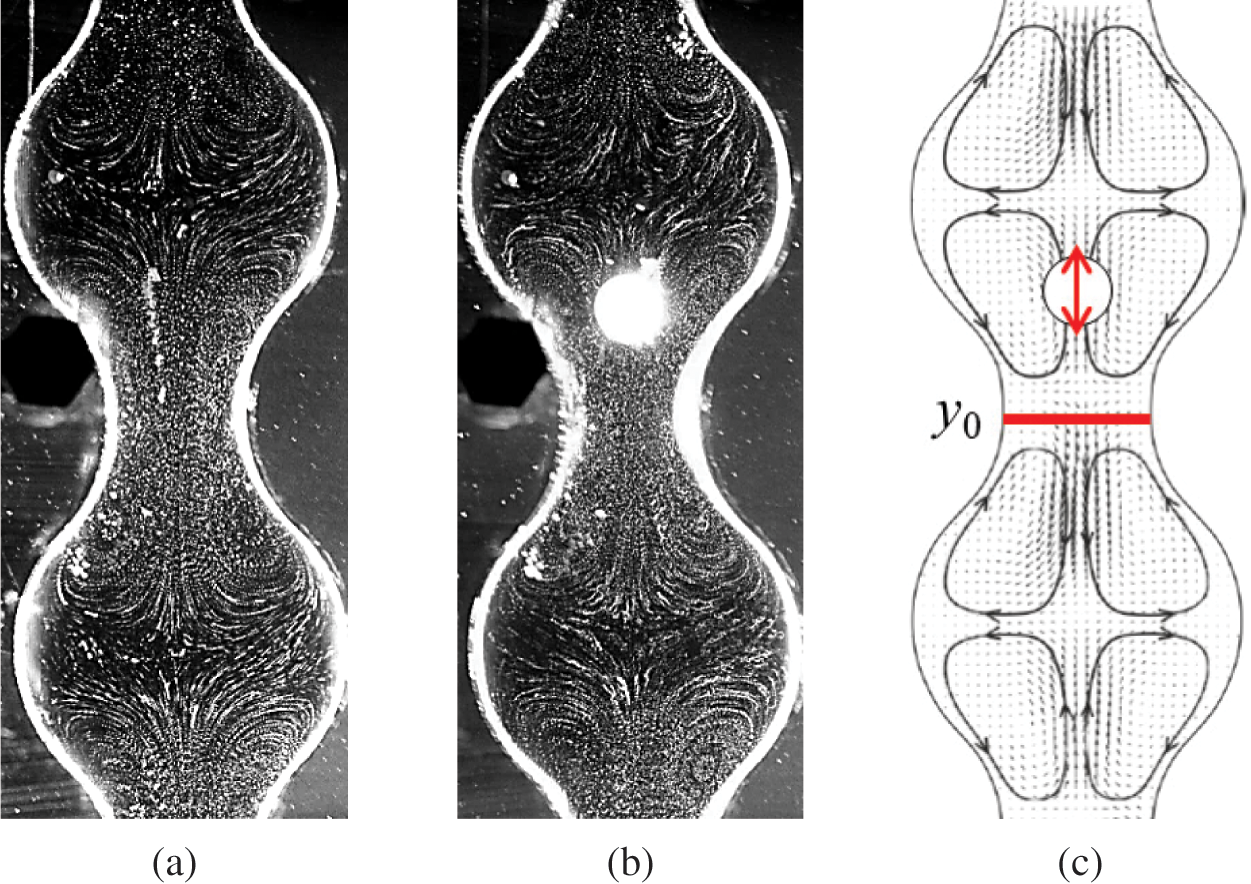
Figure 7: Qualitative representation of the characteristic structure of averaged flows in a circular vertical channel with a periodically changing cross section during oscillations of a liquid column without a body (a) and with a body dS=6 mm (b) at fvib=6 Hz and b=1.35 mm. Schematic representation of the characteristic structure of the averaged flows and the relative position of the body (c) during oscillations of the liquid column

4  Discussion

When considering the motion of the body during one oscillation period, it is observed that the body must return to its initial position as soon as it is displaced upwards by the fluid flow from the narrowing region of the channel. This ensures that the amplitude of its oscillations remains constant (refer to Fig. 3a). Any deviation from this quasi-stationary position may cause the body to slip further along the channel. When a body oscillates while suspended, its dynamics are determined by the forces acting on it. Similarly, when a body moves in a fluid under the influence of gravity, its dynamics are determined by the combined action of gravity, Archimedes’ principle, and Stokes’ law. The distance travelled by the body is proportional to half of the period of oscillation and the velocity of the body in the fluid, and it equals to 2AS . The velocity can be determined by balancing the forces acting on the body (from Stokes’ law). The parameter responsible for the threshold effect of holding the body was determined as ASΩvib2/ASΩvib2gg –the ratio of the average vibrational acceleration of a body to the acceleration of gravity. This definition characterizes and determines the intensity of the averaged vibrational force relative to the force of gravity. Fig. 8 shows the relationship between the dimensionless parameter and dimensionless frequency, according to the parameters in Fig. 6. It can be seen that the threshold for holding the phase inclusion on the plane of the dimensionless parameter is dependent on the dimensionless frequency. For different frequencies of fluid vibration and body sizes, a qualitative agreement of the ASΩvib2/ASΩvib2gg∼ω dependence can be observed. As the dimensionless frequency rises, so does the value of the parameter ASΩvib2/ASΩvib2gg required to hold-up an inclusion.

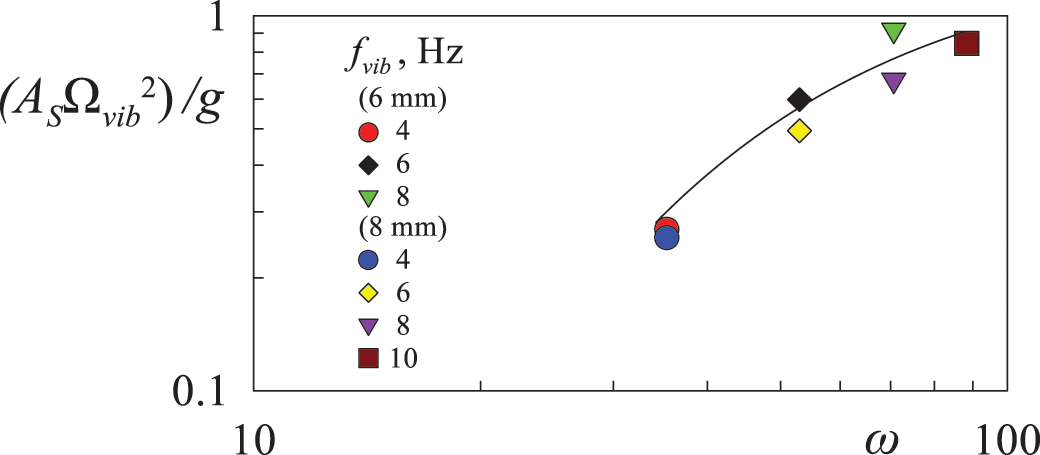
Figure 8: The dimensionless threshold value of body oscillation amplitude dependence on dimensionless frequency

In this study, the characteristics of fluid and body oscillations are considered. Fluid oscillations are detected by the oscillations of particles suspended in the fluid. Let us analyze oscillations of the dS=6 mm body and visualizer particles in the fluid near the channel axis at fvib=6 Hz and b=1.23 mm. To accurately determine the phase of body and fluid oscillations, high-speed video recording at a frequency of 600 frames per second (100 frames per period) is carried out. By measuring the y -coordinates of the visualizer particle, located near the channel axis, and the center of mass of the phase inclusion, the dependence y−y¯ on t is obtained (Fig. 9a). In this case, y¯ is the coordinate of the mean position of the particle or body, respectively. By determining the value of y−y¯ it is possible to observe how the phases of oscillations are related. The body and fluid oscillate at a given frequency. Closer examination of the one full period of oscillations at phase diagram of the y -coordinates of the center mass of the body yS and the visualizer particles yP reveals that the fluid and the body are oscillating out of phase (Fig. 9b). The curved profile of the channel causes the instantaneous velocity along the channel axis to be non-uniform. In the narrow part of the channel, the fluid displacement velocity exceeds the velocity in the wide part. The combined effect of the channel shape and the relative position of the body at different times results in different dynamics. For example, if the body is close to the narrow part of the channel and is moving downwards, the fluid starts to move upwards at high velocity and “splashes” the body back from the narrowing. The body is carried upwards by the flow and when the body reaches the widening of the channel, the fluid velocity decreases. At the extreme upper point of the body’s relative position, on the reverse course of the fluid, the heavy body begins to sink and is entrained by a relatively weak downward flow, and the cycle repeats. A significant difference in flow rate in the narrow and wide parts and the presence of a phase difference in the oscillations produce the observed body-holding effect. As soon as the flow rate differs slightly in different parts of the oscillation period, when the body approaches the narrowing, and the center of mass of the body is close to zero (see Fig. 4), the body moves to the next segment of the channel.

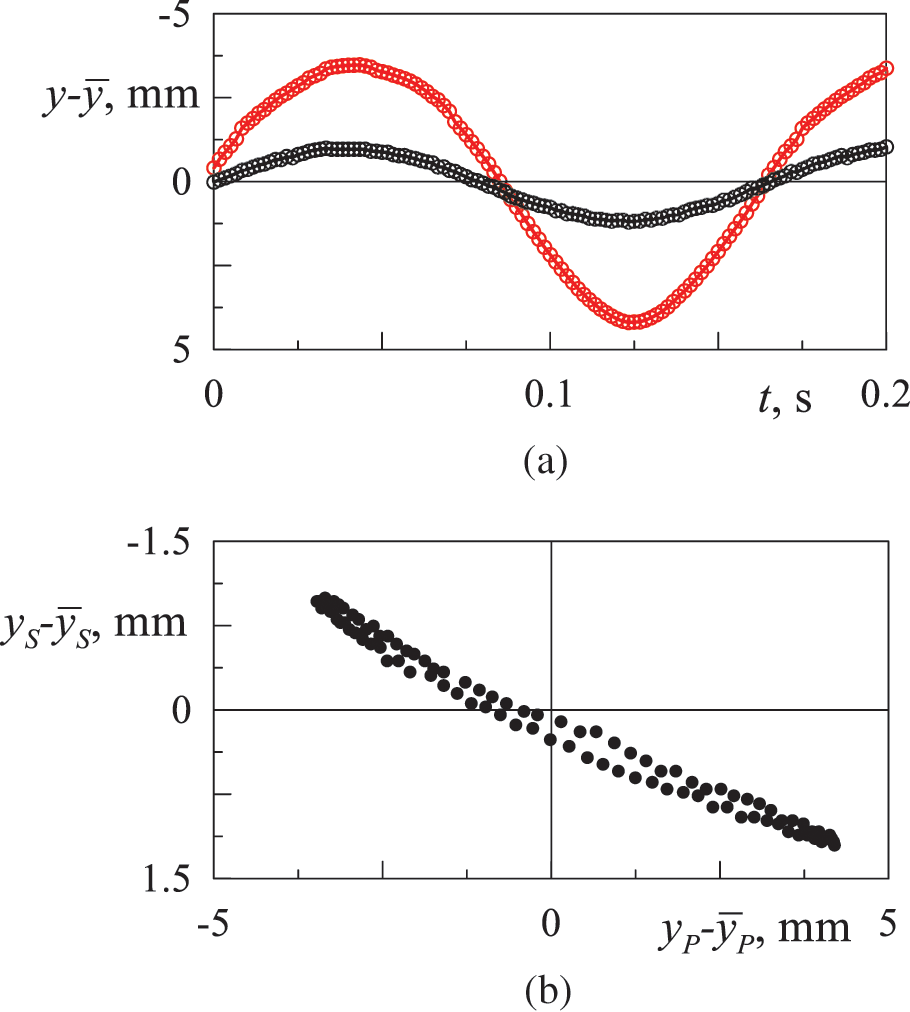
Figure 9: Time dependence of the y-coordinates of the particle visualizer (black dots) and the center of mass (red dots) of the phase inclusion (a) during oscillations of the liquid column and the phase diagram of one full period of oscillations (b) of the body and liquid

The characteristic structure of the averaged flow excited by the oscillations of the fluid is studied in a vertical channel with a variable cross section using the PIVLab programme [27]. The PIV method consists in processing pairs of frames, like in Fig. 10a at fvib=6 Hz and b=1.23 mm, the time interval between which is a multiple of the fluid oscillation period. The experiment records the dynamics of visualizer particles in the plane of the laser sheet near the axis of the variable cross section channel. For each oscillation period, there is a slight shift in the particles, and by processing a series of such photographs, an average picture of the fluid flow is obtained. Thus, the processing result is the period-averaged vorticity field close to the axis (Fig. 10b). Periodic pumping of fluid leads to the appearance of steady flow in each cell of the channel. In the considered area of dimensionless frequencies ω=35−88 the oscillating flow of fluid in the entire volume of the channel is viscous. At this, the steady flow has the form of a system of coordinately rotating rolls elongated transversally to the direction of oscillation. The flow in each cell consists of two axisymmetric toroidal vortices rotating in opposite directions. This structure is characteristic of all experimental parameters in the present study. The presence of a spherical body in the channel slightly distorts the vortex structure, but the structure and intensity are identical in the channel segments with and without the body.

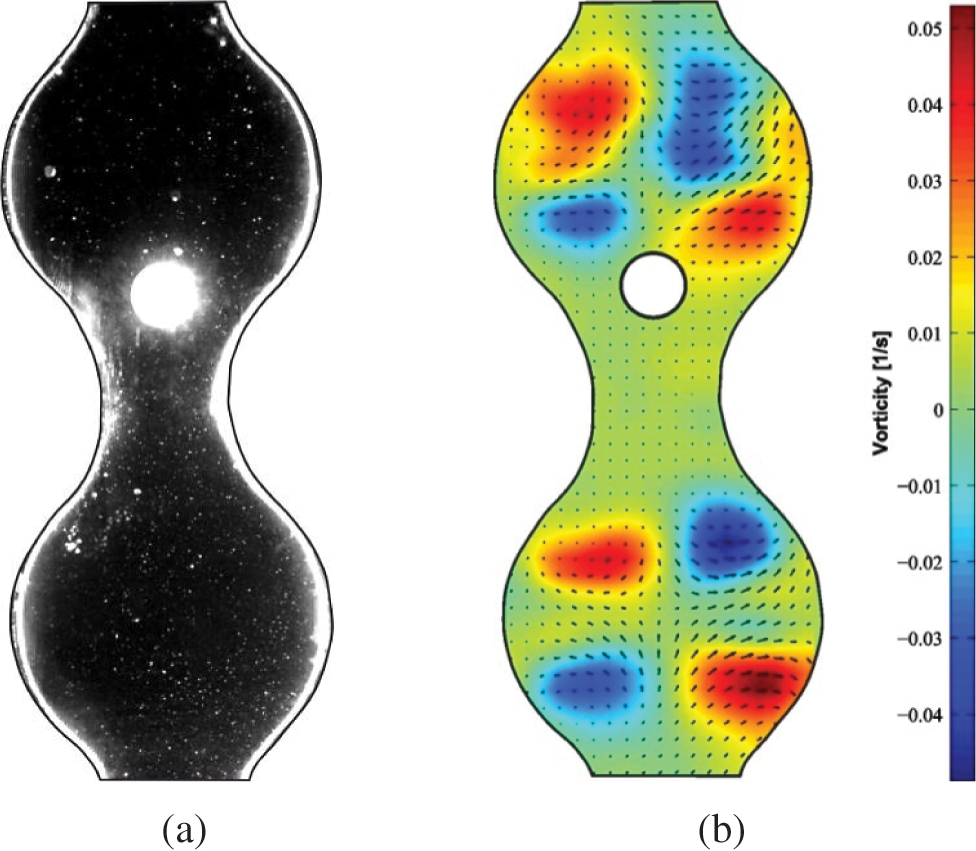
Figure 10: An example of a processed image obtained by high-speed recording (a) and the characteristic period-averaged vorticity field (b) in the plane of the laser sheet in the vicinity of the axis of the channel

The direction of rotation of the rolls is such that the fluid moves along the axis of the cavity from the narrow section of the channel to the wide section. The averaged flows have an impact on the body dynamics, but they are not the sole determining factor. Thus, the averaged flows contribute to the maintenance of the quasi-stationary position of the spherical body during the oscillations of the liquid column in a channel of variable cross section.

It can be noted that the detected vibration effect is caused by the coincidence of the frequencies and motion law ( ∼cos⁡Ωvibt ) of the body and the fluid. During the downward movement of the fluid, the body moves towards the narrowing of the channel. At the moment of upward movement of the fluid, due to the large difference in the flow rate of the fluid, it “splashes” back. In simpler terms, the body’s sinking velocity due to gravity must be balanced with the average vibration effect of the oscillating fluid flow (flow rate). It is important to note that the amplitude of body oscillations is equal to the curvature of a channel of variable cross section. The novel vibrational effect observed in the experimental study requires further careful investigation depending on the relative size of the body to the channel width, the relative density and the viscosity of the fluid. The study of phase inclusion dynamics in a wide range of dimensionless frequencies can serve as an effective tool for controlling the phase inclusion position (both light and heavy) in a variety of technological applications, particularly in mass transfer processes.

5  Conclusion

The dynamics of a spherical solid body in an oscillating fluid flow in an axisymmetric channel of variable cross section has been studied experimentally. An experimental setup has been designed and constructed which allows the setting of a periodic fluid flow in a variable cross section channel with the simultaneous possibility of introducing a phase inclusion directly into the flow. The experimental methodology has been tested. A new vibration effect is found when increasing the amplitude of oscillations at a fixed frequency. The threshold effect of phase inclusion hold-up and its oscillation relative to the mean position at a given oscillation frequency is observed. The parameter determining the threshold for the occurrence of the effect of holding the body in a quasi-equilibrium state has been identified. Within the range of dimensionless frequencies considered, the structure of averaged flows in the presence of a body in a vertical channel during oscillations of a liquid column has been defined. The discovered effect could be used to develop effective methods for controlling mass transfer in heterogeneous hydrodynamic systems (such as the mass transfer process between the phase inclusion and the surrounding liquid saturated with dissolved extractant), and also to develop a method for vibrational control of phase inclusions in such a system.

Acknowledgement: The author thanks Prof. Kozlov V.G. for his interest in the task and fruitful discussions of the results and the team of the Laboratory of Vibrational Hydromechanics of PSHPU.

Funding Statement: This work was financially supported by the Russian Science Foundation (Grant No. 23-71-01103).

Author Contributions: All the work was done by Ivan Karpunin.

Availability of Data and Materials: All data are included in this published article.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Ye, Q., Zhang, Y., Wei, J. (2021). A comprehensive review of pulsating flow on heat transfer enhancement. Applied Thermal Engineering, 196(3), 117275. https://doi.org/10.1016/j.applthermaleng.2021.117275 [Google Scholar] [CrossRef]

2. Riley, N. (2001). Steady streaming. Annual Review of Fluid Mechanics, 33(1), 43–65. https://doi.org/10.1146/annurev.fluid.33.1.43 [Google Scholar] [CrossRef]

3. Kumar, P., Pandey, K. M. (2021). A review on latest development in heat transfer through porous media in combination with nanofluids and wavy walls. Materials Today: Proceedings, 45, 7171–7175. https://doi.org/10.1016/j.matpr.2021.02.411 [Google Scholar] [CrossRef]

4. Shenoy, A., Sheremet, M., Pop, I. (2016). Convective flow and heat transfer from wavy surfaces: Viscous fluids, porous media, and nanofluids. New York, NY: Taylor and Francis Group. https://doi.org/10.1201/9781315367637 [Google Scholar] [CrossRef]

5. Mahmood, A. N., Abdulrahman, A. A., Sabri, L. S., Sultan, A. J., Majdi, H. S. et al. (2024). Flow regimes in bubble columns with and without internals: A review. Fluid Dynamics & Materials Processing, 20(2), 239–256. https://doi.org/10.32604/fdmp.2023.028015 [Google Scholar] [CrossRef]

6. Shaikh, A., Al-Dahhan, M. H. (2007). A review on flow regime transition in bubble columns. International Journal of Chemical Reactor Engineering, 5(1). [Google Scholar]

7. Patel, T., Patel, D., Thakkar, N., Lakdawala, A. (2019). A numerical study on bubble dynamics in sinusoidal channels. Physics of Fluids, 31(5), 052103. https://doi.org/10.1063/1.5092870 [Google Scholar] [CrossRef]

8. Konda, H., Kumar Tripathi, M., Chandra Sahu, K. (2016). Bubble motion in a converging-diverging channel. Journal of Fluids Engineering, 138(6), 064501. https://doi.org/10.1115/1.4032296 [Google Scholar] [CrossRef]

9. Bhaga, D., Weber, M. E. (1981). Bubbles in viscous liquids: Shapes, wakes and velocities. Journal of Fluid Mechanics, 105, 61–85. https://doi.org/10.1017/S002211208100311X [Google Scholar] [CrossRef]

10. Agnihotry, A., Prasad, N. K., Dalal, A. (2023). Numerical study of bubble rise in a three-dimensional sinusoidal channel. Physics of Fluids, 35(9), 092109. https://doi.org/10.1063/5.0165945 [Google Scholar] [CrossRef]

11. Nishimura, T., Miyashita, H., Murakami, S., Kawamura, Y. (1991). Oscillatory flow in a symmetric sinusoidal wavy-walled channel at intermediate Strouhal numbers. Chemical Engineering Science, 46(3), 757–771. https://doi.org/10.1016/0009-2509(91) [Google Scholar] [CrossRef]

12. Chakravorty, A. (2018). Process intensification by pulsation and vibration in miscible and immiscible two component systems. Chemical Engineering and Processing-Process Intensification, 133, 90–105. https://doi.org/10.1016/j.cep.2018.09.017 [Google Scholar] [CrossRef]

13. Nishimura, T., Murakami, S., Kawamura, Y. (1993). Mass transfer in a symmetric sinusoidal wavy-walled channel for oscillatory flow. Chemical Engineering Science, 48(10), 1793–1800. https://doi.org/10.1016/0009-2509(93)80349-U [Google Scholar] [CrossRef]

14. Kurtulmuo, N., Sahin, B. (2020). Experimental investigation of pulsating flow structures and heat transfer characteristics in sinusoidal channels. International Journal of Mechanical Sciences, 167(3), 105268. https://doi.org/10.1016/j.ijmecsci.2019.105268 [Google Scholar] [CrossRef]

15. Fauci, L. J. (1992). Peristaltic pumping of solid particles. Computers & Fluids, 21(4), 583–598. https://doi.org/10.1016/0045-7930(92)90008-J [Google Scholar] [CrossRef]

16. Hung, T. K., Brown, T. D. (1976). Solid-particle motion in two-dimensional peristaltic flows. Journal of Fluid Mechanics, 73(1), 77–96. https://doi.org/10.1017/S0022112076001262 [Google Scholar] [CrossRef]

17. Zeeshan, A., Ijaz, N., Bhatti, M. M. (2018). Flow analysis of particulate suspension on an asymmetric peristaltic motion in a curved configuration with heat and mass transfer. Mechanics & Industry, 19(4), 401. https://doi.org/10.1051/meca/2018022 [Google Scholar] [CrossRef]

18. Sinnott, M. D., Cleary, P. W., Harrison, S. M. (2017). Peristaltic transport of a particulate suspension in the small intestine. Applied Mathematical Modelling, 44(4), 143–159. https://doi.org/10.1016/j.apm.2017.01.034 [Google Scholar] [CrossRef]

19. Bhatti, M. M., Zeeshan, A., Ellahi, R., Shit, G. C. (2018). Mathematical modeling of heat and mass transfer effects on MHD peristaltic propulsion of two-phase flow through a Darcy-Brinkman-Forchheimer porous medium. Advanced Powder Technology, 29(5), 1189–1197. https://doi.org/10.1016/j.apt.2018.02.010 [Google Scholar] [CrossRef]

20. Ivanova, A. A., Kozlov, V. G. (2003). Vibrational convection in nontranslationally oscillating cavity (isothermal case). Fluid Dynamics, 38(2), 186–192. https://doi.org/10.1023/A:1024260716608 [Google Scholar] [CrossRef]

21. Kozlov, V. G., Sabirov, R. R., Subbotin, S. V. (2018). Steady flows in an oscillating spheroidal cavity with elastic wall. Fluid Dynamics, 53(2), 189–199. https://doi.org/10.1134/S0015462818020118 [Google Scholar] [CrossRef]

22. Subbotin, S., Kozlov, V., Shiryaeva, M. (2019). Effect of dimensionless frequency on steady flows excited by fluid oscillation in wavy channel. Physics of Fluids, 31(10), 103604. https://doi.org/10.1063/1.5119018 [Google Scholar] [CrossRef]

23. Ishaq, M., Rehman, S. U., Riaz, M. B., Zahid, M. (2024). Hydrodynamical study of couple stress fluid flow in a linearly permeable rectangular channel subject to Darcy porous medium and no-slip boundary conditions. Alexandria Engineering Journal, 91(3), 50–69. https://doi.org/10.1016/j.aej.2024.01.066 [Google Scholar] [CrossRef]

24. Simonov, O. A., Erina, Y. Y., Ponomarev, A. A. (2023). Review of modern models of porous media for numerical simulation of fluid flows. Heliyon, 9(12), e22292. https://doi.org/10.1016/j.heliyon.2023.e22292. [Google Scholar] [PubMed] [CrossRef]

25. Vlasova, O., Karpunin, I., Latyshev, D., Kozlov, V. (2020). Steady flows of a fluid oscillating in an axisymmetric channel of variable cross section, versus the dimensionless frequency. Microgravity Science and Technology, 32(3), 363–368. https://doi.org/10.1007/s12217-019-09775-x [Google Scholar] [CrossRef]

26. Kozlov, V., Karpunin, I., Kozlov, N. (2020). Finger instability of oscillating liquid-liquid interface in radial Hele-Shaw cell. Physics of Fluids, 32(10), 102102. https://doi.org/10.1063/5.0018541 [Google Scholar] [CrossRef]

27. Stamhuis, E., Thielicke, W. (2014). PIVlab-towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. Journal of Open Research Software, 2(1), 30. https://doi.org/10.5334/jors.bl [Google Scholar] [CrossRef]