Convection and Stratification of Temperature and Concentration

Nomenclature

1  Introduction

The experiments performed by Benard and their theoretical interpretation by Rayleigh can be considered the beginning of the study of natural convection in liquids and gases, after which almost 125 years have passed. Further research includes the works of Prandtl, Karman, Batchelor, Kutateladze, Landau et al. [1], Gebhart et al. [2], Bergman et al. [3], Bejan et al. [4], Cormack et al. [5], Gershuni et al. [6–8], Gershuni et al. [7], Gershuni et al. [8], Polezhaev et al. [9,10]. Unfortunately, this is an absolutely incomplete reference list since there is a huge quantity of work on the study of convective processes, and this article does not have the purpose and opportunity to consider everything related to this work. Such a large number of published scientific works is due to the variety of convective processes, fundamental interest in them, as well as the need for and importance of studying them for many applications (automotive, aviation and space technology, energy (including nuclear), technologies for obtaining new materials (including semiconductors), medicine, life support systems, fire extinguishing, etc.). It should be noted that the variety of gravitational convective flows is due not only to dimensionless parameters (liquid properties, volume size and intensity of external thermal and mass fluxes), but also to the mutual direction of gravity vectors and external thermal and mass fluxes attached to volume [9]. In this article, we will consider only one case: this is a square area with horizontal fluxes of heat and mass from the vertical boundary walls. Despite the intensive study of the processes of convective heat and mass transfer, many problems remain poorly understood due to their nonlinear nature. At certain values of the determining parameters, laminar (stationary or quasi-stationary) fluid flows can exhibit nonlinear properties that can significantly change the structure of the fluid flow and the characteristics of heat and mass transfer. For example: (1) Effect of maximum temperature (concentration) stratification [9,10], (2) well known that during vibrational action on continuous media, their anomalous nonlinear peculiarities and resonant properties may manifest themselves [8,11,12]. It must be remembered that many analytical solutions to convection problems have their own ranges of applicability. For example, based on the analysis of the equations of motion for the plane case, Batchelor [13] suggested that during convection the core is isothermal and rotates with a constant and uniform vortex of velocity, which is not always true.

In an initially homogeneous liquid located in the gravity field when heat or mass is supplied, vertical stratification in density may occur due to convective mixing. Temperature and concentration stratification in liquid volumes during convective mixing of liquids is observed in many convective processes (for example, in crystal growth processes [9,10,14,15]), both in terrestrial conditions and in microgravity. The study of such heat and mass transfer processes is relevant not only from a fundamental point of view, but also for many applications, for example, which have been indicated in [16,17]. Therefore, knowledge of the patterns of formation of stationary (quasi-stationary) flow and stratification structures in liquids is important, for example, for specialists in growing single crystals in terrestrial and space conditions, since in technological processes of obtaining materials, an urgent task is to determine the possibility of regulating temperature or concentration stratification in a liquid volume in order to obtain homogeneous perfect materials with specified properties [9,14].

In the processes of heat and mass transfer, the convective stratification of temperature and concentration plays an important role, slowing down the process of heat and mass transfer (for example, in the case of penetrating convection in vertical layers when heated from below) [2,3,9,10]. This fact is important for a wide range of applied tasks: growing perfect single crystals [14,15], problems of fire extinguishing, boiling, the safety of nuclear installations, cooling of electronic equipment and storage of liquid rocket fuel, prevention and control of environmental pollution, including from liquid finely dispersed harmful inclusions, for example, with viruses, etc.

The magnitude of the temperature and concentration stratification depends nonlinearly on the induced convection, and in zero gravity conditions, it can manifest itself more strongly than in terrestrial conditions [9].

Convective temperature and concentration stratification of a fluid can have both a positive and a negative aspect. For example, this is a negative factor in obtaining perfect homogeneous single crystals, and in density separation and in obtaining eutectic materials, this can play a positive role [9,14,15].

This article demonstrates the manifestation of nonlinear features of laminar thermal and thermo-concentration convection, as well as the influence of vibration effects on the vertical stratification of temperature and impurities [16].

2  Problem Statement and Mathematical Model

The problem of gravitational thermal and concentrational convection of an incompressible liquid in a cavity with the aspect ratio L/H=1 (where L–is length and H–is the height of the calculated region), laterally heated in the field of gravity with acceleration of free fall g, is considered. At lateral heating, constant values of temperature θ1 and θ2 ( θ1<θ2 ) and concertation s1 and s2 on the side walls are set; for velocities, non-slip conditions are set. The following boundary conditions are considered: for velocity–the non-slip condition, for dimensionless temperature T on horizontal walls–line profile T|y=0,y=1=x , and for dimensionless concertation C–no mass flow condition ∂C/∂y|y=0,y=1=0 are set. The scheme of the calculated geometry, boundary conditions and isotherms in the layer for the thermal conductivity case are shown in Fig. 1.

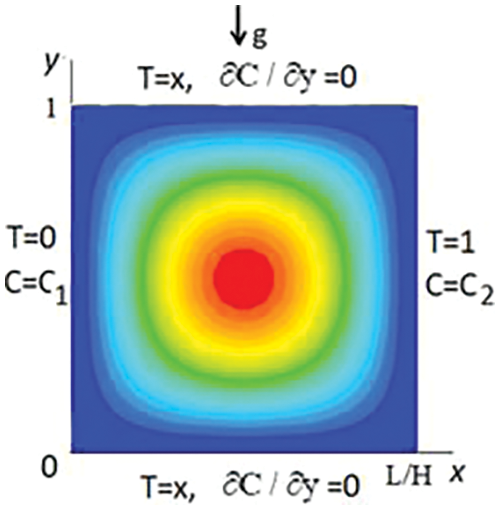
Figure 1: The calculated region and boundary conditions

The mathematical model is based on the numerical solution of the unsteady 2D Navier-Stokes equations for an incompressible fluid in the Boussinesq approximation and the equations of energy and mass transfer, which in a cartesian coordinate system, in dimensionless form, in variables: ψ -stream function, ω -vortex, T-temperature, C-concentration, can be written as follows [1,9]:

∂2ψ∂x2+∂2ψ∂y2=−ω (1)

dωdt=∂2ω∂x2+∂2ω∂y2+Gr∂T∂x+GrC∂C∂x (2)

dTdt=1Pr(∂2T∂x2+∂2T∂y2) (3)

dCdt=1Sc(∂2C∂x2+∂2C∂y2) (4)

where x, y–horizontal and vertical сartesian dimensionless coordinates; u, v–components of the velocity vector; t–time; T–dimensionless temperature; С–concentration; g –vector of the gravitational acceleration of the earth’s free fall directed opposite axis y; β , βC , ν , a , D–coefficients of temperature and concentration expansion of the liquid, kinematic viscosity, thermal conductivity and diffusion factor, respectively; in the future, we will use of dimensionless velocity and time (which was made dimensionless through the viscosity ν and height of the calculation region H). The problem is characterized by dimensionless parameters: the Grashof number Gr=gβT(θ2−θ1)H3/ν2 (or Rayleigh number Ra=Gr⋅Pr ), concentrational Grashof number GrC=gβC(s2−s1)H3/D2 ( Rac=Grc⋅Sc ), Prandtl number Pr=ν/a , Schmidt number Sc=ν/D and aspect ratio L/H = 1.

The results presented in this paper were obtained using the finite-difference scalar method [9] and the volume control method [18]. The good accuracy of numerical results was confirmed by comparison with experimental data and comparison of numerical results obtained by different numerical models [9,19].

3  Benchmark of the Model on de Vahl Davis Test Problem

The test problem of thermal convection of a viscous incompressible liquid (Pr = 0.7) in a square closed area with thermally insulated horizontal walls and with set temperatures on vertical walls (T1 = 1, T2 = 0) is considered. This de Vahl Davis task was announced more than 40 years ago as an international test for computer codes. About 40 different numerical solutions to this problem have been sent by various authors. In the paper [19], “benchmark solutions” were obtained for different Rayleigh numbers by extrapolating to a zero–step grid of solutions obtained by different methods on different grids. In Table 1, method 1 is the “benchmark solution” [19]; method 2 is the model used in this paper with mesh 65 * 65 nodes. In Fig. 2, the isolines of the stream function and the isotherms of the solution of the de Vahl Davis problem for Ra = 103 (left) and for Ra = 106 (right), obtained by method 2 are shown.

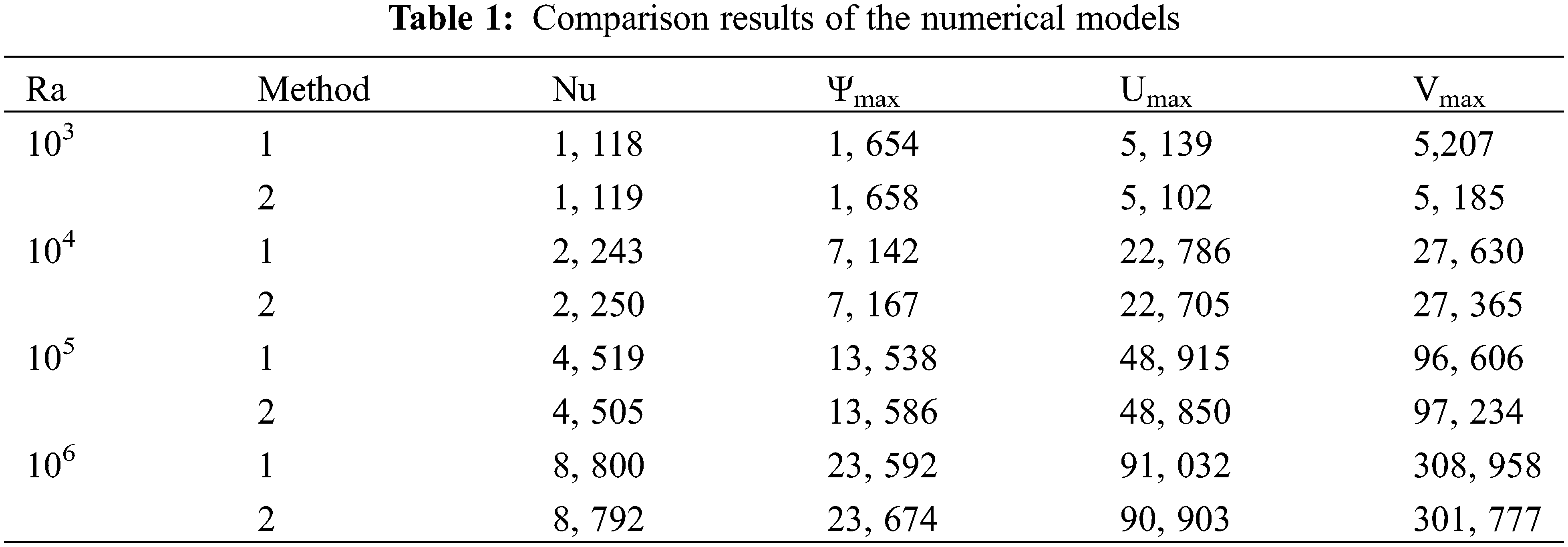
Figure 2: The stream function isolines and the isotherms of the solution of the de Vahl Davis problem for Ra = 103 (left) and for R = 106 (right)

The results of the solution of the de Vahl Davis benchmark problem presented in Table 1 and in Fig. 2. Table 1 shows: method 1 is the “benchmark solution” [19], method 2 is the solution of our model using a grid of 65 * 65 nodes (the discrepancy is less than 3%).

The results simulation for large Rayleigh numbers Ra = 107–109 and Pr = 5.8, for horizontal layers L/H = 7–12, were compared with local experimental data on the uneven grids with 141 * 33 and 141 * 65 nodes, the comparison results showed good model accuracy and are given in [9,16]. The results of this work were obtained on an uneven grid with the number of nodes 200 * 200.

4  The Results of Numerical Simulation

Gravitational convection in a square cavity heated from the side with binary mixtures with a concentration C of a light component are considered Fig. 1. Ranges of dimensionless parameters 0<Gr<108,Pr=0.7,Grc<108,10−2<Sc<102 are considered: corresponding to laminar stationary and vibrational convection. The vertical stratification was estimated by the values of derivatives of temperature (∂T/∂y) and concentration (∂C/∂y) along the vertical y coordinate.

4.1 Steady State Convection

In Fig. 3, pictures of steady-state thermal convection ( Gr=104,105,106, Pr=0.7 ) in the form of isolines of the stream function, isotherms and lines of equal concentration of impurity for different Schmidt numbers ( Sc=0.01, 0.1, 0.7, 10, 100 ) are shown.

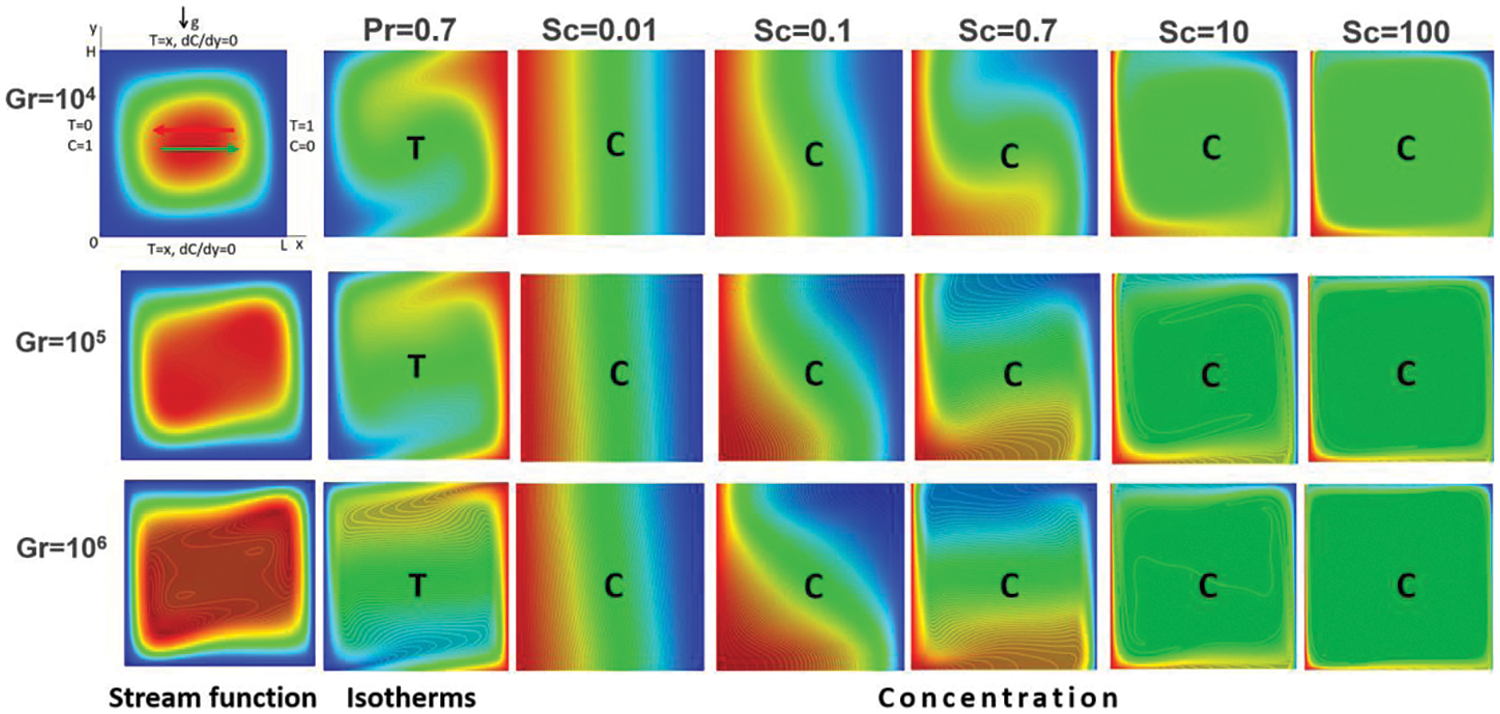
Figure 3: Isolines of the stream function, isotherms and lines of equal concentration of impurity for thermal convection for different Grashof ( Gr=104, 105, 106, Pr=0.7 ) and Schmidt numbers: Sc=0.01, 0.1, 0.7, 10, 100

At low Grashof numbers 0<Gr<104 ( Pr=0.7,L/H=1 ), the flow structure in the problem of thermal convection in a square cavity is single-vortex, with an increase in the Grashof number of more than 105, secondary vortices (“cat’s eyes”) begin to form, which shift to the upper corner near the heated wall and to the lower near the cold one, while maintaining the diagonal symmetry of the flow.

It is known that the thicknesses of the boundary layers of the velocity δ , thermal δT , concentrational δC are inversely proportional to the square root of the Reynolds, Peclet and diffusion Peclet number, respectively [3]. Analytically, only an estimated determination of the thickness of the boundary layers is possible. The structure of the boundary layers and their dependence on the Peclet number can be seen in experiments or in numerical results. In Fig. 3, the structure of the boundary layers and their dependences on Reynolds and Schmidt numbers are shown.

With an increase in the Grashof number, the flow ceases to be stationary and at Gr=106 (Fig. 4) the flow becomes quasi-stationary with weak periodic changes in velocity, and the secondary vortices of “cat’s eyes” are formed and practically do not change (Fig. 5) [2,7,9,19]. Transition on quasi-stationary mode presented in Fig. 4. It should be noted that the values of the derivatives of the temperature ∂T/∂y (or of the concentration ∂C/∂y ) are very sensitive to changes in the convective flow over time, therefore, they can be used as indicators of non-stationarity, since the slightest non-stationary changes in the convective flow are visible on changes in these derivatives. Fig. 4 on the left shows a graph with the dependencies of the average maximum and minimum temperature derivatives ∂T/∂y along the vertical coordinate in the cross-section x = 0.5 in time for Gr=106 . In Fig. 4 on the right shows the isotherms and the current function in quasi-stationary mode. At Gr=106 the flow structure and temperature distribution practically do not change, although the local values of velocity and temperature undergo weak periodic oscillations [2,7,19].

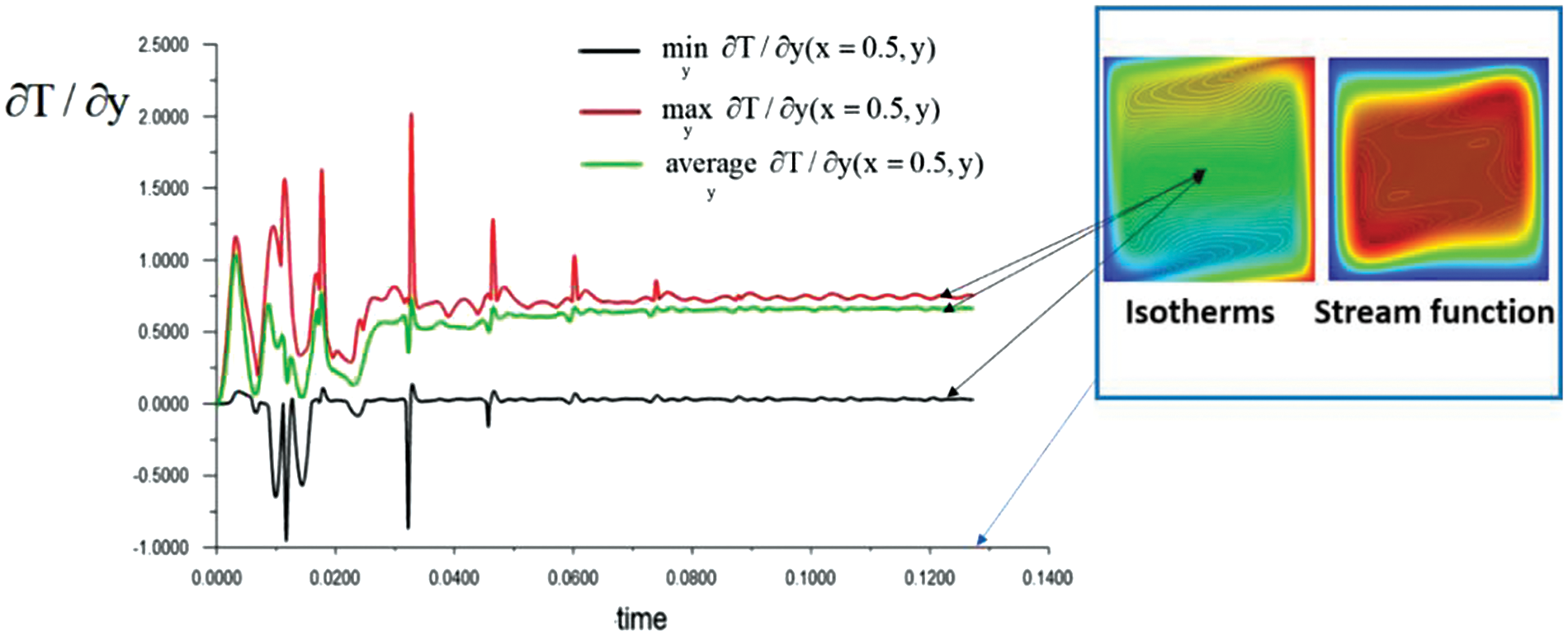
Figure 4: Time dependence of the derivative values ∂T/∂y (average, maximum and minimum values in the cross-section x = 0.5) at Gr = 106, Pr = 0.7

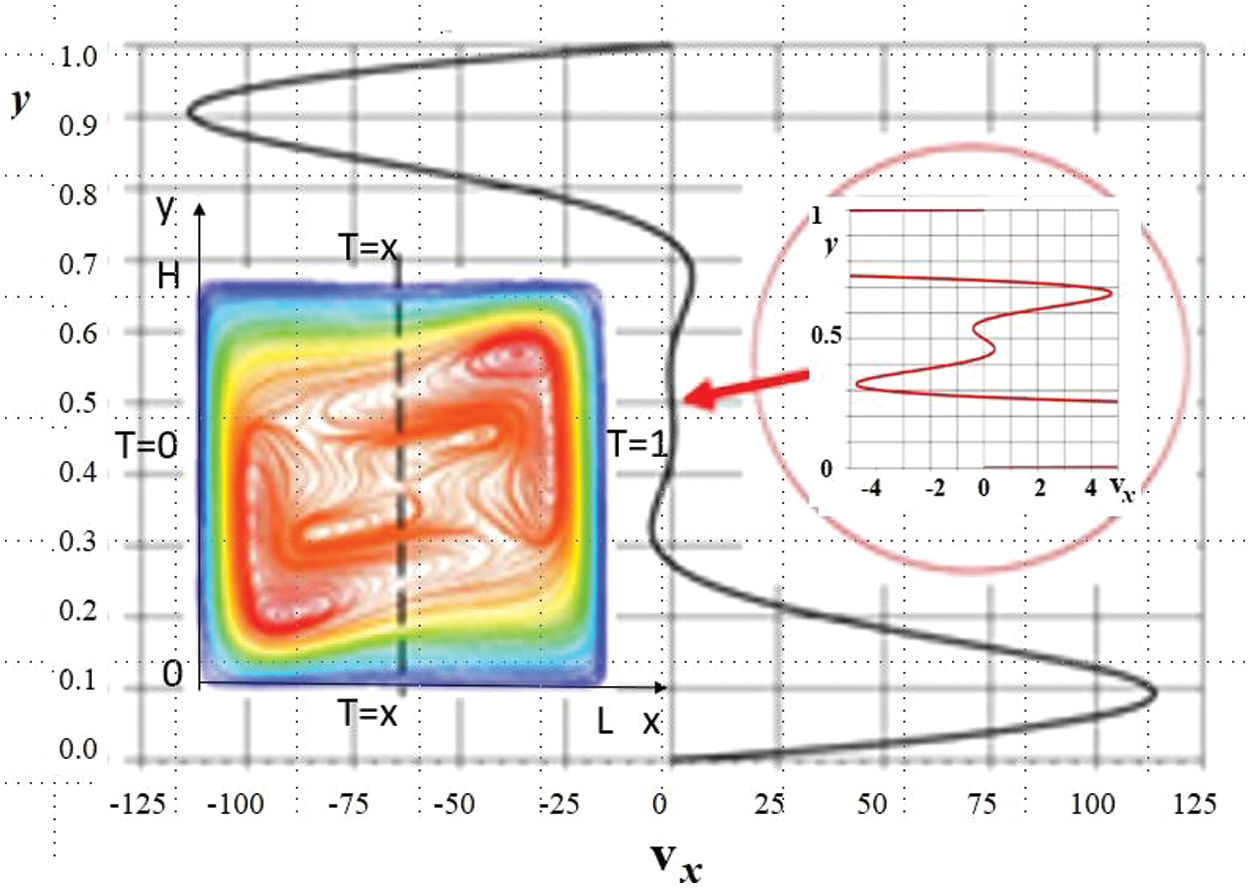
Figure 5: The profile of the horizontal velocity component vx (х = 0.5, y) in the middle vertical section for: Gr=106, Pr=0.7, L/H=1 . On the left are the tracks of the quasi-stationary flow; on the right is the vx (х = 0.5, y) profile near the center of the region on an enlarged scale

The formation and existence of stationary layered flow structures with countercurrents directed towards the main flow is shown in Fig. 5 for a square region ( Gr=106,Pr=0.7,L/H=1 ). These countercurrents are formed due to intense convective flow, steady vertical stratification of density induced by convection, and the presence of vertical and horizontal walls. The presence of countercurrents during thermal convection in elongated horizontal layers, for different properties of liquids and conditions, including for semi-infinite horizontal layers, was shown in [9,16,17].

4.2 Oscillatory Convection Flow

After reaching the Grashof number equal to Gr=107 , the laminar flow becomes periodically oscillatory (Fig. 6). Fig. 6 on the left shows a graph with the dependencies of the average maximum and minimum temperature derivatives ∂T/∂y along the vertical coordinate in the cross-section x = 0.5 in time for Gr=107 . The secondary vortices of the “cat’s eyes” (which did not move up to Gr=106 begin to be carried away by the main convective flow (counterclockwise), changing their intensity, splitting and uniting (Fig. 7). This manifests in the temperature field in the form of emerging thermals (thermal fingers) at the hot and cold walls (small, moving vortices appear on the walls-Tollmin–Schlichting waves, vortices increase in size as they move along vertical and horizontal walls). At Gr=107 , the entire flow pattern is periodically repeated over time. The fixed temperature on the walls contributes to the generation of vortices and the appearance of convective instability. In Fig. 7, the stream function (7a–7d) and isotherms (7e–7h) of oscillatory thermal convection for different time at a quasi-stationary mode are shown for different time moments for one period τ are presented for Gr=107, Pr=0.7,L/H=1 . In Fig. 7a, the values of the isolines of the stream function by color and the tracks during oscillatory thermal convection are shown (the black line with the arrows indicate the trajectory of the moving of vortices).

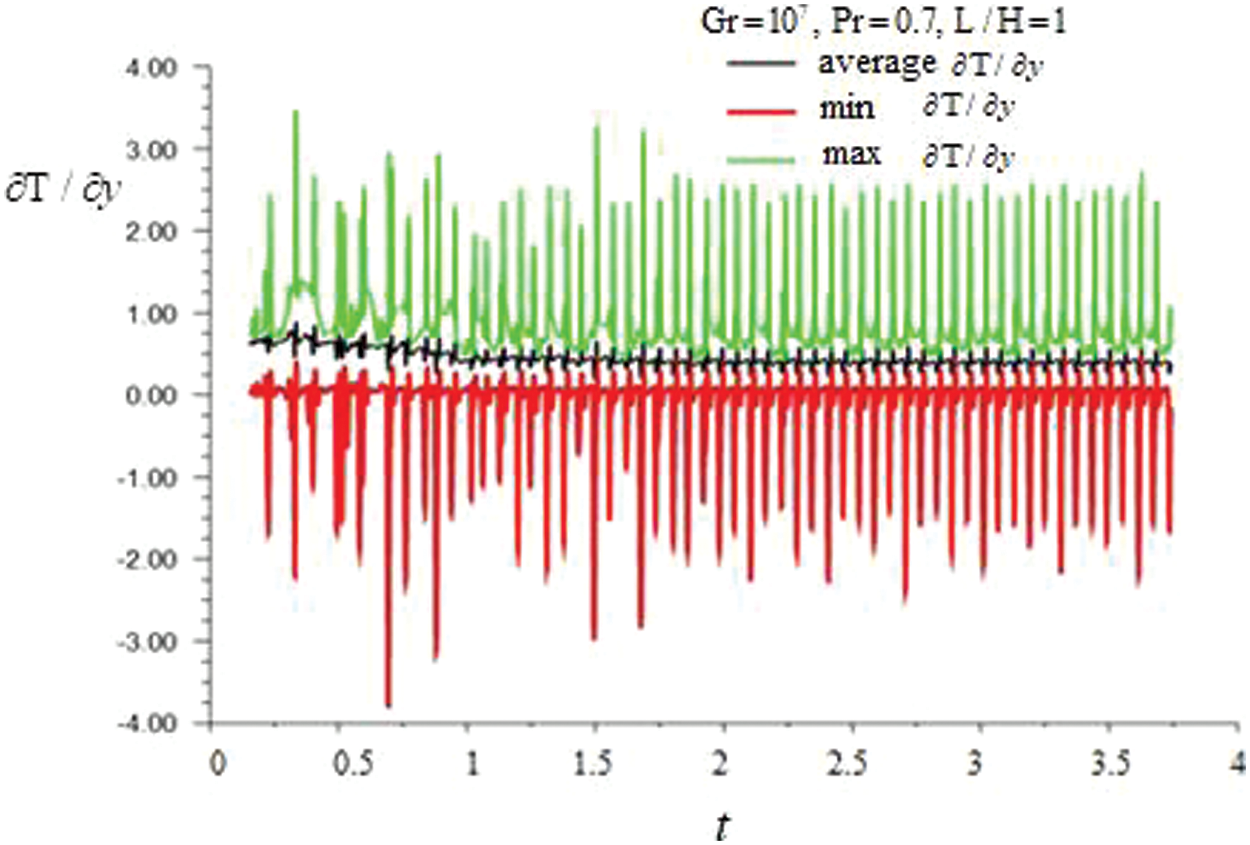
Figure 6: Time dependence of the derivative values ∂T/∂y (average, maximum and minimum values in the cross-section x = 0.5) at Gr = 107, Pr = 0.7

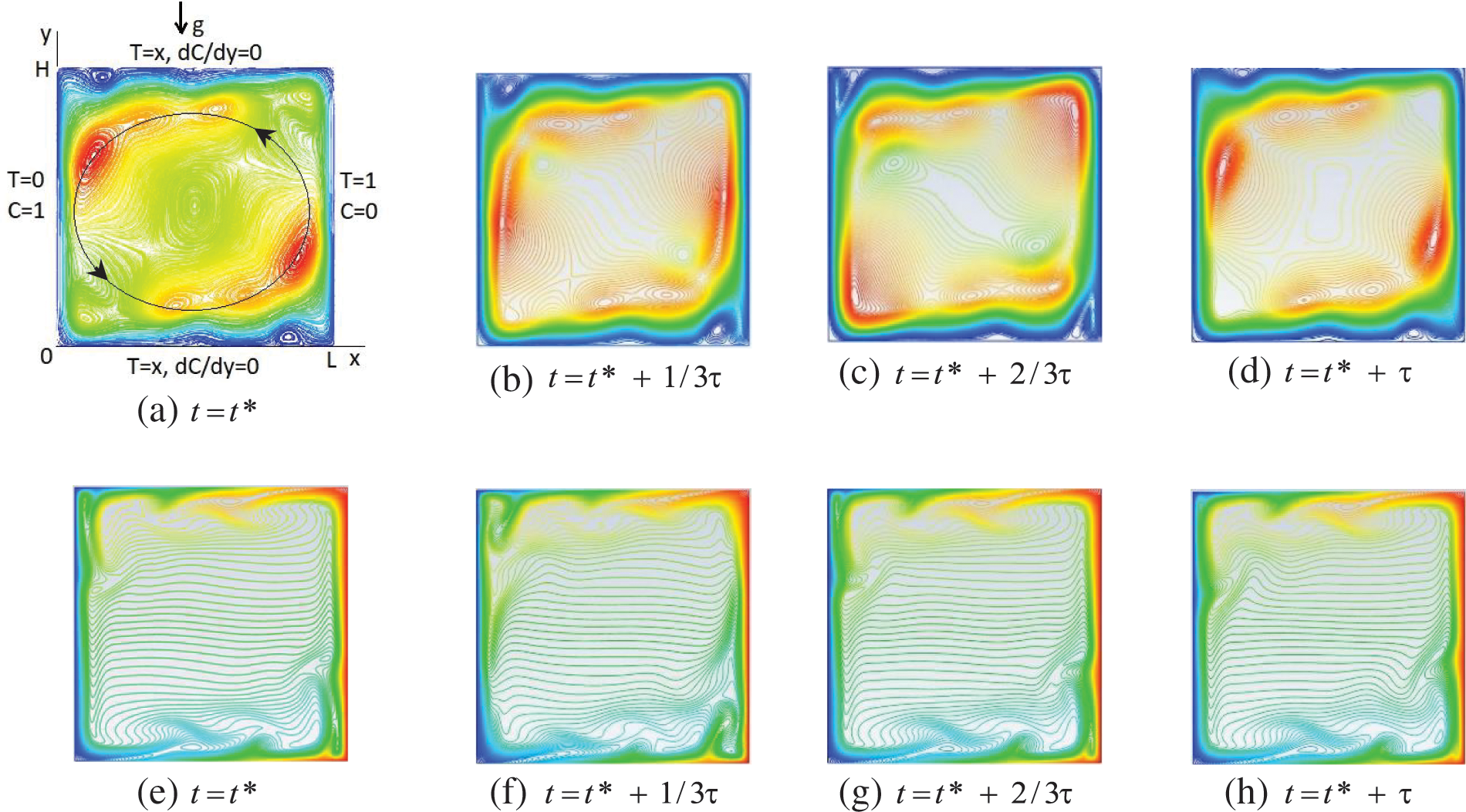
Figure 7: Isolines of the stream function (a–d) and isotherms (e–h) of oscillatory thermal convection for different time at quasi-steady-state mode for time t = t* = 3.5 ( Gr=107, Pr=0.7, L/H=1 on one oscillation period τ at approximately equal time intervals 1/3τ )

Figs. 4 and 6 show the dependences of the ∂T/∂y derivative for different Grashof numbers at Gr = 106 and Gr = 107, respectively. A comparison of these dependencies indicates the existence of a range of Rayleigh numbers at which a regular periodic oscillatory convective flow is formed: at Gr = 106, it does not exist yet (Fig. 4), at Gr = 107 it exists (Fig. 6), and at Gr = 108, the oscillatory mode of the convective flow becomes with a large number of small macro vortices, more irregular and transitional to a turbulent regime (Fig. 8). In Figs. 3, 7, 8, one can see not only the spatial change of the closed boundary layers caused by convection of different intensity, but also their change over time. It should be noted that for vibrational convection Gr = 107 in a quasi-steady state, the thickness of the boundary layers varies slightly on average over time. At Gr=108,  Pr=0.7 , the convective flow is oscillatory, but becomes less ordered than at Gr=107 (Fig. 8). Thermo-concentrational convection Gr=107\hbox, Grc=107, Pr=0.7, Sc=0.7 also has a well-defined periodic oscillatory character, but its intensity is lower than in the case of thermal convection alone (Gr = 107, Grc = 0) and the nature of the appearance of oscillations different than in thermal convection, The structure of thermo-concentration convection consists of two main vortices rotating in opposite directions (concentration convection causes the liquid to move clockwise; thermal convection-counterclockwise). These two main vortices are in confrontation each other, which determines the frequency of flow of this thermo-concentration convection. Fig. 8 shows that at oscillatory convection, the instantaneous concentration distributions depend on the Schmidt number and vary over time, but the average concentration fields have stationary and quasi-stationary modes.

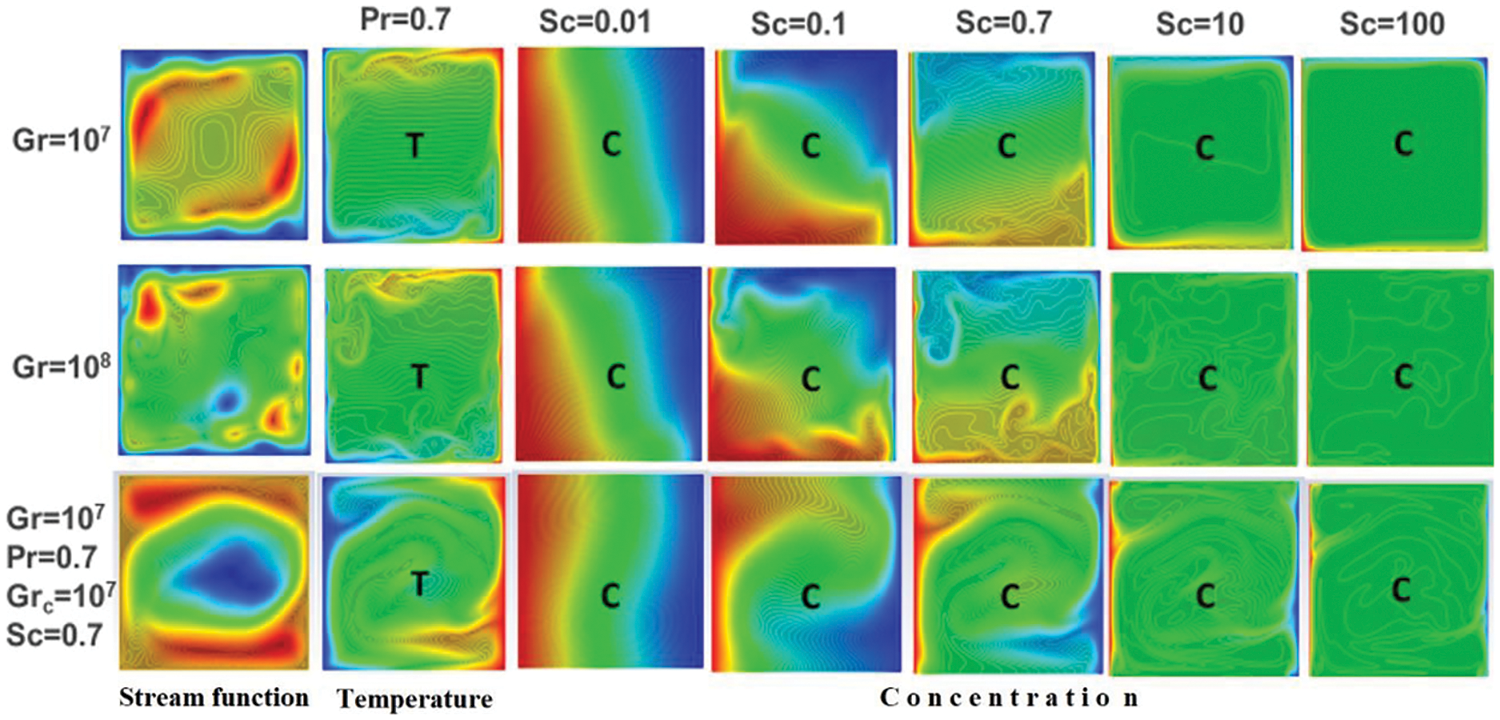
Figure 8: Isolines of the stream function, isotherms and lines of equal concentration of impurity for thermal convection for thermal Gr=107, 108,  Pr=0.7 and concentrational convection Gr=107, Grc=107, Pr=0.7,  Sc=0.7 for different Schmidt numbers: Sc=0.01, 0.1, 0.7, 10, 100

The concentration profiles in the vertical section x = 0.5 for thermal convection Gr=102, 103, 104, 105, 106, 107, Pr=0.7,  Sc=0.7 and thermo-concentrational convection Gr=107, Grc=107, Pr=0.7, Sc=0.7 are shown in Fig. 9.

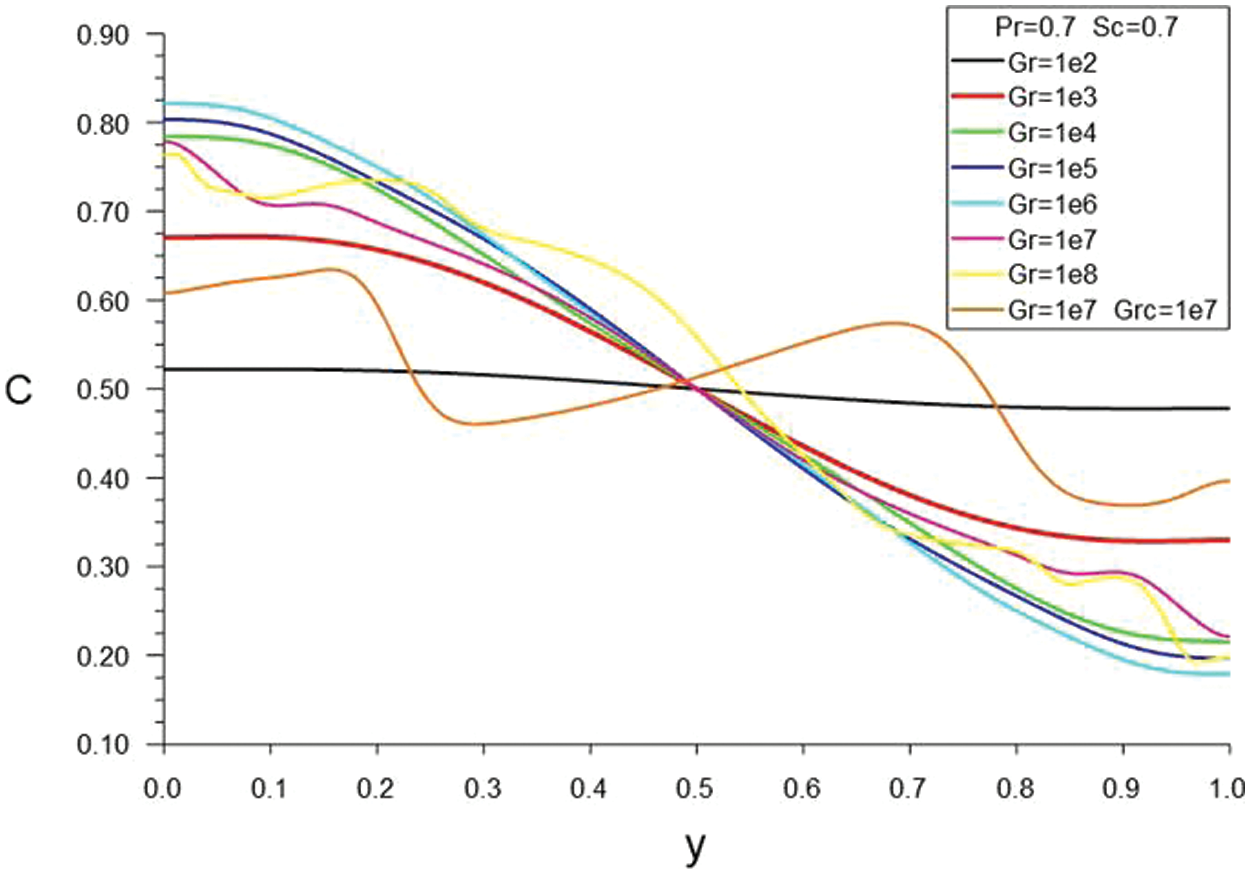
Figure 9: The concentration profiles in the vertical section x = 0.5 for Gr=102−108 and Grc=107, Pr=0.7, Sc=0.7

4.3 The Temperature and Concentration Stratification

The stratification in temperature and concentration during oscillation convection varies slightly on average over time. In Figs. 10a and in 10b the dependences of the temperature derivative ∂T/∂y on the vertical coordinate calculated in the center of the square region for the Grashof number Gr=103, 104, 105, 106, 107,  108, Pr=0.7 for thermal and thermo-concentration convection Gr=107, Grc=107, Pr=0.7, Sc=0.7 are shown. In Fig. 10, time-averaged value ∂T/∂y profiles for Gr>106 are presented. The results in Fig. 10b show that during thermo-concentration convection, the maximum temperature inhomogeneity ( ∂T/∂y ) averaged over time there is not near the walls, but closer to the core of the convective cell. This is due to the opposition of thermal and concentration convection rotating in opposite directions.

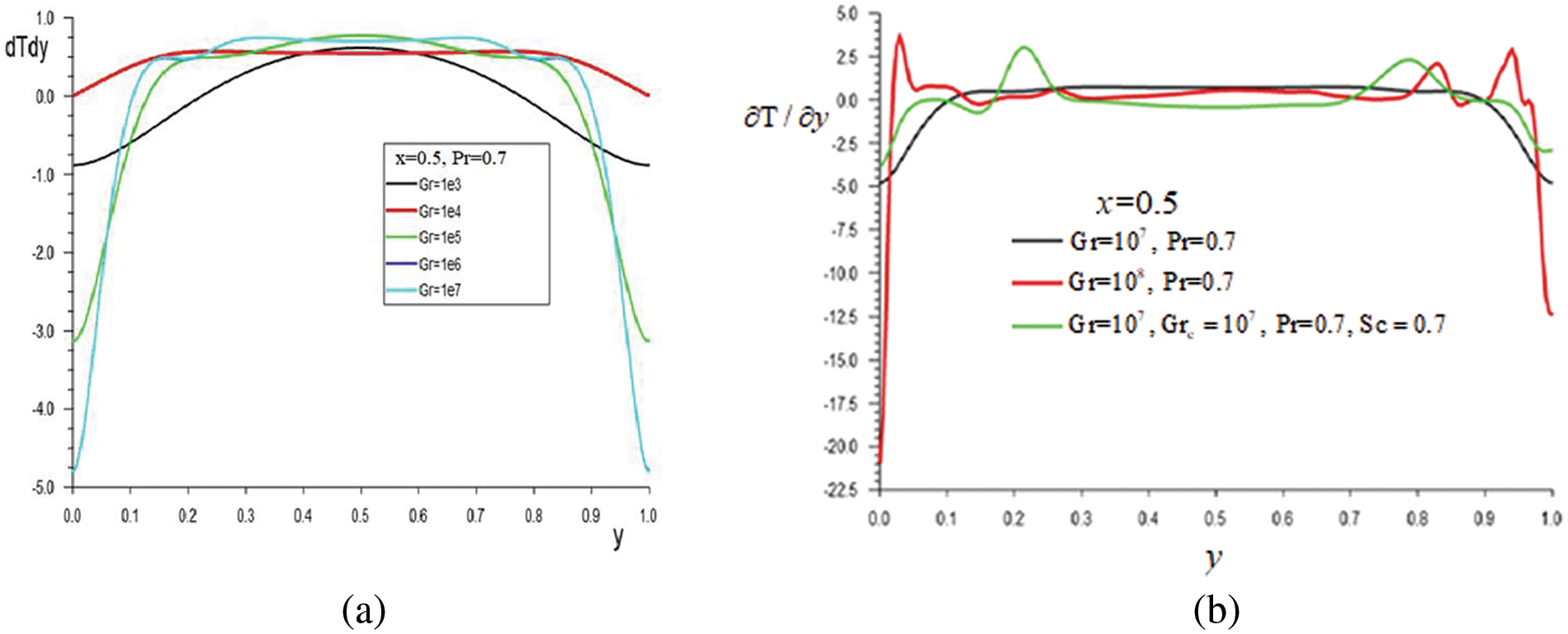
Figure 10: The dependences of the temperature derivative ∂T/∂y on the vertical coordinate (x = 0.5) calculated in the center of the square region; (a)-for the Grashof number Gr=103,104, 105, 106, 107, 108, Pr=0.7 ; (b)-for thermal ( Gr=107 and Gr=108, Pr=0.7 ) and thermo-concentration convection ( Gr=107, Grc=107, Pr=0.7, Sc=0.7 ) ( ∂T/∂y was time-averaged for Gr>106 )

In Figs. 11 and 12 for thermal convection, the dependences on the Grashof number of the values of the derivatives of temperature ( ∂T/∂y ) and concentration ( ∂C/∂y ) along the vertical coordinate calculated in the center of the region (for various Schmidt numbers: Sc = 0.1, 0.7, 10) are shown (the derivatives ∂T/∂y and ∂C/∂y were time-averaged for oscillatory mode, for Gr>106 ). The dependences on the Grashof number of the vertical derivatives of temperature and concentration calculated in the center of the region (Figs. 11, 12) show that the maximum segregation of temperature and concentration exists in the center of the calculated region. That is, maxima exist not only between the upper and lower horizontal boundary layers, where there are the greatest vertical differences in temperature and concentration, as previously shown in papers [9,10,16].

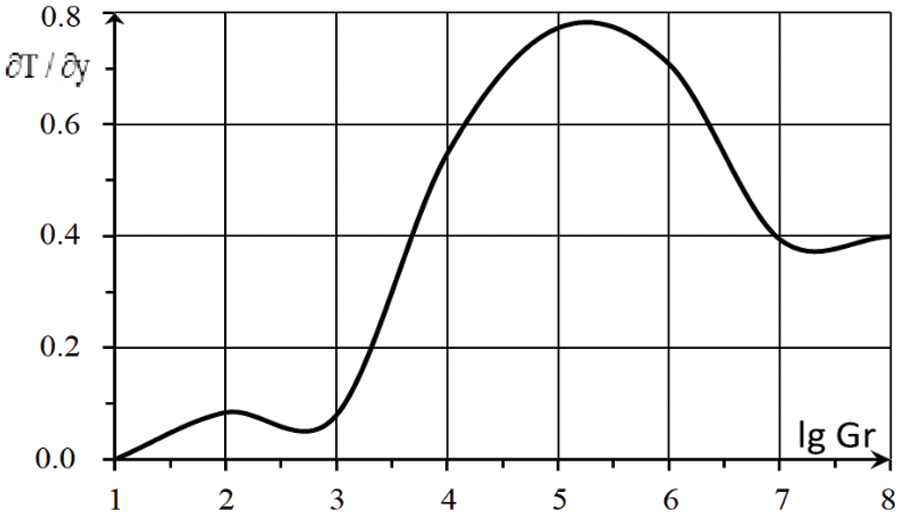
Figure 11: The dependence of the temperature derivative ∂T/∂y on the vertical coordinate in the center of the square area (x = 0.5, y = 0.5) on the Grashof number for Pr=0.7, L/H=1

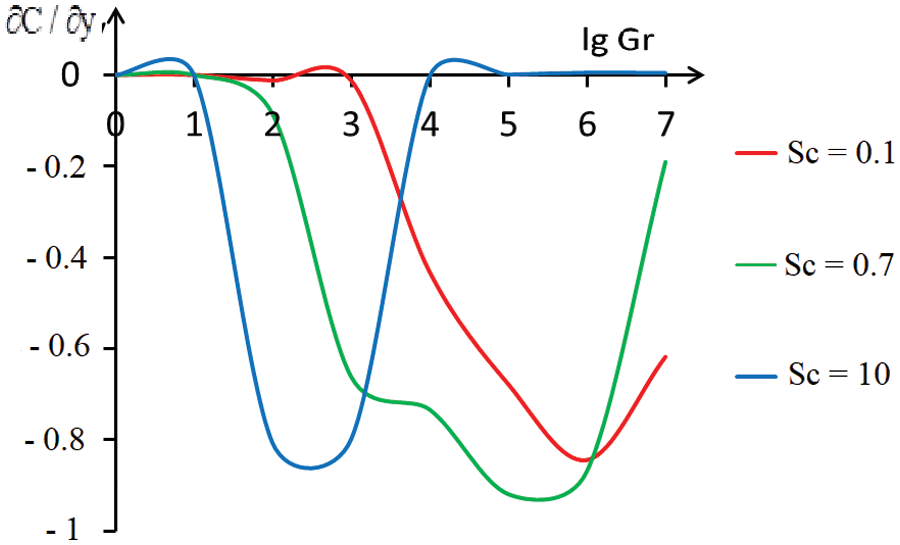
Figure 12: The dependence of the concentration derivative ∂C/∂y on the vertical coordinate in the center of the square area (x = 0.5, y = 0.5) on the Grashof number for Pr=0.7;Sc=0.1, 0.7, 10; L/H=1

The dependencies of the concentration derivative ∂C/∂y on the vertical coordinate calculated in the center of the square area on the Rayleigh number for thermal, concentration and thermo-concentration convection (Pr = 0.7, Sc = 0.7) and comparison with experiment were presented in [9].

4.4 Influence Vibration on the Temperature and Concentration Stratification

It is known that the vibration effect on a liquid can significantly affect the flow of a liquid, which leads to paradoxical phenomena [11,12,20], and to vibrational convection even in zero gravity [6,8].

The simulation of the vibrational effects on convectional flow was carried out on the basis of solving the complete (non-averaged) unsteady Navier-Stokes Eqs. (1)–(4) and the flow analysis was carried out on a quasi-steady-state mode. Two cases of vibration effects on velocity along the normal to the walls according to the law are considered:

1) horizontal vibrations from the vertical boundaries (x = 0, x = 1)

according to law vx = A sin(2πft),

2) vertical vibrations from the horizontal boundaries (y = 0, y = 1)

according to law vy = A sin(2πft).

In Fig. 13, the profiles of dimensionless velocity component Mean_vx averaged on time in vertical section (x = 0.5) for three cases: (1) horizontal vibrations from the vertical walls according to law vx = A sin(2πft), (2) vertical vibrations from the horizontal walls according to law vy = A sin(2πft), (3) thermal convection without vibrations are presented for A = 10, f = 105, Gr = 107, Pr = 0.7.

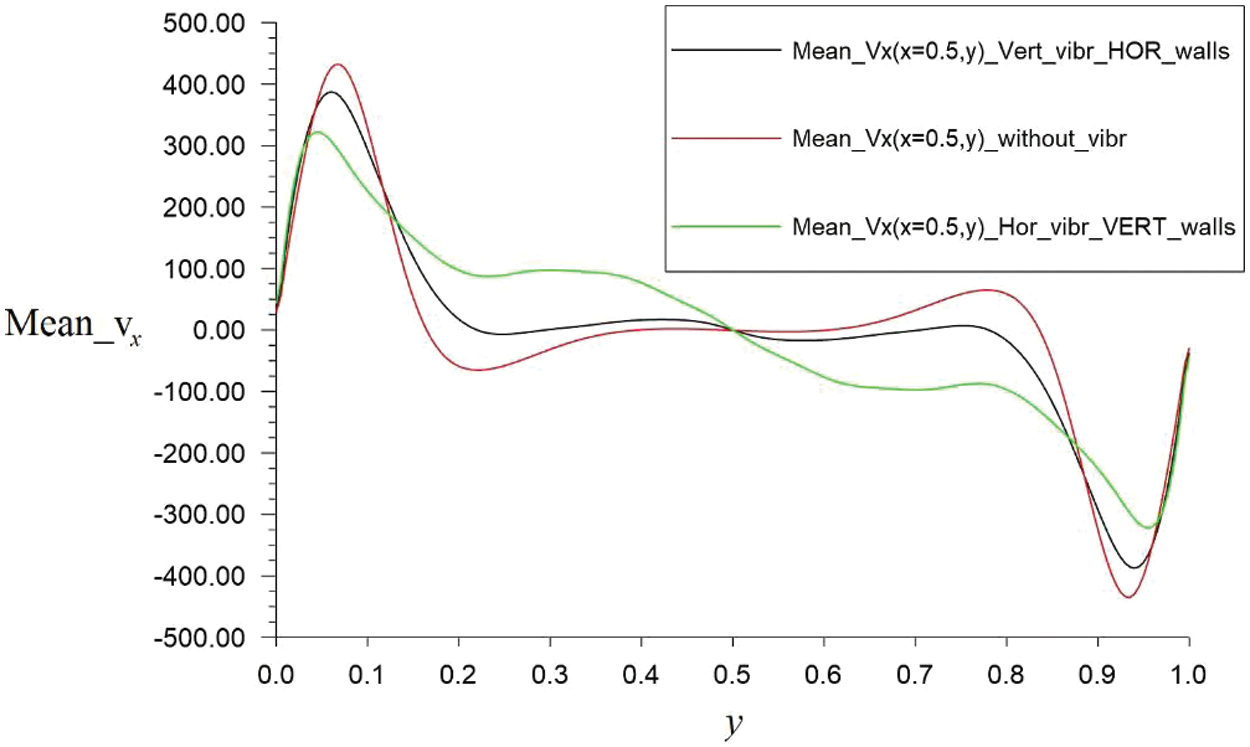
Figure 13: The profiles of the velocity component mean_vx averaged on time in vertical section (x = 0.5) for three cases (A = 10, f = 105, Gr = 107, Pr = 0.7): (1) horizontal vibrations from the vertical walls according to law vx = A sin(2πft)–green line, (2) vertical vibrations from the horizontal walls according to law vy = A sin(2πft)–black line; (3) thermal convection without vibrations–red line

The results presented in Figs. 13, 14 show that vibrations affect the velocities both in the boundary layer and in the core of the convective cell. The convective flow averaged over time under the influence of vibrations changes its character and has a more pronounced boundary between the boundary layer and the core compared to the convective flow without vibrations. Controlled vibration effects have a strong effect depending on frequency and amplitude. The vibrations make the average flow more orderly and the velocity profiles in the middle sections make more symmetry. In Fig. 14, with periodic vibration action on the convective cell from the side of its walls, the separation of the average time flow into two flow zones is observed: first is the fluid flow near the walls and second is the core slow fluid flow. This is similar to the annular Richardson effect of flow in a pipe (or in a flat diffuser) with periodic distribution of the inlet flow. These influences on horizontal velocity vx during periodical vibration vertical walls are shown in Fig. 13 (green line) and on thermal inhomogeneity in Fig. 14 (black line).

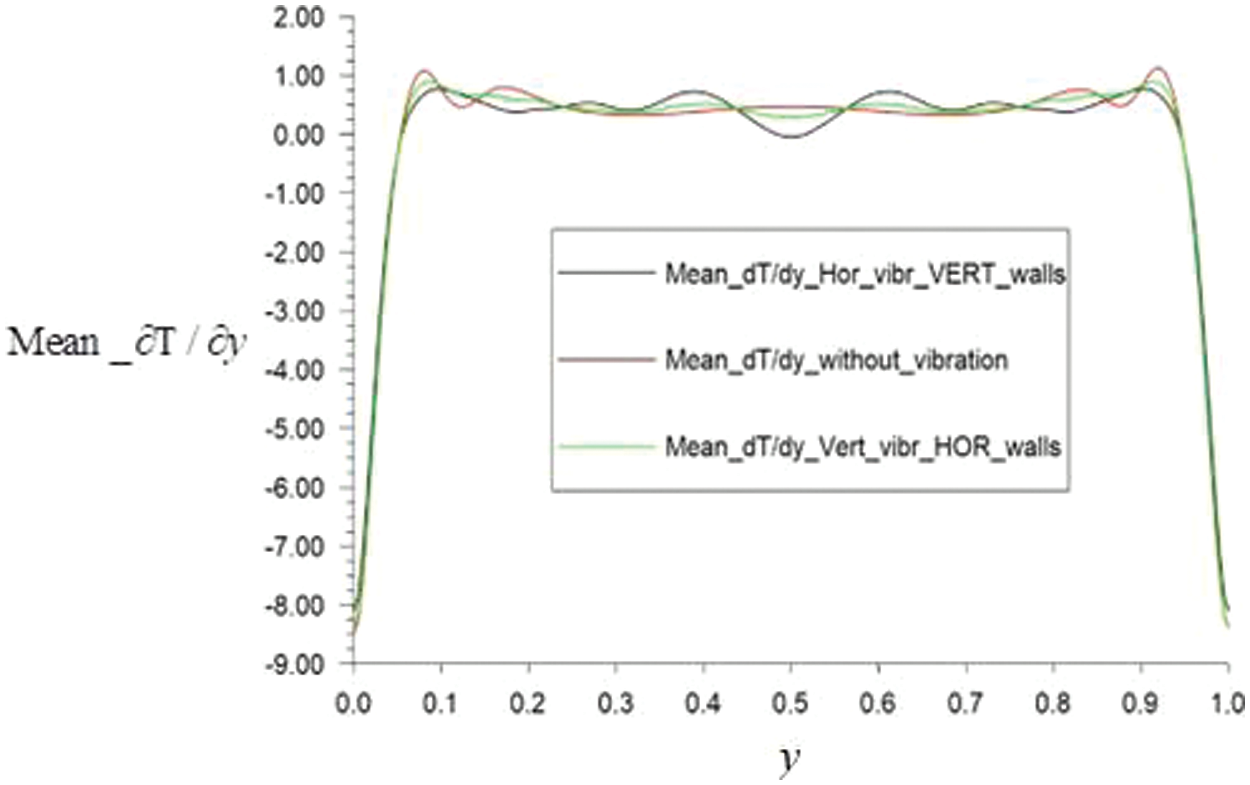
Figure 14: The profiles of the temperature derivative mean_ ∂T/∂y averaged on time in vertical section (x = 0.5) for three cases (A = 10, f = 105, Gr = 107, Pr = 0.7): (1) horizontal vibrations from the vertical walls according to law vx = A sin(2πft)–green line, (2) vertical vibrations from the horizontal walls according to law vy = A sin(2πft)–black line; (3) thermal convection without vibrations–red line

The study of vibration effects is very expensive, in terms of time and resource computer costs, therefore the effects of vibrations on heat and mass inhomogeneity for another parameters of vibration exposure requires further investigation.

5  Conclusions

Nonmonotonic dependences of vertical derivatives on temperature and concentration calculated in the center of the square region on the Grashof number were found, showing the presence of maximum heterogeneity of temperature and concentration depending on the Grashof number.

The pictures and differences of the formation of a nonstationary periodic structure of oscillatory thermal and thermo-concentration convection are shown. For thermal convection, a range of Rayleigh numbers exists where a regular periodic oscillatory convective flow is formed (for example, at Gr = 107, Pr = 0.7). The details of the formation of (quasi-stationary) countercurrents inside a square region directed opposite to the main convective flow are given. In the considered case of thermo-concentration convection (Gr = Grc = 107, Pr = Sc = 0.7 with oppositely directed heat and mass horizontal fluxes) oscillational convection is caused by the confrontation of thermal and concentration convection with opposite rotations.

The influence of vertical and horizontal vibrations on oscillatory convection is shown (Gr = 107, Pr = 0.7). Controlled vibration effects have a strong effect depending on frequency and amplitude. With periodic vibration action on the convective cell from the side of its walls, the separation of the average time flow into two flow zones is observed: first is the fluid flow near the walls and second is the core slow fluid flow. The vibrations make the average flow more orderly and the velocity profiles in the middle sections make more symmetry.

Acknowledgement: None.

Funding Statement: This work was supported by the Russian Science Foundation Grant 24-29-00101.

Author Contributions: All the work was done by the corresponding author.

Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

1. Landau, L. D., Lifshitz, E. M. (1987). Course of theoretical physics. Fluid mechanics 6, 2nd edition. Oxford: Pergamon Press. [Google Scholar]

2. Gebhart, B., Jaluria, Y., Mahajan, R. L., Sammakia, B. (1988). Buoyancy-induced flows and transport. New York: Hemisphere. [Google Scholar]

3. Bergman, T. L., Lavine, A. S., Incropera, F. P., DeWitt, D. P. (2019). Fundamentals of heat and mass transfer, 8th edition. Hoboken, NJ, USA: John Wiley & Sons, Inc. [Google Scholar]

4. Bejan, A., Al-Homoud, A. A., Imberger, J. (1981). Experimental study of high-Rayleigh-number convection in a horizontal cavity with different end temperatures. Journal of Fluid Mechanics, 109, 283–299. https://doi.org/10.1017/S0022112081001079 [Google Scholar] [CrossRef]

5. Cormack, D. E., Leal, L. G., Seinfield, J. H. (1974). Natural convection in a shallow cavity with differentially heated end walls. Part 1. Asymptotic Theory. Journal of Fluid Mechanics, 65, 231–246. https://doi.org/10.1017/S0022112074001352 [Google Scholar] [CrossRef]

6. Gershuni, G. Z., Zhukovitskii, E. M. (1976). Convective stability of incompressible fluids. Jerusalem/Wiley: Keter Publications. [Google Scholar]

7. Gershuni, G. Z., Zhukhovitskii, E. M., Tarunin, E. L. (1966). Numerical investigation of convective motion in a closed cavity. Fluid Dynamics, 1, 38–42. https://doi.org/10.1007/BF01022148 [Google Scholar] [CrossRef]

8. Gershuni, G. Z., Lubimov, D. V. (1998). Termal vibrational convection. England: John Willey & Sons Ltd. [Google Scholar]

9. Polezhaev, V. I., Bello, M. S., Verezub, N. A., Dubovik, K. G., Lebedev, A. P. et al. (1991). Convective processes in weightlessness. Nauka (In Russian). [Google Scholar]

10. Polezhaev, V. I., Fedyushkin, A. I. (1980). Hydrodynamic effects of concentration stratification in closed spaces. Fluid Dynamics, 15(3), 331–337. [Google Scholar]

11. Chelomei, V. N. (1983). Mechanical paradoxes caused by vibrations. Doklady Akademii Nauk SSSR, 270(1), 62–7 (In Russian). [Google Scholar]

12. Blekhman, I. I. (2000). Vibrational mechanics (Nonlinear dynamic effects, general approach, applications). Singapore: World Scientific. [Google Scholar]

13. Batchelor, G. K. (2000). An introduction to fluid dynamics. Cambridge, UK, New York: Cambridge University Press. [Google Scholar]

14. Dropka, N., Gradwohl, K. P. (2024). Crystal growth, bulk: Theory and models. In: Encyclopedia of condensed matter physics (second edition), pp. 231–247. Netherlands: Academic Press, Elsevier B.V. Amsterdam. https://doi.org/10.1016/B978-0-323-90800-9.00108-6 [Google Scholar] [CrossRef]

15. Fedyushkin, A. I. (2020). Effect of convection on crystal growth of calcium phosphate in a thermostat under terrestrial and space conditions. Fluid Dynamics, 55(4), 35–46. https://doi.org/10.1134/s0015462820040047 [Google Scholar] [CrossRef]

16. Fedyushkin, A. I. (2023). Stratification and segregation under laminar convection. In: Advanced hydrodynamics problems in earth sciences, pp. 153–169. Switzerland: Springer. https://doi.org/10.1007/978-3-031-23050-9_14 [Google Scholar] [CrossRef]

17. Drummond, J. E., Korpella, S. A. (1987). Natural convection in a shallow cavity. Journal Fluid Mech, 182, 543–564. [Google Scholar]

18. Patankar, S. V. (1980). Numerical heat transfer and fluid flow. New York: Hemisphere. [Google Scholar]

19. de Vahl Davis, G. (1983). Natural convection of air in a square cavity a benchmark numerical solution. International Journal for Numerical Methods in Fluids, 3, 249–264. [Google Scholar]

20. Fedyushkin, A. I. (2021). The effect of controlled vibrations on Rayleigh-Benard convection. Journal of Physics: Conference Series, 2057, 012012. https://doi.org/10.1088/1742-6596/2057/1/012012 [Google Scholar] [CrossRef]