 Open Access
Open Access
ARTICLE
On the Features of Thermal Convection in a Compressible Gas
1 Physics Department, Siberian State University of Telecommunications and Information Sciences, Novosibirsk City, 630102, Russia
2 Physics Department, Siberian State University of Geosystems and Technologies, Novosibirsk City, 630108, Russia
* Corresponding Author: Igor B. Palymskiy. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(5), 957-974. https://doi.org/10.32604/fdmp.2024.048829
Received 19 December 2023; Accepted 13 March 2024; Issue published 07 June 2024
Abstract
The fully nonlinear equations of gas dynamics are solved in the framework of a numerical approach in order to study the stability of the steady mode of Rayleigh-Bénard convection in compressible, viscous and heat-conducting gases encapsulated in containers with no-slip boundaries and isothermal top and bottom walls. An initial linear temperature profile is assumed. A map of the possible convective modes is presented assuming the height of the region and the value of the temperature gradient as influential parameters. For a relatively small height, isobaric convection is found to take place, which is taken over by an adiabatic mode when the height exceeds the critical value, or by a super-adiabatic mode in case of a relatively high temperature gradient. In the adiabatic mode, convective flow develops due to adiabatic processes given a stable initial stratification. An analytic formula for the critical height of the region is derived taking into account and neglecting the dependence of the gas viscosity on the temperature. Moreover, an analytic formula is obtained for the upper boundary of the region of applicability of the Boussinesq approximation for incompressible gases. These models for compressible gases are relevant to practical situations such as the study of convective flows in spatially extended gas mixtures when dealing with safety issues related to hydrocarbons stored in gas stations. A dangerous situation arises when the tank is almost empty but some hydrocarbon is left at the bottom of the tank. In the presence of convective flows, the vaporized fuel is mixed with the oxidizer (air) forming a gas-vapor medium. However, if the volumetric concentration of fuel vapor (hydrocarbon) is in the interval between the lower and upper concentration limits of ignition, then the gas-vapor mixture becomes explosive and any accidental spark is sufficient to cause an emergency.Keywords
Nomenclature
| u, v, P, ρ, T | Dimensionless velocity, density, pressure, temperature |
| ψy = ρu, ψx = −ρv | Relations for determining the stream function of a stationary solution |
| Ph | Equilibrium (static) pressure distribution |
| ΔT | Dimensionless difference of temperatures between lower and upper horizontal boundaries |
| H, m | Dimensional height of the region |
| Had, m | Dimensional height of the adiabatic plume motion |
| ν and χ | Kinematic and thermal diffusivity coefficients |
| Ra = Pr∙CF∙M-2ΔT | Rayleigh number |
| Rab | Critical values of Rayleigh number for incompressible fluid Boussinesq approximation |
| Rag | Critical values of Rayleigh number for compressible gas |
| Hcr | Dimensional critical height of the region |
| CF = gH/(γRT0) | Parameter of hydrostatic compressibility |
| γ | Adiabatic exponent |
| x, y and t | Dimensionless coordinates and time |
| tad, s | Dimensional time of adiabatic plume rise |
| Th(y) = 1 −ΔT∙y | Equilibrium (static) temperature distribution |
| ρh | Equilibrium (static) density distribution |
| δT, δρ | Deviations of temperature and density from the corresponding static distributions |
| ρad | Density of gas particle at adiabatic motion |
| Ek | Total energy of motion in gas while in convective motion |
| R | Specific gas constant |
| g | Standard acceleration of free fall |
| ρ0 and T0 | Characteristic values for density and temperature |
| M = ν/((γT0R)0.5H) | Mach number |
| Pr = ν/χ | Prandtl number |
| Sc | Schwarzschild number, ratio of adiabatic gradient to the given |
| Re = (2∙Ek/π)0.5/M | Reynolds number |
| Ga = gH3/ν2 | Galileo number |
Rayleigh-Bénard convection is a classical problem in fluid and gas mechanics, which has mostly been considered in terms of the Boussinesq approach for an incompressible fluid [1,2]. However, in the case of gas convection the situation is much more complicated due to gas compressibility. As a result, while studying gas convection we can only use the Boussinesq approach in laboratory studies, when the height of the layer measures a couple of centimeters (e.g., for air in normal conditions). In this case, the small height of the layer causes a relatively little change in the hydrostatic pressure; while calculations of convection in dozens and more centimeters high regions require taking into account gas compressibility described by full nonlinear equations of the gas dynamic theory [3–5].
It is necessary to consider convective flows in gas mixtures taking place in large regions when we study explosion safety issues while keeping hydrocarbons in storage reservoirs at gas stations. An explosive situation occurs when the tank is almost empty, but some small amount of hydrocarbon remains at the bottom of the tank. In the presence of convective flow, the fuel (vapors of vaporized hydrocarbon) mixes with the oxidizer (air), forming a potentially explosive gas-vapor medium. A gas-vapor mixture is explosive if the volumetric concentration of fuel vapor is between the lower and upper concentration limits of ignition. In this case, any accidental initiation (for example, a spark when turning on a switch) can lead to an emergency, the scale of which is determined by the amount of explosive gas-steam mixture formed. Since the degree of explosiveness of the mixture is determined by the concentrations of the fuel and the oxidizer, and convective processes lead to mutual movement and mixing of the fuel and oxidizer masses with changes in their local concentrations in certain areas, an explosion-proof mixture can become locally explosive and vice versa, an explosive gas mixture can become explosion-proof. The latter processes require a detailed study, and the mode, structure and intensity of convective motion are of decisive importance here, since they determine the mutual arrangement, and mixing of fuel, oxidizer and their concentrations [6–10]. Thus, it is the convective flow in this case that forms a potentially explosive gas-vapor medium from vaporized residues of liquid fuel and gaseous oxidizer. Features of the development of detonation processes in such medium have been studied in numerous works [11–15].
The features of convection in a compressible medium have been discussed in a number of monographs and discussions [16–20]. It is traditionally considered that gas compressibility under convection at laboratory scales is insignificant, and it is essential only at large (planetary) scales. In this case, both scales (laboratory and planetary) are considered asymptotic and their intersection is not taken into account.
The planetary atmosphere is treated as a compressible medium in which the flow is assumed to be adiabatic [18]. It is shown that convective flow in the atmosphere is unstable if the Schwarzschild number Sc is less than 1 and stable otherwise. The Schwarzschild number is defined in the usual way, i.e., as the ratio of the adiabatic temperature gradient to a given temperature gradient.
In this connection, we note that gas convection based on the full nonlinear equations of gas dynamics has been not adequately investigated [16], which is due to technical difficulties associated, firstly, with the large rigidity of the system of equations and with an extremely low relative pressure change [5,16].
Such rigidity of the system of equations, which leads to the need to perform calculations with an unreasonably small time step, is due to the coexistence of two types of motion-thermoacoustic waves propagating at sonic speed (analogs of pressure waves) [21] and relatively slow convective motion developing against their background. The performed methodological calculations have shown that the limitations on the time step, which ensure the stability of calculations when using explicit time schemes, are precisely determined by the need to correctly reflect the development of “fast” thermoacoustic waves, while the accuracy of the calculation is determined by both “slow” and “fast” motions. In this connection, we note that the use of implicit schemes makes it possible to multiply the time step of the calculation [2], but due to the inevitable “smearing” of “fast” thermoacoustic waves, the use of such methods is in a certain sense equivalent to the use of numerical methods with a filtering algorithm.
Some compromise is achieved with simplified models of gas convection. Derived from the equations of gas dynamics under the assumption of a small Mach number and hydrostatic compressibility parameter, the corresponding systems of equations describe the medium in which sound perturbations propagate at an infinitely large velocity. Mathematically, the structure of the obtained systems is in a certain sense similar to the structure of the viscous incompressible fluid equations with additional terms to account for compressibility [22], and, as a consequence, such a system can be successfully used in calculations of convection in regions of low heights with large variations in temperature and density [22,23]; however, calculations of convective flows in regions of bigger heights, where the compressibility of the medium begins to appear fully, require the use of full nonlinear gas dynamics equations.
Jeffrey expanded the scope of application of the Navier-Stokes equations to the case of compressible flows by taking into account the work of compression forces in the heat transfer equations [4,5]. In this case, the critical Rayleigh numbers for an incompressible medium in the Boussinesq approximation Rab and for a compressible gas Rag are related by the relation:
where Sc is the Schwarzschild number. The proposed relation describes the calculated dependence of the critical Rayleigh number on the height of the layer in the case of convection of a compressible gas with satisfactory accuracy (with an error up to 25%) and predicts adiabatic suppression of motion at its large value. By adiabatic suppression of convection here and below we mean the growth of the critical value of the Rayleigh number as the height of the layer increases.
When considering planetary-scale convective flows, it is proposed to replace a given temperature gradient with an effective temperature gradient equal to the given one but reduced by the adiabatic temperature gradient [18]. This substitution leads to the above-derived Jeffrey’s relation. The authors observed the stabilizing effect of the adiabatic gradient in atmospheric currents.
It is emphasized that the Boussinesq approximation is applicable when several conditions are satisfied, of which the most restrictive is the smallness of the Schwarzschild number [18,24]. The latter restriction is much more stringent than the restriction on the value of the product of the thermal expansion coefficient and the temperature difference commonly used in experiments [25]. It can be shown that the condition of the smallness of the Schwarzschild number is equivalent to the requirement of constancy of the critical value of the Rayleigh number.
The compressibility is very significant in near-critical gas convection and becomes decisive even at a layer thickness of about 1 mm [24]. The near-zero value of the thermodiffusion coefficient (large Prandtl numbers) here determines almost complete adiabaticity of the gas flow, and the proximity to the critical point determines a large variation of density with temperature change. Due to this, a new form of convective heat transfer in near-critical medium, known as the piston effect, becomes possible. The author mentions the existence of a region with density-stable stratification at a temperature gradient larger than adiabatic [26]. However, its study in near-critical gas is difficult due to the vanishing relative width of this region as 1/γ, which is associated with the adiabatic exponent γ approaching infinity in the vicinity of the critical point [26].
In numerical simulations, the convection of near-critical gas was considered on the basis of the gas dynamics equations with the van der Waals equation of state [26]. However, the value of these works is somewhat reduced by the use of the thermoacoustic wave filtering algorithm meant to save computational time, due to which the model used is similar to the small Mach number approximation described above with its inherent limitations.
Gas convection in a horizontal layer with horizontal boundaries free of tangential stresses is considered analytically in the linear approximation and numerically in the nonlinear approximation [27]. It is shown that convection can develop when the Schwarzschild number is strictly less than 1. It is argued that convection is impossible in the adiabatic mode and convective motion can develop only when the temperature gradient exceeds the adiabatic gradient [3,18].
Numerous works on the numerical study of convection in compressible gas have shown qualitatively correctly the presence of adiabatic suppression of convection; however, due to technical difficulties, the given values of the determining dimensionless parameters in this series of works are far from the real ones. For instance, the value of the hydrostatic compressibility criterion characterizing the relative pressure change and the resulting relative density change is overestimated by three orders of magnitude [27,28].
The necessity to take into account the adiabatic temperature gradient (gas compressibility) with corresponding corrections of the measurement results is indicated by numerous experimental works of a French group of scientists, where the temperature convection in gaseous helium at a cryogenic temperature of about 5 K was studied. It was shown that even at a relatively small height of 0.2 m, the correction for the adiabatic temperature gradient significantly changes the measured value of heat transfer [25].
Consideration of gas compressibility is particularly relevant in the experimental study of asymptotic modes of convection at extremely large values of the Rayleigh number because of the use in such experiments of regions up to 3.3 m high [29].
We should note that new technical possibilities have now appeared. The unconditional validity of the remark about the rigidity of the system of equations and the necessity to perform calculations with a small time step is partially leveled by the possibility of performing calculations according to an explicit scheme with massively parallel data processing on multicore CPUs or/and GPUs using OpenMP or CUDA technology [4,5]. The advantages of massively parallel data processing appear the stronger the larger the amount of information processed, so such computations are especially promising for detailed two-dimensional and three-dimensional calculations.
Note also that in terms of the special geometry of the region and not very high supercriticality the convection develops as a roll quasi-two-dimensional [5], which gives grounds for consideration of compressible and incompressible convective flows in the two-dimensional formulation.
The present work is devoted to the study of the features of convective instability in a bottom-heated gas layer, for certainty, in air under normal conditions. The convective two-dimensional and unsteady flow of a viscous incompressible fluid in a horizontal layer under bottom heating in the Boussinesq approximation is preliminarily considered. The critical value of the Rayleigh number and the values of the basic integral quantities are calculated, with their subsequent comparison with the corresponding values obtained in the case of a compressible gas. Then, the stability characteristics of the static convection mode of the gas layer are investigated, the role of adiabatic processes in the development of convective instability is discussed, and a diagram of convection modes is proposed. Finally, we have derived a formula for the upper limit of applicability of the Boussinesq approximation in the calculation of gas-layer convection.
2 Numeric Models and Methodology
Preliminarily, we consider the stability characteristics of the static Rayleigh-Bénard convection mode of an incompressible fluid in the Boussinesq approximation. It is obtained that the critical Rayleigh number is equal to 1971.4 at the relative horizontal extent of the flow region equal to π. For calculations of convective flows, the numerical method of longitudinal-transverse run in the modification of V.I. Polezhaev with the author’s method of calculating vortex values on rigid boundaries of the region based on the algorithm of fast Fourier transformation [2] was used on the basis of finite-difference representation of the solution. All boundaries of the region were considered rigid and isothermal and calculations were performed on a grid of (257∙65) nodes. The stream function was determined from the vortex values using the fast Fourier transform algorithm [2].
Now consider the convective flow in a compressible, viscous, and thermally conductive gas in the field of gravity, which can be described by the following system of equations [1,28]:
Here u, v, P, ρ and T are dimensionless components of velocity, pressure, density and temperature, M = ν/((γT0R)0.5H) = 4.608∙10−8∙H−1 is the Mach number, where the velocity calculated from kinematic viscosity is related to the adiabatic speed of sound, T0 = 300°K is taken as the characteristic value for temperature, the selected values of specific gas constant R = 287 J/(kg∙K), adiabatic index γ = 1. 4, kinematic viscosity ν = 16∙10−6 m2/s and Prandtl number Pr = 0.71 correspond to air, where χ denotes the gas diffusivity and CF = gH/(γRT0) = 8.130∙10−5∙H is the hydrostatic compressibility. As the length scale we chose the height of the region H, for temperature and density-their values T0 and ρ0 at the lower horizontal boundary, for the velocity-adiabatic speed of sound (γRT0)0.5, for the pressure-Rρ0T0 and time-H/(γRT0)0.5. The dependence of viscosity and thermal conductivity coefficients on temperature is neglected in the calculations. The height of the convection region in the calculations varied from 0.004 to 0.5 m.
In perspective it is supposed to consider convection of not homogeneous gas mixture in which molecular masses of gas mixture components (fuel and oxidizer) differ significantly, for example, vapor densities of gasoline and air differ in 3.5 times. Therefore, in the equation for density (the first equation of the system (1)) a term describing mass diffusion is introduced taking into account that in a perfect gas the coefficients of kinematic viscosity and mass diffusion coefficients coincide in value. Note that to the analogous equation for density, one can come also in the Boussinesq approximation [1], if to take into account the linear dependence of density on temperature and substitutes the corresponding relation in the equation for temperature. Such regularization of the density equation is not essential for relatively slow convective flows, where viscosity and heat conduction are already fully manifested due to the smallness of the Reynolds number.
Fig. 1 shows the formulation of the problem in dimensionless form. In dimensional units, the height of an area and its horizontal extent change simultaneously, but the aspect ratio remains constant, the dimensionless geometry of the region does not change and the horizontal size of the region referred to the vertical always is equal to π. And thus, the dependence of the solution to the problem on the dimensional height of the region H in the dimensionless formulation under consideration is determined only by the dependence of the parameters M and CF on H. The formulas for determining the parameters M and CF are given above.

Figure 1: Formulation of the problem
At all boundaries of the region, the values of density are derived from the system of Eq. (1) taking into account the absence of motion:
The calculations were performed using the explicit scheme in time, and since the appearance of shock waves in the solution was not expected, the convective nonlinear and diffusion terms were approximated by the monotonic scheme of [2], and thus the numerical method used was of the first order of approximation in time and the second order in space.
All calculations were performed on a grid of (241∙81) nodes with a dimensionless time step of 0.01. Test calculations on more detailed space and time grids showed sufficient accuracy and stability of the algorithm used.
All calculations were carried out near the stability threshold with the Reynolds number value as follows:
which did not exceed values of the order of 10. Here Ek denotes the total kinetic energy of the entire convective motion of the gas mass [2].
Due to the low velocity of convective flows, the main contribution to the pressure variation is made by its hydrostatic component [5].
The numerical study was organized according to the following scheme.
By calculations with different ΔT, the critical value of the temperature difference was determined, at which the solution has zero increment, i.e., it does not increase or decay in time. Then, the critical Rayleigh number was calculated from the obtained temperature difference as follows:
Here and below, we used the dimensionless temperature difference, i.e., the temperature difference related to the temperature value of the lower horizontal boundary of the region. We should note that the used technique works well for small values of H, when the perturbations of the static solution develop monotonically in time. However, oscillations were observed in the immediate vicinity of H = 0.5 m and therefore the corresponding data in Figs. 2–4 can probably be refined. In this connection, we note that regular and irregular oscillations are observed in the linear [1] and developed nonlinear [2] modes of incompressible fluid convection in the Boussinesq approximation.

Figure 2: Critical dimensionless temperature difference

Figure 3: Critical value of Rayleigh number

Figure 4: Diagram of gas convection modes
3 Analysis of Stability of Convective Flow and Applicability of the Boussinesq Approximation
Figs. 2–4 show the data as functions of the dimensional height of the region H, with H presented in meters for clarity, and the temperature difference ΔT in Figs. 2 and 4 is dimensionless.
As functions of the region height, the critical dimensionless temperature difference and the critical Rayleigh number are shown in Figs. 2 and 3. At the same time, the solid lines 1 in Figs. 2 and 3 correspond to the adiabatic temperature difference [4,5]:
lines 2 correspond to the critical temperature difference for the incompressible fluid convection in the Boussinesq approximation:
and dots represent the numerical results of the present work.
All results of systematic simulation presented here correspond to the convection mode with three vortices.
In Fig. 2, curve 3 also shows the Jeffrey’s result obtained theoretically [4,5]:
which taking into account the maximum divergence of 25%, qualitatively corresponds to the result of the present work. We should note also that at increasing H the curve (5) asymptotically passes to the adiabatic temperature difference.
According to the condition of constancy of the critical value of Rayleigh number for compressible, viscous and heat-conducting gas given in Fig. 3, we can see that the range of applicability of the Boussinesq approximation extends all over the height of the region from 1 to 10 cm. At a lower height of the region the use of the Boussinesq approximation becomes inappropriate because of large variations in temperature and density, and at higher heights-because of relatively strong changes in hydrostatic pressure and the resulting compressibility. Note also that at sufficiently large heights of the region H the calculated critical Rayleigh number grows as H4 and has close values to those calculated from the adiabatic temperature gradient.
It can be shown that at sufficiently large heights of the region, the critical temperature difference corresponds to stable stratification of the medium by density and convection develops at decreasing with height gas density due to adiabatic processes in the gas mixture.
Let us consider Eq. (2) for the gas density in the static state (in the absence of convective motion). For clarity and simplicity, let us write out asymptotic distributions for density, temperature and pressure, which can be obtained from Eq. (2) at small ΔT and CF:
The above relations show that Ph and Th always decrease with increasing y, and the density distribution at ΔT > γ∙CF (in other words, Sc < (γ − 1)/γ) corresponds to unstable stratification, and at ΔT < γ∙CF (or (γ − 1)/γ < Sc) to stable stratification, where the gas density decreases with increasing y.
At adiabatic ascent of an ideal gas particle, its adiabatic density (the density of the particle at adiabatic motion, i.e., without heat exchange with the medium) decreases according to the Poisson adiabat due to the static pressure drop:
Comparing the relations for static (6) and adiabatic (7) densities, it can be seen that the adiabatic density of the gas particle (7) is less than the static (6) and the particle floats at:
or, equivalently, Sc < 1. And at Sc > 1, the adiabatic density of the gas particle is greater than the static density (the particle returns to its initial position) and the static solution in this approximation is stable.
Thus, when choosing the value of the dimensionless temperature difference from the interval (γ − 1)∙CF < ΔT < γ∙CF (or the Schwarzschild number in the range (γ − 1)/γ < Sc < 1), convection develops at density-stable stratification, and it is the adiabaticity of gas flow that determines the possibility of convective instability at density-stable stratification. In this connection, we emphasize that the lower boundary of the region of density-stable stratification coincides with the adiabatic temperature difference (3).
The value of the dimensionless temperature difference at which density-neutral stratification is realized (the gas density does not depend on the height y) is defined as:
and the critical height of the region Hcr, above which convection under density-stable stratification is possible due to adiabatic processes (we will call such convection adiabatic), can be found as the point of intersection of the neutral stratification curve (8) and the distribution (5):
which for a gas under the considered conditions is equal to 17.3 cm.
In the author’s earlier work [5], the value of the critical height was determined as the point of intersection of the critical curves corresponding to the adiabatic temperature difference (3) and the Boussinesq approximation (4). The formula obtained in [5] differs by a constant multiplier from the above formula and gives a value of 21.7 cm, which is 25% higher than the value obtained in the present work.
We should note that without taking into account the dependence of viscosity and diffusivity of the gas on temperature, the value of the critical height (9) grows in proportion to the root of the fourth degree from the temperature of the medium.
However, the situation changes significantly if we take into account the dependence of viscosity on temperature according to Sutherland’s formula [19] and take into account the equation of state of an ideal gas. Then the formula for the dependence of kinematic viscosity on temperature and the expression for the critical height take the form:
The expression in the first brackets in the formula (10) for the critical height represents a constant, and the expression in the second bracket for simplicity we consider at high-temperature T >> C, where C = 120°K and μ0 = 18.71∙10−6 Pa∙s [19]. The value of dynamic viscosity of air here μ0 corresponds to the selected temperature T0 = 300°K.
Then, for the critical height in air, it can be obtained that:
Here the pressure P is expressed in atmospheres. It can be seen that at a high temperature the value of the critical height (11) grows linearly with increasing temperature and decreases inversely proportional to the square root of the pressure. Of course, given the range of applicability of Sutherland’s formula, we do not consider here high temperatures of the order of thousands of degrees and pressures of the order of tens of atmospheres [19].
As it is described in detail in classical monographs [1,18] and noted above, the Boussinesq approximation is applicable under a number of conditions: small temperature variation, small density variation due to temperature variation, and much smaller density variation due to hydrostatic pressure drop. In our case, these constraints are satisfied. However, in the case of a compressible gas, there appears a more significant limitation on the applicability of the Boussinesq approximation-the smallness of the ratio of the adiabatic temperature gradient to the temperature gradient in the Boussinesq approximation [24]. This ratio at small height of the region corresponds to the Schwarzschild number Sc. It can be shown that the requirement of smallness of the Schwarzschild number is equivalent to the requirement of constancy of the critical Rayleigh number.
The data in Fig. 3 show that the value of the calculated critical Rayleigh number is constant and close to that calculated for convection of an incompressible medium in the Boussinesq approximation at the height of the region from 1 to 10 cm, which determines the range of applicability of the Boussinesq approximation for convection in air under normal conditions. At smaller heights of the region the Boussinesq approximation is not applicable due to too large variations of temperature and density, and at larger heights the compressibility of the medium should be taken into account. In this connection, in addition, we note that at the height of the region from the range of applicability of the Boussinesq approximation H = 0.05 m and supercriticality r from 1.1 to 45 (supercriticality is the ratio of Rayleigh number to its critical value), the difference between the values of Nusselt number Nu and Reynolds number Re calculated by different convection models is of the order of 3% and 2%, respectively.
Simple calculations show that at the height of the region H equal to 10 cm, the value of the Schwarzschild number Sc is 0.05. Choosing this value as a threshold value for the upper limit of applicability of the Boussinesq approximation, we obtain:
It follows from relations (12) that the position of the upper limit of applicability of the Boussinesq approximation is proportional to the critical height. As a consequence, without taking into account the temperature dependence of gas viscosity and diffusivity, the position of the upper limit of applicability of the Boussinesq approximation is proportional to the root of the fourth degree of the medium temperature.
Taking into account the noted proportionality between Hb and Hcr, we can derive an asymptotic expression for the position of the upper limit of applicability of the Boussinesq approximation:
Of course, the asymptotic representation for Hb (13) is valid under the same assumptions as the corresponding asymptotics for Hcr (11).
The above consideration allows us to present the following diagram of convection modes in a compressible viscous and thermally conductive gas on the plane where dimensionless temperature difference is height of the region (Fig. 4).
The solid line 2 with points in Fig. 4 is constructed according to the analytical Jeffrey’s result (5, at H ≤ 0.2 m) and numerical results of calculations of the present work (at H > 0.2 m). Line 1 corresponds to the adiabatic temperature difference (3), and curve 3 is the line of neutral stratification (8), as it separates the regions with stable and unstable stratification of the static solution.
The critical height Hcr in Fig. 4 corresponds to the change of modes, namely, at the height of the region less than critical H < Hcr, the isobaric mode of convection (small variation of hydrostatic pressure) is realized, and at higher H > Hcr and relatively large variation of hydrostatic pressure-adiabatic and superadiabatic modes are realized. The adiabatic mode is realized in the narrow knife-shaped region in Fig. 4 and is bounded from below by the line of adiabatic temperature difference (3) (line 1 in Fig. 4) and from above by curve 3 corresponding to neutral stratification (8). The superadiabatic mode lies in Fig. 4 above the narrow knife-shaped region corresponding to the adiabatic mode and convection develops there at stable stratification; from below this mode is limited by curve 3 corresponding to neutral stratification (8). For gas under the considered conditions, the critical height Hcr is equal to 17.3 cm.
As already mentioned above, in this work, systematic research calculations were carried out only for the three-vortices convection regime. Bifurcations of convective regimes are not studied in this work, since such a goal has not yet been set.
Thus, in all calculations in this work, the convection mode has a qualitatively identical three-vortices structure. Below are shown the stream function of the stationary solution (Fig. 5), the deviations of temperature (Fig. 6) and density (Fig. 7) from their static distributions at H = 0.5 m and Sc = 1.05. The selected parameter values correspond to a point in a narrow region between the adiabatic gradient curve 1 and the solid line with dots in Fig. 4. All data in Figs. 5–7 multiplied by 107. Arrows in Fig. 5 shows the directions of rotation of the vortices. The intensity of the calculated three-vortices structure gradually decays as it approaches the neutral curve.

Figure 5: Stream function of the stationary solution
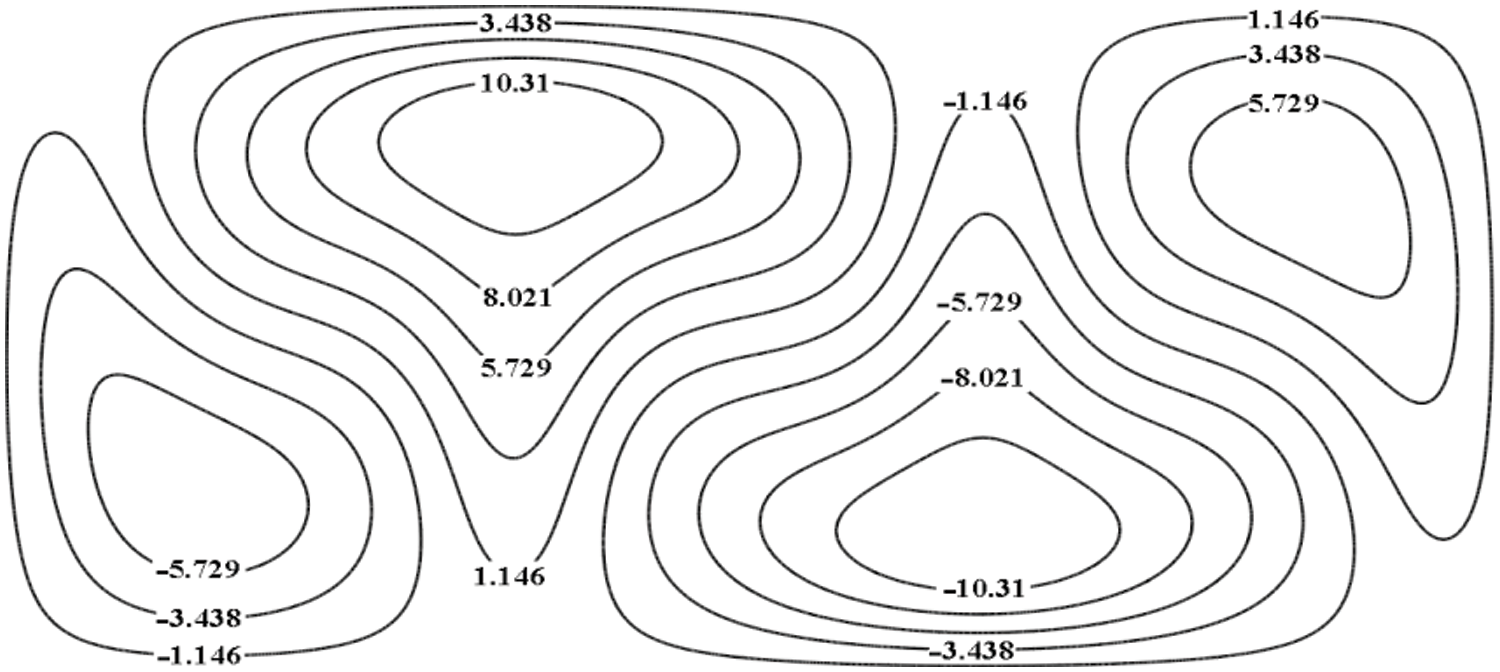
Figure 6: Temperature deviation from the static distribution

Figure 7: Density deviation from the static distribution
Convective vortices work as a kind of pumps; they lift the heated medium up to the upper horizontal boundary, and the cold medium down to the lower horizontal boundary.
Depicted in deviations from the static solution, the distributions of density and temperature differ only in sign. Namely, low temperature corresponds to a heavy medium, and high temperature corresponds to a lighter medium.
To clarify the relationship between deviations of temperature and density, we consider the equation of state, while we assume that the pressure is equal to the static pressure, and the deviations of temperature δT and density δρ from the corresponding static distributions are small. These assumptions are consistent with the assumptions about the region’s height not too high and low supercriticality adopted in this work.
Then from the equation of state we can obtain:
Now, taking into account the above relations (14) for the static distributions of temperature and density and the smallness of the values of ΔT and CF, we find:
The last relation (15) explains the correspondence obtained during calculations with the distributions of temperature and density deviations (up to sign) shown in Figs. 6 and 7, respectively.
The three-vortices convection regime with the above-mentioned correspondence between the temperature and density fields was observed with stable and unstable initial stratification, in isobaric, adiabatic, superadiabatic convection regimes and in a narrow region between the adiabatic gradient curve (curve 1 in Fig. 4) and the neutral curve (solid line with points in Fig. 4).
4 On the Role of Adiabatic Processes in the Convection of a Compressible Gas
Let us explain the role of adiabatic processes and compressibility of the medium in convection at the subcritical height of the region.
Considering that the value of the critical height Hcr (9) for convection in air under normal conditions is 17.3 cm, we consider the motion of a heated plume, for certainty, at the subcritical height of the region H = 0.1 m and at the supercritical height H = 0.5 m.
Calculations of the model problem on the rise of a heated plume (convective motion can be represented as the motion of rising and falling plumes) in a compressible medium show qualitatively different mechanisms of flow development at subcritical and supercritical heights. In the following test series of calculations, the initial conditions for the vertical velocity at the lower boundary are initiated by a rising heated plume; all other boundary conditions coincide with those described above. Observation of the plume motion is performed using special tracers, which are treated as passive admixture.
In Fig. 8, line 1 shows the density of the rising plume at H = 0.5 m and supercriticality r = 2 (the ratio of the Rayleigh number to its critical value), with line 2 corresponding to the static (initial) distribution and curve 3 to the Poisson adiabat.
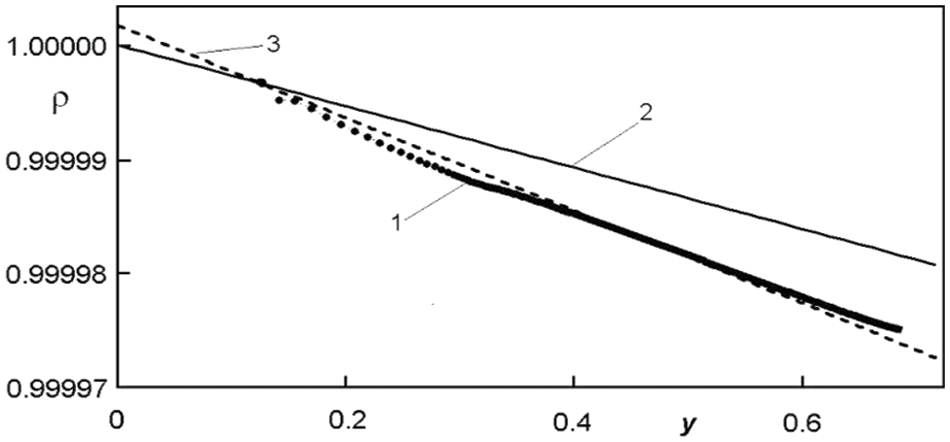
Figure 8: Density of the rising plume at H = 0.5 m
It can be seen that at the supercritical height of the region H = 0.5 m, the density of the rising plume approximates the Poisson adiabat, indicating that the flow is close to adiabatic. This is also true for the temperature distribution in the rising plume.
A significantly different situation is observed at the subcritical height of the region H = 0.1 m. Fig. 9 shows the density of the rising plume at H = 0.1 m and the same value of supercriticality r = 2; the notations are the same.

Figure 9: Density of the rising plume at H = 0.1 m
A comparison of the plume density dependences at supercritical heights (H = 0.5 m, Fig. 8) and subcritical (H = 0.1 m, Fig. 9) shows a qualitatively different mechanism of flow development, namely, at supercritical heights the plume rises adiabatically, while at subcritical heights the density rather follows a static distribution (line 2), which is due to heat conduction alone without taking convection into account. The above is also true for the temperature distribution in the rising plume. The determining role of adiabaticity is also seen at increasing supercriticality r, in the superadiabatic mode.
Adiabatic flow mode is energetically more efficient than isobaric flow mode. Physically, it is connected with the fact that at the adiabatic motion of a gas particle there is no heat exchange with the medium and it causes a large energy of a particle, increase of kinetic energy of flow and heat exchange. Thus, when the height of the region exceeds the critical value, the development of adiabatic processes should lead to intensification of the flow.
For example, let us consider the Nusselt number as a function of supercriticality r (Fig. 10) at H = 0.1 m (lower curve 1) and H = 0.5 m (upper curve 2); line 3 shows the results of verification calculations with doubled number of points in both spatial directions (480 ∙ 160). For definiteness, a two-vortices stationary convection mode is considered here.

Figure 10: Nusselt numbers as functions of supercriticality at various height of region
The approximation curves take the following form at H = 0.5 m and H = 0.1 m, correspondingly:
At the same value of supercriticality r = 10, the values of the Nusselt number at the subcritical height of the region H = 0.1 m and the supercritical one H = 0.5 m differ more than twice with a significant difference in the indices of power laws. A similar situation is observed for the Reynolds number.
Fig. 3 shows the distribution of the critical Rayleigh number as a function of the height of the region. Taking into account the constant value of the Prandtl number, the Rayleigh criterion can be interpreted as the ratio of buoyancy forces to viscous forces. The data shown in Fig. 3 show that the role of viscous forces compared to buoyancy forces gradually increases as the height of region H decreases.
Let us also consider the Galileo number:
which is the ratio of gravitational forces to viscous forces. The Galileo number (16) is directly proportional to the third power of the height of the region H. It follows from the latter that the role of viscous forces increases rapidly compared to gravitational forces as the height of region H decreases.
Taking into account that viscosity and diffusivity are related by the Prandtl number, which is considered constant in this study, we conclude that the role of viscosity and diffusivity increases as the height of the region H decreases. In turn, it is diffusivity that is responsible for the equalization of the medium temperature in the convection region, and hence it follows that the adiabatic motion at a small subcritical height of the region cannot be stable and exist long enough since the moving plume is eroded by diffusion processes related to viscosity and diffusivity, the role of which at decreasing height of the region H steadily increases.
The above is illustrated by Fig. 9, from which it can be seen that at a small subcritical height of the region H = 0.1 m the rising plume loses adiabaticity at about a height of 0.02 m, while Fig. 8 shows that at large supercritical height of the region H = 0.5 m, the rising plume moves adiabatically up to its collision with the upper horizontal boundary.
Thus, decreasing the height of the convection region H leads to the blocking of adiabatic processes.
To illustrate our conclusions, let us consider the dependence of the height Had, up to which the plume moves adiabatically, as a function of the height of the convection region H.
Our analysis of the calculated data shows that the required dependence is described by the relation (at H ≤ 0.4 m):
At small height of the region H the relation (17) showed becomes asymptotic:
Taking into account that the initial velocity of the plume in this series of calculations was set equal to 0.00205 m/s and considering it constant at a relatively small height of the adiabatic motion, we conclude that the approximate dependence of the adiabatic motion time on the height of the region has the form (at H ≤ 0.4 m):
At small height of the region H the relation (18) becomes asymptotic:
We emphasize that in the above relations the values H, Had, and tad are dimensional. And thus, a gradual decrease in the height of the convection region H leads to a consistent decrease in the adiabatic motion time and the distance covered by the rising plume in the adiabatic mode, which means a consistent blocking of adiabatic processes due to the dilution of the plume by diffusion processes related to viscosity and diffusivity, the role of which increases with decreasing height of the region H.
The degree of change in hydrostatic pressure over the height of the region and the compressibility of gas particles is determined by the value of the weight (hydrostatic) compressibility criterion CF = gH/(γRT0) = 8.13∙10−5∙H, which is equal to the relative change in hydrostatic pressure over the height of the region divided by γ.
Of course, expressed in units of relative volume, the compressibility of gas at the height of the region H = 0.5 m is a negligible value, and this creates the impression that it can be neglected and the medium can be considered incompressible. However, this impression is deceptive. In fact, exceeding the critical value of the region height allows adiabatic processes to develop, which leads to a significant intensification of the flow.
The results of calculations shown in Figs. 2 and 4 show that at H ≥ 0.322 m convection can develop at a temperature gradient much smaller than the adiabatic one, when the Schwarzschild number Sc takes values up to 1.16. The latter is probably due to the effect of gas viscosity and thermal conductivity. Thus, the statement about sufficiency and overestimation of the condition Sc > 1 for the absence of convection seems not quite reasonable [27]. This also applies to the results of linear analysis, where it is claimed that the critical value of the Schwarzschild number is always strictly less than unity [27]. However, as already mentioned, authors of this work performed the study of stability characteristics for the case of horizontal boundaries free from tangential stresses. Therefore, the transfer of conclusions from convection with rigid boundaries to that with free boundaries is not completely strict and requires additional consideration.
Let us formulate the main conclusions:
1. As follows from the diagram of convection regimes presented in the work, the critical height of the region Hcr separates the convection modes, and at the height of the region less than critical H < Hcr the isobaric mode is realized (a special case of which is the convection mode in the Boussinesq approximation), and at H > Hcr the adiabatic and superadiabatic modes are realized. In gas under normal conditions, the value of the critical height is 17.3 cm. According to the analytical formula obtained under the assumption of constant viscosity, the critical height of the region is proportional to the root of the fourth power from the absolute temperature of the gas mixture. However, the situation changes significantly if we take into account the dependence of viscosity on temperature according to the Sutherland’s formula. In this case, asymptotically at high temperature, the critical height is directly proportional to temperature and inversely proportional to the square root of the pressure. In this regard, we note that the diagram of convection regimes and all analytical formulas for the critical height were obtained for the first time and these results are new.
2. The position of the upper limit of applicability of the Boussinesq approximation is always proportional to the value of the critical height of the region, with the proportionality coefficient determined only by the value of the adiabatic index. Consequently, the conclusions valid for the upper limit of applicability of the Boussinesq approximation and for the critical height of the region are the same.
3. When the height of the region exceeds the critical value for Hcr, the flow modes change–the isobaric mode of convection changes to adiabatic and then to superadiabatic. Moreover, in the adiabatic mode convection can develop even at stable density stratification, which fundamentally distinguishes convection in a compressible medium from convection in an incompressible medium and has not been observed before. Thus, when the height of the region exceeds its critical value, consideration of gas compressibility becomes obligatory.
4. For the first time it was shown, that exceeding the height of the region of its critical value allows adiabatic processes to develop, which, as a consequence, leads to a significant intensification of the flow.
Acknowledgement: None.
Funding Statement: The author received no specific funding for this study.
Author Contributions: The author of this article confirms that all work (namely, study conception, numerical simulations, data collection and analysis and interpretation of results) on the preparation of this article was carried out by the author himself. Author reviewed all results and approved the final version of the manuscript.
Availability of Data and Materials: In the preparation of this article, only materials and data published in the open press were used. Materials and data that are not publicly accessible were not used when writing this article.
Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.
References
1. Gershuni, G. Z., Zhukhovitskii, E. M. (1976). Convective stability of incompressible fluids, pp. 1–393. Jerusalem: Israel Program for Scientific Translations. [Google Scholar]
2. Palymskiy, I. B. (2011). Turbulent Rayleigh-Bénard convection. Numerical method and calculation results, vol. 1 (In Russian). Germany: LAP. [Google Scholar]
3. Krigel’, А. М. (2016). Questions of thermodynamics of turbulent convection. Journal of Technical Physics, 86(11), 136–139 (In Russian). [Google Scholar]
4. Palymskiy, I. B., Palymskiy, V. I. (2021). Convection of compressible gas. Proceedings of Analytical and Numerical Methods in Differential Equations Conference (ANMDE 2021), vol. 2. Suranaree, Thailand. [Google Scholar]
5. Palymskiy, I. B. (2022). On the features of convection in a compressible gas. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 11(1), 29–35+3. [Google Scholar]
6. Fomin, P. A., Palymskiy, I. B. (2023). Models of the kinetics of explosive processes in multi-fuel gas mixtures, vol. 4, pp. 1–164 (In Russian). Novosibirsk: SGUGIT. [Google Scholar]
7. Palymskiy, I. B., Fomin, P. A., Gharehdash, S. (2019). On control of convection intensity of the reacting equilibrium gas. Computational Thermal Sciences, 11(4), 297–314+5. https://doi.org/10.1615/ComputThermalScien.v11.i4 [Google Scholar] [CrossRef]
8. Trotsyuk, A. V., Fomin, P. A. (2019). Modeling of an irregular cellular structure of the detonation wave in a two-fuel mixture. Combustion, Explosion and Shock Waves, 55(4), 384–389. https://doi.org/10.1134/S0010508219040026 [Google Scholar] [CrossRef]
9. Trotsyuk, A., Fomin, V., A., P. (2020). Multi-front detonation structure in two-fuel mixtures–numerical modeling. Journal of Physics: Conference Series, 1666(1), 012070. [Google Scholar]
10. Fomin, P. A., Trotsuk, A. V. (2022). Modeling the kinetics of detonation processes in gas mixtures, pp. 1–205 (In Russian). Novosibirsk: SGUGIT. [Google Scholar]
11. Fomin, P. A., Trotsyuk, A. V. (2019). Reduced model of chemical kinetic and two-dimensional structure of detonation wave in rich mixtures of methane with oxidizer. Journal of Physics: Conference Series, 1261, 12037. [Google Scholar]
12. Fedorova, N. N., Fomin, P., Valger, S. (2019). Propagation of shock waves formed by explosion of the air-propylene mixture in a T-pipeline. Journal of Physics: Conference Series, 1404, 12057. [Google Scholar]
13. Khmel, T. A., Fomin, P. A. (2019). Propagation of cellular detonation in a gas suspension in the presence of a concentration gradient. Journal of Physics: Conference Series, 1404, 12059. [Google Scholar]
14. Li, Z. H., Yu, P., Hu, J. J., Li, Y. R. (2021). Rayleigh-Bénard convection of a gas-vapor mixture with abnormal dependence of thermal expansion coefficient on temperature. International Communications in Heat and Mass Transfer, 124(61), 105245. [Google Scholar]
15. Valger, S., Fedorova, N. N., Fomin, P. A., Zhongqi, W. (2020). Blast wave dynamics caused by explosion of toroidal cloud of propylene-air mixture. AIP Conference Proceedings, 2288(1), 30082. [Google Scholar]
16. Lapin, Y. V., Strelets, M. H. (1989). Internal gas mixtures flows, pp. 1–368 (In Russian). Moskow: Science. [Google Scholar]
17. Landau, L. D., Lifshitz, E. M. (2013). Course of theoretical physics. In: Fluid mechanics, vol. 6, pp. 1–558. London: Elsevier Science & Technology Books. [Google Scholar]
18. Tritton, D. J. (2012). Physical fluid dynamics, pp. 1–536. London: Springer. [Google Scholar]
19. Smits, A. J., Dussauge, J. P. (2006). Turbulent shear layers in supersonic flow, 2nd edpp. 1–417. USA: Springer Science. [Google Scholar]
20. Verma, M. K. (2018). Physics of buoyant flows: From instabilities to turbulence, pp. 1–328. Singapore: World Scientific Publishing. [Google Scholar]
21. Zubkov, P. T., Kovalenko, M. A. (2010). Symmetry and asymmetry in a layer of compressible gas. Thermophysics of High Temperatures, 48(3), 438–443 (In Russian). [Google Scholar]
22. Wan, Z. H., Wang, Q., Wang, B., Xia, S. -N., Zhou, Q. et al. (2020). On non-Oberbeck-Boussinesq effects in Rayleigh-Bénard convection of air for large temperature differences. Journal of Fluid Mechanics, 889(10A), 1–21. [Google Scholar]
23. Wang, Q., Xia, S., Yan, R., Wan, Z. (2019). Non-Oberbeck-Boussinesq effects due to large temperature differences in a differentially heated square cavity filled with air. International Journal of Heat and Mass Transfer, 128, 479–491. https://doi.org/10.1016/j.ijheatmasstransfer.2018.06.079 [Google Scholar] [CrossRef]
24. Kogan, A., Meyer, H. (2001). Heat transfer and convection onset in a compressible fluid: 3He near the critical point. Physical Review E, 63, 56310. 1–15. https://doi.org/10.1103/PhysRevE.63.056310 [Google Scholar] [PubMed] [CrossRef]
25. Chavanne, X., Chilla, F., Chabaud, B., Castaing, B., Hebral, B. (2001). Turbulent Rayleigh-Bénard convection in gaseous and liquid he. Physics of Fluids, 13(5), 1300–11320. https://doi.org/10.1063/1.1355683 [Google Scholar] [CrossRef]
26. Amiroudine, S., Bontoux, P., Larroude, P., Gilly, B. (2001). Direct simulation of instabilities in a two-dimensional near-critical fluid layer heated from below. Journal of Fluid Mechanics, 442, 119–140. https://doi.org/10.1017/S0022112001004967 [Google Scholar] [CrossRef]
27. Gorbunov, A. A., Polezhaev, V. I. (2008). Perturbation method and numerical modeling of convection for the rayleigh problem in liquids with an arbitrary equation of state, preprint № 897 (In Russian). Moscow: Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences (IPMech RAS). [Google Scholar]
28. Polezhaev, V. I. (1967). Numerical solution of the Navier-Stokes equations for flow and heat transfer in a closed two-dimensional domain (Ph.D. Thesis) (In Russian). Research Institute of Thermal Processes, Russia. [Google Scholar]
29. Roche, P. E. (2020). The ultimate state of convection: A unifying picture of very high Rayleigh numbers experiments. New Journal of Physics, 22, 73056, 1–10. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools