Linear and Non-Linear Dynamics of Inertial Waves in a Rotating Cylinder with Antiparallel Inclined Ends

1  Introduction

A rotating homogeneous fluid can support the internal oscillatory motion known as inertial waves [1]. The existence of these waves is associated with the quasi-elastic properties of the Coriolis force, which tends to return radially displaced liquid particles to their original position. In the absence of viscosity, such a motion would be equivalent to circularly polarized oscillations. If the oscillation frequency is less than twice the rotation rate of the system , the fluid particles describe circles in an inclined direction with respect to the vector Ω . The most interesting properties of these waves are due to the unusual dispersion relation, according to which the direction of wave propagation is determined only by the wave frequency. In an unbounded fluid, the characteristic surface along which the waves propagate has the form of a cone with the aperture θ=arcsin⁡(σ/2) relative to the rotation axis, where σ is the dimensionless oscillation frequency. In closed cavities, the spectrum of possible regimes is enriched by the excitation of inertial eigenmodes [2], as well as the so-called wave attractors [3]. Wave attractor represents a limit cycle, where the trajectories of the wave beams are attracted after multiple reflections from the cavity walls. An important condition is the presence of at least one inclined wall relative to the rotation axis. The dispersion relation limits the direction of wave propagation: the beam reflected from the inclined boundary retains an angle with respect to the rotation axis and not to the normal of the boundary. Due to this, the width of the wave beam narrows after reflection, while the waves are “attracted” to one closed trajectory [4,5]. It is worth noting that wave attractors exist not only within the framework of inviscid models but are also successfully identified in the experiments [4]. In the case of spherical shell geometry, the waves can form closed trajectories that are not attractors. These regimes owe their existence to the cavity boundaries symmetry when the wave energy is periodically pumped into one closed trajectory (periodic orbit) [6,7]. A similar regime of symmetric reflection of wave beams is also observed in a rotating cylinder with two parallel inclined ends [8].

The properties of inertial waves have much in common with internal waves in a stratified fluid, where the difference between gravity and buoyancy forces plays a role of the restoring force. If the density-stratified fluid rotates, inertia-gravity waves arise [9]. In connection with the geophysical applications, the geometry of the spherical shell is of great interest for the research [6]: inertial waves are widespread in the oceans, atmosphere, liquid planetary cores and rotating stars. Nevertheless, the main features of the linear and non-linear wave regimes can be studied in the cavities that are geometrically simpler. On the one hand, the cavity geometry makes it possible to simulate different regimes; on the other hand, the simplicity of setting problems allows discovering new, previously unknown features. For example, in [4,10,11] the cavity was a rotating prism with a rectangular trapezoidal cross-section. We also note a series of works on the study of wave motion in an unevenly rotating cube. If the rotation axis passes through two opposite faces of the cube, then the flow regimes are inertial modes [12,13]. If the rotation axis passes through two opposite vertices, the sources of the waves are the corners and edges of the cube. The appearance of the sloping walls makes it possible to focus the waves into an attractor [14]. In the case of the rotation axis passing through the midpoints of two opposite edges, the spatial structure of the wave patterns becomes more complicated [15].

With an increase in the oscillation amplitude, the non-linear interactions in the wave beam lead to the development of the cascade processes. The perturbations are transmitted to the smaller scales by the mechanism of triadic interactions and dissipate due to viscosity. Most often, the wave attractors of the inertial or internal waves are used for laboratory modelling of the triadic resonance instability [11,16–18]. Nevertheless, the use of the focusing reflection is not necessary to achieve weakly non-linear regimes [19,20]. In a rotating cylinder close to the eigenfrequency of inertial mode, the triadic resonance has been known since McEwan [21] as “resonant collapse”. In a precessing cylinder, the instability satisfies the triadic resonance condition in the form of two inertial modes of the cylinder and one forced Kelvin mode [22,23]. In the case of spherical shell geometry, the triadic interactions appear against the background of the non-axisymmetric instability of the Taylor column [24].

An important issue is the transfer of wave energy to the zonal flow. Thus, the linear and non-linear fluid response in a rotating cavity with one sloping wall is experimentally studied in [4]. The wave focusing on the attractor leads to the generation of a cyclonic mean flow. This flow is localized along the axial cylinder that intersects the sloping bottom at the position where the focusing takes place. It is shown that this is the result of centrifugal instabilities, due to the mixing of angular momentum. A cylindrical cuvette with two parallel inclined ends is used in [25]. Since the attractor branches are reflected from two inclined walls, the number of mean vortices is two. When the focusing reflections are located opposite to each other (near the rotation axis), the vortices are combined into one cyclonic vortex. In the axisymmetric cavity geometry (spherical shell [26] or the annular layer with a sloping bottom [18]), the mean flow has the form of a liquid geostrophic cylinder. In [26], a forcing is introduced into the system by the circular oscillations of the inner core, and in [18]–by precessions of the upper lid representing a flat annular disk. An increase in the oscillation amplitude leads to a non-axisymmetric instability and the appearance of a periodic system (cluster) of the mean columnar vortices. In both cases, the trigger mechanism is the triadic resonance instability. Moreover, the dispersion equation allows one to interpret the vortex cluster as Rossby waves.

Considering the effects mentioned above, inertial waves can be useful for controlling fluid movement in industrial processes. An example is the concept of a soft bioreactor for the culture of microalgae [27]. The resonance of the inertial mode in a precessing cavity creates an effective mixing, resulting in nutrient transfer and more active cell growth. There are laminar planetary mixers, which use the combined effect of the rotation of a cavity around an axis and the rotation around an off-axis distance from the cavity [28]. Mean flows excited by inertial waves can be a convenient tool for controlling heat-mass transfer [29], a chemical reaction at the interface [30], fluidization, and transport of granular medium [31,32].

In this paper, we experimentally study the linear and non-linear fluid response in an unevenly rotating cylinder with two antiparallel inclined ends. Referring to geophysical applications [33], we will use the term “librations” to denote the non-uniform rotation. In contrast to [8], the azimuthal cross-section of the cavity can be conditionally divided into two parts, where the cavity length narrows and expands with radius. It allows us to investigate how the boundary conditions (fluid depth increases or decreases with radius) affect the zonal flow excited by inertial waves. At large amplitudes of librations, the wave regime with the fundamental frequency is destroyed according to the scenario of triadic interactions. For the first time, we study the relationship between subharmonics of the triadic resonance and the appearing mean vortex structures.

2  Experimental Setup and Methodology

The cavity is a circular cylinder of a radius R=26 mm with end walls inclined relative to the cross-section plane at an angle α=23∘ (Fig. 1). The cavity is filled with a low-viscosity liquid and rotates around a horizontal axis with a velocity Ω . In contrast to previous studies [8], the case of antiparallel ends inclination is considered. Thus, one of the axial sections is an isosceles trapezoid with bases L=99 mm and l=55 mm, and the one mutually perpendicular to it is a rectangle with the sides (L+l)/2=77 mm and 2R=52 mm. To excite the inertial waves, the rotation rate of the cavity periodically changes according to the law:

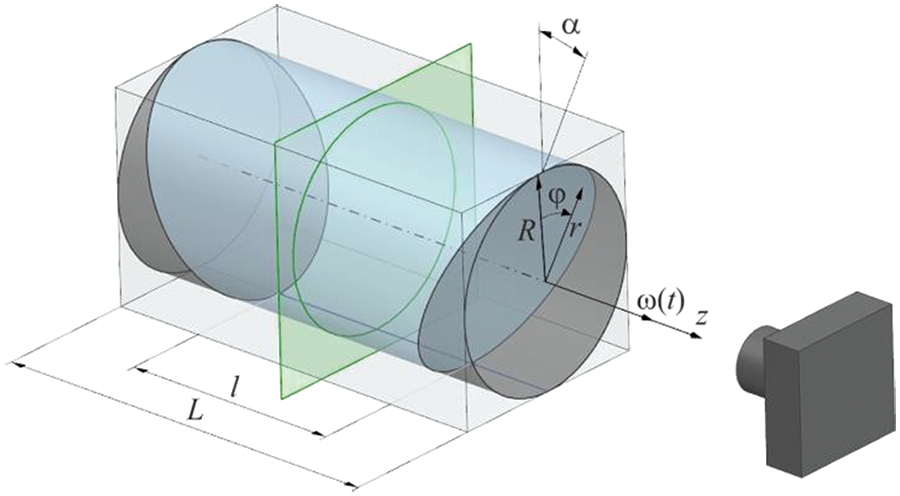
Figure 1: Sketch of a rotating cylinder with the antiparallel ends. The green plane indicates the position of laser sheet

ω(t)=Ω[1+εsin⁡(Ωlibt)], (1)

where Ω is the mean rotation rate, Ωlib is the angular libration frequency, and ε=ΔφΩlib/Ω is the modulation amplitude of the rotational oscillations; in the experiments ε≤0.15 . The parameter σ=Ωlib/Ω characterizes the dimensionless frequency of librations. In all experiments the mean rotation rate is Ω=62.8 s−1, while the libration frequency σ can be set from 0.3 to 2.0.

The experiments are carried out on the same setup as in [8]. The cuvette is installed in the ball bearings of the vertical metal supports and driven into rotation by a stepper motor (Fulling Motor FL86STH118-6004A). A high-speed camera (CamRecord CL600x2) and a continuous DPSS laser (KLM-532/h-1000) stationary in the laboratory reference frame are used to study the flow structure. The working fluid is a water-glycerol solution with kinematic viscosity ν=5 cSt. Note that to compensate for the optical distortions on the cylindrical wall, the outer boundary of the cuvette has the form of a transparent parallelepiped. A cylindrical coordinate system (r, φ, z) is used to describe the fluid motion. The z-coordinate is measured from the acute angle of the cavity end from which the observation occurs; the φ -direction is also measured from the acute angle clockwise.

The flow structure is characterized by the Ekman number E=ν/ΩR2 and in all experiments takes the value E=1.18⋅10−4 . We use Particle Image Velocimetry (PIV-method) to qualitatively visualize the flow structure and measure the quantitative flow characteristics. For this purpose, the working fluid is seeded by polyamide spherical particles with a size of 20 µm and a density of 1.04 g/cm3. When studying the azimuthal velocity field, the typical shooting frequency is 360 fps with a frame resolution of 800 × 800 pixels. For the transition from a laboratory frame to a reference frame rotating with a velocity of Ω , the entire sequence of frames is rotated against the direction of rotation with a step of 10°. Due to this, the influence of a solid-body rotation of the cavity is excluded from consideration. The velocity fields are taken in two sections z/L=0.3 and 0.5. Further cross-correlation processing is carried out using the free software PIVlab [34]. To study the velocity field in the axial section, the shooting is carried out at a frequency of 10 fps. A detailed description of the technique for obtaining instantaneous and time-averaged velocity fields is given in [25].

3  Results

3.1 Linear Regimes of Inertial Wave

In a rotating cylinder with sloping ends, librations can excite various resonance wave regimes. The strongest resonant response can be expected when the inertial modes–eigenfrequencies of a rotating fluid in a closed cavity–are excited. These regimes are characterized by large-scale fluid oscillations. On the other hand, due to the wall inclination relative to the rotation axis, inertial wave beams can focus on closed trajectories. To identify the regimes, we plot the time-averaged velocity of the oscillatory flow <U> =1N∑u as a function of the libration frequency σ (Fig. 2). Here N is the number of frame pares involved in the averaging, and u is the full average velocity in the axial section. To compare the results at different libration amplitudes, the velocity <U>  is normalized to the amplitude of the pulsational velocity at the cavity sidewall ΔφΩlibR .

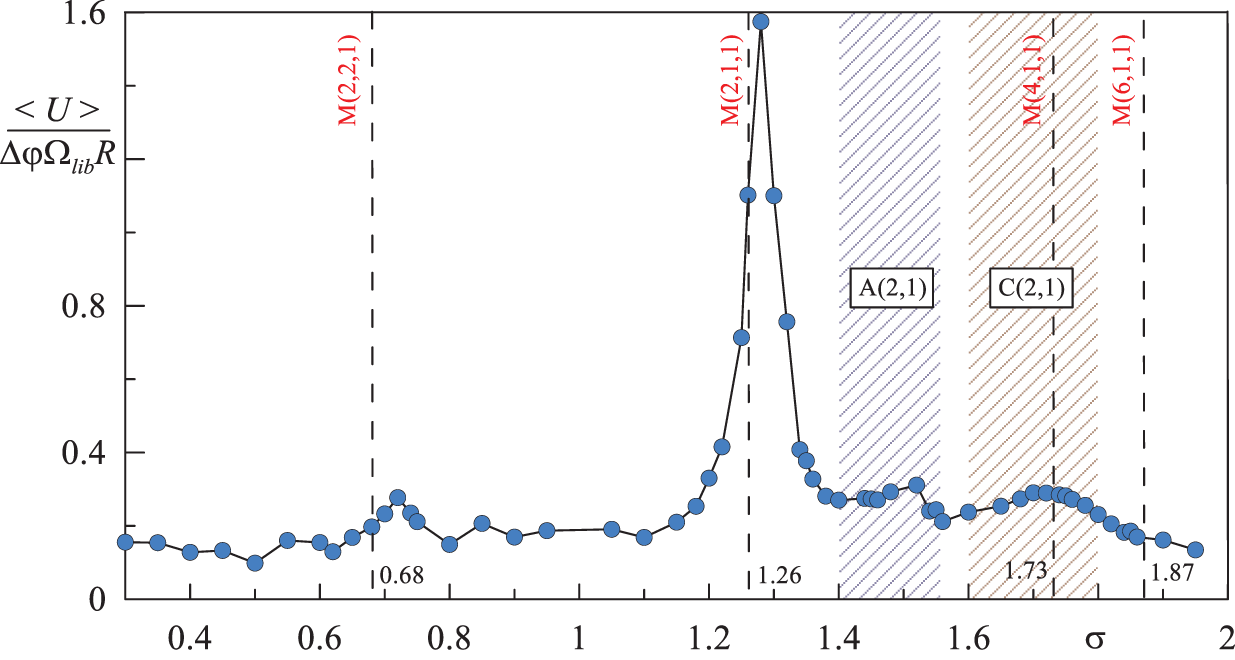
Figure 2: Time-averaged velocity of the oscillatory flow depending on the libration frequency σ ; the shading indicates the regimes of A(2,1) the wave attractor and symmetric reflection C(2,1); the vertical dashed lines show the natural frequencies of the inertial modes with k = 1

There is a set of peaks in Fig. 2: σ=0.72 , 1.28, 1.52, and 1.70. The strongest resonant response is observed at a frequency σ=1.28 (Fig. 2). The visualization of the instantaneous velocity field using the PIV-method shows that the flow structure in the libration phase Ωlibt=0 has the form of two global vortices of opposite swirl (Fig. 3a). The vortices are symmetrically inclined relative to each other, and their centres are shifted from the rotation axis to the obtuse angles of the cavity section. Over time, there is a periodic change in the direction of fluid movement in vortices and in the libration phase Ωlibt=π the vorticity has the opposite sign. At a frequency σ=0.72 , a system of six vortices is excited (Fig. 3b). Observations show that the position of the vortices in the trapezoidal section does not change with time, while the vorticity changes during the libration period. Thus, these regimes resemble standing waves or inertial modes in a rotating cylinder [35,36]. Each mode can be characterized by axial n , radial m and azimuthal k wavenumbers and is denoted as M(n,m,k). In the case under consideration, the spatial structure of the modes is strongly modified by the geometry of the cavity ends. Boundary conditions ensure the support of only non-axisymmetric modes with the azimuthal wave number k=1 and even axial wave numbers n = 2, 4, …, etc. It is worth noting that due to the non-axisymmetric structure of the modes, in a rectangular section, the position of the vorticity centres moves in a radial direction.

Figure 3: Snapshots of the velocity fields for different regimes in the libration phase Ωlibt=0 : M(2,2,1) and M(2,1,1) inertial modes (a, b); A(2,1) attractor (c, d); symmetric reflection of wave beams (e, f). The color shows the velocity magnitude; the white lines show the wave beam characteristics

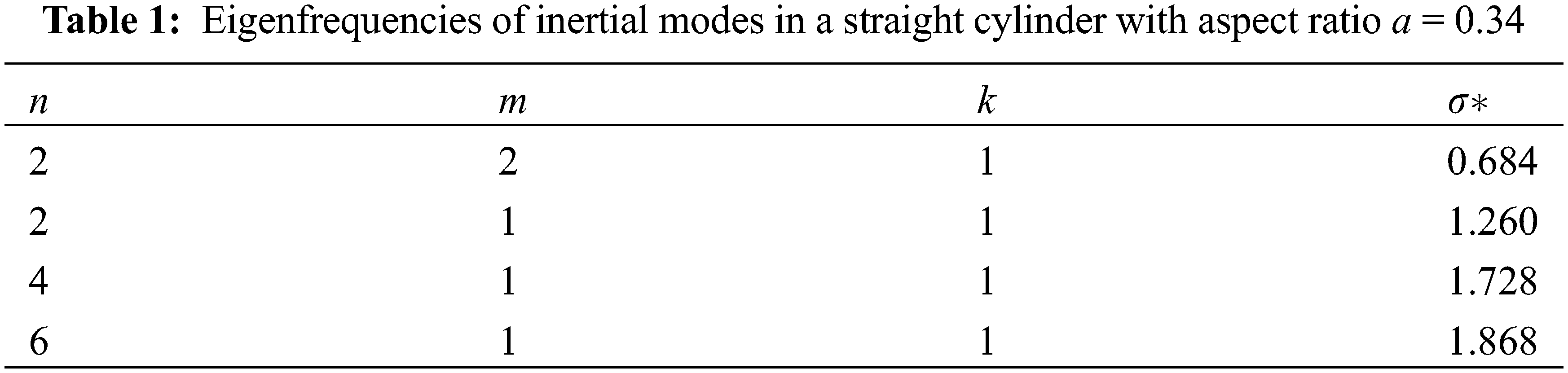
Eigenfrequencies of the inertial modes depend only on the geometry of the cavity, and their values are most easily calculated for a straight cylinder [1]. Therefore to estimate the theoretical values of frequencies σ∗ for the geometry under consideration, we introduce the average aspect ratio a=2R/(L+l)=0.34 . Then the resonant frequencies can be defined as

σ∗=(1+ξnmk2/π2n2a2)−1/2, (2)

where ξddξJ|k|(ξ)+k(1+ξ2/n2π2a2)1/2J|k|(ξ)=0 and J|k|(ξ) is the Bessel function [1]. It can be seen that the calculated values of the inertial modes (Table 1) are in good agreement with the positions of the resonance peaks in the experiments. Another extremum is observed at a frequency σ=1.73 (Fig. 2), which corresponds to the mode М(4,1,1). In this case, the structure of the oscillatory flow in the experiments slightly resembles four oscillating vortices oriented at the angles θ=arcsin⁡(σ/2) relative to the rotation axis.

Attractors are characterized by the convergence of wave beams to the limit cycle and are denoted as A(n,m), where n and m are the number of reflections from the horizontal and vertical walls in the axial section, respectively. The focusing effects into A(2,1) attractor are observed in the frequency range σ=1.4−1.55 . In this case, the wave beams propagate along a trajectory consisting of two parallelograms (Figs. 3c and 3d). At first glance, the trajectory resembles the inertial mode M(2,1,1). Nevertheless, the spatial distribution of the wave energy is different: fluid oscillates along relatively narrow shear layers. The shape of the trajectory can be predicted within the framework of the ray-tracing model with multiple reflections from the sloping walls. Figs. 3c and 3d show that the inclination θ=arcsin⁡(σ/2) and position of the wave beams in the experiment are in good agreement with the limiting focusing reflection in the model (white lines).

In the frequency range σ=1.6−1.8 , the shape of the trajectory also resembles A(2,1) attractor (Figs. 3e and 3f). Nevertheless, the ray-tracing does not predict focusing effects. From the ray theory, it follows that the closed trajectory appears due to the peculiarities of the cavity geometry and the symmetry of the location of the emission points. This regime C(2,1) is similar to the case of periodic orbits in a rotating spherical shell, which are not the attractors [6,7]. The excitation of this regime is accompanied by a local increase in the oscillatory motion (Fig. 2), and its frequencies coincide with the M(4,1,1) mode. Previously, similar regimes of the wave beam symmetric reflection were described in a rotating cylindrical cavity with a parallelogram axial section [8].

Thus, the cavity geometry supports various wave regimes, which differ in the spatial distribution of wave energy: inertial modes, inertial wave attractor and symmetric reflection of wave beams. The first regime–inertial modes–is characterized by the global fluid oscillations in the cavity. The structure of instantaneous flow is a system of oscillating vortices, the sign of vorticity in which periodically changes (Figs. 3a and 3b). The excitation of the inertial mode M(2,1,1) corresponds to the strongest inertial response of the fluid to the libration forcing (Fig. 2). The next discovered regime is the A(2,1) wave attractor. In this regime, the fluid oscillates along a relatively thin closed trajectory formed by the attractor branches (Figs. 3c and 3d). The focusing of wave beams is ensured by the presence of two inclined boundaries: sequential reflection leads to the narrowing of the wave beam and reaching the limit cycle. The last regime of symmetric wave reflection can be obtained by the first two reflections of beams emitted from the sharp cavity corners (Figs. 3e and 3f). Visually, the C(2,1) regime strongly resembles the A(2,1) attractor and is also accompanied by a local increase in the inertial response (Fig. 2). The main difference is that for the C(2,1) regime, the closed trajectory obtained in the experiments is not a limit cycle. To better understand the behaviour of fluid motion in various regimes, we attach a series of videos (see supplementary materials). The video demonstrates the dynamics of velocity fields in the axial section of the cavity; the colour shows the vorticity.

3.2 Zonal Flow

The fluid oscillations excited by librations lead to the appearance of a steady azimuthal flow. In a straight cylinder in the absence of inertial waves, this flow is retrograde, excluding the region near the side wall where the prograde flow is generated [35–37]. As shown in [38], the generation mechanism is associated with the non-linear effects in Ekman boundary layers on the end walls. The parallel inclination of the ends leads to a violation of the azimuthal flow symmetry along the coordinate z/L [25]. In the case under consideration, due to the antiparallel ends inclination, the three-dimensional effects are enhanced. Next, let us consider in detail the non-linear response of the fluid only for the resonant frequencies of the M(2,1,1) inertial mode and the A(2,1) attractor.

At a frequency σ=1.28 , the zonal flow structure is one mean vortex located at a radial distance r/R=0.5 and an angle φ=180∘ (Fig. 4a). In the figure, the cavity rotates clockwise, while the rotation direction of the liquid in the vortex is anticyclonic (blue colour). Observations show that the vortex position and the vorticity magnitude do not change with time. This can be illustrated in Fig. 4b, which shows the moving average of vorticity with a window step Δt/Tlib=3 along a ring with a radius r/R=0.5 (white dashed line in Fig. 4a): the azimuthal position of the averaged vorticity maximum is constant throughout the entire experiment time. Note that this flow structure is typical for the central part of the cavity z/L=0.5 , and near the end walls the two-dimensionality is violated. Under conditions of the inertial wave attractor, a cyclonic vortex arises with maximum vorticity at a distance r/R=0.24 and an azimuthal angle φ=20∘ (Fig. 4c). At φ=180∘ , a second vortex with anticyclonic swirl and significantly lower intensity is formed. Similarly, Fig. 4d shows that in the linear regime of the (2,1) attractor, the azimuthal distribution of the moving average of vorticity does not change with time.

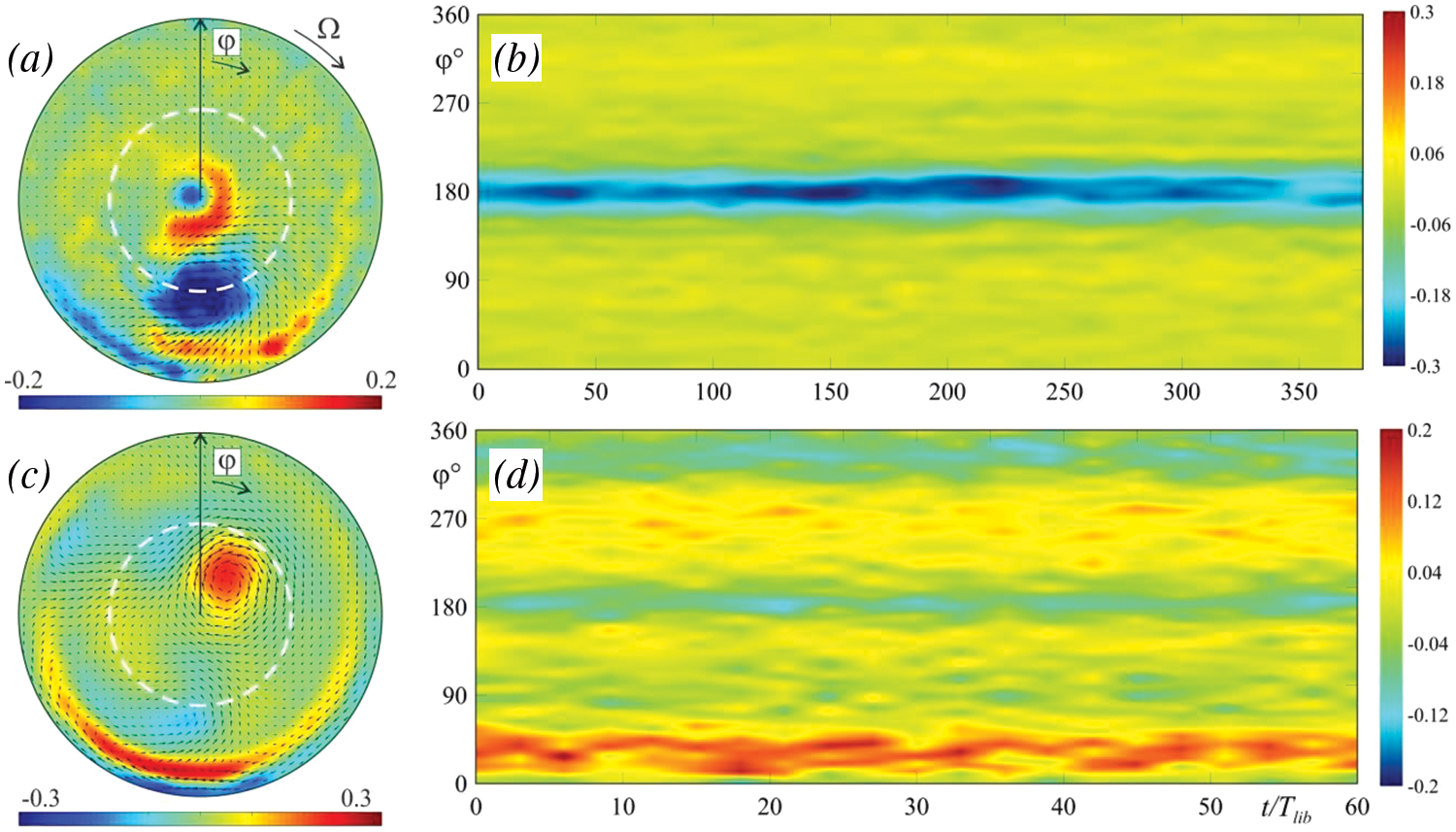
Figure 4: The averaged azimuthal velocity fields in cross-section passing through the cavity center ( z/L=0.5 ) in the linear wave regimes at σ=1.28 and ε=0.01 (a); σ=1.50 and ε=0.02 (c). The direction of the cavity rotation is clockwise; the color shows the z-component of the vorticity (positive values corresponds to the cyclonic rotation, negative values–to the anticyclonic ones); the vertical solid line shows the position of φ=0 . The time-dependence of the steady vorticity along a ring (white dashed circle on (a, c)) of a radius r/R=0.5 (b, d)

Let us discuss the mechanism of the zonal flow generation. The place of the inertial wave interaction with the sloping walls determines the position of the mean vortices. The focusing reflection of the A(2,1) attractor is located at r/R=0.30 and is shifted to the acute angles of the cavity section (Fig. 3c). This corresponds to the angular coordinate φ=0 in Fig. 4c, which is generally consistent with the visual observations of the position of the vortex. In the case of the M(2,1,1) inertial mode, the places of wave reflection are shifted to obtuse angles and are more “blurred” along sloping walls (Fig. 3b). Since the exact coordinate of the reflection point cannot be determined, we estimate the average radial position of the interaction places as r/R≈0.5 . In this case, the displacement of the reflection point corresponds to the angular coordinate φ=π , which also agrees with the position of the vortex in Fig. 4a. Thus, we can conclude that the spatial structure of the inertial wave determines the structure of the zonal flow. Apparently, this is explained by the non-linear effects in viscous boundary layers, where the mixing of angular momentum occurs due to the wave reflection. Interestingly, the cyclonic flow generation occurs in the region 270∘<φ<90∘ (close to the acute cavity corners), while the anticyclonic one–in the region 90∘<φ<270∘ (close to the obtuse corners). Thus, if the fluid depth increases (decreases) with radius, the cyclonic (anticyclonic) flow is generated.

Previously, the generation of the mean vortices was discovered in a librating cylinder with parallel inclined ends [25]. A cyclonic flow in the form of a cylindrical core arose when the A(1,1) attractor branches were reflected from the rotation axis. The change in the attractor shape and the corresponding displacement of the reflection points from the rotation axis were accompanied by the formation of a system of stationary cyclonic and anticyclonic vortices. Note that in a non-uniform rotating prism with a trapezoidal section, the inertial wave attractor also generates the cyclonic flow [4].

4  Discussions

4.1 Zonal Flow Instability and Triadic Resonances

Visual observations from the end wall show that at a critical value of ε , the steady zonal flow (Figs. 4a and 4c) is destroyed in a threshold manner. This process is accompanied by the separation of the main vortex into several pieces, which move in the azimuthal direction. Fig. 5 shows the instability thresholds depending on the frequency of librations σ (gray dots). The first minimum in the figure corresponds to the frequency σ=1.28 . This value coincides with the resonant response of the fluid at the M(2,1,1) frequency. This result is expected, since under the resonance conditions the most intense oscillatory flow occurs at the natural frequency. When the frequency changes (increase or decrease in σ ), the instability thresholds shift to the region of the large amplitudes. Another minimum is observed at a frequency σ=1.50 and corresponds to the A(2,1) attractor. The decrease in the instability threshold at a frequency σ=1.48 turned out to be a surprise. In this case, the oscillatory flow structure is qualitatively similar to σ=1.50 and represents a narrower A(2,1) attractor. Investigation of the reasons for the decrease in the instability threshold at a given frequency is beyond the scope of this work. Next, we will focus on a more detailed consideration of the non-linear regimes at frequencies σ=1.28 and σ=1.50 (red dots in Fig. 5).

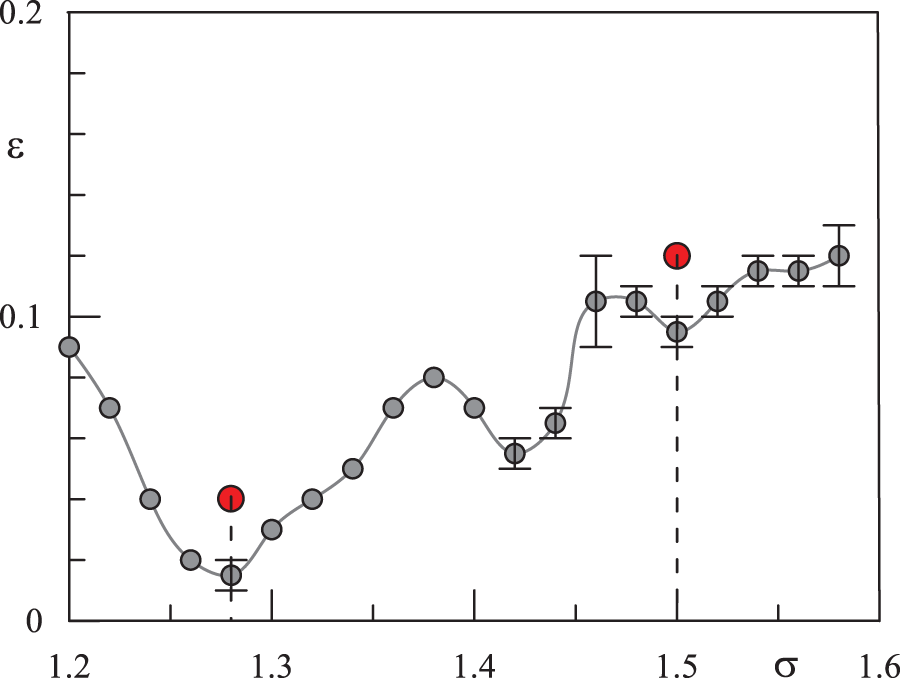
Figure 5: Azimuthal flow instability thresholds depending on the libration frequency (gray dots). The red dots correspond to the experimental results in the non-linear regimes shown in Figs. 6–9

To clarify the instability mechanism of the zonal flow, we study the instantaneous azimuthal velocity field in two cross-sections z/L=0.3 and 0.5 . Based on the PIV-data, a spectral analysis is carried out for the region 0≤r/R≤1 , 0≤φ≤2π . Further, the spectrograms are constructed in accordance with [39]:

S(ω,t)=⟨|∫−∞+∞uφ(τ)exp(−iωτ)h(t−τ)dτ |2⟩(r,φ), (3)

where h(t) is the Hamming window.

Fig. 6 shows the spectrograms of the non-linear regimes at frequencies σ=1.28 and σ=1.50 . The time moment t/Tlib=0 corresponds to the start of shooting, while the experiment begins with a gradual increase in the libration amplitude ε to the desired value with a step of Δε=0.01 . This means that the presented flow regimes were already preceded by instability. Regardless of the libration frequency, the strongest fluid response is observed at ω/Ω=σ and ω/Ω=1 . The last frequency (denoted as σrot in Figs. 6 and 7) appears as a result of the transition from a laboratory reference frame to a frame uniformly rotating with a frequency Ω . Since in experiments the direction of the rotation axis may slightly not coincide with the optical axis of the camera lens, the rotation of the frames sequence gives a precession with the mean rotation frequency. This artefact frequency is also identified in the linear regimes and does not affect the physical effects considered in this article.

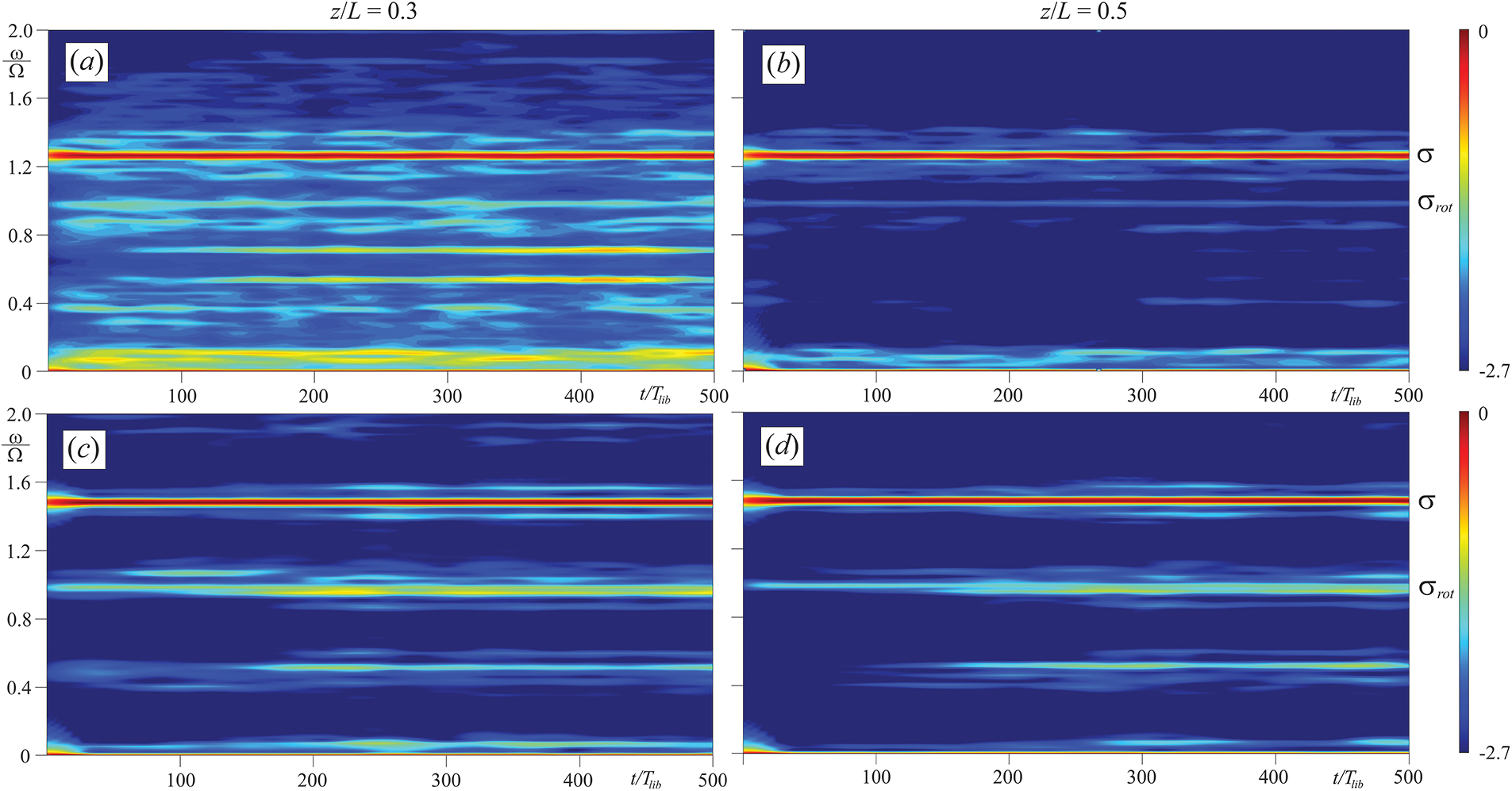
Figure 6: Spectrograms of the azimuthal velocity at σ=1.28 and ε=0.04 (a, b); σ=1.50 and ε=0.15 (c, d) and different cross-section z/L

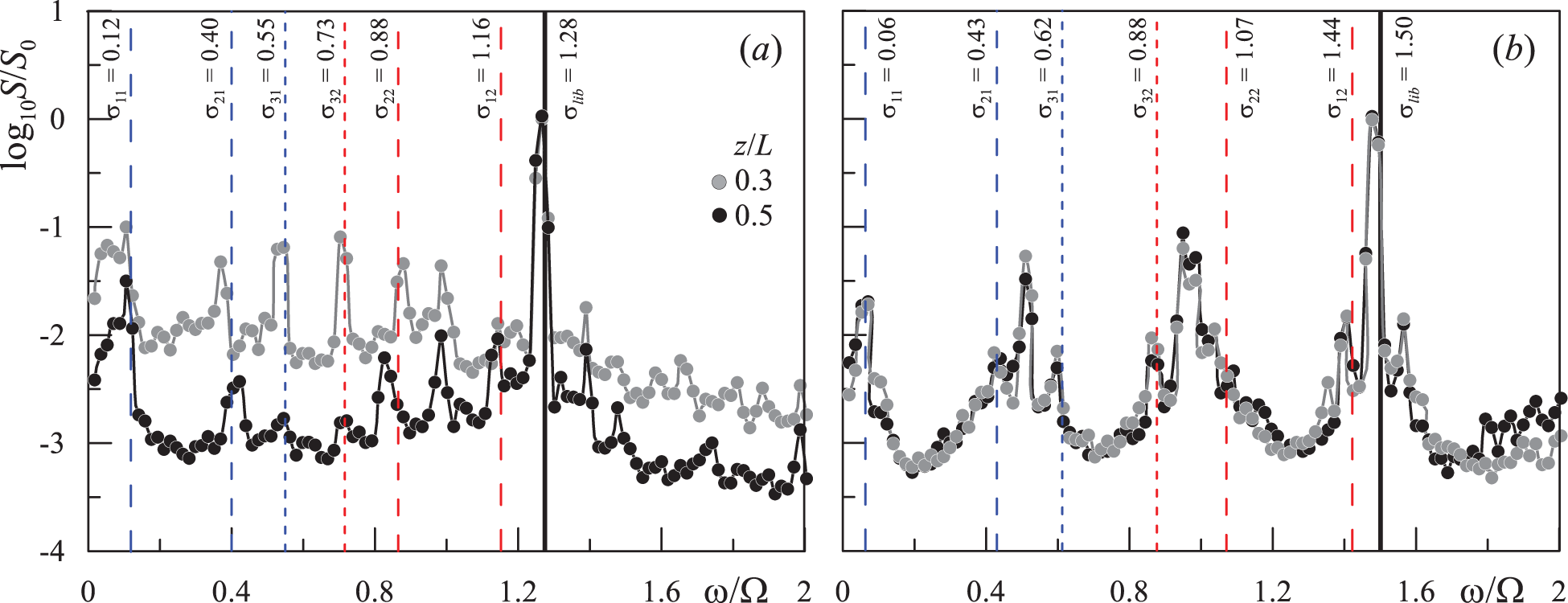
Figure 7: Spectrum of the azimuthal velocity at parameters same as in Fig. 6 and the time moment t/Tlib=300 ; the bold vertical line indicates the fundamental frequency, dashed lines indicates the frequencies of triadic resonance

In addition to the fundamental frequency, the spectra contain a large number of harmonics, which can be separated into pairs. At σ=1.28 and z/L=0.3 (Fig. 6a) the “internal” pair with frequencies σ31=0.55 and σ32=0.73 is most clearly manifested. These harmonics do not appear immediately, but only after time t/Tlib∼50 . In the middle of the cavity ( z/L=0.5 , Fig. 6b) the brighter harmonics are with frequencies σ21=0.40 and σ22=0.88 . In the time interval 0<t/Tlib<300 their amplitude is not constant, and short-term changes in the values of the frequencies themselves are also observed. For example, at t/Tlib∼130 the lower frequency decreases while the upper frequency increases. Finally, the third (“outer”) pair can be obtained from the frequencies σ11=0.12 and σ12=1.16 . The sum of each pair gives a value close to the fundamental frequency: σ=σi1+σi2 . Thus, we can assume that the main mechanism for the destruction of the mean stationary vortex is a triadic subharmonic resonance [16,40]. More detailed spectra indicating the values of all peaks for the time t/Tlib∼300 are shown in Fig. 7. Similar pairs of the triadic resonance subharmonics appear in the non-linear regime of the A(2,1) attractor (Figs. 6c and 6d). The “internal” pair corresponds to the frequencies σ31=0.62 and σ32=0.88 and occurs at t/Tlib>180 . The second pair is observed at σ21=0.43 and σ22=1.07 ; finally the third one is σ11=0.06 and σ12=1.44 . Strictly speaking, a fourth pair σ41≈0.5 and σ42≈1.0 can be distinguished in the spectrum, where one frequency corresponds to the average rotation frequency of the system. On the one hand, the inconstancy of the value σ41 with time indicates in favour of the presence of this pair. On the other hand, in Section 4.2 it will be shown that a non-linear response does not occur at these frequencies; therefore they are not highlighted separately in Fig. 7.

The experiments at frequencies σ=1.28 and σ=1.50 were carried out under the same conditions; however, the subharmonics of the triadic resonance in the cross-section z/L=0.5 manifest themselves with different intensities. In the case of the A(2,1) attractor, the position of the laser sheet does not affect the shape of the spectrum, gray and black symbols in Fig. 7b fit almost into the same dependence. On the contrary, for M(1,1,1) a significant decrease in the value of S/S0 in the cross-section z/L=0.5 is observed. Since the illumination of the visualizer particles did not differ from the attractor case, this may be related to the “three-dimensional” nature of the triadic resonance. This assumption is also supported by the fact that the values of subharmonics σ21 and σ22 in different sections are not the same (Fig. 7a). Previously, the triadic resonance instability has been widely studied in rotating and density-stratified systems, while the focus has been on the wave attractors [11,17,18,41]. The present experiments show that the triadic resonance is more easily manifested in the conditions of the resonance of the inertial mode rather than the attractor. Moreover, the spatial structure of the wave decay can be quite complex. The second point is that close to the instability threshold, a whole series of energy cascades (in this case three) occur.

Thus, the triadic resonance of inertial waves is a trigger for the destruction of the zonal flow and can be a tool for mixing. As noted earlier, in the subcritical region the flow is a single vortex elongated along the rotation axis. This flow resembles a Taylor column, in which the fluid motion along the rotation axis is prohibited [1]. The instability of the triadic resonance should lead to violation of two-dimensionality and the creation of chaotic mixing. It can be noted that mixing under conditions of triadic resonance was studied in [27]. In the non-linear regime, the streaks of the dye have been affected by the flow and spread in the fluid bulk. A detailed study of the characteristics of mixing is beyond the scope of this work.

4.2 Long-Time Evolution

Let us consider the non-linear fluid response to the triadic resonance instability. Fig. 8 shows the velocity fields averaged over the libration period at different times. At t/Tlib=0 the flow structure is a system of vortices moving in both azimuthal and radial directions (Figs. 8a and 8c). At first glance, this system behaves rather chaotically: the directions of movement of the vortices differ, while individual vortices may disintegrate or merge. Let us recall that the moment of the libration amplitude establishment was already preceded by the destruction of the main stationary flow (Fig. 4). Over time, the most intense movement is localized near the obtuse corners of the cavity ( 90∘<φ<270∘ ) (Figs. 8b and 8d). Note that at t/Tlib>100 larger vortices predominate in the velocity field. This is because the small-scale structures merge, and the mean azimuthal flow seems more regular compared to the initial moment.

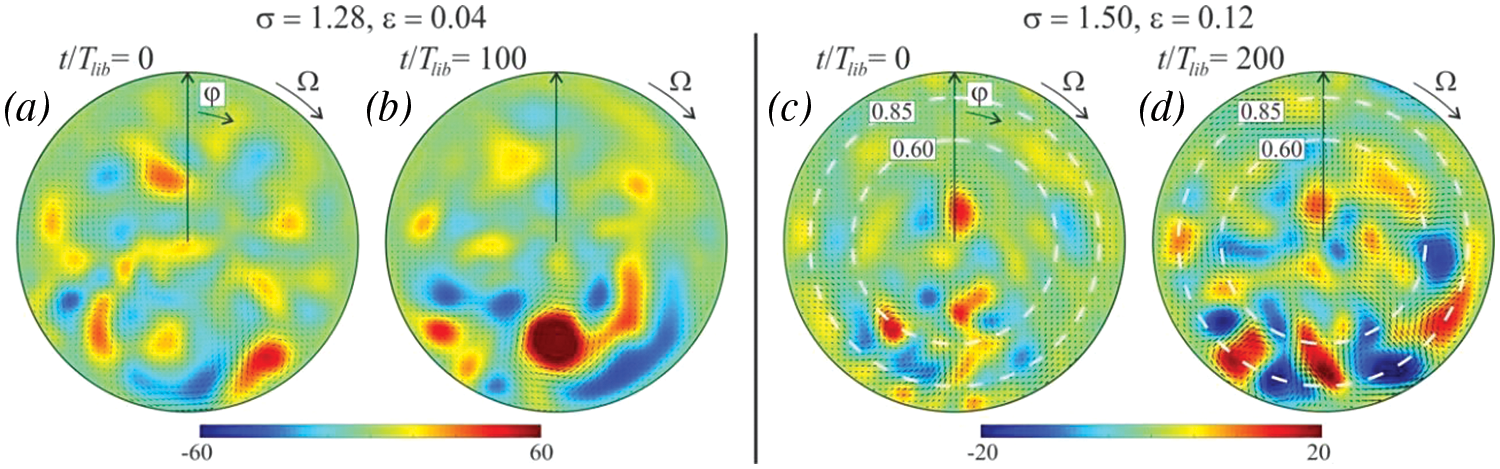
Figure 8: The mean azimuthal velocity fields in non-linear regime at σ=1.28 (a, b) and σ=1.50 (c, d) in a cross-section z/L=0.3 for different time moments. All designations are the same as in Fig. 4

To further analyze the features of the dynamics of the mean velocity field, let us focus on the frequency σ=1.50 . Fig. 9 shows the time dependence of the moving average vorticity. Similar to Fig. 4, the averaging is carried out over the libration period, but to increase the time resolution, the step between windows is Δt/Tlib=0.167 . Thus, there are 6 frames per period, which is sufficient to obtain information about the mean vortex dynamics in Fig. 8. The vortices can be located at different distances from the rotation axis, so it is possible to separately consider the vorticity along the radii r/R=0.6 (Figs. 9a–9c) and r/R=0.85 (Fig. 9d). First, the main intrigue unfolds in the vicinity of φ∼180∘ , i.e., close to the obtuse corners of the cavity, where the distance between the ends is smaller. Secondly, the diagrams can distinguish the simultaneous existence of several types of movement with different time scales. The slowest movement is discernible in the central part of the diagram and is associated with a slow prograde drift of the vorticity maximum in the direction of increasing φ . The approximate direction of the drift is shown in Fig. 9a with solid oblique lines. Taking into account that there are 4 periods in the time interval t/Tlib=0−80 , it is possible to estimate the frequency of the vortex occurrence as ≈0.05 . This value agrees well with the peak at σ11=0.06 and indicates the existence of a non-zero zonal flow.

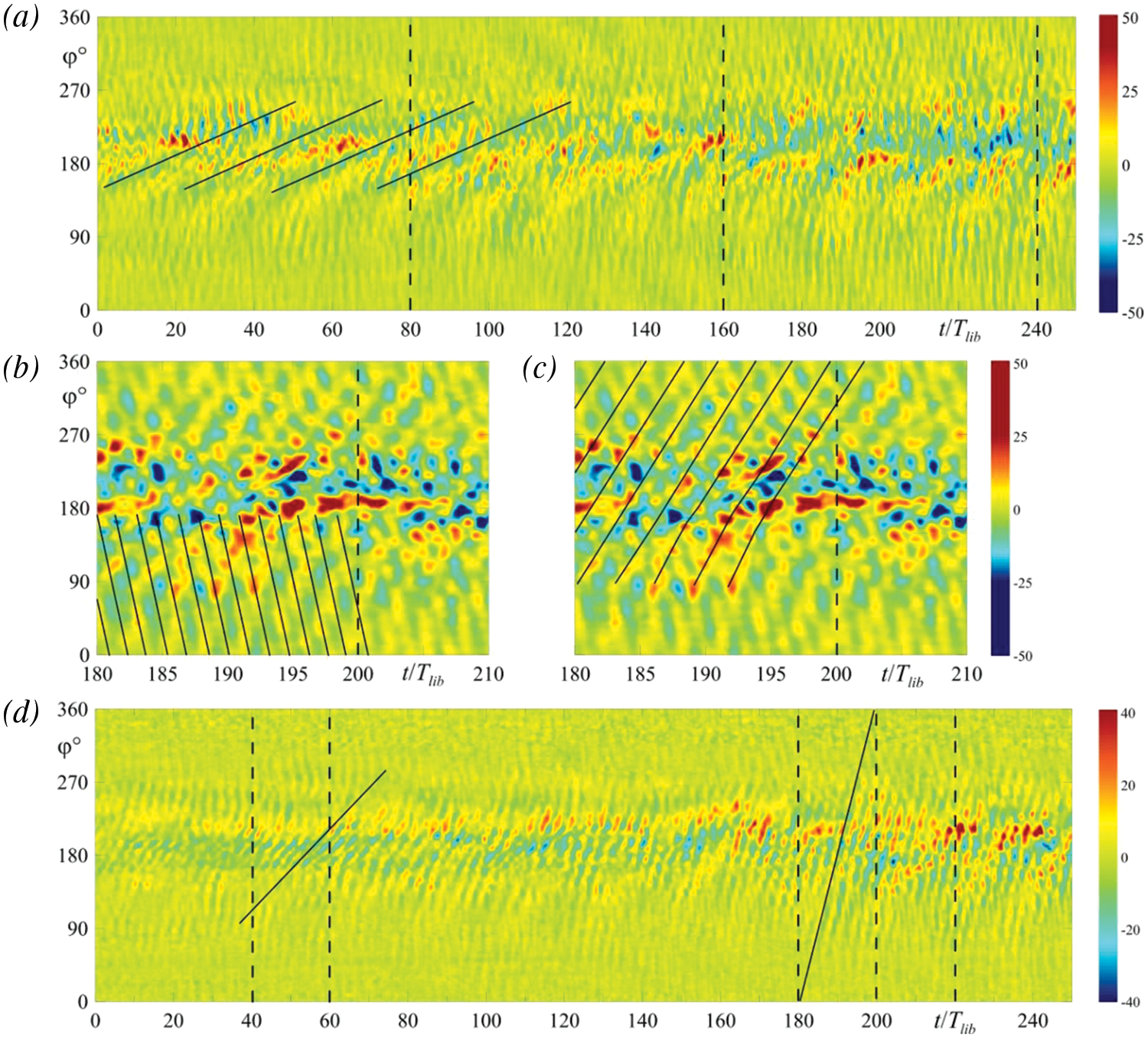
Figure 9: Time-dependence of the average vorticity moving along a ring of radius r/R=0.6 (a–c) and r/R=0.85 (d) in a cross-section z/L=0.3 at a frequency σ=1.50 . The fragments b and c correspond to the time period t/Tlib=180−210 on a larger scale

The almost vertical lines in Fig. 9a correspond to fairly fast movement against the background of the slow drift. Moreover, at certain moments in time, the vorticity forms the intertwining patterns. For a detailed study of the nature of these structures, let us consider the enlarged fragments of the diagram in a time interval t/Tlib=180−210 (Figs. 9b and 9c). It turns out that the intertwining patterns are formed by two types of movement: i) the first (“high-frequency”) is directed against the direction of the cavity rotation; ii) the second (“moderate frequency”) is directed in the direction of the cavity rotation. Estimates show that the frequency of the retrograde vortices is ≈0.65 , which also corresponds to one of the subharmonics of the triadic resonance σ31=0.62 . At the same time, the frequency of the prograde vortices ≈0.4 is very close in value to the peak at σ21=0.43 . Thus, it can be concluded that the lower subharmonics of the triadic resonance are a generator of mean vortices.

The most pronounced prograde drift with a frequency ≈0.4 is observed close to the periphery, r/R=0.85 (Fig. 9d). Moreover, the complete development of the non-linear regime occurs at t/Tlib>60 , which corresponds to the appearance of the σ21 subharmonic in the spectrogram (Fig. 6d). The main motion is also localized in the region 90∘<φ<270∘ . If we take the distance between the vorticity maximum of the same sign in the lower part of Fig. 8d as the characteristic spatial period, the azimuthal wave number can be estimated as k=8 . At the same time, the estimates show that in the time interval t/Tlib=180−210 , the dimensionless mean angular velocity of the vortex drift is ΔΩ/Ω=0.075 . Earlier it was noted that one more subharmonic with a frequency σ41≈0.5 can be distinguished in the spectrum (see Fig. 7b). Thus, in the non-linear regime of attractor, fluid oscillations with frequencies σ11=0.06 , σ21=0.43 and σ31=0.62 leads to the appearance averaged effects. Non-linear response to the frequencies σ11 and σ31 is more pronounced at a distance r/R=0.6 . At the same time, the response to a frequency σ31 is more noticeable at the periphery r/R=0.85 . In general, the flow structure resembles a set of vortices, which are located at different radii and drift in different directions. However, the analysis of the moving average does not allow one to explicitly identify the corresponding non-linear response at a given frequency. To find out the complete wave picture it is necessary to use the Hilbert transform in space and filter the wave components as in [17,26,42]. This work is beyond the scope of this article.

5  Conclusions

The linear and non-linear fluid response in a non-uniformly rotating (librating) cylindrical cavity with non-axisymmetric ends has been experimentally studied. The case of the antiparallel inclination of the ends relative to the cross-section is considered. The specific shape of the cavity geometry supports several types of inertial regimes: wave attractors, standing waves (so-called inertial modes) and symmetric reflection of the wave beams. The attractor arises due to the successive convergence of the wave beams after reflection from the inclined walls. Thus, the wave energy is localized along one closed trajectory with a sufficiently narrow beam width. The strongest resonant response is observed for the inertial modes, which are the global oscillating vortices. In a trapezoidal axial section, the position of the vorticity centres does not change with time, whereas in a rectangular section, the vortices move in the radial direction. For certain frequencies, the ray-tracing does not predict focusing effects; nevertheless, the wave beams form the closed trajectories. Unlike attractors, the branches of these trajectories at the moment of “focusing” do not lean on the inclined walls of the trapezoidal section and can be geometrically obtained as the first two reflections of the wave beams. It is worth noting that since the libration action is symmetrical, the inertial regimes with even axial wavenumbers arise.

In the linear regimes, inertial waves generate a non-axisymmetric steady azimuthal flow. The flow structure is a single vortex, the position of which is determined by the localization of the wave reflection from the inclined walls. The position of this vortex and the vorticity magnitude do not change with time. Interestingly, the generation of the cyclonic flow occurs in the region close to the acute cavity corners, while the anticyclonic–in the region close to the obtuse corners.

With an increase in the amplitude of librations, the single-vortex flow is destroyed. This process is accompanied by the separation of the main vortex into several pieces, which move in the azimuthal direction. The nature of the system’s non-linear behaviour is related to the triadic resonance instability. Regardless of the flow regime (attractor or inertial modes), several pairs of subharmonics appear in the spectrum, the sum of which is equal to the fundamental frequency. In the non-linear wave regime, the attention is on the long-time dynamics of the mean azimuthal flow. The latter is a system of vortices moving in the azimuthal and radial directions. The vorticity time diagrams show the simultaneous existence of several types of motion with different time scales. We discovered at least three frequencies: slow prograde vortex drift, fast prograde and slow retrograde drift. An estimate of the frequencies of the vortex appearance agrees well with the frequencies of the “lower” subharmonics of triads.

This work continues the study of the influence of the geometry of the end walls on the flow regimes in a rotating cylinder [8,25]. Despite the common features, the experimental setup is a rich dynamical system for studying various wave regimes, while the antiparallel inclination of the ends introduces a peculiar specificity. In contrast to parallel inclination [8,25], wave regimes with even axial wavenumbers are excited. The great interest is the non-linear response of the fluid in the form of generation of the mean single-vortex flow. The discovered dependence of the direction of the steady circulation on the cavity with radius sheds light on the mechanisms of generation of flows in geophysical systems with a β -effect due to the presence of an inclined bottom. In addition, this study raises an important question about the choice of wavenumbers in the zonal flow generated by the triadic resonance. Finally, from an applied point of view, the experimental results may be useful in the development of “soft” methods for mixing using hydrodynamic instabilities.

Acknowledgement: None.

Funding Statement: This work was supported by the Ministry of Education of the Russian Federation (Project KPZU-2023-0002).

Author Contributions: Study conception and design: S. Subbotin; data collection: M. Shiryaeva; analysis and interpretation of results: S. Subbotin, M. Shiryaeva, M. Subbotina; writing–original draft preparation: S. Subbotin, M. Shiryaeva, M. Subbotina; writing–review and editing: S. Subbotin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Greenspan, H. P. (1968). The theory of rotating fluids. Cambridge: University Press. [Google Scholar]

2. Aldridge, K. D., Toomre, A. (1969). Axisymmetric inertial oscillations of a fluid in a rotating spherical container. Journal of Fluid Mechanics, 37, 307–323. [Google Scholar]

3. Rieutord, M., Georgeot, B., Valdettaro, L. (2000). Wave attractors in rotating fluids: A paradigm for ill-posed Cauchy problems. Physical Review Letters, 85, 4277–4280. [Google Scholar] [PubMed]

4. Maas, L. R. M. (2001). Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. Journal of Fluid Mechanics, 437, 13–28. [Google Scholar]

5. Pillet, G., Maas, L. R. M., Dauxois, T. (2019). Internal wave attractors in 3D geometries: A dynamical systems approach. European Journal of Mechanics-B/Fluids, 77, 1–16. [Google Scholar]

6. Rieutord, M., Georgeot, B., Valdettaro, L. (2001). Inertial waves in a rotating spherical shell: Attractors and asymptotic spectrum. Journal of Fluid Mechanics, 435, 103–144. [Google Scholar]

7. He, J., Favier, B., Rieutord, M., Le Dizès, S. (2022). Internal shear layers in librating spherical shells: The case of periodic characteristic paths. Journal of Fluid Mechanics, 939, A3. [Google Scholar]

8. Subbotin, S., Shiryaeva, M. (2023). Inertial wave beam path in a non-uniformly rotating cylinder with sloping ends. Microgravity Science and Technology, 35(3), 32. [Google Scholar]

9. Dintrans, B., Rieutord, M., Valdettaro, L. (1999). Gravito-inertial waves in a rotating stratified sphere or spherical shell. Journal of Fluid Mechanics, 398, 271–297. [Google Scholar]

10. Maas, L. R. M., Benielli, D., Sommeria, J., Lam, F. P. A. (1997). Observation of an internal wave attractor in a confined, stably stratified fluid. Nature, 388, 557–561. [Google Scholar]

11. Brouzet, C., Ermanyuk, E. V., Joubaud, S., Pillet, G., Dauxois, T. (2017). Internal wave attractors: Different scenarios of instability. Journal of Fluid Mechanics, 811, 544–568. [Google Scholar]

12. Boisson, J., Lamriben, C., Maas, L. R. M., Cortet, P., Moisy, F. (2012). Inertial waves and modes excited by the libration of a rotating cube. Physics of Fluids, 24(7), 076602. [Google Scholar]

13. Wu, K., Welfert, B. D., Lopez, J. M. (2018). Librational forcing of a rapidly rotating fluid-filled cube. Journal of Fluid Mechanics, 842, 469–494. [Google Scholar]

14. Wu, K., Welfert, B. D., Lopez, J. M. (2020). Reflections and focusing of inertial waves in a librating cube with the rotation axis oblique to its faces. Journal of Fluid Mechanics, 896, A5. [Google Scholar]

15. Wu, K., Welfert, B. D., Lopez, J. M. (2022). Reflections and focusing of inertial waves in a tilted librating cube. Journal of Fluid Mechanics, 947, A10. [Google Scholar]

16. Scolan, H., Ermanyuk, E., Dauxois, T. (2013). Nonlinear fate of internal waves attractors. Physical Review Letters, 110, 234501. [Google Scholar] [PubMed]

17. Boury, S., Sibgatullin, I., Ermanyuk, E., Shmakova, N., Odier, P. et al. (2021). Vortex cluster arising from an axisymmetric inertial wave attractor. Journal of Fluid Mechanics, 926, A12. [Google Scholar]

18. Subbotin, S., Shmakova, N., Kozlov, V., Ermanyuk, E. (2023). Nonlinear regimes of inertial wave attractors generated by a precessing lid: Zonal flows and Rossby waves. Physics of Fluids, 35(7), 074110. [Google Scholar]

19. Xu, W., Harlander, U. (2020). Inertial mode interactions in a rotating tilted cylindrical annulus with free surface. Physical Review Fluids, 5(9), 094801. [Google Scholar]

20. Monsalve, E., Brunet, M., Gallet, B., Cortet, P. (2020). Quantitative experimental observation of weak inertial-wave turbulence. Physical Review Letters, 125, 254502. [Google Scholar] [PubMed]

21. McEwan, A. (1970). Inertial oscillations in a rotating fluid cylinder. Journal of Fluid Mechanics, 40(3), 603–640. [Google Scholar]

22. Lagrange, R., Eloy, C., Nadal, F., Meunier, P. (2008). Instability of a fluid inside a precessing cylinder. Physics of Fluids, 20(8), 081701. [Google Scholar]

23. Lagrange, R., Meunier, P., Nadal, F., Eloy, C. (2011). Precessional instability of a fluid cylinder. Journal of Fluid Mechanics, 666, 104. [Google Scholar]

24. Barik, A., Triana, S. A., Hoff, M., Wicht, J. (2018). Triadic resonances in the wide-gap spherical Couette system. Journal of Fluid Mechanics, 843, 211–243. [Google Scholar]

25. Subbotin, Shiryaeva, M. (2022). Steady vortex flow induced by inertial wave attractor in a librating cylinder with sloping ends. Microgravity Science and Technology, 34(5), 89. [Google Scholar]

26. Subbotin, S., Shmakova, N., Ermanyuk, E., Kozlov, V. (2022). Stewartson layer instability and triadic resonances in rotating sphere with oscillating inner core. Physics of Fluids, 34(6), 064103. [Google Scholar]

27. Meunier, P. (2020). Geoinspired soft mixers. Journal of Fluid Mechanics, 903, A15. [Google Scholar]

28. Yamagata, T., Sugisawa, H., Fujisawa, N. (2021). Experimental study on laminar mixing in planetary mixer. Experiments in Fluids, 62, 28. [Google Scholar]

29. Kozlov, V. G., Ivanova, A. A., Vjatkin, A. A., Sabirov, R. R. (2015). Vibrational convection of heat-generating fluid in a rotating horizontal cylinder. The role of relative cavity length. Acta Astronautica, 112, 48–55. [Google Scholar]

30. Ivanova, A. A., Kozlov, V. G., Polezhaev, D. A., Pareau, D., Stambouli, M. (2008). The concept of a vibrational cell for studying the interface chemical kinetics. Vibrational flow structure. Fluid Dynamics & Materials Processing, 4(3), 211–220. [Google Scholar]

31. Kozlov, V., Polezhaev, D. (2015). Flow patterns in a rotating horizontal cylinder partially filled with liquid. Physical Review E, 92(1), 013016. [Google Scholar]

32. Watson, P., Bonnieu, S. V., Lappa, M. (2024). Fluidization and transport of vibrated granular matter: A review of landmark and recent contributions. Fluid Dynamics & Materials Processing, 20(1), 1–29. https://doi.org/10.32604/fdmp.2023.029280 [Google Scholar] [CrossRef]

33. Le Bars, M., Cébron, D., Le Gal, P. (2015). Flows driven by libration, precession, and tides. Annual Review of Fluid Mechanics, 47, 163–193. [Google Scholar]

34. Thielicke, W., Stamhuis, E. J. (2014). PIVLab–Time-resolved digital particle image velocimetry tool for MATLAB (version: 1.41). Journal of Open Research Software, 2(1), e30. [Google Scholar]

35. Sauret, A., Cébron, D., Le Bars, M., Le Dizès, S. (2012). Fluid flows in a librating cylinder. Physics of Fluids, 24(2), 026603. [Google Scholar]

36. Subbotin, S. (2022). Steady circulation induced by inertial modes in a librating cylinder. Physical Review Fluids, 5(1), 014804. [Google Scholar]

37. Noir, J., Calkins, M. A., Lasbleis, M., Cantwell, J., Aurnou, J. M. (2010). Experimental study of libration-driven zonal flows in a straight cylinder. Physics of the Earth and Planetary Interiors, 182(1–2), 98–106. [Google Scholar]

38. Busse, F. H. (2011). Zonal flow induced by longitudinal librations of a rotating cylindrical cavity. Physica D, 240(2), 208–211. [Google Scholar]

39. Flandrin, P. (1999). Time-frequency/time-scale analysis, time-frequency toolbox for MATLab. San Diego (CAAcademic Press. [Google Scholar]

40. Sibgatullin, I. N., Ermanyuk, E. V. (2019). Internal and inertial wave attractors: A review. Journal of Applied Mechanics and Technical Physics, 60(2), 284–302. [Google Scholar]

41. Brunet, M., Dauxois, T., Cortet, P. P. (2019). Linear and nonlinear regimes of an inertial wave attractor. Physical Review Fluids, 4(3), 034801. [Google Scholar]

42. Mercier, M., Garnier, N., Dauxois, T. (2008). Reflection and diffraction of internal waves analyzed with the Hilbert transform. Physics of Fluids, 20(8), 086601. [Google Scholar]