Dynamics of Low-Viscosity Liquids Interface in an Unevenly Rotating Vertical Layer

Nomenclature

1  Introduction

The oscillatory dynamics of multiphase systems with an interface is of great scientific and practical interest. The interface can be unstable to various types of instability in dependence on the type of the fluid oscillations.

Tangential oscillations of two fluids near the interface accompanied by the discontinuity of the tangential velocity cause the excitation of the Kelvin–Helmholtz oscillatory instability [1–4], which manifests itself in the form of the quasi-stationary relief (frozen wave). It is noteworthy that the Kelvin–Helmholtz instability [5] is studied in detail for the case of stationary tangential velocity discontinuity [6,7] including the complicating factors, like: proximity of the wall [8], flows in Hele-Shaw cell [9], heat and mass transfer from viscoelastic liquid film [10]. The practical interest in the study of the Kelvin–Helmholtz instability, including the oscillatory type of the instability, is explained, in particular, by the influence of this effect on the film coating and fluid spraying [11–14]. Taking into account the above mentioned, the oscillatory dynamics of the interface between fluids in narrow gaps is of interest.

In the experiments with fluids with high viscosity contrast in narrow gaps, oscillations of the tangential pressure gradient cause tangential oscillations of fluids with different amplitudes due to different viscous interactions between fluids and the channel walls, which also causes the onset of the oscillatory Kelvin–Helmholtz instability.

A number of non-trivial phenomena were discovered [15,16] when studying the dynamics of fluids of different densities and high viscosity contrast in a narrow gap (axisymmetric Hele-Shaw cell) under modulated rotation Ω=Ωrot(1+εcos⁡Ωlibt) . Here, Ω is the angular velocity of rotation, Ωrot is the mean rotation rate, Ωlib and ε are the radian frequency and the amplitude of the modulation. It is found that the modulated rotation causes the development of a two-dimensional quasi-stationary relief at the interface. The development of the relief is associated with the onset of the Kelvin–Helmholtz instability at the interface between oscillating fluids. This is explained by the fact that a high-viscosity fluid undergoes oscillations together with the cell due to viscous interaction between the fluid and the walls of the cell. At the same time, a low-viscosity fluid rotates uniformly due to the absence of viscous interaction with the walls. It induces the discontinuity of the oscillatory tangential velocity at the interface between two fluids. The increase in the amplitude of modulation (increase in the amplitude of the tangential velocity discontinuity) results in the development of a quasi-stationary relief (Fig. 1).

Figure 1: The interface between the high-viscosity glycerol colored with blue dye and the low-viscosity and denser fluid FC-40 at frot = 4.0 rps, flib = 7 Hz, and ε  = 0.26. Photo is analogues to one, published in [16]

The high-viscosity fluid takes the form of a multi-petal flower rotating together with the cell. According to the observations, the petals undergo slight azimuthal oscillations during the period. When the modulation amplitude decreases, the transition to the axisymmetric state occurs without hysteresis. The relief appears on the surface of a more viscous fluid regardless of its density and the location of the relatively low-viscosity fluid. This phenomenon is studied theoretically and experimentally in [16]. The theoretical model is constructed for the extremely high viscosity contrast when the thickness of the Stokes boundary layer in a high-viscosity fluid exceeds the gap width while the thickness of the Stokes layer in a low-viscosity fluid is small compared to the gap width. In light of the above, an urgent issue is to clarify the effect of the viscosity contrast on the time-averaged dynamics of the interface.

This paper is aimed at experimental investigation of the dynamics of two fluids with different densities in an unevenly rotating vertical layer. Water and industrial oil I-20A are chosen as working fluids. It is noteworthy that fluids have different, but relatively low viscosities, and the Stokes boundary layers are thinner than the cell thickness in the studied range of oscillation frequencies.

2  Experimental Technique

The cell (Fig. 2) is a vertical plane layer of thickness d = 4.0 mm with circular lateral boundary of radius Rc = 56.25 mm. The walls of the cavity are made of plexiglass: The front wall is transparent while the back wall is white and opaque. The cell is filled with immiscible fluids, one was colored with blue dye. The dynamics of the interface is registered by the digital camera FUJI X-E4 and lenses FUJINON XF 50 mm f/2 R WR 2 (Fig. 3). The front side of the cell is illuminated by two LED panels 3 (LED Falcon Eyes FlatLight 600). The cell rotates around the horizontal axis of symmetry in the experiments.

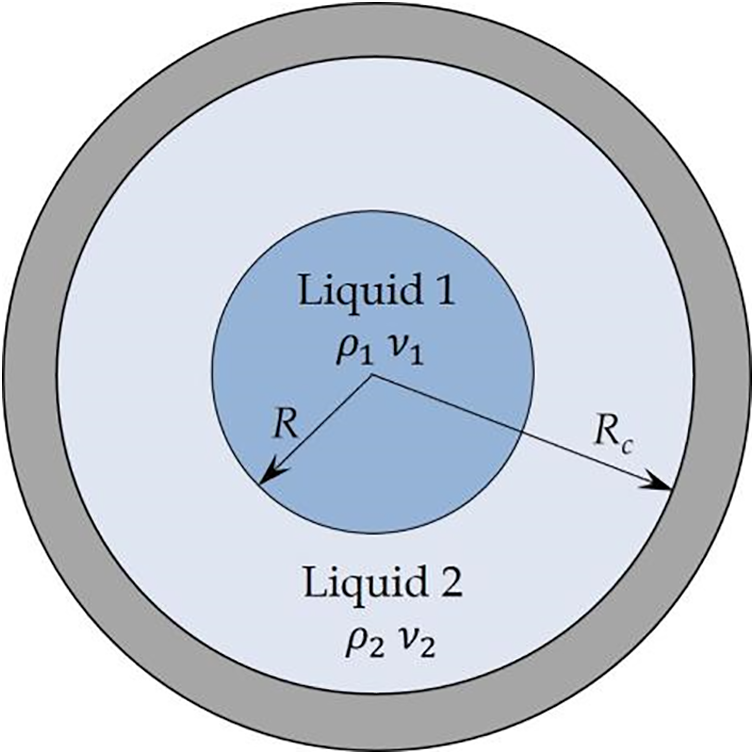
Figure 2: Formulation of the problem

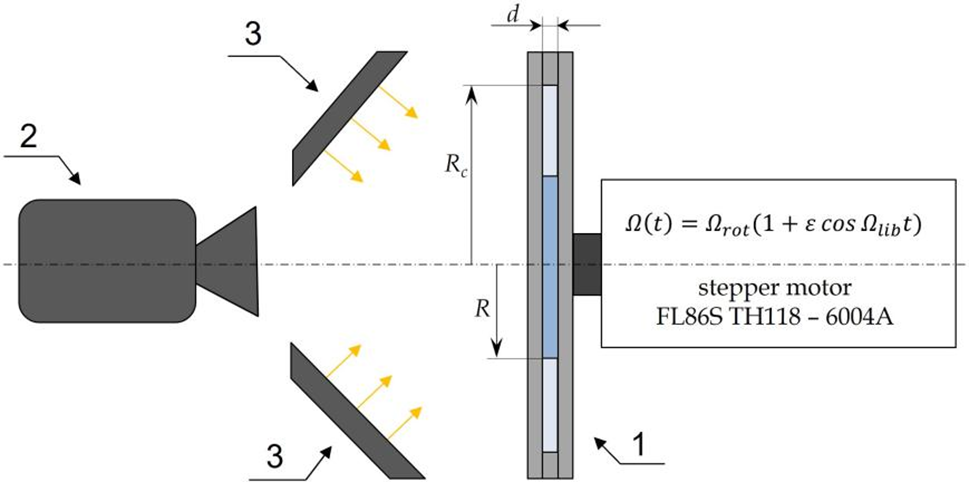
Figure 3: The scheme of the experimental setup: 1–cell, 2–camera, 3–LED panels

A stepper motor FL86S TH118–6004A is capable of rotating according to the law Ω=Ωrot(1+εcos⁡Ωlibt) , where Ωrot is the angular velocity, Ωlib is the radian frequency of oscillations, and ε is the dimensionless amplitude of modulated rotation. The rotation rate frot≡Ωrot/2π changes in the range over frot=4−6 rps, while the libration frequency flib≡Ωlib/2π changes from 2 to 6 Hz. The amplitude of modulation ε varies in the interval from 0 to 0.5.

The cell is filled with two immiscible fluids of different densities and viscosities. We use an industrial oil I-20A with a density of ρ1  = 0.89 g/cm3 and a kinematic viscosity of ν1  = 61 cSt as a more viscous fluid. A less viscous fluid (water) has a density equal to ρ2  = 1.0 g/cm3 and a kinematic viscosity equal to ν2  = 1.0 cSt. A blue dye is added to the industrial oil to increase the contrast of the visualization images. The cell rotates rapidly so that the interface is axisymmetric under the action of centrifugal force in the absence of angular velocity modulation. A less dense but more viscous fluid (industrial oil) locates near the axis of rotation while, a denser fluid (water)–in a ring layer near the lateral cylindrical wall. The interface between fluids under uniform rotation is axisymmetric with a radius R=R0 .

We vary the volume ratio of the fluids so that the radius of the unperturbed interface is equal to R0  = 27.9 and 35.2 mm. The cell is fixed to a rotating table, which is coupled with the motor shaft. We use the software ZetLab to manage the rotation rate (with an accuracy of 10−3 rps), amplitude, and frequency of oscillations. The fluid flow is registered by the digital camera located coaxially with the cell.

In each series of experiments, we set the desired rotation rate and the oscillation frequency and change the modulation amplitude from zero to maximum value with an interval of 0.04. The image of the interface is captured by a digital camera at different phases of the cell oscillations.

The image processing is done using the free software ImageJ. The tool «Threshold» is used to highlight the interface that determines the spreading area of the more viscous fluid. Then, the toll “Analyze Particles” measures the minimum and maximum diameter of the selected area. The mean radius of the wetting area is calculated at a given rotation rate, frequency and amplitude of oscillations.

3  Experimental Results

The interface between fluids is axisymmetric in the absence of oscillations (Fig. 4a). Under oscillations, a more viscous fluid with a lower density takes the form of the film attached to the end wall (Fig. 4b). A dark blue spot in the center of the cell is the area occupied by a viscous fluid; the area occupied by the film has a lower optical density. The radial size of the wetting spot increases with increasing the amplitude ε of the rotation speed modulation (Fig. 4c). It is noteworthy that the observed films are attached to both end walls. They are almost circular and have similar sizes which is clearly visible in Fig. 4c. Here, a low-viscosity fluid is located in the internal volume of the cell between two films. The dynamic stability of the films is determined by the oscillations. The wetting spot at definite Ωrot shrinks, as the modulation amplitude ε decreases, and the interface returns to its original cylindrical shape (Fig. 4a) when the oscillations are turned off.

Figure 4: The interface between oil and water at R0  = 35.2 mm, frot  = 4 rps, flib  = 3 Hz, and ε  = 0, 0.24, 0.44, and 0.46 (a–d)

The radial size of the wetting spot (radius of the fluid film) increases with the amplitude. The spreading effect is more pronounced at lower modulation frequencies. When the critical amplitude is reached, the interface becomes unstable: The film is destroyed and the feather-like structures twisted against the direction of the cell rotation appears (Fig. 4d). Here, the destroyed film turns into drops that are located between the walls of the cavity in a suspended state. The droplets tend to collect at the center of the cavity due to the centrifugal force.

The dynamics of the film coating does not undergo qualitative changes when variation of R0 (Figs. 5a, 5b); at a lower value R0 , the radius of the film coating of the end walls increases with ε , and when a critical value of R is reached, the peripheral edge of the film loses stability.

Figure 5: The interface between oil and water at R0  = 27.9 mm, frot  = 5 rps, flib  = 4 Hz and ε  = 0.42, 0.47 (a, b). The cell rotates clockwise

When the film loses stability, the size of the wetting spot decreases sharply (Fig. 4d), which corresponds to a break in the slope of the R(ε) curves at large amplitudes (Fig. 6). One can find that the dependence of the film radius on the modulation amplitude is determined by the oscillation frequency and the rotation rate. The rate of increase in the radius of the wetting spot with ε decreases with Ωrot (Fig. 6c). The film loses stability when the radius reaches the critical value R∗=42±2  mm independently on the rotation rate and frequency of oscillations (Fig. 7a); one can see that the results obtained at different rotation speeds are consistent with each other within the experimental error. The critical value of the modulation amplitude ε∗ increases with increasing oscillation frequency and reaches the maximum in the limit of high frequencies (Fig. 7b).

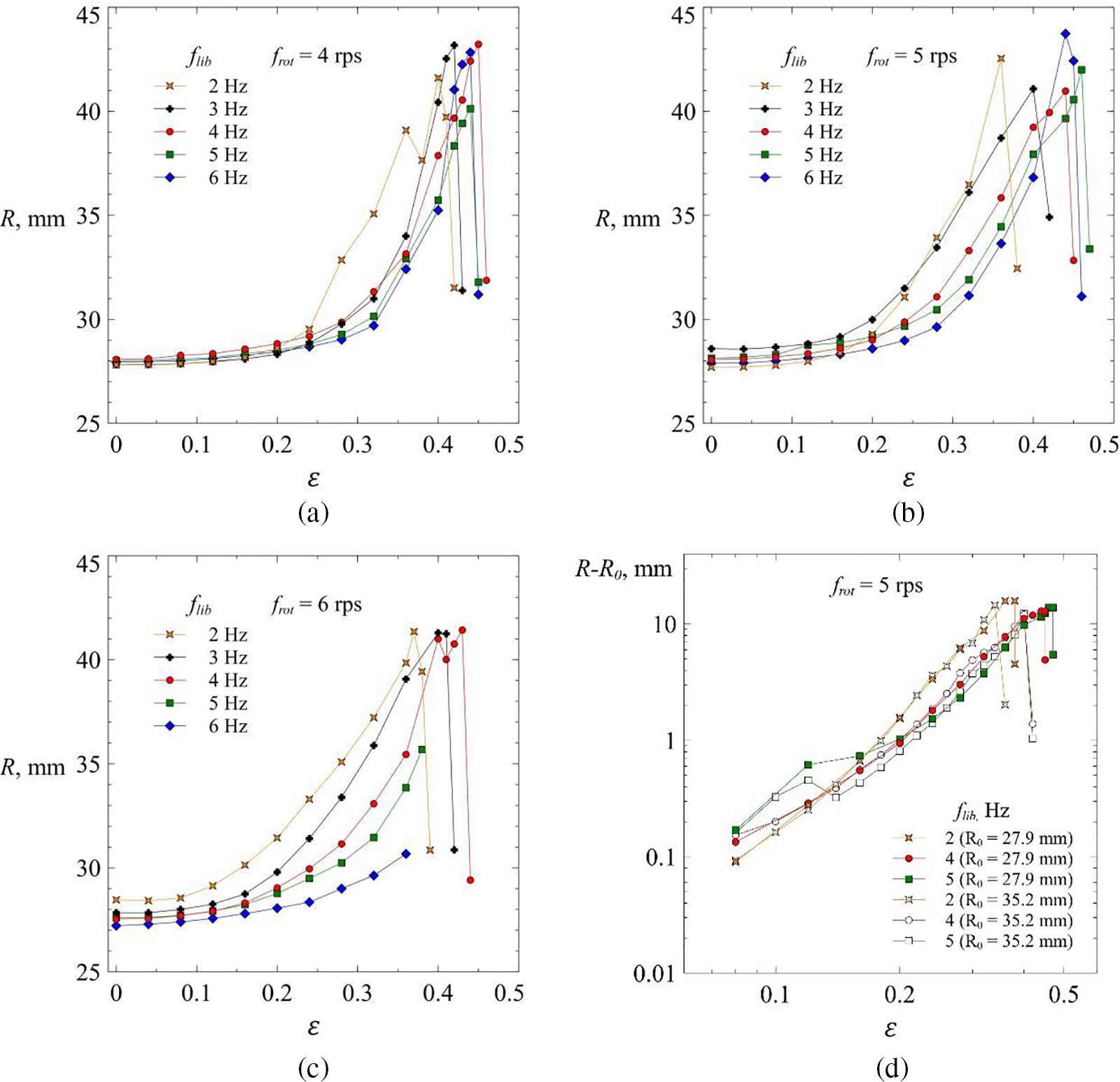
Figure 6: Dependence of the wetting radius on the amplitude of oscillations at frot  = 4, 5, and 6 rps (a–c) and oscillation frequencies flib  = 2–6 Hz; (d) displacement of the contact line at frot  = 5 rps, in log-log scale

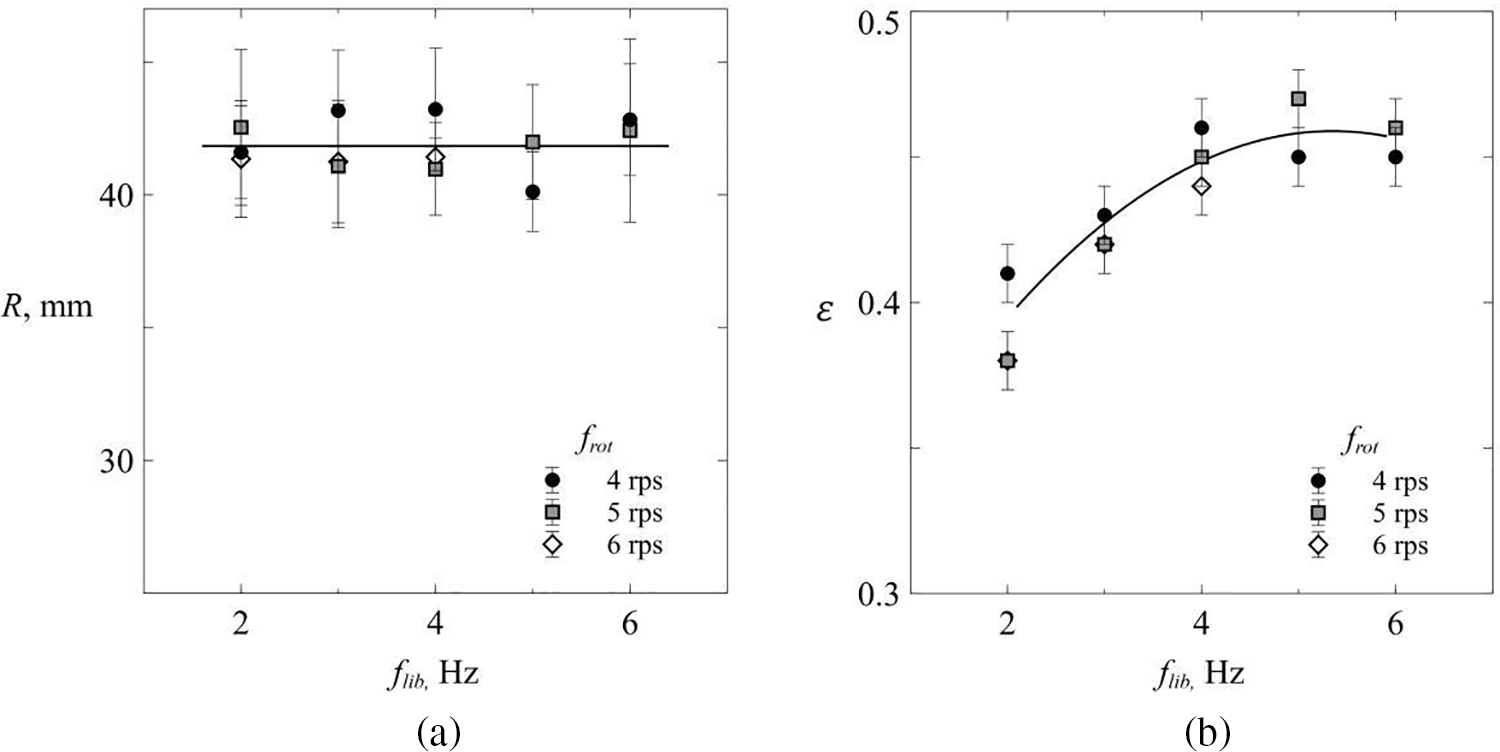
Figure 7: (a)–critical radius R* of the film on the plane (flib, R); (b)–critical amplitude ε∗ on the plan (flib, ε )

Fig. 6d shows on a log-log scale the dependence of the radial displacement of the film edge R−R0 on the initial location of the interphase boundary, depending on ε for different values R0 at a certain cavity rotation speed. One can see that the results for different initial positions of the interphase boundary R0 , are consistent with each other to within the experimental error. It is interesting that the critical stretch of the film, at which the edge of the film loses stability, has close values of (R−R0)∗=10±0.5  mm, at different R0 .

This allows us to assume that the films have the same structure at different R0 (film thickness depending on the radial coordinate, r−R0 ), and the stability is determined by the critical value of film stretch. At this, the displacement of the wetting boundary increases with the amplitude of the velocity modulation according to a law close to cubic (Fig. 6d).

At given values of the rotation rate Ωrot , the modulation amplitude ε , and the frequency, minor oscillations in the size of the wetting spot during the period are observed (Fig. 8). Moreover, the lower the libration frequency, the greater the magnitude of fluctuations in the size and optical density of the spot. The optical density of the spot can be used to characterize the thickness of the film. The maximum radius of the wetting spot is observed in the phase of maximum rotation rate (Fig. 8a).

Figure 8: The film of the viscous fluid at frot  = 4 rps, flib  = 2 Hz, and ε  = 0.4. Photos are taken at the (a) maximum and (b) minimum rotation rates

Here, the interface has a greater contrast in color compared with Fig. 8b where the rotation rate Ω(t) is close to the minimum value. This indicates a thickening of the “tongue” of a more viscous fluid in a phase of maximum rotation rate. Thus, the viscous fluid in the film undergoes azimuthal and radial oscillations with the frequency flib . In the phase of minimum rotation speed, part of the liquid from the film returns to the central column. It is noteworthy that the contact line remains in its position during the oscillation cycle due to the viscous interaction between the fluids and the cavity walls. The increase in the size of the wetting spot in a certain phase of the cell oscillations (Fig. 8a) is associated with the release of the oil film beyond the contact line in the form of a “tongue”. The increase in the thickness of the “tongue” tip in the phase of maximum rotation rate explains the increase in the optical density and the contrast in color of the interface compared to the opposite phase of the cell oscillations (Fig. 8b). A similar phenomenon, i.e., oscillations of a tongue-shaped layer of viscous liquid extending beyond the contact line, was observed in experiments with a column of a high-viscosity and light fluid in a long unevenly rotating cylinder [17].

4  Discussion

Let us discuss the nature of the radial displacement of a viscous fluid along the end wall under modulated rotation. This phenomenon is explained by the time-averaged interaction between the fluids and the end walls during the cell oscillation cycle. At this, the viscosity contrast plays an important role since the viscous interaction is considerable only within the Stokes layer of the thickness δi=2νi/Ωlib . Consider the case when the oscillation frequency is high and the thickness of the Stokes layer in both fluids is small compared with the fluid layer thickness, i.e., dimensionless frequencies of oscillations in both fluids are high: ω1≡Ωlibd2/ν1>>1 and ω2≡Ωlibd2/ν2>>1 . In the absence of oscillations, fluids rotate together with the cell, and the radial pressure gradient has a break at the axisymmetric interface.

Both fluids are entrained by the end walls and oscillate together with the cell within the Stokes boundary layers that differ in their size due to the difference in viscosities. Moreover, both fluids outside the Stokes layers rotate at the angular velocity Ωrot , and the original pressure distribution is maintained. Let us consider the dynamics of the oil film attached to the cell wall. Due to adhesion, the fluid within the Stokes layer undergoes radial and azimuthal oscillations relative to the reference frame associated with the uniformly rotating cell. The azimuthal oscillations induce the time-averaged shear stress in the oscillating boundary layers [18] and steady streaming outside them. This problem was studied theoretically by Rozenblat [19] for the case of rotational oscillations of a disk in a stationary fluid. It was shown that the averaged shear stress and the steady streaming are localized near the wall at a distance comparable to the thickness of the Stokes boundary layer. The time-averaged radial velocity depends on the distance to the oscillating wall z/δ is determined by the function F(z/δ) and is described by the formula ur=F(z/δ)Ωrot2ε2r/Ωlib (Rozenblat formula is revised for the present study), r is the distance to the axis of rotation. The maximum of the function F(z/δ) is located at a distance comparable to the thickness of the Stokes layer so that the time-averaged radial flow has a boundary layer character. Experimental studies [20] revealed the steady streaming generated in the boundary layers occurring near the end walls of a cylinder under rotational oscillations.

The results obtained in [19] for a single-phase medium are applicable to both fluids in our problem in the limit of slow rotation Ωrot<<Ωlib . Here, the time-averaged meridian flows are localized near the end walls at a distance comparable to the thickness of the Stokes boundary layer. When the fluids have different viscosities, the steady flows near the end walls of the cell are different in magnitude on different sides of the interface. When the viscosity of a less dense fluid significantly exceeds the viscosity of a denser fluid, the thickness of the Stokes layer exceeds the thickness of the working layer; the formation of a more viscous liquid film is not observed [15,16].

One can suggest that the time-averaged shear stress (which excites the averaged radial flow) in the boundary layer of a viscous fluid near the end wall perturbs the initially cylindrical interface and causes the formation of a film with a radius exceeding the radius of the interface in the middle of the layer. As shown above, the velocity of the time-averaged motion or, in other words, averaged shear stress in the Stokes boundary layer increases with distance from the axis of rotation. Then, the spreading of a film of a less dense fluid is limited by the radial pressure gradient in a denser fluid. When the thickness of the viscous film is small compared to the thickness of the layer, the pressure inside the film does not depend on the distance to the end wall and is determined by the pressure at the interface, that is, the pressure in a uniformly rotating low-viscosity fluid. This approach is standard when dealing with boundary layer flows [5]. The proposed model is the first attempt to describe film formation and requires further theoretical study.

Discuss the dynamics of the film of more viscous fluid. As follows from above, the film thickness is of order of the thickness of the Stokes boundary layer which is less than the width of the cell. The low-viscosity fluid outside the film rotates at an almost constant rate, not responding to the azimuthal oscillations of the axisymmetric cell and the film of the viscous fluid. As a consequence, a tangential discontinuity of oscillatory velocity ΔU is observed at the interface. The amplitude of this discontinuity depends on the amplitude of tangential oscillations of the cell, i.e., ΔU=Ωrotεrcos⁡(Ωlibt) . These oscillations perturb the interface and initiate the Kelvin–Helmholtz oscillatory instability in the form of the so-called “frozen waves”. On the surface of the film, the formation of quasi-stationary hills elongated along radius (frozen waves) is possible (Fig. 5a). One can suggest that the instability of the film edge is associated with the destruction (transition to the droplet phase) of the tip of the oscillating tongue of a viscous liquid, the violation of the interphase boundary in the form of a “frozen” wave can play a certain role in this case (Fig. 4d).

Discuss the origin of the anticyclonic “feathers”, i.e., traces of the viscous fluid film on the end walls. Observations show that the viscous fluid from which feathers are formed does not oscillate during velocity rate modulation. This indicates that the thickness of the viscous film that forms the “feathers” is significantly less than the thickness of the Stokes boundary layer. Moreover, both oscillatory and time-averaged flows are negligible in the viscous “feathers”. On the contrary, the low-viscosity fluid performs the azimuthal oscillations relative to the end walls and the surface of a film of viscous liquid (which oscillates along with the end walls), at this the radial steady streaming of low viscosity fluid is generated [19]. Probably, the steady streaming perturbs the wetting spots developing a feather-like pattern. Anticyclonic rotation of the low-viscosity fluid is determined solely by the cell rotation and follows from the law of conservation of angular momentum.

In conclusion, let us dwell on the role of the orientation of the rotating layer in the gravity field. Despite the fact that under the conditions of the experiment, the gravity field is several times smaller than the centrifugal force field, the orientation of the layer (and hence the axis of rotation) plays an important role. In the cavity reference frame, the gravity field rotates in the vertical plane. When the rotation axis is horizontally oriented (the layer is vertical), the time-average value of the gravity field in the rotating system equals zero. The situation changes if the layer plane deviates from the vertical. The constant axial component of the gravity field remains in the rotating system and breaks the mirror symmetry of the interphase surface and of the film coating of the opposite walls of the layer. Preliminary experiments have shown that the deviation of the rotation axis from the horizon leads to a qualitative change in the oscillatory formation of the viscous liquid film at the opposite end walls of the cavity. This effect is beyond the scope of present study and is the subject of further research.

5  Conclusion

A novel vibration effect is found in the course of an experimental study of the dynamics of two low-viscosity fluids with different densities and viscosities in an unevenly rotating circular cell. A more viscous and less dense fluid, located near the axis of rotation under the influence of centrifugal force, forms films on the end walls of the cell under oscillations. In the studied case of a vertical layer arrangement, the films on opposite end walls are similar. The similarity is violated when the layer deviates from the vertical. The dynamic stability of the films is determined by the oscillations: the wetting spot shrinks, and the interface becomes cylindrical in the absence of oscillations. Radial distribution of a more viscous fluid in the form of a film is caused by the difference in the viscous interaction of two fluids with the end walls of the rotating cell. The radius of the wetting spot increases with the modulation amplitude. Another intriguing phenomenon is the threshold destruction of the film edge when the critical radius is reached. As a result of this effect, the destroyed film turns into drops suspended in a less viscous and denser fluid. The droplets tend to collect at the center of the cavity under the action of centrifugal force. The discovered effect of creating a dynamically stable film coating due to vibration can be used to govern (intensify) the mass transfer processes at interphase boundaries.

Acknowledgement: The authors thank A.S. Selyanin for his help in experimental setup production.

Funding Statement: This research was financially supported by the Russian Science Foundation (Project 23-11-00242).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: V.K.; data collection: V.S.; analysis and interpretation of results: V.K., V.S., N.K.; draft manuscript preparation: V.K., V.S., N.K. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Lyubimov, D. V., Cherepanov, A. A. (1987). Development of a steady relief at the interface of fluids in a vibrational field. Fluid Dynamics, 22, 849–854. [Google Scholar]

2. Jia, B. Q., Xie, L., Deng, X. D., He, B. S., Yang, L. J. et al. (2023). Experimental study on the oscillatory Kelvin–Helmholtz instability of a planar liquid sheet in the presence of axial oscillating gas flow. Journal of Fluid Mechanics, 959, A18. [Google Scholar]

3. Lyubimov, D. V., Lyubimova, T. P., Cherepanov, A. A. (2003). Dynamics of interfaces in vibration fields. Moscow: FizMatLit (in Russian). [Google Scholar]

4. Yoshikawa, H., Wesfreid, J. E. (2011). Oscillatory Kelvin–Helmholtz instability. Part 1. A viscous theory. Journal of Fluid Mechanics, 675, 223–248. [Google Scholar]

5. Landau, L. D., Lifshitz, E. M. (1987). Fluid mechanics, V. 6 of course of theoretical physics. New York: Pergamon Press. [Google Scholar]

6. Funada, T., Joseph, D. D. (2001). Viscous potential flow analysis of Kelvin–Helmholtz instability in a channel. Journal of Fluid Mechanics, 445, 263–283. [Google Scholar]

7. Kim, H., Padrino, J. C., Joseph, D. D. (2011). Viscous effects on Kelvin–Helmholtz instability in a channel. Journal of Fluid Mechanics, 680, 398–416. [Google Scholar]

8. Liu, C. L., Kaminski, A. K., Smyth, W. D. (2023). The effects of boundary proximity on Kelvin–Helmholtz instability and turbulence. Journal of Fluid Mechanics, 966, A2. [Google Scholar]

9. Plouraboué, F., Hinch, E. J. (2002). Kelvin–Helmholtz instability in a Hele-Shaw cell. Physics of Fluids, 14(3), 922–929. [Google Scholar]

10. Fu, Q., Deng, X., Yang, L. (2019). Kelvin–Helmholtz instability of confined Oldroyd-B liquid film with heat and mass transfer. Journal of Non-Newtonian Fluid Mechanics, 267, 28–34. [Google Scholar]

11. Kazimardanov, M. G., Mingalev, S. V., Lubimova, T. P., Yu, G. L. (2018). Simulation of primary film atomization due to Kelvin–Helmholtz instability. Journal of Applied Mechanics and Technical Physics, 59(7), 1251–1260. [Google Scholar]

12. Senecal, P. K., Schmidt, D. P., Nouar, I., Rutland, C. J., Reitz, R. D. et al. (1999). Modeling high speed viscous liquid sheet atomization. International Journal of Multiphase Flow, 25, 1073–1097. [Google Scholar]

13. Ebner, J., Gerendás, M., Schäfer, O., Wittig, S. (2001). Droplet entrainment from a shear-driven liquid wall film in inclined ducts: Experimental study and correlation comparison. Proceedings of the ASME Turbo Expo 2001, New Orleans, Louisiana, USA. [Google Scholar]

14. Dighe, S., Gadgil, H. (2021). On the nature of instabilities in externally perturbed liquid sheets. Journal of Fluid Mechanics, 916, A57. [Google Scholar]

15. Dementeva, Y. S., Kobeleva, V. S., Kozlov, V. G. (2022). Experimental study of liquids interface oscillatory dynamics in rotating slot gap. Journal of Physics: Conference Series, 2317(1), 012013. [Google Scholar]

16. Kozlov, V., Petukhova, M., Kozlov, N. (2023). Dynamics of liquids with high viscosity contrast in unevenly rotating Hele-Shaw cell. Philosophical Transactions of the Royal Society Mathematical Physical & Engineering Sciences, 381, 20220082. [Google Scholar]

17. Kozlov, V. G., Zimasova, A. R. (2023). Dynamics of two liquids in a non-uniformly rotating horizontal cylinder. E3S Web of Conferences, 402, 14002. [Google Scholar]

18. Schlichting, H. (1968). Boundary layer theory, 7th edition. New York: McGraw-Hill. [Google Scholar]

19. Rosenblat, S. (1959). Torsional oscillations of a plane in a viscous fluid. Journal of Fluid Mechanics, 5, 206–220. [Google Scholar]

20. Lim, T. G., Hyun, J. M. (1997). Flow driven by a torsionally-oscillating shrouded endwall disk. Journal of Fluids Engineering, 119(1), 115–121. [Google Scholar]