Influence of Brownian Motion, Thermophoresis and Magnetic Effects on a Fluid Containing Nanoparticles Flowing over a Stretchable Cylinder

1  Introduction

Recently, researchers have shown considerable interest in investigating heat transfer and boundary layer flow over stretching surfaces, primarily because of their relevance in industrial processes like paper manufacturing, wire production, and plastic wrapping. Moreover, there has been a growing focus on magneto-hydrodynamic fluid flow involving nanofluids, which consist of a mixture of liquids and nanoparticles. This surge in interest is driven by numerous applications in industrial and engineering settings. It is worth noting that conventional fluids like freshwater, ethylene, and mineral oils exhibit inferior thermal properties when compared to metals, non-metals, and their oxides. Choi et al. [1] was the pioneering researcher who experimentally demonstrated the significant enhancement of thermal conductivity by adding nanoparticles to conventional base fluids. Various manufacturing processes, spanning from microelectronic devices to hybrid engines, fuel cells, nuclear reactors, transportation, biomedical and pharmaceutical applications, as well as food processing, heavily rely on utilizing temperature differences. Researchers like Ahmed et al. [2] introduced modified models to describe nanofluid behavior, with the Boussinesq approximation simplifying the buoyancy term. Ahmed et al. [3] discussed homogeneous-heterogeneous reactions in the boundary layer flow of water-based nanofluids near stagnation points. Valipour et al. [4] conducted an analysis on CNT-polyethylene nanofluids under the influence of a magnetic field. Li et al. [5] focused on thermal variations in a porous cylinder saturated with nanomaterials.

Additionally, several studies have explored the behavior of nanoparticles in non-Newtonian fluids. For example, Zeeshan et al. [6] investigated Casson nanofluids on linear stretching sheets, whereas Murthy et al. [7] extended their analysis to exponentially stretching sheets. Arian et al. [8] introduced bio-convection effects into a Reiner-Rivlin nanofluid flow in a rotating frame. Pallavarapu [9] analyzed Williamson nanofluids with Cattaneo-Cristov (CC) heat flux over a stretching sheet. Reddy et al. [10] studied Maxwell nanofluids with chemical reactions on a stretching sheet, and Zeeshan et al. [11] delved into surface chemical reactions with non-Newtonian fluids over a parabolic surface. These studies contribute to our understanding of nanofluid behavior in diverse applications.

Due to its industrial uses and significant implications for several technological processes, the investigations on the magneto-hydrodynamic flow and transfer of heat over extending cylinders have attracted a lot of interest. Crane [12] looked at the flow produced by simply stretching a sheet. The work of Crane [12] was expanded upon by other scholars, including Gupta et al. [13], Dutta et al. [14], and Char et al. [15], by including the impact of heat and mass transport analyses under various physical circumstances. Other researchers, notably Xu et al. [16], Cortell [17,18], and Hayat et al. [19], have recently looked at various facets of this topic. In the early stages of research on this topic, Wang [20] investigated the flow characteristics across stretched cylinders. In this study, because we are using the thin cylinder as a model, it is possible to assume the boundary layer thickness and radius to have the same order. The flow may thus be conceived of as axisymmetric rather than 2D, and the modified equations now incorporate the curvature component. This has an impact on the temperature and velocity fields, which in turn has an impact on the skin’s coefficient of friction and rate of heat transmission. Similarly, solutions of these types of flows have been described in various physical contexts by Ishak et al. [21], Elbashbeshy et al. [22], Bachok et al. [23], and Poply et al. [24]. Despite having various uses in several sectors including, the cooling of things, electricity production, and petroleum refining, magnetic influence has not yet been taken into consideration. There have been studies on this impact on material parameters in the literature (Dessie et al. [25], Vajravelu et al. [26], Singh et al. [27], Ahmed et al. [28], Zeeshan et al. [29] Babazadeh et al. [30], Shiekhoslami et al. [31]), with the magnetic influence on porous and free stream velocity described for linear and non-linear stretching surfaces, respectively, in Yadav et al. [32] and Singh et al. [33].

The properties of heat transportation and boundary layer flow over a stretched cylinder under the influence of a magnetic field and porous media, however, have received much attention. Numerous technical issues, including those involving magnetohydrodynamic (MHD) power generators, the petroleum industry, plasma research, and geothermal energy extraction, greatly benefit from the use of the MHD flow and heat transfer. Nield et al. [34] and Ishak et al. [35] investigated the impact of MHD caused by a stretched cylinder. Loganathan et al. [36] and Ganesan et al. [37] found that the increment of the magnetic field reduces the velocity boundary layer and thickens the temperature boundary layer.

The primary objective of this research is to assess the influence of thermophoresis and Brownian motion on the introduction of minute nanoparticles in a porous reference framework. The study incorporates the utilization of nanofluids and mixed convection. The obtained findings are juxtaposed with previously published data, considering various temperature exponent values. To illustrate the impact of these relevant parameters, the research presents graphical representations and tabulated results for concentration, velocity, and temperature configurations. The numerical computations are executed using a shooting algorithm implemented with MATLAB software.

2  Mathematical Model and Description

Let us consider the two-dimensional, incompressible, boundary layer mixed convective nanofluid flow towards a stretchable cylinder (see Fig. 1) with surface velocity U~(x)=U0xl in the axial direction and the surface temperature is Tw=T∞+T0(xL)N . A magnetic field is employed with strength B0 in the normal direction. Temperature exponent N is considered in a porous frame of reference.

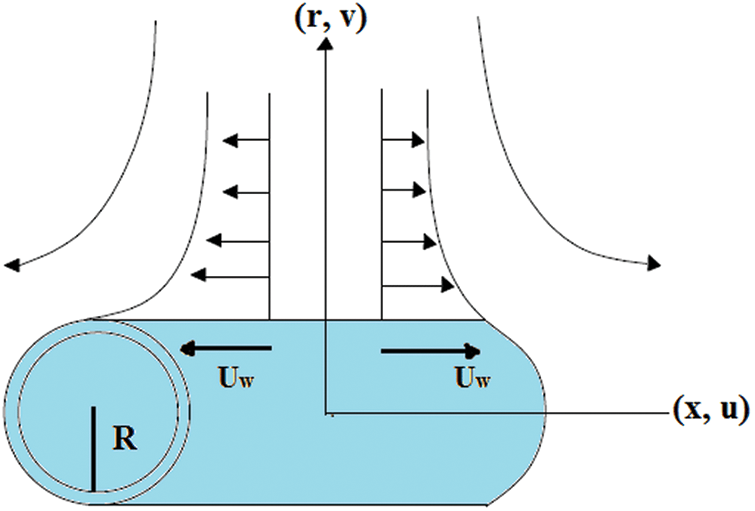
Figure 1: Physical sketch of the model

The nanofluid is governed by the following expression [33,34,37–39]:

∂(ru)∂x+∂(rν)∂r=0, (1)

u∂u∂x+ν∂u∂r=−υκu+υr∂∂r(r∂u∂x)+gβ(T~−T~∞)−σB0ρu, (2)

u∂T~∂x+ν∂T~∂r=κr∂∂r(r∂T~∂r), (3)

u∂C~∂x+v∂C~∂r=DTrT~∞∂∂r(r∂T~∂r)+DBr∂∂r(r∂C~∂r). (4)

With boundary conditions:

u=U~(x), ν=0,    T~=T~w(x),DB∂C~∂r+DTT~∞∂T~∂r=0 at r=R,

u→0,     T~→T~∞     C~→C~∞ as   r→∞, (5)

By applying similarity transformation, we have

η=r2−R22R(U~νx)12,ψ=(U~x)12Rf(η), θ(η)=T~−T~∞T~w−T~∞,ϕ(η)=C~−C~∞C~w−C~∞,u=1 r ∂ψ∂x,   v=−1r∂ψ∂r}. (6)

The reduced form of the ODE can be achieved when Eqs. (5), (6) are used into Eqs. (1)–(4).

(1+2Aη)f′′′+2Af′′+ff′′−f′2−Df′+λθ−Mf′=0, (7)

2Aθ′+(1+2Aη)θ′′+Pr(fθ′−Nf′θ)=0, (8)

(1+2γη)ϕ′′+2γNtNbθ′+2γϕ′+PrLefϕ′+(1+2γη)NtNbθ′′=0. (9)

The corresponding reduced form of Boundary conditions are:

f(0)=0,   f′(0)=0,     θ(0)=1 , Ntθ′(0)+Nbϕ′(0)=0    at r=R (10)

f′(η)→0,    θ(η)→0,   ϕ(η)→0  as    η→∞. (11)

where (v, u) are the components of velocity in the (r,x) direction, T is temperature, f is the dimensionless velocity, θ is the dimensionless temperature, ϕ is the dimensionless concentration, A is the curvature parameter, M is the magnetic field parameter, D indicates the porous medium, λ represents mixed convection,  Pr is the Prandtl number, DB is the Brownian coefficient, G is the acceleration due to gravity, Dn is the diffusion coefficient, C∞  and T∞ signify the free stream of concentration and temperature, τ is the heat capacitance, α  is the normal stress moduli, Tw is the surface temperature, B0 is magnetic induction, σ is electrical conductivity, Cw is  the surface concentration, DT is the thermophoresis coefficient, κ  denotes the thermal diffusivity of liquid, Le is the Lewis Number, Nt is the thermophoresis coefficient parameter and Nb is the Brownian motion parameter.

3  Numerical Scheme

The firing approach was employed to perform the mathematical calculations using the shooting technique as shown in the flow chart (Fig. 2). The following assumptions were made when simulating the numerical computations to arrive at the problem’s first order system.

Figure 2: Flow chart of the scheme

f=m1, f′=m2,f′′=m3,f′′′=m3′,θ=m4,θ′=m5, θ′=m5′ ϕ=m6,ϕ′=m7, ϕ′′=m′7 (12)

The dimensionless system of Eqs. (7)–(11) in view of the above defined variables are:

m3′=−(2γm3+λθ+m1m3−m22−Mm1−Dm3)(1+2γη), (13)

m5′=−[2Am5+(prfm5−prNm2m4)](1+2γη), (14)

m′7=−1(1+2γη)[2γm7+2γNtNbm5+PrLem1m7+(1+2γη)NtNbm′5]. (15)

The corresponding dimensionless boundary conditions are:

m2(0)=1+m3(0),m2(0)=0, m4(0)=0,Ntm5+Nbm7=0  (16)

m2(∞)=0, m4(∞)=0,m6(∞)=0. (17)

4  Validation

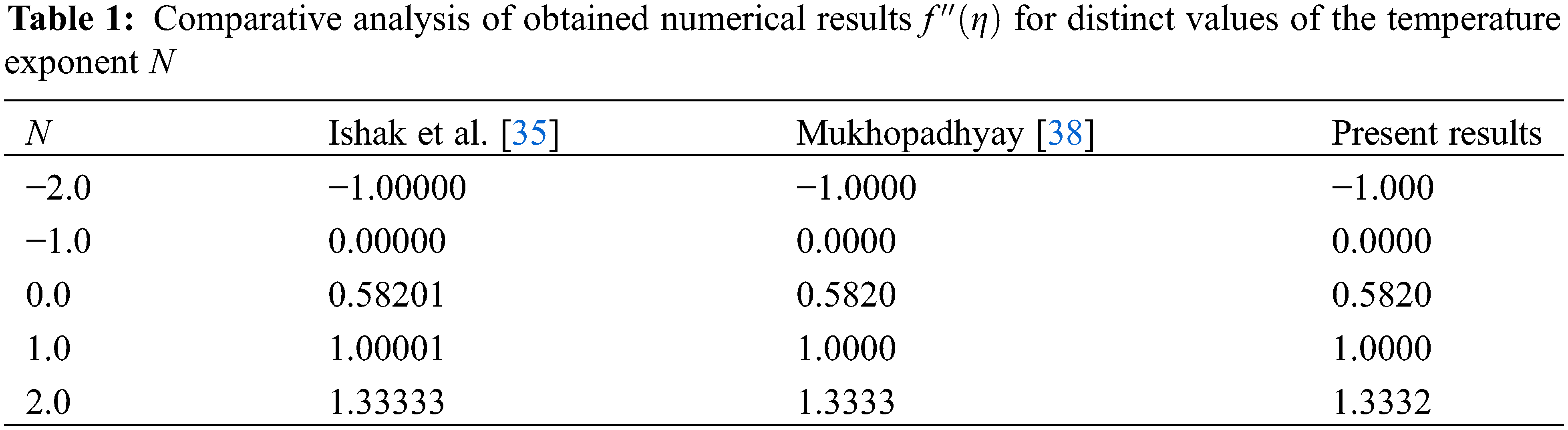
As a limiting case, the resulting numerical findings are validated in Table 1. The outcomes were compared with those obtained by Ishak et al. [35] and Mukhopadhya [38], and the numerical values show good agreement between the previous ones. There is a slight accuracy between the two investigations.

5  Results and Discussion

In this portion, the influence of emerging parameters on non-dimensional velocity profile f′ , temperature profile θ and concentration profile ϕ are investigated as shown in Figs. 3–9.

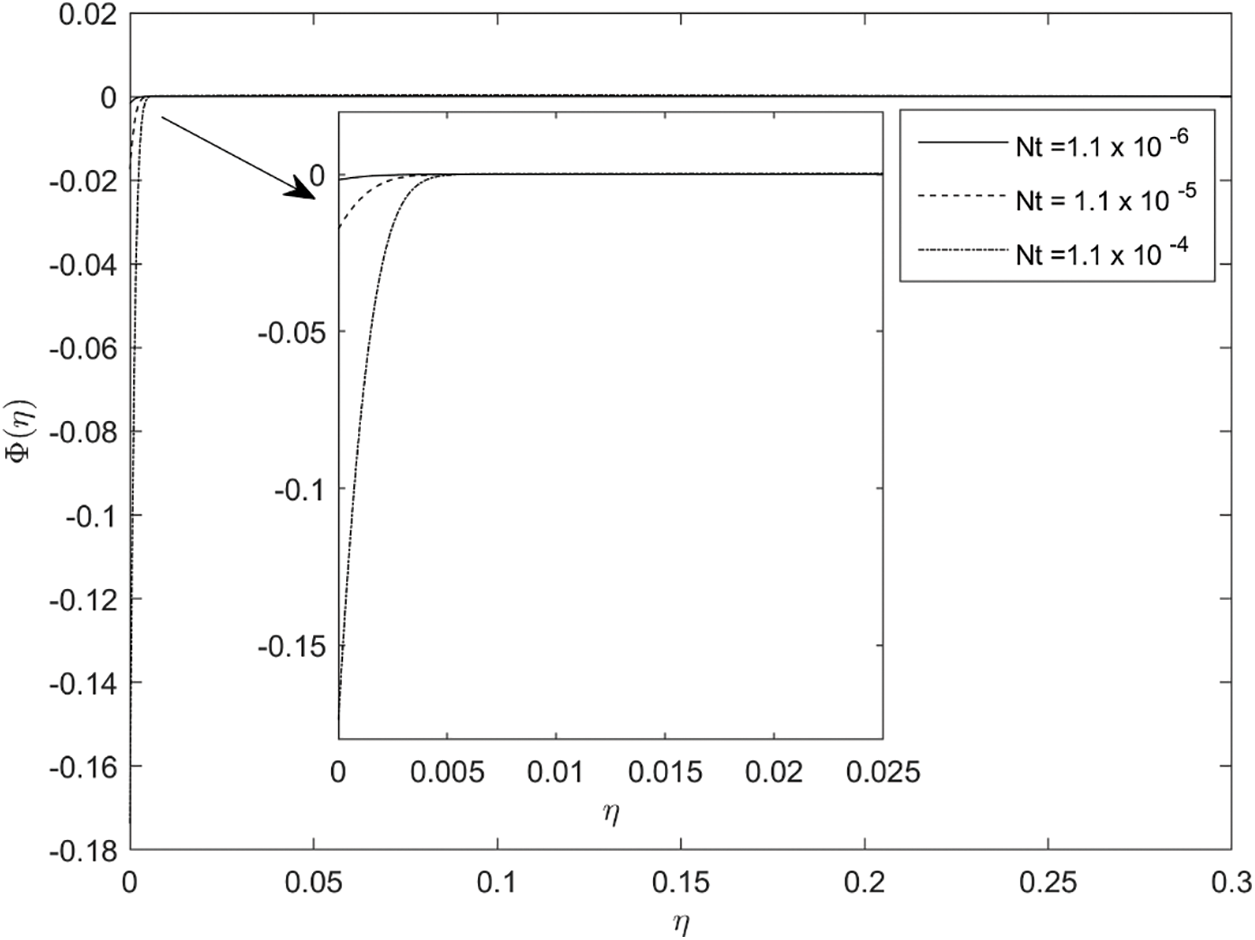
Figure 3: Implication of Nt on ϕ(η)

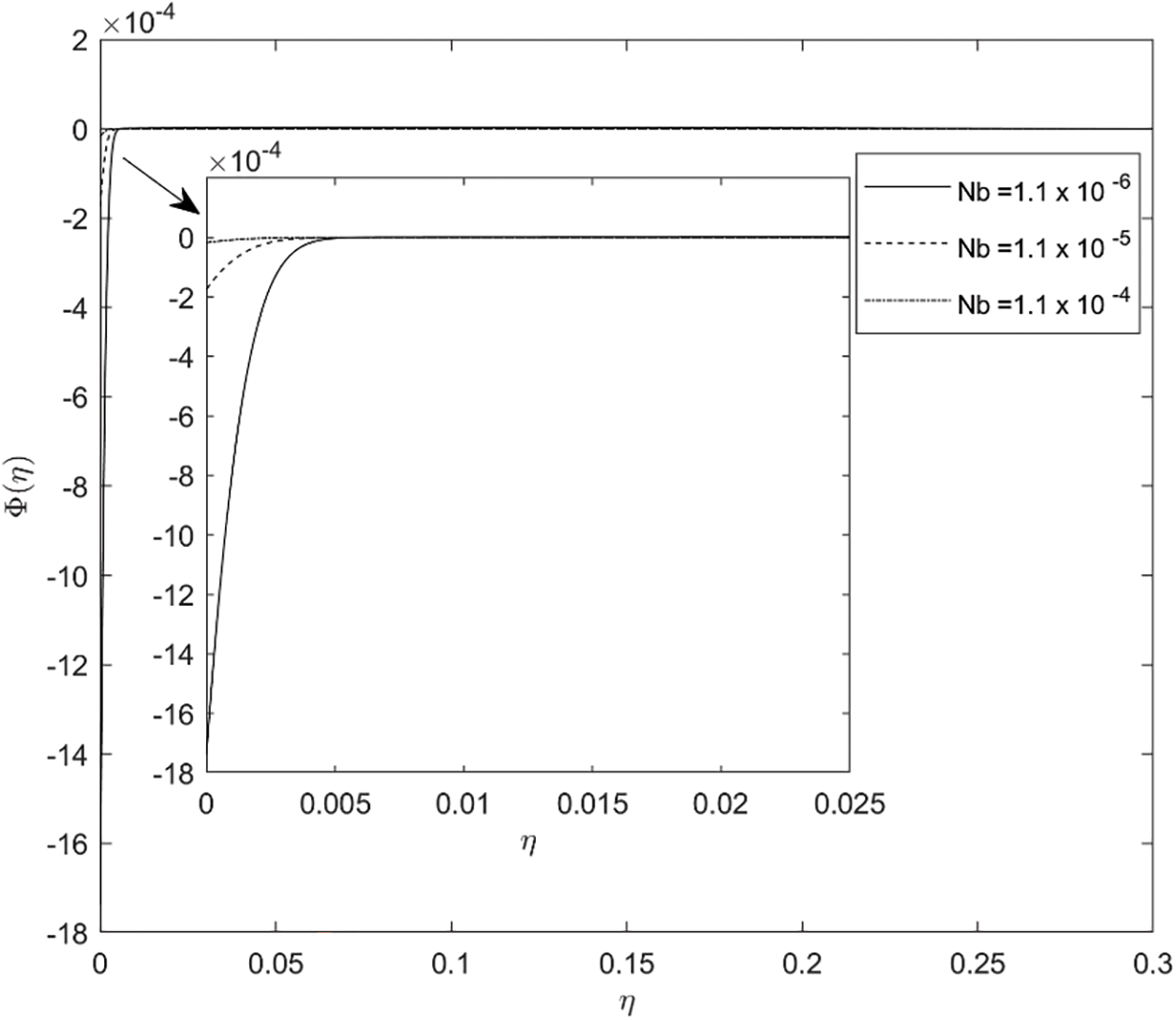
Figure 4: Implication of Nb on ϕ(η)

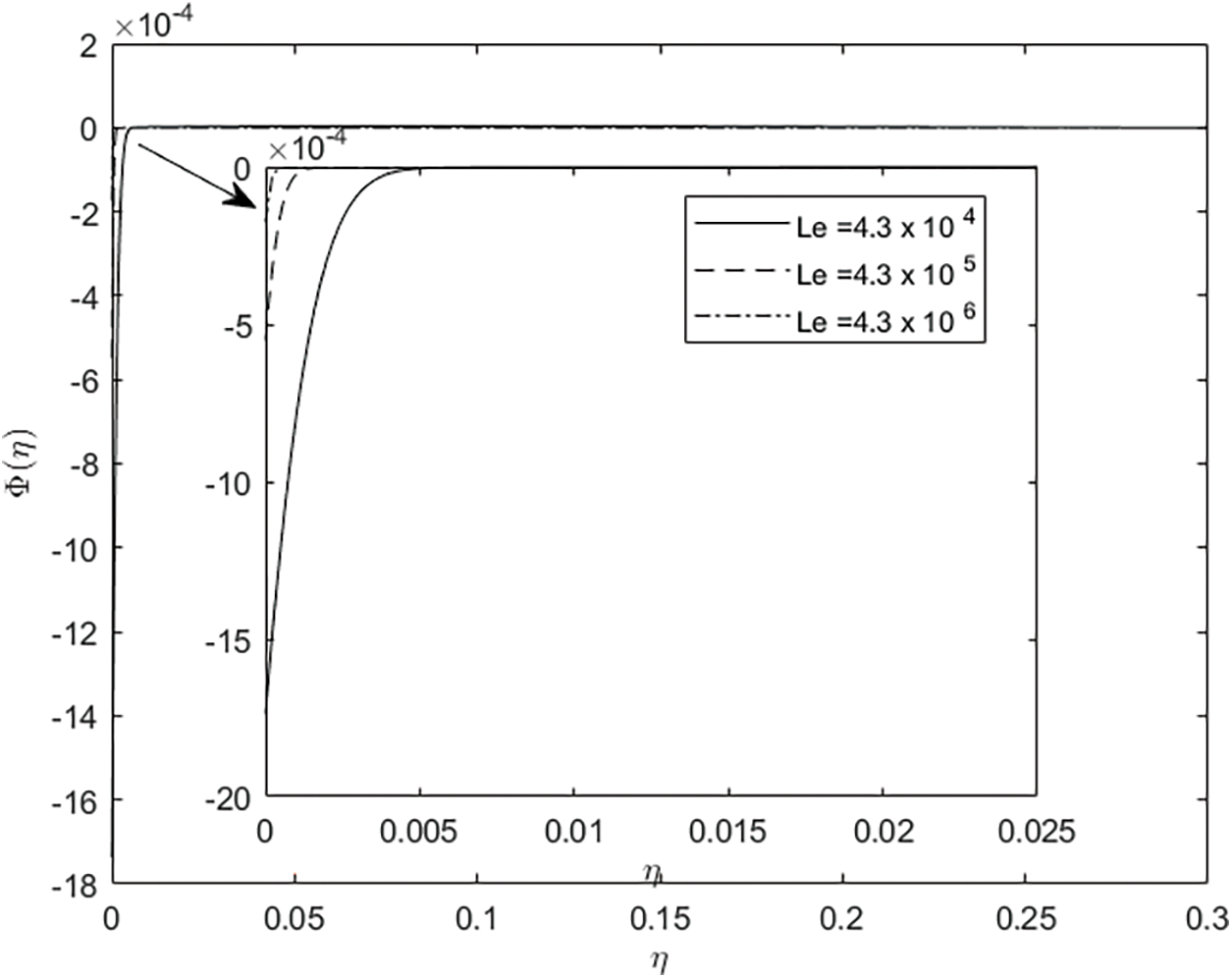
Figure 5: Implication of Le on ϕ(η)

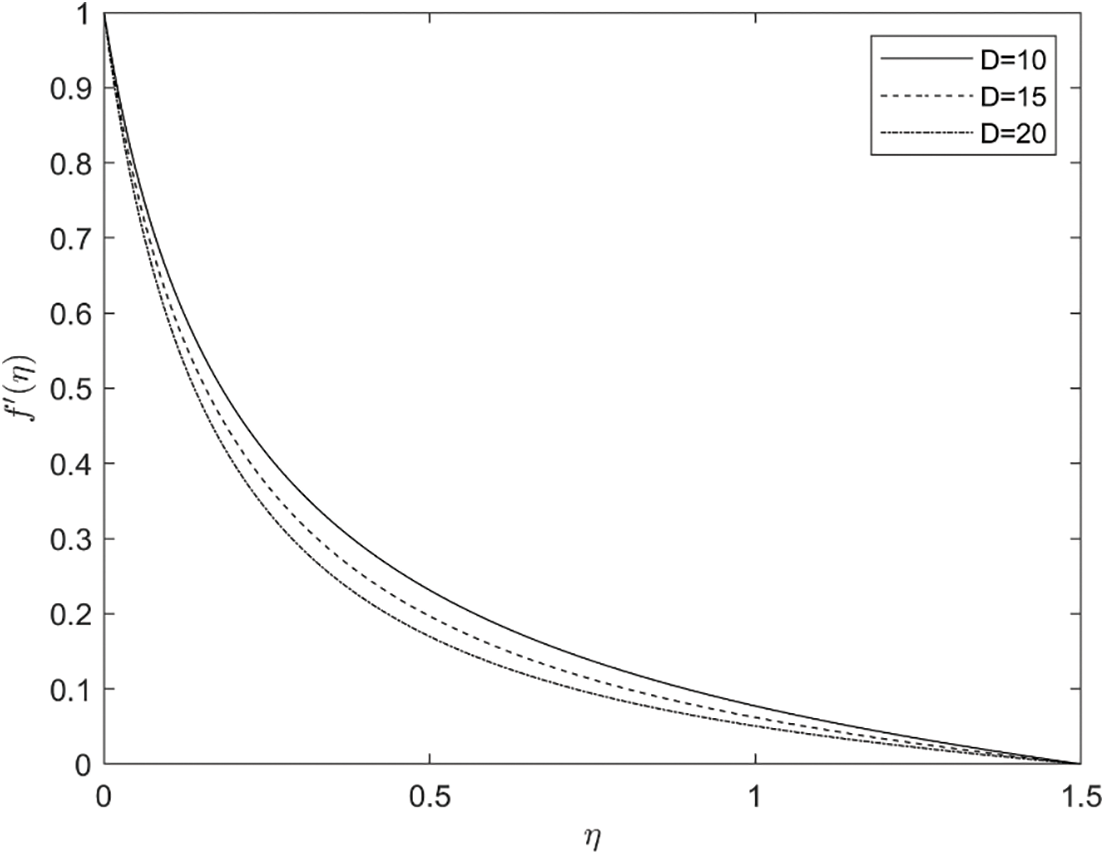
Figure 6: Implication of D on f′(η)

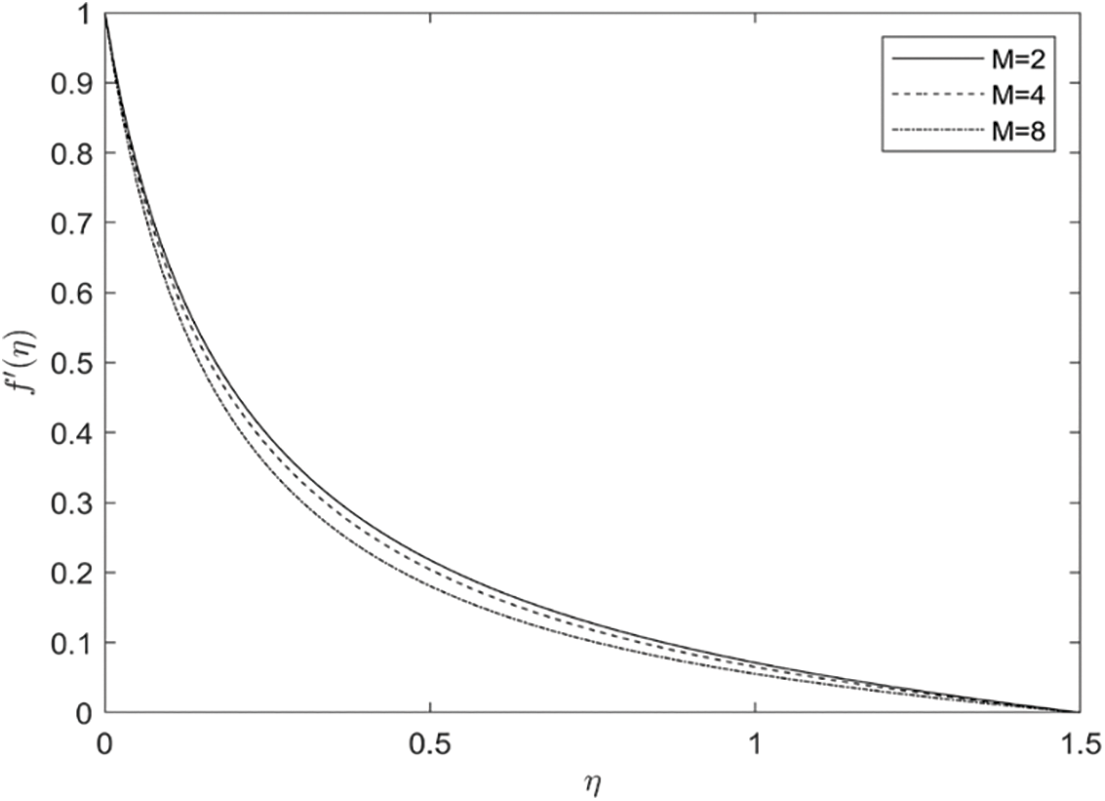
Figure 7: Implication of M on f′(η)

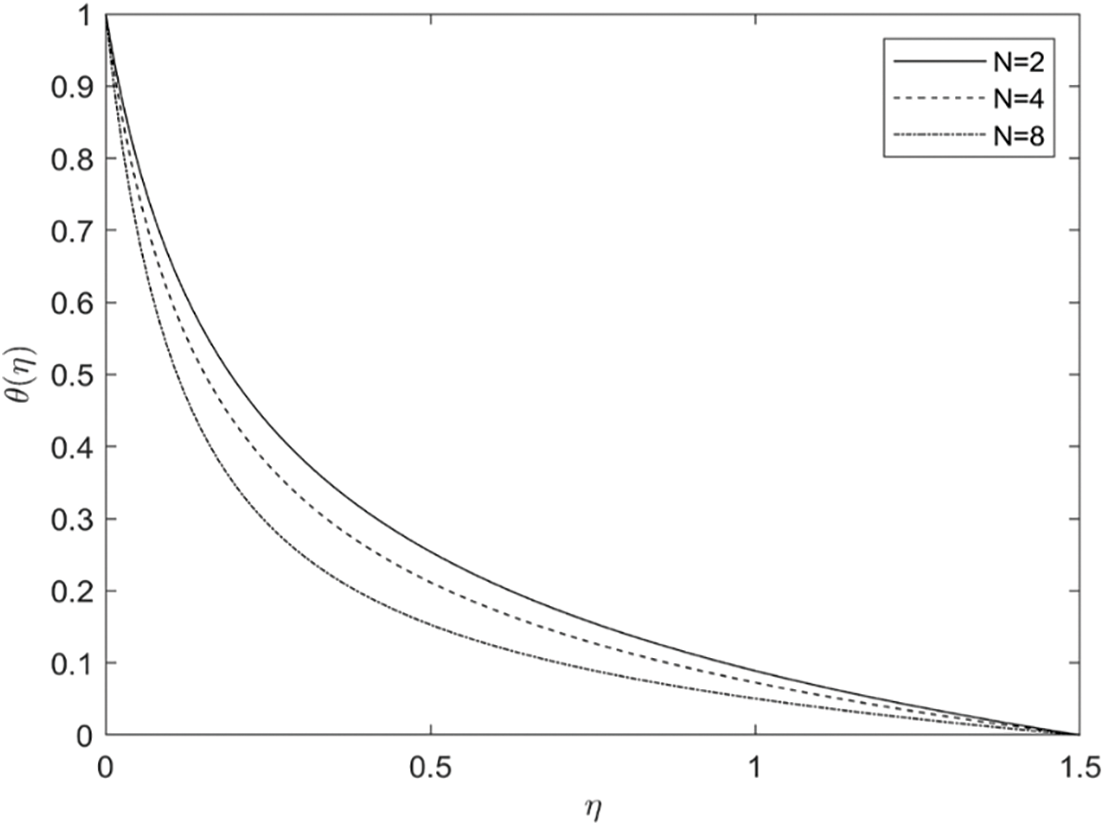
Figure 8: Implication of N on θ(η)

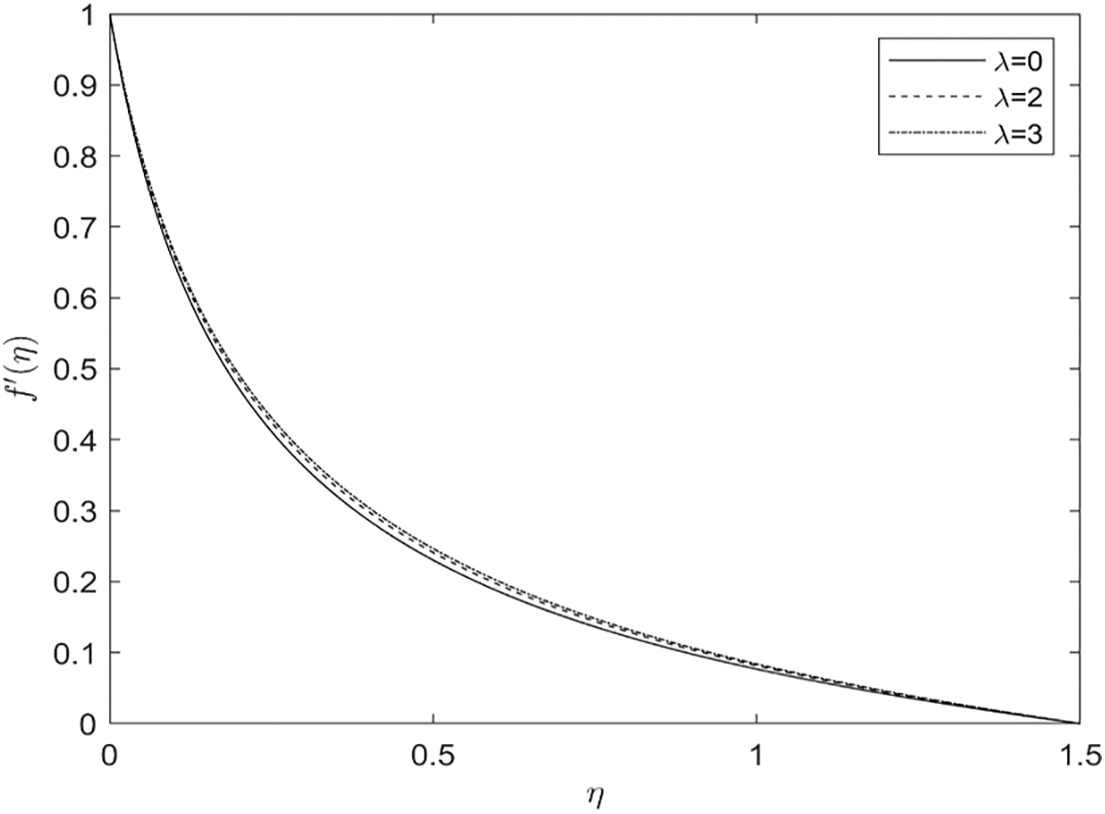
Figure 9: Implication of λ on f′(η)

Figs. 3 and 4 illustrate the concentration profiles for distinct values of the Brownian parameter ( Nb ) and the thermophoresis parameter ( Nt ). The graphs depict that a decrement occurs in the concentration profiles for higher values of Nb. Enhancing the thermophoresis process increases particle movement from the upper to the lower temperature difference, which consequently increases the nanoparticles concentration in the flow regime. Physically this happens by increasing Nb, resulting in the fluid within the barrier becoming warmer, exacerbating the random motion of particles, and thus reducing the concentration profile. The influence of Lewis number Le on the concentration profile is displayed in Fig. 5. Raising the value of Le slows down the concentration field and associated thickness of the boundary layer; because Le is not directly related to the Brownian coefficient, any increment in Le leads to a slowdown of the concentration field.

Fig. 6 illustrates the influence of the permeability parameter on the velocity profile. The pouring medium imposes a greater restriction on the fluid flow, causing its motion to reverse backwards The fluid velocity reduces while the fluid temperature and concentration profile increase for numerous values of the porosity medium ( D ). The influence of the magnetic parameter (M) on the temperature, velocity, and concentration fields is illustrated in Fig. 7. The velocity profile reduces with increments in M. From a physical perspective, a Lorentz force exists, which opposes the fluid’s motion and reduces the velocity field.

Fig. 8 illustrates the variation in temperature profile for distinct values of N, for a stretched flat plate ( γ = 0 ). Heat accumulates with rising values of N, such that temperature exceeds the thermal properties at the boundary layer’s edge when N is greater than 0. Although the temperature significantly increases with N, there is no thermal runaway for the stretched cylinder ( γ = 1 ), and so, temperature and concentration decrease with increasing values of N.

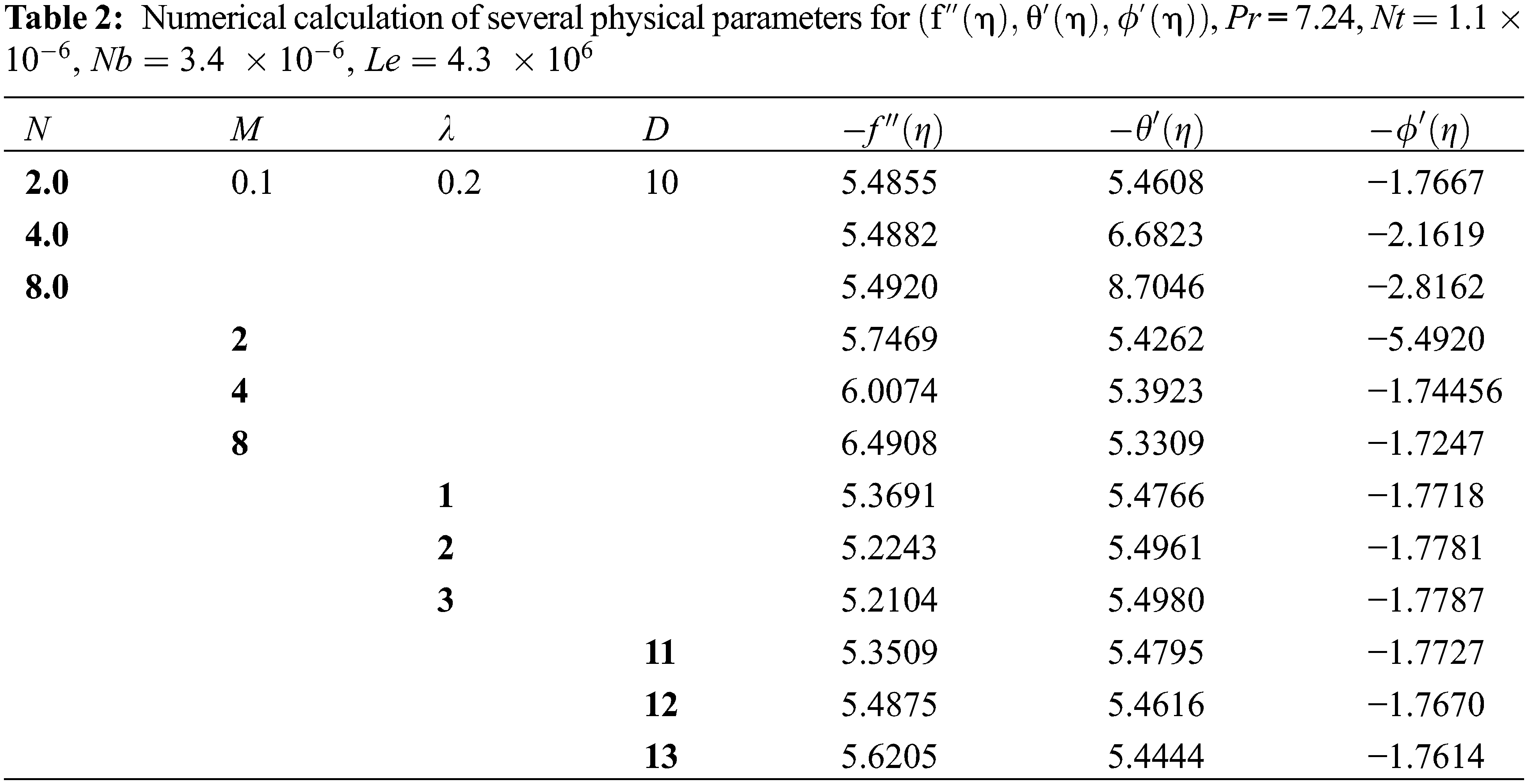
Fig. 9 illustrates the effect on velocity profile of both surfaces by convection (λ); it is noted that note fluid velocity affects both situations by raising the values of ( λ ). Technically, this is related to the enhancement of the thermal buoyancy force. So, increasing the scores of mixed convection led to increases in speed with-in a transition zone. Table 2 presents the numerical values of friction factor (f′′(η)) , heat transfer rate (θ′(η)), and concentration profile (ϕ(η)) for some physical arguments.

6  Conclusions

This paper primarily investigates the impacts of Brownian motion and thermophoresis on nanoparticles suspended in a base fluid characterized by low thermal conductivity. Thermophoresis is responsible for moving these nanoscale particles from warmer areas to cooler ones, while Brownian motion represents the random motion of particles, especially causing heavier particles to settle. Consequently, in this study, we assess the influence of magnetohydrodynamics (MHD) on the boundary layer flow around a cylindrical object, considering the Lorentz force.

•   We examine the effects of various physical parameters on velocity, temperature, and concentration, and we present these outcomes using tables and graphs. In summary, the key findings of this research are as follows: By enhancing the magnetic field M, tempera the ture, velocity and concentration profiles decrease.

•   The temperature and concentration profiles are enhanced by increases in the values of D , while the velocity profile reduces.

•   The velocity profile decreases when the parameters D and M are increased.

•   The temperature profile is lowered when the parameters A, N, and Pr are increased.

•   The concentration profile is reduced by increasing the parameters A, N, Le, and Nb.

•   There is a notable increased in the concentration profile when the thermophoresis parameter Nt incorporating the nanoparticles into the fluid increases its thermal conductivity.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: A. Majeed, A. Zeeshan; data collection: A. Zeeshan; analysis and interpretation of results: A. Majeed; draft manuscript preparation: A. Majeed, A. Zeeshan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflict of interest to report regarding the present study.

References

1. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne National Lab (ANLArgonne, IL, USA. [Google Scholar]

2. Ahmed, S., Xu, H. (2020). Mixed convection in gravity-driven thin nano-liquid film flow with homogeneous-heterogeneous reactions. Physics of Fluids, 32(2), 23604. [Google Scholar]

3. Ahmed, S., Xu, H., Sun, Q. (2020). Stagnation flow of a SWCNT Nanofluid towards a plane surface with heterogeneous-homogeneous reactions. Mathematical Problems in Engineering, 2020, 1–12. [Google Scholar]

4. Valipour, P., Aski, F. S., Mirparizi, M. (2017). Influence of magnetic field on CNT-Polyethylene nanofluid flow over a permeable cylinder. Journal of Molecular Liquids, 225, 592–597. [Google Scholar]

5. Li, Y., Shakeriaski, F., Barzinjy, A. A., Dara, R. N., Shafee, A. et al. (2020). Nanomaterial thermal treatment along a permeable cylinder. Journal of Thermal Analysis and Calorimetry, 139, 3309–3315. [Google Scholar]

6. Zeeshan, A., Mehmood, O. U., Mabood, F., Alzahrani, F. (2022). Numerical analysis of hydromagnetic transport of Casson nanofluid over permeable linearly stretched cylinder with Arrhenius activation energy. International Communications in Heat and Mass Transfer, 130, 105736. [Google Scholar]

7. Murthy, M. K., Sreenadh, S., Lakshminarayana, P., Sucharitha, G., Rushikumar, B. (2019). Thermophoresis and Brownian motion effects on three dimensional magnetohydrodynamics slip flow of a Casson nanofluid over an exponentially stretching surface. Journal of Nanofluids, 8(6), 1267–1272. [Google Scholar]

8. Arain, M. B., Bhatti, M. M., Zeeshan, A., Alzahrani, F. S. (2021). Bioconvection reiner-rivlin nanofluid flow between rotating circular plates with induced magnetic effects, activation energy and squeezing phenomena. Mathematics, 9(17), 2139. [Google Scholar]

9. Pallavarapu, L. (2022). MHD radiative flow of Williamson nanofluid with Cattaneo-Christov model over a stretching sheet through a porous medium in the presence of chemical reaction and suction/inject. Journal of Porous Media, 25(12), 1–15. [Google Scholar]

10. Reddy, M. V., Lakshminarayana, P. (2021). Cross-diffusion and heat source effects on a three-dimensional MHD flow of Maxwell nanofluid over a stretching surface with chemical reaction. The European Physical Journal Special Topics, 230, 1371–1379. [Google Scholar]

11. Zeeshan, A., Awais, M., Alzahrani, F., Shehzad, N. (2021). Energy analysis of non-Newtonian nanofluid flow over parabola of revolution on the horizontal surface with catalytic chemical reaction. Heat Transfer, 50(6), 6189–6209. [Google Scholar]

12. Crane, L. J. (1970). Flow past a stretching plate. Zeitschrift für Angewandte Mathematik und Physik ZAMP, 21(4), 645–647. [Google Scholar]

13. Gupta, P. S., Gupta, A. S. (1977). Heat and mass transfer on a stretching sheet with suction or blowing. The Canadian Journal of Chemical Engineering, 55(6), 744–746. [Google Scholar]

14. Dutta, B. K., Roy, P., Gupta, A. S. (1985). Temperature field in flow over a stretching sheet with uniform heat flux. International Communications in Heat and Mass Transfer, 12(1), 89–94. [Google Scholar]

15. Char, M. I. (1988). Heat transfer of a continuous, stretching surface with suction or blowing. Journal of Mathematical Analysis and Applications, 135(2), 568–580. [Google Scholar]

16. Xu, H., Liao, S. J. (2005). Series solutions of unsteady magnetohydrodynamic flows of non-Newtonian fluids caused by an impulsively stretching plate. Journal of Non-Newtonian Fluid Mechanics, 129(1), 46–55. [Google Scholar]

17. Cortell, R. (2005). Flow and heat transfer of a fluid through a porous medium over a stretching surface with internal heat generation/absorption and suction/blowing. Fluid Dynamics Research, 37(4), 231–245. [Google Scholar]

18. Cortell, R. (2006). Effects of viscous dissipation and work done by deformation on the MHD flow and heat transfer of a viscoelastic fluid over a stretching sheet. Physics Letters A, 357(4–5), 298–305. [Google Scholar]

19. Hayat, T., Abbas, Z., Sajid, M. (2006). Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Physics Letters A, 358(5–6), 396–403. [Google Scholar]

20. Wang, C. Y. (1988). Fluid flow due to a stretching cylinder. The Physics of Fluids, 31(3), 466–468. [Google Scholar]

21. Ishak, A., Nazar, R. (2009). Laminar boundary layer flow along a stretching cylinder. European Journal of Scientific Research, 36(1), 22–29. [Google Scholar]

22. Elbashbeshy, E. M. A., Emam, T. G., El-Azab, M. S., Abdelgaber, K. M. (2012). Laminar boundary layer flow along a stretching horizontal cylinder embedded in a porous medium in the presence of a heat source or sink with suction/injection. International Journal of Energy & Technology, 4(28), 1–6. [Google Scholar]

23. Bachok, N., Ishak, A. (2010). Flow and heat transfer over a stretching cylinder with prescribed surface heat flux. Malaysian Journal of Mathematical Sciences, 4(2), 159–169. [Google Scholar]

24. Poply, V., Singh, P., Chaudhary, K. K. (2013). Analysis of laminar boundary layer flow along a stretching cylinder in the presence of thermal radiation. WSEAS Transactions on Fluid Mechanics, 8(4), 159–164. [Google Scholar]

25. Dessie, H., Kishan, N. (2014). MHD effects on heat transfer over stretching sheet embedded in porous medium with variable viscosity, viscous dissipation and heat source/sink. Ain Shams Engineering Journal, 5(3), 967–977. [Google Scholar]

26. Vajravelu, K., Prasad, K. V., Santhi, S. R. (2012). Axisymmetric magneto-hydrodynamic (MHD) flow and heat transfer at a non-isothermal stretching cylinder. Applied Mathematics and Computation, 219(8), 3993–4005. [Google Scholar]

27. Singh, P., Jangid, A., Tomer, N. S., Sinha, D. (2010). Effects of thermal radiation and magnetic field on unsteady stretching permeable sheet in presence of free stream velocity. International Journal of Physical and Mathematical Sciences, 4(3), 396–402. [Google Scholar]

28. Ahmed, S., Xu, H., Zhou, Y., Yu, Q. (2022). Modelling convective transport of hybrid Nanofluid in a lid driven square cavity with consideration of Brownian diffusion and thermophoresis. International Communications in Heat and Mass Transfer, 137, 106226. [Google Scholar]

29. Zeeshan, A., Majeed, A., Akram, M. J., Alzahrani, F. (2021). Numerical investigation of MHD radiative heat and mass transfer of nanofluid flow towards a vertical wavy surface with viscous dissipation and Joule heating effects using Keller-box method. Mathematics and Computers in Simulation, 190, 1080–1109. [Google Scholar]

30. Babazadeh, H., Muhammad, T., Shakeriaski, F., Ramzan, M., Hajizadeh, M. R. (2021). Nanomaterial between two plates which are squeezed with impose magnetic force. Journal of Thermal Analysis and Calorimetry, 144, 1023–1029. [Google Scholar]

31. Sheikholeslami, M., Zeeshan, A., Majeed, A. (2018). Control volume based finite element simulation of magnetic nanofluid flow and heat transport in non-Darcy medium. Journal of Molecular Liquids, 268, 354–364. [Google Scholar]

32. Yadav, R. S., Sharma, P. R. (2014). Effects of porous medium on MHD fluid flow along a stretching cylinder. Annals of Pure and Applied Mathematics, 6(1), 104–113. [Google Scholar]

33. Singh, P., Poply, V. (2015). Impact of free stream velocity and variable heat flux over a permeable stretching surface. International Journal of Applied Engineering Research, 10(94). [Google Scholar]

34. Nield, D. A., Kuznetsov, A. V. (2009). The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer, 52(25–26), 5792–5795. [Google Scholar]

35. Ishak, A., Nazar, R., Pop, I. (2008). Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Conversion and Management, 49(11), 3265–3269. [Google Scholar]

36. Loganathan, P., Ganesan, P., Kannan, M. (2010). MHD effects on moving semi-infinite vertical cylinder with heat and mass transfer. International Journal of Application Mathematic and Mechanics, 6(21), 22–40. [Google Scholar]

37. Ganesan, P., Loganathan, P. (2003). Magnetic field effect on a moving vertical cylinder with constant heat flux. Heat and Mass Transfer, 39(5), 381–386. [Google Scholar]

38. Mukhopadhyay, S. (2012). Mixed convection boundary layer flow along a stretching cylinder in porous medium. Journal of Petroleum Science and Engineering, 96, 73–78. [Google Scholar]

39. Buongiorno, J. (2006). Convective transport in nanofluids. Journal of Heat Transfer, 128, 240–250. [Google Scholar]