Efficiency of a Modular Cleanroom for Space Applications

1  Introduction and Background

Indoor and cleanroom flows driven by mechanical [1,2] and natural ventilation [3], and usually disturbed by equipment and human motion [4], are highly unsteady with laminar, transient (intermittent) and turbulent regimes co-existing, and usually do not have a prevailing flow direction. These flows are highly three-dimensional across a wide range of time scales from the residual time (or eddy turn-over time) to the smallest turbulent eddy scale. Besides the high complexity of flow dynamics, the dispersion of scalar and Particulate Matter (PM) is extremely complex [1,3], for which accurate simulations and measurements are challenging. In the recent years, these have attracted even greater attention for various applications [2, 5–15]. Assessing cleanroom efficiency and effectiveness is one vital application.

A cleanroom is a closed space designed for a certain cleanliness level of pollutants in a short ventilation time, usually by using intensive mechanical ventilation. Cleanrooms are used for pharmaceutical products, medical equipment, and space applications, such as space hardware transportation facility cleanrooms. Compared to office rooms, cleanrooms have a much higher requirement [16–23], while the strictest standards have been achieved only for space applications. This paper is focused on the design of a Plastron portable cleanroom for satellite handling during launch campaigns, and the assessment of its ventilation efficiency.

Table 1 shows the ISO class numbers and the corresponding maximum numbers of particles per cubic metre of air [24], where the maximum number of particles is ten times the corresponding number of the class just one level lower. For example, the maximum number of particles ( ≥0.5μm ) is 35,200,000 per cube metre of air for the ISO9 standard, while it is 3,520,000 for the ISO8 standard. The ISO8 standard is also known as Class 100,000 cleanroom, which is equivalent to a maximum particle count of 100,000 particles ( ≥0.5μm ) per cubic foot of air. Note the ambient air quality outside the cleanroom in a typical European city environment is equivalent to the ISO9 standard. In other words, the particle concentration for the ISO8 standard is at least one tenth of that in the ambient air, while the particle concentration for the ISO6 standard is at least one thousandth of the ambient concentration. It is of crucial importance to optimise ventilation efficiency to ensure that the designed cleanroom can meet the appropriate cleanliness level in a shorter time duration, reducing energy consumption in climate change.

The peak concentration [25,26] has attracted increasing attention in recent years, such as for an estimation of exposure in a short duration for specific applications. An ‘accurate’ estimation of the peak concentration is difficult, and is usually out of the range of numerical resolution or sensor sensitivity, as the concentration is more intermittent than the flow. The temporal and spatial resolutions can significantly affect the accuracy in numerical simulations and experiments, and statistical or theoretical approaches are usually used instead. One approach is the so-called eddy diffusion model [27] assuming a constant diffusivity, based on an analytic solution for an instantaneous point source in an infinite volume [28] and symmetric (mirror) boundary conditions representing room walls. These models are not suitable for the assessment of cleanroom efficiency. To compromise computational cost and accuracy, this paper is focused on simulations of unsteady Reynolds average Navier-Stokes (URANS) equations, and a small number of large-eddy simulations (LES) for cross comparison.

1.1 Background to the Plastron Payload Processing Facility Cleanroom

The underlying requirements for the Plastron Payload Processing Facility (PPF) were identified in late 2019 but validated in 2020 as facility requirements for the Newquay Spaceport were being publicised. Plastron quickly identified that the types of affordable and fit-for-purpose facilities required for the SpacePort operations market did not exist. They also recognised that many new entrants into the NewSpace industry lacked hands-on, commercial spaceflight safety experience, which the facility designers foresaw as a considerable safety risk to the UK Launch industry. Using early market engagement, including insights from dialogues with Newquay Spaceport, the design template was determined—fundamentally, a modular facility capable of handling the propellant and pressurisation requirements for a 1,000 kg smallSat, and which could pack down to fit into shipping containers. In terms of the operational envelope for a horizontal launch operator, such as Virgin Orbit, this would ensure the facility could be transported to any spaceport used by their Boeing 747 Cosmic Girl and LauncherOne.

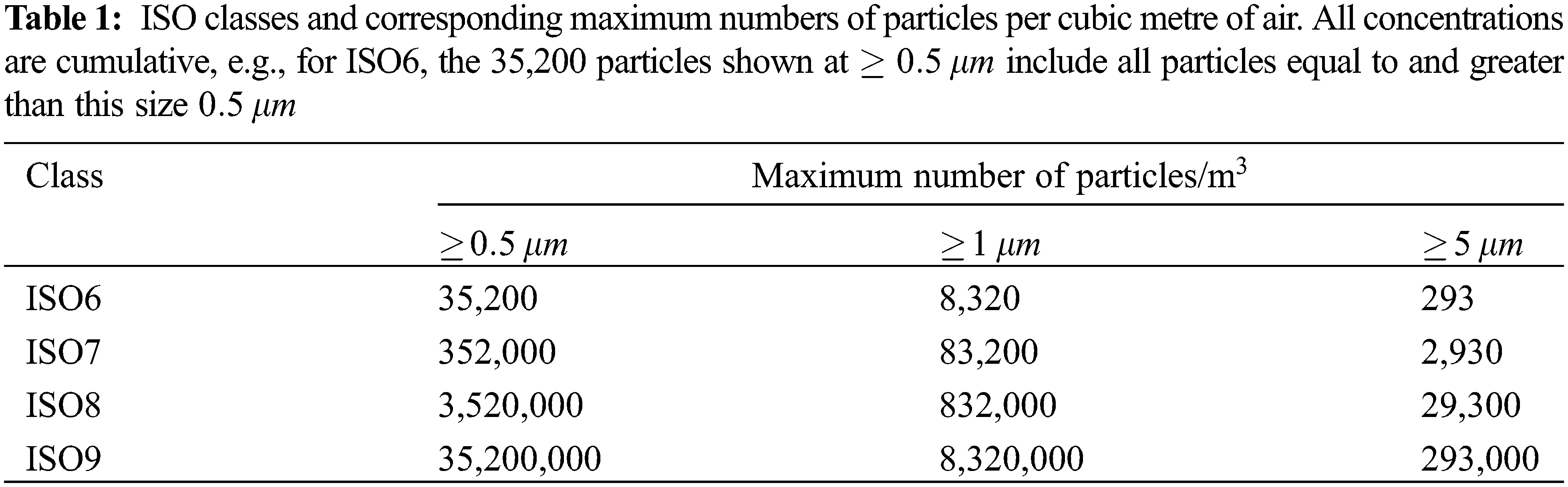
ISO8 cleanliness is vital to all customer segments in assuring flight hardware integrity throughout the Manufacture, Assembly, Integration and Test (MAIT) cycles up to launch. From our market research, it was clear the majority of commercial cleanroom system providers employ fairly rudimentary approaches, if any, for validating air quality and airflow. It was often no more complex than calculating the ratio of the total operational volume exchanged at the required frequency (e.g., 287 cubic metres every two minutes) to the volumetric flowrate of a standard fan unit, thus estimating the total number of fan units required. Plastron felt it was important to validate the air quality computationally, and so approached the SPRINT funding programme for the support required to achieve this. It was felt the research could also help discover ways to reduce operating costs and power consumption requirements, contributing to a business principle for minimising our carbon footprint. As an output of this research, the Plastron Air Control System (Fig. 1) is now a key part of the PPF.

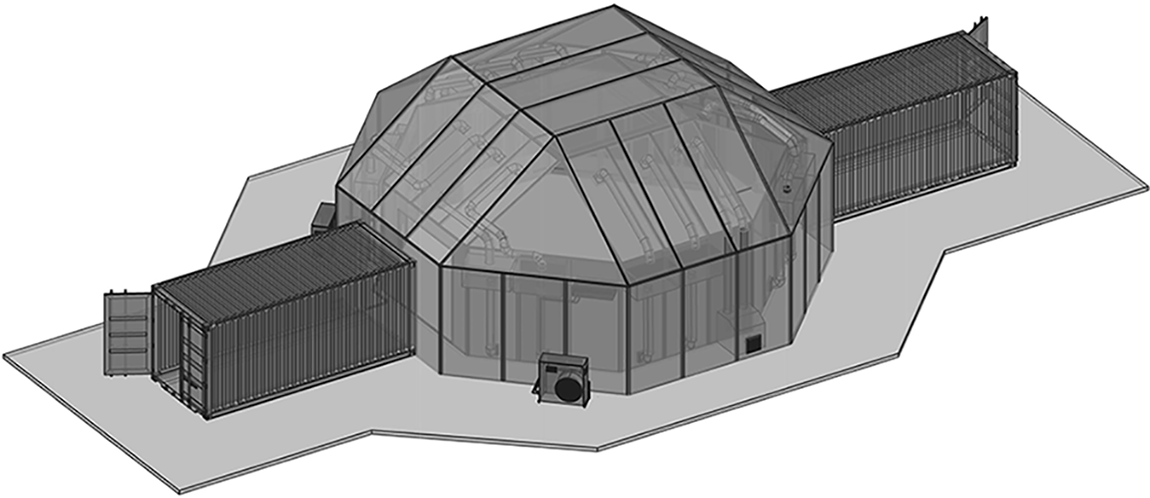
Figure 1: The plastron air control system is incorporated into a fully functional satellite processing facility. The facility comprises three elements: the main cleanroom environment, an adjacent hazardous processing environment and a garment changing room

1.2 Outline of Our Work

Satellite components, assemblies and systems have to be manufactured and assembled in extremely clean environments to ensure contamination does not compromise the function of the hardware before launch or once in orbit. Plastron developed their state-of-the-art facility to meet the NewSpace space sector requirement for rapidly and more cheaply producing flight hardware without compromising on hazardous safety or product quality standards. Central to what makes a cleanroom viable for satellite assembly is the air quality, where the concentration of microscopic particles suspended in the air needs to be below a required threshold.

The standard for air quality in space hardware cleanrooms is ECSS Basic Specification 24,900, which includes requirements for the maximum suspended air particulate concentration levels. The research focus was to prove the air quality throughout the operational volume met the ISO8 standard at a minimum. Advanced computational fluid dynamics (CFD) modelling was used to assess how well the air management system design of the product achieved the ISO8 standard.

Two research stages were identified. Phase 1: the baseline study helped validate the ISO8 requirement. Phase 2: investigating how system redundancy can support climate control zones in the facility as well as reduce overall power consumption. To complete this research and assure the quality of the Plastron facility, the baseline Air Control System was modelled, tested and incrementally evolved between tests. A brief summary of the project is shown below:

I. Completing dynamic simulations of the effect of equipment and human motion, and evaluating the designed cleanroom against the ISO8 standard.

II. Repeating simulations with the inclusion of air inlet diffusers and evaluating the cleanroom against the ISO8 standard.

III. Extending operational volume to cover an additional 30 m3 , and evaluating the cleanroom against the ISO8 standard.

IV. Evaluating cleanroom-within-a-cleanroom against the ISO8 standard, and supporting the ability for ISO6 optical payloads to be handled in a Plastron.

During the project, more than one hundred cases were numerically tested, for identifying an optimum design of the inlet shape and location and testing various industrial requests. To form a concise scientific paper being of interest of researchers in academia and industry, only a small part of data and their analysis from tasks I and II are reported here. The main purpose of this paper was to highlight the novel concept of cleanroom design, rather than to give most details of the various designs.

2  Methodology

2.1 Governing Equations

The incompressibe unsteady Reynolds average Navier-Stokes (URANS) equations [7,8,14,15] and the incompressibe large-eddy simulation (LES) Navier-Stokes equations [2,8,25] can be shown in the same form:

∂u¯i∂xi=0 (1)

∂u¯i∂t+∂u¯iu¯j∂xj=−1ρ∂p¯∂xi+∂∂xj(ν∂u¯i∂xj−τij), (2)

where ‘ ¯ ’ denotes a time averaged quantity for URANS approach, or a grid-filtered quantity for LES approach, ui¯ is the URANS velocities, or the LES filtered velocities, p¯ is the URANS pressure or the LES filtered pressure, ρ the density, and ν the kinematic viscosity. τijr is turbulent stress tensor for URANS, or the subgrid-scale (SGS) stress tensor for LES,

τij=uiuj¯−u¯iu¯j, (3)

and is modelled based on the Boussinesq approximation,

τij=−2νtS¯ij+13δijτkk, (4)

where the Kronecker delta δij = 1 for i=j , otherwise δij=0 . νt is the turbulent (URANS) or SGS (LES) viscosity. S¯ij is the rate-of-strain tensor,

S¯ij=12(∂u¯i∂xj+∂u¯j∂xi). (5)

The k−ϵ Realizable model [29] was used for the URANS approach, while the WAVE SGS model [30] was adopted for the LES approach. For more details of these two models, the readers are advised to read the above references.

The transport equation for a passive scalar is

∂C∂t+∂u¯jC∂xj=∂∂xj[(K+Kt)∂C∂xj]+S, (6)

where C is the URANS averaged, or the LES filtered scalar (PMs) concentration. For simplicity, C is a dimensionless quantity, which is the concentration normalized by the concentration in normal room air (Table 1). K is the molecular diffusivity and Kt is the turbulent, or SGS turbulent diffusivity computed as

Kt=νtSct, (7)

where Sct is the turbulent or the SGS Schmidt number. A constant Sct=0.7 was assumed [25].

2.2 Geometry of the Baseline Cleanroom and the Accommodated Satellite Model

Fig. 2 shows the dimensions of the baseline cleanroom (see a 3D view in Fig. 3). The total volume of the cleanroom is approximately 287 m3. The dimensions of the satellite and human models (Fig. 3b) are as follows. The satellite and wheel base had a total height of mm, including a ground clearance of mm. The base had dimensions of mm × mm and extends up to mm above the ground. The satellite dimensions were mm × mm with a vertical extent of mm. The human model had a total height of mm with a ground clearance of mm. The satellite was stationary. The human body had dimensions of mm × mm with a height of mm. The human head was mm × mm with a height of mm. The human moved around the satellite along a circle at a constant speed of 0.75 m/s.

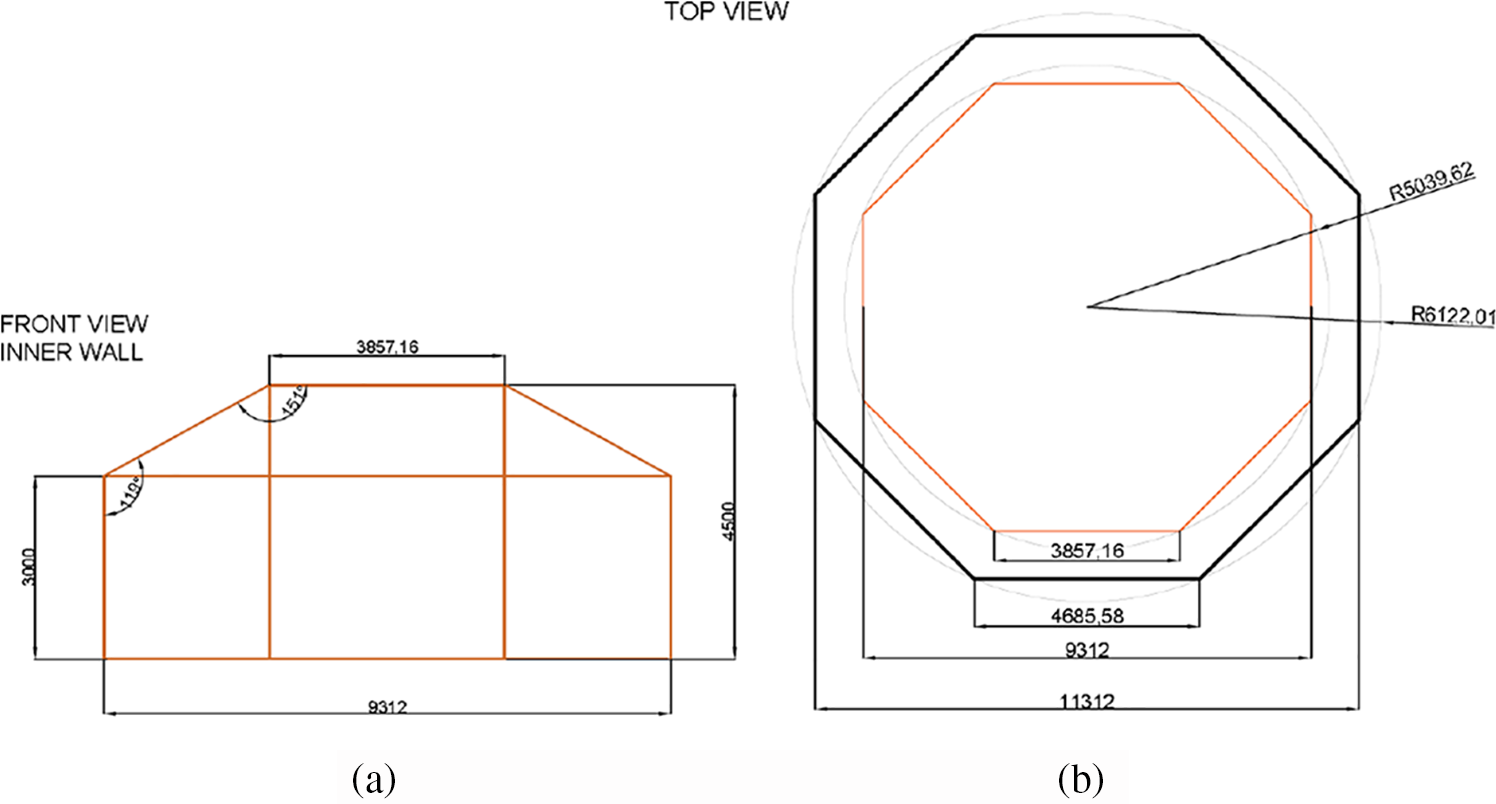
Figure 2: Dimensions of the cleanroom. Units are in mm . (a) Front view of the internal wall. (b) Top view of the inner and outer walls, black line: outer walls, orange line: inner walls. Only the inner wall was simulated in the CFD. The origin of the right-hand coordinate system is placed on the centre of the cleanroom ground, with x from left to right, and z upwards

Figure 3: 3D geometry of the CFD domain of the baseline room. (a) An isometric view of the 3D CFD domain. (b) An isometric view of the satellite model (the larger object) placed on the clean ground and a human standing (the smaller object) walking around the satellite model along a circle at a speed of 0.75 m/s

The baseline total mass flow rate through the 12 inlets was 3.4 kg/s, resulting in an air change rate (ACR) approximately of 40. It is crucial to define the turn-over time T,

T=Vroom/Qtotal, (8)

where Vroom is the room volume, Qtotal is the total volume flow rate. The dimensionless ventilation time tv/T was used for presenting the scaling of ventilation for different room sizes and flow rates.

2.3 Adopted Numerical Settings

LES was only used for evaluating URANS simulations in Section 3, while URANS was used in all other simulations. The 2nd order accuracy implicit scheme was used for the temporal discretisation. The 2nd order accuracy upwind and bounded-central schemes were used for the discretisation of the convection term in the URANS and LES N-S equations, respectively. The 2nd order accuracy central scheme was used for the diffusion term in both URANS and LES. The 1st order upwind scheme was used for the convection terms for k and ϵ equations of the k−ϵ Realisable model. The SIMPLE scheme was used for solving the incompressible velocity-pressure coupling N-S equations (Eq. (2)). 5 iterations per time step were required following the early published studies [31], which forced the continuity and momentum equations to converge to a residual of 10−2 or less. Given a large number of test cases to be carried out in time. This option was inevitably chosen to compromise between accuracy and efficiency.

To ensure fully developed flows, the flow initialisation periods for URANS and LES were and s, respectively, when the concentration of particles (C in Eq. (8)) was set equal to a constant dimensionless concentration of 1.0 in the cleanroom, and as the inlet boundary condition. After the flow initialisation was complete, the ‘filtering system’ was switched on by setting the concentration C=0 for the inlet boundary condition, which defined the start time of ventilation time ( tv = 0).

2.4 Mesh Sensitivity Analysis

Because the URANS and LES were much more computationally expensive than the steady RANS, and more than one hundred cases were to be simulated, we decided to design a low cost baseline mesh with the viscous sublayer resolved, by following the early work [2]. Foat et al. [2] used LES to simulate the cuboid-shape room designed by [1], of which the volume was about one third of the current cleanroom (Fig. 3a). The structured mesh used in [2] had 5.4 million cells, with the near-wall grids resolving the viscous sublayer. By using a prism layer (PL) mesh with the viscous-sublayer resolved (Fig. 4 and Table 2), and a unstructured Cartesian mesh in the current study, we estimated 5 million cells were sufficient to generate data meeting the requirements. It is to be noted the [1] room had an ACR = 10 h−1 with an inlet Reynolds number approximately of 5000, which suggested a turbulent inflow. Downstream from the inlet, the turbulent flow could decay to laminar flow, while passing through the long cuboid-shape room. The current cleanroom had a much stronger mechanical ventilation with an ACR = 40 h−1 and an inlet Reynolds number approximately of 30,000. It was expected that the RANS and LES models could produce more accurate predictions in the current study.

Figure 4: Mesh of the ‘empty’ CFD domain including the inlets (diffusers) and outlets, with 3 levels of refinement and a boundary layer mesh resolving the viscous sublayer. (a) Front view of a vertical x−z plane across the centre of the cleanroom (see Fig. 2). (b) Top view of a horizontal x−y plane at a height z = 1 m. The baseline mesh size was 0.025 m. The total number of cells was 6.1 million

Table 2 shows the baseline mesh settings, with three levels of refinement in the near wall regions. The time step was set to meet the condition of CFL <1 . The total number of cells of the baseline mesh was 5.0 million. Further mesh refinements were carried out in critical regions, such as the near-inlet regions, resulting in a total number of 6.1 million cells (Fig. 4). Fig. 5 presents typical dimensionless wall-normal resolution ‘ y1+ ’, showing all first cells on the walls and the inlet surfaces are within the viscous sublayer with ‘ y1+<9 ’. On the outlet surfaces, some first cells show ‘ y1+ ’ just exceeding 10.

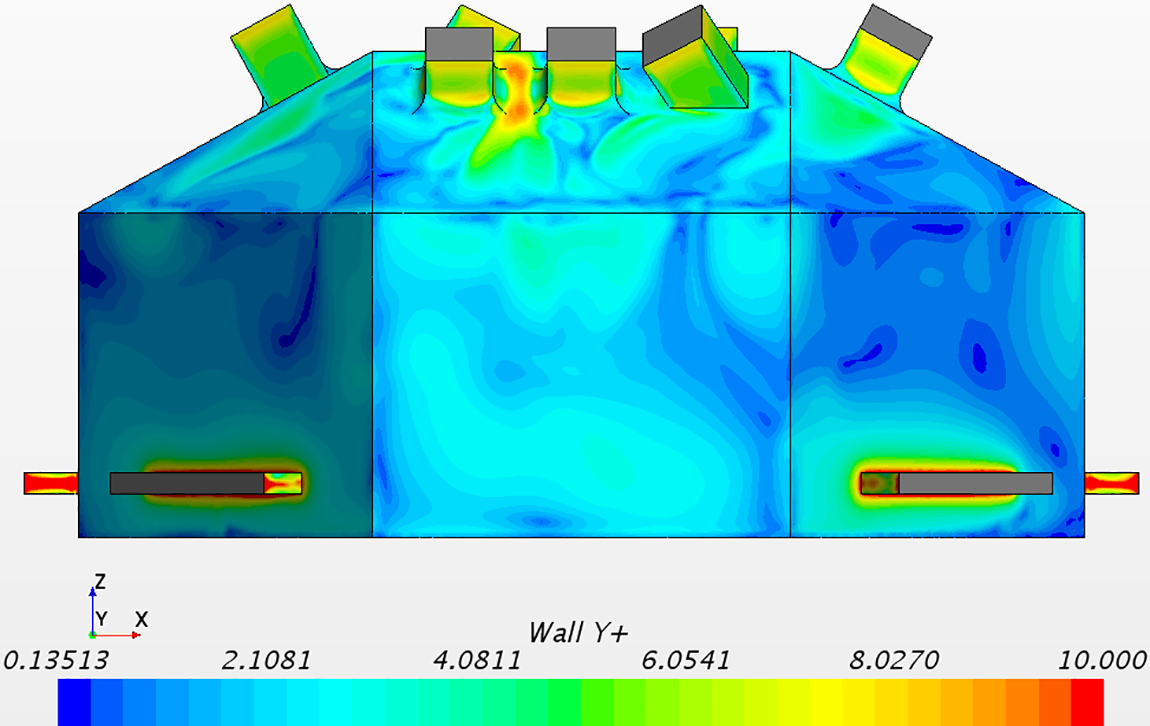
Figure 5: Dimensionless wall-normal resolution ‘ y1+ ’ for a typical case

Besides the rigorous mesh sensitivity tests carried out in [2], we tested two mesh resolutions for one design configuration. Table 3 shows a mesh sensitivity analysis with a focus on the volume averaged concentration and the maximum concentration. After 6 min ventilation, the ratios of the absolute discrepancies in the room-volume averaged concentration and the maximum concentration to the corresponding data were 5% and 8%, respectively. Hereafter, the refined mesh was used for testing all designs.

2.5 Other Uncertainties

We assessed the uncertainty due to the turbulent model. Given the resolution was close to the LES resolution in [2], an LES test based on the same mesh as the URANS was carried out to assess the discrepancy between the URANS and LES data (see details in Section 3.1). The effect on the cleanroom ventilation efficiency due to human motion disturbance was assessed (Section 4.1) by using the moving mesh approach, i.e., overset mesh. The uncertainties due to mesh resolution (Section 2.4), turbulent model (Section 3.1), thermal stratification, small objects in the cleanroom, and effectiveness of the filtering system, must be considered in the final design and the operation.

3  Baseline Room Simulations and Evaluation

The first part of this section is the assessment of URANS models for the portable cleanroom with a high ACR value, comparing with a well-established LES. The second part of this section is on the design of the inlet diffuser geometry and the location of the inlet, in order to optimise the ventilation efficiency.

3.1 Comparison between LES and URANS

To evaluate the URANS model, an LES was carried out based on the same mesh (i.e., the refined mesh). The refined mesh had a similar resolution to the early published work [2], e.g., with the viscous sublayer resolved. The flow and concentration fields were carefully examined, to ensure a cyclone-type flow being formed, and the pollutant being well mixed. Fig. 6 shows a comparison of flow field on a horizontal plane at z=2 m between the URANS and LES methods. The velocity shown in Fig. 6a is Reynolds-averaged velocity, whereas the velocity shown in Fig. 6b is instantaneous velocity. Both the URANS and LES data show an evident anti-clockwise cyclone type flow.

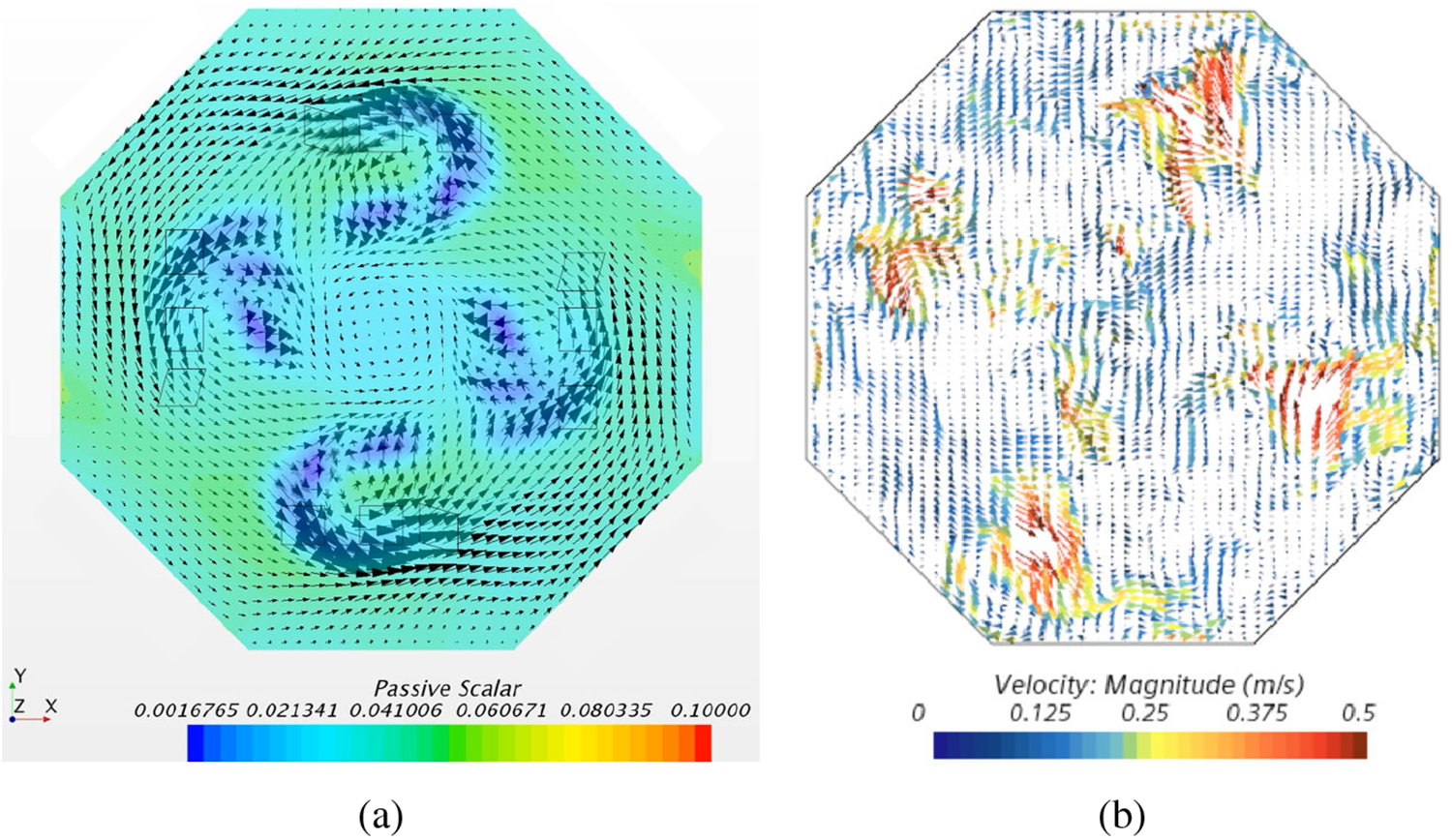
Figure 6: (a) URANS velocity vectors and scalar concentration at a horizontal plane at z=2 m after 900 s initialisation and 180 s ventilation; (b) LES instantaneous velocity vectors after 450 s initialisation

The Q criterion was studied to check the flow field, defined as

Q=12(ΩijΩij−SijSij), (9)

whereΩij=12(∂ui∂xj−∂uj∂xi),

andSij=12(∂ui∂xj+∂uj∂xi).

Positive Q values identify rotation-dominated regions of the flow, while negative Q values identify shear-dominated regions of the flow. Fig. 7 shows a comparison of Q-criteria on a vertical x−z plane across the centre of the cleanroom, demonstrating an evident consistency between the URANS and LES data, despite the LES data provide more details of the instantaneous flow structures. Both the URANS and LES data show a strong shear near the diffuser surfaces and the outlets.

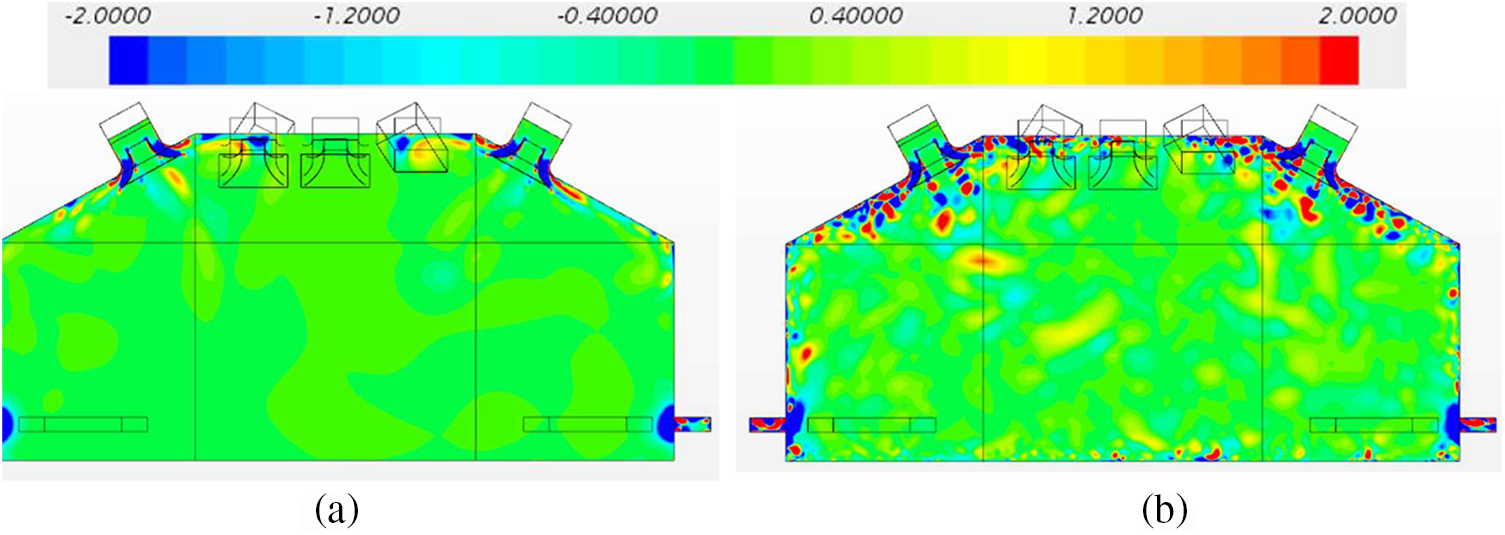
Figure 7: A comparison of Q-criteria on a vertical x−z between URANS and LES

Fig. 8 shows contours of instantaneous concentration on a vertical plane across the centre of the room after 6 mins ventilation. Both the LES and URANS data show evident effectiveness of the implemented diffusers. The LES data shows more isolated instantaneous pollutant clouds, while the RANS data shows more evenly distributed pollutant contours. Nevertheless, a consistency of the overall picture is evidently shown in Fig. 8. Quantitative comparison between URANS and LES was also carried out. Fig. 9 shows an excellent agreement of volume averaged concentration between the “Baseline room, LES” and the URANS “Baseline room, with diffuser”. The maximum (peak) concentration was also carefully examined. Fig. 10 shows a consistency of peak concentration between the “Baseline room, LES” and the URANS “Baseline room, with diffuser”. Both Figs. 9 and 10 suggest that URANS is a reliable tool for such applications. Given its higher efficiency compared to LES, the URANS was chosen in the rest of the study.

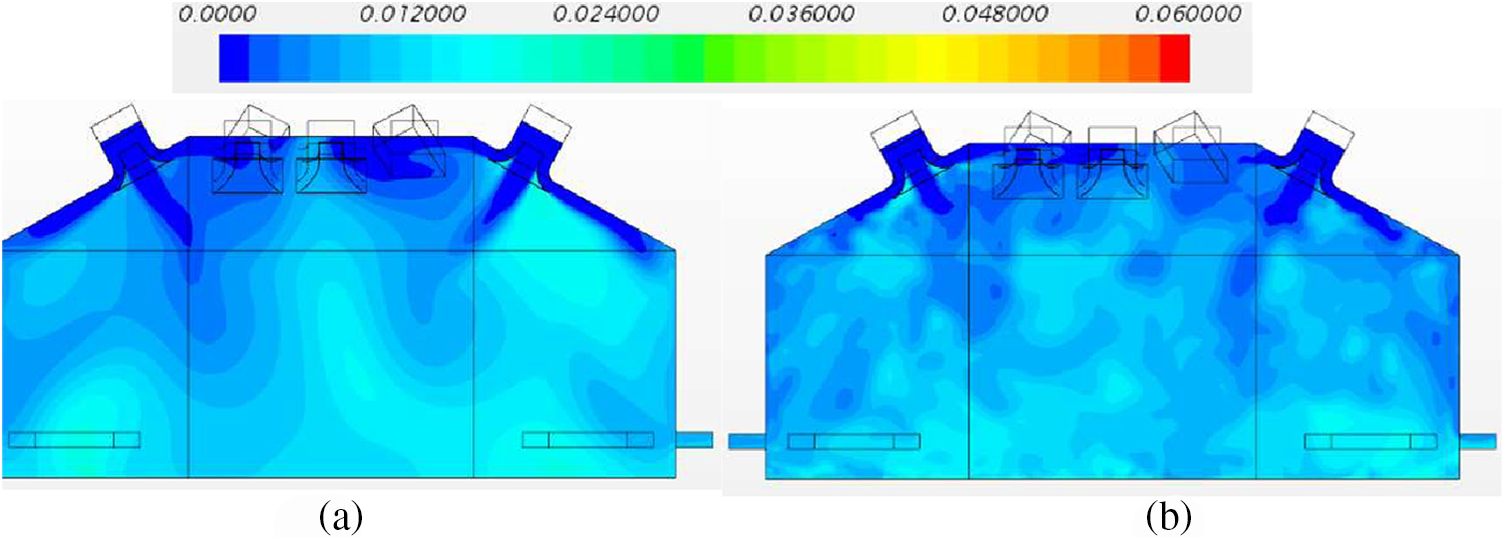
Figure 8: Instantaneous concentration on a vertical x−z at 6 mins ventilation. (a) URANS, (b) LES

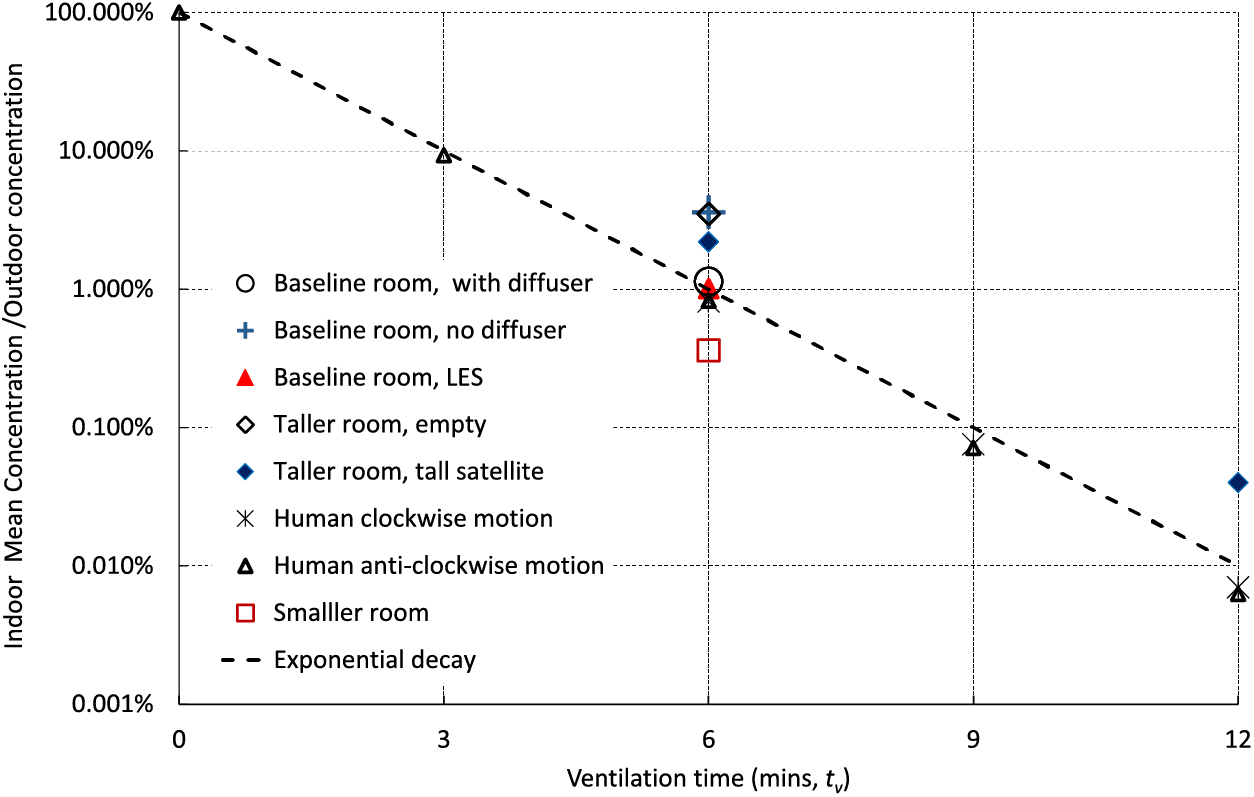
Figure 9: The ratio of cleanroom-volume averaged concentration to normal room concentration against the ventilation time tv . 100%, 10%, 1% and 0.1% are respectively equivalent to ISO9, ISO8, ISO7 and ISO6. The height of the tall room is 6 m. Human motion speed is 0.75 m/s . The volume of smaller room is 75% of the baseline room. The taller room is 1.5 m taller than the basline room

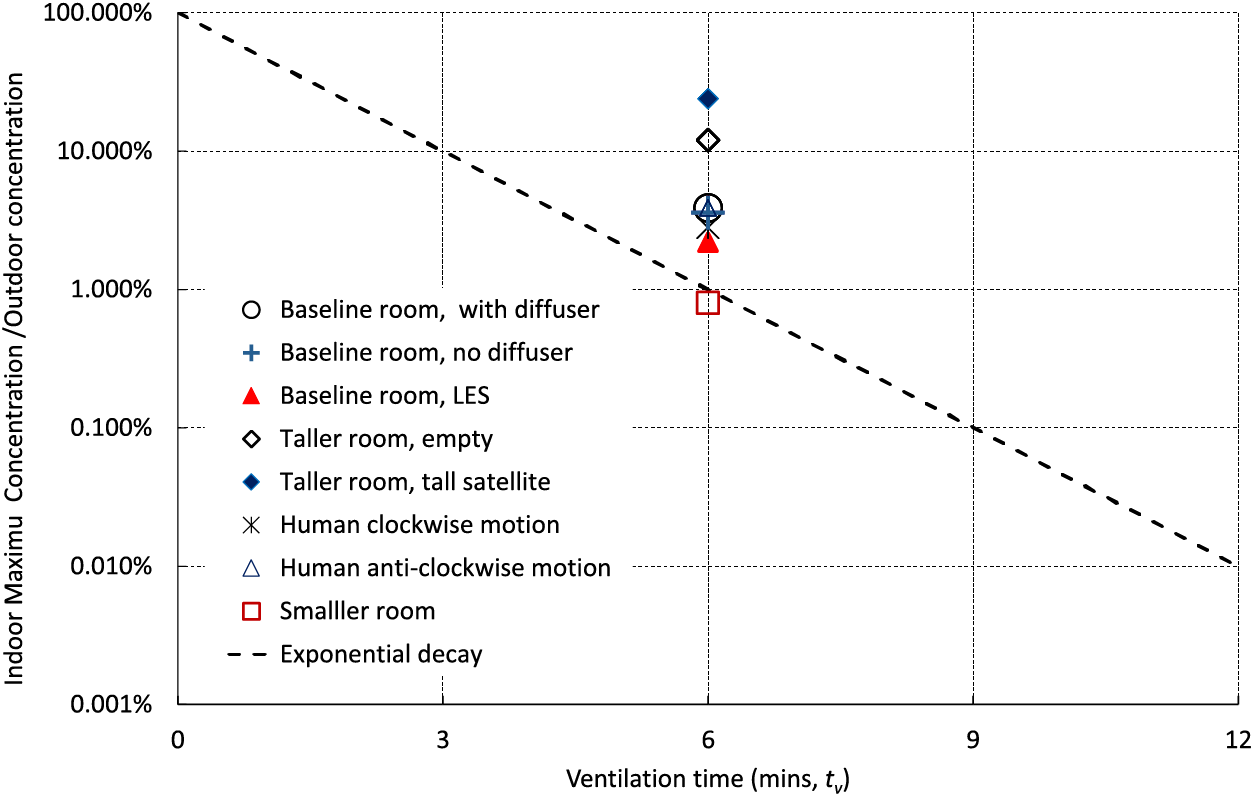
Figure 10: The ratio of cleanroom maximum concentration to the outdoor concentration at ventilation time tv = 6 min. Other settings the same as in Fig. 9

3.2 Identifying Optimum Location, Angle and Shape of the Inlets

A number of configurations of 12 inlet locations, and their various pitching angles were tested. The configuration shown in Fig. 3a was the most effective one to form a cyclone type flow. In particular we carried out tests to determine how inlet airflow could be distributed more effectively, leading to a more efficient air cycling. The baseline inlet design was adapted from the square design outlined in [32]. The central section was changed to allow the flow to have more momentum to reach deep into the room. Subsequent changes were made to help the flow spread across the ceiling panels. No diffuser was used on the pitched inlets (Fig. 3). This was to maintain the strength of the large scale rotation of the flow around the cleanroom. Fig. 9 presents a comparison of ventilation efficiency between “Baseline room, empty, no diffuser” and “Baseline room, empty, diffuser”, showing that the inclusion of diffusers increases efficiency by more than 3 times. Therefore, these diffusers were included in the rest of the tests.

4  Advanced Modelling Cleanroom

4.1 Disturbance of the Satellite and Human Motion

The disturbance of the satellite and human motion was assessed extensively. The ratio of the volume of the satellite model to the cleanroom was less than 1.5% (Figs. 3b and 11). However, the accommodation of the satellite model visibly improved the ventilation efficiency. This was likely because placing the satellite model at the centre of the room enhanced the airflow circulation around the room.

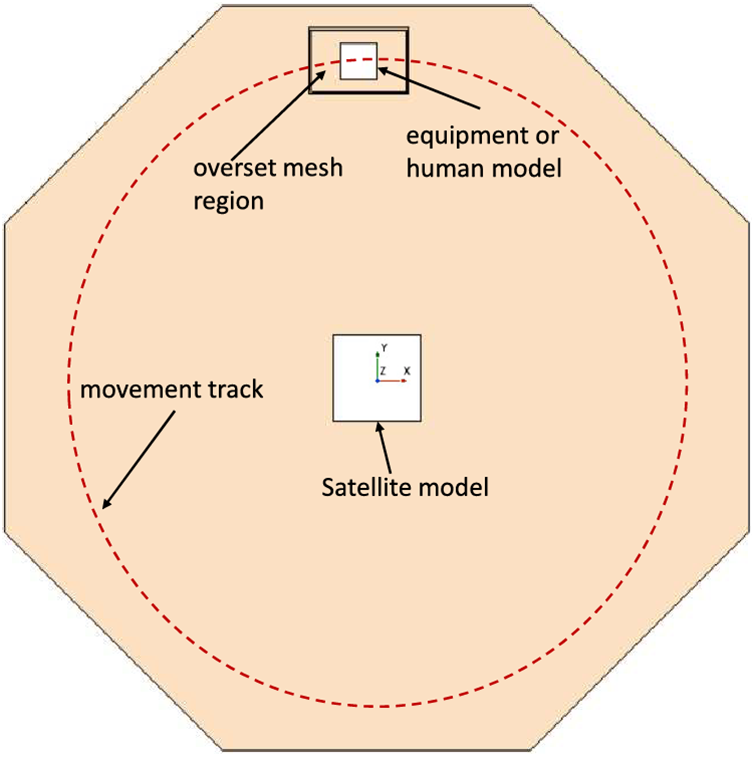
Figure 11: A sketch top view of the cleanroom ground with the overset mesh region (i.e., the human body region), the satellite model, and the moving equipment or human model (see Fig. 3b). The dashed line denotes the movement track

Fig. 11 shows a sketch top view of the cleanroom ground with the overset mesh region (i.e., the near human model region), the satellite model, and the moving human model (see Fig. 3b). The dashed line denotes the human motion track. The speed of the human motion is 0.75 m/s. The overset mesh [33] was used to simulate human motion either in clockwise or in anti-clockwise directions.

Fig. 9 shows that the impact of human motion on the effectiveness of ventilation at the ventilation time tv = 6 mins is negligible compared to the cases “Baseline room, empty, diffuser”. The two cases “Human clockwise motion” and “Human anti-clockwise motion” present almost identical concentration data, both in an evident exponential decay against ventilation time tv .

4.2 Smaller Cleanroom

These tests were to convert the cleanroom volume to include only three quadrants (i.e., the case “Smaller room, empty” shown in Figs. 9 and 12), while the same total flow rate was kept the same to achieve a high cleanliness level of ISO6 quicker than the baseline room. Fig. 9 shows that the volume-averaged concentration at tv = 6 mins was reduced by more than 3 times compared to the baseline cleanroom.

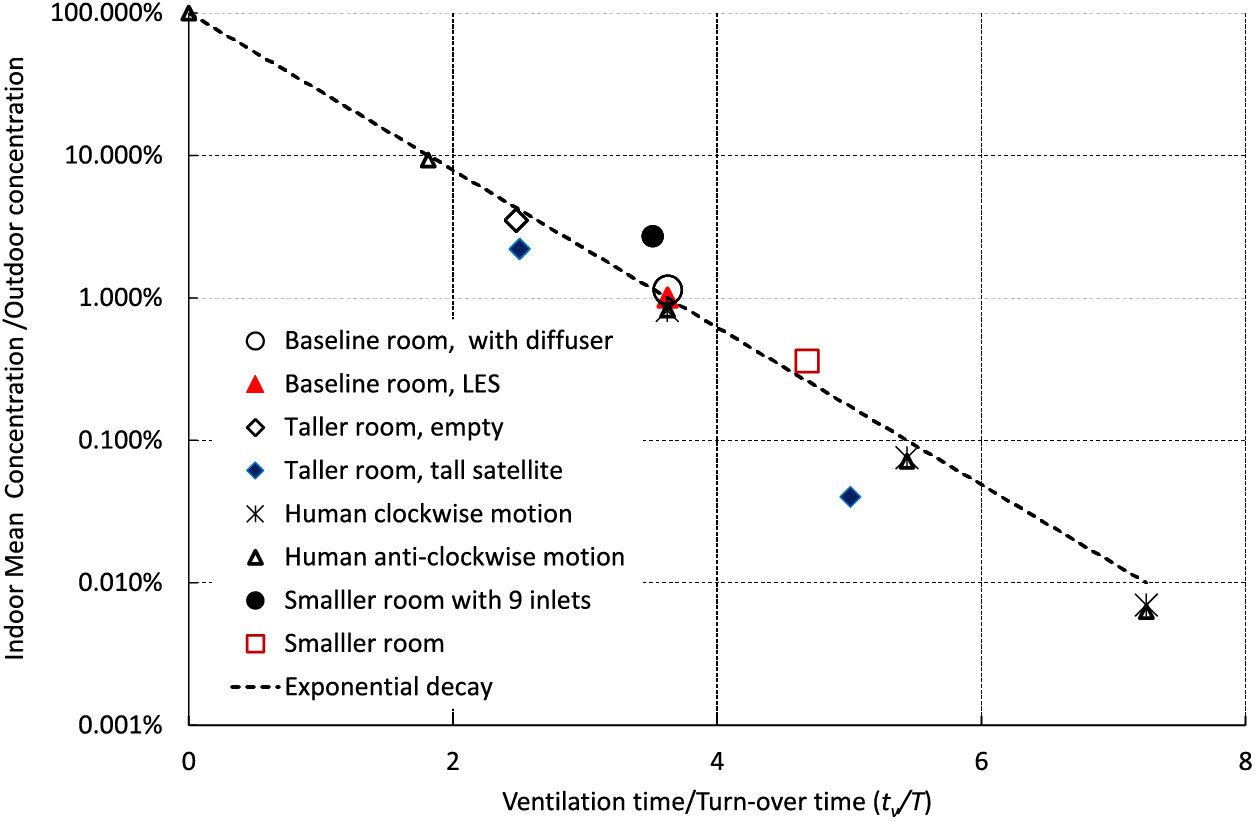
Figure 12: The ratio of cleanroom-volume averaged concentration to normal room concentration against dimensionless ventilation time tv/T . The height of the tall room is 6 m, of which the volume is 140% of the baseline room. The volume of smaller room is 75% of the baseline room. All cases have the baseline total flow rate, except the case ‘Smaller room with 9 inlets’ has a total flow rate being 75% of the baseline one

To produce more data for future designs, such as for different sizes of cleanroom and different inlet flow rates, a smaller flow rate was tested. The case “Smaller room with 9 inlets” shown in Fig. 12 had three quarters of the flow rate for the case ‘Smaller room, empty’, showing that different flow rates for the same cleanroom yield a consistent trend of cleanness level against dimensionless ventilation time.

4.3 Summary of the Tested Designs

This section summarises the tested designs with a focus on room volume averaged concentration and maximum concentration against dimensional ventilation time tv and dimensionless time tv/T . Fig. 9 presents a summary of ventilation efficiency of the tested designs. Again, the 100%, 10%, 1% and 0.1% ratios of cleanroom concentration to normal room concentration are respectively equivalent to ISO9, ISO8, ISO7 and ISO6 levels of cleanliness. The concentration decayed exponentially at a reduction rate of approximately 0.1 every 3 mins. For all test cases for the baseline room volume and 12 inlets, the ISO8, ISO7 and ISO6 levels of cleanliness were achieved within 3, 6 and 9 mins, respectively. The high ACR ≈40 , the high Reynolds number flow, and the well-designed inlet shape and position, lead to a well-mixed air in the cleanroom (see Fig. 8). This suggests volume-averaged concentration a reasonable criterion for measuring the ventilation efficiency.

The maximum concentration can be considered as another criterion for measuring the air quality and ventilation efficiency, albeit it is difficult to estimate accurately and should be used cautiously. Fig. 10 shows the ratio of cleanroom maximum concentration to the outdoor average concentration at ventilation time tv = 6 mins. The maximum concentration was usually several times greater than the volume-averaged concentration (Fig. 9). The dimensionless maximum concentration for the taller cleanroom was the greatest, suggesting the challenging design of a tall cleanroom.

Fig. 12 shows the ratio of cleanroom concentration to normal room concentration against dimensionless ventilation time tv/T . All data collapse well close to an exponential decay curve (i.e., the straight dashed line shown on Fig. 12), suggesting a constant decay rate. At tv/T = 9, the dimensionless concentration reduces to 0.001%, which is equivalent to the ISO3 standard.

The vital concept is the design of the three-dimensional operational cleanroom with the specific inlet configuration. The entirety of the key design aspects consisting of the quasi-axisymmetric room, as well as the chamferred ceiling is critical to the product’s efficiency. Based on the constant exponential decay shown in Fig. 12, the ventilation rate can be estimated for a given cleanroom size, a required ISO level of cleanliness at a required ventilation time. A new cleanroom must have the similar configuration as the baseline cleanroom, including the configuration of the inlets. A change of the plan shape, the roof shape, or the height-width ratio of a cleanroom, deserves more cautious adjustment of the ventilation efficiency prediction. Nevertheless, Fig. 12 provides a baseline prediction.

5  Conclusion and Discussion

The first test cleanroom in the study was the Plastron UK Standard Cleanroom Product, known as the Plastron PPF and which provided 75 square metres of operational floor space in an ISO8 environment with a 4.5 m ceiling limit. This operational environment equated to 287 cubic metres, which had to be filtered 10–25 times per hour in order to maintain constant ISO8 air cleanliness. The product was designed for hazardous testing and handling of spacecraft prior to launcher encapsulation. By using CFD on the Southampton local supercomputer IRIDIS5 to carry out a number of simulations of flow and PM dispersion, we have designed a prototype cleanroom, which meets the ISO8 standard. One special design with a smaller child section inside the parent cleanroom was able to meet the ISO6 standard.

The following concluding remarks have been drawn from the research: (1) it is critical to optimise the location and shape of the air intakes and their orientation angles, to balance pollutant convection and diffusion. (2) the URANS model is a cost-effective approach for assessing the efficiency of cleanroom with intensive mechanical ventilation. (3) the equipment or human motion inside the cleanroom can slightly improve ventilation efficiency, assuming they only occupy a small area of the cleanroom. (4) slightly increasing or reducing the cleanroom size, or changing the ventilation flow rate, does not significant affect the exponential decay rate of the pollutant concentration. (5) the ratio of volume-averaged concentration to outdoor concentration against the dimensionless ventilation time are in an exponential decay curve for all the tested cases, suggesting this curve can be used as an baseline for future new cleanroom designs. Based on this documented constant exponential decay of dimensionless concentration, the ventilation rate can be estimated for a given cleanroom size, a required ISO level of cleanliness at a required ventilation time. Nevertheless, if a change is to be made for the plan shape, the roof shape, or the height-width ratio of a cleanroom, a cautious adjustment is recommended for a prediction of the ventilation efficiency.

Acknowledgement: Computational work has been undertaken on Southampton University’s Iridis systems.

Funding Statement: The research was funded by Space Research and Innovation Network (www.sprint.ac.uk) for Technology Grants (OW131743P4V4M, OW131797P4V2B, ZX and CY). ZX is also grateful to NERC (www.nerc.ac.uk) for the Grant (NE/W002841/1, ZX) to complete the writing of the paper.

Author Contributions: The authors confirm contribution to the paper as follows: study conception: ZX, CY; cleanroom design: CY, CS, GS, MR; air management system design: CY, CS GS, MR; CFD simulations: MC, ZX; project management: ZX, CY, CS; data collection: MC, MR; analysis and interpretation of results: ZX, CY, MC, MR, CS, GS; draft manuscript preparation: ZX, MC, CY. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Readers can access the data used in the study on request to the corresponding author ZX.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Nielsen, P. V. (1990). Specification of a two-dimensional test case: (IEA). Aalborg: Institut for Bygningsteknik, Aalborg Universitet. [Google Scholar]

2. Foat, T. G., Parker, S. T., Castro, I. P., Xie, Z. T. (2018). Numerical investigation into the structure of scalar plumes in a simple room. Journal of Wind Engineering and Industrial Aerodynamics, 175, 252–263. [Google Scholar]

3. Linden, P. F. (1999). The fluid mechanics of natural ventilation. Annual Review of Fluid Mechanics, 31(1), 201–238. [Google Scholar]

4. Papakonstantis, I. G., Hathway, E. A., Brevis, W. (2018). An experimental study of the flow induced by the motion of a hinged door separating two rooms. Building and Environment, 131, 220–230. [Google Scholar]

5. Khan, M. A. I., Delbosc, N., Noakes, C. J., Summers, J. (2015). Real-time flow simulation of indoor environments using lattice boltzmann method. Building Simulation, 8, 405–414. [Google Scholar]

6. Durrani, F., Cook, M. J., McGuirk, J. J. (2015). Evaluation of LES and RANS CFD modelling of multiple steady states in natural ventilation. Building and Environment, 92(3), 167–181. [Google Scholar]

7. Nielsen, P. V. (2015). Fifty years of CFD for room air distribution. Building and Environment, 91(3), 78–90. [Google Scholar]

8. van Hooff, T., Blocken, B., Tominaga, Y. (2017). On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Building and Environment, 114(4), 148–165. [Google Scholar]

9. Manolesos, M., Gao, Z., Bouris, D. (2018). Experimental investigation of the atmospheric boundary layer flow past a building model with openings. Building and Environment, 141(6458), 166–181. [Google Scholar]

10. Gough, H., Sato, T., Halios, C., Grimmond, C., Luo, Z. et al. (2018). Effects of variability of local winds on cross ventilation for a simplified building within a full-scale asymmetric array: Overview of the silsoe field campaign. Journal of Wind Engineering and Industrial Aerodynamics, 175, 408–418. [Google Scholar]

11. Higton, T. D., Burridge, H. C., Hughes, G. O. (2021). Natural ventilation flows established by a localised heat source in a room with a doorway and a high-level vent. Building and Environment, 203, 108093. [Google Scholar]

12. Kosutova, K., van Hooff, T., Vanderwel, C., Blocken, B., Hensen, J. (2019). Cross-ventilation in a generic isolated building equipped with louvers: Wind-tunnel experiments and CFD simulations. Building and Environment, 154(9), 263–280. [Google Scholar]

13. Parker, D., Burridge, H., Partridge, J., Hacker, J., Linden, P. (2021). Vertically distributed wall sources of buoyancy. Part 2. Unventilated and ventilated confined spaces. Journal of Fluid Mechanics, 907, A16. [Google Scholar]

14. Liu, F., Qian, H., Luo, Z., Zheng, X. (2021). The impact of indoor thermal stratification on the dispersion of human speech droplets. Indoor Air, 31(2), 369–382 [Google Scholar] [PubMed]

15. Li, Q., Liang, J., Wang, Q., Chen, Y., Yang, H. et al. (2022). Numerical investigations of urban pollutant dispersion and building intake fraction with various 3D building configurations and tree plantings. International Journal of Environmental Research and Public Health, 19(6), 3524 [Google Scholar] [PubMed]

16. Hu, S., Wu, Y., Liu, C. (1996). Measurements of air flow characteristics in a full-scale clean room. Building and Environment, 31(2), 119–128. https://doi.org/10.1016/0360-1323(95)00039-9 [Google Scholar] [CrossRef]

17. Tung, Y. C., Hu, S. C., Xu, T., Wang, R. H. (2010). Influence of ventilation arrangements on particle removal in industrial cleanrooms with various tool coverage. Building Simulation, 3, 3–13. [Google Scholar]

18. Sadrizadeh, S., Holmberg, S. (2015). Effect of a portable ultra-clean exponential airflow unit on the particle distribution in an operating room. Particuology, 18(9), 170–178. [Google Scholar]

19. Wagner, J. A., Greeley, D. G., Gormley, T. C., Markel, T. A. (2019). Comparison of operating room air distribution systems using the environmental quality indicator method of dynamic simulated surgical procedures. American Journal of Infection Control, 47(1), e1–e6 [Google Scholar] [PubMed]

20. Tan, H., Wong, K. Y., Othman, M. H. D., Kek, H. Y., Tey, W. Y. et al. (2022). Controlling infectious airborne particle dispersion during surgical procedures: Why mobile air supply units matter? Building and Environment, 223(6), 109489. [Google Scholar]

21. Sadeghian, P., Duwig, C., Sköldenberg, O., Tammelin, A., Hosseini, A. R. et al. (2022). Numerical investigation of the impact of warming blankets on the performance of ventilation systems in the operating room. Advances in Building Energy Research, 16(5), 589–611. [Google Scholar]

22. Tan, H., Wong, K. Y., Othman, M. H. D., Kek, H. Y., Nyakuma, B. B. et al. (2023). Why do ventilation strategies matter in controlling infectious airborne particles? A comprehensive numerical analysis in isolation ward. Building and Environment, 231(13), 110048. [Google Scholar]

23. Tan, H., Wong, K. Y., Othman, M. H. D., Nyakuma, B. B., Sheng, D. D. C. V. et al. (2023). Does human movement-induced airflow elevate infection risk in burn patient’s isolation ward? a validated dynamics numerical simulation approach. Energy and Buildings, 283(1), 112810. [Google Scholar]

24. ISO (2015). ISO 14644-1: 2015. Cleanrooms and associated controlled environments—Part 1: Classification of air cleanliness by particle concentration. ISO Geneva. [Google Scholar]

25. Xie, Z. T., Hayden, P., Robins, A. G., Voke, P. R. (2007). Modelling extreme concentrations from a source in a turbulent flow over a rough wall. Atmospheric Environment, 41(16), 3395–3406. [Google Scholar]

26. Santos, J. M., Reis, N., Castro, I., Goulart, E. V., Xie, Z. T. (2019). Using large-eddy simulation and wind-tunnel data to investigate peak-to-mean concentration ratios in an urban environment. Boundary-Layer Meteorology, 172(3), 333–350. [Google Scholar]

27. Foat, T. (2021). Modelling vapour transport in indoor environments for improved detection of explosives using dogs (Ph.D. Thesis). University of Southampton. [Google Scholar]

28. Crank, J. (1979). The mathematics of diffusion. USA: Oxford University Press. [Google Scholar]

29. Shih, T. H., Liou, W. W., Shabbir, A., Yang, Z., Zhu, J. (1995). A new k-ε viscosity model for high reynolds number turbulent flows. Computers & Fluids, 24(3), 227–238. [Google Scholar]

30. Nicoud, F., Ducros, F. (1999). Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow, Turbulence and Combustion, 62(3), 183–200. [Google Scholar]

31. Xie, Z. T., Castro, I. P. (2006). LES and RANS for turbulent flow over arrays of wall-mounted obstacles. Flow, Turbulence and Combustion, 76(3), 291–312. [Google Scholar]

32. Mohammed, R. H. (2013). A simplified method for modeling of round and square ceiling diffusers. Energy and Buildings, 64(1), 473–482. [Google Scholar]

33. Oxyzoglou, I., Xie, Z. T. (2020). Effects of heaving motion on the aerodynamic performance of a double element wing in ground effect. Fluid Dynamics & Material Processing, 16(6), 1093–1114. [Google Scholar]