 Open Access
Open Access
ARTICLE
Numerical Analysis of the Magnetic Dipole Effect on a Radiative Ferromagnetic Liquid Flowing over a Porous Stretched Sheet
1 Department of Mathematics, Narasaraopeta Engineering College, Narasaraopet, India
2 Department of Physics, Faculty of Sciences, University of 20 Août 1955-Skikda, Skikda, Algeria
3 Department of Mathematics, RVR & JC College of Engineering, Guntur, India
4 Department of Mathematics, Koneru Lakshmaiah Education Foundation, Vaddeswaram, India
* Corresponding Author: F. Mebarek-Oudina. Email:
Fluid Dynamics & Materials Processing 2024, 20(2), 293-310. https://doi.org/10.32604/fdmp.2023.030325
Received 31 March 2023; Accepted 05 May 2023; Issue published 14 December 2023
Abstract
The effects of a magnetic dipole on a nonlinear thermally radiative ferromagnetic liquid flowing over a stretched surface in the presence of Brownian motion and thermophoresis are investigated. By means of a similarity transformation, ordinary differential equations are derived and solved afterwards using a numerical (the BVP4C) method. The impact of various parameters, namely the velocity, temperature, concentration, is presented graphically. It is shown that the nanoparticles properties, in conjunction with the magnetic dipole effect, can increase the thermal conductivity of the engineered nanofluid and, consequently, the heat transfer. Comparison with earlier studies indicates high accuracy and effectiveness of the numerical approach. An increase in the Brownian motion parameter and thermophoresis parameter enhances the concentration and the related boundary layer. The skin-friction rises when the viscosity parameter is increased. A larger value of the ferromagnetic parameter results in a higher skin-friction and, vice versa, in a smaller Nusselt number.Graphic Abstract
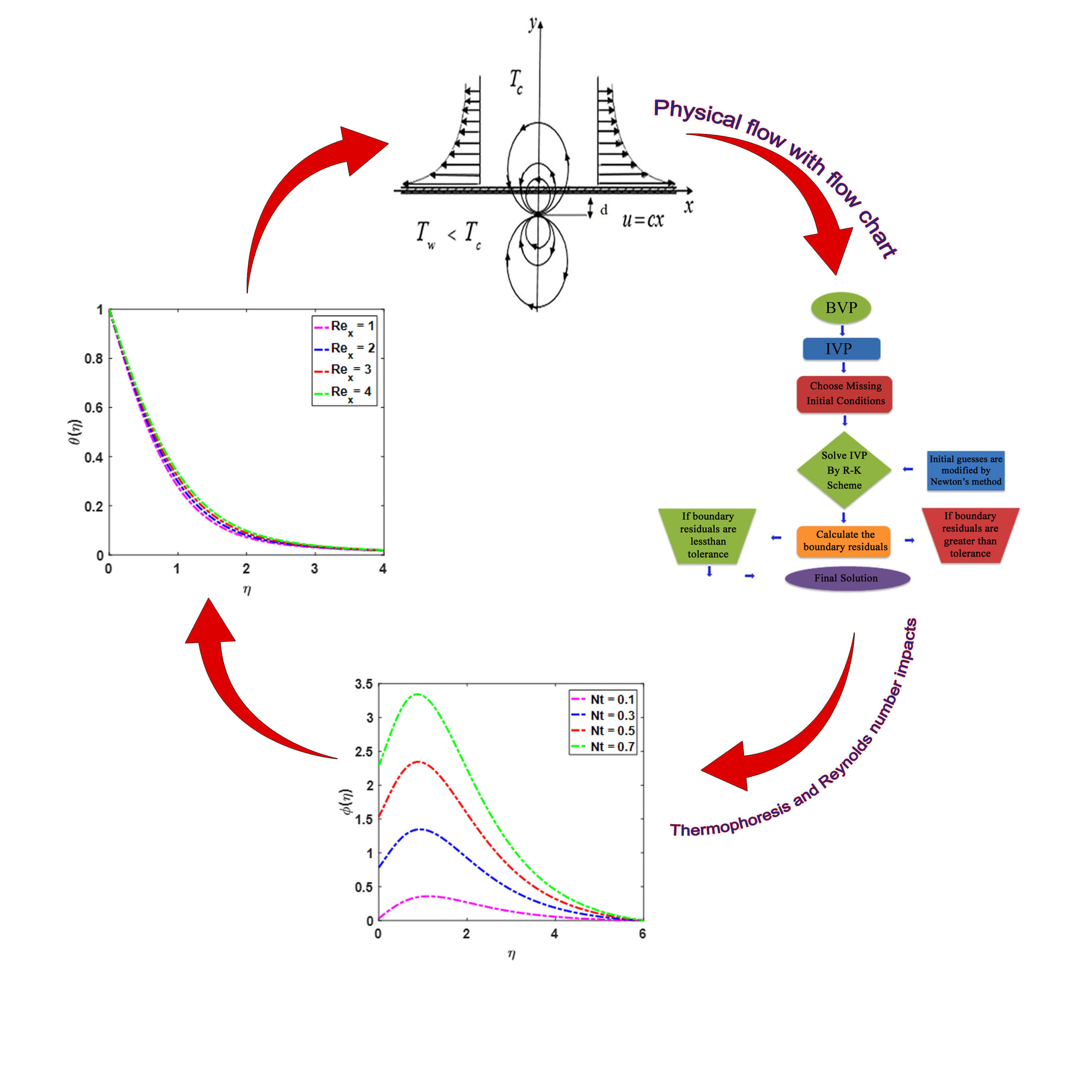
Keywords
Ferrofluids are well suited for use in the hard drive rotary seals and fresh motors with revolving shafts, the vibration damping systems of speakers. Due to their paramagnetic properties, ferro liquids have recently enticed the attention of scientists. Electronics, materials science, thermal engineering, biomechanical engineering, aerospace, and a wide variety of other technical disciplines find ferrofluid useful in a wide variety of applications. Ferrofluid is a contrast researcher used in resonance magnetic imaging in the medical field. Convection of a magnetite water nanofluid driven by gravity and assisted by radiating heat transfer via a swinging vertical surface in a magnetic region was suggested by Seth et al. [1]. Naturally, entropy formation and convection of ferrofluid were described by Astanina et al. [2], an open trapezoidal chamber partly filled with a porous material. Natural convection and entropy production were studied by Gibanov et al. [3] in an open chamber via a variety of horizontal permeable blocks imbued with ferrofluid. Heat transfer ferrofluid with a non-uniformly magnetic region in a channel via sinusoidal walls was explored by Asadi et al. [4].
Bodies of different temperatures may exchange energy in three ways, one of which is thermal radiation. The term “thermal radiation” refers to the emission of electromagnetic waves from a substance, which causes it to warm up (variation of its internal energy). Radiation from the ultraviolet to the far-field infrared may be transmitted through this material, with the exact range being a function of the temperature at which the material is cooled or heated. The whole body is constantly emitting thermal radiation and also receiving radiation from nearby and distant sources. However, the chemical make-up of the transmitter, receiver, and medium being traversed all play a role in the transfer and reception of heat radiation. The ability to transfer and store heat is related to a body’s surface radiation (specific temperatures).
The term “nanofluid” was used to describe a fluid containing particles on the nanoscale. With their long-term stability, minimal clogging, and thermal conductivity, nano-liquids have the potential to be useful in power engines, nuclear reactors, microelectronics, pharmaceuticals, solar energy, and so on [5–11]. Furthermore, there are no side consequences to dealing with nanoparticles, such as a drop in pressure, erosion, or sedimentation. A comprehensive study found that the most prevalent methods for enhanced heat transmission in nanofluids include Brownian motion-induced convection and consecutive transmission via propagating nanoparticle pathways. Numerous scholars [12–17] have examined Brownian motion and thermophoresis consequences in great depth. With heat augmentation as their ultimate aim, their research examined a wide variety of technical setups. Ahmed et al. [18] investigated the MHD flow of viscous nanomaterial across a stretchy plate. Flow entropy, Joule, and frictional heating are assessed. Hayat et al. [19] examined about the materials for the transport of low-quality ferrofluids across elastic substrates. Flow in a non-Darcy-Forchheimer medium is considered. Ahmed et al. [20] numerically analyzed the micropolar fluid flow across permeable parallel plates with finite difference method. Ahmad et al. [21] analyzed computationally about the flow of a viscous fluid across a deformable plate with radiation and entropy generation. Hayat et al. [22] looked at the radiative flow of a ferromagnetic Williamson fluid over a flat surface with a magnetic dipole that could let fluid through. Ahmed et al. [23] reported Comparative study of five water-based nanofluids showed that the upper sheet is squeezed towards the lower sheet, while the lower sheet is porous. Hayat et al. [24] discussed the phenomenon of ferromagnetic flow of rate-type liquid across a stretched surface. Ahmad [25] explored the Finite difference approach for computational investigation of enhanced heat transfer in Ag-H2O, TiO2-H2O, and Ag-TiO2-H2O. Many researchers [26–32] have conducted a variety of studies on ferromagnetic fluid and its related applications.
Brownian motion is the movement of random particles. It is very important in science and biology. Brownian motion is caused by the way molecules in the medium around them keep hitting each other. This kind of movement happens when molecules of close liquids or gases hit each other. The molecules of the liquid or gas that cover the tiny or minute particles in liquids or gases affect the particles. Thermophoresis is when big molecules change their position or move in response to a large-scale temperature difference. The effect can be seen because different particles react in different ways. Brownian motion and thermophoresis both works, as shown by the sources [33–42].
So far, no studies have attempted to disentangle the effects of 2-D nano-particles moment on steady flow across a ferromagnetic stretched surface. As a result, we extended, the modifiable thermal effects of ferrofluid submerged in porous media were studied by Munazza et al. [43]. An influence of magnetic dipole with nonlinear thermal ferromagnetic radiation liquid across a stretching region is investigated numerically using a broad range of relevant parameters. Some more industrial and engineering applications are found in [44,45].
An efficacious BVP4C method is performed to acquire the solution. The time-dependent flow case of this problem should be considered in future research. Also, if the flow medium is changed then the new problem may give a better alternative for a rapid heat transfer process, and also the same problem in the presence of distinct geometries will be very interesting to be explored.
A steady 2-D flow of a viscous, incompressible, and electrically non-conducting magnetite ferrofluid driven through an impermeable stretching sheet is considered. “Flow assumptions are: The flow is caused by the action of two equal and opposite forces along the horizontal direction which is taken as the x-axis, and the direction normal to the flow as the y-axis. The sheet is stretched with a velocity u(x) which is proportional to the distance from the origin. A magnetic dipole is located some distance below the sheet. The center of the dipole lies on the y-axis at a distance ‘a’ below the x-axis. Its magnetic field points in the positive x-direction and the strength of the magnetic field is sufficient to saturate the ferrofluid. The stretching sheet is kept at a fixed temperature Tw below the Curie temperature Tc, while the liquid elements far away from the sheet are supposed to be at temperature T = Tc and hence incapable of being magnetized until they begin to cool upon entering the thermal BL adjacent to the sheet’’ [43].
Consideration is given to the case of a magnetite ferrofluid that is viscous and incompressible, 2-D stead flow, propelled by an impermeable stretching sheet. Fig. 1 shows a schematic depiction of the model’s physical flow.

Figure 1: A schematic depiction of the model’s physical flow
Underlying flow presumptions are:
1) The x-axis denotes the direction of the flow, which is created by the interaction of two forces acting in opposing directions.
2) The y-axis is normal to the flow.
3) Velocity is used to stretch the sheet, varies inversely with x from the origin.
4) Far under the sheet, there exists a magnetic dipole.
5) The magnetic field is enough to strongly saturate the ferro-fluid, points in the positive x-direction.
6) To prevent magnetization of the stretched sheet, we maintained a constant temperature Tw under heath Curie temp (Tc).
7) Fluid components distant are considered with T = Tc.
The scalar magnetic potential, its components, and the magnitude of magnetic field H are [43]
From Eqs. (3) and (4), we have
Ferrofluid boundary layer equations follow [43,45]:
The BCs are [17,21] the problem is
The heat flux
and
The similarity transformations are [30]
All the parameters are given in the nomenclature.
The dimensionless equations are
The relative boundary conditions are
Physically significant numbers include Sk, Nu and Sh which may be stated as
Here
The MATLAB BVP4C method is used to numerically account for the resulting linked non-linear Eqs. (16)–(18) and boundary conditions (19) and (20). Researchers all across the world have relied on this solution to get them through the boundary value issue. The equations are expressed as a system of equivalent first-order ordinary differential equations before the solver can be used. Eqs. (16)–(18) are then coded into the BVP4C solver. The syntax of the solver, sol = BVP4C (@OdeBVP, @OdeBc, solinit, options) contains the function handle @OdeBVP, into which the Eqs. (16)–(18) are coded. Then, the boundary conditions (19) and (20) are coded into the function handle @OdeBC with an error is less than 10−6.
Below is the numerical approach flow chart (see Fig. 2) used to solve the model.

Figure 2: Flow chart
The following is a summary of the pros and cons of utilizing the BVP4C program:
Advantages:
1. Rate of convergence.
2. Accuracy.
3. Stability.
4. The program is usually written for a dedicated simulation problem.
Disadvantages:
1. The simulation software cannot be modified or upgraded since its source code is unavailable.
2. The mathematical model of the simulated system must be obtained, which might be a challenging task.
Here, we presented the physical meanings of the findings from the relevant numerical calculations. As a result, we extended Saeed et al. [10] and noted that velocity profile gradient decreases when ferrofluid and viscosity parameter rise. The fixed values in the work are: β = 0.5; α = 0.5; Г = 0.4; λ1 = 0.5; γ1 = 0.5; Rex = 2; Tr = 3; δ = 0.2; Le = 0.5; Nt = 0.1; Nb = 0.1. The consequences of β on velocity profiles are shown in detail in Fig. 3. When β is enhanced, it shows an enhancement in velocity. Physically, when the ferromagnetic parameter is increased in fluid motion, the momentum barrier layer rises.

Figure 3: Appearance of β on velocity
The consequences of α on velocity profiles are shown in detail in Fig. 4. When α is enhanced, it shows a reduction in velocity. Physically, when the fluid moves away from the magnetic dipole, the effects of viscous forces weaken, leading to a speed decrease.

Figure 4: Appearance of α on velocity
The consequences of Г on velocity profiles are shown in detail in Fig. 5. When Г is enhanced, it shows an enhancement in velocity. This happens as a result of an increase in magnetic permeability, which produces a rise in velocity. Physically, the magnetic field produced by the magnetic dipole raises the velocity of the ferrofluid.
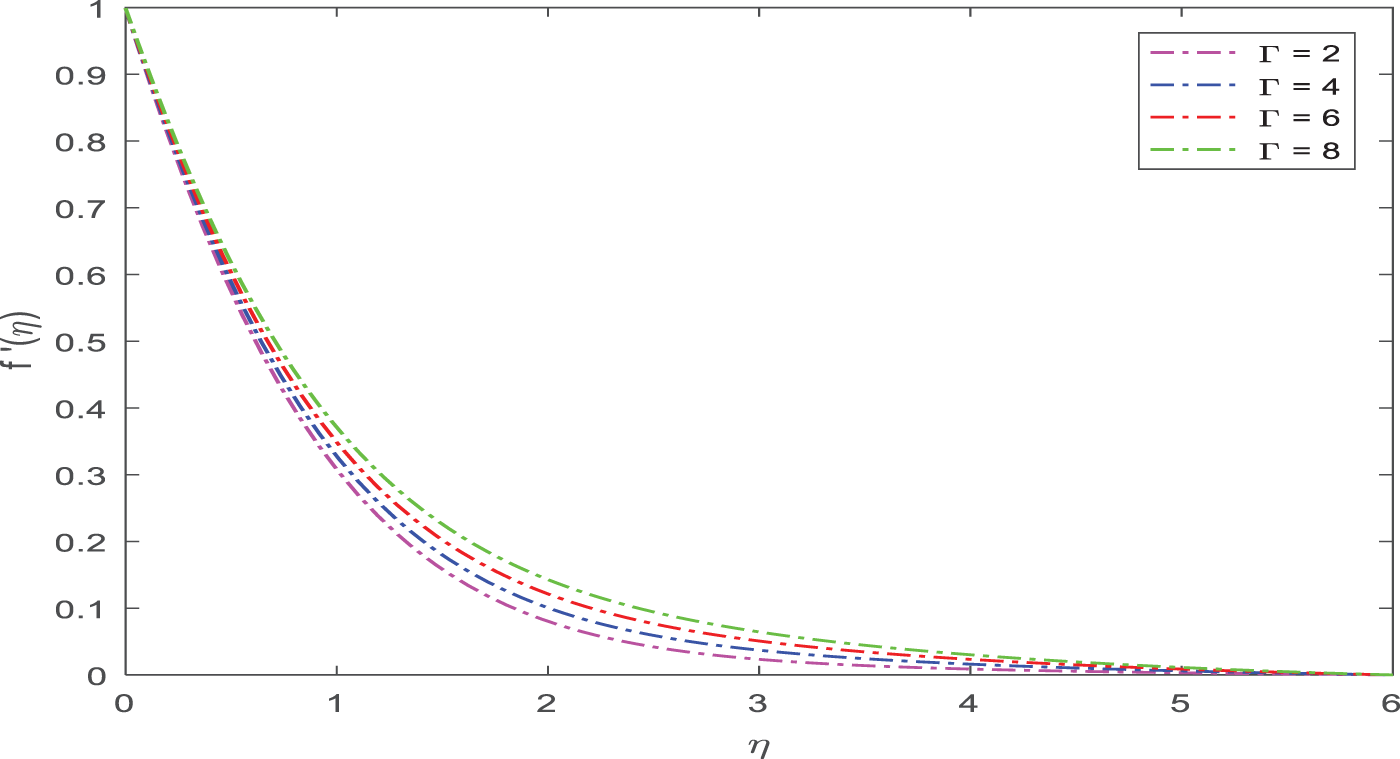
Figure 5: Appearance of Г on velocity
The consequences of λ1 on velocity profiles are shown in detail in Fig. 6. When λ1 is enhanced, it shows an enhancement in velocity. Physically, this is brought on by a laminar flow that increases in velocity due to a low Reynolds number.
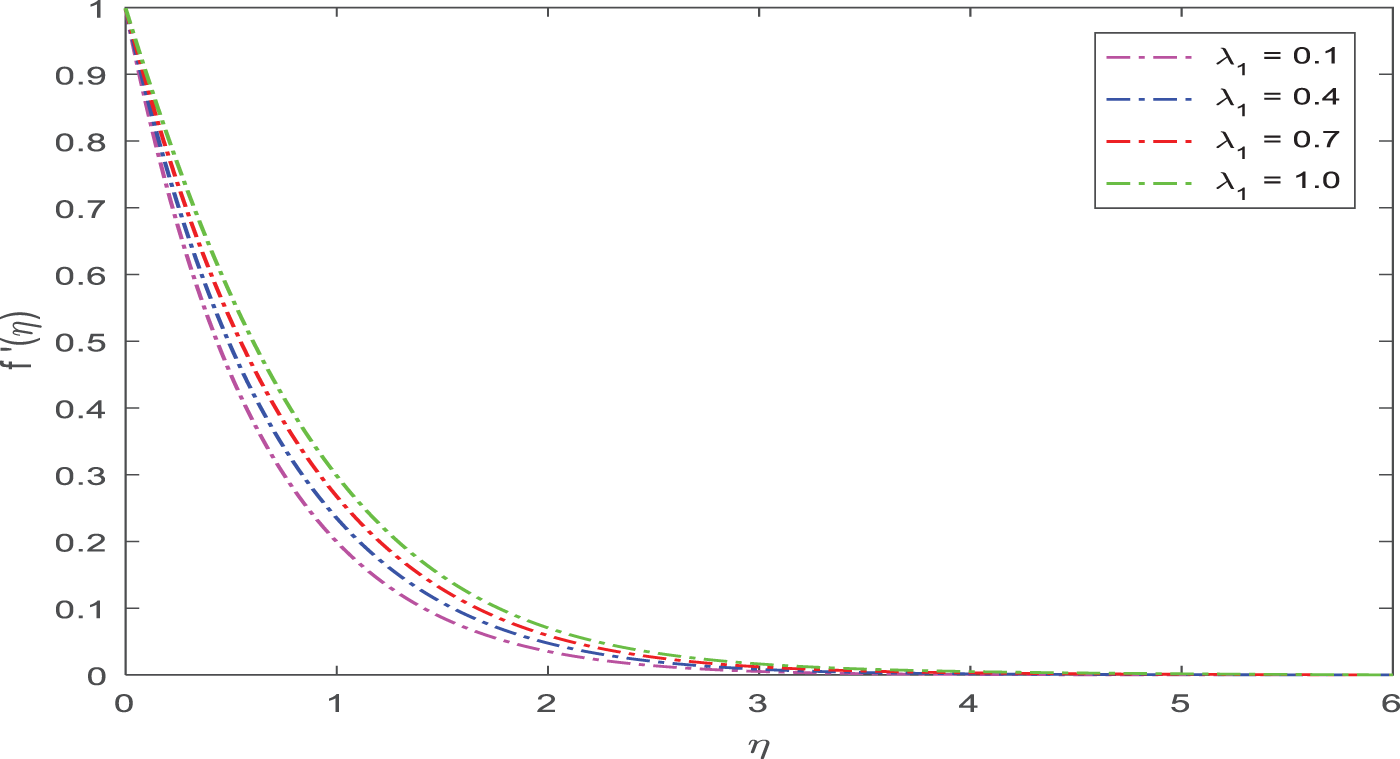
Figure 6: Appearance of λ1 on velocity
The consequences of γ1 on velocity profiles are shown in detail in Fig. 7. When γ1 is enhanced, it shows a reduction in velocity.
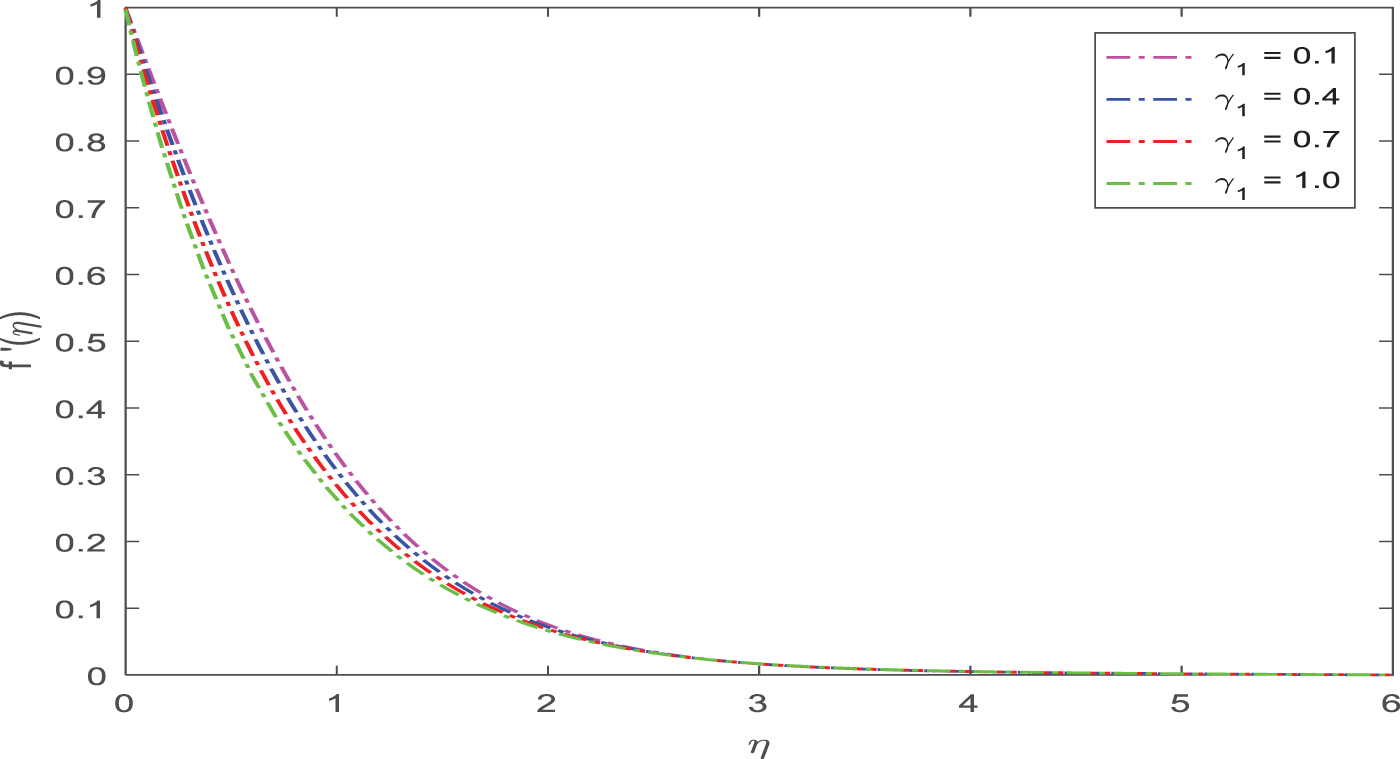
Figure 7: Appearance of γ1 on velocity
The consequences of ε on velocity profiles are shown in detail in Fig. 8. When ε is enhanced, it shows an improvement in velocity.
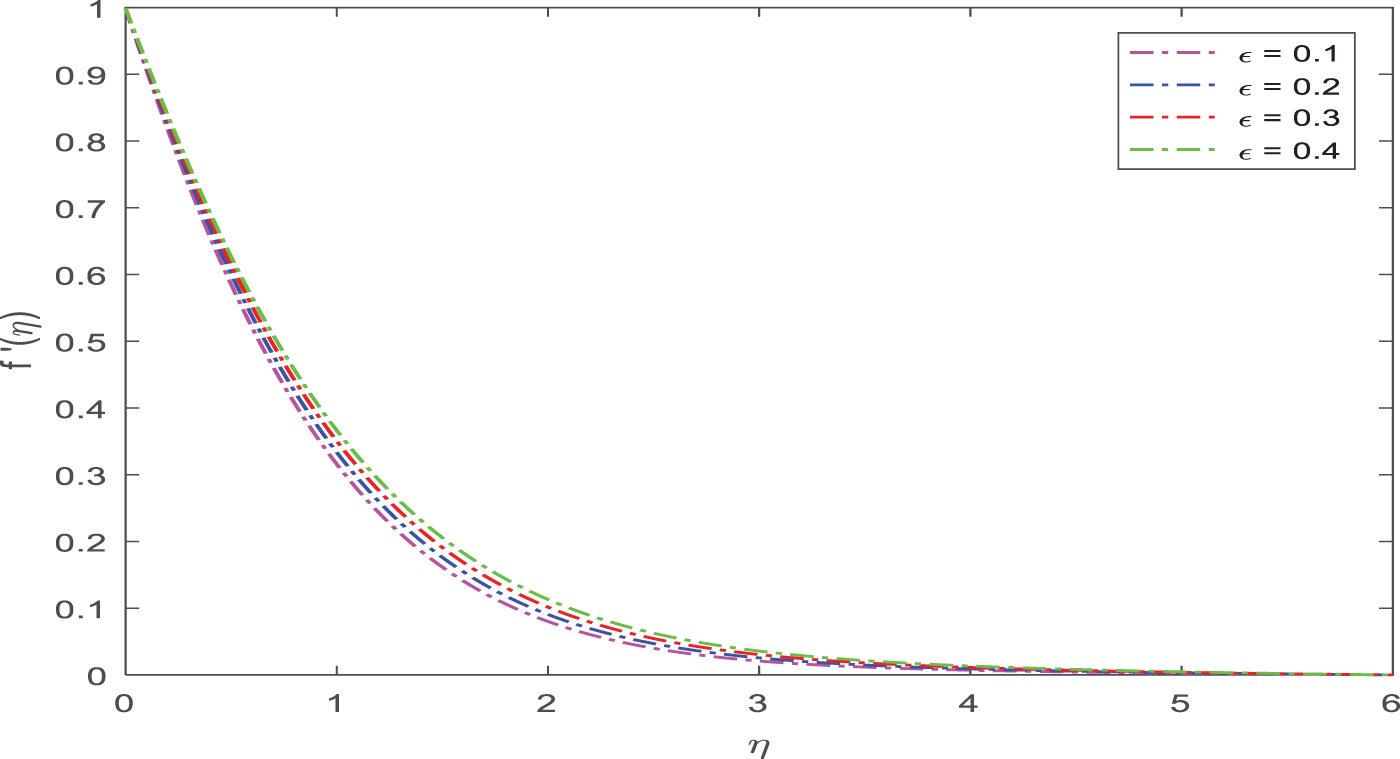
Figure 8: Appearance of ε on velocity
The impact of Pr on temperature distribution is discussed using a scatter plot, seen in Fig. 9. Therefore, when Pr increases temperature declines. Physically, the thickness of the thermal boundary layer is decreased if there is a rise in the Prandtl number. The ratio of the momentum diffusivity to the thermal diffusivity is referred to as the Prandtl number. In issues involving heat transport, the relative thickness of the momentum and thermal boundary layers is controlled by the parameter Pr.
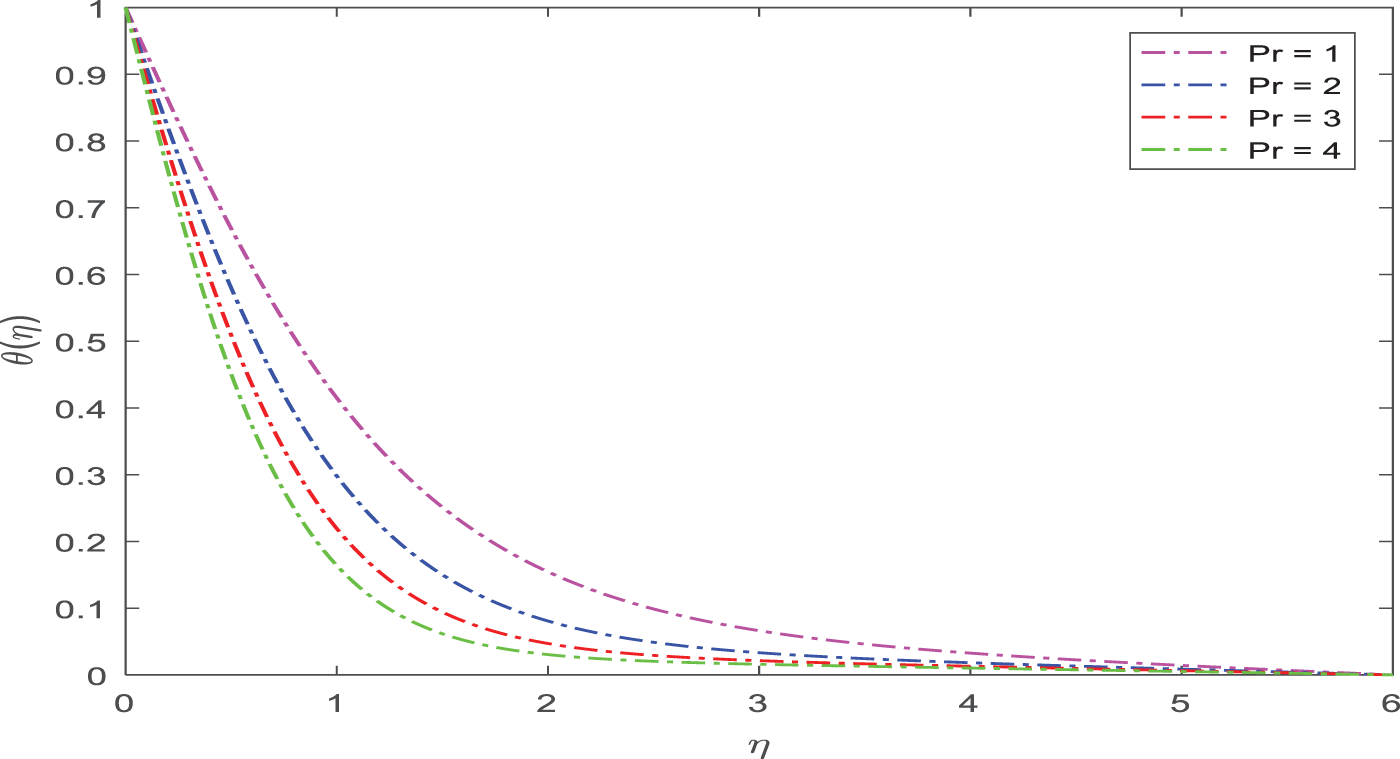
Figure 9: Appearance of Pr on temperature
The impact of Rex on temperature distribution is discussed using a scatter plot, seen in Fig. 10. Therefore, when Rex increases, temperature improves.

Figure 10: Appearance of Rex on temperature
The influence of Tr on temperature is discussed using a scatter plot, seen in Fig. 11. Therefore, when Tr increases, temperature improves. Physically, the intensity of the radiation is influenced by the temperature of the material since thermal radiation is produced by the temperature of the material. If the temperature of the matter is greater than the temperature of the surrounding environment, the net heat transfer occurs away from the surface of the matter; otherwise, it occurs toward the surface.
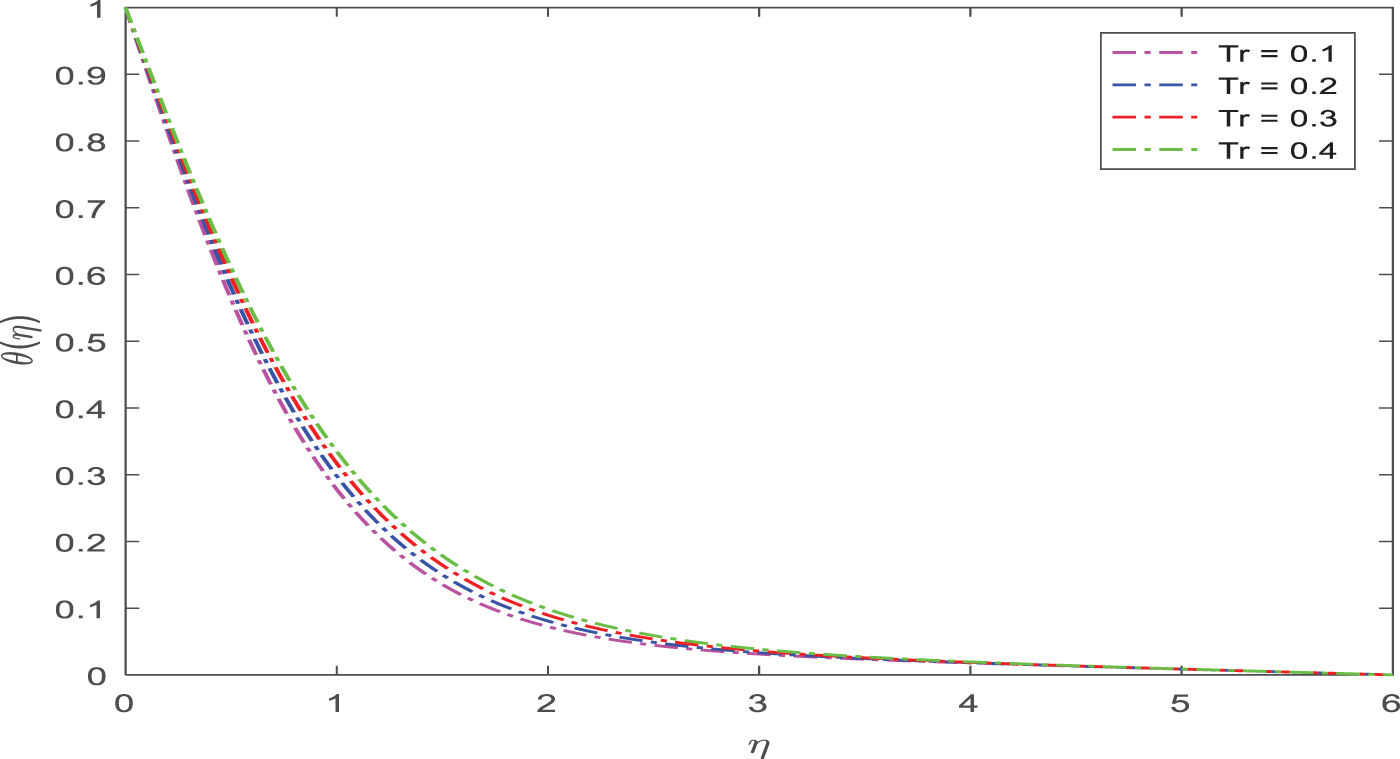
Figure 11: Appearance of Tr on temperature
The consequences of the Lewis number on constituent concentration are seen in Fig. 12. With an improvement in the Lewis number, concentration profiles flatten off. It establishes a direct physical connection between the hydrodynamic layer and the mass-transfer boundary layer’s relative thickness.

Figure 12: Appearance of Le on concentration
The consequences of the thermophoresis parameter Nt on the distribution of concentrations are seen in Fig. 13. Concentration fields are seen to increase as Nt grows. As Nt grows, the thermophoresis force increases, moving the nanoparticles from a warm to a cold region; this, in turn, causes the concentration distributions to grow. In most cases, free convection processes, which are those in which the flow is created by the buoyancy force induced by a temperature gradient, are the ones in which thermophoresis is more prominent. The nanoparticles move in the direction of a lowering temperature, and the process of heat transfer is improved when the bulk density is lowered.
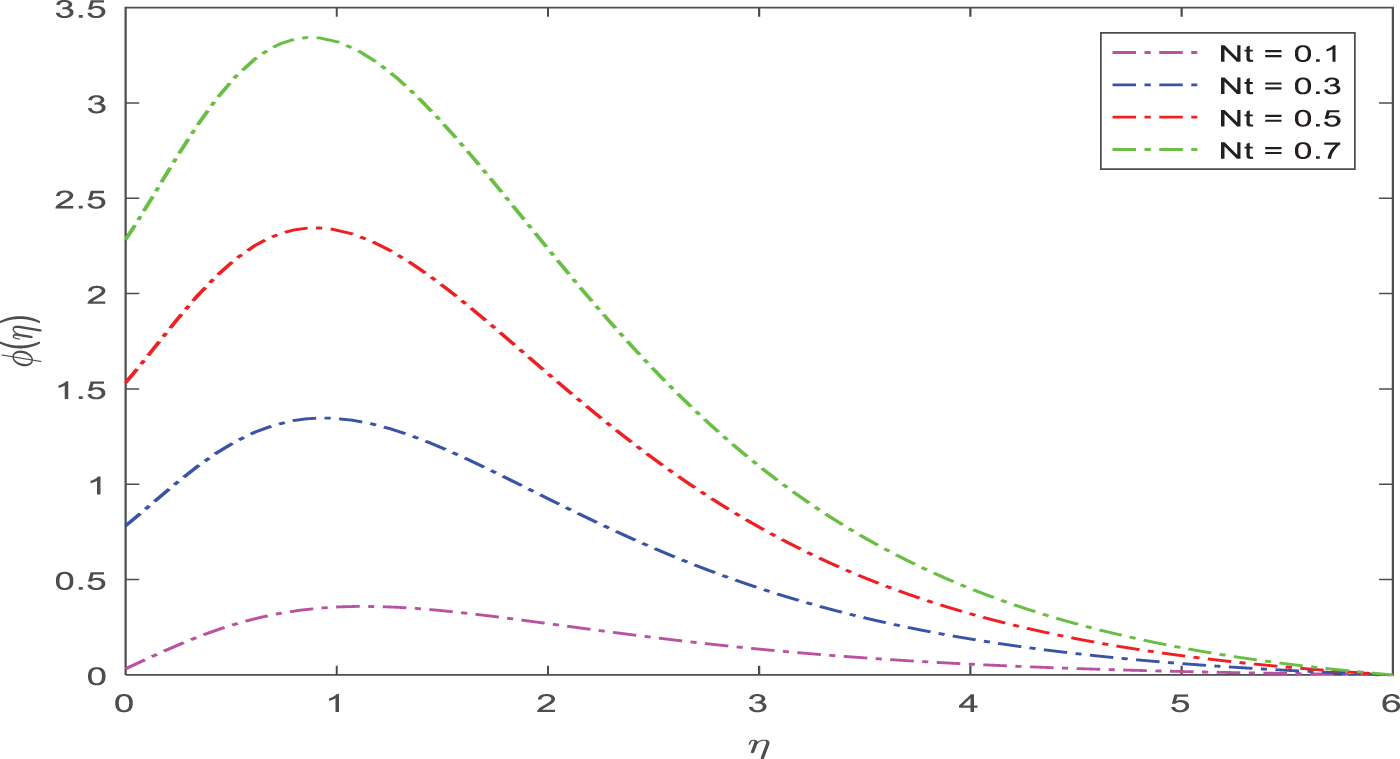
Figure 13: Appearance of Nt on concentration
Fig. 14 shows how the limit layer viscosity and concentration distribution both grow with increasing Nb concentrations. As Nb increases, the liquid’s macroscopic particles become more likely to randomly move and collide with one another. As a result, there will be a higher concentration of liquid. By increasing Nb, fluid velocity may be arbitrarily decreased. The particles in a fluid are always moving because of a phenomenon known as Brownian movement. Because of this, particles are prevented from settling down, which contributes to the stability of colloidal solutions. With the use of this motion, a genuine solution may be differentiated from a colloid in an effective manner.
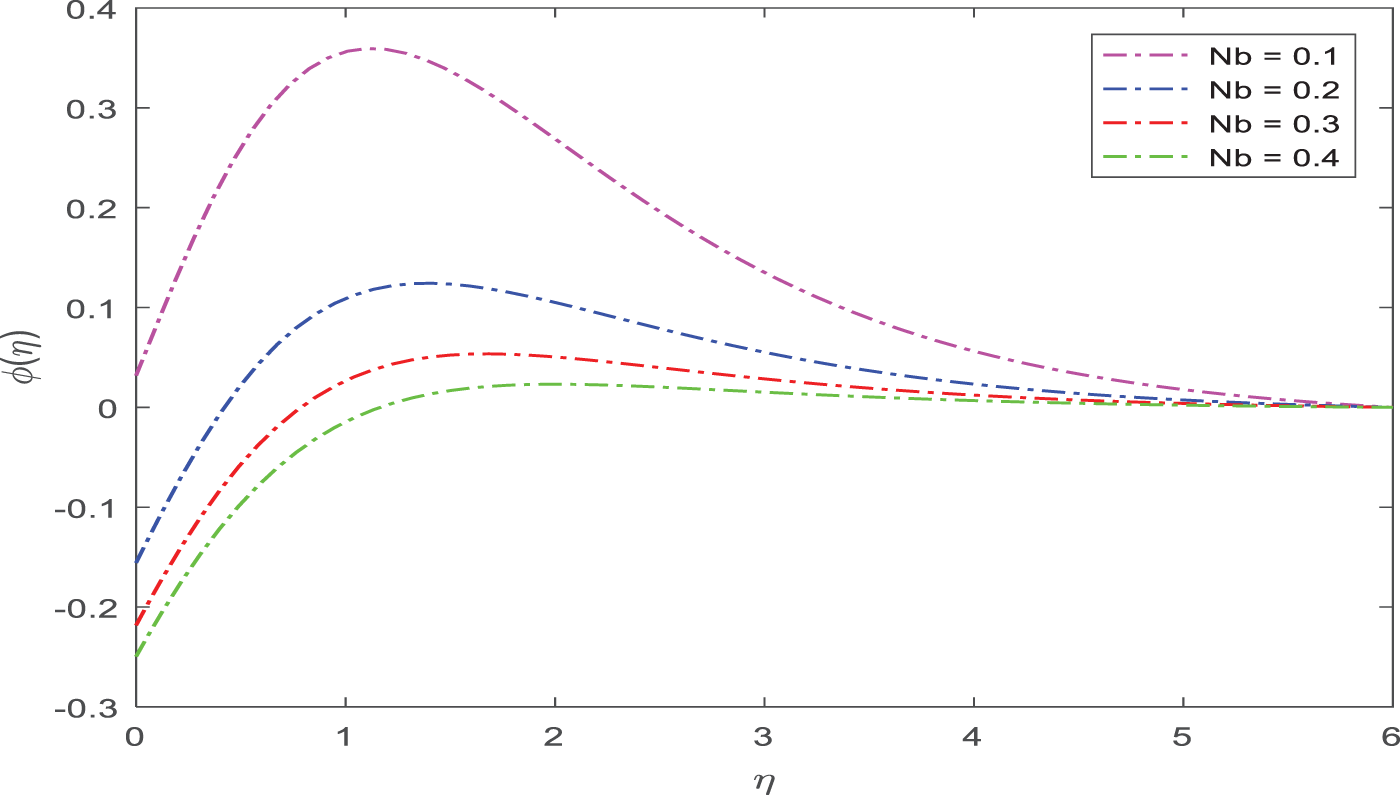
Figure 14: Appearance of Nb on concentration
A plot of the Cf viscosity parameter vs. the Lewis number is shown in Fig. 15. The Cf rises when the viscosity parameter is increased.
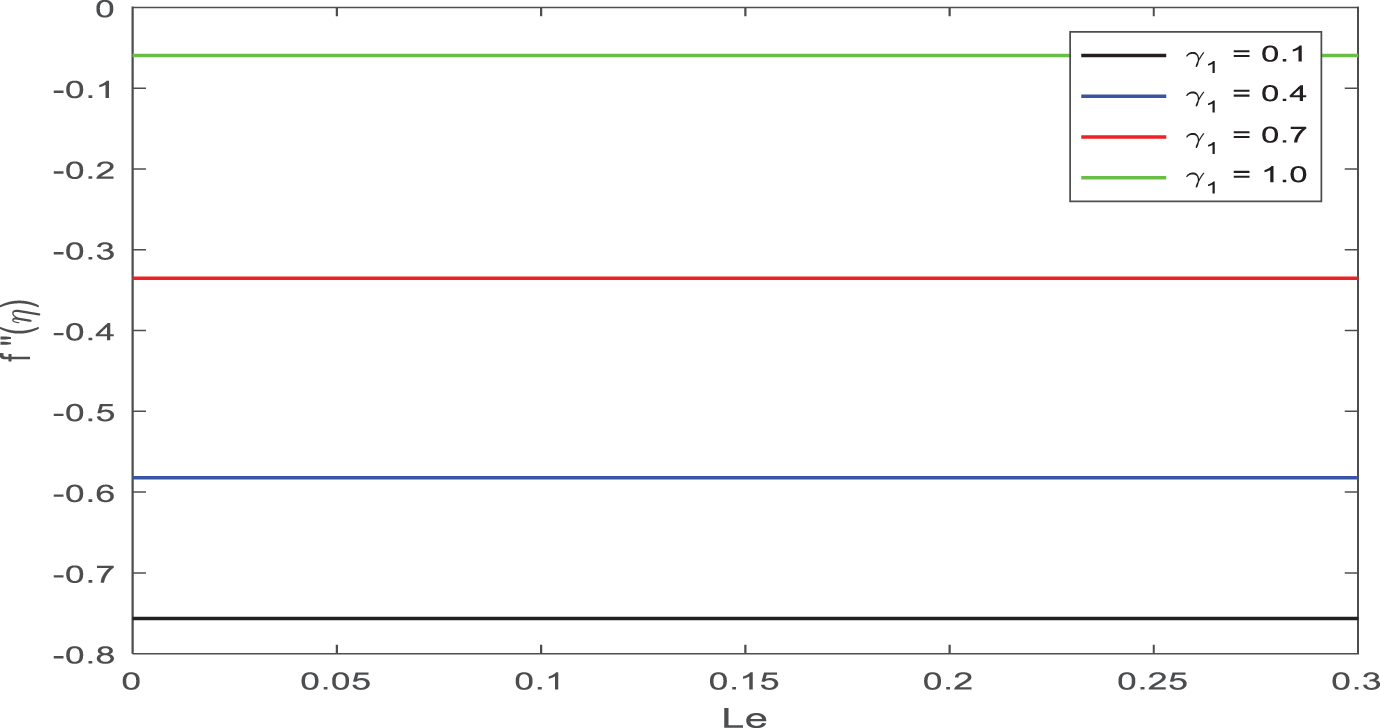
Figure 15: Appearance of γ1 on Cf against Le
Skin-friction on ferromagnetic parameter influence vs. radiation parameter is shown in Fig. 16. Increasing the value of the ferromagnetic parameter results in a higher Cf.
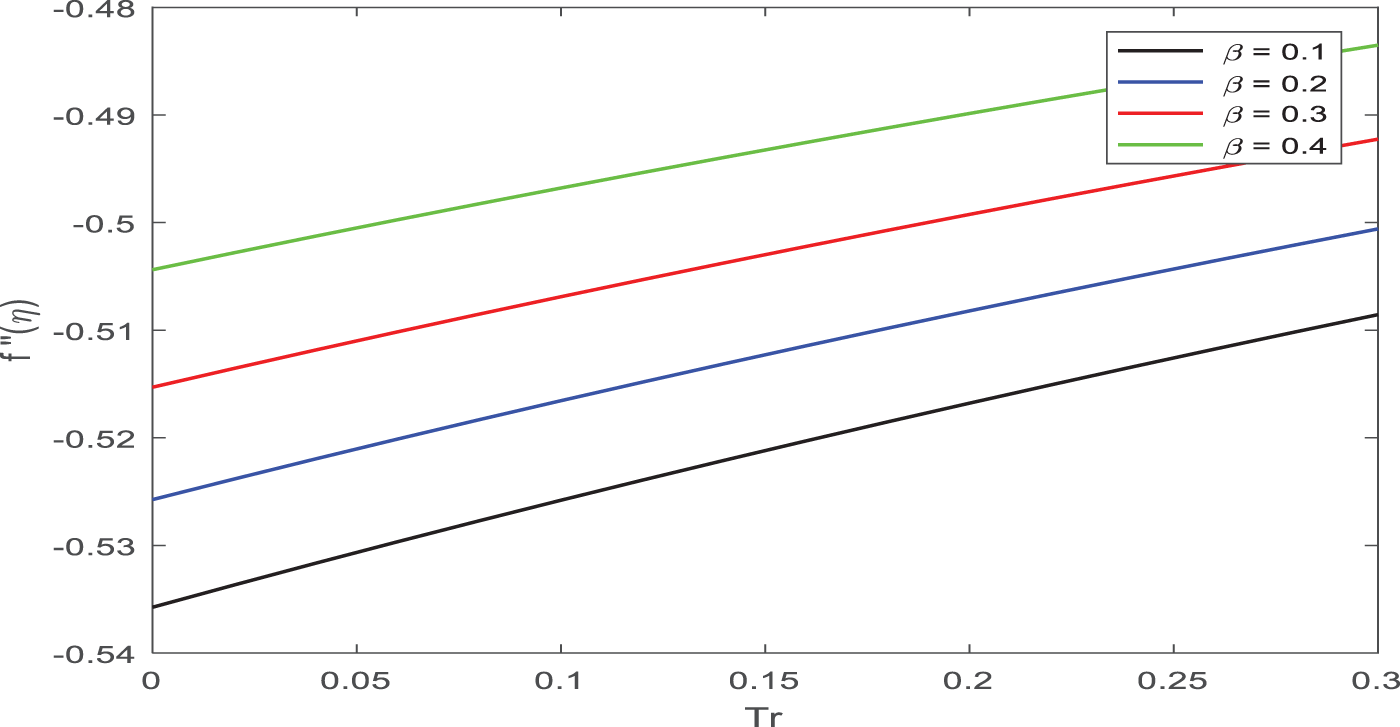
Figure 16: Appearance of β on Cf against Tr
The relationship between the Nu viscosity parameter and the Lewis number is seen in Fig. 17. With rising levels of the viscosity parameter, the Nusselt number drops.
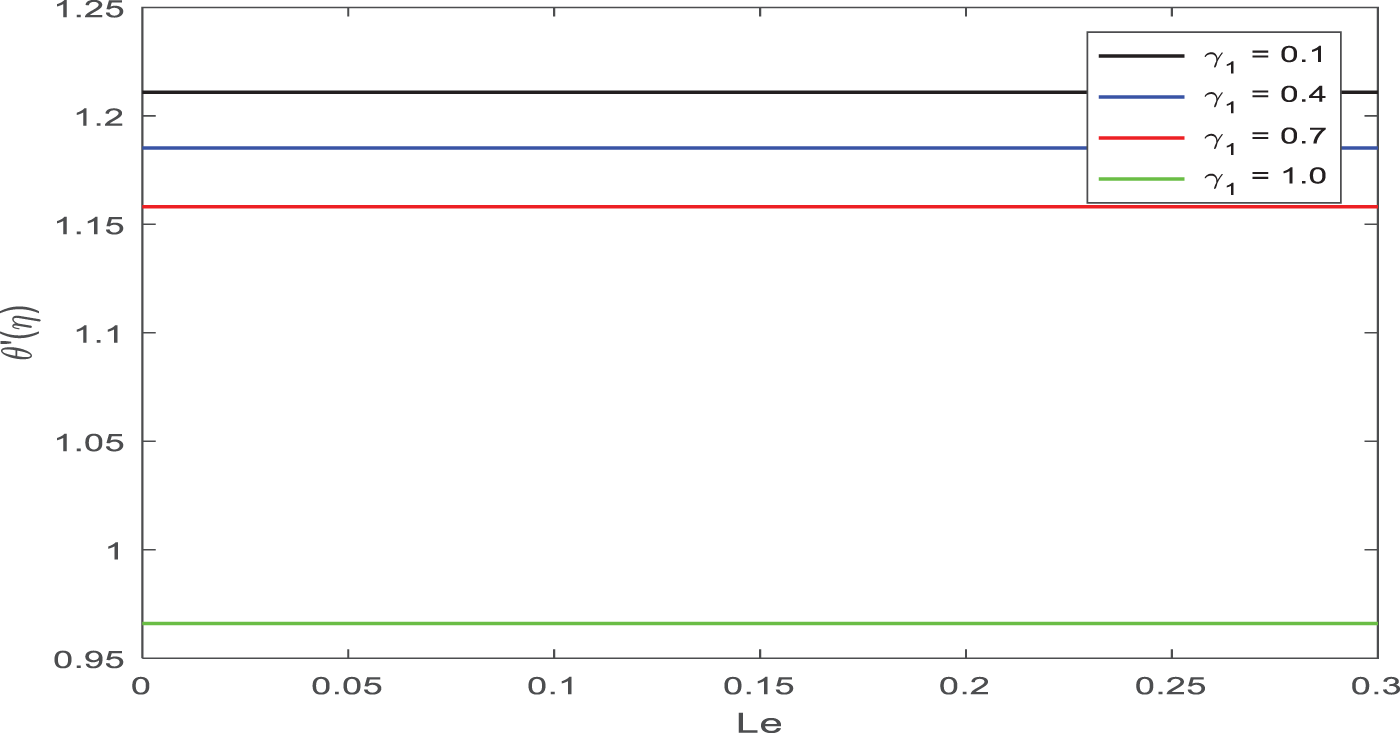
Figure 17: Appearance of γ1 on Nu against Le
Nusselt number on ferromagnetic parameter influences, on the radiation parameter are shown in Fig. 18.
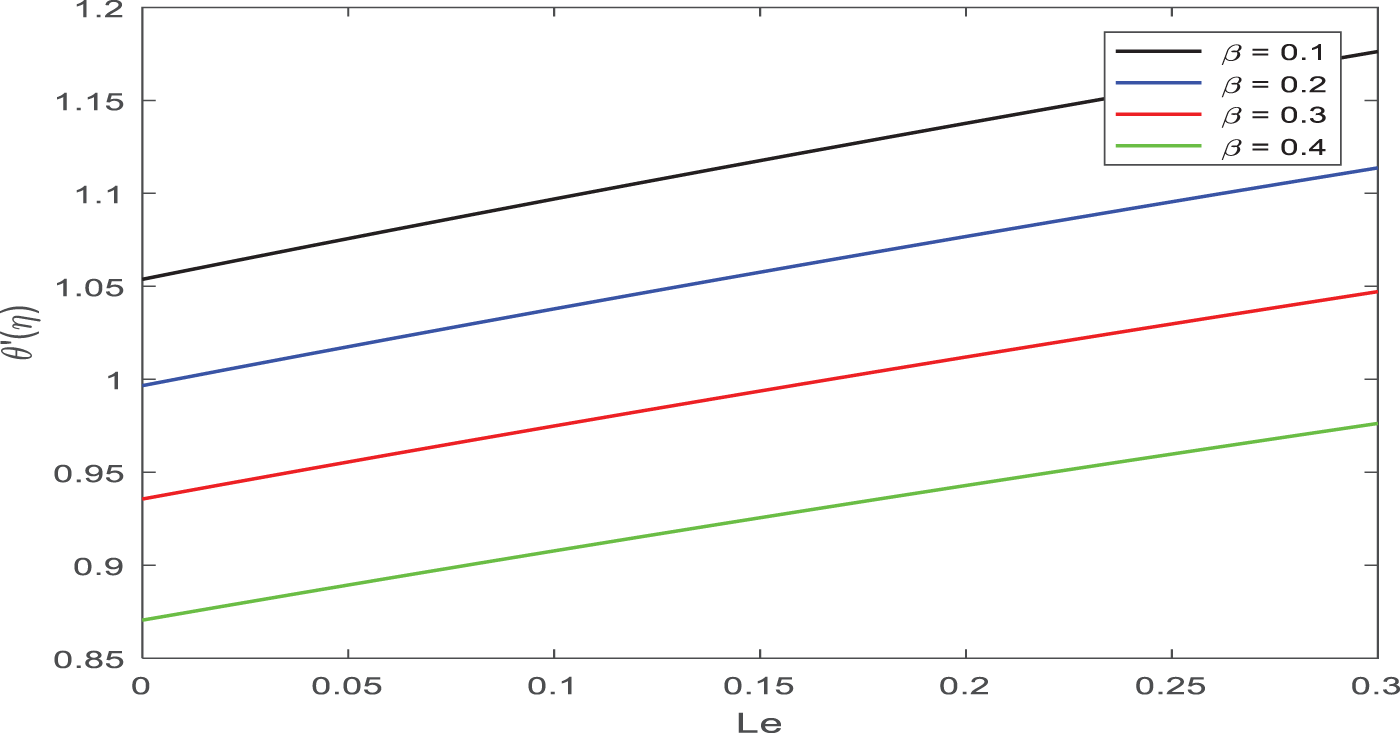
Figure 18: Appearance of β on Nu against Tr
The Nusselt number falls as the ferromagnetic parameter rises. The impact of the Sherwood number on the thermophoresis parameter is shown in Fig. 19.
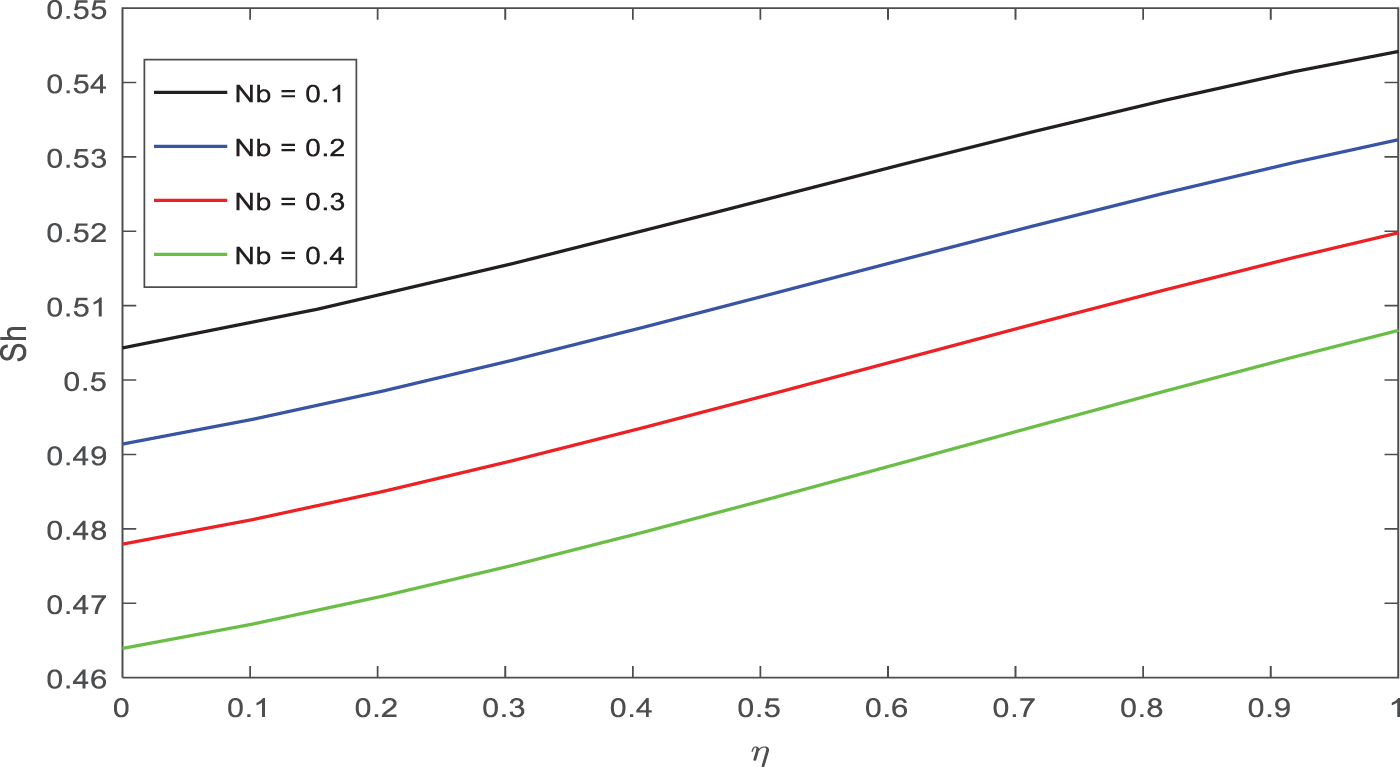
Figure 19: Appearance of Nb on Sh against η
The impact of the Sherwood number on the Brownian motion parameter is seen in Fig. 20. As the parameter for Brownian motion heightens, so does the Sh.
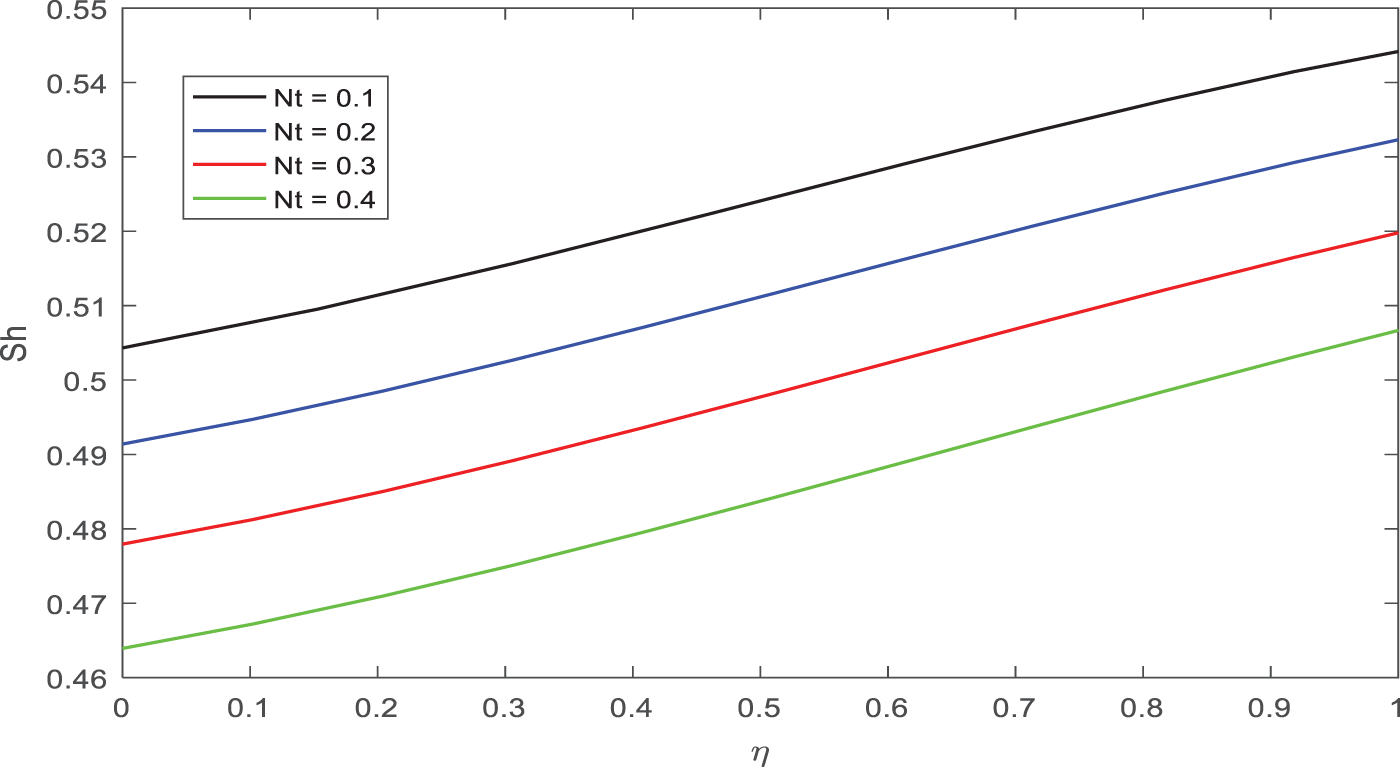
Figure 20: Appearance of Nt on Sh against η
Figs. 21 and 22 depict the comparison of the prior work [43] and the current study on temperature and velocity. The comparison is a really strong agreement. Results that are compared to earlier studies show high accuracy and effectiveness.
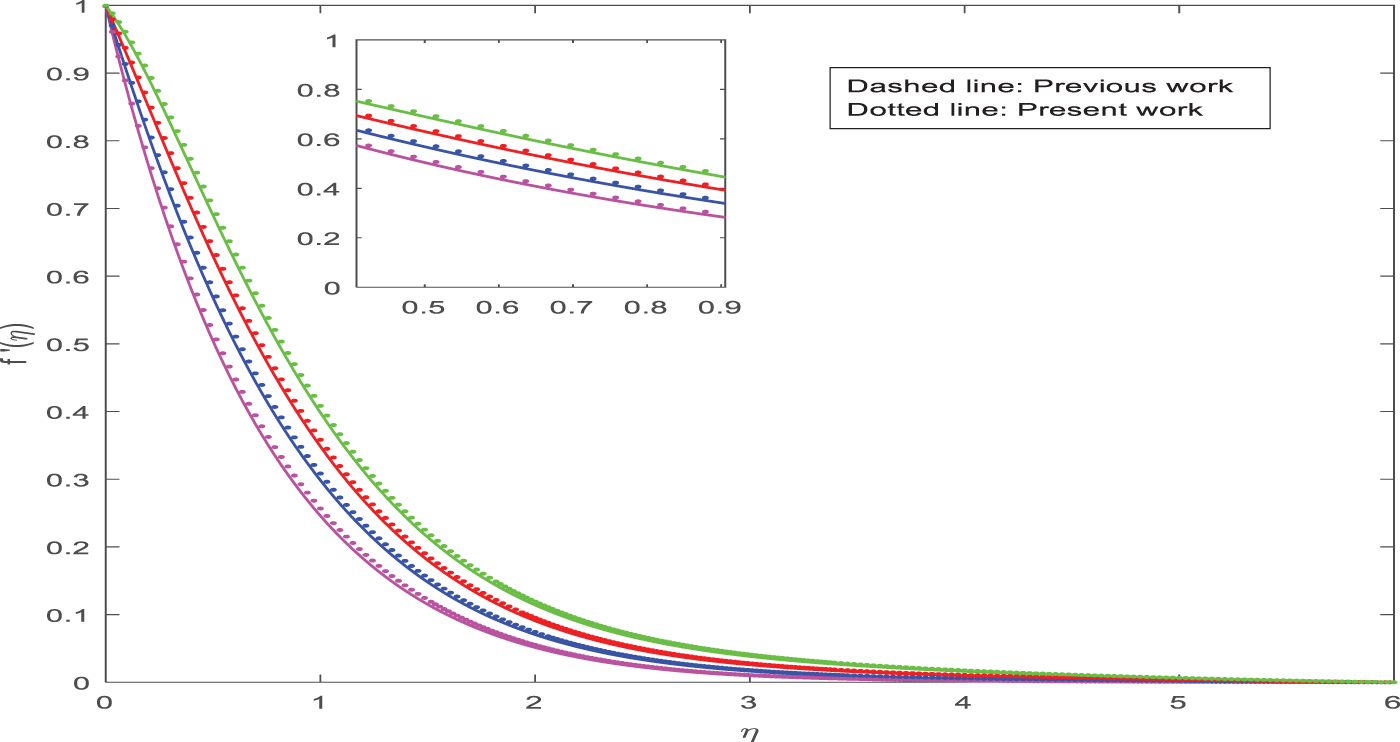
Figure 21: Comparison of velocity for λ1 between published work [43] and present work
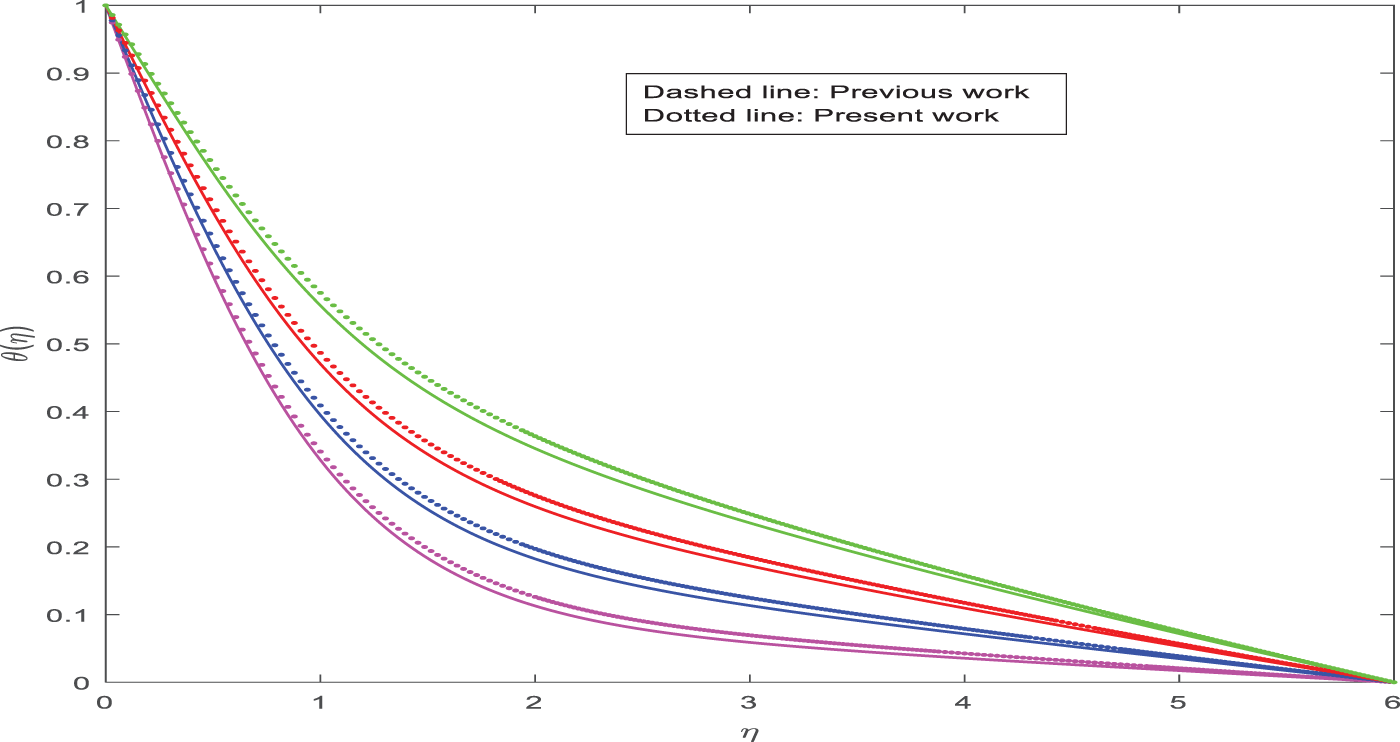
Figure 22: Comparison of temperature for β between published work [43] and present work
The effects of the magnetic dipole on nonlinear thermal ferromagnetic fluid across a stretching region are investigated numerically using a broad range of relevant parameters. Also, it was carried out to learn more about the steady flow of ferro-fluids in a porous media with Brownian motion and thermo-phoresis impact. By using the right similarity transformation, ordinary differential equations are derived. The equations are solved afterward using the BVP4C approach. Two variables, the distance, and the ferromagnetic parameter, affect the velocity in different ways.
• Increasing Prandtl boosts both the temperatures and nanoparticle concentration magnitudes throughout the boundary layer regime.
• An increase in Prandtl leads to an increase in the temperatures as well as the thermal boundary layer raises.
• Increasing the Brownian motion parameter and thermophoresis parameter enhances concentration and its boundary layer.
• An increase in Lewis numbers has a strong dampening effect on the measured concentration of nanoparticles.
• An enhanced impact in velocity due to the Ferro-magnetic parameter has been observed.
• The skin-friction rises when the viscosity parameter is increased.
• Increasing the value of the ferromagnetic parameter results in a higher skin-friction.
• With rising levels of the viscosity parameter, the Nusselt number falls.
• The Nusselt number reduces, as the ferromagnetic parameter rises.
• As the growing of thermophoresis parameter, the reduction behaviors on the Sherwood number are noted.
Acknowledgement: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: All authors have the same contribution. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All necessary data are presented in the manuscript.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Seth, G. S., Mandal, P. K. (2018). Gravity driven convective flow of magnetite water nanofluid and radiative heat transfer past an oscillating vertical plate in the presence of magnetic field. Latin American Applied Research, 48, 7–13. [Google Scholar]
2. Astanina, M., Sheremet, M., Oztop, H., Abu-Hamdeh, N. (2018). MHD natural convection and entropy generation of ferrofluid in an open trapezoidal cavity partially filled with a porous medium. International Journal of Mechanical Sciences, 136, 493–502. [Google Scholar]
3. Gibanov, N., Sheremet, M., Oztop, H. (2018). MHD natural convection and entropy generation in an open cavity having different horizontal porous blocks saturated with a ferrofluid. Journal of Magnetism and Magnetic Materials, 452, 193–204. [Google Scholar]
4. Asadi, A., Hossein Nezhad, A., Sarhaddi, F., Keykha, T. (2019). Laminar ferrofluid heat transfer in presence of non-uniform magnetic field in a channel with sinusoidal wall: A numerical study. Journal of Magnetism and Magnetic Materials, 471, 56–63. [Google Scholar]
5. Naseem, T., Shahzad, A., Sohail, M., Askar, S. (2023). Axisymmetric flow and heat transfer in TiO2/H2O nanofluid over a porous stretching-sheet with slip boundary conditions via a reliable computational strategy. Energies, 16, 681. [Google Scholar]
6. Nazir, U., Sohail, M., Kumam, P., Elmasry, Y., Sitthithakerngkiet, K. et al. (2022). Thermal and solute aspects among two viscosity models in synovial fluid inserting suspension of tri and hybrid nanomaterial using finite element procedure. Scientific Reports, 12(1), 1–14. [Google Scholar]
7. Hou, E., Nazir, U., Naz, S., Sohail, M., Nadeem, M. et al. (2023). Novel analysis of two kinds hybrid models in ferro martial inserting variable Lorentz force past a heated disk: An implementation of finite element method. Computer Modeling in Engineering & Sciences, 135(2), 1393–1411. https://doi.org/10.32604/cmes.2022.022500 [Google Scholar] [CrossRef]
8. Mebarek-Oudina, F., Chabani, I. (2023). Review on nano enhanced PCMs: Insight on nePCM application in thermal management/storage systems. Energies, 16(3), 1066. https://doi.org/10.3390/en16031066 [Google Scholar] [CrossRef]
9. Ramesh, K., Mebarek-Oudina, F., Ismail, A. I., Jaiswal, B. R., Warke, A. S. et al. (2023). Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sciencia Iranica, 30(2), 376–390. https://doi.org/10.24200/sci.2022.58629.5822 [Google Scholar] [CrossRef]
10. Durgaprasad, P., Varma, S. V. K., Hoque, M. M., Raju, C. S. K. (2018). Combined consequencess of Brownian motion and thermophoresis parameters on three-dimensional (3D) Casson nanofluid flow across the porous layers slendering sheet in a suspension of graphene nanoparticles. Neural Computing and Applications, 31(10), 6275–6286. [Google Scholar]
11. Ali, A., Mebarek-Oudina, F., Barman, A., Das, S., Ismail, A. I. (2023). Peristaltic transportation of hybrid nano-blood through a ciliated micro-vessel subject to heat source and Lorentz force. Journal of Thermal Analysis and Calorimetry, 148(14), 7059–7083. https://doi.org/10.1007/s10973-023-12217-x [Google Scholar] [CrossRef]
12. Rafique, K., Anwar, M. I., Misiran, M., Khan, I., Seikh, A. H. et al. (2019). Brownian motion and thermophoretic diffusion consequencess on micropolar type nanofluid flow with soret and dufour impacts over an inclined sheet: Keller-box simulations. Energies, 12(21), 4191. [Google Scholar]
13. Lin, Y., Jiang, Y. (2018). Consequencess of Brownian motion and thermophoresis on nanofluids in a rotating circular groove: A numerical simulation. International Journal of Heat and Mass Transfer, 123(2), 569–582. [Google Scholar]
14. Kumar, R. N., Gowda, R. J. P., Madhukesh, J. K., Prasannakumara, B. C., Ramesh, G. K. (2021). Impact of thermophoretic particle deposition on heat and mass transfer across the dynamics of Casson fluid flow over a moving thin needle. Physica Scripta, 96(7), 075210. [Google Scholar]
15. Akbar, S., Sohail, M. (2022). Three dimensional MHD viscous flow under the influence of thermal radiation and viscous dissipation. International Journal of Emerging Multidisciplinaries: Mathematics, 1(3), 106–117. [Google Scholar]
16. Mebarek-Oudina, F., Preeti, S. A. S., Vaidya, H., Lewis, R. W. et al. (2023). Hydromagnetic flow of magnetite-water nano-fluid utilizing adapted Buongiorno model. International Journal of Modern Physics B, 2450003. https://doi.org/10.1142/S0217979224500036 [Google Scholar] [CrossRef]
17. Raza, J., Mebarek-Oudina, F., Ali Lund, L. (2022). The flow of magnetised convective Casson liquid via a porous channel with shrinking and stationary walls. Pramana—Journal of Physics, 96(4), 229. https://doi.org/10.1007/s12043-022-02465-1 [Google Scholar] [CrossRef]
18. Ahmad, S., Hayat, T., Alsaedi, A. (2020). Numerical analysis of entropy generation in viscous nanofluid stretched flow. International Communications in Heat and Mass Transfer, 117, 104772. https://doi.org/10.1016/j.icheatmasstransfer.2020.104772 [Google Scholar] [CrossRef]
19. Hayat, T., Ahmad, S., Ijaz Khan, M., Alsaedi, A. (2017). Non-darcy forchheimer flow of ferromagnetic second grade fluid. Results in Physics, 7(15), 3419–3424. https://doi.org/10.1016/j.rinp.2017.08.041 [Google Scholar] [CrossRef]
20. Ahmad S., Khan Z. H. (2022). Numerical solution of micropolar fluid flow with heat transfer by finite difference method. International Journal of Modern Physics B, 36(4), 2250037. https://doi.org/10.1142/S0217979222500370 [Google Scholar] [CrossRef]
21. Ahmad, S., Hayat, T., Alsaedi, A. (2021). Computational analysis of entropy generation in radiative viscous fluid flow. Journal of Thermal Analysis and Calorimetry, 143(3), 2665–2677. https://doi.org/10.1007/s10973-020-09684-x [Google Scholar] [CrossRef]
22. Hayat, T., Ahmad, S., Khan, M. I., Alsaedi, A. (2018). Exploring magnetic dipole contribution on radiative flow of ferromagnetic Williamson fluid. Results in Physics, 8(132), 545–551. https://doi.org/10.1016/j.rinp.2017.11.040 [Google Scholar] [CrossRef]
23. Ahmad, S., Khan, M. I., Hayat, T., Khan, M. I., Alsaedi, A. (2018). Entropy generation optimization and unsteady squeezing flow of viscous fluid with five different shapes of nanoparticles. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 554(2), 197–210. https://doi.org/10.1016/j.colsurfa.2018.06.017 [Google Scholar] [CrossRef]
24. Hayat, T., Ahmad, S., Khan, M. I., Alsaedi, A. (2018). Simulation of ferromagnetic nanomaterial flow of Maxwell fluid. Results in Physics, 8, 34–40. https://doi.org/10.1016/j.rinp.2017.11.021 [Google Scholar] [CrossRef]
25. Ahmad, S. (2023). Computational analysis of comparative heat transfer enhancement in Ag-H2O, TiO2-H2O and Ag-TiO2-H2O: Finite difference scheme. Journal of the Taiwan Institute of Chemical Engineers, 142(9), 104672. https://doi.org/10.1016/j.jtice.2023.104672 [Google Scholar] [CrossRef]
26. Hassan, M., Fetecau, C., Majeed, A., Zeeshan, A. (2018). Effects of iron nanoparticles’ shape on convective flow of ferrofluid under highly oscillating magnetic field over stretchable rotating disk. Journal of Magnetism and Magnetic Materials, 465(4), 531–539. https://doi.org/10.1016/j.jmmm.2018.06.019 [Google Scholar] [CrossRef]
27. Majeed, A., Zeeshan, A., Ellahi, R. (2017). Chemical reaction and heat transfer on boundary layer Maxwell Ferro-fluid flow under magnetic dipole with Soret and suction effects. Engineering Science and Technology, an International Journal, 20(3), 1122–1128. https://doi.org/10.1016/j.jestch.2016.11.007 [Google Scholar] [CrossRef]
28. Majeed, A., Zeeshan, A., Majeed Noori, F., Usman, M. (2019). Influence of rotating magnetic field on Maxwell saturated ferrofluid flow over a heated stretching sheet with heat generation/absorption. Mechanics & Industry, 20, 502. https://doi.org/10.1051/meca/2019022 [Google Scholar] [CrossRef]
29. Majeed, A., Zeeshan, A., Gorla, R. (2018). Convective heat transfer in a dusty ferromagnetic fluid over a stretching surface with prescribed surface temperature/heat flux including heat source/sink. Journal of the National Science Foundation of Sri Lanka, 46(3), 399–409. https://doi.org/10.4038/jnsfsr.v46i3.8492 [Google Scholar] [CrossRef]
30. Wang, F., Sohail, M., Nazir, U., El-Zahar, E. R., Park, C. et al. (2022). An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial. Nanotechnology Reviews, 11(1), 1620–1632. [Google Scholar]
31. Ramesh, G. K., Madhukesh, J. K., Aly, E. H., Pop, I. (2022). Modified Buongiorno’s model for biomagnetic hybrid nanoliquid past a permeable moving thin needle. International Journal of Numerical Methods for Heat & Fluid Flow, 32(11), 3551–3578. [Google Scholar]
32. Soomro F. A., Haq R. U., Hamid M. (2021). Brownian motion and thermophoretic effects on non-Newtonian nanofluid flow via Crank–Nicolson scheme. Archive of Applied Mechanics, 91(7), 3303–3313. https://doi.org/10.1007/s00419-021-01966-6 [Google Scholar] [CrossRef]
33. Hu, G. J., Ali Shah, N., Mahrous, Y. M., Sharma, P., Raju, C. S. K. et al. (2021). Radiated magnetic flow in a suspension of ferrous nanoparticles over a cone with brownian motion and thermophoresis. Case Studies in Thermal Engineering, 25(4), 100915. https://doi.org/10.1016/j.csite.2021.100915 [Google Scholar] [CrossRef]
34. Kalpana, G., Madhura, K. R., Ramesh Kudenatti, B. (2022). Magnetohydrodynamic boundary layer flow of hybrid nanofluid with the thermophoresis and Brownian motion in an irregular channel: A numerical approach. Engineering Science and Technology, an International Journal, 32(18048), 101075. https://doi.org/10.1016/j.jestch.2021.11.001 [Google Scholar] [CrossRef]
35. Izamarlina, A., Alias, J., Abdullah, S. (2023). Brownian motion and thermophoresis effects in co-flowing carbon nanotubes towards a moving plate. Results in Physics, 44(8), 106165. https://doi.org/10.1016/j.rinp.2022.106165 [Google Scholar] [CrossRef]
36. Mahnoor, S., Khan, M., Ahmed, A. (2023). Study of thermophoresis and Brownian motion phenomena in radial stagnation flow over a twisting cylinder. Ain Shams Engineering Journal, 14(2), 101869. https://doi.org/10.1016/j.asej.2022.101869 [Google Scholar] [CrossRef]
37. Naseem, T., Nazir, U., Sohail, M. (2021). Contribution of Dufour and Soret effects on hydromagnetized material comprising temperature-dependent thermal conductivity. Heat Transfer, 50(7), 7157–7175. [Google Scholar]
38. Javed, M., Imran, N., Arooj, A., Sohail, M. (2021). Meta-analysis on homogeneous-heterogeneous reaction effects in a sinusoidal wavy curved channel. Chemical Physics Letters, 763(4), 138200. [Google Scholar]
39. Ramesh, G. K., Madhukesh, J. K. (2021). Activation energy process in hybrid CNTs and induced magnetic slip flow with heat source/sink. Chinese Journal of Physics, 73, 375–390. [Google Scholar]
40. Sohail, M., Ali, U., Zohra, F. T., Al-Kouz, W., Chu, Y. M. et al. (2021). Utilization of updated version of heat flux model for the radiative flow of a non-Newtonian material under Joule heating: OHAM application. Open Physics, 19(1), 100–110. [Google Scholar]
41. Shahzad, A., Liaqat, F., Ellahi, Z., Sohail, M., Ayub, M. et al. (2022). Thin film flow and heat transfer of Cu-nanofluids with slip and convective boundary condition over a stretching sheet. Scientific Reports, 12(1), 14254. [Google Scholar] [PubMed]
42. Puneeth, V., Manjunatha, S., Madhukesh, J. K., Ramesh, G. K. (2021). Three dimensional mixed convection flow of hybrid casson nanofluid past a non-linear stretching surface: A modified Buongiorno’s model aspects. Chaos, Solitons & Fractals, 152(1), 111428. [Google Scholar]
43. Munazza, S., Bilal, A., Qazi Mahmood ul, H. (2022). Variable thermal consequencess of viscosity and radiation of ferrofluid submerged in porous medium. Ain Shams Engineering Journal, 13(4), 101653. https://doi.org/10.1016/j.asej.2021.101653 [Google Scholar] [CrossRef]
44. Dharmaiah, G., Mebarek-Oudina, F., Sreenivasa Kumar, M., Chandra Kala, K. (2023). Nuclear reactor application on Jeffrey fluid flow with Falkner-skan factor, Brownian and thermophoresis, non linear thermal radiation impacts past a wedge. Journal of the Indian Chemical Society, 100(2), 100907. https://doi.org/10.1016/j.jics.2023.100907 [Google Scholar] [CrossRef]
45. Andersson, H. I., Valnes, O. A. (1998). Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mechanica, 128(1), 39–47. https://doi.org/10.1007/BF01463158 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools