An Investigation into Forced Convection of a Nanofluid Flowing in a Rectangular Microchannel under the Influence of a Magnetic Field

1  Introduction

Nanofluids are gaining popularity in research owing to their ability to improve heat transport and cooling in a variety of systems. New studies demonstrate that graphene-containing nanofluids have a stronger capacity to boost the displacement heat transfer coefficient than traditional nanofluids, even at low concentrations [1,2]. The introduction of this significant material into the challenge of heat transfer seems necessary with the development of the amazing material known as graphene, which has an extraordinary thermal conductivity coefficient [3]. The use of graphene oxide as a hybrid can be more productive because, despite the fact that graphene nanoparticles are an excellent material for nanofluids, the large-scale synthesis of graphene is challenging and expensive [4].

It should be noted that one of the active strategies for increasing the rate of heat transfer is the influence of magnetic fields on nanoparticles. To accomplish this, it was determined what effect the application of different frequencies and the strength of the external magnetic field had on the improvement of heat transfer at various concentrations and Reynolds numbers (Re) [5].

The findings reveal that the heat transfer rate of the tested hybrid nanofluid improves in the presence of a constant and alternating magnetic field, with the alternating field being more important than the constant field [6]. Furthermore, the findings demonstrate that in the absence of a magnetic field and a Re of 571, the average increase in displacement heat transfer of a ferrofluid with a concentration of 0.5 reached 14.3% as compared to pure water, but this value further increased when the field was applied [7]. Permanent and alternating magnetization levels are respectively 21 and 28.9 percent [8].

Ferrofluids are a unique class of nanofluids. They are made up of a stable colloidal mixture of magnetic nanoparticles with a diameter of 5–15 nm that are uniformly dissolved in the base fluid, along with a non-magnetic carrier fluid (like water or oil) [9]. Researchers’ attentions have recently been focused on the conduction and convection heat transfer of nanofluids, particularly ferrofluids, and numerous studies have examined the thermal conductivity coefficient and the impact of various parameters on it, including nanoparticle size, concentration, and temperature [10–14]. Sezer et al. [15] looked at the thermal conductivity coefficient of carbon nanotubes using various base fluids. Their findings showed a notable rise in heat conductivity. They demonstrated in a different study that ethylene glycol’s thermal conductivity will increase by 25.8% when CuO nanoparticles are added.

Several studies have also linked the methods of improving the thermal conductivity of nanofluids to Brownian motion of particles, layering of liquid at the interface with the solid phase, photon heat transfer, and cluster formation [16–18].

Shahsavar et al. [19] have looked at the impact of volume fraction and temperature on the thermal conductivity of Fe3O4 ferrofluid. They believed that the rise in thermal conductivity with temperature was due to the intensification of the particles’ Brownian motion. These investigations have demonstrated that adding nanoparticles to the base fluid boosts the thermal conductivity coefficient.

Because magnetic nanoparticles can react appropriately to the force caused by the use of an external magnetic field, some studies also measured the coefficient of magnetic response when an external magnetic field is used [20,21]. It should be noted that the use of an external magnetic field is considered as one of the active methods for increasing heat transfer rate. Concentrated ferrofluid thermal conductivity is impacted by a magnetic field [22].

Shahsavar et al. [23] investigated the effects of variables like concentration and surfactant on the thermal conductivity coefficient and viscosity of a ferrofluid in the presence of an external magnetic field. Their research shows that as the magnetic field strength increases, thermal conductivity and viscosity increase until saturation is reached. Meanwhile, changes in the microscopic structure (mass and chain structure) in the presence of a magnetic field parallel to the temperature gradient was responsible for the increase in thermal conductivity [12].

Soudagar et al. [24] observed a significant increase in the thermal conductivity of nanofluid with iron oxide particles that were under the magnetic field and reported the highest increase in thermal conductivity and volume concentration. Ghazvini et al. [25] reported that the thermal conductivity coefficient was shown to rise by 30% as a function of the transverse magnetic field and temperature. A constant magnetic field was applied to a circulating Fe3O4/H2O ferro-nano-fluid with different concentrations (1%, 2%, and 5%) by Taşkesen et al. [26]. They found that the magnetic field could improve convective heat transfer by 8.32%. Gürdal et al. [27] investigated the flow of Fe3O4/H2O in a tube with dimples under magnetic field effect, and reported that the Nusselt number (Num) increases as the Reynolds number and magnetic field intensity increase. The Num rises by 115.31 percent in comparison to the flow of distilled water in a smooth tube at 0.3 T. Gürdal et al. [28] explained the effect on a hybrid nanofluid flow under the influence of a magnetic field under fully developed hydrodynamic and developing thermal flow conditions. The magnetic field improved the Num and friction factor. In the absence of a magnetic field, hybrid nanofluid flow in a dimpled tube with a magnetic field of magnitude 0.3 T increases the Num and friction factor by 11.87% and 6.19%, respectively.

The hydrodynamic and thermal behavior of a ferrofluid in a horizontal and curved conduit under a linear magnetic field of varying intensities was examined using the mixed two-phase model and the finite element method [29]. Bezaatpour et al. [30] discovered that the Kelvin force and centrifugal force are responsible for the increase in the heat transfer coefficient in the curved tube over the straight tube in the presence of an external magnetic field. Namburu et al. [31] numerically studied a number of nanofluids in turbulent flow. According to their research, the Num increases as the Re and volume concentration of nanoparticles increase. They demonstrated that the nanofluid containing SiO2 would have the highest Num despite having the lowest thermal conductivity coefficient.

Alumina/water nanofluid heat transfer in microchannels with asymmetric heat was investigated by other researchers for its effect on nanoparticle movement by magnetic fields [32]. Pakravan et al. [33] showed that the nanoparticles separate from the heated walls and almost certainly assemble on the wall with the lower heat flow. Additionally, the migration of nanoparticles towards the wall is sped up with greater heat flux, increasing the rate of heat transfer.

The same nanofluid’s magnetic hydrodynamic behavior in a vertical loop was also studied by other researchers. They demonstrated that the applied boundary conditions have a significant impact on the rate of heat transfer and pressure drop of nanofluid [34].

Another study examined the forced displacement heat transfer in the laminar flow regime in a pipe with a constant heat flux and constant magnetic field [35]. Ghofrani et al. [35] found that merely introducing iron oxide nanoparticles to the base fluid enhances the displacement heat transfer, and that adding a magnetic field amplifies this improvement even further.

In this study, the influence of a magnetic field on nanoparticles was offered as one of the active strategies for enhancing heat transfer rate. To accomplish this purpose, the influence of an external magnetic field strength, as well as the effect of applying various frequencies on the improvement of heat transfer in different Re and concentrations, was explored, and the ideal frequency was determined.

2  Method

The schematic representation of the microchannel can be seen in Fig. 1. The heat flux that is introduced into the microchannel by the fins and the bottom of the channel is dissipated as a result of its transfer to the fluid that is moving through the channels. A consistent magnetic field is exerting its effect in a transverse direction along the length of L1 in the section of the channel that is located lower down. Cobalt ferrite/graphene particles were utilized, and each particle had a diameter of 39.4 nm and a volume percentage of 2%. W and H, respectively, denote the width and height of each individual channel. As shown in Fig. 1, the length of the channels is denoted by the value L, the width of the blades is denoted by the value WcW, and the depth of the floor layer is denoted by the value t. Both Tables 1 and 2 provide information on the size of the channel as well as the characteristics of the nanofluid. Because the number of calculations for all channels will be large, one of the middle channels is selected and due to the existing symmetry, half of this channel is selected for calculations. Therefore, the calculation range is the same as Fig. 1 which applies the symmetrical boundary conditions on the left and right walls.

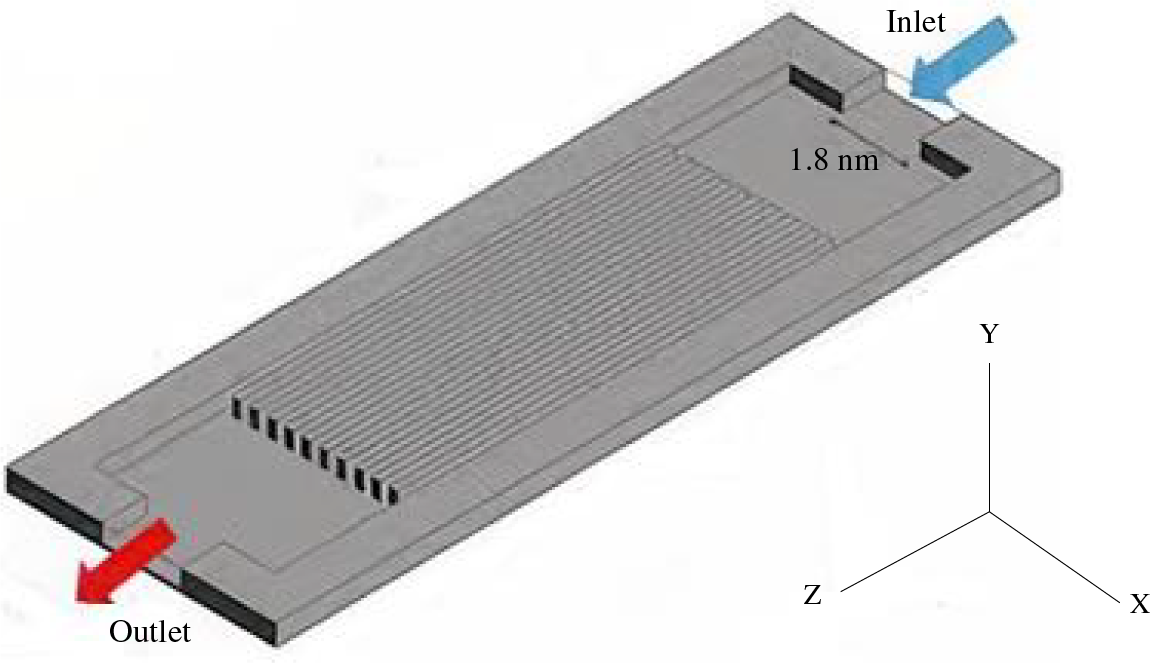
Figure 1: Thermal well microchannel

The governing equations with the assumption of incompressible and stable flow are as follows [18]:

∂U∂X+∂V∂Y+∂W∂Z=0 (1)

U∂V∂X+V∂V∂Y+W∂V∂Z=−∂P∂Y+μnfρnf×αf1RePr(∂2 V∂2X+∂2 V∂2Y+∂2 V∂2Z)  (2)

U∂W∂X+V∂W∂Y+W∂W∂Z=∂P∂Z nfρnf×α1RePt(∂2 W∂2X+∂2 W∂2Y∂2 W∂2Z)−H2ReW (3)

U∂θ∂X+V∂θ∂Y+W∂θ∂Z=αnfαf1RePr(∂2θ∂2X+∂2θ∂2Y+∂2θ∂2Z) (4)

U∂U∂X+V∂U∂Y+W∂U∂Z=∂P∂X+μnfρnf×αf1RePT(∂2U∂2X+∂2U∂2Y+∂2U∂2Z)−Ha2ReU (5)

The first order central differencing scheme was used to discretization the equation of motion. A central difference derived equations that are integrated using an explicit time integration approach (Eq. (6)). Although this approach is conditionally stable, it does not necessitate the employment of implicit iterative techniques. The central difference method necessitates that for each time step. In the central difference method, the solution to the current time step depends only on the solution of previous steps.

dfdx|x=f(x+Δx)−f(x−Δx)2Δx (6)

where, f represents the objective function and x illustrated the direction.

The energy conservation equation for the solid part is solved:

KS(∂2θ∂2X+∂2θ∂2Y+∂2θ∂2Z)=0 (7)

In the above Equation, ρnf is the density of the nanofluid, αbf is the thermal diffusivity of the base fluid, Re = uinDh/Vbf, is the Re, Pr = Vbf/αbf, is the Parantel number, and Ha is the dimensionless Hartmann number.

The bottom surface of the channel’s floor is exposed to a heat flux that is equivalent to 200 W/cm2. The heat that is transferred from the channel’s top surface is not very much because the forced displacement heat transfer rate that takes place in the channel and on the insulated surface is thought to be much higher than the natural displacement heat transfer mechanism that actually takes place on this surface. It is assumed that both the right and left walls are symmetrical because of symmetry. In addition, it is assumed that on symmetrical planes, the temperature gradient and the normal velocity are both equal to zero. The fluid initially enters the channel at the intake, where its temperature is 279 K and its velocity is constant.

A constant pressure is considered at the outlet. Because the length of the channel is long enough, therefore, the fluid at the outlet is assumed to be fully developed, and hence the axial gradient (∂∂x) is considered equal to zero. To investigate the fully developed condition, the length of the channel was increased, as a result of which no significant changes were seen. In the line connecting the solid and the velocity at the axial position z = L of the fluid, the condition of no slippage of velocity and no jump of temperature is true:

V→=0Tnf=TSKnf∂Tnf∂n=KS∂TS∂n (8)

Knf and Ks are the thermal conductivities of the nanofluid and solid part, respectively.

To obtain the suitable grid size and number of mesh according to the solution time, the problem was solved with different number of meshes and the Num of the channel was measured in each step. Fig. 2 shows an assessment of the effect of mesh size on the modeling results. Tthe results do not change significantly after 980836 meshes and the results independent from grid size. Therefore, the number of networks given by x × y × z = 50 × 100 × 150 was chosen as the final network.

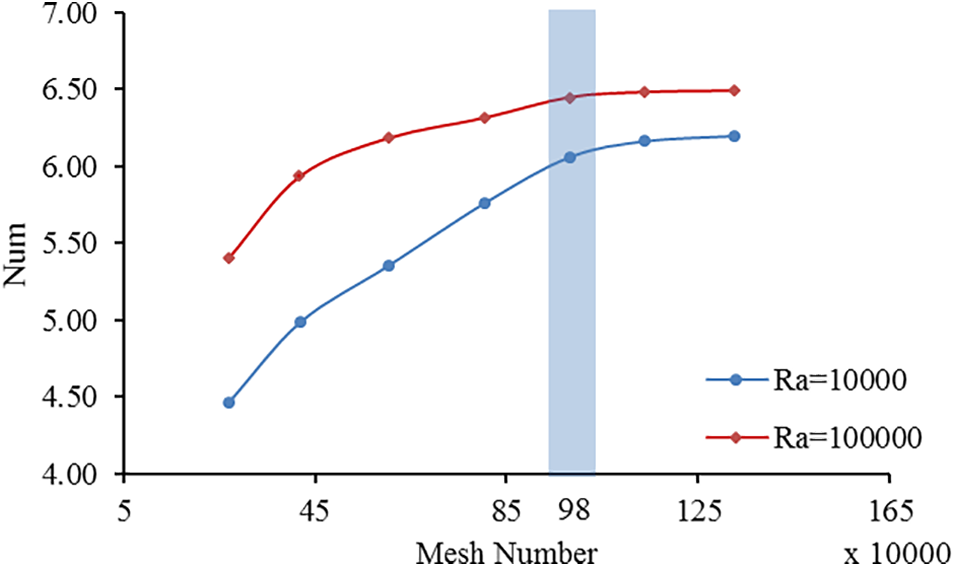
Figure 2: Assessment of the effect of mesh size on modeling results

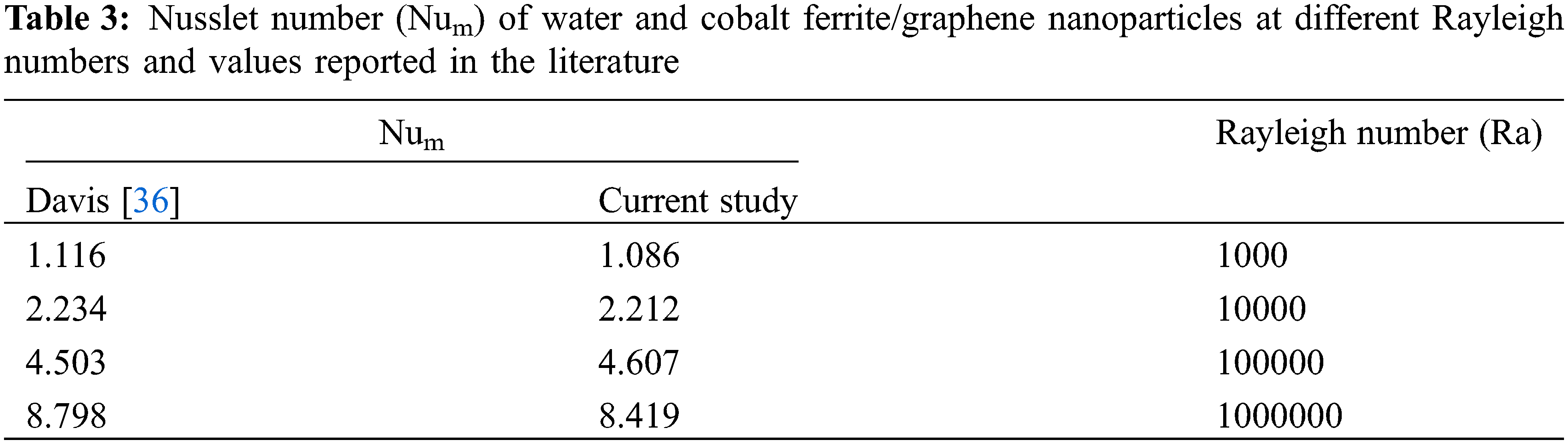
To check the solution method and ensure the correctness of the numerical results obtained from it, it was compared with the results of Davis [36], for which the agent fluid is air, and the Num of the hot wall was measured for different Rayleigh numbers, as presented in Table 3.

After being numerically stated using the finite volume approach and the SIMPLE algorithm in steady state, the nonlinear governing equations with boundary conditions are then discretized and solved. The technique of discretization used for the commutative term is the second-order high-order approach. The foundation for convergence is the total difference between the average speed and temperature in two phases of the solution, and the criteria for convergence is a difference in dimensionless terms that is less than 0.002.

3  Results and Discussion

After verifying the test apparatus with clean water, we ran experiments to see how the ferrofluid heats up under various circumstances. This section contains an analysis of the acquired findings.

Fig. 3 depicts the velocity contour in the channel’s inlet, central and outlet area, taking into account that it was assumed that entrance velocity to be uniform in the boundary conditions, so the velocity profile is almost uniform at the beginning of the entrance area due to the thinness of the boundary layer. The velocity contour in the fully developed region is shown in Fig. 3. The maximum velocity occurs at the greatest distance from the wall in this region, as the boundary layer grows to the center of the channel (at the center of the channel). By applying a magnetic field in the lower part of the channel, the fluid velocity profile under the influence of the Lorentz force (Ha = 30) can be controlled to become close to the channel’s inlet velocity profile.

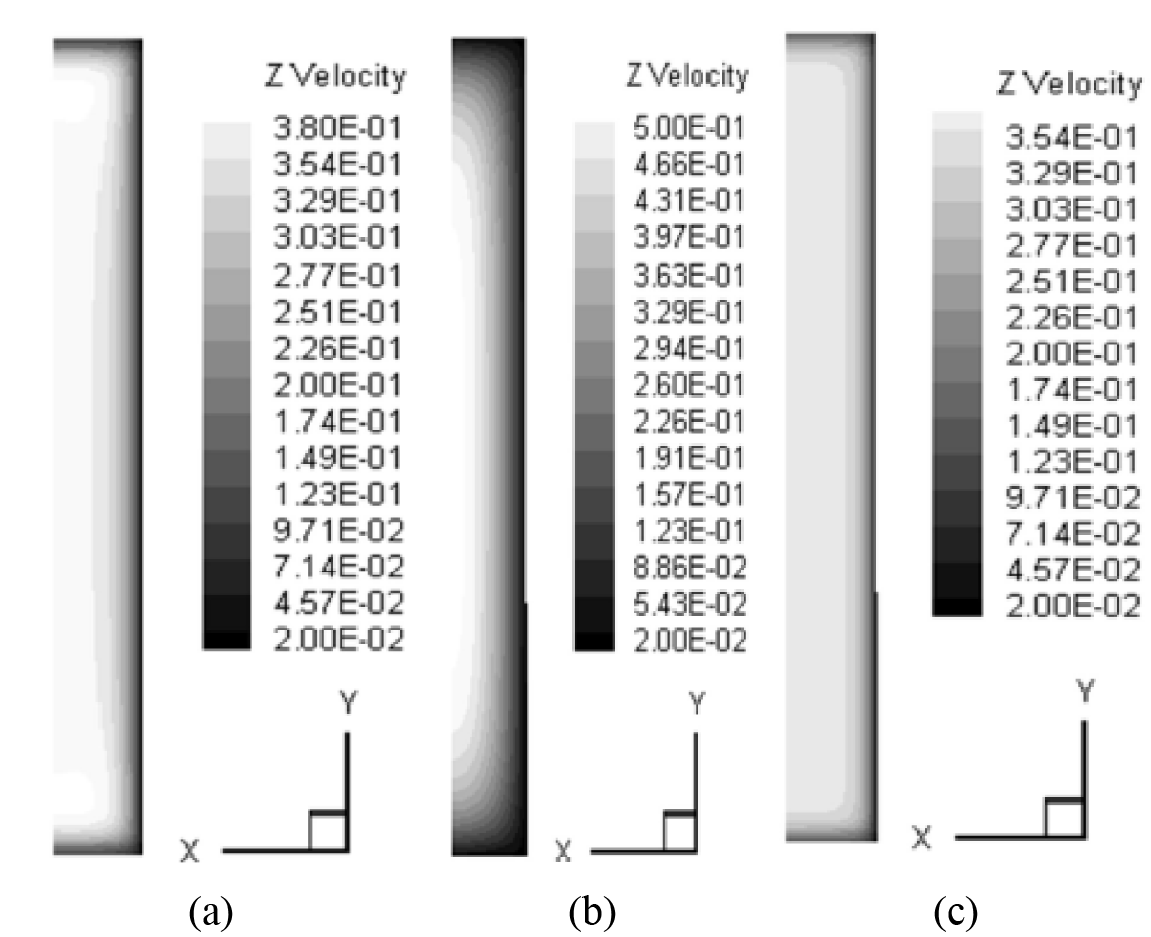
Figure 3: The velocity contour in the channel (a) inlet (b) central, and (c) outlet

In the absence of a magnetic field, a series of tests were carried out on pure water and the ferrofluid at three distinct weight concentrations (0.25%, 0.5%, and 1%), and it was done in two Reynolds numbers 550 and 1750.

Fig. 4 shows the role of magnetic nanoparticles in increasing the nanofluid, displacement heat transfer coefficient, so that displacement heat transfer improves with increasing concentration. It should be noted that the values of Num would be higher at higher Re. Since the displacement heat transfer coefficient is proportional to the thermal conductivity coefficient of the fluid, its increase by nanoparticles led to an increase in the displacement heat transfer coefficient. For instance, the average increase of Num compared to pure water was 18 and 26, respectively, in Re = 1750 with concentrations of 0.5% and 1%, respectively. It is also clear from the comparison of the two graphs that the changes in Num was greater at higher Reynolds numbers, which indicates that the heat transfer area is fully thermally developed. As can be seen from Fig. 5, increasing the concentration of nanofluid improves heat transfer, so that, the average increase in heat transfer in Re = 1750 and concentration 0.25% is 9%, which is in the concentration 1% compared to pure water, it reached 27%.

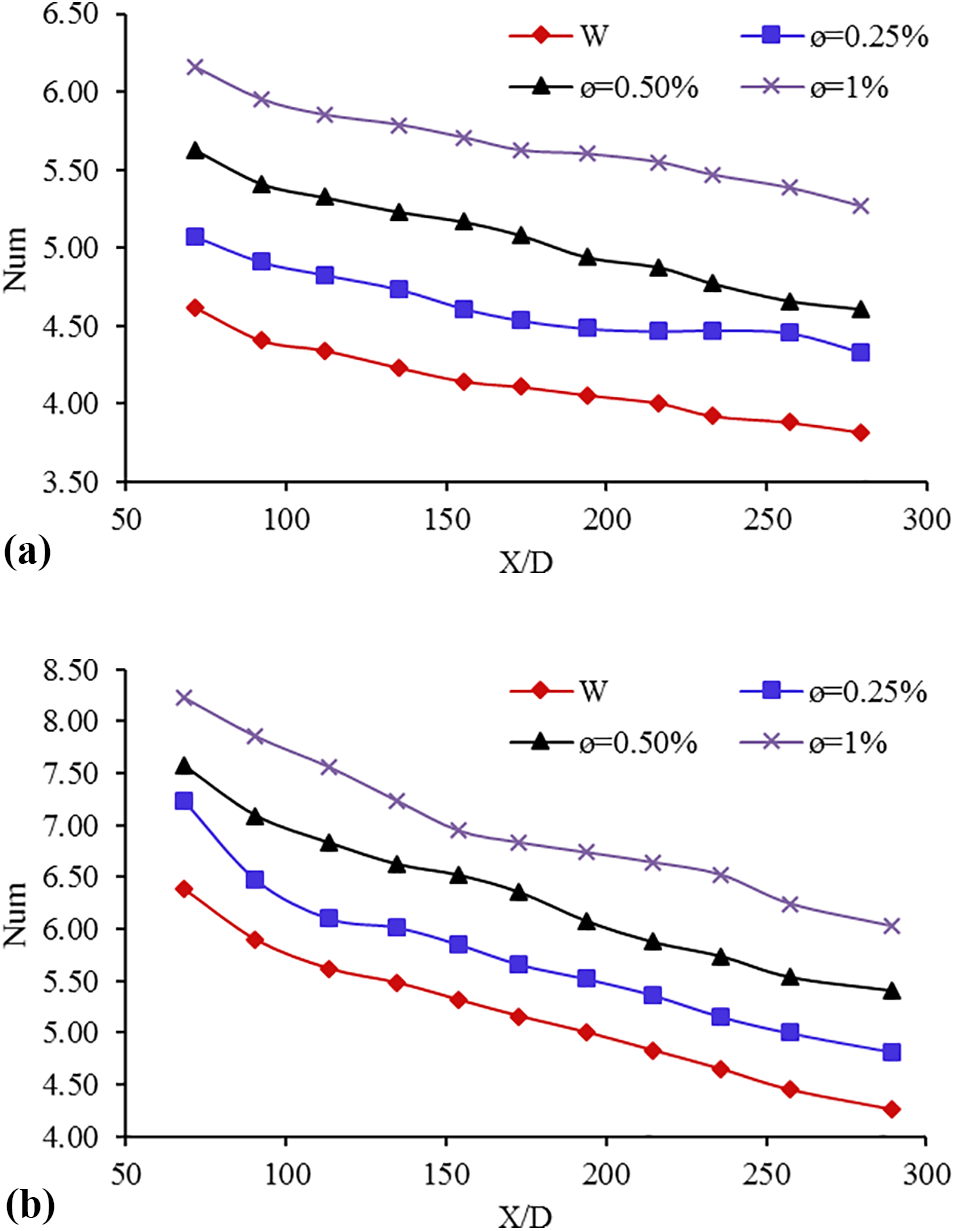
Figure 4: Changes of Num for the ferrofluid in different concentrations at (a) Re = 550 and (b) Re = 1750 in the absence of a magnetic field

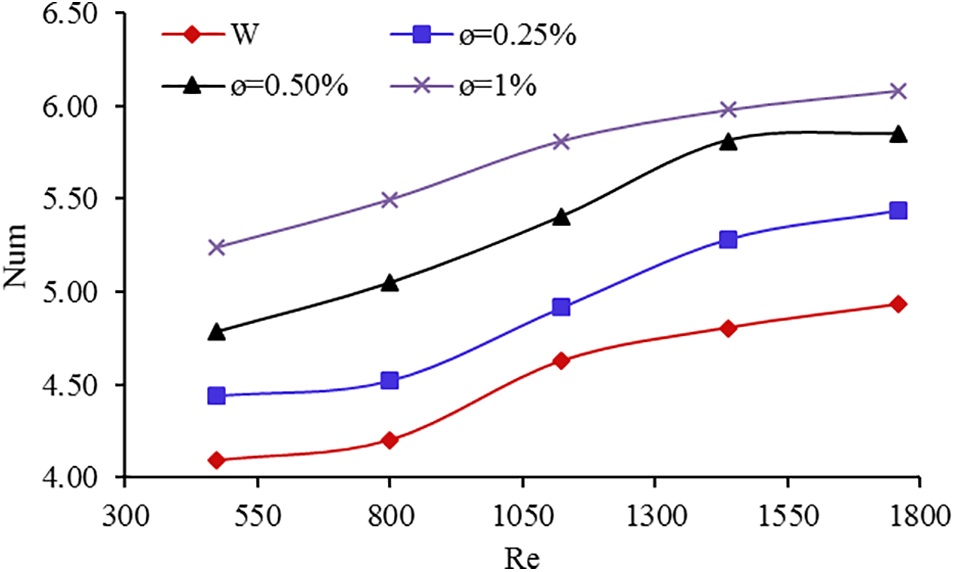
Figure 5: Average Num as a function of Re and nanoparticle concentration

An investigation of the displacement heat transfer of ferrofluid under the application of a constant and alternating magnetic field was made. A magnetic field with a maximum flux density of 800 Gauss was applied to the ferrofluid flow at Re of 550 and 1750 at concentrations of 0.5% by weight. It should be noted that the arrangement of electromagnets along the tube is such that a magnetic field is formed perpendicular to the passing nanofluid flow. In addition, to investigate the effect of the frequency of the field in the case that the alternating field is applied to the microchannel, three periodic periods equal to 0.20, 0.067 and 0.034 s have been considered, the frequency of which were 5, 15 and 30 Hz, respectively.

The impact of a constant and alternating magnetic field on the ferrofluid forced displacement heat transfer was explored. The electromagnets are arranged in this configuration such that the first electromagnet is 800 mm from the inlet and the second electromagnet is 800 mm from the outlet.

The impact of a constant and alternating magnetic field on the ferrofluid forced displacement heat transfer was explored using the configuration shown in Fig. 6. The electromagnets are arranged in this configuration such that the first electromagnet is 800 mm from the pipe’s entry and on the thermocouples T3 and T4 and three more electromagnets on both sides of the pipe, with equal distances of 100 mm and on the thermocouples T5, T6, T7, T8, T9, and T10.

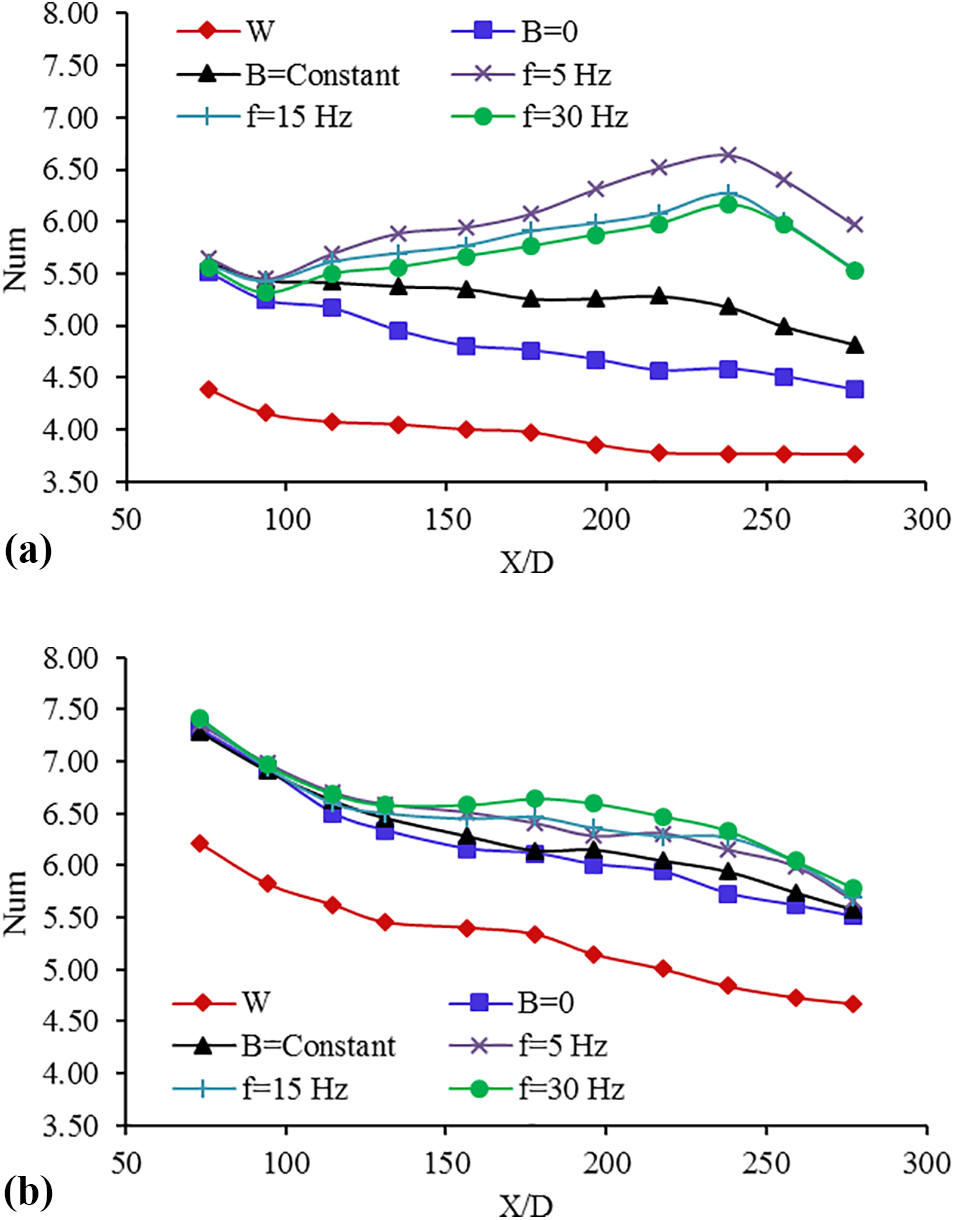
Figure 6: Variations of Num under magnetic field for (a) Re = 550 and (b) Re = 1750

To accurately examine parameters such as Re and ferrofluid concentration in the case where a magnetic field is applied, the effect of applying a constant and alternating magnetic field on the heat transfer of forced displacement in D and the case of constant concentration, variable Re and vice versa has been done. Figs. 4 and 5 show the changes in Num of the ferrofluid under constant and alternating magnetic field for the ferrofluid with a concentration of 0.5% by weight and at Re of 550, 1750.

In addition, the forced displacement heat transfer of the ferrofluid under constant and alternating fields has been investigated and compared to the absence of a magnetic field (B = 0) and the condition where pure water flows within the tube (Fig. 6). As can be seen, the application of the magnetic field has increased the heat transfer rate to the point where the local heat transfer coefficient at the site of the thermocouple T10, where the final electromagnet is placed (x/D = 243.2) is the highest. The displacement heat transfer coefficient then declines and approaches the value of the displacement heat transfer coefficient in the absence of a field (B = 0).

Because the displacement heat transfer coefficient is proportional to the thermal conductivity coefficient and inversely proportional to the thickness of the thermal boundary layer, the forced displacement heat transfer can be increased in two ways: increasing the thermal conductivity coefficient fluid and decreasing the thickness of the thermal boundary layer. As a result, when the ferrofluid passes through the area of the tube affected by the magnetic field, the nanoparticles are drawn to the surface of the tube by the Kelvin magnetic force. The transport of particles towards the wall and their aggregation in this region increases the ferrofluid concentration in this area, resulting in a local increase in the thermal conductivity coefficient and, as a consequence, an increase in forced displacement heat transfer.

It was deduced from Fig. 6 that when the Re increases, the influence of the magnetic field on enhancing the heat transfer rate diminishes. For example, at Re 550, the highest heat transfer increase relative to the ferrofluid in the absence of a magnetic field is 20.9%, whereas this figure drops to 11.3% at Re 1750. The reason for this reduction can be inferred from the fact that at low Re, magnetic nanoparticles move at a slower rate, giving the magnetic field enough time to exert a magnetic force on the nanoparticles and attract them to the wall, causing the disturbance of the layer’s boundary to be greater.

In addition, we reasoned that the increase in the heat transfer rate under the alternating field by switching the magnetic field off and on, the nanoparticles practically cannot accumulate near the wall and for this reason, the viscosity of the ferrofluid has not increased or the increase in viscosity is not significant.

It should be mentioned that in some research, the application of a constant magnetic field has led to a decrease in the heat transfer rate, or at least it has not had a significant effect. While in some other research, the application of this type of field has resulted in an increase in the heat transfer coefficient. By examining these research, it seems that three factors including thermal conductivity coefficient, boundary layer thickness and ferrofluid viscosity are effective in increasing or decreasing the heat transfer rate of ferrofluid displacement under constant magnetic field.

The increase in thermal conductivity caused by nanoparticle accumulation near the wall and the decrease in the thickness of the thermal boundary layer leads to an increase in the displacement heat transfer coefficient, whereas the increase in the viscosity of the ferrofluid caused by the application of a constant field and, as a result, a decrease in the speed of the fluid flow, leads to a decrease in the heat transfer coefficient. Meanwhile, some researchers believe that when the magnetic field intensity is low, viscosity is the dominant factor, and thus heat transfer is reduced under a constant magnetic field, whereas when the intensity is high, the coefficient of thermal conductivity and the thickness of the boundary layer, two factors, are important. They are regarded as the critical parameters in terms of boosting the heat transfer rate.

Furthermore, they reasoned that the increase in heat transfer rate under the alternating field by switching the magnetic field off and on, the nanoparticles virtually cannot concentrate near the wall, and therefore the viscosity of the ferrofluid has not risen or is not substantial. As a result, the negative impact of viscosity increase is thought to be less than the beneficial effect of disruption of the negative boundary layer. The action of a steady magnetic field, however, raises the concentration of nanofluid in this location, increases the local coefficient of thermal conductivity, and therefore enhances the forced displacement heat transfer.

On the other hand, the accumulation of nanoparticles near the wall acts as an obstacle against the flow of the ferrofluid and causes disturbances in the thermal boundary layer, which leads to an increase in heat transfer under a constant magnetic field and also causes changes and disturbances in the thermal boundary layer and shape, and the flow and heat transfer will increase further. While in magnetic fields with higher intensity, increasing the thermal conductivity coefficient and reducing the thickness of the boundary layer are the main reasons for increasing the heat transfer rate.

4  Conclusions

In the absence of a magnetic field, the use of magnetic nanoparticles leads to the improvement of the heat transfer coefficient of the ferrofluid displacement. In addition, under the application of a constant and alternating magnetic field, the displacement heat transfer is improved in such a way that this increase is greater in the case where the field is of an oscillating type. It should be mentioned that this improvement is more at lower Re and higher weight concentrations. A decrease in the strength of the magnetic field causes a decrease in the changes in the thermal conductivity coefficient and the thickness of the thermal boundary layer, and as a result, it results in less improvement in heat transfer. Heat transfer under the effect of a constant magnetic field increases with increasing Re, but with alternating magnetic field, it depends on both the Re and field frequency. At each Re, there is an optimal value for the field frequency at which the heat transfer reaches its maximum value. The optimal frequency depends on the Re and increases with the increase of the Re. Also, the optimal frequency is independent of the intensity of the magnetic field. Forced displacement heat transfer under the effect of constant and alternating magnetic field increases with increasing nanofluid concentration and magnetic field intensity.

It may also be said that, at the beginning of the channel, owing to the substantial pressure variations caused by the expansion of the boundary layer, the pressure difference force applied in this area is considerable. Because the frictional force is constant owing to the constant channel cross-section, the Poisson number begins with a very high value and achieves a constant limit value after the developed area. By introducing a magnetic field, and keeping in mind that the magnetic field’s force is directed against the flow, the pressure gradient along the channel rises abruptly in order to maintain the flow rate and, as a result, the average speed.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Muataz S. Alhassan, Azher M. Abed, Ameer A. Alameri; data collection: Andrés Alexis Ramírez-Coronel, I. B. Sapaev; analysis and interpretation of results: Muataz S. Alhassan, David-Juan Ramos-Huallpartupa, Andrés Alexis Ramírez-Coronel; draft manuscript preparation: Rahman S. Zabibah, Azher M. Abed. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Fu, L., Liao, K., Tang, B., Jiang, L., Huang, W. (2020). Applications of graphene and its derivatives in the upstream oil and gas industry: A systematic review. Nanomaterials, 10(6), 1013. [Google Scholar] [PubMed]

2. Razali, S. Z., Yunus, R., Kania, D., Rashid, S. A., Ngee, L. H. et al. (2022). Effects of morphology and graphitization of carbon nanomaterials on the rheology, emulsion stability, and filtration control ability of drilling fluids. Journal of Materials Research and Technology, 21, 2891–2905. [Google Scholar]

3. Balandin, A. A. (2011). Thermal properties of graphene and nanostructured carbon materials. Nature Materials, 10(8), 569–581. [Google Scholar] [PubMed]

4. Kanti, P., Sharma, K. V., Khedkar, R. S., Rehman, T. (2022). Synthesis, characterization, stability, and thermal properties of graphene oxide based hybrid nanofluids for thermal applications: Experimental approach. Diamond and Related Materials, 128, 109265. [Google Scholar]

5. Tekir, M., Taskesen, E., Aksu, B., Gedik, E., Arslan, K. (2020). Comparison of bi-directional multi-wave alternating magnetic field effect on ferromagnetic nanofluid flow in a circular pipe under laminar flow conditions. Applied Thermal Engineering, 179, 115624. [Google Scholar]

6. Rauf, A., Mushtaq, A., Shah, N. A., Botmart, T. (2022). Heat transfer and hybrid ferrofluid flow over a nonlinearly stretchable rotating disk under the influence of an alternating magnetic field. Scientific Reports, 12(1), 17548. [Google Scholar] [PubMed]

7. Olia, H., Torabi, M., Bahiraei, M., Ahmadi, M. H., Goodarzi, M. et al. (2019). Application of nanofluids in thermal performance enhancement of parabolic trough solar collector: State-of-the-art. Applied Sciences, 9(3), 463. [Google Scholar]

8. Raouf, I., Lee, J., Kim, H. S., Kim, M. H. (2021). Parametric investigations of magnetic nanoparticles hyperthermia in ferrofluid using finite element analysis. International Journal of Thermal Sciences, 159, 106604. [Google Scholar]

9. Kole, M., Khandekar, S. (2021). Engineering applications of ferrofluids: A review. Journal of Magnetism and Magnetic Materials, 537, 168222. [Google Scholar]

10. Safaei, M. R., Hajizadeh, A., Afrand, M., Qi, C., Yarmand, H. et al. (2019). Evaluating the effect of temperature and concentration on the thermal conductivity of ZnO-TiO2/EG hybrid nanofluid using artificial neural network and curve fitting on experimental data. Physica A: Statistical Mechanics and its Applications, 519, 209–216. [Google Scholar]

11. Giwa, S. O., Sharifpur, M., Ahmadi, M. H., Meyer, J. P. (2021). A review of magnetic field influence on natural convection heat transfer performance of nanofluids in square cavities. Journal of Thermal Analysis and Calorimetry, 145, 2581–2623. [Google Scholar]

12. Tekir, M., Gedik, E., Arslan, K., Kadir Pazarlıoğlu, H., Aksu, B. et al. (2022). Hydrothermal behavior of hybrid magnetite nanofluid flowing in a pipe under bi-directional magnetic field with different wave types. Thermal Science and Engineering Progress, 34, 101399. [Google Scholar]

13. Tekir, M., Taskesen, E., Gedik, E., Arslan, K., Aksu, B. (2022). Effect of constant magnetic field on Fe3O4-Cu/water hybrid nanofluid flow in a circular pipe. Heat and Mass Transfer, 58(5), 707–717. [Google Scholar]

14. Altunay, F. M., Pazarlıoğlu, H. K., Gürdal, M., Tekir, M., Arslan, K. et al. (2022). Thermal performance of FeO/water nanofluid flow in a newly designed dimpled tube under the influence of non-uniform magnetic field. International Journal of Thermal Sciences, 179, 107651. [Google Scholar]

15. Sezer, N., Atieh, M. A., Koç, M. (2019). A comprehensive review on synthesis, stability, thermophysical properties, and characterization of nanofluids. Powder Technology, 344, 404–431. [Google Scholar]

16. Jang, S. P., Choi, S. U. S. (2004). Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Applied Physics Letters, 84(21), 4316–4318. [Google Scholar]

17. Shima, P. D., Philip, J., Raj, B. (2009). Role of microconvection induced by Brownian motion of nanoparticles in the enhanced thermal conductivity of stable nanofluids. Applied Physics Letters, 94(22), 223101. [Google Scholar]

18. Sadeghzadeh, M., Maddah, H., Ahmadi, M. H., Khadang, A., Ghazvini, M. et al. (2020). Prediction of thermo-physical properties of TiO2-Al2O3/water nanoparticles by using artificial neural network. Nanomaterials, 10(4), 697. [Google Scholar] [PubMed]

19. Shahsavar, A., Salimpour, M. R., Saghafian, M., Shafii, M. B. (2015). An experimental study on the effect of ultrasonication on thermal conductivity of ferrofluid loaded with carbon nanotubes. Thermochimica Acta, 617, 102–110. [Google Scholar]

20. Skumiel, A., Józefczak, A., Hornowski, T., Abowski, M. (2003). The influence of the concentration of ferroparticles in a ferrofluid on its magnetic and acoustic properties. Journal of Physics D: Applied Physics, 36(24), 3120–3124. [Google Scholar]

21. Bezaatpour, M., Goharkhah, M. (2019). Effect of magnetic field on the hydrodynamic and heat transfer of magnetite ferrofluid flow in a porous fin heat sink. Journal of Magnetism and Magnetic Materials, 476, 506–515. [Google Scholar]

22. Gan Jia Gui, N., Stanley, C., Nguyen, N. T., Rosengarten, G. (2018). Ferrofluids for heat transfer enhancement under an external magnetic field. International Journal of Heat and Mass Transfer, 123, 110–121. [Google Scholar]

23. Shahsavar, A., Jamei, M., Karbasi, M. (2021). Experimental evaluation and development of predictive models for rheological behavior of aqueous Fe3O4 ferrofluid in the presence of an external magnetic field by introducing a novel grid optimization based-Kernel ridge regression supported by sensitivity. Powder Technology, 393, 1–11. [Google Scholar]

24. Soudagar, M. E. M., Nik-Ghazali, N. N., Abul Kalam, M., Badruddin, I. A., Banapurmath, N. R. et al. (2018). The effect of nano-additives in diesel-biodiesel fuel blends: A comprehensive review on stability, engine performance and emission characteristics. Energy Conversion and Management, 178, 146–177. [Google Scholar]

25. Ghazvini, M., Maddah, H., Peymanfar, R., Ahmadi, M. H., Kumar, R. (2020). Experimental evaluation and artificial neural network modeling of thermal conductivity of water based nanofluid containing magnetic copper nanoparticles. Physica A: Statistical Mechanics and its Applications, 551, 124127. [Google Scholar]

26. Taşkesen, E., Tekir, M., Pazarlıoğlu, H. K., Gurdal, M., Gedik, E. et al. (2023). The effect of MHD flow on hydrothermal characteristics of ferro-nano-fluid in circular pipe. Experimental Heat Transfer, 36(5), 617–631. https://doi.org/10.1080/08916152.2022.2065384 [Google Scholar] [CrossRef]

27. Gürdal, M., Pazarlıoğlu, H. K., Tekir, M., Arslan, K., Gedik, E. et al. (2023). Experimental investigation on thermo hydraulic performance of ferronanofluid flow in a dimpled tube under magnetic field effect. Experimental Heat Transfer, 36(3), 312–330. https://doi.org/10.1080/08916152.2022.2027575 [Google Scholar] [CrossRef]

28. Gürdal, M., Pazarlıoğlu, H. K., Tekir, M., Altunay, F. M., Arslan, K. et al. (2022). Implementation of hybrid nanofluid flowing in dimpled tube subjected to magnetic field. International Communications in Heat and Mass Transfer, 134, 106032. [Google Scholar]

29. Qureshi, M. A., Hussain, S., Sadiq, M. A. (2021). Numerical simulations of MHD mixed convection of hybrid nanofluid flow in a horizontal channel with cavity: Impact on heat transfer and hydrodynamic forces. Case Studies in Thermal Engineering, 27, 101321. [Google Scholar]

30. Bezaatpour, M., Rostamzadeh, H., Bezaatpour, J. (2021). Hybridization of rotary absorber tube and magnetic field inducer with nanofluid for performance enhancement of parabolic trough solar collector. Journal of Cleaner Production, 283, 124565. [Google Scholar]

31. Namburu, P. K., Das, D. K., Tanguturi, K. M., Vajjha, R. S. (2009). Numerical study of turbulent flow and heat transfer characteristics of nanofluids considering variable properties. International Journal of Thermal Sciences, 48(2), 290–302. [Google Scholar]

32. Malvandi, A., Ganji, D. D. (2015). Effects of nanoparticle migration and asymmetric heating on magnetohydrodynamic forced convection of alumina/water nanofluid in microchannels. European Journal of Mechanics—B/Fluids, 52, 169–184. [Google Scholar]

33. Pakravan, H. A., Yaghoubi, M. (2013). Analysis of nanoparticles migration on natural convective heat transfer of nanofluids. International Journal of Thermal Sciences, 68, 79–93. [Google Scholar]

34. Naphon, P., Wiriyasart, S. (2017). Pulsating TiO2/water nanofluids flow and heat transfer in the spirally coiled tubes with different magnetic field directions. International Journal of Heat and Mass Transfer, 115, 537–543. [Google Scholar]

35. Ghofrani, A., Dibaei, M. H., Hakim Sima, A., Shafii, M. B. (2013). Experimental investigation on laminar forced convection heat transfer of ferrofluids under an alternating magnetic field. Experimental Thermal and Fluid Science, 49, 193–200. [Google Scholar]

36. de Vahl Davis, G. (1983). Natural convection of air in a square cavity: A bench mark numerical solution. International Journal for Numerical Methods in Fluids, 3(3), 249–264. [Google Scholar]