 Open Access
Open Access
ARTICLE
Enhancing Thermal Performance of Building Envelopes Using Hemp Wool and Wood Wool with Phase Change Materials
1 Laboratory of Energy, Faculty of Sciences of Tetuan, University of Abdelmalek Essaadi, Tetuan, 93002, Morocco
2 LEM3, ENIM, University of Lorraine, Metz, 57078, France
3 LERMAB, IUT Henri Poincaré de Longwy, University of Lorraine, Longwy, 54400, France
* Corresponding Author: Salma Kouzzi. Email:
(This article belongs to the Special Issue: Materials and Energy an Updated Image for 2023)
Fluid Dynamics & Materials Processing 2024, 20(12), 2741-2755. https://doi.org/10.32604/fdmp.2024.055890
Received 09 July 2024; Accepted 21 August 2024; Issue published 23 December 2024
Abstract
This study investigates the potential for enhancing the thermal performance of external walls insulation in warmer climates through the combination of phase change materials (PCMs) and bio-based materials, specifically hemp wool and wood wool. Experimental tests using the heat flow method (HFM), and numerical simulations with ANSYS Fluent software were conducted to assess the dynamic thermal distribution and fluid-mechanical aspects of phase change materials (PCMs) within composite walls. The results demonstrate a notable reduction in peak indoor temperatures, achieving a 58% reduction with hemp wool with a close 40% reduction with wood wool when combined with PCMs. Fluid-mechanical analysis indicates that PCMs act as efficient indoor temperature regulators by storing excess heat during hot periods and releasing it later during phase transitions. Furthermore, the homogeneous distribution of the liquid fraction and natural convection during phase change contribute significantly to the improvement in heat transfer rates, resulting in a 96% reduction compared to hemp wool and wood wool without PCMs.Keywords
Nomenclature
| | Density |
| | Thermal conductivity ( |
| | Temperature (K) |
| Ts | Solidus temperature (K) |
| Tl | Liquidus temperature (K) |
| | Outside temperature |
| | Inside temperature |
| t | Time (s) |
| Cp | Specific heat capacity (J/(kg.K)) |
| L | Latent heat (kJ/kg) |
| | Thickness |
| HW | Hemp Wool |
| WW | Wood Wool |
| PCM | Phase Change Materials |
| HFM | Heat Flow Method |
The future of energy and sustainable construction is a growing area of interest and concern. According to the IEA’s “World Energy Outlook 2022” report [1], enhancing the energy efficiency of buildings is crucial for achieving greenhouse gas emission reduction targets and combating climate change. The Global State of Buildings and Construction Report 2022 [2] indicates that the building sector contributes almost 40% of global energy consumption and about one-third of greenhouse gas emissions.
Various studies have focused on evaluating and improving the energy consumption of buildings by reducing heating and cooling needs. Hoseinzadeh et al. [3] underlined the importance of implementing specific strategies based on geographical and climatic conditions to achieve energy-saving improvements in buildings located in a mountainous, humid zone.
Researchers have evaluated insulation materials used in buildings to address energy losses through building envelopes. They highlight the importance of selecting appropriate insulation materials to enhance energy performance, taking into account their environmental aspects [4], and examining thermal inertia and insulation effectiveness in building structures [5].
The use of phase-change material (PCM) in exterior walls has been explored for their energy efficiency and CO2 emissions reduction benefits [6], as well as their potential in enhancing thermal regulation in specific climatic conditions [7]. Research on PCMs demonstrates their ability to store and release substantial thermal energy, thereby attenuating temperature variations in buildings and reducing energy consumption [8]. El-Ganaoui et al. [9] have provided innovative analytical solutions to heat transfer problems involving phase changes and interfaces, forming the basis for numerous advances. Recent advancements in PCM technology highlight their potential for storing thermal energy in buildings [10,11]. Hekimoğlu et al. [12] noted the integration of PCMs into building cooling systems, which reduces the thermal load on air-conditioning systems and minimizes energy consumption, while Zhan et al. [13] focused on the integration of PCMs in buildings in hot climates.
Anter et al. [14] demonstrated the efficiency of integrating PCMs into building walls for thermal energy savings, highlighting the importance of optimizing the design, choice, and quantity of PCMs to maximize thermal benefits. M’hamdi et al. [15] analyzed the energy, environmental, and economic impacts of different building envelopes incorporating PCMs in different climates, showing that PCMs can reduce energy consumption and carbon emissions while offering economic benefits [16,17].
The potential of bio-based materials to enhance the sustainability and energy efficiency of buildings has also been studied [18–20]. These materials have demonstrated promising thermal and hygrothermal performances [21,22] and a low carbon footprint [23,24]. Using bio-based materials with PCMs improves energy performance in buildings [25], but careful assessment of their hygrothermal behavior is essential to prevent building deterioration [26,27].
Researchers have explored the combined use of PCMs with other insulating materials to enhance energy efficiency, such as dynamic insulation boards [28] and recycled waste paper in building enclosures, demonstrating potential for improved thermal performance and sustainability [29].
Recent studies have tackled the importance of fluid dynamics in these systems. Numerical simulations by Wang et al. [30] explored the coupling between solid-liquid phase change and thermal flow, providing valuable insights into fluid behavior in these materials. These studies also underline the crucial role of convection in the behavior of PCMs, as demonstrated by Lappa [31], with significant impacts on boundary conditions, material properties, and the integration of nanoparticles. A multi-physics modeling approach that considers the interactions between heat, mass, and fluid movement is necessary to study natural convection phenomena and heat transfer in phase change materials.
Optimizing material configurations is vital for maximizing building energy efficiency [32]. The application of new technologies, numerical modeling, and advanced simulation methods like Computational Fluid Dynamics (CFD) have been used to analyze and optimize thermal performance and design in buildings [33].
Zhou et al. [34] used CFD modeling to validate the thermal performance of dynamic Trombe walls incorporating PCMs, providing a better understanding of heat flows and more efficient solutions.
Integration PCMs and bio-based materials with advanced modeling techniques has shown promise in improving building efficiency [35]. Khoukhi et al. [36] focused on the effect of varying the dynamic thermal conductivity of insulation materials on temperature variation across wall assemblies.
While PCMs may have varying thermal performance depending on environmental conditions, they may be less effective in extreme climates or environments with minimal temperature variations [37]. To achieve thermal performance equivalent to conventional insulating materials, bio-based materials may require a greater thickness of insulating panels [38].
The importance of thermal performance in building envelopes is well-recognized for its impact on energy efficiency and occupant comfort. Traditional insulation materials often fail to provide adequate thermal regulation, especially in warmer climates.
While numerous studies have explored the use of PCMs and bio-based materials individually for thermal regulation, there is a significant research gap exploring the synergistic effects of combining these materials to maximize their benefits.
This article addresses this gap by investigating the potential benefits of combining PCMs with biobased insulation materials, specifically Wood Wool (WW) and Hemp Wool (HW), in building envelopes to enhance thermal performance. By exploring the latent heat storage capabilities of PCMs and the natural insulating properties of bio-based materials, this research aims to develop sustainable and efficient insulation solutions.
This study’s novelty lies in the experimental and numerical analysis of these composite materials, providing valuable insights into their thermal behavior and practical applications. The research subjects the wall to a sinusoidal outside temperature, simulating typical summer day weather in Morocco, through experimental analysis using the heat flow method and numerical simulations using ANSYS Fluent software. The study provides insights into the dynamic thermal distribution within the insulation wall, with thorough assessment of the thermal performance and fluid mechanical aspects associated with the transition phase change of the different scenarios to determine indoor temperature reduction and heat transfer decrease.
The Heat Flow Method (HFM) [39] experimental study investigates two different external wall insulation configurations using HW as the main material for its numerous advantages and thermal properties. The study also explores the impact of adding PCM on temperature variation to take advantage of its thermal storage capacity for regulating internal temperature.
HW, with its low thermal conductivity, helps limit heat transmission through walls, ultimately reducing the need for heating and cooling and lowering energy costs. PCM materials have the ability to store and release large amounts of heat energy by transitioning between solid and liquid phases. The study will analyze the thermal properties of HW and the effects of PCM integration, aiming to enhance insulation designs and optimize the thermal performance of buildings.
The experiments focused on the thermal distribution within the external insulation wall. The heat flow method was utilized by placing the sample between two isothermal aluminum heat exchange plates connected to thermostatically controlled water baths [40], as illustrated in Fig. 1.
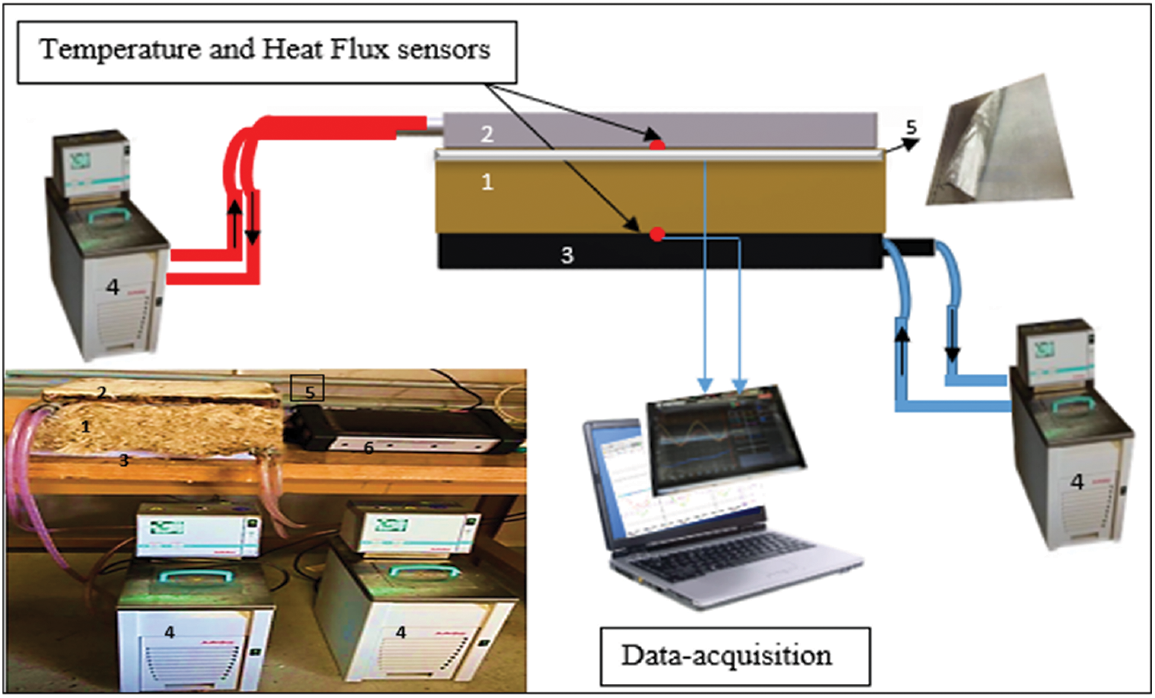
Figure 1: Experimental setup of HFM. 1: Insulation sample, 2: Isothermal heat exchange plate
The thermal response of the wall with and without the PCM layer was examined by collecting temperature measurements
The heat flux is monitored by HFS sensors with dimensions of 50 × 50 × 0.5 mm3; on the upside and underside of the sample.
In Case 1 of the experiment, the sample consisted of HW (30 × 30 × 7
The upper part of the specimen underwent temperature variations ranging from 20°C to 40°C over time, following a sinusoidal pattern described in Eq. (8), while the temperature of the lower part remained constant at 22°C throughout the experiment. Data was collected at 60 s intervals over a 24 h period.
The distribution of temperature in a wall due to heat transfer by conduction in a transient regime is determined by the heat equation, also known as the thermal diffusion equation. This equation illustrates how temperature changes over time and space based on the thermal properties of the material. The simplified form of the basic linear heat Eq. (1), according to Fourier’s law, is typically written as:
where the
In the case of phase change material (PCM), such as melting/solidification phenomena, additional considerations and equations may be required:
The heat equation with convection become:
where u is the velocity vector of the fluid. If the dynamic field is concerned, additional melting/solidification model can be added, using well known models as Darcy law and other approximations to take into account the fluid flowing only in the liquid zone.
The simulation was conducted using ANSYS Fluent student version 2023 R2 software [44], allowing to analyze the temperature, velocity, liquid fraction and heat flux within PCM + (HW and WW) during phase change processes.
To model the temperature distribution using the heat Eq. (1), numerical methods, and assumptions about the wall material subjected to transient unidirectional heat transfer were taken into account [45,46].
The simulation of fluid flow and heat transfer in PCMs involves solving the Navier-Stokes equations Eq. (5) for fluid motion, coupled with the energy equation for heat transfer. Here, we consider the Boussinesq approximation for natural convection, which assumes that density variations are significant only in the buoyancy term.
The continuity, momentum, and energy equations for an incompressible fluid with phase change are as follows:
Continuity Equation:
Momentum Equation (Navier-stokes):
where P is the pressure,
To model the phase change, the enthalpy-porosity technique is often used. In this method, the liquid fraction fs is determined based on the temperature field:
Energy Equation with phase change:
where Ts and Tl are the solidus and liquidus temperatures, respectively.
Heat transfer analysis of the wall envelope was simulated by the user-defined function (UDF) representing outdoor temperature variation on a typical summer day, modeled as a sinusoidal temperature oscillation.
Here t is the time, and
The temperature evolution T (x, t) in the model was studied under certain assumptions [47]. These assumptions include considering laminar flow, neglecting radiation effects due to slow temperature changes, assuming adiabatic horizontal walls, and considering walls to be homogeneous and isotropic. In addition, the model assumes that the thermal properties of the material are constant in space and time and that there are no internal heat sources. These assumptions provide a simplified framework for understanding the temperature distribution within the system.
Boundary conditions for this case require a specific value to be specified, with both the external wall and inner wall having a Dirichlet condition as the type of boundary condition imposed.
Boundary conditions
The bottom and top of the insulation wall are adiabatic:
The temperature at x = 0 is
The finite element method (FME) is used to solve these equations with ANSYS Fluent by discretizing the heat equations and solving them numerically on a mesh of the wall to determine the temperature distribution.
Geometric modeling was performed using the Design Modeler tool in ANSYS software. The study considered four different wall scenarios, as shown in Fig. 2. A quadratic mesh was then generated, comprising 40,000 elements for PCM/HW and PCM/WW, and 35,000 elements for HW or WW.
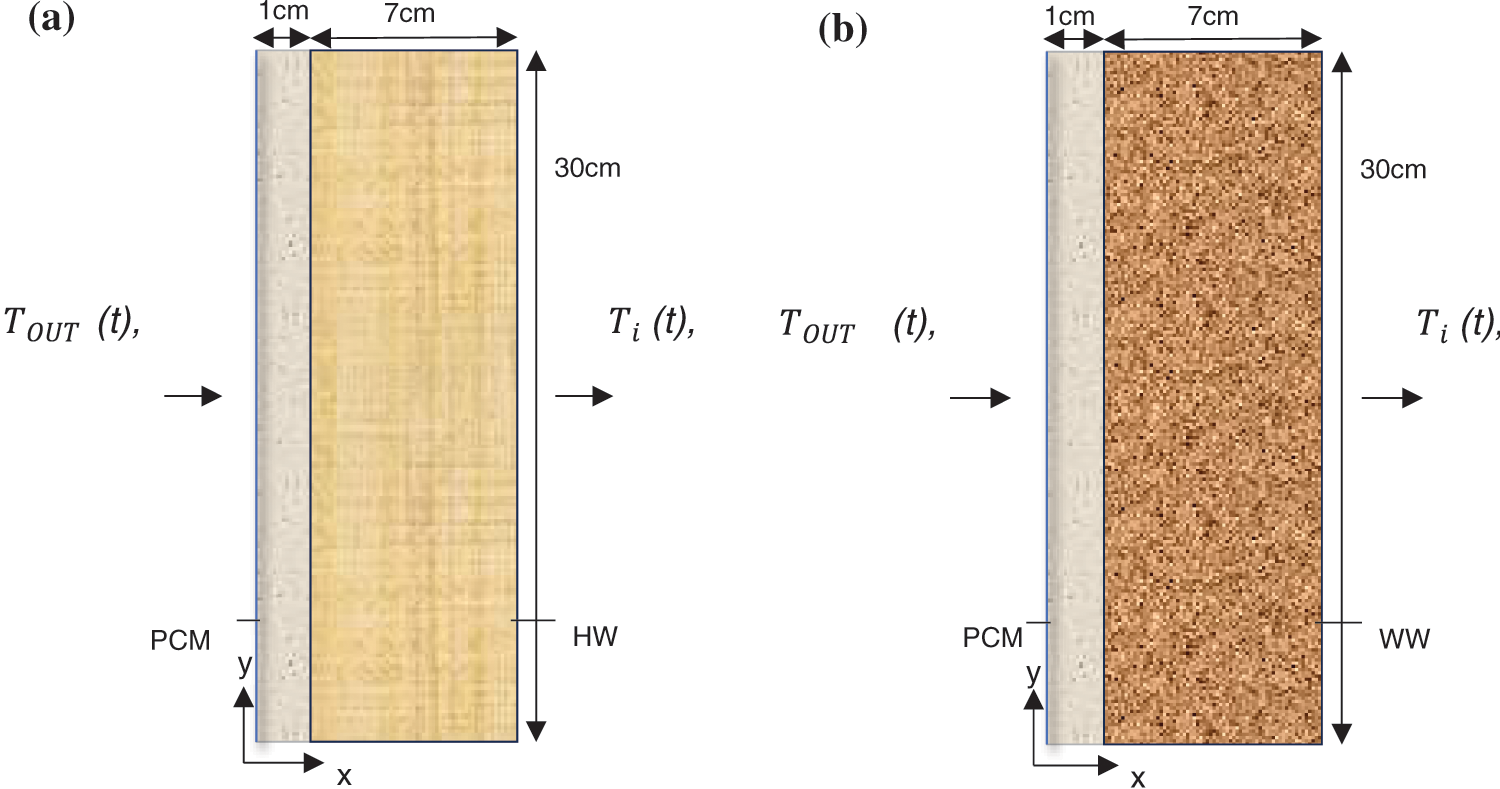
Figure 2: The schematic heat transfer of the insulation wall: (a) PCM + HW, (b) PCM + WW
Simulations were solved using a pressure-based and transient solver configured with implicit pressure and coupled operator splitting, along with a second-order upwind scheme.
Running the simulation allowed for calculating the temperature distribution across the walls and plotting the temperature evolution inside the wall over a 24 h period to analyze heat transfer through the wall.
In the present study, simulation results were compared with experimental data for validation purposes, using two plates with imposed temperatures, one simulating outdoor conditions and the other indoor conditions. The test involved an envelope containing a 7-cm-thick layer of HW (Case 1). Subsequently, a multi-layer envelope was examined, consisting of a 1 cm layer of PCM added to the HW (Case 2). The dimensions of these configurations were 30 × 30 × 7 cm3 and 30 × 30 × 8 cm3, respectively.
Fig. 3 depicts the measured temperature vs. time for HW and PCM_HW on the top (x = 0) and bottom (x = e) surfaces of the sample in comparison with simulation results, where x = 0 represents outdoor conditions and x = e represents indoor temperature. To validate the simulated results, the average error (AE) was calculated using Eq. (10):
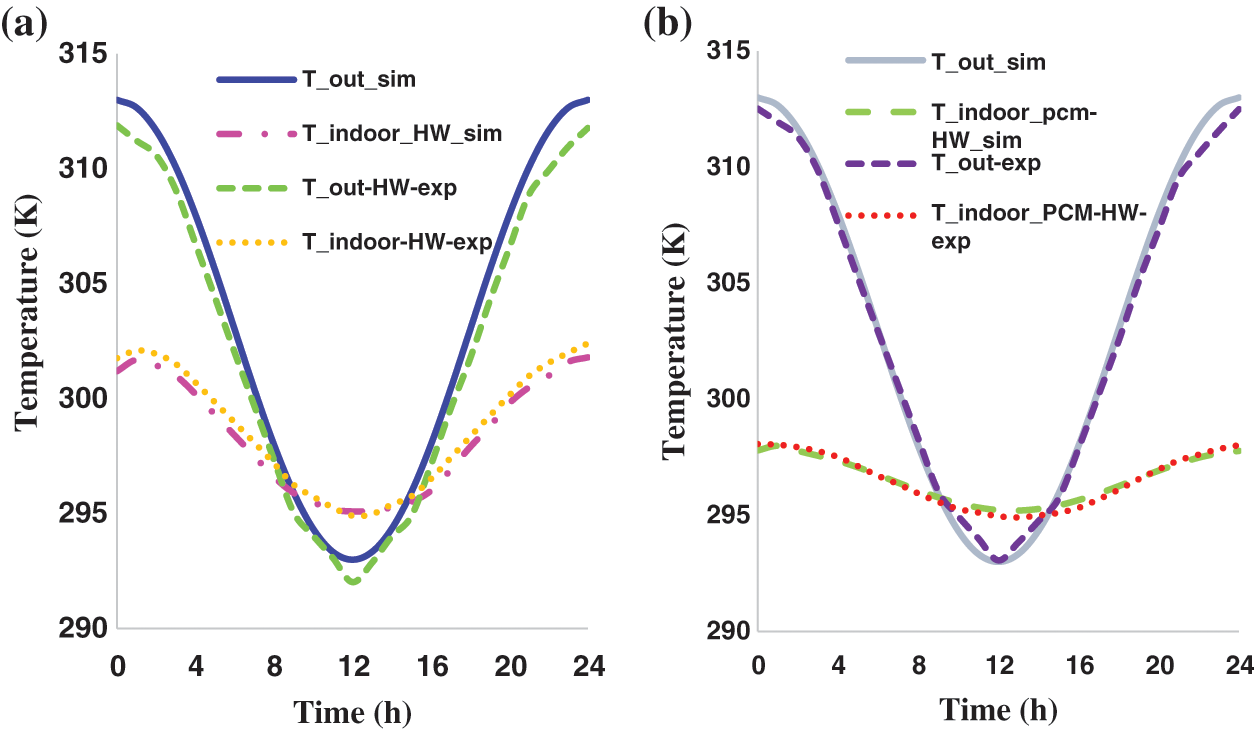
Figure 3: Comparison between the simulated and experimental temperature results for (a) HW and (b) HW with PCM
The average error of the numerical model is 0.14% in the first case and 0.06% in the second case. The small discrepancies between the experimental and numerical results may be attributed to the infiltration of free air into the HW layers. These low relative errors demonstrate the accuracy of the numerical model compared to the experiment, affirming its validity and reliability for further studies.
A 24 h test was conducted on a typical summer day using a reference insulating wall made of WW (Case 3). Subsequently, a similar test was performed by adding a layer of PCM (Case 4). Both tests were carried out utilizing ANSYS Fluent and adhering to the same numerical methodology outlined previously.
Fig. 4 compares the experimental and simulated heat fluxes for PCM + HW over 24 h period. Both data sets show similar profiles, with an initial peak (initial phase change), followed by a significant decrease with negative flux (liquid to solid), and then a rise towards the end (heat absorption). Some differences amplitude and timing are observed between the experimental and simulated results. These discrepancies could be attributed to various factors, such as simplifications in the simulation model, experimental measurement errors, or inherent material property variations.
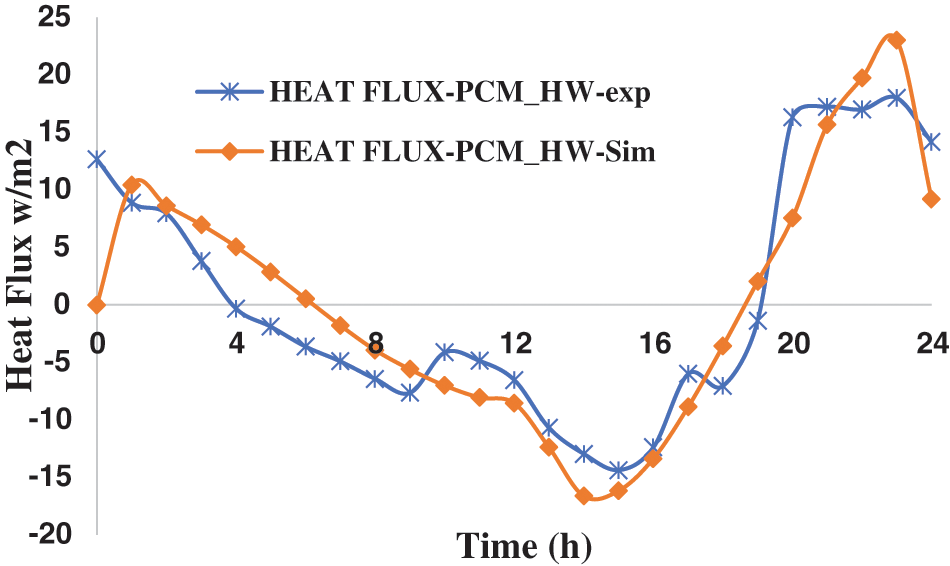
Figure 4: Comparison of experimental and simulated heat flux in PCM + HW composite over time
Thermal performance was evaluated in this study by comparing the interior thermal characteristics, such as thermal amplitude, time lag, and decrement factor [48], for walls made of eco-materials (HW and WW) with and without a PCM layer. The graphs presented in Fig. 5. illustrate the impact of incorporating PCM into HW (a) and WW (b) walls insulation on the surface temperature. The results show that the addition of PCM layers help in reducing internal temperature variations and providing a more stable indoor surface temperature profile compared to HW and WW alone.
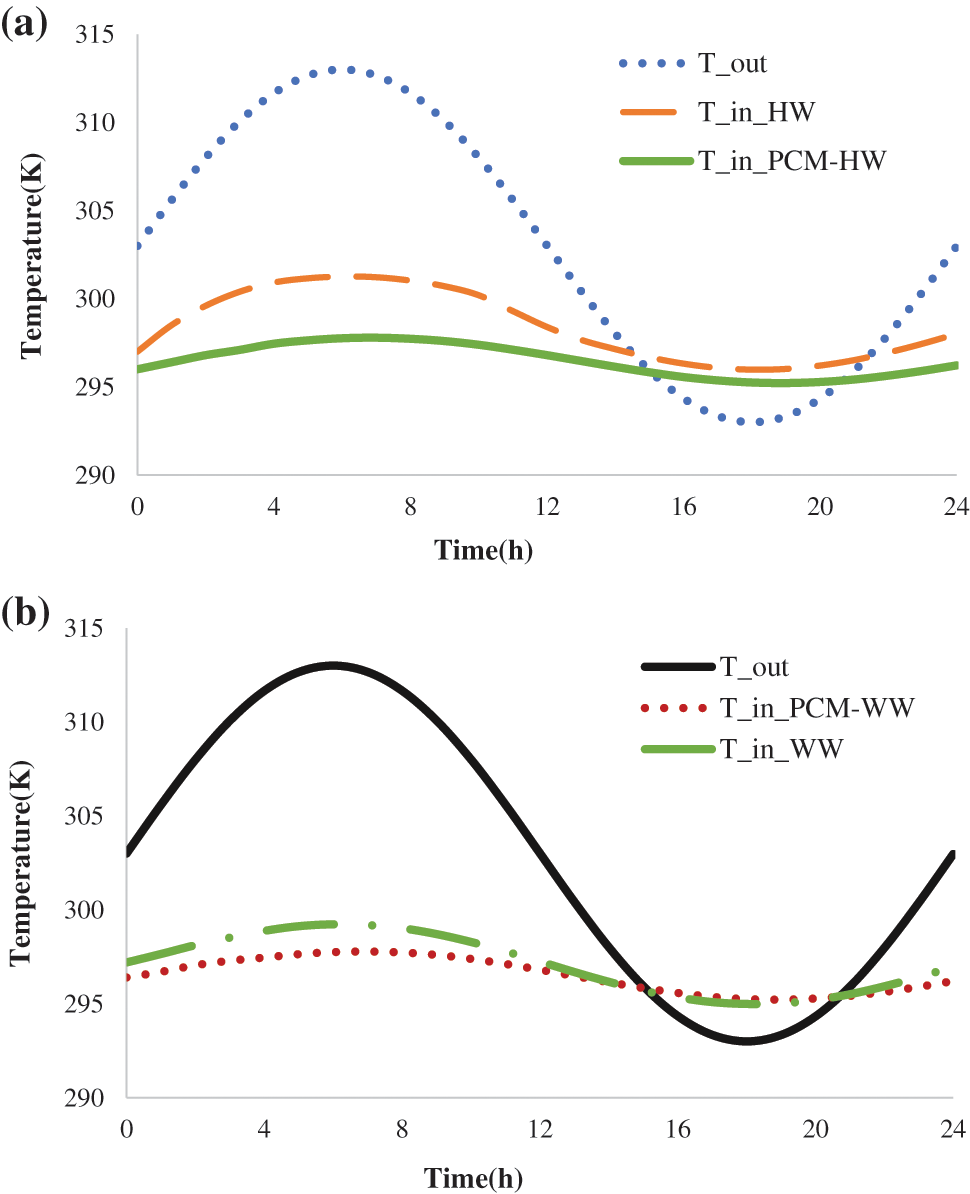
Figure 5: The impact of incorporating PCM into the HW (a) and WW (b) insulating wall on surface temperature
The thermal amplitude of PCM_HW is 2.79 in comparison to HW 6.7, with a 58.36% reduction, and 2.56 for PCM_WW in comparison to WW 4.25, with a 39.62% reduction.
The lag time for PCM_HW and PCM_WW is 1 h relative to the external environment, indicating that the addition of PCM helps to minimize overheating hours. The decrement factor for PCM_HW and PCM_WW was calculated to be 0.14 and 0.13, respectively, using the formula provided by Jin et al. [49]. The determination of the decrement factor is largely dependent on thermophysical properties and wall thickness [50]. A lower decrement factor indicates a higher level of indoor thermal comfort.
Fig. 6 illustrates the distribution of surface temperatures for different types of walls insulation: HW, WW, PCM + WW, and PCM + HW.

Figure 6: Temperature distribution within the wall insulation; Case 1: HW, Case 2: PCM_HW, Case 3: WW and Case 4: PCM_WW
Walls with PCM layers (Cases 2 and 4) have a more uniform temperature distribution and lower temperatures, especially on the indoor side, as indicated by the blue areas in the contours. This highlights the effectiveness of adding PCM layers in enhancing the thermal regulation of wall insulations.
4.3 Fluid-Mechanical Aspect in Phase Change Materials
In this section, the fluid-mechanical properties of phase change material (PCM) used in conjunction with HW and WW are analyzed. Specifically, the velocity, liquid fraction, and heat flux within the PCM composites. These aspects are considered crucial for evaluating the thermal insulation performance and efficiency of PCM-based materials in various applications.
4.3.1 Liquid Fraction Evolution
The liquid fraction allows visualizing the evolution of the liquid fraction in the phase change material (PCM), as shown in Fig. 7. The curves indicate similar melting and solidification cycles for PCM, with a slight phase advance for PCM + HW compared to PCM + WW. The right visualization illustrates the contour of the liquid fraction distribution at t = 22 h for both composite walls, where it’s clearly shown the presence of wavy colors in the distribution suggesting natural convection effects within the PCM.
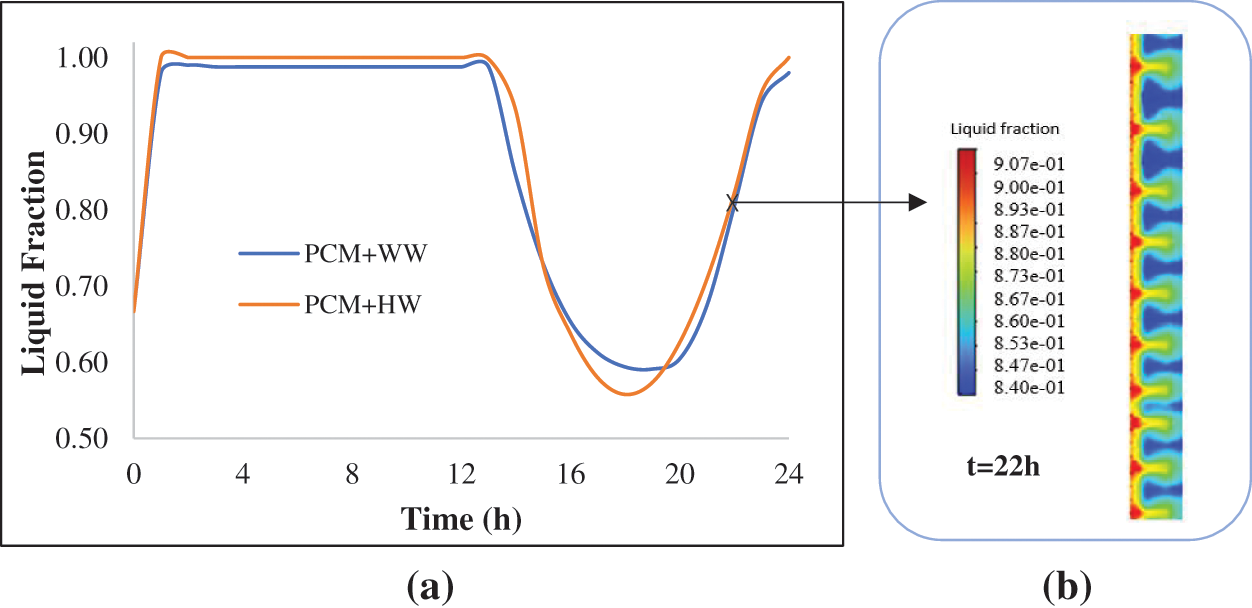
Figure 7: (a) Liquid fraction distribution in PCM for PCM + HW and PCM + WW Composites (b) Liquid fraction distribution in the PCM part of the composite at t = 22 h
The faster progression towards a complete liquid state for PCM + HW can be attributed to the distinct thermal properties of HW and WW. Hemp wool’s lower thermal conductivity (0.04 W/m.K) compared to Wood wool (0.046 W/m.K) results in less heat being conducted away from the PCM layer, allowing for more rapid melting. During the liquid phase, natural convection within the PCM helps in distributing the absorbed heat more uniformly across the wall. This phenomenon prevents localized overheating and contributes to a more uniform temperature across the external wall insulation.
Thus the incorporation of PCM in building materials, as observed in the studies by Mahdaoui et al. [51] and Hamdaoui et al. [52], significantly improves thermal performance by promoting balanced heat distribution and a more controlled phase transition.
Analyzing the velocity field helps study the natural convection effects within the molten PCM.
The graph in Fig. 8 shows the velocity distribution in PCM for both PCM + HW and PCM + WW composites over a 24 h period. The velocity curves for both composites are similar, with PCM + HW showing slightly higher velocities between 2 and 12 h.
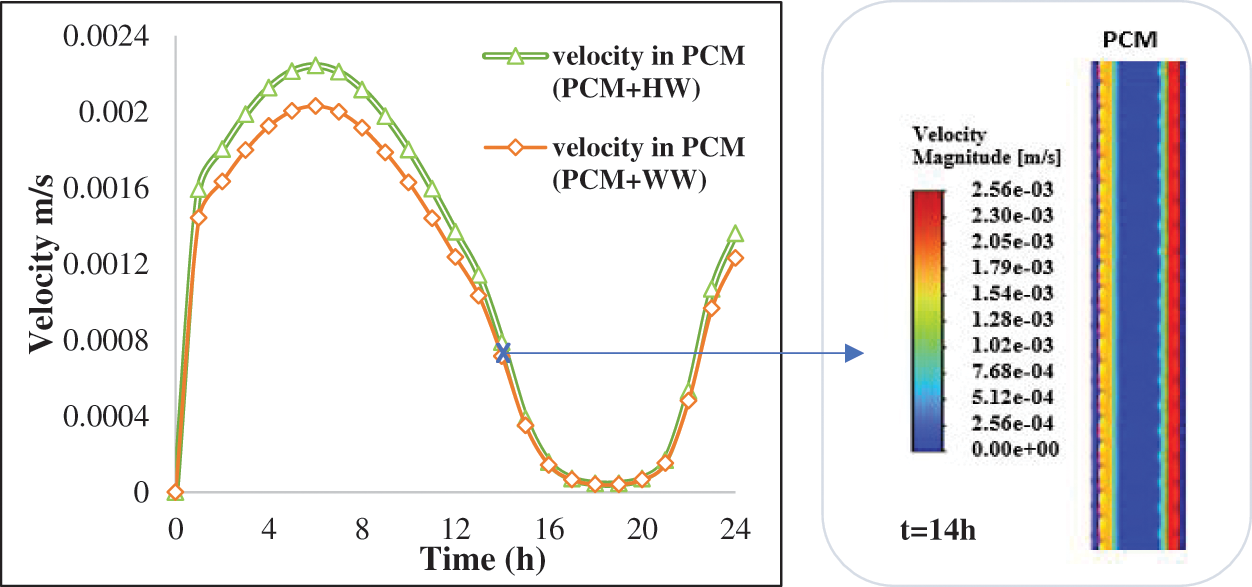
Figure 8: Velocity distribution in PCM for PCM + HW and PCM + WW composites
Since the profile contour of velocity for both composites are similar, the velocity magnitude visualization at 14 h (right side of the figure) shows higher velocities near the edges of the PCM layer, suggesting the presence of convection currents within the melted PCM. This natural convection plays a crucial role in heat distribution within the composites.
Due to the temperature gradients causing density differences in the molten PCM, higher velocities were noticed near the edges indicating the formation of boundary layers, where buoyancy-driven flow is strongest. This behavior aligns with studies on PCM in similar configurations. Soliman et al. [53] Observed comparable convection effects in their simulations of PCM confined in cylindrical enclosures under constant heat flux. However, adding bio-based materials (HW and WW) could improve heat storage and release by slightly enhancing convective movements without creating major imbalances. As described by Cheng et al. [54], enhancing the thermal conductivity of stabilized PCM can optimize underfloor heating systems, which could be similar to the effect observed with HW and WW.
Heat flux is a key parameter for evaluating the thermal performance of insulation materials.
Fig. 9 demonstrates the impact of integrating PCM on heat flux. The curves for the two composites with PCM + HW and PCM + WW are quite similar, suggesting that the PCM dominates the thermal behavior of the composite. The PCM composites show a period of significant heat absorption (negative flux), followed by a period of heat release (positive flux). This can be attributed to the high latent heat of the PCM allowing to absorb a significant amount of thermal energy during phase change and release it later. Achieving an average reduction of the heat transfer rate of 95.82% compared to WW without PCM and a decrease of 95,65% compared to HW without PCM. The results demonstrate the enhanced thermal management capabilities of PCM incorporated to biobased insulation materials. The studies by Bouzennada et al. [55] and Babaharra et al. [56] highlighted the importance of managing heat flux in PCM applications, claiming that well-controlled heat flux improves the thermal storage capacity; the results of this study support these conclusions.
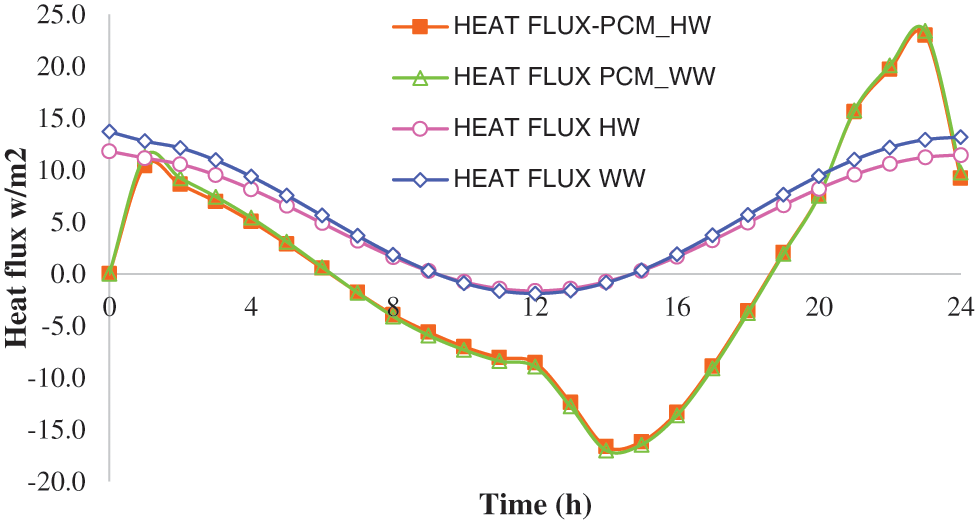
Figure 9: Comparison of heat flux in HW and WW insulation materials with and without PCM
This study asserts the significant potential of the combination PCM and biobased insulation materials to enhance the thermal performance of building envelopes.
The combination of phase change material (PCM) with biobased insulation materials resulted in significant reductions in temperature oscillations within walls. PCM_HW exhibited a temperature decreases of 3.8 K, while PCM_WW showed a reduction of 1.45 K compared to their respective reference wall insulation without PCM.
PCM composites demonstrated superior thermal management capabilities. The addition of PCM to both Hemp Wool and Wood Wool significantly improved their effectiveness as thermal insulation materials, providing more stable indoor temperatures. This enhancement in thermal stability contributes to improved occupant comfort and reduced energy needs for heating and cooling.
Regarding heat flux, the addition of PCMs resulted in a significant reduction in heat transfer rates. An average decrease of 96% for PCM + (HW, WW) compared to HW and WW without PCM.
The homogeneous distribution of the liquid fraction within the PCM layer and moderate velocities indicate efficient thermal energy storage and release process, which is crucial for maintaining consistent thermal performance in sustainable building applications and contribute to the effectiveness of the composite insulation system.
Future research will explore the hygrothermal performances of these materials, examining how PCM integration affects moisture management and thermal behavior over extended periods. Moreover, exploring the wider impact of PCM usage on sustainable construction and environmental management will provide valuable insights into their role in ecofriendly building solutions.
Acknowledgement: We would like to thank PHC Maghreb for its financial support to the first author and LERMAB Laboratory for agreeing to host.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: conception and design: Salma Kouzzi; data collection: Salma Kouzzi; simulation: Salma Kouzzi, Mouniba Redah; analysis and interpretation of results: Salma Kouzzi, Souad Morsli; draft manuscript preparation: Salma Kouzzi, Mouniba Redah; writing: Salma Kouzzi, Souad Morsli, Mouniba Redah; review and editing: Salma Kouzzi, Mohammed El Ganaoui, Souad Morsli; supervision and administration: Mohammed El Ganaoui, Mohammed Lhassane Lahlaouti. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. World Energy Outlook 2022. International Energy Agency IEA. Available from: https://www.iea.org/reports/world-energy-outlook-2022. [Accessed 2023]. [Google Scholar]
2. Environment UN. Global status report for buildings and construction. UNEP-UN Environment Programme. Available from: http://www.unep.org/resources/publication/2022-global-status-report-buildings-and-construction. [Accessed 2023]. [Google Scholar]
3. Hoseinzadeh S, Hadi Zakeri M, Shirkhani A, Chamkha AJ. Analysis of energy consumption improvements of a zero-energy building in a humid mountainous area. J Renew Sustain Energy. 2019 Feb 15;11(1):15103. [Google Scholar]
4. Struhala K, Ostrý M. Life-cycle assessment of phase-change materials in buildings: a review. J Clean Prod. 2022 Feb 15;336:130359. [Google Scholar]
5. Zilberberg E, Trapper P, Meir IA, Isaac S. The impact of thermal mass and insulation of building structure on energy efficiency. Energy Build. 2021 Jun 15;241:110954. [Google Scholar]
6. Arıcı M, Bilgin F, Krajčík M, Nižetić S, Karabay H. Energy saving and CO2 reduction potential of external building walls containing two layers of phase change material. Energy. 2022 Aug 1;252:124010. [Google Scholar]
7. Dhayanithi J, Hotta TK. Optimization of temperature distribution in building envelopes of Ahmedabad region using nano-encapsulated phase change material. Energy and Built Environ. 2024 Mar. doi:10.1016/j.enbenv.2024.03.004. [Google Scholar] [CrossRef]
8. Wang X, Li W, Luo Z, Wang K, Shah SP. A critical review on phase change materials (PCM) for sustainable and energy efficient building: design, characteristic, performance and application. Energy Build. 2022 Apr 1;260:111923. [Google Scholar]
9. El Ganaoui M, Hristov J. Analytical and innovative solutions for heat transfer problems involving phase change and interfaces. Comptes rendus. Mécanique. 2012;340(7):91. [Google Scholar]
10. Hassan F, Jamil F, Hussain A, Ali HM, Janjua MM, Khushnood S, et al. Recent advancements in latent heat phase change materials and their applications for thermal energy storage and buildings: a state of the art review. Sustain Energy Technol Assess. 2022 Feb 1;49:101646. [Google Scholar]
11. Rashid FL, Al-Obaidi MA, Dulaimi A, Mahmood DMN, Sopian K. A review of recent improvements, developments, and effects of using phase-change materials in buildings to store thermal energy. Designs. 2023 Aug;7(4):90. [Google Scholar]
12. Hekimoğlu G, Sarı A. A review on phase change materials (PCMs) for thermal energy storage implementations. Mat Today: Proc. 2022 Jan 1;58:1360–7. [Google Scholar]
13. Zhan H, Mahyuddin N, Sulaiman R, Khayatian F. Phase change material (PCM) integrations into buildings in hot climates with simulation access for energy performance and thermal comfort: a review. Constr Build Mater. 2023 Sep 15;397:132312. [Google Scholar]
14. Anter AG, Sultan AA, Hegazi AA, El Bouz MA. Thermal performance and energy saving using phase change materials (PCM) integrated in building walls. J Energy Storage. 2023 Sep 1;67:107568. [Google Scholar]
15. M’hamdi Y, Baba K, Tajayouti M, Nounah A. Energy, environmental, and economic analysis of different buildings envelope integrated with phase change materials in different climates. Sol Energy. 2022 Sep 1;243:91–102. [Google Scholar]
16. Nouhaila B, Mouhib T, Bendriaa F. Creation of energy-efficient building envelope based on phase-change materials (PCM). Eximia Sci. 2022 Aug 18;5(1):78–102. [Google Scholar]
17. Sharma R, Jang JG, Hu JW. Phase-change materials in concrete: opportunities and challenges for sustainable construction and building materials. Materials. 2022 Jan;15(1):335. [Google Scholar] [PubMed]
18. Pittau F, Carcassi OG, Servalli M, Pellegrini S, Claude S. Hygrothermal characterization of bio-based thermal insulation made of fibres from invasive alien lake plants bounded with mycelium. IOP Conf Ser: Earth Environ Sci. 2022 Sep;1078(1):12069. [Google Scholar]
19. Zhou Y, Trabelsi A, El Mankibi M. Hygrothermal properties of insulation materials from rice straw and natural binders for buildings. Constr Build Mater. 2023 Apr 3;372:130770. doi:10.1016/j.conbuildmat.2023.130770. [Google Scholar] [CrossRef]
20. Kouzzi S, Ganaoui ME, Kheiri A, Bouardi AE. Local materials, between regional diversity and energy performance to build efficient buildings in a transborder context (morocco-spain). E3S Web Conf. 2022;353:1003. doi:10.1051/e3sconf/202235301003. [Google Scholar] [CrossRef]
21. Koh CH, Gauvin F, Schollbach K, Brouwers HJH. Investigation of material characteristics and hygrothermal performances of different bio-based insulation composites. Constr Build Mater. 2022 Sep 5;346:128440. doi:10.1016/j.conbuildmat.2022.128440. [Google Scholar] [CrossRef]
22. Jensen NF, Møller EB, Hansen KK, Rode C. Hygrothermal assessment of solid masonry walls internally insulated with bio-based insulation materials. AIP Conf Proc. 2023 Nov 9;2918(1):20024. doi:10.1063/5.0173596. [Google Scholar] [CrossRef]
23. Reibert D, Tzanetos F, Sydow S, Bialuch I, Lee TH, Abraham TG, et al. Integration of bio-based insulation materials as a contribution to the biological transformation of production technology. Procedia CIRP. 2022 Jan 1;110:305–10. doi:10.1016/j.procir.2022.06.055. [Google Scholar] [CrossRef]
24. Mouton L, Allacker K, Röck M. Bio-based building material solutions for environmental benefits over conventional construction products—life cycle assessment of regenerative design strategies (1/2). Energy Build. 2023 Mar 1;282:112767. [Google Scholar]
25. Wu D, Rahim M, El Ganaoui M, Bennacer R, Liu B. Multilayer assembly of phase change material and bio-based concrete: a passive envelope to improve the energy and hygrothermal performance of buildings. Energy Convers Manage. 2022 Apr 1;257:115454. [Google Scholar]
26. Bakkour A, Ouldboukhitine SE, Biwole P, Amziane S. A review of multi-scale hygrothermal characteristics of plant-based building materials. Constr Build Mater. 2024 Jan 19;412:134850. [Google Scholar]
27. Fischer H, Korjenic A. Hygrothermal performance of bio-based exterior wall constructions and their resilience under air leakage and moisture load. Buildings. 2023 Oct;13(10):2650. [Google Scholar]
28. Gopalan A, Antony ASM, Suresh R, Sahoo S, Livingston LMM, Titus A, et al. Performance enhancement of building energy through the combination of dynamic insulation panels and phase changing materials. Energy Rep. 2022 Nov 1;8:945–58. [Google Scholar]
29. Abdulmunem AR, Hussein NF, Samin PM, Sopian K, Hussien HA, Ghazali H. Integration of recycled waste paper with phase change material in building enclosure. J Energy Storage. 2023 Aug;64:107140. [Google Scholar]
30. Wang J, Zhang X. Coupled solid-liquid phase change and thermal flow simulation by particle method. Int Commun Heat Mass Transf. 2020 Apr 1;113:104519. [Google Scholar]
31. Lappa M. A mathematical and numerical framework for the simulation of oscillatory buoyancy and marangoni convection in rectangular cavities with variable cross section. In: Computational methods in applied sciences. Cham: Springer; 2018. p. 419–58. [Google Scholar]
32. Dardouri S, Mankai S, Almoneef MM, Mbarek M, Sghaier J. Energy performance based optimization of building envelope containing PCM combined with insulation considering various configurations. Energy Rep. 2023 Nov 1;10:895–909. [Google Scholar]
33. Wu D, Rahim M, Li W, El Ganaoui M, Bennacer R. Simulation of the hygrothermal behavior of a building envelope based on phase change materials and a bio-based concrete. Fluid Dyn Mater Proc. 2022;18(5):1483–94. doi:10.32604/fdmp.2022.021917. [Google Scholar] [CrossRef]
34. Zhou S, Razaqpur AG. CFD modeling and experimental validation of the thermal performance of a novel dynamic PCM Trombe wall: comparison with the companion static wall with and without PCM. Appl Energy. 2024 Jan 1;353:121985. [Google Scholar]
35. Karanafti A, Theodosiou T, Tsikaloudaki K. Assessment of buildings’ dynamic thermal insulation technologies—a review. Appl Energy. 2022 Nov 15;326:119985. doi:10.1016/j.apenergy.2022.119985. [Google Scholar] [CrossRef]
36. Khoukhi M, Abdelbaqi S, Hassan A, Darsaleh A. Impact of dynamic thermal conductivity change of EPS insulation on temperature variation through a wall assembly. Case Stud Therm Eng. 2021 Jun 1;25:100917. doi:10.1016/j.csite.2021.100917. [Google Scholar] [CrossRef]
37. Ling H, Chen C, Wei S, Guan Y, Ma C, Xie G, et al. Effect of phase change materials on indoor thermal environment under different weather conditions and over a long time. Appl Energy. 2015 Feb 15;140:329–37. doi:10.1016/j.apenergy.2014.11.078. [Google Scholar] [CrossRef]
38. Cosentino L, Fernandes J, Mateus R. A review of natural bio-based insulation materials. Energies. 2023 Jan;16(12):4676. doi:10.3390/en16124676. [Google Scholar] [CrossRef]
39. ISO 9869-1:2014. Thermal insulation–Building elements–In-situ measurement of thermal resistance and thermal transmittance. ISO; 2014. Available from: https://www.iso.org/standard/59697.html. [Accessed 2024]. [Google Scholar]
40. Escudero C, Martin K, Erkoreka A, Flores I, Sala JM. Experimental thermal characterization of radiant barriers for building insulation. Energy Build. 2013 Apr 1;59:62–72. [Google Scholar]
41. King JAJr. Hydrocarbon-based PCM applications, 2010. Available from: https://cdn2.hubspot.net/hub/55819/file-14755587-pdf/docs/buildings-xi/dupont_energain.pdf. [Accessed 2024]. [Google Scholar]
42. Mnasri F, Bahria S, Slimani MEA, Lahoucine O, El Ganaoui M. Building incorporated bio-based materials: experimental and numerical study. J Build Eng. 2020 Mar 1;28:101088. [Google Scholar]
43. Biofib’Isolation. Isolation chanvre thermique et écologique: BIOFIB’CHANVRE-Biofib’Isolation. Biofib’Isolation-Notre culture, votre confort. 2021. Available from: https://www.biofib.com/biofib-chanvre/. [Accessed 2023]. [Google Scholar]
44. Tickoo PS. ANSYS workbench 2023 R2: a tutorial approach. 6th ed. Schererville, Indiana, USA: CADCIM Technologies; 2023. p. 677. [Google Scholar]
45. Mageed RH, Kurji HJ, Abdulrasool AA. A numerical study to determine the effect of an insulator location on the transient heat transfer. J Ecol Eng. 2023 Oct 1;24(10):105–14. [Google Scholar]
46. Zhang L. Analysis of energy saving effect of green building exterior wall structure based on ANSYS simulation analysis. Environ Technol Innov. 2021 Aug 1;23:101673. [Google Scholar]
47. Essid N, Eddhahak-Ouni A, Neji J. Experimental and numerical thermal properties investigation of cement-based materials modified with PCM for building construction use. J Archit Eng. 2020 Sep;26(3):4020018. [Google Scholar]
48. Rathore PKS, Gupta NK, Yadav D, Shukla SK, Kaul S. Thermal performance of the building envelope integrated with phase change material for thermal energy storage: an updated review. Sustain Cities Soc. 2022 Apr 1;79:103690. [Google Scholar]
49. Jin X, Zhang X, Cao Y, Wang G. Thermal performance evaluation of the wall using heat flux time lag and decrement factor. Energy Build. 2012 Apr 1;47:369–74. [Google Scholar]
50. Fathipour R, Hadidi A. Analytical solution for the study of time lag and decrement factor for building walls in climate of Iran. Energy. 2017 Sep 1;134:167–80. [Google Scholar]
51. Mahdaoui M, Hamdaoui S, Ait Msaad A, Kousksou T, El Rhafiki T, Jamil A, et al. Building bricks with phase change material (PCMthermal performances. Constr Build Mater. 2021 Feb;269:121315. [Google Scholar]
52. Hamdaoui S, Bouchikhi A, Azouggagh M, Akour M, Ait Msaad A, Mahdaoui M. Building hollow clay bricks embedding phase change material: thermal behavior analysis under hot climate. Sol Energy. 2022 May 1;237:122–34. [Google Scholar]
53. Soliman AS, Zhu S, Xu L, Dong J, Cheng P. Numerical simulation and experimental verification of constrained melting of phase change material in cylindrical enclosure subjected to a constant heat flux. J Energy Storage. 2021 Mar 1;35:102312. [Google Scholar]
54. Cheng W, Xie B, Zhang R, Xu Z, Xia Y. Effect of thermal conductivities of shape stabilized PCM on under-floor heating system. Appl Energy. 2015 Apr 15;144:10–8. [Google Scholar]
55. Bouzennada T, Mechighel F, Filali A, Kolsi L. Study of the usability of sinusoidal function heat flux based on enthalpy-porosity technique for PCM-related applications. J Therm Anal Calorim. 2020 Sep 1;141(5):1769–84. [Google Scholar]
56. Babaharra O, Choukairy K, Hamdaoui S, Khallaki K, Hayani Mounir S. Thermal behavior evaluation of a radiant floor heating system incorporates a microencapsulated phase change material. Constr Build Mater. 2022 May 2;330:127293. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF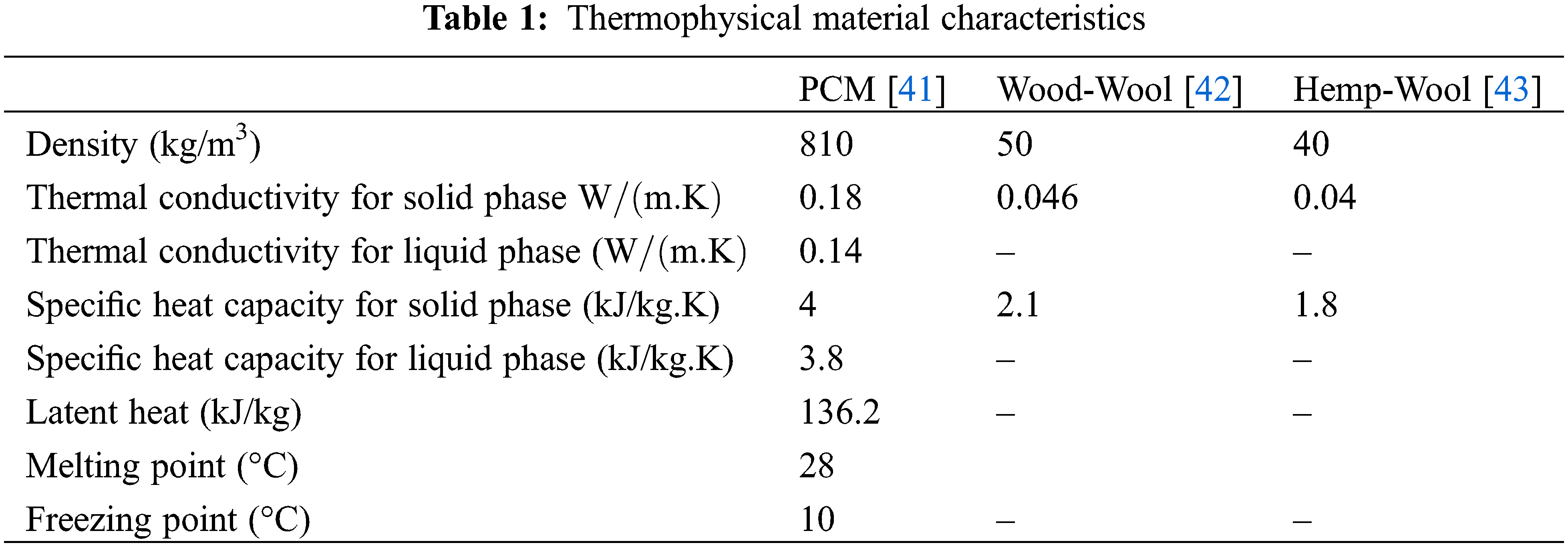
 Downloads
Downloads
 Citation Tools
Citation Tools