A Method Based on Thermo-Vibrational Effects for Hydrogen Transportation and Storage

1  Introduction

The global trend is the transition to clean and renewable energy sources, one of which is hydrogen. On the one hand, its use in the energy sector leads to a reduction in harmful emissions, and on the other, its transportation and storage are associated with the risk of explosion and increased requirements for the tightness of containers and pipelines.

In the Russian Federation, hydrogen and hydrogen-containing mixtures are transported through pipelines for use in the gas and oil transportation industries, combustion chambers are being developed for hydrogen-containing fuels in aviation, and combustion processes of hydrogen jets are being studied in the energy sector.

In this regard, there is an urgent problem of ensuring safety when working with hydrogen. The article discusses mechanisms that allow minimizing the kinetic energy of hydrogen flow during its transportation and storage.

The features of vibration-convective flow in closed cavities are also studied by other scientists. In [1], set of fixed mutual orientations of vibration and heating directions at which the state of mechanical quasiequilibrium [2,3] is possible have been determined The theory of vibrational-convective stability was extended to binary mixtures in [4–7]. In [8,9], the influence of the vibration direction at a fixed angle between the heating direction and gravity was considered. In [10,11], the issues of controlling the structure of vibration convection modes are considered. Works [12,13] are devoted to the consideration of porosity, temperature inversion of density. Thermovibrational convection in a horizontal layer of fluid between isothermal solid boundaries heated to different temperatures in the presence of longitudinal vibrations is considered in [14]. It is shown that the model predicts the drastic excitation of stationary supercritical vibrational convection in the case of heating from the top. Cyclic variation of the gravitational Rayleigh number leads to hysteretic transitions between stationary solutions. The importance of viscoelastic properties of fluids is considered in [15–17]. The simulations [18] of thermal vibrational convection in cubic cavities have shown that an increase in the system (spatial) dimensionality has a dramatic influence on the richness of the fundamental modes of convection that can be excited.

Under a simple condition previously obtained in [19], two mechanisms of thermal vibrational and thermal gravitational convection can completely suppress each other in a cylindrical cavity. To determine the structures that arise when this condition is met, a study was conducted [20] for the square shape of the cavity. Research [20] presented an analytical model of vibrogravitational gas flow, implemented by the Sturm-Liouville method for microgravity conditions that correspond to very small Grashof numbers (Gr < 100). The problem is solved for a square cavity with a constant gas temperature gradient without the possibility of changing it–the temperature distribution is specified linearly as a boundary condition. An analytical condition was also obtained for minimizing the intensity of the vibrogravitational flow, in which the vibrational convection mechanism compensates for the gravitational one:

Grsin⁡α−Grv4sin⁡2β=0 (1)

This paper presents a mathematical model implemented by an explicit finite difference method (FDM), in which the distribution of gas temperatures is not specified as a boundary condition but is determined by direct numerical modeling. The problem was solved for low-speed, small Reynolds numbers (Re < 100), convective flow of hydrogen under Earth conditions, which increased the Grashof number to 104.

In addition, since the applied problem of ensuring safety during the transportation and storage of hydrogen is being solved, it is necessary to assess the limits of applicability of Condition (1) for Grashof numbersequal to 104.

2  Problem Formulations, Assumption System

The assumption system is formulated as follows:

1. Pure hydrogen in the gaseous state is considered as the working fluid; the thermophysical properties are described through the Prandtl number (Pr = 0.7);

2. Gravity is taken into account using the Grashof number (Gr);

3. The hydrogen is viscous and incompressible due to small Reynolds numbers (Re < 100), the Boussinesq approximation is considered;

4. Gas-dynamic processes are considered in a two-dimensional non-stationary formulation;

5. It is assumed that vibrations act on the entire volume of hydrogen according to the harmonic law; the vibration intensity is given by the Grashof vibration number (Grv);

6. The stability of the calculation scheme was ensured by fulfilling the Courant-Friedrichs-Levy condition;

7. Wall roughness is not taken into account due to low flow rates;

8. The walls are impenetrable, non-deformable;

9. The aeroelasticity of the structure is not taken into account due to low flow velocities;

10. Due to their small size, electromagnetic processes are not taken into account;

11. Radiative convection is not taken into account due to the low radioactivity of the hydrogen.

Unsteady regimes of vibration-convective flow of viscous incompressible pure hydrogen in the gaseous phase in an infinite cavity of square cross-section are investigated. For one pair of opposite faces a constant temperature difference is maintained, and the other pair is thermally insulated. The geometric formulation of the problem (Fig. 1) was used similarly to work [11].

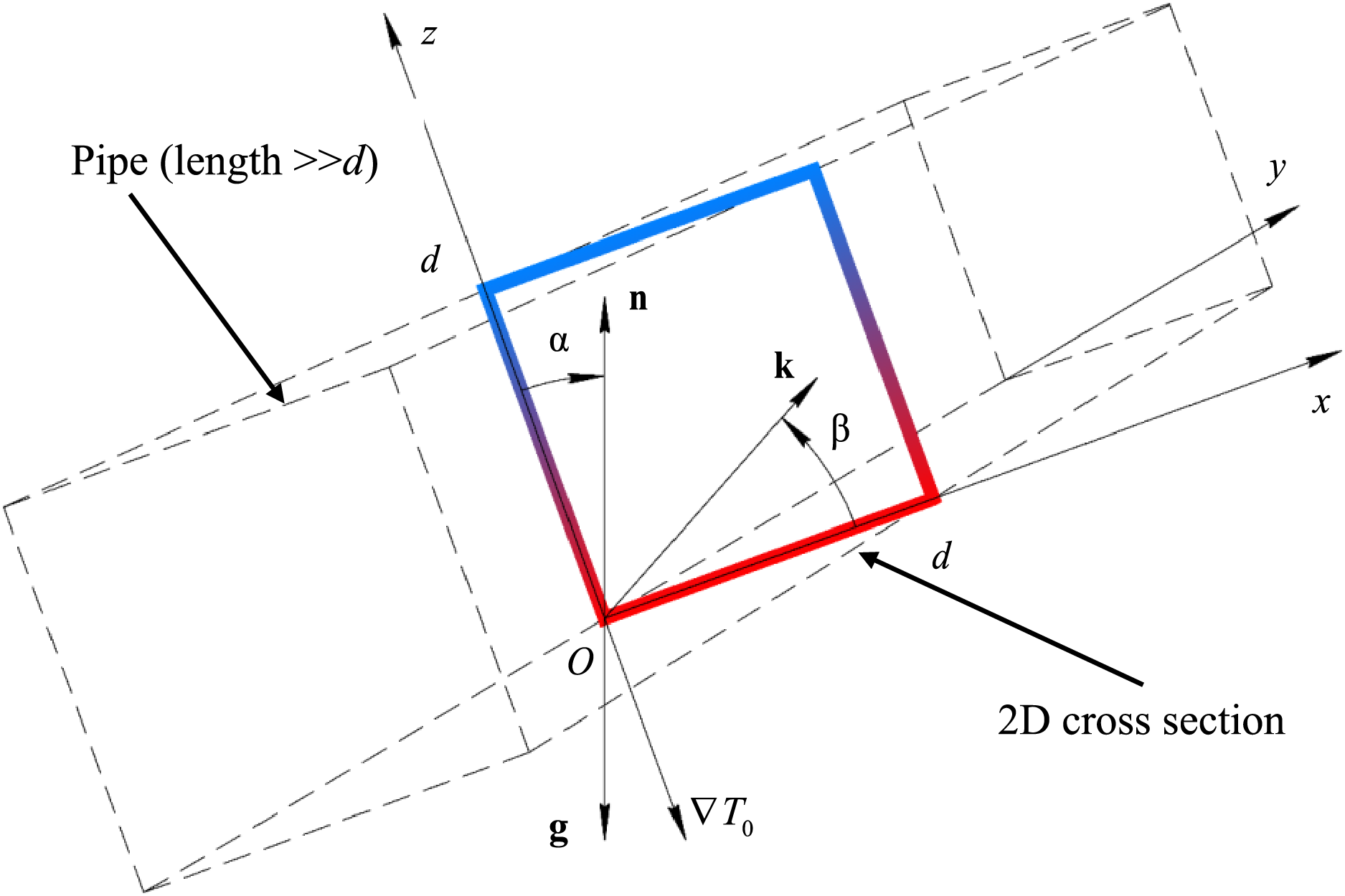
Figure 1: 2D pipe cross section

The cavity is in α gravitational field with intensity g = −gn, where n is a unit vector directed upwards. The angle α of inclination is counted clockwise from the axis z to n. The range of angle α change is 0≤α≤2π , and at α = 0 the upward direction coincides with the axis z.

The cavity performs harmonic oscillations with amplitude a and cyclic frequency ω along a unit vector k located in the plane XOZ. Angle β, which specifies the direction of vibration, is counted counterclockwise from the axis x to k. The range of angle β change is 0≤β≤π , and at β = 0 the direction of vibrations coincides with the axis x.

The results of more than 170 numerical experiments using the developed mathematical model were obtained and analyzed.

3  Mathematical Model

The problem is solved in dimensionless variables, to go to which the following dimensionless quantities are used: the unit of length is the side of the cavity d , time– d2/d2νν , speed– ν/νdd and temperature– Θ .

The problem solution is found in a two-dimensional formulation using a two-field method and Navier-Stokes equation [2] in Helmholtz form [20]:

∂φ∂t+∇⋅(Vφ)=Δφ+Gr(n×∇T)y+Grv[∇(W⋅k)×∇T]y,∂T∂t+∇⋅(VT)=ΔTPr,ΔF=(∇T×k)y,Δψ+φ=0,V=curl ψ, φ=curl V, W=curl F,z=0,1:ψ=∂ψ∂x=0,F=0;x=0,1:ψ=∂ψ∂z=0,F=0;z=0,1:T=1,0;x=0,1:∂T∂x=0. (2)

where the index y means that only the vector component (scalar) along the axisy is used. The dimensionless Grashof number, the vibrational Grashof number and the Prandtl number are determined using dimensional parameters:

Gr=gbΘd3v2,Grv=12(aωbΘdv)2,Pr=vχ, (3)

where the coefficient of the thermal expansion of the fluid b=1273,15[1K] .

The variables of this system are temperature T and dynamic flow parameters: stream function – ψ and vorticity – φ :

φ=(0, φ,0), ψ=(0, ψ,0), F=(0, F,0). (4)

Analytically in [20], the Navier-Stokes equation was obtained in the Boussinesq approximation in the Helmholtz form, where the vorticity function is represented through the vibrational and gravitational components of the convective gas flow:

Δφ+Gr(n×∇T)y+Grv[∇(W⋅k)×∇T]y=Δφ−Grsin⁡α+Grvsin2β4++Grv7π2sin2β2500{sin(πz)[sh(πx)+sh(π−πx)]−sin(πx)[sh(πz)+sh(π−πz)]}−     −Grv7π2cos2β1250{cos(πz)[ch(πx)−ch(π−πx)]+cos(πx)[ch(πz)−ch(π−πz)]}=0. (5)

In this work, a mathematical model has been developed in a two-field formulation (vorticity function φ and stream function ψ ), implemented by the finite difference method using an explicit scheme for solving non-stationary equations of free thermal convection on a uniform structured rectangular mesh:

xi=ih, i=0, 1,..., N;zk=kh, k=0, 1,..., N, (6)

where h=1/N –dimensional mesh step; N=64 .

The Poisson equation was solved by the method of sequential upper relaxation using the Gauss-Seidel method for the stream function.

By approximating the derivatives in expressions (61), (62), which are given in [20], by central differences, finitedifference equations for the stream function and vorticity at the internal nodes of the mesh model are obtained. Resolving them relative to the central node of the template, we obtained iterative expressions using the Gauss-Seidel method:

φn= Δt{φki+1−2φki+φki−1h2+φk+1i−2φki+φk−1ih2+Gr2h[(Tki+1−Tki−1)cos⁡α−(Tk+1i−Tk−1i)sin⁡α]+−Grv2h[(Fk+1i−Fk−1i)sin⁡β(Tki+1−Tki−1)++(Fki+1−Fki−1)cos⁡β(Tk+1i−Tk−1i)]−−Vxkiφki+1−φki−12h−Vzkiφki+1−φki−12h++φxkiVki+1−Vki−12h−φzkiVki+1−Vki−12h}+φn−1(i, k), (7)

In a similar way, iterative formulas for solving the Poisson equation were obtained to find the stream function ψn(i, k) at internal mesh nodes:

ψki=(φkih2+ψki+1+ψki−1+ψk+1i+ψk−1i)/4, (8)

where φn(i, k) derived from (5).

For vorticity at the boundaries, the Thom formulas are used:

φ0,kn+1=−2ψ1,kn+1h2,φN,kn+1=−2ψN−1,kn+1h2,φi,0n+1=−2ψi,1n+1h2,φi,Nn+1=−2ψi,N−1n+1h2, (9)

Based on the obtained values of the stream function field, a new temperature field is calculated at the next iterative step:

Tn= Δt[1h2Pr(Tki+1+Tki−1+Tk+1i+Tk−1i−4Tki) −+ (ψk+1i+ψk−1i)(Tki+1−Tki−1)4h2−(ψki+1+ψki−1)(ψk+1i+ψk−1i)4h2]+Tn−1(i,k) (10)

The procedure for obtaining a numerical solution is described below:

Step 1.At the zero iteration ( n=0 ), the initial state was set:

ψi,k0=0,φi,k0=0,Ti,k0=1−z. (11)

or determined from the previous calculation.

Step 2.Using Formula (7), we determine the vorticity values φn+1(i, k) at the next iteration ( n+1 ) at the internal mesh nodes.

Step 3.Based on the calculated values φn+1(i, k) at the internal mesh nodes, we obtain, using Formula (8), the values of the stream function ψn(i, k) at the internal mesh nodes.

Step 4.Based on the calculated values ψn(i, k) at the internal mesh nodes, we obtain, using Formula (10), the values of the temperature field Tn(i, k) at the internal mesh nodes.

Step 5.Using new values of the stream function at the boundary mesh nodes, using (9) we determine the boundary values of vorticity at the next iteration.

Steps 2–5 are repeated until stable values of ψ , φ and T are obtained. The values of the specified grid functions, together with physical and numerical parameters for a given value of the Grashof vibration number Grv and inclination angle β , are stored in external memory.

4  Numerical Simulation Results

When Condition (1) is met, the flow in an infinite cavity of square pipe cross-section has a minimum intensity of kinetic energy (Fig. 2). With a slight deviation of any of the parameters, the kinetic energy of the averaged flow increases. It should be taken into account that there is some small deviation from the real minimum, which is determined in the process of a numerical experiment.

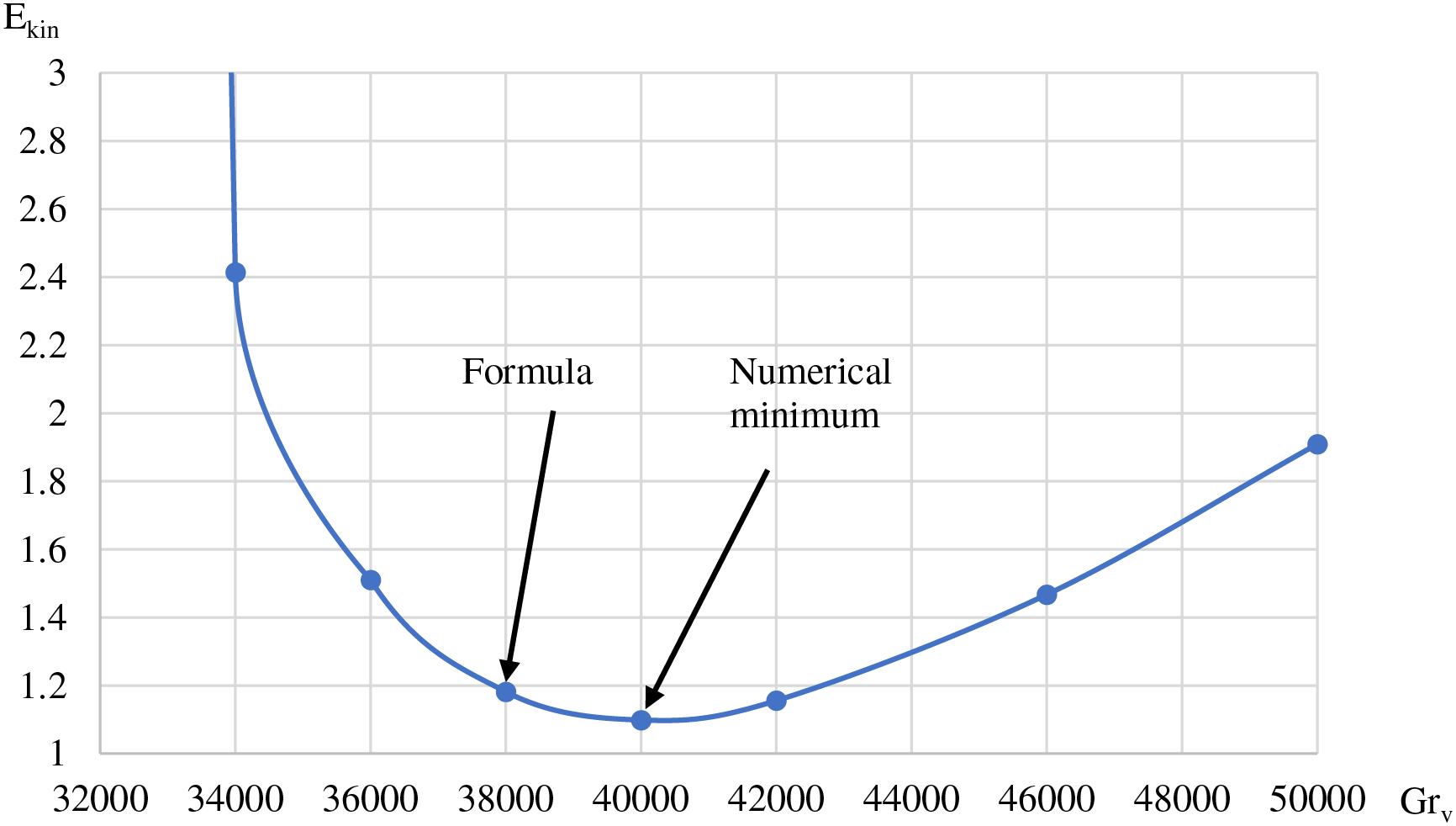
Figure 2: Dependence of kinetic energy on the vibrational Grashof number ( Gr=9500 , α=60∘ , β=60∘ )

The motion intensity was estimated according to the kinetic energy formula for convective flow:

E=12∫01∫01ψφdxdz. (12)

A simplex lattice plan was compiled, on the basis of which a number of numerical experiments were carried out for a wide range of cavity inclinations and vibration directions, as well as Grashof numbers, in order to determine the limits of applicability of the solution and analyze the influence of each parameter of convection mechanisms on the flow intensity.

The calculation results are presented in Figs. 3–8.

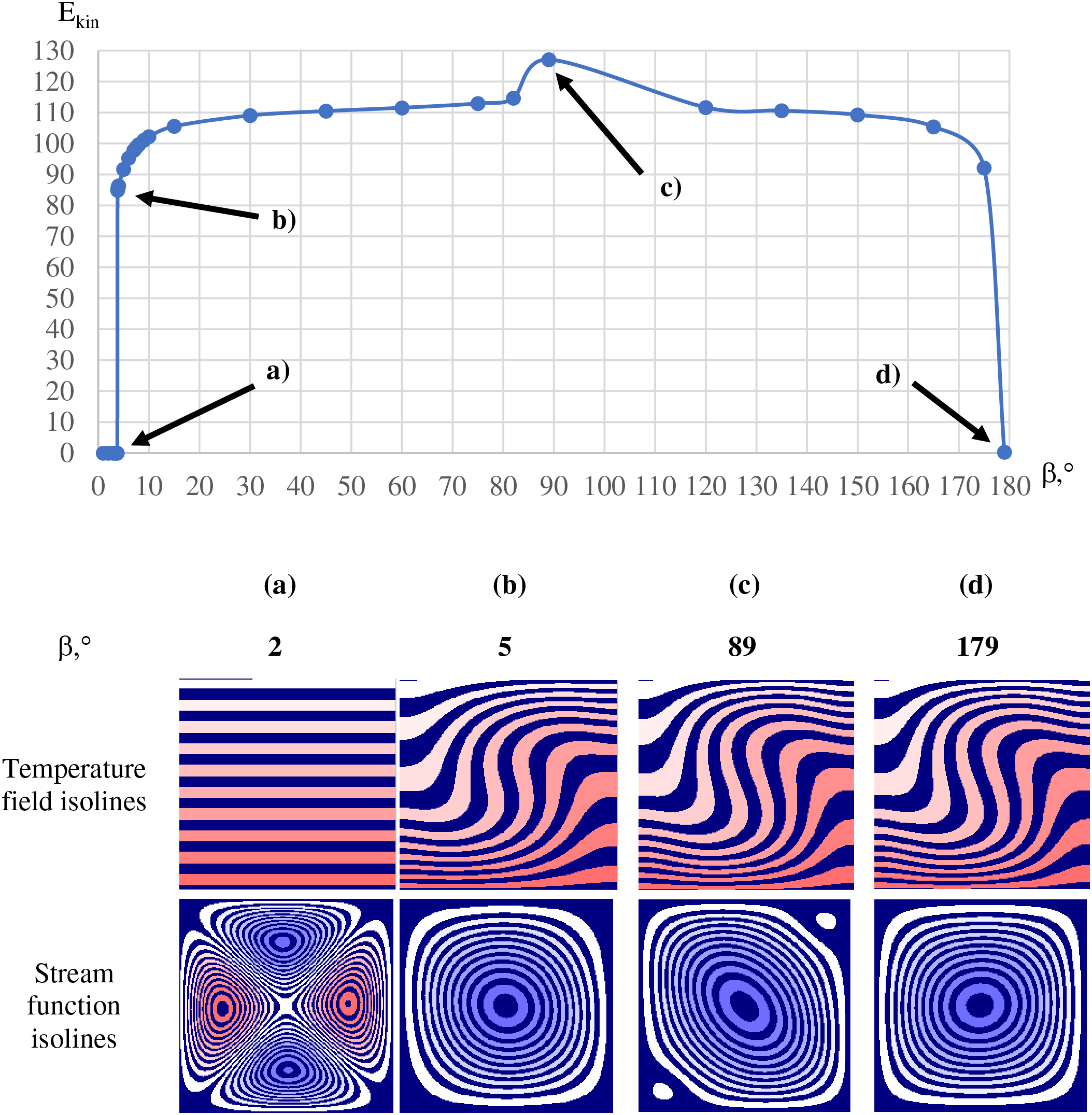
Figure 3: Dependence of kinetic energy on β ( Gr=9500 , α=1∘ )

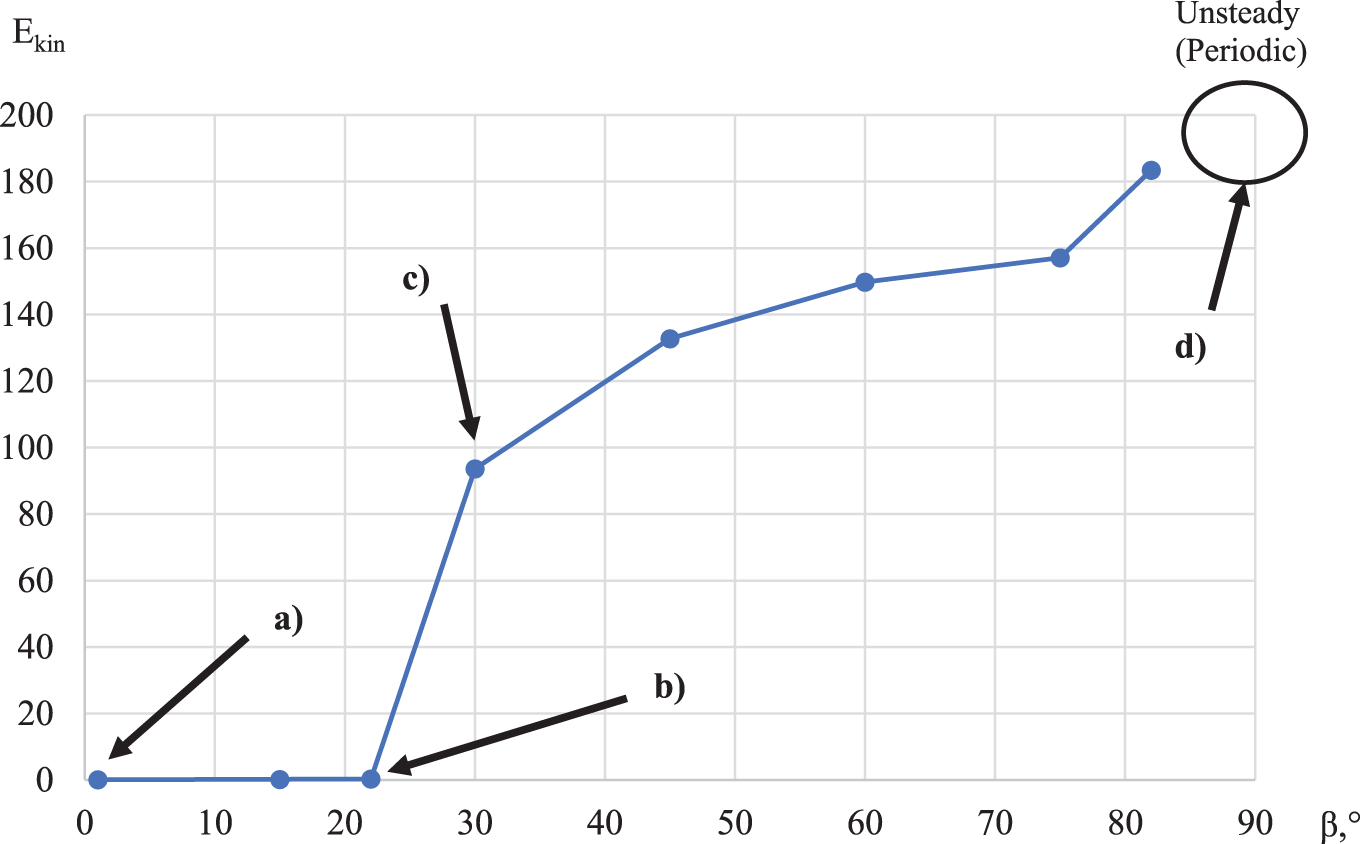
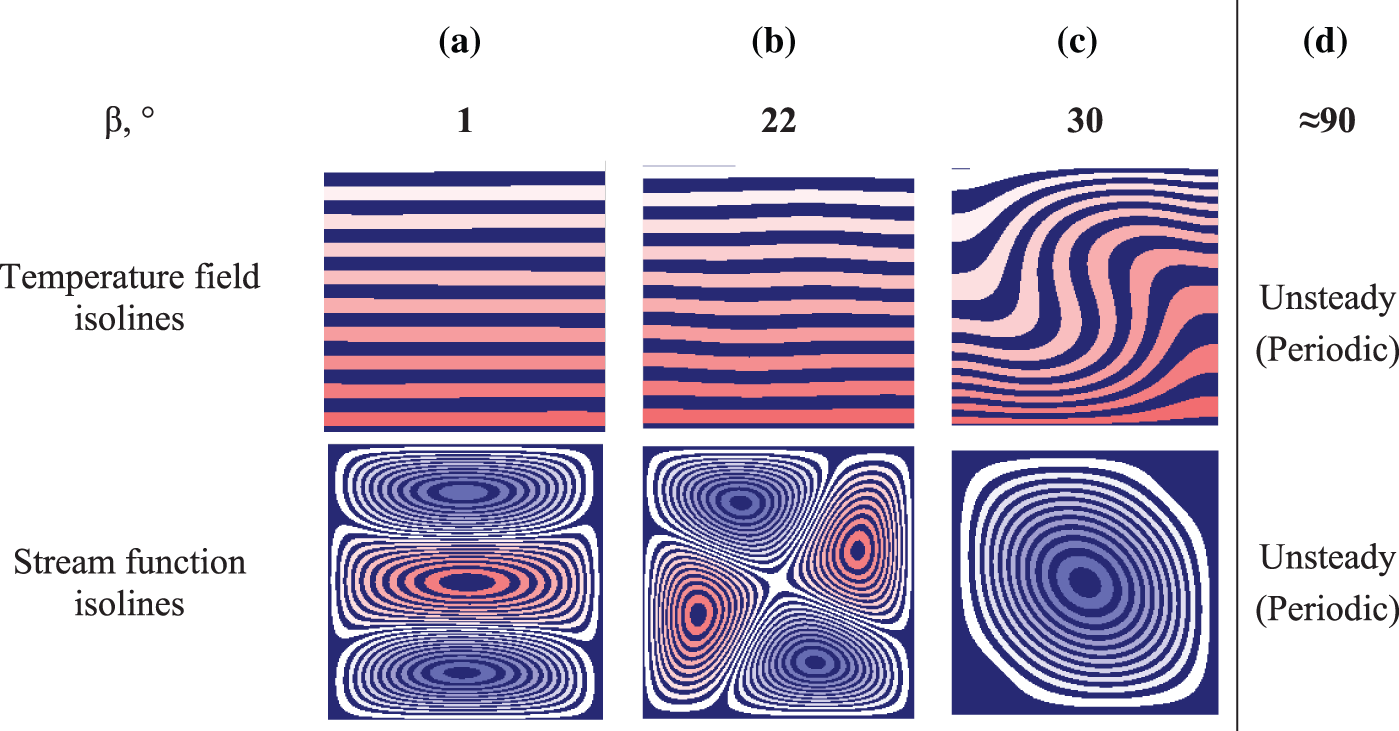
Figure 4: Dependence of kinetic energy on β ( Gr=9500 , α=30∘ )

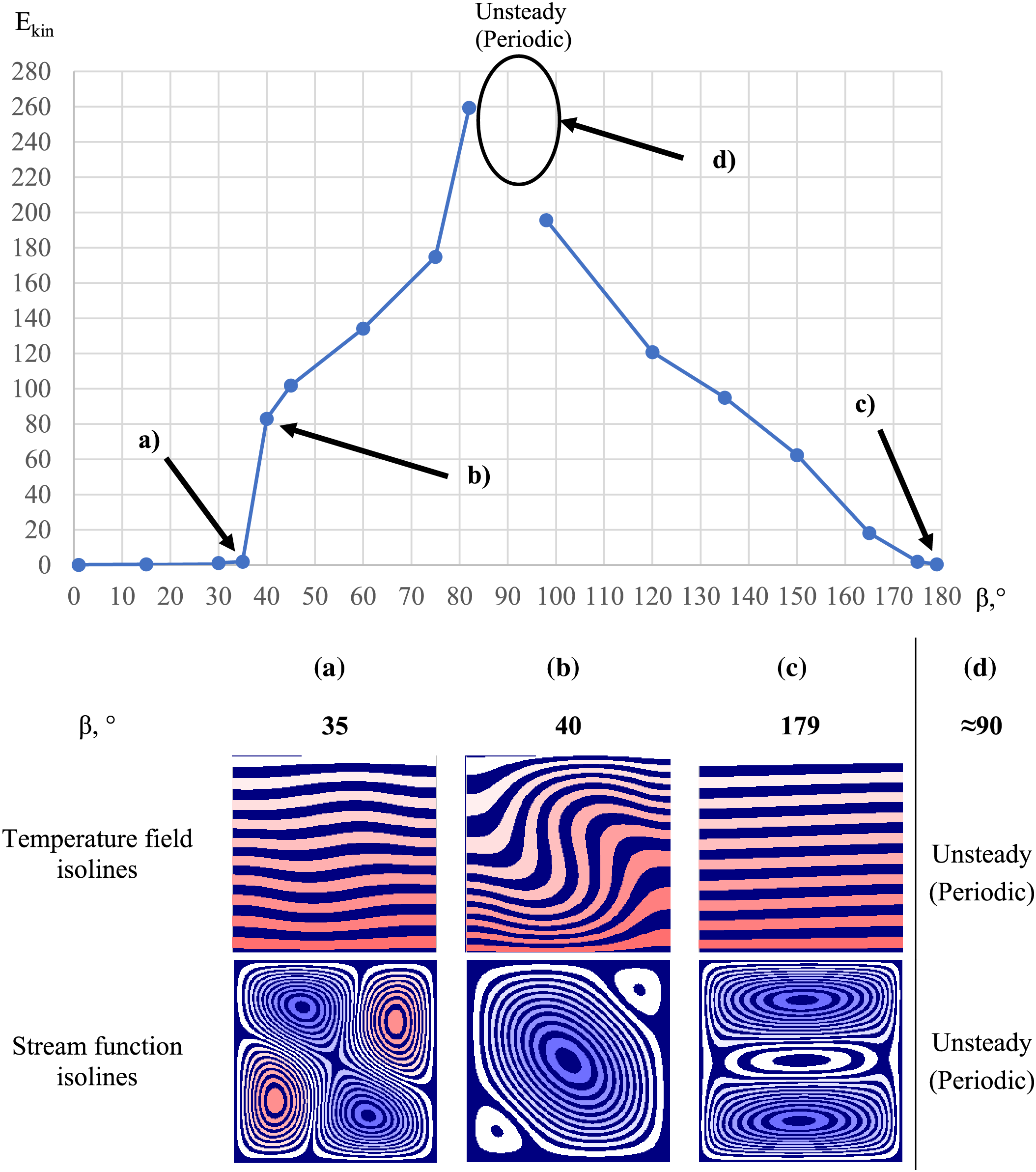
Figure 5: Dependence of kinetic energy on β ( Gr=9500 , α=60∘ )

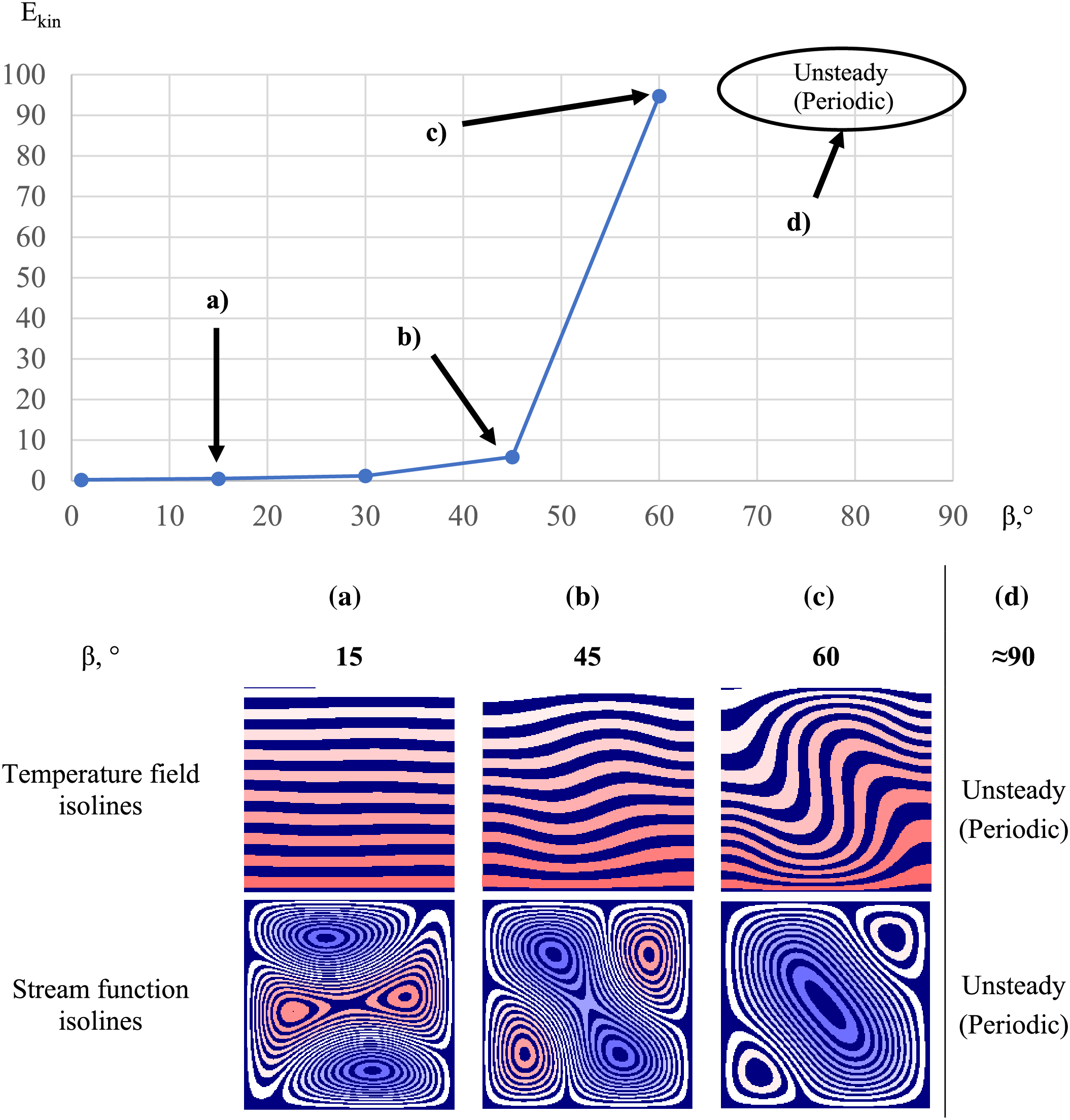
Figure 6: Dependence of kinetic energy on β ( Gr=9500 , α=90∘ )

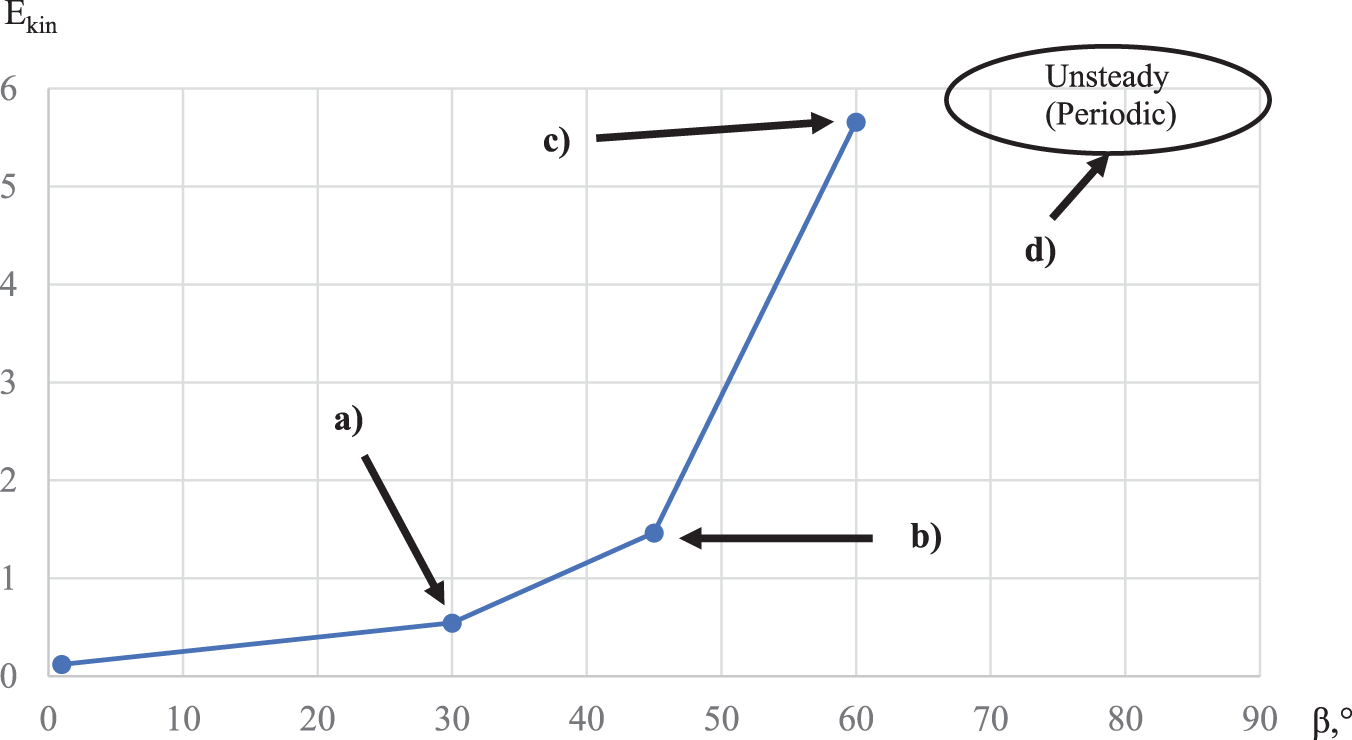
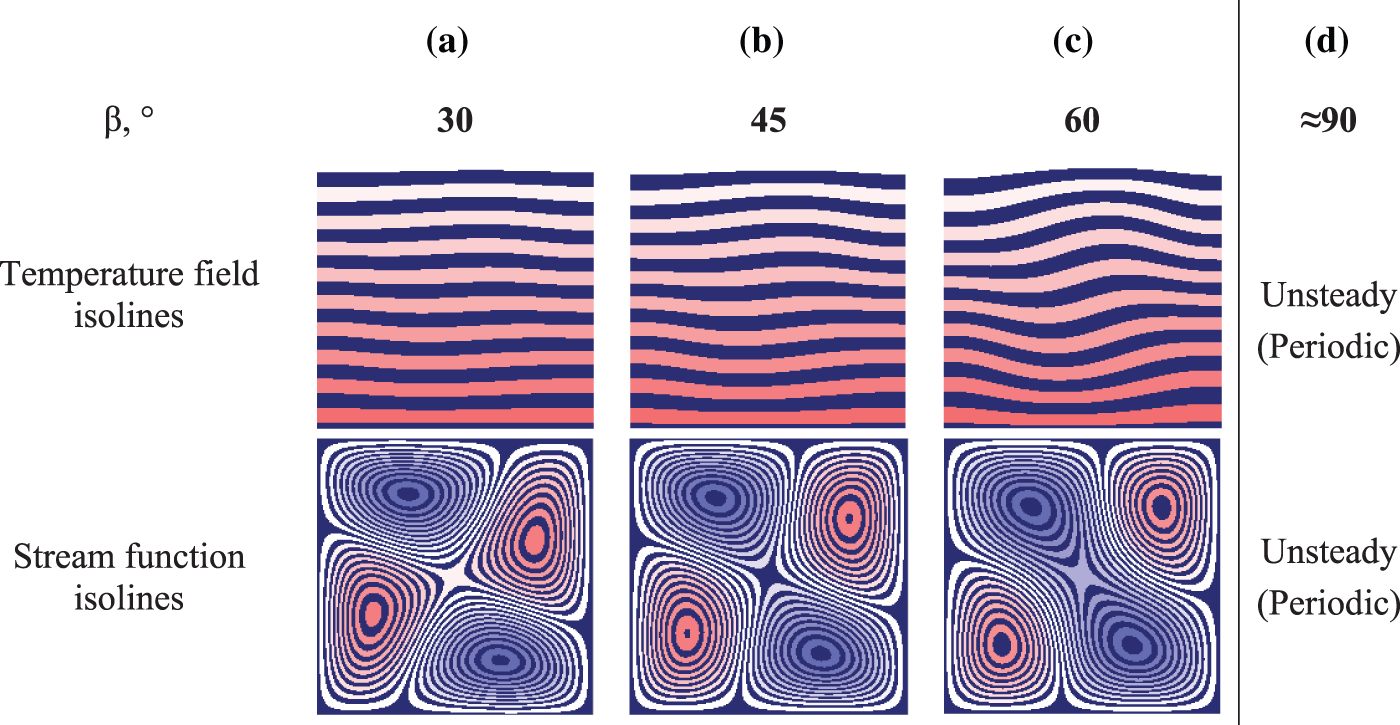
Figure 7: Dependence of kinetic energy on β ( Gr=9500 , α=135∘ )

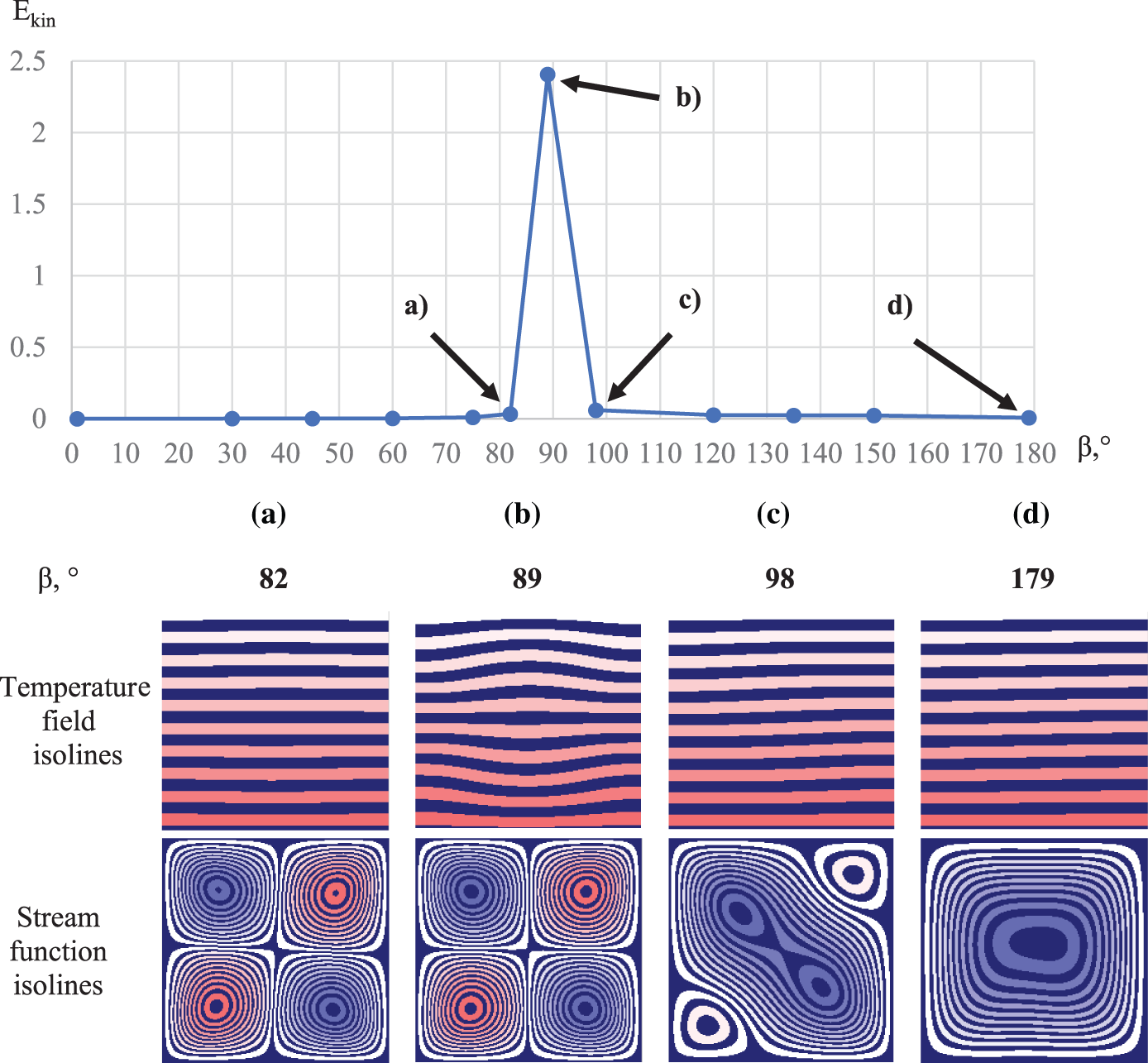
Figure 8: Dependence of kinetic energy on β ( Gr=9500 , α=179∘ )

Analysis of the obtained results showed that for any values of Gr (Grashof numbers) and α (inclination angles of the acceleration action vector relative to the temperature influence vector), there are two characteristic ranges of β values (inclination angles of the vibration action vector relative to the temperature influence vector). In the first range, for values of angles β from to βk , the kinetic energy is close to , that is, the effect of acceleration on the intensity of the convective flow is almost completely compensated by the effect of vibration. In the second range for values of angles β from βk to π/π22 , kinetic energy is significant.

In the case when the vibration vector is directed along the normal to the heated surface, i.e., is co-directional to the heat flux at β = 90˚, it was not possible to find a stationary solution for some cavity angles α. This is due to the nonstationary behavior of the gas flow, as well as to the fact that the solution is periodic in time.

In this case, the value of the angle βk depends almost linearly on the angle α and depends little on the Grashof number (Fig. 9).

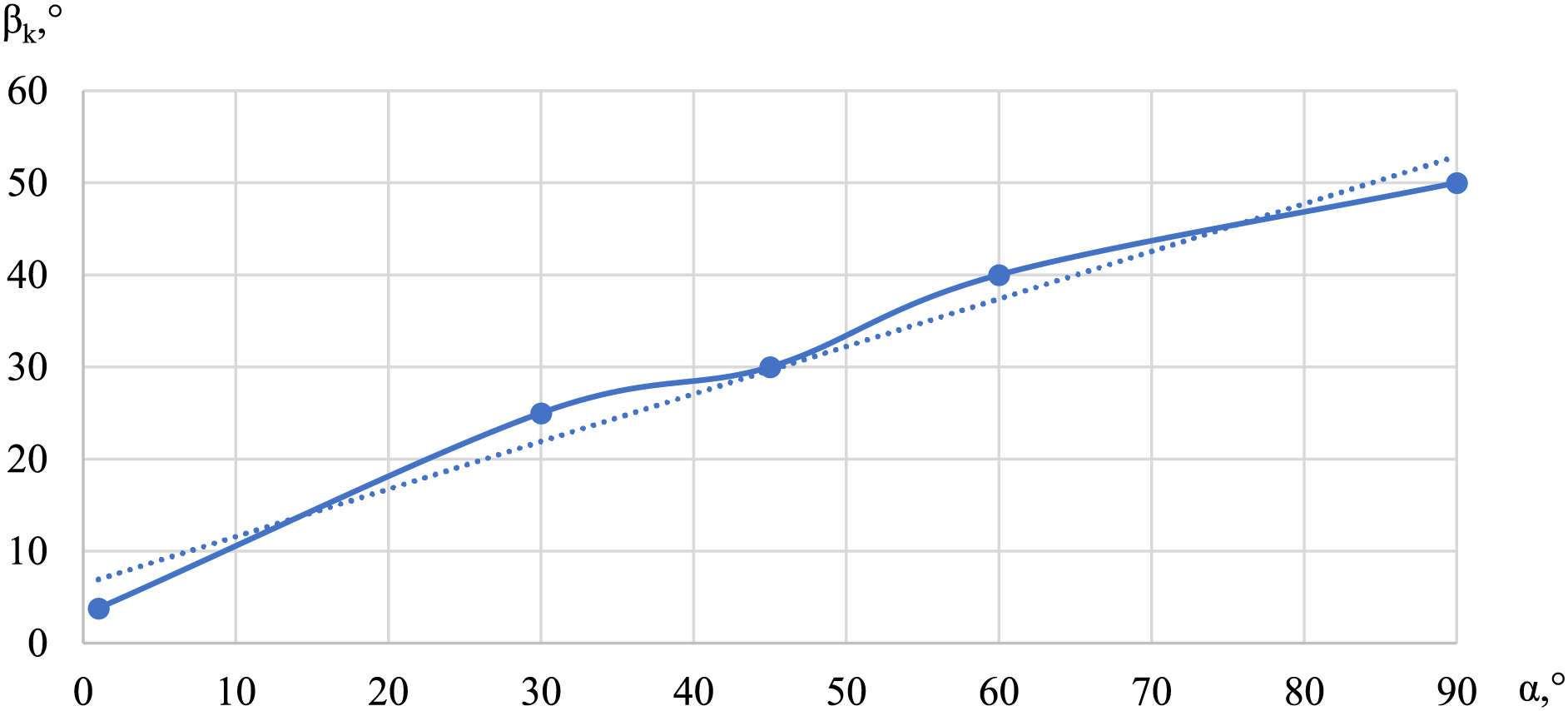
Figure 9: Dependence of βk (the inclination angle of the vibration impact vector relative to the temperature impact vector, at which the vibration effect ceases to compensate for the effect of acceleration on the intensity of the convective flow) by α (the inclination angle of the acceleration impact vector relative to the temperature impact vector)

A sharp transition to a developed flow at increased flow intensity occurs at the same time when, in an infinite cavity of square cross-section, a significant maximum deviation from the linear temperature distribution is not realized, and the isotherms have a complex curved structure.

When hydrogen in a cavity is exposed only to gravity and temperature, the flow intensity, determined by kinetic energy, has a nonlinear dependence on the angle of inclination of the cavity (Fig. 10). In this case, there is an increased intensity of the flow, comparable for cases when two mechanisms of vibrogravitational convection cannot compensate each other.

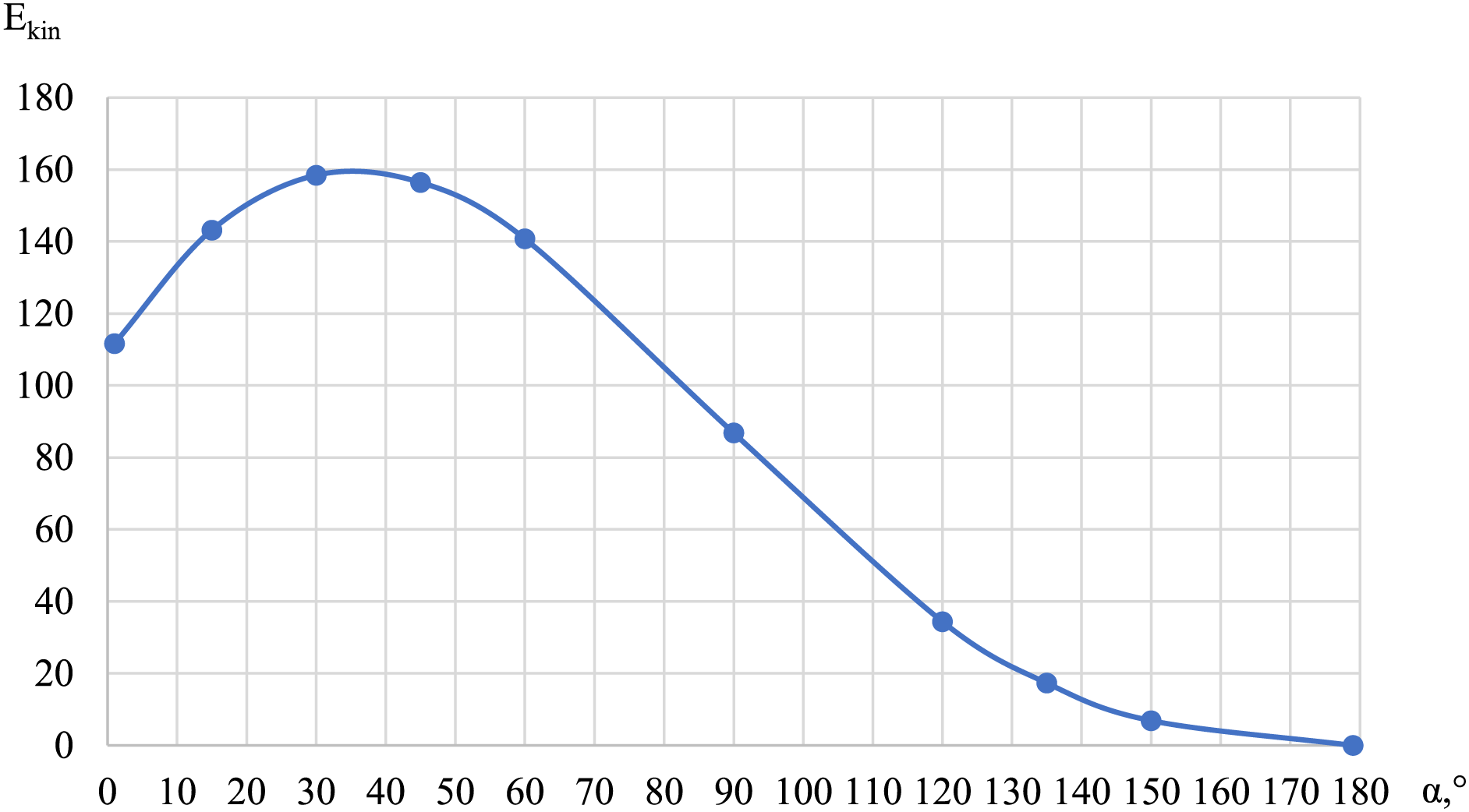
Figure 10: Dependence of kinetic energy on the angle of inclination of the vector of the influence of gravity relative to the vector of the influence of temperature, which shows how much the intensity of kinetic energy can be compensated ( Gr=9500 )

It should also be noted that for cases where the flow in the cavity is realized at the limiting values of the angle of influence of vibration βk , and the condition for minimizing kinetic energy stops working; in this case, there also remains some point, different from Condition (1), at which the minimum kinetic energy will be realized (Fig. 11).

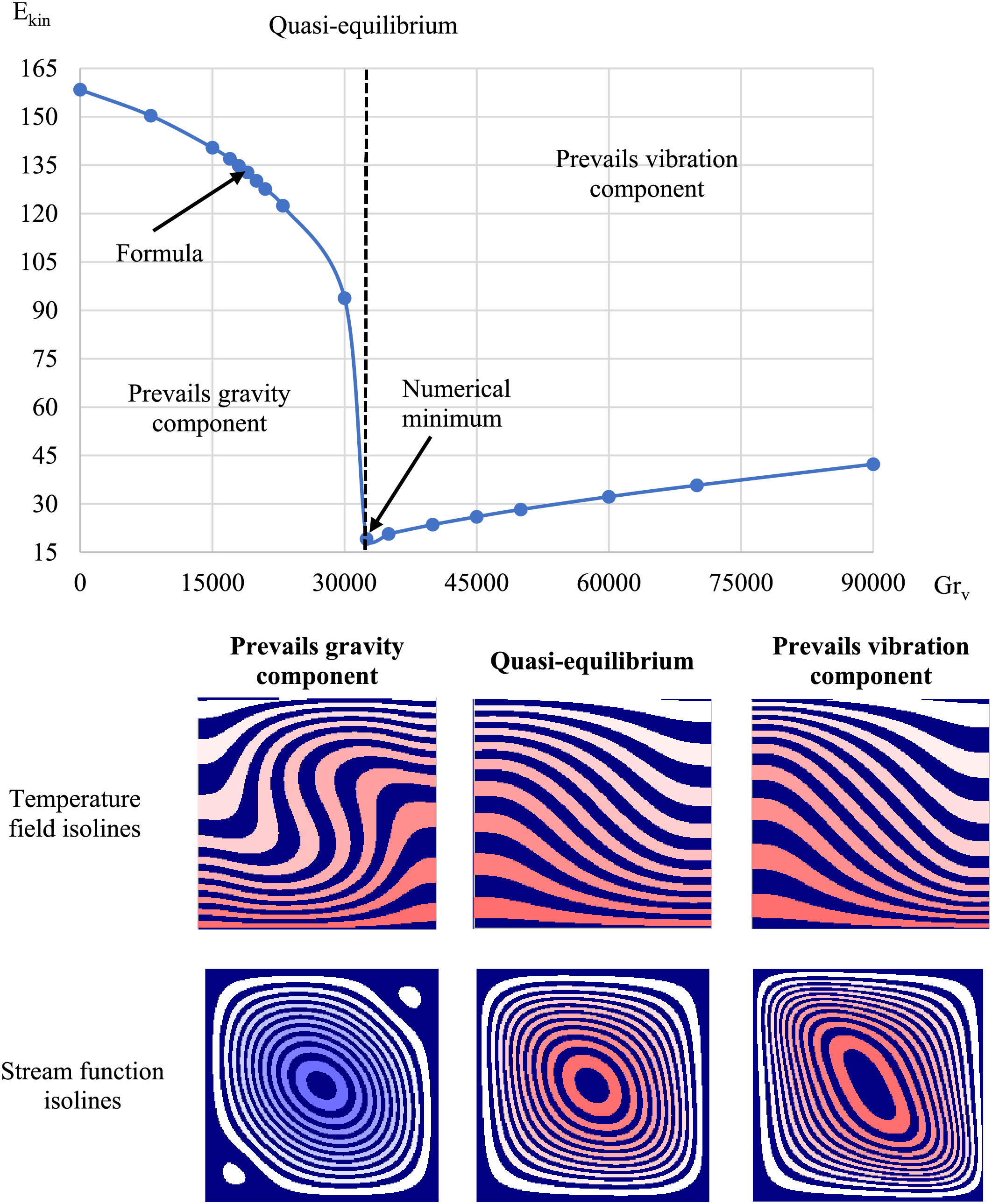
Figure 11: Dependence of kinetic energy on the vibration Grashof number for the limiting values of the vibration impact angle βk ( Gr=9500 , α=30∘ , β=45∘ )

5  Conclusion

1. From the obtained results, it can be concluded that Condition (1) works as long as the temperature field does not change significantly with respect to its initial linear distribution and indicates the parameter values at which the intensity of the averaged flow is practically equal to zero;

2. In the case where the intensity of convective flow significantly changes the initial temperature distribution, calculations have shown that a combination of parameters is possible at which the intensity of the flow as in the case of a linear temperature distribution, can be practically above zero. The role of Formula (1) is now reduced to the fact that it can be used to find the region near which one should search for the point where both convection mechanisms almost completely compensate each other, as can be seen in Fig. 11. In the following, we would like to define a correction to Condition (1), which allows us to determine the minimum of kinetic energy in the general case;

3. The effect of mutual suppression of the mentioned mechanisms of thermal convection obtained in calculations should be used in solving one of the main problems–hydrogen leakage through the walls of pipes and cavities.

Acknowledgement: None.

Funding Statement: The research was carried out with financial support from the Russian Ministry of Education and Science, project FSNM-2023-0004 “Hydrogen energy. Materials and technology for storage, transportation and use of hydrogen and hydrogen-containing mixtures”.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tatiana P. Lyubimova, Vladimir Ya. Modorskii, Albert N. Sharifulin; data collection: Sergey A. Plotnikov, Sergey S. Neshev; analysis and interpretation of results: Stanislav L. Kalyulin, Sergey A. Plotnikov, Albert N. Sharifulin; draft manuscript preparation: Stanislav L. Kalyulin, Sergey S. Neshev. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data on which this paper is based is available from the authors upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Demin VA, Gershuni GZ, Verkholantsev IV. Mechanical quasi-equilibrium and thermovibrational convective instability in an inclined fluid layer. Int J Heat Mass Transf. 1996;39(9):1979–91. doi:10.1016/0017-9310(95)00239-1. [Google Scholar] [CrossRef]

2. Gershuni GZ, Lyubimov DV. Thermal vibrational convection. New York: Willey; 1998. p. 1–372. [Google Scholar]

3. Sharifulin AN. Vibrational convection in cylindrical cavity under arbitrary direction of heating. Convective Flows Perm. 1981;22–9. [Google Scholar]

4. Gershuni GZ, Kolesnikov AK, Legros JC, Myznikova BI. On the vibrational convective instability of a horizontal, binary-mixture layer with the Soret effect. J Fluid Mech. 1997;330:251–69. doi:10.1017/S002211209600376X. [Google Scholar] [CrossRef]

5. Gershuni GZ, Kolesnikov AK, Legros JC, Myznikova BI. On the convective instability of a horizontal binary mixture layer with Soret effect under transversal high frequency vibration. Int J Heat Mass Transf. 1999;42(3):547–53. doi:10.1016/S0017-9310(98)00154-9. [Google Scholar] [CrossRef]

6. Smorodin BL, Myznikova BI, Legros JC. Evolution of convective patterns in a binary-mixture layer subjected to a periodical change of the gravity field. Phys Fluids. 2008;20(9):496. doi:10.1063/1.2978065. [Google Scholar] [CrossRef]

7. Elhajjar B, Mojtabi A, Charrier-Mojtabi MC. Influence of vertical vibrations on the separation of a binary mixture in a horizontal porous layer heated from below. Int J Heat Mass Transf. 2009;52(1–2):165–72. [Google Scholar]

8. Bouarab S, Mokhtari F, Kaddeche S, Henry D, Botton V, Medelfef A. Theoretical and numerical study on high frequency vibrational convection: influence of the vibration direction on the flow structure. Phys Fluids. 2019;31(4):043605. [Google Scholar]

9. Mokhtari F, Kaddeche S, Henry D, Bouarab S, Medelfef A, Botton V. Three-dimensional effect of high frequency vibration on convection in silicon melt. Phys Rev Fluids. 2020;5(12):123501. [Google Scholar]

10. Shevtsova V, Ryzhkov II, Melnikov DE, Gaponenko YA, Mialdun A. Experimental and theoretical study of vibration-induced thermal convection in low gravity. J Fluid Mech. 2010;648:53–82. [Google Scholar]

11. Gaponenko Y, Shevtsova V. Mixing under vibrations in reduced gravity. Microgravity Sci Technol. 2008;20:307–11. [Google Scholar]

12. Kolchanova EA, Kolchanov NV. The interaction of thermal vibrational and thermal gravitational mechanisms of convection onset in a fluid-porous layer. Microgravity Sci Technol. 2021;33(3):1–15. doi:10.1007/s12217-021-09895-3. [Google Scholar] [CrossRef]

13. Lyubimov DV, Sharifulin VA, Lyubimova TP, Sharifulin AN. Thermal vibrational convection of water near its density inversion point in a cylindrical cavity with constant heat flux at the boundaries in low gravity conditions. Microgravity Sci Technol. 2019;31(3):269–78. doi:10.1007/s12217-019-9686-1. [Google Scholar] [CrossRef]

14. Sharifulin VA. Thermovibrational low-mode model of convection in a horizontal layer with longitudinal vibrations. J Sib Fed Univ Math Phys. 2017;10(2):158–69. doi:10.17516/1997-1397-2017-10-2-158-169. [Google Scholar] [CrossRef]

15. Boaro A, MacDowall G, Lappa M. Symmetry properties and bifurcations of viscoelastic thermovibrational convection in a square cavity. Phys Rev E. 2023;108(6):065101. doi:10.1103/PhysRevE.108.065101. [Google Scholar] [PubMed] [CrossRef]

16. Boaro A, Lappa M. Competition of overstability and stabilizing effects in viscoelastic thermovibrational flow. Phys Rev E. 2021;104(2):25102. doi:10.1103/PhysRevE.104.025102. [Google Scholar] [PubMed] [CrossRef]

17. Boaro A, Lappa A. Multicellular states of viscoelastic thermovibrational convection in a square cavity. Phys Fluids. 2021;33(3):33105. doi:10.1063/5.0041226. [Google Scholar] [CrossRef]

18. Crewdson G, Lappa M. Spatial and temporal evolution of three-dimensional thermovibrational convection in a cubic cavity with various thermal boundary conditions. Phys Fluids. 2021;34(1):014108. [Google Scholar]

19. Sharifulin AN. Controllable equilibrium of an inhomogeneously heated liquid in a vibrational field. J Exp Theor Phy. 2010;110(1):157–61. doi:10.1134/S1063776110010188. [Google Scholar] [CrossRef]

20. Sharifulin AN, Plotnikov SA, Lyubimova TP. Influence of the directions of vibrations and gravity on the formation of vortex structures of a nonuniformly heated fluid in a square cavity. Microgravity Sci Technol. 2022;34(5):97. doi:10.1007/s12217-022-10016-x. [Google Scholar] [CrossRef]