Stability of a Viscous Liquid Film in a Rotating Cylindrical Cavity under Angular Vibrations

Nomenclature

1  Introduction

The problem of the dynamics and stability of interphase boundaries is relevant in scientific and applied aspects [1,2]. The stability of rimming flows in rotating cavities is actual for fundamental science and is an important technological problem, the study of which has been the subject of many works [3–7]. The instability of the interface can be excited by gravity in various rotating hydrodynamic systems, two low-viscosity immiscible liquids of different densities [8], and the surface of a granular medium in a liquid [9,10]. Of great interest in this regard is the effect of rotational vibration on the shape of the boundary discovered in [11]. It was found in [11] that when modulating the rotation speed of a cylindrical cavity containing two liquids, when the denser liquid covering the lateral boundary has a high viscosity, the interphase axisymmetric boundary loses stability. With an increase in the amplitude of the rotation speed modulation, a quasi-stationary relief in the form of a “frozen” wave appears on the interface in a threshold manner. The relief has the form of an azimuthally periodic system of two-dimensional crests and troughs extended along the axis of rotation, which are rotating together with the container and performing slight azimuthal oscillations relative to the cavity with the libration frequency. It was shown that the appearance of the frozen two-dimensional wave on the surface of a viscous liquid film is associated with the development of Kelvin–Helmholtz oscillatory instability. The physical model proposed in [11], which describes the development of the frozen wave on the surface of the layer (film) of the viscous liquid on the inner wall of the rotating horizontal cylinder, is based on the results of systematic theoretical [12–16] (and later [17]) and experimental [18–20] studies of the Kelvin–Helmholtz oscillatory instability without rotation. A feature of the cited works is that the instability of the plane interphase boundary is studied during tangential oscillations of liquids relative to the interface caused by translational vibrations. The experimental results [11] are in agreement with the model constructed, which reflects the behavior of the interphase boundary only to certain approximations. The latter include: relatively slow rotation, when the Coriolis force does not play a role; high viscosity of the liquid covering the cavity wall, when the entire layer of viscous liquid is completely entrained by the wall during its azimuthal oscillations; high-frequency modulation of the rotation speed, at which the low-viscosity liquid filling the remaining volume of the cavity rotates at a constant speed due to the absence of viscous interaction with the denser liquid. The latter means that the thickness of the Stokes layer in the low-viscosity liquid near the interface is negligibly thin due to the high contrast of liquid viscosities. Finally, the radius of the interface in the rotating cylinder is assumed large compared to the capillary length, while the length of the frozen wave is small compared to the azimuthal length of the interface. The above makes it relevant to study the influence, on the effect of excitation of the quasi-stationary relief at the boundary of the viscous-liquid layer during the non-monotonous rotation of the cavity, of such factors as: the thickness of the viscous liquid layer, the contrast of viscosities and the rotation speed of the cavity.

The relevance of the study of interface dynamics is determined by the importance of the fundamental and technological problem of controlling mass transfer across the interface [21,22]. At the same time, vibrational methods for controlling the interface dynamics are of particular interest due to the convenience and simplicity of the vibration effect on hydrodynamic systems [23,24]. Note that the effect of rotational vibrations (rotation rate modulation) on the shape of the interphase boundary, discovered experimentally in [11], is original and qualitatively new; the excitation of the oscillating motion of liquids near the interphase boundary in this case is determined by the different interactions of liquids with the boundaries of the cavity and with each other, due to high contrast of viscosities. At the same time, the experimental results and the physical model [11] refer to the case of relatively slow rotation, when rotation (Coriolis force) does not play an important role.

The present study is an advancement over [11]; the objective of this work is the experimental investigation of the dynamics of the boundary of a viscous-liquid layer with variations in the thickness of the viscous liquid layer and the rotation rate. The studies are performed with liquids of lower contrast of viscosities in a wide range of amplitudes and frequencies of rotation rate modulation with varying thicknesses of the viscous liquid layer. The novel and important result: it is found that the rotation has a stabilizing effect, which can be characterized by a dimensionless rotation rate, and the threshold of axisymmetric interface stability is determined by the product of vibrational parameter and the dimensionless rotation rate to some power.

2  Experimental Setup and Procedure

2.1 Experimental Setup

The stability of the interface between two liquids in a horizontal long cylinder is studied experimentally for the case when the rotation velocity is modulated against a background of uniform rotation. The liquids are: low viscosity and low density PMS-5 silicone oil and more dense and viscous glycerol. The coefficient of interfacial tension at the PMS-5–glycerol interface was measured using the hanging drop technique. The liquids properties as well as the viscosity contrast coefficient of liquids K≡ν2/ν1 are presented in Table 1. The definition of the viscosity contrast coefficient corresponds to [14], in fact, this coefficient characterizes the ratio of the thicknesses of Stokes boundary layers in liquids.

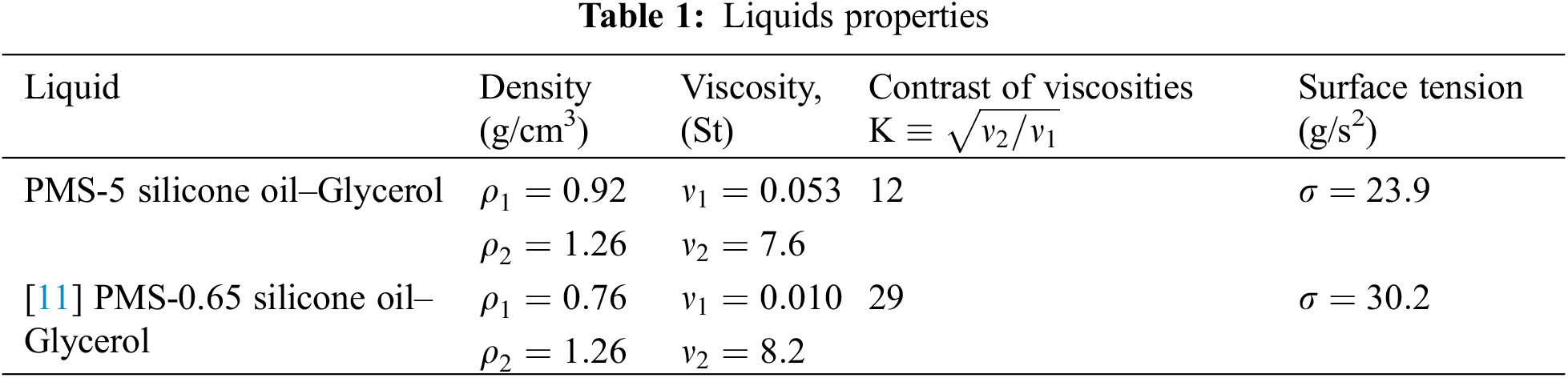
The experiments are carried out at a relatively rapid rotation of the cavity, when the entire system is in the centrifuged state, while the viscous heavy liquid under the influence of the centrifugal force is located near the cavity wall, forming an axisymmetric layer of thickness h0, and the light, low-viscosity liquid is located in the center of the cavity in the form of a cylinder with a radius Rin (Fig. 1). The experiments are carried out with the layers of viscous liquid of different thicknesses, h0 = 3.3, 4.6 mm.

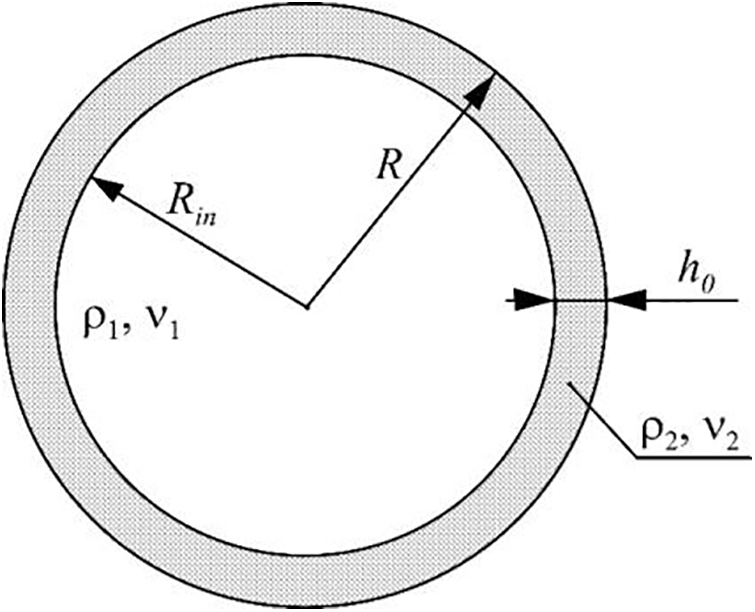
Figure 1: Scheme of the liquid distribution in the cavity cross section without librations

The results obtained are compared with the results of a similar experiment [11], performed with a pair of liquids silicone oil PMS-0.65–glycerin, with a higher contrast of viscosities K=29 . The liquid properties are also presented in Table 1. The layer thickness in [11] was h0 = 3.0 mm.

The experimental setup (Fig. 2) is a horizontal cylindrical cavity with a radius R=3.0 cm and a length L=7.4 cm. The cavity rotation according to the law Ω=Ωrot(1+εcos⁡Ωlibt) is set by a stepper motor type FL86STH118-6004A. Here Ωrot is the rotation speed, Ωlib –circular frequency of modulation, ε – dimensionless amplitude of rotation speed modulation. The cavity rotation rate varies in the range frot≡Ωrot/2π=3−6  rps, the frequency of the velocity modulation varies within flib≡Ωlib/2π=3−7 Hz and the amplitude of the rotation velocity modulation changes in the interval ε=0−0.9 .

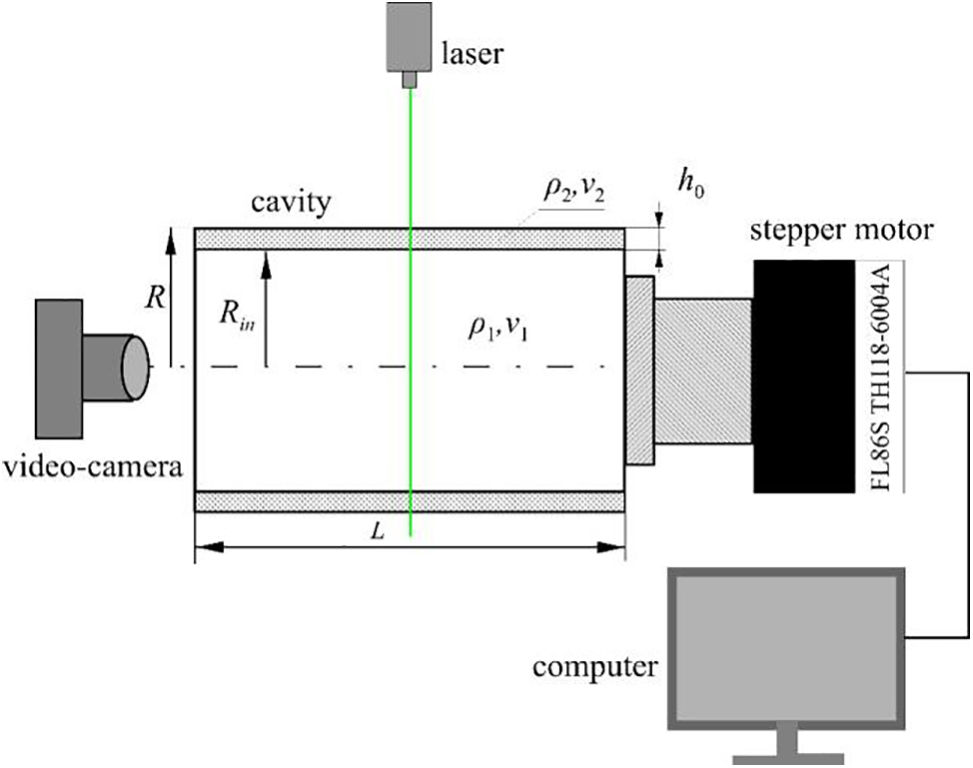
Figure 2: Scheme of the experimental setup

The cavity is machined inside a Plexiglas parallelepiped of square cross-section. The transparent flanges and polished edges of the cuvette allow liquids to be observed practically without optical distortion both from the end and from the side. A detailed description of the cuvette design can be found in [11]. When studying the shape of the interphase boundary in cross-section, the cuvette is illuminated with a green light sheet from a laser of the type KLM-532/h-1000 with the power of 1 W. The laser sheet thickness is 2 mm. The plane of the laser sheet is perpendicular to the axis of the cavity rotation. Taking into account the two-dimensionality of the vibration structures, the optimal position for the laser light sheet is selected to be on the median of the cavity length in experiments. To exclude the extraneous light the side walls of the cavity, except the slot for the light sheet, are covered with black self-adhesive film. The viscous liquid (glycerol) is visualized by rhodamine, which fluoresces red under the green laser light. The concentration of the dissolved rhodamine does not exceed 10−3 percent and its presence does not affect the physical properties of the liquid. Rhodamine does not dissolve in the low-viscosity liquid, which provides a high brightness contrast at the interface. The use of a red filter during the video recording of the interface eliminates the stray light and enhances the contrast of the boundary image.

Photo and video recording of the interface between two liquids is carried out through the front transparent end of the cavity using a high-speed video camera (type CamRecord Optronis CL600 × 2) installed coaxially with the axis of the cavity rotation. The images are captured with a resolution of 800 × 800 pix (and further processed using a computer), with a frame rate of 420 fps, sufficient to study the shape of the interphase boundary and its transformation during the period of velocity modulation.

2.2 Experimental Technique

The experiment begins with the cuvette being rapidly rotated ( frot > 15  rps) while the interface between the liquids takes an axisymmetric shape. Within a few tens of seconds, under the action of centrifugal force, the end surface is cleared of droplets of viscous (more dense) liquid. After this, the rotation velocity is gradually decreased to the required value frot . The observation of the boundary shape is carried out with a step-by-step increase in the amplitude of the velocity modulation at a given frequency flib . In Fig. 3a, the interface is visible as a bright light line enclosed between dark stripes. The developed technique for visualizing one of the liquids (with higher refractive index) with rhodamine allows one to see the interface in the form of a thin line. The appearance of a dark stripe on the side of the viscous liquid layer is explained by the phenomenon of total internal reflection–the refractive index of glycerin exceeds that of low-viscosity oil in the central part of the cavity.

Figure 3: Pictures of interface when modulating the rotation velocity at frot = 3 rps, flib = 4 Hz: a–d) ε = 0; 0.52, 0.54, 0.56. Pictures of interface at frot = 3 rps, flib = 3 Hz: e–f) ε = 0.45, 0.49. The blue line in Fig. 3a shows the boundary of the cavity in the cross-sectional plane of the light sheet, working fluids are PMS-5 and glycerol, h0 = 4.6 mm

It was found that with the increase in the amplitude of the rotation velocity modulation ε, the axisymmetric interface loses its stability in a threshold manner, and a quasi-stationary two-dimensional relief with an azimuthal periodicity develops on it (Fig. 3b–d). Two-dimensional crests of viscous liquid extended along the axis of rotation move together with the cavity. With the increase in the velocity modulation amplitude, the height of the frozen wave increases as well. The threshold value of the modulation amplitude ε and the azimuthal wave number of the wave in the threshold depend on the rotation velocity and the velocity modulation frequency.

As noted above, in the subthreshold area the interface has an axisymmetric shape. It should be noted that if the frequency of librations flib coincides with the rotation velocity frot the interphase boundary loses axial symmetry before the Kelvin–Helmholtz instability occurs: the boundary shifts from the rotation axis in the radial direction. The displacement increases with the velocity modulation amplitude. With a small displacement, the boundary retains a circular shape. As it approaches the boundary of the rotating cavity, the interphase boundary loses its circular shape (Fig. 3e). A theoretical description of this effect is available in [25]. It was shown that the violation of the axial symmetry of the interphase boundary is associated with the average force field formed in the rotating reference frame by the action of the gravity field transverse to the axis of rotation. It should be noted that if the frequencies coincide, frot=flib , the development of the frozen wave instability is also observed upon reaching a certain threshold value of the libration amplitude ε. The wave develops in a part of the boundary, which is limited to the area where the layer thickness is the smallest (Fig. 3f). The present study is devoted to the stability of an axisymmetric unperturbed boundary, which is formed in the entire studied range of libration frequencies and rotation rates when the libration and rotation frequencies do not coincide. The study of the boundary dynamics, when the rotation velocity and the libration frequency coincide, is beyond the scope of this work.

3  Experimental Results

3.1 Interface Stability

The studies have shown that at small libration amplitudes, the boundary retains an axisymmetric shape. The threshold excitation of the wave relief in the studied range of parameters has a supercritical character–the development of the wave with the increase in the modulation amplitude ε and its disappearance while decreasing ε occur without hysteresis. In most of the cases considered, with different frot and h0, when increasing the frequency of librations, the threshold value of the modulation amplitude decreases (Fig. 4a,b). Only at the lowest rotation velocity, frot = 3 rps, the stability threshold slightly varies with the libration frequency flib. A comparison to the results of the experiments [11] performed at K=29 (Fig. 4a) shows that the threshold curves [11] have a similar appearance, but are located higher. The confidence intervals for all points shown in Fig. 4 are Δε=0.005 , they are not presented so as not to clutter the picture. The confidence interval is determined by the step of ε increase (decrease) during the experiment, which is 0.01; the threshold is determined by visually recognizing the appearance of relief. With increasing the thickness of the viscous liquid layer, the stability threshold grows (Fig. 4b).

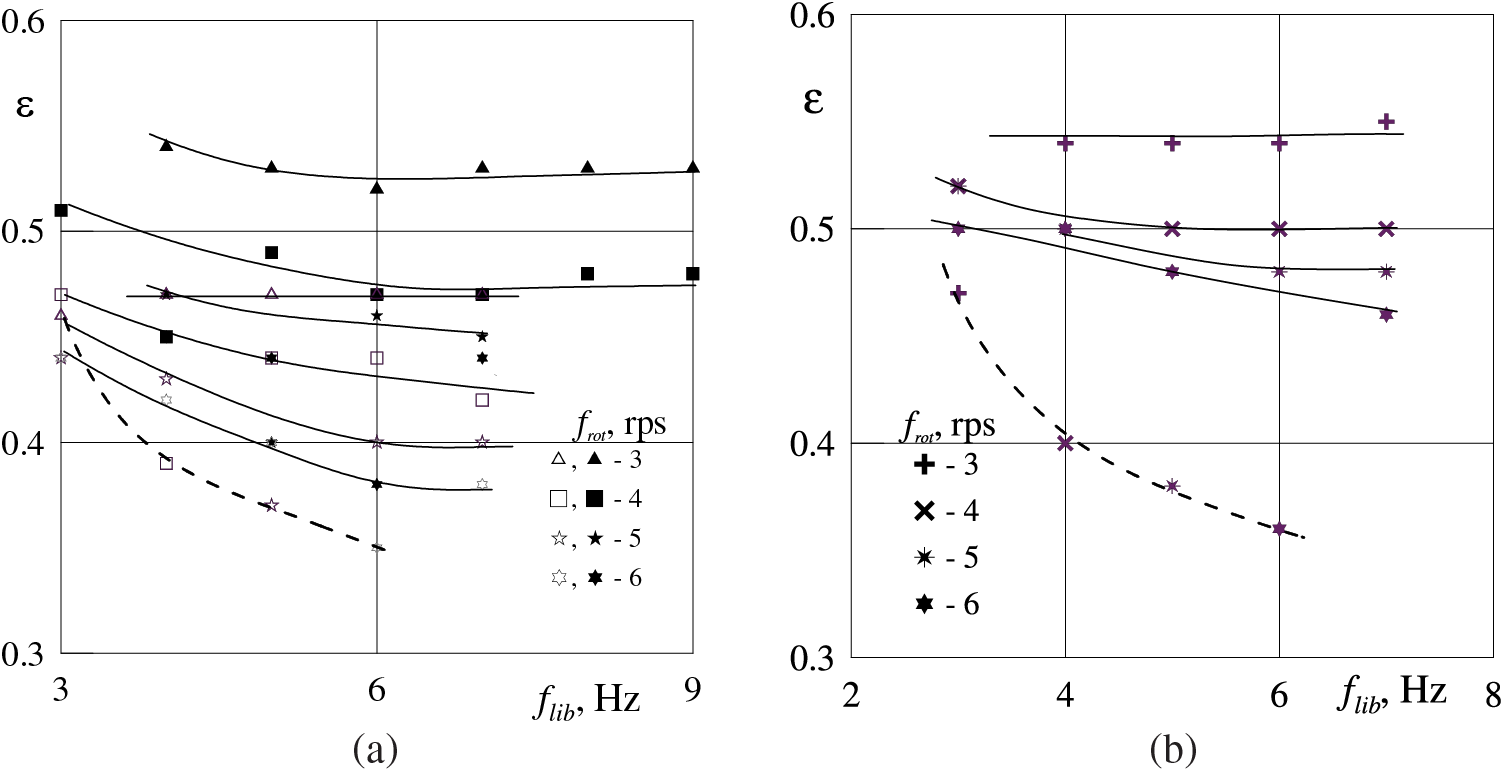
Figure 4: Stability threshold curves for an axisymmetric PMS-5–glycerol boundary on the plane (flib,ε) : а) h0 = 3.3 mm–empty points (for comparison the thresholds for the PMS-0.65–glycerol pair are shown in filled symbols at h0 = 3.0 mm [11]); b) h0 = 4.6 mm. The dashed lines show the stability threshold when the libration frequency coincides with the rotation velocity

It is important to note that some points in Fig. 4a,b fall out of the monotonic dependencies corresponding to a given rotation velocity and are located significantly lower. These points correspond to the case when the libration frequency exactly coincides with the rotation velocity. If the frequency difference exceeds at least a few percent, this phenomenon does not appear. This displacement is due to the fact that when libration and rotation frequencies coincide, a loss of symmetry of the interphase boundary is observed (Fig. 3е). As a result of the boundary radial displacement the thickness of the viscous fluid layer decreases on a part of the perimeter. The loss of symmetry and the displacement of the interphase boundary occurs in a non-threshold manner and increases with the amplitude of the velocity modulation. Instability, in this case, is limited along the perimeter–the frozen wave develops in the area where the layer has the smallest thickness (Fig. 3f). It is interesting that the threshold points obtained in the layers of different initial thicknesses h0, are consistent with each other. The local nature of the instability explains the agreement of the thresholds for different initial volumes of viscous liquid–the threshold value is determined not by the average-along-layer thickness, but by the local one, which apparently takes on similar values at different fillings. As noted above, the object of this study is axisymmetric layers; the cases of frequency coincidence when the layers are not axisymmetric, will not be considered in further analysis and discussion.

Fig. 5 shows the threshold values of the modulation amplitude depending on the libration frequency for different thicknesses of viscous liquid at different rotation velocities. It can be seen that with the increase in the layer thickness when going from h0 = 3.3 mm to h0 = 4.6 mm the threshold value increases. The comparison of the fragments а and b (Fig. 5) shows a decrease in the critical amplitude of the velocity modulation when increasing the rotation velocity. Note that the studied thicknesses meet the condition h0 < δ2 , where δ2≡2ν2/Ωlib is the thickness of the Stokes layer in the viscous liquid. This limitation is due to the fact that the studied mechanism of the generation of an oscillating tangential velocity discontinuity [11] is based on the entrainment of a viscous fluid by the cavity wall performing rotational oscillations.

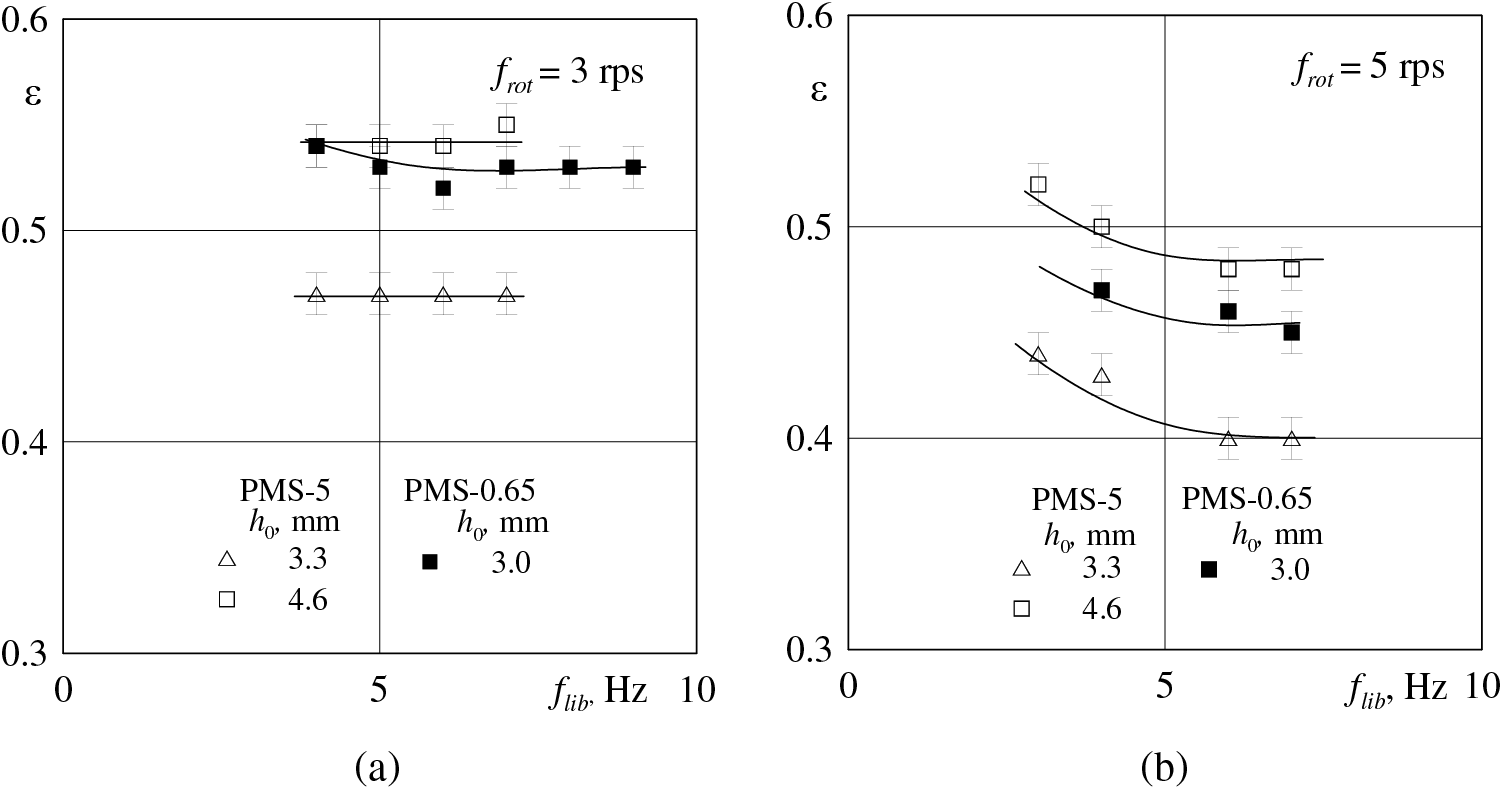
Figure 5: Dependence of the threshold value of the modulation amplitude ε at the interface PMS-5–glycerol on the frequency of librations at different thicknesses h0 for different rotation velocities frot: a)−3 rps, b)−5 rps. For comparison, the filled symbols show the results of experiments for the pair of liquids PMS-0.65–glycerin [11]

The observations performed allow us to conclude that the stability threshold (threshold value of the velocity modulation amplitude): a) increases with the thickness of the viscous fluid layer; b) decreases with increasing the rotation velocity; c) decreases with the frequency of librations, and at high frequencies ceases to change. From a comparison with the results of [11], it follows that the contrast in liquid viscosities significantly changes the threshold value of the velocity modulation amplitude. At this, the rotation speed has a significant influence on the threshold. An explanation of the role of rotation speed and thickness of the viscous fluid layer will be given in paragraph 4, when analyzing the results in the space of the governing dimensionless parameters.

3.2 Shape of the Interphase Boundary

The observations show that in the supercritical area, the number of wavelengths over the perimeter of the interphase boundary takes on an integer value. The wavelength λ is calculated based on the length of the unperturbed interface and the number of waves. In the supercritical region with the increase in the libration amplitude ε (at constant values of the rotation velocity frot and the libration frequency flib) the length of the frozen wave remains practically unchanged in the studied range of parameters frot,, flib and h0.

The wavelength in the threshold of the instability development practically does not change with the frequency of librations (at a given rotation velocity) (Fig. 6) in the area flib > 4 Hz. At flib < 4 Hz, a wave of greater length develops at the threshold. The large scatter of experimental points is due to the fact that an integer number of waves fits onto the perimeter, this means that the relative error of the measured wavelengths is more than 10 percent. At rotation speeds frot = 4 and 5 rps, the wavelengths are consistent within experimental errors (represented in Fig. 6 by one curve, the lowest).

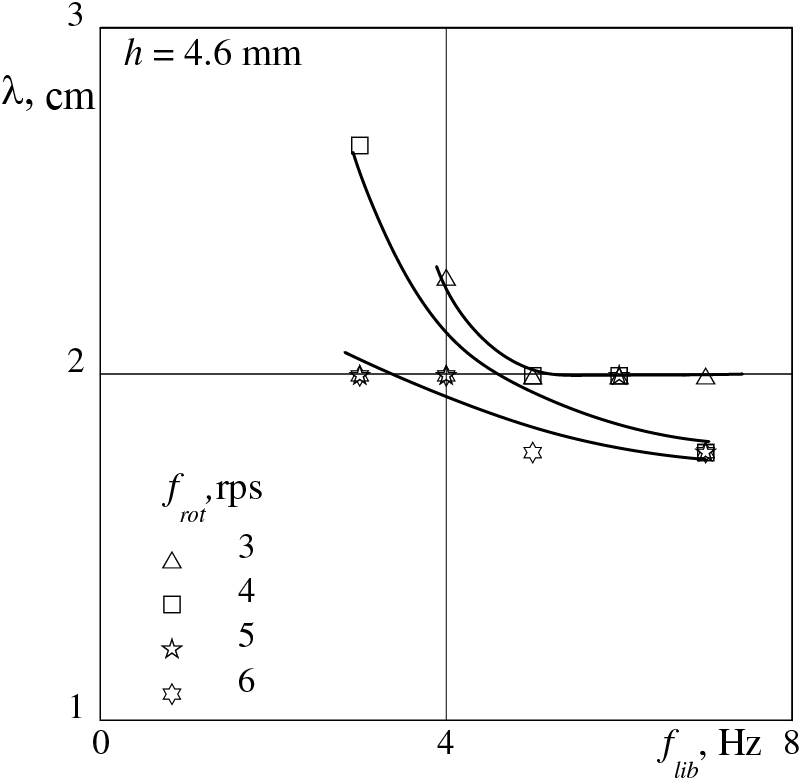
Figure 6: The wavelength λ at the threshold of the relief appearance at the interface of PMS-5–glycerol versus the frequency of librations flib at different rotation velocities frot, h0 = 4.6 mm

At a fixed rotation velocity, the wavelength decreases while increasing the libration frequency (Fig. 7).

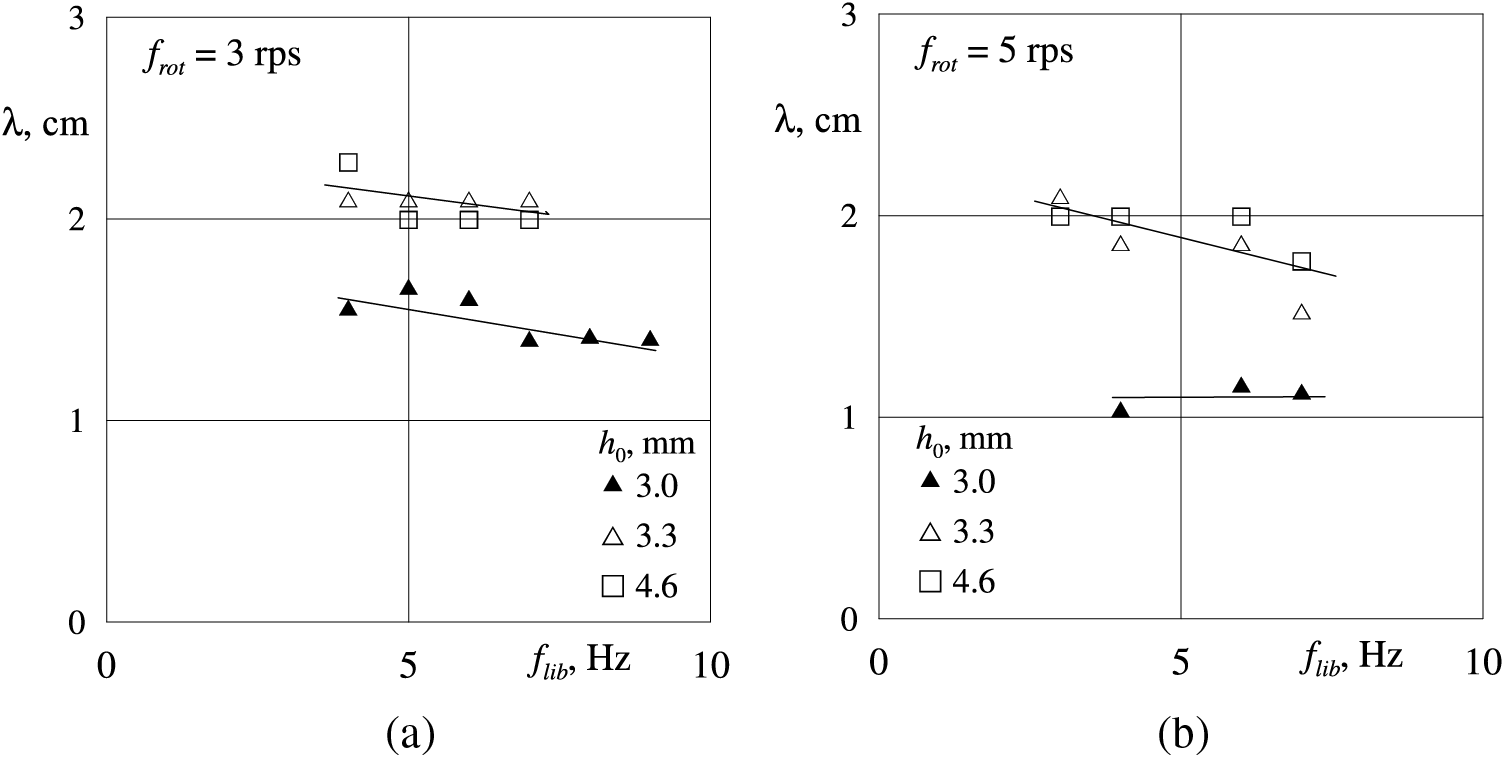
Figure 7: Dependence of the wavelength λ in the threshold of relief appearance on the interface PMS-0.65–glycerol (solid symbols) and PMS-5–glycerol on the frequency of librations at different thicknesses of the viscous liquid layer for rotation velocities frot: a) 3 rps, b) 5 rps

Fig. 7 shows that at a given rotation speed, the results of measuring the wavelength of the azimuthal relief in layers of different thicknesses (3.3 and 4.6 mm) are consistent with an accuracy of scatter, associated, first of all, with the integer value of the waves falling on the perimeter. Thus, the thickness of the viscous liquid layer h0 has little effect on the wavelength. From a comparison of wavelengths at the glycerol–PMS-0.65 interface [11] (presented by solid symbols in Fig. 7) it follows that the wavelength at the threshold for this pair of liquids is less than at the boundary of the glycerol–PMS-5 liquids. Thus, the contrast of liquids viscosities plays an important role. It should be noted that an increase in the rotation speed in all cases is accompanied by a decrease in the wavelength of the structures (compare fragments a and b in Fig. 7).

4  Analysis of Results

The appearance of a frozen wave at the interface is associated with the development of oscillatory Kelvin–Helmholtz (K–H) instability, excited by an oscillating tangential velocity discontinuity at the boundary. This phenomenon is known and studied experimentally and theoretically in the case of tangential oscillations of liquids relative to a flat interface. Such oscillations of liquids are excited, for example, under the action of horizontal translational harmonic oscillations of a cavity filled with liquids. Liquids of different densities oscillate along the interface in an oscillating inertial field. A theoretical model of this phenomenon was developed in [12] for non-viscous liquids. Subsequently, the stability of the interface between viscous liquids was examined theoretically and experimentally. In [14,16,19], it is shown that an increase in viscosity contrast leads to a significant decrease in the stability threshold.

In [11], the excitation of oscillatory instability was discovered in a non-uniformly rotating cylinder with two liquids with a high viscosity contrast. The rotation was carried out at a fairly high speed, and the system was in a centrifuged state with an axisymmetric interface. In this case, the more viscous liquid had a higher density and was located near the outer boundary of the cavity. The nature of the occurrence of an oscillating tangential velocity discontinuity at the interface between liquids was that the viscous liquid near the boundary of the cavity, with uneven rotation, was completely entrained by the cavity wall and performed rotational oscillations along with it, that is, the thickness of the liquid layer was less than the thickness of the Stokes layer. At the same time, the low-viscosity liquid in the middle part of the cavity rotated uniformly at a constant speed, since the Stokes boundary layers in it were of negligible thickness. The theoretical model built in [11], based on the results of studies in the case of translational oscillations [13,14,19], included the approximation Ωrot << Ωlib ; ω2≡Ωlibh02/ν2 << 1 , ω1≡Ωlibh02/ν1 >> 1 , λcap << R . Thus, in the description of the phenomenon, the curvature of the surface is neglected (it is assumed that the wavelength is much less than the circumference), and the rotation speed is assumed to be small, that is, the effect of the Coriolis force is not taken into account. Note that in the described phenomenon, a high viscosity contrast (high viscosity of one of the liquids) plays a fundamental role, since it is the viscous liquid that performs tangential oscillations along the interface as a result of viscous drag by the oscillating wall.

The vibrational parameter B, which determines the threshold for the development of Kelvin–Helmholtz oscillatory instability [12,13], is transformed under the conditions of the present problem. It characterizes the amplitude of the oscillating tangential velocity discontinuity at the interface between two fluids when one fluid oscillates relative to the other in an averaged centrifugal force field and, in accordance with [11], is determined by the expression

B=πρRinε22(1−ρ2)(1+0.5ε2)λcap (1)

where, ρ≡ρ1ρ2 , λcap=2πσ(ρ2−ρ1)Ωrot2Rin(1+0.5ε2) .

In this case, the role of the static force field in a rotating system is played by the centrifugal force averaged over the period, and the effect of the gravity field on the fluid in the cavity, which rotates quite rapidly relative to the horizontal axis, is neglected. Note that the results of experiments [11], carried out on liquids with a high viscosity contrast and on a relatively thin layer of viscous liquid, at high libration frequency were in satisfactory agreement with theoretical and experimental results for translational vibrations of the cavity in the absence of rotation [14,19].

The following questions remains: a) what is the role of the relative thickness of the viscous fluid layer, b) what role does the contrast of liquids viscosities play, c) how does the Coriolis force affect oscillatory K–H instability in rotating cylinder. The dimensionless frequency ω2≡Ωlibh02/ν2 is responsible for the first point, which characterizes the ratio of the thickness of the viscous fluid layer to the thickness of the Stokes layer, and therefore the degree of entrainment of the viscous fluid layer by the oscillating wall. It is proposed to characterize the influence of the Coriolis force by the dimensionless rotation speed ωrot≡Ωroth02/ν1 , this parameter characterizes the ratio of the Coriolis force to viscous forces (in this form–in a layer of low-viscosity fluid).

By analogy with [11], we will plot the dependence of the threshold value of the vibration parameter B on the relative frequency of librations Ωlib/Ωrot (Fig. 8). The figure shows that the stability threshold (critical value of parameter B) at a given rotation speed decreases with the relative frequency of librations Ωlib/Ωrot in all cases. At the same time, in a separate series of experiments performed on a layer of viscous liquid of a fixed thickness, the threshold curves are stratified by rotation speed; with increasing frot, the threshold curves rise, maintaining their shape.

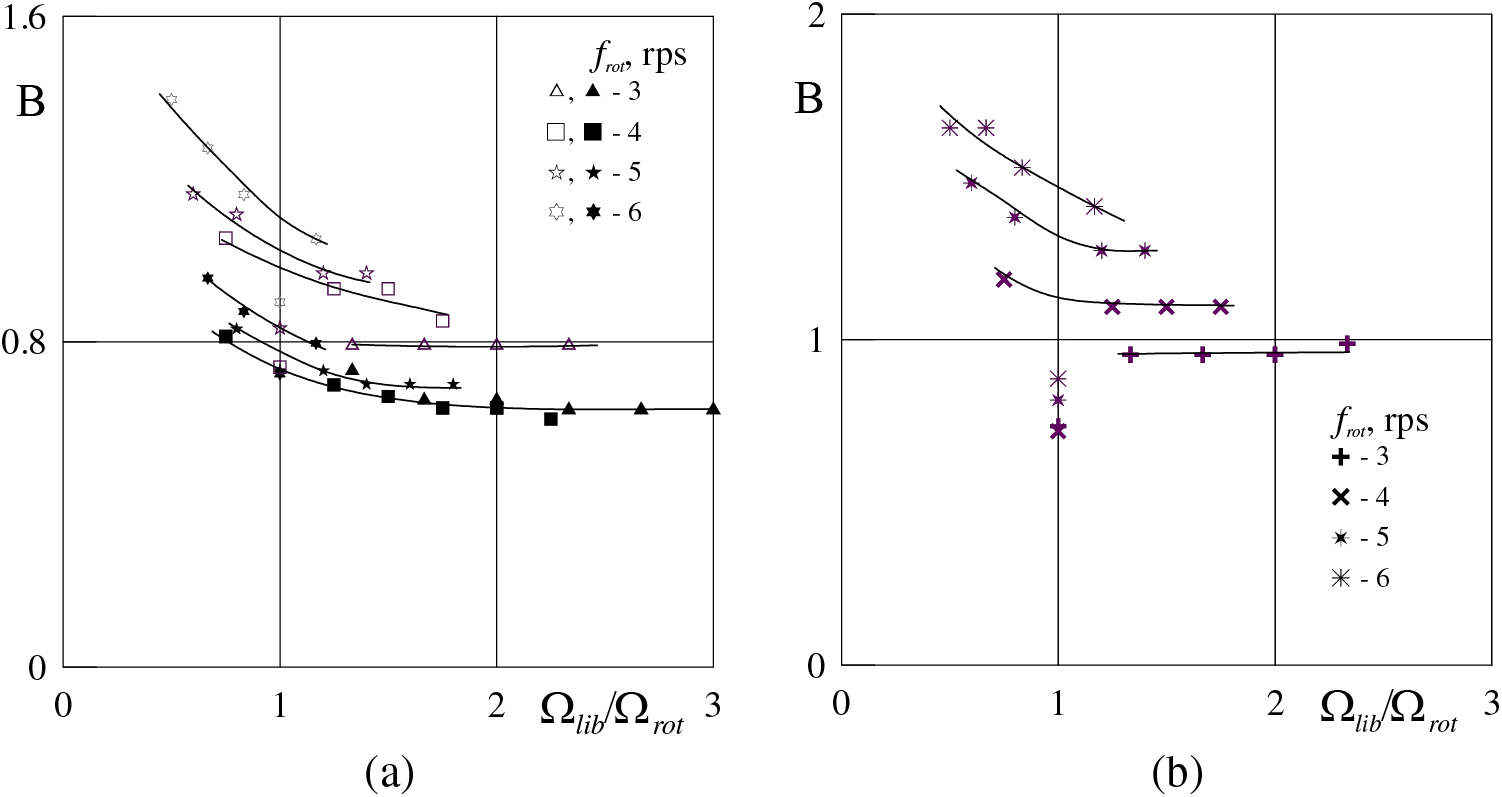
Figure 8: Dependence of the threshold value of parameter B on the relative frequency of librations: a) h0 = 3.3 mm (light symbols); b) h0 = 4.6 mm; the results were obtained on a pair of liquids: glycerin–PMS-5 with a viscosity contrast of K = 12. In fragment a, dark symbols show the results [11] obtained on pair: glycerol–PMS-0.65; K = 29, h0 = 3.0 mm

Comparison with the results of [11], obtained on a pair of liquids “glycerol–PMS-0.65”, indicates that reducing the viscosity contrast increases stability (Fig. 8). An increase in the thickness of viscous liquid layer is also accompanied by an increase in stability; with an increase in the layer thickness h0 = 3.3 mm (Fig. 8a) to h0 = 4.6 mm (Fig. 8b), the family of curves corresponding to different rotation speeds shifts upward. With relatively slow rotation Ωlib/Ωrot > 2 , the stability threshold ceases to change with the relative frequency of librations. Note that in Fig. 8, the points in case of libration and rotation frequencies coincidence, at Ωlib/Ωrot=1 , fall out of the monotonic dependences and locate significantly lower.

The dimensionless wavelength λ/λcap, as can be seen from Fig. 9, at close values of h0 depends on the contrast of liquid viscosities: λ/λcap goes up with the viscosity contrast. The dependences obtained for different pairs of liquids have a similar shape. It should be noted that a significant scatter of experimental points is determined by the condition of an integer number of waves falling on the perimeter of the interface.

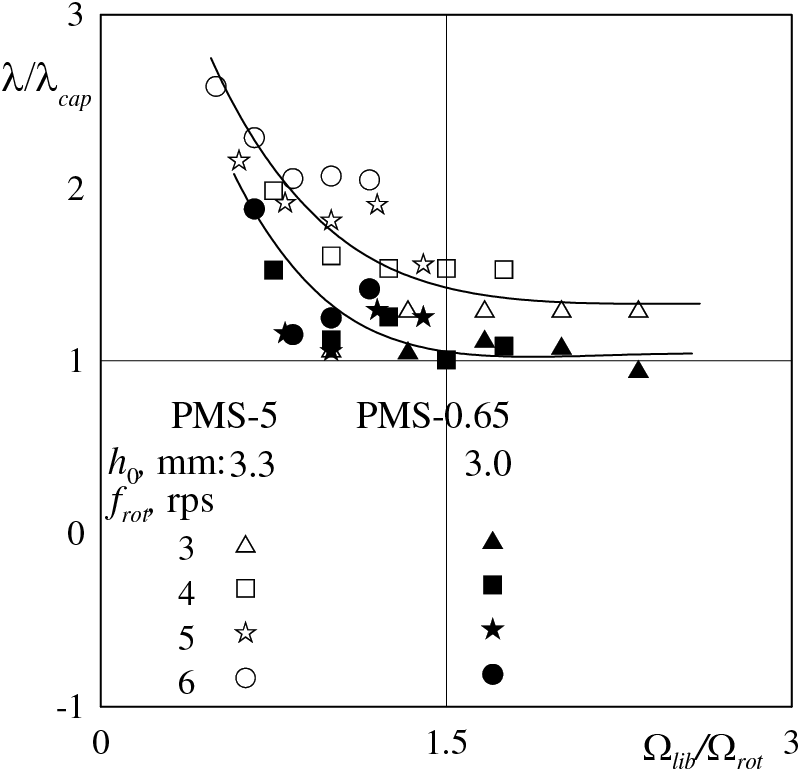
Figure 9: Dimensionless parameter λ/λcap versus the relative frequency of librations, PMS-5–glycerol; for comparison, results of [11]: PMS-0.65–glycerol

From Fig. 9, it follows that for each pair of liquids, the points obtained at similar thicknesses fit within one dependence within the error. In the case of K = 12 the curve lies higher than with K = 29. It is worth noting that at low values of rotation speed, the dimensionless wavelength ceases to change, and the value of λ/λcap approaches a value close to unity. This value agrees satisfactorily with the theoretical one in the case of translational oscillations of liquids (thick layers) near a flat boundary [12,14].

Let us dwell on the stratification of the threshold curves (Fig. 8) by rotation speed (dependence of the stability threshold on the rotation speed)–with increasing rotation speed, the threshold curves shift to the region of higher values of the vibrational parameter B. As noted above, the physical model of the development of oscillatory Kelvin–Helmholtz instability does not take into account the action of the Coriolis force. Let us use the dimensionless rotation speed ωrot=Ωroth02/ν1 , which characterizes the ratio of the thickness of the layer of a viscous liquid to the thickness of the Ekman layer in a low-viscosity liquid (more precisely, the square of this ratio) in a rotating cavity. From the analysis of the results obtained, it follows that the stabilizing effect of rotation on the stability of the interphase boundary in the experiment has a power-law dependence, and the stability threshold can be described by the complex B/ωrot0.35 (Fig. 10).

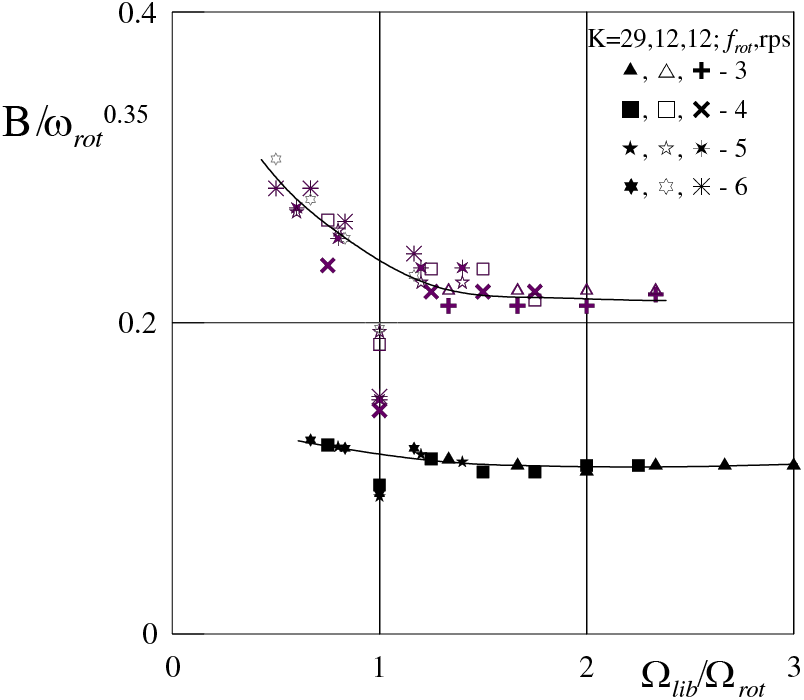
Figure 10: Threshold of the interphase stability on the parameters plane, relative frequency of librations–dimensionless complex B/ωrot0.35 , for pairs of liquids with different viscosity contrasts, PMS-5–glycerin (K = 12, present study) and PMS-0.65–glycerin (K = 29, [11])

All points obtained at different rotation speeds and stratified in Fig. 8 are in satisfactory agreement on the plane of these parameters (Fig. 10) (symbols in Figs. 8 and 10 coincide). This indicates that rotation has a stabilizing effect on the stability of the interphase boundary, and the stabilizing effect could be characterized by dimensionless rotation speed ωrot .

The threshold points are located much lower at Ωlib/Ωrot=1 . This is explained by the fact that at this the frozen waves excite only on a part of the interphase boundary, where the layer thickness is much smaller than h0, which means that the dimensionless rotation speed, being calculated through the local thickness of the viscous liquid layer, is also smaller. This could explain the decrease in the threshold value of B/ωrot0.35 at Ωlib/Ωrot=1 .

5  Conclusion

The behavior of a viscous liquid film on the wall of rapidly rotating cylinder subjected to angular vibrations is experimentally studied. The cavity is filled with an immiscible low-viscosity liquid of lower density. It is found that with an increase in the amplitude of rotational vibrations, the axisymmetric interphase boundary loses stability–а periodic 2D frozen wave appears on the liquid-film interface in a threshold manner. The frozen wave excitation is associated with the oscillatory Kelvin–Helmholtz instability, and the stability threshold is determined by vibrational parameter. The experiments carried out allow us to draw two important conclusions. The first concerns the role of the viscosity contrast coefficient K, which characterizes the ratio of the thicknesses of Stokes layers in liquids on opposite sides of the interface. It is shown that as the viscosity contrast decreases, the threshold for excitation of instability increases. This conclusion is qualitatively consistent with the results of theoretical and experimental studies of the oscillatory instability of the K–H in plane geometry [14] in a different formulation: the layers of the liquid are considered thick, there is no rotation, and tangential oscillations of liquids are caused by uniform oscillating external force fields. The second important result concerns the role of cavity rotation. It was discovered that rotation plays a stabilizing role and leads to an increase in the threshold value of the vibrational parameter B∗ (at a given relative frequency of librations) according to a power law B∗∼ωrotn . Under the conditions of the experiments performed (at sufficiently high values of the viscosity contrast K = 12 and K = 29) n≈0.35 . The use of a dimensionless complex B/ωrot0.35 makes it possible to coordinate experimental points obtained at different rotation speeds at a certain value of the contrast in liquid viscosities. Note that the found dependence well approximates the results of the present experiments. At the same time, one can expect a transformation of the dependence (in particular, the exponent n) with a change in K.

The results obtained shed light on the features of a new phenomenon discovered in [11]–instability of the interface between liquids with a high contrast of viscosities in a cylindrical cavity undergoing modulated rotation. The discovered stabilizing effect of dimensionless rotation rate on the oscillatory instability of the interface is qualitatively new and promising in terms of applied development of vibrational methods for controlling the interfaces; it requires further systematic experimental and theoretical research. To develop this direction, the following is planned: a systematic experimental study of the dynamics of the interface depending on the relative volume of liquids and their properties with the viscosity contrast and dimensionless rotation speed variation; theoretical modeling of the found phenomenon.

Acknowledgement: The authors thank A.S. Selyanin for his help in experimental setup production.

Funding Statement: Victor Kozlov and Alsu Zimasova were financially supported by the Russian Science Foundation (Project 23-11-00242), Nikolai Kozlov had no specific support.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Victor Kozlov and Nikolai Kozlov; data collection: Alsu Zimasova; analysis and interpretation of results: Victor Kozlov, Alsu Zimasova and Nikolai Kozlov; draft manuscript preparation: Victor Kozlov, Alsu Zimasova and Nikolai Kozlov. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Joseph DD, Renardy Y. Fundamentals of two-fluid dynamics. Part I: Mathematical theory and applications. New York: Springer; 1993. [Google Scholar]

2. Joseph DD, Renardy Y. Fundamentals of two-fluid dynamics. Part II: Lubricated transport, drops and miscible liquids. New York: Springer; 1993. [Google Scholar]

3. Phillips OM. Centrifugal waves. J Fluid Mech. 1960;7(3):340–52. doi:10.1017/S0022112060000128. [Google Scholar] [CrossRef]

4. Benilov ES, Lapin VN. Inertial instability of flows on the inside or outside of a rotating horizontal cylinder. J Fluid Mech. 2013;736:107–29. doi:10.1017/jfm.2013.530. [Google Scholar] [CrossRef]

5. Preziosi L, Joseph DD. The run-off condition for coating and rimming flows. J Fluid Mech. 1988;187:99–113. doi:10.1017/S0022112088000357. [Google Scholar] [CrossRef]

6. Seiden G, Thomas PJ. Complexity, segregation, and pattern formation in rotating-drum flows. Rev Mod Phys. 2011;83(4):1323–65. doi:10.1103/RevModPhys.83.1323. [Google Scholar] [CrossRef]

7. Thoroddsen S, Mahadevan L. Experimental study of coating flows in a partially-filled horizontally rotating cylinder. Exp Fluids. 1997;23(1):1–13. doi:10.1007/s003480050080. [Google Scholar] [CrossRef]

8. Kozlov NV, Kozlova AN, Shuvalova DA. Dynamics of immiscible liquids in a rotating horizontal cylinder. Phys Fluids. 2016;28:112102. doi:10.1063/1.4966980. [Google Scholar] [CrossRef]

9. Dyakova V, Polezhaev D. Pattern formation on the surface of the granular medium in a horizontal rotating cylinder filled with fluid. Phys Rev Fluids. 2022;7(4):044302. doi:10.1103/PhysRevFluids.7.044302. [Google Scholar] [CrossRef]

10. Dyakova V, Polezhaev D. Shear instability at the interface between fluid and granular medium in a horizontal rotating cylinder. Phys Fluids. 2023;35(4):043336. doi:10.1063/5.0147504. [Google Scholar] [CrossRef]

11. Kozlov VG, Zimasova AR, Kozlov NV. Stability of liquid-liquid interface in unevenly rotating horizontal cylinders. Interfacial Phenom Heat Transf. 2024;12(1):63–74. doi:10.1615/InterfacPhenomHeatTransfer.2023050051. [Google Scholar] [CrossRef]

12. Lyubimov DV, Cherepanov AA. Development of a steady relief at the interface of fluids in a vibrational field. Fluid Dyn. 1987;22:849–54. [Google Scholar]

13. Lyubimov DV, Lyubimova TP, Cherepanov AA. Dynamics of interfaces in vibration fields. Moscow: FizMatLit; 2003 (In Russian). [Google Scholar]

14. Yoshikawa H, Wesfreid JE. Oscillatory Kelvin-Helmholtz instability. Part 1. A viscous theory. J Fluid Mech. 2011;675:223–48. doi:10.1017/S0022112011000140. [Google Scholar] [CrossRef]

15. Kim H, Padrino JC, Joseph DD. Viscous effects on Kelvin-Helmholtz instability in a channel. J Fluid Mech. 2011;680:398–416. doi:10.1017/jfm.2011.206. [Google Scholar] [CrossRef]

16. Lyubimov DV, Ivantsov AO, Lyubimova TP, Khilko GL. Numerical modeling of frozen wave instability in fluids with high viscosity contrast. Fluid Dyn Res. 2016;48(6):061415. doi:10.1088/0169-5983/48/6/061415. [Google Scholar] [CrossRef]

17. Porter J, Salgado Sánchez P, Shevtsova V, Yasnou V. A review of fluid instabilities and control strategies with applications in microgravity. Math Model Nat Phenom. 2021;16:24. doi:10.1051/mmnp/2021020. [Google Scholar] [CrossRef]

18. Ivanova AA, Kozlov VG, Evesque P. Interface dynamics of immiscible fluids under horizontal vibration. Fluid Dyn. 2001;36(3):362–8. doi:10.1023/A:1019223732059. [Google Scholar] [CrossRef]

19. Talib E, Jalikop SV, Juel A. The influence of viscosity on the frozen wave instability: theory and experiment. J Fluid Mech. 2007;584:45–68. doi:10.1017/S0022112007006283. [Google Scholar] [CrossRef]

20. Yoshikawa H, Wesfreid JE. Oscillatory Kelvin-Helmholtz instability. Part 2. An experiment in fluids with a large viscosity contrast. J Fluid Mech. 2011;675:249–67. doi:10.1017/S0022112011000152. [Google Scholar] [CrossRef]

21. Nagl R, Zimmermann P, Zeiner T. Interfacial mass transfer in quaternary liquid-liquid systems. Chem Eng Process: Process Intensif. 2022;171:108501. doi:10.1016/j.cep.2021.108501. [Google Scholar] [CrossRef]

22. Nagl R, Zimmermann P, Zeiner T. Interfacial mass transfer in water-toluene systems. J Chem Eng Data. 2020;65(2):328–36. doi:10.1021/acs.jced.9b00672. [Google Scholar] [CrossRef]

23. Bushueva A, Polezhaev D. Averaged dynamics of fluids near the oscillating interface in a Hele-Shaw cell. Fluid Dyn Mater Process. 2024;20(4):847–57. doi:10.32604/fdmp.2024.048271. [Google Scholar] [CrossRef]

24. Bushueva A, Polezhaev D. Mass transfer of solute in an oscillating flow in a two-dimensional channel. Phys Fluids. 2024;36:045150. doi:10.1063/5.0204206. [Google Scholar] [CrossRef]

25. Kozlov V, Petukhova M, Kozlov N. Dynamics of liquids with high viscosity contrast in unevenly rotating Hele-Shaw cell. Phil Trans R Soc A. 2023;381(2245):20220082. doi:10.1098/rsta.2022.0082. [Google Scholar] [PubMed] [CrossRef]