Fuzzy Comprehensive Analysis of Static Mixers Used for Selective Catalytic Reduction in Diesel Engines

1  Introduction

Increasingly stringent restrictions on ship exhaust emissions are being imposed by various countries and international organizations because of growing concerns on air pollution and climate change.

Selective catalytic reduction (SCR) systems are key technologies used in modern ship exhaust treatment [1,2]. The system uses a specified catalytic reaction to convert the toxic nitrogen oxides from ship exhaust into harmless nitrogen and water vapor, which significantly reduces nitrogen oxide emissions. This improves air quality and protects the marine environment and coastal areas [3].

Improper mixing of the reducing agent (NH3) and flue gas in the SCR system results in challenges, such as a reduction in the NOx conversion rate, an increase in the NH3 slip rate, and the blockage of the air preheater. Therefore, the uniformity of the distribution of the flue gas parameters at the inlet of the SCR reactor is crucial for operational safety and cost-effectiveness [4]. These parameters include the flue gas temperature and velocity, as well as the distribution of NH3 in the flue gas. To ensure a uniform distribution of these parameters, many factors, such as the flue gas flow rate, nozzle structure, nozzle number, nozzle arrangement position, and distance between the nozzle and reactor, must be considered. Owing to the limited space in the engine room of the ship, static mixers are installed in the pipeline ahead of the reactor to attain a uniform distribution of flue gas parameters at the reactor inlet within a short distance [5,6].

Static mixers are efficient passive mixing devices with no moving parts. These mixing units consist of structures fixed within the pipe that change the flow state of the fluid to attain favorable dispersion and thorough mixing between different fluids. Such devices have been widely used to enhance chemical reactions, heat transfer, and fluid mixing [7,8]. Currently, there are numerous structural forms of static mixers in the market that exhibit varying mixing effects and are used in different applications [9]. However, not all available mixers are suitable for diesel engine SCR systems because the specific environment of an SCR system imposes unique requirements on the static mixer installed in a pipeline. (i) A relatively low proportion of NH3 gas is mixed with the flue gas (the volume ratio is typically less than 1:100), which makes uniform mixing a challenge. (ii) The concentration, velocity, and temperature fields must be uniform before the catalytic reaction stage of the SCR system is attained. (iii) The installation space of the SCR system is usually limited and narrow; thus, NH3 must be evenly mixed with flue gas within a short distance. (iv) The pressure loss must be low; otherwise, a large exhaust backpressure will form in the diesel engine, which affects the overall performance [10].

There are a limited number of studies on the development of static mixers for SCR systems. In general, there are no standard or clear starting points when selecting an appropriate type of static mixer. Therefore, a method for evaluating static mixers and comparing their performances is required. When static mixers are evaluated, the following aspects are generally considered:

(1) Pressure loss

Owing to the limited on ships, SCR systems are generally combined with silencers for layout purposes. The silencer and the catalyst component of the SCR system contribute to the reduction in pressure. This sets the requirement for the pressure loss of the static mixer, which must not be exceedingly high. Generally, the reduction in pressure of a silencer is approximately 1000 Pa, whereas that of a static mixer is lower than 500 Pa.

(2) Mixing distance

The mixing distance refers to the distance from the urea spray nozzle to the point at which the mixed gas reaches the mixing section after passing through the mixer. Different static-mixer configurations have varying mixing distances; additionally, different standards for mixing uniformity require different mixing distances. Many applications prefer shorter mixing distances because these distances are associated with improved mixing performance.

(3) Mixing quality

The mixing quality is evaluated based on the uniformity of the velocity, temperature, and composition of a specified section. The degree of uniformity is typically measured using the relative standard deviation. The ratio of the standard deviation to the average value is known as the unevenness or variation coefficient. The higher the variation coefficient, the greater the unevenness of the mixing. The maximum allowable unevenness temperature is 10%–15% for the velocity and 5%–10% for the composition.

(4) Structural form

While designing a mixer, the structure of the mixing unit must be simple and easy to process.

These aspects are interconnected, mutually influential, and even conflicting. Improving one aspect of performance may reduce the influence of another [11]; therefore, their effects must be considered.

Many studies have compared the performances of static mixers based on varying mixing indices; however, only a single aspect of performance is generally considered, such as the pressure reduction characteristics, mixing characteristics, or heat transfer characteristics. Zhu et al. [12] used numerical models to assess the pressure reduction of vaporizers and mixers in high-pressure marine SCR systems. Fernandes et al. [13] used mixing efficiency and pressure reduction to evaluate the performance of spiral, KVM, and T-tube mixers. Liu et al. [14] showed that the mixing effect is enhanced when the number of mixing elements is increased; however, this also increased pressure loss. Jang et al. [15] evaluated the mixing performance based on the uniformity of NH3 and axial velocity distributions. Haddadi et al. [16] investigated the hydrodynamics and mixing behavior in an SMX mixer at a low Reynolds number; the power consumption and mixing distribution were used to evaluate its performance. Xiao et al. [17] used the coefficient of variation (CoV) and separation strength to evaluate the mixing effect. Medina et al. [18] defined the M number, which is the dimensionless ratio of the mixing level to the energy loss, and assessed the effects of the mixer based on the entropy change and pressure loss. These evaluation methods and criteria consider the mixing performance and pressure loss of the mixer and not the velocity field or mixing distance after mixing. As mentioned previously, the SCR system of a marine diesel engine requires uniform composition and velocity fields within a short distance. Thus, these methods are not applicable in this study and require further improvement.

This study introduces a fuzzy comprehensive evaluation method using the fuzzy set theory, fuzzy linear transformation principle, and maximum membership degree principle in fuzzy mathematics to consider multiple factors and conduct a comprehensive evaluation. Therefore, the pressure losses, mixing distances, mixing qualities, and velocity fields of various static mixers were comprehensively evaluated.

2  Fuzzy Comprehensive Evaluation Method

A fuzzy comprehensive evaluation is a mathematical method used to address fuzzy problems. The principle of fuzzy mathematics is leveraged for the quantification of factors that are unclear and difficult to quantify, and to comprehensively evaluate the objects or phenomena affected by various fuzzy factors. This method is useful for handling complex problems with fuzziness, particularly those that are difficult to describe using exact numerical values [19]. Fig. 1 shows the basic steps: establish the fuzzy comprehensive evaluation factor set U, establish the evaluation set V, perform a single factor fuzzy evaluation to obtain the evaluation matrix R, establish the weight set W, select the synthesis operator to synthesize W and R, obtain the fuzzy comprehensive evaluation set F, and analyze the evaluation results.

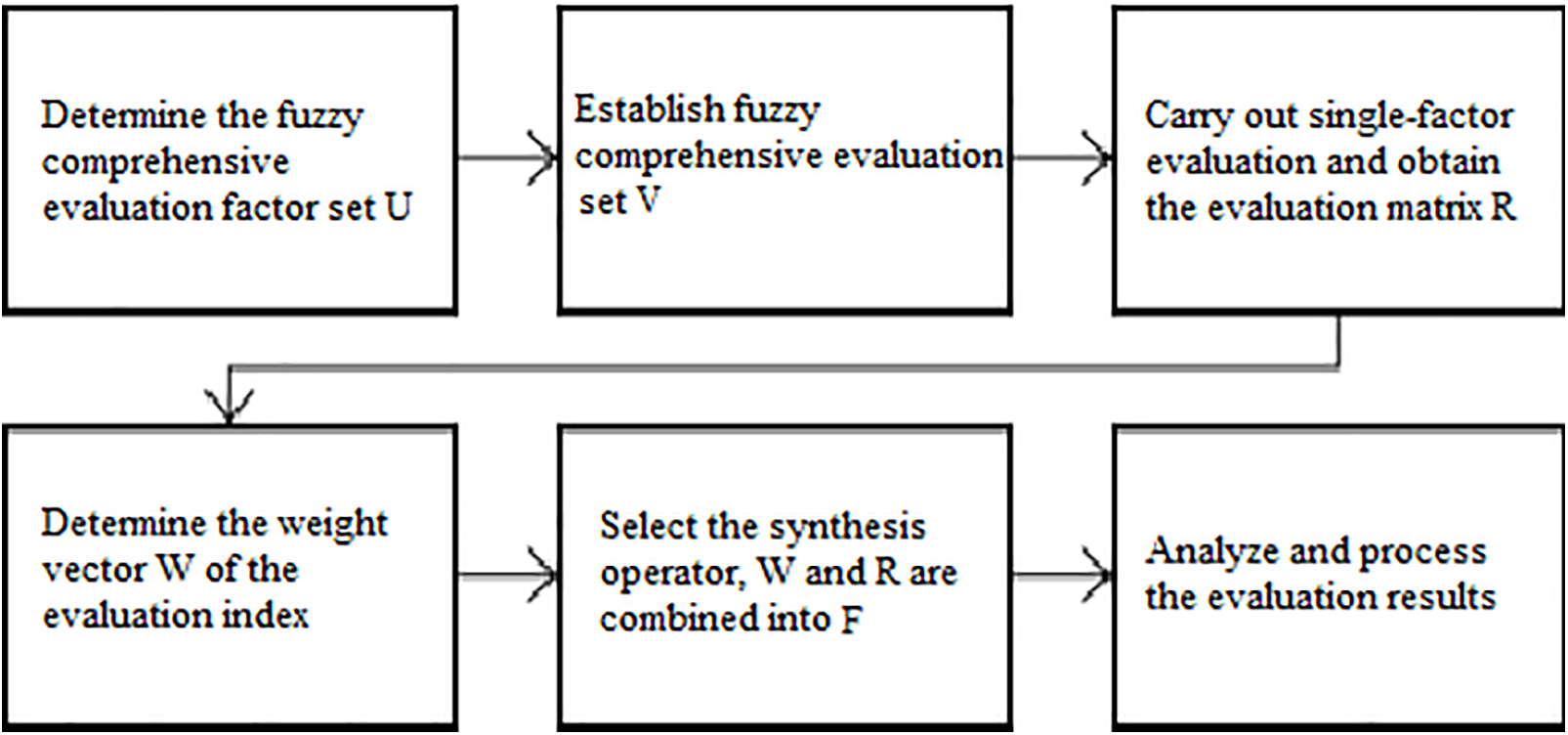
Figure 1: Flow chart of the evaluation of fuzzy factors

The evaluation set F is expressed as follows:

F=W∗R=(w1,w2,⋯,wn)∗[ r11r12⋅⋅⋅r1mr21r22⋅⋅⋅r2m⋮⋮⋮rn1rn2⋅⋅⋅rnm ]=(b1,b2,⋯,bn) (1)

where F is the fuzzy comprehensive evaluation set and R is the evaluation matrix of the fuzzy relationship. The jth column in R represents the degree of membership of each evaluation factor value to the jth level standard and indicates the possibility of an assessment of an aspect of a specified evaluation object by an evaluation subject. A specific value was assigned by the membership function. W is the factor weight set, which represents the importance of each factor and the magnitude of its effects. The success of the model is associated with the appropriateness of the weight selection. Weight can be determined using several methods, including the Delphi method, expert investigation method, weighted average method, and the analytic hierarchy process. Finally, bj (j = 1, 2, …, m) is a fuzzy comprehensive evaluation index, where bj represents the membership degree of the evaluation object to the jth element in the judgment set when all factors are considered. Set B is the fuzzy set for the evaluation set V.

3  Simulation Model and Results

3.1 Simulation Model and Boundary Conditions

A 9L20C diesel engine, which operates at a constant speed, was used as the generator of the ship considered in this study. Siemens equipped its ship with a SINOX system. The tailpipe of the diesel engine was equipped with an SCR system and a static mixer was installed inside the pipe. In this study, a static mixer was modeled and simulated for the exhaust pipe of a 9L20C diesel engine.

The diameter (D) of the exhaust pipe was 0.4 m. To facilitate the calculation, the urea injection process was simplified using a circular inlet located in the center of the exhaust pipe; additionally, water vapor was introduced into the exhaust pipe from the inlet instead of a urea solution. The concentration of water vapor in the pipe was changed by adjusting the inlet area. Air was used to replace the diesel engine flue gas. Because the flue gas was in a turbulent flow state, the turbulence in the pipe was described using the κ-ε turbulence model, which has high convergence speed, low memory requirements, and can effectively solve external flow challenges with complex geometry. The velocities of the water vapor and air at the inlet were considered equal for the calculations, ensuring the uniformity of the velocity field for the static mixer. Thus, the changes in the velocity field caused by different mixers were compared.

The inlet boundary conditions of the mass flow rate were adopted for the air and water vapor; additionally, the calculation was based on a compressible gas. The end of the pipe was set as the boundary condition for the pressure outlet where the pressure was set to zero. A schematic representation of the model is shown in Fig. 2.

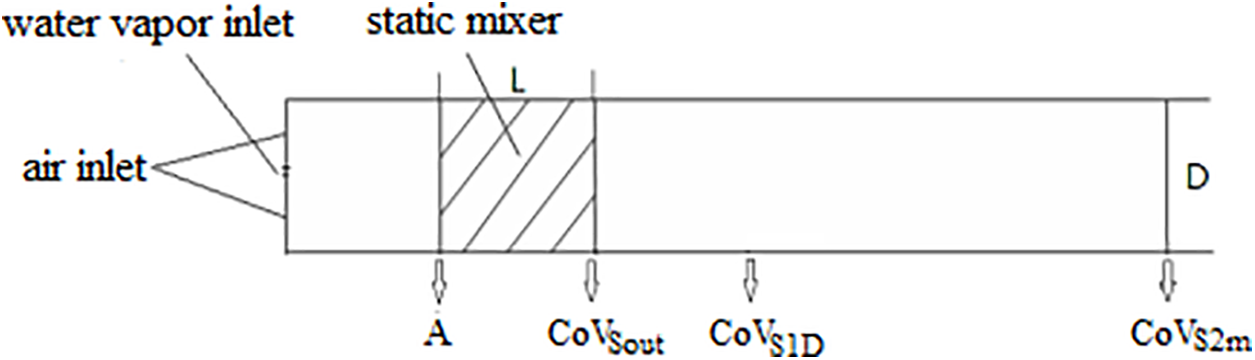
Figure 2: Schematic of the simulation calculation model

During evaluation, the mixer was placed 0.4 m from the inlet, and the installation space left for the mixer was 0.4 m. Thus, the length-to-diameter ratio of the mixer was L/D = 1. The performance of each mixer was compared using the flue gas parameters of a 9L20C diesel engine at 100% load. The exhaust velocity was 48 m/s and the exhaust temperature was 623 K.

3.2 Static Mixer Selection and Construction Type

Although the structures of static mixers vary according to their mixing characteristics, they can be roughly divided into the following categories:

1. The mixer changes the shape of the fluid flow section and volume, causing immediate expansion or shrinkage. The mixing between fluids depends on the turbulence of the fluid (for example, GK static mixer, cone static mixer, and HEV static mixer).

2. The mixer causes fluid separation and confluence, inducing mixing through fluid collision (for example, an SK static mixer).

3. The fluid is forced through and around a maze structure, providing time and collisions for mixing (for example, an SV static mixer).

4. The mixer induces a vortex as the fluid passes through the obstacle (for example, a star-shaped static mixer).

In this study, six typical static mixers (GK, cone, star-shaped, SK, SV, and HEV) were selected for three-dimensional modeling and performance simulations using the Fluent software (Fig. 3). A fuzzy comprehensive evaluation method was used to evaluate the performance of each static mixer.

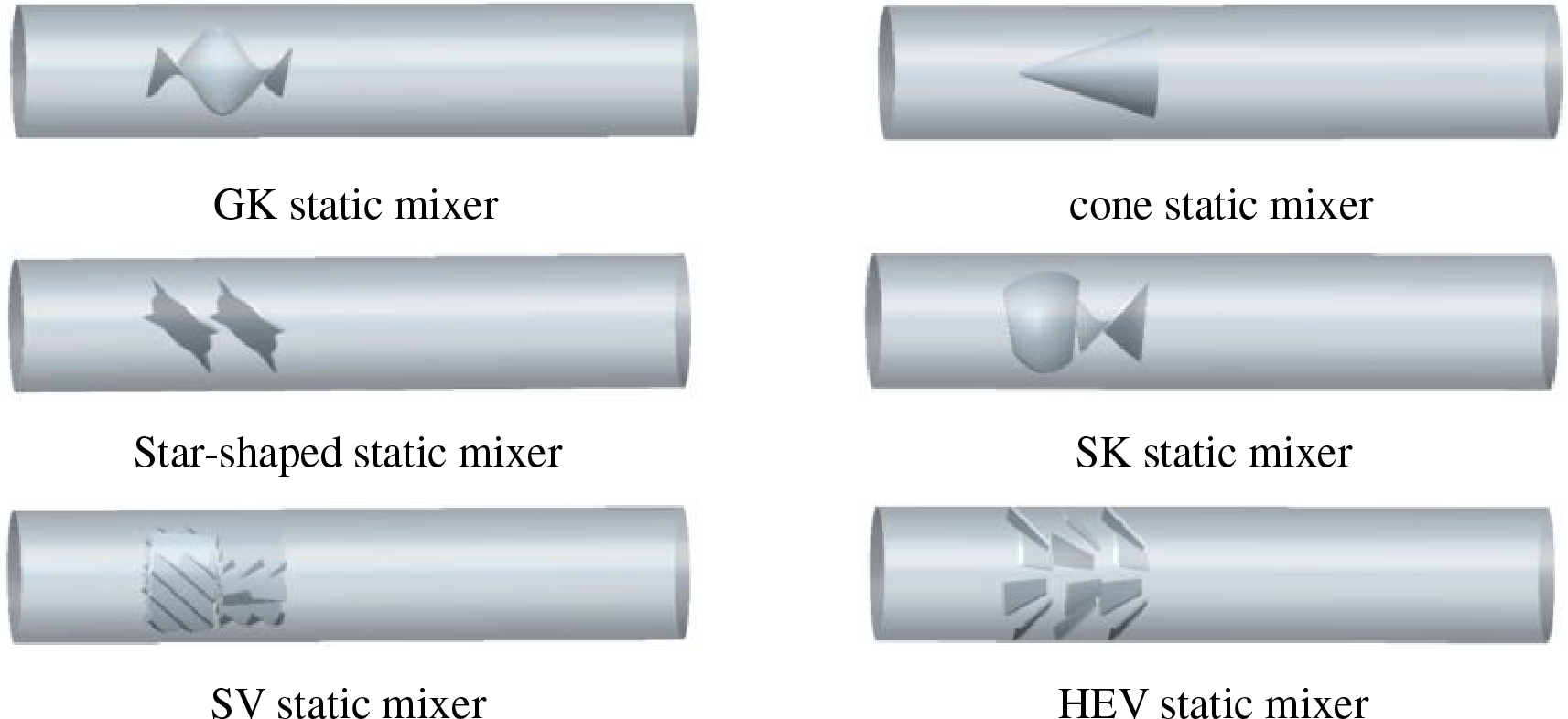
Figure 3: Three-dimensional model of six static mixers

3.3 Simulation Results and Data Processing

The velocity field for the vertical plane of the 2 m long exhaust pipe equipped with a mixer for a flue gas velocity of 48 m/s is shown in Fig. 4. The concentration and pressure fields are not displayed owing to space limitations.

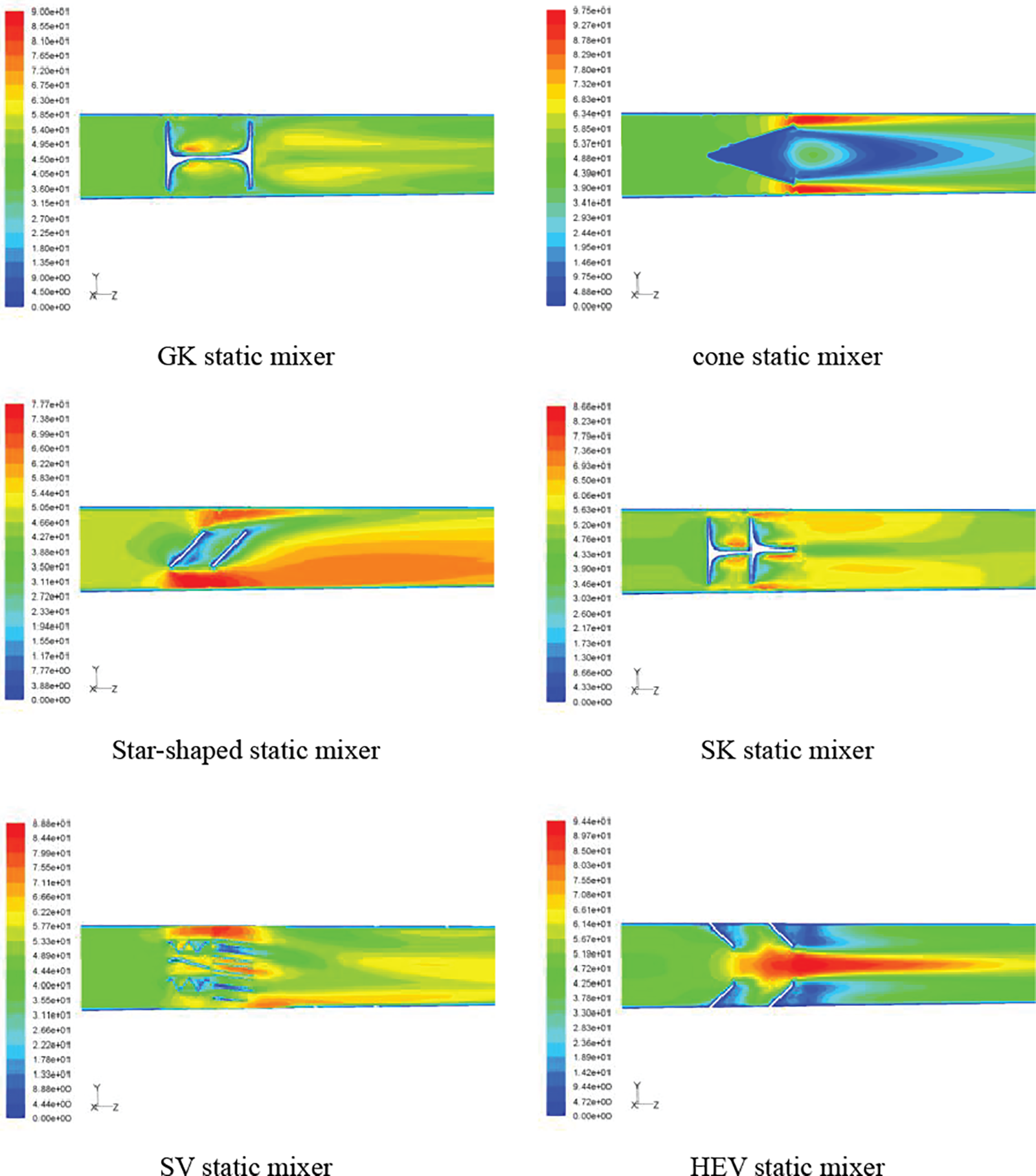
Figure 4: Cloud map of the velocity field distribution in the pipeline using each static mixer

The static mixers significantly affect the flow field, and each mixer induces different structural forms (Fig. 4). The flow rate of the fluid in the pipeline was high, and the circulation area was small. Owing to the different interflow-spheric velocities, the fluid was subjected to shear force and deformed because of stretching, thus enhancing interfluid mixing. The velocity field gradually returned to uniformity over a specified distance after mixing.

When calculating the uniformity of the temperature, speed, and concentration of the pipe cross section, the sampling points across the entire section must be evenly selected. Subsequently, the value of each point was recorded, and the formula was used to calculate uniformity. A higher number of sampling points provided more accurate results; however, the workload increased. Therefore, a number of sampling points must be selected to satisfy the required accuracy without significantly increasing the computational load. Herein, the accuracy of the calculation was sufficient and stabilized when 45 sampling points were used. Increasing the number of sampling points only increased the workload. The 45 sampling points were selected in the pipeline section, as shown in Fig. 5. The intersection points of the grid lines indicate the locations of the selected sampling points.

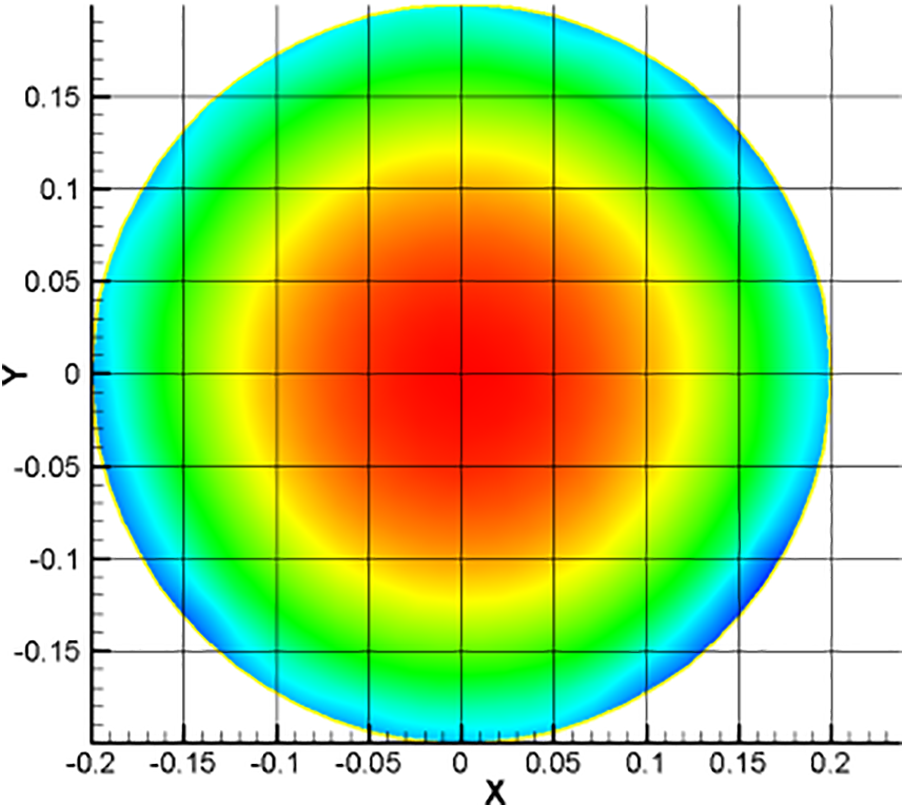
Figure 5: NH3 gas concentration distribution and selection of the sampling points for the pipe cross-section

4  Application of the Fuzzy Comprehensive Evaluation Method

Before establishing the quality of the static mixer evaluation index, the effect of inflow velocity on the performance of the static mixer must be determined. The mixing of an NH3 gas at a concentration of c¯ = 0.1 using a GK static mixer was used as an example. The flow velocities were set as 8, 16, 32, and 48 m/s. CoV was calculated for the velocity (Table 1) and composition (Table 2) at the outlet of the mixer and after the mixer at distances that were a function of D (1 to 6 D).

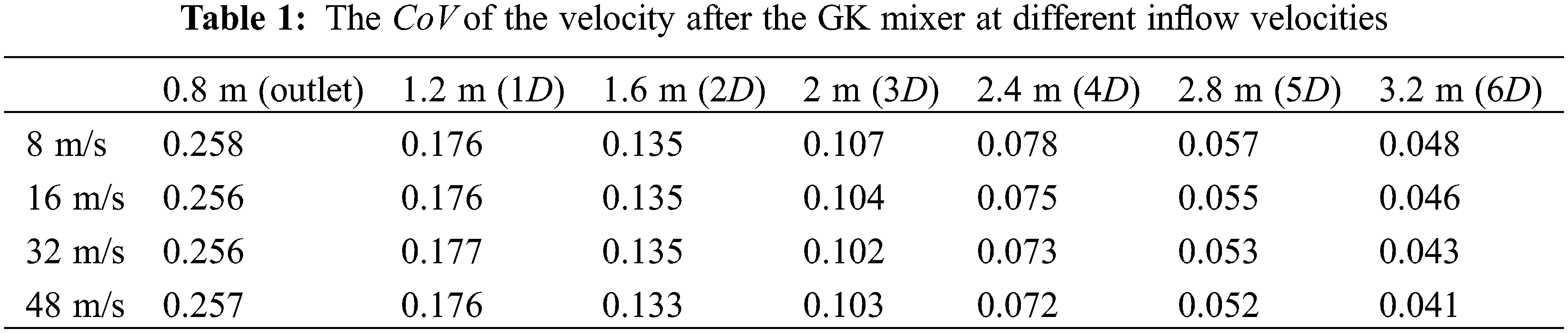
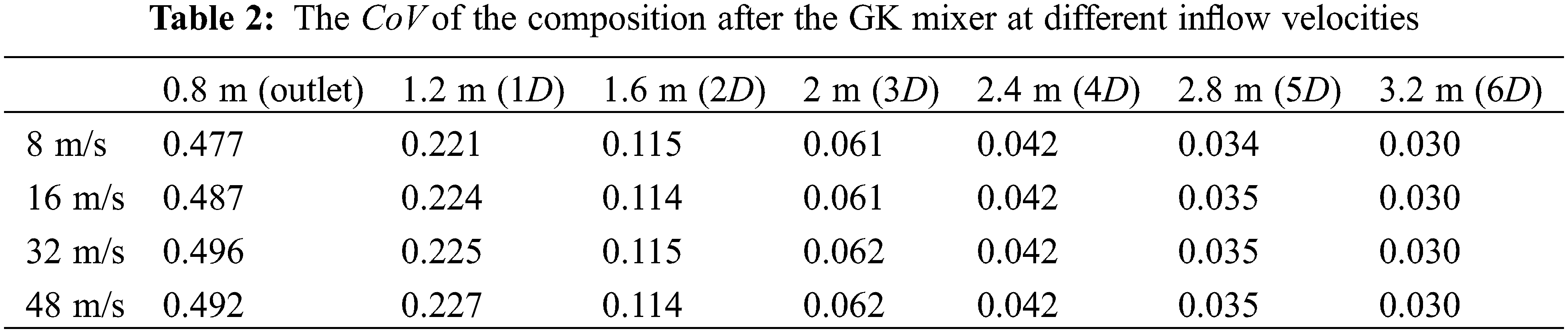
Although the velocities of the incoming flow were different, the relative velocities of the two components were zero because the velocities of the two components at the inlet were equal, and the shear force between the two components was maintained. Because the two components used in the calculation were gases, no breakup of the droplets and particles was observed. Therefore, the magnitude of the incoming flow velocity did not affect the mixture composition. Therefore, the CoV values of the composition and velocity after mixing were only related to the form of the static mixer. Consequently, the distance required for the velocity field to reach uniformity after the static mixer did not change with the incoming flow velocity.

4.1 Establishing the Fuzzy Evaluation Factor Set

Considering the mixing characteristics of the static mixers, the CoV for the composition at the outlet of the straight pipe section fitted the exponential function:

CoVSout=σ/c¯=A⋅exp⁡(−BLD), (2)

where:

σ: Standard deviation of the mixer outlet concentration;

c¯ : Average concentration;

L: Length of the mixer;

D: Equivalent diameter of the straight pipe.

A is the CoV of the composition at the inlet of the mixer when the pipe is empty. This is important, because the presence of a mixture in a pipe can affect the incoming flow. Even when the evaluated mixers were placed at the same position in the pipeline, the compositional CoV at the inlet varied owing to the structural differences of the mixers. Using this definition, the conditions at the mixer inlet can be inferred from the value of A:

B=D/L∗ln⁡(A/CoVSout), (3)

Thereafter, the index was defined as C = ln(CoVSout/CoVS1D). When L = D, the value of B represents the natural logarithm of the attenuation multiple of the component nonuniformity at the outlet section of the mixer with a unit length-diameter ratio (L/D = 1). The value of C represents the natural logarithm of the attenuation multiple of CoV for a composition at a distance of one diameter length (1D) after mixing [20]. The B and C values indicate the mixing and residual mixing abilities of the mixer, respectively.

The pressure loss factor, Z, is commonly used to evaluate pressure loss characteristics and represents the ratio of the pressure loss generated by the fluid flowing through the static mixer to the pressure loss of the blank pipe. The mixer disturbs the incoming gas and the static pressure recovery characteristics are related to the flow pattern at the outlet of the static mixer. The shrinkage effect often causes a high pressure loss when the reduction in pressure is calculated directly based on the inlet and outlet positions of the mixer. Therefore, when evaluating the pressure loss characteristics of the static mixer, the static pressure recovery of the mixer is considered, and the pressure drop factor Z is corrected to Z′, which is defined as the ratio of the pressure loss generated by the fluid flowing through the static mixer to the pressure loss of the empty tube with an average unit diameter (1D). However, when calculating the pressure drop of the mixer and empty tube, the selected pressure measurement point is the pressure recovery point before and after the mixer; particularly, the position where the pressure loss of the mixer is lowest. For example, the positions of the forward and rear pressure measurement points of the GK mixer are 0.5D and 2D, respectively. The locations of the measurement points for the blank pipe were selected in this manner.

Additionally, the distance (LV) required for the velocity field to achieve uniformity after mixing must be considered. The LV/D ratio was used for calculations.

Because of the low quantity of urea injected into the SCR system, the temperature change was negligible; thus, the CoV for temperature was not considered in the evaluation.

Finally, the fuzzy evaluation factor set was U = {B, C, LV/D, Z}.

4.2 Establishing the Evaluation Set

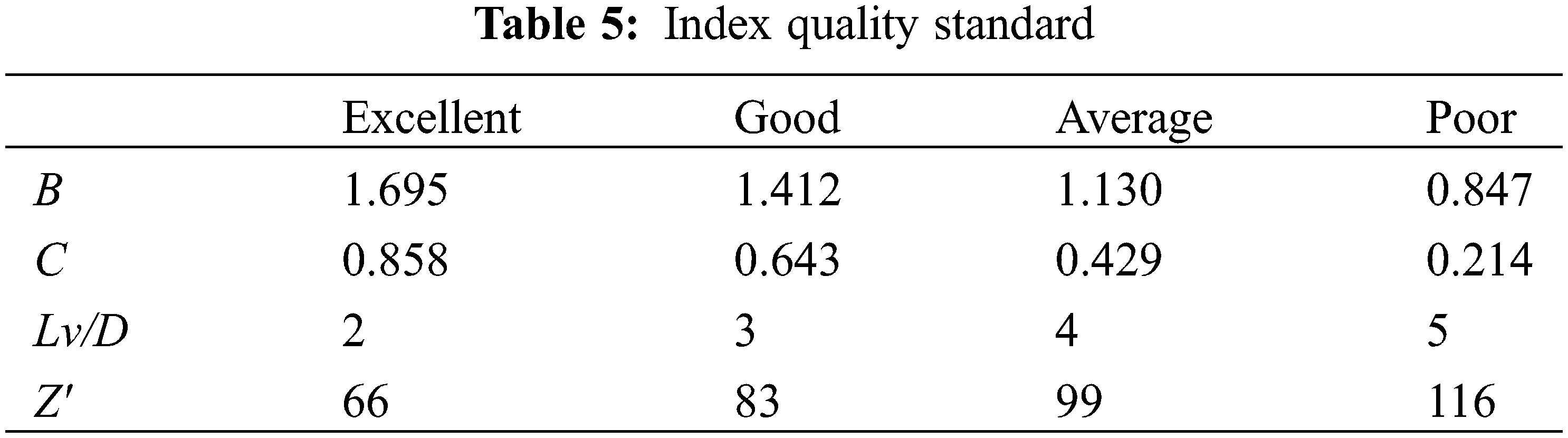
Different grades are often assigned owing to the different evaluation criteria for each index. To facilitate unified measurements, each index was evaluated according to a four-level standard, particularly the comment set V = {excellent, good, average, poor}.

To establish the quality standard of indices B and C, a GK-type mixer with L/D = 1 was placed at different positions in the pipeline (starting at 0.1 m along the pipeline), and the changes in B and C with the change in mixer position were assessed (Fig. 6). The following conclusions were drawn:

1)   For the same pipe position, the value of A increased when the concentration decreased. The greater the difference in the proportion of the two components, the more difficult the achievability of uniformity, which was consistent with existing theory and experience.

2)   At the same concentration, c¯ , the closer the mixer was to the inlet of the pipeline, the greater the values of A, BGK, and CGK; additionally, the change in A was more exponential.

Figure 6: Changes in the indices under varying concentrations and installation positions

The performances of the six static mixers were then calculated using different concentrations, and the results are listed in Table 3.

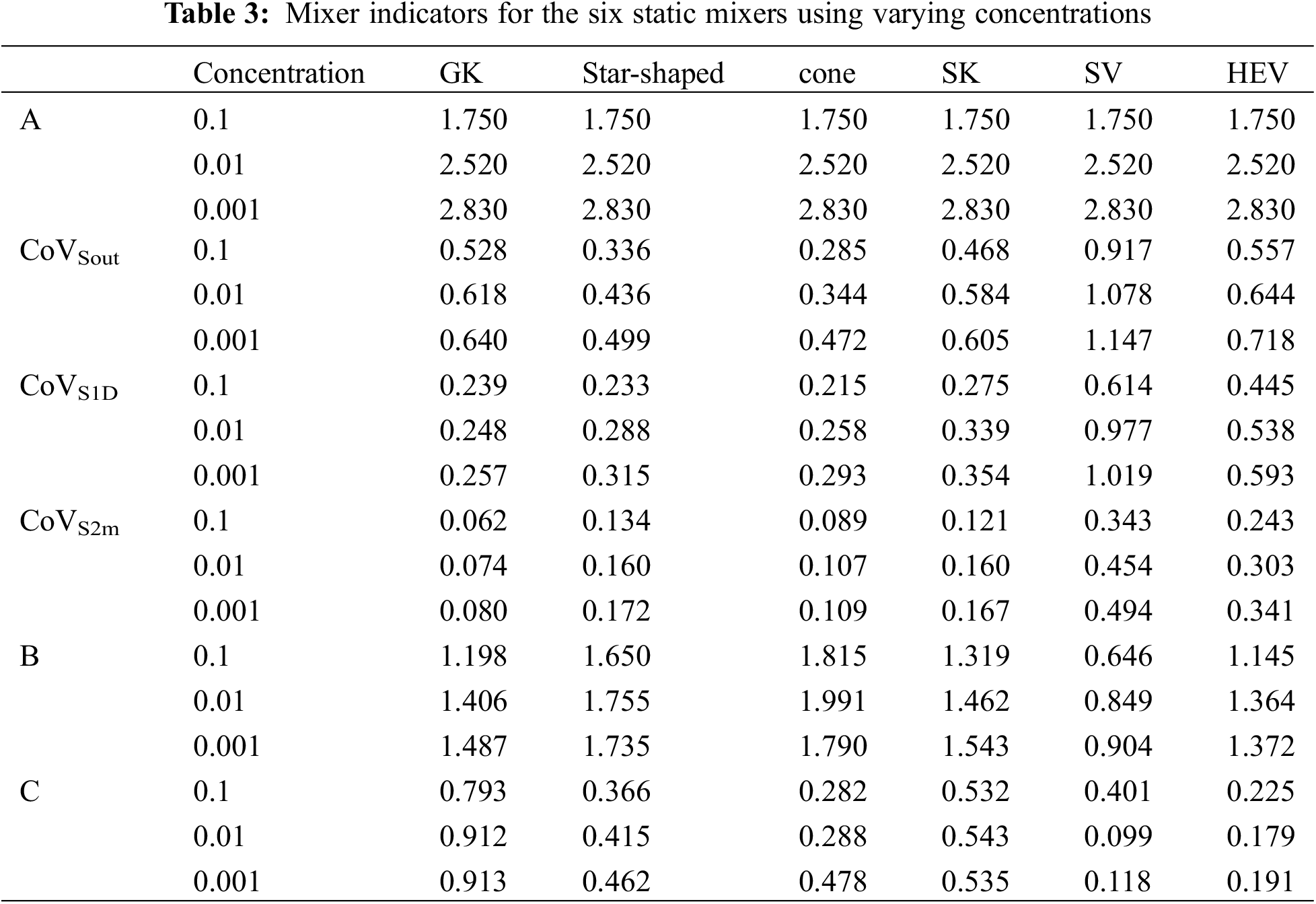
An improved mixing performance and lower CoV composition were observed as the values of B and C increased. Changes in the values of B and C were associated with changes in the value of A. The relationship was fitted as shown in Fig. 7.

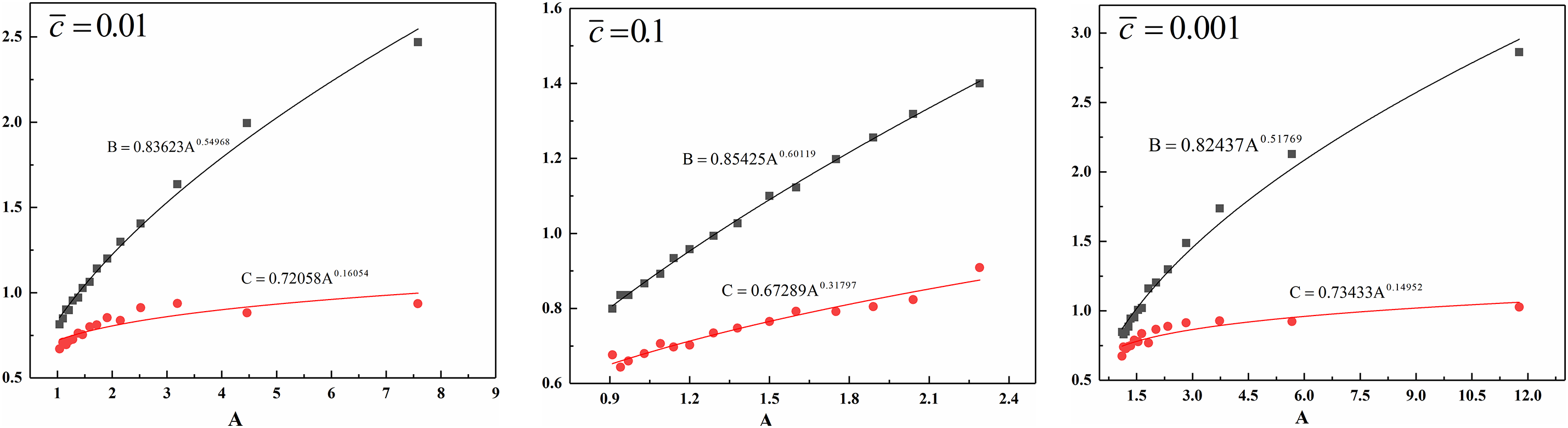
Figure 7: The fitting of BGK and CGK vs. A

Statistical analyses showed that the mixers were reasonably classified by B = 1.2BGK and C = CGK. The same method was used to calculate LV/D and Z′, as shown in Table 4.

The pressure loss of the GK static mixer was lower than that of the other mixers. Therefore, the modified pressure-loss factor, Z′GK, was considered an excellent standard. An LV/D < 2 was considered excellent, and an LV/D > 5 was considered poor. The evaluation of the quality of the four indicators is summarized in Table 5.

4.3 Establishing the Fuzzy Relation Matrix

The membership degree was determined and calculated using the membership function by comparing the index values of the mixers with the quality standard of each index. In general, membership functions can exhibit various shapes, such as triangles, trapezoids, and Gaussians, depending on the characteristics of the system and its application. The change in the performance of the static mixer was a gentle process. Additionally, the trapezoidal membership function was most appropriate, assuming the following three forms:

f(x)={1x≥a1x−a2a1−a2a2 < x < a10x≤a2f(x)={0x≥a1a1−xa1−a2a2 ≤ x < a1x−a3a2−a3a3 < x < a20x≤a3f(x)={0x≥a1a1−xa1−a2a2 < x < a11x≤a2, (4)

where f(x) is the membership degree of an evaluation factor; x is the measured value of the evaluation factor in the sample; a1, a2, and a3 are the standard values of the adjacent levels; and the fuzzy matrix R can be determined by the membership degree.

The larger the B and C values, the better the performance of the static mixer. Conversely, the lower the values of LV/D and Z′, the better the performance of the static mixer. Therefore, excellent B and C values adopt the upper-level membership function, poor B and C values adopt the lower-level membership function, poor LV/D and Z′ values adopt the upper-level membership function, excellent LV/D and Z′ values adopt the lower-level membership function, and good and average values adopt the intermediate-level membership function.

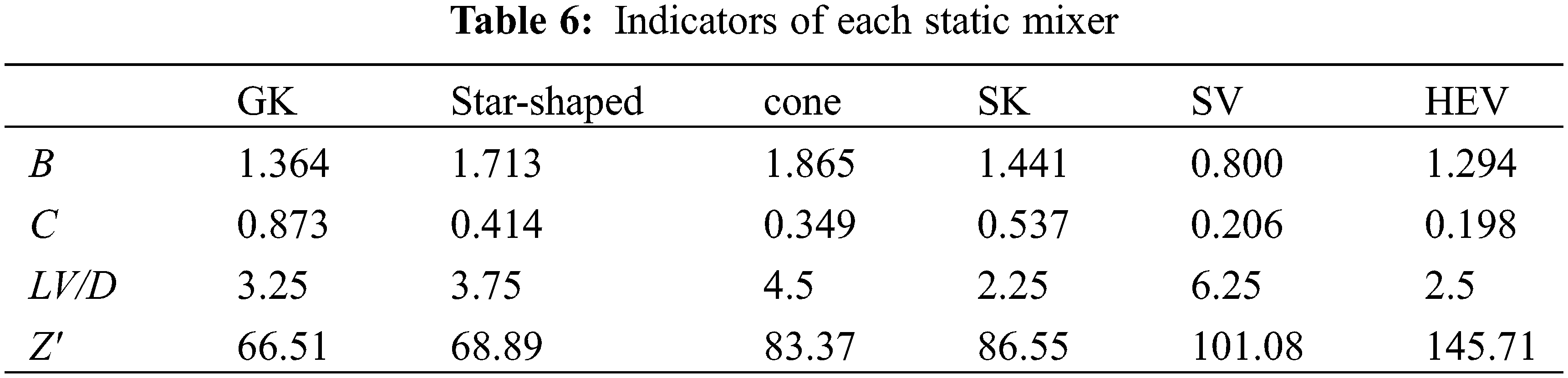
The B and C values at different concentrations in Table 4 were taken as weighted averages so that each static mixer index could be calculated, as shown in Table 6.

By substituting the data into the corresponding membership function, the fuzzy relation matrix for each static mixer was obtained as follows:

RGK=[00.8300.1700100000.7500.25000.9700.03000]  Rstar=[1000000.9300.07000.2500.75000.8300.17000]

Rcone=[1000000.6280.372000.50.500.9770.0230]  RSK=[0.1020.8980000.5040.49600.750.250000.7780.2220]

RSV=[000100010001000.8780.122]  RHEV=[00.5820.418000010.50.5000001]

4.4 Establishing the Weight Set of Evaluation Indices

In the fuzzy comprehensive evaluation model, the weight reflects the position and importance of each factor in the comprehensive decision-making process, which affects the results of the comprehensive evaluation. The methods used to determine the weights include the statistical average method, CoV method, analytic hierarchy process, weighted statistical method, Delphi method, expert investigation method, and public evaluation method.

An expert investigation method is used to determine the weights of the evaluation indices. By consulting field experts, the weight vector for each evaluation factor was obtained as follows:

w=[0.3,0.2,0.2,0.3]

4.5 Fuzzy Comprehensive Evaluation

A comprehensive fuzzy evaluation was performed to calculate the fuzzy vector, F. By combining the weight vector (W) with the fuzzy relation matrix (R) of each evaluated mixer, vector F of each evaluated mixer was obtained.

F = W∗R, (5)

The synthesis operator selected the weighted average type operator (×, +):

FGK=[0.4910.4080.1010]         Fstar=[0.5490.1010.3360.014]

Fcone=[0.3000.2930.2330.174]     FSK=[0.1810.6540.1660]

FSV=[000.2630.734]             FHEV=[0.1000.2750.1250.500]

To quantitatively analyze each static mixer, the evaluation result vector must be single-valued. Excellent, good, average, and poor grades were assigned 100, 80, 60, and 30, respectively. Thus, the four fuzziness evaluation levels were mapped onto the following vector:

G=[100806030]T

The comprehensive evaluation value of the mixer was calculated using the following formula:

S = F∗G, (6)

SGK=FGK∗G=87.800     Sstar=Fstar∗G=83.560

Scone=Fcone∗G=72.630    SSK=FSK∗G=80.296

SSV=FSV∗G=37.812      SHEV=FHEV∗G=54.492

The order of comprehensive performance from high to low was:

GK > star−shaped > SK > cone > HEV > SV

From a structural perspective, the curve contour of the GK static mixer changed continuously and slowly, whereas the contour changes of the other static mixers were immediate. Therefore, the degree of turbulence in the GK mixer was lower than that of the other static mixers, resulting in a marginally lower mixing effect and heat transfer capacity; however, its fluid resistance was also the lowest, leading to reduced energy consumption. Ultimately, the GK static mixer exhibited a higher cost performance than that of the other static mixers in the SCR system of the 9L20C diesel engine.

The comprehensive evaluation results were consistent with those of the previous analysis, indicating that the established evaluation model was effective.

5  Conclusion

The fuzzy comprehensive evaluation considers the velocity field after the mixer and accounts for the L/D mixing unit, which is more suitable for scenarios that require low-pressure losses and distances to attain uniformity. The selected evaluation indices were the B value, C value, Z′ of the pressure drop, and ratio of the required distance to the equivalent diameter of the pipe LV/D when the velocity field after the mixer attained uniformity. From the simulations of the six static mixers under different conditions, the following results were obtained:

1) When the inlet velocities of the two components were the same, and the concentration was constant, the change in the CoV of the composition and velocity after mixing was maintained by changing the speed. This shows that the CoV values for the composition and velocity after mixing were only related to the form of the static mixer and not to the magnitude of the incoming flow velocity. Thus, the distances required for the uniformity of the composition and velocity fields after static mixing did not change with the incoming flow velocity.

2) The mixing performance was related to the installation position and concentration of the mixer. At the same installation position, a lower concentration resulted in an increase in the difficulty of even mixing. At the same concentration, higher B and C values as the closeness of the installation position to the inlet of the pipeline increased. The change in these values increased exponentially as the values of A changed.

3) The fuzzy comprehensive evaluation method was objective and effectively evaluated the static mixer.

The fuzzy comprehensive evaluation method can be used for the selection of static mixers and to evaluate the performances of mixers after structural optimization. This method can be used to determine the optimal working conditions when designing a new static mixer and to evaluate the applications of vehicle SCR systems and other static mixers. Overall, the fuzzy comprehensive evaluation method can be used to comprehensively evaluate multiple parameters of a mixer, and to design, develop, and select static mixers. This can reduce the technical development cycle and enhance the development of the SCR mixer systems.

Acknowledgement: This work was financially aided by the National Natural Science Foundation of China (52276122).

Funding Statement: This work was supported by the National Natural Science Foundation of China (52276122), Min Kuang.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xin Luan; data collection: Hailong Chen; analysis and interpretation of results: Xin Luan, Guoqing Su; writing—original draft preparation: Xin Luan, Guoqing Su, Hailong Chen; writing—review and editing: Min Kuang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Lee JU, Hwang S, Han SH. Numerical and experimental study on NOx reduction according to the load in the SCR system of a marine boiler. J Mar Sci Eng. 2023;11(777):777. doi:10.3390/jmse11040777. [Google Scholar] [CrossRef]

2. Foteinos MI, Christofilis GI, Kyrtatos NP. Large two-stroke marine diesel engine operation with a high-pressure SCR system in heavy weather conditions. J Ship Res. 2021;65(3):179–93. doi:10.5957/JOSR.05190027. [Google Scholar] [CrossRef]

3. Lee C. Performance evaluation of a urea-selective catalytic reduction system in a marine diesel engine. Proc IMechE, Part M: J Eng Marit Environ. 2017;231(3):801–8. doi:10.1177/1475090216667238. [Google Scholar] [CrossRef]

4. Rumac F, Glujić D, Bernečić D. The influence of SCR on main engine parameters. Sci J Marit Res. 2022;36(1):113–22. doi:10.31217/p.36.1.13. [Google Scholar] [CrossRef]

5. Mehdi G, Zhou S, Zhu YQ, Hussain S, Hussain A. A CFD analysis of static mixer to study its impacts on SCR performance in marine diesel engine. In: 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies, 2019; Sukkur, Pakistan. [Google Scholar]

6. Venkatesh A, Ramesh K. Design of static mixer to improve the uniformity index in urea SCR system. Int J Sci Adv Res Technol (IJSART). 2019;5(5):1002–7. [Google Scholar]

7. Medina H, Anthony JM, Eldredge T. Evaluating the performance of static mixers using the M-number: the case of the Koflo® mixer. Eng Res Express. 2023;5(1):015026. doi:10.1088/2631-8695/acb9d6. [Google Scholar] [CrossRef]

8. Cristopher MU, Nijso B, Lisa K, Jeroen O. Adjoint-based design optimization of a Kenics static mixer. Results Eng. 2024;21:101856. doi:10.1016/j.rineng.2024.101856. [Google Scholar] [CrossRef]

9. Valdes JP, Kahouad L, Mater OK. Current advances in liquid-liquid mixing in static mixers: a review. Chem Eng Res Des. 2022;177(1):694–731. doi:10.1016/j.cherd.2021.11.016. [Google Scholar] [CrossRef]

10. Yiğit G, Güner Ö. Effect of exhaust backpressure on performance of a diesel engine: neural network based sensitivity analysis. Int J Automot Technol. 2022;23(1):215–23. doi:10.1007/s12239-022-0018-x. [Google Scholar] [CrossRef]

11. Ranim C, Fouad A. Performance comparison between novel and commercial static mixers under turbulent conditions. Chem Eng Process-Process Intensif. 2023;193:109559. doi:10.1016/j.cep.2023.109559. [Google Scholar] [CrossRef]

12. Zhu YQ, Li TH, Xia C, Feng YM, Zhou S. Simulation analysis on vaporizer/mixer performance of the high-pressure SCR system in a marine diesel. Chem Eng Proc Process Intensif. 2020;148:107819. doi:10.1016/j.cep.2020.107819. [Google Scholar] [CrossRef]

13. Fernandes LA, Marcon LRC, Rouboa A. Simulation of flow conditions for natural gas and hydrogen blends in the distribution natural gas network. Int J Hydrog Energy. 2024;59:199–213. doi:10.1016/j.ijhydene.2024.01.014. [Google Scholar] [CrossRef]

14. Liu Y, Rao A, Ma F, Li X, Wang J, Xiao Q. Investigation on mixing characteristics of hydrogen and natural gas fuel based on SMX static mixer. Chem Eng Res Des. 2023;197:738–49. doi:10.1016/j.cherd.2023.07.040. [Google Scholar] [CrossRef]

15. Jang JW, Na SY, Roh HW, Ahn SY, Choi GM. Spraying and mixing characteristics of urea in a static mixer applied marine SCR system. Energies. 2021;14(18):5788. doi:10.3390/en14185788. [Google Scholar] [CrossRef]

16. Haddadi MM, Hosseini SH, Rashtchian D, Olazar M. Comparative analysis of different static mixers performance by CFD technique: an innovative mixer. Chin J Chem Eng. 2020;28(3):672–84. doi:10.1016/j.cjche.2019.09.0043. [Google Scholar] [CrossRef]

17. Xiao YH, Zhao H, Tian XN, Sun T. Design and evaluation of novel static mixers for SCR application. J Mar Eng Technol. 2023;23(1):55–66. doi:10.1080/20464177.2023.2275352. [Google Scholar] [CrossRef]

18. Medina H, Thomas M, Eldredge T, Adebanjo A. The M number: a novel parameter to evaluate the performance of static mixers. J Fluids Eng. 2019;141(12):1–10. doi:10.1115/1.4044070. [Google Scholar] [CrossRef]

19. Apostolos S, Theophanes G. A modern introduction to fuzzy mathematics. New York: Wiley; 2020. [Google Scholar]

20. Tian XN, Xiao YH, Zhou PL, Zhang WP, Chu ZH, Zheng W. Study on the mixing performance of static mixers in selective catalytic reduction (SCR) systems. J Mar Eng Technol. 2015;14(2):57–60. doi:10.1080/20464177.2015.1096615. [Google Scholar] [CrossRef]